Displacement Error Propagation From Embedded Markers to Brain Strain

Abstract

Head injury model validation has evolved from against pressure to relative brain–skull displacement, and more recently, against marker-based strain. However, there are concerns on strain data quality. In this study, we parametrically investigate how displacement random errors and synchronization errors propagate into strain. Embedded markers from four representative configurations are used to form unique and nonoverlapping tetrahedrons, triangles, and linear elements. Marker displacements are then separately subjected to up to ±10% random displacement errors and up to ±2 ms synchronization errors. Based on 100 random trials in each perturbation test, we find that smaller strain errors relative to the baseline peak strains are significantly associated with larger element sizes (volume, area, or length; p < 0.05). When displacement errors are capped at the two extreme levels, the earlier “column” and “cluster” configurations provide few usable elements with relative strain error under an empirical threshold of 20%, while about 30–80% of elements in recent “repeatable” and “uniform” configurations are considered otherwise usable. Overall, denser markers are desired to provide exhaustive pairwise linear elements with a range of sizes to balance the need for larger elements to minimize strain error but smaller elements to increase the spatial resolution in strain sampling. Their signed strains also provide unique and unambiguous information on tissue tension and compression. This study may provide useful insights into the scrutinization of existing experimental data for head injury model strain validation and to inform how best to design new experiments in the future.

Introduction

Traumatic brain injury (TBI) remains a major public health problem in the world [1,2]. It is both an acute disorder and, for some patients, a chronic neurological disease as well with long-term consequences affecting their quality of life [3]. The etiology of TBI can be broadly classified into either blast or blunt impact [4]. Blast-induced TBI is initiated by an explosive blast wave traveling through the brain, which often occurs in the military population [5]. In comparison, blunt impact-induced TBI is the result of sudden acceleration and/or deceleration event, where the head strikes another object or is subject to whiplash without a direct contact. It can happen in both the military and the civilian populations due to falls and automotive crashes [4]. For the civilian population, contact sports and recreational activities are also significant contributors, especially for incidents of mild severities [6].

Regardless of the TBI etiology, energy external to the head is transmitted into the brain through the organ-to-cell length scales [7], which leads to stresses and strains in specific regions of the brain to cause tissue damage and subsequent neurological consequences. Therefore, it is important to understand how injury occurs from the biomechanical perspective in order to design effective countermeasures to reduce the incidence and/or severity of TBI. Given that measurable impact accelerations inform the severity of blunt impact, there have been numerous efforts using impact kinematics to assess the risk of TBI, including various forms based on linear acceleration [8,9], rotational acceleration [10,11], and their combination [12–14]. Nevertheless, there is general consensus that brain deformation in terms of strain/strain rate, rather than impact kinematics, is the primary mechanism of blunt-induced TBI, including mild traumatic brain injury [4,15,16].

Due to ethical reasons, the only feasible approach to estimating high-rate brain strain and strain rate in a live human is through impact simulation. Although it remains a significant challenge to develop a detailed and sufficiently biofidelic head injury model, once developed and validated, a head injury model would offer a cost-effective and most ethical approach to studying TBI based on the validated response variable. Therefore, efforts to develop sophisticated head injury models have been ongoing for almost half a century now [16–18]. However, a fundamental question about how to validate a head injury model to ensure its sufficient biofidelity remains unresolved. Multiple studies have reported that different “validated” head injury models based on relative brain–skull displacements could produce different brain strains even under identical impact loading conditions [19,20]. This suggests that displacement-based model validations are, in fact, ineffective in discriminating head injury models and are unable to assess their biofidelity performances when studying strain-induced injury. Without a proper validation, the use of a head injury model would be severely compromised.

The primary challenge of validating a human head injury model is the lack of appropriate “ground-truth” experimental data about the biomechanical responses of a living brain thought responsible for the injury. Extensive experimental work exists across physical [21] and animal [22,23] injury models, human surrogates [24,25], and human volunteers [26]. These studies provide a wealth of biomechanical data relevant to TBI or at subconcussive levels. However, nonhuman data are not appropriate for validating a human head injury model due to substantial differences in brain morphology and anatomy. in vivo data from human volunteers are capable of providing detailed brain strain for model validation at impact levels far below injury. Nevertheless, on their own are insufficient to inform the model biofidelity at much higher, potentially injury-causing, impact levels, in part due to the nonlinear and rate-dependent material properties of the brain [16,27,28].

In order to assess model biofidelity to study TBI, the validation of human head injury models has so far largely relied on high-rate experimental data from cadaveric human heads [16]. Although they are subject to postmortem tissue deterioration, cadaveric heads are the best candidate to approximate high-rate biomechanical responses of a living brain. Early work has used cadaveric brain pressure [29,30] for validation. However, brain pressure is now recognized as of little value in validating brain shear deformation or strain responses because of brain's near incompressibility [4]. In fact, brain pressure can be analytically determined by the magnitude and direction of linear acceleration, and brain mass and shape [31,32].

To inform brain shear deformation, relative brain–skull displacements were tracked using embedded neutral density targets (NDTs) with high-speed biplanar X-ray by striking or stopping a cadaveric head [33,34]. These datasets have been extensively used for the validation of human head injury models in the last two decades [16,17], even though they were not “specifically designed” for model validation [16,35]. More recently, the technique has been further improved with a new marker placement configuration [35,36]. In addition, a new tracking technique called sonomicrometry has also been adopted to measure relative brain–skull displacements, where crystal receivers are embedded more or less uniformly throughout a large part of the brain [37]. Over the years, the time between cadaveric head donor death and testing has reduced from 5–10 days [33,34], 7 days [35,36], to 56 h [37], which reduces deterioration and improves biofidelity.

Nevertheless, displacement-based model validation, alone, does not indicate the biofidelity of model strain responses [38,39]. This should not be surprising given that strain is the spatial gradient of displacement field, and the difference between displacement and strain is analogous to displacement versus velocity in the temporal domain. Recognizing this disconnect, attention has shifted toward model validation against marker-based strain derived from relative brain–skull displacement trajectories, using either a “triad” [40] or a “tetra” [38] approach. However, these two methods do not compare the same strain between model and experiment (e.g., model-estimated volumetric versus experimentally derived surface strain, and averaged strain across selected elements versus that from a sparse set of markers, respectively). Therefore, they may not be effective in model validation, as recognized [39,41]. To rectify, a generalized marker-based strain validation framework has also been proposed, which compares strains from the same set of markers but using either model-estimated or experimentally measured displacement trajectory data [39]. This ensures the same strain to be compared between model and experiment.

Still, concerns remain on the “quality” in marker-based strain [42], as the experimental environment is typically “noisy” [40] and measurement errors seem inevitable. Although error sources have been exhaustively discussed for the NDT technique [43], a quantitative error estimate in strain, nevertheless, does not exist. A recent study examines the influence of data filtering algorithms on the localization accuracy of embedded sonomicrometry crystals during head impact [44]. Similarly, nonetheless, it does not inform how errors in the measured displacements propagate into brain strain.

Therefore, the objective of this study is to evaluate how errors in measured relative brain–skull displacements propagate into marker-based strain. This is important to assess the confidence in any subsequent strain-based model validation, which has not been investigated before. By definition, strain is a measure of change in geometrical shape, which requires first forming markers into geometrical elements for strain quantification. Thus, we suspect that the error propagation depends on element geometry or how the markers are placed and grouped into elements for strain calculation. As a result, we select four representative marker placement configurations for scrutiny, including the column [33], cluster [34], “prescribed, scalable, and repeatable” [35], and the more or less uniform [37] configuration. The three element construction strategies from the generalized marker-based strain validation framework [39] are also evaluated. The three strategies are to form unique and nonoverlapping three-dimensional (3D) tetrahedrons, two-dimensional (2D) triangles, and one-dimensional (1D) linear elements, respectively (albeit all elements remain in a 3D space). They provide different components of the complex 3D strain tensor for comparison.

Given that an exact marker displacement error model does not exist, we resort to two simplest error models to randomly and separately perturb displacement data misalignment in magnitude and in time to understand how marker displacement errors propagate into strain. Regardless of this limitation, this study may be important for providing critical insight into how best to utilize existing cadaveric experimental data [33–37], or how best to design new experiments [45], for improved head injury model strain validation in the future.

Materials and Methods

Experimental Datasets.

From a wide range of cadaveric head impact experiments now available, we selected four cases of representative marker placement configurations with a similar peak rotational velocity ($v_{\mathrm{rot}}$) of ∼20 rad/s and an impulse duration ($\Delta t$) of ∼60 ms for the major $v_{\mathrm{rot}}$ peak in the resultant rotational velocity profile. This choice minimized potential confounding factors related to different impact severities in our findings. The selected cases were C755-T2 [33], C393-T3 [34,46], NDTB-T2 [36], and Vrot20dt60 [37,39]. The first three cases used NDTs as embedded markers, while the remaining one employed sonomicrometry crystals for displacement measurement.

Case C755-T2 employed a column configuration for NDTs. Two vertical columns of NDTs were implanted in the temporoparietal and occipitoparietal regions of the right hemisphere, respectively. Each column contained six NDTs with an average spacing of 10–11 mm. For C393-T3 that used a cluster configuration, two clusters of seven NDTs each were implanted into both brain hemispheres in a “1–5–1” scheme, with the marker in the center of ∼10 mm from the other six. The enclosing volume of the cluster encompassed ∼4 ml of brain tissue. For NDTB-T2, NDTs were implanted following a prescribed, scalable, and repeatable way (abbreviated as a repeatable configuration): markers were prescribed to be radially distributed in one hemisphere while along three vertical columns in the other in a scalable manner. Essentially, this method used a consistent and repeatable approach to determining marker locations while accounting for different head sizes. It was intended to reduce experimental variation and to aid model validation [35].

Finally, case Vrot20dt60 employed a sonomicrometry technique to track the motion of embedded crystals (receivers) relative to those embedded in the skull (transmitters). A total of 24 receiver crystals were implanted more or less uniformly throughout a large part of the brain (hence, referred to as a uniform configuration). However, data only from 19 receivers were usable [37], which were employed in this study for analysis. The detailed comparisons of the four selected cases are in Table 1.

Table 1.

Summary of kinematics characteristics for the four selected impacts, including the plane of head rotation, peak rotational velocity magnitude ($v_{\mathrm{rot}}^p$) and duration ($\Delta t$), and peak rotational acceleration magnitude ($a_{\mathrm{rot}}^p$) and its corresponding duration

	C755-T2	C393-T3	NDTB-T2	Vrot20dt60
Plane of rotation	Sagittal	Coronal	Sagittal	Coronal
$v_{\mathrm{rot}}^p$ (rad/s)	19.2	26.6	22.0	22.3
$\Delta t$ for $v_{\mathrm{rot}}^p$ (ms)	60	65	62	63
$a_{\mathrm{rot}}^p$ (krad/s2)	1.9	11.8	1.3	1.4
$\Delta t$ for $a_{\mathrm{rot}}^p$ (ms)	21.0	3.9	30.9	34.4

Marker Displacement and Marker-Based Strain.

For all cases, the published relative brain–skull displacement time history curves were manually digitized. The digitized data were resampled at a temporal resolution of 1 ms and further smoothed with a five-point moving average approach (smooth.m in matlab) to minimize digitization errors.

We followed the earlier “generalized marker-based strain validation” strategy [39] to form elements for strain sampling. For each case, the markers' undeformed locations were used to create unique and nonoverlapping tetrahedrons via Delaunay triangulation (delaunay.m in matlab). Their unique 2D triangular surface boundary elements were also obtained. In addition, pairwise 1D linear elements ($N=\left(1/2\right)n\left(n-1\right)$, where $n$ is the number of markers) were also created between two arbitrary markers to sample brain strain.

Table 2 compares the number and geometrical characteristics of marker-based elements in terms of size (volume, area, and length, respectively) and shape. The shape was measured in terms of element aspect ratio (i.e., the ratio between the largest and smallest element edge, applicable only to tetrahedrons and triangles), which is also a typical measure of element quality. Figure 1 shows 3D tetrahedral elements for the selected cases after transforming them into the whim V2.0 model space [47], which provides perspectives for visualization.

Table 2.

Summary of the number and geometrical characteristics of the marker-based elements in terms of size (volume, area, and length for tetrahedrons, triangles, and linear elements, respectively) and aspect ratio for the four selected cases and marker configurations

Impact case	C755-T2	C393-T3	NDTB-T2	Vrot20dt60
Marker configuration	Column	Cluster	Repeatable	Uniform
Number of markers	10	13	11	19
Number of tetrahedrons (volume, mm3)	18 (84.8 ± 77.3)	29 (211.4 ± 230.9)	18 (8235.2 ± 6386.5)	53 (5005.7 ± 5125.6)
Aspect ratio (tetrahedrons)	5.7 ± 2.0	2.5 ± 0.7	4.1 ± 0.6	4.2 ± 2.9
Number of triangles (area, mm2)	12 (164.9 ± 125.2)	66 (112.8 ± 71.5)	42 (1239.1 ± 925.9)	122 (813.7 ± 518.5)
Aspect ratio (triangles)	4.0 ± 1.7	2.1 ± 0.7	3.0 ± 1.3	2.7 ± 2.2
Number of linear elements (length, mm)	45 (28.9 ± 17.0)	78 (26.4 ± 13.4)	55 (64.5 ± 27.6)	171 (51.9 ± 20.7)

Fig. 1.

Brain marker configurations and their 3D tetrahedral elements in the whim V2.0 space [47] for the four selected cases. The dimensions of the whim were scaled according to the corresponding cadaveric head size [39]. See Fig. S1, available in the Supplemental Materials on the ASME Digital Collection, for additional isoviews.

Error Models

Error sources for marker displacement measurements have been extensively discussed. For NDT datasets [43], in addition to brain–skull coupling limitation due to gas evacuation inherent to cadaveric experiments, the greatest data processing concerns were about the measurement of skull target locations in the anatomical coordinates. This would introduce absolute errors in their initial positions and path directions, but not relative errors between sequential points in the displacement trajectory. Another potential source of error is the manual tracking and image enhancement of individual NDTs, which was estimated to range 0.19–2.14%. Digital signal filtering effects could also introduce error in the displacement measurement as well as head kinematics measurement, which were subjectively evaluated to provide “reasonable” data trends. The earlier tests also suffered from a relatively low camera pixel resolution (384 × 240) and frame rate (250 fps) [33], which were subsequently improved with upgraded imaging systems (e.g., 512 × 512 or 1024 × 1024 and 1000 fps [33,34], and recently 1200 × 1200 and 1250 fps [36]). NDT density effects could also introduce error but was estimated to be less than 1.5% of the maximum excursion via a computational simulation. Finally, there are errors in signal synchronization or phase shift that could cause measured displacement to delay up to 4 ms relative to the measured skull kinematics [43].

For the sonomicrometry data [37,44], while the technique does not suffer from limitations with camera resolution, image distortion, parallax, and errors encountered in coordinate system transformation, according to the authors, it is susceptible to trilateration error in determining crystal receiver displacements. The absolute distance errors were estimated to typically range 2–6% of the measured distance [44]. Other error sources include: (1) systematic noises from electrical signal, acoustic reflection, and delayed wavefront triggering; and (2) signal bias/magnitude shift errors due to uncertainty of the brain's speed of sound, CT measurement of the crystal initial positions, and sonomicrometry system, itself, such as cable tethering.

Nevertheless, these discussions do not provide sufficient information to establish an exact error model or magnitude. Therefore, we assumed two simplest error models for parametric analysis: random magnitude errors and synchronization errors. The former considered signal misalignment in magnitude, while the latter accounted for signal misalignment in the temporal domain. They were further assumed to be uncorrelated and independent among markers. These simplest error models could serve as a starting point for considering a more sophisticated error model in the future when relevant information becomes available.

To introduce random magnitude errors, an origin-centered sphere with a radius of x% (with x ranging from 1 to an empirical value of 10 at a step size of 1) was created for each marker and at every time-step (at a resolution of 1 ms). It represented the maximum percentage of displacement error magnitude for perturbation. The maximum error of 10% was chosen out of convenience to allow easy scaling to any other error magnitude. Then, a point within the sphere was randomly generated following a uniform distribution, whose coordinates were projected onto the x, y, and z axes to determine the corresponding scaling factors (sx, sy, and sz). The displacement percentage error component relative to the corresponding baseline displacement (dx, dy, and dz) was then determined (dis_err) and added to the baseline displacement. This process is illustrated in Fig. 2.

Fig. 2.

Illustration of how displacement random magnitude errors are generated. The spherical radius in (a) represents the maximum error magnitude ratio relative to the baseline measurement, which is capped at x%, with x ranging from 1 to 10 at a step size of 1. For illustration, the range of displacements from 100 random trials for the x-component time-history is shown for a selected case (b), where the maximum displacement random error is capped at 50% to improve visualization (note, a maximum value of 10% was used in analysis). The displacement time history curve for a typical trial is also presented.

To introduce synchronization errors, displacement time history curves for each marker along the three anatomical directions were randomly but synchronously shifted by up to ±2 ms (at a temporal resolution of 1 ms) relative to the baseline following a uniform distribution. This would lead to a maximum of 4 ms error between two displacement time history curves as suggested from experiment.

Data Analysis

For each error perturbation condition, 100 random trials were conducted for each selected impact case to evaluate maximum principal Green strain for each element at each time-step. Strain calculation was performed using an inhouse matlab (version 2020a) routine, which was verified for correctness against abaqus (version 2018; Dassault Systèmes, Johnston, RI) to produce identical results. The resulting time-varying strain curves would allow comparing against the baseline using the commonly adopted correlation and analysis (cora) score [48], which assesses an aggregated similarity score based on weighted values in curve shape, phase shift, and magnitude. However, this measure was shown to be ineffective in discriminating head injury models, as models with similar cora scores (using either the default or “recommended” settings [46]) can lead to differences in whole-brain strain magnitude by 2–3 times [39]. Therefore, here we chose to compare peak strain magnitudes between the perturbed strains and the baseline. This was justified, given that only strain peak magnitude from model simulation is used at present for injury prediction that does not consider temporal shape or phase of strain time history data.

Specifically, the fifth and 95th percentile strain magnitudes for each element among the 100 random trials were obtained at every time point. Their difference at the time when the baseline strain value reached the peak (regardless of the negative or positive peak for 1D linear elements) was used to quantify strain uncertainty. The resulting ratio relative to the baseline strain peak magnitude was finally used to assess relative strain error, ${\epsilon }_{\mathrm{err}}$.

Element size in terms of volume, area, and length was calculated for 3D tetrahedral, 2D triangular, and 1D line elements, respectively. Pearson correlation was conducted between ${\epsilon }_{\mathrm{err}}$ and element size/quality to report their respective main statistical effects. Statistical significance was reached when the $p$ value was less than 0.05. For each marker configuration, the number and percentage of “usable” elements are also reported when the displacement errors were at the extreme magnitudes. Usable elements were empirically defined as those with relative ${\epsilon }_{\mathrm{err}}$ less than 20% of the baseline peak strain magnitude. They were meant to quantify the relative performance of marker placement configurations for strain validation in the future (all elements remained in the analysis). Finally, for the synchronization error characterizing signal temporal misalignment, we also performed the correlation between average ${\epsilon }_{\mathrm{err}}$ and impact kinematics variables, $\Delta t$ and $a_{\mathrm{rot}}^p$.

Results

Displacement Random Error.

For this error model concerning displacement magnitude errors, average ${\epsilon }_{\mathrm{err}}$ across each element type increased linearly with the capped displacement percentage error magnitude, for all marker configurations (Fig. 3). Nevertheless, the ${\epsilon }_{\mathrm{err}}$ versus displacement error ratios (i.e., line slopes) depended on the marker configuration, where the largest ratio occurred in the cluster configuration for triangular elements (7.8; Fig. 3(b)). Incidentally, marker configurations in the recent NDT and sonomicrometry experiments had the smallest ratios overall (1.9–2.4 and 2.5–3.0, respectively).

Fig. 3.

Average relative strain error, ${\epsilon }_{\mathrm{err}}$, increases linearly with respect to the capped maximum marker displacement error magnitude. The error ratios, as shown in each subfigure, depend on the marker configuration. Inset shows the standard deviations when displacement random errors are capped at the ±10% level. Numbers in subfigures indicate the fitted line slope for the corresponding element type.

As an illustration, time-varying marker-based strains using the cluster and uniform configurations are shown for each element type using their respective smallest ${\epsilon }_{\mathrm{err}}$ among peers when the maximum allowable displacement percentage error was capped at ±10% (Fig. 4). Illustrations for their largest ${\epsilon }_{\mathrm{err}}$ among peers are reported in Fig. S2, available in the Supplemental Materials on the ASME Digital Collection.

Fig. 4.

Time-varying baseline strains and the strain uncertainty ranges (fifth to 95th percentiles) due to displacement random errors (magnitude capped at ±10% level) from 100 random trials for the cluster (top; case C393-T3) and uniform (bottom; case Vrot20dt60) configurations for the three element types. The elements were selected to represent the smallest relative strain errors with respect to the baseline at the time when the latter reached its peak value (dashed vertical lines; either negative or positive for linear elements).

Correlations between ${\epsilon }_{\mathrm{err}}$ and element size and quality were conducted separately at the ±10% level of displacement magnitude error using independent data combined from all marker configurations. Significant and negative correlations were found between ${\epsilon }_{\mathrm{err}}$ and element size (Pearson correlation coefficients ranged from −0.47 to −0.41; $p$ < 0.001; Fig. 5). However, no significant correlation was found between ${\epsilon }_{\mathrm{err}}$ and aspect ratios regardless of the element type. With the displacement errors capped at the ±10% level, the number and percentage of usable elements suitable for strain validation are reported in Table 3.

Fig. 5.

Significant and negative correlations between ${\epsilon }_{\mathrm{err}}$ and element size (left: tetrahedrons; middle: triangles; and right: linear elements) due to displacement random errors when the magnitude was capped at the ±10% level. Values of ${\epsilon }_{\mathrm{err}}$ are capped at 100% to improve visualization.

Table 3.

Summary of the number and percentage (in parenthesis) of elements that had an ${\epsilon }_{\mathrm{err}}$ below an empirical 20% threshold relative to the baseline strain peak magnitude when the displacement random error magnitude was capped at the ±10% level

	C755-T2	C393-T3	NDTB-T2	Vrot20dt60
Tetrahedrons	1 (5.6)	0 (0)	12 (66.7)	23 (43.4)
Triangles	1 (5.6)	0 (0)	30 (66.7)	60 (49.2)
Linear elements	12 (26.7)	0 (0)	44 (80.0)	104 (60.8)

Displacement Synchronization Error.

This error model was related to signal phase shift. Similarly, average ${\epsilon }_{\mathrm{err}}$ across each element type also increased linearly with the synchronization error for all marker configurations (albeit, limited to two time points and the error-free baseline origin; Fig. 6). The zero-crossing line slopes depended on the marker configuration. The largest ratios occurred in the column and cluster configurations, while the smallest ratios occurred in the more recent repeatable and uniform configurations.

Fig. 6.

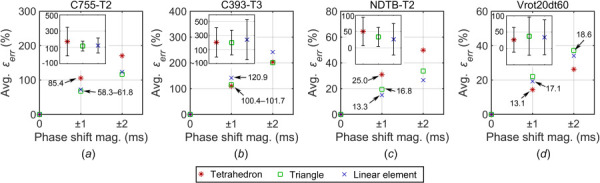
Average relative strain error, ${\epsilon }_{\mathrm{err}}$, increases linearly with respect to the synchronization error or phase shift magnitude, which depend on the marker configuration. Inset shows the standard deviations when the synchronization error was at ±2 ms level. Numbers in subfigures indicate the fitted line slopes for the corresponding element type.

Figure 7 illustrates strain uncertainty due to displacement synchronization errors for the same two selected marker configurations for each element type (with their respective smallest ${\epsilon }_{\mathrm{err}}$; illustrations for their largest ${\epsilon }_{\mathrm{err}}$ among peers are reported in Fig. S3, available in the Supplemental Materials on the ASME Digital Collection). Although the uncertain ranges could be large at some time points especially for the cluster configuration (top row), only values at the time when the baseline strain reached the peak were used for analysis.

Fig. 7.

Time-varying baseline strains and the strain uncertainty ranges from 100 random trials due to displacement synchronization errors (at ±2 ms level) for the cluster (top; case C393-T3) and uniform (bottom; case Vrot20dt60) configurations for the three element types. The elements were selected to represent the smallest relative strain errors with respect to the baseline at the time when the latter reached the peak (dashed vertical lines; either negative or positive for linear elements).

Similar to the displacement random errors, ${\epsilon }_{\mathrm{err}}$ was negatively correlated with element size (range from −0.42 to −0.30; $p$ < 0.05; Fig. 8), while correlation between ${\epsilon }_{\mathrm{err}}$ and aspect ratio did not reach significance. The number and percentage of usable elements are reported in Table 4.

Fig. 8.

Significant and negative correlations between ${\epsilon }_{\mathrm{err}}$ and element size (left: tetrahedrons; middle: triangles; and right: linear elements) due to displacement synchronization errors when the magnitude was capped at the ±2 ms level. Values of ${\epsilon }_{\mathrm{err}}$ are capped at 100% to improve visualization.

Table 4.

Summary of the number and percentage (in parenthesis) of elements that had an ${\epsilon }_{\mathrm{err}}$ below an empirical 20% threshold relative to the baseline strain magnitude when the displacement synchronization error magnitude was capped at the ±2 ms level

	C755-T2	C393-T3	NDTB-T2	Vrot20dt60
Tetrahedrons	0 (0)	0 (0)	5 (27.8)	34 (64.2)
Triangles	0 (0)	0 (0)	16 (35.6)	66 (54.1)
Linear elements	2 (4.4)	0 (0)	38 (69.1)	103 (60.2)

Finally, average ${\epsilon }_{\mathrm{err}}$ was obtained for each element type. It was found to have a significant and negative correlation with the duration of the major rotational acceleration peak, and a significant and positive correlation with the peak magnitude of rotational acceleration for the impact cases (Fig. 9; $p$ < 0.05).

Fig. 9.

With displacement synchronization errors, average ${\epsilon }_{\mathrm{err}}$ across each element type and all marker configurations is significantly and negatively correlated with the impact duration ($\Delta t$) of the major rotational acceleration peak (a), while positively correlated with the peak magnitude of rotational acceleration, $a_{\mathrm{rot}}^p$ (b)

Discussion

Validation of a head injury model is critical and fundamental to ensure sufficient biofidelity before any real-world application. Yet, this remains a significant challenge due to the lack of appropriate high-rate experimental data that are unavailable from live humans due to ethical reasons. The majority of head injury models have been validated against relative brain–skull displacement trajectories from cadaveric experiments [16,17]. However, this strategy is ineffective in discriminating head injury models for their strain responses [19,20]. This suggests the need to validate models against measured strains in order to study strain-induced brain injury, as performed in an animal injury model [23]. However, utilizing marker-based strain from measured displacements for validation of a human head injury model at high rate only emerged relatively recently [38–40]. Given that displacement measurement errors are inevitable [43,44], a study on how marker displacement errors propagate into strain seems important to assess the effectiveness of the marker-based strain validation, which appears not to have been recognized before.

By parametrically perturbing marker displacements following two simplest error models, we found that relative strain error (${\epsilon }_{\mathrm{err}}$) at the time of peak baseline strain strongly depended on how the markers were placed to form elements for strain calculation. For both displacement random error and synchronization error models and all element types (tetrahedral, triangular, and linear elements), ${\epsilon }_{\mathrm{err}}$ linearly increased with the increase of the error magnitude (Figs. 3 and 6). The error also significantly and negatively correlated with element size, with a correlation coefficient ranging from −0.5 to −0.3 (Figs. 5 and 8). This suggests that larger elements are more tolerant of displacement errors, while smaller elements are more susceptible to displacement errors when evaluating strain. Practically, markers cannot be too close to each other either, as that would affect motion of the brain. This is in contrast to conventional finite element simulations where smaller elements are often desired to improve accuracy. However, such an observation is not surprising, considering that when element size is too small or at least two markers are too close to each other, displacement errors may approach to element size in magnitude, which would induce dramatic change in element shape or large strains and even could destroy the element leading to a negative volume/area, or reversing the sign of the linear strain. This is evident in Figs. 5 and 8, where largest ${\epsilon }_{\mathrm{err}}$ mostly occurred when element size approached to zero, especially for tetrahedral and triangle elements.

Nevertheless, no significant correlation existed between ${\epsilon }_{\mathrm{err}}$ and aspect ratios for the aggregated data, regardless of the error model. This suggests that element shape may not be important for displacement error propagation into brain strain. In contrast, we found a significant and positive correlation between the baseline peak strain magnitudes and the aspect ratios, for both tetrahedral and triangle elements (Fig. S4, available in the Supplemental Materials on the ASME Digital Collection). Therefore, elements with larger aspect ratios (poorer quality) tend to induce larger strains. This may have implications when averaging strains [38–40] from elements with significantly different shapes, as values from elements of poor qualities would dominate.

Error Model

The time-varying strain uncertainty range generally correlated well with the baseline strain, itself, for the random error model (Fig. 4). This was expected because the applied error magnitude was proportional to that of displacement. Therefore, the perturbed strain curves followed the same shape and phase of the baseline strain. This contrasted with the synchronization error, however, where smaller strain uncertainty ranges were often observed when the baseline strain reached its peak (Fig. 7). This was also expected, as this type of error perturbed the relative phase of displacement curves between markers. When relative brain–skull displacement reached the peak, the change in displacement magnitude due to time shift, or the displacement curve slope at this time point, would be small. This would lead to a small error in strain.

However, the strain uncertainty was much more pronounced at other time points when displacement temporal gradient was high, or, when the marker was “moving” fast relative to skull. This observation explains the striking differences between the two selected impacts (Fig. 7). Case C393-T3 had a much shorter peak strain duration than Vrot20dt60 (∼20 ms versus ∼50 ms). We suspected that this was because C393-T3 had a much higher peak rotational acceleration and shorter acceleration impulse (11.8 krad/s² and 3.9 ms, respectively) compared to others (1–2 krad/s² and ∼20–35 ms, respectively; Table 1). This was confirmed by the significant correlation between the average strain errors aggregated from all element types and the acceleration impulse duration (Fig. 9). With such a large uncertainty in strain over time, it would be questionable whether cora is applicable for assessment due to the high weighting factors on curve shape and phase shift [38,40].

Marker Configuration

Marker configuration played a significant role in displacement error propagation because it dictated how markers formed geometrical elements. At the same displacement error level regardless of the error model, relative strain errors were more sensitive for the earlier column and cluster configurations because their marker-based elements were much smaller in size than those in the more recent repeatable and uniform configurations. For example, the average tetrahedron volume for the column configuration was only ∼1% of the repeatable configuration (Table 2).

At the random error magnitude of ±10% and synchronization error of ±2 ms, the two earlier marker configurations led to few or no usable elements for potential model validation with ${\epsilon }_{\mathrm{err}}$ less than an empirical threshold of 20% of the baseline strain magnitude (Tables 3 and 4). In contrast, both the recent repeatable and uniform configurations were more tolerant of displacement errors regardless of the error model. At the same error levels, they offered approximately 40–80% and 30–70% of the elements that could be considered usable for potential model validation, for the two error models, respectively.

Element Type

We used the well-established Delaunay approach to create volumetric and surface elements from the group of markers for brain strain sampling. This strategy ensured that the brain region was sampled deterministically without ambiguity or overlapping, as there could be multiple possible ways to create tetrahedrons and triangles (e.g., when the number of noncoplanar or noncolinear markers are more than 4 and 3, respectively). The additional pairwise linear elements between two arbitrary markers would also ensure a complete sampling, which, unlike tetrahedrons and triangles, do not suffer from poor element quality. Linear elements also uniquely offer signed strains—positive for tension and negative for compression [39]. To simplify data analysis in our current study, we did not differentiate tension versus compression. Nevertheless, signed strains from linear elements provide unique information on tissue tension and compression not available in maximum principal or shear strain exported from tetrahedrons or triangles [38,40].

Identifying specific threshold values for element sizes in order to ensure robust strain-based model validation is beyond the scope of our study, because the necessary quantitative information on displacement error is currently unavailable. Nevertheless, our parametric study does suggest employing larger elements to minimize marker displacement error propagation into strain. This is somewhat in competition with the desire for denser markers or smaller elements to increase the spatial resolution of brain strain for validation [39]. Therefore, a tradeoff seems necessary in practice. One possible compromise is to use dense markers to generate pairwise 1D linear elements, which allows limiting to a subset of them with sufficient lengths for strain validation. This may be another advantage over tetrahedrons or triangles from the Delaunay method, as the latter elements are formed in local regions which may not guarantee to have sufficient sizes.

One may wonder if results from 1D linear elements can still be referred to as “strain,” given that tissue strain is inherently 3D for a realistic head injury model. However, it is understood that simple linear strains as well as principal and shear strains from tetrahedrons and/or triangles can all be considered as different projections or components of the complete 3D strain tensor. Using exhaustive pairwise 1D linear elements could ensure unambiguous validation not attainable from directionally insensitive maximum principal or shear strains [39], as illustrated in Fig. S5, available in the Supplemental Materials on the ASME Digital Collection.

Implications

It is important to recognize that strains from sparse markers, regardless of the sampling strategy, are spatially averaged that do not have the necessary spatial resolution to inform the accuracy of localized tissue strain. For example, pairwise linear elements from the four configurations were on the order of several centimeters (Table 2), 10–20 times larger than typical FE elements for the majority of brain models (∼1–5 mm). The substantial difference in spatial scale indicates that a successful marker-based strain validation of a head injury model does not necessarily ensure its accuracy in estimating elementwise strain. Nevertheless, this coarse-grained strain validation may still be important to gain the necessary confidence in local tissue strain estimated from model simulation that is often used for injury prediction and correlation.

In addition, a strain-based model validation rating method is yet to be developed. With pairwise 1D linear strains, it is possible to construct a symmetric adjacency matrix to encode signed strains from either experiment or impact simulation, and at every time point. This is illustrated using the uniform marker configuration at one time point (Fig. 10). The difference between model-simulated, strain-encoded matrix and that from measured displacements would reveal the degree of model–experiment agreement. The compact matrix-form may facilitate the development of a quantitative validation quality measure in the future, for example, by simple summation of absolute strain peak magnitude differences, or adopting a cora-like method to rate the quality of each individual strain time history curve. The strain error magnitudes could serve as appropriate weighting factors when aggregating from all individual ratings. A marker-specific rating may also be possible, which would effectively indicate the spatiotemporal coherence of the corresponding local tissue relative to other parts of the brain (e.g., marker #11 in Fig. 10). These ideas will be explored in the future.

Fig. 10.

Illustration using a 19 × 19 adjacency matrix (171 unique nonzero elements) to encode pairwise 1D linear strains at one instance in time. Pairwise linear strains for a given marker (#11 as shown) relative to the remaining 18 markers are represented by the corresponding row (or column, due to symmetry), excluding itself in the matrix diagonal. The example corresponds to impact case, Vrot20dt30, at 24 ms when the simulated strains reached the first major peak using the anisotropic whim V1.0 [39]. Color (or grayscale) bar on the right indicates signed 1D Green–Lagrangian strain.

Limitations

A limitation of this study is the lack of a precise, quantitative error model to characterize marker displacement errors. The assumed displacement random error and synchronization error were also blindly applied to all marker configurations and impact experiments without considering whether they were equally applicable. Therefore, even though the column and cluster configuration performed poorly in comparison to other configurations in this study (Tables 3 and 4), the results reported here do not necessarily invalidate previous efforts using the associated impact experiments for validation [39,40], as they were not designed for this type of strain-based validation [16,35]. For example, the two clusters in C393-T3 were meant to be used separately for strain sampling [38], but the markers were combined for element formulation in this study (Fig. 1(b)).

In addition, the usable elements identified in this study were based on fixed error levels (either at ±10% level of displacement magnitude error, Table 3; or at ±2 ms level of synchronization error, Table 4). The strain error threshold for usable elements of 20% was also chosen somewhat arbitrarily but based on our best intuition and experience. Importantly, these parametric investigations were intended to probe and quantify how assumed displacement errors propagate into marker-based strain using the four representative marker configurations from their respective impact cases. Note, these results could change when analyzing different impact cases, with a different threshold for usable elements (e.g., a more stringent 10% relative to baseline strain magnitude), or at a more specific error level (e.g., 5%). Although results in this study are not to be generalized, the approach established herein would remain applicable for future studies when displacement errors can be better approximated and quantified.

Further, the two error models were applied separately, and the displacement errors were also assumed uncorrelated among markers and between time points. Nevertheless, our study would be an important first step toward a more definitive understanding of how marker displacement errors propagate in practice. Additionally, we only tested at the maximum error level of ±2 ms for displacement synchronization error with a temporal resolution of 1 ms, even though the measured signals were sampled at much higher rates (e.g., 10 kHz [37] to 20 kHz [34,35]). This choice was made because the displacement curves had to be manually digitized at a relatively coarse temporal resolution, which could suffer from digitization errors not accounted for in this study.

Despite these limitations, it is important to quantify how marker placement configurations and element size and shape influence displacement error propagation into strain. This would allow informing how best to utilize existing experimental data [33–37] (e.g., to select a subset of appropriate marker-based elements, preferably pairwise 1D linear elements). In addition, it may be possible to use model-simulated displacement to parametrically probe how displacement errors are to propagate into brain strain prior to designing new experiments [45] for an initial insight, even though the model may not have been fully validated (e.g., as illustrated in Fig. 10). Earlier experiments did not seem to have considered displacement error propagation into strain at the time of design. Regardless, once a more refined and quantitative marker displacement error model becomes available, it is straightforward to reanalyze displacement error propagation using the framework established herein. Finally, the same analysis may potentially be extended to strain rate, which was not considered in this study.

Conclusion and Recommendations

In this study, we parametrically studied how marker displacement errors propagate into brain strain under two assumed error models, displacement magnitude error and synchronization error. We identified that strains in larger elements are more tolerant of displacement errors for all element types, including 3D tetrahedrons, 2D triangles, and 1D linear elements. Pairwise 1D linear elements may offer an effective compromise between the need for larger (less susceptible to errors) and smaller (for increased spatial resolution) elements in validation. Their signed strains also provide unique and unambiguous information on local tissue tension and compression not available from directionally insensitive maximum principal or shear strains used for tetrahedrons and triangles. Based on these findings, a few actionable recommendations may be proposed below to facilitate the use of existing data and to aid future experimental designs. They may contribute toward a standardized approach to head injury model strain-based validation, which would promote harmonization of diverse head injury models and their injury findings [17–20].

• For an existing experiment, it is recommended to use the same approach established in this study to quantify strain error magnitude propagated from assumed displacement errors under the prescribed impact condition. This will scrutinize which elements might be more tolerant of displacement errors and are, thus, more reliable for marker-based strain validation.

• To place markers in the brain in a new experiment, it is recommended to use one or a few different head computational models to first probe how marker displacement errors could propagate into strain. A parametric optimization may be particularly helpful to maximize the quality and usefulness of marker-based strain. Using multiple head injury models to converge to a more or less common result may also be preferable, given the cost and effort associated with each cadaveric head impact test.

Funding Data

• NIH (Grant No. R01 NS092853; Funder ID: 10.13039/100000002).

Conflict of Interest

No competing financial interests exist.

Supplementary Material

Supplementary Material

Supplementary Files