Abstract
BACKGROUND:
To evaluate the predictability of the Kane formula in estimating postoperative refractive outcome with various corneal curvatures and axial lengths (ALs) besides comparing with existing intraocular lens (IOL) formulae.
MATERIALS AND METHODS:
A prospective cross-sectional study was carried out among patients having uneventful cataract surgery at an eye hospital. A total of 50 eyes were considered for the study. The corresponding A-constant for the model of IOL implanted into the patient's eye was taken along with the actual power of IOL implanted and corresponding predicted power for the IOL power inserted were taken for all the chosen formulae and was termed as "Adjusted Predicted Refractive Power." This was compared with the actual refractive outcome and the absolute error (AE) was measured. The eyes were separated into groups in terms of corneal curvature as flat (<42D), medium (42D–46D), and steep (>46D) corneas. In terms of AL, it was grouped as short (≤22 mm), medium (>22.0–<24.0 mm), and long (>24.0 mm) eyes.
RESULTS:
The study included 50 eyes and the mean AE for all the selected formulae were calculated for each group. Over the entire corneal curvature range, none of the formulae showed any significance when compared with the Kane formula (P > 0.05). In short AL, SRK-T formula had a statistical significance over the Kane formula (P = 0.043), whereas no other group had any significance over the Kane formula in AL groups.
CONCLUSION:
The study shows, all formulae (SRK-T, Holladay1, Hoffer Q, Hill RBF, Barrett Universal II, Kane) are interchangeable to predict the IOL power for any of the corneal curvature and ALs.
Keywords: Axial length, corneal curvature, intraocular lens power, kane formula, refractive outcome
Introduction
Advancements in technology and improvement in techniques have made cataract surgery safe and effective in restoring vision to millions of people worldwide. The need to describe and quantify refractive outcomes arise from the fact that in many cases, the predicted postoperative refraction is not the same as the final postoperative refraction.
Many of the recent studies have reported that Barrett Universal II formula has the lowest absolute error (AE) compared with other modern formulae.[1,2,3,4,5]
The Kane formula is a new intraocular lens (IOL) power formula created using several large data sets from selected high-volume surgeons which uses a combination of theoretical optics, thin lens formulae and "big data" techniques to make its prediction. The Kane formula uses the axial length (AL), keratometry, anterior chamber depth (ACD), lens thickness (LT), central corneal thickness, and gender of the patient to make its predictions.[6,7,8,9]
Many studies have compared different formulae by taking different parameters and made conclusions on the accuracy and predictability of refractive outcomes. To the best of our knowledge, none of the studies have assessed the predictability of the Kane formula involving various corneal curvatures. Hence, this work aims at finding out the Predictability of the Kane formula in estimating postoperative refractive outcome with various corneal curvatures alongside comparison with existing IOL formulae.
Materials and Methods
This prospective study was conducted in the ophthalmology department of an eye hospital at Palakkad, Kerala with the ethics approval obtained from the institutional ethics committee viz., "Ahalia International Foundation." Informed consent was obtained from all the subjects participated in the study. The subjects willing for cataract surgery were chosen for the study and analyzed further. A total of 50 eyes undergoing phacoemulsification were included in the study.
Patients above 20 years and preoperative astigmatism of ≤1.50 D along with uneventful cataract surgery by phacoemulsification technique were included in the study. Since corneal astigmatism beyond 1.50 D requires peripheral corneal relaxing incisions and toric IOL implantations,[10] higher corneal astigmatism were not included. The surgeries were performed by two experienced surgeons who were masked.
Factors that might impact the postoperative refractive outcome related to irregular corneas (post LASIK, post LASIK ectasia, postgraft, keratoconus, etc.,), dense cataracts, Intraoperative complications (anterior or posterior capsule tear, vitreous prolapse, or zonular dehiscence) along with postoperative complications (persistent corneal edema) including improper positioning of IOL, surgically induced astigmatism, multifocal IOL, toric IOLs, and other ocular pathologies were also excluded from the study. Similarly, postoperative corrected distance visual acuity worse than 6/12, refraction performed before 4 weeks postoperatively were also excluded.
Preoperative eye examinations included refraction, cataract grading, and biometry. Preoperative biometry was performed using Acutome A-scan plus version 7.00.02. Postoperative refraction was performed by a single experienced optometrist. After measuring the AL, ACD, and LT, the IOL power along with corresponding refractive prediction error for SRK-T, Holladay I, and Hoffer Q were calculated. Online IOL power calculators were used for Hill RBF,[11] Barrett Universal II[12] and Kane[13] formulae. The A constants for all the formulae were taken in accordance to the type of IOL chosen by the patient. In this study, predominantly three types of IOLs were chosen, UltraSert Acrysof IQ, Auroflex hydrophilic aspheric, and Acriol galaxyfold. The IOL power along with the predicted power nearer to zero correspondings to each formula for the chosen A-constant was recorded.
In this study, six IOL power calculation formulae (SRT-T, Holladay1, Hoffer Q, Hill RBF, Barrette, and Kane) were chosen and since a single IOL power can be fixed, the actual IOL which got implanted in the patient was taken as the fixed IOL power and the corresponding predicted refractive outcome for the implanted IOL power was recorded and termed as "Adjusted Predicted Refractive Power" for each formula.
After finding out the adjusted predicted refractive power, the difference between the adjusted predicted refractive power and the postoperative refractive spherical equivalent was taken as the AE.[14]
The mean adjusted prediction error (MPE, which is the average of adjusted predicted refractive power), mean absolute error (MAE, which is the average of absolute errors), median absolute error (MedAE) and SD of the adjusted prediction error as well as the percentage of eyes that had absolute error within ± 0.00 - 0.12D, ± 0.13 - 0.25 and > ± 0.25D were calculated for each formula. Eyes were divided into subgroups based on corneal curvature as: Flat (<42D), medium (42D–46D) and steep (>46D) corneas and as short (≤22 mm), medium (>22.0–<24.0 mm), and long (>24.0 mm) ALs. One-month postoperative refraction was done after 28–30 days of surgery.
For analysis, values were transcribed manually from the patient's electronic medical record into Microsoft Excel 2007 spreadsheet. Normality of the data was tested with Kolmogorov–Smirnov test. Statistical significance of AE of all the formulae over the Kane formula was analyzed with t-test. Descriptive statistics were done to find out the mean age and also for calculating the mean and SD of various parameters in all the groups. Regression analysis was done between corneal curvature and AE of each formula, similarly between AL and AE. A P < 0.05 was considered significant. Statistical analysis was performed using Microsoft excel 2007 and IBM SPSS free version (Statistical Package for the Social Sciences) IBM SPSS Inc, New York, USA.
Results
In this study, a total of 50 eyes from 43 subjects undergoing cataract surgery with IOL implantation were included. They were separated into six groups based on corneal curvature and AL.
The mean age of the patients included in the study for all the groups together was 62.48 ± 11.57 years. For flat, medium and steep K groups, it was 62 ± 9.98, 62 ± 9.98 and 58 ± 17.2 years respectively. For short, medium, and long AL groups, the mean age was found to be 59.4 ± 9.8, 62 ± 12.2, and 69 ± 6.4 years, respectively. For other variables, the mean parameters for all groups together are shown in Table 1.
Table 1.
Mean and standard deviation of all variables for the entire group
| Parameter | Mean±SD (range) |
|---|---|
| Mean keratometry (D) | 44.53±1.77 (41-48.13) |
| AL (mm) | 22.85±0.75 (21.23-24.8) |
| Anterior chamber depth (mm) | 3.27±0.53 (2.41-5.46) |
| Lens thickness (mm) | 4.33±0.77 (2.18-5.58) |
| IOL power (D) | 22.05±1.94 (17-26) |
| Sex (male:female) | 31:19 |
SD: Standard deviation, IOL: Intraocular lens, AL: Axial length
In the corneal curvature cohort, none of the formulae showed any significance when compared with the Kane formula (P > 0.05). The MAE for flat K was found to be greater for the Kane formula. The order of descending for MAE was found to be Kane > Barrett/Hill RBF > Hoffer Q > Holladay 1> SRK-T. Similarly, for medium K, the successive decrease of MAE was found to be Barrett > Kane> Hill RBF > Hoffer Q/SRK-T > Holladay 1and for steep K, Hoffer Q > Kane> Barrett > Hill RBF/Holladay1/SRK-T as shown in Table 2.
Table 2.
Mean absolute error of each formula for corneal curvature cohort
| Formula | Flat K (D) | Medium K (D) | Steep K (D) |
|---|---|---|---|
| Kane | 0.46±0.15 | 0.39±0.30 | 0.29±0.32 |
| Barrett | 0.41±0.32 | 0.40±0.29 | 0.26±0.23 |
| Hill RBF | 0.41±0.20 | 0.36±0.30 | 0.25±0.25 |
| Hoffer Q | 0.37±0.18 | 0.35±0.27 | 0.34±0.15 |
| Holladay1 | 0.32±0.19 | 0.33±0.26 | 0.25±0.16 |
| SRK-T | 0.31±0.33 | 0.35±0.26 | 0.25±0.20 |
Percentage of eyes having AE within the range of 0.00–0.12D, ±0.13–0.25D and > ±0.25D was calculated for all the formulae in flat, medium, and steep corneal curvature cohorts and is given in Table 3.
Table 3.
Percentage of eyes within ±0-0.12D, ±0.13-0.25D and >±0.25D accuracy for all the formulas in flat, medium and steep corneal curvature groups
| Error range in diopters (D) | Kane (%) | Barrett (%) | Hill RBF (%) | Hoffer Q (%) | Holladay 1 (%) | SRK-T (%) | |
|---|---|---|---|---|---|---|---|
| Flat K | ±0-0.12 | 0 | 25 | 0 | 0 | 0 | 50 |
| ±0.13-0.25 | 0 | 0 | 25 | 25 | 50 | 0 | |
| >±0.25 | 100 | 75 | 75 | 75 | 50 | 50 | |
| ±0-0.12 | 22 | 19 | 24 | 22 | 24 | 22 | |
| Medium K | ±0.13-0.25 | 13 | 16 | 22 | 27 | 22 | 22 |
| >±0.25 | 65 | 65 | 54 | 51 | 54 | 56 | |
| ±0-0.12 | 56 | 33.3 | 44 | 11 | 11 | 23 | |
| Steep K | ±0.13-0.25 | 0 | 33.3 | 12 | 11 | 67 | 44 |
| >±0.25 | 44 | 33.3 | 44 | 78 | 22 | 33 | |
| For overall K | ±0-0.12 | 26 | 22 | 26 | 18 | 20 | 24 |
| ±0.13-0.25 | 10 | 18 | 20 | 24 | 32 | 24 | |
| >±0.25 | 64 | 60 | 54 | 58 | 48 | 52 |
Percentage of eyes having AE within Zero–0.12D, ±0.13–0.25D, and > ±0.25D for all the formulae in the corneal curvature cohort (flat, medium, and steep K together) is represented in Figure 1.
Figure 1.
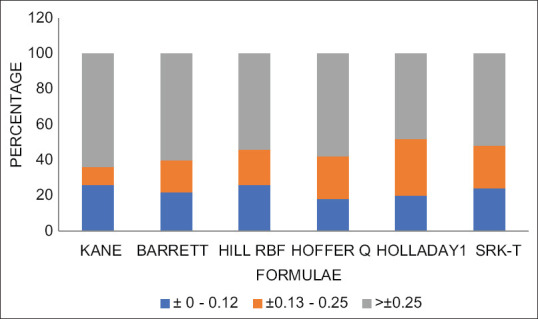
Percentage of absolute error within the range 0.00–0.12D, ±0.13–0.25D and >±0.25D for the entire corneal curvature cohort (flat, medium and steep K together)
In the short AL cohort, Kane formula predicted more MAE tha SRK-T and was statistically significant with a P = 0.043. The MAE for each AL is shown in Table 4.
Table 4.
Mean absolute error of each formula for axial lengths
| Formula | Short AL | Medium AL | Long AL |
|---|---|---|---|
| Kane | 0.47±0.31 | 0.37±0.29 | 0.27±0.30 |
| Barrett | 0.39±0.30 | 0.39±0.29 | 0.24±0.25 |
| Hill RBF | 0.38±0.30 | 0.35±0.29 | 0.22±0.27 |
| Hoffer Q | 0.33±0.27 | 0.36±0.25 | 0.29±0.24 |
| Holladay1 | 0.33±0.30 | 0.33±0.24 | 0.17±0.21 |
| SRK-T | 0.35±0.33 | 0.34±0.24 | 0.11±0.13 |
AL: Axial length
Percentage of eyes having AE within 0.00–0.12D, ±0.13–0.25D, and > ±0.25D for each formula in short, medium, and long AL cohorts is given in Table 5.
Table 5.
Percentage of eyes within ±0-0.12D, ±0.13-0.25D and >±0.25D for all the formulas in short, medium and long axial length
| Error range in diopters (D) | Kane (%) | Barrett (%) | Hill RBF (%) | Hoffer Q (%) | Holladay 1 (%) | SRK-T (%) | |
|---|---|---|---|---|---|---|---|
| Short AXL | ±0-0.12 | 22 | 12 | 11 | 33 | 23 | 23 |
| ±0.13-0.25 | 0 | 44 | 33 | 11 | 44 | 33 | |
| >±0.25 | 78 | 44 | 56 | 56 | 33 | 44 | |
| ±0-0.12 | 24 | 22 | 27 | 14 | 19 | 19 | |
| Medium AXL | ±0.13-0.25 | 14 | 13 | 16 | 27 | 24 | 24 |
| >±0.25 | 62 | 65 | 57 | 59 | 57 | 57 | |
| ±0-0.12 | 50 | 50 | 50 | 25 | 50 | 75 | |
| Long AXL | ±0.13-0.25 | 0 | 0 | 0 | 25 | 25 | 0 |
| >±0.25 | 50 | 50 | 50 | 50 | 25 | 25 | |
| For overall AXL | ±0-0.12 | 26 | 22 | 26 | 18 | 20 | 24 |
| ±0.13-0.25 | 10 | 18 | 20 | 24 | 28 | 24 | |
| >±0.25 | 64 | 60 | 54 | 58 | 52 | 52 |
AXL: Axial Length
Percentage of eyes within ± 0–0.12D, ±0.13–0.25D, and > ±0.25D accuracy for all the formulas in the entire AL cohort (short, medium, and long AL) is represented in Figure 2.
Figure 2.
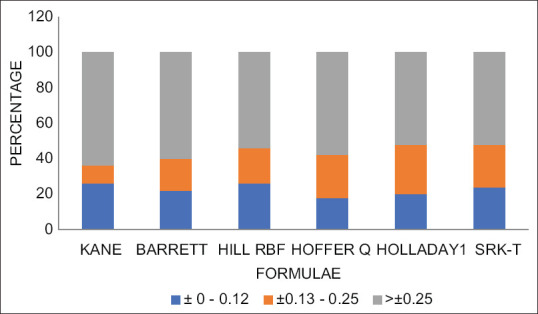
Percentage of absolute error within the range of 0.00–0.12D, ±0.13–0.25D and > ±0.25D in the entire axial length cohort (short, medium and long axial length)
Discussion
This study revealed that all IOL formulae were equally effective in predicting the refractive outcome postoperatively for all the corneal curvatures and AL groups, except for short AL, where the SRK-T formula was found to be closer to predictive error as compared to Kane formula, which was statistically significant.
In this study, for flat corneal curvature cohort (K < 42D), greater percentage of eyes fell within zero–0.12D of refractive prediction for SRK-T when compared with another study by Olga Reitblat et al.[2] where the Barrett Universal II formula was found accurate for the range within ± 0.50D. For medium corneal curvature, not many studies had mentioned about the accuracy of any formulae, whereas this study revealed that Hill RBF and Holladay 1 formulae had the greatest percentage of eyes within zero–0.12D. For steep corneal curvature, previous study[15] reported that SRK-T formulae had better accuracy within ±0.50D whereas in this work Kane formula had better accuracy than other formulae with more precise prediction of refractive error within zero–±0.12D. For the entire corneal curvature range, both Kane and Hill RBF formulae showed greater percentage of eyes within zero–0.12D. Comparison of previous studies with the present study on the accuracy of different formulae for the entire corneal curvature and AL groups is given in Table 6.
Table 6.
Comparison of previous studies with present study on accuracy of different formulae for the entire corneal curvature group and axial length groups
| Flat K (<42D) | Medium K (42D-46D) | Steep K (>46D) | Entire K | Short AL (≤22 mm) | Medium AL (>22.0-<24.0 mm) | Long AL (>24.0 mm) | Entire AL | |
|---|---|---|---|---|---|---|---|---|
| Reitblat et al.[2] | SRK-T | - | SRK-T | - | - | - | - | - |
| Kuthirummal et al.[4] | - | - | - | - | Barrett | Barrett | Barrett | - |
| Connell and Kane[6] | - | - | - | - | - | Kane | - | - |
| Cooke and Cooke[16] | - | - | - | - | Barrett and Olsen | Barrett and Olsen | - | - |
| Zhang et al.[17] | - | - | Barrett | - | - | - | - | - |
| Wang et al.[18] | - | - | - | - | - | - | Barrett | - |
| Hoffer[19] | - | - | - | - | Hoffer Q and Holladay 2 | Hoffer Q and Holladay 1 | SRK-T and Holladay 2 | - |
| Savini et al.[20] | - | - | SRK-T | - | - | - | - | - |
| Kamiya et al.[21] | - | - | SRK-T | - | - | - | - | - |
| This study (±0-0.12D) | SRK-T | Holladay 1 and Hill RBF | Kane | Kane and Hill RBF | Hoffer Q | Hill RBF | SRK-T | Kane and Hill RBF |
AL: Axial length
In AL cohort, Hoffer Q formula was found to be more precise within the range of zero–0.12D in short AL whereas in the previous study,[16,17,22] Barrett formula was found to be more accurate when measurements were made using partial coherence interferometry and Olsen formula was good when optical low coherence reflectometry (OLCR) was used. In both, the case the range was within ±0.50D. In earlier studies,[6,15,17] Kane, Hoffer Q and Barrett Universal II formulae were found more accurate. In the medium AL cohort, Hill RBF formula had the greatest percentage of accuracy within zero–0.12D in this study whereas, other studies reported Barrett universal II formula was more accurate predictor within ±0.50D and Olsen formula performed better with OLCR.[16,17] In the long AL group, the SRK-T formula was more precise within zero–±0.12D in this study, though other studies reported that Barrett and Kane formulae performed better.[6,17,18,22] For overall AL group in this study, Kane and Hill RBF formulae was found more precise within zero–0.12D, although an earlier study reported that the Barrett Universal II formula performed better.[18] The potential limitation of this study is the small sample size where only 50 eyes could be taken for the study purpose. The study failed to maintain an equal number of eyes in each of the groups.
Conclusion
According to this study, statistically, all the formulae (SRK-T, Holladay1, Hoffer Q, Hill RBF, Barrett Universal II, Kane) are interchangeable to predict the IOL power for any corneal curvature and AL. Clinically, for flat K, SRK-T is preferable, and for medium K, both Holladay 1 and Hill RBF formulae can be used. For steep K, Kane formula is preferable. In case of AL, Hoffer Q is preferable in short AL, Hill RBF for medium AL, and SRK-T for long AL. For the overall range of corneal curvature and AL, both Kane and Hill RBF formulae can be used interchangeably.
Financial support and sponsorship
Nil.
Conflicts of interest
There are no conflicts of interest.
References
- 1.Kane JX, Van Heerden A, Atik A, Petsoglou C. Intraocular lens power formula accuracy: Comparison of 7 formulas. J Cataract Refract Surg. 2016;42:1490–500. doi: 10.1016/j.jcrs.2016.07.021. [DOI] [PubMed] [Google Scholar]
- 2.Reitblat O, Levy A, Kleinmann G, Lerman TT, Assia EI. Intraocular lens power calculation for eyes with high and low average keratometry readings: Comparison between various formulas. J Cataract Refract Surg. 2017;43:1149–56. doi: 10.1016/j.jcrs.2017.06.036. [DOI] [PubMed] [Google Scholar]
- 3.Zhou D, Sun Z, Deng G. Accuracy of the refractive prediction determined by intraocular lens power calculation formulas in high myopia. Indian J Ophthalmol. 2019;67:484–9. doi: 10.4103/ijo.IJO_937_18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kuthirummal N, Vanathi M, Mukhija R, Gupta N, Meel R, Saxena R, et al. Evaluation of Barrett universal II formula for intraocular lens power calculation in Asian Indian population. Indian J Ophthalmol. 2020;68:59–64. doi: 10.4103/ijo.IJO_600_19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Iijima K, Kamiya K, Iida Y, Shoji N. Comparison of predictability using barrett universal II and SRK/T formulas according to keratometry. J Ophthalmol. 2020;2020:1–5. doi: 10.1155/2020/7625725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Connell BJ, Kane J×. Comparison of the Kane formula with existing formulas for intraocular lens power selection. BMJ Open Ophthalmol. 2019;4:e000251. doi: 10.1136/bmjophth-2018-000251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xia T, Martinez CE, Tsai LM. Update on intraocular lens formulas and calculations. Asia Pac J Ophthalmol (Phila) 2020;9:186–93. doi: 10.1097/APO.0000000000000293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kane JX, Connell B, Yip H, McAlister JC, Beckingsale P, Snibson GR, et al. Accuracy of intraocular lens power formulas modified for patients with keratoconus. Ophthalmology. 2020;127:1037–42. doi: 10.1016/j.ophtha.2020.02.008. [DOI] [PubMed] [Google Scholar]
- 9.Cheng H, Wang L, Kane JX, Li J, Liu L, Wu M. Accuracy of artificial intelligence formulas and axial length adjustments for highly myopic eyes. Am J Ophthalmol. 2021;223:100–7. doi: 10.1016/j.ajo.2020.09.019. [DOI] [PubMed] [Google Scholar]
- 10.Lee YC. Astigmatism considerations in cataract surgery. Tzu Chi Med J. 2013;25:19–22. [Google Scholar]
- 11.Hill WE Hill-RBF Calculator Version 3.0. [Last accessed on 2020 Dec 19]. Available from: https://rbfcalculator.com .
- 12.Barrett Universal II Formula. [Last accessed on 2020 Dec 19]. Available from: https://calc.apacrs.org/barrett_universal2105/
- 13.Kane K. Kane Formula. [Last accessed on 2020 Dec 19]. Available from: https://www.iolformula.com .
- 14.Wang L, Koch DD, Hill W, Abulafia A. Pursuing perfection in intraocular lens calculations: III. Criteria for analyzing outcomes. J Cataract Refract Surg. 2017;43:999–1002. doi: 10.1016/j.jcrs.2017.08.003. [DOI] [PubMed] [Google Scholar]
- 15.Aristodemou P, Cartwright NE, Sparrow JM, Johnston RL. Improving refractive outcomes in cataract surgery: A global perspective. World J Ophthalmol. 2014;4:140–6. [Google Scholar]
- 16.Cooke DL, Cooke TL. Comparison of 9 intraocular lens power calculation formulas. J Cataract Refract Surg. 2016;42:1157–64. doi: 10.1016/j.jcrs.2016.06.029. [DOI] [PubMed] [Google Scholar]
- 17.Zhang C, Dai G, Pazo EE, Xu L, Wu X, Zhang H, et al. Accuracy of intraocular lens calculation formulas in cataract patients with steep corneal curvature. PLoS One. 2020;15:e0241630. doi: 10.1371/journal.pone.0241630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang Q, Jiang W, Lin T, Zhu Y, Chen C, Lin H, et al. Accuracy of intraocular lens power calculation formulas in long eyes: A systematic review and meta-analysis. Clin Exp Ophthalmol. 2018;46:738–49. doi: 10.1111/ceo.13184. [DOI] [PubMed] [Google Scholar]
- 19.Hoffer KJ. Clinical results using the Holladay 2 intraocular lens power formula. J Cataract Refract Surg. 2000;26:1233–7. doi: 10.1016/s0886-3350(00)00376-x. [DOI] [PubMed] [Google Scholar]
- 20.Savini G, Abbate R, Hoffer KJ, Mularoni A, Imburgia A, Avoni L, et al. Intraocular lens power calculation in eyes with keratoconus. J Cataract Refract Surg. 2019;45:576–81. doi: 10.1016/j.jcrs.2018.11.029. [DOI] [PubMed] [Google Scholar]
- 21.Kamiya K, Iijima K, Nobuyuki S, Mori Y, Miyata K, Yamaguchi T, et al. Predictability of intraocular lens power calculation for cataract with keratoconus: A multicenter study. Sci Rep. 2018;8:1312. doi: 10.1038/s41598-018-20040-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Melles RB, Holladay JT, Chang WJ. Accuracy of intraocular lens calculation formulas. Ophthalmology. 2018;125:169–78. doi: 10.1016/j.ophtha.2017.08.027. [DOI] [PubMed] [Google Scholar]


