Screening and Selection: The Case of Mammograms

Abstract

We analyze selection into screening in the context of recommendations that breast cancer screening start at age 40. Combining medical claims with a clinical oncology model, we document that compliers with the recommendation are less likely to have cancer than younger women who select into screening or women who never screen. We show this selection is quantitatively important: shifting the recommendation from age 40 to 45 results in three times as many deaths if compliers were randomly selected than under the estimated patterns of selection. The results highlight the importance of considering characteristics of compliers when making and designing recommendations.

Whether and when to recommend screening for potential diseases is a highly controversial and evolving policy area, with active academic research.¹ Much of the debate—both in public policy and in academia—centers on the causal impact of screening for a typical individual covered by the recommendation. Estimating this causal impact is challenging for several well-known reasons. First, there are the usual challenges to causal inference. Second, many of the potential costs and benefits of screening are difficult to measure and to monetize.² In this paper, we highlight another important—and, we believe, overlooked—challenge in analyzing and designing screening recommendations: the typical individual covered by a recommendation may be very different from the typical individual who responds to the recommendation. As a result, the estimated impact of screening for a randomly-selected individual may be quite different from the impact for an affected individual.

We explore this distinction in the context of the current controversy over whether to recommend annual mammograms for women starting at age 40. Results from randomized trials have consistently failed to show statistically significant mortality benefits of mammograms for women in their 40s. In 2009, these results prompted the US Preventive Services Task Force (USPTF) to change its recommendation for routine mammograms to begin at age 50 rather than at age 40. This change generated substantial public controversy (Kolata 2009; Saad 2009; Berry 2013).

This debate has focused on the costs and benefits of mammograms for typical (“average-risk”) 40-year-old women, with little attention paid to what types of women respond to a screening recommendation and whether the costs and benefits for them may differ from the average woman. To investigate the type of women who respond, we draw on two primary data sources. The first is insurance claims data on mammogram choices and their results (negative, false positive, or true positive) for privately-insured women aged 35–50 from the Health Care Cost Institute (HCCI). The second is cancer registry data, from the National Cancer Institute’s Surveillance, Epidemiology, and End Results (SEER) database, on the size and stage of detected tumors for women aged 35–50 who were diagnosed with breast cancer. We supplement some of the descriptive analyses with additional information from the Behavioral Risk Factor Surveillance System Survey (BRFSS), which allows us to observe additional health behaviors and demographics of women who do and do not receive mammograms at various ages.

The visual evidence shows sharp and pronounced changes in behavior and outcomes at age 40. There is a 25-percentage-point jump in the annual mammogram rate at age 40, from 10 percent to 35 percent of women. We then compare characteristics of the women who respond to the recommendation for a mammogram (i.e. “compliers” in the terminology of Angrist, Imbens, and Rubin 1996) to characteristics of always-takers (i.e. women who choose mammograms even in the absence of the recommendation, which is before age 40). We find that compliers have a lower incidence of cancer than always-takers: there is a roughly 30 percent decline (from 0.84% to 0.56%) in the share of screened women diagnosed with cancer (i.e. true positives) at age 40. Given the high rate of false positives—about 90 percent of initial positive mammograms turn out to be false positives—the sharp increase in the mammogram rate at age 40 translates into a substantial increase in the number of women experiencing false positives, from about 10 per thousand women to about 40 per thousand women. This is consistent with false positives being a key concern that motivated moving the recommended age of beginning mammography from 40 to 50 (Nelson et al. 2009). Moreover, among those diagnosed with cancer, the registry data show a sharp decline in the average tumor’s stage and size starting at age 40, compared to earlier ages. For example, the share of detected tumors that are in a late stage (invasive tumors) as opposed to early stage (in-situ tumors) falls by about 6 percentage points (or 7 percent) at age 40.

These descriptive results indicate that women who respond to the recommendation for a mammogram have lower risk of cancer than those who seek mammograms in the absence of the recommendation. For non-cancer characteristics, we can also compare compliers to never-takers (women who do not get mammograms even once the recommendation is in effect). We find that, relative to never-takers, compliers are more likely to undertake other types of recommended preventive care, such as cervical cancer screening tests and flu shots. This pattern is consistent with findings that when a health behavior is recommended, those who comply with the recommendation tend to exhibit other positive health behaviors (Oster 2020). It also echoes the observation that women who comply with assignment to mammograms in an RCT setting are healthier than never-takers (Kowalski 2019).³

To assess the implications of these findings and to quantify costs and health outcomes under various counterfactual selection scenarios, we specify a model of mammogram demand that is a function of a woman’s age, her (undiagnosed) cancer type (no cancer, in-situ, or invasive), and whether or not a mammogram is recommended at her age. We estimate the model by method of moments, using two key inputs. First, we leverage our data on the observed patterns of mammogram decisions and mammogram outcomes (specifically, cancer type) for women by age. Second, we bring in a clinical oncology model of the underlying rate of onset of breast cancer by age, as well as the cancer’s clinical progression in the absence of detection and treatment.

The clinical model allows us to estimate the cancer characteristics of never-takers. In the absence of a clinical model, these cancer characteristics are inherently difficult (or impossible) to observe: cancer incidence is not observed in the non-screened population, and almost all detected cancer is treated immediately upon detection. The clinical model of breast cancer incidence and progression is drawn from a large-scale, coordinated project funded by the National Cancer Institute (NCI) involving seven different research groups (Clarke et al. 2006); since there is naturally some uncertainty about the underlying model, we confirm that our main findings are not sensitive to a range of alternative assumptions about the onset and distribution of cancer type by age.

The estimates from our model indicate that women who would select into mammograms in the absence of the recommendation (“always-takers”) have much higher rates of both in-situ and invasive cancer than the general population. We refer to this as “positive selection” into mammograms (positive with respect to cancer incidence). However, our estimates indicate that the women who select into mammograms due to the recommendation (“compliers”) are much less likely to have invasive cancer—and are no more likely to have in-situ cancer—than women who do not select into mammograms (“never-takers”). The relative degree of selection pre- and post- the age-40 recommendation is identified directly from our data; the clinical model of underlying cancer incidence is needed to assess whether the observed selection either pre- or post-age 40 is positive with respect to the underlying population, whose cancer incidence is not directly observed.

We apply our model and its estimates to illustrate how the nature of selection in response to the recommendation affects the impact of the recommendation. Specifically, we estimate that shifting the recommendation from age 40 to age 45 results in more than three times as many deaths—at similar cost savings—if we assume that compliers with the recommendation are randomly drawn from the population rather than drawn based on the estimated selection patterns. We view this as a particularly instructive counterfactual, since assuming that the women who respond are randomly drawn from the population is conceptually similar to using estimates of the impact of mammography from randomized experiments (with full compliance). Because in practice those who respond to the recommendation have a much lower rate of invasive cancer than the underlying population, the mortality cost of moving the recommendation to age 45 is lower than under random selection. Conversely, our model also illustrates that if it were feasible to target the recommendations to those with higher rates of cancer, the mortality cost of moving the recommendation from age 40 to 45 could be substantially larger than even the random selection assumption would imply. This is consistent with recent interest in reducing over-diagnosis by developing targeted, precision screening for women at higher risk (Elmore 2016; Esserman, Shieh, and Thompson 2009).

Our paper relates to several distinct literatures. Most narrowly, it speaks to the large body of work on mammograms, which we describe in the next section. But beyond the specific application of mammograms, it speaks to a broader health policy debate about whether and when to recommend medical screening tests (e.g., Welch, Schwartz, and Woloshin 2011). A central challenge that has limited empirical research on this topic is that—in the datasets typically available to researchers—the testing decision is observed but the outcome of the test is not. An attractive feature of our setting is that the outcome of the test (i.e. cancer incidence and type of cancer) is measurable both in claims data and in registry data. In this sense our analysis is similar in spirit to Abaluck et al. (2016), who are able to measure the outcome of imaging tests for pulmonary embolism in claims data, which they use to investigate whether and when that imaging test is being “overused”. Both our paper and Abaluck et al. (2016) share a common feature with the racial profiling literature on stop and frisks (Anwar and Fang 2006; Persico 2009): the object of interest is only observed conditional on an action. This raises an empirical challenge for analyzing how the action (in our case, screening) relates to the underlying object of interest (in our case, the underlying incidence of cancer and cancer types). In our setting, we overcome this empirical challenge by combining two insights. First, the recommendation at age 40 serves as an exogenous source of variation in the screening rate, allowing us to estimate the cancer type of the marginal person affected by the recommendation. Second, the clinical oncology model of cancer incidence and growth allows us to use the observed moments (namely, outcomes conditional on screening under different regimes) to model outcomes under counterfactual regimes.

More broadly, our paper speaks to the value of complementing reduced-form estimates of causal effects with economic models of behavior, and particularly of selection. Reduced-form methods—both quasi-experimental and randomized experiments—aim to estimate causal effects by shutting down any endogenous choices. In practice, however, most policies involve an element of choice, so that the ultimate impact of the policy depends not only on the distribution of causal treatment effects but also on which women select into treatment. In this sense, our paper relates broadly to the literature on Roy selection, or selection on gains. In the health care context specifically, Einav et al. (2013) emphasize that the impact on health care spending of offering a high-deductible health insurance plan may be very different than what would be estimated from random assignment of high-deductible plans across individuals, because the types of people who choose high-deductible plans can have very different health care utilization responses to cost sharing than a typical individual. Our analysis speaks to a similar issue, in the context of evaluating recommendations for disease screening.

The rest of the paper proceeds as follows. Section I summarizes the relevant institutional details of our empirical context (breast cancer and mammography), and describes the existing evidence regarding the effect of mammograms and of various policy interventions that are designed to increase mammography rates. Section II describes our data and presents descriptive results. Section III presents our model of mammogram choice and describes how we estimate it using the observed descriptive patterns together with a clinical oncology model. Section IV presents the model estimates and discusses their implications for the impact of changing the recommended age of beginning mammography under both observed and counterfactual selection patterns. The last section concludes by using our findings to speculate about possible policy implications more broadly.

I. Empirical context

A. Breast cancer

The earliest stages of breast cancer typically produce no symptoms and are not detectable in the absence of screening technologies.⁴ As breast cancer progresses, it can spread within the breast, to adjacent tissues, to adjacent lymph nodes, and to distant organs (known as metastases). In clinical settings, tumors are classified according to the size of the tumor, the extent to which it has spread to lymph nodes, and whether it has metastasized. Public health research typically relies on a standardized classification—namely, the SEER classification system—which includes four stages: in-situ, local, regional, and distant; the last three stages are collectively referred to as “invasive” tumors.

Our analysis focuses on the distinction between in-situ and invasive tumors, a distinction that has been a key focus of the policy debate around mammography recommendations. In-situ refers to abnormal cells that have not invaded nearby tissues, instead remaining confined to the ducts or glands in which they originated. Some but not all in-situ tumors will become invasive. Expected survival time varies greatly by stage at diagnosis: women who are diagnosed with localized breast cancer are 99% as likely as cancer-free women to survive to 5 years after diagnosis, compared to 85% for regional breast cancer, and 27% for distant-stage breast cancer.⁵ Within a stage, survival also varies with tumor size. For example, among women with regional disease, 5-year survival (again, relative to comparable cancer-free women) is 95% for tumors smaller than 2 centimeters in diameter, 85% for tumors of 2–5 centimeters, and 72% for tumors greater than 5 centimeters.⁶

B. Mammography

Asymptomatic breast cancer can be detected by a mammogram, which is a low-dose X-ray procedure that allows visualization of the internal structure of the breast. If an abnormality is detected on a routine screening mammogram, the woman is typically called back in for a diagnostic mammogram and—if needed—a confirmatory biopsy (Cutler 2008; Hubbard et al. 2011). Once a diagnosis has been confirmed, the woman may undergo surgery to remove the tumor, in addition to other treatments which aim to reduce the risk of recurrence, such as radiation therapy, chemotherapy, hormone therapy, and/or targeted therapy.

Mammography is based on the theory of early detection of invasive cancer, rather than detection and removal of precancerous lesions (Humphrey et al. 2002). The efficacy of mammography is the subject of considerable debate. Mechanically, mammography is most beneficial if machines can detect tumors in their earliest stages, and if tumors (on average) rapidly become more difficult to treat the longer they go undetected. The benefits from mammography will be lower if a tumor is slow to advance from stage to stage, if mortality when treatment begins at a later stage is similar to when tumors are treated earlier, or if mammogram machines are unlikely to correctly identify tumors. In practice, because most women diagnosed with breast cancer are treated immediately upon detection, there is little information about the natural history of breast cancer tumors, making it difficult to know how an individual tumor would have progressed had it not been treated (Zahl, Maehlen, and Welch 2008). This complicates attempts to quantify the benefits of mammography.

In principle, the major potential health benefit of mammography is reduced mortality. However, in practice, randomized trials of the impact of mammograms on mortality have documented mixed results (Habbema et al. 1986; Alexander et al. 1999; Miller et al. 2000, 2002; Nyström et al. 2002; Bjurstam et al. 2003; Moss et al. 2006). There have been nine trials in total, with the first one dating back to the 1960s (Welch and Black 2010). Their estimates of relative risk reduction in breast-cancer mortality due to invitation to mammography range from 0% to 31% (Welch and Passow 2014), but many of these studies have lacked the statistical power to separately determine effects in different age groups (Humphrey et al. 2002). In particular, while most studies indicate that mammography reduces mortality among average-risk women over age 50, recent trials specifically designed to study mammography in younger women (aged 40–49) have estimated statistically insignificant reductions in breast-cancer mortality in this age group (Bjurstam et al. 2003; Moss et al. 2006).

The potential costs of mammography include financial, physical, and psychological costs. These costs arise from the initial screening, the frequent finding of false positives, and the treatment of cancers that would not have become clinically relevant in a woman’s lifetime (often referred to as “over-diagnosis”) (Jørgensen and Gøtzsche 2009). Some of these costs, such as the financial cost of a screening, are easy to quantify, while others are much more difficult to estimate. Estimates of the rate of over-diagnosis of breast cancer (from both observational work and inferences from randomized control trials) range from less than 5% to more than 50% of diagnosed breast cancers (Zackrisson et al. 2006; Jørgensen and Gøtzsche 2009; Bleyer and Welch 2012; Oeffinger et al. 2015; Harding et al. 2015; Welch et al. 2016; Jørgensen et al. 2017).⁷

C. Age-specific mammogram recommendation and its impact

Several studies have combined the existing evidence to quantify the costs and benefits of mammograms (e.g., Welch and Passow 2014; Ong and Mandl 2015). For example, Welch and Passow (2014) estimate that for every 1,000 women aged 40–49 who undergo annual mammography for 10 years, 0.1–1.6 women will avoid dying from breast cancer, while 510–690 will have at least one false-positive result and up to 11 women will be over-diagnosed and (unnecessarily) treated. As the estimates of the costs and benefits of mammography have evolved, so have the recommendations by medical associations regarding which groups of women should receive mammograms, and how often.

In the 1980s, following the first randomized trials of routine mammography, the National Institutes of Health (NIH), the National Cancer Institute (NCI), and eleven other health care organizations issued recommendations for routine screenings of women over age 40 (Kolata 2009). These recommendations became the subject of controversy over time as more trials were published, and the US federal government subsequently reconsidered its position. In 1997, an NIH panel concluded that there was insufficient evidence to recommend routine screening for women in their 40s, a finding that was controversial (one radiologist described the finding as a “death sentence” for women (Taubes 1997)). After public pressure, the Senate encouraged an advisory board to reject that conclusion (Kolata 2009). In 2009, following the publication of experimental data that failed to show statistically significant mortality benefits of mammograms for women in their 40s, the US Preventive Services Task Force (USPSTF) recommended that women begin screening at age 50. Again, this conclusion generated backlash from patient advocacy groups like the American Cancer Society, which at the time recommended annual screening for women aged 40 and above (American Cancer Society 2018).⁸ This negative reaction was exacerbated by fears that the Affordable Care Act (ACA, then being drafted) would allow insurers to refuse to cover mammograms for younger women. The USPSTF stood by its recommendation, but a poll found that 84% of women aged 35–49 did not plan to follow the new recommendations, and the ACA was modified to mandate that insurers reimburse mammograms for women aged 40 and over (Saad 2009). Although in the last few years most patient advocacy organizations have begun to moderate their stances, the question of whether mammography should be recommended in the 40–49 age group remains controversial.

Importantly, both the academic literature and the policy debate over the costs and benefits of mammograms have primarily focused on the average impacts of mammograms at specific ages. For example, Welch and Passow (2014) extrapolate results from mammography RCTs to the entire population without considering selection effects. In contrast, our focus is on the characteristics of women whose decision to get a mammogram is influenced by the mammogram recommendation, and how their underlying cancer incidence and characteristics may differ from that of a randomly-selected woman in the population.

Several papers have examined the mammogram response to recommendations (Kadiyala and Strumpf 2011, 2016; Jacobson and Kadiyala 2017). Most closely related to our work on the selected response to mammogram recommendations is Kadiyala and Strumpf (2016), who document a sharp increase in self-reported mammograms at age 40 and estimate that most of the “newly detected” cancers are early-stage cancers. Also closely related is the work of Kim and Lee (2017) and Bitler and Carpenter (2016), who document that women who elect to receive mammograms in response to price reductions are in better health than those who get the mammogram even without the price reduction or those who don’t get the mammogram even with the price reduction. Finally, Kowalski (2019) shows that the compliers in a Canadian mammography RCT are healthier on both cancer dimensions (i.e., rates of breast cancer) and non-cancer dimensions (e.g. body mass and smoking) than the never-takers.

II. Data and descriptive patterns

A. Data and variable construction

Our analysis of mammogram choices and outcomes focuses on women aged 35–50 and draws on two primary data sources. The first is claim-level data provided by the Health Care Cost Institute (HCCI), consisting of all claims paid by three large commercial insurers (Aetna, Humana, and UnitedHealthcare) from January 2008 through December 2012. Together, these three insurers represented about one-quarter of individuals under age 65 with commercial insurance (HCCI 2012). The data capture the billing-related information contained in the claims that these insurers pay out to medical providers; this includes the exact date and purpose of each claim, as well as the amount paid by the insurer and the amount owed out of pocket. The data also include a (masked) person identifier as well as the individual’s birth year and gender.

The claim-level information in the HCCI data allow us to construct variables measuring whether an individual had a screening mammogram,⁹ whether the result was positive or negative, and whether a positive result was a true positive or false positive. Our coding of screening mammograms (hereafter “mammograms”)—as well as their outcomes—broadly follows the approach of Segel, Balkrishnan, and Hirth (2017), which we cross-validated using Medicare claims data linked to cancer registry data (see Appendix A for more details).

The complete HCCI data contain about 28.7 million privately-insured women aged 25–64, and over 70 million woman-years. We limit the data to woman-years aged 35–50 who are covered continuously for at least three years between January 2008 and December 2012; we keep all the years of coverage except the first and last (since for every woman-year we need to observe the previous year to define screening mammograms and the subsequent year to measure outcomes). This results in about 7.4 million woman-years, and 3.7 million distinct women over the years from January 2009 to December of 2011.

The primary drawback of the HCCI data is that we are not able to observe information on a breast cancer diagnosis beyond its detection. To overcome this limitation of the HCCI data, we also analyze the National Cancer Institute’s (NCI) Surveillance, Epidemiology, and End Results (SEER) database. This is an administrative, patient-level cancer registry of all cancer diagnoses in 13 US states, covering about one quarter of the US population (SEER 2019). We analyze all the breast cancer diagnoses in the data between 2000 and 2014 for women aged 35–50 at the time of diagnosis; this covers about 212,000 diagnoses. All cancer diagnoses are required to be reported, with data collected directly from the cancer patients’ medical records at the time of diagnosis (rather than self reports).¹⁰ For each diagnosed cancer, the SEER data contain information about the size and stage of each tumor at diagnosis. They also contain basic demographics for the patient including age at time of diagnosis, race, and insurance coverage, as well as subsequent mortality information through December 2013.

In our HCCI sample, the average woman’s age is 43 and 27% of woman-years are under 40. In the SEER data, because cancer risk increases with age, the average age at diagnosis is a bit higher (44.6) and only 13% of the SEER diagnoses occur in women under 40. In SEER, where we can observe race, slightly over three-quarters of the sample is white. And unlike the HCCI data where, by construction, everyone is privately insured, in the SEER data only 84% are privately insured, while 13% are on Medicaid.

Table 1 documents mammogram rates and test results in the HCCI data. About 30% of woman-years are associated with a mammogram. The vast majority (89.6%) of mammograms are negative, and another 9.7% are false positives. Only 0.7% are true positives. Among all woman-years with a mammogram, total (insurer plus out-of-pocket) health care spending in the 12 months starting from (and including) the mammogram averages $5,000; while it is slightly higher (by about $1,000) for those with a false positive, it is dramatically higher for those with true positives, averaging almost $50,000. Out-of-pocket spending in the 12 months post-mammogram is about $2,800 for women with a positive mammogram, compared to $715 for women with a negative mammogram and $950 for women with a false positive.

Table 1:

Summary statistics

	No.of Observations		Health Care Spending ($US)
	N (000s)	Share	Total	Out-of-pocket
No mammogram	5,166.2	0.701	4,300	625
Mammogram	2,206.9	0.299	4,985	751
Conditional on mammogram:
Negative	1,977.8	0.896	4,552	715
False positive	214.6	0.097	6,106	952
True Positive	14.4	0.007	47,639	2,821

Table shows summary statistics from insurance claims data on a set of 35–50 year old privately insured women from 2008–2012, for mammograms between 2009–2011. Each observation is a woman-year. 12-month spending measures health care spending in the 12 months after the mammogram (including the mammogram itself) for those with a mammogram. For those without a mammogram, we draw a reference date from the distribution of actual mammograms in that year. All reference dates are set to be the first of the given month. Spending is measured in the 12 months after this reference date.

The SEER data provide more information on tumor stage and tumor size for the 212,000 true positives (i.e. diagnoses) we observe. Just over 15% are in-situ; the rest are invasive. Of the invasive, about 57% are localized, 38% are regional, and the remaining 5% are distant.

B. Mammograms and outcomes, by age

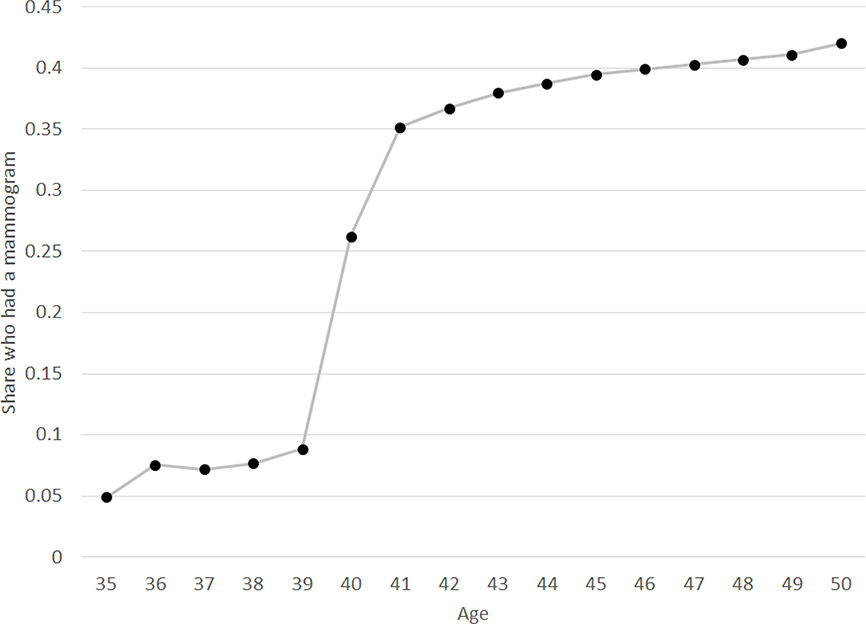
Figure 1 shows the age profile of annual mammogram rates in the HCCI data. Because we observe birth year, the mammogram rate at age, say, 40 is the share of women who got a mammogram in the year they turned 40. Between ages 39 and 41, the mammogram rate jumps by over 25 percentage points, from 8.9% to 35.2%. This pronounced jump in mammogram rates at age 40 has been previously documented in self-reported data (Kadiyala and Strumpf 2011, 2016).¹¹ One might be concerned that the existence of a recommendation for mammograms at age 40 could bias upward self-reports at that age. However, our analysis, which uses claims data, confirms a real change in mammogram behavior at 40. Indeed, as we show in Appendix Figure A.1, the increase in mammogram rates that we estimate at age 40 in the HCCI data is very similar to what we estimate using self-reported data (from the Behavioral Risk Factor Surveillance System Survey, or BRFSS), although—consistent with prior work (Blustein 1995; Cronin et al. 2009)—we estimate lower mammogram rates at every age in claims data compared to self-reported data.

Figure 1: Mammogram rates by age.

Figure shows share of women who had a mammogram by age, from insurance claims data on a set of privately insured woman-years from 2008–2012, for mammograms between 2009–2011. Because we observe birth year, age is measured as of the start of the calendar year. Thus the mammogram rate at age 40 is the share of women who got a mammogram in the year they turned 40. Error bars (small, and therefore not visible in the figure) reflect 95% confidence intervals. N = 7,373,302 woman-years.

We examine the outcomes of these mammograms—negative, false positive, and true positive—by age in the HCCI data. As shown in Appendix Figure A.2, the vast majority (85 to 90 percent) of mammograms are negative, and almost all of the remainder are false positives; spending is much higher for true positives than false positives and negatives.

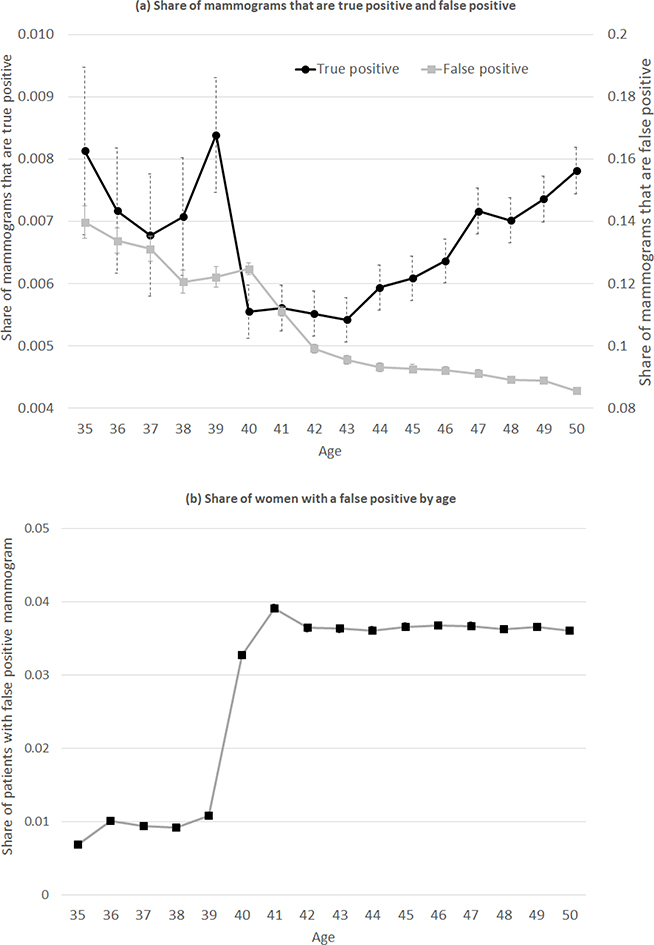
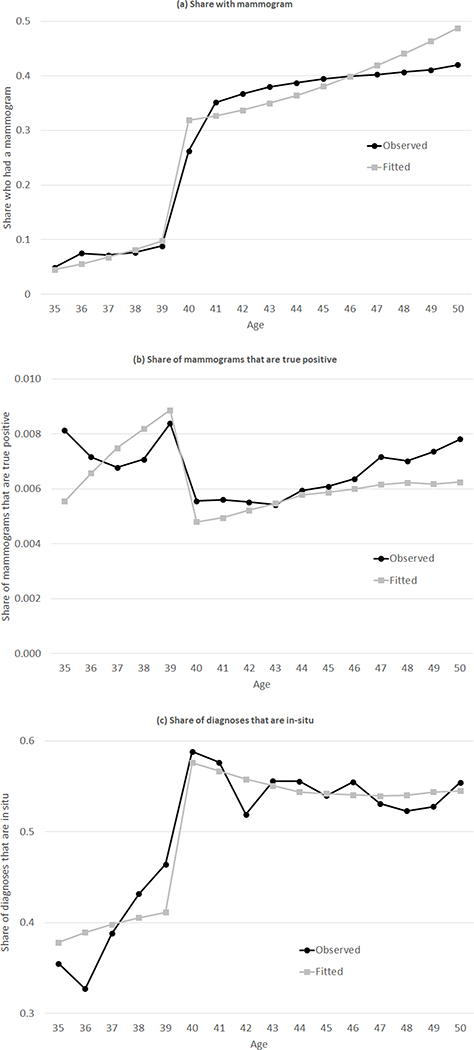
Figure 2a shows the share of mammograms that are true positive and false positive by age. Between ages 39 and 41, the share of true positives falls by one-third (from 0.84% to 0.56%). This indicates that the marginal women who choose to have a mammogram because of the screening recommendation at age 40 (i.e. “compliers”) have lower underlying rates of cancer (i.e. true positive diagnoses) than those who choose to get screened at younger ages before the recommendation kicks in (“always-takers”).

Figure 2: Mammogram outcomes by age.

Sample is limited to the set of privately insured woman-years from the private insurance claims data who had a mammogram. N = 7,373,302 woman-years. For each age (measured by the age at the beginning of the calendar year), panel (a) shows the share of mammograms that are true positive (left hand axis) and false positive (right hand axis); the omitted category is mammograms that are negative. Panel (b) presents the share of women with a false positive by age; this reflects both mammogram rates by age from Figure 1, and the share of mammograms with a false positive by age from panel (a). Error bars reflect 95% confidence intervals.

The share of mammograms that are false positive is generally declining smoothly in age because the probability of a false positive is higher for women with denser breast tissue, and density generally decreases with age (Susan G. Komen Foundation 2018). The exception is a small “spike” in false positives around age 40; this likely is attributable to the fact that the probability of a false positive mammogram is highest for a woman’s first mammogram (American Cancer Society 2017b). Note, however, that while the share of mammograms that are false positive is trending fairly smoothly in age, the share of women experiencing a false positive rises considerably at age 40, since there is a 25-percentage-point increase in the share of women who have a mammogram. This is shown in Figure 2b: the share of women experiencing a false positive mammogram quadruples at age 40, from about 10 to 40 per thousand women.

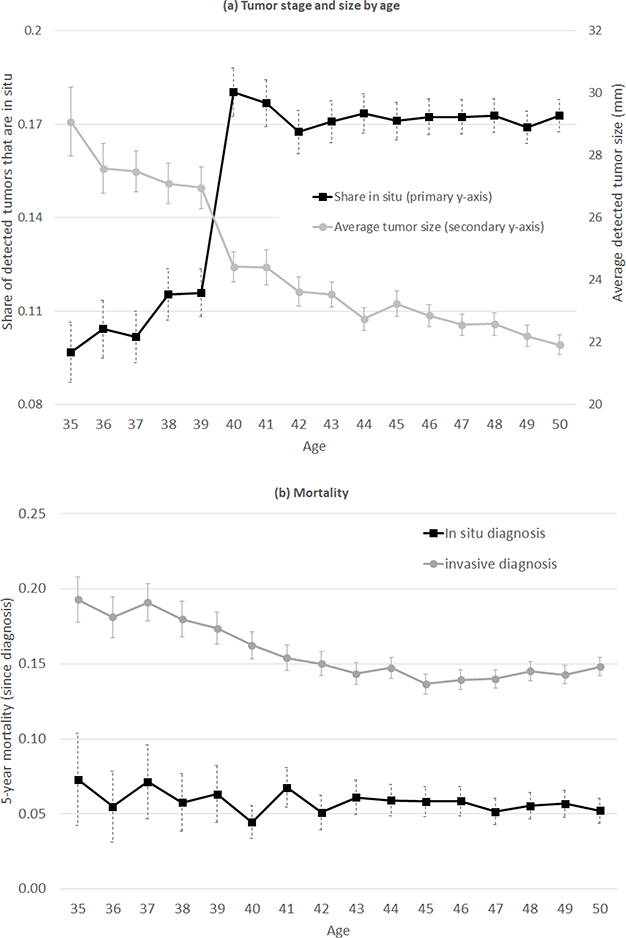
Figure 3a documents the age profile of tumor type among all diagnoses in the SEER data. Between ages 39 and 41, the share of detected tumors that are in-situ (as opposed to invasive) rises by 6 percentage points, from 11.6 percent to 17.9 percent; this is consistent with prior findings from Kadiyala and Strumpf (2016). The average size of a detected tumor falls by over 10 percent, from 27.3mm at age 39 to 24.4mm at age 41, although the pattern is less dramatic since detected tumor size is also falling (albeit less rapidly) at earlier ages.

Figure 3: Tumor characteristics and mortality by age.

Panel (a) shows diagnosed breast cancer tumors by age in the SEER data from 2000–2015; N =197,956 breast cancer diagnoses. Primary y-axis shows share of breast cancer tumors that are in-situ; secondary y-axis shows average size of diagnosed tumors. Panel (b) shows 5-year mortality for diagnosed breast cancer tumors separately by age of diagnoses and by tumor stage (in-situ and invasive) in the SEER data from 2000–2010 to account for five-year mortality outcomes by 2015; N = 147,243 diagnoses with non-missing 5-year mortality. Error bars reflect 95% confidence intervals.

Finally, Figure 3b documents 5-year mortality post-diagnosis in the SEER data by age of diagnosis, separately for tumors initially diagnosed as in-situ and invasive tumors. Mortality is almost three times higher for invasive tumors compared to in-situ tumors. For example, at age 40, the five-year mortality rate is 16.2% for invasive tumors compared to 4.5% for in-situ tumors. However, the mortality rate is roughly flat by age within tumor type.

C. Who responds to the recommendation?

The preceding descriptive results from both the HCCI and SEER data suggest that the women brought into screening by the recommendation at age 40 have a lower cancer disease burden than those who sought screening prior to the age-40 recommendation. This manifests in lower rates of cancer, detection of cancer at earlier stages, and smaller tumors conditional on cancer detection among compliers compared to always-takers.

Naturally, we are also interested in comparing compliers to never-takers: those who do not get screened even after the age-40 recommendation is in effect. Since the cancer status of women who do not get screened is inherently difficult (or impossible) to observe, we will draw on a clinical model of breast cancer incidence and progression to estimate the cancer profile of never-takers. Before turning to this exercise in the next section, we can use the available data to compare compliers and never-takers on various non-cancer characteristics.

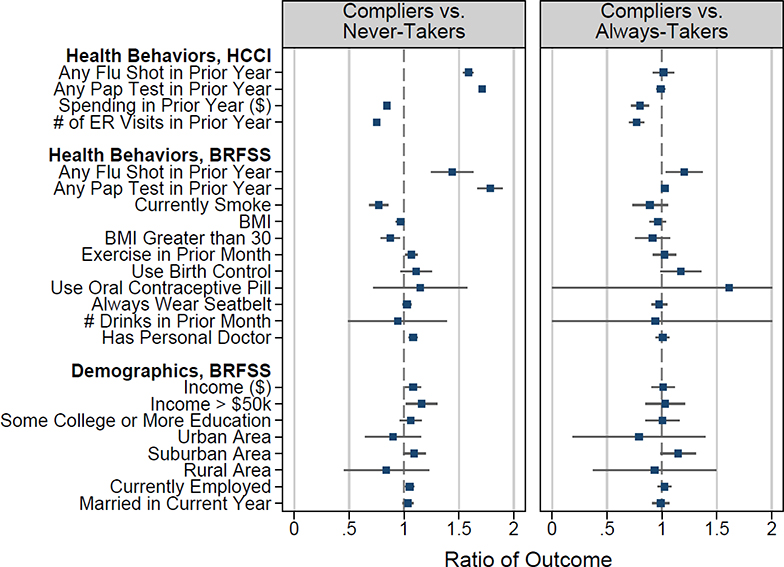
Specifically, we use the discrete onset of the recommendation at age 40 in a regression discontinuity framework to implement the Abadie (2002, 2003) approach to characterizing compliers and never-takers. Figure 4 shows the results. The left-hand panel compares various characteristics of compliers and never-takers; for completeness, the right-hand panel compares compliers to always-takers. The top panel examines preventive health behaviors and prior health care use in the HCCI data. The bottom two panels examine insured women in the BRFSS data; these data allows us to observe additional health behaviors and demographic characteristics. Appendix B contains more detail on the estimation approach and also shows the average characteristics of the population and the subset who receive a mammogram, by age.

Figure 4: Characteristics of who selects into mammograms.

Figure reports the ratio of health care use, behavior, and demographics for compliers relative to always-takers (left panel) and compliers relative to never-takers (right panel). The mean characteristics for these groups were calculated using regression coefficients from the estimation of equation (A.1) as described in Appendix B. Error bars represent 95% confidence intervals. Standard errors are constructed using a bootstrap with 100 repetitions clustered at the age level. The error bars for “Use Oral Contraceptive Pill” and “# Drinks in Prior Month” in the right panel are truncated at zero and two for scaling; the actual bootstrap confidence intervals are larger. The sample in the first section is a set of privately insured woman-years from HCCI from 2008–2012, for mammograms between 2009–2011. The sample in the second and third sections is from BRFSS for even years 2000–2012, restricted to women with any health insurance (the data do not distinguish between public or private insurance status). Details for each outcome are listed in Appendix Figures A.3, A.4, and A.5.

Overall, Figure 4 suggests that women who receive a mammogram as a result of the recommendation are more likely to comply with other recommended preventive care than women who do not get a mammogram even in the presence of the recommendation. In particular, both data sets indicate that compliers are more likely to get flu shots and Papanicolaou tests (also known as Pap tests, which are used to screen for cervical cancer) than never-takers. The HCCI data also indicate that compliers have lower health care spending and have fewer emergency room visits than never-takers. These results are consistent with Oster (2020)’s finding that when a health behavior is recommended, those who take it up also tend to exhibit other positive health behaviors. The results are also broadly consistent with related patterns reported by Kowalski (2019) in the context of selection into participation in clinical trials. Interestingly, however, we find no evidence of pronounced differences between compliers and never-takers on non-healthcare dimensions; they look similar on other health behaviors (such as seat belt use and alcohol consumption) as well as on basic demographics.

III. Model and estimation

The empirical patterns documented in the preceding section indicate that the women who respond to the mammogram recommendation have a lower incidence of cancer than those who seek mammograms in the absence of a recommendation. To evaluate the implications of this selection for alternative, counterfactual timings of the screening recommendation (such as at age 45 instead of age 40), we write down a stylized model of mammogram decision making. We then estimate this model using the observed patterns shown in Section II combined with a clinical oncology model of the underlying cancer incidence in the population and tumor evolution in the absence of detection. The clinical oncology model provides the (hitherto absent) crucial information on the cancer disease burden of women who respond to the mammogram recommendation compared to women who do not. Naturally, we explore sensitivity to alternative clinical assumptions.

A. A descriptive model of mammogram choice

Consider a woman i in a given year she is observed in the data.¹² We model the annual decision of whether or not to have a mammogram; annual decision frequency seems natural given that mammogram screening tends not to be done more frequently than once a year. Absent any recommendation to do so, we assume that the “organic” decision to have a mammogram follows a simple probit, so that

$$\mathrm{Pr}\left(m_i^o=1\right)=\mathrm{Pr}\left({\alpha }^o+{\gamma }^o{a}_i+{\delta }_{in-situ}^{o}I\left(c_i^{in-situ}\right)+{\delta }_{invasive}^{o}I\left(c_i^{invasive}\right)+{\epsilon }_i^o>0\right),$$ (1)

where $m_i^o$ is an indicator for whether woman i had a mammogram in that observed year, a_i is woman i’s age that year, $c_i=\{c_i^{in-situ},c_i^{invasive})$ describes woman i’s undiagnosed cancer status that year, and ${\epsilon }_i^o$ is a (standard) Normally distributed error term. Following our discussion in Section II, our baseline specification summarizes cancer status c_i with two indicator variables, one that indicates an in-situ tumor and another that indicates an invasive tumor; the omitted category is no cancer.

If it is recommended that woman i obtain a mammogram, we model her response to the recommendation as a second, subsequent decision that is taken within the same year. That is, if a woman has already decided to have a mammogram “organically” based on equation (1), a recommendation has no additional impact. But for women who decided not to have a mammogram organically (that is, $m_i^o=0$), a second decision point arises due to the recommendation, and we model this second decision point in a similar fashion, except that the parameters are allowed to be different:

$$\mathrm{Pr}\left(m_i^r=1|m_i^o=0\right)=\mathrm{Pr}\left({\alpha }^r+{\gamma }^r{a}_i+{\delta }_{in-situ}^{r}I\left(c_i^{in-situ}\right)+{\delta }_{invasive}^{r}I\left(c_i^{invasive}\right)+{\epsilon }_i^r>0\right),$$ (2)

where ${\epsilon }_i^r$ is a (standard) Normally distributed error term, drawn independently from ${\epsilon }_i^o$.¹³ This model assumes that the impact of the recommendation is (weakly) monotone for all women. For each woman, it only increases the probability that she has a mammogram, a feature that seems (to us) natural.¹⁴

Since we do not directly observe whether a mammogram was taken for organic reasons or in response to a recommendation, the probability that woman i obtains a mammogram in the year she is observed is given by

$$\mathrm{Pr}\left(m_i=1\right)=\{\begin{array}{cc}\mathrm{Pr}\left(m_i^o=1\right)& \text{if}\text{not}\text{recommended}\\ \mathrm{Pr}\left(m_i^o=1\right)+\mathrm{Pr}\left(m_i^r=1|m_i^o=0\right)\mathrm{Pr}\left(m_i^o=0\right)& \text{if}\text{recommended}\end{array}$$

We use the model’s results to quantify the degree of selection into mammograms in the presence and absence of a recommendation, and to examine how the nature of this selection affects the impact of recommendations. To do so, we use the model estimates to predict mammogram rates and mammogram outcomes under the current recommendation to begin mammograms at age 40 as well as under a counterfactual recommendation to begin at age 45. Consistent with our focus on selection, we also examine how alternative, counterfactual selection into mammograms in response to the recommendation would change the impact of changing the recommended age of beginning mammography from 40 to 45.

Discussion.

Importantly, this is a descriptive, or statistical model of mammogram choice, rather than a behavioral one. This is most apparent from the fact that we use the cancer status c_i as an explanatory variable, when naturally this cancer status is unknown by undiagnosed women. Cancer status c_i is also unobserved by the econometrician; we describe below the clinical model of tumor evolution which we use to “fill in” these missing data, thus essentially integrating over the population distribution of this cancer status component.

We take this modeling approach for several reasons. First, many of the outcomes in this setting are difficult to assess or monetize, e.g. the stress and anxiety associated with false-positive test results or the non-monetary costs associated with the breast cancer treatment (even if successful). This makes it difficult to translate the rich set of outcomes into a single metric of utility. Second, our key focus is on the impact of the recommendation policy. With a perfectly informed population of women, recommendations should have no impact, yet the data in Section II show a clear increase in the mammogram rate in response to the age 40 recommendation. We could try to attribute this recommendation-induced increase in mammogram rate to improved information, but this would require us to make assumptions about what type of information is being revealed and how, or why women did not have such information to begin with. We prefer instead to remain agnostic about the behavioral channel by which the recommendation affects screening rates. Finally, a descriptive model of decision making does not require us to try to reconcile observed patterns of decisions with optimal behavior, or model deviations from optimality. The drawback is, of course, that we will not be able to engage with other policy changes or with the impact of changes in the recommendation policy on individual welfare directly, but rather will only evaluate changes in recommendation policies through their effect on observed outcomes.

Another key feature of our setup is that we model the mammogram decision to be a static—and perhaps naive—one. The decision is static in the sense that we assume that women do not take into account, for example, the time elapsed since their most recent mammogram (if any).¹⁵ The decision is naive in the sense that we assume that women, when deciding to get a mammogram or not, do not explicitly take into account their propensity to get a mammogram in future years. This assumption seems not unrealistic, and simplifies the model. This assumption is particularly important in the context of our counterfactual exercise, which holds the estimated model as given while we change the age at which it is recommended to begin mammography. Specifically, in considering the changes that occur when the mammogram recommendation begins at age 45 instead of 40, our static model assumes that this would have no impact on women aged 39 or younger. In a dynamic model with forward-looking agents, however, it could increase the propensity of women under age 40 to get a mammogram. Our current model could in principle capture such dynamics implicitly by allowing serial correlation in ${\epsilon }_i^o$ and in ${\epsilon }_i^r$. However, because we have a relatively short panel, and because we only use age to match the two main data sets, it would be hard to identify such a serial correlation structure. Consistent with this being a fairly inconsequential assumption, Figure 2 shows very low rates of pre-recommendation mammograms, and no evidence that mammogram rates decline in the year or two that are right before age 40 (when forward-looking women might anticipate their future mammogram).

B. Implementation

A clinical model of tumor appearance and evolution.

To complete the empirical specification, we specify a clinical oncology model of tumor appearance and tumor evolution. The oncology model has two important roles in our analysis, one for estimation and another for our counterfactual exercises. For estimation, the key role of the oncology model is that it allows us to “impute” cancer status for the “never-takers,” i.e., the women who do not get screened even when it is recommended. This clinical model delivers two key elements. First, it produces the underlying incidence of cancer (and cancer type) by age. This cannot be directly observed in data since cancer incidence is only observed conditional on screening. Intuitively, since we observe the rate of cancer among those who get screened and the share of women who get screened, then, with the estimate of the overall rate of cancer from the clinical model, we can deduce the rate of cancer in the unscreened population. Second, the clinical model provides (counterfactual) predictions for the rate at which tumors would progress in the absence of detection and treatment (the so-called “natural history” of the tumor). Since breast cancer is usually treated once diagnosed, rather than being monitored without treatment, it is difficult (perhaps impossible) to directly estimate the natural history of tumors from existing data. This latter element is particularly important for our counterfactual exercises, in which the effect of different selection patterns depends on the share of cancer cases that get diagnosed, as well as how early tumors are found. In order to assess how clinically important early diagnosis is (e.g., in its effect on mortality), a model of tumor evolution is needed.

For the clinical model, we draw on an active literature creating clinical/biological models of cancer arrival and growth. Specifically, we draw on the work of the Cancer Intervention and Surveillance Modeling Network (CISNET) project funded by the National Cancer Institute to analyze the role of mammography in contributing to breast cancer mortality reductions over the last quarter of the 20th century. As part of this effort, seven different groups¹⁶ developed models of breast cancer incidence and progression (Clarke et al. 2006). For convenience, we focus on one of these models, the Erasmus model (Tan et al. 2006). As we discuss below, we also confirm that our main results are not sensitive to alternative specifications designed to produce markedly different estimates for the key objects (the underlying incidence of cancer and cancer types).

We briefly summarize the Erasmus model here; Appendix C describes the model in much more detail. Starting with a cancer-free population of 20-year-old women, the Erasmus model assumes that breast tumors appear at a given age-specific rate (that is increasing in age). When they appear, tumors are endowed with a given invasive potential and initial rate of growth, and then evolve accordingly over time with respect to those two characteristics. Tumors can either be invasive, leading to death of the women if not detected early enough, or be in-situ. In-situ tumors are not themselves harmful but may either transform into a harmful invasive tumor or remain benign. In some sense, a key issue in the debate over mammograms is the extent to which tumors that are detected early (e.g. in-situ tumors) would have become harmful if not detected or would have remained benign; Marmot et al. (2013) discusses how, depending on the method of analysis, a wide variety of estimates can be obtained when trying to answer this question. The Erasmus model further classifies tumors by whether or not they are detectable by screening, which in the case of invasive tumors depends on their size and in the case of in-situ tumors depends on their sub-type. Finally, the model assumes that beyond a certain size, invasive tumors are fatal.

The original Erasmus model was calibrated using a combination of Swedish trial data and US (SEER) population data. To better match the cancer incidence rates in the SEER data (birth cohorts 1950–1975), we introduce a proportional shifter of overall cancer incidence and calibrate this parameter on the SEER data. Appendix Figure A.6 shows the calibrated model’s predictions—under the assumption of no screening—of the share of women with cancer at each age, and the share of existing cancers that are in-situ (rather than invasive) by age.

Estimation and identification.

We estimate the model using method of moments. The observed moments we try to match are the mammogram screening rate at each age (Figure 1), the true positive rate at each age (Figure 2a), and the share of tumors at each age that are in-situ conditional on true positive (as in Figure 3a).¹⁷ Because identification is primarily driven by the discontinuous change in screening rates at age 40, we weight more heavily moments that are closer to age 40 than moments that are associated with younger and older ages.¹⁸

To generate the corresponding model-generated moments, we simulate a panel of women starting at age 20, and use the clinical model described above to generate cancer incidence and tumor growth for each woman. We then apply our mammogram decision model, by age and recommendation status, to each simulated woman who is alive and has yet to be diagnosed with cancer. The simulated cohort allows us to see the fraction of women with a detectable (by mammogram) tumor at each age, and thus generate the mammogram rate, and the true positive rate (by cancer type) conditional on screening. As mentioned above, for cancer type, we distinguish only between in-situ and invasive tumors.

With this simulated population of women, an assumed value of parameters associated with the mammogram decisions with and without recommendation (equations (1) and (2)) and the observed policy recommendation (40 and above), the model generates an age-specific share of women who are screened, and the tumor characteristics (in-situ and invasive rates), conditional on getting screened. We then search for the parameters that minimize the (weighted) distance between these generated moments and the observed moments described above.

Although the model is static, it does have a dynamic element because we calculate the model-generated moments only for women who were not diagnosed with cancer in previous years, and for those who did not die (from breast cancer or other causes) prior to the given age. Specifically, because the mammogram decision applies to women who have yet to be diagnosed with cancer, fitting the model requires calculating the rate of cancer among the population who is eligible to be screened, which includes those who have currently undiagnosed cancer or no cancer, but does not include those who are dead or already diagnosed. Appendix D provides more detail on this and other aspects of the estimation.

For our counterfactual exercises, the estimates from the mammogram choice model—and the assumption that choices would be smooth in age through age 40 in the absence of the recommendation—allow us to predict mammogram decisions and outcomes under counterfactual scenarios. Crucially, the model estimates allow us to forecast the cancer characteristics of women who (counterfactually) do not get screened and whose cancer may therefore progress in the absence of diagnosis. The key parameters are δ^o and δ^r, which capture the nature of selection into mammogram screening. Positive selection (i.e. positive δ) implies that women with cancer (or with invasive vs. in-situ cancer) are more likely to get a mammogram than are woman without cancer. A negative δ implies the opposite. Both types of selection are plausible. Positive selection could arise, for example, if women with a greater risk of breast cancer (e.g. due to family history) are more likely to get a mammogram; negative selection could arise, for example, if women with certain underlying characteristics (e.g. risk aversion) are both more likely to get a mammogram and also more likely to avoid risk factors linked to breast cancer. Importantly, by allowing δ^o and δ^r to be different, the model allows for the nature of selection to be different for organic and recommendation-driven mammograms. Identification of these selection effects is driven by comparing the share of cancer in the population (which is data provided by the clinical oncology model) to the true positive mammogram rates. The extent to which this relationship changes discretely at age 40, when the recommendation kicks in, allows us to separately identify δ^o and δ^r.

IV. The impact of alternative screening policies

A. Model fit and parameter estimates

Figure 5 presents the model fit to the key moments, which we view as quite reasonable. The parameter estimates are shown in Table 2. It may be easiest to see the implications of these parameters in the context of our counterfactual results, but one can already infer the general pattern by focusing on the four δ parameters, which indicate the extent of selection into mammogram. The two δ^o parameters are positive and relatively large, indicating strong positive selection into the “organic” decision to have a mammogram. For example, for the average woman-year in the sample (that is, using the distribution of ages in the sample), the estimated coefficients imply that the “organic” mammogram rates for women with either an in-situ or invasive tumor are much higher (0.30 and 0.57, respectively) relative to the “organic” mammogram rates for cancer-free women (0.20).

Figure 5: Model fit.

Figure shows model fit by comparing the observed patterns of mammogram rates, outcomes, and types of diagnoses by age to the fitted values from the model based on the parameter estimates from Table 2. The observed data on mammograms (Panel (a)) was previously shown in Figure 1; the observed data on share of mammograms that are true positives was previously shown in Figure 2a; the observed data on the share of diagnoses that are in-situ is a modified version of the data shown in Figure 3a. While Figure 3a presented the share of all diagnosed cancers that are in-situ, we match the share of mammogram-diagnosed cancers that are in-situ, as shown in Panel (c). Appendix D provides more detail.

Table 2:

Parameter estimates

Parameter	Estimate	95% Confidence Interval
αo	−5.21	[−5.63, −4.48]
γo	0.10	[0.08, 0.11]
δoin-situ	0.36	[0.29, 0.97]
δoinvasive	1.13	[0.98,56.73]
αr	0.29	[−0.63, 1.18]
γr	−0.03	[−0.05, 0.00]
δrin-situ	−0.01	[−0.20, 0.77]
δrinvasive	−4.67	[−143, −0.01]

Table shows the parameter estimates from the mammogram decision model. Confidence intervals are calculated using 100 repetitions of the bootstrap.

In contrast, the two δ^r parameters tell a different story. The estimates suggest that there is no differential selection into the “recommended” decision for women with in-situ tumors (relative to cancer-free women), and that essentially no woman with an invasive tumor selects into mammogram due to the recommendation. This result is driven by precisely the patterns in the data that identify these parameters, and which were presented in Figure 3a. Namely, conditional on diagnosis, the share of in-situ tumors rises sharply at age 40, so that virtually all the increase in detected cancers reflects in-situ tumors. As we show below, this pattern has a critical effect on our results, because women without cancer or with in-situ tumors—who constitute the primary incremental positive mammogram results may not face drastic health implications if those tumors would instead be discovered several years later.

We note that the large confidence intervals on ${\delta }_{invasive}^o$ and ${\delta }_{invasive}^r$ reflect the fact that the estimates imply that virtually all women with invasive tumors who get screened do so organically, with essentially no women with invasive tumors getting screened in response to the recommendation; as a result, the likelihood function is fairly at for high values of ${\delta }_{invasive}^o$ and low values of ${\delta }_{invasive}^r$. But for exactly the same reason, these imprecise estimates of the parameter have little impact on the counterfactual results, as reflected by the much tighter standard errors associated with the counterfactuals of interest reported in the next section.

B. Implications

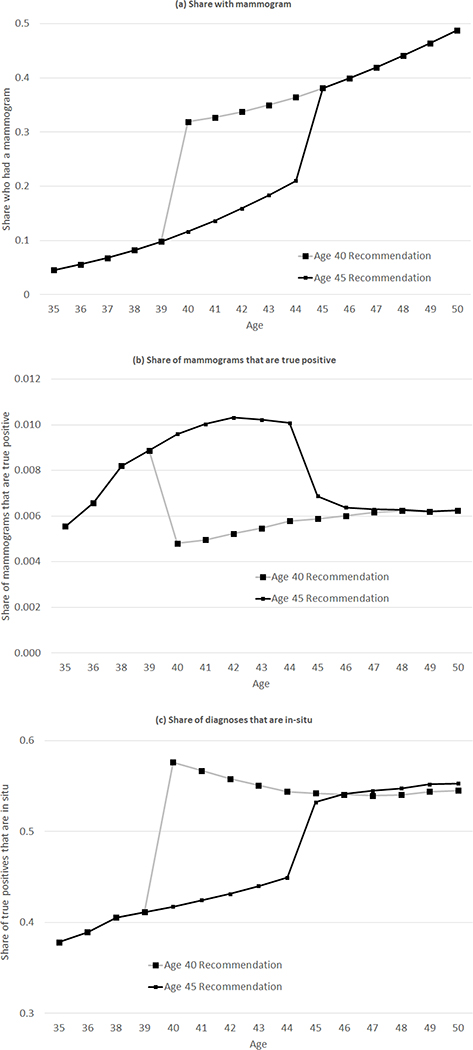
We apply the estimated parameters from Table 2 to analyze outcomes under various counterfactual recommendations. For concreteness, we focus on outcomes under the current recommendation to begin mammograms at age 40 as well as under a counterfactual recommendation to begin at age 45. Our model is well suited for such a counterfactual exercise: we simply assume that mammogram decisions are based on the “organic” decision until age 45, and only at age 45 is there a second, recommendation-induced decision. Given the static nature of the model, mammogram rates will remain the same until age 40, and would be the same (conditional on cancer status) from age 45 and on, but will decrease for women aged 40–44 without a recommendation. We choose a counterfactual recommendation that begins at age 45 because this is not too far out of sample, and also in the range of realistic policy alternatives; Canada, for instance, recommends routine screening beginning at age 50 (Kadiyala and Strumpf 2011). Of course, such counterfactuals do require us to rely on our assumption of a linear age profile in order to predict outcomes for always-takers beyond age 40 in a counterfactual world in which the recommendation does not occur until age 45; while this strikes us as not unreasonable, given that the linear specification in age seems to fit the data well, it is of course an important (and untestable) assumption.

For both the age 40 and age 45 recommendations, we also examine how alternative, counterfactual selection into mammograms in response to the recommendation would change the recommendation’s impact. The main outcomes we generate under the various counterfactuals are age-specific mammogram rates, mammogram outcomes (specifically, negative, false positive, and true positive, as well as tumor type), total health care spending, and mortality. We do not attempt to quantify other potential consequences of a change in recommendation (such as the opportunity to use less invasive treatments for early-stage diagnoses, or increased anxiety from false positive results, which are more uncertain (Welch and Passow 2014)).

Throughout the counterfactual exercises, mammogram rates are generated directly from the parameter estimates in Table 2, and mammogram outcomes are generated based on the parameter estimates in Table 2 and the underlying incidence and natural history of breast cancer tumors from the Erasmus model. We also use the Erasmus model’s parameters in order to map detection of tumors to subsequent mortality, allowing us to translate the estimated changes in detection into implied changes in mortality. Finally, we use the auxiliary data from Figure A.2b on how health care spending varies with age and mammogram outcomes to translate the estimated change in mammogram rates and mammogram outcomes into implied spending changes. Appendix E provides more details behind these counterfactual calculations.

Shifting the age of recommendation from 40 to 45.

Table 3 shows the implications of shifting the recommendation from age 40 to age 45, given the estimated response to recommendations from Table 2. We focus on the implications for women ages 35–50.

Table 3:

Impact of changing the mammogram recommendation age from 40 to 45

	Rec at Age 40	Rec at Age 45	Change
A. Screening and spending (per woman)
Mammograms	4.70 (0.06)	3.80 (0.14)	−0.90 (0.08)
Negative	4.22 (0.05)	3.42 (0.12)	−0.81 (0.07)
False positives	0.46 (0.01)	0.36 (0.02)	−0.09 (0.01)
True positives	0.0208 (0.0024)	0.0204 (0.0024)	−0.0004 (0.0001)
In-situ diagnoses	0.0063 (0.0005)	0.0060 (0.0005)	−0.0004 (0.0001)
Invasive diagnoses	0.0145 (0.0019)	0.0145 (0.0019)	0.0000 (0.0001)
Total health care spending ($)	71,326 (128)	71,007 (155)	−319 (29)
B. Mortality (per 1,000 women by age 50)
Dead	15.98 (0.53)	16.03 (0.53)	0.05 (0.03)
Dead from breast cancer	8.23 (0.53)	8.28 (0.53)	0.05 (0.03)
Dead from other reason	7.75 (0.00)	7.75 (0.00)	0.00 (0.00)
Years alive, per woman	15.87 (0.00)	15.87 (0.00)	−0.0002 (0.0001)

Table reports model predictions for various outcomes under the status quo recommendation that mammograms begin at age 40 (column 1) and the counterfactual recommendation that mammograms begin at age 45 (column 2). The predictions are generated using the parameter estimates from Table 2, and simulated women’s life histories under a non-screening regime based on the clinical oncology model. Panel A reports the average number of mammograms and different mammogram outcomes per woman over ages 35–50. Panel B shows the share of women dead (and from different causes) by age 50, as well as the number of years alive on average between 35 and 50. Standard errors are calculated using 100 repetitions of the bootstrap.

Panel A summarizes the implications for screening and spending; Figure 6 shows how the age profile of screening and screening outcomes change with this counterfactual. Changing the recommended age from 40 to 45 reduces the average number of mammograms a woman receives between ages 35 and 50 from 4.7 to 3.8, an almost 20 percent decline. By design, all of the “lost” mammograms occur between ages 40 and 44. Naturally, the vast majority of these “lost” mammograms would have been negative (89.5%) or false positive (10.4%). Moving the recommendation to age 45 decreases the average number of false positives a woman experiences over ages 30–45 by 0.09. The fraction of true positive mammograms that are “lost” due to the later recommendation, while small in absolute number (0.0004 per woman), is not negligible, and it constitutes an approximately 6% reduction in the cancer detection rate. Of the “lost” true positives, however, all are in-situ since our estimates imply that the recommendation effectively induces no additional women with invasive cancer to get screened. Thus, any changes in mortality are due to in-situ tumors that go unscreened and later become invasive.

Figure 6: Impact of changing the mammogram recommendation age from 40 to 45, by age.

Figure reports the model predictions - by age - for mammogram rates, mammogram outcomes, and the share of diagnoses that are in-situ, based on the parameter estimates from Table 2. As in Table 3, we report the model predictions both under the status quo recommendation that mammograms begin at age 40 and the counterfactual recommendation that mammograms begin at age 45.

The last row of Panel A shows that changing the recommendation age to 45 reduces total health care spending over ages 35–50 per woman by about $320, or about half a percent. This reduction in spending arises from a combination of a level and composition effect. The dominant factor is naturally the decline in the overall number of mammograms. We estimate that women who have a mammogram in a given year are expected to spend approximately $570 more (on average, averaging over ages 40–44) over the subsequent 12 months relative to women with no mammograms, and that moving the recommendation age to 45 results in 0.9 fewer mammograms per woman. This would mechanically result in approximately $510 lower spending. The estimated spending reduction is lower ($320) because of selection. The “lost” mammograms are disproportionately negative or false positive, and the true positive mammogram results are associated with, by far, the highest expected subsequent spending (see Figure A.2b). True-positive mammograms account for a larger share of mammograms in the counterfactual scenario (0.53%, relative to 0.44% under the age-40 recommendation).

Panel B documents the implications of this counterfactual for health outcomes. The lower detection rate of cancers is associated with 5 more women per 100,000 who are dead by the age of 50; all of this increase in deaths comes from increased breast cancer mortality. The results thus suggest that, relative to an age-45 recommendation, an age-40 recommendation increases spending by about $32 million per 100,000 women (during the ages of 35–50), and prevents about 5 additional deaths by age 50 per 100,000 women; the cost per life saved is thus about $6 million.

Naturally, these mortality implications are driven by the assumptions in the clinical oncology model, about which there is a range of views (Clarke et al. 2006; Welch and Passow 2014). In addition, our analysis considers only the costs in terms of health care spending, and does not consider the disutility of stress and anxiety created by false positives or additional medical care. For both reasons, our goal here is not to emphasize a specific estimate of the cost per life saved per se, but rather to examine whether and how this type of counterfactual policy exercise can be affected by the nature of selection into mammograms in response to the recommendation, a question we turn to in the next section.

Consequences of selection patterns in response to mammogram.

Table 4 illustrates the importance of selection in response to the recommendation. To do so, Panel A replicates the results from Table 3, while Panels B and C contrast them with what the results would be under alternative selection responses to the recommendation. Under both alternative selection models, we maintain our estimated selection associated with the “organic” mammogram decision, but vary the nature of selection into mammograms in response to the recommendation. One case (Panel B) assumes no selection, which is conceptually consistent with the idea of using estimated mammogram treatment effects from randomized experiments to inform the recommendation policy (as in, for example, Welch and Passow 2014); in practice we do this by assuming that δ^r = 0.¹⁹ The other case (Panel C) assumes that selection in response to the recommendation is positive, and is the same as in the organic decision; we implement this counterfactual by assuming that δ^r is equal to our estimated δ^o.

Table 4:

Spending differences for different components of spending

	Recommendation at		Difference
	Age 40	Age 45
A. Estimated Selection
Mammograms (per woman)	4.70 (0.06)	3.80 (0.14)	−0.90 (0.08)
Total health care spending ($ per woman)	71,326 (128)	71,007 (155)	−319 (29)
Dead by age 50 (per 1,000 women)	15.98 (0.53)	16.03 (0.53)	0.05 (0.03)
B. No Selection
Mammograms (per woman)	4.70 (0.06)	3.80 (0.14)	−0.90 (0.08)
Total health care spending ($ per woman)	71,364 (111)	71,024 (147)	−340 (37)
Dead by age 50 (per 1,000 women)	15.84 (0.47)	16.02 (0.53)	0.18 (0.06)
C. Consistent Selection
Mammograms (per woman)	4.70 (0.06)	3.80 (0.14)	−0.90 (0.08)
Total health care spending ($ per woman)	71,450 (87)	71,068 (134)	−382 (48)
Dead by age 50 (per 1,000 women)	15.54 (0.39)	15.99 (0.52)	0.45 (0.13)

Table reports model predictions under the status quo recommendation that mammograms begin at age 40 (column 1) and the counterfactual recommendation that mammograms begin at age 45 (column 2). Each panel reports results under different assumptions about the nature of selection both in the absence and presence of a recommendation. Panel A reports results based on the estimated selection patterns; these results repeat findings shown previously in Table 3. Panel B repeats the same exercises as in Panel A, but instead of using the estimated selection (i.e. the δ^o and δ^r parameters shown in Table 2), we instead assume “no selection” (i.e. we set δ^o = δ^r = 0). Panel C also repeats the exercises in Panel A but now assumes “consistent selection” (i.e. we set δ^r equal to our estimates of δ^o in Table 2). In both Panel B and C, we hold the overall mammogram rate fixed at Panel A’s predicted age-specific mammogram rates (which of course varies in column 1 and column 2), so that the counterfactuals across panels consider differences in selection, not in levels. To do this we adjust the intercept α_r for each age and counterfactual to match the age-specific mammogram rates in Panel A, assuming the simulated life histories and cancer status remains constant. The small differences in mammograms in Panel A and Panel C are due to changes in the denominator of simulated life histories. Specifically, since fewer women die in Panel C, there are more years where they could potentially obtain a mammogram. Standard errors are calculated using 100 repetitions of the bootstrap.

In both counterfactual selection cases we consider, we adjust the model to maintain the same age-specific mammogram rates under a given recommendation regardless of the assumed selection, so that only the nature of selection changes; Appendix E provides more detail. By design, therefore, the mammogram rates (first row of each panel) remain almost the same across all three selection models,²⁰ and therefore the spending effect associated with each of these cases also remains almost identical (second row of each panel). In contrast, the importance of selection is shown in the third row of each panel: different patterns of selection affect the reduction in deaths from moving the recommendation to age 40 compared to age 45. For example, while our estimates that are based on observed selection imply that moving the recommendation from 45 to 40 saves 5 additional lives (by age 50) per 100,000 women, which corresponds to a cost of about $6.3 million per life saved, random selection would imply over three times as many lives saved (18 per 100,000), corresponding to a cost of about $1.9 million per life saved. At a more extreme case of selection, assuming that the strong positive selection associated with “organic” selection would also apply to the selection in response to the recommendation, would imply almost nine times as many lives saved (45 per 100,000 women), corresponding to a cost per life saved of about $0.86 million.

The qualitative results are intuitive. As selection associated with the recommendation is more negative (i.e. women who respond are less likely to have cancer), the recommendation for earlier mammograms is less effective in finding tumors that would have not been found otherwise or tumors that would otherwise be found only later. However, if the selection associated with the recommendation were very positive (i.e. women who respond are more likely to have cancer), an earlier recommendation would be more effective. Thus, out of the three selection scenarios considered, earlier recommendation is most beneficial if the selection response to the recommendation is the same as under organic selection, which was highly positive (Panel C). While it is not immediately clear how in practice to achieve such strong positive selection in response to the recommendation, this result suggests that better targeting of the recommended mammogram to women with higher a-priori risk of cancer could—if feasible—have dramatic effects on the mortality benefits from the recommendation.²¹ The comparison between our estimated selection (panel A) and the “no selection” case (panel B) is an intermediate case. Because we estimate negative selection for invasive tumors, an earlier recommendation is more effective (i.e. more women with cancer would be screened) under random selection, and the cost per life saved is therefore lower.

Sensitivity.

The data allow us to estimate characteristics of always-takers and compliers, and to see that compliers have a lower incidence of cancer than always-takers (see Figures 2a and 3a). However, our counterfactuals require us to also estimate the cancer status of never-takers, as well as how cancer would evolve if (counterfactually) screening occurred at a later age. For both of these endeavors, we relied heavily on the underlying natural history (“clinical”) model of breast cancer. We therefore examine the sensitivity of our conclusions to changing key features of this model, such as the underlying incidence rate of cancer, the share of in-situ tumors that will become invasive if not treated, and the share of tumors that are non-malignant, i.e. have no potential to be invasive and therefore would never result in a breast cancer mortality.

This sensitivity analysis serves to highlight a point we have tried to emphasize throughout: the reader should not place much (or any) weight on our particular, quantitative estimates of the cost per life saved of recommending that mammography begin at 40 instead of at 45; these are quite sensitive to the assumptions underlying the clinical model. By contrast, the qualitative result we focus on—how the nature of the selection response to the recommendation affects any estimate of the impact of an earlier recommendation—is quite robust to alternative assumptions in the underlying clinical model. Appendix F discusses the specifics of how we implement the sensitivity analysis and presents the results in detail.

V. Summary and possible policy implications

The debate over whether and when to recommend screening for a particular disease involves a host of empirical and conceptual challenges with which the existing literature has grappled, including how to estimate the “health” return to early screening, how to measure non-health benefits or costs, and how to monetize all of these factors (Humphrey et al. 2002; Nelson et al. 2009; Marmot et al. 2013; Welch and Passow 2014; Ong and Mandl 2015). We make no pretense of “resolving” these issues. Instead, we suggest an additional important and largely overlooked factor that can—and should—be considered: the nature of selection in response to the recommendation.

We illustrate this point in the specific context of the (controversial) recommendation that women should begin regular mammogram screenings at age 40. We document that this recommendation is associated with a sharp (25 percentage point) increase in mammogram rates, and that those who respond to the recommendation have substantially lower rates of cancer incidence than those who choose to get mammograms in the absence of the recommendation (i.e. before age 40). Conditional on having cancer, women who respond to the recommendation also have lower rates of the more lethal invasive cancer, relative to the less lethal in-situ cancer. These data speak directly to the relative cancer risks of women who select mammograms in the absence and presence of a recommendation. To further assess how the cancer risk of those who select mammograms when recommended compares to those who do not select mammograms even when recommended, we draw on a clinical oncology model to estimate the underlying cancer incidence in the non-screened population (since this is not directly observed). These results suggest that those who choose mammograms in the absence of a recommendation have substantially higher rates of both invasive and in-situ cancer than women who do not get screened; women who choose mammograms in response to the recommendation have similar rates of in-situ cancer to unscreened women but much lower rates of invasive cancer than unscreened women.

To illustrate the potential consequences of these selection responses to recommendations, we write down a stylized model of the mammogram decision, which depends on age, cancer status, and recommendation. We estimate this model using the observed empirical patterns combined with the clinical oncology model, the latter of which provides both the underlying incidence of cancer and the (counterfactual) tumor evolution in the absence of detection. We then apply the model to assess the implications for spending and mortality of changing the recommended age for beginning mammograms from 40 to 45. The specific numbers that we estimate will naturally be sensitive to the modeling assumptions; moreover, our estimates do not attempt to measure all of the the potential impacts of mammograms, such as stress.

Our focus instead is on the consequences of the selection response to the recommendation, which our estimates suggest are non-trivial. Specifically, we consider the impact of moving the recommended age of beginning mammography from 45 to 40, and how this varies under alternative selection responses to the recommendation. We hold the change in mammogram rates (and consequently the cost increase) from changing the recommended age constant, and show that the mortality implications from earlier recommended mammograms vary markedly with selection patterns. For example, under the observed selection pattern, the number of lives saved by moving the recommendation from age 45 to 40 is less than a third of what it would be if those who responded to the recommendation were instead drawn at random from the population. This difference arises because we estimate that those who respond to the recommendation have much lower rates of invasive cancer. Conversely, our results also suggest that if it were feasible to target the recommendations to those with higher rates of cancer, shifting the recommendation from age 45 to 40 would save substantially more lives than either the observed selection patterns or random selection.

These findings suggest that the ongoing debates over whether and when to recommend screening for a disease should consider not only average costs and benefits from screening, but also the nature of selection associated with those who respond to the recommendation. They also suggest that future work exploring the impact of existing policy instruments or the design of potential new ones should consider not just aggregate impacts on mammography rates, but also the cancer incidence for compliers.

While our empirical focus has been on recommendations, these are of course only one part of a broader set of policy efforts that have been deployed or discussed for increasing disease screening. In the case of mammograms, another widely-used instrument has been lowering the financial costs of screenings. For example, in 1991 the federal government launched the National Breast and Cervical Cancer Early Detection Program to provide free screenings to women below 250 percent of the federal poverty line (Lee et al. 2014). In the same year, Medicare expanded its coverage to include bi-annual screening mammograms; subsequently, in 1998, Medicare expanded coverage further to include annual screening mammograms and to waive the deductible (O’Sullivan et al. 1997; Kelaher and Stellman 2000; Habermann et al. 2007). On the private insurance side, a number of states have mandated that insurance plans must cover mammography (Bitler and Carpenter 2016). Beyond these financial levers, there are also policy efforts to reduce non-financial barriers to mammograms. These include, for example, increasing ease of access to mammograms through programs such as mobile mammography clinics (Vang, Margolies, and Jandorf 2018), and outreach efforts designed to educate women about the benefits of mammograms and informing them of the services available to them (Levano et al. 2014).

Related to these efforts, an existing literature has studied the impact of various policy instruments on mammography rates. It has found, for example, that lowering out-of-pocket financial costs increases mammogram rates (Kelaher and Stellman 2000; Habermann et al. 2007; Finkelstein et al. 2012; Fedewa et al. 2015; Mehta et al. 2015; Bitler and Carpenter 2016; Cooper et al. 2017; Kim and Lee 2017), while increasing the distance a woman must travel to get a mammogram decreases mammogram rates (Lu and Slusky 2016). Only a few of these studies have examined differential responses to the policy by underlying health characteristics. This existing work suggests that, like our findings on the response to guidelines, those who get mammograms in response to a lower price and those who comply with assignment to mammogram treatment in a clinical trial tend to be healthier than never-takers and always-takers (Bitler and Carpenter 2016; Kim and Lee 2017; Kowalski 2019). While one of course must be careful in generalizing too much from a few studies, our read of this existing literature is that these alternative interventions are not obviously better targeted than recommendations in terms of the compliers, at least in the context of mammograms.

The combined evidence therefore highlights the importance of trying to better target the existing instruments. This is challenging since underlying cancer incidence, tumor stage, and tumor size are not observable without screening. However, our descriptive analyses in Section II—comparing compliers to never-takers on a host of observable characteristics—suggest that never-takers are also less likely than compliers to engage in other recommended health behaviors, such as flu shots and Pap tests. This finding is consistent with the idea that those who comply with recommendations tend to exhibit other positive health behaviors (Oster 2020). It also suggests that coordinated efforts, which attempt to draw in women who otherwise would not engage in any preventive health behaviors, could be high-value. If we are willing to extrapolate our qualitative results from breast cancer to these related contexts, our findings suggest that trying to get such women to undertake a slew of recommended health behaviors might be well-targeted at reaching women at higher risk of not only breast cancer, but perhaps also cervical cancer and the flu.

Recent analyses by clinical researchers also suggest other observables that might be useful in targeting mammograms to higher-risk groups, instead of (or in conjunction with) age-based screening recommendations. For example, Evans et al. (2019) describe the results of a randomized trial that begins regular mammograms at age 34 for women with a mother or sister who has been diagnosed with breast cancer, and an ongoing trial is investigating the impact of risk-based screening relative to standard annual screening (Esserman et al. 2017). Motivated by such work, researchers have proposed that the recommended age of beginning mammography should be based on individual risk factors such as age of first birth, number of children, and breast density (Evans, Howell, and Howell 2020; Mukama et al. 2020). Our findings underscore the potential value of such targeting, given that compliance with the existing recommendation is only about one-third, and compliers appear to be disproportionately low-risk for cancer. They also suggest the importance of analyzing the impact of targeted instruments, not only for recommendations but also for price subsidies and other policy instruments.

More broadly, our findings suggest that considering and improving selection into screening is a first-order factor in an effective design and analysis of interventions to increase screenings. However, the extent to which we can generalize our findings in this paper, in the context of mammograms, to other types of screening and preventive medicine remains an open question. The controversy surrounding the recommendation that mammography start at age 40 may generate stronger selection than in other, less controversial settings (e.g., flu shots). Whether this is true or not is an important question that we leave for future work.