Abstract
Meta-analyses from the 1990s have previously established a significant, small-to-moderate, and negative correlation between math achievement and math anxiety. Since these publications, research has continued to investigate this relation with more diverse samples and measures. Thus, the goal of the present meta-analysis was to provide an update of the math anxiety-math achievement relation and its moderators. Analyzing 747 effect sizes accumulated from research conducted between 1992 and 2018, we found a small-to-moderate, negative, and statistically significant correlation (r = −.28) between math anxiety and math achievement. The relation was significant for all moderator subgroups, with the exception of the relation between math anxiety and assessments measuring the approximate number system. Grade level, math ability level, adolescent/adult math anxiety scales, math topic of anxiety scale, and math assessments were significant moderators of this relation. There is also a tendency for published studies to report significantly stronger correlations than unpublished studies but, overall, large, negative effect sizes are under-reported. Our results are consistent with previous findings of a significant relation between math anxiety and math achievement. This association starts in childhood, remains significant through adulthood, is smaller for students in grades 3 through 5 and postsecondary school, is larger for math anxiety than for statistics anxiety and for certain math anxiety scales, and is smaller for math exam grades and samples selected for low math ability. This work supports future research efforts to determine effective math achievement and math anxiety interventions, which may be most helpful to implement during childhood.
Keywords: meta-analysis, math anxiety, math achievement, grade level
Research aimed at understanding how to improve achievement in mathematics has long been stimulated by the importance of its use in everyday life (OECD, 1999). More recently, a clear national and international priority has been made to increase engagement in fields that require strong mathematics skills, such as fields in science, technology, engineering, and mathematics (STEM; Corbett & Hill, 2015; Olson & Riordan, 2012). Despite this importance, recent work has shown declines in math achievement in students across the globe (Gottfried, Marcoulides, Gottfried, Oliver, & Guerin, 2007; Kastberg, Chan, & Murray, 2016; Wijsman, Warrens, Saab, Van Driel, & Westenberg, 2016). For example, the 2015 Program for International Student Assessments (PISA) report found a significant decline from 2012 to 2015 in the average 15-year-old students’ math achievement scores from at least a third of countries sampled, including the United States, China (i.e., Hong Kong), and Brazil (OECD, 2016). In light of this decline, it is imperative to continue to work to understand the nature of math achievement and associated factors.
Negative affect related to math has been a critical focus of the research aimed at understanding how to increase math knowledge (Aiken, 1970; Foley et al., 2017; McLeod, 1994). One affective factor that has been found to play a central role in math achievement is math anxiety, defined as the fear and worry related to math stimuli and situations (Ashcraft, 2002; Richardson & Suinn, 1972). Meta-analyses investigating the relation between math anxiety and math achievement from the 1990s highlight the primacy of this relation; both Hembree’s (1990) and Ma’s (1999) statistical analyses of the strength of the association found significant small-to-moderate negative associations between math anxiety and math achievement (Hembree: rs ranged from −.25 to −.40; Ma: r = −.27). Overall, aggregated evidence from these two meta-analyses suggest that many students with higher levels of math anxiety tend to also have lower levels of math achievement.
Over the past twenty years since the last of these statistical reviews, research studying the relation between math anxiety and math achievement has continued to flourish. A closer look at these previous meta-analyses, along with publications that have surfaced since their release, reveals that there are specific questions that need to be clarified surrounding the nature of the relation between math anxiety and math achievement. For example, although recent work has been conducted with different age groups, it is unclear whether the relation is consistently evident in student populations younger than grade 4 (Ganley & McGraw, 2016; Harari, Vukovic, & Bailey, 2013) or in non-student adult populations (Hart & Ganley, 2019). The scope of recent research has become more nuanced with regard to the demographics of samples studied and measures used to assess math anxiety and math achievement. As such, a synthesis of this work can provide a clearer picture of the magnitude of the relation, particularly for complexities of the relation that remain unclear.
There were two aims for the present study. The primary aim was to conduct a meta-analysis that takes into account the surge of research that has occurred since Ma’s (1999) meta-analysis on the overall association between math anxiety and math achievement. The secondary aim was to investigate whether this relation is moderated by certain factors. Specifically, we examined whether sample demographic characteristics of gender, race/ethnicity, country, or grade level moderated the relation between math anxiety and math achievement. We also examined whether teachers or samples selected for low math ability had differential relations compared to non-teacher samples and samples not selected for low math ability, respectively. Finally, we examined whether measure characteristics, such as the types of measures used to assess math anxiety and math achievement or the content area assessed by the math assessment, moderated the relation.
Importance of Math Anxiety and Math Achievement
Math anxiety and math achievement have both been theorized to be important correlates of educational and career outcomes (Wigfield & Eccles, 2000). High levels of math anxiety as well as low math achievement and beliefs about math ability early in development have been found to significantly relate to avoidance of later educational opportunities in math (Espino, Pereda, Recon, Perculeza, & Umali, 2017; Hembree, 1990; Hurst & Cordes, 2017; Meece, Wigfield, & Eccles, 1990). Math anxiety has also been found to relate to the adoption of achievement goal types that are linked with reduced content mastery, such as performance-avoidance and mastery-avoidance goal orientations (Gonzalez-DeHass, Furner, Vásquez-Colina, & Morris, 2017). Furthermore, math anxiety and math achievement have been associated, separately, with high school and college career interests and choices in STEM fields (Ahmed, 2018; Lauermann, Chow, & Eccles, 2015; Watt, et al., 2017). For example, one study found that students who had consistently low or decreasing math anxiety from middle school through high school were more likely to choose STEM majors during postsecondary education than were students with consistently high or increasing math anxiety from middle to high school (Ahmed, 2018).
Throughout development, math anxiety and math achievement guide people down pathways that lead to different learning outcomes, educational pursuits, and career choices. Despite the importance of math anxiety and math achievement in shaping these pathways, inequities in these factors have been reported for certain groups, including females, people of racial and ethnic minority backgrounds, and students with learning disabilities (Catsambis, 1994; Devine et al., 2012; Dowker, Sarkar, & Looi, 2016; Else-Quest, Hyde, & Linn, 2010; Fan, Chen, & Matsumoto, 1997; Hall, Davis, Bolen, & Chia, 1999; Sonnenschein & Galindo, 2015; Suárez-Pellicioni, Núñez-Peña, & Colomé, 2016). For example, some evidence suggests a greater tendency for females to self-report high levels of math anxiety compared to males (Devine, Fawcett, Szűcs, & Dowker, 2012; Hart & Ganley, 2018; Wigfield & Meece, 1988). Regarding math achievement, other work has found gender differences that vary in direction of math performance levels. Some findings have suggested that boys have lower math achievement and other findings have suggested the same for girls, with many of the differences in findings between studies primarily depending on the measure of math achievement used, age of sample, and ability level of students (Cimpian, Lubienski, Timmer, Makowski, & Miller, 2016; Voyer & Voyer, 2014). As another example of group inequities, some studies have found that samples of African American students achieve lower math scores compared to samples of mostly European American students (Else-Quest, Mineo, & Higgins, 2013; Hall et al., 1999; Sonnenschein & Galindo, 2015), although socioeconomic status may explain these racial and ethnic differences (Lubienski, 2002). Given that math anxiety and math achievement are instrumental in understanding a person’s academic and career choices, it is important to understand whether group inequities found in math anxiety and math achievement, separately, are also prevalent in their relation. In the case where there is a stronger relation between math anxiety and math achievement for certain groups that also tend to have lower achievement or higher anxiety, these groups would be most in need of targeted interventions to reduce math anxiety or improve math skills in order to minimize negative academic-related outcomes.
Math Anxiety-Math Achievement Link
Numerous theories have been posited to explain the negative relation between math anxiety and math achievement, with much of the initial work rooted in theories derived from the general anxiety and test anxiety literatures (Eysenck & Calvo, 1992; Liebert & Morris, 1967; Wine, 1971) and adapted to accommodate the math-specific context. The primary theories explaining the anxiety-performance relation are described briefly below (for detailed reviews, see Beilock & Maloney, 2015, Carey, Hill, Devine, & Szucs, 2016, or Foley et al., 2017).
One major theory explaining the anxiety-performance link is the processing efficiency theory. In this theory, cognitive worry interferes with cognitive capacities required for efficient and accurate performance (Eysenck & Calvo, 1992). This reduction in efficiency is theorized to be attributable primarily to an overload of working memory resources (Ashcraft, Kirk, & Hopko, 1998; Caviola, Mammarella, Cornoldi, & Lucangeli, 2012). Thus, in the presence of a math-related stressor such as solving a multiplication problem or learning about the commutative property of multiplication, math anxiety is proposed to use working memory resources, which would otherwise be available to solve the problem or learn math content. An expanded version of this theory, the attentional control theory, further proposes that initial attention to a task is controlled by either the stimulus-driven system or the goal-directed system (Eysenck, Derakshan, Santos, & Calco, 2007). In the case of math anxiety, a math stressor activates the stimulus-driven system, which then undermines the goal-directed system of completing the math task (Eysenck et al., 2007). Furthermore, negative cognitive biases, such as tendencies to attend to specific stimuli and interpret them as threatening, are thought to be part of the initial processing components that enable the distraction, making it difficult for an individual to focus on the details of a math problem and instead fixate on the negative thoughts (Macleod & Mathews, 2012). Taken together, these theories suggest that, in the presence of math stimuli, the attention of a person with math anxiety, who may have a tendency to attend to and interpret math stimuli as threatening, gets redirected from the goal of completing the task to the math stressor. Ultimately, this redirection of attention reduces the available working memory to efficiently and accurately complete the math task at hand.
Another theory has suggested a causal relation in the opposite direction of the attentional control theory, whereby poor math achievement causes heightened math anxiety. The deficit model suggests that poor basic number processing (e.g., counting, subitizing) is the primary reason for anxiety during math situations (Maloney, Risko, Ansari, & Fugelsang, 2010; Núñez-Peña & Suárez-Pellicioni, 2014; Tobias, 1986). This theory suggests that deficits in basic numerical processing lead to negative encounters with math, which then creates anxiety during subsequent math-related experiences and tasks. Several studies have provided empirical support for this model, finding that students with high math anxiety perform worse than their lower math anxiety counterparts in number magnitude representation skills (Maloney et al., 2010; Núñez-Peña & Suárez-Pellicioni, 2014). Some researchers have further extended the math deficit model to individuals with math learning disabilities, providing empirical evidence suggesting that these populations are more susceptible to math anxiety than individuals without math learning disability (Lai, Zhu, Chen, & Li, 2015; Wu, Wilcutt, Escovar, & Menon, 2014). However, other work has failed to find support for this interpretation (Devine, Hill, Carey, & Szűcs, 2017).
Though the attentional control theory and the deficit model could be seen as competing conceptualizations of the math anxiety-math achievement link, the opposing causal directions found between studies testing these theories may instead be artifacts of study design. Specifically, longitudinal studies often find that early math achievement influences later math anxiety (Ma & Xu, 2004; Meece, Wigfield, & Eccles, 1990), while experimental studies find that math anxiety causes math achievement difficulties due to math anxiety’s online use of working memory capacities (Ashcraft, Krause, & Hopko, 2007). Importantly, some work has attempted to reconcile both theories by suggesting that these two causal pathways occur simultaneously (Ashcraft et al., 2007; Carey et al., 2016; Pekrun, 2006). More generally, Pekrun’s control-value theory of achievement emotions suggests that achievement emotions and achievement are reciprocally related in a feedback loop (Pekrun, 2006). With regard to the domain of math and the emotion of anxiety, the reciprocal theory combines the two theoretical perspectives of the attentional control theory and the deficit model that assume different causal relations, and proposes that math anxiety and math achievement are causally related to each other bidirectionally (Devine et al., 2012; Gunderson, Park, Maloney, Beilock, & Levine, 2018; Ma & Xu, 2004). Research has found supporting evidence for this perspective, finding differing magnitudes of causal importance between math anxiety and math achievement depending on the age of the sample (Cargnelutti, Tomasetto, & Passolunghi, 2017; Gunderson et al., 2018; Pekrun et al., 2017).
Potential Moderators of the Math Anxiety-Math Achievement Link
Based on previous empirical evidence, the relation between math anxiety and math achievement has been theorized to vary depending on a number of sample and study factors. For example, the two meta-analyses from the 1990s that investigated this relation found several factors differentiated the strength of the negative correlation, including the gender of primary and secondary school students (Hembree, 1990) and the assessments used to measure math achievement (Ma, 1999). Of importance, many changes in social-contextual factors and study measures have occurred over the last 25 years that may contribute to varying strengths in the relation that were not evident or have changed since the publication of previous meta-analyses. Accordingly, it is important to conduct an updated and thorough moderator analysis on the current available work in order to understand the nuanced between-study differences that may impact the strength of the reported math achievement-math anxiety relation. It is also important to note that, for the moderators, the difference in the relations between subgroups (i.e., males, females) is generally theorized to vary in magnitude (i.e., small versus moderate correlation) and not in direction (i.e., positive versus negative correlation), which is generally found to be negative.
Demographics of sample.
Gender.
Previous research has found gender differences in self-reported math anxiety, with higher self-reported scores found for girls than for boys and for women than for men (Devine, et al., 2012; Hart & Ganley, 2019). Small gender differences have also been found in math achievement, although the direction is less clear-cut (Cimpian et al., 2016; Hyde, Fennema, & Lamon, 1990). The evidence so far on gender differences in the relation between math anxiety and math achievement has also been mixed. The two meta-analyses from the 1990s that investigated this relation each came to a different conclusion on this topic: Hembree (1990) found a stronger negative correlation for male students compared to female students in grades 5 through 12 but not for students in postsecondary school, whereas Ma (1999) found the correlations to be similar for females and males. Some theory (Aiken, 1970) as well as recent empirical evidence (Hill et al., 2016) adds yet another possible conclusion, suggesting that a stronger negative relation between math anxiety and math achievement exists for females compared to males. In the present meta-analysis, we will attempt to clarify these contradictory findings by empirically testing whether gender moderates the relation between math anxiety and math achievement, using the combined power of effect sizes from studies reporting correlations for completely male or female samples.
Race, ethnicity, and country.
In addition to gender differences in the relation between math anxiety and math achievement, there may be significant differences that are evident between racial groups, ethnic groups, or country of origin. Variability in math achievement and math anxiety, separately, has been found between samples from different countries and samples of different racial and ethnic backgrounds (Cipora, Szczygiel, Willmes, & Nuerk, 2015; Else-Quest, Mineo, & Higgins, 2013; OECD, 2016; Pretorius & Norman, 1992; Young & Young, 2016; Zabulionis, 2001). Importantly, there may be variations that stem from the education systems between countries and within countries that may be associated with the differences seen in math anxiety and math achievement between racial/ethnic groups and countries. Investigating whether the differences further appear in the relation between math anxiety and math achievement will serve to better inform the roles of educational practices and policies between countries and for different racial/ethnic groups.
When examining the influence of race on the correlation between math anxiety and math achievement, previous work has found that the magnitude of the correlation did not differ for samples that consisted of a homogenous race (e.g., effect sizes from majority European sample or majority Asian sample combined into one group) compared to samples that were racially diverse (Ma, 1999). However, it is unclear whether there is enough information available from different racial groups within a specific country in the current literature that will allow for meaningful comparisons between these more specific groups (e.g., majority African American sample, majority Asian American sample, majority European American sample). We will examine whether these potential differences can be tested in the present study.
Additionally, some work has been done to clarify whether there are differences in the relation between math anxiety and math achievement between countries (Engelhard, 1990; Foley et al., 2017; Verkijika & De Wet, 2015). However, confounds related to the age of the study samples may limit the generalizability of study findings. For example, analyses conducted from international, large-cohort data sets of 15-year-old students, such as the PISA, have reported significant differences across countries in the magnitude of the negative relation between math anxiety and math achievement (Foley et al., 2017; Lee, 2009). Several other studies investigating this relation in younger student samples across different countries have found varying correlations, ranging from not significant to significant (Hill et al., 2016; Ganley & McGraw, 2016; Krinzinger et al., 2009; Vukovic, Kieffer, Bailey, & Harari, 2013). Both of these examples suggest that differences in the size and significance of the relation for between different countries may be due to the age of the sample as well as the country of the sample. To date, no work has examined between-country differences in the relation between math anxiety and math achievement with a study sample encompassing participants of various age levels. Thus in the present meta-analysis, we aim to fill these gaps and examine whether the relation between math anxiety and math achievement appears different across varying racial and ethnic groups and across countries with samples of all ages.
Age and grade level.
Research has investigated the relation between math anxiety and math achievement in students of different ages. Notably though, the two meta-analyses from the 1990s did not report effect sizes from samples of students younger than grade 4 (Hembree, 1990; Ma, 1999). The absence of younger samples in these two meta-analyses likely occurred because no research investigating this relation had been conducted on younger students; at this point in time, there were not many, if any, valid measures available to assess math anxiety in students younger than grade 4 (Suinn, Taylor, & Edwards, 1988).
In the years since these publications, multiple researchers have developed and validated math anxiety measures for use with students as young as grade 1, with some of this work finding evidence for high levels of math anxiety in some students at these young ages (Ganley & McGraw, 2016; Harari et al., 2013; Ramirez, Gunderson, Levine, & Beilock, 2013; Wu, Amin, Barth, Malcarne, & Menon, 2012). Importantly though, studies investigating the relation between math anxiety and math achievement in young children have found inconsistent results (Harari et al., 2013; Hill et al., 2016; Jameson, 2014; Krinzinger, Kaufmann, & Willmes, 2007; Thomas & Dowker, 2000). Some evidence suggests that the association between math anxiety and math achievement for 6 to 9-year-olds is not significant (Thomas & Dowker, 2000), whereas other research has found significant associations in samples of young children (Harari et al., 2013; Krinzinger et al., 2007). Some of this work suggests that, when found to be significant, this relation in younger children is due to general anxiety that is not math-specific (Hill et al., 2016). The relation found in samples of young children may also be confounded by geographic differences or anxiety measure differences, a possibility that is discussed in other sections of this manuscript.
As for adolescents and young adults, a large body of research has found small-to-moderate negative correlations between math anxiety and math achievement in middle school, high school, and undergraduate student samples (Hembree, 1990; Ma, 1999). A large amount of this work has been with undergraduate college students, and this methodological choice is likely due to the ease with which an undergraduate sample can be accessed for research purposes in a university setting. Some recent work has also examined whether the relation may differ in non-student adult samples (Beilock, Gunderson, Ramirez, & Levine, 2010; Hart & Ganley, 2019; Maloney, Ramirez, Gunderson, Levine, & Beilock, 2015), finding similar small-to-moderate correlations in these samples. Overall though, it is currently unclear whether the magnitude of the relation varies in size at different points of development.
Teachers.
In addition to demographic characteristics such as gender, race, and age, a person’s career choice may moderate the relation between math anxiety and math achievement. Specifically, teachers, often elementary-level educators, have been a group of professionals that have been studied with regard to their math anxiety. Previous research has found higher levels of math anxiety for elementary education majors compared to people in other college majors like the social sciences and business (Hembree, 1990). This higher than typical math anxiety in teacher samples may have short- and long-term impacts on the students they educate. Some research further suggests that teachers’ math anxiety may impact their students’ math performance (Beilock et al., 2010; Ramirez, Hooper, Kersting, Ferguson, & Yeager, 2018). Thus, a comparison of this relation for teacher samples compared to other samples is imperative as it is unclear whether teacher math anxiety is more or less related to their math knowledge when compared to the rest of the population.
Students with low math ability.
Another subsample where we may find a different relation between math anxiety and math achievement is students with low math ability. More broadly, research has found that math anxiety levels were similar for students with low and average levels of math ability (Hembree, 1990). Importantly though, according to the deficit model described earlier in this paper, which theorizes that poor math performance leads to math anxiety, it is suggested that students with low math ability may have higher math anxiety than their counterparts with average math abilities. Some behavioral studies as well as brain imaging studies have found supporting evidence for this hypothesis (Lindskog, Winman, & Poom, 2017; Maloney et al., 2010; Núñez-Peña & Suárez-Pelicioni, 2014). However, whether there is a difference in the magnitude of the relation between math anxiety and math achievement for students with low math ability compared to students who do not have low math ability is still unclear. Therefore, it is important to understand whether a differential trend exists in this relation for students with low math ability compared to samples that are not selected for low math ability.
Measure characteristics.
Math anxiety scales.
With the current availability of a variety of scales to assess math anxiety, it may be useful for researchers to know how each scale differentially relates to math achievement when selecting their study measures. One of the first and most well-known scales to measure math anxiety is the 98-item Math Anxiety Rating Scale (MARS; Richardson & Suinn, 1972). In his 1999 meta-analysis, Ma compared the correlations of samples using the MARS (k = 15) to samples using other, non-MARS scales (k = 22). Importantly, he found no differences in the correlations between these two groups of studies, suggesting that the MARS and non-MARS scales produced similar correlations with math achievement.
However, since Ma’s (1999) meta-analysis, many newer and shorter math anxiety scales have been developed using the most current psychometric methods (e.g., Ganley & McGraw, 2016; Harari et al., 2013; Hopko, Mahadevan, Bare, & Hunt, 2003; Núñez-Peña, Guilera, & Suárez-Pellicioni, 2014). Some scales have also been adapted from previous scales for a variety of reasons, such as to accommodate young children’s language abilities (e.g., Ganley & McGraw, 2016; Harari et al., 2013), to be translated and better understood in other languages and countries (e.g., Carey, Hill, Devine, & Fuchs, 2017), and to assess anxiety in more specific math content areas like statistics (e.g., Baloğlu, 2002). In light of the number of novel math anxiety scales, it is important to examine whether the math anxiety scale used moderates the relation between math anxiety and math achievement.
Components of math anxiety.
Some of the work investigating math anxiety has treated it as a unidimensional construct (Richardson & Suinn, 1972); however, some researchers have investigated whether math anxiety is multidimensional (Ganley & McGraw, 2016; Lukowski et al., 2016; Rounds & Hendel, 1980; Plake & Parker, 1982). Evidence from factor analyses has indicated that math anxiety is multidimensional, suggesting that, depending on the items used within a scale, math anxiety can be made up of a variety of components. One distinction that has been made is between worry, or the cognitive dimension of anxiety, and emotionality, or the physiological dimension of anxiety (Liebert & Morris, 1967). Worry consists of negative expectations and self-deprecating thoughts about a math situation, whereas emotionality refers to the dread and unpleasant physical sensations associated with a math situation.
Another distinction has been made between math learning anxiety and math evaluation anxiety (Plake & Parker, 1982; Hopko et al., 2003). Math learning anxiety involves responses to situations surrounding learning in a math classroom, such as seeing the teacher write a math equation on the board and opening up a math textbook. Math evaluation anxiety involves responses to studying for and taking math tests. These two components were found to make up a shortened 24-item version of the 98-item MARS (Richardson & Suinn, 1972), developed by Plake & Parker (1982). Beyond these four components, research has also found other similar components to these that involve anxiety associated with various aspects of math situations and tasks, such as numerical processing anxiety (Wu et al., 2012), math problem-solving anxiety (Gierl & Bisanz, 1995), and math error anxiety (Jameson, 2013). Although there may be overlap between these categories (i.e., an item may ask about feeling worried while learning math, combining components of worry and math learning anxiety), researchers have primarily distinguished math anxiety between worry and emotionality or between math learning anxiety and math evaluation anxiety components of math anxiety.
Some research has been done to examine whether there are differences in the relations with math achievement for different components of math anxiety (Ganley & McGraw, 2016; Lukowski et al., 2016). For example, Wigfield & Meece (1982) found that the component of worry had weaker relations with two assessments of math achievement (both rs = .02) than did the component of negative affective reactions and math achievement (rs = −.22 and −.26). Thus, it is important to understand whether, in the work currently available, the component of math anxiety is an important distinction to take into account when examining the relation between math anxiety and math achievement.
Math assessments.
In addition to the math anxiety scale used, the strength of the relation between math anxiety and math achievement may also depend on the type of assessment used to measure math achievement. In general, the strength of the relation between anxiety and performance is strong for high-stakes achievement measures, such as the SAT (Cassady & Johnson, 2002). High-stakes testing situations may invoke high levels of anxiety and, as suggested by the attentional control theory, this may lead to a stronger association with achievement than other testing situations. However, meta-analytic work has shown a lower-magnitude correlation between math anxiety and math achievement for standardized achievement tests in comparison to researcher-made math tests and teacher reports of children’s math achievement (Ma, 1999). It is not yet known whether evidence from recent work supports the potential theory that a stronger relation exists between math anxiety and high-stakes, standardized math tests compared to low-pressure testing situations, like researcher-developed measures. Additionally, it may be important to test whether there are differences in the relation with math anxiety for more diverse math achievement measures, such as exam scores in math classes, and between more specific contexts of standardized achievement measures, such as college entrance exams and tests administered in lab experiments.
Math content.
Previous work has found significant, small-to-moderate correlations between math anxiety and different math content areas, such as computation (r = −.25), math concepts (r = −.27), problem solving (r = −.27), and abstract reasoning (r = −.40; Hembree, 1990). Despite these significant correlations, most of these effect sizes were constrained to samples in grade 7, high school, and postsecondary school. To extend this work, it is prudent to further examine what the relation between math anxiety and math achievement looks like for more specific math content areas typically developed or learned during childhood, such as approximate number system or basic number knowledge. Additionally, with the number of studies that have examined this relation in the past 25 years, it may be possible to expand the search to include samples of a wider range of ages.
Though previous work did find significant relations between math anxiety and math achievement for some content areas (Hembree, 1990), math content area has yet to be tested as a moderator of the relation between math anxiety and math achievement. There is some empirical evidence indicating that there may be different relations between math anxiety and math tests that assess certain math content; for example, difficult math problems with high cognitive demands are more impacted by math anxiety in comparison to those math problems demanding less cognitive resources (Ashcraft, 2002). Additionally, early math skills have been found to be important for later math skills (Jordan, Kaplan, Raminemi, & Locuniak, 2009; Siegler et al., 2012); as such, testing whether there are differential relations between math anxiety and different content areas that typically develop and are learned during specific points in development could have important implications on our understanding of math learning and practices in education.
The Present Study
Throughout the past several decades, researchers have made a strong collective effort to understand the factors that significantly relate to math achievement, homing in on math anxiety as a crucial correlate. In the current meta-analysis, we investigated two main research questions. First, we examined the strength of the overall correlation between math anxiety and math achievement across studies investigating this relation from 1992 through 2018. Second, we conducted a moderator analysis to investigate whether the size of the correlation between math anxiety and math achievement differed depending on study and sample characteristics, specifically 1) gender, 2) race/ethnicity, 3) country, 4) grade level, 5) teacher samples, 6) low math ability samples, 7) math anxiety scale, 8) component of math anxiety, 9) math assessment type, and 10) content area of math assessment.
Method
Study Search and Selection
The search for relevant articles for the present study consisted of two techniques. The first technique was based on Ma’s (1999) meta-analytic search techniques. We conducted an online database search across three journal databases that focus on literature in psychology, education, and medicine: PsycInfo, Educational Resources Information Center (ERIC), and Medline. In order to remain consistent with the search terms and Boolean operators across databases, we used the ProQuest platform for each database search. We queried any available document that contained our search terms, including both peer-reviewed publications and grey literature, such as dissertations, theses, reports, and conference proceedings. The selected year criteria for these database searches ranged from January of 1992, the year of Ma’s (1999) last relevant study, to any documents or publications available in May of 2018.
In order to conduct an exhaustive search through our query of online databases, we expanded on the three search terms of mathematics, anxiety, and achievement originally used by Ma (1999). We included the following search terms, making sure to select for articles that included both the word math, or a related synonym, and the word anxiety (denoted by the connecting AND): mathematics, math, maths, arithmetic, numerical, geometry, statistics, calculus, OR algebra AND statistics anxiety, mathematics anxiety, math anxiety, OR maths anxiety. We specifically searched for these terms if they appeared anywhere in a document.
For our second search technique to procure relevant studies for our literature search, we sent a message to the Cognitive Development Society (CDS) listserv and requested unpublished data or manuscripts on the relation of math anxiety and math achievement that could be included in the present meta-analysis. Of note, this solicitation of data from the CDS listserv also included several unpublished effect sizes from studies in the labs headed by two of the authors of the current study.
Studies were eligible to be included in the meta-analysis if they met the following inclusionary criteria. First, studies had to either report a zero-order correlation coefficient between math anxiety and math achievement or have collected data that made the calculation of a zero-order correlation coefficient possible. If the relation was not reported directly in the paper but data were collected, or if multivariate regression coefficients were reported, zero-order correlations were requested from authors via email. Second, studies had to measure math achievement or math performance using a math-related assessment. Studies assessing math achievement as student’s self-reported beliefs about their math ability or overall GPA scores that were not specific to math were excluded. Third, if a study tested an intervention, we included effect sizes from experimental groups only if data were available for both math anxiety and math achievement prior to the intervention. For experimental study control groups, effect sizes from assessments measured before and after the intervention were included.
As a fourth inclusion criterion, we chose to examine only studies published in the English language to reduce potential errors in translation or interpretation. A fifth inclusion criterion was that the achievement and anxiety measures had to be collected and matched by participant and not be collected on separate groups of people (e.g., they could not have math achievement for teachers and math anxiety for students). The sixth, and final, inclusion criterion was that correlational studies were to be included even if they reported on longitudinal data. Correlation coefficients from longitudinal studies with up to two time points were obtained between time point (i.e., time 1 math anxiety with time 1 math achievement, time 1 math anxiety with time 2 math achievement, etc.). Correlation coefficients from longitudinal studies with more than two time points were obtained for each time point separately, rather than for a composite of all time points or between each and every time point (e.g., for three time points, we coded three correlations: time 1 math anxiety with time 1 math achievement, time 2 math anxiety with time 2 math achievement, and time 3 math anxiety with time 3 math achievement).
Coding Procedures and Included Studies
Figure 1 displays a flow chart of the article selection process. The two database searches yielded a total of 1556 relevant documents. We excluded 293 repeated titles, making a final count of 1263 independent documents found through the initial database search. These documents were then subject to close review using the previously outlined inclusion criteria. At each round, questions regarding coding specific articles were discussed as a group through a private, online messaging system and through ad hoc meetings as needed, with the first and second authors resolving any questions unanimously. Training for each round of coding consisted of reviewing the inclusion criteria as a group prior to coding articles and answering any questions that arose until all criteria were well understood.
Figure 1.
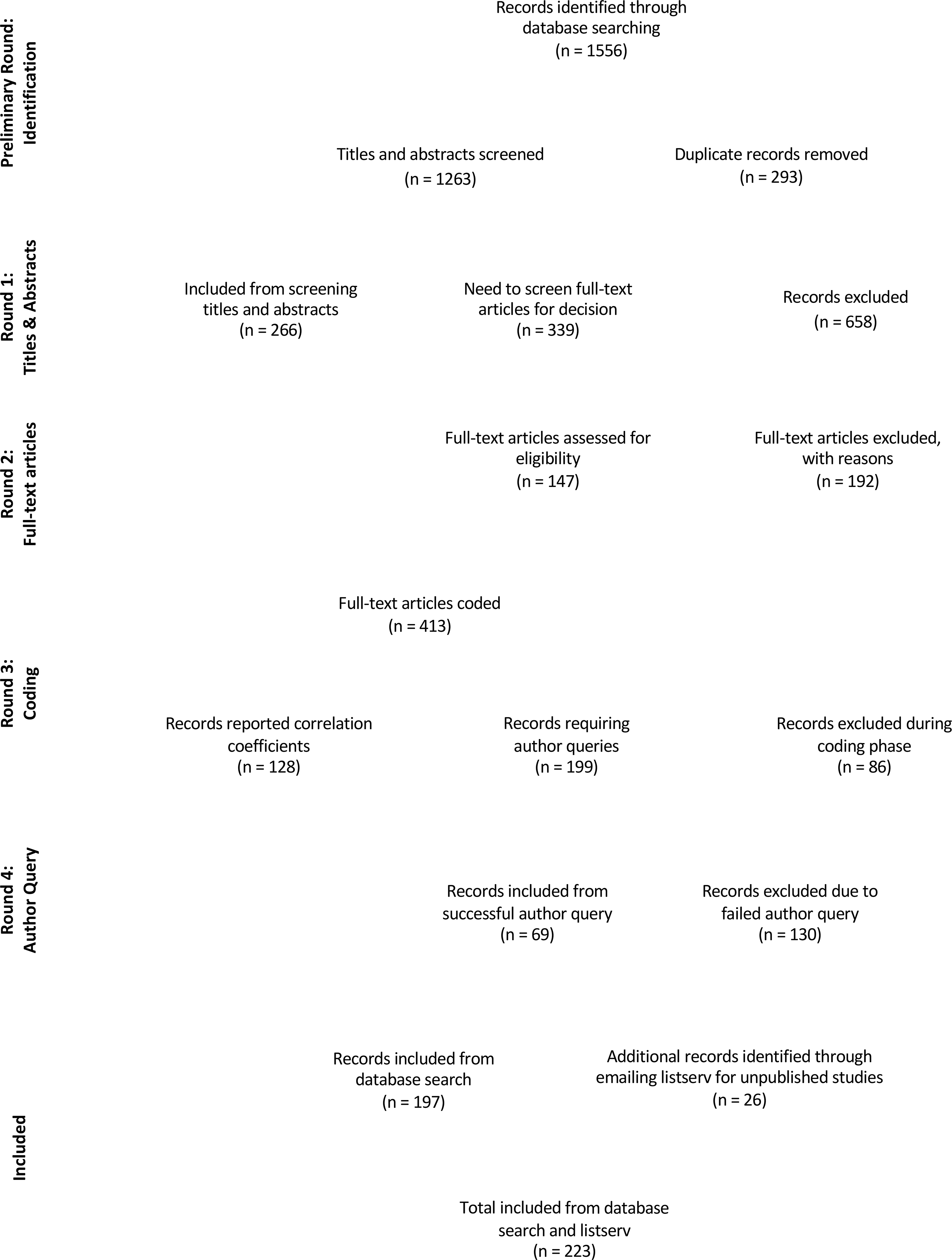
Flow Diagram of the Excluded and Included Studies.
In Round 1 of narrowing down a final study sample, the first four authors reviewed the study titles and abstracts obtained from the online database search and separated these articles into yes, no, and maybe categories based on inclusion criteria. During Round 1, we excluded the 658 articles that were coded no, included the 266 articles that were coded yes, and determined that the inclusion of the remaining 339 maybe documents was unclear and subject to further inspection in Round 2.
Round 2 consisted of reviewing full-text documents separately for each of the articles identified as maybes from Round 1 and categorizing them into yes or no categories, again based on inclusion criteria. We split the articles so that each article was coded by two coders selected from the first four authors. If the two coders’ category choices did not match for an article, these articles were discussed at a roundtable discussion among the first four authors to determine whether or not the study was eligible to be included, using the abstract and full text of the article to make the decision. Out of the 339 articles subject to Round 2, we excluded 192 studies and included 147 studies.
The 413 included articles from Round 1 and Round 2 were coded for descriptive information and information for moderation analyses during Round 3. The following study information from included studies in Rounds 1 and 2 were entered into a Qualtrics survey: correlation coefficients, sample size, gender, race/ethnicity, country, age and grade level, teacher sample, low math ability sample, math anxiety scale, math assessment type, and math content area. These studies were divided between all six authors, all of whom attended a 1-hour training session to learn how to extract the necessary information for each relevant variable prior to coding. In this round, we further excluded 86 studies. Out of the remaining 327 studies that were included and coded during Round 3, 128 studies reported at least 1 correlation coefficient that could be used in this meta-analysis.
The remaining 199 studies did not include the necessary correlation coefficient(s) and were subject to Round 4, where authors were emailed to request correlation information. Corresponding authors of specific studies were contacted by email by the first or second author. During Round 4, we received responses with the information that we needed from authors for 69 of these studies (35%). We excluded the remaining 130 studies from the 199 studies subject to Round 4 because we were unable to obtain the effect size information needed for inclusion.
Thus, overall, the two online database search waves yielded 197 relevant studies to include in this meta-analysis. The second search technique of emailing the CDS listserv yielded information from 26 unpublished data sets and manuscripts. In total, we included 223 studies in the present meta-analysis.
Inter-rater reliability.
Twenty percent of the studies included in Round 3 were selected to be double-coded and split between all six coders. The index of agreement rate was calculated for all data extracted by coders who double-coded the article for the inclusion variable, the number of effect sizes, correlation, sample size, gender, race/ethnicity, country, grade level, teachers, students with low math ability, math anxiety scale (separate for child, adolescent/adult, and scale topic), components of math anxiety, math achievement scale, and math content.
We first calculated the agreement rate for the inclusion variable that indicated whether the coder decided to include the study in our sample, based on our inclusion criteria. We then calculated the agreement rate for the number of effect sizes that each coder decided was pertinent from each study. If coders disagreed on the inclusion variable, the study was not included in the agreement rate calculation for the number of effect sizes and moderator variables. Finally, we calculated the agreement rate for each of the moderator variables, based on the final codes that these originally entered codes would have been categorized into for the moderator analyses (see Coding Procedures section). If coders disagreed on the number of effect sizes, we only coded the agreement rate for moderator variables for the effect sizes that overlapped between the coders. Because we had different pairs of raters selected from six possible raters code a random subset of these studies, agreement rate was calculated for each pair of raters (15 possible pairs) and averaged across them for each variable.
The average agreement rate for each variable is reported in Table S1. The average agreement rate was 91% for the inclusion variable, 75% for the number of effect sizes, 85% for the correlation coefficient, and 72% for the sample size. Average agreement rates for the moderator variables ranged from 84% to 100%, with an average of 94.8%. To ensure accurate coding of variables from included studies, most included study variables were checked for accuracy by another independent coder or verified by the first author.
Demographic information.
For each effect size, demographic and measure information were recorded in an online Qualtrics survey and then coded for the moderator analysis into particular categories. The coding scheme is outlined below.
Gender.
Gender was entered as the percentage of males reported in the sample for each effect size. If gender information was not available in the document, gender was entered as not reported. Reported gender information was then coded into two categories: 1) samples made up of 100% male participants (k = 38) and 2) samples made up of 100% female participants (k = 52). Any samples with greater than 0, less than 100%, or not reported male percentages were not included in the gender moderator analysis (k = 657).
Race/ethnicity.
Race/ethnicity was entered as whether the sample associated with each effect size consisted of 75% or more 1) White, 2) Black, 3) Hispanic, or 4) Asian participants, 5) whether the sample consisted of a racially or ethnically diverse group (i.e., no race or ethnicity was more than 75% of the sample), or 6) whether the racial or ethnic breakdown of the sample was not reported. From this initial coding scheme, we found few effect sizes that consisted of primarily Black (k = 1), Hispanic (k = 1), or Asian participants (k = 42). We also found that a large percentage of the effect sizes that had reported race/ethnicity information were from the United States (75%), and that all except one of the Asian samples were from Asia. Thus, to reduce potential confounds related to country, we only included effect sizes for samples from the United States in the race/ethnicity moderator analysis. We ended up coding our race/ethnicity variable into two categories: 1) effect sizes with samples consisting of 75% or more White participants (k = 104) and 2) effect sizes with samples consisting of less than 75% White participants (k = 72). Any effect sizes without race/ethnicity information reported were not included in the race/ethnicity moderator analysis (k = 571).
Country.
Country information was entered as either the country or countries reported by the paper for the sample for each effect size or as not reported if country information was not available. There were 52 countries represented (see Table S2 for individual country correlations), and 23 out of these 52 countries (44.2%) had only k=1 (i.e., only one effect size represented the relation for that one country). Thus, we grouped countries according to their respective continent. We will refer to the “country” moderator as the “continent” moderator when describing our analyses in the remainder of the paper. We had effect sizes representing samples from six continents: North America (k = 389), South America (k = 26), Europe (k = 204), Asia (k = 103), Africa (k = 11), and the geographic region of Oceania, which includes the countries of Australia and New Zealand (k = 8). Samples that did not report country information were not included in the continent moderator analysis (k = 6).
To account for the variation in cultures among the many countries within these continents, we conducted supplemental moderator analyses by country or region for each continent. North America, South America, Oceania, and Africa each had a small enough number of countries to compare at the country level. However, Asia and Europe were represented by effect size estimates from a large number of countries (i.e., Asia = 16 countries; Europe = 26 countries). Thus, we tested region as a moderator. Asia was divided into five regions (i.e., North, South, East, West, Southeast; Pariona, 2018) and Europe into four regions (i.e., North, South, East, West; Nag, 2018). We have included a figure of the overall effect sizes for these Asian and European regions (as well as the other continents) in Figure S1. Supplemental moderator analyses for each continent and region, separately, are presented in Table S3 and pairwise comparisons for significant moderators are presented in Table S4.
Grade level.
Grade level(s) (i.e., year in school) of the sample for each effect size was selected from one or more of the following choices: kindergarten, grade 1, grade 2, grade 3, grade 4, grade 5, grade 6, grade 7, grade 8, grade 9, grade 10, grade 11, grade 12, community college students, undergraduate students, graduate students, non-student adults, or not reported. Mean age, standard deviation of age, minimum age, and maximum age of each sample were also recorded if reported in the study.
For samples with no reported grade level but with a reported age, we estimated the grade according to the average compulsory age for students entering into each grade from the United States, based on the mean age or the highest category for the range of age if reported (Education Commission of the States, 2018). For samples that included participants from two grades across multiple categories (e.g., grades 5 and 6) we first estimated the grade based on mean age if available. If mean age was not reported and samples were from consecutive grades (i.e., grades 8 and 9), we coded the sample into the category for the highest grade of the two. If mean age was not reported and the samples were from two nonconsecutive grades (e.g., grades 6 and 9), we coded the sample into the category for the average grade rounded up (e.g., rounded up to grade 8 from grade 7.5). If more than two consecutive grades were reported with an odd number of grades, and several of them overlapped across multiple groups (e.g., grades 6 through 10), we first estimated the grade based on mean age, if available. If the mean age was not reported, a mean grade was calculated based on the median grade of the total grade range reported, and subsequently coded into the grade category in which that median grade was included (e.g., samples with students in grades 7 through 9 were calculated to be in grade 8 and coded as being in the grade category for grades 6 through 8). If more than two grades were reported that were not consecutive (e.g., grades 7, 8, and 10), the average grade was taken, rounded to the closest integer, and coded into the corresponding category (e.g., the average of grades 7, 8, and 10 is grade 8.33 and would be rounded to grade 8 and would fall under the category for grades 6 through 8). For those samples that included students in an even number of multiple, consecutive grade levels that spanned across multiple categories, we coded them into the higher of the middle categories (e.g., samples with students in grades 7 through 10 were coded into the high school category because grade 9 is high school).
There were no samples of kindergarten participants. For our analysis, we coded grade levels into six broader categories: (1) grades 1 through 2 (early elementary; k = 68), (2) grades 3 through 5 (late elementary; k = 89), (3) grades 6 through 8 (middle/junior-high school; k = 116), (4) grades 9 through 12 (high school or pre-university; k = 99), (5) undergraduate and graduate students (postsecondary; k = 355), and (6) non-student adult samples (k = 20).
Teachers.
Effect sizes were coded as representing teacher samples if the study reported that the sample was made up of pre-service or practicing teachers (k = 58). We compared the average effect size obtained with teacher samples to the average effect size obtained for non-teacher samples (k = 689).
Students with low math ability.
If the study reported that the authors selected a complete sample based on having low math ability, we coded them as such (k = 18). We compared effect sizes of selected samples with low math ability to effect sizes for samples not selected based on ability level (k = 729).
Measures information.
Math anxiety scale.
Math anxiety measures were categorized in three different ways. Table 1 lists definitions and examples of each of these three categorizations for math anxiety scale. We first categorized math anxiety scales based on whether they were originally developed to assess children’s math anxiety. Child math anxiety scales were coded into six categories: 1) Math Anxiety Rating Scale – Elementary (MARS-E; k = 42; Suinn, Taylor, & Edwards, 1988), 2) Scale for Early Mathematics Anxiety (SEMA; k = 19; Wu et al., 2012), 3) versions of the Math Anxiety Scale for Young Children (MASYC; k = 22; Harari et al., 2013; Ganley & McGraw, 2016), 4) Children’s Math Anxiety Questionnaire (CMAQ; k = 36; Ramirez et al., 2013), 5) Math Anxiety Questionnaire (MAQ; k = 11; Thomas & Dowker, 2000), and 6) all other math anxiety scales made for children (k = 25). For this variable, any math anxiety scale that was not developed to assess math anxiety in children was coded as missing and excluded from the moderator analysis for children’s math anxiety scales (k = 592).
Table 1.
Math Assessment and Math Anxiety Scale Categories, Definitions, and Examples
| Category | Definition | Example measures/items |
|---|---|---|
| Type of Math Anxiety Scale | ||
| Child Math Anxiety | Developed for the intended use of measuring math anxiety in children | Scale for Early Math Anxiety |
| Adolescent and Adult Math Anxiety | Developed with the intended or primary use of measuring math anxiety in adolescents or adults or with no intention of measuring a specific age group/grade level during childhood | Math Anxiety Rating Scale |
| Math Anxiety | Items in a measure developed for the intended use of measuring anxiety in a broad math context | Math Anxiety Rating Scale |
| Statistics Anxiety | Items in a measure developed for the intended use of measuring anxiety in a statistics context | Statistics Anxiety Scale |
| Components of Math Anxiety | ||
| Worry | Cognitive dimension of anxiety; negative expectations and self-deprecating thoughts about a math situation* | -- |
| Emotionality | Physiological dimension of anxiety; feelings of dread, nervousness, and unpleasant physiological reactions to math situations* | -- |
| Math Evaluation Anxiety | Anxiety felt while taking a math test or while doing math in front of others | -- |
| Math Learning Anxiety | Anxiety felt in the classroom or while engaging in a math task | -- |
| Type of Math Assessment | ||
| Standardized high-stakes | Measures used for selection into institutions or receipt of license or degree | SAT, ACT |
| Standardized measures for research | Measures with a standard protocol, often validated to measure achievement, may have manual | Woodcock-Johnson Applied Problems |
| Non-standardized or research-made | Measures with no standard protocol or created by the researcher without validation | Subtraction problems created by researcher |
| Course grade | Grade assigned for a particular math course | Developmental Algebra course grade |
| Exam/test grade | Grade from course exam on specific math material | Statistics mid-term exam |
| Content of Math Assessment | ||
| Approximate Number System | Tasks that measure intuitive number and magnitude system with non-symbolic representations | The Dots Task |
| Basic Number Knowledge | Knowledge about numerosity, relations of numbers, counting words, and symbolic numbers** | Number line task |
| Whole Number Calculation | Single or multi-digit addition, subtraction, multiplication, and division** | Woodcock-Johnson Math Fluency |
| Word Problem Solving | Tasks with a problem narrative where relevant information needs to be isolated, number sentences constructed, and missing numbers solved for in order to find the answer | WIAT Math Reasoning Subtest |
| Fractions, Decimals, & Percentages | Knowledge of part-whole relation and interpreting measurement of fractions** | Knowledge of Fractions Assessment |
| Geometry | Tasks asking about shape, size, position of figures relative to others, and properties of space** | KeyMath3 Geometry Subtest |
| Algebra | Knowledge and application of pre-learned symbol manipulation arguments** | KeyMath3 Algebra Subtest |
| Statistics, Data Analysis, & Probability | Knowledge in analysis and interpretation of data | Statistics Concept Inventory |
Note.
definition adapted from Liebert & Morris, 1967
definition adapted from Peng, Namkung, Barnes, & Sun, 2015.
We then categorized math anxiety scales based on whether they were originally developed to assess adolescent and postsecondary/adult math anxiety. Ten categories were coded for adolescent and postsecondary/adult math anxiety measures: 1) Math Anxiety Rating Scale (MARS) and MARS-based measures (k = 197; e.g., Hopko et al., 2003; Richardson & Suinn, 1972), 2) one-item math anxiety measures (k = 18; e.g., Núñez-Peña et al., 2014), 3) Fennema Sherman Math Anxiety Scale (FSMAS; k = 44; Fennema & Sherman, 1976), 4) MARS-based measures created for adolescents (k = 8), like the MARS-Adolescents (MARS-A; Suinn & Edwards, 1982), 5) the math anxiety scale used by the Programme for International Student Assessment (PISA; k = 56), 6) Achievement Emotion Questionnaire Math Anxiety Subscale (AEQ; k = 7; Pekrun, Goetz, Frenzel, Barchfeld, & Perry, 2011), 7) Math Anxiety Scale created by Betz (MAS; k = 25; Betz, 1978), 8) Math Anxiety Scale created by Meece (MAS; k = 15; Meece, 1981), 9) Math Anxiety Scale created by Bai and colleagues (k = 19; Bai, Wang, Pan, & Frey, 2009), and 10) all other measures (k = 123). For this variable, any math anxiety scale that was specified to assess math anxiety in children was coded as missing and excluded from the moderator analysis for adolescent and adult math anxiety scales (k = 235).
Math anxiety topic.
We also created a third math anxiety scale variable where we coded whether the anxiety topic assessed was math or statistics specific. For this variable, if the anxiety scale explicitly stated that the anxiety topic being assessed was for statistics then the scale was coded as statistics anxiety (k = 80). If the scale did not specify that it assessed anxiety in the subject of statistics, then it was coded as math anxiety (k = 667).
Components of math anxiety.
Table 1 lists definitions and example items for four of the most commonly measured components of math anxiety: worry, emotionality, math evaluation anxiety, and math learning anxiety. This moderator was coded into six categories that differentiated between these four components: 1) worry (k = 14), 2) emotionality, including affect, dread, and negative reactions (k = 7), 3) both worry and emotionality (k = 11), 4) math evaluation anxiety, including test and examination anxiety (k = 55), 5) math learning anxiety, including class/course anxiety (k = 35), and 6) both math evaluation and math learning anxiety (k = 120). If the study explicitly specified that the correlation was between one of these specific components of math anxiety and math achievement, then it was coded in its respective category. In addition, widely-used scales that had previous factor analyses conducted, like the MARS (Richardson & Suinn, 1972) with factor analysis done by Rounds & Hendel (1978) and the AMAS (Hopko et al., 2003), were coded using the factor structure found in the construct validation studies, unless a different factor structure was found and stated for a newer individual study or if the effect size was for one of the multiple components. If the effect size did not explicitly specify that the math anxiety scale was assessing one of these categories or if it was measuring categories that overlapped with other categories that were not included (e.g., math performance adequacy anxiety) then it was excluded from the moderator analysis (k = 505).
Math assessment.
Table 1 lists definitions and examples of each category for type of math assessment. Math assessments were coded into five categories that characterized the type of assessment: 1) standardized criterion-referenced or norm-referenced assessment used for high-stakes testing (k = 56), 2) standardized assessment used for research purposes (k = 322), 3) non-standardized researcher-made or other assessments (k = 166), 4) course grades (k = 113), and 5) class exam grades (k = 90). If a math assessment contained a composite score made up of several measures that could be coded into one of the five categories, that measure was coded into the appropriate category. If assessments overlapped across more than one category, these effect sizes were coded in the “non-standardized researcher-made or other assessments” category.
Math content.
We adapted the math content category definitions from Peng, Namkung, Barnes, & Sun (2016) as a model for coding math content in the current meta-analysis. Table 1 provides definitions and examples of these categories. The content of the math assessment was determined from each article and initially coded into whichever content area(s) they measured. Effect sizes were then used for the moderator analysis if the assessment measured achievement in only one content area: 1) approximate number system (k = 14), 2) basic number knowledge (k = 30), 3) whole number calculation (k = 113), 4) word problem solving (k = 20), 5) fractions, decimals, or percentages (k = 10), 6) geometry (k = 9), 7) algebra (k = 34), and 8) statistics, data analysis, and probability (k = 105). If the math assessment assessed multiple content areas, the effect size was excluded from the math content moderator analysis (k = 412).
Data Analysis
Overall average effect size.
We used Pearson’s r correlation coefficient as the effect size for the present meta-analysis. Under the assumption that the effect size would be based on variables using scales that were continuous rather than rank-ordered or categorical, we requested Pearson correlation coefficients from authors who reported Spearman’s correlation coefficient. Pearson correlation coefficients were converted to Fisher’s Z-scores to approximate a normal distribution of the population effect sizes (Cohn & Becker, 2003).
Due to varying sample and measure characteristics used to assess math anxiety and math achievement, the overall average effect size model was fitted as a random-effects model. The sample of included effect sizes was considered to come from a universal number of populations instead of one single population; therefore, the true effect size that a study estimates is considered to be random and made up of the true estimate plus the sampling error variance and between-studies variance. Once the true effect size estimate was calculated, we transformed the overall Fisher’s z-score back to a Pearson’s r correlation coefficient for interpretation and reporting purposes.
Effect sizes for samples with multiple reported correlation coefficients (i.e., dependent samples) violate the assumption of independent samples; therefore, we conducted multilevel meta-analyses to model the nested structure of the data. This technique accounts for correlations between the dependent effect sizes and models the Level-1 (effect size) and Level-2 (sample) correlations (Maas & Hox, 2004). To conduct these multilevel meta-analyses, the metafor package from the statistical program R was used with the restricted maximum likelihood estimation method (Viechtabauer, 2010).
Heterogeneity of effect sizes.
To determine if there was a significant amount of unexplained between-study heterogeneity (i.e., large between-samples variance beyond within-sample variance) in the combined estimate of overall effect size and whether it would be appropriate to test for moderators to account for this unexplained heterogeneity (Cooper, Hedges, & Valentine, 2009), we calculated the Q-statistic and its significance. This statistic tests the null hypothesis that the study effect sizes are estimates from a single population against the alternative hypothesis that the observed variance in study effect sizes is greater than would be expected by chance if all studies shared a common population effect size (Cochran, 1954). In addition, we also calculated the associated I2 -statistic. This is a descriptive statistic that indicates how much of the variability across studies is due to heterogeneity as opposed to chance due to sampling error (Higgins & Thompson, 2002).
Analyzing variability in effect sizes.
We tested whether the amount of unexplained variance across the effect sizes was attributable to specific demographic or measure characteristics from the sample of studies. We used an ANOVA framework and performed separate omnibus tests for each moderator variable to determine whether there were significant differences in the size of the effect sizes between the groups in each moderator. If the omnibus test was significant, we tested for further significant differences between effect sizes for each subgroup of the moderator using pair-wise comparisons for every possible pair of subgroups. To reduce the false discovery rate, we applied the Benjamini-Hochberg correction to each group of pair-wise comparisons (Benjamini & Hochberg, 1995). Finally, to obtain overall effect sizes for each subgroup within a moderator, we conducted random-effects multi-level models for each subgroup using datasets that only contained effect sizes for the specific subgroup.
Publication bias.
We used several indices to assess publication bias. First, we tested whether there were significantly different correlations for effect sizes that came from published studies compared to unpublished work. We categorized the moderator variable of publication status into two groups, 1) published studies (k = 520) and 2) unpublished work including theses, dissertations, and unpublished studies (k = 227).
Next, we checked whether the effect sizes included in the meta-analytic sample are distributed symmetrically around the average overall effect size. This method to assess potential publication bias provides a visual and statistical test that detects the difference in effect sizes from large study samples compared to effect sizes from small study samples. Small study samples are more likely to be published only if they produce positive results, compared to large study samples that are more likely to be published regardless of the result (Sterne & Harbord, 2004). We created and visually inspected a funnel plot, which graphs each effect size by its standard error in a scatter plot, which is an indicator of the sample size of the study. We expect the funnel plot to show an even distribution of the effect sizes around the true population effect size, with effect sizes getting more precise and closer to the true effect size as the sample size increases. The funnel plot would indicate publication bias against small studies if it is visually evident that negative results (i.e., weak or positive correlations between math anxiety and math achievement) are associated with large standard errors (i.e., lower half of plot).
We also statistically tested for asymmetry by conducting Egger’s test, a meta-regression analysis that estimates effect size precision (i.e., the standard error) as a predictor of the correlation coefficient, in a multi-level model (Egger, Smith, Schneider, & Minder, 1997). If the meta-regression analysis is significant, it indicates the intercept of the dependent variable (i.e., the correlation coefficient) is significantly different from zero, suggesting that the effect sizes are not distributed evenly around the true population effect size.
Finally, we also used the trim-and-fill method on the effect sizes in the meta-analytic sample. The trim-and-fill method determines the adjusted estimate of the average overall effect size and its significance after filling in sparse areas of the funnel plot and removing outliers (Duval & Tweedie, 2000). The trim-and-fill method is an indicator of how biased an overall effect size is from the current meta-analytic sample compared to the effect size from a sample that may more accurately account for the missing effect sizes that may not have been published and therefore are not represented on the funnel plot (i.e., file drawer problem; Rosenthal, 1979).
Results
Overall Average Correlation Between Math Anxiety and Math Achievement
The 223 studies included in the present meta-analysis consisted of 747 correlation coefficients from 332 independent samples with approximately 385,441 individual participants (see supplemental materials for coded information for each effect size [Tables S5 and S6] and references of included studies). Overall, the average correlation between math anxiety and math achievement was small-to-moderate, negative, and significant (r = −.28, 95% Confidence Interval [CI] [−.29, −.26]). As indicated by the Q-statistic and I2-statistic, there was a significant amount of unexplained variance across the range of effect sizes included in the calculation of the overall average effect size (Q = 7784.61, p < .0001, df = 747; I2 = 90.42), suggesting that these effect sizes did not come from the same population and validating our use of a random-effects model.
Moderation Effects of Demographic and Measure Characteristics
Next, we conducted moderator analyses to examine potential demographic or measure characteristics that might explain the variation found in the relation between math anxiety and math achievement. Average effect sizes for subgroups within each moderator were negative and statistically significant, with the exception of the average effect size for the approximate number system subgroup within the math content moderator (r = −.09, 95% CI [−.18, .005], p = .06). Table 2 shows F-test results, Q-statistics, variance explained by Level-1 and Level-2 for each moderator analysis, and I2-statistics. Even after accounting for differences in the subgroups within each moderator, a significant amount of heterogeneity still remained in the overall effect size for each moderator analysis. P-values obtained from pairwise comparisons for subgroups of significant moderators were interpreted based on Benjamini-Hochberg adjusted cutoffs. We report comparisons that remained significant after the Benjamini-Hochberg correction was taken into account.
Table 2.
Multi-level Model Results for Overall and Moderator Analyses
| Moderator | F(df1, df2) | Between-study variance (Level-1) |
Within-study variance (Level-2) |
QE(df) | I2 |
|---|---|---|---|---|---|
| Overall | -- | .01 | .02 | 7797.56(749)** | 90.39% |
| Gender | 1.19(1, 88) | .02 | .01 | 494.51(88)** | 82.00% |
| Race | 0.28(1, 174) | .003 | .01 | 609.50(174)** | 71.29% |
| Continent | 1.56(5, 735) | .01 | .02 | 7354.65(735)** | 89.94% |
| Grade level | 6.64(5, 741)** | .01 | .02 | 6582.82(741)** | 88.67% |
| Teachers | 0.59(1, 745) | .01 | .02 | 7755.88(745)** | 90.38% |
| Low math ability | 6.29(1, 745)* | .01 | .02 | 7732.83(745)** | 90.35% |
| Child math anxiety scale | 1.26(5, 149) | .01 | .02 | 735.33(149)** | 79.06% |
| Adolescent/Adult math anxiety scale | 6.87(9, 502)** | .004 | .02 | 5233.87(502)** | 90.24% |
| Anxiety scale by topic | 12.14(1, 745)** | .01 | .02 | 7199.63(745)** | 89.64% |
| Components of math anxiety | 3.02(5, 236)* | .01 | .01 | 1273.77(236)** | 81.08% |
| Math assessment | 2.34(4, 742)* | .01 | .02 | 7398.40(742)** | 89.92% |
| Math content area | 1.40(7, 327) | .01 | .02 | 1176.00(327)** | 71.60% |
Note.
p < .05
p < .001
F = omnibus test; df = degrees of freedom; QE = Residual Heterogeneity; I2 = Heterogeneity Percentage.
Moderation Effects of Demographic Characteristics
Gender.
Figure 2 contains a forest plot for effect sizes across demographic characteristics. The subgroups for testing gender as a moderator were samples with 100% male participants (k = 38; r = −.24, 95% CI [−.29, −.17]) and those with 100% female participants (k = 52; r = −.28, 95% CI [−.34, −.23]). The analysis indicated that the average effect size for males was not significantly different from the average for females (F[1, 88] = 1.19, p = .28).
Figure 2.
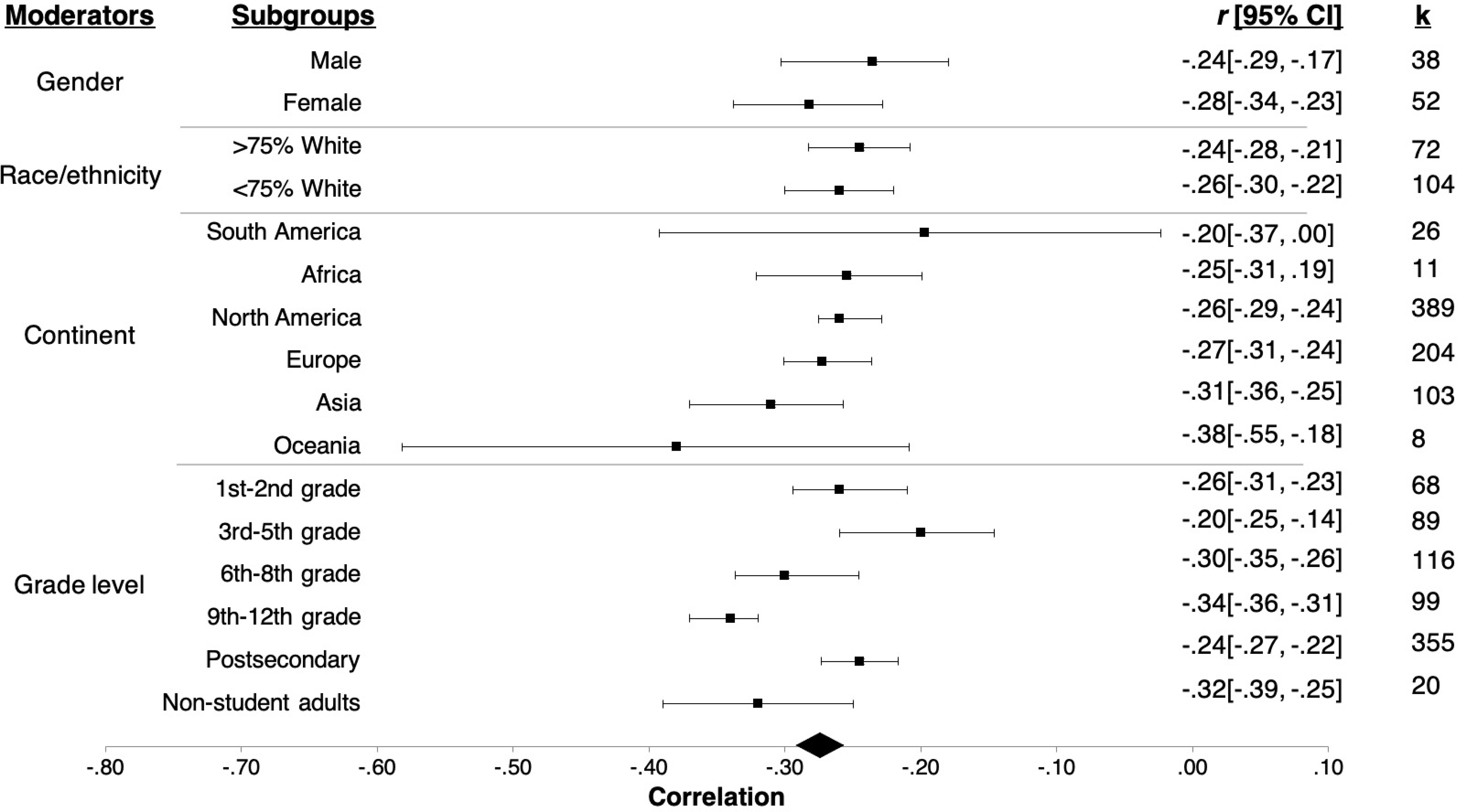
Average Effect Sizes for Demographic Moderators.
Race/ethnicity.
The subgroups for testing race/ethnicity as a moderator were samples with greater than 75% White participants (k = 72; r = −.26, 95% CI [−.30, −.22]) and samples with less than 75% White participants (k = 104; r = −.24, 95% CI [−.28, −.21]). The moderator analysis indicated that the average effect sizes for these two groups did not significantly differ from one another (F[1, 174] = 0.28, p = .60).
Continent.
The subgroups for testing continent as a moderator were North America (k = 389; r = −.26, 95% CI [−.29, −.24]), South America (k = 26; r = −.20, 95% CI [−.37, .00]), Europe (k = 204; r = −.27, 95% CI [−.31, −.24]), Asia (k = 103; r = −.31, 95% CI [−.36, −.25]), Africa (k = 11; r = −.25, 95% CI [−.31, −.19]), and Oceania (k = 8; r = −.38, 95% CI [−.55, −.18]). The omnibus test for the continent moderator analysis was not statistically significant (F[5, 735] = 1.56, p = .17), indicating that there were no statistically significant differences in the relations between math anxiety and math achievement between samples from each of the six continents. The results of the supplemental continent moderator analyses and pairwise comparisons are reported in Tables S3 and S4.
Grade.
The subgroups for testing grade level as a moderator were Grades 1 and 2 (k = 68, r = −.26; 95% CI [−.31, −.23]), Grades 3 through 5 (k = 89, r = −.20; 95% CI [−.25, −.14]), Grades 6 through 8 (k = 116, r = −.30; 95% CI [−.35, −.26]), Grades 9 through 12 (k = 99, r = −.34; 95% CI [−.36, −.31]), undergraduate and graduate students (k = 355, r = −.24; 95% CI [−.27, −.22]), and non-student adult samples (k = 20, r = −.32; 95% CI [−.39, −.25]). The omnibus test for the grade level moderator analysis was statistically significant (F[5, 741] = 6.64, p < .001), indicating that at least one of the subgroups within the grade level moderator variable is statistically significantly different from at least one of the other subgroups.
Pairwise comparisons indicated several statistically significant differences between grade levels in the average correlation between math anxiety and math achievement (Table 3). Students in Grades 1 and 2 demonstrated a statistically significantly lower magnitude correlation than students in Grades 9 through 12 (b = −.07, p = .02). The average correlation for students in Grades 3 through 5 was significantly weaker than the average correlation between math anxiety and math achievement for students in Grades 6 through 8 (b = −.11, p = .004), Grades 9 through 12 (b = −.14, p < .001), and non-student adults (b = −.14, p = .02). In addition, the average correlation between math anxiety and math achievement for students in Grades 6 through 8 (b = .07, p = .01) and Grades 9 through 12 (b = .10, p < .001) were significantly stronger than the average correlation found for postsecondary student samples.
Table 3.
Univariate Pairwise Comparisons of Grade Level and Low Math Ability Moderator
| Demographic | beta | 95% CI |
k | |
|---|---|---|---|---|
| LL | UL | |||
| Grade level | ||||
| 1–2 vs. 3–5 | .08*† | .02 | .15 | 157 |
| 1–2 vs. 6–8 | −.04 | −.11 | .04 | 184 |
| 1–2 vs. 9–12 | −.07* | −.14 | −.01 | 167 |
| 1–2 vs. PS | .03 | −.05 | .10 | 423 |
| 1–2 vs. Non-student adults | −.05 | −.14 | .03 | 88 |
| 3–5 vs. 6–8 | −.11** | −.19 | −.04 | 205 |
| 3–5 vs. 9–12 | −.14*** | −.21 | −.08 | 188 |
| 3–5 vs. PS | −.05 | −.11 | .02 | 444 |
| 3–5 vs. Non-student adults | −.14* | −.25 | −.02 | 109 |
| 6–8 vs. 9–12 | −.03 | −.09 | .02 | 215 |
| 6–8 vs. PS | .07** | .02 | .12 | 471 |
| 6–8 vs. Non-student adults | −.02 | −.13 | .08 | 136 |
| 9–12 vs. PS | .10*** | .05 | .14 | 454 |
| 9–12 vs. Adult | .01 | −.08 | .10 | 119 |
| PS vs. Non-student adults | −.09 | −.19 | .01 | 375 |
| Low math ability | ||||
| Low math ability vs. non-low math ability | −.21** | −.37 | −.04 | 747 |
Note.
p < .05
p < .01
p < .001
predictor variables no longer significant after
Benjamini-Hochberg correction; k = number of effect sizes
PS = Postsecondary.
We also were interested in further examining this relation to determine whether the grade level differences in the relation between math anxiety and math achievement were evident across all math content areas or just specific math content areas. We conducted post-hoc grade level moderator analyses separately for samples with achievement measures that assessed only one math content area (Table S7). We found that relations between math anxiety and specific math content areas were mostly similar across grade levels except for assessments measuring basic number knowledge (F[3, 26] = 6.42, p = .002) and algebra (F[3, 30] = 3.26, p = .04). Pairwise comparisons, shown in Table S8, indicated that students in Grades 1 and 2 (r = −.40, p = .004) showed a significantly stronger correlation between math anxiety and basic number knowledge than did students in Grades 3 through 5 (r = .0009, p = .99; b = .40, p < .001) and postsecondary school students (r = −.12, p = .23; b = .29, p = .03). Students in Grades 3 through 5 had weaker relations between math anxiety and basic number knowledge than did students in Grades 6 through 8 (r = −.17, p = .12; b = −.17, p = .001). The relation between math anxiety and algebra knowledge was significantly weaker in magnitude for postsecondary school students (r = −.17, p <.001) compared to the relation for students in Grades 6 through 8 (r = −.32, p = .06; b = .21, p = .01) and Grades 9 through 12 (r = −.40, p = .18; b = .29, p < .001).
Teachers.
Figure 3 contains a forest plot for effect sizes for subgroup analyses for teacher and low ability groups. The subgroups for testing teacher samples as a moderator were pre-service and practicing teacher samples (k = 58, r = −.31; 95% CI [−.37, −.24]) and non-teacher samples (k = 689, r = −.27; 95% CI [−.29, −.26]). The omnibus test for the teacher moderator analysis was not statistically significant (F[1, 745] = 0.59, p = .44), indicating that there was no statistically significant difference in the relations between math anxiety and math achievement for pre-service and practicing teacher samples compared to non-teacher samples.
Figure 3.
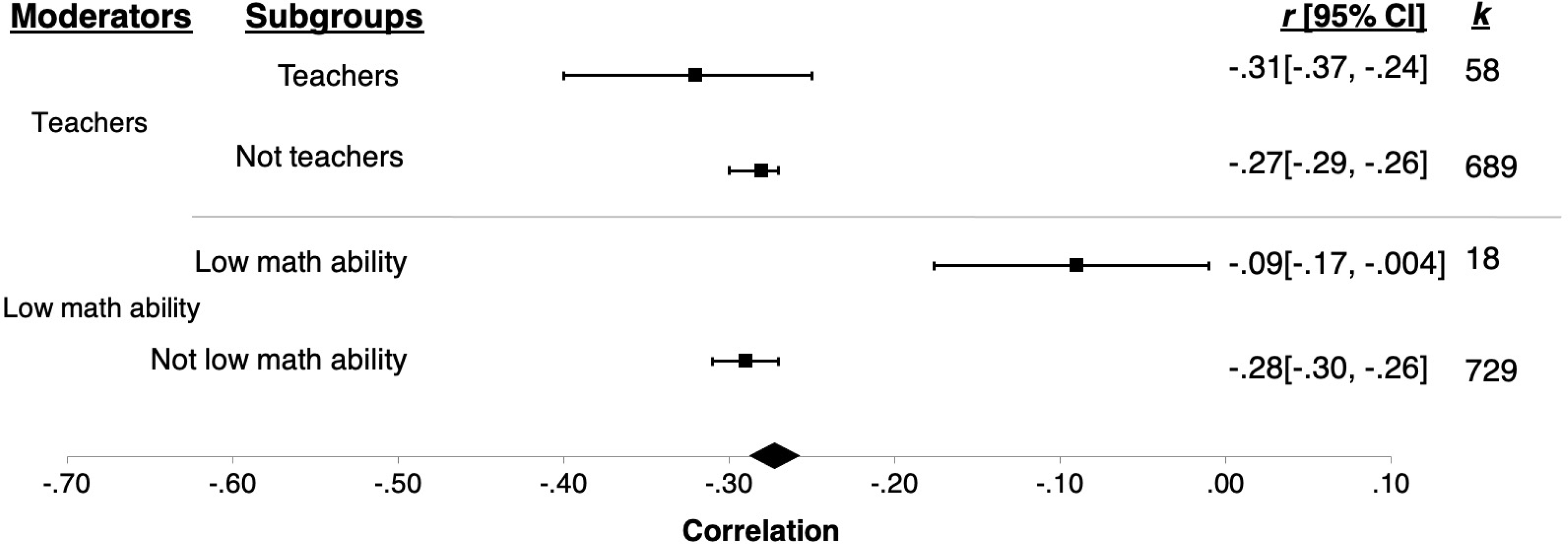
Average Effect Sizes for Teacher and Low Math Ability Moderators.
Students with low math ability.
The subgroups for testing students with low math ability as a moderator were samples selected for low math ability (k = 18, r = −.09; 95% CI [−.17, −.004]) and samples not selected for low math ability (k = 729, r = −.28; 95% CI [−.30, −.26]). The moderator analysis for low math ability samples was statistically significant (F[1, 745] = 6.29, p = .01), indicating that the correlation coefficient for the relation between math achievement and math anxiety for samples selected for low math ability was significantly weaker than the relation between math achievement and math anxiety for samples not selected for low math ability (b = −.21, p = .01; Table 3).
Moderation Effect of Measure Characteristics
Math anxiety scales.
Figure 4 contains a forest plot for effect sizes across math anxiety scales and components of math anxiety.
Figure 4.
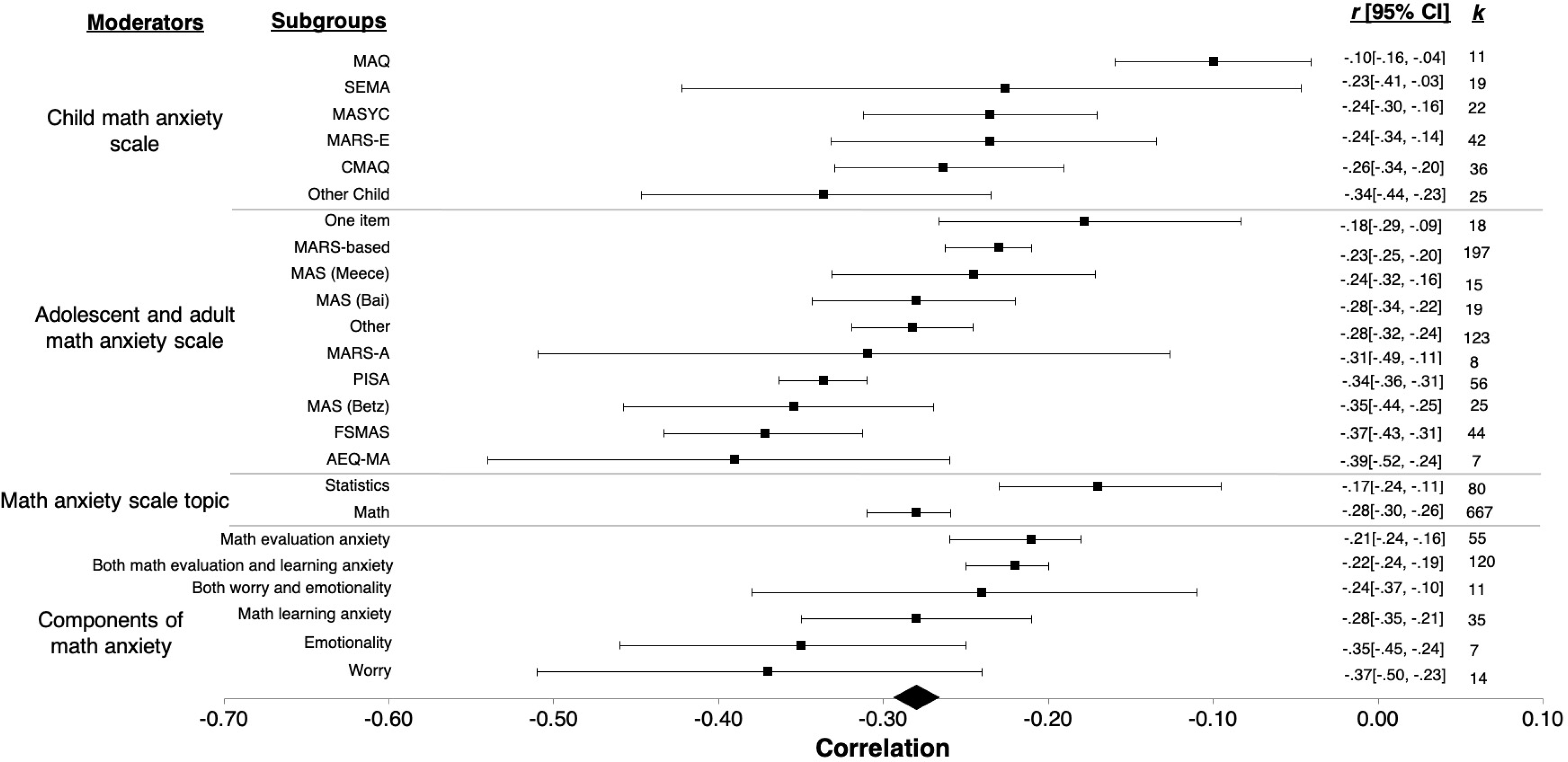
Average Effect Sizes for Math Anxiety Scale and Components of Math Anxiety Moderators.
Child math anxiety scales.
The subgroups within the child math anxiety scales moderator variable were the MARS-E (k = 42, r = −.24, 95% CI [−.34, −.14]), SEMA (k = 19, r = −.23. 95% CI [−.41, −.03]), MASYC (k = 22, r = −.24, 95% CI [−.30, −.16]), CMAQ (k = 36, r = −.26, 95% CI [−.34, −.20]), MAQ (k = 11, r = −.10, 95% CI [−.16, −.04]), and other child math anxiety scales (k = 25, r = −.34, 95% CI [−.44, −.23]). The omnibus test conducted for the six subgroups within child math anxiety scales was not statistically significant (F[5, 149] = 1.26, p = .28), indicating that there were no statistically significant differences in the relations between math anxiety and math achievement across different types of math anxiety scales typically used for children.
Adolescent and adult math anxiety scales.
The subgroups within the adolescent and adult math anxiety scales moderator variable were the MARS (k = 197, r = −.23; 95% CI [−.25, −.20]), one-item (k = 18, r = −.18; 95% CI [−.27, −.09), FSMAS (k = 44, r = −.37; 95% CI [−.43, −.31]), MARS-A (k = 8, r = −.31; 95% CI [−.49, −.11]), PISA (k = 56, r = −.34; 95% CI [−.36, −.31]), AEQ-MA (k = 7, r = −.39; 95% CI [−.52, −.24]), MAS-Betz (k = 25, r = −.35; 95% CI [−.44, −.25]), MAS-Meece (k = 15, r = −.24; 95% CI [−.32, −.16]), MAS-Bai (k = 19, r = −.28; 95% CI [−.34, −.22]), and other scales (k = 123, r = −.28; 95% CI [−.32, −.24]). The omnibus test performed for the ten categories within adolescent and adult math anxiety measures was statistically significant (F[9, 502] = 6.87, p < .001), indicating that at least one of the subgroups within the adolescent and adult math anxiety moderator variable is statistically significantly different from at least one of the other subgroups.
Results are listed in Table 4 for pairwise comparisons between subgroups of adolescent and adult math anxiety scales. MARS-based scales were found overall to have a significantly weaker relation with math achievement than did the FSMAS (b = −.16, p < .001), PISA (b = −.12, p < .001), the AEQ-MA (b = −.18, p = .003) and MAS-Betz (b = −.14, p = .003). Similarly, one-item math anxiety scales were found to have an average correlation coefficient with math achievement that was significantly weaker than the relation between math achievement and FSMAS (b = −.21, p = .001), PISA (b = −.16, p < .001), and the AEQ-MA (b = −.39, p < .001).
Table 4.
Univariate Pairwise Comparisons of Adolescent/Adult and Math Topic Math Anxiety Measure Moderators
| 95% CI |
||||
|---|---|---|---|---|
| Measure | beta | LL | UL | k |
| Adolescent/Adult Math Anxiety Measure | ||||
| MARS vs. One item | 0.03 | −0.05 | 0.10 | 215 |
| MARS vs. FSMAS | −0.16*** | −0.23 | −0.09 | 241 |
| MARS vs. MARS-A | −0.11 | −0.23 | 0.02 | 205 |
| MARS vs. PISA | −0.12*** | −0.16 | −0.08 | 253 |
| MARS vs. AEQ | −0.18** | −0.29 | −0.06 | 204 |
| MARS vs. MAS (Betz) | −0.14*** | −0.22 | −0.05 | 222 |
| MARS vs. MAS (Meece) | −0.02 | −0.13 | 0.09 | 212 |
| MARS vs. MAS (Bai) | −0.05 | −0.15 | 0.06 | 216 |
| MARS vs. Other | −0.05 | −0.10 | 0.002 | 320 |
| One item vs. FSMAS | −0.21*** | −0.33 | −0.09 | 62 |
| One item vs. MARS-A | −0.14 | −0.34 | 0.06 | 26 |
| One item vs. PISA | −0.16*** | −0.24 | −0.08 | 74 |
| One item vs. AEQ | −0.39*** | −0.50 | −0.27 | 25 |
| One item vs. MAS (Betz) | −0.18**† | −0.32 | −0.04 | 43 |
| One item vs. MAS (Meece) | −0.06 | −0.19 | 0.07 | 33 |
| One item vs. MAS (Bai) | −0.10 | −0.22 | 0.03 | 37 |
| One item vs. Other | −0.06 | −0.15 | 0.02 | 141 |
| FSMAS vs. MARS-A | 0.05 | −0.12 | 0.23 | 52 |
| FSMAS vs. PISA | 0.05 | −0.01 | 0.11 | 100 |
| FSMAS vs. AEQ | −0.02 | −0.17 | 0.13 | 51 |
| FSMAS vs. MAS (Betz) | 0.02 | −0.10 | 0.14 | 69 |
| FSMAS vs. MAS (Meece) | 0.14*† | 0.01 | 0.28 | 59 |
| FSMAS vs. MAS (Bai) | 0.12 | −0.01 | 0.24 | 63 |
| FSMAS vs. Other | 0.10**† | 0.02 | 0.18 | 167 |
| MARS-A vs. PISA | 0.0003 | −0.11 | 0.11 | 64 |
| MARS-A vs. AEQ | −0.08 | −0.35 | 0.18 | 15 |
| MARS-A vs. MAS (Betz) | −0.03 | −0.25 | 0.18 | 33 |
| MARS-A vs. MAS (Meece) | 0.07 | −0.16 | 0.31 | 23 |
| MARS-A vs. MAS (Bai) | 0.06 | −0.16 | 0.27 | 27 |
| MARS-A vs. Other | 0.05 | −0.09 | 0.19 | 131 |
| PISA vs. AEQ | −0.06 | −0.15 | 0.04 | 63 |
| PISA vs. MAS (Betz) | −0.02 | −0.10 | 0.06 | 81 |
| PISA vs. MAS (Meece) | 0.10*† | 0.02 | 0.19 | 71 |
| PISA vs. MAS (Bai) | 0.07 | −0.01 | 0.15 | 75 |
| PISA vs. Other | 0.06*† | 0.01 | 0.11 | 179 |
| AEQ vs. MAS (Betz) | 0.05 | −0.14 | 0.23 | 32 |
| AEQ vs. MAS (Meece) | 0.16 | −0.03 | 0.35 | 22 |
| AEQ vs. MAS (Bai) | 0.13 | −0.04 | 0.30 | 26 |
| AEQ vs. Other | 0.12 | −0.01 | 0.25 | 130 |
| MAS (Betz) vs. MAS (Meece) | 0.11 | −0.05 | 0.28 | 40 |
| MAS (Betz) vs. MAS (Bai) | 0.09 | −0.06 | 0.24 | 44 |
| MAS (Betz) vs. Other | 0.08 | −0.02 | 0.18 | 148 |
| MAS (Meece) vs. MAS (Bai) | −0.03 | −0.13 | 0.07 | 34 |
| MAS (Meece) vs. Other | −0.04 | −0.16 | 0.08 | 138 |
| MAS (Bai) vs. Other | −0.01 | −0.12 | 0.10 | 142 |
| Anxiety Topic | ||||
| Math vs. Statistics | .09*** | .04 | .14 | 747 |
Note.
p < .05
p < .01
p < .001
predictor variables no longer significant after
Benjamini-Hochberg correction; CI = Confidence Interval; LL = Lower Level; UL = Upper Level; k = number of effect sizes; MARS = Math Anxiety Rating Scale; FSMAS = Fennema Sherman Math Anxiety Scale; MARS-A = Math Anxiety Rating Scale – Adolescents; PISA = Programme for International Student Assessments; AEQ = Achievement Emotion Questionnaire; MAS = Math Anxiety Scale.
Anxiety scale topic.
The subgroups within the anxiety scale topic moderator were math anxiety (k = 667, r = −.28, 95% CI [−.30, −.26]) and statistics-specific anxiety (k = 80, r = −.17, 95% CI [−.24, −.11]). The moderator analysis for anxiety scale topic was statistically significant (F[1, 745] = 12.14, p = .001), indicating that the correlation coefficient for the relation between math achievement and anxiety scales assessing math anxiety was significantly stronger than the relation between math achievement and scales assessing statistics-specific anxiety (b = .09, p = .001).
We were also interested in determining whether the stronger relation between math achievement and math anxiety held even when examining only statistics-specific achievement. We conducted two additional post-hoc anxiety scale topic moderator analyses, one using effect sizes that only assessed statistics content knowledge and the other analysis using effect sizes that assessed everything except statistics content (Table S7). We found that the moderator did not remain statistically significant for achievement assessments of only statistics knowledge (F[1, 103] = 0.14, p = .71), indicating that math anxiety (r = −.23, p <.001, k = 49) and statistics anxiety (r = −.19, p < .001, k = 56) were similarly related to achievement in statistics. Additionally, we found that when the effect sizes consisted of scales assessing other types of math achievement, the moderator was still significant (F[1, 640] = 20.76, p < .001), with nonstatistics math content having a stronger relation with math anxiety (r = −.29, p < .001, k = 618) compared to statistics anxiety scales (r = −.10, p = .005, k = 23).
Components of math anxiety.
The subgroups within the components of math anxiety were worry (k = 14, r = −.37, 95% CI [−.50, −.23]), emotionality (k = 7, r = −.35, 95% CI [−.45, −.24]), both worry and emotionality (k = 11, r = −.24 95% CI [−.37, −.10]), math evaluation anxiety (k = 55, r = −.21, 95% CI [−.24, −.16]), math learning anxiety (k = 35, r = −.28, 95% CI [−.35, −.21]), and both math evaluation and learning anxiety (k = 120, r = −.22, 95% CI [−.24, −.19]). The omnibus test performed for the six categories within components of math anxiety was statistically significant (F[5, 236] = 3.02, p = .01), indicating that at least one of the subgroups is statistically significantly different from at least one of the other subgroups. Results for pairwise comparisons (Table 5) indicated that the relation between math achievement and the worry component of math anxiety was stronger than the relation between math achievement and math evaluation anxiety (b = .18, p = .002) and between math achievement and both math evaluation and learning anxiety (b = .17, p = .001). The relation between math achievement and emotionality (b = .15, p = .003) and between math achievement and math learning anxiety (b = .08, p = .01) was also stronger than the relation between math achievement and both math evaluation and learning anxiety.
Table 5.
Univariate Pairwise Comparisons of Math Anxiety Component Subgroups
| Subscale | beta | 95% CI |
k | |
|---|---|---|---|---|
| LL | UL | |||
| Worry vs. Emotionality | .04 | −.08 | .16 | 21 |
| Worry vs. Both Worry and Emotionality | .13 | −.11 | .37 | 25 |
| Worry vs. Math Evaluation Anxiety | .18** | .07 | .30 | 69 |
| Worry vs. Math Learning Anxiety | .10 | −.05 | .26 | 49 |
| Worry vs. Both Math Evaluation and Learning Anxiety | .17*** | .07 | .27 | 134 |
| Emotionality vs. Both Worry and Emotionality | .12 | −.07 | .32 | 18 |
| Emotionality vs. Math Evaluation Anxiety | .14*† | .02 | .26 | 62 |
| Emotionality vs. Math Learning Anxiety | .08 | −.08 | .25 | 42 |
| Emotionality vs. Both Math Evaluation and Learning Anxiety | .15** | .05 | .25 | 127 |
| Both Worry and Emotionality vs. Math Evaluation Anxiety | .03 | −.10 | .15 | 66 |
| Both Worry and Emotionality vs. Math Learning Anxiety | −.03 | −.22 | .15 | 46 |
| Both Worry and Emotionality vs. Both Math Evaluation and Learning Anxiety | .02 | −.10 | .13 | 131 |
| Math Testing Anxiety vs. Math Learning Anxiety | −.04 | −.09 | .02 | 90 |
| Math Testing Anxiety vs. Both Math Evaluation and Learning Anxiety | −.002 | −.05 | .05 | 175 |
| Math Learning Anxiety vs. Both Math Evaluation and Learning Anxiety | .08** | .02 | .14 | 155 |
Note.
p < .05*
p < .01**
p < .001***
predictor variables no longer significant after Benjamini-Hochberg correction; CI = Confidence Interval; LL = Lower Level; UL = Upper Level; k = number of effect sizes.
Math assessments.
Figure 5 contains a forest plot for effect sizes across math assessments and content area. The subgroups within the math assessment moderator were high-stakes standardized math tests (k = 56, r = −.26, 95% CI [−.30, −.23]), standardized measures for research purposes (k = 322, r = −.29, 95% CI [−.31, −.27]), researcher-made and non-standardized measures for research (k = 166, r = −.29, 95% CI [−.34, −.25]), course grades in math classes (k = 113, r = −.27, 95% CI [−.31, −.23]), and exam grades on math assessments (k = 90, r = −.20, 95% CI [−.24, −.15]). The omnibus test for the math assessment moderator was statistically significant (F[4, 742] = 2.34, p = .054) and pairwise comparisons for this moderator are shown in Table 6. Specifically, the overall relation found between math anxiety and math exam grades was weaker than the relation between math anxiety and standardized assessments used for research (b = −.08, p = .002) and between math anxiety and non-standardized research measures and other math assessments (b = −.09, p = .01).
Figure 5.
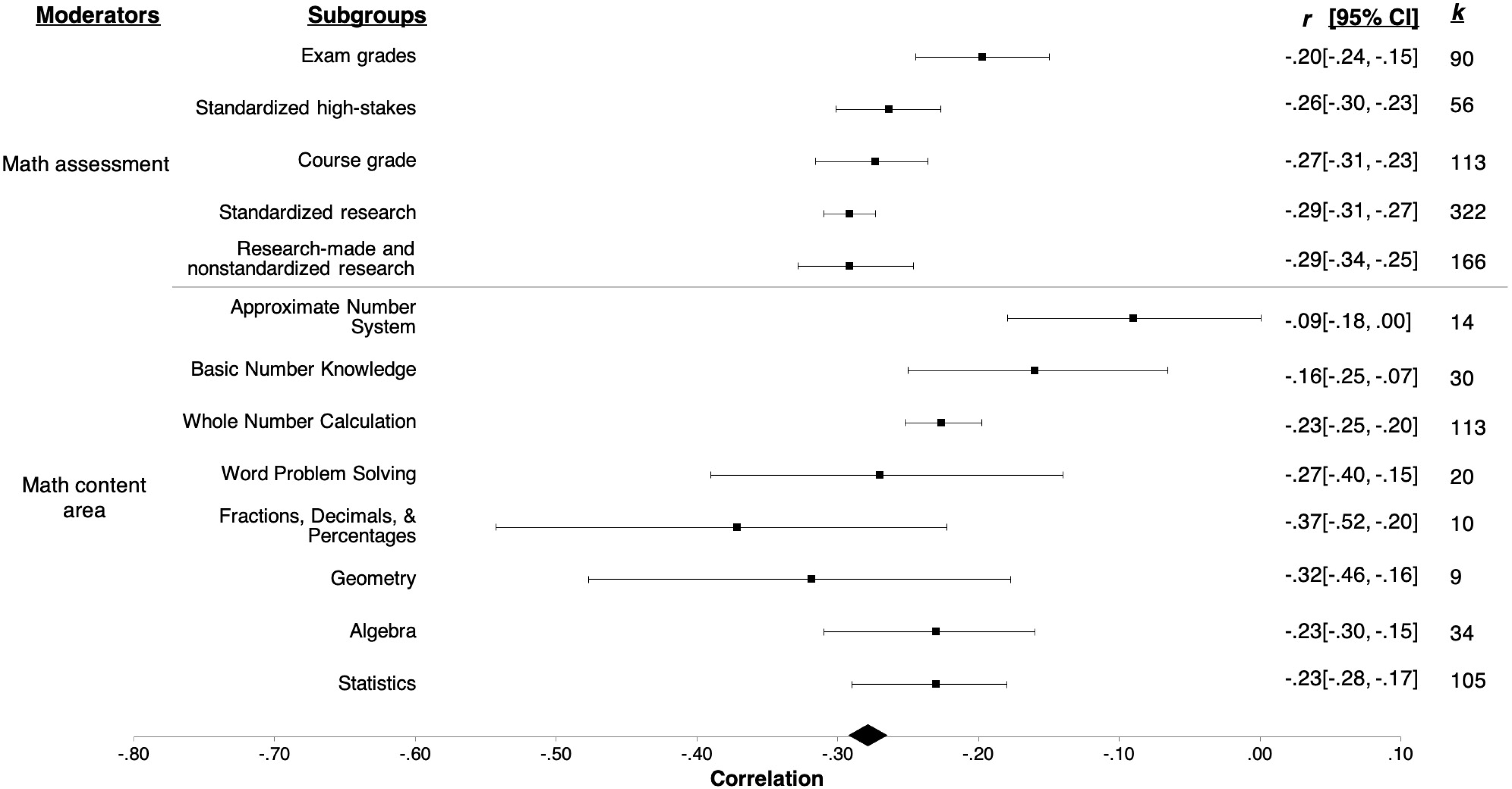
Average Effect Sizes for Math Assessment and Math Content Area Moderators.
Table 6.
Univariate Pairwise Comparisons of Math Assessment Subgroups
| Subscale | beta | 95% CI |
k | |
|---|---|---|---|---|
| LL | UL | |||
| High stakes tests vs. Standardized research assessments | −.005 | −.06 | .05 | 378 |
| High stakes tests vs. Nonstandardized research assessments and Other tests | −.05 | −.12 | .01 | 222 |
| High stakes tests vs. Course grade | −.02 | −.08 | .04 | 169 |
| High stakes tests vs. Exam grade | .06 | −.002 | .13 | 146 |
| Standardized research assessments vs. Nonstandardized research assessments and Other tests | .01 | −.03 | .05 | 488 |
| Standardized research assessments vs. Course grade | .01 | −.03 | .05 | 435 |
| Standardized research assessments vs. Exam grade | .08** | .03 | .14 | 412 |
| Nonstandardized research assessments and Other tests vs. Course grade | .02 | −.05 | .08 | 279 |
| Nonstandardized research assessments and Other tests vs. Exam grade | .09* | .02 | .15 | 256 |
| Course grade vs. Exam grade | .06*† | .003 | .11 | 203 |
Note.
p < .05*
p < .01**
predictor variables no longer significant after Benjamini-Hochberg correction; CI = Confidence Interval; LL = Lower Level; UL = Upper Level; k = number of effect sizes.
Math content.
The subgroups within the math content area moderator were approximate number system (k = 14, r = −.09, 95% CI [−.18, .005]), basic number knowledge (k = 30, r = −.16, 95% CI [−.25, −.07]), whole number calculation (k = 113, r = −.23, 95% CI [−.25, −.20]), word problem solving (k = 20, r = −.27, 95% CI [−.40, −.15]), fractions, decimals, and percentages (k = 10, r = −.37, 95% CI [−.52, −.20]), geometry (k = 9, r = −.32, 95% CI [−.46, −.16]), algebra (k = 34, r = −.23, 95% CI [−.30, −.15]), and statistics knowledge (k = 105, r = −.23, 95% CI [−.28, −.17]). The omnibus test for the math content area moderator analysis was not statistically significant (F[7, 327] = 1.40, p = .21), indicating that there were no statistically significant differences in the relations between math anxiety and math assessments in different math content areas.
Publication bias
The moderator analysis for publication status was statistically significant (F[1, 745] = 12.02, p < .001). There was a significantly stronger negative correlation between math anxiety and math achievement reported in published studies (k = 520, r = −.29, 95% CI [−.32, −.27]) than for unpublished studies (k = 227, r = −.23, 95% CI [−.25, −.21]).
Visual inspection of the funnel plot of the effect sizes by their standard errors (black dots in Figure 6), with higher standard errors at the bottom of the plot, indicated that the spread of the effect sizes was not perfectly symmetrical. Many of the effect sizes were located around and just to the right of the line denoting the overall average correlation (r = −.28), suggesting that most of the effect sizes in the meta-analytic sample represent reporting small-to-moderate negative effect sizes from studies with various sample sizes. A statistically significant Egger test (z = 2.59, p = .01) confirmed the presence of funnel plot asymmetry. The potential missing studies in the left half of the plot, as shown by the sparseness of effect sizes in that area compared to the right half, may indicate higher magnitude negative effect sizes from samples of all sizes are missing from our meta-analytic sample. The trim-and-fill analysis indicated that 129 effect sizes (white dots in Figure 6), primarily clustered in the left half of the asymmetrical plot, are potentially missing and needed to fill in the sparse areas of the funnel plot. The result of the trim-and-fill analysis suggested that, after adjusting the funnel plot to become symmetrical, the adjusted overall correlation coefficient would remain statistically significant and similar in magnitude to the original overall correlation coefficient (r = −.29, p < .001).
Figure 6.
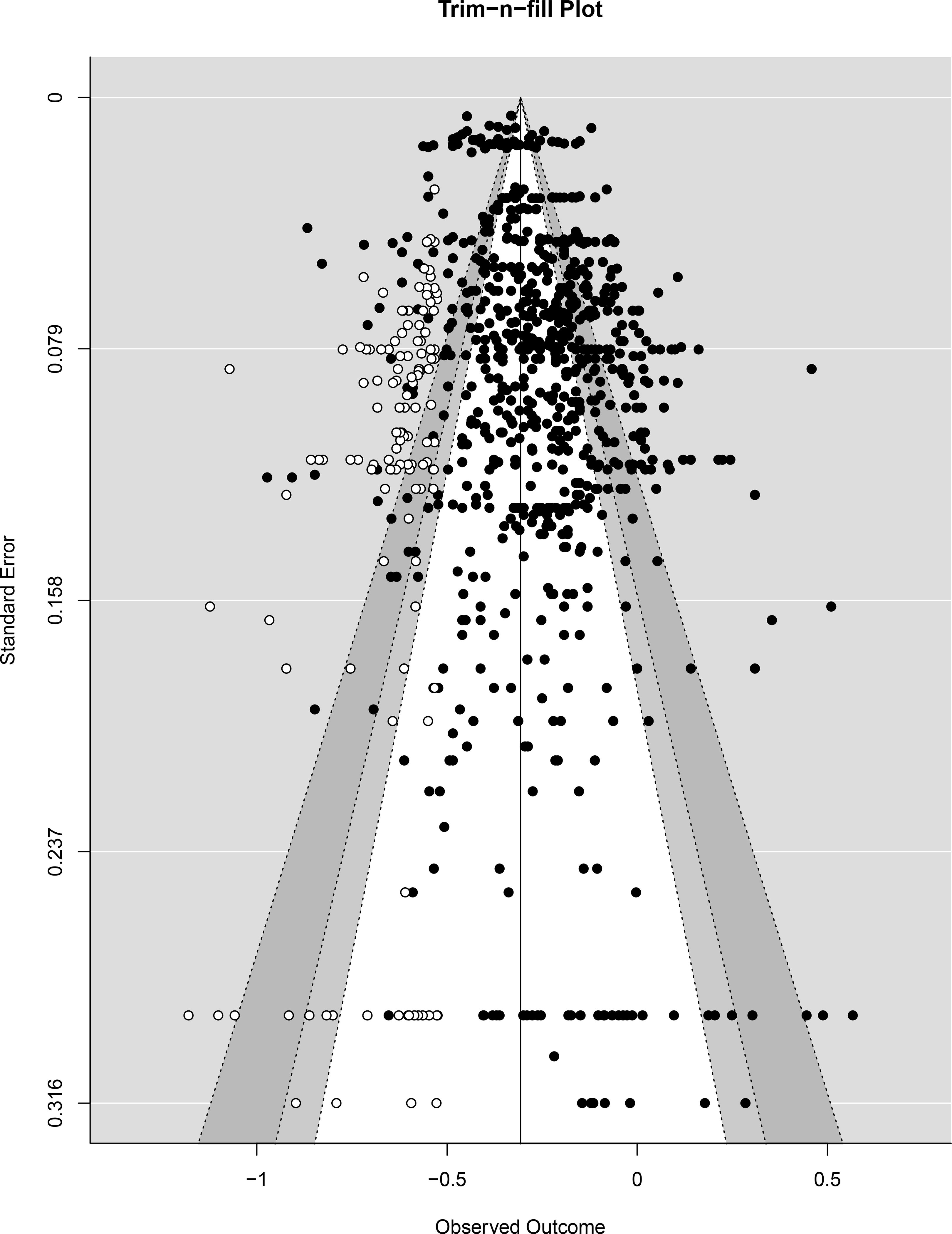
Funnel plot of Fisher’s Z-transformed correlations for all included effect sizes (black dots) and trim-and-fill analysis (white dots).
Discussion
Math achievement and math anxiety have been studied together for more than half a century (Dreger & Aiken, 1957). Previous meta-analyses have provided us with some knowledge about the association between math anxiety and math achievement, specifically that the association is negative and small-to-moderate, with patterns of high math anxiety often co-occurring with low math achievement (Hembree, 1990; Ma, 1999). Since the publication of previous meta-analyses in the 90s, the trend to study these constructs together has continued to grow. Reviews summarizing the wave of research from more recent years have primarily focused on examining the potential mechanisms behind the association between math anxiety and math achievement (Beilock & Maloney, 2015; Foley et al., 2017), leaving a need for an updated and thorough statistical summary of the work conducted on this relation since the start of the 21st century. Thus, the aims of the present meta-analysis were to 1) calculate an overall average weighted effect size based on recent work on the relation between math anxiety and math achievement and 2) conduct moderator analyses in order to determine whether the magnitude of the correlation differs depending on the demographic characteristics of the sample or the measures used to assess math anxiety or math achievement.
Overall Average Effect Size
We found an overall average correlation of −.28 across all included samples in our meta-analysis, indicating that math anxiety and math achievement tend to have a small-to-moderate negative association. Our findings are similar to the overall average correlation of −.27 found by Ma (1999) and fall within the range of correlations of −.25 to −.40 reported by Hembree (1990). Our results also reveal that there is significant heterogeneity in the spread of effect sizes that estimate the overall relation between math anxiety and math achievement. This suggests that variability in these effect sizes is due to the inclusion of samples that do not represent a homogenous population, supporting our methodological choice to conduct random-effects and mixed-effects models.
Moderators
We found that, after grouping effect sizes by subgroups within our moderators, significant negative relations between math anxiety and math achievement remained for most of our subgroups. We also found there were several significant differences in the size of the relation between subgroups within some moderators. Importantly, although our moderator analyses were able to provide some valuable information about potential sources of variability in the size of the effect sizes for the relation between math anxiety and math achievement, the estimates of heterogeneity for all the moderator analyses indicated that there was still a significant amount of variance left unexplained. These findings suggest that there may be other factors, like different levels of working memory (Ramirez, Chang, Maloney, Levine, & Beilock, 2016) or motivation in math (Wang et al., 2015), or a combination of factors including those not currently incorporated in the present study, that may be able to explain remaining variability found in the correlations included in this meta-analysis. Another important note to consider is that, despite weighting effect sizes by their standard errors and testing moderators of math assessments and anxiety scales, there still may be differences in the relation between math anxiety and math achievement that are due to the inherent differences between large-scale samples with equivalent and standardized measures (such as the PISA) and small-scale studies that use convenience samples and often use researcher-developed measures.
Demographic characteristics as moderators.
Gender, race/ethnicity, and continent.
It has been hypothesized in some work that the relation between math anxiety and achievement would be stronger for women than for men (Aiken, 1970), but that has not been found overall in either the current or previous meta-analyses. Specifically, Hembree (1990) found the opposite, that males in grades 5 through 12 demonstrated a stronger correlation between math anxiety and math achievement compared to females in that same age group. Contrary to these findings, we found in the current meta-analysis that the correlations for gender, when broken down by samples with either 100% male or 100% female participants, were similar in strength and magnitude, as did Ma (1999). Previous research has found gender differences in levels of self-reported math anxiety, with greater math anxiety reported by girls than by boys (Devine, Fawcett, Szűcs, & Dowker, 2012). Small gender differences have also been found in math achievement during middle childhood and adolescence, with the slight advantage switching between males and females and depending on the age of the sample and the type of math assessment (Else-Quest, Hyde, & Linn, 2010). Despite these differences in levels of math anxiety and math achievement scores separately, our meta-analytic results based on a pooled, diverse sample of studies, found that the association between math achievement and math anxiety is similar for males and females.
With regard to differences in the math anxiety-math achievement relation among different racial and ethnic groups, we found similar relations for samples from the United States made up of 75% or more White participants and samples that consisted of 75% or less White participants (i.e., majority non-White participants or racially diverse sample). This finding aligns with the results from Ma’s (1999) meta-analysis where he found similar magnitude correlations for ethnically homogenous versus ethnically heterogeneous samples. Importantly though, the present moderation analysis of race and ethnicity differences is subject to certain limitations. Specifically, the number of effect sizes from different race and ethnic groups was small and only data from samples within the United States were analyzed. However, given that cultural differences within racial and ethnic groups vary greatly depending on the specific racial and ethnic group being studied (Betancourt & López, 1993), it may be that differences in the relation between math anxiety and math achievement may only arise when looking across a variety of racial and ethnic groups from different countries rather than examining all minority groups from only one country. Thus, future work should examine the relation between math anxiety and math achievement from a variety of racial and ethnic groups from different countries in order to provide insight on the role of specific cultural practices within a specific racial or ethnic group.
The results of the previously untested moderator of the continent of origin of the study sample suggest that there are no significant differences in the strength of the relation between math anxiety and math achievement across the six continents tested in the current paper. Although some work has found that, overall, the correlation tends to be smaller in magnitude for samples from Asian countries (i.e., rs = −.12 to −.31) compared to North American and many European countries (i.e., rs = −.26 to −.51, Lee, 2009), this was not found to be the case in the current paper when testing for differences in effect size magnitude between continents, rather than between countries. However, as previously noted, cultures and educational systems between the countries within a continent are very different. We do provide some evidence in our supplemental analyses that there are differences in the relation at the country- and region-level within continents, yet many of these overall effect sizes are represented by only one sample. Although there may not be significant differences in the relation between math anxiety and math achievement at the continent-level, there is some support for the idea that the correlation varies depending on the country or region being studied. As such, research to collect more data in a larger number of samples from different countries is needed in order to gain a more precise understanding of where around the globe the relation differs and to further study cultural mechanisms that may be driving these differences.
Grade level.
Previous meta-analyses have found significant associations between math anxiety and achievement for students in grades ranging from grade 4 to college level (Hembree, 1990) but no significant differences in the magnitude of the relation based on grade level (Ma, 1999). In the current meta-analysis, we were able to include data from students in grades as early as grade 1 all the way up to samples made up of non-student adults. Our findings support previous work indicating that a significant relation between math anxiety and math achievement exists throughout different development periods, as well as adding that a significant relation exists for samples in early elementary school and beyond formal schooling in adulthood.
The significant differences we did find between grade level categories in the relation between math anxiety and math achievement suggest that the magnitude of the association varies across development. During early elementary school, the relation between math anxiety and achievement is significantly stronger compared to the same relation during high school. However, some research has found that general anxiety, a factor not considered in the present meta-analysis, explains the relation found between math anxiety and math achievement in young children (Dowker et al., 2016; Hill et al., 2016). As such, more work is needed to address and understand the mechanisms driving the stronger relation found between math anxiety and math achievement during early childhood.
Our findings also suggest that the relation between math anxiety and math achievement across grades does not follow a linear trend across development. Specifically, the correlation for students in grades 3 through 5 was significantly weaker than the relation for students in each of the other grade categories, with the exception of grades 1 and 2 and postsecondary students. Our supplemental analyses suggest that the weaker relation could be driven by differences in the relation between math anxiety and basic number knowledge for students in grades 3 through 5 compared to students in grades 1 and 2 and grades 6 through 8 (Tables S7 and S8). Overall, future research should consider the math content area as an important factor that may contribute to grade-level differences, particularly for students in late elementary school, in the math anxiety–math achievement association.
Moving on from late elementary to middle school, we do see a statistically significant increase in the relation between math anxiety and math achievement. Once students reach high school, the relation is found to be significantly stronger than that of the relation during late elementary school. High school students may experience increased pressure to perform well in school while preparing for selection into postsecondary school entry (Clinedinst & Koranteng, 2017), which could explain this increase in the co-occurrence of high math anxiety with low math achievement. Postsecondary school students, on the other hand, demonstrate a weaker relation in comparison to students in earlier development. Students who reach postsecondary education may represent a population of students with higher math achievement that experience less math anxiety as a result of their higher math ability, potentially reducing the strength of the relation between math anxiety and math achievement at that point in development.
Finally, we found that the relation does not disappear for non-student samples. Instead, the magnitude of the correlation is equivalent to the correlation for students in most of the other grade levels, with the exception of postsecondary school students, who demonstrate a weaker relation between math anxiety and math achievement than do non-student adults. This overall finding suggests a need for more research to further understand how the association between math anxiety and math achievement develops from childhood to adulthood.
It is important to note that the grade levels we coded in this study are based on the ages typically included in grade levels within the United States, and therefore these grades may differ internationally. In addition, some samples represented participants across a wide age range spanning across multiple grade level categories, yet we coded these groups into one category that matched the average age.
Teachers.
With regard to pre-service and practicing teacher samples, we found that, on average, studies examining these samples reported significant correlations between math anxiety and math achievement. In addition to the significant correlations found for non-student adult samples, these findings further emphasize why it is important to study this relation after high school graduation; clearly, this association is not a phenomenon that develops and then disappears once people have graduated from primary and secondary school. Future work should not only aim to create and implement interventions geared toward math anxiety or math achievement for student samples, but they may also explore the implementation of these interventions to non-student adults and teachers. Furthermore, there is some work suggesting that students majoring in elementary education have higher math anxiety than people in other college majors (Hembree, 1990), and that this math anxiety can influence their students’ beliefs and math achievement (Beilock et al., 2010). Importantly, we did not find the relation between math anxiety and math achievement to be significantly different between teacher and non-teacher samples. Though teachers have become a focus of research due to higher levels of anxiety, their anxiety does not appear to be more or less related to their math performance compared to other segments of the population.
Students with low math ability.
For the moderator analyses for low math ability samples, we did find a significant difference in the relation between math anxiety and math achievement for samples selected for low math ability compared to those not selected. Specifically, samples selected for low math ability had weaker, although still significant, associations than did samples not selected for low math ability. These findings are contrary to some work extending the deficit model of the relation between math anxiety and math achievement to populations with math learning disabilities (Lai, Zhu, Chen, & Li, 2015; Wu, Wilcutt, Escovar, & Menon, 2014). Instead, we find that, overall, the achievement of samples with low math ability is less related to math anxiety than it is for those samples that represent a wider range of math ability. Of course, it is important to note that the range of math achievement for many of these selected samples is typically restricted due to the cutoffs used for selection, and as such a stronger relation may not be as clear as it is for samples with more variability in their math achievement. In sum, more work needs to be done to better understand the weaker relations found for samples selected for low math ability compared to samples representing a larger range of math ability.
Measure characteristics as moderators.
Math anxiety scales.
With regard to the scales used to measure math anxiety, Ma (1999) previously found that the relations with math achievement did not significantly differ when using the MARS compared to a non-MARS measure. However, the 37 studies included in Ma’s (1999) meta-analysis represented only six individual math anxiety instruments. A number of new scales to measure math anxiety have emerged since then, and therefore we were able to test for effect size differences between scales that were developed to measure math anxiety separately in children and in adolescents and adults. Although some studies utilized child-, adolescent-, or adult-oriented measures in samples other than the age group they were intended for, creating separate variables for child as well as adolescent and adult anxiety measures allowed us to account for a majority of the confounding effect of age.
Overall, we found that math anxiety had a significant relation with math achievement for all math anxiety scale groups coded in this meta-analysis for children, adolescents, and adults. For the six child math anxiety scales, our results suggested that a similar relation can be expected with math achievement no matter which child math anxiety scale is used.
However, for adolescent and adult math anxiety scales, we found that several measures, specifically the group made up of MARS-based scales and one-item scales, had significantly weaker relations with math achievement than did the PISA math anxiety scale, the Fennema Sherman Math Anxiety Scale (FSMAS), the Achievement Emotion Questionnaire Math Anxiety Scale (AEQ), and the Math Anxiety Scale by Betz (MAS [Betz]; 1988). On the one hand, the one-item scale may not tap enough into specific math situations (due to only being one item rather than having a range of situations from multiple items) to consistently be associated with math achievement. On the other hand, scales like the original 98-item MARS may have way too many items that may lead to poor data quality and similarly reduce the potential association that math anxiety can have with math achievement. The MARS category in the current paper, however, includes shorter MARS-based measures also, like the MARS-revised (Plake & Parker, 1982) and the Abbreviated Math Anxiety Scale (Hopko et al., 2003); thus, the number of items may not fully explain the differences. It could also be that another one of the moderators we tested, specifically the components of math anxiety, plays a role in the differences found in the relations between math achievement and these scales (results discussed in next section). However, none of the math anxiety scales that were stronger (i.e., PISA, AEQ, FSMAS, MAS [Betz]) or weaker (i.e., MARS-based, one item) were consistently in any of the categories that we coded for in the components of math anxiety variable. Thus, the reason for the differences found here still remains an unanswered question. Overall, future research is needed to investigate these and other potential reasons why differences exist in the relations between math achievement and scores on these adolescent and adult math anxiety scales.
We also found that math anxiety scales assessing anxiety in the broader subject of math were significantly more related to math achievement than scales assessing anxiety in statistics. This finding suggests that the relation between math anxiety and math achievement is different depending on the math content of the anxiety scale. However, we also found that math anxiety topic is a significant moderator only in the case of assessments testing non-statistics math content (i.e., more related to math anxiety scales that to statistics anxiety scales). Statistics anxiety and math anxiety were similarly related to math achievement when the assessment was testing statistics content. These findings indicate that the content of the math assessment is also an important moderator of this relation, with the content of statistics playing a role in whether we find differences in the relation between math achievement and broader math anxiety scales compared to the relation between math achievement and statistics-specific anxiety scales.
Components of math anxiety.
With regard to the moderator of components of math anxiety, one might have expected that the strongest correlation would be between math evaluation anxiety and math achievement, because math achievement was primarily represented by math tests in this meta-analysis and the component of math evaluation anxiety specifically targets the situation of a math test. However, we found stronger relations between math achievement and the cognitive worry component of math anxiety compared to those effect sizes measuring math anxiety through the single component of math evaluation and through both components of math evaluation and learning anxiety. The relation with math achievement was also stronger with math anxiety measured as math learning anxiety and emotionality, separately, than those relations measured with both components of math evaluation and learning anxiety. This suggests that the negative relation between math anxiety and math achievement is stronger, at least when compared to items that ask about testing or testing and both learning situations in math, when the anxiety items ask about negative expectations and self-deprecating thoughts related to math stimuli or situations or when they ask about the process of learning in math as well as when they ask about physiological reactions during math situations. The stronger correlations found with the worry component of anxiety provide some evidence for the attentional control theory. This theory hypothesizes that, in a math context, anxious thoughts and worry take up limited cognitive resources that are needed to complete a math-related task, which subsequently reduces both efficiency and accuracy on the task (Eysenck et al., 2007).
Math assessments.
Regarding math achievement measures, a previous meta-analysis found weaker relations between math anxiety and commercially-developed and psychometrically-validated assessments than between math anxiety and researcher-made achievement measures and math teachers’ grades (Ma, 1999). This finding is unexpected when considering other work that shows that greater levels of anxiety are more often associated with high-stakes testing (Cassady & Johnson, 2002), which would fit into the psychometrically-validated test group from Ma’s (1999) meta-analysis. In the present meta-analysis, we were able to expand on the types of math assessments to include high-stakes standardized testing situations, standardized tests used for research, non-standardized research tests, math course grades, and math exam grades.
Similar to the previous meta-analysis, we found significant relations between math anxiety and each of these types of math assessments; however, the moderator effect we found was different from that found in Ma’s 1999 meta-analysis. We were able to separate what the 1999 meta-analysis considered to be an “other” category into three categories of non-standardized researcher-made math assessments, exam grades, and math course grades (or math GPA). We found that the relation was weaker between math anxiety and math exam grades compared to the relations between math anxiety and standardized measures for research and between math anxiety and non-standard researcher made measures. In other words, the relation between math achievement and math anxiety was significantly stronger, and more negative, when the achievement measure consisted of standardized tests used for research and non-standardized research-made compared to when the math assessment consisted of a math test or exam that were not high-stakes and mostly math class-level exams. Our lack of significant findings with regard to the high-stakes math tests subgroup also opposes the notion that, specifically with math-related tests, high-stakes exams are more related with math anxiety than other forms of math assessments. We find that the relation between math anxiety and high-stakes exams is similar to the relation between math anxiety and other types of math tests.
These findings have implications for education practitioners, parents, and researchers alike. For educators, knowing that the relation between math achievement and math anxiety is consistently weaker when the math assessment consists of a math exam that is often encountered in a regular classroom setting may be useful when preparing curriculum and using class math tests as sources of math knowledge that are less related with the math anxiety that a student may have. For parents, the weaker relation can also provide some relief for the various types of math assessments their children encounter throughout the school year. For researchers investigating the math anxiety-math achievement association in lab studies and experiments, this finding suggests that results from lab experiments and research projects are more likely to find stronger relations with math anxiety than when using math exam grades as measures of math achievement. Thus, it may be beneficial for researchers to know ahead of time that the relation between math anxiety and math achievement may be different depending on the measure of achievement they decide to use, whether it be already available exam grades provided by teachers or whether they decide to collect their own math achievement data.
Math content.
In the final moderation analysis based on measure characteristics, we tested whether the math content area of the math achievement measure was a moderator of the relation between math anxiety and math achievement. Hembree (1990) had previously reported significant relations, but did not test for differences in the relations between math anxiety and a variety of math content areas, such as computation, math concepts, problem solving, abstract reasoning, and spatial ability, for students in grade 7, high school, and postsecondary school. In the present analysis, we tested the relations between math anxiety and math achievement for assessments testing knowledge in a single content area for samples representing a wider grade level range than previously tested (i.e., grade 1 students through non-student adults). Our results indicated that there are significant negative correlations between math anxiety and most types of single-content math assessments, with the exception of the content area of approximate number system (ANS: r = −.09; other areas: rs ranged from −.20 to −.38).
We did not find evidence that math content area moderated the relation with math anxiety. Our supplemental analyses did suggest that there are grade-level differences for certain math content areas, but this is not the case when taking all grade levels into account. Some theories, such as the attentional control theory described earlier in this paper, have suggested that math anxiety disrupts cognitive resources such as working memory during achievement tasks (Eysenck, Derakshan, Santos, & Calco, 2007). Some previous research also indicates that math anxiety has negative consequences with complex math that requires greater use of cognitive resources (Ashcraft, 2002); however, our current findings suggest that the relation is similar across math content areas, whether they measure achievement in more basic math knowledge or more advanced content.
Publication Bias
Publication bias was assessed in the present meta-analysis in order to examine whether there is a tendency to publish stronger effect sizes compared to weaker ones and whether the available effect sizes included in our meta-analytic samples are representative of the true effect size or skewed due to missing studies (i.e., the “file drawer problem”; Rosenthal, 1979). Previous work has found that published studies reported weaker correlation between math anxiety and math achievement than did unpublished studies, which suggests an unexpected “positive publication bias” (Ma, 1999). In the current meta-analysis, we found the opposite to be the case, where effect sizes published in peer-reviewed journals were significantly stronger than the effect sizes reported in unpublished and grey literature. This finding supports the typical pattern of “negative” publication bias, in which smaller effect sizes and non-significant findings tend to not be published.
Additionally, our funnel plot and Egger test results indicate the presence of a skew against large effect sizes for all sample sizes in the distribution of the included effect sizes within the meta-analytic sample. The trim-and-fill method results further suggest that there are effect sizes missing and that inclusion of those effect sizes would produce a statistically significant, moderate, and negative adjusted overall effect size, similar to the original effect size reported here. Based on all of our publication indices, although the file drawer problem is an issue, our average weighted effect size is not significantly impacted by the potentially missing studies. Moreover, previous work has suggested that the trim-and-fill method should be used as a sensitivity analysis instead of an index of publication bias (Peters et al., 2007). It is unknown whether publication bias is the only cause of funnel plot asymmetry; often meta-analyses with large between-study heterogeneity in their effect sizes are due to tested or untested moderators. In these cases, use of the trim-and-fill method underestimates the true effect size when there is no publication bias. Overall, the publication bias evidenced by our indices is likely not a critical issue that would negatively impact the interpretation or significance of our main meta-analytic results.
Connections with Recent Work
One important note to mention is that, simultaneous to us working on this meta-analysis, two other research groups worked on and subsequently published meta-analyses of the relation between math anxiety and math performance (Namkung, Peng, & Lin, 2019; Zhang, Zhao, & Kong, 2019). There are some key differences in the search strategies, inclusion and exclusion criteria, and effect size extraction techniques between these two recently published meta-analyses and the present one that should be mentioned. In general, our study was more thorough and inclusive, as we chose to include adult samples, include unpublished data, and conduct author queries for missing information. This led us to have many more effect sizes (k = 747) compared to Zhang et al. (k = 84) and Namkung et al. (k = 478). Despite these differences, the main findings were generally similar across studies, suggesting that we are homing in on the magnitude of the relation between math anxiety and achievement. Our overall correlation was −.28 compared to a correlation of −.32 in Zhang et al. and −.34 in Namkung et al. An investigation of the articles included across the meta-analyses shows a lot of overlap, suggesting that we did not miss research included in these other studies. Therefore, our study makes an important unique contribution to this literature, while also being generally consistent with the findings of these other research groups.
Limitations
Although meta-analyses provide an opportunity to aggregate a large number of effect sizes from many studies that assess relevant factors, which then increases the power to draw more accurate, statistically-driven conclusions about the relations, the current set of analyses is not exhaustive in explaining the relation between math anxiety and math achievement. One limitation of a meta-analysis that considers only the zero-order correlation is that other relevant factors that may account for the relation, such as test anxiety (Devine et al., 2012) or math confidence (Hembree, 1990), are not examined in conjunction with the variables of interest. Thus, there may be confounding variables we do not account for that are influencing the relations we found between math anxiety and math achievement.
Another limitation is that any unexplained variance that remains in the accumulated effect sizes after accounting for all moderators tested suggests that there are other study factors, not included in the meta-analysis, that may also moderate the relation tested. For example, environmental factors, such as math activities done in the home (del Rio, Susperreguy, Strasser, & Salinas, 2017), have been previously highlighted as potentially important moderators of the relation between math anxiety and math achievement. Although many of the reasons posited to explain the significant moderators require direct testing through studies beyond a meta-analysis, additional work is needed to better explain the factors that influence the strength of the relation between math anxiety and math achievement.
Additionally, this study is limited to the relation between the emotion of anxiety in math and achievement. However, the study of the relations between different emotions and math achievement and how it differs from the relation between math anxiety and math achievement may also be an important gap to fill for future meta-analytic work.
Meta-analyses are dependent on the quality of the studies that are included in them, particularly because they rely on effect size parameters from studies that vary in the rigor of their study designs (Gersten, Baker, & Lloyd, 2000). Thus, another limitation of this meta-analysis is that the quality of the included studies was not examined as a moderator. There are instruments that have been previously developed to measure quality of reviews (Oxman & Guyatt, 1991), which have been used as templates for researchers to assess study quality in a meta-analysis (Downs & Black, 1998). Future meta-analyses on this topic should consider study quality as an important potential moderator.
There were also some limitations related to our search strategy and timeline. The search was done for articles available or published between January of 1992 through May of 2018. Thus, we may be missing studies that have been published since our last search that may impact the findings reported in our meta-analysis. Importantly though, we did solicit effect sizes from unpublished and ongoing studies from researchers in the area and were able to include 26 additional effect sizes from unpublished data that may have been published in the interim between our last search and our writing up of the results. Second, the search terms and databases used may not be expansive or broad enough to capture all available and relevant articles. Specifically, relevant studies, may have been missing due to the narrowness of the search terms used (i.e., math anxiety versus anxiety). While the results may still be generalizable, it is important to consider that there are likely some missing effect sizes that may be relevant for understanding the relation between math anxiety and math achievement.
An additional issue with our search strategy is the omission of the OECD 2013 report containing PISA 2012 data (OECD, 2013). PISA is a large international effort to gauge achievement levels every four years from over 510,000 high school students from 65 countries (OECD, 2013). The PISA 2012 data were published in a 2013 report, but this report was not found in the three journal databases we searched and therefore we did not include it in our sample. However, we did include effect sizes from previous PISA years and a few country’s effect sizes from PISA 2012 when empirical studies contained these effect sizes (i.e., Lee, 2013; Thien & Ong, 2015). The PISA 2012 sample consists of 15-year old students, and their average correlation across countries was −.34, which is the same magnitude of the correlation for high school students in the present study. This suggests the findings from our meta-analysis would likely not change with the inclusion of all PISA 2012 results.
Another limitation of the current meta-analysis is related to the low response rate by contacted authors for correlation information from potentially included studies. We sent first- or corresponding-authors email requests for correlation coefficient information for almost 200 studies, but the response rate was only 35%. The date criteria we chose extended as far back as 1992, and many researchers had likely moved from their original institutions or changed their originally listed email addresses by the time they were contacted. We opted to email authors rather than contact them through other modes of communication, which may have impacted the response rate. Although the response rate was low, the trim-and-fill analysis indicated that even if we were to uncover the file drawer problem and add 130 missing studies to fill in the unrepresented areas of our funnel plot, this addition would not have impacted the magnitude of the average correlation we found in our meta-analysis.
Additionally, the inter-rater reliabilities for two variables had lower-than-desired values (<80%; sample size: 72%; number of effect sizes: 75%). One reason for the low inter-rater reliability was because of the challenge of accurately coding information from experimental studies, specifically for control and experimental groups, separately. Some other reasons include one coder not finding the sample size in the paper and listing it as needing an author query, one coder reporting the full sample and the other coder reporting the analytic sample for that effect size, and true coding errors. Importantly though, a large number of the codes from experimental studies required an author query and thus the number of effect sizes and sample size variables were subsequently checked by the first author, which may help to increase the overall inter-rater reliability for these variables.
Finally, many of the effect sizes in our meta-analytic sample come from small convenience samples. Additionally, many of the samples are from Western countries (N = 626/744; 84%) and college students (N = 355/750; 47%). This minimal diversity and lack of representativeness are a limitation of our meta-analytic results, specifically for the race and ethnicity and continent moderator analyses we were able to conduct and present in this paper. Research on the relation between math anxiety and math achievement needs to continue to seek out more diverse and more representative samples to fully understand whether there are truly varying associations between math anxiety and math achievement for certain moderators.
Implications
In the ever-evolving sectors of education, researchers, teachers, and education policy-makers must constantly stay updated on the factors related to math achievement. Moreover, the implications of this relation during childhood and adolescence on future career and educational pathways is significant for both individuals’ career successes and society’s needs of a larger STEM workforce (Wigfield & Eccles, 2000; Wang & Degol, 2013). Math anxiety has been previously implicated as an important factor related to math achievement (Hembree, 1990; Ma, 1999). The present meta-analysis provides further support for the importance of the co-occurrence of math anxiety and math achievement. This relation is critical for people of all ages, a diverse set of demographics, and for different scale and assessment characteristics.
These current findings inform the development and implementation of interventions that aim to reduce math anxiety and/or increase math achievement. Previous experimental work has investigated the effectiveness of strategies such as writing sessions prior to a math task (Park, Ramirez, & Beilock, 2014) or reappraisal of anxiety (Jamieson, Mendes, Blackstock, & Schmader, 2010) to reduce math anxiety. Other work has focused on reducing the math achievement-math anxiety link by targeting math problem solving through cognitive tutoring (Supekar, Iuculano, Chen, & Menon, 2015). Importantly, the present work indicates that the association is detectable in children as young as students in grade 1. Thus, interventions such as those just described may be prudent for students as young as those in early elementary and could target math anxiety or achievement in content areas as foundational as basic number knowledge and whole number calculations.
Conclusions
The present meta-analysis provides an updated summary of the association between math anxiety and math achievement and moderators of the relation. We found that a small-to-moderate negative association is evident and robust for students as young as grades 1 and 2 all the way to up to non-student adults. These significant, small-to-moderate relations are evident across all types of math content areas, with the exception of content measuring the approximate number system. The strength of the relation with math achievement differs depending on the math anxiety scale used and the math topic that the anxiety scale asks about, a finding that can inform the choice of math anxiety scales for future research. Finally, the relation between math anxiety and math achievement is stronger for samples that are not selected for low math ability compared to samples that are selected for low math ability, providing some evidence against current research suggesting that samples selected for low math ability tend to have stronger relations between their achievement in math and of math anxiety. Overall, this work has both theoretical implications for current theories explaining the math anxiety math achievement and practical implications that will advise the future development of effective interventions to lower math anxiety, reduce its relation with math achievement, and improve math achievement in the long run.
Supplementary Material
Public Significance Statement:
The present meta-analysis finds a robust association between math anxiety and math achievement, indicating that people who report higher feelings of anxiety towards math tend to have lower math achievement. The relation is weaker for people at certain grade levels (grades 3 through 5 and college students), depends on the scales used to measure math anxiety, is stronger for math anxiety compared to statistics anxiety, and is weaker for math exam grades and for low math ability samples. Math anxiety is experienced by many individuals throughout development. Its association with math achievement makes math anxiety an important factor to consider for improving math experiences, academic outcomes, and STEM career participation.
Acknowledgments
The research reported in this paper was supported in part by the Eunice Kennedy Shriver National Institute of Child Health and Human Development, National Institutes of Health (Award #HD052120) and Institute of Education Sciences, U.S. Department of Education, through Grant R305A170463 to Florida State University. Views expressed herein are those of the authors and have neither been reviewed nor approved by the granting agencies.
Footnotes
The data and associated files for this meta-analysis are available at https://osf.io/szrhx
References
*References with effect sizes included in the present meta-analysis
**References with effect sizes of unpublished manuscripts or raw data at the time of request for unpublished literature included in the present meta-analysis
- *Abu-Hilal MM (2000). A structural model for predicting mathematics achievement: Its relation with anxiety and self-concept in mathematics. Psychological Reports, 86(3), 835–847. 10.2466/pr0.2000.86.3.835 [DOI] [PubMed] [Google Scholar]
- *Ader E, & Erktin E (2010). Coping as self-regulation of anxiety: A model for math achievement in high-stakes tests. Cognition, Brain, Behavior, 14(4), 311–332. https://search.proquest.com/docview/820543402?accountid=6724 [Google Scholar]
- *Agus M, Penna MP, Peró-Cebollero M, Guàrdia-Olmos J, & Pessa E (2016). Investigating the probabilistic reasoning in verbal–numerical and graphical–pictorial formats in relation to cognitive and non-cognitive dimensions: The proposal of a model. Personality and Individual Differences, 94, 44–53. 10.1016/j.paid.2016.01.003Get [DOI] [Google Scholar]
- Ahmed W (2018). Developmental trajectories of math anxiety during adolescence: Associations with STEM career choice. Journal of Adolescence, 67, 158–166. doi: 10.1016/j.adolescence.2018.06.010 [DOI] [PubMed] [Google Scholar]
- Aiken LR Jr (1970). Attitudes toward mathematics. Review of Educational Research, 40(4), 551–596. doi: 10.3102/00346543040004551 [DOI] [Google Scholar]
- *Aoude SG (2014). Factors affecting the performance of students in university remedial mathematics courses [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 75, Issue 1–A(E)). [Google Scholar]
- *Ariapooran S (2017). Mathematics motivation, anxiety, and Pprformance in female deaf/hard-of-hearing and hearing students. Communication Disorders Quarterly, 38(3), 172–178. 10.1177/1525740116681271 [DOI] [Google Scholar]
- **Arias JM (2016). Replication of study 2 in “Is math anxiety always bad for math learning? The role of math motivation” by Wang Z, Lukowski SL, Hart SA, Lyons IM, Thompson LA, Kovas Y, Mazzocco MM, Plomin R & Petrill SA (2015, Psychological Science). Unpublished manuscript. Stanford University, Stanford, California. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashcraft MH (2002). Math anxiety: Personal, educational, and cognitive consequences. Current Directions in Psychological Science, 11(5), 181–185. doi: 10.1111/1467-8721.00196 [DOI] [Google Scholar]
- Ashcraft MH, Kirk EP, & Hopko D (1998). On the cognitive consequences of mathematics anxiety. In Donlan C (Ed.), Studies in Developmental Psychology. The Development of Mathematical Skills (pp. 175–196). Hove, England: Psychology Press/Taylor & Francis (UK). [Google Scholar]
- Ashcraft MH, Krause JA, and Hopko D (2007). Is math anxiety a mathematical learning disability? In Berch DB and Mazzocco MMM (Eds.), Why Is Math So Hard For Some Children? The Nature and Origins of Mathematical Learning Difficulties and Disabilities (pp. 329–348). Baltimore, MD: Paul H Brookes Publishing Co. [Google Scholar]
- *Auxter AE (2017). The problem with word problems: An exploratory study of factors related to word problem success [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 77, Issue 12–A(E)). [Google Scholar]
- Ayotola A, & Adedeji T (2009). The relationship between gender, age, mental ability, anxiety, mathematics self-efficacy and achievement in mathematics. Cypriot journal of educational sciences, 4(2), 113–124. 10.1016/j.sbspro.2009.01.169 [DOI] [Google Scholar]
- *Bai H (2011). Cross-validating a bidimensional mathematics anxiety scale. Assessment, 18(1), 115–122. 10.1177/1073191110364312 [DOI] [PubMed] [Google Scholar]
- Bai H, Wang L, Pan W, & Frey M (2009). Measuring mathematics anxiety: Psychometric analysis of a bidimensional affective scale. Journal of Instructional Psychology, 36(3), 185–193. [Google Scholar]
- *Baloglu M (2001). An application of structural equation modeling techniques in the prediction of statistics anxiety among college students [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 62, Issue 2–A, p. 456). [Google Scholar]
- *Baloğlu M (2002). Psychometric properties of the statistics anxiety rating scale. Psychological Reports, 90(1), 315–325. doi: 10.2466/pr0.2002.90.1.315 [DOI] [PubMed] [Google Scholar]
- Bandalos DL, Yates K, & Thorndike-Christ T (1995). Effects of math self-concept, perceived self-efficacy, and attributions for failure and success on test anxiety. Journal of Educational Psychology, 87(4), 611–623. 10.1037/0022-0663.87.4.611 [DOI] [Google Scholar]
- *Bangert AW (1996). Peer assessment: An instructional strategy for effectively implementing performance-based assessments [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 56, Issue 9–A, p. 3505). [Google Scholar]
- **Barner D, Alvarez G, Sullivan J, Brooks N, Srinivasan M, & Frank MC (2016). Learning mathematics in a visuospatial format: A randomized, controlled trial of mental abacus instruction. Raw data. [DOI] [PubMed] [Google Scholar]
- **Barner D, Athanasopoulou A, Chu J, Lewis M, Marchand E, Schneider R, & Frank M (2016). A one-year classroom-randomized trial of mental abacus instruction for first- and second-grade students. Raw data. [Google Scholar]
- **Barroso C, Ganley CM, & Hart SA (2017). Psychology majors study cohort 2. Raw data. [Google Scholar]
- **Barroso C, Ganley CM, & Hart SA, Clendinning J, Rogers N (2018). Undergraduate music theory majors sample. Raw data. [Google Scholar]
- **Batchelor JH (2016). A mixed methods study of the effects of clicker use on math anxiety and achievement in mathematics. (Doctoral dissertation, Iowa State University). 10.31274/etd-180810-5502 [DOI] [Google Scholar]
- *Beasley TM, Long JD, & Natali M (2001). A confirmatory factor analysis of the mathematics anxiety scale for children. Measurement and Evaluation in Counseling and Development, 34(1), 14–26. 10.1080/07481756.2001.12069019 [DOI] [Google Scholar]
- Beilock SL, Gunderson EA, Ramirez G, & Levine SC (2010). Female teachers’ math anxiety affects girls’ math achievement. Proceedings of the National Academy of Sciences, 107(5), 1860–1863. doi: 10.1073/pnas.0910967107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beilock SL, & Maloney EA (2015). Math anxiety: A factor in math achievement not to be ignored. Policy Insights from the Behavioral and Brain Sciences, 2(1), 4–12. doi: 10.1177/2372732215601438 [DOI] [Google Scholar]
- **Benedict M (2017). The Effect of Gender on Math Anxiety: How adults think they feel versus how they actually feel. (Unpublished masters thesis). Carleton University, Ottawa, Canada. [Google Scholar]
- Benjamini Y, & Hochberg Y (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society: Series B (Methodological), 57(1), 289–300. [Google Scholar]
- *Bessant KC (2000). Affective and cognitive components of statistics course performance. (Doctoral dissertation, University of Manitoba). http://hdl.handle.net/1993/19534 [Google Scholar]
- Betancourt H, & López SR (1993). The study of culture, ethnicity, and race in American psychology. American Psychologist, 48(6), 629–637. doi: 10.1037/0003-066X.48.6.629 [DOI] [Google Scholar]
- Betz N (1978). Prevalence, distribution and correlates of math anxiety in college students. Journal of Counseling Psychology, 24, 551–558. doi: 10.1037/0022-0167.25.5.441 [DOI] [Google Scholar]
- *Birenbaum M, & Eylath S (1994). Who is afraid of statistics? Correlates of statistics anxiety among students of educational sciences. Educational Research, 36(1), 93–98. 10.1080/0013188940360110 [DOI] [Google Scholar]
- *Birgin O, Baloğlu M, Çatlıoğlu H, & Gürbüz R (2010). An investigation of mathematics anxiety among sixth through eighth grade students in Turkey. Learning and Individual Differences, 20(6), 654–658. 10.1016/j.lindif.2010.04.006 [DOI] [Google Scholar]
- *Bisse WH (1995). Mathematics anxiety: A multi-method study of causes and effects with community college students. (Unpublished doctoral dissertation). Northern Arizona University, Flagstaff, Arizona. [Google Scholar]
- *Bosmans G, & De Smedt B (2015). Insecure attachment is associated with math anxiety in middle childhood. Frontiers in Psychology, 6, 1596. 10.3389/fpsyg.2015.01596 [DOI] [PMC free article] [PubMed] [Google Scholar]
- **Braham EJ, & Libertus ME (2018). When approximate number acuity predicts math performance: The moderating role of math anxiety. PloS one, 13(5), e0195696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Buelow MT, & Barnhart WR (2017). The influence of math anxiety, math performance, worry, and test anxiety on the Iowa gambling task and balloon analogue risk task. Assessment, 24(1), 127–137. 10.1177/1073191115602554 [DOI] [PubMed] [Google Scholar]
- *Buelow MT, & Frakey LL (2013). Math anxiety differentially affects WAIS-IV arithmetic performance in undergraduates. Archives of Clinical Neuropsychology, 28(4), 356–362. 10.1093/arclin/act006 [DOI] [PubMed] [Google Scholar]
- *Bull H (2009). Identifying maths anxiety in student nurses and focusing remedial work. Journal of Further and Higher Education, 33(1), 71–81. doi: 10.1080/03098770802638689 [DOI] [Google Scholar]
- *Canu WH, Elizondo M, & Broman-Fulks JJ (2017). History of ADHD traits related to general test and specific math anxiety in college students. Learning and Individual Differences, 58, 56–63. 10.1016/j.lindif.2017.07.008 [DOI] [Google Scholar]
- *Carey E, Hill F, Devine A, & Szücs D (2016). The chicken or the egg? The direction of the relationship between mathematics anxiety and mathematics performance. Frontiers in Psychology, 6, 1987. doi: 10.3389/fpsyg.2015.01987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carey E, Hill F, Devine A, & Szűcs D (2017). The modified abbreviated math anxiety scale: A valid and reliable instrument for use with children. Frontiers in Psychology, 8, 11. doi: 10.3389/fpsyg.2017.00011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Cargnelutti E, Tomasetto C, & Passolunghi MC (2017). How is anxiety related to math performance in young students? A longitudinal study of Grade 2 to Grade 3 children. Cognition and Emotion, 31(4), 755–764. doi: 10.1080/02699931.2016.1147421 [DOI] [PubMed] [Google Scholar]
- *Casad BJ, Hale P, & Wachs FL (2015). Parent-child math anxiety and math-gender stereotypes predict adolescents’ math education outcomes. Frontiers in Psychology, 6, 1597. 10.3389/fpsyg.2015.01597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Casey MB, Nuttall RL, & Pezaris E (1997). Mediators of gender differences in mathematics college entrance test scores: A comparison of spatial skills with internalized beliefs and anxieties. Developmental psychology, 33(4), 669–680. 10.1037//0012-1649.33.4.669 [DOI] [PubMed] [Google Scholar]
- Cassady JC, & Johnson RE (2002). Cognitive test anxiety and academic performance. Contemporary Educational Psychology, 27(2), 270–295. doi: 10.1006/ceps.2001.1094 [DOI] [Google Scholar]
- *Catapano M (2013). Tenth-grade high school students’ mathematical self-efficacy, mathematics anxiety, attitudes toward mathematics, and performance on the New York State Integrated Algebra Regents Examination. (Order No. 3572381). Available From ProQuest Central Student. (1442456200). Retrieved from https://search.proquest.com/docview/1442456200?accountid=6724
- *Çatlıoğlu H, Gürbüz R, & Birgin O (2014). Do pre-service elementary school teachers still have mathematics anxiety? Some factors and correlates. Bolema: Boletim de Educação Matemática, 28(48), 110–127. 10.1590/1980-4415v28n48a06 [DOI] [Google Scholar]
- Catsambis S (1994). The path to math: Gender and racial-ethnic differences in mathematics participation from middle school to high school. Sociology of Education, 67, 199–215. doi: 10.2307/2112791 [DOI] [Google Scholar]
- Caviola S, Mammarella IC, Cornoldi C, & Lucangeli D (2012). The involvement of working memory in children’s exact and approximate mental addition. Journal of Experimental Child Psychology, 112(2), 141–160. doi: 10.1016/j.jecp.2012.02.005 [DOI] [PubMed] [Google Scholar]
- *Caviola S, Primi C, Chiesi F, & Mammarella IC (2017). Psychometric properties of the Abbreviated Math Anxiety Scale (AMAS) in Italian primary school children. Learning and Individual Differences, 55, 174–182. 10.1016/j.lindif.2017.03.006 [DOI] [Google Scholar]
- *Cheema JR, & Sheridan K (2015). Time spent on homework, mathematics anxiety and mathematics achievement: Evidence from a US sample. Issues in Educational Research, 25(3), 246–259. http://www.iier.org.au/iier25/cheema.html [Google Scholar]
- *Cheung KC (2017). The effects of resilience in learning variables on mathematical literacy performance: a study of learning characteristics of the academic resilient and advantaged low achievers in Shanghai, Singapore, Hong Kong, Taiwan and Korea. Educational Psychology, 37(8), 965–982. 10.1080/01443410.2016.1194372 [DOI] [Google Scholar]
- *Chiesi F, & Primi C (2010). Cognitive and non-cognitive factors related to students’ statistics achievement. Statistics Education Research Journal, 9(1), 6–26. 10.1177/0734282911404985 [DOI] [Google Scholar]
- *Chiesi F, Primi C, & Carmona J (2011). Measuring statistics anxiety: Cross-country validity of the Statistical Anxiety Scale (SAS). Journal of Psychoeducational Assessment, 29(6), 559–569. 10.3389/fpsyg.2015.01833 [DOI] [Google Scholar]
- Cimpian JR, Lubienski ST, Timmer JD, Makowski MB, & Miller EK (2016). Have gender gaps in math closed? Achievement, teacher perceptions, and learning behaviors across two ECLS-K cohorts. AERA Open, 2(4), 1–19. doi: 10.1177/233285841667361726942210 [DOI] [Google Scholar]
- *Cipora K, Szczygieł M, Willmes K, & Nuerk HC (2015). Math anxiety assessment with the abbreviated math anxiety scale: applicability and usefulness: insights from the polish adaptation. Frontiers in Psychology, 6, 1833. doi: 10.3389/fpsyg.2015.01833 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clinedinst M, & Koranteng AM (2017). State of college admission. http://hdl.handle.net/10919/83148.
- *Coates JD (1998). Mathematics anxiety and its relationship to students’ perceived teacher and parent attitudes toward mathematics. Mathematics anxiety and its relationship to students’ perceived teacher and parent attitudes toward mathematics [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 58, Issue 12–A, p. 4590). [Google Scholar]
- Cochran WG (1954). The combination of estimates from different experiments. Biometrics 10(1), 101–129. doi: 10.2307/3001666 [DOI] [Google Scholar]
- Cohn LD, & Becker BJ (2003). How meta-analysis increases statistical power. Psychological Methods, 8(3), 243–253. doi: 10.1037/1082-989X.8.3.243 [DOI] [PubMed] [Google Scholar]
- **Conlon R, Hicks A, Barroso C, & Ganley CM (2018). Anxiety Timing Study. Raw data. [Google Scholar]
- *Cook RP (1998). An exploration of the relationship between mathematics anxiety level and perceptual learning style of adult learners in a community college setting [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 58, Issue 10–A, p. 3801). [Google Scholar]
- Cooper H, Hedges LV, & Valentine JC (Eds.). (2009). The Handbook of Research Synthesis and Meta-analysis. Russell Sage Foundation. [Google Scholar]
- Corbett C, & Hill C (2015). Solving the Equation: The Variables for Women’s Success in Engineering and Computing. American Association of University Women. 1111 Sixteenth Street NW, Washington, DC: 20036. [Google Scholar]
- *Cortina JM (1995). On the meaning and measurement of test appropriateness. (Unpublished doctoral dissertation). Michigan State University, East Lansing, Michigan. [Google Scholar]
- *D’Aloisio BE (2016). Investigating predictors of academic success in a foundational business mathematics course. (Doctoral dissertation, Rhode Island College). 10.28971/242016db105 [DOI] [Google Scholar]
- *Daches Cohen L, & Rubinsten O (2017). Mothers, intrinsic math motivation, arithmetic skills, and math anxiety in elementary school. Frontiers in psychology, 8, 1939. 10.3389/fpsyg.2017.01939 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Davis MM (2010). An exploration of factors affecting the academic success of students in a college quantitative business course [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 71, Issue 1–A, p. 102). [Google Scholar]
- del Río MF, Susperreguy MI, Strasser K, & Salinas V (2017). Distinct Influences of Mothers and Fathers on Kindergartners’ Numeracy Performance: The Role of Math Anxiety, Home Numeracy Practices, and Numeracy Expectations. Early Education and Development, 28(8), 939–955. doi: 10.1080/10409289.2017.1331662 [DOI] [Google Scholar]
- Devine A, Hill F, Carey E, & Szűcs D (2018). Cognitive and emotional math problems largely dissociate: Prevalence of developmental dyscalculia and mathematics anxiety. Journal of Educational Psychology, 110(3), 431–444. doi: 10.1037/edu0000222 [DOI] [Google Scholar]
- *Devine A, Fawcett K, Szűcs D, & Dowker A (2012). Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behavioral and Brain Functions, 8(33). doi: 10.1186/1744-9081-8-33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Devine A, Hill F, Carey E, & Szűcs D (2018). Cognitive and emotional math problems largely dissociate: Prevalence of developmental dyscalculia and mathematics anxiety. Journal of Educational Psychology, 110(3), 431–444. 10.1037/edu0000222 [DOI] [Google Scholar]
- *Donelle L (2008). Risk comprehension of online colorectal cancer information: An assessment of health numeracy [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 68, Issue 11–A, p. 4531). [Google Scholar]
- **Douglas H, & LeFevre J (2016). Modeling Relations Between Math Anxiety and Cognition: Limited evidence for a cognitive deficits hypothesis. Unpublished manuscript. [Google Scholar]
- Dowker A, Sarkar A, & Looi CY (2016). Mathematics anxiety: what have I learned in 60 years?. Frontiers in Psychology, 7, 508. doi: 10.3389/fpsyg.2016.00508 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Downs SH, & Black N (1998). The feasibility of creating a checklist for the assessment of the methodological quality both of randomised and non-randomised studies of health care interventions. Journal of Epidemiology & Community Health, 52(6), 377–384. doi: 10.1136/jech.52.6.377 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dreger RM, & Aiken LR Jr (1957). The identification of number anxiety in a college population. Journal of Educational Psychology, 48(6), 344–351. doi: 10.1037/h0045894 [DOI] [Google Scholar]
- Duval S, & Tweedie R (2000). Trim and fill: a simple funnel-plot–based method of testing and adjusting for publication bias in meta-analysis. Biometrics, 56(2), 455–463. doi: 10.1111/j.0006-341X.2000.00455.x [DOI] [PubMed] [Google Scholar]
- *Dutko JA (2016). Understanding mathematics anxiety: The relationships between fourth grade students’ math anxiety, multiplication fact fluency, and problem solving ability [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 76, Issue 9–A(E)). [Google Scholar]
- Education Commission of the States (2018). 50-State Comparison: State Kindergarten Through Third Grade Policies, retrieved from https://www.ecs.org/kindergarten-policies/.
- Egger M, Smith GD, Schneider M, & Minder C (1997). Bias in meta-analysis detected by a simple, graphical test. Bmj, 315(7109), 629–634. doi: 10.1136/bmj.315.7109.629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Else-Quest NM, Hyde JS, & Linn MC (2010). Cross-national patterns of gender differences in mathematics: a meta-analysis. Psychological Bulletin, 136(1), 103–127. doi: 10.1037/a0018053 [DOI] [PubMed] [Google Scholar]
- Else-Quest NM, Mineo CC, & Higgins A (2013). Math and science attitudes and achievement at the intersection of gender and ethnicity. Psychology of Women Quarterly, 37(3), 293–309. doi: 10.1177/0361684313480694 [DOI] [Google Scholar]
- Engelhard G (1990). Math anxiety, mother’s education, and the mathematics performance of adolescent boys and girls: Evidence from the United States and Thailand. The Journal of Psychology, 124(3), 289–298. doi: 10.1080/00223980.1990.10543224 [DOI] [PubMed] [Google Scholar]
- *Erturan S, & Jansen B (2015). An investigation of boys’ and girls’ emotional experience of math, their math performance, and the relation between these variables. European Journal of Psychology of Education, 30(4), 421–435. 10.1007/s10212-015-0248-7 [DOI] [Google Scholar]
- Espino M, Pereda J, Recon J, Perculeza E, & Umali C (2017). Mathematics anxiety and its impact on the course and career choice of grade 11 students. International Journal of Education, Psychology and Counselling, 2, 99–119. http://www.ijepc.com/PDF/IJEPC-2017-05-09-08.pdf [Google Scholar]
- Eysenck MW, & Calvo MG (1992). Anxiety and performance: The processing efficiency theory. Cognition & Emotion, 6(6), 409–434. doi: 10.1080/02699939208409696 [DOI] [Google Scholar]
- Eysenck MW, Derakshan N, Santos R, & Calvo MG (2007). Anxiety and cognitive performance: attentional control theory. Emotion, 7(2), 336. doi: 10.1037/1528-3542.7.2.336 [DOI] [PubMed] [Google Scholar]
- Fan X, Chen M, & Matsumoto AR (1997). Gender differences in mathematics achievement: Findings from the National Education Longitudinal Study of 1988. The Journal of Experimental Education, 65(3), 229–242. doi: 10.1080/00220973.1997.9943456 [DOI] [Google Scholar]
- *Fannin-Carroll KD (2015). The effect of math anxiety on the academic success of developmental mathematics students at a texas community college [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 75, Issue 9–A(E)). [Google Scholar]
- *Farnsworth DM Jr. (2009). Math Performance as a Function of Math Anxiety and Arousal Performance Theory. (Doctoral dissertation, The University of North Dakota, Grand Forks, North Dakota: ). https://commons.und.edu/theses/896 [Google Scholar]
- *Farquharson F (2005). A comparison of community college students’ anxiety, motivation, and achievement in two learning models for teaching developmental algebra: Instructor-directed computer-mediated model and traditional lecture model [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 65, Issue 11–A, p. 4138). [Google Scholar]
- *Faust MW, Ashcraft MH, & Fleck DE (1996). Mathematics anxiety effects in simple and complex addition. Mathematical Cognition, 2(1), 25–62. 10.1080/135467996387534 [DOI] [Google Scholar]
- *Federici RA, & Skaalvik EM (2014). Students’ Perceptions of Emotional and Instrumental Teacher Support: Relations with Motivational and Emotional Responses. International Education Studies, 7(1), 21–36. 10.5539/ies.v7n1p21 [DOI] [Google Scholar]
- Fennema E, & Sherman JA (1976). Fennema-Sherman mathematics attitudes scales: Instruments designed to measure attitudes toward the learning of mathematics by females and males. Journal for Research in Mathematics Education, 7(5), 324–326. doi: 10.2307/748467 [DOI] [Google Scholar]
- *Ferla J, Valcke M, & Cai Y (2009). Academic self-efficacy and academic self-concept: Reconsidering structural relationships. Learning and individual differences, 19(4), 499–505. 10.1016/j.lindif.2009.05.004 [DOI] [Google Scholar]
- *Finney SJ, & Schraw G (2003). Self-efficacy beliefs in college statistics courses. Contemporary Educational Psychology, 28(2), 161–186. 10.1016/S0361-476X(02)00015-2 [DOI] [Google Scholar]
- **Foley A (2015). Visuospatial working memory and arithmetic strategies. Unpublished manuscript. University of Chicago, Chicago, Illinois. [Google Scholar]
- Foley AE, Herts JB, Borgonovi F, Guerriero S, Levine SC, & Beilock SL (2017). The math anxiety-performance link: A global phenomenon. Current Directions in Psychological Science, 26(1), 52–58. doi: 10.1177/0963721416672463 [DOI] [Google Scholar]
- *Frenzel AC, Pekrun R, & Goetz T (2007). Girls and mathematics—A “hopeless” issue? A control-value approach to gender differences in emotions towards mathematics. European Journal of Psychology of Education, 22(4), 497. 10.1007/BF03173468 [DOI] [Google Scholar]
- *Gan SKE, Lim KMJ, & Haw YX (2016). The relaxation effects of stimulative and sedative music on mathematics anxiety: A perception to physiology model. Psychology of Music, 44(4), 730–741. 10.1177/0305735615590430 [DOI] [Google Scholar]
- **Ganley CM (2014). Test framing study. Raw data. [Google Scholar]
- **Ganley CM, & Hart SA (2017). Common Core Paper. Raw data. [Google Scholar]
- *Ganley CM, & McGraw AL (2016). The development and validation of a revised version of the math anxiety scale for young children. Frontiers in psychology, 7, 1181. 10.3389/fpsyg.2016.01181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Ganley CM, Conlon R, McGraw AL, Barroso C, & Geer EA (2016). Anxiety Intervention Study. Raw data. [Google Scholar]
- *Ganley CM, & Vasilyeva M (2011). Sex differences in the relation between math performance, spatial skills, and attitudes. Journal of Applied Developmental Psychology, 32(4), 235–242. 10.1016/j.appdev.2011.04.001 [DOI] [Google Scholar]
- **Gashaj, & Roebers (2015). Mathematics and Motor Study. Unpublished Manuscript.
- **Geer EA, & Ganley CM (2017). Spatial and social project. Raw data. [Google Scholar]
- *Gibson-Dee KA (2016). Hope, expectation, math anxiety, and achievement in college algebra students: Examining an instructional strategy using multi-level modeling. (Doctoral dissertation, University of South Florida, Tampa, Florida: ). https://scholarcommons.usf.edu/etd/6506 [Google Scholar]
- Gierl MJ, & Bisanz J (1995). Anxieties and attitudes related to mathematics in grades 3 and 6. The Journal of experimental education, 63(2), 139–158. [Google Scholar]
- Gersten R, Baker S, & Lloyd JW (2000). Designing high-quality research in special education: Group experimental design. The Journal of Special Education, 34(1), 2–18. doi: 10.1177/002246690003400101 [DOI] [Google Scholar]
- **Gilligan KA, Thomas MSC, & Farran EK (2016). Mathematics in the Primary Years: The role of dispositional factors. Unpublished Manuscript. University of Surrey, Guildford, England. [Google Scholar]
- *Goetz T, Bieg M, Lüdtke O, Pekrun R, & Hall NC (2013). Do girls really experience more anxiety in mathematics?. doi: Psychological science, 24(10), 2079–2087. 10.1177/0956797613486989 [DOI] [PubMed] [Google Scholar]
- *González A, Rodríguez Y, Faílde JM, & Carrera MV (2016). Anxiety in the statistics class: Structural relations with self-concept, intrinsic value, and engagement in two samples of undergraduates. Learning and Individual Differences, 45, 214–221. 10.1016/j.lindif.2015.12.019 [DOI] [Google Scholar]
- Gonzalez-DeHass AR, Furner JM, Vásquez-Colina MD, & Morris JD (2017). Pre-service elementary teachers’ achievement goals and their relationship to math anxiety. Learning and Individual Differences, 60, 40–45. doi: 10.1016/j.lindif.2017.10.002 [DOI] [Google Scholar]
- *Gorvine BJ, & Smith HD (2015). Predicting student success in a psychological statistics course emphasizing collaborative learning. Teaching of Psychology, 42(1), 56–59. 10.1177/0098628314562679 [DOI] [Google Scholar]
- Gottfried AE, Marcoulides GA, Gottfried AW, Oliver PH, & Guerin DW (2007). Multivariate latent change modeling of developmental decline in academic intrinsic math motivation and achievement: Childhood through adolescence. International Journal of Behavioral Development, 31(4), 317–327. doi: 10.1177/0165025407077752 [DOI] [Google Scholar]
- Gunderson EA, Park D, Maloney EA, Beilock SL, & Levine SC (2018). Reciprocal relations among motivational frameworks, math anxiety, and math achievement in early elementary school. Journal of Cognition and Development, 19(1), 21–46. doi: 10.1080/15248372.2017.1421538 [DOI] [Google Scholar]
- *Guven B, & Cabakcor BO (2013). Factors influencing mathematical problem-solving achievement of seventh grade Turkish students. Learning and Individual Differences, 23, 131–137. 10.1016/j.lindif.2012.10.003 [DOI] [Google Scholar]
- *Hadfield OD, Littleton CE, Steiner RL, & Woods ES (1998). Predictors of preservice elementary teacher effectiveness in the micro-teaching of mathematics lessons. Journal of Instructional Psychology, 25(1), 34–47. [Google Scholar]
- *Hafner EW (2008). The relationship between math anxiety, math self-efficacy, and achievement among a sample of eighth grade students [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 69, Issue 2–A, p. 503) [Google Scholar]
- Hall CW, Davis NB, Bolen LM, & Chia R (1999). Gender and racial differences in mathematical performance. The Journal of Social Psychology, 139(6), 677–689. doi: 10.1080/00224549909598248 [DOI] [PubMed] [Google Scholar]
- *Hamid MHS, Shahrill M, Matzin R, Mahalle S, & Mundia L (2013). Barriers to Mathematics Achievement in Brunei Secondary School Students: Insights into the roles of mathematics anxiety, self-esteem, proactive coping, and test stress. International Education Studies, 6(11), 1–14. 10.5539/ies.v6n11p1 [DOI] [Google Scholar]
- *Hanna D, & Dempster M (2009). The effect of statistics anxiety on students’ predicted and actual test scores. The Irish Journal of Psychology, 30(3–4), 201–209. 10.1080/03033910.2009.10446310 [DOI] [Google Scholar]
- *Harari RR, Vukovic RK, & Bailey SP (2013). Mathematics anxiety in young children: an exploratory study. The Journal of Experimental Education, 81(4), 538–555. doi: 10.1080/00220973.2012.727888 [DOI] [Google Scholar]
- *Harding JL (2015). The effect of cooperative learning groups on mathematics and statistics anxiety in a college mathematics class. (Unpublished doctoral dissertation). Robert Morris University, Pittsburgh, Pennsylvania. [Google Scholar]
- *Harpole CA (1996). Effects of a mental rotations curriculum on mathematical conceptualization and math anxiety in eighth-grade male and female students [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 57, Issue 2–A, p. 0612). [Google Scholar]
- *Hart SA, Daucourt M, & Ganley CM (2017). Individual differences related to college students’ course performance in calculus II. Journal of Learning Analytics, 4(2), 129–153. 10.18608/jla.2017.42.11 [DOI] [Google Scholar]
- **Hart SA, & Ganley CM (2016). Psychology Majors Study Cohort 1. Raw data. [Google Scholar]
- *Hart SA, & Ganley CM (2019). The nature of math anxiety in adults: Prevalence and correlates. Journal of Numerical Cognition, 5(2), 122–139. 10.5964/jnc.v5i2.195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Hart SA, Ganley CM, & Purpura DJ (2016). Understanding the home math environment and its role in predicting parent report of children’s math skills. PloS one, 11(12), e0168227. 10.1371/journal.pone.0168227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Hart SA, Logan JA, Thompson L, Kovas Y, McLoughlin G, & Petrill SA (2016). A latent profile analysis of math achievement, numerosity, and math anxiety in twins. Journal of educational psychology, 108(2), 181. 10.1037/edu0000045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Helming L (2013). Motivation and Math Anxiety for Ability Grouped College Math Students. (Doctoral dissertation). ERIC. (1773213371; ED563200). [Google Scholar]
- Hembree R (1990). The nature, effects, and relief of mathematics anxiety. Journal for Research in Mathematics Education, 21(1), 33–46. doi: 10.2307/749455 [DOI] [Google Scholar]
- *Henschel S, & Roick T (2017). Relationships of mathematics performance, control and value beliefs with cognitive and affective math anxiety. Learning and Individual Differences, 55, 97–107. 10.1016/j.lindif.2017.03.009 [DOI] [Google Scholar]
- Higgins JP, & Thompson SG (2002). Quantifying heterogeneity in a meta-analysis. Statistics in Medicine, 21(11), 1539–1558. doi: 10.1002/sim.1186 [DOI] [PubMed] [Google Scholar]
- *Hill F, Mammarella IC, Devine A, Caviola S, Passolunghi MC, & Szűcs D (2016). Maths anxiety in primary and secondary school students: Gender differences, developmental changes and anxiety specificity. Learning and Individual Differences, 48, 45–53. doi: 10.1016/j.lindif.2016.02.006 [DOI] [Google Scholar]
- *Hoffman B (2010). “I think I can, but I’m afraid to try”: The role of self-efficacy beliefs and mathematics anxiety in mathematics problem-solving efficiency. Learning and Individual Differences, 20(3), 276–283. 10.1016/j.lindif.2010.02.001 [DOI] [Google Scholar]
- *Hong E, & Karstensson L (2002). Antecedents of state test anxiety. Contemporary Educational Psychology, 27(2), 348–367. 10.1006/ceps.2001.1095 [DOI] [Google Scholar]
- *Hoover JD, & Healy AF (2017). Algebraic reasoning and bat-and-ball problem variants: Solving isomorphic algebra first facilitates problem solving later. Psychonomic Bulletin & Review, 24(6), 1922–1928. 10.3758/s13423-017-1241-8 [DOI] [PubMed] [Google Scholar]
- *Hopko DR, Hunt MK, & Armento ME (2005). Attentional task aptitude and performance anxiety. International Journal of Stress Management, 12(4), 389. 10.1037/1072-5245.12.4.389 [DOI] [Google Scholar]
- Hopko DR, Mahadevan R, Bare RL, & Hunt MK (2003). The abbreviated math anxiety scale (AMAS) construction, validity, and reliability. Assessment, 10(2), 178–182. doi: 10.1177/1073191103010002008 [DOI] [PubMed] [Google Scholar]
- *Hunt TE, Bhardwa J, & Sheffield D (2017). Mental arithmetic performance, physiological reactivity and mathematics anxiety amongst UK primary school children. Learning and Individual Differences, 57, 129–132. 10.1016/j.lindif.2017.03.016 [DOI] [Google Scholar]
- *Hunt TE, Clark-Carter D, & Sheffield D (2015). Exploring the Relationship Between Mathematics Anxiety and Performance: An eye-tracking approach. Applied Cognitive Psychology, 29(2), 226–231. 10.1002/acp.3099 [DOI] [Google Scholar]
- **Hurst M, & Cordes S (2012). FDN Study 1. Unpublished Manuscript. Boston College, Boston, Massachusetts. [Google Scholar]
- **Hurst M, & Cordes S (2013). FDN Study 2. Unpublished Manuscript. Boston College, Boston, Massachusetts. [Google Scholar]
- Hurst M, & Cordes S (2017). When Being Good at Math Is Not Enough: How Students’ Beliefs About the Nature of Mathematics Impact Decisions to Pursue Optional Math Education. In Understanding Emotions in Mathematical Thinking and Learning (pp. 221–241). Academic Press. [Google Scholar]
- *Hutt GK (2007). Experiential learning spaces: Hermetic transformational leadership for psychological safety, consciousness development and math anxiety related inferiority complex depotentiation (Doctoral dissertation, Case Western Reserve University, Columbus, Ohio: ). http://rave.ohiolink.edu/etdc/view?acc_num=case1175892374 [Google Scholar]
- Hyde JS, Fennema E, & Lamon SJ (1990). Gender differences in mathematics performance: a meta-analysis. Psychological Bulletin, 107(2), 139–155. doi: 10.1037/0033-2909.107.2.139 [DOI] [PubMed] [Google Scholar]
- *Imbo I, & Vandierendonck A (2007). Do multiplication and division strategies rely on executive and phonological working memory resources?. Memory & Cognition, 35(7), 1759–1771. 10.3758/BF03193508 [DOI] [PubMed] [Google Scholar]
- *Imbo I, & Vandierendonck A (2007). The development of strategy use in elementary school children: Working memory and individual differences. Journal of experimental child psychology, 96(4), 284–309. 10.1016/j.jecp.2006.09.001 [DOI] [PubMed] [Google Scholar]
- *Iossi LH (2009). The mathematics anxiety of bilingual community college students. (Doctoral Dissertation, Florida International University). [Google Scholar]
- *Ironsmith M, Marva J, Harju B, & Eppler M (2003). Motivation and Performance in College Students Enrolled in Self-Paced Versus Lecture-Format Remedial Mathematics Courses. Journal of Instructional Psychology, 30(4). 276–284. [Google Scholar]
- *Jameson MM (2013). The development and validation of the Children’s Anxiety in Math Scale. Journal of Psychoeducational Assessment, 31(4), 391–395. [Google Scholar]
- Jameson MM (2014). Contextual factors related to math anxiety in second-grade children. The Journal of Experimental Education, 82(4), 518–536. doi: 10.1080/00220973.2013.813367 [DOI] [Google Scholar]
- Jamieson JP, Mendes WB, Blackstock E, & Schmader T (2010). Turning the knotw in your stomach into bows: Reappraising arousal improves performance on the GRE. Journal of Experimental Social Psychology, 46(1), 208–212. doi: 10.1016/j.jesp.2009.08.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Jamieson JP, Peters BJ, Greenwood EJ, & Altose AJ (2016). Reappraising stress arousal improves performance and reduces evaluation anxiety in classroom exam situations. Social Psychological and Personality Science, 7(6), 579–587. 10.1177/1948550616644656 [DOI] [Google Scholar]
- *Jansen BR, Louwerse J, Straatemeier M, Van der Ven SH, Klinkenberg S, & Van der Maas HL (2013). The influence of experiencing success in math on math anxiety, perceived math competence, and math performance. Learning and Individual Differences, 24, 190–197. 10.1016/j.lindif.2012.12.014 [DOI] [Google Scholar]
- *Jansen BR, Schmitz EA, & van der Maas HL (2016). Affective and motivational factors mediate the relation between math skills and use of math in everyday life. Frontiers in psychology, 7, 513. 10.3389/fpsyg.2016.00513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Jenßen L, Dunekacke S, Eid M, & Blömeke S (2015). The relationship of mathematical competence and mathematics anxiety. Zeitschrift für Psychologie. 10.1027/2151-2604/a000197 [DOI] [Google Scholar]
- Jordan NC, Kaplan D, Ramineni C, & Locuniak MN (2009). Early math matters: kindergarten number competence and later mathematics outcomes. Developmental Psychology, 45(3), 850–867. doi: 10.1037/a0014939 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Justicia-Galiano MJ, Martín-Puga ME, Linares R, & Pelegrina S (2017). Math anxiety and math performance in children: The mediating roles of working memory and math self-concept. British Journal of Educational Psychology, 87(4), 573–589. 10.1111/bjep.12165 [DOI] [PubMed] [Google Scholar]
- *Justicia-Galiano MJ, Pelegrina S, Lechuga MT, Gutiérrez-Palma N, Martín-Puga EM, & Lendínez C (2016). Math anxiety and its relationship to inhibitory abilities and perceived emotional intelligence. Anales De Psicología/Annals of Psychology, 32(1), 125–131. 10.6018/analesps.32.1.194891 [DOI] [Google Scholar]
- *Karimi A, & Venkatesan S (2009). Mathematics anxiety, mathematics performance and overall academic performance in high school students. Management and Labour Studies, 34(4), 556–562. 10.1177/0258042X0903400406 [DOI] [Google Scholar]
- Kastberg D, Chan JY, & Murray G (2016). Performance of US 15-Year-Old Students in Science, Reading, and Mathematics Literacy in an International Context: First Look at PISA 2015. NCES 2017–048. National Center for Education Statistics. [Google Scholar]
- *Keeley J, Zayac R, & Correia C (2008). Curvilinear relationships between statistics anxiety and performance among undergraduate students: Evidence for optimal anxiety. Statistics Education Research Journal, 7(1), 4–15. [Google Scholar]
- *Khabiri PS (1994). The role of metacognition, effort and worry in math problem-solving requiring problem translation [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 54, Issue 9–A, p. 3379). [Google Scholar]
- *Kim J, & McLean JE (1994). The Relationships between Individual Difference Variables and Test Performance in Computerized Adaptive Testing. Paper presented at the Annual Meeting of the Mid-South Educational Research Association, Nashville, TN. [Google Scholar]
- *Kimber CT (2009). The effect of training in self-regulated learning on math anxiety and achievement among preservice elementary teachers in a freshman course in mathematics concepts. (Doctoral dissertation, Temple University, Philadelphia, Pennsylvania: ). https://digital.library.temple.edu/digital/collection/p245801coll10/id/27309/ [Google Scholar]
- *Koponen V, & Lasonen J (1994). Finnish Vocational High School Students’ Perceptions of Themselves as Learners of Mathematics. International Journal of Vocational Education and Training, 2(1), 21–37. [Google Scholar]
- **Kowalsky AL (2017). The role of fingers in adults’ numerical processing. Unpublished manuscript. Florida State University, Tallahassee, Florida. [Google Scholar]
- **Krinzinger H (2016). Math anxiety questionnaire cross-sectional (group testing of MAQ). Unpublished manuscript. RWTH Aachen University, Aachen, Germany. [Google Scholar]
- *Krinzinger H, Kaufmann L, & Willmes K (2009). Math anxiety and math ability in early primary school years. Journal of Psycho-Educational Assessment, 27(3), 206–225. 10.1177/0734282908330583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Kyttälä M, & Björn PM (2010). Prior mathematics achievement, cognitive appraisals and anxiety as predictors of Finnish students’ later mathematics performance and career orientation. Educational Psychology, 30(4), 431–448. 10.1080/01443411003724491 [DOI] [Google Scholar]
- *Kyttälä M, & Björn PM (2014). The role of literacy skills in adolescents’ mathematics word problem performance: Controlling for visuo-spatial ability and mathematics anxiety. Learning and Individual Differences, 29, 59–66. 10.1016/j.lindif.2013.10.010 [DOI] [Google Scholar]
- *Lai Y, Zhu X, Chen Y, & Li Y (2015). Effects of mathematics anxiety and mathematical metacognition on word problem solving in children with and without mathematical learning difficulties. PloS one, 10(6), e0130570. doi: 10.1371/journal.pone.0130570 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Lalonde RN, & Gardner RC (1993). Statistics as a second language? A model for predicting performance in psychology students. Canadian Journal of Behavioural Science/Revue canadienne des sciences du comportement, 25(1), 108–125. 10.1037/h0078792 [DOI] [Google Scholar]
- **Lauer JE, Esposito AG, & Bauer PJ (2016). The role of anxiety in math and spatial performance: Developmental change and specificity across the elementary-school years. Unpublished manuscript. Emory University, Atlanta, Georgia. [Google Scholar]
- Lauermann F, Chow A, & Eccles JS (2015). Differential effects of adolescents’ expectancy and value beliefs about math and English on math/science-related and human services-related career plans. International Journal of Gender, Science and Technology, 7(2), 205–228. http://genderandset.open.ac.uk/index.php/genderandset/article/view/393 [Google Scholar]
- *Lawson VJ (1993). Mathematics anxiety, test anxiety, instructional methods, and achievement in a developmental mathematics class [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 53, Issue 10–A, p. 3479). [Google Scholar]
- *Leap EM (2013). A Quasi-Experimental Study Investigating the Effect of Scent on Students’ Memory of Multiplication Facts and Math Anxiety. ERIC. (1720060993; ED557536). [Google Scholar]
- *Lee J (2009). Universals and specifics of math self-concept, math self-efficacy, and math anxiety across 41 PISA 2003 participating countries. Learning and Individual Differences, 19(3), 355–365. doi: 10.1016/j.lindif.2008.10.009 [DOI] [Google Scholar]
- *Lee K, & Cho S (2018). Magnitude processing and complex calculation is negatively impacted by mathematics anxiety while retrieval-based simple calculation is not. International Journal of Psychology, 53(4), 321–329. 10.1002/ijop.12412 [DOI] [PubMed] [Google Scholar]
- **LeFevre JA, Penner-Wilger M, Pyke AA, Shanahan T, & Deslauriers WA (2014). Putting Two and Two Together: Declines in Arithmetic Fluency among Young Canadian Adults, 1993 to 2005. Technical Report 2014–01 (No. 2014–01). https://ir.library.carleton.ca/pub/20945/ [Google Scholar]
- *Lester D (2007). Predicting performance in a psychological statistics course. Psychological Reports, 101(1), 334–334. 10.10.2466/PR0.101.1.334 [DOI] [PubMed] [Google Scholar]
- *Lester D (2016). Predicting success in psychological statistics courses. Psychological Reports, 118(3), 772–777. 10.1177/0033294116647687 [DOI] [PubMed] [Google Scholar]
- Liebert RM, & Morris LW (1967). Cognitive and emotional components of test anxiety: A distinction and some initial data. Psychological Reports, 20(3), 975–978. doi: 10.2466/pr0.1967.20.3.975 [DOI] [PubMed] [Google Scholar]
- *Lim SY, & Chapman E (2013). An investigation of the Fennema-Sherman mathematics anxiety subscale. Measurement and Evaluation in Counseling and Development, 46(1), 26–37. 10.1177/0748175612459198 [DOI] [Google Scholar]
- *Lim SY, & Chapman E (2013). Development of a short form of the attitudes toward mathematics inventory. Educational Studies in Mathematics, 82(1), 145–164. 10.1007/s10649-012-9414-x [DOI] [Google Scholar]
- *Lim SY, & Chapman E (2015). Identifying affective domains that correlate and predict mathematics performance in high-performing students in Singapore. Educational Psychology, 35(6), 747–764. 10.1080/01443410.2013.860221 [DOI] [Google Scholar]
- *Lindskog M, Winman A, & Poom L (2017). Individual differences in nonverbal number skills predict math anxiety. Cognition, 159, 156–162. doi: 10.1016/j.cognition.2016.11.014 [DOI] [PubMed] [Google Scholar]
- *Lloyd SA, & Robertson CL (2012). Screencast tutorials enhance student learning of statistics. Teaching of Psychology, 39(1), 67–71. 10.1177/0098628311430640 [DOI] [Google Scholar]
- Lubienski ST (2002). A closer look at Black-White mathematics gaps: Intersections of race and SES in NAEP achievement and instructional practices data. Journal of Negro Education, 269–287. doi: 10.2307/3211180 [DOI] [Google Scholar]
- *Lukowski SL, DiTrapani J, Jeon M, Wang Z, Schenker VJ, Doran MM, ... & Petrill SA (2016). Multidimensionality in the measurement of math-specific anxiety and its relationship with mathematical performance. Learning and individual differences. 10.1016/j.lindif.2016.07.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Luo W, Hogan D, Tan LS, Kaur B, Ng PT, & Chan M (2014). Self-construal and students’ math self-concept, anxiety and achievement: An examination of achievement goals as mediators. Asian Journal of Social Psychology, 17(3), 184–195. 10.1111/ajsp.12058 [DOI] [Google Scholar]
- *Luo W, Lee K, Ng PT, & Ong JXW (2014). Incremental beliefs of ability, achievement emotions and learning of Singapore students. Educational Psychology, 34(5), 619–634. 10.1080/01443410.2014.909008 [DOI] [Google Scholar]
- Ma X (1999). A meta-analysis of the relationship between anxiety toward mathematics and achievement in mathematics. Journal for Research in Mathematics Education, 520–540. [Google Scholar]
- Ma X, & Xu J (2004). The causal ordering of mathematics anxiety and mathematics achievement: a longitudinal panel analysis. Journal of Adolescence, 27(2), 165–179. doi: 10.1016/j.adolescence.2003.11.003 [DOI] [PubMed] [Google Scholar]
- Maas CJ, & Hox JJ (2004). Robustness issues in multilevel regression analysis. Statistica Neerlandica, 58(2), 127–137. doi: 10.1046/j.0039-0402.2003.00252.x [DOI] [Google Scholar]
- *Macher D, Paechter M, Papousek I, & Ruggeri K (2011). Statistics anxiety, trait anxiety, learning behavior, and academic performance. European Journal of Psychology of Education, 27(4), 483–498. 10.1007/s10212-011-0090-5 [DOI] [Google Scholar]
- *Macher D, Paechter M, Papousek I, Ruggeri K, Freudenthaler HH, & Arendasy M (2013). Statistics anxiety, state anxiety during an examination, and academic achievement. British Journal of Educational Psychology, 83(4), 535–549. 10.1111/j.2044-8279.2012.02081.x [DOI] [PubMed] [Google Scholar]
- MacLeod C, & Mathews A (2012). Cognitive bias modification approaches to anxiety. Annual Review of Clinical Psychology, 8, 189–217. doi: 10.1146/annurev-clinpsy-032511-143052 [DOI] [PubMed] [Google Scholar]
- *Maloney EA, Ramirez G, Gunderson EA, Levine SC, & Beilock SL (2015). Intergenerational effects of parents’ math anxiety on children’s math achievement and anxiety. Psychological Science, 26(9), 1480–1488. doi: 10.1177/0956797615592630 [DOI] [PubMed] [Google Scholar]
- Maloney EA, Risko EF, Ansari D, & Fugelsang J (2010). Mathematics anxiety affects counting but not subitizing during visual enumeration. Cognition, 114(2), 293–297. doi: 10.1016/j.cognition.2009.09.013 [DOI] [PubMed] [Google Scholar]
- *Maree JG, Fletcher L, & Erasmus P (2013). The relationship between emotional intelligence, study orientation in mathematics and the mathematics achievement of the middle adolescent. Journal of Psychology in Africa, 23(2), 205–211. 10.1080/14330237.2013.10820616 [DOI] [Google Scholar]
- *Maree JG, Van Der Walt MS, & Ellis SM (2009). Developing a study orientation questionnaire in mathematics for primary school students. Psychological Reports, 104(2), 425–438. 10.2466/PR0.104.2.425-438 [DOI] [PubMed] [Google Scholar]
- McLeod DB (1994). Research on affect and mathematics learning in the JRME: 1970 to the present. Journal for Research in Mathematics Education, 25(6), 637–647. doi: 10.2307/749576 [DOI] [Google Scholar]
- *McMullan M, Jones R, & Lea S (2012). Math anxiety, self-efficacy, and ability in British undergraduate nursing students. Research in Nursing & Health, 35(2), 178–186. 10.1002/nur.21460 [DOI] [PubMed] [Google Scholar]
- Meece JL (1981). Individual differences in the affective reactions of middle and high school students to mathematics: A social cognitive perspective [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 42, Issue 5–A, pp. 2035–2036). [Google Scholar]
- Meece JL, Wigfield A, & Eccles JS (1990). Predictors of math anxiety and its influence on young adolescents’ course enrollment intentions and performance in mathematics. Journal of Educational Psychology, 82(1), 60–70. doi: 10.1037/0022-0663.82.1.60 [DOI] [Google Scholar]
- *Melius J (2012). Mathematics anxiety and mathematics self-efficacy in relation to medication calculation performance in nurses (Doctoral dissertation, University of North Texas , Denton, Texas: ). https://digital.library.unt.edu/ark:/67531/metadc115119/m1/116/ [Google Scholar]
- *Merritt WP (2012). Exploring math anxiety as it relates to math achievement, gender, and race [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 73, Issue 3–A, p. 943). [Google Scholar]
- *Miller H, & Bichsel J (2004). Anxiety, working memory, gender, and math performance. Personality and Individual Differences, 37(3), 591–606. 10.1016/j.paid.2003.09.029 [DOI] [Google Scholar]
- *Mkhize MV, & Maistry SM (2017). Pre-service accounting teachers’ attitudes to mathematics. South African Journal of Education, 37(2). 10.15700/saje.v37n2a1372 [DOI] [Google Scholar]
- *Morony S, Kleitman S, Lee YP, & Stankov L (2013). Predicting achievement: Confidence vs self-efficacy, anxiety, and self-concept in Confucian and European countries. International Journal of Educational Research, 58, 79–96. 10.1016/j.ijer.2012.11.002 [DOI] [Google Scholar]
- *Morsanyi K, Primi C, Handley SJ, Chiesi F, & Galli S (2012). Are systemizing and autistic traits related to talent and interest in mathematics and engineering? Testing some of the central claims of the empathizing–systemizing theory. British Journal of Psychology, 103(4), 472–496. 10.1186/1744-9081-10-31 [DOI] [PubMed] [Google Scholar]
- *Morsanyi K, Busdraghi C, & Primi C (2014). Mathematical anxiety is linked to reduced cognitive reflection: a potential road from discomfort in the mathematics classroom to susceptibility to biases. Behavioral and Brain Functions, 10(1), 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nag OS (2018, February 1). Europe Countries and Regions. Retrieved from https://www.worldatlas.com/articles/the-four-european-regions-as-defined-by-the-united-nations-geoscheme-for-europe.html
- Namkung JM, Peng P, & Lin X (2019). The relation between mathematics anxiety and mathematics performance among school-aged students: a meta-analysis. Review of Educational Research, 89(3), 459–496. [Google Scholar]
- *Nasser FM (2004). Structural model of the effects of cognitive and affective factors on the achievement of Arabic-speaking pre-service teachers in introductory statistics. Journal of Statistics Education, 12(1), 1–19. http://jse.amstat.org/v12n1/nasser.html [Google Scholar]
- *Nasser F, & Birenbaum M (2005). Modeling mathematics achievement of Jewish and Arab eighth graders in Israel: The effects of learner-related variables. Educational Research and Evaluation, 11(3), 277–302. 10.1080/13803610500101108 [DOI] [Google Scholar]
- *Necka EA, Sokolowski HM, & Lyons IM (2015). The role of self-math overlap in understanding math anxiety and the relation between math anxiety and performance. Frontiers In Psychology, 6, 1543. 10.3389/fpsyg.2015.01543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Novak E, & Tassell JL (2015). A dataset for education-related majors’ performance measures with pre/post-video game practice. British Journal of Educational Technology, 46(5), 932–936. 10.1111/bjet.12287 [DOI] [Google Scholar]
- *Novak E, & Tassell JL (2017). Studying preservice teacher math anxiety and mathematics performance in geometry, word, and non-word problem solving. Learning and Individual Differences, 54, 20–29. 10.1016/j.lindif.2017.01.005 [DOI] [Google Scholar]
- *Núñez-Peña MI (2013). 2013 undergraduate student data. Raw data. [Google Scholar]
- *Núñez-Peña MI (2014). 2014 undergraduate student data. Raw data. [Google Scholar]
- Núñez-Peña MI, Guilera G, & Suárez-Pellicioni M (2014). The single-item math anxiety scale: An alternative way of measuring mathematical anxiety. Journal of Psychoeducational Assessment, 32(4), 306–317. doi: 10.1177/0734282913508528 [DOI] [Google Scholar]
- Núñez-Peña MI, & Suárez-Pellicioni M (2014). Less precise representation of numerical magnitude in high math-anxious individuals: an ERP study of the size and distance effects. Biological Psychology, 103, 176–183. doi: 10.1177/0734282913508528 [DOI] [PubMed] [Google Scholar]
- Organisation for Economic Co-operation and Development (1999). Measuring Student Knowledge and Skills: A New Framework for Assessment. OECD Publishing. [Google Scholar]
- OECD. (2013). PISA 2012 Results: Ready to Learn (Volume III): Students’ Engagement, Drive and Self-Beliefs, PISA, OECD Publishing, Paris, 10.1787/9789264201170-en. [DOI] [Google Scholar]
- Organisation for Economic Co-operation and Development (2016). PISA 2015 Results (Volume I): Excellence and Equity in Education. OECD Publishing. doi: 10.1787/9789264266490-en. [DOI] [Google Scholar]
- Olson S, & Riordan DG (2012). Engage to Excel: Producing One Million Additional College Graduates with Degrees in Science, Technology, Engineering, and Mathematics. Report to the President. Executive Office of the President. [Google Scholar]
- *Otts CD (2010). Self-Regulation and math attitudes: effects on academic performance in developmental math courses at a community college. (Ed. D. Dissertation, University of Kansas, Lawrence, Kansas: ). http://hdl.handle.net/1808/7081 [Google Scholar]
- *Owens AR (1993). The relationship between selected affective and cognitive variables to academic achievement and persistence with peer tutoring [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 54, Issue 1–A, p. 108). [Google Scholar]
- Oxman AD, & Guyatt GH (1991). Validation of an index of the quality of review articles. Journal of clinical epidemiology, 44(11), 1271–1278. doi: 10.1016/0895-4356(91)90160-B [DOI] [PubMed] [Google Scholar]
- *Paechter M, Macher D, Martskvishvili K, Wimmer S, & Papousek I (2017). Mathematics anxiety and statistics anxiety. Shared but also unshared components and antagonistic contributions to performance in statistics. Frontiers In Psychology, 8, 1196. 10.3389/fpsyg.2017.01196 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pajares MF (1995). Mathematics self-efficacy as a mediating mechanism on mathematics problem-solving performance: A path analysis. (Doctoral Dissertation, University of Florida, Gainesville, Florida: ). https://ufdc.ufl.edu/AA00034641/00001 [Google Scholar]
- *Pajares F (1996). Self-efficacy beliefs and mathematical problem-solving of gifted students. Contemporary Educational Psychology, 21(4), 325–344. 10.1006/ceps.1996.0025 [DOI] [PubMed] [Google Scholar]
- *Pajares F, & Graham L (1999). Self-efficacy, motivation constructs, and mathematics performance of entering middle school students. Contemporary Educational Psychology, 24(2), 124–139. 10.1006/ceps.1998.0991 [DOI] [PubMed] [Google Scholar]
- *Pajares F, & Kranzler J (1995). Self-efficacy beliefs and general mental ability in mathematical problem-solving. Contemporary Educational Psychology, 20(4), 426–443. 10.1006/ceps.1995.1029 [DOI] [PubMed] [Google Scholar]
- Pariona A (2018, February 10). The Five Regions of Asia - Asia Countries and Regions. Retrieved from https://www.worldatlas.com/articles/the-four-regions-of-asia.html.
- *Park DE (2015). Motivational frameworks among children in early elementary school [ProQuest Information & Learning]. In Dissertation Abstracts International: Section B: The Sciences and Engineering (Vol. 76, Issue 2–B(E)). [Google Scholar]
- Park D, Ramirez G, & Beilock SL (2014). The role of expressive writing in math anxiety. Journal of Experimental Psychology: Applied, 20(2), 103–111. doi: 10.1037/xap0000013 [DOI] [PubMed] [Google Scholar]
- *Parks MQ (2009). Possible effects of calculators on the problem-solving abilities and mathematical anxiety of students with learning disabilities or attention deficit hyperactivity disorder. (Unpublished doctoral dissertation). Walden University, Minneapolis, Minnesota. [Google Scholar]
- Pekrun R (2006). The control-value theory of achievement emotions: Assumptions, corollaries, and implications for educational research and practice. Educational psychology review, 18(4), 315–341. doi: 10.1007/s10648-006-9029-9 [DOI] [Google Scholar]
- Pekrun R, Goetz T, Frenzel AC, Barchfeld P, & Perry RP (2011). Measuring emotions in students’ learning and performance: The Achievement Emotions Questionnaire (AEQ). Contemporary Educational Psychology, 36(1), 36–48. doi: 10.1016/j.cedpsych.2010.10.002 [DOI] [Google Scholar]
- Pekrun R, Lichtenfeld S, Marsh HW, Murayama K, & Goetz T (2017). Achievement emotions and academic performance: Longitudinal models of reciprocal effects. Child development, 88(5), 1653–1670. doi: 10.1111/cdev.12704 [DOI] [PubMed] [Google Scholar]
- Peng P, Namkung J, Barnes M, & Sun C (2016). A meta-analysis of mathematics and working memory: Moderating effects of working memory domain, type of mathematics skill, and sample characteristics. Journal of Educational Psychology, 108(4), 455–473. doi: 10.1037/edu0000079 [DOI] [Google Scholar]
- Peters JL, Sutton AJ, Jones DR, Abrams KR, Rushton L, & Moreno SG (2010). Assessing publication bias in meta-analyses in the presence of between-study heterogeneity. Journal of the Royal Statistical Society: Series A (Statistics in Society), 173(3), 575–591. [Google Scholar]
- *Piearcy RK (1997). The relationship between mathematics anxiety, cerebral hemispheric dominance, and final course grade of students in college algebra [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 57, Issue 7–A, p. 2926). [Google Scholar]
- Plake BS, & Parker CS (1982). The development and validation of a revised version of the Mathematics Anxiety Rating Scale. Educational and Psychological Measurement, 42(2), 551–557. doi: 10.1177/001316448204200218 [DOI] [Google Scholar]
- *Pletzer B, Wood G, Moeller K, Nuerk HC, & Kerschbaum HH (2010). Predictors of performance in a real-life statistics examination depend on the individual cortisol profile. Biological Psychology, 85(3), 410–416. 10.1016/j.biopsycho.2010.08.015 [DOI] [PubMed] [Google Scholar]
- Pretorius TB, & Norman AM (1992). Psychometric data on the statistics anxiety scale for a sample of South African students. Educational and Psychological Measurement, 52(4), 933–937. doi: 10.1177/0013164492052004015 [DOI] [Google Scholar]
- *Prieto G, & Delgado AR (2007). Measuring math anxiety (in Spanish) with the Rasch rating scale model. Journal of Applied Measurement, 8(2), 149. [PubMed] [Google Scholar]
- *Radišić J, Videnović M, & Baucal A (2015). Math anxiety—contributing school and individual level factors. European Journal of Psychology of Education, 30(1), 1–20. 10.1007/s10212-014-0224-7 [DOI] [Google Scholar]
- *Ramirez G (2014). The cognitive mechanism underlying the math anxiety-performance relationship in early elementary school [ProQuest Information & Learning]. In Dissertation Abstracts International: Section B: The Sciences and Engineering (Vol. 75, Issue 1–B(E)). [Google Scholar]
- *Ramirez G (2017). Motivated forgetting in early mathematics: A proof-of-concept study. Frontiers in Psychology, 8, 2087. 10.3389/fpsyg.2017.02087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Ramirez G, Chang H, Maloney EA, Levine SC, & Beilock SL (2016). On the relationship between math anxiety and math achievement in early elementary school: The role of problem solving strategies. Journal of Experimental Child Psychology, 141, 83–100. doi: 10.1016/j,jecp.2015.07.014 [DOI] [PubMed] [Google Scholar]
- *Ramirez G, Gunderson EA, Levine SC, & Beilock SL (2013). Math anxiety, working memory, and math achievement in early elementary school. Journal of Cognition and Development, 14(2), 187–202. doi: 10.1080/15248372.2012.664593 [DOI] [Google Scholar]
- Ramirez G, Hooper SY, Kersting NB, Ferguson R, & Yeager D (2018). Teacher math anxiety relates to adolescent students’ math achievement. AERA Open, 4(1), 1–13. doi: 10.1177/2332858418756052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Rayner V, Pitsolantis N, & Osana H (2009). Mathematics anxiety in preservice teachers: Its relationship to their conceptual and procedural knowledge of fractions. Mathematics Education Research Journal, 21(3), 60–85. 10.1007/BF03217553 [DOI] [Google Scholar]
- *Ribeiro FS, Tonoli MC, Ribeiro DPDSA, & Santos FHD (2017). Numeracy deficits scrutinized: Evidences of primary developmental dyscalculia. Psychology & Neuroscience, 10(2), 189. 10.1037/pne0000082 [DOI] [Google Scholar]
- Richardson FC, & Suinn RM (1972). The mathematics anxiety rating scale: psychometric data. Journal of Counseling Psychology, 19(6), 551–554. doi: 10.1037/h0033456 [DOI] [Google Scholar]
- *Roberts SO, & Vukovic RK (2011). The relation between parental involvement and math anxiety: implications for mathematics achievement. Paper presented at the meeting of the Society for Research on Educational Effectiveness, Washington, D.C. [Google Scholar]
- *Rolison JJ, Morsanyi K, & O’Connor PA (2016). Can I count on getting better? Association between math anxiety and poorer understanding of medical risk reductions. Medical Decision Making, 36(7), 876–886. 10.1177/0272989X15602000 [DOI] [PubMed] [Google Scholar]
- Rounds JB, & Hendel DD (1980). Measurement and dimensionality of mathematics anxiety. Journal of Counseling Psychology, 27(2), 138. [Google Scholar]
- Rosenthal R (1979). The file drawer problem and tolerance for null results. Psychological Bulletin, 86(3), 638–641. doi: 10.1037/0033-2909.86.3.638 [DOI] [Google Scholar]
- *Rushing BH Jr. (1997). Effects of study skill and systematic desensitization training on mathematics anxiety, mathematics achievement, mathematics self-efficacy, and cognitive interference among university students enrolled in developmental mathematics [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 57, Issue 7–A, p. 2927). [Google Scholar]
- *Sandoz EK, Butcher G, & Protti TA (2017). A preliminary examination of willingness and importance as moderators of the relationship between statistics anxiety and performance. Journal of Contextual Behavioral Science, 6(1), 47–52. 10.1016/j.jcbs.2017.02.002 [DOI] [Google Scholar]
- *Satake E, & Amato PP (1995). Mathematics anxiety and achievement among Japanese elementary school students. Educational and Psychological Measurement, 55(6), 1000–1007. 10.1177/0013164495055006009 [DOI] [Google Scholar]
- **Schmitz EA, Salemink E, Wiers RW, & Jansen BR (2015). Development of the Components of the Math Anxiety Questionnaire. Unpublished data. [Google Scholar]
- *Schnell K, Tibubos AN, Rohrmann S, & Hodapp V (2013). Test and math anxiety: A validation of the German Test Anxiety Questionnaire. Polish Psychological Bulletin, 44(2), 193–200. 10.2478/ppb-2013-0022 [DOI] [Google Scholar]
- *Schoeck AM (1994). The effectiveness of cognitive/relaxation training in reducing test anxiety and math anxiety and improving arithmetic performance with ninth- and tenth-grade students [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 54, Issue 12–A, p. 4395). [Google Scholar]
- *Schommer-Aikins M, Unruh S, & Morphew J (2015). Epistemological belief congruency in mathematics between vocational technology students and their instructors. Journal of Education and Training Studies, 3(4), 137–145. 10.11114/jets.v3i4.859 [DOI] [Google Scholar]
- *Scott JS (2002). Modeling aspects of students’ attitudes and performance in an undergraduate introductory statistics course [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 62, Issue 9–A, p. 2973). [Google Scholar]
- *Scott S (2014). The Effects of Math Tutoring Sessions for Parents on Eighth Grade Students’ Mathematics Achievement and Anxiety. (Doctoral dissertation, Liberty University, Lynchburg, Virginia: ). https://digitalcommons.liberty.edu/doctoral/838/ [Google Scholar]
- *Seng ELK (2015). The influence of pre-university students’ mathematics test anxiety and numerical anxiety on mathematics achievement. International Education Studies, 8(11), 162–168. 10.5539/ies.v8n11p162 [DOI] [Google Scholar]
- *Si J, Li H, Sun Y, Xu Y, & Sun Y (2016). Age-related differences of individuals’ arithmetic strategy utilization with different level of math anxiety. Frontiers in Psychology, 7, 1612. 10.3389/fpsyg.2016.01612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Siebers WM (2015). Relationship between math anxiety and student achievement of middle school students (Doctoral dissertation, Colorado State University, Fort Collins, Colorado: ). http://hdl.handle.net/10217/166940 [Google Scholar]
- Siegler RS, Duncan GJ, Davis-Kean PE, Duckworth K, Claessens A, Engel M, ... & Chen M (2012). Early predictors of high school mathematics achievement. Psychological Science, 23(7), 691–697. doi: 10.1177/0956797612440101 [DOI] [PubMed] [Google Scholar]
- *Skaalvik EM (2002). Self-enhancing and self-defeating ego goals in mathematics lessons: Relationships among task and avoidance goals, achievement, self-perceptions, anxiety, and motivation (A Scientific Educology). International Journal of Educology, 16(1), 54–76. [Google Scholar]
- *Solazzo LA (2008). The role of gender, cognition, anxiety, and competence beliefs in predicting mathematics achievement (Doctoral dissertation, Fordham University, Bronx, New York: ). https://research.library.fordham.edu/dissertations/AAI3303095). [Google Scholar]
- *Soni A, & Kumari S (2017). The role of parental math anxiety and math attitude in their children’s math achievement. International Journal of Science and Mathematics Education, 15(2), 331–347. 10.1007/s10763-015-9687-5 [DOI] [Google Scholar]
- Sonnenschein S, & Galindo C (2015). Race/ethnicity and early mathematics skills: Relations between home, classroom, and mathematics achievement. The Journal of Educational Research, 108(4), 261–277. doi: 10.1080/00220671.2014.880394 [DOI] [Google Scholar]
- **Sowinski C (2016). Numerical Building Blocks: Exploring Domain-Specific Cognitive Predictors of Mathematics. Unpublished manuscript. [Google Scholar]
- **Sowinski C, Dunbar K, & LeFevre J (2014). Calculation fluency test. Unpublished technical report). Math Lab, Carleton University, Ottawa, Canada. [Google Scholar]
- *Standing LG, Sproule RA, & Leung A (2006). Can business and economics students perform elementary arithmetic?. Psychological Reports, 98(2), 549–555. 10.2466/pr0.98.2.549-555 [DOI] [PubMed] [Google Scholar]
- *Stankov L, Morony S, & Lee YP (2014). Confidence: the best non-cognitive predictor of academic achievement?. Educational Psychology, 34(1), 9–28. 10.1080/01443410.2013.814194 [DOI] [Google Scholar]
- *Steiner ET, & Ashcraft MH (2012). Three brief assessments of math achievement. Behavior Research Methods, 44(4), 1101–1107. 10.3758/s13428-011-0185-6 [DOI] [PubMed] [Google Scholar]
- Sterne JA, & Harbord RM (2004). Funnel plots in meta-analysis. The Stata Journal, 4(2), 127–141. [Google Scholar]
- *Stiegelmeyer C (2012). The relationship between mathematical knowledge of numbers and operations and mathematics beliefs of prospective teachers. (Doctoral dissertation). ERIC. (1651830853; ED545857). [Google Scholar]
- Suárez-Pellicioni M, Núñez-Peña MI, & Colomé À (2016). Math anxiety: A review of its cognitive consequences, psychophysiological correlates, and brain bases. Cognitive, Affective, & Behavioral Neuroscience, 16(1), 3–22. doi: 10.3758/s13415-015-0370-7 [DOI] [PubMed] [Google Scholar]
- Suinn RM, & Edwards R (1982). The measurement of mathematics anxiety: The mathematics anxiety rating scale for adolescents—MARS-A. Journal of Clinical Psychology, 38(3), 576–580. doi: [DOI] [PubMed] [Google Scholar]
- Suinn RM, Taylor S, & Edwards RW (1988). Suinn mathematics anxiety rating scale for elementary school students (MARS-E): Psychometric and normative data. Educational and Psychological Measurement, 48(4), 979–986. doi: 10.1177/0013164488484013 [DOI] [Google Scholar]
- *Suinn RM, & Winston EH (2003). The mathematics anxiety rating scale, a brief version: Psychometric data. Psychological Reports, 92(1), 167–173. 10.2466/pr0.2003.92.1.167 [DOI] [PubMed] [Google Scholar]
- Supekar K, Iuculano T, Chen L, & Menon V (2015). Remediation of childhood math anxiety and associated neural circuits through cognitive tutoring. Journal of Neuroscience, 35(36), 12574–12583. doi: 10.1523/JNEUROSCI.0786-15.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Thien LM, & Ong MY (2015). Malaysian and Singaporean students’ affective characteristics and mathematics performance: evidence from PISA 2012. SpringerPlus, 4(1), 563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas G, & Dowker A (2000). Mathematics anxiety and related factors in young children. Paper presented at British Psychological Society Developmental Section Conference, Bristol, UK. [Google Scholar]
- *Thompson R, Wylie J, Mulhern G, & Hanna D (2015). Predictors of numeracy performance in undergraduate psychology, nursing and medical students. Learning and Individual Differences, 43, 132–139. 10.1016/j.lindif.2015.08.008 [DOI] [Google Scholar]
- *Tissot SL (1997). An examination of ethnic variation in gender differences in mathematics attitudes and performance [ProQuest Information & Learning]. In Dissertation Abstracts International: Section B: The Sciences and Engineering (Vol. 58, Issue 4–B, p. 2158). [Google Scholar]
- Tobias S (1986). Anxiety and cognitive processing of instruction. In Schwarzer R (Ed.), Self-related cognitions in anxiety and motivation (pp. 35–54). Hillsdale, NJ: Erlbaum. [Google Scholar]
- *Tobias S, & Everson H (1995). Development and Validation of an Objective Measure of Metacognition. Paper presented at the annual meeting of the American Educational Research Association in San Francisco, CA. [Google Scholar]
- *Townsend MA, Moore DW, Tuck BF, & Wilton KM (1998). Self-concept and anxiety in university students studying social science statistics within a co-operative learning structure. Educational Psychology, 18(1), 41–54. 10.1080/0144341980180103 [DOI] [Google Scholar]
- *Trezise K, & Reeve RA (2014). Working memory, worry, and algebraic ability. Journal Of Experimental Child Psychology, 121, 120–136. 10.1016/j.jecp.2013.12.001 [DOI] [PubMed] [Google Scholar]
- *Tsao YL (2004). Exploring the connections among number sense, mental computation performance, and the written computation performance of elementary preservice school teachers. Journal of College Teaching & Learning, 1(12), 71–90. 10.19030/tlc.v1i12.2022 [DOI] [Google Scholar]
- *Tubbs L (2015). Teaching methods in mathematics and their impact on sixth-grade students’ mathematics anxiety, attitudes, and achievement [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 76, Issue 1–A(E)). [Google Scholar]
- *Van der Beek JP, Van der Ven SH, Kroesbergen EH, & Leseman PP (2017). Self-concept mediates the relation between achievement and emotions in mathematics. British Journal of Educational Psychology, 87(3), 478–495. 10.1111/bjep.12160 [DOI] [PubMed] [Google Scholar]
- Verkijika SF, & De Wet L (2015). Using a brain-computer interface (BCI) in reducing math anxiety: Evidence from South Africa. Computers & Education, 81, 113–122. doi: 10.1016/j.compedu.2014.10.002 [DOI] [Google Scholar]
- *Vidović VV (1999). Self-referenced cognitions and mathematics grades in secondary school. Studia Psychologica, 41(2), 133–142. [Google Scholar]
- Viechtbauer W (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3). doi: 10.18637/jss.v036.i03 [DOI] [Google Scholar]
- Voyer D, & Voyer SD (2014). Gender differences in scholastic achievement: A meta-analysis. Psychological Bulletin, 140(4), 1174–1204. doi: 10.1037/a0036620 [DOI] [PubMed] [Google Scholar]
- *Vukovic RK, Kieffer MJ, Bailey SP, & Harari RR (2013). Mathematics anxiety in young children: Concurrent and longitudinal associations with mathematical performance. Contemporary Educational Psychology, 38(1), 1–10. doi: 10.1016/j.cedpsych.2012.09.001 [DOI] [Google Scholar]
- *Vukovic RK, Roberts SO, & Green Wright L (2013). From parental involvement to children’s mathematical performance: The role of mathematics anxiety. Early Education & Development, 24(4), 446–467. 10.1080/10409289.2012.693430 [DOI] [Google Scholar]
- Wang MT, & Degol J (2013). Motivational pathways to STEM career choices: Using expectancy-value perspective to understand individual and gender differences in STEM fields. Developmental Review, 33(4), 304–340. doi: 10.1016/j.dr.2013.08.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Wang Z, Hart SA, Kovas Y, Lukowski S, Soden B, Thompson LA, ... & Petrill SA (2014). Who is afraid of math? Two sources of genetic variance for mathematical anxiety. Journal of Child Psychology and Psychiatry, 55(9), 1056–1064. 10.1111/jcpp.12224 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Wang Z, Lukowksi SL, Hart SA, Lyons IM, Thompson LA, Kovas Y, … & Petrill SA (2015). Is math anxiety always bad for math learning? The role of math motivation. Psychological Science, 26(12), 1863–1876. doi: 10.1177/0956797615602471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watt HM, Hyde JS, Petersen J, Morris ZA, Rozek CS, & Harackiewicz JM (2017). Mathematics—A critical filter for STEM-related career choices? A longitudinal examination among Australian and US adolescents. Sex Roles, 77(3–4), 254–271. doi: 10.1007/s11199-016-0711-1 [DOI] [Google Scholar]
- *Watts BK (2011). Relationships of mathematics anxiety, mathematics self-efficacy and mathematics performance of adult basic education students (Doctoral dissertation, Capella University, Minneapolis, Minnesota: ). https://search.proquest.com/docview/862498506 [Google Scholar]
- Wigfield A, & Eccles JS (2000). Expectancy–value theory of achievement motivation. Contemporary Educational Psychology, 25(1), 68–81. doi: 10.1006/ceps.1999.1015 [DOI] [PubMed] [Google Scholar]
- Wigfield A, & Meece JL (1988). Math anxiety in elementary and secondary school students. Journal of Educational Psychology, 80(2), 210–216. doi: 10.1037/0022-0663.80.2.210 [DOI] [Google Scholar]
- Wijsman LA, Warrens MJ, Saab N, Van Driel JH, & Westenberg PM (2016). Declining trends in student performance in lower secondary education. European Journal of Psychology of Education, 31(4), 595–612. doi: 10.1007/s10212-015-0277-2 [DOI] [Google Scholar]
- *Wilder S (2012). Gender differences in factors pertaining to math anxiety among college students (Doctoral dissertation, University of Akron, Akron, Ohio: ). http://rave.ohiolink.edu/etdc/view?acc_num=akron1327538414 [Google Scholar]
- *Williams JE (1994). Anxiety measurement: Construct validity and test performance. Measurement and Evaluation in Counseling and Development, 27(1), 302–7. [Google Scholar]
- Wine J (1971). Test anxiety and direction of attention. Psychological Bulletin, 76(2), 92–104. doi: 10.1037/h0031332 [DOI] [PubMed] [Google Scholar]
- *Wu S, Amin H, Barth M, Malcarne V, & Menon V (2012). Math anxiety in second and third graders and its relation to mathematics achievement. Frontiers in psychology, 3, 162. doi: 10.3389/fpsyg.2012.00162 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Wu SS, Chen L, Battista C, Watts AKS, Willcutt EG, & Menon V (2017). Distinct influences of affective and cognitive factors on children’s non-verbal and verbal mathematical abilities. Cognition, 166, 118–129. 10.1016/j.cognition.2017.05.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Wu SS, Willcutt EG, Escovar E, & Menon V (2013). Mathematics achievement and anxiety and their relation to internalizing and externalizing behaviors. Journal of Learning Disabilities, 47(6), 503–514. doi: 10.1177/0022219412473154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- *Yáñez-Marquina L, & Villardón-Gallego L (2017). Math anxiety, a hierarchical construct: Development and validation of the scale for assessing math anxiety in secondary education. Ansiedad y Estrés, 23(2–3), 59–65. 10.1016/j.anyes.2017.10.001 [DOI] [Google Scholar]
- Young JR, & Young JL (2016). Young, Black, and anxious: Describing the Black student mathematics anxiety research using confidence intervals. Journal of Urban Mathematics Education, 9(1), 79–93. 10.21423/jume-v9i1a275 [DOI] [Google Scholar]
- Zabulionis A (2001). Mathematics and science achievement of various nations. Education Policy Analysis Archives, 9, 33. [Google Scholar]
- *Zachai J (1999). Adult learners’ math self-concept as a barrier to passing California State University’s Entry Level Mathematics (ELM) Test [ProQuest Information & Learning]. In Dissertation Abstracts International Section A: Humanities and Social Sciences (Vol. 60, Issue 4–A, p. 1048). [Google Scholar]
- *Zakaria E, & Nordin NM (2007). The effects of mathematics anxiety on matriculation students as related to motivation and achievement. Eurasia Journal of Mathematics, Science & Technology Education, 4(1). 27–30. 10.12973/ejmste/75303 [DOI] [Google Scholar]
- *Zettle RD (2003). Acceptance and commitment therapy (ACT) vs. systematic desensitization in treatment of mathematics anxiety. The Psychological Record, 53(2), 197–215. 10.1007/BF03395440 [DOI] [Google Scholar]
- Zhang J, Zhao N, & Kong QP (2019). The relationship between math anxiety and math performance: a meta-analytic investigation. Frontiers in psychology, 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


