Abstract
The left ventricle of the heart is a fundamental structure in the human cardiac system that pumps oxygenated blood into the systemic circulation. Several valvular conditions can cause the aortic and mitral valves associated with the left ventricle to become severely diseased and require replacement. However, the clinical outcomes of such operations, specifically the postoperative ventricular hemodynamics of replacing both valves, are not well understood. This work uses computational fluid–structure interaction (FSI) to develop an improved understanding of this effect by modeling a left ventricle with the aortic and mitral valves replaced with bioprostheses. We use a hybrid Arbitrary Lagrangian–Eulerian/immersogeometric framework to accommodate the analysis of cardiac hemodynamics and heart valve structural mechanics in a moving fluid domain. The motion of the endocardium is obtained from a cardiac biomechanics simulation and provided as an input to the proposed numerical framework. The results from the simulations in this work indicate that the replacement of the native mitral valve with a tri-radially symmetric bioprosthesis dramatically changes the ventricular hemodynamics. Most significantly, the vortical motion in the left ventricle is found to reverse direction after mitral valve replacement. This study demonstrates that the proposed computational FSI framework is capable of simulating complex multiphysics problems and can provide an in-depth understanding of the cardiac mechanics.
Keywords: Fluid–structure interaction, Immersogeometric analysis, Cardiac biomechanics and hemodynamics, Bioprosthetic heart valves, Aortic and mitral valve replacement
1. Introduction
In the cardiac system, the left ventricle (LV) is responsible for receiving oxygenated blood from the left atrium (LA) and pumping it into the the human systemic circulation. The two heart valves associated with the LV, the aortic valve (AV) and the mitral valve (MV), work in coordination to ensure unidirectional flow through the cardiac system. On the left side of the heart, the higher pressure and associated increases in cyclic loading make the AV and MV more susceptible to cardiac diseases than the valves on the right side of the heart [1]. Valvular heart diseases [2] can severely deteriorate the normal function of these valves and fundamentally disrupt the cardiac hemodynamics. For patients with severe valvular diseases, heart valve replacement is one of the most viable intervention options, resulting in around 75,000 prosthetic implants in the United States and around 170,000 to 250,000 implants in the world annually [3, 4]. Recently, surgical bioprosthetic heart valves (BHVs), which are tri-radially symmetric devices that are designed to mimic the anatomy of the AV, have become the predominant choice for valve replacement operations [5]. Although the anatomies of the AV and MV are entirely different, it is a common practice to use the same BHV design (e.g. Medtronic Mosaic valve [6]) for both aortic and mitral valve replacements [7]. While the asymmetry of the native MV is believed to result in a circulatory flow pattern in the LV that aids in the washout of ventricular blood during systole [8, 9], the replacement of the native MV with a symmetric BHV may alter this flow pattern and negatively influence the cardiac hemodynamics [10, 11]. Furthermore, the clinical outcomes after combined aortic and mitral valve surgery are not well known [12]. In an effort to develop an improved understanding of these effects, this work proposes a computational fluid–structure interaction (FSI) framework for the simulation of LV with both the AV and MV replaced with surgical BHVs.
The simulation of the intricate structures and function of the cardiac system requires suitable modeling and analysis methods that can accurately capture the physical complexity of this system. However, most of the previous LV simulations have utilized simplified assumptions regarding the LV geometry, deformation, or boundary conditions [13-16], which significantly reduce the feasibility of effectively replicating the in-vivo cardiac motions or hemodynamics. In recent years, vascular simulations (i.e. simulations of blood flows inside the vessels connected to the heart) have reached a relatively mature state [17-21] with even clinical applications [22-25]. At the same time, cardiac hemodynamics simulations (i.e. simulations of blood flows in the four chambers of the heart) still face many challenges, despite the advancements that have been made over the last decade [26-30]. Some of these challenges include obtaining the time-dependent large-scale heart-chamber deformation, resolving the complex hemodynamics, and considering their interactions with the structural mechanics of the heart valves [31]. As a result, realistic and robust numerical modeling of the cardiac system requires advanced FSI formulations and methodologies.
To approach the computational challenges of this complex system, traditional boundary-fitted methods for moving domain simulations, including the Arbitrary Lagrangian–Eulerian (ALE) [32-34] and Space–Time (ST) [35-37] methods, have been successfully applied to modeling the hemodynamics of wall-bounded biomedical problems [38-42]. However, for simulations that consider the geometries and motions of the heart valves, the large structural deformation of the valve leaflets can severely distort the boundary-fitted fluid elements if they are continuously deformed from a single reference configuration of the computational domain. Sophisticated mesh management algorithms are often required [43-45] to handle this type of problem. In addition, the heart valve experiences contact between the leaflets. Some existing specialized contact algorithms either impose a small distance to separate surfaces that would otherwise come into contact [46] or prescribe locations where the contact would occur [30, 47, 48]. While these assumptions are often sufficient for some idealized scenarios, they are inadequate for general valvular FSI simulations.
In light of these limitations for cardiac applications, immersogeometric analysis (IMGA) [49] was proposed as a geometrically flexible method to model and simulate heart valve FSI problems [50-54]. This novel method makes direct use of the CAD boundary representation (B-rep) of a complex design structure by immersing it into a non-boundary-fitted discretization of the surrounding fluid domain [55-59]. This approach effectively deals with FSI problems involving structures with complex motion that leads to large deformations of the fluid domain, including changes of topology [60, 61]. Algorithms developed for structural contact and impact problems [62, 63] can also be directly adopted in the IMGA simulations. The variational formulation for immersogeometric FSI analysis was derived using a dynamic augmented Lagrangian (DAL) approach to weakly enforce kinematic and traction constraints [64, 65]. A hybrid ALE/IMGA methodology, in which a single computation combines both a boundary-fitted, deforming-mesh treatment of some fluid–structure interfaces and a non-boundary-fitted treatment of others, was also developed under the same framework [50]. A comprehensive review of IMGA and its recent developments and applications in heart valve simulations can be found in Hsu and Kamensky [66].
In this work, based on the different types of deformation present in the LV and BHV subproblems, we formulate an FSI framework in which the LV is treated with a boundary-fitted, deforming-mesh ALE approach and the BHVs are treated with a non-boundary-fitted IMGA approach. Within this hybrid ALE/IMGA concept, a variety of advanced technologies are seamlessly integrated, including geometry modeling [67], fluid dynamics [68], structural mechanics [69, 70], and structural contact/impact [71]. Such a versatile technology is well suited for the multiscale, multiphysics modeling environment of cardiac flows. The detailed geometry and deformation information for the LV are obtained over the complete cardiac cycle from a separate cardiac biomechanics simulation, which is based on the technology proposed in Krishnamurthy et al. [72], and used as an input to the cardiac FSI simulation. A high-quality fluid domain finite element mesh is created and deformed in time in a boundary-fitted fashion following the endocardial surface information obtained from the biomechanics simulation of the LV. Using the corresponding annulus information, we construct two BHVs, one attached to the aortic annulus and one to the mitral annulus, and immerse them into the background LV fluid meshes. These two distinct approaches are integrated within our hybrid ALE/IMGA framework to solve for the complex hemodynamics of the LV coupled to the structural mechanics of the BHVs. Particular emphasis is placed on understanding the alteration in the left ventricular hemodynamic pattern that may result from these valve replacements.
This paper is organized as follows. In Section 2, we present the main constituents of the hybrid ALE/IMGA framework for solving the cardiac and valvular FSI problem. Section 3 details the techniques for obtaining the LV geometry and its time-dependent motion over a complete cardiac cycle, and the problem setup of the ventricular FSI simulation. The results are presented in Section 4, in which we demonstrate and discuss the LV flow pattern after bioprosthetic aortic and mitral valve replacement. Finally, we draw conclusion and motivate future research in Section 5.
2. Fluid–structure interaction methodology
In this section, we present the main constituents of the hybrid ALE/IMGA FSI framework for simulating cardiac problems. We start with the discussion of the DAL FSI framework. We then provide a comprehensive overview on the numerical formulations for all the subproblems in the FSI system. Finally, we demonstrate how the numerical ingredients are integrated together within the ALE/IMGA framework.
2.1. Mathematical model of the FSI problem
The LV FSI problem is governed by a partial differential equation (PDE) system, described using the augmented Lagrangian framework, that consists of the fluid subproblem, the structure subproblem, and a Lagrange multiplier constraint problem to enforce the compatibility of kinematics and tractions at the fluid–structure interface [49, 66, 73]. For a thin structure Γt in a fluid domain Ωt, the FSI problem can be expressed as: Find a fluid velocity and fluid pressure , a structure displacement with its material time derivative denoted as u2, and a Lagrange multiplier such that for all test functions , , , and ,
| (1) |
where and are trial solution and test function spaces, B(·, ·) and F(·) are functionals defining the fluid and structure subproblems, denoted by subscript 1 and 2 respectively, and β is a penalty parameter that enforces the compatibility of kinematics on the immersed thin structure. The presence of the Lagrange multiplier and penalty terms facilitates the development of certain numerical schemes based on the “augmented Lagrangian” concept [73], as it is valid regardless of matching or non-matching discretizations at the fluid–structure interface. For this reason, although the augmented Lagrangian framework was originally developed for boundary-fitted simulations, it can be straightforwardly applied to the context of immersed interface problems.
Remark 1. If the fluid and structural velocities and the corresponding test functions are explicitly assumed to be continuous (i.e., u1 = u2 and w1 = w2) at the interface, the second and third lines of Eq. (1) drop out and the FSI formulation of Eq. (1) reduces to a form suitable for matching fluid–structure interface meshes.
2.2. Hemodynamics
The fluid subproblem (hemodynamics) is governed by the Navier–Stokes equations of incompressible flows on a moving domain. The ALE formulation is adopted to account for the motion of the deforming LV, which is tracked by a boundary-fitted mesh that morphs with it. Advanced mesh moving techniques [74-76] are used to preserve the mesh quality throughout the entire cardiac cycle. The advantage of the ALE formulation is that the kinematic constraints on the boundaries are naturally satisfied by construction. The ALE formulation has been proven effective in a variety of vascular flow simulations [77, 78], for which comprehensive reviews can be found in Takizawa et al. [79].
The ALE form of the Navier–Stokes equations is discretized using a variational multiscale (VMS) approach [68, 80-84], in which the stabilization parameter is modified to improve the conservation of mass in the presence of an immersed thin structure [64]. We introduce a collection of disjoint fluid elements {Ωe} such that , and replace the semi-linear form B1 and linear functional F1 in Eq. (1) with their ALE–VMS counterparts, which take the forms of
| (2) |
and
| (3) |
where ρ1 is the fluid mass density, ε is the symmetric gradient operator, σ1(u1, p) = −pI + 2με(u1), where μ is the dynamic viscosity, f1 is a prescribed body force, h1 is a prescribed traction on indicates time differentiation with respect to a fixed point from some reference configuration Ω0, is the fine scale velocity ansatz,
| (4) |
p′ is the fine scale pressure,
| (5) |
and the mesh {Ωe} deforms with velocity . The detailed definition of the stabilization parameters τM, τC, and can be found in Kamensky et al. [64]. The first three terms of the right hand side of Eq. (2) correspond to the standard Galerkin form of the Navier–Stokes equations, and the rest of the terms are the VMS entries, which can be interpreted both as a stabilized formulation and a large-eddy simulation (LES) turbulence model [68, 85-89].
Finally, the formulation of the fluid subproblem is enhanced by a weakly enforced no-slip boundary condition operator on the LV surface. Let (ΓD)t ∈ Γt be the part of the boundary where Dirichlet velocity boundary conditions are applied. We replace the traditional strong enforcement of Dirichlet boundary conditions by adding the following weak-boundary-condition operator to the left hand side of the fluid subproblem:
| (6) |
The first two terms of the above equation are the consistency and adjoint consistency terms, respectively [90]. The last two terms provide additional numerical stabilities and help better satisfy the no-slip and no-penetration boundary conditions by penalizing the fluid velocity u1 toward the prescribe velocity g on the Dirichlet boundary. The third term is imposed on , which is the “inflow” part of (ΓD)t where . The τB in the fourth term is chosen element-wise as τB = 4μ/hn, where hn is the wall-normal element size at the boundary. This definition ensures the stability of the formulation, yet does not overshadow the consistency and adjoint consistency terms that are responsible for the excellent robustness and accuracy of the weak enforcement of boundary conditions. The formulation allows the flow to slip on the boundary when the fluid mesh in the boundary layer is coarse, which mimics the presence of a wall function and therefore avoids the excessive resolution requirement of the boundary-layer meshes [68, 90-92].
2.3. Heart valve structure modeling
The BHV structures are modeled by an isogeometric hyperelastic thin shell formulation developed in Kiendl et al. [69]. The formulation is based on the Kirchhoff–Love assumption with an arbitrary hyperelastic constitutive model. Let (Γsh)t ∈ Γt denote the midsurface of the BHVs and (Γsh)0 being its reference configuration, the semi-linear form B2 and linear functional F2 defining the nonlinear elasticity problem can be expressed as
| (7) |
| (8) |
where ρ2 is the structure mass density, hth is the shell thickness, ∂(·)/∂t∣x indicates the time derivative taken with respect to a fixed material point X, ξ3 is the shell through-thickness coordinate, f2 is a prescribed body force, h2 is the net fluid traction acting on the BHV leaflets, E is the Green–Lagrange strain tensor depending entirely on the shell midsurface displacement y, Dw2E is the variation of E in the direction w2, and S is the second Piola–Kirchhoff stress tensor. In this work, the BHV leaflets are assumed to be incompressible and are modeled as a Fung-type material. Specifically, S is computed as
| (9) |
where
| (10) |
In the above equations, C = 2E + I is the left Cauchy–Green deformation tensor, pl is a Lagrange multiplier that can be analytically determined using the plane stress condition to enforce incompressibility, I1 = tr C, and c0, c1, and c2 are material parameters.
The Fung-type material model uses a combination of linear and exponential functions of the first strain invariant [93-95] to describe the tissue stiffening under tensile loading. For the small strain regimes, such as those present in the open aortic BHV configuration during LV systole, the tissue remains compliant, since the unloaded collagen fibers are highly undulated and only provide very low stiffness. The extracellular matrix dominates the material stiffness, and is modeled here by the incompressible neo-Hookean term proposed by Fan and Sacks [96]. As the strain increases, the magnitude of the exponential term begins to dominate, which mimics the drastic increase in the stiffness of stretched biological tissues, such as when the aortic BHV closes subject to the large transvalvular pressure load during LV diastole.
Remark 2. In this work, the contact between the leaflets is assumed to be frictionless and is modeled using a penalty-based approach detailed in Kamensky et al. [49], in which a repulsive force is applied to the leaflet structures that come into contact. In our hybrid ALE/IMGA framework, since the discretization of the BHVs are independent from the fluid, other existing contact algorithms may be directly incorporated. For example, the volumetric-potential-based algorithms developed by Kamensky et al. [71, 97] are suitable options to model self contact and frictions.
2.4. Fluid–structure coupling
The thin-shell BHV structures described in the previous section are “immersed” into the background LV fluid mesh. The coupling between the fluid and thin shell is achieved using the IMGA approach through a combination of the penalty and the Lagrangian multiplier field shown in Eq. (1). The semi-linear forms and linear functionals in the fluid and structure subproblems are discretized in time using the generalized-α method [98]. Note that the fluid–structure interface is not conforming to the fluid mesh elements ∪eΩe. Therefore, the Lagrange multiplier field on needs to be approximated in the context of the non-boundary-fitted discretization. Following the DAL approach [64, 66], the Lagrange multiplier is discretized in space and updated semi-implicitly in each time step. In short, in the case in which a thin shell is immersed into the fluid, the tangential component of the Lagrange multiplier is eliminated such that the non-sliding condition is only enforced by the tangential component of the penalty, βTAN. The normal component λ = λ · nsh is stored at the quadrature points of the thin shell Γsh (with nsh being its unit outward normal vector) in the form of a scalar, and is used together with the normal penalty βNOR to enforce the no-penetration conditions. λ is updated in time by
| (11) |
where n + αf is an intermediate time level between steps n and n + 1 that is predicted by the generalized-α method. The constant parameter r ≥ 0, which is inspired by the perturbed Lagrangian approach [99], ensures well-posedness in the steady limit. Kamensky et al. [64, 100] analyzed the stability and accuracy of this methodology as well as the choices of the parameters. Following their recommendation, we set r = 10−5 for the semi-implicit time integration scheme for Lagrange multiplier in Eq. (11).
Remark 3. The hybrid ALE/IMGA framework falls under the concept of the Fluid–Solid Interface-Tracking/Interface-Capturing Technique (FSITICT) [101]. In such a paradigm, interfaces that are feasible to track are tracked (e.g. the LV motion), and those that are too challenging to track are captured (e.g. the BHVs). In the present work, the immersion of the non-boundary-fitted BHV structures into a boundary-fitted discretization of the deforming LV is a typical example of FSITICT. The FSITICT was recently introduced to compressible flow simulations with application to rotorcraft aerodynamics [58].
3. Ventricular fluid–structure interaction simulation
In this section, we present the implementation details for simulating blood flow inside an LV model in which the native AV and MV are replaced with BHVs. Based on the LV motion obtained from a cardiac biomechanics simulation, we use an interactive geometry framework [67] to construct the fluid mesh and BHV models, and specify the boundary conditions of the FSI problem in a complete cardiac cycle.
3.1. Structural analysis of LV motion
The physiological LV wall motion used in this work is generated through a standalone structural simulation of the cardiac mechanics [70, 72]. A brief summary of this technology is presented here. A biventricular cardiac model, which includes both the left and the right ventricles, orifices, and valve annuli, is constructed using cubic-Hermite finite element meshes. The model dimensions, including the volume of both ventricles and wall (myocardium) thickness, were adjusted using data from available literature [102]. Although high order smoothness can be achieved in the interior of Hermite elements, maintaining continuity of the fields across element boundaries requires additional mathematical constraints, especially at extraordinary nodes that are connected to a non-regular number of edges (3, or ≥ 5). Following the work of Krishnamurthy et al. [72], a local-to-global map [103] that transforms global ensemble derivatives into local element derivatives is used to maintain the continuity at extraordinary nodes. In addition, the accurate myocardial fiber architecture is crucial to the physiological realism of the LV structural mechanics. A coordinate frame interpolation method is developed to maintain the consistency of the fiber orientation within the elements, even in the presence of extraordinary nodes [104]. The passive material properties of the myocardial tissue are modeled by the hyperelastic constitutive model [105]. This is a nonlinear hyperelastic constitutive law for which the strain energy is an exponential function of the right Cauchy–Green strain tensor in the fiber direction and the transverse direction as separate terms. Using the three-wall segment (TriSeg) model [106], the muscle contraction is modeled as a time-dependent active stress that is added to the passive stress in the 3D finite element formulation. Finally, to obtain the deformation of the biventricular model for the complete cardiac cycle, the 3D finite element model is coupled with a lumped-parameter closed-loop circulation model that represents the rest of the cardiovascular system. For details on the setup and numerical methodologies used for the cardiac structural model, we refer the readers to the cited literature.
3.2. Geometry modeling and mesh generation
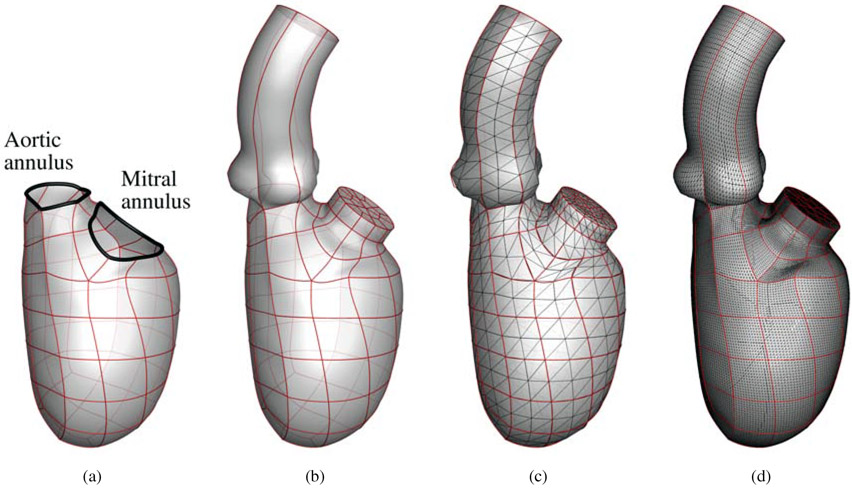
For this cardiac flow study, the endocardial surface obtained from the cardiac biomechanics simulation is used as an input for the ventricular FSI simulation. Starting from the geometry of the biventricular model described in Section 3.1, we extract the portion that includes the full LV endocardium and the mitral and aortic flow tracts, as show in Fig. 1(a). We then attach an idealized aorta to the aortic annulus, and a cylindrical LA extension to the mitral annulus to allow flow development before the MV. The smooth annular connections, between the idealized aorta and the aortic annulus, and between the cylindrical LA extension and the mitral annulus, are achieved via cubic spline interpolation. Fig. 1(b) illustrates the geometry that is used for the FSI simulation as the reference configuration, with the edges denoting the patch boundaries. Starting from the reference configuration, the motions of the aorta and the LA extension are prescribed with the following constraints. The centerlines of the aorta and LA extension are only allowed to translate in space from the reference configuration, with their lower endpoints attached to the centers of the aortic and mitral annuli, respectively. The diameters of the aorta and the LA extension are scaled following the change of the aortic and mitral annuli, respectively. Throughout the cardiac cycle, the annular connections are kept smooth.
Figure 1:
Reference fluid domain mesh generation: (a) the spline patches making up the left ventricle model; (b) LV model with an idealized aorta and LA extension; (c) coarse triangulation of the model; (d) fine triangulation of the model that is used as the resolution in the FSI simulation.
Due to their flexibility and adaptivity, we use pure tetrahedral elements to discretize the moving fluid domain. We start by discretizing the spline patches into a triangular mesh. Since the spline patches are part of the biventricular finite element mesh, the smoothness between neighboring patches is automatically maintained, and we can split each patch into triangles that share nodes on the patch boundaries (Fig. 1(c)). Note that Fig. 1(c) shows a very coarse mesh that is only used to illustrate the surface discretization. We locate the surface element nodes in the parametric space of the spline patches. The parametric coordinates are used to interpolate the current locations of the nodes when the LV deforms, and are then used as boundary conditions to deform the fluid domain in the FSI simulation. Finally, the volumetric mesh is generated based on the refined surface triangular mesh illustrated in Fig. 1(d). As a result, a total of 1,232,871 elements are generated for the volumetric mesh. The volumetric mesh is updated at each time step by solving the equations of elastostatics [74-76, 107], with the prescribed displacement boundary conditions on the surface nodes extracted from the LV structural motion obtained in Section 3.1 and the aorta and LA motions previously described in this section. Note that the temporal resolution of the LV motion from the structural analysis is limited, so we use periodic cubic splines to smoothly interpolate the LV motion into arbitrarily small time steps.
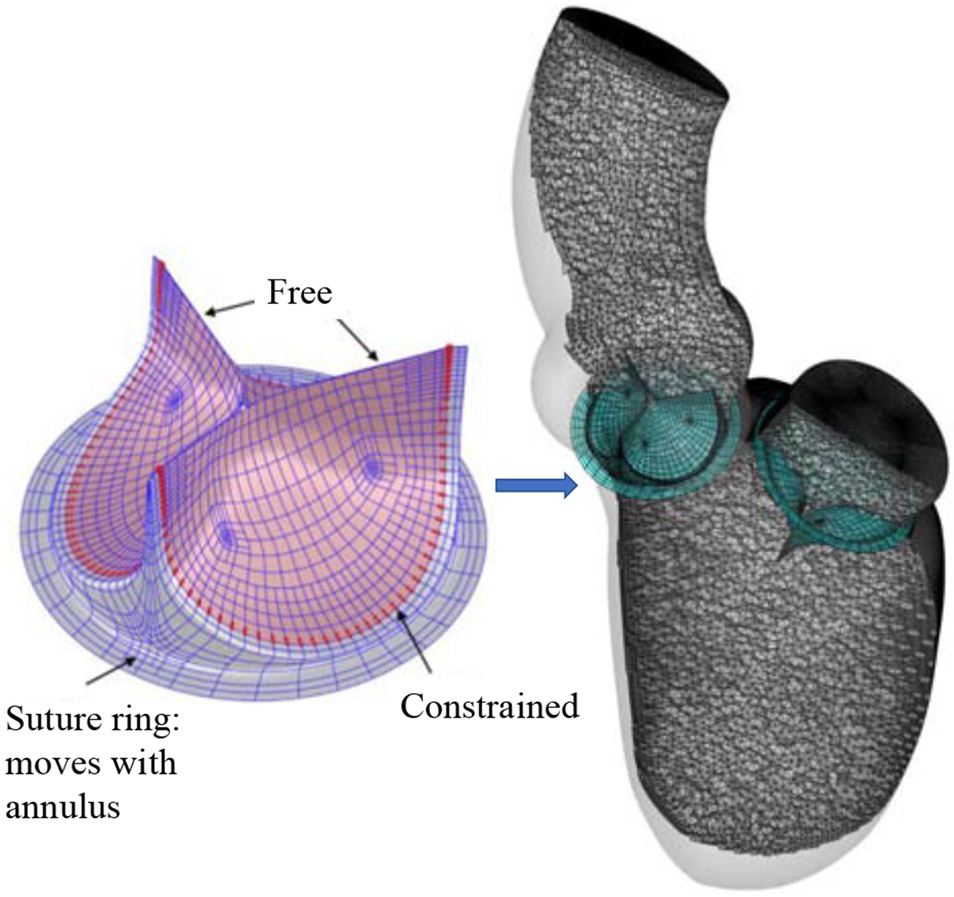
For the BHVs in this paper, we use the T-spline model from Hsu et al. [51]. The T-spline mesh for the aortic BHV comprises 382 and 1020 Bézier elements for each leaflet and the stent, respectively, and a total of 2262 T-spline control points. The T-spline mesh for the mitral BHV comprises 354 and 1020 Bézier elements for each leaflet and the stent, respectively, and a total of 2169 T-spline control points. We scale and locate the BHVs such that the suture rings of the AV and MV stents match the aortic and mitral annuli, respectively. The sizes of the BHVs for AV and MV replacements are 20 mm and 24 mm (based on stent diameter), respectively. Fig. 2 illustrates the parameterization of the BHV model, and the reference configuration in which two BHVs are implanted into the LV, with the MV replacement placed in an inverted configuration.
Figure 2:
The BHV model discretization and configuration of the AV and MV implants, which are immersed into the LV fluid domain. The control points with constrained motion are highlighted by red color in the left-hand-side figure.
The attached edges of the leaflets are clamped to the stent by constraining the relative motions of the two rows of control points adjacent to the stent. These control points are highlighted in Fig. 2. We model the surgical suturing between the BHV stent and the annulus by intersecting the suture ring with the LV wall. Fig. 2 shows the geometric intersection of the stent with the fluid domain boundary. The intersection seals the space between the BHV and the LV fluid domain boundaries, such that the blood can only flow through the orifices of the BHVs when they are open. The intersection is maintained during the entire cardiac cycle by matching the movements of the suture rings to the motions of the AV and MV annuli.
3.3. FSI simulation details
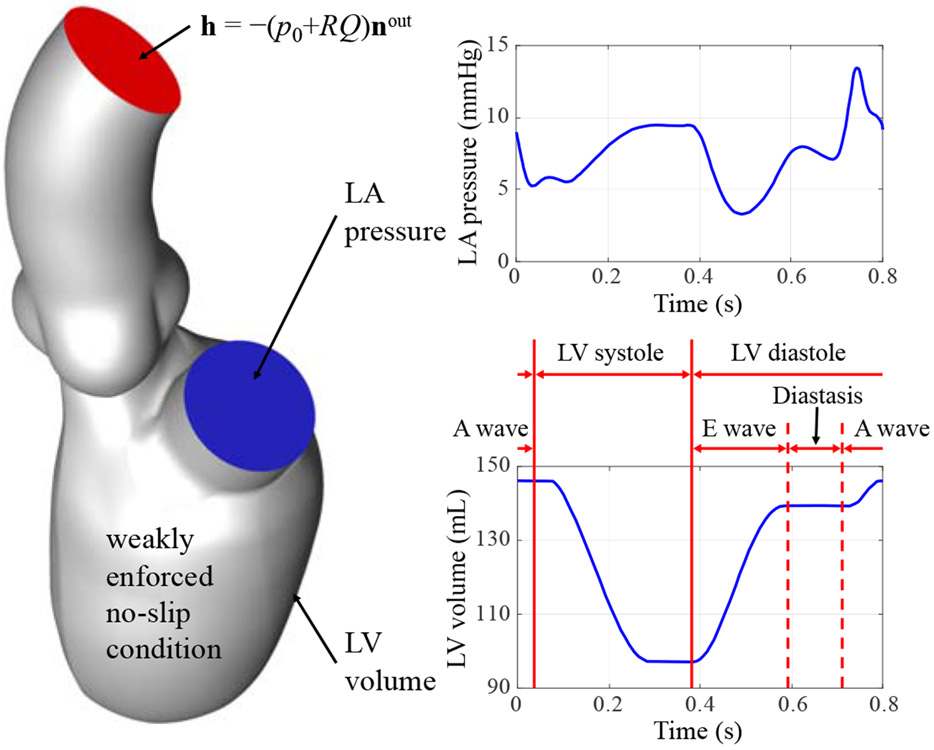
The flow boundary conditions are shown in Fig. 3. In the FSI simulation, we apply the left atrial pressure based on the simulations from Krishnamurthy et al. [70] as a traction boundary condition at the mitral inflow tract. The applied pressure profile, shown in Fig. 3, is periodic with a time period of 0.8 s. A resistance boundary condition is applied at the outflow boundary of the ascending aorta in the form of a traction −(p0 + RQ)nout, where p0 is the end-diastolic aortic pressure, nout is the outward-facing normal of the fluid domain, R is a resistance constant, and Q is the volumetric flow rate through the outflow.
Figure 3:
Setup for the FSI simulation. Different phases of the cardiac cycle are labeled on the LV volume curve.
In the present computation, we set p0 = 40 mmHg and R = 70 (dyn s)/cm5. The end-diastolic aortic pressure value, which is lower than the normal physiological level, is consistent with the LV structural simulation of a patient who is in the early stages of heart failure with ventricular dyssynchrony that has not progressed to dilated cardiomyopathy [70]. Backflow stabilizations [108] are used at the mitral inflow tract and the aorta outlet boundary, by adding the following term to the fluid subproblem:
| (12) |
where γ = 0.5, , and is the ith outflow boundary. On all other boundaries, weakly enforced no-slip boundary conditions are applied. The different phases of the cardiac cycle (e.g. the LV systole and diastole) are labeled on the LV volume profile in Fig. 3. The normal and tangential velocity penalization parameters used in our FSI formulation are and . The time step size is Δt = 1.0 × 10−4 s so that a total of 8000 time steps are used in a complete cardiac cycle. The fluid density and viscosity in the fluid domain are set as ρ1 = 1.0 g/cm3 and μ = 3.0 × 10−2 g/(cm s), respectively, to model the physical properties of human blood [109, 110].
Remark 4. The simulations are carried out in a parallel computing environment on the Lonestar5 Linux cluster [111] of the Texas Advanced Computing Center [112]. The system consists of 1252 compute nodes, each with two Intel E5-2690 v3 12-core (Haswell) processors and 64 GB of DDR4 memory. We partition the fluid mesh into 96 subdomains, and use the parallelization strategy presented in Hsu et al. [113]. With these configurations, a complete cardiac cycle takes 38 to 42 hours to simulate.
The material parameters in Eq. (10) are set to c0 = 5.0× 106 dyn/cm2, c1 = 2.0 × 105 dyn/cm2, and c2 = 100.0. Based on the three-point bending tests of glutaraldehyde-treated bovine pericardium reported by Mirnajafi et al. [114], we set the coefficient c0 such that it provides a similar small-strain bending stiffness. The parameters c1 and c2 are selected based on the assumption that the BHVs in this paper are comparable to the pericardial BHV leaflet models in Sun et al. [115]. The mass density of the leaflets is set to 1.0 g/cm3. The thickness of the leaflets is 0.0386 cm, which is selected as a typical thickness of adult bovine pericardial tissue [116, 117]. The stents are assumed to be rigid, considering their large stiffness compared with the leaflets.
4. Results and discussions
4.1. FSI simulation results
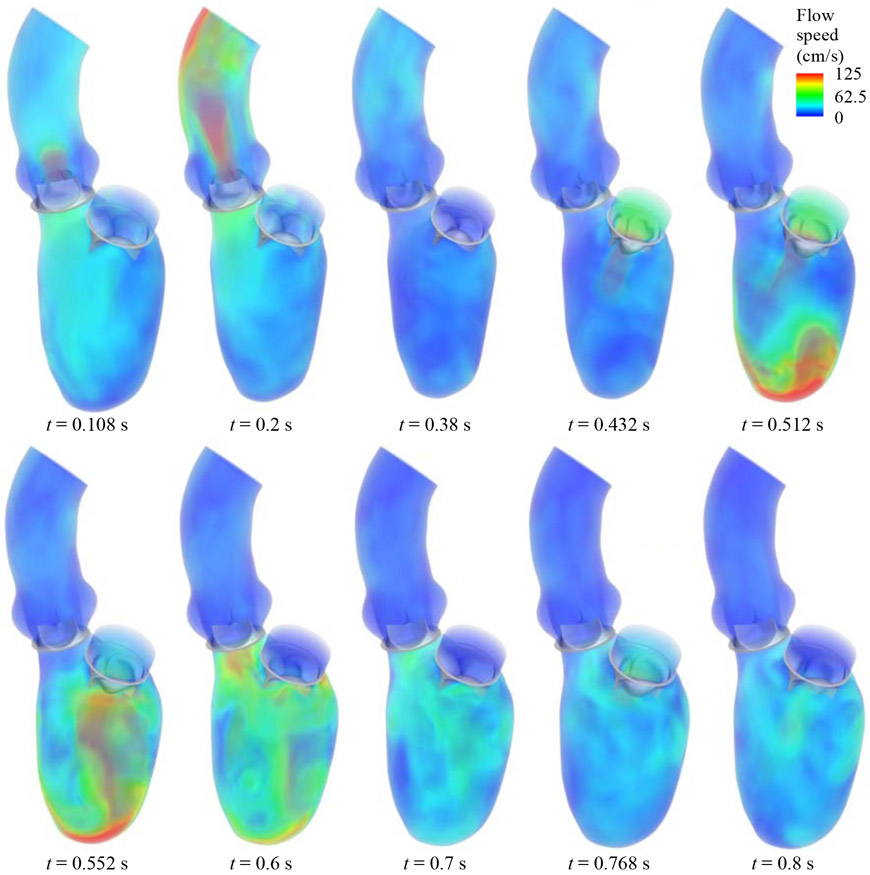
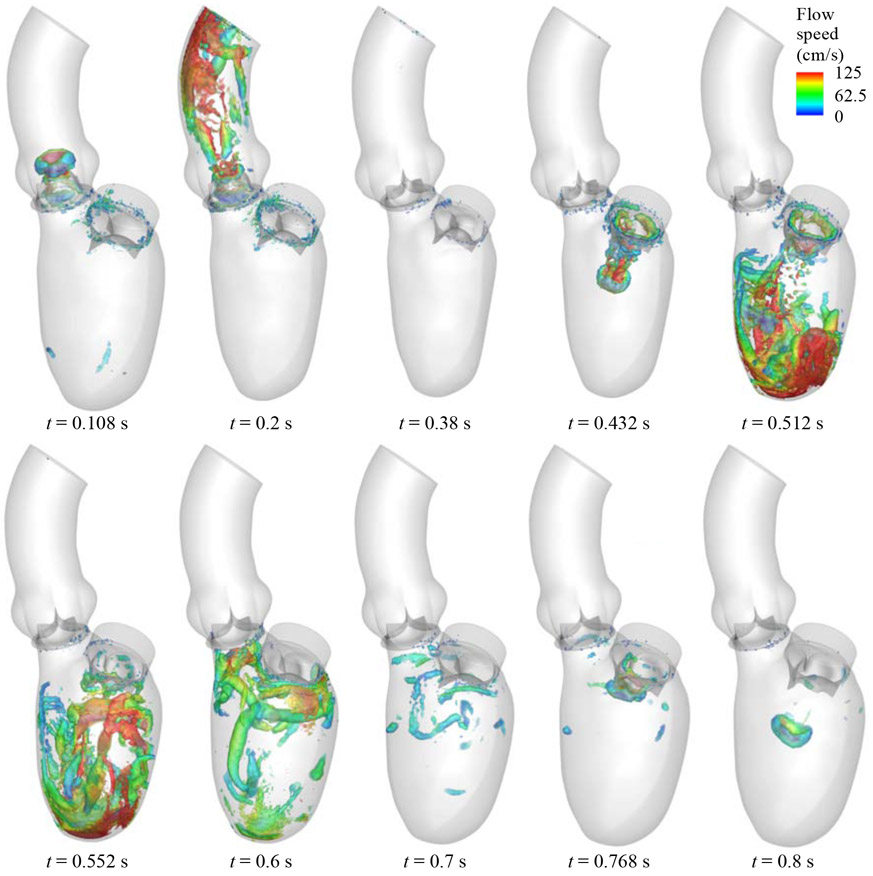
The FSI simulation is carried out for four cardiac cycles in order to achieve a statistically periodic steady state. To evaluate the variations between cycles, the volumetric flow rate entering the mitral inflow tract is monitored and compared between the third and fourth cycles. The L2-norm of flow rate difference between the two cycles is below 3% of the L2-norm of fourth-cycle flow rate. All the results presented in this section are based on the fourth cycle. Several snapshots of the BHV deformation and the details of the flow field at several time points during the cardiac cycle are presented in Fig. 4. The visualization of flows and structures clearly demonstrates the response of the valves to the left ventricular motions and hemodynamics. The entire cardiac cycle can be divided into several representative time intervals, as detailed on the LV volume profile in Fig. 3. During the 0.05 s to 0.38 s time interval, the contraction of the LV volume causes the aortic BHV to open and allow blood flow into the aorta. This time period corresponds to the systole of the LV, during which the mitral BHV closes and prevents the flow from reversing to the LA. The next part of the cycle, between 0.38 s and 0.8 s, is the diastole of the LV. In the early diastole (E wave) from 0.38 s to 0.6 s, the mitral BHV fully opens and a large amount of blood fills into the LV chamber while the LV wall relaxes. The mitral BHV closes during the 0.6 s to 0.72 s time period of diastasis. Finally, the atrial contraction during the A wave propels additional blood flows into the LV, and reopens the mitral BHV at 0.768 s. Due to the shorter duration and lower strength of the A wave, the mitral BHV opening during this period is minor compared to its opening during the E wave. As a result, most of the blood flow transfer from the LA to the LV is completed during the E wave.
Figure 4:
Visualization of the FSI results for the flow field in the LV and the BHV motions in a complete cardiac cycle.
Fig. 5 visualizes the vortical structures at the same time frames as Fig. 4. The vortical structures are created using isosurfaces of the second invariant of the velocity gradient matrix, i.e. the λ2 criterion [118]. Some of the same flow phenomena that were observed in Fig. 4 are also clearly visible from the vortical structures. The vortex ring generated by the mitral jet during LV diastole is one of the most distinguishable features of intraventricular flows. During the E wave, the vortex ring demonstrates that the flow forms a jet as it moves to the apex, from 0.432 s to 0.512 s. Once the blood flow reaches the apex, it reverses and moves upwards toward the valves. The vortical structures at 0.552 s indicate that the flows are well mixed in the LV. During the A wave, the small ring-structured vortex can be clearly observed. This vortex is generated from the minor mitral BHV opening created by the atrial kick from the LA contraction, and moves into the LV while the flows in the other regions remain mostly at rest.
Figure 5:
Vortical structures colored by the velocity magnitude in a complete cardiac cycle.
4.2. Effects of BHV on hemodynamic pattern
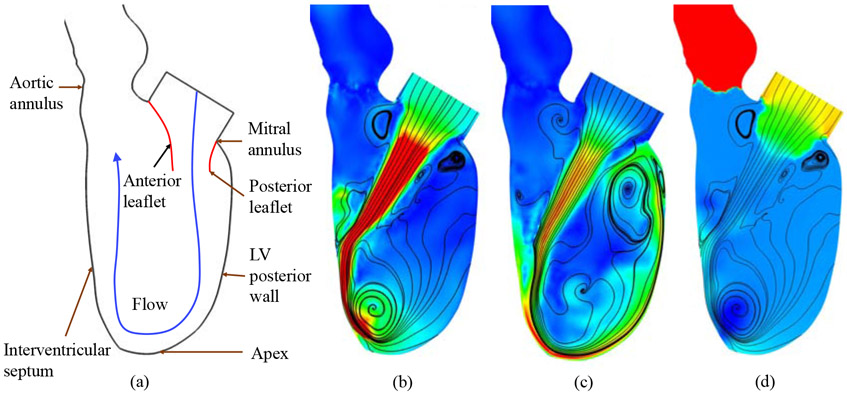
The asymmetry of the native MV leaflets guides the flow to impinge toward the LV posterior wall [8, 9] during LV diastole. The flow continues in the same direction until it reaches the apex of the LV, where it turns and is redirected toward the outflow tract (the AV annulus). A schematic of the flow pattern is depicted in Fig. 6(a). The jet flow that reaches the apex is considered to be important for enhancing apical washout in the LV [9]. Without proper apical washout, the blood flow could reach a stasis in the apex region and cause subsequent thrombus formation [119, 120]. In addition, with the clockwise circulatory pattern, the systolic contraction of the LV would propel blood flow that is already moving toward the aortic valve, such that the momentum loss is minimal.
Figure 6:
Comparison of flow circulatory patterns in the LV during diastole: (a) schematic of the flow direction resulting from a typical native valve [8]; (b) streamlines and velocity magnitude contours for the BHV FSI results at t = 0.472 s; (c) streamlines and velocity magnitude contours for the BHV FSI results at t = 0.552 s; (d) pressure contours at t = 0.472 s. Velocity magnitude contours are plotted using a color scale ranging from 0 (blue) to ≥ 200 cm/s (red) in (b) and (c). Pressure contours are plotted using a color scale ranging from ≤ −5 (blue) to ≥ 5 mmHg (red) in (d).
With the implant of a symmetric BHV in the MV annulus, obvious changes in the flow pattern can be observed. The most prominent change is the direction of the flow jet entering the LV. Fig. 6(b) shows that the flow is essentially perpendicular to the MV annulus plane, and it impacts the interventricular septum instead of impinging toward the posterior wall. Subsequently, the flow turns counterclockwise toward the apex, and the blood flow circulates back toward the MV along the posterior wall, as suggested by Fig. 6(c). As a result, the replacement of the native MV with a symmetric BHV changes the direction of the diastolic vorticity inside the LV. In spite of the direction change of the vorticity, it can be observed that the apical washout is still present. Fig. 6(c) shows a high speed flow, which may result from the smaller orifice areas of BHVs compared to healthy native MVs [6, 121], that changes direction in the apex region. From a heart-workload perspective, a negative effect of the high-speed jet is that the resulting large kinetic energy of blood typically indicates increased workload done by the expanding LV. On the other hand, the high speed jet can actually enhance the apical washout and the blood mixing in the LV, which is desirable as it reduces the risk of stasis [119, 120].
Potential adverse effects can also result from the altered pressure distribution in the LV. The impact of the jet on the interventricular septum will increase the pressure on the septum, compared with the native MV case in which the jet moves along the posterior wall, as shown in Fig. 6(d). As a result, the septal tissue may be exposed to higher stresses than those that result from the native MV. In addition, the normal equilibrium developed under pre-implant physiological conditions may be modified after valve replacement. It was also reported that the LV may suffer from changes in geometry after MV replacements [122], which can worsen with the removal of the chordae tendineae during conventional MV replacement surgeries [123, 124]. Further studies of these post-operative phenomena, including the effect of hemodynamic changes on LV chamber geometry, are necessary to investigate the subsequent impact of replacing the native MV with a BHV.
5. Conclusions, limitations, and future work
5.1. Conclusions
This study focuses on using advanced hybrid ALE/IMGA modeling and simulation to better understand the hemodynamics in the LV with BHV implants. The structures and kinematics of the BHVs are expected to have a significant influence on the LV hemodynamics. However, the computational challenges presented by such a complex application pose a substantial obstacle for numerical investigations that use classical methods. Such challenges include large-scale structural deformations, as well as contact/impact between heart valve leaflets. To overcome these issues, this work employs the IMGA method to model the interactions between the blood flow and the valve in a non-boundary-fitted approach. Combined with a penalty-based contact algorithm, these methods produce a physiologically realistic valvular FSI modeling approach. In conjunction with these valve models, the ALE–VMS method is utilized to model the hemodynamics that result from LV wall motion, which incorporates the accuracy provided by boundary-fitted approaches. Through the combination of these advanced technologies, numerical simulations of the LV FSI system are carried out using a computational approach that balances robustness and accuracy. These simulation results predict the LV intraventricular flow field after AV and MV replacements. Several unique phenomena in the LV, such as the valve opening and flow behavior that is caused by the atrial kick, are accurately captured. The effect of BHV replacements on the vortex direction reversal in the specific LV presented in this paper is particularly highlighted since this hemodynamic change may have a profound impact on the LV workload and structural behavior.
5.2. Limitations and future work
The primary intent of this paper is to develop an FSI modeling and simulation framework for cardiac and valvular problems. Although this framework is intended to provide a flexible approach to model many cardiac conditions, the presented results and observations are specific to the boundary conditions and geometries specified in this paper, and the conclusions should not be generalized to all other possible variations. In the future, the proposed hybrid ALE/IMGA framework could be applied to simulate a diverse set of cardiac conditions, including variations in boundary conditions and geometries, which would further demonstrate its robustness and physiological realism. The proposed framework could also be extended and applied to different cardiac applications, especially those hearts with prosthetic valve replacements, and to include four-chamber models [104] and atrioventricular valves [125, 126]. Efficiently exploring the myriad of parameters that are present in the wide variety of cardiac problems would require some form of automated optimization. Previous work has demonstrated that the FSI system can be optimized using a surrogate management framework (SMF) [127], and similar combinations of the SMF and hybrid ALE/IMGA framework could provide an effective tool for future numerical studies of cardiac systems.
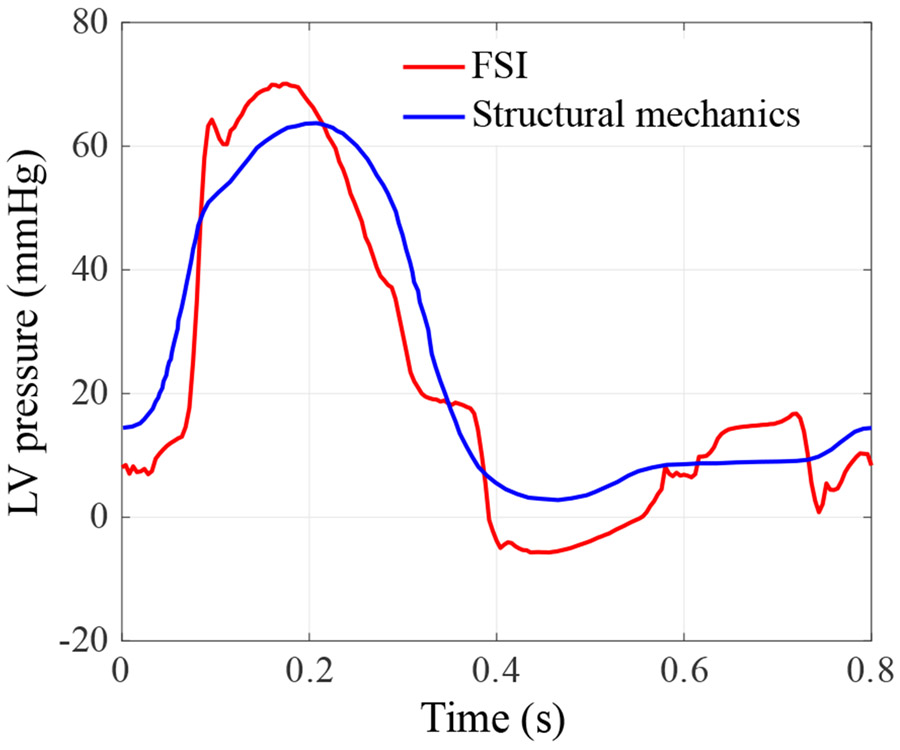
The specific heart geometry in this paper is from a patient with mild heart failure with ventricular dyssynchrony that has not progressed to dilated cardiomyopathy [70]. The cardiac motion for such a patient in the early stages of heart failure is expected to remain within a normal range. Although the LV motion and the boundary conditions in this paper are within a reasonable range, the following assumptions and simplifications had to be taken to make the FSI simulation more tractable. First, all the motions of the boundaries, including the LV and the ascending aorta, are prescribed. With the BHV replacements, the altered pressure may not be consistent with the prescribed volume change, and as a result, the effect of LV and aorta compliance is likely not well reproduced. In addition, the LA is simplified to a cylindrical section that is attached to the mitral inflow tract, which artificially alters the mechanism driving the flow through the MV during the A wave. Instead of being driven by the contraction of LA, the flow is driven by the suction created by the prescribed LV volume expansion. This explains the LV pressure profile discrepancy in Fig. 7 between 0.72 s and 0.8 s, where an obvious pressure drop is observed in the FSI simulated LV pressure. Some other limitations of this work include the simple resistance boundary condition applied at the outlet of the ascending aorta. This limitation can be addressed in the future by incorporating Windkessel-type boundary conditions [128].
Figure 7:
The intraventricular pressure of the FSI simulation throughout a complete cardiac cycle. The intraventricular pressure is obtained by space-averaging the blood pressure in the LV. The LV pressure used in the structural mechanics simulation of the LV motion is plotted for reference.
The paradigm proposed in this work provides an effective tool to better understand the fluid and structural behaviors in the cardiac system. Despite the realistic modeling approaches presented in this work, the BHV structures and the deformation of the LV are limited to the idealized data that is available for these geometries and the structural simulation of the LV. The simplification of these model inputs produces more idealized FSI simulation results that will be improved in the future by connecting the present hybrid ALE/IMGA framework to medical imaging technologies [52]. Incorporating these data has significant potential to lead to highly realistic patient-specific modeling and simulation. Such an integrated tool could be beneficial for developing novel implant strategies that focus on replicating the native blood flows after BHV replacement operations. Eventually, this physics-based computational FSI framework could help reduce the morbidity and mortality in cardiac disease treatments through improved surgical planning and personalized medical device design.
Highlights.
FSI framework for a left ventricle with two bioprosthetic implants is proposed
Hemodynamics of left ventricle and structural mechanics of valve implants are modeled
Replacing native mitral valve with tri-radially symmetric valve changes hemodynamics
6. Acknowledgments
E.L. Johnson, M.S. Sacks, and M.-C. Hsu were partially supported by the National Heart, Lung, and Blood Institute of the National Institutes of Health under award numbers R01HL129077 and R01HL142504. A. Krishnamurthy was partially supported by the same institute under award number R01HL131753 and by the National Science Foundation under award number 1750865. All this support is gratefully acknowledged. We also thank the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources that have contributed to the research results reported in this paper.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest Statement
The authors declare no conflict of interest.
References
- [1].Yoganathan AP, He Z, and Jones SC. Fluid mechanics of heart valves. Annual Review of Biomedical Engineering, 6:331–362, 2004. [DOI] [PubMed] [Google Scholar]
- [2].Nishimura RA, Otto CM, Bonow RO, Carabello BA, Erwin JP, Guyton RA, OGara PT, Ruiz CE, Skubas NJ, Sorajja P, Sundt TM, and Thomas JD. 2014 AHA/ACC guideline for the management of patients with valvular heart disease. Circulation, 129:e521e643, 2014. [DOI] [PubMed] [Google Scholar]
- [3].Li RL, Russ J, Paschalides C, Ferrari G, Waisman H, Kysar JW, and Kalfa D. Mechanical considerations for polymeric heart valve development: biomechanics, materials, design and manufacturing. Biomaterials, 225:119493, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Schoen FJ and Butany J. Cardiac valve replacement and related interventions. In Cardiovascular Pathology, pages 529–576. Elsevier, 2016. [Google Scholar]
- [5].Soares JS, Feaver KR, Zhang W, Kamensky D, Aggarwal A, and Sacks MS. Biomechanical behavior of bioprosthetic heart valve heterograft tissues: Characterization, simulation, and performance. Cardiovascular Engineering and Technology, 7(4):309–351, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Magne J, Mathieu P, Dumesnil JG, Tanné D, Dagenais F, Doyle D, and Pibarot P. Impact of prosthesis-patient mismatch on survival after mitral valve replacement. Circulation, 115:1417–1425, 2007. [DOI] [PubMed] [Google Scholar]
- [7].Eichinger WB, Botzenhardt F, Gunzinger R, Kemkes BM, Sosnowski A, Maïza D, Coto EO, and Bleese N. European experience with the Mosaic bioprosthesis. The Journal of Thoracic and Cardiovascular Surgery, 124(2):333–339, 2002. [DOI] [PubMed] [Google Scholar]
- [8].Pedrizzetti G, Domenichini F, and Tonti G. On the left ventricular vortex reversal after mitral valve replacement. Annals of Biomedical Engineering, 38(3):769–773, 2010. [DOI] [PubMed] [Google Scholar]
- [9].Seo JH, Vedula V, Abraham T, Lardo AC, Dawoud F, Luo H, and Mittal R. Effect of the mitral valve on diastolic flow patterns. Physics of Fluids, 26(12):121901, 2014. [Google Scholar]
- [10].Daebritz SH, Sachweh JS, Hermanns B, Fausten B, Franke A, Groetzner J, Klosterhalfen B, and Messmer BJ. Introduction of a flexible polymeric heart valve prosthesis with special design for mitral position. Circulation, 108:II–134–II–139, 2003. [DOI] [PubMed] [Google Scholar]
- [11].Mächler H, Perthel M, Reiter G, Reiter U, Zink M, Bergmann P, Waltensdorfer A, and Laas J. Influence of bileaflet prosthetic mitral valve orientation on left ventricular flow-an experimental in vivo magnetic resonance imagingstudy. European Journal of Cardio-Thoracic Surgery, 26(4):747–753, 2004. [DOI] [PubMed] [Google Scholar]
- [12].Turina J, Stark T, Seifert B, and Turina M. Predictors of the long-term outcome after combined aortic and mitral valve surgery. Circulation, 100(suppl II):II–48–II–53, 1999. [DOI] [PubMed] [Google Scholar]
- [13].Carmody CJ, Burriesci G, Howard IC, and Patterson EA. An approach to the simulation of fluid–structure interaction in the aortic valve. Journal of Biomechanics, 39(1):158–169, 2006. [DOI] [PubMed] [Google Scholar]
- [14].Dahl SK, Vierendeels J, Degroote J, Annerel S, Hellevik LR, and Skallerud B. FSI simulation of asymmetric mitral valve dynamics during diastolic filling. Computer Methods in Biomechanics and Biomedical Engineering, 15(2):121–130, 2012. [DOI] [PubMed] [Google Scholar]
- [15].Le TB and Sotiropoulos F. On the three-dimensional vortical structure of early diastolic flow in a patient-specific left ventricle. European Journal of Mechanics-B/Fluids, 35:20–24, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Le TB and Sotiropoulos F. Fluid–structure interaction of an aortic heart valve prosthesis driven by an animated anatomic left ventricle. Journal of Computational Physics, 244:41–62, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Marsden AL, Vignon-Clementel IE, Chan F, Feinstein JA, and Taylor CA. Effects of exercise and respiration on hemodynamic efficiency in CFD simulations of the total cavopulmonary connection. Annals of Biomedical Engineering, 35:250–263, 2007. [DOI] [PubMed] [Google Scholar]
- [18].Marsden AL, Bernstein AD, Reddy VM, Shadden S, Spilker R, Chan FP, Taylor CA, and Feinstein JA. Evaluation of a novel Y-shaped extracardiac fontan baffle using computational fluid dynamics. Journal of Thoracic and Cardiovascular Surgery, 137:394–403.e2, 2009. [DOI] [PubMed] [Google Scholar]
- [19].Kim HJ, Vignon-Clementel IE, Coogan JS, Figueroa CA, Jansen KE, and Taylor CA. Patient-specific modeling of blood flow and pressure in human coronary arteries. Annals of Biomedical Engineering, 38(10):3195–3209, 2010. [DOI] [PubMed] [Google Scholar]
- [20].Les AS, Shadden SC, Figueroa CA, Park JM, Tedesco MM, Herfkens RJ, Dalman RL, and Taylor CA. Quantification of hemodynamics in abdominal aortic aneurysms during rest and exercise using magnetic resonance imaging and computational fluid dynamics. Annals of Biomedical Engineering, 38(4):1288–1313, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Eslami P, Tran J, Jin Z, Karady J, Sotoodeh R, Lu MT, Hoffmann U, and Marsden A. Effect of wall elasticity on hemodynamics and wall shear stress in patient-specific simulations in the coronary arteries. Journal of Biomechanical Engineering, 142(2):024503, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Taylor CA, Fonte TA, and Min JK. Computational fluid dynamics applied to cardiac computed tomography for noninvasive quantification of fractional flow reserve: Scientific basis. Journal of the American College of Cardiology, 61(22):2233–2241, 2013. [DOI] [PubMed] [Google Scholar]
- [23].Lee JM, Choi G, Hwang D, Park J, Kim HJ, Doh J-H, Nam C-K, Na S-H, Shin E-S, Taylor CA, and Koo B-K. Impact of longitudinal lesion geometry on location of plaque rupture and clinical presentations. JACC: Cardiovascular Imaging, 10(6):677–688, 2017. [DOI] [PubMed] [Google Scholar]
- [24].Taylor CA, Gaur S, Leipsic J, Achenbach S, Berman DS, Jensen JM, Dey D, Btker HE, Kim HJ, Khem S, Wilk A, Zarins CK, Bezerra H, Lesser J, Ko B, Narula J, Ahmadi A, Øvrehus KA, St Goar F, De Bruyne B, and Nørgaard BL. Effect of the ratio of coronary arterial lumen volume to left ventricle myocardial mass derived from coronary CT angiography on fractional flow reserve. Journal of Cardiovascular Computed Tomography, 11(6):429–436, 2017. [DOI] [PubMed] [Google Scholar]
- [25].Modi BN, Sankaran S, Kim HJ, Ellis H, Rogers C, Taylor CA, Rajani R, and Perera D. Predicting the physiological effect of revascularization in serially diseased coronary arteries: Clinical validation of a novel CT coronary angiography-based technique. Circulation: Cardiovascular Interventions, 12(2):e007577, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Doost SN, Zhong L, Su B, and Morsi YS. The numerical analysis of non-Newtonian blood flow in human patient-specific left ventricle. Computer Methods and Programs in Biomedicine, 127:232–247, 2016. [DOI] [PubMed] [Google Scholar]
- [27].Bavo AM, Pouch AM, Degroote J, Vierendeels J, Gorman JH, Gorman RC, and Segers P. Patient-specific CFD simulation of intraventricular haemodynamics based on 3D ultrasound imaging. Biomedical engineering online, 15(1):107, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Bavo AM, Pouch AM, Degroote J, Vierendeels J, Gorman JH, Gorman RC, and Segers P. Patient-specific CFD models for intraventricular flow analysis from 3D ultrasound imaging: Comparison of three clinical cases. Journal of Biomechanics, 50:144–150, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Mao W, Caballero A, McKay R, Primiano C, and Sun W. Fully-coupled fluid-structure interaction simulation of the aortic and mitral valves in a realistic 3D left ventricle model. PloS One, 12(9):e0184729, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Terahara T, Takizawa K, Tezduyar TE, Tsushima A, and Shiozaki K Ventricle-valve-aorta flow analysis with the SpaceTime Isogeometric Discretization and Topology Change. Computational Mechanics, 65: 1343–1363, 2020. [Google Scholar]
- [31].Mittal R, Seo JH, Vedula V, Choi YJ, Liu H, Huang HH, Jain S, Younes L, Abraham T, and George RT. Computational modeling of cardiac hemodynamics: Current status and future outlook. Journal of Computational Physics, 305:1065–1082, 2016. [Google Scholar]
- [32].Hughes TJR, Liu WK, and Zimmermann TK. Lagrangian–Eulerian finite element formulation for incompressible viscous flows. Computer Methods in Applied Mechanics and Engineering, 29:329–349, 1981. [Google Scholar]
- [33].Donea J, Giuliani S, and Halleux JP. An arbitrary Lagrangian–Eulerian finite element method for transient dynamic fluid–structure interactions. Computer Methods in Applied Mechanics and Engineering, 33(1–3):689–723, 1982. [Google Scholar]
- [34].Donea J, Huerta A, Ponthot J-P, and Rodriguez-Ferran A. Arbitrary Lagrangian–Eulerian methods. In Encyclopedia of Computational Mechanics, Volume 3: Fluids, chapter 14. John Wiley & Sons, 2004. [Google Scholar]
- [35].Tezduyar TE, Behr M, and Liou J. A new strategy for finite element computations involving moving boundaries and interfaces – the deforming-spatial-domain/space–time procedure: I. The concept and the preliminary numerical tests. Computer Methods in Applied Mechanics and Engineering, 94(3):339–351, 1992. [Google Scholar]
- [36].Tezduyar TE, Behr M, Mittal S, and Liou J. A new strategy for finite element computations involving moving boundaries and interfaces – the deforming-spatial-domain/space–time procedure: II. Computation of free-surface flows, two-liquid flows, and flows with drifting cylinders. Computer Methods in Applied Mechanics and Engineering, 94(3):353–371, 1992. [Google Scholar]
- [37].Tezduyar TE and Takizawa K. Space–time computations in practical engineering applications: A summary of the 25-year history. Computational Mechanics, 63:747–753, 2019. [Google Scholar]
- [38].Takizawa K, Tezduyar TE, and Sasaki T. Aorta modeling with the element-based zero-stress state and isogeometric discretization. Computational Mechanics, 59:265–280, 2017. [Google Scholar]
- [39].Sasaki T, Takizawa K, and Tezduyar TE. Aorta zero-stress state modeling with T-spline discretization. Computational Mechanics, 63:1315–1331, 2019. [Google Scholar]
- [40].Takizawa K, Tezduyar TE, Uchikawa H, Terahara T, Sasaki T, and Yoshida A. Mesh refinement influence and cardiac-cycle flow periodicity in aorta flow analysis with isogeometric discretization. Computers & Fluids, 179:790–798, 2019. [Google Scholar]
- [41].Sasaki T, Takizawa K, and Tezduyar TE. Medical-image-based aorta modeling with zero-stress-state estimation. Computational Mechanics, 64:249–271, 2019. [Google Scholar]
- [42].Yu Y, Zhang YJ, Takizawa K, Tezduyar TE, and Sasaki T. Anatomically realistic lumen motion representation in patient-specific space–time isogeometric flow analysis of coronary arteries with time-dependent medical-image data. Computational Mechanics, 65(2):395–404, 2020. [Google Scholar]
- [43].Johnson AA and Tezduyar TE. Parallel computation of incompressible flows with complex geometries. International Journal for Numerical Methods in Fluids, 24:1321–1340, 1997. [Google Scholar]
- [44].Johnson AA and Tezduyar TE. 3D simulation of fluid-particle interactions with the number of particles reaching 100. Computer Methods in Applied Mechanics and Engineering, 145:301–321, 1997. [Google Scholar]
- [45].Johnson AA and Tezduyar TE. Advanced mesh generation and update methods for 3D flow simulations. Computational Mechanics, 23: 130–143, 1999. [Google Scholar]
- [46].Sathe S and Tezduyar TE. Modeling of fluid–structure interactions with the space–time finite elements: Contact problems. Computational Mechanics, 43:51–60, 2008. [Google Scholar]
- [47].Takizawa K, Tezduyar TE, Terahara T, and Sasaki T. Heart valve flow computation with the integrated Space–Time VMS, Slip Interface, Topology Change and Isogeometric Discretization methods. Computers & Fluids, 158:176–188, 2017. [Google Scholar]
- [48].Terahara T, Takizawa K, Tezduyar TE, Bazilevs Y, and Hsu M-C. Heart valve isogeometric sequentially-coupled FSI analysis with the space–time topology change method. Computational Mechanics, 65: 1167–1187, 2020. [Google Scholar]
- [49].Kamensky D, Hsu M-C, Schillinger D, Evans JA, Aggarwal A, Bazilevs Y, Sacks MS, and Hughes TJR. An immersogeometric variational framework for fluid–structure interaction: Application to bioprosthetic heart valves. Computer Methods in Applied Mechanics and Engineering, 284:1005–1053, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Hsu M-C, Kamensky D, Bazilevs Y, Sacks MS, and Hughes TJR. Fluid–structure interaction analysis of bioprosthetic heart valves: Significance of arterial wall deformation. Computational Mechanics, 54: 1055–1071, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Hsu M-C, Kamensky D, Xu F, Kiendl J, Wang C, Wu MCH, Mineroff J, Reali A, Bazilevs Y, and Sacks MS. Dynamic and fluid–structure interaction simulations of bioprosthetic heart valves using parametric design with T-splines and Fung-type material models. Computational Mechanics, 55:1211–1225, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Xu F, Morganti S, Zakerzadeh R, Kamensky D, Auricchio F, Reali A, Hughes TJR, Sacks MS, and Hsu M-C. A framework for designing patient-specific bioprosthetic heart valves using immersogeometric fluid–structure interaction analysis. International Journal for Numerical Methods in Biomedical Engineering, 34(4):e2938, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Wu MCH, Zakerzadeh R, Kamensky D, Kiendl J, Sacks MS, and Hsu M-C. An anisotropic constitutive model for immersogeometric fluid–structure interaction analysis of bioprosthetic heart valves. Journal of Biomechanics, 74:23–31, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Johnson EL, Wu MCH, Xu F, Wiese NM, Rajanna MR, Herrema AJ, Ganapathysubramanian B, Hughes TJR, Sacks MS, and Hsu M-C. Thinner biological tissues induce leaflet flutter in aortic heart valve replacements. Proceedings of the National Academy of Sciences, 117:19007–19016, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Xu F, Schillinger D, Kamensky D, Varduhn V, Wang C, and Hsu M-C. The tetrahedral finite cell method for fluids: Immersogeometric analysis of turbulent flow around complex geometries. Computers & Fluids, 141:135–154, 2016. [Google Scholar]
- [56].Hsu M-C, Wang C, Xu F, Herrema AJ, and Krishnamurthy A. Direct immersogeometric fluid flow analysis using B-rep CAD models. Computer Aided Geometric Design, 43:143–158, 2016. [Google Scholar]
- [57].Wang C, Xu F, Hsu M-C, and Krishnamurthy A. Rapid B-rep model preprocessing for immersogeometric analysis using analytic surfaces. Computer Aided Geometric Design, 52–53:190–204, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Xu F, Bazilevs Y, and Hsu M-C. Immersogeometric analysis of compressible flows with application to aerodynamic simulation of rotorcraft. Mathematical Models and Methods in Applied Sciences, 29:905–938, 2019. [Google Scholar]
- [59].Zhu Q, Xu F, Xu S, Hsu M-C, and Yan J. An immersogeometric formulation for free-surface flows with application to marine engineering problems. Computer Methods in Applied Mechanics and Engineering, 361:112748, 2020. [Google Scholar]
- [60].Xu S, Xu F, Kommajosula A, Hsu M-C, and Ganapathysubramanian B. Immersogeometric analysis of moving objects in incompressible flows. Computers & Fluids, 189:24–33, 2019. [Google Scholar]
- [61].Wu MCH, Muchowski HM, Johnson EL, Rajanna MR, and Hsu M-C. Immersogeometric fluid–structure interaction modeling and simulation of transcatheter aortic valve replacement. Computer Methods in Applied Mechanics and Engineering, 357:112556, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Wriggers P. Computational Contact Mechanics, 2nd ed. Springer-Verlag, Berlin Heidelberg, 2006. [Google Scholar]
- [63].Laursen TA. Computational Contact and Impact Mechanics: Fundamentals of Modeling Interfacial Phenomena in Nonlinear Finite Element Analysis. Springer-Verlag, Berlin Heidelberg, 2003. [Google Scholar]
- [64].Kamensky D, Evans JA, and Hsu M-C. Stability and conservation properties of collocated constraints in immersogeometric fluid-thin structure interaction analysis. Communications in Computational Physics, 18:1147–1180, 2015. [Google Scholar]
- [65].Yu Y, Kamensky D, Hsu M-C, Lu XY, Bazilevs Y, and Hughes TJR. Error estimates for projection-based dynamic augmented Lagrangian boundary condition enforcement, with application to fluid–structure interaction. Mathematical Models and Methods in Applied Sciences, 28(12):2457–2509, 2018. [Google Scholar]
- [66].Hsu M-C and Kamensky D. Immersogeometric analysis of bioprosthetic heart valves, using the dynamic augmented Lagrangian method. In Tezduyar TE, editor, Frontiers in Computational Fluid–Structure Interaction and Flow Simulation, pages 167–212. Springer International Publishing, Cham, 2018. [Google Scholar]
- [67].Hsu M-C, Wang C, Herrema AJ, Schillinger D, Ghoshal A, and Bazilevs Y. An interactive geometry modeling and parametric design platform for isogeometric analysis. Computers and Mathematics with Applications, 70:1481–1500, 2015. [Google Scholar]
- [68].Bazilevs Y, Calo VM, Cottrel JA, Hughes TJR, Reali A, and Scovazzi G. Variational multiscale residual-based turbulence modeling for large eddy simulation of incompressible flows. Computer Methods in Applied Mechanics and Engineering, 197:173–201, 2007. [Google Scholar]
- [69].Kiendl J, Hsu M-C, Wu MCH, and Reali A. Isogeometric Kirchhoff–Love shell formulations for general hyperelastic materials. Computer Methods in Applied Mechanics and Engineering, 291:280–303, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Krishnamurthy A, Villongco CT, Chuang J, Frank LR, Nigam V, Belezzuoli E, Stark P, Krummen DE, Narayan S, Omens JH, McCulloch AD, and Kerckhoffs RCP. Patient-specific models of cardiac biomechanics. Journal of Computational Physics, 244:4–21, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Kamensky D, Xu F, Lee C-H, Yan J, Bazilevs Y, and Hsu M-C. A contact formulation based on a volumetric potential: Application to isogeometric simulations of atrioventricular valves. Computer Methods in Applied Mechanics and Engineering, 330:522–546, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Krishnamurthy A, Gonzales MJ, Sturgeon G, Segars WP, and McCulloch AD. Biomechanics simulations using cubic Hermite meshes with extraordinary nodes for isogeometric cardiac modeling. Computer Aided Geometric Design, 43:27–38, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Bazilevs Y, Hsu M-C, and Scott MA. Isogeometric fluid–structure interaction analysis with emphasis on non-matching discretizations, and with application to wind turbines. Computer Methods in Applied Mechanics and Engineering, 249:28–41, 2012. [Google Scholar]
- [74].Tezduyar TE. Finite element methods for flow problems with moving boundaries and interfaces. Archives of Computational Methods in Engineering, 8:83–130, 2001. [Google Scholar]
- [75].Stein K, Tezduyar T, and Benney R. Mesh moving techniques for fluid–structure interactions with large displacements. Journal of Applied Mechanics, 70:58–63, 2003. [Google Scholar]
- [76].Tezduyar TE and Sathe S. Modeling of fluid–structure interactions with the space–time finite elements: Solution techniques. International Journal for Numerical Methods in Fluids, 54:855–900, 2007. [Google Scholar]
- [77].Gerbeau J-F, Vidrascu M, and Frey P. Fluid–structure interaction in blood flows on geometries based on medical imaging. Computers and Structures, 83:155–165, 2005. [Google Scholar]
- [78].Nobile F and Vergara C. An effective fluid–structure interaction formulation for vascular dynamics by generalized Robin conditions. SIAM Journal on Scientific Computing, 30:731–763, 2008. [Google Scholar]
- [79].Takizawa K, Bazilevs Y Tezduyar TE Long CC Marsden AL, and Schjodt K. ST and ALE-VMS methods for patient-specific cardiovascular fluid mechanics modeling. Mathematical Models and Methods in Applied Sciences, 24(12):2437–2486, 2014. [Google Scholar]
- [80].Masud A and Khurram RA. A multiscale finite element method for the incompressible Navier–Stokes equations. Computer Methods in Applied Mechanics and Engineering, 195:1750–1777, 2006. [Google Scholar]
- [81].Khurram RA and Masud A. A multiscale/stabilized formulation of the incompressible Navier–Stokes equations for moving boundary flows and fluid–structure interaction. Computational Mechanics, 38:403–416, 2006. [Google Scholar]
- [82].Calderer R and Masud A. A multiscale stabilized ALE formulation for incompressible flows with moving boundaries. Computational Mechanics, 46:185–197, 2010. [Google Scholar]
- [83].Masud A and Calderer R. Residual-based turbulence models for moving boundary flows: Hierarchical application of variational multiscale method and three-level scale separation. International Journal for Numerical Methods in Fluids, 73(3):284–305, 2013. [Google Scholar]
- [84].Calderer R, Zhu L, Gibson R, and Masud A. Residual-based turbulence models and arbitrary Lagrangian–Eulerian framework for free surface flows. Mathematical Models and Methods in Applied Sciences, 25(12):2287–2317, 2015. [Google Scholar]
- [85].Brooks AN and Hughes TJR. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier–Stokes equations. Computer Methods in Applied Mechanics and Engineering, 32:199–259, 1982. [Google Scholar]
- [86].Hughes TJR, Mazzei L, Oberai AA, and Wray A. The multiscale formulation of large eddy simulation: Decay of homogeneous isotropic turbulence. Physics of Fluids, 13:505–512, 2001. [Google Scholar]
- [87].Bazilevs Y, Yan J, de Stadler M, and Sarkar S. Computation of the flow over a sphere at Re = 3700: A comparison of uniform and turbulent inflow conditions. Journal of Applied Mechanics, 81(12):121003, 2014. [Google Scholar]
- [88].Yan J, Deng X, Korobenko A, and Bazilevs Y. Free-surface flow modeling and simulation of horizontal-axis tidal-stream turbines. Computers & Fluids, 158:157–166, 2017. [Google Scholar]
- [89].Yan J, Korobenko A, Tejada-Martínez AE, Golshan R, and Bazilevs Y. A new variational multiscale formulation for stratified incompressible turbulent flows. Computers & Fluids, 158:150–156, 2017. [Google Scholar]
- [90].Bazilevs Y and Hughes TJR. Weak imposition of Dirichlet boundary conditions in fluid mechanics. Computers & Fluids, 36:12–26, 2007. [Google Scholar]
- [91].Yan J, Augier B, Korobenko A, Czarnowski J, Ketterman G, and Bazilevs Y. FSI modeling of a propulsion system based on compliant hydrofoils in a tandem configuration. Computers & Fluids, 141:201–211, 2016. [Google Scholar]
- [92].Zhu Q and Yan J. A moving-domain CFD solver in FEniCS with applications to tidal turbine simulations in turbulent flows. Computers & Mathematics with Applications, 2019. 10.1016/j.camwa.2019.07.034. [DOI] [Google Scholar]
- [93].Tong P and Fung Y-C. The stress-strain relationship for the skin. Journal of Biomechanics, 9(10):649–657, 1976. [DOI] [PubMed] [Google Scholar]
- [94].Fung Y-C. Biomechanics: Mechanical Properties of Living Tissues. Springer-Verlag, New York, second edition, 1993. [Google Scholar]
- [95].Sun W, Sacks MS, Sellaro TL, Slaughter WS, and Scott MJ. Biaxial mechanical response of bioprosthetic heart valve biomaterials to high in-plane shear. Journal of Biomechanical Engineering, 125(3): 372–380, 2003. [DOI] [PubMed] [Google Scholar]
- [96].Fan R and Sacks MS. Simulation of planar soft tissues using a structural constitutive model: Finite element implementation and validation. Journal of Biomechanics, 47(9):2043–2054, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [97].Kamensky D, Behzadinasab M, Foster JT, and Bazilevs Y. Peridynamic modeling of frictional contact. Journal of Peridynamics and Nonlocal Modeling, 1(2):107–121, 2019. [Google Scholar]
- [98].Chung J and Hulbert GM. A time integration algorithm for structural dynamics with improved numerical dissipation: The generalized-α method. Journal of Applied Mechanics, 60:371–75, 1993. [Google Scholar]
- [99].Simo JC, Wriggers P, and Taylor RL. A perturbed Lagrangian formulation for the finite element solution of contact problems. Computer Methods in Applied Mechanics and Engineering, 50(2):163–180, 1985. [Google Scholar]
- [100].Kamensky D, Hsu M-C, Yu Y, Evans JA, Sacks MS, and Hughes TJR. Immersogeometric cardiovascular fluid–structure interaction analysis with divergence-conforming B-splines. Computer Methods in Applied Mechanics and Engineering, 314:408–472, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101].Tezduyar TE, Takizawa K, Moorman C, Wright S, and Christopher J. Space–time finite element computation of complex fluid–structure interactions. International Journal for Numerical Methods in Fluids, 64: 1201–1218, 2010. [Google Scholar]
- [102].Hudsmith LE, Petersen SE, Francis JM, Robson MD, and Neubauer S. Normal human left and right ventricular and left atrial dimensions using steady state free precession magnetic resonance imaging. Journal of Cardiovascular Magnetic Resonance, 7(5):775–782, 2005. [DOI] [PubMed] [Google Scholar]
- [103].Gonzales MJ, Sturgeon G, Krishnamurthy A, Hake J, Jonas R, Stark P, Rappel W-J, Narayan SM, Zhang Y, Segars WP, and McCulloch AD. A three-dimensional finite element model of human atrial anatomy: New methods for cubic hermite meshes with extraordinary vertices. Medical Image Analysis, 17(5):525–537, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [104].Jafari A, Pszczolkowski E, and Krishnamurthy A. A framework for biomechanics simulations using four-chamber cardiac models. Journal of Biomechanics, 91:92–101, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [105].Holzapfel GA and Ogden RW. Constitutive modelling of passive myocardium: A structurally based framework for material characterization. Philosophical Transactions of the Royal Society A, 367(1902): 3445–3475, 2009. [DOI] [PubMed] [Google Scholar]
- [106].Lumens J, Delhaas T, Kirn B, and Arts T. Three-wall segment (TriSeg) model describing mechanics and hemodynamics of ventricular interaction. Annals of Biomedical Engineering, 37(11):2234–2255, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [107].Tezduyar TE, Behr M, Mittal S, and Johnson AA. Computation of unsteady incompressible flows with the finite element methods – Space–time formulations, iterative strategies and massively parallel implementations. In New Methods in Transient Analysis, PVP-Vol.246/AMD-Vol.143, pages 7–24, New York, 1992. ASME. [Google Scholar]
- [108].Esmaily-Moghadam M, Bazilevs Y, Hsia T-Y, Vignon-Clementel IE, and Marsden AL. A comparison of outlet boundary treatments for prevention of backflow divergence with relevance to blood flow simulations. Computational Mechanics, 48:277–291, 2011. [Google Scholar]
- [109].Kenner T. The measurement of blood density and its meaning. Basic Research in Cardiology, 84(2):111–124, 1989. [DOI] [PubMed] [Google Scholar]
- [110].Rosencranz R and Bogen SA. Clinical laboratory measurement of serum, plasma, and blood viscosity. American Journal of Clinical Pathology, 125:78–86, 2006. [DOI] [PubMed] [Google Scholar]
- [111].TACC Lonestar5 User Guide. https://portal.tacc.utexas.edu/user-guides/lonestar5. 2020.
- [112].Texas Advanced Computing Center (TACC). http://www.tacc.utexas.edu. 2020.
- [113].Hsu M-C, Akkerman I, and Bazilevs Y. High-performance computing of wind turbine aerodynamics using isogeometric analysis. Computers & Fluids, 49:93–100, 2011. [Google Scholar]
- [114].Mirnajafi A, Raymer J, Scott MJ, and Sacks MS. The effects of collagen fiber orientation on the flexural properties of pericardial heterograft biomaterials. Biomaterials, 26(7):795–804, 2005. [DOI] [PubMed] [Google Scholar]
- [115].Sun W, Abad A, and Sacks MS. Simulated bioprosthetic heart valve deformation under quasi-static loading. Journal of Biomechanical Engineering, 127(6):905–914, 2005. [DOI] [PubMed] [Google Scholar]
- [116].Kim H, Lu J, Sacks MS, and Chandran KB. Dynamic simulation of bioprosthetic heart valves using a stress resultant shell model. Annals of Biomedical Engineering, 36(2):262–275, 2008. [DOI] [PubMed] [Google Scholar]
- [117].Caballero A, Sulejmani F, Martin C, Pham T, and Sun W. Evaluation of transcatheter heart valve biomaterials: Biomechanical characterization of bovine and porcine pericardium. Journal of the Mechanical Behavior of Biomedical Materials, 75:486–494, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [118].Jeong J and Hussain F. On the identification of a vortex. Journal of Fluid Mechanics, 285:69–94, 1995. [Google Scholar]
- [119].Delemarre BJ, Visser CA, Bot H, and Dunning AJ. Prediction of apical thrombus formation in acute myocardial infarction based on left ventricular spatial flow pattern. Journal of the American College of Cardiology, 15(2):355–360, 1990. [DOI] [PubMed] [Google Scholar]
- [120].Delewi R, Zijlstra F, and Piek JJ. Left ventricular thrombus formation after acute myocardial infarction. Heart, 98(23):1743–1749, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Li M, Dumesnil JG, Mathieu P, and Pibarot P. Impact of valve prosthesis-patient mismatch on pulmonary arterial pressure after mitral valve replacement. Journal of the American College of Cardiology, 45 (7):1034–1040, 2005. [DOI] [PubMed] [Google Scholar]
- [122].Ren J-F, Aksut S, Lighty GW Jr, Vigilante GJ, Sink JD, Segal BL, and Hargrove WC. Mitral valve repair is superior to valve replacement for the early preservation of cardiac function: Relation of ventricular geometry to function. American Heart Journal, 131(5):974–981, 1996. [DOI] [PubMed] [Google Scholar]
- [123].Okita Y, Miki S, Kusuhara K, Ueda Y, Tahata T, Yamanaka K, and Higa T. Analysis of left ventricular motion after mitral valve replacement with a technique of preservation of all chordae tendineae. Comparison with conventional mitral valve replacement or mitral valve repair. The Journal ofThoracic and Cardiovascular Surgery, 104(3):786–795, 1992. [PubMed] [Google Scholar]
- [124].Popovic Z, Barac I, Jovic M, Panic G, Miric M, and Bojic M. Ventricular performance following valve replacement for chronic mitral regurgitation: Importance of chordal preservation. Journal of Cardiovascular Surgery, 40(2):183–190, 1999. [PubMed] [Google Scholar]
- [125].Lee C-H, Laurence DW, Ross CJ, Kramer KE, Babu AR, Johnson EL, Hsu M-C, Aggarwal A, Mir A, Burkhart HM, Towner RA, Baumwart R, and Wu Y. Mechanics of the tricuspid valve–from clinical diagnosis/treatment, in-vivo and in-vitro investigations, to patient-specific biomechanical modeling. Bioengineering, 6:47, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [126].Laurence DW, Johnson EL, Hsu M-C, Baumwart R, Mir A, Burkhart HM, Holzapfel GA, Wu Y, and Lee C-H. A pilot in silico modeling-based study of the pathological effects on the biomechanical function of tricuspid valves. International Journal for Numerical Methods in Biomedical Engineering, 36:e3346, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [127].Wu MCH, Kamensky D, Wang C, Herrema AJ, Xu F, Pigazzini MS, Verma A, Marsden AL, Bazilevs Y, and Hsu M-C. Optimizing fluid–structure interaction systems with immersogeometric analysis and surrogate modeling: Application to a hydraulic arresting gear. Computer Methods in Applied Mechanics and Engineering, 316:668–693, 2017. [Google Scholar]
- [128].Westerhof N, Lankhaar J-W, and Westerhof BE. The arterial Windkessel. Medical & Biological Engineering & Computing, 47:131–141, 2009. [DOI] [PubMed] [Google Scholar]