Data mining of functional RNA structures in genomic sequences

Abstract

The normal functions of genomes depend on the precise expression of messenger RNAs and noncoding RNAs (ncRNAs) such as transfer RNAs and microRNAs in eukaryotes. These ncRNAs and functional RNA structures (FRSs) act as regulators or response elements for cellular factors and participate in transcription, posttranscriptional processing, and translation. Knowledge discovery of these FRSs in huge DNA/RNA sequence databases is a very important step to reach our goal of going from genomic sequence data to biological knowledge for understanding RNA-based regulation. Analyses of a large number of FRSs have indicated that the FRS can be well characterized by some quantitative measures such as significance and well-ordered scores of the local segment. Various data mining tools have been developed and successfully applied to FRS discovery in genomic sequence databases. Here, we summarize our efforts in the computational discovery of structured features of ncRNAs and FRSs within complex genomes by EDscan and SigED.

INTRODUCTION

It is known that almost all of the genome is transcribed; however, only a small proportion (~2%) of the human genome encodes protein. There is an abundance of noncoding RNAs (ncRNAs) encoded in human and other eukaryotic genomes. It has been demonstrated that ncRNAs and functional RNA structures (FRSs) play important and diverse roles in the cell by interacting with proteins and other nucleic acids. Well-documented instances include transcriptional mediation,¹ RNA processing and modification,² messenger RNA (mRNA) stability³ and localization, and translation of mRNA into protein.⁴ Among them, a number of distinct FRSs located in viral mRNAs also play crucial roles in their transcription, nuclear export, and translation, including the transactivation response element, Rev response element of HIV, and the internal ribosome entry sequence (IRES) found in the 5′ untranslated region (UTR) of picornaviruses.⁵

mRNA has long been recognized as the immediate source of information for translation from sequences containing a four base alphabet of nucleotides (nts) to the 20 amino acid alphabet of proteins. Although mRNA is transcribed as if single stranded, almost every mRNA has structure that includes various double-stranded helical base paired regions formed by fold-back in an antiparallel orientation between complementary segments (A:U, G:C, and G:U) and the formation of unpaired loops. The loops include hairpin, internal, bulge, and multi-branch loops. The energy of an RNA structure is determined by summing the energy contributions from all of the stacked base pairs and loops it contains. The thermodynamic stability of an RNA fragment in the genome is often measured by the free energy of the formation of the folded segment.^6,7

The sequences of FRSs and ncRNAs are evolutionary products that have survived because they execute a biological function efficiently. Knowledge discovery⁸ using a large numbers of FRSs indicates that they have well-ordered conformations and are uniquely folded. One of the major goals of our data mining of sequence data is to discover potential FRSs in genomic transcripts, to correlate them with known experimental properties, and to suggest candidates for further experimental studies. A number of data mining tools have been developed to search for ncRNAs and FRSs in genomes.^9–11 Examples include genome-scale predictions of ncRNAs and FRSs, such as transfer RNAs (tRNAs), ribosomal RNAs (rRNAs), microRNAs (miRNAs), and riboswitches by comparative genomic analysis, that mainly rely on the conservation of an RNA primary sequence and/or an RNA structure. Advances in data mining FRSs in genomic sequences by comparative genomics and covariance analysis from other groups are fully discussed in the recent review paper.¹¹ However, there is no effective data mining approach to detect an FRS that lacks sequence or structure homology to one of the known FRSs. This latter point is the main focus of attention of this paper. Here, we mainly discuss our efforts in discovering the FRSs that lack homology information in genomic sequences, and the characterization of their distinct properties by the quantitative measures E_diff and Zscr_e of a local RNA segment and its statistical significance score SigZscr_e. In general, computational prediction of our potential FRSs in genomic sequences has been further verified by experimental testing of expression levels, functional assays by deletion or mutagenesis, and structural analysis.

FRSs ARE UNIQUELY FOLDED

Computational simulations and data mining for the evolutionary constraints that determine the distinct conformations of folded FRSs are often used to explore the structural feature of FRSs. It has been suggested that the FRSs possess well-ordered conformations that are both thermodynamically stable and uniquely folded.¹² Using a quantitative measure, maximal similarity score (MSS) between two RNA structures based on a tree-edit distance algorithm,⁸ the uniqueness of an RNA structure can be estimated by evaluating the difference between the average MSS computed from the structure of the natural RNA sequence and structures folded from its randomly shuffled sequences, and those MSS scores computed from the random structures versus random structures folded from the randomly shuffled sequences. For a test dataset that includes 100 tRNAs, 14 RNase P RNAs, and four other FRSs selected randomly from a database, data analyses⁸ indicated that the structural conformations of the 114 natural ncRNAs and the other four FRSs were significantly different from those of their corresponding random structures. The thermodynamic stability and the well-ordered conformation of the FRSs were unlikely to occur by chance. Furthermore, it also indicated that the measure of thermodynamic stability alone is not enough for us to characterize all the structural properties of FRSs.

QUANTITATIVE MEASURES OF FRS EVALUATION

On the basis of the knowledge discovery of what constitutes a well-ordered structural feature of FRSs, FRS can be characterized by both the thermodynamic stability and the distinct conformation of an FRS within a genomic sequence. Several groups^13,14 have also suggested that FRSs can be characterized by mutational robustness, linguistic complexity, and Shannon entropy. Previously, we often characterized an FRS by using two quantitative measures,^15,16 the significance score (SigScr) and the stability score (StbScr) computed from a genomic sequence. The normalized z-score, SigScr, indicates the difference in the thermodynamic stability between the structure of a local, natural segment and the average derived from its randomly shuffled sequences. The greater the negative value of SigScr, the more significant the folded structure in the segment. Similarly, the normalized z-score, StbScr, signifies the difference in the thermodynamic stability between a specific segment at a given place and the average of all other overlapping fragments of the same size generated by sliding the window in steps of one nt along the genomic sequence. The more negative the values of StbScr, the more stable the folded structure in the fragment.

In a recently developed data mining tool,¹⁷ FRSs were evaluated by the measure E_diff. The measure E_diff of a local segment, S, is used to characterize the properties of both the thermodynamic stability and the distinctness of the conformation of structures folded in S of the genomic sequence. E_diff is defined as the difference in free energies between the folded optimal structure (OS) and its corresponding optimal restrained structure (ORS) in which all the previous base pairings in the OS are forbidden, that is, E_diff = E_f − E.As shown in Figure 1, the E_diff value of miRNA let-7 precursor is 24.7 kcal/mol; however, the E_diff value of its corresponding randomly shuffled sequence is only 1.1 kcal/mol. Thus, E_diff signifies the uniqueness of the conformation folded in the segment.^17–20 The greater the E_diff of the folded segment, the more well-ordered the folded structure (WFS) is expected to be. To facilitate comparison of E_diff computed from different segments with various sizes, a normalized score Zscr_e of E_diff for each overlapping segment is used in the data mining, that is Zscr_{e =} (E_diff − E_diff(w))/std(w), where sample mean E_diff(w) and sample standard deviation std(w) are computed from the sample composed of all overlapping segments made by sliding a window along the genomic sequence.

FIGURE 1 |.

The optimal structure (OS) and corresponding optimal restrained structure (ORS) computed from Caenorhabditis elegans let-7 precursor sequence (a) and its randomly shuffled sequence (b). The computed lowest free energies of OS and ORS for the natural functional RNA are −38.5 (E) and −13.8 (E_f) kcal/mol, and from the randomly shuffled sequence are −15.0 (E) and 13.9 (E_f) kcal/mol, respectively. E_diff values are 24.7 kcal/mol for the let-7 precursor and 1.1 kcal/mol for its randomly shuffled sequence. It is quite obvious that the greater E_diff of the folded let-7 wild-type sequence indicates a significantly more well-ordered OS.¹⁷

To estimate the statistical extremes of Zscr_e in a very long genomic sequence, we need a good statistical model to describe the Zscr_e distribution in the sample. What is the general behavior of Zscr_e in a random sample that is associated with the natural genomic sequence? Statistical analysis indicated that the Zscr_e data were asymmetric with a sample mean, m = 0, sample standard deviation, std = 1.0.The distribution of Zscr_e is skewed in the positive direction with a long tail, and it does not follow a normal distribution.²¹ To estimate the statistical significance of E_diff and/or Zscr_e, a normalized z-score, SigZscr_e, is calculated by dividing the difference between the E_diff of the real and the average of the randomized sequences by the sample standard deviation of those E_diff measures computed from the randomized sequences. In the random sample, the distribution of the random variable SigZscr_e (RS) is expected to approximately follow a normal distribution.¹⁸ The statistical significance of E_diff can be easily estimated from the normal distribution. In many cases, WFSs with high SigZscr_e do correlate with FRSs and other biologically interesting properties.

DATA MINING TOOLS FOR DETECTING FRSs IN GENOMES

FRSs were characterized by SigScr and StbScr; the main approach¹⁵ of our data mining is to explore an RNA sequence by choosing successive overlapping segments by sliding a fixed window with a step of one nt along the genomic sequence. The SigScr scores are calculated by comparing their lowest free energies computed from the actual segment sequences to those from a number of randomly shuffled sequences of the same size and base composition. At the same time, a comparison is also made between the local thermodynamic stability and the average of all overlapping segments. As a result, the StbScr is also computed. The FORTRAN programs SIGSTB¹⁶ and SEGFOLD¹⁵ are the operational codes for these computations. In general, unusually stable or unstable folding regions (UFRs) can be found by more extensive searches using various segment sizes to define the extent of the unusual regions in an mRNA.^15,16 For a large data sample, a linearly transformed noncentral Students’ t distribution (LTNSTD) is used to delineate the distributions of SigScr and StbScr computed in the entire genome. Statistical tests²² have indicated that LTNSTD is a good statistical model to describe the behavior of the two scores in the large sample. The significant UFRs that are either much more stable or unstable than expected by chance are discovered on the basis of the derived LTNSTD. In many cases,^16,23–26 UFRs do correlate with FRSs and other biologically interesting properties.

Using the same scan approach and a specific quantitative measure E_diff, data mining tool EDscan¹⁷ is used to compute E_diff and Zscr_e and SigED¹⁸ is used to compute SigZscr_e by sliding a window along the genomic sequence. In the computation of E_diff, E_diff = E_f − E, we first have to determine the secondary structure of the OS folded in S, in addition to computing the value of E in S. By prohibiting all base pairings in the folded OS, we then compute the lowest free energy of the local segment S again. Thus, we need to fold S twice under the two specific conditions to compute E_diff. For a given RNA sequence, a dynamic programming algorithm is used to predict an OS with the given energy rules⁷ in all of our approaches.

In general, the local maxima of Zscr_e are extracted to determine the optimized WFSs from a more extensive search¹⁷ using various segment sizes in the RNA sequence. The statistical significance of the computed WFSs is further tested by using Monte Carlo simulations (SigED). In SigED,¹⁸ the E_diff computed from actual segment sequences is compared with those from a number of randomly shuffled sequences, and as a result, SigZscr_e is calculated. In the random sample, the distribution of the random variable SigZscr_e (RS) is expected to approximately follow a normal distribution.¹⁸ The statistical significance of E_diff of WFS can be easily estimated from the normal distribution. In many cases,^17,20,21,27 WFSs do correlate with FRSs and other biologically interesting properties.

Once the UFR and WFS are found in a genomic sequence, then similar structural features are looked for in their homologous RNAs by using EFFOLD, COMFOLD, and RNAGA. Homologous FRSs can be further searched for using sequence databases by HomoStRscan based on both the primary sequence and the higher-ordered structures. This is different from approaches used by other groups,¹¹ which require comparative genomics to determine significant RNA motifs. More details about all these programs can be found online at http://protein3d.ncifcrf.gov/shuyun/rna2d.html.

DATA MINING OF FRSs IN THE 5′ AND 3′ UTRs OF mRNAs

In most eukaryotic, mRNAs translation into protein begins at the first initiation codon, AUG, found in the 5′ end. A notable exception was first found in poliovirus RNA, which has multiple unused AUG triplets in its long ~760 nt 5′ UTR. Computational analyses and experimental studies revealed that a special UFR called an IRES allowed the translational machinery of the infected cell to skip over the upstream AUGs (uAUG). Following this discovery, we used our computational tools to find similar structures in not only all the other viruses with analogous biology to poliovirus but also in other viral and cellular mRNAs that often have long, GC-rich, and structured 5′ UTRs with multiple uAUGs as well. The common structural core²³ of these divergent viral IRESs shares a similar four-way junction motif to group I introns. However, the common structural core computed for these cellular IRESs²⁴ shows a distinct, three-way junction (Y-shaped stem-loop) motif that is followed by a sequence that is complementary to the 3′ end of the human 18S rRNA. This complementary sequence is just a few nt upstream from the initiation codon (AUG). There are a growing number of interesting cases in which it has been shown that the conserved Y-shaped stem-loop motifs^25,26,28 play an important role in regulation of expression at a posttranscriptional level. Some possible roles for IRES regulation are alternative expressions in different cellular environments in developmental differentiation and in response to different stresses.

In general, human mRNAs have long 3′ UTRs with an average length of ~740 nt. It is conceivable that the 3′ UTR is not traversed by ribosomes. Therefore, the 3′ UTR seems to be a place for the assembly of complexes that can contribute to a wide range of control by posttranscriptional regulation. In studying the rapLR1 mRNA of an antioncogenic protein, we detected two remarkable FRSs in its long 2377 nt 3′ UTR. The conserved structural feature of the two FRSs is a long stalk-like stem-loop.²⁹ When this long mRNA was tested in vitro, it was not translated efficiently, but if the long 3′ UTR was eliminated, translation was greatly increased. This suggested that the long double-stranded RNA (dsRNA) played a negative regulatory role by which the mRNA is degraded in a manner that is similar to that found in the RNA interference pathway. Our database search indicated that the occurrence rate for such large dsRNA in 3′ UTRs is ~0.19% in human mRNA; however, about 2887 miRNA-like stem-loops are found in human 3′ UTRs.¹⁹ These miRNA-like stem-loops may play a role in the translational repression of gene expression. Interestingly, more FRSs have been recently determined in 3′ UTRs.^20,27 For example, two significant UFRs were found in the 3′ UTR of turnip crinkle virus (TCV) that join together to fold into a three-dimensional structure resembling a tRNA-like shape.²⁷ Experimental data further indicate that the FRS includes a ribosome-binding structural element and plays a key role in the switch between viral translation and replication of TCV.²⁷

FINDING CONSERVED STRUCTURAL FEATURES OF miRNAs IN GENOMES

In searching for significant WFSs in the intergenic sequences of human and other genomes, we found a large number of distinct stem-loops of miRNAs^18,21,30 by EDscan and SigED. The statistical analysis³⁰ of the computed E_diff for these miRNAs and their corresponding randomly shuffled sequences indicated that the miRNA stem-loops are distinct, well ordered, and can be well characterized by the score E_diff (see Table 1). To perform data mining for well-ordered stem-loops in genomic sequences, a specific version of EDscan, called StemED,³⁰ can be used to improve the prediction. In StemED, only stem-loops folded in the local segment are considered in computing E_diff so that the accuracy of the predictions are less sensitive to the window size used (Figure 2). Also, the computational complexity is decreased to O (L × n²) from O (L × n³) where L is the length of the genomic sequence and n is the size of the sliding window. The extensive computational search requirements for ncRNAs in genomes indicate that EDscan and SigED are generally very useful for finding FRSs that are expected to be both significantly more ordered and thermodynamically more stable than expected by chance.

TABLE 1.

Statistical Analysis of Computed E_diff (kcal/mol) for miRNA Precursors from the miRBase Database (2005) and Their Corresponding 500 Randomly Shuffled Sequences³⁰

		Sample Mean and Standard Deviation (std) Computed from
miRNAs		Natural Sequence		Randomly Shuffled Sequence
Genome	Number	Ediff (std)	SigZscr (std)	Ediff (std)	SigZscr (std)
Human	207	20.52 (5.89)	6.11 (2.25)	3.50 (0.55)	0.0 (1.0)
Mouse	208	19.14 (6.19)	5.76 (2.34)	3.43 (0.52)	0.0 (1.0)
Rat	187	20.40 (6.13)	5.93 (2.15)	3.54 (0.46)	0.0 (1.0)
Gallus gallus	121	19.81 (5.02)	6.13 (1.77)	3.30 (0.36)	0.0 (1.0)
Fly	78	18.22 (4.68)	5.80 (1.73)	3.14 (0.41)	0.0 (1.0)
Caenorhabditis elegans	116	20.15 (7.03)	6.09 (2.40)	3.36 (0.41)	0.0 (1.0)
Caenorhabditis briggsae	50	21.84 (6.03)	6.77 (2.30)	3.36 (0.34)	0.0 (1.0)
Arabidopsis thaliana	92	30.54 (8.22)	8.48 (2.17)	3.99 (0.80)	0.0 (1.0)
Oryza sativa	122	30.35 (9.89)	7.72 (2.61)	4.35 (0.66)	0.0 (1.0)

FIGURE 2 |.

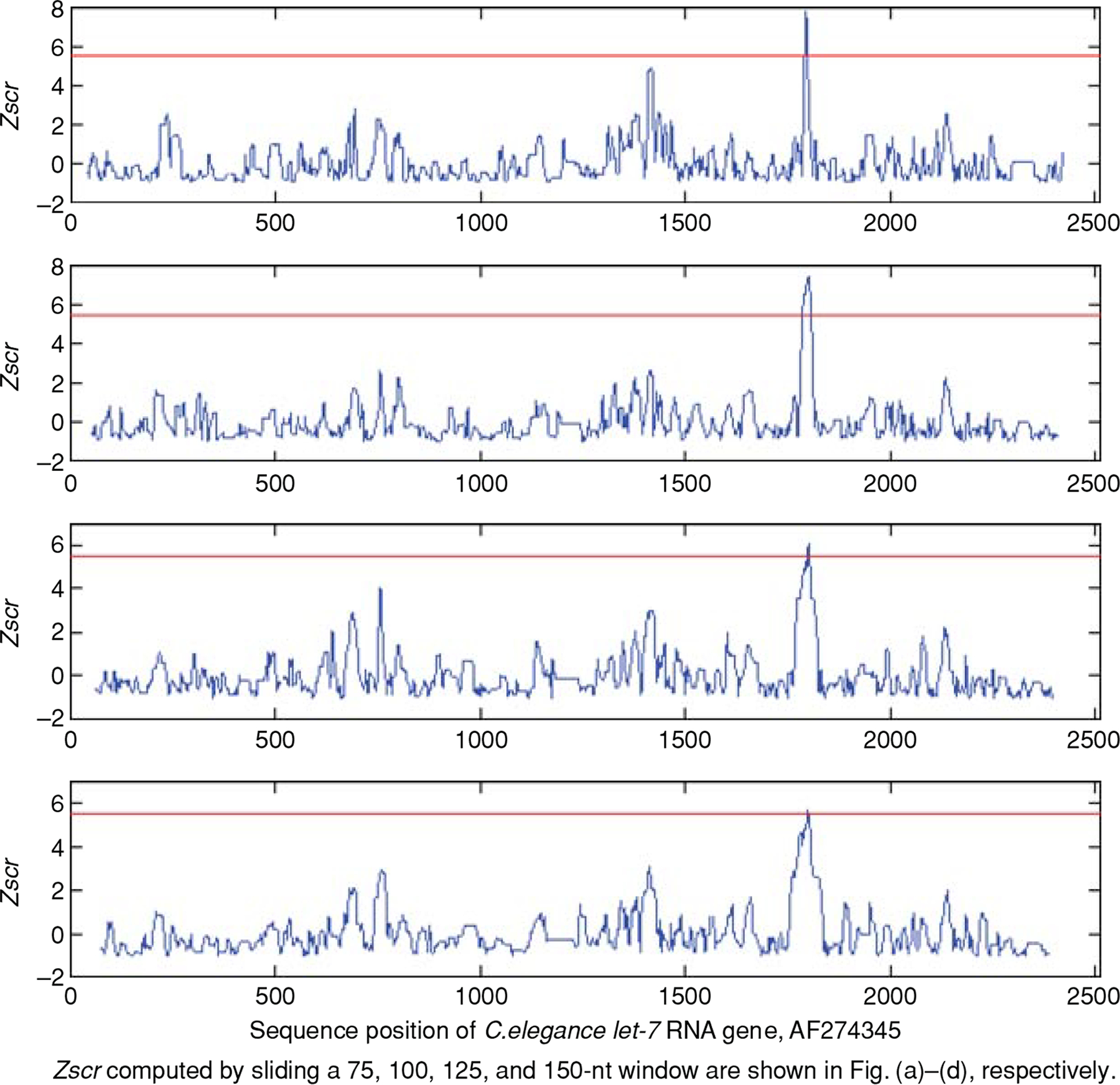
Zscr_e of local segments computed for the genomic sequence of Caenorhabditis elegans (accession no. AF274345). Zscr_e were computed by moving a set of windows with sizes of 75-nt (shown in row 1), 100-nt (row 2), 125-nt (row 3), and 150-nt (row 4) in steps of 3 nt from 5′ to 3′ along the sequence by StemED. The plot was made by plotting the Zscr_e against the position of the middle nt of these overlapping segments. The reported stem-loop of let-7 can be easily distinguished in each plot by the maximal Zscr_e as denoted the by peak in the plot.³⁰

CONCLUSION

Computational methods can discover RNA structures that are associated with important biological properties. The need for this kind of data mining is growing in proportion to the size of sequence databases. Rapid advances in computational biology are providing new approaches for understanding complex biological systems. Advances in molecular biology and medicine require the combined efforts of bioinformaticians and molecular biologists. Such integrative approaches hold promise for elucidating gene function and RNA-based regulation of gene expression. With the continued improvement in integrating algorithms that combine statistical and computational tools for RNA folding, pattern search, sequence, and structure comparison, computational methods can be improved to discover FRSs that are associated with important biological properties.