Digital light processing 3D prints liquid crystal elastomers for artificial muscle-like actuation and optomechanical self-sensing.
Abstract
Artificial muscles based on stimuli-responsive polymers usually exhibit mechanical compliance, versatility, and high power-to-weight ratio, showing great promise to potentially replace conventional rigid motors for next-generation soft robots, wearable electronics, and biomedical devices. In particular, thermomechanical liquid crystal elastomers (LCEs) constitute artificial muscle-like actuators that can be remotely triggered for large stroke, fast response, and highly repeatable actuations. Here, we introduce a digital light processing (DLP)–based additive manufacturing approach that automatically shear aligns mesogenic oligomers, layer-by-layer, to achieve high orientational order in the photocrosslinked structures; this ordering yields high specific work capacity (63 J kg−1) and energy density (0.18 MJ m−3). We demonstrate actuators composed of these DLP printed LCEs’ applications in soft robotics, such as reversible grasping, untethered crawling, and weightlifting. Furthermore, we present an LCE self-sensing system that exploits thermally induced optical transition as an intrinsic option toward feedback control.
INTRODUCTION
Some of the more interesting differences between natural muscles and motors that drive today’s machinery (e.g., electric motors or internal combustion engines) are (i) variable recruitment of actuator elements (i.e., fibers) over micro- to macroscale volumes to adjust their isometric and isotonic force-velocity profiles, (ii) the ability to be placed locally to where force must be applied (as in octopus tentacles or our eyelids), and (iii) mechanical compliance (1). These abilities, despite comparably lower efficiency relative to our typical motor choices, when combined with higher energy density fuel (e.g., carbohydrates, fat, and protein), make muscle a good choice for animals to generally adapt in the widely varying and unpredictable conditions of the natural world (2). Inspired by muscle’s general capabilities, varying soft actuator motifs have been synthesized to mimic one or more of their attributes (3–6). Biohybrid robotic approaches have even adopted natural muscle tissues directly for mobility (7, 8).
Among all the candidate actuation schemes (9–13), thermomechanical liquid crystal elastomers (LCEs) are particularly appealing, as this class of soft matter natively demonstrates variable recruitment, localized actuation, and mechanical compliance and have been reported to apply contractile stresses similar to those of natural muscle (σLCE ≈ 270 kPa; σmuscle ≈ 350 kPa) (14). LCEs actively combine the entropic elasticity of elastomers with the self-organization of liquid crystals. In the liquid crystalline (LC) phase (e.g., nematic), the molecular orientation of mesogenic units align polymer chains into a strained conformation; above a clearing temperature (e.g., nematic-to-isotropic temperature or TNI) entering the isotropic phase, the molecular orientation is lost and the polymer backbone subsequently relaxes into a thermodynamically more favorable random coil conformation (15). Despite being relatively slow and energy inefficient compared to natural muscle (16), this phase- and temperature-dependent polymer chain conformation change can still lead to muscle-like, large, reversible macroscopic shape morphing.
Although LCEs with uniaxial alignment have been reported to exhibit spontaneous length change up to 400% (L/L0), their global deformations are mostly limited to single–degree-of-freedom (DOF) tensile strokes (17, 18). On the other hand, muscles, although similarly limited to contractile actuation, can be arrayed in such a way as to achieve almost infinite DOF, as in the muscular hydrostat appendages of an octopus tentacle (19). Bridging the gap between the single-DOF demonstrations of conventional LCEs and the infinite-DOF examples in nature (e.g., tongues, trunks, and tentacles) demands new manufacturing techniques (20). A portfolio of recently presented self-assembly methods using surface interactions via micropatterned molds have been shown to faithfully align and cross-link LCE chemistries for both two-dimensional (2D) and 3D shape morphing (21–24); finite anchoring energies, however, can only prescribe alignment for limited thickness (h < 100 μm) (25), preventing useful work comparable to that of natural muscle groups to be exerted by the fabricated thin LCE membranes. More recently, direct ink writing (DIW)–based 3D printing has been exploited to simultaneously orient LC mesogens along the direction of extrusion path while photocrosslinking the LCE network. These strategies have successfully yielded soft robotic actuators with complex, dynamic functional architectures that can undergo 2D-to-3D and 3D-to-3D′ shape transformations (26–34). One disadvantage is that the success of DIW is limited by the print time scaling with both part size and resolution: Smaller extrusion nozzles are needed for higher orientational order and longer path lengths for larger parts; both increase the print time substantially (35).
In addition to generating high DOF movements, skeletal muscle fibers (usually 20 in number) can also provide mechanical sensing feedback to the nervous system through the connected Golgi tendon organ. This confluent sensing is essential for proprioception in complex animals (36). Although there have been tremendous advancements in nearly all smart material actuator systems to incorporate the perception of mechanical deformation (i.e., self-sensing) and recently we have witnessed this feature being coupled to LCEs via liquid metal–based resistive or capacitive sensing schemes (37, 38), presently there is no pure LCE system that comprises sensory feedback for control. This absence will likely limit the benefits of using LCEs in robots unless seamless integration of sensing can be achieved.
In this work, we introduce two new concepts to address all these challenges: (i) the use of digital light processing (DLP) to 3D print LCE soft actuators and (ii) the use of optoelectrical measurement of mechanical strain that imparts self-sensing to the printed LCE actuators. We achieve shear flow–induced alignment of LC mesogens via a built-in shear separation mechanism and fabricate monolithic LCE actuators for programmable bending and large tensile strokes. We demonstrate how these actuation motifs permit manipulation and locomotion modes such as gripping, crawling, and weightlifting at the highest specific work capacity yet reported for 3D printed LCE soft actuators (Γ = 63 J kg−1). Furthermore, we achieve real-time feedback of the LCE actuators using optoelectronics suitable for robotics, flexible electronics, and medical devices.
RESULTS
DLP of LCEs
To formulate our LCE liquid resin, we chose a previously reported one-pot thiol-acrylate/thiol-ene click reaction (Fig. 1A) (31) because of its rapid reaction kinetics and low nematic-to-isotropic phase transition temperature (TNI = 39°C; Fig. 1B). After mixing mesogenic diacrylates 1,4-bis-[4-(3-acryloyloxypropyloxy)benzoyloxy]-2-methylbenzene (RM257) and 1,4-bis-[4-(6-acryloyloxypropyloxy)benzoyloxy]-2-methylbenzene (RM82) with flexible dithiol linker 2,2′-(ethylenedioxy)diethanethiol (EDDT) and trivinyl cross-linker 1,3,5-triallyl-1,3,5-triazine-2,4,6(1H,3H,5H)-trione (TATATO), we found that the mixture lacks the flow properties experimentally preferred for continuous DLP at room temperature (Tm = 41°C; Fig. 1B) (39). We added organic solvents, dichloromethane (DCM) and tetrahydrofuran (THF), to modify its rheological behavior (apparent viscosity η < 1 Pa s; fig. S1). These volatile solvents were later removed after printing (fig. S2). The addition of 1 weight % (wt%) photoinitiator diphenyl(2,4,6-trimethylbenzoyl)phosphine oxide (TPO) led to efficient photocuring with nearly 90% gelation within 3 s of ultraviolet (UV) irradiation (UV projector: λ = 405 nm, I = 11.4 mW cm−2; Fig. 1C). We fabricated LCE actuators using a commercially available, open source desktop DLP 3D printer, Ember by Autodesk, primarily because of its built-in shear separation mechanism (also known as minimal force mechanics). Figure 1D shows a schematic illustration of the cyclic rotation of the resin tray. Originally set up to reduce suction force between printed parts and the build window, this rotational motion was reprogrammed to achieve spatial control over director alignment in the LCE (see text S1 for details; fig. S3). The shear force imposed on the photopolymerizable LCE liquid resin while sliding over each thin layer (20 μm) aligns LC mesogens in the backbone of flexible polymer chains. Within the time scale of relaxation, the polymer chains are polymerized and cross-linked via projected UV light to lock in the in-plane orientational order, forming a low-modulus main-chain LCE. This alignment procedure is similar to the well-established shear flow field method for fabricating LCE microactuators in a confined space (15). In addition to the built-in shear alignment that achieves mechanical orientation of LCE without precrosslinking, the spatial and temporal control of UV light for selective photopolymerization further enables rapid fabrication of numerous actuators in parallel with high resolution (40). To inhibit each layer of polymerized resin from adhering to the build window, we replaced the conventional polydimethylsiloxane (PDMS) window with polymethylpentene (PMP), as the latter material has much lower surface tension (<20 mN m−1), higher oxygen permeability [12,000 Barrer; 1 Barrer = 10−10 cm3 (STP) cm/cm2 s cm Hg] and excellent optical transmittance (>90% at 405 nm for a 25-mm sample) (41). We reprogrammed the sliding motion of the resin tray to enable (i) fast approaching speed that enhances the effect of uniaxial shear-induced alignment (42) and (ii) slow separation speed that maximizes the shear separation force. To verify the spatial control over director alignment during the DLP printing of LCE, we observed birefringence with clear contrast via polarized optical microscopy (POM) and thus confirmed the uniaxially ordered elastomer (Fig. 2A). The stress-strain curves of the printed LCE measured in parallel or perpendicular to the optical axis (shearing direction) are also indicative of the existence of orientational order (Fig. 2B). To further quantify the shear-induced alignment, we need to calculate the order parameter (S) of the LCEs that are either nonshear printed as a control group or shear printed but with different shearing speeds up to the printer’s upper limit of 40 mm s−1 (Fig. 2C). These parameters were determined from the dichroic ratio of infrared (IR) absorption at 3343 cm−1 to the in-plane aromatic stretching overtone of the LC mesogen core (see text S2 for details; fig. S4) (14). We found that nonsheared printing yields LCEs with order parameter S < 0.1, suggesting globally isotropic nature. High-speed shear printing produces prominent orientational order scaling with the shearing speed, with a maximum S = 0.45. As a result, we chose the approaching speed as 40 mm s−1 and the separation speed as 8 mm s−1. In this case, the time needed to print each thin layer of 20-μm thickness, including approaching—photocuring—separation, is 10 s; this time step results in a draw rate of roughly 120 μm min−1 in the z direction with maximum build area of 64 mm by 40 mm.
Fig. 1. DLP of LCEs.
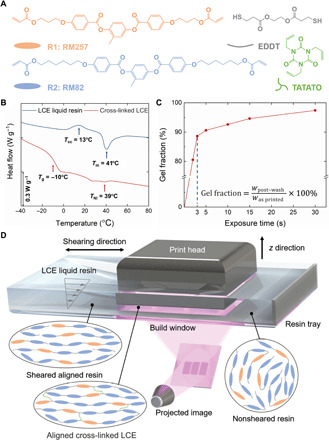
(A) Chemical structures of mesogenic monomers (RM257 and RM82), flexible linker (EDDT), and cross-linker (TATATO) used to synthesize the thermomechanical LCEs. (B) Differential scanning calorimetry curves showing glass transition temperature (Tg) and nematic-to-isotropic transition temperature (TNI) of the cross-linked LCE, as well as melting temperature (Tm) and cold crystallization temperature (Tcc) of the LCE liquid resin. (C) Polymerization speed of the thiol-acrylate/thiol-ene click reaction measured by the gel fraction of LCE exposed to UV irradiation with different duration. (D) Schematic illustration of shear alignment caused by the cyclic rotation of the resin tray. (Inset) From left to right, morphologies of molecular orientation in the sheared aligned resin, aligned cross-linked polymer, and nonsheared resin.
Fig. 2. Characterizations of orientational order.
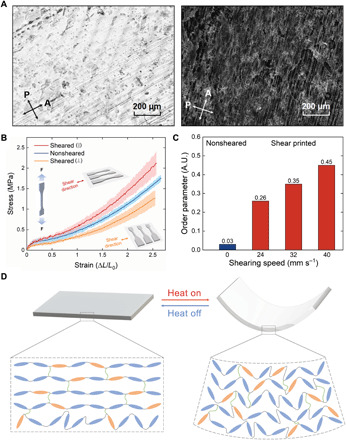
(A) POM images of printed LCE showing birefringence caused by shear-induced alignment. (B) Stress-strain curves of LCEs that are parallel shear printed, nonshear printed, and perpendicular shear printed with respect to the direction of the axial stress in tensile testing. SD is demonstrated as the colored shaded areas. (C) Comparison of order parameters calculated from nonshear printed LCE and shear printed LCE with different shearing speeds. (D) Principle of thermal bending (T > TNI) in the printed LCE actuators. (Inset) Schematic showing reversible reconfiguration of cross-linked LCE polymer network in the layered structure. A.U., arbitrary units.
Thermal actuation
Although anisotropic main-chain LCEs usually undergo large, linear contraction along the direction of nematic director, in practice, we observed that our DLP-fabricated LCE freestanding actuators generate bending rather than tensile stroke in response to heat stimulation above TNI (=39°C). We attributed this phenomenon to the asymmetric photocuring of the LCE as part of the actuator that is immersed in the liquid resin bath: a thin surface layer (h < 10 μm) will always form on the bottom when the residue resin cures in open air and thus remains isotropic. Under thermal actuation, the aligned top portion experiences a phase transition and shrinks uniaxially, while the bottom surface maintains nearly constant length, resembling the bending mechanism of elastomeric bilayers. We took advantage of this intrinsic bilayer architecture and fabricated LCE bending actuators (Fig. 2D).
To assess the pros and cons of this system when compared with prior work, we first examined the effect of applied temperature (Fig. 3A). We started to notice lateral bending as the homogeneous temperature of the hot plate reached 40°C. The bending curvature continues scaling with increasing temperature for every 10°C until a plateau around 70°C, where we observed the onset of perigon bending (360°). Hence, we set 70°C as the benchmark homogeneous temperature for further characterization. Next, we printed bending actuators (surface area, 18 mm by 15 mm) with various total thicknesses ranging from 100 to 500 μm (Fig. 3B). As expected, the curvature increases drastically as the thickness of the actuator is decreased (assuming that thickness of the isotropic bottom surface layer remains the same), most likely because of the bending stiffness (EI) scaling with thickness (h) following the relationship, EI ∝ Eh3, where E is the Young’s modulus (43).
Fig. 3. Thermomechanical shape morphing.

(A) Thermal bending of LCE actuators in response to homogeneous heat of different temperatures. (B) Thermal bending of LCE actuators that are printed with different thickness. (C) Thermal bending of LCE actuators that are printed with different fraction of shearing (FS) along their thickness. (D) Response time for actuation and relaxation of LCE actuators that are printed with different fraction of shearing along their thickness. (E) Cyclic actuation and relaxation (10 cycles) of printed LCE actuators in response to intermittent heat stimulation of high (~140°C) and low (~90°C) temperature gusts. Superimposed photos under different experimental conditions are shown in inlets; all scale bars, 1 cm. Photo credit: Shuo Li, Cornell University.
Another unique capability of DLP arises from the combination of stacking shear printed layers with nonshear printed ones. Here, we fabricated LCE actuators of the same surface area and total thickness (10 layers, h = 200 μm) but with different fraction of shearing (FS = number of layers shear printed/total number of printed layers). As we intentionally insert additional nonshear printed isotropic layers, the bending deformation becomes more suppressed, which is in qualitative agreement with previous experimental observations of nematic LCE-polystyrene bilayers (Fig. 3C) (44). Moreover, thermally responsive materials, such as LCEs, have their response time limited by the characteristic low thermal conductivity. Traditionally, to reduce the response time (especially during relaxation led by heat dissipation), the most effective approach is to reduce the material in thickness, inevitably leading to adverse actuation performance (45). By inserting nonsheared layers during DLP, we provided additional restoring force to a thicker structure (albeit lower force output), thus reducing the relaxation time from 10 s to less than 5 s, with limited compromise to the thickness of the bending actuators (Fig. 3D). Last, we investigated the reversibility of the printed LCE actuators with built-in nonshear printed layers (FS = 0.7). We measured bending deformation with the same cycle time under two different conditions of rapid hot air heating: 1-s higher temperature (~140°C) gusts followed by 5-s room temperature cooling and 2-s lower temperature (~90°C) gusts followed by 4-s room temperature cooling (Fig. 3E). Both cases exhibited highly repeatable LCE actuation and relaxation for up to 10 cycles. In practice, we found that these actuators can be reversibly triggered for more than hundreds of cycles.
In addition to actuation speed, we evaluated another important criterion for the overall actuation performance in DLP printed LCEs, the energy density ρE, which is approximated as ρE = Eεa2/2, where E is Young’s modulus at room temperature and εa is the actuation strain (46). The first quantity E can be extracted from the tensile stress-strain curves (in our elastomeric system, E is actually the tangent modulus; Fig. 2B). To obtain the second quantity εa, we simulated thermally induced self-folding using the commercial finite-element analysis software COMSOL Multiphysics (see text S3 for details; fig. S5). As a result, our LCE bending actuators, as shown in Fig. 3C, can deform to a uniaxial strain εa = 0.60 with Young’s modulus E = 1.02 MPa, yielding an energy density of 1.84 × 105 J m−3, which is among the highest reported energy densities for all 3D printed shape programmable soft materials (10).
Object manipulation and untethered locomotion
To demonstrate the object manipulation ability of our printed LCEs, we printed a gripper (dimensions, 18 mm by 15 mm by 0.2 mm; m = 75 mg) with all 10 layers sheared (FS = 1) to maximize its bending curvature toward stronger grasping force. As shown in Fig. 4A, an L-shaped thin string attached to the center of mass suspends the LCE gripper and assists in lifting a much heavier object, such as a metal spring (m = 600 mg). When the gripper is approaching the preheated spring, it curls along the axis perpendicular to its shear printing direction and wraps around the spring without any external control. We then transfer the autonomously grasped spring to a receiver container and showed that the LCE gripper could maintain that firm grip for more than 25 s even during our continuous twisting of the string (movie S1).
Fig. 4. Object manipulation and locomotion.

(A) A soft robotic gripper (dimensions, 18 mm by 15 mm by 0.2 mm; fraction of shearing FS = 1.0) is used for (a and b) controlled grasping, (c to e) delivering, and (f) releasing of a preheated metal spring. Scale bar, 2 cm. (B) Crawling of a soft maneuvering robot (dimensions, 18 mm by 13 mm by 0.2 mm, FS = 0.7) on a ratchet surface. (a to e, left) Designed heat actuation sequence shows bending of forelimb, torso, and hindlimb of the crawling robot for effective locomotion. (a to e, right) Snapshots of the crawling robot demonstrate the corresponding gaits. Photo credit: Shuo Li, Cornell University.
We then demonstrated the crawling of a soft robot (dimensions, 18 mm by 13 mm by 0.2 mm) by taking advantage of localized heat stimulation (Fig. 4Band movie S2). We printed the crawler with FS = 0.7 to enable faster shape recovery upon cooling. The nozzle diameter of the heat gun is 6 mm. Inspired by the gait sequence of pneumatically actuated quadrupeds (47), our undulation sequence is designed as four steps, starting from the rest state (Fig. 4B, a): (i) heating the forelimb (roughly the front one-third segment) pulled the robot up by leaning the front edge against the anchoring point (Fig. 4B, b); (ii) heating the torso (roughly the middle one-third segment) further lifted the spine up and dragged the rear edge toward a new anchoring point ahead of its prior location (Fig. 4B, c); (iii) heating the hindlimb (roughly the rear one-third segment) bent it to a larger extent, storing elastic energy (Fig. 4B, d); and (iv) turning off the heat, the release of that elastic energy when combined with relaxation of forelimb, torso, and hindlimb in sequence propelled the robot forward, entering a new rest state that is ready for another actuation sequence (Fig. 4B, e). We drove the robot in this gait sequence at a speed of 20 mm min−1 (~1.1 body lengths min−1 or 66.7 body lengths hour−1) on a ratchet surface.
Weightlifting
When tethered to hanging weights in the direction of shear printing (in this case, vertical), the LCE polymer network is strained along the same direction, with all rod-like LC mesogens aligned parallel to the polymer backbone. In this way, the bending actuator can be transformed into a linear one. To demonstrate their weightlifting capability and gauge a work capacity for these printed LCEs, we fabricated thick (40 layers, h = 800 μm, FS = 1) dog bone–shaped actuators. Next, we mounted hangers and weights to their shoulders with only the gauge section (dimensions, 25 mm by 2 mm by 0.8 mm) exposed to exert thermomechanical contraction force in response to applied heat (Fig. 5A and movie S3). On the basis of the algorithm, as introduced in (26), strain is calculated as the decrement in displacement (ΔL < 0) relative to the reference length (L0) before loading at room temperature. We found that the specific work, defined as work done per unit mass of actuator (m = 56 mg), is nearly proportional to the mass of the loaded weight up to a maximum of 40 g (more than 700 times the actuator’s own weight), with the actuation strain subject to gradual decay (Fig. 5C). Most notably, the maximum specific work done by this system is 63 J kg−1, higher than that of most 3D printed LCEs and that of human skeletal muscles (30, 48). This high specific work capacity is attributable to the increase in actuator’s thickness (or total number of aligned layers), which elevates the output force markedly (22). We also examined the tensile stroke as a function of applied temperature (Fig. 5D and movie S4). The result indicates that the nematic-to-isotropic transition is not the major driving force that governs the temperature-dependent deformation in our LCE actuator. For both temperature regimes (below and above TNI) up to 90°C, we observed different negative correlations in the temperature dependence, identical to what was reported in prior work (49). This dependence on temperature is evidence of entropic elasticity that contributes to actuation whether nematic, isotropic, or altogether amorphous. The benefit of printing under LC phase, therefore, may be in the ease of aligning the mesophase during printing and not necessarily the nematic-to-isotropic transition, although one may take advantage of this variation in negative slope near the phase transition for applications that involve tunable thermomechanical responses.
Fig. 5. Weightlifting.
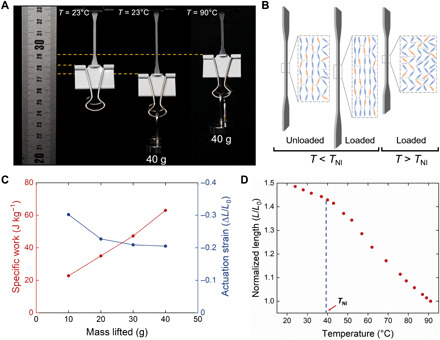
(A) Image sequence of an LCE actuator (h = 800 μm, m = 56 mg) lifting a 40-g weight in response to applied temperature. (B) Reversible reconfiguration of polymer network of the three cases as shown in (A). (C) Specific work and actuation strain of the actuator when lifting different weights. (D) Uniaxial actuation of the LCE under mechanical load of 40 g. Photo credit: Shuo Li, Cornell University.
Optomechanical self-sensing
Analogous to the use of liquid crystals in modern display technology, shape-memory LCEs can also manipulate optical birefringence for optomechanical transduction, such as temperature-controlled deformation sensors. According to Warner and Terentjev (50), cross-linked LCEs always form polydomain textures (often referred to as Schlieren texture) even with proper director alignment. The characteristic length scale of these textures is often comparable to the wavelength of visible and near-IR spectrum. Therefore, the LCE material is completely opaque below TNI as a result of strong scattering of light; it becomes transparent in the isotropic phase (T > TNI) because of the disappearance of misoriented domains (fig. S6).
On the basis of this working principle, we embedded optical sensing in the LCE matrix by coupling miniature optoelectronic components with a bending actuator. As shown in Fig. 6A, the DLP printed LCE cantilever actuator (dimensions, 15 mm by 5 mm by 0.8 mm) can experience two modes of bending deformation that is either thermally induced (e.g., with 90°C gusts; mode 1) or nonthermally induced (e.g., toggled to cause bending; mode 2). In mode 1, the initially opaque polydomain LCE became transparent to light on entering the isotropic state in response to heat stimulation. This optical clarity allows coupled light beams, via an IR light-emitting diode (LED), for example, to propagate through from one end; some radiates to the environment, and the remaining is bounced back at the other end and subsequently received by a photodetector (e.g., an IR photodiode) placed next to the light source. By this means, we can measure the optical signal of this lossy LCE waveguide to indicate its own bending deformation (fig. S7): the higher the applied temperature, the more the actuator is deformed, the more transparent the material, and the stronger the received optical signal (see text S4 for details; Fig. 6B). In mode 2, although the magnitude of bending is similar, the LCE keeps its polydomain state intact, preventing coupled light beams from propagating, and thus, the photodetector will not capture notable signal change (movie S5). This prototypical demonstration combines soft thermomechanical actuation with optoelectronic strain sensing previously used in other classes of soft actuators, introducing a self-sensing LCE actuator for potential feedback control (51, 52). The same principle may also extend to polydomain-monodomain phase transition, for monitoring elongation and consequent stiffening in the same material system (50).
Fig. 6. Optomechanical self-sensing.
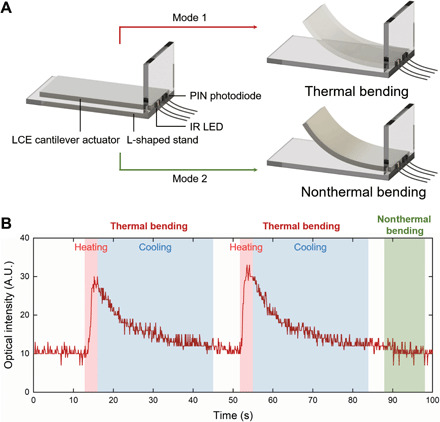
(A) Left: Schematic of the LCE bending actuator (dimensions, 15 mm by 5 mm by 0.8 mm) and optoelectronic components. Right: Bending deformation of the actuator in two modes [(top) mode 1: thermally induced bending causes the disappearance of Schlieren texture and thus transparency in the actuator; (bottom) mode 2: nonthermally induced (external force) bending does not change the polydomain Schlieren texture, so the actuator remains whitish opaque]. (B) Optical signals detecting and differentiating thermally induced bending and nonthermally induced bending.
DISCUSSION
We presented the DLP-based 3D printing of thermally driven LCEs with programmable orientational order in the LC mesogens. By controlling the printing parameters, we rapidly printed artificial muscle-like soft actuators with tunable bending curvatures and response times (a printing time comparison to DIW is shown in text S5). As these actuators are thermally driven, we were able to power them remotely via convective heat sources. In particular, we demonstrated LCE bending actuators for object grasping and crawling locomotion, as well as linear actuators for weightlifting that demonstrate a specific work capacity of 63 J kg−1 and tensile stroke of 50%, both exceeding the maximums of human skeletal muscles (~40 J kg−1 and 20%, respectively) (48, 53). In addition, we leveraged the orientational order–dependent optical properties of thermomechanical LCEs to introduce a self-sensing LCE actuator. This design enabled us to continuously monitor shape morphing in an intrinsically nonlinear soft structure and distinguish the deformation that is either thermally or nonthermally induced, taking the field one step further toward a natural muscle-like sensorimotor system in LCEs for feedback on motion and the environment.
The actuation frequency (~0.2 Hz) of our DLP printed LCE actuators, however, is still below the lower limit in that of natural muscles (1 to 200 Hz) (2), most plausibly because of the intrinsically low thermal conductivity of bulk LCEs, which also leads to a low efficiency of energy conversion in almost all thermally driven soft actuating materials (45). By embedding microheaters (e.g., KMHP-100 MEMS Micro-Hotplate, Kebaili Corp.) or spatially patterning the 3D printed LCEs in such a way as to take advantage of faster convection, both the speed and the density of actuation could be increased. Nonetheless, our printed structures are mostly prismatic, and our shear printing is currently limited to uniaxial alignment. By incorporating UV absorbing dyes and other additives to the LCE liquid resin, considerable opportunities exist to expand this work to nonprismatic geometries with higher resolution (39, 41). With the equipment of additional linear motors or spinning components for bidirectional or rotational shearing, we believe that more complicated director fields, such as topological defect patterns for controllable deformations in auxetic lattices and Gaussian curvatures can be realized toward sophisticated and multifunctional robotics (46, 51).
MATERIALS AND METHODS
Experimental design
The objectives of this study was to prove that shear force–induced molecular orientation can properly align LC mesogenic units in a main-chain LCE chemistry during the layer-by-layer DLP printing without any prealignment. To evaluate the fabrication process, we developed and demonstrated DLP-fabricated soft robotic actuators for object manipulation, locomotion, and weightlifting. We also exploited the phase-dependent optical transition in LCE for self-sensing.
Materials
Diacrylate LC monomers RM257 and RM82 were purchased from Wilshire Technologies. EDDT, TATATO, TPO, radical inhibitor butylated hydroxytoluene (BHT), anhydrous DCM, and anhydrous THF were purchased from Sigma-Aldrich. All reagents and solvents were used as received without further purification.
Preparation of LCE liquid resin
To initiate the thiol-acrylate/thiol-ene click reaction, we mixed EDDT, RM257, RM82, and TATATO at a molar ratio of 1.0:0.2:0.6:0.133 and dissolved them in a solvent blend (45 wt% DCM and 35 wt% THF) along with 1 wt% TPO in an amber vial. BHT (2 wt%) was also added to inhibit rapid thermal polymerization. The mixture was stirred at 200 rpm on a 65°C hot plate for 2 hours to complete oligomerization.
DLP of LCE actuators
All DLP files were created using CAD software SolidWorks, imported and sliced to photopatterns in Autodesk Print Studio, and converted to tar.gz format before being sent to print on Autodesk Ember. The aluminum substrate on the printhead was anodized to black to suppress surface reflection and enhance adhesion between the printed part and the printhead (Surface Finish Technologies Inc.). A 3-mm-thick PMP window (RT18, Goodfellow Corp.) was attached to a custom-built polytetrafluoroethylene resin tray and bonded using a silicone adhesive (Sil-Poxy, Smooth-On Inc.) after 45 s of oxygen plasma activation. The oligomerized liquid resin was transferred to the resin tray and let stand still for 5 min before printing. The xy resolution of the printer was measured as 50 μm (1280 × 800 pixels of UV projector over the maximum build area of 64 mm by 40 mm) for thinner structures (h < 200 μm, <10 layers) and ~100 to 200 μm for thicker structures (200 μm < h < 800 μm, 10 to 40 layers) because of stronger light scattering. The z resolution was 10 μm. Postcuring under higher-intensity UV (25 mW cm−2) was performed on all printed parts both sides for 90 s, followed by 70°C vacuum bakeout for 24 hours to remove all residue solvents.
Thermal actuation and image analysis
Bending actuation in response to applied heat was carried out by placing the DLP printed LCE actuators on a hot plate and waiting until the bending deformation reached equilibrium. Thermal bending and weightlifting were recorded by a Sony α7 III camera with a Sony 28-70 mm lens. All bending curvatures were calibrated and measured using ImageJ software. Movies of LCE soft robot locomotion and optical sensing in LCE actuator were recorded by an Apple iPhone 11 Pro Max. Temperature profiles were recorded using an FLIR E4 thermal imaging camera.
Preparation of samples for order parameter measurements
Cryo-microtome was used to freeze and slice printed LCEs into 10-μm-thin films (surface area > 1.5 mm by 1.5 mm) for POM (Olympus BX 51 equipped with crossed polarizers) imaging and polarized–Fourier transform IR microscope (Bruker Hyperion) analysis.
Differential scanning calorimetry
Differential scanning calorimetry (TA Instruments Q1000) was used to measure the melting point (Tm) and cold crystallization temperature (Tcc) of LCE liquid resin, as well as the nematic-to-isotropic transition temperature (TNI) and glass transition temperature (Tg) of cross-linked solid LCE. Both samples (=10 mg) were heated to 100°C to erase any thermal history, cooled to −50°C at a ramp rate of 5°C min−1, and then heated to 100°C at a ramp rate of 10°C min−1. Data shown were collected from the second heating cycle.
Mechanical testing
Uniaxial tensile tests were performed using a Zwick/Roell Z010 testing machine equipped with 10-kN load cell and pneumatic grips. Strain rate was set to 20 mm min−1. Dog bone specimens were prepared by positioning the samples in parallel or perpendicular to the shearing direction during printing or applying no shear during printing, following the protocol as described in the main text and caption of Fig. 2B.
LCE resin rheology
Rheological properties of the LCE liquid resin were characterized using an Anton Paar MCR 301 rotational rheometer. Measurements were conducted using a cone-and-plate system (CP50) with a 0.2-mm gap at room temperature.
Assembly of optical sensor and processing of optical signals
A DLP printed LCE cantilever actuator, an IR LED (SFH 4254, Osram Opto Semiconductors GmbH), and a PIN photodiode (SFH 2700 FA, Osram Opto Semiconductors GmbH) were fixed to a 3D printed (UMA 90, M1 Printer, Carbon Inc.) L-shaped rigid plastic stand. The LED and photodiode were placed in parallel, contacting the anchoring edge of the cantilever, so that the photodiode could receive optical signals reflected on the other side. A current-to-voltage (I/V) converter circuit (fig. S8) was used to transform light intensity (I) received by photodiode to electrical signals (V) collected by a microcontroller (Arduino Uno R3). The raw data were presented in real-time through the Processing software. The sampling frequency was 30 Hz.
Statistical analysis
Error bars in various data plots indicate the SDs over at least three tests on the specimens. All data were processed using OriginPro.
Acknowledgments
We thank P. Carubia and J. Yin for technical assistances and K. Wang and W. Pan for helpful discussions. Funding: This work was supported by Air Force Office of Scientific Research (AFOSR) under grant no. FA9550-18-1-0243, Office of Naval Research (ONR) under grant no. N00014-17-1-2837, and NSF under grant nos. EFMA-1830924, DMR-1719875, and CMMI-1825444. Part of the study was performed at the Cornell Energy Systems Institute, Cornell Center for Materials Research Shared Facilities, which are supported through the NSF MRSEC program (grant no. DMR-1719875), and Cornell NanoScale Facility, a member of the National Nanotechnology Coordinated Infrastructure (NNCI), which is supported by the NSF (grant no. NNCI-2025233). Author contributions: S.L. and R.F.S. designed the research. S.L., H.B., Z.L., X.Z., C.H., and L.W.W. performed experiments. S.L., H.B., Z.L., and R.F.S. analyzed experimental results. H.B. conducted theoretical modeling. S.L., H.B., and R.F.S. wrote the manuscript. All authors edited versions of the manuscript. R.F.S. supervised the research and managed the project. Competing interests: R.F.S. is a board member of Organic Robotics Corporation. All other authors declare that they have no financial or other competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/30/eabg3677/DC1
REFERENCES AND NOTES
- 1.Fenwick A. J., Wood A. M., Tanner B. C. W., Effects of cross-bridge compliance on the force-velocity relationship and muscle power output. PLOS ONE 12, e0190335 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Alexander R. M., Bennet-Clark H. C., Storage of elastic strain energy in muscle and other tissues. Nature 265, 114–117 (1977). [DOI] [PubMed] [Google Scholar]
- 3.Acome E., Mitchell S. K., Morrissey T. G., Emmett M. B., Benjamin C., King M., Radakovitz M., Keplinger C., Hydraulically amplified self-healing electrostatic actuators with muscle-like performance. Science 359, 61–65 (2018). [DOI] [PubMed] [Google Scholar]
- 4.Duduta M., Hajiesmaili E., Zhao H., Wood R. J., Clarke D. R., Realizing the potential of dielectric elastomer artificial muscles. Proc. Natl. Acad. Sci. U.S.A. 116, 2476–2481 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cacucciolo V., Shintake J., Kuwajima Y., Maeda S., Floreano D., Shea H., Stretchable pumps for soft machines. Nature 572, 516–519 (2019). [DOI] [PubMed] [Google Scholar]
- 6.Kim Y., Parada G. A., Liu S., Zhao X., Ferromagnetic soft continuum robots. Sci. Robot. 4, eaax7329 (2019). [DOI] [PubMed] [Google Scholar]
- 7.Nawroth J. C., Lee H., Feinberg A. W., Ripplinger C. M., McCain M. L., Grosberg A., Dabiri J. O., Parker K. K., A tissue-engineered jellyfish with biomimetic propulsion. Nat. Biotechnol. 30, 792–797 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Park S.-J., Gazzola M., Park K. S., Park S., Di Santo V., Blevins E. L., Lind J. U., Campbell P. H., Dauth S., Capulli A. K., Pasqualini F. S., Ahn S., Cho A., Yuan H., Maoz B. M., Vijaykumar R., Choi J.-W., Deisseroth K., Lauder G. V., Mahadevan L., Parker K. K., Phototactic guidance of a tissue-engineered soft-robotic ray. Science 353, 158–162 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ilievski F., Mazzeo A. D., Shepherd R. F., Chen X., Whitesides G. M., Soft robotics for chemists. Angew. Chemie Int. Ed. 50, 1890–1895 (2011). [DOI] [PubMed] [Google Scholar]
- 10.Kim Y., Yuk H., Zhao R., Chester S. A., Zhao X., Printing ferromagnetic domains for untethered fast-transforming soft materials. Nature 558, 274–279 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Sydney Gladman A., Matsumoto E. A., Nuzzo R. G., Mahadevan L., Lewis J. A., Biomimetic 4D printing. Nat. Mater. 15, 413–418 (2016). [DOI] [PubMed] [Google Scholar]
- 12.Aharoni H., Xia Y., Zhang X., Kamien R. D., Yang S., Universal inverse design of surfaces with thin nematic elastomer sheets. Proc. Natl. Acad. Sci. U.S.A. 115, 7206–7211 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shahsavan H., Aghakhani A., Zeng H., Guo Y., Davidson Z. S., Priimagi A., Sitti M., Bioinspired underwater locomotion of light-driven liquid crystal gels. Proc. Natl. Acad. Sci. U.S.A. 117, 5125–5133 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Thomsen D. L., Keller P., Naciri J., Pink R., Jeon H., Shenoy D., Ratna B. R., Liquid crystal elastomers with mechanical properties of a muscle. Macromolecules 34, 5868–5875 (2001). [Google Scholar]
- 15.Ohm C., Brehmer M., Zentel R., Liquid crystalline elastomers as actuators and sensors. Adv. Mater. 22, 3366–3387 (2010). [DOI] [PubMed] [Google Scholar]
- 16.Davidson Z. S., Shahsavan H., Aghakhani A., Guo Y., Hines L., Xia Y., Yang S., Sitti M., Monolithic shape-programmable dielectric liquid crystal elastomer actuators. Sci. Adv. 5, eaay0855 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ahir S. V., Tajbakhsh A. R., Terentjev E. M., Self-assembled shape-memory fibers of triblock liquid-crystal polymers. Adv. Funct. Mater. 16, 556–560 (2006). [Google Scholar]
- 18.Yekutieli Y., Sagiv-Zohar R., Aharonov R., Engel Y., Hochner B., Flash T., Dynamic model of the octopus arm. I. Biomechanics of the octopus reaching movement. J. Neurophysiol. 94, 1443–1458 (2005). [DOI] [PubMed] [Google Scholar]
- 19.Hochner B., An embodied view of octopus neurobiology. Curr. Biol. 22, R887–R892 (2012). [DOI] [PubMed] [Google Scholar]
- 20.Hannan M. W., Walker I. D., Kinematics and the implementation of an elephant’s trunk manipulator and other continuum style robots. J. Robot. Syst. 20, 45–63 (2003). [DOI] [PubMed] [Google Scholar]
- 21.Xia Y., Cedillo-Servin G., Kamien R. D., Yang S., Guided folding of nematic liquid crystal elastomer sheets into 3D via patterned 1D microchannels. Adv. Mater. 28, 9637–9643 (2016). [DOI] [PubMed] [Google Scholar]
- 22.Guin T., Settle M. J., Kowalski B. A., Auguste A. D., Beblo R. V., Reich G. W., White T. J., Layered liquid crystal elastomer actuators. Nat. Commun. 9, 2531 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yamada M., Kondo M., Miyasato R., Naka Y., Mamiya J., Kinoshita M., Shishido A., Yu Y., Barrett C. J., Ikeda T., Photomobile polymer materials—Various three-dimensional movements. J. Mater. Chem. 19, 60–62 (2009). [Google Scholar]
- 24.Chen L., Wang M., Guo L.-X., Lin B.-P., Yang H., A cut-and-paste strategy towards liquid crystal elastomers with complex shape morphing. J. Mater. Chem. C 6, 8251–8257 (2018). [Google Scholar]
- 25.Kowalski B. A., Tondiglia V. P., Guin T., White T. J., Voxel resolution in the directed self-assembly of liquid crystal polymer networks and elastomers. Soft Matter 13, 4335–4340 (2017). [DOI] [PubMed] [Google Scholar]
- 26.Ambulo C. P., Burroughs J. J., Boothby J. M., Kim H., Shankar M. R., Ware T. H., Four-dimensional printing of liquid crystal elastomers. ACS Appl. Mater. Interfaces 9, 37332–37339 (2017). [DOI] [PubMed] [Google Scholar]
- 27.Gantenbein S., Masania K., Woigk W., Sesseg J. P. W., Tervoort T. A., Studart A. R., Three-dimensional printing of hierarchical liquid-crystal-polymer structures. Nature 561, 226–230 (2018). [DOI] [PubMed] [Google Scholar]
- 28.López-Valdeolivas M., Liu D., Broer D. J., Sánchez-Somolinos C., 4D printed actuators with soft-robotic functions. Macromol. Rapid Commun. 39, 1700710 (2018). [DOI] [PubMed] [Google Scholar]
- 29.Roach D. J., Kuang X., Yuan C., Chen K., Qi H. J., Novel ink for ambient condition printing of liquid crystal elastomers for 4D printing. Smart Mater. Struct. 27, 125011 (2018). [Google Scholar]
- 30.Kotikian A., Truby R. L., Boley J. W., White T. J., Lewis J. A., 3D printing of liquid crystal elastomeric actuators with spatially programed nematic order. Adv. Mater. 30, 1706164 (2018). [DOI] [PubMed] [Google Scholar]
- 31.Saed M. O., Ambulo C. P., Kim H., De R., Raval V., Searles K., Siddiqui D. A., Cue J. M. O., Stefan M. C., Shankar M. R., Ware T. H., Molecularly-engineered, 4D-printed liquid crystal elastomer actuators. Adv. Funct. Mater. 29, 1806412 (2019). [Google Scholar]
- 32.Zhang C., Lu X., Fei G., Wang Z., Xia H., Zhao Y., 4D printing of a liquid crystal elastomer with a controllable orientation gradient. ACS Appl. Mater. Interfaces 11, 44774–44782 (2019). [DOI] [PubMed] [Google Scholar]
- 33.Kotikian A., McMahan C., Davidson E. C., Muhammad J. M., Weeks R. D., Daraio C., Lewis J. A., Untethered soft robotic matter with passive control of shape morphing and propulsion. Sci. Robot. 4, eaax7044 (2019). [DOI] [PubMed] [Google Scholar]
- 34.Davidson E. C., Kotikian A., Li S., Aizenberg J., Lewis J. A., 3D printable and reconfigurable liquid crystal elastomers with light-induced shape memory via dynamic bond exchange. Adv. Mater. 32, 1905682 (2020). [DOI] [PubMed] [Google Scholar]
- 35.Wallin T. J., Pikul J., Shepherd R. F., 3D printing of soft robotic systems. Nat. Rev. Mater. 3, 84–100 (2018). [Google Scholar]
- 36.D. L. Smith, S. A. Plowman, in Sports-Specific Rehabilitation, R. Donatelli, Ed. (Elsevier, 2007), pp. 15–38. [Google Scholar]
- 37.Ford M. J., Ambulo C. P., Kent T. A., Markvicka E. J., Pan C., Malen J., Ware T. H., Majidi C., A multifunctional shape-morphing elastomer with liquid metal inclusions. Proc. Natl. Acad. Sci. U.S.A. 116, 21438–21444 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kent T. A., Ford M. J., Markvicka E. J., Majidi C., Soft actuators using liquid crystal elastomers with encapsulated liquid metal joule heaters. Multifunct. Mater. 3, 025003 (2020). [Google Scholar]
- 39.Wang K., Pan W., Liu Z., Wallin T. J., Dover G., Li S., Giannelis E. P., Menguc Y., Shepherd R. F., 3D printing of viscoelastic suspensions via digital light synthesis for tough nanoparticle–elastomer composites. Adv. Mater. 32, 2001646 (2020). [DOI] [PubMed] [Google Scholar]
- 40.Patel D. K., Sakhaei A. H., Layani M., Zhang B., Ge Q., Magdassi S., Highly stretchable and UV curable elastomers for digital light processing based 3D printing. Adv. Mater. 29, 1606000 (2017). [DOI] [PubMed] [Google Scholar]
- 41.Wallin T. J., Pikul J. H., Bodkhe S., Peele B. N., Mac Murray B. C., Therriault D., McEnerney B. W., Dillon R. P., Giannelis E. P., Shepherd R. F., Click chemistry stereolithography for soft robots that self-heal. J. Mater. Chem. B 5, 6249–6255 (2017). [DOI] [PubMed] [Google Scholar]
- 42.LeDuc P., Haber C., Bao G., Wirtz D., Dynamics of individual flexible polymers in a shear flow. Nature 399, 564–566 (1999). [DOI] [PubMed] [Google Scholar]
- 43.Rogers J. A., Lagally M. G., Nuzzo R. G., Synthesis, assembly and applications of semiconductor nanomembranes. Nature 477, 45–53 (2011). [DOI] [PubMed] [Google Scholar]
- 44.Agrawal A., Yun T., Pesek S. L., Chapman W. G., Verduzco R., Shape-responsive liquid crystal elastomer bilayers. Soft Matter 10, 1411–1415 (2014). [DOI] [PubMed] [Google Scholar]
- 45.He Q., Wang Z., Wang Y., Minori A., Tolley M. T., Cai S., Electrically controlled liquid crystal elastomer–based soft tubular actuator with multimodal actuation. Sci. Adv. 5, eaax5746 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Mirfakhrai T., Madden J. D. W., Baughman R. H., Polymer artificial muscles. Mater. Today 10, 30–38 (2007). [Google Scholar]
- 47.Shepherd R. F., Ilievski F., Choi W., Morin S. A., Stokes A. A., Mazzeo A. D., Chen X., Wang M., Whitesides G. M., Multigait soft robot. Proc. Natl. Acad. Sci. U.S.A. 108, 20400–20403 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kim K. J., Hyeon J. S., Kim H., Mun T. J., Haines C. S., Li N., Baughman R. H., Kim S. J., Enhancing the work capacity of electrochemical artificial muscles by coiling plies of twist-released carbon nanotube yarns. ACS Appl. Mater. Interfaces 11, 13533–13537 (2019). [DOI] [PubMed] [Google Scholar]
- 49.Ware T. H., McConney M. E., Wie J. J., Tondiglia V. P., White T. J., Voxelated liquid crystal elastomers. Science 347, 982–984 (2015). [DOI] [PubMed] [Google Scholar]
- 50.M. Warner, E. M. Terentjev, in Liquid Crystal Elastomers (Oxford Univ. Press, 2003), pp. 95–119. [Google Scholar]
- 51.Li S., Zhao H., Shepherd R. F., Flexible and stretchable sensors for fluidic elastomer actuated soft robots. MRS Bull. 42, 138–142 (2017). [Google Scholar]
- 52.Bai H., Li S., Barreiros J., Tu Y., Pollock C. R., Shepherd R. F., Stretchable distributed fiber-optic sensors. Science 370, 848–852 (2020). [DOI] [PubMed] [Google Scholar]
- 53.Haines C. S., Lima M. D., Li N., Spinks G. M., Foroughi J., Madden J. D. W., Kim S. H., Fang S., Jung de Andrade M., Goktepe F., Goktepe O., Mirvakili S. M., Naficy S., Lepro X., Oh J., Kozlov M. E., Kim S. J., Xu X., Swedlove B. J., Wallace G. G., Baughman R. H., Artificial muscles from fishing line and sewing thread. Science 343, 868–872 (2014). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/30/eabg3677/DC1


