Layer-engineered interlayer excitons

Long valley polarization lifetime and tunable photoluminescence have been realized for interlayer excitons by layer engineering.

Abstract

Photoluminescence (PL) from excitons serves as a powerful tool to characterize the optoelectronic property and band structure of semiconductors, especially for atomically thin two-dimensional transition metal dichalcogenide (TMD) materials. However, PL quenches quickly when the thickness of TMD materials increases from monolayer to a few layers, due to the change from direct to indirect band transition. Here, we show that PL can be recovered by engineering multilayer heterostructures, with the band transition reserved to be a direct type. We report emission from layer-engineered interlayer excitons from these multilayer heterostructures. Moreover, as desired for valleytronics devices, the lifetime, valley polarization, and valley lifetime of the generated interlayer excitons can all be substantially improved as compared with that in the monolayer-monolayer heterostructure. Our results pave the way for controlling the properties of interlayer excitons by layer engineering.

INTRODUCTION

Layered transition metal dichalcogenides (TMDs) MX₂ (M = W and Mo, and X = S and Se) provide a platform for fundamental research and optoelectronic devices using an atomically thin material (1). For optoelectronic applications, to have efficient light emission, a semiconductor with a direct bandgap nature is required (2–4). However, bilayer or multilayer MX₂ has an indirect bandgap, quenching its light emission to a large extent (2, 5). In this work, we show that van der Waals (vdW) heterostructures (6) formed by the stacking of two different MX₂ can convert an indirect bandgap material to a direct type and therefore recover its photoluminescence (PL) emission.

In particular, the light emission of interlayer excitons (IXs) (7–9) in our monolayer (1L) WSe₂/few-layer (mL) MoS₂ heterostructures shows fascinating valley properties (7–9), where the lifetimes, valley polarization, and valley relaxation lifetimes improve remarkably. Valley, defined as local band extreme in momentum space, represents one potential degree of freedom to carry and process information (10–12) in valley spintronics. Therein, a long valley lifetime and high valley degree of polarization (DOP) is desired. However, the picosecond time scale depolarization process of the intralayer excitons in the monolayer TMDs markedly limits its application (13, 14). For the IXs in the bilayer heterostructures, the electrons and holes are separated in different layers, thus reducing the electron-hole exchange interaction. This spatially indirect nature of the IXs results in their high valley polarization and long lifetime (7, 9, 15–17), which brings promising opportunities for high-temperature exciton condensation (17, 18) and valley physics (7, 9, 15–17, 19–22). Different knobs have been shown to be effective ways to tune the properties of IXs, for instance, the twist angles (19, 23–27). The IXs formed in a bilayer heterostructure with small twist angles lead to the Moiré physics (19, 25–27).

In this study, we show that, in addition to controlling the stacking angle in a bilayer heterostructure system, varying the number of layers provides another natural degree of freedom to modulate the vdW heterostructure properties. Two types of heterostructures are analyzed with different layer-dependent behaviors: mL-WSe₂/1L-MoS₂ and 1L-WSe₂/mL-MoS₂. For 1L-WSe₂/mL-MoS₂, the increase of layer numbers reduces the electron and hole cloud overlap, further increasing the valley lifetime of excitons, while the valley polarization almost vanishes for mL-WSe₂/1L-MoS₂ cases. In addition, we found that, for 1L-WSe₂/mL-MoS₂, a tiny magnetic field can suppress the valley relaxation and increase the valley lifetime from tens of nanoseconds by two orders to several microseconds. The suppression of valley relaxation has been directly observed from the time-resolved PL emission due to the slow valley relaxation in these multilayer vdW heterostructures. In the end, a more robust valley polarization can be sustained until room temperature in these multilayer heterostructures.

RESULTS AND DISCUSSION

IX spectrum

Figure 1 shows the microscopic image and the PL spectrum for different WSe₂/MoS₂ heterostructure samples. Figure 1 (A and B) shows the schematic of a multilayer heterostructure formed by different layers of MoS₂ and WSe₂. The electrons and holes are separated into the MoS₂ layer and the WSe₂ layers, respectively, forming the IXs (see inset in Fig. 1A). Figure 1C shows a typical optical image for the mL (here, m = 1 to 4) WSe₂/1L-MoS₂ sample, and Fig. 1D shows the image for 1L-WSe₂/mL-MoS₂ samples. The two-dimensional (2D) layers are first exfoliated mechanically from bulk crystals on polydimethylsiloxane (PDMS) stamps and then transferred to form the heterostructure by a dry transfer method. The details for sample preparation can be found in the methods section. We used second harmonic generation (SHG) to check the alignment to be AA stacking (section S1 and fig. S1) and Raman spectroscopy to characterize the sample quality, layer numbers, and interlayer coupling strength of the heterostructures (section S2 and figs. S2 and S3).

Fig. 1. Observation of IXs in mL-WSe₂/1L-MoS₂ and 1L-WSe₂/mL-MoS₂ heterostructures.

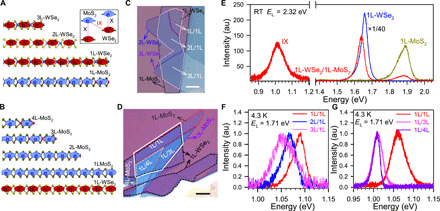
(A and B) A schematic of the IXs in mL-WSe₂/1L-MoS₂ and 1L-WSe₂/mL-MoS₂ heterostructures (HS), respectively. The inset shows a type II band alignment of WSe₂/MoS₂ heterostructure [intralayer exciton (X); interlayer exciton (IX)]. For IX, the electrons and holes are separated in MoS₂ and WSe₂ layers, respectively. (C and D) The optical microscope image of the mL-WSe₂/1L MoS₂ (labeled as mL/1L; m = 1 to 3) sample (S1) and 1L-WSe₂/mL-MoS₂ (labeled as 1L/mL; m = 1, 3, and 4) sample (S2). WSe₂ and MoS₂ with different layers are marked with dashed lines of different colors. The heterostructure regions are marked with solid white lines. Scale bars, 10 μm. (E) The PL spectra of intralayer excitons in monolayer WSe₂ and MoS₂ and IXs in 1L-WSe₂/1L-MoS₂ heterostructure sample at room temperature (RT). (F and G) The PL spectra of IXs in mL-WSe₂/1L-MoS₂ heterostructure and 1L-WSe₂/mL-MoS₂ heterostructure at low temperature. au, arbitrary units.

IX emission and intralayer exciton emission spectrum are shown in Fig. 1E. We note that the IX emission from the heterostructure lies in the infrared range, which is far away from the visible range of all intralayer exciton emission from WSe₂ and MoS₂. Thus, a pure IX signal can be obtained by using long-pass filters (e.g., a 1064-nm long pass). Figure 1 (F and G) shows the low-temperature PL spectra of IXs from the mL-WSe₂/1L-MoS₂ heterostructure (sample in Fig. 1C) and 1L-WSe₂/mL-MoS₂ heterostructure (sample in Fig. 1D). We can see that clear IX PL has been observed for all the samples with different spectrum shifts. When the number of WSe₂ (MoS₂) layers is increased, the IX PL spectra show a redshift up to 50 meV relative to that in the 1L/1L heterostructure case. We prepared several other heterostructure samples, with and without hexagonal Boron Nitride (hBN) encapsulation, and observed similar results (more sample images and characterizations are presented in section S3 and figs. S4 to S10). This redshift can be understood as a consequence of the increase in the effective dielectric constant with increasing number of layer (28). Also, we anticipate that this redshift is mainly due to the shifts of valence band of mL-WSe₂ and conduction band of mL-MoS₂, as well as the changes of IX binding energy in multilayer heterostructures (29). This makes IX energy highly tunable with the bandgap engineering (30). More results and discussions related to this PL redshift in multilayer heterostructure are shown in section S4 and figs. S11 and S12 in that section.

Temperature dependence of IX PL intensity

To understand more about the nature of the IX transition and band structure of the stacked heterostructure, we investigate the temperature dependence of PL emissions. Figure 2 (A and B) shows the PL intensity mapping of IXs in mL-WSe₂/1L-MoS₂ heterostructure at 4.3 K and room temperature, respectively. Here, the intralayer exciton emission is blocked by a 1064-nm long-pass filter, and therefore, only IX emission is relevant in the PL mapping. The intensity change as a function of temperature is shown in Fig. 2C. For both 1L-WSe₂/1L-MoS₂ and 2L-WSe₂/1L-MoS₂ cases, PL intensity decreases as the temperature increases (also see section S5 and figs. S13 to S15). This PL temperature dependence is consistent with the case of monolayer MoS₂ intralayer exciton (31) and IXs in 1L-WSe₂/1L-MoS₂ heterostructure (8) and can be understood by considering the reduced momentum mismatch between the band extrema and the increased radiative transition probability with decreased temperatures (8, 31, 32).

Fig. 2. Temperature dependence of IXs in mL-WSe₂/1L-MoS₂ and 1L-WSe₂/mL-MoS₂ heterostructures.

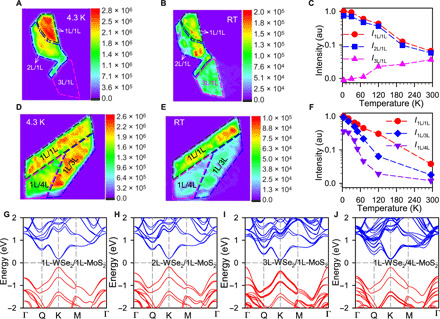
(A and B) The PL intensity map of the IXs in mL-WSe₂/1L-MoS₂ (mL/1L; m = 1 to 3) HS at 4.3 K and room temperature, respectively. (C) The PL intensity of IXs in mL-WSe₂/1L-MoS₂ as a function of temperature. The PL intensity is the average values of multiple positions of each mL-WSe₂/1L-MoS₂ region. (D and E) The PL intensity map of the IXs in 1L-WSe₂/mL-MoS₂ (mL/1L; m = 1, 3, and 4) HS at 4.3 K and room temperature, respectively. A 1064-nm long pass was used to ensure that only the IX signal can be detected. (F) The PL intensity of IXs in 1L-WSe₂/mL-MoS₂ as a function of temperature. The PL intensity is the average values of multiple positions of each 1L-WSe₂/mL-MoS₂ region. (G to J) The calculated electronic energy structure of 1L-WSe₂/1L-MoS₂, 2L-WSe₂/1L-MoS₂, 3L-WSe₂/1L-MoS₂, and 1L-WSe₂/4L-MoS₂ heterostructures, respectively.

In contrast to the 1L-WSe₂/1L-MoS₂ and 2L-WSe₂/1L-MoS₂ case, when the number of WSe₂ layers is more than two in mL/1L heterostructure (e.g., m = 3), the PL intensity of the IXs tends to increase with increasing temperature (Fig. 2C). Similar results are observed in other samples (see section S5 and figs. S13 and S14). This indicates that the 3L-WSe₂/1L-MoS₂ heterostructure can be a momentum indirect bandgap semiconductor. This comes from the fact that the valence band maximum from multilayer WSe₂ changes from K to Γ point when the number of layers is increased to three. In this case, the indirect K-Γ transition is in the ground state, while the direct K-K transition has higher energy than the indirect K-Γ transition. Therefore, the PL emission intensity will increase with a higher temperature. We note that these results are consistent with the recent direct measurement of the valence band of 1L-3L WSe₂ by the micrometer-scale angle-resolved photoemission spectroscopy (microARPES) (33).

In contrast to the case in mL-WSe₂/1L-MoS₂ heterostructure, the IX PL intensity in 1L-WSe₂/mL-MoS₂ (m = 1, 3, and 4) heterostructure regions is strong at low temperature, and it decreases with increasing temperature (Fig. 2, D to F, and fig. S16). Similar behavior has been observed in other samples up to m = 6 (see section S5 and fig. S14). These results suggest that the 1L-WSe₂/mL-MoS₂ heterostructure is a direct bandgap semiconductor, and the bright state is the ground state, at least for MoS₂ up to four layers. To confirm these analyses, we calculate the band structures of the 1L-WSe₂/mL-MoS₂ heterostructure and mL-WSe₂/1L-MoS₂ heterostructure based on the density functional theory (DFT). These calculated results (see Fig. 2, G to J, and figs. S16 and S17) agree well with the experimental observations. Similar calculated results of 1L-WSe₂/1L-MoS₂ also show its direct bandgap nature (8, 34), which is consistent with our results. On the other hand, we should note that the parameters and methods should be carefully chosen owing to its effects on the theory calculated results (34, 35).

In addition, we also note that IX PL intensity in 2L-WSe₂/3L-MoS₂ heterostructure decreases with increasing temperature, indicating that it is a direct bandgap semiconductor (see section S5 and fig. S14). This result is in line with our analysis above that the conduction band minimum/CBM (valence band maximum/VBM) is mainly affected by MoS₂ (WSe₂) layers with both 3L-MoS₂ CBM and 2L-WSe₂ VBM located at K (K′) point, although both 2L-WSe₂ and 3L-MoS₂ are indirect bandgap semiconductor. Our DFT calculation further confirms the direct band of 2L-WSe₂/3L-MoS₂ heterostructure (see section S5 and fig. S19). These results open the door to design the direct bandgap heterostructure semiconductors for future optoelectronic device applications based on the layer engineering of multilayer TMDs. More results and discussion regarding the power dependence of the IX in 1L-WSe₂/mL-MoS₂ can be found in section S5 and fig. S20.

Valley polarization for IXs in multilayer heterostructures

Valley polarization has been used to probe the valley index in 2D TMDs. A natural question is as follows: How about the IX valley polarization in our multilayer heterostructures? With the optical selection rule (Fig. 3A), the valley is coupled with the PL circular polarization, and therefore, we can characterize the valley properties through circular polarization–resolved PL measurement. Figure 3B shows the corresponding valley DOP mapping, and Fig. 3 (C and D) shows the corresponding circularly polarized PL spectra, respectively. Here, we define $\text{DOP}=\frac{{\mathit{I}}_{{\mathrm{\sigma }}^{‐}{\mathrm{\sigma }}^{‐}}-{\mathit{I}}_{{\mathrm{\sigma }}^{‐}{\mathrm{\sigma }}^{+}}}{{\mathit{I}}_{{\mathrm{\sigma }}^{‐}{\mathrm{\sigma }}^{‐}}+{\mathit{I}}_{{\mathrm{\sigma }}^{‐}{\mathrm{\sigma }}^{+}}}$, where I_σ^jσ^k represents the PL intensity with σ^j excitation and σ^k detection, and σ⁺(σ⁻)denotes the right (left) circularly polarized light. As shown in Fig. 3B, all heterostructure regions show a high valley DOP. This indicates that the valley optical selection rule is valid in the 1L-WSe₂/mL-MoS₂ heterostructure, i.e., σ⁻(σ⁺) IX emission coupled primarily to K (K′) valley. The observation also agrees with the recent report for the K-K transition nature for the IX emission in the infrared range for the monolayer-monolayer case (8, 26). Similar results are obtained for other 1L-WSe₂/mL-MoS₂ samples (see section S6 and figs. S22 to S26). Moreover, The IX valley polarization of 1L-WSe₂/mL-MoS₂ heterostructure is quite robust and can persist up to room temperature, which is desired for valley device applications (see section S6 and fig. S24).

Fig. 3. Circularly polarized PL spectra of IXs in 1L-WSe₂/mL-MoS₂ heterostructures.

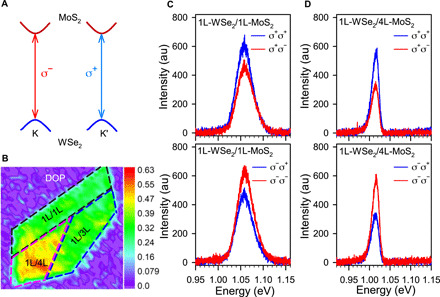
(A) A simplified schematic of valley optical selection rule for IXs in K and K′ valley. The electrons and holes are located at K (K′) point of the MoS₂ conduction band and WSe₂ valence band, respectively. (B) The valley DOP mapping of IXs in the multilayer HS calculated from the polarized PL intensity mapping measurement results. (C and D) The circularly polarized PL spectra of IXs from 1L-WSe₂/1L-MoS₂ and 1L-WSe₂/4L-MoS₂ heterostructure regions, respectively. σⁱσ^j represents excitation with σⁱ and detection with σ^j circular polarization.

On the contrary, we find that the DOP for mL-WSe₂/1L-MoS₂ (m > 1) heterostructure is negligible (see section S6 and fig. S21). Upon resonant excitation with σ⁻ (σ⁺) circularly polarized light (726 nm), the WSe₂ excitons are selectively created. Then, an ultrafast charge transfer process takes the electrons from the multilayer WSe₂ layers to the K (K′) valley of monolayer MoS₂ layer (36–38), leaving only the holes in the multilayer WSe₂ layers (36–38). Therefore, the vanishing valley polarization in the 2L-WSe₂/1L-MoS₂ case can only be attributed to the hole interlayer hopping between the WSe₂ layers. This can be further confirmed by calculating the charge density distribution of holes in WS₂ layers (see section S6 and fig. S21). In addition, in the 3L-WSe₂/1L-MoS₂ case, the VBM locates at Γ valley, which can couple equally to both polarizations. Consequently, the valley polarization of IX vanishes in mL-WSe₂/1L-MoS₂ (m > 1) and 2L-WSe₂/3L-MoS₂ heterostructures (see section S6 and fig. S25). This is in stark difference with 1L-WSe₂/mL-MoS₂ heterostructure. In the latter case, the VBM at the K (K′) valley is mainly contributed by 1L-WSe₂, where the orbital mixing of the VBM is largely suppressed. Meanwhile, the interlayer hopping for electrons between mL-MoS₂ layers vanishes at K points due to the symmetry of the d_z² orbital (33). Hence, the valley optical selection rule of IXs in the 1L-WSe₂/1L-MoS₂ case is maintained for 1L-WSe₂/mL-MoS₂ heterostructures.

Enhanced valley lifetime for layer-engineered IXs at zero magnetic field

We found that IX in 1L-WSe₂/mL-MoS₂ (m > 1) heterostructure has a longer lifetime and valley lifetime than IX in 1L-WSe₂/1L-MoS₂ heterostructure. Figure 4 (A to C) shows the time-resolved circularly polarized PL of IXs from 1L-WSe₂/mL-MoS₂ heterostructure regions in Fig. 1D. For the copolarized emission (i.e., the collected emission polarization is the same as the excitation polarization), the data fit very well with a biexponential function. The slowest decay component is up to hundreds of nanoseconds, which is an order of magnitude longer than previously reported results for IX lifetimes (7, 17, 39). All decay components are slower in the 1L-WSe₂/3L-MoS₂ and 1L-WSe₂/4L-MoS₂ region as compared to the values in the 1L-WSe₂/1L-MoS₂ region. In contrast, the lifetime of IXs in mL-WSe₂/1L-MoS₂ heterostructure is decreased with more WSe₂ layers (section S7 and fig. S27). These results indicate that the number of MoS₂ layers can be used to increase the lifetime of IXs.

Fig. 4. Layer-engineered depolarization lifetime of IX in 1L-WSe₂/mL-MoS₂ heterostructures.

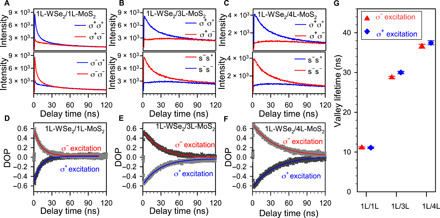
(A to C) Time-resolved circularly polarized PL of IXs from 1L-WSe₂/1L-MoS₂, 1L-WSe₂/3L-MoS₂, and 1L-WSe₂/4L-MoS₂ HS regions, respectively. The IX lifetime of a few hundred nanoseconds was observed. The temperature for PL decay measurements is 4.3 K. (D to F) The time-resolved valley DOP of IXs obtained from the measured time-resolved circularly polarized PL in (A) to (C). (G) The valley DOP lifetimes under left and right circularly polarized light excitation.

On the basis of the time-resolved PL data, we calculate the valley (DOP) lifetime. Figure 4 (D to F) shows the time-resolved DOP at 4.3 K. We fit the data with a single exponential decay function to obtain the valley lifetime. We find that the valley lifetime of IXs depends on the number of MoS₂ layers. The DOP decay shows a similar trend with the count decay, i.e., it is getting slower as the number of MoS₂ layers is increased. In particular, the valley lifetime increases from 11 ± 0.2 ns in the 1L-WSe₂/1L-MoS₂ region to 29 ± 0.3 ns in the 1L-WSe₂/3L-MoS₂ region and 37 ± 0.5 ns in the 1L-WSe₂/4L-MoS₂ region (Fig. 4G). We get similar results for different samples (section S7 and figs. S28 and S29). These results indicate that the valley lifetime has been increased by three to four times with the increasing number of MoS₂ layers.

The layer dependence of the IX lifetime and valley lifetime can be explained by considering that both exciton oscillator strength and electron-hole exchange interaction are suppressed in multilayer heterostructure when the wave function overlap between electron and hole is reduced (16). Similar to the case of multiple quantum well (40), the electron wave function spreads more as the number of MoS₂ layers is increased. As a result, the reduced electron-hole wave function overlap of IXs in 1L-WSe₂/mL-MoS₂ heterostructure leads to a longer exciton lifetime and valley lifetime. More results and discussion about the temperature dependence of the valley lifetime in 1L-WSe₂/mL-MoS₂ heterostructure can be found in section S8 and fig. S30.

Magnetic field enhanced valley polarization and valley lifetime

With applied magnetic field, we found that the valley polarization and valley lifetime can be further enhanced for IXs in 1L-WSe₂/mL-MoS₂. Figure 5A shows copolarized and cross-polarized PL spectra. One can clearly see the enlarged difference in spectrum between the two cases, representing an enhanced valley polarization. To examine the magnetic field dependence in more detail, we plot DOP under different magnetic fields, as shown in Fig. 5B. It shows that the amplitude of DOP has increased markedly from ~0.1 to 0.2 to ~0.7 to 0.8 by applying a tiny magnetic field. This is the case for all three situations of IXs in 1L-WSe₂/mL-MoS₂ (m = 1, 3, and 4). This implies that the origin of increased DOP is similar in these three cases. For IXs in 1L-WSe₂/4L-MoS₂, a prolonged valley lifetime has been shown in Fig. 5 (C and D) as well. Considering that we are exciting resonantly with the WSe₂ bright A exciton transition (726 nm), the magnetic field–induced increased DOP and prolonged valley lifetime can be attributed to the suppression of valley relaxation of WSe₂ excitons with magnetic fields. The suppression of the valley mixing by small perpendicular magnetic field has been discussed in some reports (15, 41). For the IX, the increased DOP and valley lifetime of IX emission are attributed to the suppression of Maialle-Silva-Sham–like intervalley scattering (13) of the long-lived intralayer exciton before it decays to become an IX (15). More magnetic field–dependent results of IXs in 1L-WSe₂/mL-MoS₂ are presented in section S9 and figs. S31 to S33.

Fig. 5. Suppression of valley relaxation under magnetic field for IXs in 1L-WSe₂/mL-MoS₂ heterostructures.

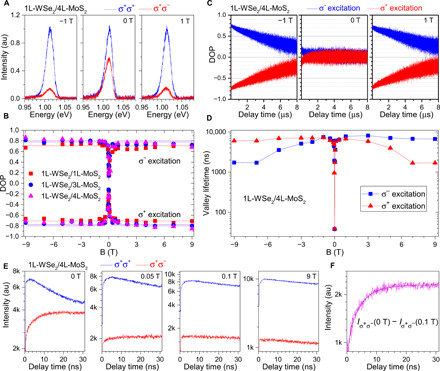
(A) Valley polarization for IXs in 1L-WSe₂/4L-MoS₂ under three magnetic fields: −1, 0, and 1 T. An enhanced valley polarization under magnetic field has been observed. (B) Magnetic dependence of DOP. Valley mixing has been suppressed for all m = 1, 3, and 4 cases. (C) Time-resolved DOP for IXs in 1L-WSe₂/4L-MoS₂ at −1, 0, and 1 T (0.125-MHz repetition rate is used here). An enhanced valley polarization lifetime has been observed under magnetic field. (D) The magnetic field dependence of valley DOP lifetime under left and right circularly polarized light excitation, respectively. (E) Time-resolved photon emission at different magnetic fields. (F) The magnetic field suppressed valley relaxation characterization. The temperature for all measurements under magnetic fields is around 4.3 K.

It is worth noting that the valley relaxation is slow in 1L-WSe₂/4L-MoS₂ such that the valley mixing time constant is comparable with the PL decay lifetime. This leads to the fact that the cross-polarized PL count shows an initial count increase, rather than an exponential decay, as shown in Fig. 5E. To extract the information for this valley mixing mechanism, we ramp up the magnetic field. One can clearly see the suppression of the cross-polarized PL counts with the increase of magnetic field, which comes from the suppression of valley mixing. One can give an estimation of the valley mixing time constant of 5 ± 1 ns in this case, by fitting the cross-polarized PL count at 0 T or simply subtracting the count rate in the magnetic field from the zero-field case (Fig. 5F). We should note that this valley mixing time scale is much slower than that in monolayer TMDs (42). Our result represents the first direct observation of valley mixing in the time domain from PL emission, thanks to the prolonged exciton lifetimes in multilayer heterostructure.

In summary, we studied the IXs from multilayer WSe₂/MoS₂ heterostructures. We demonstrated that the layer number of WSe₂ and MoS₂ offers an additional degree of freedom to modulate the emission spectra, as well as enhancing the exciton lifetime, valley polarization, and valley lifetime of IXs. The 1L-WSe₂/mL-MoS₂ heterostructure preserves the direct bandgap at least for MoS₂ up to four layers. These results demonstrate that novel phenomena can be achieved by layer engineering of multilayer 2D semiconductor materials, which offers a systematic approach readily extended to other 2D materials. While we did not use a deterministic layer engineering method in our report, recent advances in 2D material fabrication method allows this method (43). This deterministic layer engineering method combined with the twist angle manipulation in vdW heterostructure will bring many opportunities for fundamental research and optoelectronic device applications.

MATERIALS AND METHODS

Sample fabrication

1L-MoS₂ and mL-MoS₂ and 1L-WSe₂ and mL-WSe₂ are first exfoliated mechanically from bulk crystals on PDMS stamps. The alignment between MoS₂ and WSe₂ layers is done by first choosing these samples that have two sharp edges with a 120° angle. We then used the dry transfer method to stack MoS₂ and WSe₂ samples by aligning the edge of the top and bottom samples onto an ultralow doping Si substrate that is covered by 285 nm of SiO₂ to form the WSe₂/MoS₂ and hBN/WSe₂/MoS₂/hBN heterostructures at room temperature. Last, the heterostructure samples were annealed under ultrahigh vacuum (around 10 to 6 mbar) at 200°C for 3 hours.

Optical measurements

PL measurement

A homemade confocal microscope is used to perform the polarization and spatially resolved PL spectroscopy. The polarization state of the excitation and the detection are controlled by a combination of polarizers, half-wave plates, and quarter-wave plates installed on the excitation and detection. The PL spectra were obtained by a spectrometer (Andor Shamrock) with a charge-coupled device (CCD) detector. Unless otherwise stated, a laser with 726 nm was used as the excitation source at low temperatures. A 50× objective lens with a spot size of 1 μm [numerical aperture (NA) = 0.65] is used to collect the signal. The sample temperature is controlled using a cryostat (Montana Instruments and Attocube, Attodry 1000). For pulse experiments, a 726-nm diode laser (full width at half maximum of <80 ps, maximum repetition rate is 80 MHz) is used for exciting the sample. The intensity map is obtained by detecting the emission using a superconducting single-photon detector while scanning the excitation position on the sample by using a galvo system. If not otherwise stated, the continuous wave (CW) laser power for the PL measurement at low temperatures is around 100 μW. For PL decay measurements, the CW-equivalent laser power for pulse laser is around 0.25 μW.

Raman measurement

The Raman spectra were measured at room temperature with the T64000 Raman system, equipped with a liquid nitrogen–cooled CCD. A 100× objective lens (NA = 0.95) is used to collect the signal. The excitation wavelength for Raman spectra measurement is 532 nm. The laser power for Raman measurements is around 200 μW.

SHG measurements

The SHG measurements are performed at room temperature. A pulse laser from a Ti:Sapphire oscillator (Spectra Physics, Tsunami) with a peak at around 870 nm, a repetition rate of 80 MHz, and a pulse duration of 100 fs was used as the excitation source. The laser power is around 0.6 mW.

Theoretical calculations

We performed first-principles calculations using the Vienna ab initio simulation package (44) with the projector augmented wave method (45). The Perdew-Burke-Ernzerhof type (46) generalized gradient approximation was used for the exchange-correlation functional. The heterostructures were constructed by taking the average of the experimental lattice constant of bulk materials [the lattice constant for MoS₂ is a = b = 3.168 Å (47) and for WSe₂ is a = b = 3.282 Å (48)]. We set the interlayer distance to 6.67 Å between MoS₂ and WSe₂ initially and then relax the interlayer distance and atomic coordinates. The cutoff energy was set to 500 eV, and a 16 × 16 × 1 Γ-centered k-point mesh was used for the Brillouin zone sampling. The convergence criteria for the energy and force were set to 10⁻⁵ eV and 0.01 eV/Å, respectively. A vacuum layer with a thickness of 20 Å was taken to avoid artificial interactions between periodic images. The vdW corrections were taken into account by the approach of Dion et al. (49). To get a more accurate energy gap, we also used the more sophisticated Heyd-Scuseria-Ernzerhof hybrid functional method (HSE06) for the exchange-correlation potential (50) to calculate the band structure for the 1L/1L heterostructure.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/30/eabh0863/DC1