New mechanism and exact theory of superconductivity from strong repulsive interaction

A mechanism for pairing in purely repulsive Fermi systems is developed, leading to unconventional superconducting behaviors.

Abstract

We introduce a general mechanism for superconductivity in Fermi systems with strong repulsive interaction. Because kinetic terms are small compared to the bare repulsion, the dynamics of charge carriers is constrained by the presence of other nearby carriers. By treating kinetic terms as a perturbation around the atomic limit, we show that pairing can be induced by correlated multiparticle tunneling processes that favor two itinerant carriers to be close together. Our analytically controlled theory provides a quantitative formula relating T_c to microscopic parameters, with maximum T_c reaching about 10% of the Fermi temperature. Our work demonstrates a powerful method for studying strong coupling superconductivity with unconventional pairing symmetry. It also offers a realistic new route to realizing finite angular momentum superfluidity of spin-polarized fermions in optical lattice.

INTRODUCTION

Superconductivity in conventional metals results from an effective attraction between electrons mediated by the exchange of phonons (1, 2). While this attraction is much weaker than the bare Coulomb repulsion (3), the latter is drastically renormalized downward by retardation effects (4). Thanks to the vast difference between Fermi and Debye energy, the phonon-mediated attraction can overscreen the Coulomb repulsion to enable electron pairing and superconductivity (5). On the other hand, this crucial retardation condition fails in systems with narrow bands or low carrier density. Yet, superconductivity has been found in a growing number of materials in such strong-coupling regime. Two famous examples are (i) strontium titanate, the most dilute bulk superconductor with Fermi energy as small as 1 meV (6), and (ii) magic-angle graphene with a record-low density n_2D ∼ 10¹¹ cm⁻² and a very small bandwidth of ∼10 meV (7–10). The ratio of superconducting transition temperature T_c and Fermi temperature E_F/k_B far exceeds typical values, reaching as high as 0.01 in strontium titanate (6) and 0.1 in magic-angle graphene (8). Finding electronic mechanisms for strong-coupling superconductivity in narrow band systems has long been a subject of great interest and challenge (11–18).

In this work, we introduce a new mechanism for superconductivity stemming from the strong repulsive interactions. Because kinetic terms are small compared to the bare repulsion, the dynamics of charge carriers is constrained by the presence of other nearby carriers. In this regime, pairing can be induced by correlated multiparticle tunneling processes that favor two itinerant carriers to be close together. To illustrate this physical phenomenon, we introduce a simple two-band model of interacting spin-polarized fermions on a two-dimensional lattice. In our model, an insulating state occurs at the filling of n = 1 fermion per unit cell, and superconductivity emerges upon particle or hole doping. On the basis of a perturbative expansion around the atomic limit, we rigorously show that, despite the strong bare repulsion, a nonretarded short-range pairing interaction between doped fermions arises. It is generated by coupling to high-energy composite excitations, which mediate correlated-tunneling terms, effectively keeping pairs of carriers close to one another. The resulting superconductor is unconventional by all standards. It has f-wave pairing symmetry and changes from having a full gap to point nodes above a critical doping. T_c is controlled by the bare interaction strength and the bandgap, reaching as large as T_c ∼ 0.1 E_F/k_B when they are of comparable magnitude. Our theory is analytically controlled by a small coupling constant that emerges in the narrow band limit. Our work demonstrates a reliable and robust mechanism for unconventional superconductivity from repulsion in narrow band systems.

Our model is broadly inspired by a recent work by Slagle and one of us (19), who proposed a mechanism for pairing from purely classical electrostatic repulsion in a doped charge transfer insulator. The essential ingredient there is a charge 2e excitation dubbed “trimer,” which is a composite object consisting of two doped electrons tightly bound to a dipole. For certain extended Coulomb repulsion, a trimer is energetically more favored than two separate electrons. Under appropriate conditions, the presence of preformed trimers can lead to Wigner crystal or superconducting ground states at small doping.

While we also start with the problem of doping an insulator, our work differs fundamentally from (19). We find superconductivity without invoking trimers or any preformed pairs at low energy. Instead, pairing arises from correlated quantum hopping of doped fermions induced by virtual composite excitations at high energy. We demonstrate this novel mechanism by introducing and solving the simplest model of spin-polarized fermions interacting on a bipartite lattice. Last but not the least, our solution reveals distinct superconducting states at different ranges of doping and provides a quantitative formula for T_c in terms of microscopic parameters.

RESULTS

We consider spin-polarized fermions on a bipartite lattice with repulsive interactions, described by the Hamiltonian

$$\begin{array}{c}\mathrm{\mathscr{H}}={\mathrm{\mathscr{H}}}_0+{\mathrm{\mathscr{H}}}_{\mathit{t}},\\ {\mathrm{\mathscr{H}}}_0=\mathit{V}{\displaystyle \sum _{\langle \mathit{r},{\mathit{r}}^{\prime }\rangle }}{\mathit{n}}_{\mathit{r}}{\mathit{n}}_{{\mathit{r}}^{\prime }}+\mathrm{\Delta }{\displaystyle \sum _{\mathit{r}\in \mathit{B}}}{\mathit{n}}_{\mathit{r}},\\ {\mathrm{\mathscr{H}}}_{\mathit{t}}=-\mathit{t}{\displaystyle \sum _{\langle \mathit{r},{\mathit{r}}^{\prime }\rangle }}({\mathit{c}}_{\mathit{r}}^{†}{\mathit{c}}_{{\mathit{r}}^{\prime }}+\mathit{hc})\end{array}$$ (1)

where ℋ₀ contains the nearest-neighbor interaction—the dominant interaction for spin-polarized fermions on a lattice—and the sublattice potential difference between the two inequivalent A and B sites, while ℋ_t describes tunneling between adjacent sites. Despite the simplicity of our model, in this work, we unveil its remarkably rich phase diagram as a function of filling and interaction strength. We shall derive the low-energy properties of the system with a fully controlled perturbative expansion in the narrow band limit t ≪ Δ, which we further complement with field-theoretic analysis and extensive exact diagonalization (ED) studies. For concreteness, we thereafter focus on the honeycomb lattice.

In the strong coupling limit, the ground state of ℋ at n = 1 is an insulator with all A sites occupied and all B sites empty, as shown in Fig. 1. Its insulating property is ensured by the large gap E_D = 2V + Δ, which corresponds to the energy necessary to transfer an electron from an A site to B, or equivalently, creating a dipole. The inclusion of tunneling, small compared to E_D, slightly decreases the charge transfer gap without any notable change to the insulating ground state.

Fig. 1. Model and virtual processes.

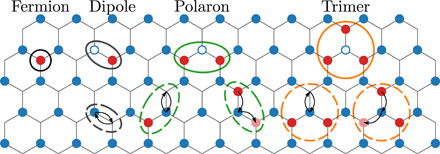
Low-energy fermions added above the n = 1 insulating background live on the B lattice. Excitations above this f-band are dipoles, polarons, and trimers (solid circles), whose virtual occupation leads to the effective model Eq. 2 (dashed circles).

Since ℋ is invariant under particle-hole transformation ${\mathit{c}}_{\mathit{A}}\to {\mathit{c}}_{\mathit{A}}^{†},{\mathit{c}}_{\mathit{B}}\to -{\mathit{c}}_{\mathit{B}}^{†}$ combined with spatial inversion that interchanges the two sublattices, it suffices to consider n > 1 filling below. At finite doping n = 1 + δ (δ > 0), low-energy configurations of the system remain with all A sites occupied to avoid the large charge transfer gap. Because of the Pauli exclusion principle, the δ additional fermions must live on the B lattice and, in the limit t = 0, form a highly degenerate manifold with an energy E_f = Δ + 3V per doped charge that we refer to as f-band.

Besides these fermions on B sites, there exist various types of composite excitations at higher energy, which involve holes on A sites, as depicted in Fig. 1. For example, a B fermion can bind with a neighboring dipole to form a charge e Fermi polaron, which has energy E_P = E_f + V + Δ. More interesting is the charge 2e trimer, which consists of three neighboring B fermions surrounding a hole on the center A site. It can also be viewed as two neighboring B fermions tightly bound to a dipole. A trimer costs energy E_T = 2E_f + Δ, which is greater than the energy of two separate B fermions by Δ. These composite excitations—dipoles, polarons, and trimers—are hereafter collectively referred to as the charge-transfer complex.

In the presence of small quantum tunneling t ≪ Δ, doped carriers in the f-band constitute the only low-energy excitations in our system. They virtually couple to the charge-transfer complex at high energy. This coupling results in a narrow dispersive f-band of doped carriers and induces short-range interactions between them. We shall show that the induced interaction leads to pairing within the f-band. To that purpose, we analytically carry out a Schrieffer-Wolff transformation ℋ′ = e^iSℋe^−iS to decouple the f-band from high-energy degrees of freedom (20, 21). As detailed in the Supplementary Materials, this procedure accounts for all possible virtual processes (see Fig. 1) and leads to the following effective Hamiltonian for doped fermions, which is exact to second order in t/Δ and at any f-band filling

$$\begin{array}{c}{\mathrm{\mathscr{H}}}^{\prime }={\displaystyle \sum _{\langle \mathit{i},\mathit{j}\rangle }}{\mathit{t}}_{\mathit{f}}({\mathit{f}}_{\mathit{i}}^{†}{\mathit{f}}_{\mathit{j}}+\mathit{hc})+{\mathit{V}}_{\mathit{f}}{\mathit{n}}_{\mathit{i}}{\mathit{n}}_{\mathit{j}}\\ +{\displaystyle \sum _{(\mathit{ijk})\in \mathrm{\Delta }}}\mathrm{\lambda }({\mathit{f}}_{\mathit{i}}^{†}{\mathit{n}}_{\mathit{j}}{\mathit{f}}_{\mathit{k}}+{\mathit{P}}_{\mathit{ijk}})+{\mathit{U}}_3{\mathit{n}}_{\mathit{i}}{\mathit{n}}_{\mathit{j}}{\mathit{n}}_{\mathit{k}}\end{array}$$ (2)

The f_i fermionic operators denote the doped fermions on the triangular B lattice, and their vacuum is the n = 1 insulating state described above. The sums labeled by 〈i, j〉 and (i, j, k) ∈ △, respectively, run over all bonds and all upper triangles of the B lattice, while P_ijk stands for the inclusion of ${\mathit{f}}_{\mathit{i}}^{†}{\mathit{n}}_{\mathit{j}}{\mathit{f}}_{\mathit{k}}$ with all possible permutations of the indices i, j, and k.

The effective Hamiltonian ℋ′ for doped fermions consists of single-particle tunneling, correlated (density-dependent) tunneling, and two-body and three-body density interactions. Their origins can be understood as follows. The tunneling from k to i in the upper triangle (ijk) arises from two consecutive hopping processes. The virtual intermediate state involved is either a polaron or a trimer, depending on the occupation of site j (see Fig. 1). The resulting tunneling amplitude is thus t²[(1 − n_j)/(E_P − E_f) + n_j/(E_T − 2E_f)], from which the expression of t_f and λ are derived

$${\mathit{t}}_{\mathit{f}}=\frac{{\mathit{t}}^2}{\mathrm{\Delta }+\mathit{V}}$$ (3a)

$$\mathrm{\lambda }=\frac{{\mathit{t}}^2}{\mathrm{\Delta }}-\frac{{\mathit{t}}^2}{\mathrm{\Delta }+\mathit{V}}$$ (3b)

The interaction coefficients V_f and U₃ come from processes where an A fermion hops back and forth between neighboring sites (see Fig. 1). For example, V_f measures the difference of energy between two neighboring doped charges on B sites and two well-separated ones. The former configuration can couple to a trimer state whereas the latter cannot, thus leading to an attraction −t²/Δ. Accounting for all processes, we find

$${\mathit{V}}_{\mathit{f}}=-\frac{{\mathit{t}}^2}{\mathrm{\Delta }}+\frac{4{\mathit{t}}^2}{\mathrm{\Delta }+\mathit{V}}-\frac{3{\mathit{t}}^2}{\mathrm{\Delta }+2\mathit{V}}$$ (3c)

$${\mathit{U}}_3=\frac{3{\mathit{t}}^2}{\mathrm{\Delta }}-\frac{6{\mathit{t}}^2}{\mathrm{\Delta }+\mathit{V}}+\frac{3{\mathit{t}}^2}{\mathrm{\Delta }+2\mathit{V}}$$ (3d)

In Eqs. 3a to 3d, the denominators Δ, Δ + V, and Δ + 2V are the energy costs of intermediate states involving trimer, polaron, and dipole, respectively. When longer-range interactions are included, these denominators are tuned accordingly. Higher-order corrections to the effective Hamiltonian ℋ′ are small provided that the narrow band condition t ≪ Δ is satisfied, regardless of interaction strength V.

At small V ≪ Δ, the effective interactions in the f-band are found to be ${\mathit{V}}_{\mathit{f}}^0=2{(\mathit{t}/\mathrm{\Delta })}^2\mathit{V}, {\mathrm{\lambda }}^0={(\mathit{t}/\mathrm{\Delta })}^2\mathit{V}$, and ${\mathit{U}}_3^0=0$ to first order in V/Δ. These values simply correspond to the projection of the bare repulsion V into the f-band, whose wave functions have small amplitudes ∼t/Δ on A sites. As V increases, interband mixing quickly becomes important and our exact results (Eqs. 3a to 3d) reveal a dramatic departure of the “dressed” interaction from the projected interaction. As opposed to the projected interactions, V_f starts to decrease at V ≈ 0.29Δ and changes sign from repulsive to attractive at V = Δ. Similarly, λ and U₃ show manifest deviations from the projected estimates for V > 0.1Δ and saturate at large V/Δ (see the Supplementary Materials). In the rest of this work, we shall mainly consider the case V < Δ, where the induced V_f, λ, and U₃ turn out to be positive and small compared to the single-particle bandwidth W = 9t_f.

To reveal the tendency toward pairing, we study the formation of two-particle bound states, the analog of “Cooper problem” in a doped insulator. Pair formation is evidenced by the positivity of the pair binding energy

$$\begin{array}{cc}\hfill {\mathrm{\epsilon }}_{\mathit{b}}& =2[\mathit{E}(1)-\mathit{E}(0)]-[\mathit{E}(2)-\mathit{E}(0)]\hfill \\ & =2\mathit{E}(1)-\mathit{E}(2)-\mathit{E}(0)\hfill \end{array}$$ (4)

with E(m) being the ground state energy of a system with m charges added above n = 1 filling. As detailed in the Supplementary Materials, we analytically solve the lattice Hamiltonian Eq. 2 in the case of two doped fermions and obtain ε_b as a function of V/Δ as shown in Fig. 2. It is found positive in the entire range V/Δ. This result shows an effective pairing interaction between low-energy fermions. It is worth noting that the two-particle bound states cannot be captured by the projected interaction ${\mathit{V}}_{\mathit{f}}^0=2{\mathrm{\lambda }}^0$, which proves that pairing is induced by virtual interband excitations. We further confirm the formation of pairs in the original model Eq. 1 with ED (see the Supplementary Materials). Pairs are already present for V < Δ despite a repulsive induced nearest-neighbor interaction (V_f > 0). This highlights the essential role of correlated hopping λ in the effective model for pairing.

Fig. 2. Doped charges form bound pairs.

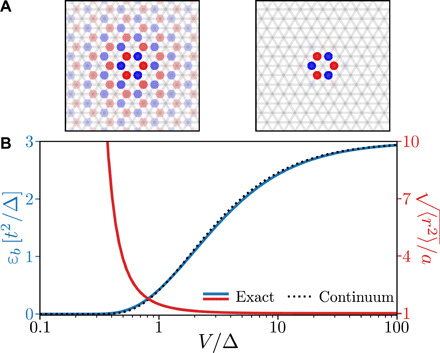
(A) The transition from weakly to tightly bound pairs, depicted for V/Δ = 0.5 (left) and 10 (right), constitutes a probe of the BCS-BEC crossover at low doping. (B) Pair binding energy ε_b and bound state size as a function of V/Δ from the exact solution of the two fermion problem. The prediction of the continuum model (dashed line) perfectly matches the full-fledged lattice calculation, a stringent test of our derivation.

The two-particle bound state we found has zero total momentum, is symmetric under threefold rotation, and changes sign under reflection that flips one of the primitive vectors a_j, i.e., it has f-wave pairing symmetry. The size of the bound state shrinks with increasing V/Δ, as shown in the inset of Fig. 2 for V/Δ = 0.5 and 100. At small V/Δ, the pair wave function is highly extended over many lattice sites, while in the opposite limit V/Δ → ∞, two nearest-neighbor fermions form the most tightly bound pair “resonating” within a single upper triangle (see the Supplementary Materials). Our solution of the two-particle problem suggests a crossover between Bardeen–Cooper–Schrieffer (BCS) and Bose–Einstein condensate (BEC) states at small particle density, tuned by V/Δ.

The presence of a two-particle bound state is a striking feature of our mechanism, distinct from the Kohn-Luttinger one (22), and relies on the presence of a filled Fermi sea to mediate an effective attraction between electrons. Here, on the contrary, pairing is already present for two doped fermions and is induced by the virtual excitations of the insulating state.

We now extend our analysis to finite, but small, doping concentrations δ above n = 1. In this regime, the physics of dilute doped fermions is governed by long-wavelength properties that transcend the details on the lattice scale. This motivates us to derive a low-energy theory by taking the continuum limit of the lattice Hamiltonian. This is achieved by rewriting the lattice Hamiltonian in terms of fermionic fields in momentum space and retaining only modes near the bottom of the f-band. The band dispersion $\mathrm{\epsilon }(\mathbf{k})\mathit{=}2{\mathit{t}}_{\mathit{f}}{\sum }_{\mathit{j}=1}^3\text{cos} (\mathbf{k}·{\mathbf{a}}_{\mathit{j}})$ with t_f > 0 has two degenerate minima located at the ±K points of the Brillouin zone. Therefore, low-energy degrees of freedom are described by two long-wavelength fermionic fields ψ_τ(q) = f(τK + q) with qa ≪ 1, distinguished by the valley index τ = ±. In the Supplementary Materials, we find the following continuum Hamiltonian for ψ_τ

$$\widetilde{\mathrm{\mathscr{H}}}=\int \mathrm{d}\mathit{x} {\displaystyle \sum _{\mathrm{\tau }=\pm }} {\mathrm{\psi }}_{\mathrm{\tau }}^{†}\left[\frac{-{\nabla }^2}{2\mathit{m}}\right]{\mathrm{\psi }}_{\mathrm{\tau }}+\mathit{g}{\mathrm{\psi }}_{+}^{†}{\mathrm{\psi }}_{+}{\mathrm{\psi }}_{-}^{†}{\mathrm{\psi }}_{-}$$ (5)

where the effective mass and interaction strength are entirely determined from the lattice parameters

$$\begin{array}{c}\mathit{m}=2/(3{\mathit{t}}_{\mathit{f}}{\mathit{a}}^2),\\ \mathit{g}=6{\mathit{a}}^2({\mathit{V}}_{\mathit{f}}-2\mathrm{\lambda })<0\end{array}$$ (6)

The resulting quantum field theory describes a two-flavor fermion gas in the continuum with attractive contact interaction. The two flavors correspond to the valley degree of freedom associated with the underlying lattice, from which the field theory is derived. This theory is asymptotically exact in the low doping limit where s-wave scattering between fermions of opposite valleys is the dominant interaction.

This attractive interaction leads to the formation valley-singlet two-particle bound states, which exactly correspond to the f-wave pairs observed on the lattice (see Fig. 2). The pair amplitude f(+K)f(−K) is odd under the reflection that interchanges the two valleys. To verify the validity of our continuum model, we calculate the two-particle binding energy ε_b in the field theory and, using the parameters m and g given by Eqs. 3a to 3d and 6, compare it with the exact solution of the lattice model. The expression for ε_b is

$$\begin{array}{c}\frac{{\mathrm{\epsilon }}_{\mathit{b}}}{{\mathrm{\epsilon }}_{\text{uv}}}={[{\mathit{e}}^{1/{\mathit{g}}_0}-1]}^{-1},\\ {\mathit{g}}_0=\frac{9}{\mathrm{\pi }}\frac{2\mathrm{\lambda }-{\mathit{V}}_{\mathit{f}}}{\mathit{W}}=\frac{6}{\mathrm{\pi }}\frac{{\mathit{V}}^2}{\mathrm{\Delta }(\mathrm{\Delta }+2\mathit{V})}\end{array}$$ (7)

with ε_uv = πW/9 being an energy cutoff that we fix with the exact binding energy at V → ∞ (see the Supplementary Materials). The exponent g₀ in Eq. 7, defined by the ratio of effective pairing interaction g and the bandwidth, only depends on the ratio V/Δ in the narrow band regime t ≪ Δ. A perfect agreement between continuum theory and the lattice model is found at all values of V/Δ (see Fig. 2). This proves the accuracy of our mapping from the lattice model to continuum theory.

Let us summarize our achievements so far. We have transformed the strongly repulsive model (Eq. 1), where the repulsion V far exceeds the single-particle bandwidth, into an effective Hamiltonian for doped particles featuring attractive interaction. The nature of the ground state at low density depends on the strength of this attraction, measured by the dimensionless coupling constant g₀. If g₀ is small, the binding energy is small compared to the Fermi energy and the doped charge forms a weakly attractive Fermi gas. On the other hand, a large g₀ will produce tightly bound pairs. One can tune between these two regimes by increasing the ratio V/Δ, as shown Fig. 2A.

The attractive Fermi gas in two dimensions is known to be superconducting at low temperature and exhibits a BCS-BEC crossover as the ratio between pair binding and Fermi energies changes from small to large values (23–25). In the region of weakly bound pairs ε_b ≪ E_F, the critical temperature is given by ${\mathit{k}}_{\mathit{B}}{\mathit{T}}_{\mathit{c}}={\mathit{e}}^{\mathrm{\gamma }-1}\sqrt{2{\mathit{E}}_{\mathit{F}}{\mathrm{\epsilon }}_{\mathit{b}}}/\mathrm{\pi }$, with γ ≃ 0.577 being Euler’s constant (26, 27). In terms of the dimensionless coupling constant g₀ (Eq. 7), we obtain the explicit formula for T_c

$${\mathit{k}}_{\mathit{B}}{\mathit{T}}_{\mathit{c}}={\mathit{e}}^{\mathrm{\gamma }-1}\sqrt{\frac{2{\mathit{E}}_{\mathit{F}}\mathit{W}}{9\mathrm{\pi }}}{\mathit{e}}^{-1/(2{\mathit{g}}_0)}$$ (8)

where the Gorkov-Melik-Barkhudarov corrections have been included to correctly describe the strong coupling nature of the superconducting state (28, 29). As an example, this formula safely applies at δ = 0.1 if V < 0.7Δ, where we both have exp (1/g₀) > 10 and ε_b ≲ E_F/2 (24), as confirmed thereafter by ED.

On the other side of the crossover ε_b ≫ E_F, the physics depends on the interaction between the bosonic pairs. When these bosons repel, the system exhibits a Berezinskii–Kosterlitz–Thouless transition toward a BEC at low temperature (30), while it collapses if bosons attract (31, 32). Between the extreme BCS and BEC limits, the critical temperature satisfies the very general bound k_BT_c ≤ E_F/8 (33), which limits the largest achievable T_c.

The BCS-BEC crossover of the two-dimension Fermi gas can be achieved by tuning either carrier density or the interaction strength g₀, which is controlled by V/Δ in our model. We plot in Fig. 3 the critical temperature T_c as a function of doping concentration δ and V/Δ. At very low doping where E_F < ε_b, the system lies in the BEC regime and T_c increases rapidly with δ. At some critical concentration, the system undergoes the BEC-BCS crossover and finally follows Eq. 8.

Fig. 3. Critical temperature.

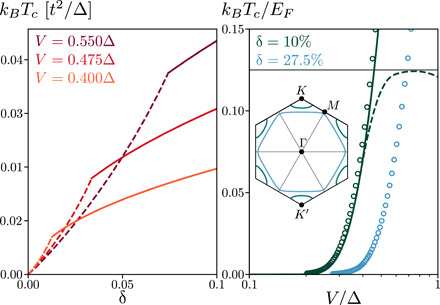
Critical temperature of the continuum model in the exact BCS (solid line; Eq. 8) and BEC (dashed line) limits, as a function of doping and V/Δ. A gray horizontal line highlights the bound k_BT_c < E_F/8. The self-consistent lattice mean-field solutions (dots) agree with the continuum theory for small doping, but differ when the ±K pockets merge (inset).

It is worth emphasizing that our exact BCS formula Eq. 8 applies provided that the dimensionless coupling constant g₀ is small, even when the bare repulsion V far exceeds the bandwidth W. This is because doped fermions at the conduction band bottom ±K reside entirely on B sublattice and therefore avoid the direct nearest-neighbor repulsion V. In the weak-coupling regime V ≪ Δ, the attraction g₀ ∝ (V/Δ)² between low-energy carriers is induced by virtual interband particle-hole pairs or excitons and leads to exponentially small T_c. However, our expression of g₀ is nonperturbative in V and remains exact at V ∼ Δ ≫ W, where strong-coupling superconductivity and maximum T_c are attained. For instance, at doping δ = 0.1, T_c reaches 0.1E_F ≃ 0.032t²/Δ around V = 0.43Δ, which is about 0.5% of the quasiparticle bandwidth W = 9t_f ≃ 6.3t²/Δ.

MATERIALS AND METHODS

We support the emergence of superconductivity with evidence from ED on finite size lattices. While the original model Eq. 1 exhibits positive ε_b (see the Supplementary Materials), we focus on the effective model Eq. 2, which allows reaching larger system sizes. First, the superfluid behavior of the system is probed by the charge stiffness (34)

$$\mathit{D}=\frac{1}{16{\mathrm{\pi }}^2}{\frac{{\mathit{L}}_1}{{\mathit{L}}_2}\frac{{\mathrm{\partial }}^2\mathit{E}(\mathit{N},\mathrm{\varphi })}{\mathrm{\partial }{\mathrm{\varphi }}^2}\mid }_{\mathrm{\varphi }=0}$$ (9)

at doping δ = N/(L₁ × L₂), with N being the number of doped fermions and (L₁, L₂) being the number of sites along the two basis vectors of the triangular lattice. D measures the sensitivity of the ground state energy E(N, ϕ) to twisted boundary conditions ψ_{r + L1} = e^2iπϕψ_r. A positive value of D > 0 in the thermodynamic limit implies dissipationless charge transport and gives a direct signature of the Meissner effect (35). In the range of parameters considered, our system clearly exhibits (with small finite-size effect) the h/2e flux periodicity of superconductors (36) and shows positive D (see Fig. 4, A to B), which proves superconductivity in the ground state. The charge stiffness of a BCS superconductor with a parabolic dispersion relation is known exactly: D = E_F/4π (33). Our results for V < Δ are correctly captured by this prediction, especially at low doping concentrations where fermions live close to the band minima.

Fig. 4. Numerical evidence of superconductivity.

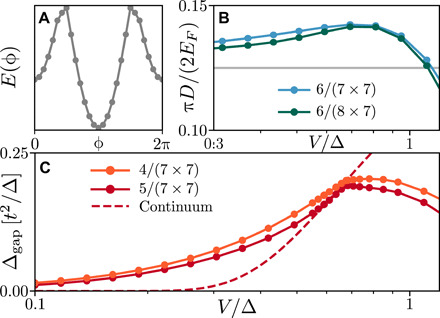
(A) The ground state energy exhibits the characteristic flux dependence of a superconductor, as shown here for V = Δ and six particles on an 8 × 6 lattice. (B)The charge stiffness divided by the Fermi energy is constant in the BCS limit, reaching 1/8 for small doping (gray). (C) Superconducting gap as a function of V/Δ for different doping concentrations. It follows the continuum prediction (dashed line) up to V/Δ ≃ 0.7.

To demonstrate the strong-coupling nature of the superconducting state, we consider the superconducting gap

$${\mathrm{\Delta }}_{\text{gap}}=\frac{{(-1)}^{\mathit{N}}}{2}[\mathit{E}(\mathit{N}+1)+\mathit{E}(\mathit{N}-1)-2\mathit{E}(\mathit{N})]$$ (10)

Our continuum theory Eq. 5 predicts ${\mathrm{\Delta }}_{\text{gap}}=\sqrt{2{\mathit{E}}_{\mathit{F}}{\mathrm{\epsilon }}_{\mathit{b}}}$ up to V ∼ Δ. This leads to a ratio of the gap and critical temperature Δ_gap/k_BT_c = πe^{1 − γ} ≃ 4.796 (26–28), which is much larger than the universal value 1.764 in BCS theory for weak-coupling superconductors (37). This is because the phonon-induced retarded attraction in conventional metals is limited to electrons within a Debye energy from the Fermi surface, whereas in our theory, the induced pairing interaction is instantaneous on the time scale of inverse bandwidth (ℏ/W), so that all carriers in the narrow band are subject to the pairing interaction. For sufficiently large V or at very small doping concentrations, the system lies in the BEC regime and the gap-to-T_c ratio can take arbitrarily large values.

Our numerical results for δ ≃ 0.1, shown in Fig. 4C, confirm the superconducting behaviors identified above with a robust gap Δ_gap increasing with V up to V/Δ = 0.7. Near this point, our numerical results agree with the mean field prediction, and the gap reaches as large as Δ_gap = 0.84E_F. This allows the system to reach a critical temperature of 0.1E_F as described above. For V ≲ 0.5Δ, the numerically extracted gaps Δ_gap lie above the continuum theory prediction due to finite size effects. In that regime, the finite lattice considered cannot fully accommodate the bound state that arises in the thermodynamic limit (see Fig. 2). This effective confinement increases the energy of the bound pairs, resulting in an overestimate of the superconducting gap. Despite this discrepancy, the simultaneous presence of a positive Δ_gap and a nonzero charge stiffness stands as a strong probe of superconductivity in our model for V < 0.7Δ.

In addition to the BCS-BEC superconductivity at low density, our model shows very rich physics at higher doping concentrations, where lattice effects become important. By performing mean-field calculation on the model Eq. 2, we find f-wave pairing for doping δ < 1/3 (see the Supplementary Materials). The corresponding critical temperatures, as shown in Fig. 3, are calculated with the linearized gap equation

$$\frac{1}{\mathrm{\alpha }}=\frac{1}{N_s}\sum _{\mathbf{q}}\frac{{[{\sum }_j \text{sin} (\mathbf{q}·{\mathbf{a}}_j)]}^2}{\mid {\mathrm{\xi }}_{\mathbf{q}}\mid }\text{tanh} \left(\frac{\mid {\mathrm{\xi }}_{\mathbf{q}}\mid }{2k_B{T}_c}\right)$$ (11)

with ξ_k = ε(k) − μ and α = 2λ − V_f − (2β + δ)U₃, where β = (3N_s)⁻¹∑_qf_FD(ξ_q)∑_j cos (q · a_j) originates from three-body interactions. Here, N_s denotes the total number of sites, and the chemical potential is fixed by $\mathrm{\delta }=N_s^{-1}{\sum }_{\mathbf{q}}{f}_{\text{FD}}({\mathrm{\xi }}_{\mathbf{q}})$, with f_FD being the Fermi-Dirac distribution.

At low doping, the f-wave superconducting state has a full pairing gap, and its T_c obtained from lattice model calculation agrees well with our previous result based on continuum theory. At higher doping concentration δ > δ_c ≈ 1/4, the gap vanishes at six nodes on the Fermi surface along the ΓM direction, where the f-wave gap function vanishes. This change in gap structure is due to the change of Fermi surface topology across the van Hove singularity, where the two pockets around ±K merge into a single Fermi surface enclosing the Γ point (see Fig. 3).

The above conclusions are confirmed by our ED study, which shows clear evidence of nodal superconductivity at $\frac{1}{4}<\mathrm{\delta }\le \frac{1}{3}$. We also find that the superconducting state is remarkably robust against longer-range bare repulsion. These numerical results can respectively be found in the Supplementary Materials.

Last, our ED study reveals nonsuperconducting states in the ultrastrong coupling regime V ≳ Δ (see the Supplementary Materials). The detailed description of these competing phases is left for further study, the focus of this work being the fully controlled theory of superconductivity emerging from repulsive interactions at V < Δ.

DISCUSSION

Our work opens a new route to unconventional superconductivity in atomic Fermi gas and electron systems. Encouragingly, optical lattices with honeycomb geometry and tunable bandgap have already been realized (38, 39). Many recent advances in dipolar or Rydberg atom systems with longer-range interactions (40, 41) have enabled the implementation of one-dimensional t − V Hamiltonian (42) and hold great promise for the realization of our model in the near future.

Our mechanism for strong-coupling superconductivity mediated by charge-transfer complex, or interband excitations, may also shed insight into graphene-based moiré superlattices, where the small bandwidth and high k_BT_c/E_F ratio (up to ∼0.1) place important constraints on viable theories. It will be interesting to develop accurate low-energy models for these systems and analyze superconductivity in the narrow band limit as exemplified in our work. In this regard, we note that correlated hopping and direct repulsion also appear in effective Hamiltonian for narrow bands in twisted bilayer graphene (43–45). Our theory suggests that renormalization by virtual interband excitations is necessary to obtain strong-coupling superconductivity. Moreover, our simple model may be relevant to twisted double bilayer graphene (46) and trilayer graphene-boron nitride heterostructures (47), where signs of spin-polarized superconductivity have been reported (48, 49). We leave to future work the extension of our theory to spinful systems and its application to various strongly correlated materials.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/30/eabh2233/DC1