A high-resolution PET demonstrator using a silicon “magnifying glass”

Abstract

To assist ongoing investigations of the limits of the tradeoff between spatial resolution and noise in PET imaging, several PET instruments based on silicon-pad detectors have been developed. The latest is a segment of a dual-ring device to demonstrate that excellent reconstructed image resolution can be achieved with a scanner that uses high-resolution detectors placed close to the object of interest or surrounding a small field-of-view in combination with detectors having modest resolution at larger radius. The outer ring of our demonstrator comprises conventional BGO block detectors scavenged from a clinical PET scanner and located at a 500mm radius around a 50mm diameter field-of-view. The inner detector—in contrast to the high-Z scintillator typically used in PET—is based on silicon-pad detectors located at 70mm nominal radius. Each silicon detector has 512 1.4mm x 1.4mm x 1mm detector elements in a 16 x 32 array and is read out using VATA GP7 ASICs (Gamma Medica-Ideas, Northridge, CA). Even though virtually all interactions of 511 keV annihilation photons in silicon are Compton-scatter, both high spatial resolution and reasonable sensitivity appears possible. The system has demonstrated resolution of ~0.7mm FWHM with Na-22 for coincidences having the highest intrinsic resolution (silicon-silicon) and 5–6mm FWHM for the lowest resolution BGO-BGO coincidences. Spatial resolution for images reconstructed from the mixed silicon-BGO coincidences is ~1.5mm FWHM demonstrating the “magnifying-glass” concept.

1. Introduction

Positron emission tomography or PET is a widely employed imaging method in medicine and biomedical research [1]. Briefly, the subject is injected with a radiolabeled tracer that localizes according to specific metabolic pathways. Upon decay, the radionuclide emits a positron that annihilates with a nearby electron releasing two 511 keV photons traveling in nearly opposite directions. Detection of these photons in time-coincidence localizes the annihilation to a line-of-response (LOR) and from a collection of 10⁷ – 10⁸ such events, the 3D distribution of radiotracer can be reconstructed.

Magnifying PET geometries—where a detector having high spatial resolution located close to a region of interest works in coincidence with a conventional PET detector having more modest resolution—have been investigated in a number of studies spanning the past decade. Clinthorne and Park proposed instruments for small animal and patient imaging based on high-resolution detectors used in conjunction with standard PET detectors [2–5]. Tai and co-workers have referred to the concept as “virtual pinhole PET” and have developed several demonstration instruments [6–8]. Huh, et al, have evaluated the concept of an endorectal insert for high resolution prostate imaging and are presently developing a LYSO/silicon photomultiplier based instrument [9]. The goal of the MADEIRA project is to develop a high-resolution add-on probe for clinical PET [10]. More recently, Zhou and co-workers have termed the concept “zoom-in” PET and have investigated the advantage of augmenting conventionally acquired PET data with information from a higher resolution detector [11,12].

To explore potential performance advantages of magnifying geometries for PET applications ranging from small animal imaging to organ-specific high resolution imaging probes for human subjects, we have constructed a demonstration instrument consisting of a partial outer ring of conventional PET detectors supplemented by a partial inner ring of high-resolution silicon detectors. This paper describes the basic principles, construction, and initial images obtained from the device.

2. Principles and Design

2.1. Magnifying PET geometry

The principles of a magnifying geometry are discussed by Park, et al. [5]. We restrict the following discussion to geometries in which a full ring of high resolution detectors (or emulation thereof) surrounds a small field-of-view. This high resolution detector ring is itself inserted into the larger diameter bore of a conventional PET instrument. Since the inner detector may not have high detection efficiency for 511 keV photons, there are three significant classes of PET coincidence events that can be reconstructed: (1) those in which both annihilation photons interact in the high resolution detector ring (referred to as Si-Si here); (2) those in which both photons are detected in the outer, low-resolution ring (BGO-BGO); (3) and hybrid events (Si-BGO) where one event interacts in the high resolution ring and the other in the low resolution ring. That the Si-Si and BGO-BGO events result in the highest and lowest resolution data, respectively, is clear. The spatial uncertainty of the Si-BGO events, however, varies significantly along the coincidence LOR between the high- and low-resolution detectors as described next.

2.2. Intrinsic spatial resolution in a magnifying geometry

Intrinsic resolution is dominated by the detector (either high- or low-resolution) to which the positron source is physically closest. Thus, resolution in a small FOV surrounded by high-resolution detectors will be dominated by the performance of that detector as shown through the following expression:

$$R_D\approx 2.35\sqrt{\left({\left(1-\alpha \right)}^2\left({\sin }^2{\theta }_1{\sigma }_{D1}^2+{\cos }^2{\theta }_1{\sigma }_{C1}^2\right)+{\alpha }^2\left({\sin }^2{\theta }_2{\sigma }_{D2}^2+{\cos }^2{\theta }_2{\sigma }_{C2}^2\right)\right)}$$ (1)

where σ_C and σ_D are the standard deviations in estimating position in each detector in the circumferential or transverse and depth directions, respectively, α is the fractional distance of the source along a coincidence LOR intersecting the two detectors at the angles of incidence shown in Fig. 1. Note that the expression conveniently accounts for depth-of-interaction uncertainty that often degrades resolution at large angles of incidence. Eq. (1) is derived by calculating the covariance of a point along the mean LOR at distance α × D from D₁ given the position variance in the LOR endpoints. Element (1,1) of this matrix quantifies the variation transverse to the LOR at that location. To obtain the combined resolution, uncertainty due to acolinearity of the annihilation radiation, which can be quantified as 0.0088 × (α – α²) × D millimeters (where D is also in millimeters), adds in quadrature to the resolution in eq. (1).

Fig. 1.

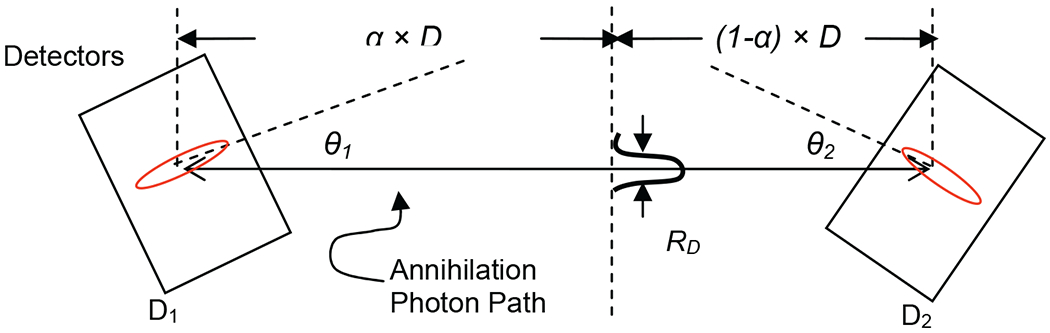
Diagram illustrating detector geometry and parameters used for approximating intrinsic resolution in Equation (1).

As an example, assuming normal incidence on both detectors, the intrinsic resolution for a source 3cm from a detector having 1mm FWHM resolution and 40cm from a detector having 6mm FWHM resolution would be 1.1mm FWHM including the effects of acolinearity of the annihilation radiation in soft-tissue. At 10cm from the higher resolution detector, this decreases to 1.7mm FWHM.

2.3. Tradeoff between reconstructed resolution and noise

Although intrinsic measurement uncertainty plays a significant role in overall system performance, spatial resolution in the reconstructed image can actually be better than that suggested by the intrinsic resolution if the system aperture function is appropriately modeled in the reconstruction process [1]. Such resolution recovery, however, increases the noise level or variance in reconstructed images. This increase is highly non-linear as a function of reconstructed resolution as shown in Fig. 2(a) where the approximate standard deviation at the center of a uniformly emitting disk source occupying the full FOV is plotted against desired spatial resolution in reconstructed images for simulated PET systems having Gaussian resolutions of 4mm, 6mm, and 8mm FWHM (curves were calculated using the modified uniform Cramér-Rao bound, which is applicable to SPECT and PET imaging systems [13, 16]). Each curve has been normalized to unity at the intrinsic resolution of the simulated scanner. Note how quickly noise increases as one attempts to operate at points better than the intrinsic resolution. As an example, operating the 4mm system at 3mm FWHM reconstructed resolution increases the standard deviation by a factor of 10. To achieve the same noise level as a reconstruction with 4mm FWHM resolution, 100× the number of events would need to be collected.

Fig. 2.

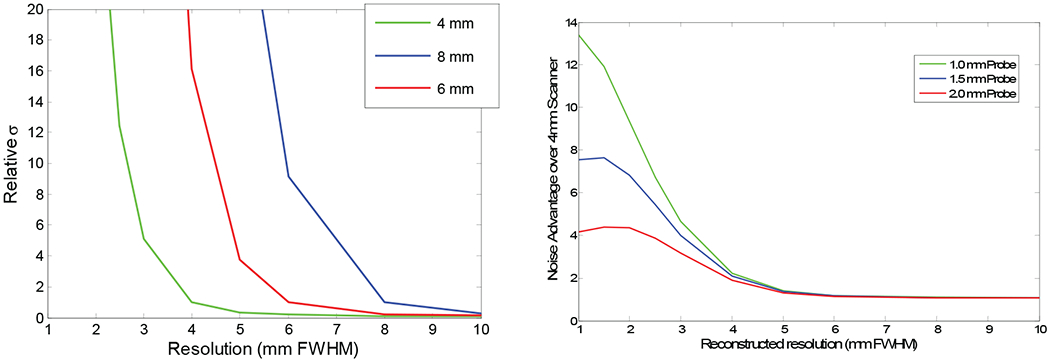
(a) Standard deviation vs. reconstructed image resolution for detectors supporting intrinsic resolution of 4mm, 6mm, and 8mm FWHM. Standard deviation has been normalized to unity for reconstructed resolution equal to the intrinsic resolution, (b) Noise advantage as a function of reconstructed image resolution for an additional 12% of data having intrinsic resolutions of 1.0mm, 1.5mm, and 2.0mm FWHM added to 4mm FWHM data.

Fig. 2(b) demonstrates the effect of adding a small amount (12%) of additional data having resolutions of 1mm, 1.5mm, and 2mm FWHM to PET data from a system having 4mm intrinsic resolution. Curves shown are the standard deviation of reconstructions from the combined datasets divided by that of the 4mm dataset alone and are plotted against desired reconstructed resolution. At operating points above 4mm FWHM, there is little advantage to including information from a high resolution detector while there is a considerable performance improvement at operating points better than 4mm FWHM. And as expected, the advantage increases for detectors having higher resolution.

2.4. Silicon as an unconventional PET detector

The previous section demonstrates that adding a modest amount of data having high intrinsic resolution to lower resolution data can have a significant impact on performance. In a conventional PET scanner, detectors typically comprise high-density scintillators such as BGO or LYSO read out by photodetectors. It remains challenging to achieve submillimeter spatial resolution with this approach as well as appropriate depth of interaction resolution (i.e., 3D position resolution). Solid-state detectors based on silicon, however, can readily achieve submillimeter performance in 3D. Even though attenuation length of silicon for 511 keV photons is 5cm as opposed to 1cm for BGO and 1.1cm for LYSO, information in the previous section demonstrates that silicon may well outperform the more conventional scintillation detectors when the goal is resolution in the neighborhood of 1mm FWHM.

3. Demonstrator Design

To evaluate the use of silicon as a PET detector for the primary purpose of rodent imaging within a 50mm FOV, we have assembled the demonstration instrument shown in Fig. 3(a). The instrument consists of a partial ring of 24 BGO detectors at 500mm radius within which a partial “ring” of silicon pad detectors at nominal radius 70mm has been inserted. To reduce the overall event rate on the detectors, the source has been collimated to a 1mm thick slice using tungsten plates and the silicon detectors have been located on edge as shown in Fig. 3(b) to achieve high detection efficiency for the slice. A full set of PET data is acquired by rotating the object in 6° steps and recording Si-Si, Si-BGO, and BGO-BGO coincidences. Raw coincidence information is recorded in a structured list containing position and energy as well as a time-stamp for each trigger, which allows acquired data to be post-processed to change energy thresholds or timing window widths, for example.

Fig. 3.

(a) Dual partial-ring PET demonstrator showing BGO block detectors at 500mm radius and silicon pad detectors at ~70 mm radius surrounding 45mm diameter field-of-view. Full PET dataset is acquired by rotating object. (b) Close-up showing edgewise positioning of 1mm thick silicon pad detector, object turntable and tungsten slice collimator.

3.1. BGO block detectors

The 24 BGO block detectors were scavenged from a CTI 931 (ca. 1985) PET scanner and each comprises a 4x8 BGO crystal array of 6mm x 12mm crystals read out by a 2 x 2 array of 25mm square PMTs. The detectors are oriented such that the 6mm width is along the circumference of the ring. PMT outputs are routed to a simple CR-RC shaping amplifier and then to a peak-sensing ADC. Timing resolution for BGO-BGO coincidences is ~12 ns FWHM while typical energy resolution for the 511 keV peak is 20% FWHM. Although the performance of these detectors is inferior to modern LYSO (or LSO) based devices, they provide an excellent demonstration of the magnifying PET concept using Si-BGO coincidences.

3.2. Silicon pad detectors

The silicon detectors currently used in this instrument are 1mm thick and each have 512 1.4mm x 1.4mm pads arranged in a 16 x 32 array [14]. Each detector is read out by four VATAGP-7 ASICs developed for this application by Gamma Medica-Ideas [15] and a VME bus based interface. Since virtually all interactions of 511 keV photons will be Compton scattering, the triggering threshold for PET measurements was set to nominally 30 keV but varied by channel depending on inherent offset. While the ASIC has trim-DACs for each channel to allow triggering at the same energy, these were not calibrated for the measurements presented below. Energy resolution with this setup is approximately 2 keV FWHM (although this does not directly impact PET performance of the instrument). Timing resolution is relatively poor due to both time-walk of the leading-edge trigger in the ASIC, which can be corrected off-line, and variations due to 3D interaction location in the detector and uncertainty in the Compton recoil electron path. Coincidence resolution between two silicon detectors operated at 136 V bias is ~50ns FWHM. Increasing the bias and correcting the pulse-height dependent time-walk improves timing performance but was not done since the random coincidence rate was sufficiently low in the single-slice geometry.

4. Imaging Performance

4.1. Reconstructions from simulated data

To understand what to expect from reconstructions of a resolution phantom and to explore the advantages of simultaneously reconstructing a single image from all three types of coincidence events, single-slice Monte Carlo data was generated by projecting a simulated resolution phantom through the system response and then adding Poisson noise. Measurement sensitivities, detector normalizations, and intrinsic resolutions were consistent with those of the demonstrator. Specifically, 50 million total detected events were used (3% Si-Si, 14% Si-BGO, and 83% BGO-BGO) with Si-Si resolution of 0.7mm FWHM, Si-BGO resolution of 1.2mm FWHM and BGO-BGO resolution of 3.2 mm FWHM (all Gaussian shaped and based on the approximation in Section 2.2). These figures correspond to an idealized version of the demonstrator and performance of the actual system is expected to be significantly worse due primarily to significant mis-positioning in the BGO detectors and to a lesser extent inaccuracies in modeling the response of the real device.

Reconstructions from the simulated data using a regularized maximum likelihood (ML) reconstruction [16] are shown in Fig. 4 for a resolution phantom consisting of 4.8mm, 4.0mm, 3.2mm, 2.4mm, 1.6mm and 1.2mm diameter rods separated by two rod diameters center-to-center. The top row shows images reconstructed from the individual coincidence events (Si-Si–100 iterations, Si-BGO–500 iterations, and BGO-BGO–1000 iterations). Performance is as expected with the Si-Si events demonstrating the best resolution (and spot-shape fidelity) but also the highest noise. BGO-BGO resolution is the worst and the reconstruction also shows aliasing for the wedges containing the three smallest diameter spots due to undersampling. Reconstructions from the Si-BGO events greatly improve upon this with resolution closer to that of the Si-Si reconstruction. Note, however, that the smaller spots in the Si-BGO and BGO-BGO reconstructions tend to be overly sharp with diameters smaller than actual and that the larger spots in the Si-BGO reconstructions suffer from edge overshoot.

Fig. 4.

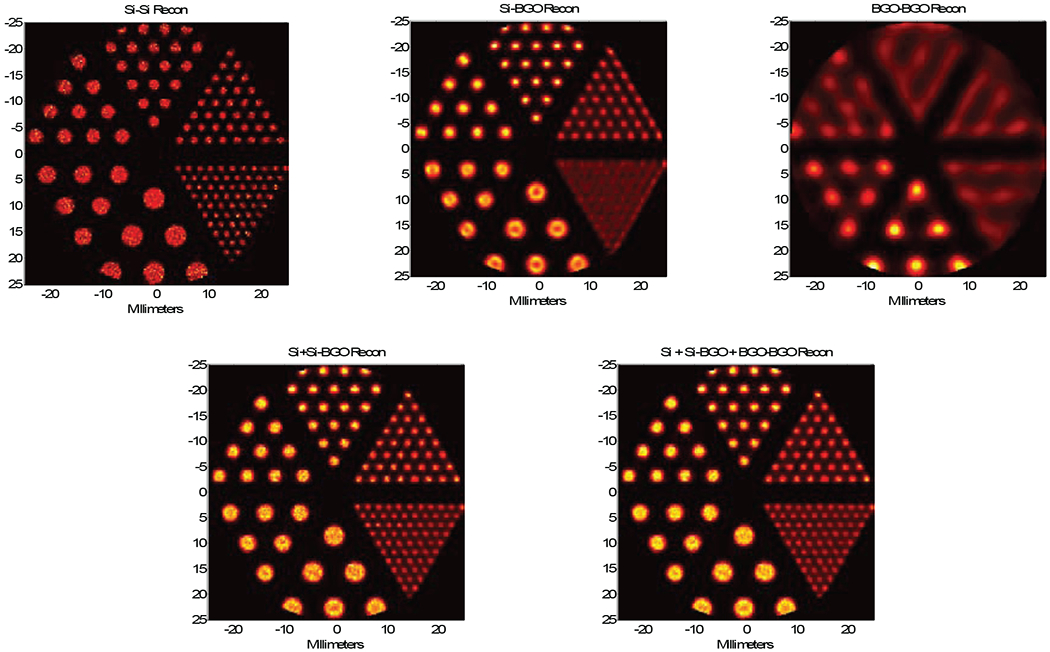
Top row left-to-right: Si-Si reconstruction from simulated data, Si-BGO reconstruction, BGO-BGO reconstruction. Note noise in Si-Si reconstruction as well as distortion of spot shapes in Si-BGO and BGO-BGO reconstructions. Bottom row: composite reconstructions using Si-Si and Si-BGO data (left) and all events (right).

The image at the bottom left in Fig. 4 combines both Si-Si and Si-BGO events (500 iterations). Resolution is improved over the reconstruction from Si-BGO events alone and noise is reduced over using only Si-Si events. Moreover, the spot shape has better fidelity. As predicted in [16], adding the lowest resolution BGO-BGO events adds little, if anything, to overall performance and slows convergence of the iterative ML reconstruction (1000 iterations).

4.2. Reconstructions from demonstrator measurements

For data acquisition using the demonstrator, the silicon threshold was set to ~30 keV, the BGO energy window from 300–700 keV, and the Si-Si, Si-BGO, and BGO-BGO timing windows to 425ns, 230ns, and 25ns, respectively. Since virtually all interactions of 511 keV photons are Compton scatter in the silicon, the energy of a valid event ranges from the 30 keV threshold through ~340 keV. Due to both the small FOV and the single-slice geometry, the rate of detected events resulting from Compton-scatter in the object is low although this warrants additional investigation for geometries lacking such collimation. Presently, wide timing windows are needed to accommodate time-walk associated with the large range of silicon pulse-heights. In a system capable of operating at counting rates necessary for small animal imaging, the wide windows will lead to an unacceptable random coincidence rate. Improved time resolution for silicon, however, is under active investigation in our laboratory. Typical random coincidences in this geometry for Si-Si events were <5% of the total for the resolution phantom studies. Detector normalization factors were calculated using both measurements and modeling for each coincidence event class. Calculated object attenuation was included in the normalization.

Fig. 5 shows images reconstructed from micro-Jaszczak resolution phantom measurements acquired using the demonstration instrument using ~185 MBq of ¹⁸F-fluorodeoxyglucose (FDG) over an interval of 5 hours. Rod sizes in the resolution phantom are the same as for the simulation in the previous section (4.8mm, 4.0mm, 3.2mm, 2.4mm, 1.6mm, and 1.2mm) and the order is the same as for the reconstructions shown in Fig. 4 (Si-Si–40 iterations, Si-BGO–200 iterations, BGO-BGO–1000 iterations). In this case, Si-Si events comprise 3.4%, Si-BGO 20.5%, and BGO-BGO 76.1% of the 1.2 x 10⁷ collected coincidences. For reconstruction, the same system model for reconstructing the simulated data in Fig. 5 was used (responses of 0.7mm, 1.2mm, and 3.2mm FWHM for Si-Si, Si-BGO, and BGO-BGO events, respectively). The hot ring around the resolution phantom is real and not visualized in the Si-Si reconstruction due to the slightly smaller FOV size (45 mm vs. 50mm diameter). Trends in these reconstructions correspond to those in Fig. 4 with the exception that the Si-Si reconstruction is significantly noisier due to fewer coincidence events. Composite reconstructions are shown in the bottom row using 200 iterations for Si-Si+Si-BGO (left image) and 1000 iterations for all events (right). While reconstruction from Si-Si and Si-BGO events is perhaps slightly better than either reconstruction alone (the outer ring is correctly reconstructed and the blurring slightly less for the smallest diameter spots), reconstruction from all events reduces performance somewhat. This is due both to a significantly slower convergence rate for the combined data and to inaccuracies in modeling the actual response of the BGO-BGO events. If modeling is consistent, there is no reason that including the lowest resolution events should decrease performance. Nevertheless, when the desired operating point is at a resolution much higher than the intrinsic resolution of the BGO-BGO events, one will lose little performance by disregarding them as shown in Fig. 4.

Fig. 5.

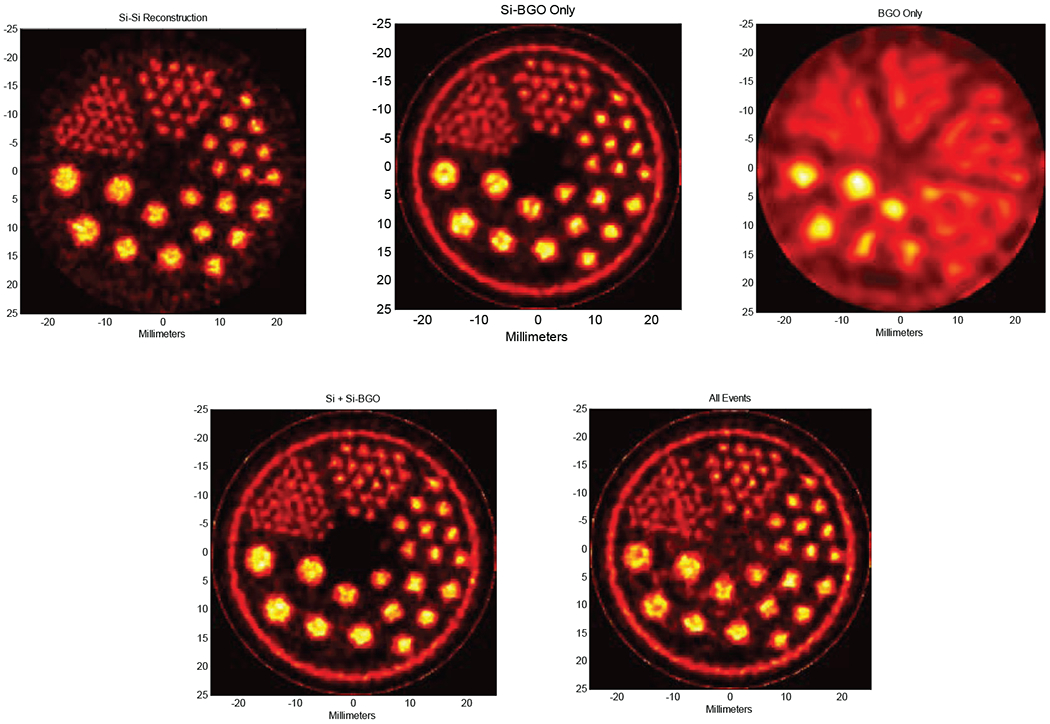
Reconstructions from data measured with the demonstrator shown in Fig. 3. Top row left-to-right: reconstructions of a micro-Jaszczak resolution phantom from Si-Si, Si-BGO, and BGO-BGO events alone. Bottom row left: reconstruction from Si-Si and Si-BGO events. Bottom right: reconstruction using all events.

5. Conclusions

To assist in our ongoing investigation of high resolution PET in magnifying geometries we have constructed a demonstration instrument consisting of low resolution BGO detectors and high resolution silicon pad detectors. Preliminary reconstructions of resolution phantom data acquired using the device were presented and performance qualitatively agreed with Monte Carlo simulations from an idealized system. In the coming months, this instrument will be used to evaluate a number of high-resolution PET imaging configurations including those applicable to small animals as well as probes for prostate and head-and-neck imaging in human subjects.