Angular Resolution Enhancement of Diffusion MRI Data Using Inter-Subject Information Transfer

Abstract

Diffusion magnetic resonance imaging is widely used to investigate diffusion patterns of water molecules in the human brain. It provides information that is useful for tracing axonal bundles and inferring brain connectivity. Diffusion axonal tracing, namely tractography, relies on local directional information provided by the orientation distribution functions (ODFs) estimated at each voxel. To accurately estimate ODFs, data of good signal-to-noise ratio and sufficient angular samples are desired, but unfortunately, are not always practically available. In this paper, we propose to improve ODF estimation by using inter-subject correlation. Specifically, diffusion-weighted images acquired from different subjects, when transformed to the space of a target subject, can not only provide signal denoising with additional information, but also drastically increase the number of angular samples for better ODF estimation. This is largely because of the incoherence of the angular samples generated when the diffusion signals are reoriented and warped to the target space. Experiments on both synthetic data and real data show that our method can reduce noise-induced artifacts, such as spurious ODF peaks, and yield more coherent orientations.

1. Introduction

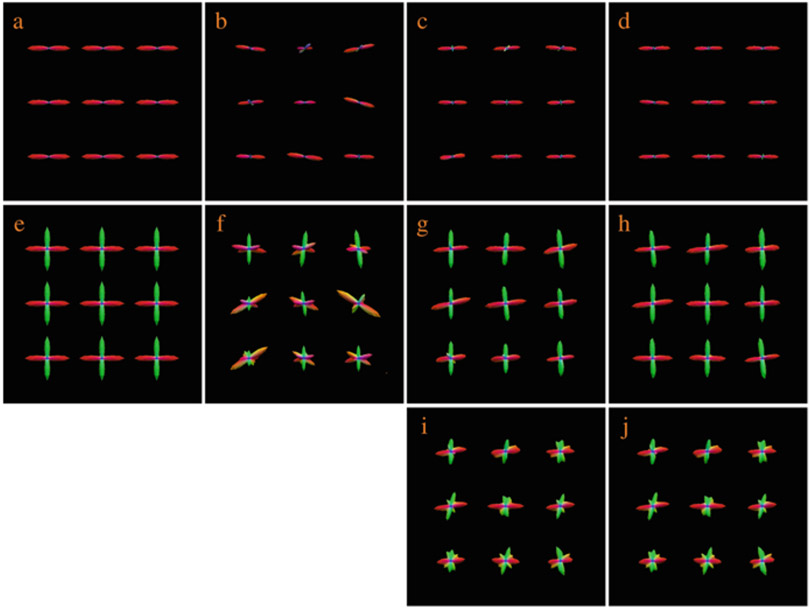
Diffusion magnetic resonance imaging (MRI) provides information on brain circuitry by observing the diffusion patterns of water molecules in the human brain. To trace the brain connections, diffusion tractography algorithms rely on information provided by local fiber orientations, which are often represented by a quantity called the orientation distribution function (ODF). Accurate ODF estimation is key to successful tractography. Precise tractography can be used to study the integrity and changes of white matter tracts in relation to development and disorders [1-8]. Two major factors affect the estimation of ODFs: (1) The number of diffusion-sensitizing gradient directions used to acquire the diffusion data, and (2) The signal-to-noise ratio (SNR) of the data. Figure 1 shows that ODF estimation improves when a sufficient number of gradient directions are used (top row), and gets worse with heavy noise (bottom row).

Fig. 1.

Influence of the number of gradient directions and noise on ODF estimation. (a) Ground truth. (b)–(e) ODFs estimated using 6, 21, 81, and 321 gradient directions with 9% noise. (f)–(i) ODFs estimated using 21 diffusion directions with 3%, 5%, 7%, and 9% noise. Gaussian noise (i.e. $\mathcal{N}(0,v(p∕100))$) is added in the complex domain of the signal, determined by the percentage p, where v is the maximum signal value (150 in our case)

Varentsova et al. [9] introduced a post-processing approach to increase the number of gradient directions for improving ODF estimation in an atlas. The key idea is to make use of the orientation incoherence of the diffusion signals when they are reoriented and warped to a common space. This incoherence is a direct result of the variation of brain shape and the position of the head when scanned. A major drawback of this approach is that only rotation is considered when reorienting the diffusion signals. We show that this deteriorates ODF estimation when transformations such as shearing are involved. This approach is also limited due to its implicit assumption that the images are perfectly aligned after spatial registration. This assumption almost never holds in the real-world scenario and will cause blurring of structures that are misaligned.

A number of methods for denoising the diffusion MRI data have been proposed [10, 11]. These methods are effective for enhancing the signal SNR, but to improve the ODF estimation, removing noise is not sufficient—another important aspect is to enhance angular resolution. In this paper we seek to better estimate ODFs by concurrent edge-preserving signal denoising and angular resolution enhancement. Inspired by our previous work in MRI denoising [12], we extend the non-local means (NLM) algorithm [13] to leverage both self and inter-subject similarity. The underlying assumption is that the possibility of finding repeating structures from a collection of scans of different individuals is higher than a single scan from the same individual. In transferring information from images of multiple individuals to the space of the target individual for denoising, we make available signals from incoherent gradient directions for improving ODF estimation. This is illustrated in Fig. 2, where we show that the effective number of gradient directions can be significantly increased by inter-subject information transfer. For this purpose, we propose a signal reorientation method that utilizes the full affine transform estimated locally from a non-linear deformation field. This differs from [9], which uses only the rotation component of the affine transform. Finally, we integrate both block-matching based denoising and angular resolution enhancement into a unified framework to improve ODF estimation.

Fig. 2.

Angular resolution enhancement using inter-subject information transfer. The green points on the sphere indicate the original gradient directions. Transferring incoherent samples from ten other images increases the effective number of gradient directions, as indicated by the red points

2. Method

2.1. Overview

Suppose we have a group of reference images acquired from different individuals (possibly also including the target individual), the goal is to improve ODF estimation for the target image with the help of the reference images. This is achieved in three steps: (1) block matching, (2) reorientation, and (3) ODF estimation. Each step is detailed below. See Fig. 3 for an overview.

Fig. 3.

Overview. Three components of our method: (1) block matching for identifying corresponding voxels from the reference images, (2) reorientation of the reference diffusion signals, and (3) ODF estimation

2.2. Block Matching

We first warp all the reference images to the target space. For each voxel in the target image, we then determine the matching voxels in the reference images via robust block matching, similar to that used in NLM [13]. A similarity weight is determined for each matching voxel and will be used for ODF estimation. NLM relies on repeating structures in an image. However, this might be challenging due to the complex anatomy of the human brain and fine unique structures might not find matching candidates. To address this issue, we extend NLM by performing block matching across images, significantly increasing the chance of finding similar structures. Gross misalignment between images is first dealt with using non-linear registration and residual misalignment is then overcome using block matching.

Let $\mathcal{N}({\mathbf{x}}_i)$ be a 3D block neighbourhood centered at ${\mathbf{x}}_i\in {\mathbb{R}}^3$. The size of $\mathcal{N}({\mathbf{x}}_i)$ is (2d + 1)³, where d is the neighborhood radius. Let ${\mathcal{V}}_k({\mathbf{x}}_i)$ be the search volume centered at x_i in reference image k. The size of ${\mathcal{V}}_k({\mathbf{x}}_i)$ is (2M + 1)³, where M is the search radius. Let u(x_i) be the intensity value at x_i, then $u(\mathcal{N}({\mathbf{x}}_i))$ is a vector that represents the intensity values of all voxels within $\mathcal{N}({\mathbf{x}}_i)$. The unnormalized weight, indicating similarity between the neighborhoods of a voxel, x_i, in the target image, and a voxel, ${\mathbf{x}}_j\in {\mathcal{V}}_k({\mathbf{x}}_i)$, in the reference image is computed as $w_{\text{NLM}}({\mathbf{x}}_i,{\mathbf{x}}_j)=\text{exp}\left\{-\frac{\Vert u(\mathcal{N}({\mathbf{x}}_i))-u(\mathcal{N}({\mathbf{x}}_j)){\Vert }_2^2}{h_i^2}\right\}$, where h_i controls the attenuation of the exponential function. Coupé et al. [14] suggested to set $h_i=\sqrt{2\beta {\widehat{\sigma }}_i^2\mid \mathcal{N}({\mathbf{x}}_i)\mid }$, where $\mid \mathcal{N}({\mathbf{x}}_i)\mid$ is the cardinality of $\mathcal{N}({\mathbf{x}}_i)$, β is a constant that is set to 1, ${\widehat{\sigma }}_i$ is an estimate of the standard deviation of the noise at x_i, which is spatial-adaptively estimated following the method described in [15].

For each voxel in the target image, block matching leads to a set of corresponding voxels and associated similarity weights in the reference images. Specifically, given x_i in the target, we have Ω(x_i) = ⋃_k{(S(q, x_j; k), $w_{\text{NLM}}({\mathbf{x}}_i,{\mathbf{x}}_j;k)){\}}_{{\mathbf{x}}_j\in {\mathcal{V}}_k}\cup \{(S(\mathbf{q},{\mathbf{x}}_i;0),1)\}$, where S(q, x_j; k), k > 0 is the diffusion-attenuated signal collected at x_j with wavevector q in the kth reference dataset, and S(q, x_i; 0) is the signal measured in the target dataset.

2.3. Reorientation

The diffusion signal S(q, x_j) in Ω(x_i) has to be reoriented before it can be used for ODF estimation. We note that the MR signal attenuation E(q, x_j) = S(q, x_j)/S₀(x_j), where S₀(x_j) is the base signal without diffusion-sensitizing gradient. Then, the ODF $\psi (\widehat{\mathbf{u}},{\mathbf{x}}_j,q^{\prime })$, contributed by the sampling shell with radius q′ in q-space can be computed as [16]

$$\psi (\widehat{\mathbf{u}},{\mathbf{x}}_j,q^{\prime })\approx \int E(\mathbf{q},{\mathbf{x}}_j)\delta ({\widehat{\mathbf{q}}}^{\mathrm{T}}\widehat{\mathbf{u}})\delta (\Vert \mathbf{q}\Vert -q^{\prime })\mathrm{d}\mathbf{q},$$ (1)

where $\widehat{\mathbf{q}}=\mathbf{q}∕\Vert \mathbf{q}\Vert$, $\widehat{\mathbf{u}}$ is a unit vector that represents a spatial direction, and δ(·) is the Dirac delta function. Given a local affine matrix A(x_j) computed at x_j, the integral of the ODF must be maintained after transformation

$$\int \psi (\widehat{\mathbf{u}},{\mathbf{x}}_j,q^{\prime })\mathrm{d}\widehat{\mathbf{u}}=\int \mid {\mathbf{A}}^{-1}({\mathbf{x}}_j)\Vert {\mathbf{J}}_{{\mathbf{A}}^{-1}({\mathbf{x}}_j)\widehat{\mathbf{u}}}\mid \psi \left(\frac{{\mathbf{A}}^{-1}({\mathbf{x}}_j)\widehat{\mathbf{u}}}{\Vert {\mathbf{A}}^{-1}({\mathbf{x}}_j)\widehat{\mathbf{u}}\Vert },q^{\prime }\right)\mathrm{d}\widehat{\mathbf{u}},$$ (2)

where ${\mathbf{J}}_{{\mathbf{A}}^{-1}({\mathbf{x}}_j)\widehat{\mathbf{u}}}$ is a transformation associated with $\widehat{\mathbf{u}}\to \frac{\widehat{\mathbf{u}}}{\Vert {\mathbf{A}}^{-1}({\mathbf{x}}_j)\widehat{\mathbf{u}}\Vert }$. After applying A⁻¹(x_j) to $\widehat{\mathbf{u}}$ on both sides of (1) and simplifying, we have

$$\begin{gathered} \mid {\mathbf{A}}^{-1}({\mathbf{x}}_j)\Vert {\mathbf{J}}_{{\mathbf{A}}^{-1}({\mathbf{x}}_j)\widehat{\mathbf{u}}}\mid \psi \left(\frac{{\mathbf{A}}^{-1}({\mathbf{x}}_j)\widehat{\mathbf{u}}}{\Vert {\mathbf{A}}^{-1}({\mathbf{x}}_j)\widehat{\mathbf{u}}\Vert },q^{\prime }\right)\approx \\ \int \underset{\text{Reoriented Signal Profile}}{\underbrace{E\left(\frac{{\mathbf{A}}^{\mathrm{T}}({\mathbf{x}}_j)\widehat{\mathbf{q}}}{\Vert {\mathbf{A}}^{\mathrm{T}}({\mathbf{x}}_j)\widehat{\mathbf{q}}\Vert }\Vert \mathbf{q}\Vert ,x_j\right)}}\delta ({\widehat{\mathbf{q}}}^{\mathrm{T}}\widehat{\mathbf{u}})\delta (\Vert \mathbf{q}\Vert -q^{\prime })\mathrm{d}\mathbf{q}, \end{gathered}$$ (3)

where ∣ · ∣ denotes the determinant and ∥ · ∥ is the ℓ₂ norm. If we let

$$\widehat{E}(\mathbf{q},{\mathbf{x}}_j)=E\left(\frac{{\mathbf{A}}^{\mathrm{T}}({\mathbf{x}}_j)\widehat{\mathbf{q}}}{\Vert {\mathbf{A}}^{\mathrm{T}}({\mathbf{x}}_j)\widehat{\mathbf{q}}\Vert }\Vert \mathbf{q}\Vert ,{\mathbf{x}}_j\right)\to \widehat{E}\left(\frac{{\mathbf{A}}^{-\mathrm{T}}({\mathbf{x}}_j)\widehat{\mathbf{q}}}{\Vert {\mathbf{A}}^{-\mathrm{T}}({\mathbf{x}}_j)\widehat{\mathbf{q}}\Vert }\Vert \mathbf{q}\Vert ,{\mathbf{x}}_j\right)=E(\mathbf{q},{\mathbf{x}}_j),$$ (4)

we can see that the reorientation involves transforming the signal measured at q, i.e., E(q, x_j), to $\frac{{\mathbf{A}}^{-\mathrm{T}}({\mathbf{x}}_j)\widehat{\mathbf{q}}}{\Vert {\mathbf{A}}^{-\mathrm{T}}({\mathbf{x}}_j)\widehat{\mathbf{q}}\Vert }\Vert \mathbf{q}\Vert$. The reoriented signal is hence $\widehat{S}(\mathbf{q},{\mathbf{x}}_j)=\widehat{E}(\mathbf{q},{\mathbf{x}}_j)S_0({\mathbf{x}}_j)$. We denote the reoriented version of Ω(x_i) as $\widehat{\Omega }({\mathbf{x}}_i)$.

2.4. ODF Estimation

To estimate the ODF at x_i, $\widehat{\Omega }({\mathbf{x}}_i)$ is decomposed into a linear combination of diffusion basis functions (DBFs). By dropping off x_i for simplicity, the decomposition is given by

$$S(\mathbf{q})=\sum _{j=0}^N{\alpha }_j{f}_j(\mathbf{q}\mid {\lambda }_1,{\lambda }_2,{\lambda }_3),$$ (5)

where α_j is the volume fraction associated with the jth tensor DBF f_j(·) and {λ₁, λ₂, λ₃} are the three eigenvalues of the tensor. The DBF is defined as $f_j(\mathbf{q}\mid {\lambda }_1,{\lambda }_2,{\lambda }_3)=\text{exp}(-t{\mathbf{q}}^{\mathrm{T}}{\mathbf{D}}_j\mathbf{q})=\text{exp}(-b{\widehat{\mathbf{q}}}^{\mathrm{T}}{\mathbf{D}}_j\widehat{\mathbf{q}})$, where D_j is a tensor defined by {λ₁, λ₂, λ₃} and principal diffusion direction μ_j, t is the diffusion time, and b is the diffusion weighting. For 1 ⩽ j ⩽ N, the tensors are anisotropic with principal diffusion directions distributed uniformly on a unit sphere. For j = 0, the tensor is isotropic to model free water diffusion. By representing each element of set $\widehat{\Omega }({\mathbf{x}}_i)$ as (s_n, w_n) and each DBF as a column of matrix F_n, we can solve for the volume fraction vector α = [α₀, … , α_N]^T using ℓ₁-penalized weighted least-squares [17]:

$$\underset{\alpha }{\text{arg}\text{min}}\left\{\sum _n{w}_n\Vert ({\mathbf{s}}_n-{\mathbf{F}}_n\alpha ){\Vert }_2^2+\gamma \Vert \alpha {\Vert }_1\right\}\text{s.t.}\alpha ⩾0,$$ (6)

where ∥ · ∥₁ is the ℓ₁-norm and γ ≥ 0 is a tuning parameter. F_n is the DBF matrix corresponding to s_n, computed based on its reoriented gradient directions. If no reorientation is applied, F_n is identical for all n. The ODF can then be computed as

$$\psi (\widehat{\mathbf{u}})=\frac{1}{S_0}\sum _{j=0}^N{\alpha }_j\varphi (\widehat{\mathbf{u}},{\mathbf{D}}_j).$$ (7)

When $\varphi (\widehat{\mathbf{u}},{\mathbf{D}}_j)=\frac{1}{4\pi Z}{\mid {\mathbf{D}}_j\mid }^{-\frac{1}{2}}({\widehat{\mathbf{u}}}^{\mathrm{T}}{\mathbf{D}}_j^{-1}\widehat{\mathbf{u}}{)}^{-\frac{1}{2}}$, with Z being the normalization constant, we have the diffusion ODF proposed by Tuch [16]. When $\varphi (\widehat{\mathbf{u}},{\mathbf{D}}_j)=\frac{1}{4\pi }{\mid {\mathbf{D}}_j\mid }^{-\frac{1}{2}}({\widehat{\mathbf{u}}}^{\mathrm{T}}{\mathbf{D}}_j^{-1}\widehat{\mathbf{u}}{)}^{-\frac{3}{2}}$, we have the constant-solid-angle diffusion ODF [18]. Finally, when $\varphi (\widehat{\mathbf{u}},{\mathbf{D}}_j)=\delta (\mid {\widehat{\mathbf{u}}}^{\mathrm{T}}{\widehat{\mathbf{v}}}_j\mid -1)$, with ${\widehat{\mathbf{v}}}_i$ being the eigenvector of D_j corresponding to the largest eigenvalue, we have the fiber ODF [19, 20].

3. Experiments

3.1. Data

Synthetic Dataset

A set of single pixel images were generated to evaluate the performance of our method in reconstructing ODFs from low angular resolution noisy data. Both single-direction and two-direction cases were considered. For the latter, the angular separation between two directions was set to 45° and 90°. Six ground truth images for these two cases were generated using 6 and 21 gradient directions. Ten reoriented images were generated for each ground truth image by applying affine transformations to the principal directions of the tensors. The affine transformations include random rotation ([−90°, 90°]) around the axis perpendicular to the image plane and shearing ([−0.5, 0.5]) within the image plane. Four levels of Rician noise (3%, 5%, 7% and 9%) were added to the ground truth image and the reoriented images. The noise-perturbed ground truth image was used as the target image and the noisy reoriented images were the reference images.

Real Dataset

The real dataset consists of diffusion-weighted (DW) images from 11 subjects. One subject was used as the target and the whole subjects as references. All images were acquired using a Siemens 3T TRIO MR scanner following a standard imaging protocol: 30 diffusion directions isotropically distributed on a hemisphere, b = 1000 s/mm², one image with no diffusion weighting, 128×128 imaging matrix, voxel size of 2 × 2 × 2 mm³, TE= 81 ms, TR= 7618 ms, 1 average.

3.2. Results

In all experiments, we set block radius d = 1 and search radius M = 2 for block matching and tuning parameter γ = 0.01 for sparse estimation. The number of reference images was 11, including the target image. The diffusivities of the anisotropic tensors λ₁, λ₂, λ₃ were estimated from the corpus callosum. Those of the isotropic tensor were estimated from the ventricles. A total of 321 orientations, generated by subdividing the faces of an icosahedron three times and discarding antipodal symmetric directions, were used as the principal diffusion directions of the DBFs.

For the synthetic dataset, we utilized our reorientation algorithm described in Sect. 2.3, we applied the affine transformation to the tensors in the reference images. For the real dataset, the reference DW images were registered to the target space by diffeomorphic demons [21] using the reference and target fractional anisotropy (FA) images, though other non-rigid registration algorithms [22] may be used. Based on the estimated deformation field, the reference DW images were warped to the target space using a DW spatial warping method [17]. The warped reference DW images were then used for multi-channel block matching with respect to the target DW images.

For quantitative evaluation, Orientational Discrepancy (OD) measure [23] was used. OD is a measure of the angular difference between two sets of directions. After calculating the ODFs for the diffusion MRI data, the ODF peaks were detected following the method described in [17] and then the resulting peaks were compared with the ground truth using OD as the metric. We repeatedly generated the synthetic data and ran the experiment 900 times. The mean and standard deviation of OD values were reported.

Figure 4 shows that our method significantly reduces the mean OD on the two-direction crossing synthetic data. The small mean OD indicates that the estimated peaks are close to the ground truth. Compared with the results given by using the target image only, the maximum improvement is 26.81° when the noise level is 9 %. This is for the case of 6 gradient directions, where each pair of directions are separated by an angle of 90°.

Fig. 4.

Average OD comparison using two-direction synthetic data. Three cases were compared: (1) using only the target image; (2) using the proposed method; and (3) using the proposed method but only rotation was used for reorientation. Four noise levels and two sets of gradient directions were involved. The error bars indicate the standard deviations. For the proposed method, ten reference images were used

The ODF glyphs are shown for visual inspection in Fig. 5. The estimated ODF glyphs look very similar to the ground truth. We ran the same experiment by performing only rotation for reorientation, as done in [9]. The results, shown in Fig. 5, indicate that this will cause spurious peaks that are not observed in the ground truth. The superiority of our method over the rotation-only approach is confirmed in Fig. 4.

Fig. 5.

Comparison of ODFs. (a) and (e) Ground truth ODFs. (b) and (f) ODFs estimated using only the target, which was generated using 5% noise and six gradient directions; (c) and (g) ODFs estimated using the proposed method with five reference images. (d) and (h) ODFs estimated using the proposed method with ten reference images. (i) and (j) Results when only rotation was used for reorientation

For the real data, the ODFs are shown in Fig. 6. We can observe that the ODFs estimated using the target alone and with the reference images but without block matching exhibit spurious peaks. The ODFs are also not as coherent as those estimated using the proposed method.

Fig. 6.

ODF results for the real data. (Far left) Reference FA image. ODFs estimated using (left) the target dataset only, (middle) 11 reference images but without block matching, and (right) the proposed method with 11 reference images

Tractography results, shown in Fig. 7, indicate that the proposed method gives cleaner and richer fiber tracts compared with the other two methods. When block matching is not used, a significant amount of fiber tracts are missing. The proposed method gives fuller and smoother fiber tracts.

Fig. 7.

Tractography. Three representative sets of tractography results using (Left) the target dataset only, (Middle) the proposed method without block matching, and (Right) the proposed method. The fiber bundles are extracted using different ROIs, including CCtoM1: precentral gyrus and corpus callosum, CST: precentral gyru and posterior limb of the internal capsule, FMAJOR: occipital cortex and corpus callosum

4. Conclusion

We have proposed a method for improving ODF estimation by using correlated information between subjects. Information from multiple reference datasets is used to simultaneously remove noise and to enhance angular resolution. Extensive experiments on both synthetic and real data show improved ODF estimation, despite using noisy data with insufficient angular sampling. Further validation on tractography performance demonstrates the efficacy of our approach in reconstructing clean and rich fiber tracts.