A machine learning regression model for the screening and design of potential SARS-CoV-2 protease inhibitors

Abstract

The widespread infection caused by the 2019 novel corona virus (SARS-CoV-2) has initiated global efforts to search for antiviral agents. Drug discovery is the first step in the development of commercially viable pharmaceutical products to deal with novel diseases. In an effort to accelerate the screening and drug discovery workflow for potential SARS-CoV-2 protease inhibitors, a machine learning model that can predict the binding free energies of compounds to the SARS-CoV-2 main protease is presented. The optimized multiple linear regression model, which was trained and tested on 226 natural compounds demonstrates reliable prediction performance (r² test = 0.81, RMSE test = 0.43), while only requiring five topological descriptors. The externally validated model can help conserve and maximize available resources by limiting biological assays to compounds that yielded favorable outcomes from the model. The emergence of highly infectious diseases will always be a threat to human health and development, which is why the development of computational tools for rapid response is very important.

Supplementary Information

The online version contains supplementary material available at 10.1007/s13721-021-00326-2.

Introduction

The corona virus disease of 2019 (COVID-19) caused by the 2019 novel corona virus (SARS-CoV-2) that was first reported in Wuhan, China, has already reached pandemic levels. It is a global health concern that has claimed thousands of lives and requires urgent interventions to control the situation. The efficient transmission of the disease as well as its ability to kill healthy adults have necessitated for the accelerated development of vaccines and drugs that can combat the virus (Gates 2020). Several vaccines have already been granted emergency use authorization in multiple countries (Terry 2021). However, for developing countries, vaccine distribution is accompanied by problems in supply, storage and logistics (Callaway 2020). The urgency of the matter has led to the repurposing of approved drugs to be administered for the management of COVID-19 patients (Li and de Clercq 2020). Consequently, the World Health Organization (WHO) initiated a large global trial called Solidarity, which aims to determine if available drugs are capable of treating COVID-19 (Kupferschmidt and Cohen 2020). Another viable strategy for developing antiviral drugs against SARS-CoV-2 is searching for natural products that can inhibit key processes in the viral life cycle. Natural products are ideal sources to be considered since they are readily available and looking into their activities against the virus can help identify promising leads much faster. Moreover, promising natural products may be derivatized into more potent antiviral agents, thereby shortening the design phase in the drug discovery process (Rastelli et al. 2020).

The characterization of the SARS-CoV-2 main protease (Jin et al. 2020) is a significant step forward for the discovery and development of antiviral drugs since this enzyme plays a key role in viral replication and transcription. Studies have, therefore, emerged that dock compounds to the binding site of the SARS-CoV-2 protease to visualize binding interactions and determine the binding affinity of the docked compounds onto the protein (Aanouz et al. 2020; Das et al. 2020; Ton et al. 2020). However, docking simulations can be hardware-intensive and time consuming, especially if the simulations are to be validated by molecular dynamics simulations (Chen 2015). On the other hand, experimental assays for candidate compounds can be demanding to the availability of resources and personnel. Mathematical models are key components in the chemical product design (CPD) and computer-aided molecular design (CAMD). For CPD, models are often used in identifying product candidates which can be further analyzed and prototyped (Zhang et al. 2020). For CAMD, models serve as guide on how the molecule can be modified or synthesized to reach or enhance the desired properties (Mapari and Camarda 2020).

In an effort to accelerate the drug candidate discovery workflow for the SARS-CoV-2, a machine learning model that predicts the binding free energy of compounds was constructed in this study. This model can be utilized to reduce dependence of screening endeavors on hardware-demanding tasks, such as docking and molecular dynamics simulations, as well as for both CPD and CAMD applications. Furthermore, it would allow rapid screening and identification of compounds as potential SARS-CoV-2 protease inhibitor. From a CAMD perspective, the model can also guide attempts on molecular modifications that can increase the binding affinity of lead compounds toward the viral enzyme. In addition, the model may catalyze the design of a process for the commercial-scale synthesis of identified compounds.

Methodology

Dataset

The list of compounds and their binding free energy (BFE) towards the SARS-CoV-2 main protease (PDB ID: 6LU7) were taken from Yan et al. (2020), and Gentile et al. (2020). The first set of compounds are from Chinese Patent Drugs which have established their role in treating respiratory diseases in China. The second set of compounds are marine natural products with an excellent binding with the target protein SARS-CoV-2 MPro. In total, there are 226 compounds that were converted into their corresponding SMILES format. Thereafter, their corresponding 230 chemical descriptors were calculated using the “rcdk” R package (Guha 2007). These molecular descriptors are the independent variables or predictor variables, while the binding free energy is the dependent variable or outcome variable. The resulting data set serves as the input features for the regression models. The dataset is available in the supporting information.

Reduction of molecular descriptors

Filtering of the molecular descriptors was first done by setting thresholds for variance, Pearson correlation, and % of zero values. Through the r function “nearZeroVar”, predictors with near zero variance or less than 10% unique values were removed. These are descriptors with only 1 or 2 values all throughout the data set. Next, highly correlated predictors were removed, wherein variables with at least 0.90 Pearson correlation coefficient were eliminated. A built-in R function called "cor" was used. The last threshold was set for % of zero values wherein variables with at least 75% zero values were removed.

The resulting dataset was further subjected to lasso regression as the feature selection method. Lasso (Least Absolute Selection and Shrinkage Operator) regression imposes constraints on the sum of the absolute values of the model parameters resulting to the shrinkage of some coefficients to zero. Thus, variables with strong associations with the outcome variable are identified. Sixty percent of the data was used to train the model followed by tenfold cross-validation using the “caret” package (Kuhn 2008). Lasso regression was performed using the package “glmnet”. Diagnostic tests were performed using the R package “olsrr” (Hebbali 2017).

Selection of appropriate machine learning algorithm for regression

Using “caret” package in R, the data set was subjected to the create regression models based on the following algorithms: support vector regression (SVR), classification and regression trees (CART), random forest, and multiple linear regression (MLR). Model performance was evaluated using the coefficient of determination (R²), and the root mean square error (RMSE).

External validation

The optimized regression model was externally validated using studies that employed Autodock Vina as the docking platform and the 6LU7 protease as the receptor. The binding free energies of compounds from these studies were predicted using the optimized regression model. Compounds that appeared in the training and testing sets were excluded in the external validation set.

Results and discussion

Reduction of molecular descriptors

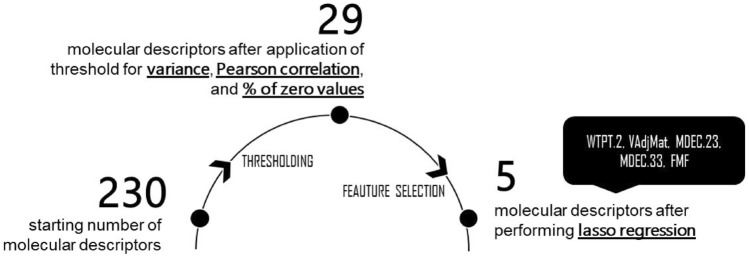
The starting data are composed of 226 natural products compounds. Each compound has 230 molecular descriptors, which are the independent variables or predictors. Upon removing predictors that did not meet the Pearson correlation, variance, and % zero values threshold, the molecular descriptors were reduced to 29. Feature selection with data splitting and tenfold cross-validation were used to come up with fewer and better sets of predictor variables. Smaller number of predictors is desirable to have a simple model and to prevent overfitting. 137 compounds were grouped as the training set, and the remaining 89 compounds as the test set. Lasso regression narrowed down the molecular descriptors to WTPT.2 (molecular ID/number of atoms), VAdjMat (vertex adjacency information magnitude), MDEC.23 (molecular distance edge between all secondary and tertiary carbons), MDEC.33 (molecular distance edge between all tertiary carbons), and FMF (fraction of size of Murcko framework versus the size of the whole molecule). In the training data, lasso regression had an R² of 0.838 and RMSE of 0.518. For the testing data, the R² was 0.743 and the RMSE was 0.578. The regression model has a good coefficient of determination (R²) values in the training and testing sets denoting that the selected molecular descriptors are able to explain more than 70% of the binding free energies (Fig. 1).

Fig. 1.

Narrowing down the number of molecular descriptions by applying thresholds and feature selection to achieve a parsimonious model

Examination of lasso regression assumptions

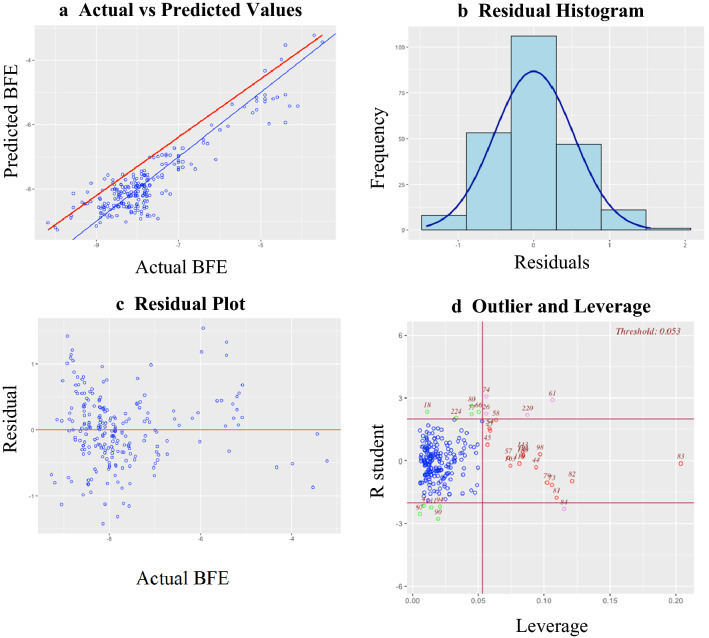
To further assess the set of variables selected by lasso regression for model building, diagnostic tests were run using the "olsrr" package. Figure 2 shows the diagnostic plots generated. The model was linear (Fig. 2a) and had normally distributed residuals indicated by the bell shape curve centered at 0 (Fig. 2b). Normality of residuals was further assessed using the Shapiro–Wilk test. Lasso regression had a test statistic of 0.9932 and a p value of 0.3913. The p value is greater than 0.05, meaning the null hypothesis is not rejected and thus, lasso regression has normally distributed residuals. The residual plots of the model as seen in Fig. 2c had a scattered pattern indicating homoscedasticity. However, some of the data points were very far from the 0-line suggesting that there were outliers. Using the outlier and leverage plot in Fig. 2d, the influential points had been pinpointed. Breusch Pagan test was also performed to further justify the homoscedasticity. In the lasso regression model, the chi square test statistic was 0.00548, which was very small, and the p value for the chi square statistic was 0.941, far greater than 0.05. Thus, the null hypothesis was not rejected, and the lasso regression model was considered homoscedastic. In Table 1, the variance inflation factor (VIF) of all variables were less than 5 and their tolerance were all greater than 0.10. This means that there was no severe multicollinearity in the variables of the lasso regression model.

Fig. 2.

Results of diagnostics performed on the lasso regression model using the “olsrr” package. a The actual vs predicted values plot shows if the model is linear and how well the data points fit the regression line. b Residual histogram checks if the residuals are normally distributed. c The residual plot shows if the model is homoscedastic. d Outlier and leverage plot detects the observations influencing the model. Blue points are normal, red points are leverages, green points are outliers, and pink points are both outliers and leverages

Table 1.

Computed VIF and tolerance for each of the five molecular descriptors selected by lasso regression

Variables	Tolerance	VIF
WTPT.2	0.260	3.842
VAdjMat	0.501	1.996
MDEC.23	0.538	1.859
MDEC.33	0.762	1.313
FMF	0.303	3.303

Variance inflation factor (VIF) and tolerance are metrics to detect multicollinearity

In summary, lasso regression exhibited linearity, homoscedasticity, normality, and had no severe multicollinearity. All of the assumptions of linear regression were met. Thus, WTPT.2, VAdjMat, MDEC.23, MDEC.33, and FMF are the molecular descriptors that were used in predictive model.

Selection of machine learning algorithm

Four machine learning algorithms were compared to find the best predictive model, multiple linear regression (MLR), support vector regression (SVR), classification and regression trees (CART), and artificial neural networks (ANN). For each machine learning algorithm, two models were generated. Both had the same predictor variables namely: WTPT.2, VAdjMat, MDEC.23, MDEC.33, and FMF. The first model entries made use of all 226 compounds in the data set. The second model entries utilized a refined data set composed of 203 compounds. In the refined data set, 23 outliers, high leverage, and outlier and high leverage data points were removed based on the outlier and leverage diagnostic plot in Fig. 2d. All models exhibited satisfactory predictive ability in terms of the r-squared and the RMSE for both training and test sets as shown in Table 2. In determining the best model, comparing the training set performance alone may be misleading because of overfitting. This was the case with the CART model, which had an exemplary performance in the training set. However, when it was run in the testing set, it was not able to perform at the same exemplary level. This suggests that the CART model was overfitted. Upon examination of the model performances, the refined multiple linear regression model stood out. It had a good performance in the training set, and the best performance in the testing set. Furthermore, it had the most consistent RMSE. MLR is easy to implement and has a strong theoretical foundation. Out of the four machine learning algorithms, MLR is the simplest and the only one considered as interpretable (Kaur et al. 2020). SVR, CART, and ANN are all black box models, which have input-to-output implementations that are not fully explainable (Rudin 2019). Thus, MLR was deemed as the best model.

Table 2.

Summary of prediction performance of the machine learning models

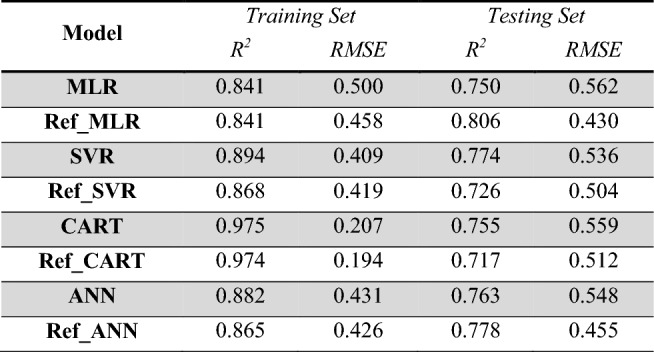
Gray-shaded rows used the original dataset composed of 226 compounds. White rows used the refined dataset composed of 203 compounds

The predictive regression model

The refined MLR model assumed the form of:

$$\begin{array}{cc}\hfill \widehat{\text{BFE}}& =-2.2378\left(\text{WTPT}.2\right)-1.1727\left(\text{VAdjMat}\right)+0.00028\left(\text{MDEC}.23\right)\hfill \\ \hfill & -0.0122\left(\text{MDEC}.33\right)-1.5875\left(\text{FMF}\right)+5.1811\text{.}\hfill \\ \hfill \end{array}$$

Larger values of WTPT.2, VAdjMat, MDEC.33, and FMF would make the Binding Free Energy (BFE) more negative and, thus, more favorable to bind with the SARS-CoV-2 MPro. Out of the five predictor variables, WTPT.2 had the greatest contribution to the model because it had the largest coefficient. WTPT.2 is dependent on molecular ID, which is unique for each molecule yet conveys structural significance. This underscores the importance of molecular structure which is consistent with the accepted knowledge about host–guest interaction.

WTPT.2 is a weighted path descriptor equal to molecular ID/ number of atoms. The molecular ID is based on Randic’s molecular IDs (Randic 1984). Molecules with longer chains and more ring structures would have larger molecular IDs, but their number of atoms would also increase. So, the value of WTPT.2 is more or less steady. VAdjMa is the vertex adjacency information magnitude with the formula 1 + log2 (m), wherein m is equal to the number of heavy–heavy bonds. A bond is considered a heavy–heavy bond if it is between two non-hydrogen atoms. Larger molecules would have a greater number of m, but this increase in m imparts a very slow increase in VAdjMat because of the logarithm function. MDEC.23 and MDEC. 33 are both based on the molecular distance edge (MDE) operators of Liu et al. (1998). MDEC.23 calculates the MDE between all secondary and tertiary carbons, while MDEC.33 calculates the MDE between all tertiary carbons. Consequently, branched and substituted molecules would have a higher MDEC. FMF is a ratio of the heavy atoms in the Murcko framework and the heavy atoms in the molecular structure (Yang et al. 2010). The Murcko framework is composed of ring structures and linker atoms connecting cyclic moieties with each other (Bemis and Murcko 1996). Aliphatic molecules do not have a Murcko framework so their FMF is 0. Cyclic and aromatic structures are then favorable structures to increase the FMF. Therefore, based on the interpretations of the model’s molecular descriptors, large hydrophobic molecules, specifically substituted cyclic molecules would have a high affinity with the SARS-CoV-2 main protease (PDBID: 6LU7).

This model trend was consistent with the properties of the SARS-CoV-2 main protease active site. It is composed of four subsites: S1, S1′, S2, and S4 (Yang et al. 2005). The S1 pocket is capable of both hydrogen bonding and accommodating bulky rings like lactam structures. S1’ houses a cysteine residue. S2 subsite is characterized as a deep hydrophobic pocket that can accommodate large residues. S4 is also a hydrophobic pocket but smaller than S2. Thus, hydrophobic interactions at the active site play a significant role in binding, explaining why the model predicted a more favorable binding with cyclic substituted molecules.

External validation

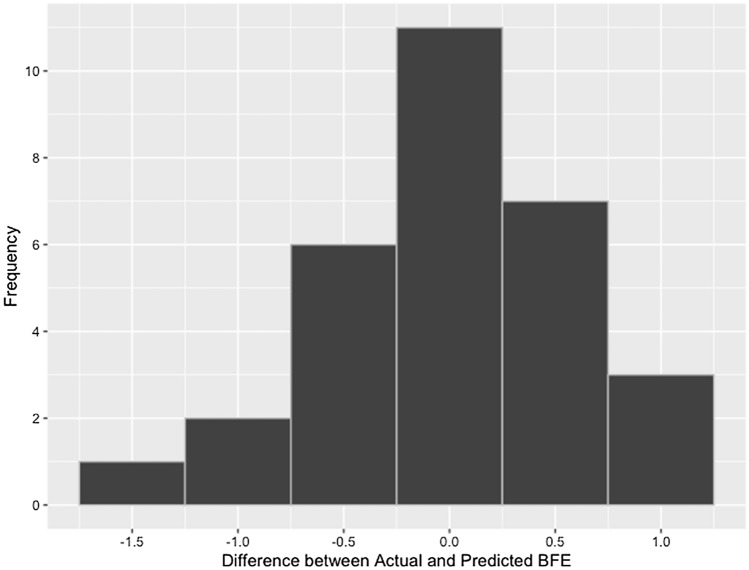
The performance of the MLR model was further assessed by conducting external validation, as summarized in Table 3. The model performed well, wherein the difference between the actual and predicted values ranged from − 1.37 to 1.11; while the percentage errors were between 0.58 and 16.01%. As shown in Fig. 3, the bulk of the externally validated data had only ± 0.75 difference from the actual BFE. The results of the external validation highlighted the robustness of the formulated model, since the compounds used for validation came from three independent studies (Farabi et al. 2020; Khaerunnisa et al. 2020; Prasanth et al. 2020), with differences in the manner in which the docking simulations were conducted.

Table 3.

Results of the external validation. References for the reported BFE: compounds 1–7 (Farabi et al. 2020), compounds 8–17 Khaerunnisa et al. 2020, compounds 18–30 Prasanth et al. 2020

	CAS no.	Compound name	Reported BFE	Predicted BFE	Difference	% error
1	154-23-4	Catechin	− 7.24	− 7.19	− 0.05	0.68
2	39728-80-8	Zingerol	− 5.40	− 5.52	0.12	2.19
3	539-86-6	Allicin	− 4.03	− 3.65	− 0.38	9.41
4	520-18-3	Kaempferol	− 8.58	− 7.21	− 1.37	16.01
5	480-41-1	Naringenin	− 7.89	− 7.17	− 0.72	9.10
6	22608-11-3	Demethoxycurcumin	− 7.99	− 7.21	− 0.78	9.73
7	4670-05-7	Theaflavin	− 9.00	− 8.77	− 0.23	2.51
8	480-10-4	Astragalin	− 8.80	− 7.99	− 0.81	9.25
9	21637-25-2	Isoquercitrin	− 8.70	− 7.97	− 0.73	8.40
10	482-36-0	Hyperoside	− 8.60	− 8.02	− 0.58	6.73
11	81-27-6	Sennoside A	− 8.30	− 8.80	0.50	6.08
12	1415-73-2	Aloin A	− 8.20	− 7.89	− 0.31	3.76
13	38953-85-4	Isovitexin	− 8.00	− 7.93	− 0.07	0.85
14	3463-92-1	Carpaine	− 7.90	− 8.04	0.14	1.80
15	529-92-0	Cusparine	− 7.90	− 7.70	− 0.20	2.58
16	54983-96-9	Piperitol	− 7.80	− 8.00	0.20	2.54
17	520-36-5	Kaempferol	− 7.80	− 7.17	− 0.63	8.05
18	6750-60-3	Spathulenol	− 6.60	− 6.54	− 0.06	0.85
19	83-48-7	Stigmasterol	− 7.10	− 7.46	0.36	5.03
20	925213-53-2	Subamolide A	− 5.50	− 6.11	0.61	11.05
21	530-57-4	Syringic_acid	− 5.50	− 5.53	0.03	0.58
22	21453-69-0	Lirioresinol B	− 7.40	− 7.75	0.35	4.74
23	12798-57-1	Procyanidin-B5	− 7.70	− 8.81	1.11	14.41
24	607-80-7	Sesamin	− 7.60	− 8.32	0.72	9.54
25	485-19-8	Reticuline	− 7.00	− 7.27	0.27	3.86
26	65230-04-8	Anhydrocinnzeylanine	− 6.60	− 7.16	0.56	8.56
27	523-80-8	Apiole	− 5.40	− 6.25	0.85	15.78
28	499-75-2	Carvacrol	− 5.30	− 5.27	− 0.03	0.60
29	87-44-5	Caryophyllene	− 6.20	− 6.33	0.13	2.15
30	23953-63-1	Carpacin	− 5.40	− 6.16	0.76	14.04

Fig. 3.

Distribution of differences between actual and predicted BFE

A QSAR model for SARS-CoV-2 main protease inhibitor, built on 40 compounds, reported that the topological surface area, molecular weight, XLogP, hydrogen bond donors, hydrogen bond acceptors descriptors were needed to create the model that exhibited r² test = 0.753 (Islam et al. 2020). Another model, constructed from 25 compounds, utilized solute hydrogen bond acidity, mordred autocorrelation, molecular distance edge, and two fingerprint descriptors: unsaturated non-aromatic heteroatom-containing ring size 6, and O=C–C–C–C–C–N, this model had r² = 0.944 (Amin et al. 2021). Thus, the presented regression model introduces new variables that can predict the binding interaction of compounds with the viral enzyme. Furthermore, the multiple linear regression model built in this study was formulated using at least 200 compounds. Some of the relevant MLR models have so far utilized 100 compounds or less (Amin et al. 2021; De et al. 2020; Ghosh et al. 2021; Kumar and Roy 2020). Deep learning and other machine learning models can screen bigger number of compounds, but they lack interpretability, which highlights the simplicity, transparency and interpretability of MLR models. The key point of the MLR model is the formulated equation of the line, which contains all the information needed to predict and explain the results. The MLR model therefore has transparency in the model building steps and interpretability of the results, both of which are not present in black box models. The parsimonious machine learning model built in this study is targeted towards chemical product design (CPD) and computer-aided molecular design (CAMD) applications. The model can be used to guide attempts on molecular modifications that can increase the binding affinity of lead compounds toward the viral enzyme. In addition, the formulated regression model may catalyze the design of a process for the commercial-scale synthesis of identified compounds.

Conclusion

A multiple linear regression that can accurately predict the binding free energies of compounds towards the SARS-CoV-2 main protease was presented. During the model building process, the performances of MLR, SVR, CART, and ANN were compared. The one with the best performance was the MLR model with an r² test = 0.81 and RMSE test = 0.43. The regression model utilized five topological descriptors, WTPT.2, VAdjMat, MDEC.23, MDEC.33, and FMF, and was thoroughly validated. Based on the model, large, substituted, cyclic molecules have high affinity towards the SARS-CoV-2 main protease. Moreover, since the outcome of the model is an estimate of the binding free energy, systematic molecular modifications can be carried out to increase the affinity of the candidate compounds to the target protein. The parsimony and reliability of the formulated regression model can potentially accelerate the discovery and development of protease inhibitors.

Supplementary Information

Below is the link to the electronic supplementary material.

Funding

This work was supported by Department of Science and Technology—Science Education Institute Accelerated Science and Technology Human Resource Development Program—National Science Consortium (DOST-SEI ASTHRDP-NSC).

Declarations

Conflict of interest

None.