Skip to main content
PMC home page
Sensors (Basel, Switzerland) logoLink to Sensors (Basel, Switzerland)
. 2021 Jul 13;21(14):4781. doi: 10.3390/s21144781

An Approximation for Metal-Oxide Sensor Calibration for Air Quality Monitoring Using Multivariable Statistical Analysis

Diego Sales-Lérida 1,*, Alfonso J Bello 2, Alberto Sánchez-Alzola 2, Pedro Manuel Martínez-Jiménez 1
Editors: Klaus Schäfer, Matthias Budde
PMCID: PMC8309700  PMID: 34300517

Abstract

Good air quality is essential for both human beings and the environment in general. The three most harmful air pollutants are nitrogen dioxide (NO2), ozone (O3) and particulate matter. Due to the high cost of monitoring stations, few examples of this type of infrastructure exist, and the use of low-cost sensors could help in air quality monitoring. The cost of metal-oxide sensors (MOS) is usually below EUR 10 and they maintain small dimensions, but their use in air quality monitoring is only valid through an exhaustive calibration process and subsequent precision analysis. We present an on-field calibration technique, based on the least squares method, to fit regression models for low-cost MOS sensors, one that has two main advantages: it can be easily applied by non-expert operators, and it can be used even with only a small amount of calibration data. In addition, the proposed method is adaptive, and the calibration can be refined as more data becomes available. We apply and evaluate the technique with a real dataset from a particular area in the south of Spain (Granada city). The evaluation results show that, despite the simplicity of the technique and the low quantity of data, the accuracy obtained with the low-cost MOS sensors is high enough to be used for air quality monitoring.

Keywords: air quality, metal-oxide sensor, monitoring, multivariable regression models, model calibration

1. Introduction

Good air quality is essential for both humanity and the natural environment. Economic activities such as energy production, industry and agriculture, as well as the dramatic rise in traffic, release air pollutants into the environment that can lead to serious problems for our health [1]. In fact, the poor quality of air is the cause of more than 400,000 premature deaths in Europe each year, as well as a decrease in quality of life by causing or exacerbating asthma and respiratory problems [2,3].

There are several pollutants involved in air quality characterization, such as SOx, CO, NOx, O3, or particulate matter pollution [4,5]. From all of them, three of the most harmful air pollutants, in terms of damage to ecosystems, are nitrogen dioxide (NO2), ozone (O3) and particulate matter (specifically PM2.5, which is directly related to traffic) [6,7,8,9]. Thus, it is very important to monitor and analyze these elements in the air, especially in towns and cities, in order to detect dangerously high levels and take actions to reduce pollution [10,11].

In this regard, several agencies around the world are responsible for the air quality monitoring of their corresponding regions, such as the European Environment Agency (EEA) in Europe, or the Environmental Protection Agency (EPA) in the United States. Their data give relevant and reliable information to policymaking agents [12]. In particular, the use of air quality models to assess the potential changes in urban air quality concentrations is a fundamental element of air quality management. In this type of modeling, the input data require high spatio-temporal resolution to capture the variability in the urban environment. However, one of the main technical difficulties nowadays is the lack, or low quality, of input data on concentrations [13]. Due to the high cost of monitoring stations, only a few examples of this type of infrastructure have been deployed in cities, providing limited spatial coverage [14].

In order to address this problem, recent environmental agencies’ reports suggest that cities should participate in the input data acquisition, complementing official monitoring data with additional measurements of local air quality [13]. In this sense, the cities are increasingly aware of the potential for low-cost ‘citizen science’ sensors to help support the results of their air quality modeling [15,16]. These sensors offer air pollution monitoring at a lower cost and smaller size than conventional methods, making it possible for them to be installed in many more locations [17,18,19]. However, the accuracy of input data in air quality modeling is as important as the quantity of measures. Thus, the use of citizen science and citizen participation in air quality monitoring by means of these low-cost sensors is only feasible if they can provide accurate information [20,21].

Currently, the three most popular types of low-cost air quality sensors are electrochemical sensors (EC), metal-oxide sensors (MOS) and photoionization detectors (PID) [22,23]. Since the objective is to achieve the widest possible distribution of air monitoring sensors in cities, their price is an essential factor. In this sense, the cost of EC and PID sensors is prohibitive for most consumers (they can cost more than EUR 100). On the contrary, the cost of MOS sensors, which are usually below EUR 10, as well as their small dimensions, make them an excellent option for use by citizens [24,25]. However, it should be noticed that, in air quality monitoring, the pollutant concentration that sensors should capture is usually very small: in the order of parts per billion (ppb) or “μg/m3”. In this sense, the World Health Organization (WHO) casts some doubts on the reliability of low-cost sensors when the calibration methods provided by manufacturers are employed, because these methods may be questionable regarding very low concentrations [26]. Thus, the WHO, as well as the EEA [10], only recommends the use of these devices for air quality monitoring through an exhaustive calibration process and subsequent precision analysis [27,28].

In most of the works in the literature, sensor calibration is performed under laboratory conditions [29,30,31]. In this type of approach, controlled environments are created by injecting known concentrations of the specific pollutants to be measured. However, in these ideal laboratory conditions, other variables that are present in real environments are not taken into account. On the one hand, there could be particles of other components that are different from the pollutants to be measured in the specific region where the sensors should be used which are not considered in a laboratory. On the other hand, although other environmental factors in the specific region can be simulated in a laboratory, such as the temperature and relative humidity of the air, they may differ from the actual conditions [32].

In order to face these problems, several on-field calibration techniques have been proposed in the literature [33,34,35,36], which are based on the data obtained from the monitoring stations of the regional government agencies. This way, sensors are calibrated using the specific environmental conditions of the region where they will be used, and are, therefore, adapted to its temperature, humidity and air composition. In most of these works, the proposed calibration techniques are complex and not very intuitive, and they are applied by experts in the field. In addition, in those studies, a large amount of calibration data is available from sensors, since they have been placed close to the reference monitoring stations for long periods of time. However, we should remember that the objective of these low-cost sensors is the use of citizen science and citizen participation in air quality monitoring. Thus, in real situations, the sensors will be calibrated by field workers who are usually not so expert in applying complex techniques, and the available data for calibration may be limited, since locations close to monitoring stations cannot be used for long periods of time.

In this work, we present an on-field calibration technique for low-cost MOS sensors that tries to solve both problems commented on above: it can be easily applied by non-expert operators, and it can be used even with only a small amount of calibration data. The proposed technique is based on the well-known regression analysis tool [37,38,39], which is widely used for data modeling in a great variety of fields. In our approach, we have studied the different kinds of regression techniques in the literature, and we have selected the most appropriate one, taking into account the number of independent variables, the type of dependent variables and the shape of the regression curve. We apply and evaluate this technique with a real dataset from a particular area in the south of Spain (Granada city). The training and test data were used to fit and validate the model, respectively, using the R software [40]. The evaluation results show that, despite the simplicity of the technique and the low quantity of data, the accuracy obtained with the low-cost MOS sensors is high enough to be used for air quality monitoring. In addition, the proposed method is adaptive, in the sense that the calibration can be refined as more data become available.

The rest of the paper is organized as follows. In Section 2, we briefly present the sensors that are usually employed to measure the air pollutant concentrations, giving more details to the low-cost MOS used in this work, we describe and analyze the dataset used to validate the calibration technique, and we explain the calibration methodology. In Section 3, we apply this methodology to fit the pollutant concentrations corresponding to ozone (O3), nitrogen dioxide (NO2) and carbon monoxide (CO). The obtained results are statistically studied and discussed in Section 4, while Section 5 contains the main conclusions of this paper.

2. Material and Methods

2.1. Sensors

Before going into details about the sensors used in this work to measure air pollutant concentrations, we should clarify that the unit selected to express these concentrations will be “μg/m3” because this is the form used by the European Commission for regulation in the European framework.

The European air quality standards set by the Ambient Air Quality Directive (EU, 2008) for the protection of human health [41], the air quality guidelines (AQGs) set by the World Health Organization (WHO) [42], and their subsequent revisions, define several aspects of values for the different pollutants, like typical qualitative levels, the averaging period, the time by which limit values can be overcome in a year, or alert values. In Spain, there are certain laws that refer to these standards; the most recent of their revisions were passed on 28 January 2011 in the form of the directive RD102/2011. Table 1 shows some of its aspects.

Table 1.

Qualitative levels as referred to for the quantitative levels of each pollutant, and the averaging period used in each of them, following the European EEA standards.

Qualitative
Index		 SO2 μg/m3
(24 h Average Value)		 O3 μg/m3
(8 h Average Value)		 NO2 μg/m3
(1 h Average Value)		 CO μg/m3
(8 h Measured Value)		 PM10 μg/m3
(24 h Measured Value)
Good 0–63 0–60 0–100 0–5000 0–25
Moderate 63–125 60–120 100–200 5000–10,000 25–50
Poor 125–187 120–180 200–300 10,000–15,000 50–75
Very Poor >187 >180 >300 >15,000 >75
Open in a new tab

As mentioned in Section 1, in this study we have proposed the use of MOS sensors, since they are the most accessible to users from an economic point of view. These sensors are composed of a semiconductor layer, generally, tin dioxide (SnO2), which makes them especially sensitive to other oxides, and, by controlling the doping of the semiconductor, it is possible to make the material more sensitive to certain parameters. Therefore, when there are higher concentrations of these parameters in sampled air, the conductivity of this layer changes its values. It is worth mentioning that this conductivity keeps a direct relation with temperature, and, in general terms, they change in a proportional form. In addition, it should be noticed that, after a certain temperature, the sensibility to target gases can decrease, negatively affecting the quality of sensor detection. To take advantage of this property, electrodes are inserted into the detection layer of the sensor in order to increase its temperature in a controlled way (by using a heating circuit, such as a voltage divider with resistors) [43,44,45].

In particular, the MOS sensors used in this work are the ones incorporated in the devices developed in the “EcoBici (Kers bike)” research project (file number G-GI3002/IDIC) which resulted in a patented invention, application number P201600319 and publication number ES2638715 [46]. These devices were designed to take air quality values, accumulating the data and being able to configure the time in which the averages are sent to a web server, in real time, through the deployment of a sensor network using XBee technology (protocol ZigBee). The parameters measured by these devices are CO, O3 and NO2. It should be noticed that these sensors are non-specific sensors since they can measure other gases apart from the main gas [43], but these secondary gases are not those considered in this paper. It is worth mentioning that O3 and NO2 are linked by the Leighton relationship. Nevertheless, the proposed methodology is not affected by this relationship since it is already considered in the parameter estimation.

For the calibration tests, the devices were adapted to send the temporal average of the three parameters every 10 min in order to be synchronized with the calibration equipment. Figure 1 shows the three sensors incorporated in EcoBici end devices, which include an MQ-7 sensor for CO measuring [43], an MQ-131 sensor for O3 [44] and an MiCS-2714 sensor for NO2 [45].

Figure 1.

Figure 1

Open in a new tab

Telemetering devices from the EcoBici project.

The concentration values given by the curves in datasheets [43,44,45] are much higher than the values that should be measured in terms of air quality. Although some of the sensor manufacturers guarantee that the device is able to detect the presence of gas at tens of ppb, our own experience can confirm the information from the WMO, cited in Section 1, and discourage the use of these curves for low concentrations.

In order to carry out the measurement campaign for field calibration, we used the highly sophisticated equipment located in the sampling stations belonging to the Environment Council of the Andalusian government. In these sampling stations, which are mostly composed of measurement analyzers, the pollutant concentrations are taken continuously, 24 h/day, 365 days per year, except for breakdowns. The cost of this type of equipment generally exceeds the barrier of EUR 10,000, and it is used to analyze a single parameter. It should be noted that each autonomous community or region has its own criteria to collect the data. In the case of Andalusia, the analyzers used in their stations take a sample of the ambient air, previously conditioned and homogenized, and analyze it in periods ranging from 10 s to 10 min, depending on the pollutant to be analyzed. This information is averaged in 10 min periods, stored and published by the Spanish Ministry of Air Quality [47], and on the Andalusian Council website (available from the following day) [48].

In order to select the most suitable sampling stations for calibration campaigns, several factors should be taken into account, such as the latest calibration reviews of the station, accessibility, and measurements range obtained of the different parameters in the station in several days. Regarding the data range, it is highly important to choose a station that can provide a wide range of values in the different parameters to be calibrated. For example, if a station where quantitative O3 values do not exceed 50 ppb after several days is selected, the sensor may not be properly calibrated for higher concentration values. According to this criterion, a station localized in Granada city was selected from more than 100 Andalusian Council monitoring stations. Figure 2 shows a photo of the Granada sampling station, where it is possible to identify the EcoBici devices on it, next to the station analyzers.

Figure 2.

Figure 2

Open in a new tab

Field calibration of 10 EcoBici devices on the front of an Andalusian Council sampling station in Seville City.

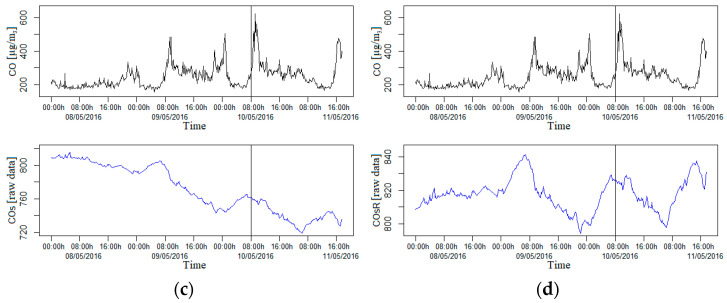
Finally, it is important to take into account the particular conditions of temperature and humidity in Granada city, since both parameters affect the best adjustment of sensors, as will be seen in the data section. In fact, both parameters were requested by the agency in charge of the sampling station after the measurement campaign. In any case, if these data could not be obtained from the corresponding agency, another option would be to place temperature and humidity sensors in the devices.

2.2. Description of Dataset

The real dataset of the work in the present paper involves measurements, taken by both analyzers and sensors, of three particular gaseous pollutants: ozone, nitrogen dioxide and carbon monoxide, in addition to temperature and humidity measurements by the agency. The observations are collected in 490 registers which were taken from midnight, 00:00 h, 08/05/2016 until 09:30 h, 11/05/2016, at a ten-minute frequency. The respective pollutant variables corresponding to the analyzers, from now on also called patterns, have been denoted as “O3”, “NO2” and “CO”, the respective pollutant variables corresponding to the sensors as “O3s”, “NO2s” and “COs”, the temperature variable as “temp”, and the humidity variable as “hum”. To obtain a better fit of the models, we have added a new variable, called “COsR”, which is a version of COs without trend. The rectified COsR time series has been obtained by the ratio of the sensor values and its adjusted least squares regression line. Moreover, we have translated the time series to the sensor range modifying the scale. Therefore, finally, we count 9 variables of work in the dataset: temp, hum, O3, NO2, CO, O3s, NO2s, COs and COsR.

The following sections show how to predict the pattern values for the gaseous pollutants O3, NO2 and CO, applying multivariable regression models and selecting the best fit by using the measurements of the sensors, O3s, NO2s and COs, and the values of temperature and humidity. That is, a general expression of the model would be:

Y = f(X1, X2, …, X5), (1)

where Y represents the pattern values, (X1, X2, …, X5) represent the measurements of the sensors and the temperature and humidity values, and f represents the convenient functional form of the model.

2.3. Methodology

The prediction and model assessment (or validation) are closely related to each other. Particularly, in our task, several models have been considered, of which, those that we have observed to best fit in each case will be analyzed and presented. It is important to mention that, although we have considered different more complex functional forms for the regression models, they have not managed to significantly improve the fits obtained by simple multilinear regression models in all cases. Therefore, the expression of the model used for the fit takes the form:

Y = α0 + α1 X1 + α2 X2 + α3 X3 + α4 X4 + α5 X5, (2)

where αi ∈ ℝ, for i = 0,1, …,5, are the independent term and the contribution of the variables Xi in the model. Both fitting to a dataset and choosing the best multilinear regression model can be easily done using the lm and step functions from the R stats package (there are many works on the internet that show how to do it, such as [49,50]).

In order to evaluate the best fitting model, we have performed the following method. We have split the sample into two disjoint subsets to estimate the prediction error, treating one subset as the training set and the other as the test set (split by vertical lines in Figure 3 and Figure 4). We used the training set to regress each gaseous pollutant on the rest of the variables. Afterward, we predicted a new gaseous pollutant value by applying the fitted model to the new values of the test set. The prediction was compared with the real response value and the prediction ability of the regression model. This provided a measure for the quality of the prediction, which was evaluated by its mean squared prediction error.

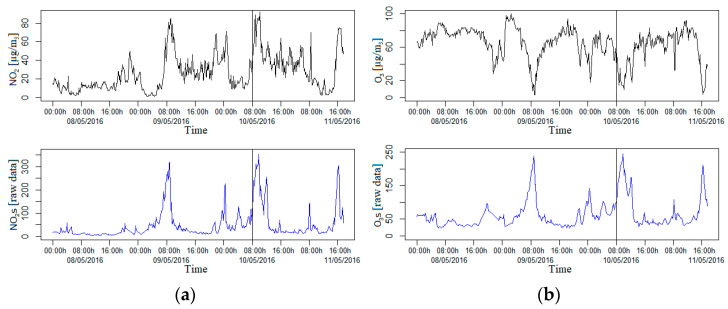
Figure 3.

Figure 3

Figure 3

Open in a new tab

(a–d) Plots of the evolution over time of the indicated gaseous pollutants in black lines for the patterns and in blue lines for the sensors (and for the transformation of the variable COs, COsR). Each vertical line separates the training dataset (on the left) from the test dataset (on the right).

Figure 4.

Figure 4

Open in a new tab

(a) The red line corresponds with the evolution over time of the temperature; (b) the blue line corresponds with the evolution in time of the humidity. Each vertical line separates the training dataset (on the left) from the test dataset (on the right).

Training and Test Sets

The methodology applied for each pollutant is similar. Firstly, we evaluate the different regression models using the dataset with all records and choose the one that best fits. Secondly, in order to perform a prediction test, we divide the whole dataset into two subsets: the training dataset and the test dataset.

The training dataset contained the measurements corresponding to the period from 00:00 h on 08/05/2016 until 08:00 h on 10/05/2016. Thirdly, using this subset, we fit the regression model chosen by fixing the coefficients of the model using the least squares method. The test dataset contained the measurements corresponding to the period from 08:10 h on 10/05/2016 until 09:30 h on 11/05/2016. It is important to mention that the test dataset contained an entire daily cycle, which let us include the possible daily periodicities. Fourthly, with the regression model fitted in the previous phase, we obtain the predictions for the test dataset and compare the results with respect to the pattern values of the test dataset.

3. Results

3.1. Analysis of Dataset

We can observe in Figure 3a that, in a different proportion, the evolution over time of the measurements taken by the sensor for nitrogen dioxide is closely related and also directly to the pattern values. In addition, in the same sense, we can observe in Figure 3b that there is a high association between ozone measurements, but in this case with an inverse relationship. The previous observations are supported by the correlation coefficients: ρ(O3,O3s) = −0.8227, ρ(NO2,NO2s) = 0.6118.

In Figure 3c, we do not observe the existence of an evident relationship between the carbon monoxide measurements captured by the sensor and its corresponding pattern values. In addition, ρ(CO,COs) = −0.3735, which is a low correlation. In line with COs, it is possible to appreciate the existence of a decreasing trend in concentration over time that does not exist in the pattern values curve. In order to better visualize any relationship, we have decided to eliminate the slope of the curve, creating the new variable COsR. However, as we can see in Figure 3d, there is still no evidence of any relationship after removing the slope, and, in this case, an even lower correlation is obtained (ρ(CO,COsR) = −0.1467). We kept the variable COsR in the dataset because the results in the model-fitting work improved.

3.2. Fitting Ozone

3.2.1. Selection of the Model

In the case of ozone, first, we considered a multilinear regression model with different combinations among the measurements of the sensors for O3s, NO2s and COs, in addition to the temperature and humidity measurements. Afterward, we chose the measures of COs instead of its version without a decreasing trend, COsR, obtaining a better adjustment and results. In particular, the model that best fits is:

O3 = α0 + α1 COsR + α2 NO2s + α3 O3s + α4 temp + α5 hum, (3)

where αi ∈ ℝ, for i = 0,1, …,5.

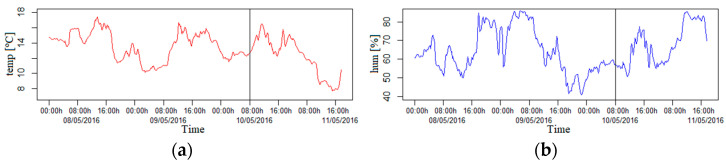
Adjusting the model by the least squares method to the dataset with all records, we obtain the αi values contained in Table 2. We observed that all variables considered were significant for the model. In addition, we know that the model manages to explain 75.08% of the total variability of O3, and the predictions of the model have a correlation of 0.8665 with the measures of the O3 pattern. In the left plot of Figure 5, we compared the values predicted by the model with the measurements of the O3 pattern. We can see in the histogram of the net prediction errors of the model that visually these do not differ too much from adjusting to a normal distribution (although the normality hypothesis was rejected when the Shapiro–Wilk test was applied).

Table 2.

The table contains the summary of the model described in Equation (3), adjusted to the dataset with all records. We can see the estimated values and the standard errors of the coefficients, the test statistics and p-values of their significance tests (for i = 0,1, …,5, the null hypothesis is αi = 0), the statistics of the residuals and the goodness of fit.

Coefficients Estimate Std. Error t Value p-Value
α0 −406.43899 54.43049 −7.467 3.85 × 10−13
α1 0.66569 0.07036 9.461 <2 × 10−16
α2 0.09424 0.02109 4.468 9.82 × 10−6
α3 −0.56357 0.03175 −17.752 <2 × 10−16
α4 −1.01488 0.31333 −3.239 0.00128
α5 −0.44478 0.07294 −6.098 2.20 × 10−9
Residuals:
Min 1Q Median 3Q Max
−31.110 −5.171 1.232 6.224 30.671
R-squared: 0.7508
Open in a new tab
Figure 5.

Figure 5

Open in a new tab

(a) The fitted values by the model and the pattern values for ozone; (b) the histogram of the net prediction errors of the model.

3.2.2. Evaluation of the Selected Model

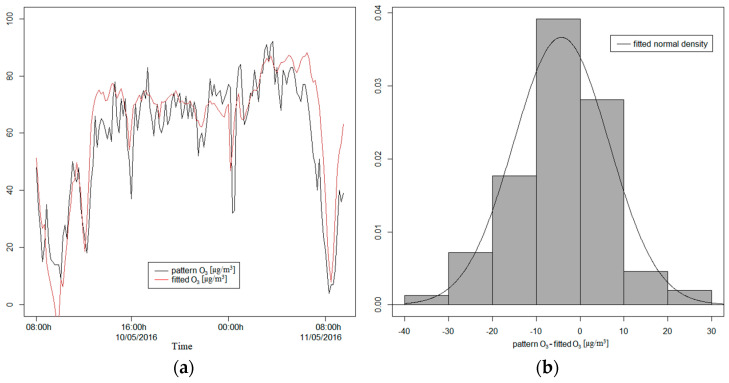
Now, adjusting the model by the least squares method to the training dataset, we obtain the αi values contained in Table 3. We can see that all variables considered in the model are significant and that it manages to explain 71.27% of the total variability of O3 for the training dataset. In Figure 6, for the test dataset, we can compare the values predicted by the model with the measurements of the O3 pattern and, in the histogram of the net prediction errors of the model, we can observe that these do not differ from a normal distribution. In addition, applying the Shapiro–Wilk test, we obtain a p-value of 0.4424, being able to consider the net prediction errors as normal, with mean μ = −4.2807 and standard deviation σ = 10.8789. The predictions of the model have a correlation of 0.8824 with the measures of the O3 pattern for the test dataset.

Table 3.

The table contains the summary of the model described in Equation (3), adjusted to the training dataset.

Coefficients Estimate Std. Error t Value p-Value
α0 −413.68158 69.18787 −5.979 5.81 × 10−9
α1 0.69410 0.08865 7.830 6.68 × 10−14
α2 0.10644 0.02793 3.812 0.000165
α3 −0.61144 0.04218 −14.497 <2 × 10−16
α4 −1.99947 0.42228 −4.735 3.25 × 10−6
α5 −0.43273 0.08206 −5.274 2.42 × 10−7
Residuals:
Min 1Q Median 3Q Max
−32.143 −4.406 1.603 5.626 19.206
R-squared: 0.7127
Open in a new tab
Figure 6.

Figure 6

Open in a new tab

Both graphs with the test dataset. (a) The fitted values by the model and the pattern values for ozone; (b) the histogram of the net prediction errors of the model.

3.3. Fitting Nitrogen Dioxide

As in the ozone case, firstly we have selected the best fit for nitrogen dioxide, which corresponds to the following multilinear regression model:

NO2 = α0 + α1 COs + α2 NO2s + α3 O3s + α4 temp + α5 hum, (4)

where αi ∈ ℝ, for i = 0,1, …,5.

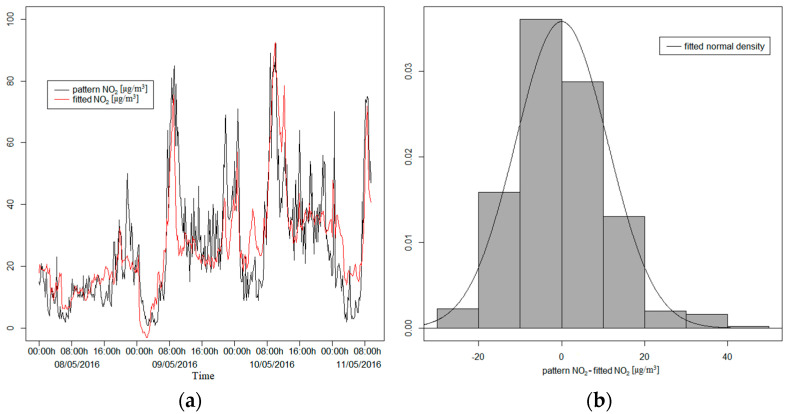
In Table A1 we can see the αi values when we fit the model to the dataset with all records. It can also be seen that all variables are significant for the model, and that the model manages to explain 68.10% of the total variability of NO2. The model predictions have a correlation of 0.8252 with the NO2 pattern. In Figure A1, it is possible to compare the NO2 values predicted by the model with those of the pattern and the histogram of the net prediction errors of the model, which do not differ too much from adjusting to a normal distribution.

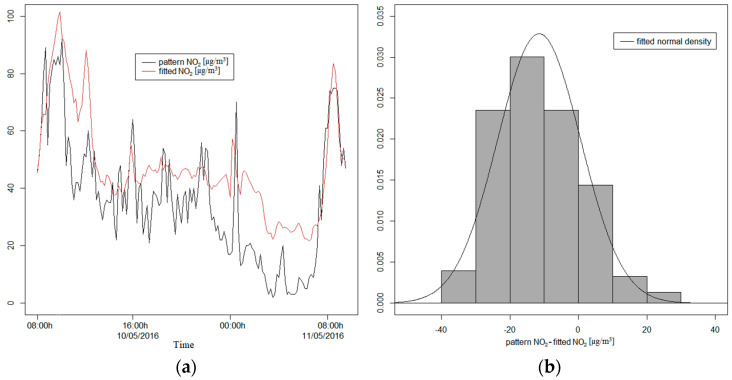
To evaluate the chosen model, it was adjusted to the training dataset, obtaining the αi values contained in Table A2. In this case, all variables considered are also significant and it managed to explain 65.55% of the total variability of NO2. In Figure A2, for the test dataset, we can see the NO2 values predicted by the model, and in the histogram of the net prediction errors of the model, we can see that they also did not differ from a normal distribution. The predictions of the model had a correlation of 0.8301 with the measures of the NO2 pattern for the test dataset.

3.4. Fitting Carbon Monoxide

The selected model for carbon monoxide has the following expression:

CO = α0 + α1 COsR + α2 NO2s + α3 O3s + α4 temp + α5 hum, (5)

where αi ∈ ℝ, for i = 0,1, …,5.

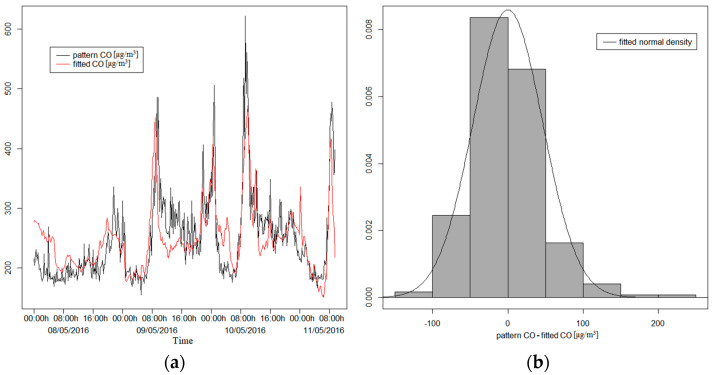
In this case, adjusting the model to the dataset with all records, the model explains 57.93% of the total variability of CO, and the corresponding predictions have a correlation of 0.7611 with the CO pattern. In Table A3 we can see the αi values that were obtained, all variables being significant. We can also see the predictions of the model and the histogram of its net prediction errors in Figure A3.

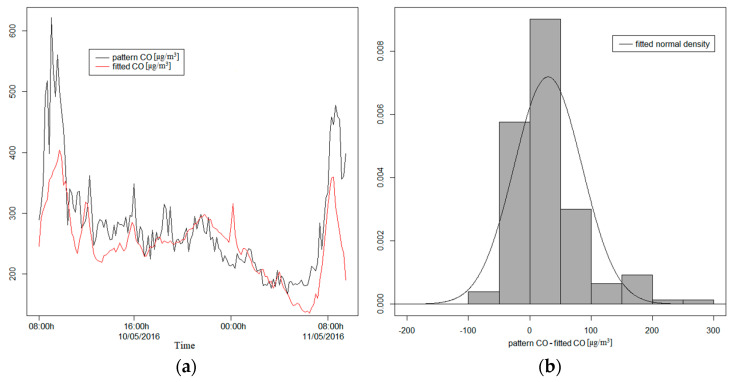
Regarding the evaluation of the selected model, once it was adjusted to the training dataset, it explained 47.49% of the total variability and its predictions had a correlation of 0.7769 with the CO pattern. All variables considered are significant for the model, as we can see in Table A4, in addition to the values of the coefficients. In Figure A4, for the test dataset, we can observe the CO values predicted by the model and the histogram of the net prediction errors of the model, which do not differ from a normal distribution.

4. Discussion

We observed that all the models generated overcame the global significance contrasts (p-values < 0.01) and almost all the individual significance contrasts. In particular, the p-values of NO2s from Table A3 and Table A4 show that the null hypothesis cannot be rejected by 10% of the significance level (0.09886 and 0.15552, respectively), the reason why the coefficient of NO2s in the model of CO is statistically equal to 0. Nevertheless, when this variable is removed from the model, although it simplifies it, neither the adjustment nor the prediction improves. Furthermore, an extension of the dataset will induce the NO2 sensor to have a higher influence in the model, providing a better fit for them, as happens with the other pollutants. For this reason, we decided to keep this variable in the model.

Focusing on ozone measurements, and considering all the datasets, the model obtained explains 75.08% of the variability of the data (R-squared), leaving less than 25% to the residuals. We also observed a high direct correlation (0.8665) with the measures of this pollutant pattern. This coefficient indicated a good correspondence between the observations and the predictions of this sensor. Moreover, the histogram of the prediction errors was not normally distributed (Shapiro–Wilk test rejected), although we observed a rough 0 symmetry distribution (Figure 5b).

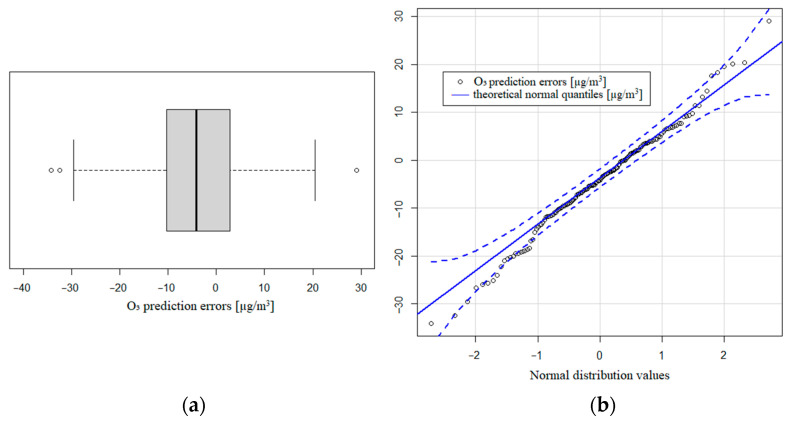
Nevertheless, when we consider the training dataset for this pollutant, the least square model when adjusted has a lower value of R-squared (71.27%), although it is close to the previous goodness of fit. In this case, the model overcomes the Shapiro–Wilk test on the prediction errors (they follow a normal distribution n(−4.28;10.88), p-value = 0.4424). It can be seen that 95% of the central prediction errors are between −23 and 12.2 µg/m3 with a median of −4.2 µg/m3. The interquartile range is 13.1 µg/m3. In the boxplot shown in Figure 7a, we observe only 3 outlier values from 337 data points. In Figure 7b, the theoretical normal quantiles, compared to prediction errors, display a good agreement in the central quantiles (points near the straight blue line).

Figure 7.

Figure 7

Open in a new tab

(a) Boxplot of O3 prediction errors; (b) theoretical normal quantiles compared to prediction errors.

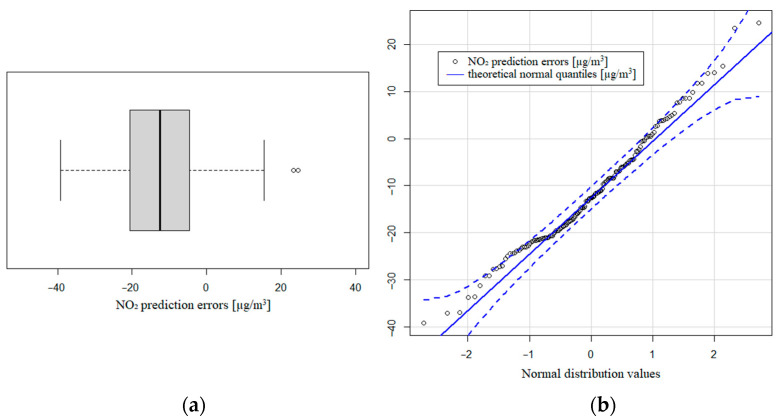
In the case of nitrogen dioxide, we observed that the model obtained explained 68.10% of the variability with a 0.8252 correlation with the NO2 pattern. The prediction errors histogram has a slight right asymmetry, although it does not differ excessively from a normal distribution (Figure A1b). Focusing on the training data, we observed a similar value of R-squared (65.55%), and the prediction errors were distributed with the same right asymmetry as before. The mean value of the prediction errors was negative (−11.5 µg/m3), with a standard deviation of 12.14 µg/m3. These values indicated that the prediction values were greater than the real values, so the model overestimated the NO2 values. The asymmetric coefficient is 0.4292, so the distribution shows a right asymmetry with more concentration of negative values of the prediction errors. This bias also shows that the model was overestimating the pattern value measures. We found that 95% of the central prediction errors are between −28.3 and 9.1 µg/m3 with a median of −12.6 µg/m3. The interquartile range is 16.2 µg/m3. Figure 8a shows the rough symmetry of the NO2 distribution and Figure 8b presents the deviation of the theoretical normal quantities and the NO2 prediction errors.

Figure 8.

Figure 8

Open in a new tab

(a) Boxplot of NO2 prediction errors; (b) theoretical normal quantiles compared to prediction errors.

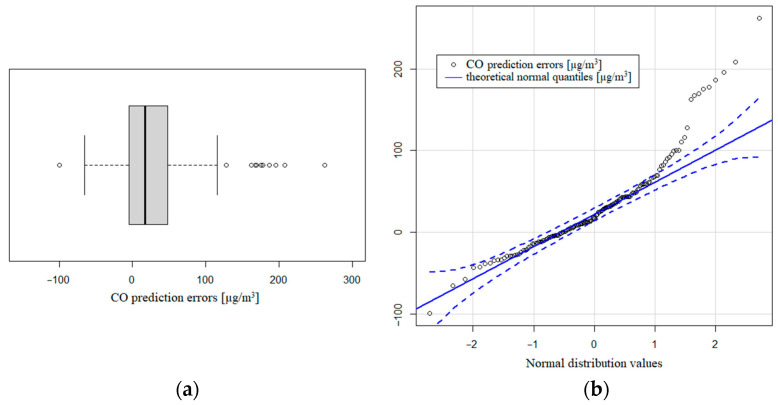
Regarding the carbon monoxide values, we needed to use the detrended measures of the CO sensor (COs) because the fit is better than COsR. In this case, the variability explained is lower (57.93%) regarding all the data, dropping to 47.49% of the total variability considering the training dataset. Clearly, the distribution of the prediction errors did not follow a normal distribution, with a strong right asymmetry with some values well over 100 µg/m3 (asymmetric coefficient: 1.4045). The mean value is 29.84 µg/m3 with a standard deviation of 55.51 µg/m3. These values indicate that the prediction values were lower than the real ones, so the model underestimated the CO values. Clearly, the adjustment of CO was not as good as the fit of the other pollutants, even after the detrending process. We found that 95% of the central prediction errors were between −34.3 and 164.5 µg/m3, with a median of −17.5 µg/m3. The interquartile range is also the highest one, with 53 µg/m3. Figure 9a shows the clear right asymmetry of the CO distribution and Figure 9b presents the deviation of the theoretical normal quantities and the CO prediction errors.

Figure 9.

Figure 9

Open in a new tab

(a) Boxplot of CO prediction errors; (b) theoretical normal quantiles compared to prediction errors.

5. Conclusions

In this paper, we present an on-field calibration technique for low-cost MOS sensors, using an adaptive method based on multivariate regression and rigorous statistical analysis. The results show a good adjustment with, at worst, almost 50% of the variability explained by the model. In particular, we found 71.27%, 65.55% and 47.49% of the variability explained for O3, NO2 and CO, respectively. Considering the short time interval used to estimate the model (less than 2.5 days), and achieving these adjustment values, it is expected that expanding the time series would improve the results.

In the case of O3, we obtained the best fit. Ozone prediction errors followed a symmetrical distribution with no bias (the Shapiro–Wilks normality test passed 95% confidence). On the other hand, the NO2 and CO prediction errors distribution had a right symmetry, which indicates a greater tail of the distribution in positive values. In these pollutants, the prediction values are generally overestimated with respect to the pattern ones. Overall, we observed a better quality on the fit with higher data.

We observed that the values of CO have the worst fit, which affected the R-squared with the variables considered. To model it, we needed to detrend the sensor measures of monoxide to include them in the calculus. Despite that, the prediction errors were greater than the others, with an average of 29 µg/m3 and a marked right bias. We consider that this lack of adjustment in CO was caused by the high time of response of the sensor, the daily variability of this pollutant and the short time interval. Although its calibration may be improved using other more complex models, we consider that for a first approach, the linear multivariate regression is the best-balanced model.

Despite the limitations of the sensors and the dataset used, we obtained a good fit of these gaseous pollutants with respect to the values of the analyzers, while using measurements obtained with low-cost MOS sensors. After the application of our methodology, we observed that the O3 and NO2 adjusted parameters can be used to give reliable information to citizens and could be used by government agencies for policymaking.

In future works, we will explore other and more complex statistical modeling to enhance the results. We will also verify the possibility of calibrating other MOS sensors through the use of sensors calibrated with the proposed methodology, instead of using control stations. In addition, two of the main disadvantages of the MQ-7 sensor are the delay in the response of the measure and the discontinuous operation mode. In relation to the delay, this is due to the fact that it was designed to measure in ranges 100 times greater than those measured in air quality. Nowadays, new CO sensors working in continuous mode, with the capacity for measuring lower concentrations, has emerged, and these will be considered to replace MQ-7 sensors in future experiments.

Acknowledgments

The researchers would like to thank the University of Cadiz for the grant obtained through its “Programa de Fomento e Impulso de la actividad de Investigación y Transferencia”. The authors would also like to thank to the Environmental Technology researching group and Acoustic Engineering Laboratory researching group, TEP-181 and TEP-195, respectively, for the access to the devices and data of the EcoBici Project (number G-GI3002/IDIC). Alfonso J. Bello acknowledges the support received from the 2014–2020 ERDF Operational Program and by the Department of Economy, Knowledge, and Business and the University of the Regional Government of Andalusia, Spain, under grant: FEDER-UCA18-107519.

Appendix A

This section contains tables and figures that complement Section 3.3 and Section 3.4.

Table A1.

The table contains the summary of the model described in Equation (4) adjusted to the dataset with all records.

Coefficients Estimate Std. Error t Value p-Value
α0 205.52408 13.85254 14.837 <2 × 10−16
α1 −0.38428 0.02208 −17.402 <2 × 10−16
α2 −0.10342 0.02386 −4.335 0.000017738
α3 0.48487 0.03688 13.146 <2 × 10−16
α4 4.89923 0.43472 11.270 <2 × 10−16
α5 0.41505 0.07775 5.338 0.000000144
Residuals:
Min 1Q Median 3Q Max
−29.964 −7.158 −1.064 5.946 45.364
R-squared: 0.681
Open in a new tab

Figure A1.

Figure A1

Open in a new tab

(a) The fitted values by the model and the pattern values for nitrogen dioxide; (b) the histogram of the net prediction errors of the model.

Table A2.

The table contains the summary of the model described in Equation (4) adjusted to the training dataset.

Coefficients Estimate Std. Error t Value p-Value
α0 306.28198 23.25716 13.169 <2 × 10−16
α1 −0.56296 0.03834 −14.685 <2 × 10−16
α2 −0.12499 0.02869 −4.357 1.76 × 10−5
α3 0.53380 0.04452 11.989 <2 × 10−16
α4 6.29591 0.55686 11.306 <2 × 10−16
α5 0.72325 0.09612 7.525 5.04 × 10−13
Residuals:
Min 1Q Median 3Q Max
−25.390 −6.507 −0.237 5.456 40.765
R-squared: 0.6555
Open in a new tab

Figure A2.

Figure A2

Open in a new tab

Both graphs with the test dataset. (a) The fitted values by the model and the pattern values for nitrogen dioxide; (b) the histogram of the net prediction errors of the model.

Table A3.

The table contains the summary of the model described in Equation (5) adjusted to the dataset with all records.

Coefficients Estimate Std. Error t Value p-Value
α0 3604.9455 261.9849 13.760 <2 × 10−16
α1 −4.4098 0.3387 −13.021 <2 × 10−16
α2 0.1679 0.1015 1.654 0.09886
α3 1.1791 0.1528 7.716 6.90 × 10−14
α4 4.5623 1.5081 3.025 0.00262
α5 1.6188 0.3511 4.611 5.13 × 10−6
Residuals:
Min 1Q Median 3Q Max
−132.41 −26.88 −3.60 25.60 210.30
R-squared: 0.5793
Open in a new tab

Figure A3.

Figure A3

Open in a new tab

(a) The fitted values by the model and the pattern values for carbon monoxide; (b) the histogram of the net prediction errors of the model.

Table A4.

The table contains the summary of the model described in Equation (5) adjusted to the training dataset.

Coefficients Estimate Std. Error t Value p-Value
α0 4077.0760 321.4378 12.684 <2 × 10−16
α1 −5.0366 0.4119 −12.229 <2 × 10−16
α2 0.1847 0.1297 1.424 0.15552
α3 0.8636 0.1959 4.407 0.00001417
α4 6.0151 1.9619 3.066 0.00235
α5 2.0935 0.3812 5.492 0.00000008
Residuals:
Min 1Q Median 3Q Max
−72.537 −27.893 −3.568 22.071 224.530
R-squared: 0.4749
Open in a new tab

Figure A4.

Figure A4

Open in a new tab

Both graphs with the test dataset. (a) The fitted values by the model and the pattern values for carbon monoxide; (b) the histogram of the net prediction errors of the model.

Author Contributions

D.S.-L., A.J.B., A.S.-A. and P.M.M.-J. contributed to conceptualization, organization, and performance analysis of this paper, including writing and review. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no potential conflict of interest.

Footnotes

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

References

  • 1.Brunekreef B., Holgate S.T. Air pollution and health. Lancet. 2002;360:1233–1242. doi: 10.1016/S0140-6736(02)11274-8. [DOI] [PubMed] [Google Scholar]
  • 2.Stanaway G., Afshin A., Gakidou E., Lim S., Abate K., Cristiana A., Abbasi N., Abbastabar H., Abd-Allah F., Abdela J., et al. Global, regional, and national comparative risk assessment of 84 behavioural, environmental and occupational, and metabolic risks or clusters of risks for 195 countries and territories, 1990–2017: A systematic analysis for the Global Burden of Disease Study 2017. Lancet. 2018;392:1923–1994. doi: 10.1016/S0140-6736(18)32225-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Jaimini U., Banerjee T., Romine W., Thirunarayan K., Sheth A., Kalra M. Investigation of an indoor air quality sensor for asthma management in children. IEEE Sens. Lett. 2017;1:1–4. doi: 10.1109/LSENS.2017.2691677. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Marinello S., Butturi M.A., Gamberini R. How changes in human activities during the lockdown impacted air quality parameters: A review. Environ. Prog. Sustain. Energy. 2021;40:e13672. doi: 10.1002/ep.13672. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Losacco C., Perillo A. Particulate matter air pollution and respiratory impact on humans and animals. Environ. Sci. Pollut. Res. 2018;25:33901–33910. doi: 10.1007/s11356-018-3344-9. [DOI] [PubMed] [Google Scholar]
  • 6.Orellano P., Reynoso J., Quaranta N., Bardach A., Ciapponi A. Short-term exposure to particulate matter (PM10 and PM2.5), nitrogen dioxide (NO2), and ozone (O3) and all-cause and cause-specific mortality: Systematic review and meta-analysis. Environ. Int. 2020;142:105876. doi: 10.1016/j.envint.2020.105876. [DOI] [PubMed] [Google Scholar]
  • 7.Liu J.C., Peng R.D. Health effect of mixtures of ozone, nitrogen dioxide, and fine particulates in 85 US counties. Air Qual. Atmos. Health. 2018;11:311–324. doi: 10.1007/s11869-017-0544-2. [DOI] [Google Scholar]
  • 8.Olstrup H., Johansson C., Forsberg B., Åström C. Association between mortality and short-term exposure to particles, ozone and nitrogen dioxide in Stockholm, Sweden. Int. J. Environ. Res. Public Health. 2019;16:1028. doi: 10.3390/ijerph16061028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Ritz B., Hoffmann B., Peters A. The effects of fine dust, ozone, and nitrogen dioxide on health. Dtsch. Ärzteblatt Int. 2019;116:881. doi: 10.3238/arztebl.2019.0881. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.European Environment Agency (EEA) Air Quality in Europe-2019 Report. No 10/2019. [(accessed on 12 March 2021)];2019 Available online: https://www.eea.europa.eu/publications/air-quality-in-europe-2019.
  • 11.United States Environmental Protection Agency (EPA) Report: EPA’s FYs 2020–2021 Top Management Challenges. No 20-N-0231. [(accessed on 12 March 2021)];2020 Available online: https://www.epa.gov/sites/production/files/2020-07/documents/_epaoig_20200721-20-n-0231_0.pdf.
  • 12.Kuklinska K., Wolska L., Namieśnik J. Air quality policy in the U.S. and the EU—A review. Atmos. Pollut. Res. 2015;6:129–137. doi: 10.5094/APR.2015.015. [DOI] [Google Scholar]
  • 13.European Environment Agency (EEA) Europe’s Urban Air Quality-Re-Assessing Implementation Challenges in Cities. Nº24-2018. [(accessed on 12 March 2021)];2018 Available online: https://www.eea.europa.eu/publications/europes-urban-air-quality.
  • 14.Castell N., Dauge F.R., Schneider P., Vogt M., Lerner U., Fishbain B., Broday D., Bartonova A. Can commercial low-cost sensor platforms contribute to air quality monitoring and exposure estimates? Environ. Int. 2017;99:293–302. doi: 10.1016/j.envint.2016.12.007. [DOI] [PubMed] [Google Scholar]
  • 15.Motlagh N.H., Lagerspetz E., Nurmi P., Li X., Varjonen S., Mineraud J., Siekkinen M., Rebeiro-Hargrave A., Hussein T., Petaja T., et al. Toward massive scale air quality monitoring. IEEE Commun. Mag. 2020;58:54–59. doi: 10.1109/MCOM.001.1900515. [DOI] [Google Scholar]
  • 16.Kaivonen S., Ngai E.C.H. Real-time air pollution monitoring with sensors on city bus. Digit. Commun. Netw. 2020;6:23–30. doi: 10.1016/j.dcan.2019.03.003. [DOI] [Google Scholar]
  • 17.Munir S., Mayfield M., Coca D., Jubb S.A., Osammor O. Analysing the performance of low-cost air quality sensors, their drivers, relative benefits and calibration in cities—A case study in Sheffield. Environ. Monit. Assess. 2019;191:94. doi: 10.1007/s10661-019-7231-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Gryech I., Ben-Aboud Y., Guermah B., Sbihi N., Ghogho M., Kobbane A. MoreAir: A Low-Cost Urban Air Pollution Monitoring System. Sensors. 2020;20:998. doi: 10.3390/s20040998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Piedrahita R., Xiang Y., Masson N., Ortega J., Collier-Oxandale A., Jiang Y., Li K., Dick R., Lv Q., Hannigan M., et al. The next generation of low-cost personal air quality sensors for quantitative exposure monitoring. Atmos. Meas. Technol. 2014;7:3325–3336. doi: 10.5194/amt-7-3325-2014. [DOI] [Google Scholar]
  • 20.Che W., Frey H.C., Fung J.C., Ning Z., Qu H., Lo H.K., Lau A.K. PRAISE-HK: A personalized real-time air quality informatics system for citizen participation in exposure and health risk management. Sustain. Cities Soc. 2020;54:101986. doi: 10.1016/j.scs.2019.101986. [DOI] [Google Scholar]
  • 21.Wesseling J., de Ruiter H., Blokhuis C., Drukker D., Weijers E., Volten H., Tielemans E. Development and implementation of a platform for public information on air quality, sensor measurements, and citizen science. Atmosphere. 2019;10:445. doi: 10.3390/atmos10080445. [DOI] [Google Scholar]
  • 22.Thorson J., Collier-Oxandale A., Hannigan M. Using A Low-Cost Sensor Array and Machine Learning Techniques to Detect Complex Pollutant Mixtures and Identify Likely Sources. Sensors. 2019;19:3723. doi: 10.3390/s19173723. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Rai A.C., Kumar P., Pilla F., Skouloudis A.N., Di Sabatino S., Ratti C., Yasar A., Rickerby D. End-user perspective of low-cost sensors for outdoor air pollution monitoring. Sci. Total Environ. 2017;607–608:691–705. doi: 10.1016/j.scitotenv.2017.06.266. [DOI] [PubMed] [Google Scholar]
  • 24.Burgués J., Marco S. Low Power Operation of Temperature-Modulated Metal Oxide Semiconductor Gas Sensors. Sensors. 2018;18:339. doi: 10.3390/s18020339. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Martinez D., Burgués J., Marco S. Fast Measurements with MOX Sensors: A Least-Squares Approach to Blind Deconvolution. Sensors. 2019;19:4029. doi: 10.3390/s19184029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.World Meteorological Organization Low-Cost Sensors for the Measurement of Atmospheric Composition: Overview of Topic and Future Applications Europe’s Urban Air Quality. [(accessed on 12 March 2021)]; Available online: https://library.wmo.int/doc_num.php?explnum_id=9881.
  • 27.Masson N., Piedrahita R., Hannigan M. Approach for quantification of metal oxide type semiconductor gas sensors used for ambient air quality monitoring. Sens. Actuators B Chem. 2014;208:339–345. doi: 10.1016/j.snb.2014.11.032. [DOI] [Google Scholar]
  • 28.Maag B., Zhou Z., Thiele L. A Survey on Sensor Calibration in Air Pollution Monitoring Deployments. IEEE Internet Things J. 2018;5:4857–4870. doi: 10.1109/JIOT.2018.2853660. [DOI] [Google Scholar]
  • 29.Afshar-Mohajer N., Zuidema C., Sousan S., Hallett L., Tatum M., Rule A.M., Thomas G., Peters T.M., Koehler K. Evaluation of low-cost electro-chemical sensors for environmental monitoring of ozone, nitrogen dioxide, and carbon monoxide. J. Occup. Environ. Hyg. 2018;15:87–98. doi: 10.1080/15459624.2017.1388918. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Schultealbert C., Baur T., Schütze A., Böttcher S., Sauerwald T. A novel approach towards calibrated measurement of trace gases using metal oxide semiconductor sensors. Sens. Actuators B Chem. 2017;239:390–396. doi: 10.1016/j.snb.2016.08.002. [DOI] [Google Scholar]
  • 31.Leidinger M., Schultealbert C., Neu J., Schütze A., Sauerwald T. Characterization and calibration of gas sensor systems at ppb level—A versatile test gas generation system. Meas. Sci. Technol. 2017;29:015901. doi: 10.1088/1361-6501/aa91da. [DOI] [Google Scholar]
  • 32.Wei P., Ning Z., Ye S., Sun L., Yang F., Wong K.C., Westerdahl D., Louie P.K.K. Impact Analysis of Temperature and Humidity Conditions on Electrochemical Sensor Response in Ambient Air Quality Monitoring. Sensors. 2018;18:59. doi: 10.3390/s18020059. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Jiang Y., Zhu X., Chen C., Ge Y., Wang W., Zhao Z., Cai J., Kan H. On-field test and data calibration of a low-cost sensor for fine particles exposure assessment. Ecotoxicol. Environ. Saf. 2021;211:111958. doi: 10.1016/j.ecoenv.2021.111958. [DOI] [PubMed] [Google Scholar]
  • 34.Spinelle L., Gerboles M., Villani M.G., Aleixandre M., Bonavitacola F. Field calibration of a cluster of low-cost available sensors for air quality monitoring. Part A: Ozone and nitrogen dioxide. Sens. Actuators B Chem. 2015;215:249–257. doi: 10.1016/j.snb.2015.03.031. [DOI] [Google Scholar]
  • 35.De Vito S., Massera E., Piga M., Martinotto L., Di Francia G. On field calibration of an electronic nose for benzene estimation in an urban pollution monitoring scenario. Sens. Actuators B Chem. 2008;129:750–757. doi: 10.1016/j.snb.2007.09.060. [DOI] [Google Scholar]
  • 36.Peterson P.J.D., Aujla A., Grant K.H., Brundle A.G., Thompson M.R., Vande Hey J., Leigh R.J. Practical Use of Metal Oxide Semiconductor Gas Sensors for Measuring Nitrogen Dioxide and Ozone in Urban Environments. Sensors. 2017;17:1653. doi: 10.3390/s17071653. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Berry W.D., Feldman S. Multiple Regression in Practice (Sage University Paper Series, Quantitative Applications in the Social Sciences) Sage; Beverly Hills, CA, USA: 1985. [Google Scholar]
  • 38.Montgomery D.C., Peck E.A., Vining G.G. Introduction to Linear Regression Analysis. 5th ed. John Wiley & Sons, Inc.; Hoboken, NJ, USA: 2012. [Google Scholar]
  • 39.Yan X., Su X.G. Linear Regression Analysis: Theory and Computing. World Scientific Publishing Co. Pte. Ltd.; Singapore: 2009. [Google Scholar]
  • 40.R Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2020. [(accessed on 28 May 2021)]. Available online: https://www.R-project.org/ [Google Scholar]
  • 41.Official Journal of the European Union Directive 2008/50/EC of the European Parliament and the Council of 21 May 2008 on Ambient Air Quality and Cleaner Air for Europe. June 2008. [(accessed on 28 May 2021)]; Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2008:152:0001:0044:en:PDF.
  • 42.World Meteorological Organization Global Air Quality Guidelines. [(accessed on 28 May 2021)]; Available online: https://www.euro.who.int/en/health-topics/environment-and-health/air-quality/activities/update-of-who-global-air-quality-guidelines.
  • 43.Technical Data MQ-7 Gas Sensor. [(accessed on 12 March 2021)]; Available online: https://www.sparkfun.com/datasheets/Sensors/Biometric/MQ-7.pdf.
  • 44.MQ-131 Ozone Gas Sensor. [(accessed on 12 March 2021)]; Available online: https://aqicn.org/air/view/sensor/spec/o3.winsen-mq131.pdf.
  • 45.Data Sheet MiCS-2714. [(accessed on 12 March 2021)]; Available online: https://www.sgxsensortech.com/content/uploads/2014/08/1107_Datasheet-MiCS-2714.pdf.
  • 46.Sales-Lérida D., Sales-Márquez D., Hernandez-Molina R., Cueto-Ancela J.L. Sistema de Telemedición de Calidad Del Aire Para la Visualización en Tiempo Real de una Red de Dispositivos Compactos. Number ES2638715. Spain Patent. 2018 Aug 16;
  • 47.Visor de Calidad del Aire. [(accessed on 12 March 2021)]; Available online: https://www.miteco.gob.es/es/calidad-y-evaluacion-ambiental/temas/atmosfera-y-calidad-del-aire/calidad-del-aire/visor/default.aspx.
  • 48.Informes Diarios de Calidad del Aire. [(accessed on 12 March 2021)]; Available online: http://www.juntadeandalucia.es/medioambiente/site/portalweb/menuitem.7e1cf46ddf59bb227a9ebe205510e1ca/?vgnextoid=7e612e07c3dc4010VgnVCM1000000624e50aRCRD&vgnextchannel=910f230af77e4310VgnVCM1000001325e50aRCRD.
  • 49.How to Perform Multiple Linear Regression in R. [(accessed on 3 July 2021)]; Available online: https://www.statology.org/multiple-linear-regression-r/
  • 50.A Complete Guide to Stepwise Regression in R. [(accessed on 3 July 2021)]; Available online: https://www.statology.org/stepwise-regression-r/

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Articles from Sensors (Basel, Switzerland) are provided here courtesy of Multidisciplinary Digital Publishing Institute (MDPI)

RESOURCES