Prediction model of in-hospital mortality in intensive care unit patients with heart failure: machine learning-based, retrospective analysis of the MIMIC-III database

Abstract

Objective

The predictors of in-hospital mortality for intensive care units (ICUs)-admitted heart failure (HF) patients remain poorly characterised. We aimed to develop and validate a prediction model for all-cause in-hospital mortality among ICU-admitted HF patients.

Design

A retrospective cohort study.

Setting and participants

Data were extracted from the Medical Information Mart for Intensive Care (MIMIC-III) database. Data on 1177 heart failure patients were analysed.

Methods

Patients meeting the inclusion criteria were identified from the MIMIC-III database and randomly divided into derivation (n=825, 70%) and a validation (n=352, 30%) group. Independent risk factors for in-hospital mortality were screened using the extreme gradient boosting (XGBoost) and the least absolute shrinkage and selection operator (LASSO) regression models in the derivation sample. Multivariate logistic regression analysis was used to build prediction models in derivation group, and then validated in validation cohort. Discrimination, calibration and clinical usefulness of the predicting model were assessed using the C-index, calibration plot and decision curve analysis. After pairwise comparison, the best performing model was chosen to build a nomogram according to the regression coefficients.

Results

Among the 1177 admissions, in-hospital mortality was 13.52%. In both groups, the XGBoost, LASSO regression and Get With the Guidelines-Heart Failure (GWTG-HF) risk score models showed acceptable discrimination. The XGBoost and LASSO regression models also showed good calibration. In pairwise comparison, the prediction effectiveness was higher with the XGBoost and LASSO regression models than with the GWTG-HF risk score model (p<0.05). The XGBoost model was chosen as our final model for its more concise and wider net benefit threshold probability range and was presented as the nomogram.

Conclusions

Our nomogram enabled good prediction of in-hospital mortality in ICU-admitted HF patients, which may help clinical decision-making for such patients.

Strengths and limitations of this study.

• We developed the first in-hospital mortality prediction nomogram using logistic regression with included variables selected by the extreme gradient boosting algorithm.

• The area under the receiver operating characteristic curve, calibration curves, decision curve analysis and survival curves were enrolled to evaluate the performance of this novel nomogram model in both the primary cohort and validation cohort.

• Least absolute shrinkage and selection operator regression and machine learning were applied to screen independent risk factors.

• Data were collected from patient medical records and we relied on the accuracy of the records.

Introduction

Heart failure (HF), a syndrome due to a heart function disorder, is the terminal phase of all heart diseases. As a major cause of cardiovascular morbidity and mortality, HF has become an overwhelming threat to human health and social development.¹ Despite the recent progress in diagnosis and evidence-based management, the outcomes concerning HF remain unsatisfactory.²

As a life-threatening disease, especially concerning combined advanced organ dysfunction or other severe complications, a large proportion of HF patients may immediately require advanced, high-technology, life-saving care that is available only in intensive care units (ICUs), characterised with high-intensity staffing in terms of nurse and physician-to-patient ratios. Approximately 10%–51% of patients hospitalised with HF in the USA have been reported to be admitted to an ICU.^{3 4} ICU-admitted patients have been reported to have significantly higher adjusted in-hospital mortality compared with those admitted to hospital wards only.⁵ The in-hospital mortality rate for patients who have received treatment in an ICU has been reported to be 10.6%, whereas the in-hospital mortality rate for all HF patients has been reported to be 4.0%.⁶ Given the considerably higher in-hospital mortality rate, accurately predicting prognosis and receiving intensive treatment with closer follow-up may be of greater benefit to ICU-admitted HF patients. Although several in-hospital mortality prediction models are available,^7–10 the accuracies of these methods are unsatisfactory (the C-statistic of these models range from 0.75 to 0.776）and have not been widely implemented. Moreover, limited data are available on prediction models concerning ICU-admitted HF patients.

Identifying patients at the highest risk of poor outcomes following hospital discharge can improve outcomes for ICU-admitted HF patients. Machine-learning algorithms can automatically reconstruct relationships between variables and response values from big data and improve the performance of traditional methods, such as logistic regression analyses, in identifying critical predictors.¹¹ This study aimed to develop and validate a predictive model for in-hospital mortality among ICU-admitted HF patients using data from the Medical Information Mart for Intensive Care (MIMIC-III) database.

Data source

The MIMIC-III database (V.1.4, 2016) is a publicly available critical care database containing de-identified data on 46 520 patients and 58 976 admissions to the ICU of the Beth Israel Deaconess Medical Center, Boston, USA, between 1 June 2001 and 31 October 2012. These data include comprehensive information, such as demographics, admitting notes, International Classification of Diseases-9th revision (ICD-9) diagnoses, laboratory tests, medications, procedures, fluid balance, discharge summaries, vital sign measurements undertaken at the bedside, caregivers notes, radiology reports and survival data.¹² After successful completion of the National Institutes of Health Protecting Human Research Participants web-based training course, we obtained approval to extract data from MIMIC-III for research purposes (Certification Number: 28860101).

Patient and public involvement

Patients and/or the public were not directly involved in this study.

Study patients

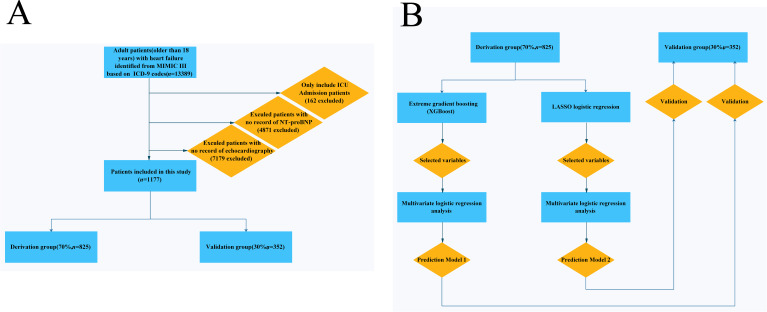
Patients with a diagnosis of HF, identified by manual review of ICD-9 codes, and who were ≥15 years old at the time of ICU admission were included in the study; two researchers conducted the ICD-9 code review. Patients without an ICU record or data missing for left ventricular ejection fraction (LVEF) or N-terminal pro-brain natriuretic peptide (NT-proBNP) were excluded from the study. Figure 1A illustrates the flow chart showing the selection of patients into the study. A total of 13 389 patients with a diagnosis of HF were screened and 1177 adult patients were included in this study (figure 1A).

Figure 1.

(A) Flowchart of patient selection (n=1177). (B) Model development flowchart. ICD-9, 9th revision of the International Classification of Diseases; ICU, intensive care unit; LASSO, least absolute shrinkage and selection operator; MIMIC-III, Medical Information Mart for Intensive Care III; NT-proBNP, N-terminal pro-brain natriuretic peptide; XGBoost, extreme gradient boosting.

Data extraction

Using Structured Query Language queries (PostgreSQL, V.9.6), demographic characteristics, vital signs and laboratory values data were extracted from the following tables in the MIMIC-III dataset: ADMISSIONS, PATIENTS, ICUSTAYS, D_ICD DIAGNOSIS, DIAGNOSIS_ICD, LABEVENTS, D_LABIEVENTS, CHARTEVENTS, D_ITEMS, NOTEEVENTS and OUTPUTEVENTS. Based on previous studies,7–9 13–15 clinical relevance, and general availability at the time of presentation, we extracted the following data: demographic characteristics (age at the time of hospital admission, sex, ethnicity, weight and height); vital signs (heart rate (HR), systolic blood pressure (SBP), diastolic blood pressure (DBP), mean blood pressure, respiratory rate, body temperature, saturation pulse oxygen (SPO₂), urine output (first 24 hours); comorbidities (hypertension, atrial fibrillation, ischaemic heart disease, diabetes mellitus, depression, hypoferric anaemia, hyperlipidaemia, chronic kidney disease (CKD) and chronic obstructive pulmonary disease (COPD)) and laboratory variables (haematocrit, red blood cells, mean corpuscular haemoglobin, mean corpuscular haemoglobin concentration, mean corpuscular volume (MCV), red blood cell distribution width (RDW), platelet count, white blood cells, neutrophils, basophils, lymphocytes, prothrombin time (PT), international normalised ratio (INR), NT-proBNP, creatine kinase, creatinine, blood urea nitrogen (BUN) glucose, potassium, sodium, calcium, chloride, magnesium, the anion gap, bicarbonate, lactate, hydrogen ion concentration (pH), partial pressure of CO₂ in arterial blood and LVEF), using Structured Query Language (SQL) with PostgreSQL (V.9.6). Demographic characteristics and vital signs extracted were recorded during the first 24 hours of each admission and laboratory variables were measured during the entire ICU stay. Comorbidities were identified using ICD-9 codes. For variable data with multiple measurements, the calculated mean value was included for analysis. The primary outcome of the study was in-hospital mortality, defined as the vital status at the time of hospital discharge in survivors and non-survivors.

Missing data handling

Variables with missing data are common in the MIMIC-III, however, eliminating patients with incomplete data can bias the study. Therefore, imputation is an important step in data preprocessing. All screening variables contained <25% missing values (online supplemental table 1). For normally distributed continuous variables, the missing values were replaced with the mean for the patient group. For skewed distributions related to continuous variables, missing values were replaced with their median. There were no missing dichotomous variables in our study.¹⁶

Statistical analysis

We present baseline patient characteristics in both samples using a percentage of the total for categorical variables and mean±SD or median and IQR for continuous variables, depending on the normality of distribution. For categorical variables, we used a two-sided Pearson’s χ² test or Fisher’s exact tests to assess differences in proportions between the two groups. For all continuous variables, we used a two-sided one-way analysis of variance or Wilcoxon rank-sum tests when comparing the two groups.

Figure 1B illustrates the methodology used to develop the prediction model. A total of 52 demographic, clinical and biochemical variables were considered as candidate predictors based on existing literature, expert knowledge and availability in clinical practice. Table 1 summarises the predictor variables and summary statistics. Two methods were used to select the most important predictors for the in-hospital mortality prediction model from the derivation group. First, we used extreme gradient boosting (XGBoost),¹⁷ a supervised machine-learning and data-mining tool, which involves a meta-algorithm, to construct a strong ensemble learner from weak learners, such as regression trees.¹⁸ The parameters of a regression tree consist of the tree structures and the weights of the leaf nodes. They are sequentially optimised to minimise an objective function, consisting of a fitting loss term plus a regularisation term, using gradient methods. XGBoost retrofits the tree-learning algorithm for handling sparse data by raising a weighted quantile sketch to approximate an optimisation calculation and design a column block structure for parallel learning. The XGBoost algorithm can indicate the contributions of each of the predictors, making it possible to choose the most relevant predictors. The 20 top-ranked variables were selected for further analysis. Second, we used the least absolute shrinkage and selection operator (LASSO) method,¹⁹ which involves regression analysis to perform both variable selection and regularisation. This enhances the prediction accuracy and interpretability of a statistical model and is suitable for reduction in high-dimensional data. Variables with non-zero coefficients in the LASSO regression model were selected for further analysis.

Table 1.

Characteristics of participants

	Total (n=1177)	Derivation group (n=825)	Validation group (n=352)	P value for derivation vs validation	Alive (n=1017)	Died (n=159)	P value for alive vs dead
Age, mean (SD), years	74.06 (13.43)	74.05 (13.49)	74.06 (13.32)	0.998	73.71 (13.45)	76.24 (13.22)	0.027
BMI, mean (SD)	29.88 (7.94)	30.00 (8.23)	29.59 (7.25)	0.467	30.11 (8.07)	28.17 (6.67)	0.016
Heart rate, mean (SD), bpm	84.58 (16.02)	84.52 (15.84)	84.70 (16.45)	0.863	83.75 (15.99)	89.82 (15.25)	<0.001
Systolic blood pressure, mean (SD), mm Hg	118.00 (17.37)	118.71 (17.90)	116.33 (15.95)	0.032	118.91 (17.32)	112.18 (16.61)	<0.001
Diastolic blood pressure, mean (SD), mm Hg	59.53 (10.68)	59.64 (10.50)	59.30 (11.12)	0.618	59.90 (10.90)	57.18 (8.88)	0.003
Mean blood pressure, mean (SD), mm Hg	75.20 (10.62)	75.44 (10.70)	74.64 (10.43)	0.239	75.60 (10.69)	72.65 (9.84)	0.001
Respiratory rate, mean (SD), bpm	20.80 (4.00)	20.82 (3.99)	20.76 (4.03)	0.821	20.62 (3.90)	21.98 (4.42)	<0.001
Temperature, mean (SD), °C	36.68 (0.61)	36.68 (0.61)	36.66 (0.61)	0.512	36.70 (0.59)	36.54 (0.70)	0.002
SPO2, mean (SD), %	96.27 (2.30)	96.24 (2.34)	96.35 (2.19)	0.458	96.34 (2.14)	95.86 (3.10)	0.015
Urine-output (first 24 hours), median (Q1–Q3), mL	1675.00 (992.50–2480.00)	1630.00 (1000.00–2475.00)	1717.50 (938.50–2488.75)	0.932	1773.50 (1078.75–2586.25)	1050.00 (674.50–1626.50)	<0.001
LVEF, mean (SD), %	48.72 (12.87)	48.82 (12.74)	48.48 (13.18)	0.679	48.83 (12.55)	47.92 (14.77)	0.408
Haematocrit, mean (SD), %	31.91 (5.20)	31.77 (5.13)	32.25 (5.36)	0.151	31.94 (5.19)	31.69 (5.27)	0.571
Red cells, mean (SD), ×10∧12/L	3.58 (0.63)	3.55 (0.62)	3.62 (0.65)	0.088	3.58 (0.62)	3.54 (0.70)	0.411
MCH, mean (SD), pg	29.54 (2.62)	29.58 (2.59)	29.44 (2.69)	0.394	29.53 (2.58)	29.63 (2.87)	0.647
MCHC, mean (SD), %	32.86 (1.40)	32.87 (1.40)	32.84 (1.40)	0.701	32.88 (1.41)	32.75 (1.36)	0.275
MCV, mean (SD), fL	89.90 (6.53)	90.01 (6.47)	89.66 (6.67)	0.396	89.81 (6.43)	90.47 (7.16)	0.242
RDW, mean (SD), %	15.95 (2.13)	16.01 (2.25)	15.81 (1.82)	0.139	15.83 (2.07)	16.75 (2.33)	<0.001
White cells, mean (SD), /×10∧9/L	10.54 (4.29)	10.54 (4.31)	10.53 (4.23)	0.980	10.20 (4.11)	12.78 (4.78)	<0.001
Platelet count, median (Q1–Q3), ×10∧9/L	222.67 (168.91–304.25)	222.12 (168.91–301.38)	224.03 (168.97–306.78)	0.582	226.09 (173.40–305.33)	198.56 (134.68–262.07)	<0.001
Neutrophils, mean (SD), %	80.11 (11.13)	79.99 (10.63)	80.39 (12.21)	0.591	79.79 (10.41)	82.12 (14.77)	0.020
Basophils, median (Q1–Q3), %	0.30 (0.20–0.50)	0.30 (0.20–0.50)	0.30 (0.20–0.50)	0.286	0.30 (0.20–0.50)	0.20 (0.10–0.40)	<0.001
Lymphocytes, median (Q1–Q3), %	10.48 (6.65–15.46)	10.62 (6.94–15.31)	10.00 (6.10–16.18)	0.870	11.00 (7.10–16.00)	7.00 (4.14–10.53)	<0.001
PT, mean (SD), s	17.48 (7.39)	17.40 (7.13)	17.66 (7.98)	0.585	17.07 (6.50)	20.09 (11.18)	<0.001
INR, median (Q1–Q3)	1.30 (1.14–1.74)	1.30 (1.15–1.75)	1.30 (1.13–1.70)	0.461	1.28 (1.13–1.70)	1.46 (1.20–2.00)	<0.001
NT-proBNP, median (Q1–Q3), pg/mL	5840.00 (2251.00–14 968.00)	6217.00 (2341.00–15 555.00)	4994.00 (2088.38–13 629.75)	0.102	5302.00 (2143.00–13 666.50)	9469.00 (3082.50–3662.75)	<0.001
Creatine kinase (CK), median (Q1–Q3), IU/L	89.25 (46.00–185.19)	85.00 (46.92–185.88)	99.00 (44.00–185.00)	0.509	90.00 (47.00–182.13)	83.12 (37.85–38.63)	0.794
Creatinine, median (Q1–Q3), mg/dL	1.29 (0.94–1.90)	1.27 (0.94–1.88)	1.33 (0.95–1.94)	0.549	1.25 (0.93–1.81)	1.45 (0.97–2.21)	0.007
Blood urea nitrogen, median (Q1–Q3), mg/dL	30.67 (20.83–45.25)	30.67 (20.56–45.08)	30.49 (22.25–45.36)	0.580	29.25 (20.11–43.00)	39.62 (27.06–57.16)	<0.001
Glucose, mean (SD), mEq/L	148.80 (51.49)	148.07 (52.09)	150.49 (50.12)	0.462	148.14 (50.46)	153.01 (57.63)	0.270
Potassium, mean (SD), mEq/L	4.18 (0.41)	4.17 (0.41)	4.18 (0.42)	0.662	4.15 (0.39)	4.32 (0.53)	<0.001
Sodium, mean (SD), mEq/L	138.89 (4.15)	138.85 (4.17)	138.98 (4.12)	0.636	139.01 (3.98)	138.20 (5.02)	0.023
Calcium, total, mean (SD), mg/dL	8.50 (0.57)	8.49 (0.58)	8.54 (0.56)	0.169	8.54 (0.55)	8.24 (0.62)	<0.001
Chloride, mean (SD), mEq/L	102.28 (5.34)	102.27 (5.43)	102.32 (5.14)	0.875	102.17 (5.21)	103.10 (6.00)	0.040
Anion gap, mean (SD), mEq/L	13.93 (2.65)	13.91 (2.68)	13.96 (2.58)	0.763	13.68 (2.41)	15.46 (3.52)	<0.001
Magnesium, mean (SD), mg/dL	2.12 (0.25)	2.12 (0.26)	2.13 (0.24)	0.420	2.11 (0.24)	2.17 (0.29)	0.011
PH, mean (SD)	7.38 (0.07)	7.38 (0.07)	7.37 (0.07)	0.041	7.38 (0.06)	7.36 (0.07)	<0.001
Bicarbonate, mean (SD), mEq/L	26.91 (5.17)	26.90 (5.23)	26.94 (5.02)	0.906	27.37 (4.98)	24.00 (5.42)	<0.001
Lactate, median (Q1–Q3), mmol/L	1.60 (1.20–2.20)	1.60 (1.20–2.20)	1.65 (1.25–2.20)	0.309	1.60 (1.20–2.10)	2.00 (1.36–3.08)	<0.001
PCO2, mean (SD), mm Hg	45.54 (12.86)	45.48 (12.95)	45.67 (12.65)	0.846	45.82 (12.85)	44.07 (12.85)	0.141
Gender				0.685			0.437
Male (n, %)	559 (47.49%)	395 (47.88%)	164 (46.59%)		478 (47.00%)	80 (50.31%)
Female (n, %)	618 (52.51%)	430 (52.12%)	188 (53.41%)		539 (53.00%)	79 (49.69%)
Hypertension				0.072			0.013
No (n, %)	332 (28.21%)	220 (26.67%)	112 (31.82%)		274 (26.94%)	58 (36.48%)
Yes (n, %)	845 (71.79%)	605 (73.33%)	240 (68.18%)		743 (73.06%)	101 (63.52%)
Atrial fibrillation				0.918			<0.001
No (n, %)	646 (54.89%)	452 (54.79%)	194 (55.11%)		578 (56.83%)	67 (42.14%)
Yes (n, %)	531 (45.11%)	373 (45.21%)	158 (44.89%)		439 (43.17%)	92 (57.86%)
Ischaemic heart disease				0.857			0.614
No (n, %)	1076 (91.42%)	755 (91.52%)	321 (91.19%)		928 (91.25%)	147 (92.45%)
Yes (n, %)	101 (8.58%)	70 (8.48%)	31 (8.81%)		89 (8.75%)	12 (7.55%)
Diabetes mellitus				0.390			0.086
No (n, %)	681 (57.86%)	484 (58.67%)	197 (55.97%)		579 (56.93%)	102 (64.15%)
Yes (n, %)	496 (42.14%)	341 (41.33%)	155 (44.03%)		438 (43.07%)	57 (35.85%)
Hypoferric anaemia				0.822			<0.001
No (n, %)	778 (66.10%)	547 (66.30%)	231 (65.62%)		653 (64.21%)	124 (77.99%)
Yes (n, %)	399 (33.90%)	278 (33.70%)	121 (34.38%)		364 (35.79%)	35 (22.01%)
Depression				0.417			0.037
No (n, %)	1037 (88.11%)	731 (88.61%)	306 (86.93%)		888 (87.32%)	148 (93.08%)
Yes (n, %)	140 (11.89%)	94 (11.39%)	46 (13.07%)		129 (12.68%)	11 (6.92%)
Hyperlipidaemia				0.275			0.067
No (n, %)	730 (62.02%)	520 (63.03%)	210 (59.66%)		620 (60.96%)	109 (68.55%)
Yes (n, %)	447 (37.98%)	305 (36.97%)	142 (40.34%)		397 (39.04%)	50 (31.45%)
Chronic renal insufficiency				0.937			<0.001
No (n, %)	747 (63.47%)	523 (63.39%)	224 (63.64%)		625 (61.46%)	122 (76.73%)
Yes (n, %)	430 (36.53%)	302 (36.61%)	128 (36.36%)		392 (38.54%)	37 (23.27%)
Chronic obstructive pulmonary disease				0.697			0.105
No (n, %)	1088 (92.44%)	761 (92.24%)	327 (92.90%)		935 (91.94%)	152 (95.60%)
Yes (n, %)	89 (7.56%)	64 (7.76%)	25 (7.10%)		82 (8.06%)	7 (4.40%)
Race/ethnicity				0.265			0.021
Non-black (n, %)	1020 (86.66%)	709 (85.94%)	311 (88.35%)		872 (85.74%)	147 (92.45%)
Black (n, %)	159 (13.52%)	116 (14.06%)	41 (11.65%)		145 (14.26%)	12 (7.55%)
In-hospital death				0.406			–
No (n, %)	1017 (86.48%)	709 (85.94%)	308 (87.75%)		–	–
Yes (n, %)	159 (13.52%)	116 (14.06%)	43 (12.25%)		–	–

Data are presented as mean±SD, % or median (IQR).

BMI, body mass index; INR, international normalised ratio; LVEF, left ventricular ejection fraction; MCH, mean corpuscular haemoglobin; MCHC, mean corpuscular haemoglobin concentration; MCV, mean corpuscular volume; NT-proBNP, N-terminal pro-brain natriuretic peptide; PaCO₂, partial pressure of carbon dioxide in artery; PH, hydrogen ion concentration; PT, lymphocytes, prothrombin time; RDW, red blood cell distribution width; SPO₂, saturation pulse oxygen.

To investigate independent risk factors of in-hospital mortality, univariate logistic regression analysis was used to assess the significance of variables selected by each method in the derivation group. Variables significantly associated with in-hospital mortality were candidates for multivariate binary logistic regression. Potential non-linearity relationships between candidate continuous variables and in-hospital mortality were explored using a smoothing plot, and nomograms were formulated based on the results of multivariate logistic regression analysis. The nomogram was based on proportionally converting each regression coefficient in multivariate logistic regression to a 0–100-point scale. The prediction models were evaluated in terms of discrimination and calibration. Calibration curves were plotted to assess the calibration of the in-hospital mortality nomogram. Discrimination was assessed by calculating the area under the curve (AUC) of the receiver operating characteristic (ROC) curve and C-statistic testing. The 95% CI was calculated using 500 bootstrap resamples. Decision curve analysis (DCA)²⁰ was used to compare the clinical net benefit associated with the use of these models. The model with the highest AUC and highest clinical net benefit was used to develop a nomogram predicting in-hospital mortality.

The American Heart Association Get With The Guidelines-Heart Failure (GWTG-HF) risk score is a well-validated, widely accepted scoring system for risk stratification regarding in-hospital mortality.⁹ This prediction model was validated in our study groups and compared with our developed model. Because the final published version was a risk score, the calculated GWTG-HF risk score for each of the study patients was used for further analysis. A non-parametric approach, using generalised U statistical theorising to generate an estimated covariance matrix,²¹ was used to analyse areas under the ROC curves and estimate differences in the discriminatory power between the models.

A two-tailed p value of <0.05 indicated statistical significance in all analyses. All analyses were performed using EmpowerStats (V.2.17.8; http://www.empowerstats.com) and R software (V.3.1.4; https://www.R-project.org).

Results

Patient characteristics

The MIMIC-III database contained 58 976 ICU admissions. As shown in the data extraction flowchart (figure 1A), a total of 13 389 patients with a diagnosis of HF were screened. Patients without an ICU record or those with missing LVEF or NT-proBNP data were excluded, and 1177 adult patients were included in this study. According to the grouping method of a previous study,⁹ all patients were randomly divided into a derivation (n=825, 70%) and a validation (n=352, 30%) group.

In our study population of severely ill ICU-admitted patients, the in-hospital mortality rate was higher than that of other HF patients previously reported. There were 159 (13.52%) in-hospital patient deaths. Table 1 shows comparisons of demographics and variables between the derivation and validation groups, and between those who died and survived during hospitalisation. SBP and pH values were lower in the validation group. There were no significant differences in other selected variables between the derivation and validation groups. Consistent with previous reports, the in-hospital mortality rate for African American patients was significantly lower, while that of older patients was considerably higher. A high number of patients who died during their hospital stay had atrial fibrillation, but were found to be less likely to have hypertension, hypoferric anaemia, depression or CKD compared with patients who survived hospitalisation. Patients who died also had lower serum bicarbonate, calcium, sodium, lymphocyte, basophil, platelet count, and body mass index (BMI) levels, and lower pH values. However, HR, RDW, white blood cells, neutrophils, PT, INR, NT-proBNP, creatinine, BUN, potassium, chloride, the anion gap, magnesium and lactate levels in patients who died during their hospital stay were significantly increased. Additionally, urine output in the first 24 hours, SPO₂, temperature and blood pressure levels were decreased in patients who died during their hospital stay. There was no significant difference in LVEF between the surviving and non-surviving patients.

Selected variables

Figure 1B illustrates the methodology that we followed to develop the model.

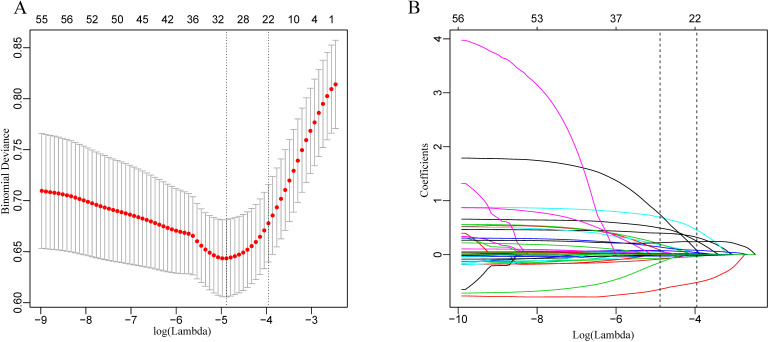
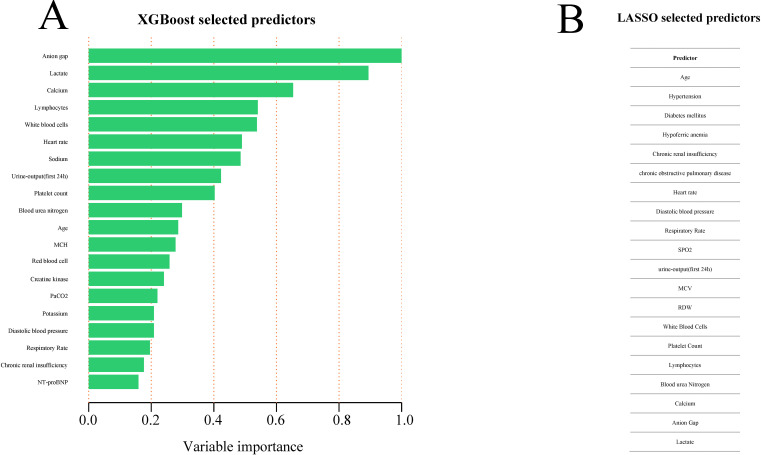
The LASSO regularisation process resulted in 20 potential predictors on the basis of 825 patients in the derivation group (figure 2A, B). Using XGBoost, the 52 selected variables were used to identify patients who had died during their hospital stay in the derivation group. The proportional importance of the 20 top-ranked input variables in the XGBoost model is shown in figure 3A. Figure 3B shows the LASSO-selected predictors (shrinkage parameter, λ=0.0192).

Figure 2.

Demographic and clinical feature selection using the least absolute shrinkage and selection operator (LASSO) binary logistic regression model. (A) Tuning parameter (λ) selection in the LASSO model used 10-fold cross-validation via minimum criteria. The partial likelihood deviance (binomial deviance) curve was plotted versus log(λ). Dotted vertical lines were drawn at the optimal values by using the minimum criteria and the one SE of the minimum criteria (the 1-SE criteria). λ value of 0.0192, with log (λ), −3.9545 was chosen (1-SE criteria) according to 10-fold cross-validation. (B) LASSO coefficient profiles of the 52 features. A coefficient profile plot was produced against the log (λ) sequence. The vertical line was drawn at the value selected using 10-fold cross-validation, where optimal resulted in 20 features with non-zero coefficients.

Figure 3.

Predictor variables selection. (A) Importance of the predictor variables selected by XGBoost algorithm scaled to a maximum of 1.0. (B) Predictor variables selected by LASSO. LASSO, least absolute shrinkage and selection operator; MCH, mean corpuscular haemoglobin; MCV, mean corpuscular volume; NT-proBNP, N-terminal pro-brain natriuretic peptide; PaCO₂, partial pressure of carbon dioxide in the artery; RDW, red blood cell distribution width; SPO₂, saturation pulse oxygen; XGBoost, extreme gradient boosting.

Model development

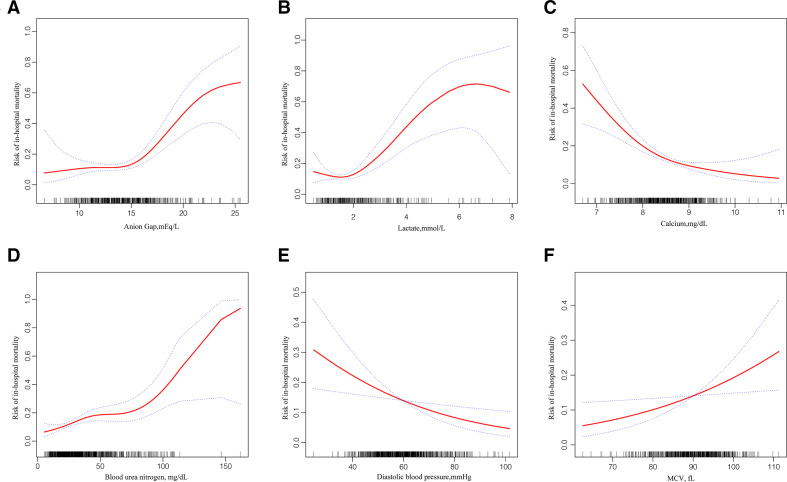
For the derivation group, tables 2 and 3 show the variables selected using XGBoost and LASSO regression that was significantly associated with in-hospital death in the univariate analysis. Statistically significant variables screened from the univariate analysis were included in the non-conditional binary multivariate logistic regression. Among the XGBoost-selected variables, multivariate logistic regression identified anion gap; lactate, calcium, BUN and DBP levels and the presence of CKD as the most significant mortality risk predictors. Among the variables screened using LASSO regression, in addition to the six variables above, hypoferric anaemia and MCV were also identified as statistically significant variables using multivariate likelihood ratio (LR). For continuous variables entered into the multivariate LR model mentioned previously, potential non-linearity in the prediction of in-hospital mortality was explored using a smoothing plot. Hence, the associations of the anion gap and lactate levels with mortality risk were confined to an anion gap of >14.73 mEq/L and a lactate level of >1.5 mmol/L, respectively (figure 4A, B, table 4). A non-linearity relationship was not found in relation to calcium, BUN, DBP and MCV levels (figure 4C-F).

Table 2.

Univariate and multivariate logistic regression analyse variables screened by extreme gradient boosting in the development group

		Univariate analysis			Multivariate analysis
		OR	95% CI	P value	OR	95% CI	P value
Anion gap, mEq/L		1.23	1.15 to 1.32	<0.0001	1.15	1.04 to 1.27	0.0083
Lactate, mmol/L		1.78	1.48 to 2.14	<0.0001	1.51	1.20 to 1.90	0.0004
Calcium, mg/dL		0.39	0.27 to 0.55	<0.0001	0.38	0.26 to 0.56	<0.0001
Lymphocytes, %		0.92	0.88 to 0.95	<0.0001	NA
White cells, ×10∧9/L		1.11	1.06 to 1.16	<0.0001	NA
Heart rate, bpm		1.03	1.02 to 1.04	<0.0001	NA
Sodium, mEq/L		0.95	0.91 to 0.99	0.0197	NA
Urine-output (first 24 hours), mL		1.00	1.00 to 1.00	<0.0001	NA
Platelet count, ×10∧9/L		1.00	0.99 to 1.00	0.0028	NA
Blood urea nitrogen, mg/dL		1.02	1.01 to 1.03	<0.0001	1.03	1.01, 1.04	<0.0001
Age, years		1.02	1.00 to 1.04	0.0197	NA
MCH, pg		1.07	0.99 to 1.16	0.0981	NA
Red cells, ×10∧12/L		0.82	0.58 to 1.14	0.233	NA
Creatine kinase (CK), IU/L		1.00	1.00 to 1.00	0.1528	NA
PaCO2, mm Hg		0.98	0.96 to 1.00	0.0398	NA
Potassium, mEq/L		1.92	1.23 to 2.99	0.0042	NA
Diastolic blood pressure, mm Hg		0.97	0.95 to 0.99	0.0056	0.97	0.95 to 0.99	0.0203
Respiratory rate, bpm		1.10	1.04 to 1.15	0.0002	NA
Chronic renal insufficiency	No	1
	Yes	0.48	0.30 to 0.76	0.0016	0.24	0.14 to 0.43	<0.0001
NT-proBNP, pg/mL		1.00	1.00 to 1.00	0.0047	NA

MCH, mean corpuscular haemoglobin; NA, not available; NT-proBNP, N-terminal pro-brain natriuretic peptide; PaCO₂, partial pressure of carbon dioxide in the artery.

Table 3.

Univariate and multivariate logistic regression analyse variables screened by least absolute shrinkage and selection operator regression in the development group

		Univariate analysis			Multivariate analysis
		OR	95% CI	P value	OR	95% CI	P value
Age, years		1.02	1.00 to 1.04	0.0197	NA
Hypertension	No	1
	Yes	0.45	0.30 to 0.68	0.0001	NA
Diabetes mellitus	No	1
	Yes	0.62	0.41 to 0.95	0.0269	NA
Hypoferric anaemia	No	1			1
	Yes	0.50	0.31 to 0.79	0.0033	0.49	0.29 to 0.83	0.0076
Chronic renal insufficiency	No	1			1
	Yes	0.48	0.30 to 0.76	0.0016	0.27	0.15 to 0.48	<0.0001
Chronic obstructive pulmonary disease	No	1
	Yes	0.39	0.14 to 1.08	0.0708	NA
Heart rate, bpm		1.03	1.02 to 1.04	<0.0001
Diastolic blood pressure, mm Hg		0.97	0.95 to 0.99	0.0056	0.97	0.95 to 0.99	0.0153
Respiratory rate, bpm		1.10	1.04 to 1.15	0.0002	NA
SPO2, %		0.91	0.84 to 0.98	0.0151	NA
Urine-output (first 24 hours), mL		1.00	1.00 to 1.00	<0.0001	NA
MCV, fL		1.04	1.01 to 1.07	0.0188	1.05	1.01 to 1.09	0.0066
RDW, %		1.18	1.09 to 1.27	<0.0001	NA
White cells, ×10∧9/L		1.11	1.06 to 1.16	<0.0001	NA
Platelet count, ×10∧9/L		1.00	0.99 to 1.00	0.0028	NA
Lymphocytes, %		0.92	0.88 to 0.95	<0.0001	NA
Blood urea nitrogen, mg/dL		1.02	1.01 to 1.03	<0.0001	1.03	1.01 to 1.04	<0.0001
Calcium, mg/dL		0.39	0.27 to 0.55	<0.0001	0.37	0.25 to 0.55	<0.0001
Anion gap, mEq/L		1.23	1.15 to 1.32	<0.0001	1.15	1.03 to 1.27	0.0092
Lactate, mmol/L		1.78	1.48 to 2.14	<0.0001	1.53	1.21 to 1.95	0.0005

MCV, mean corpuscular volume; NA, not available; RDW, red blood cell distribution width; SPO₂, saturation pulse oxygen.

Figure 4.

Unadjusted relationship between anion gap (A), calcium (B), blood urea nitrogen (C), lactate (D), diastolic blood pressure (E), MCV (F) and the risk of in-hospital mortality by using Lowess smoothing technique. The y-axis represents the risk of in-hospital mortality. The x-axis spans the range of the variable of interest. MCV, mean corpuscular volume.

Table 4.

Threshold effect analysis of two non-linearity variables

Exposure	Anion gap	Lactate
Turning point (K)	14.73	1.5
<K slope 1	1.01 (0.88, 1.17) 0.8475	0.41 (0.16, 1.05) 0.0619
>K slope 2	1.40 (1.24, 1.57) <0.0001	2.09 (1.67, 2.61) <0.0001
Slope 2–slope 1	1.38 (1.10, 1.72) 0.0053	5.08 (1.80, 14.30) 0.0021
Predicted at K	−2.11 (−2.45, –1.78)	−2.35 (−2.65, –2.04)
LRT	0.006	0.003
95% CI of TP (K)	10.33 to 18.12125	0.86 to 3.33

Two-piece-wise regression was used to examine the threshold effect of the risk factor on the outcome.

LRT, likelihood ratio test; TP, turning point.

We established an in-hospital mortality prediction algorithm (PA) using XGBoost-selected variables as follows: log odds of mortality=4.62536+0.24559×anion gap+0.61542×lactate−1.04993×calcium+0.02687×BUN−1.76330×CKD−0.05633×DBP.

The variance inflation factors (VIFs) for these variables were 1.3, 1.2, 1.1, 1.4, 1.2 and 1.1, respectively.

Based on LASSO regression, the selected variables for the in-hospital mortality PA were as follows: log odds of mortality=3.75020+0.31313×anion gap+0.55440×lactate−1.18119×calcium+0.02857×BUN−1.764666 CKD−0.06122×DBP−1.16783×hypoferric anaemia presence+0.01596×MCV.

The VIFs for these variables were 1.3, 1.2, 1.1, 1.4, 1.2, 1.1, 1.1 and 1, respectively.

Model validation

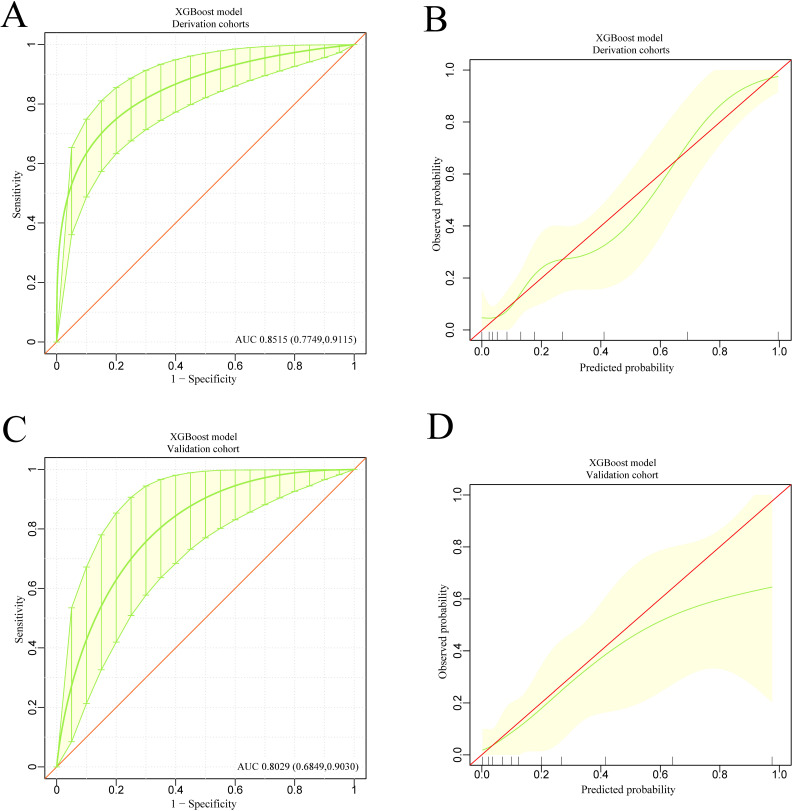
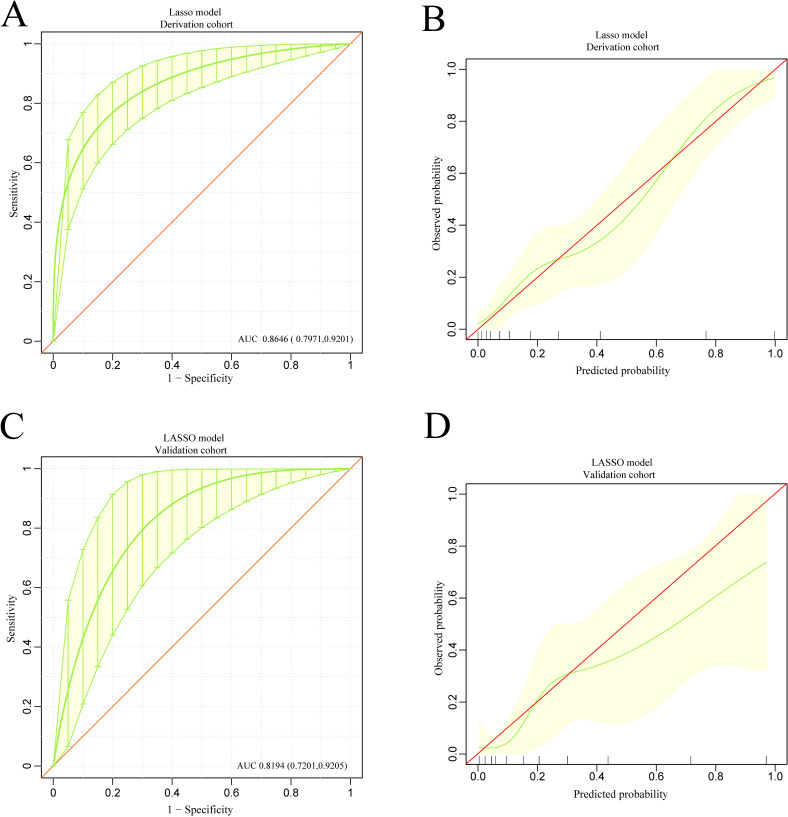
The discrimination and calibration of the XGBoost-based model and the LASSO regression-based model in the derivation and validation groups are shown in figure 5A–D and figure 6A–D, respectively. Using bootstrapping validation, the area under the ROC curve values for the XGBoost model and the LASSO regression model were found to be 0.8515 (95% CI 0.7749 to 0.9115) and 0.8646 (95% CI 0.7971 to 0.9201) in the derivation group, respectively, and 0.8029 (95% CI 0.6849 to 0.9030) and 0.8194 (95% CI 0.7201 to 0.9205) in the validation group, respectively. The 95% CIs of the calibration belt in both the derivation and validation groups did not cross the diagonal bisector line, suggesting that the prediction models had a strong concordance performance in both groups; this indicates the two models performed well in both groups.

Figure 5.

The discrimination and calibration performance of XGBoost model. Plots (A) and (C) show the ROC curves of the XGBoost model in the derivation and validation groups, respectively (AUC=0.8515 versus 0.8029). The light yellow area represents the 95% CIs. 500 bootstrap resamples was used to calculate a relatively corrected AUC and 95% CI. The light yellow area represents the 95% CIs. Calibration curves of the XGBoost model in the derivation (B) and validation (D) groups. Calibration curves depicted the calibration of the XGBoost model in terms of the agreement between the predicted risk of in-hospital mortality and observed in-hospital mortality. The 45° red line represents a perfect prediction, and the green lines represent the predictive performance of the XGBoost model. The closer the green line fit is to the ideal line, the better the predictive accuracy of the XGBoost model is. The light yellow area represents the 95% CIs. AUC, area under the curve; ROC, receiver operating characteristic; XGBoost, extreme gradient boosting.

Figure 6.

The discrimination and calibration performance of the LASSO model. Plots (A) and (C) show the ROC curves of the LASSO model in the derivation and validation groups, respectively (AUC=0.8646 versus 0.8194). 500 bootstrap resamples used to calculate a relatively corrected AUC and 95% CI. The light yellow area represents the 95% CIs. Calibration curves of the LASSO model in the derivation (B) and validation (D) groups. The light yellow area represents the 95% CIs. AUC, area under the curve; LASSO, least absolute shrinkage and selection operator; ROC, receiver operating characteristic.

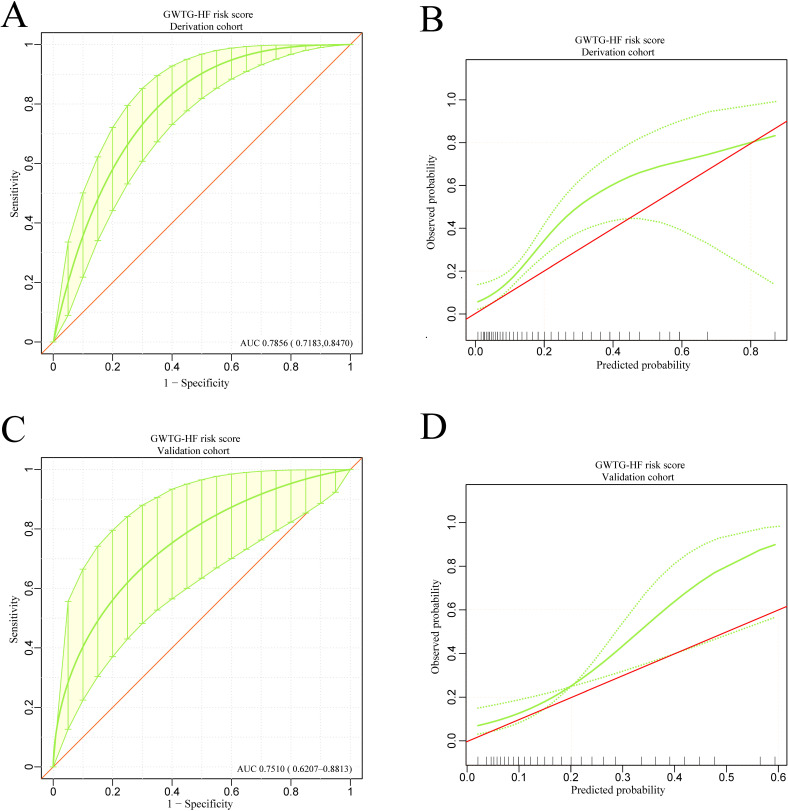
The GWTG-HF risk score is based on information concerning patient age, SBP, BUN, HR, serum sodium, COPD and non-African American ethnicity to predict the risk of in-hospital mortality for patients hospitalised with HF We calculated the GWTG-HF score for all study patients. The discrimination and calibration performance were also validated in our study groups. The ROC curve and the calibration curve of the GWTG-HF risk score in the derivation and validation groups are shown in figure 7A–D. The area under the ROC curve values in the derivation and validation groups were 0.7856 (95% CI 0.7183 to 0.8470) and 0.7510 (95% CI 0.6207 to 0.8813), respectively. Bootstrapping validation was also used. The calibration curve demonstrated that the agreement between prediction and observation in both groups did not present as well as the models above. The DCA showed that a threshold probability within a range from 0 to 0.46 added more net benefit (figure 8A).

Figure 7.

The discrimination and calibration performance of GWTG-HF risk score model. Plots (A) and (C) show the ROC curves of the GWTG-HF risk score model in the derivation and validation groups, respectively (AUC=0.7856 versus 0.7510). 500 bootstrap resamples used to calculate a relatively corrected AUC and 95% CI. Calibration curves of the GWTG-HF risk score model in the derivation (B) and validation (D) groups. The area between two green dotted lines represents the 95% CIs. AUC, area under the curve; GWTG-HF, Get With The Guidelines-Heart Failure; ROC, receiver operating characteristic.

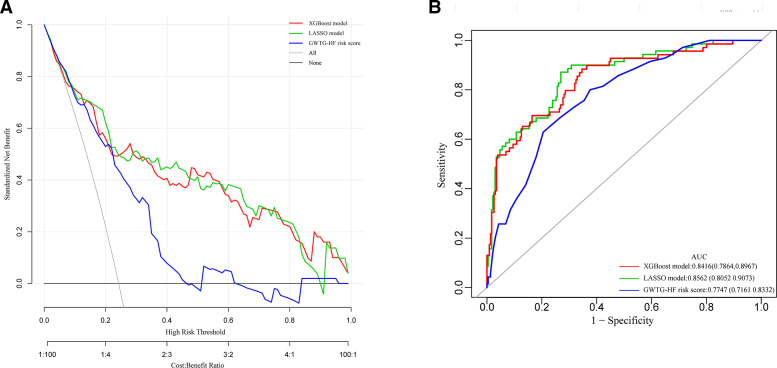
Figure 8.

(A) Pairwise comparison of ROC curves for XGBoost model, LASSO model and GWTG-HF risk score model. (B) Decision curve analysis for XGBoost model, LASSO model and GWTG-HF risk score model. The y-axis measures the net benefit. The red line represents the XGBoost model. The light green line represents the LASSO model. The purple line represents the GWTG-HF risk score model. The grey line represents the assumption that all patients die in the hospital. The black line represents the assumption that no patients die in the hospital. Plot (B) shows the net benefit threshold probability range of the three models respectively, between which using the models in the current study to predict in-hospital mortality adds more benefit than the die-all-patients scheme or the die-none scheme. GWTG-HF, Get With The Guidelines-Heart Failure; LASSO, least absolute shrinkage and selection operator; ROC, receiver operating characteristic; XGBoost, extreme gradient boosting.

The DCA for XGBoost-based model and the LASSO regression-based model are presented in figure 8A. Analysis showed that when the threshold probability for a doctor or a patient was >0 in the XGBoost model, or within a range from 0 to 0.89 in the LASSO model, the models added more net benefit than the ‘treat all’ or ‘treat none’ scheme.

Model comparison

To assess the predictive effectiveness of the XGBoost, LASSO regression and GWTG-HF risk score models, we compared the ROC curves of the three models using generalised U statistics to generate an estimated covariance matrix in our total study population. Figure 8B shows that the area under the ROC curve values for the XGBoost, LASSO regression and GWTG-HF risk score models were 0.8416 (95% CI 0.7864 to 0.8967), 0.8562 (95% CI 0.8052 to 0.9073) and 0.7747 (95% CI 0.7161 to 0.8332), respectively, which were confirmed to be 0.8378, 0.8518 and 0.7743 via bootstrapping validation.

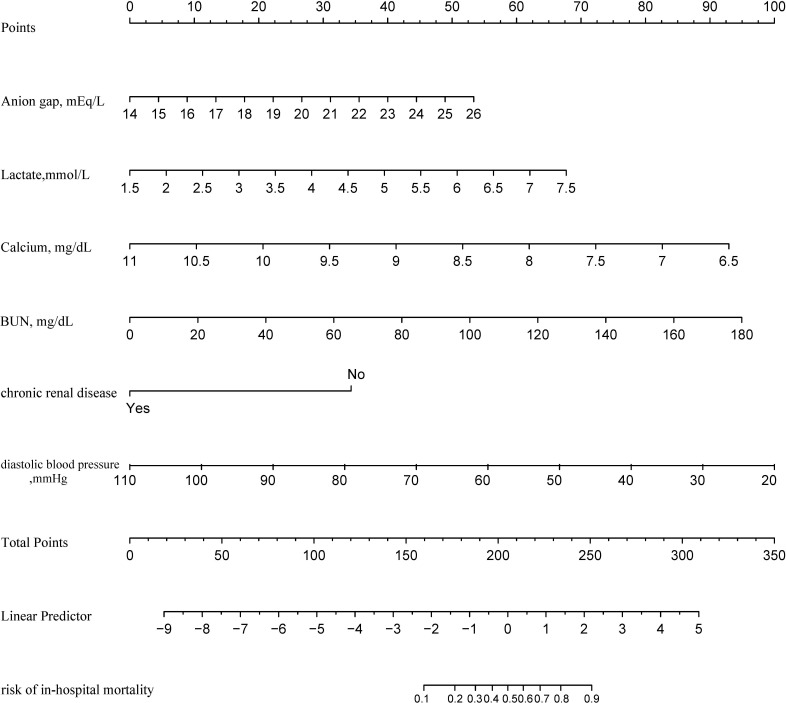
The predictive effectiveness of the XGBoost model and the LASSO regression model were both considerably better than the GWTG-HF risk score model (p<0.05) (table 5). There was no statistical significance difference between the XGBoost model and the LASSO regression model discrimination performance (p=0.1961) (table 5). However, the XGBoost model was more concise because only six variables were included, whereas the LASSO regression model comprised eight variables. Furthermore, as shown in figure 8A, the XGBoost model had a wider net benefit threshold probability range. Therefore, the XGBoost-based model generated in the derivation group was chosen as our final model and is presented as the nomogram in figure 9. In the nomogram, each predictor corresponds to a specific point through drawing a line straight upward to the points axis. The sum of the points located on the total points axis represents the probability of in-hospital mortality when drawing a line directly down to the risk identified on the in-hospital mortality axis.

Table 5.

Pairwise comparison of prediction effectiveness for XGBoost model, LASSO model and GWTG-HF risk score model

Models	XGBoost model vs LASSO regression model			LASSO regression model vs GWTG-HF risk score model			XGBoost model vs GWTG-HF risk score model
	XGBoost model	LASSO regression model	P (compare)	LASSO regression model	GWTG-HF risk score model	P (compare)	XGBoost model	GWTG-HF risk score model	P (compare)
ROC area (AUC)	0.8498	0.8378	0.1961	0.8518	0.7743	0.0299	0.8378	0.7834	0.0471
95% CI lower	0.7993	0.7772		0.8011	0.7097		0.7826	0.7239
95% CI upper	0.8998	0.8921		0.8998	0.8274		0.8847	0.8352
Specificity	0.7273	0.6537		0.7308	0.6239		0.6537	0.6234
Sensitivity	0.8696	0.8841		0.8714	0.8000		0.8841	0.8116
Accuracy	0.7600	0.7067		0.7632	0.6645		0.7067	0.6667
Positive-LR	3.1884	2.5527		3.2367	2.1273		2.5527	2.1549
Negative-LR	0.1793	0.1774		0.1759	0.3205		0.1774	0.3022
Diagnose-OR	17.7778	14.3922		18.3968	6.6364		14.3922	7.1300
Postive-pv	0.4878	0.4326		0.4919	0.3889		0.4326	0.3916
Negative-pv	0.9492	0.9497		0.9500	0.9125		0.9497	0.9172

AUC, area under the curve; GWTG-HF, Get With The Guidelines-Heart Failure; LASSO, least absolute shrinkage and selection operator; LR, likelihood ratio; PV, predictive value; ROC, receiver operating characteristic; XGBoost, extreme gradient is boosting.

Figure 9.

Developed risk of in-hospital mortality nomogram. Each predictor corresponds to a specific point by drawing a line straight upward to the Points axis. After sum of the scores is located on the Total Points axis, the sum represents the probability of in-hospital mortality by drawing straight down to the risk of in-hospital mortality axis. BUN, blood urea nitrogen.

Sensitivity and specificity for predicting in-hospital mortality at different cut-off values are summarised in table 6. At a cut-off value of ≥0.50, specificity was 95% and sensitivity was 53%. Although higher cut-off values resulted in higher specificity, sensitivity rapidly fell to a point at which the model identified that only 50% of patients in-hospital mortality may have been omitted.

Table 6.

Values of sensitivity, specificity and predictive values of the nomogram scores at different cut-off values

Nomogram score/predicted probability	Specificity	Sensitivity	Accuracy	PPV	NPV
≥0.10	0.40	0.95	0.51	0.29	0.97
≥0.20	0.65	0.84	0.69	0.38	0.94
≥0.30	0.80	0.63	0.76	0.44	0.90
≥0.40	0.84	0.58	0.79	0.48	0.89
≥0.50	0.95	0.53	0.86	0.71	0.89
≥0.60	0.95	0.32	0.82	0.60	0.85
≥0.70	0.96	0.21	0.81	0.57	0.83
≥0.80	0.96	0.16	0.80	0.50	0.82
≥0.90	0.99	0.05	0.80	0.50	0.80

The predicted probability/nomogram score is a numeric value representing the prediction model score of the individual patient. The nomogram score can be used as a test parameter, and a positive test result can be defined as a score that is equal to or exceeds a specific cut-off value. A negative test result is defined as a score less than the cut-off value.

NPV, negative predictive value; PPV, positive predictive value.

Discussion

Using data derived from the MIMIC-III database, we developed the first in-hospital mortality prediction nomogram with variables selected by XGBoost model using logistic regression analysis. By using XGBoost and LASSO regression, we screened out independent risk factors for in-hospital mortality of ICU-admitted HF patients. The nomogram may facilitate clinical decision-making for advanced management of ICU-admitted HF patients.

Patients hospitalised with HF often require admission to the ICU. Data from 341 hospitals in the United States showed that the median ICU admission rate concerning hospitalised HF patients was 10% (IQR, 6%–16%).³ ICU admission rates have been reported to be 11.9% in the FINN-AKVA (Finish Acute Heart Failure Study),²² 10.7% in the RO-AHFS registry study²³ and 45% in the ALARM-HF study.²⁴ Many studies have shown that ICU-admitted patients with advanced HF have considerably higher in-hospital mortality rates than HF patients who have been admitted to hospital wards only. The all-cause in-hospital mortality rates for ICU-admitted HF patients and for all study HF patients were 10.6% versus 4.0% in the ADHERE study,⁶ 17.3% versus 6.5% in the RO-AHFS study²³ and 17.8% versus 4.5% in the ALARM-HF study, respectively.²⁴ A decision to admit to intensive care varies depending on both clinician expectations and resource availability, so both factors will add unmeasured variance to outcome studies.

Our study population comprised ICU-admitted patients with advanced HF, and the in-hospital mortality rate was 13.52% (n=159 patients). This rate was considerably higher than that with other HF in-hospital mortality prediction models based on all HF patients, regardless of ICU admission. In the ADHERE in-hospital mortality risk stratification models, their study population in-hospital mortality rate was 4.2%⁷; in the OPTIMIZE-HF(Optimize Heart Failure) prediction models, it was 3.8%.⁸ In the GWTG-HF risk score model, the rate was 2.86%,⁹ and in the risk prediction score system, a single-centre elderly Chinese patient-based model established by Jia et al,¹³ it was 5.58%.

Although the higher in-hospital mortality rate among ICU-admitted HF patients is mainly due to underlying severity of illness, an accurate prognosis is fundamental to many clinical decisions concerning ICU-admitted HF patients. To avoid shortcomings such as over-fitting, and predictor variables with skewed distributions using conventional LR analysis, the XGBoost algorithm and LASSO regression analysis were used to screen independent risk factors of in-hospital mortality using data on demographic characteristics, vital signs, comorbidities and laboratory variables. The anion gap and lactate, calcium, BUN, CKD and DBP levels were included in the XGBoost-based and LASSO-based multiple regression equations. The presence of hypoferric anaemia and MCV were included in the LASSO-based multiple regression equation.

A lot of variables were reported to correlate with mortality in heart failure patients, such as gender, age, BMI, smoking, LVEF, NYHA (New York Heart Association) classification, diabetes mellitus, chronic obstructive lung disease, low SBP, serum creatinine levels, not receiving beta-blockers and not receiving ACEIs/ARBs (Angiotensin-Converting Enzyme Inhibitors/Angiotensin II Receptor Blockers).²⁵ Whereas, our study showed that LVEF was not a predictor of in-hospital mortality of ICU-admitted HF patients. This was also observed in previous small number HF cohorts.^26–29 This may be partly attributed to our relatively small sample size of participants and the duration of hospitalisation is a relatively shorter time. Our study found that the HF patient who had comorbidity of atrial fibrillation had higher in-hospital mortality. Whereas atrial fibrillation is not an independent impact factor that strong enough to affects the outcome after adjusting for other covariates. This is consistent with the previous reports.^7–9

Whether HR was a predictor, the heart failure mortality prediction models showed differently. Some models believe that it affects prognosis strongly^{8 10} and some models disagree.^{7 30 31} In our model, the HR did not appear in the final model. BMI also encountered the same situation. Our study failed to prove that BMI was a predictor of in-hospital mortality of ICU-admitted HF patients. This may be due to the different populations studied and our relatively small sample size. Whether ‘the obesity paradox’ bias our result is hard to say, because critical care-related outcome³² and heart failure³³ both have ‘the obesity paradox’, respectively. We would therefore like to explore these confusions in future studies.

Both hypocalcaemia and hypercalcaemia were reported to associated with an increased short-term mortality risk in heart failure patient.³⁴ Our study showed that hypercalcaemia indicated an adverse outcome. Free serum calcium ions, a very important electrolyte, play a major role in excitation, contraction and relaxation coupling of the myocardium. The alterations of serum calcium homeostasis may adversely affect the prognosis of heart failure patients. Besides, the amount of calcium-binding proteins are significantly altered in end-stage heart failure.³⁵

Given the varying characteristics of the study patients involved, our multivariate logistic regression models did not consider age and HR as independent predictive factors, which have otherwise both been independently identified as associated with an increased risk of mortality in the GWTG-HF risk score model⁹ and the OPTIMIZE-HF prediction model.⁸ BUN levels also substantially contributed to the overall point score in our model, and an elevated BUN level has been associated with increased in-hospital mortality.^7–9 Contrary to previous studies,^7–9 ICU-admitted patients with advanced HF and with CKD as a comorbidity had a lower in-hospital mortality rate in our study. This finding may be due to the ability of patients with CKD to better compensate for changes in cardiac function and to have an earlier chance of receiving continuous renal replacement therapy, which is a therapeutic scheme also recommended in HF management. One study showed that early creatinine changes, 48–72 hours after hospital admission, significantly affected the prognosis in HF patients.³⁶ Given the 12-year date range of MIMIC-III, there may also be unmeasured outcome variance over time.

Consistent with previous studies,^{13 37} our study also identified an acid–base balance as a strong prognostic predictor. Using the Lowess smoothing technique, a non-linearity relationship was found between the anion gap and lactate levels (figure 4). After two-piece-wise regression analysis, with the anion gap at >4.73 mEq/L and the lactate level at >1.5 mmol/L (table 4), these factors were found to be independently associated with increased risk of mortality. Altered calcium homeostasis has been reported to be associated with increased short-term mortality risk.³⁴ Moreover, patients with HF and hypocalcaemia had an increased in-hospital mortality. Our analysis identified DBP as a prognostic predictor rather than SBP, which had been selected in previous prediction models. Other studies have also found that low DBP increased the risks of adverse outcomes in HF patients.^{38 39}

Compared with the GWTG-HF risk score, which has been reported to be a well-validated in-hospital mortality prediction tool for HF patients, both the XGBoost model and the LASSO regression model showed superiority in predictive effectiveness among our study population. Both models demonstrated good discrimination and calibration power in the derivation and validation groups. To obtain a more concise and wider net benefit threshold probability range, we selected the XGBoost model to develop our prediction nomogram.

This study had some limitations. First, apart from the patients’ clinical status, the decision to admit patients to an ICU may be a result of multiple other factors, including practitioner discretion, institutional policies and procedures, and hospital capacity, which may bias our prediction scores. Second, the data extracted from MIMIC database is spread across a number of years (2001–2012), during which the treatment of heart failure had changed greatly, which may weaken the application of our model. Third, as a single-centre study, the population was relatively small. Although the robustness of our nomogram was tested extensively with internal validation using bootstrap testing, it remains uncertain whether the results of this study can be applied to other populations, and further studies with larger numbers of patients in various clinical settings are required to confirm our results. Fourth, data were collected from patient medical records and we relied on the accuracy of the records. Fifth, as this was a retrospective study, we were unable to avoid selection bias. However, we strictly set the inclusion criteria so that the cases and the control patient groups could reflect actual conditions as accurately as possible. Finally, our model may only help to recognise critical clinical situations at bedside quickly, do not provide any more information about potential life-threatening pathophysiological mechanisms.

Conclusion

We developed the first in-hospital mortality prediction nomogram for ICU-admitted HF patients, which can be introduced and routinely be used in the ICUs monitoring techniques to automatically warn the ICU staff at any stage of the disease. With a high AUC of 0.8416 (95% CI 0.7864 to 0.8967) and a wide net benefit threshold range (>0.1), this nomogram can be widely used to enhance more accurate clinical decision-making. Involving a small number of routinely collected variables, this tool can be easily used at the bedside.

Data availability statement

Extra data can be accessed via the Dryad data repository at http://datadryad.org/ with the doi: 10.5061/dryad.0p2ngf1zd.

Ethics statements

Patient consent for publication

Not required.

Ethics approval

All the data presented in this study were extracted from an online database named ‘MIMIC III’, which was approved by the review boards of the Massachusetts Institute of Technology and Beth Israel Deaconess Medical Center. Thus, requirement for individual patient consent was waived because the study did not impact clinical care, and all protected health information was deidentified.