Functional boundaries in the human cerebellum revealed by a multi-domain task battery

Abstract

There is compelling evidence that the human cerebellum is engaged in a wide array of motor and cognitive tasks. A fundamental question centers on whether the cerebellum is organized into distinct functional subregions. To address this question, we employed a rich task battery designed to tap into a broad range of cognitive processes. During four functional MRI sessions, participants performed a battery of 26 diverse tasks comprising 47 unique conditions. Using the data from this multi-domain task battery, we derived a comprehensive functional parcellation of the cerebellar cortex and evaluated it by predicting functional boundaries in a novel set of tasks. The new parcellation successfully identified distinct functional subregions, providing significant improvements over existing parcellations derived from task-free data. Lobular boundaries, commonly used to summarize functional data, did not coincide with functional subdivisions. The new parcellation provides a functional atlas to guide future neuroimaging studies.

Converging lines of research provide compelling evidence that the cerebellum is engaged in a broad range of cognitive functions, well beyond its historical association with sensorimotor control¹. Anatomical tracing studies in non-human primates have revealed reciprocal connections with parietal and prefrontal association cortices². Individuals with lesions to the cerebellum exhibit behavioral impairments on tasks designed to assess non-motor processes such as duration discrimination, attentional control, spatial cognition, emotion perception and executive and language function. Perhaps most intriguing, neuroimaging studies consistently reveal activations of the cerebellar cortex during a diverse set of motor, cognitive, and social and affective tasks³.

This raises the question of whether the cerebellum can be meaningfully subdivided into a discrete set of regions, reflecting distinct functional contributions across diverse task domains. In contrast to the cerebral cortex, the cytoarchitectonic organization is remarkably uniform across the entire cerebellar cortex. Due to this homogeneity, neuroimaging and neuropsychological studies have mostly relied on the macroanatomical folding of the cerebellum along the superior to inferior axis into ten lobules (numbered I–X)⁴. More recently, functional parcellations based on task-free functional magnetic resonance imaging (fMRI) data have been proposed^5–7. However, the degree to which these proposed boundaries correspond to functional divisions remains unclear. Task-based studies have been limited by the lack of a comprehensive neuroimaging data set. A few studies have employed data sets involving multiple tasks^7,8, but the small number of task conditions (<7) and the lack of a common measurement baseline have made it difficult to derive and evaluate task-based functional parcellations. The functional heterogeneity of the cerebellum has also been explored using meta-analytic approaches⁹, which have the disadvantage that data for different tasks come from different groups of participants.

In the present study, we aimed to fully characterize the functional organization of the cerebellar cortex by employing a large and diverse task battery comprising 47 unique conditions designed to engage a broad range of sensorimotor, cognitive and social/affective processes. Using a block design, activation for each task was measured over four fMRI scanning sessions against a common baseline. Our task set was successful in eliciting activation across the entirety of the cerebellar cortex, allowing us to derive a novel parcellation that characterizes the functional profile of cerebellar subregions in unprecedented detail. The breadth of the task sets also enabled us to summarize the functional specialization of each region in terms of the underlying latent motor, cognitive and social/affective features.

We developed a metric to evaluate the strength of the proposed functional boundaries. This allowed us to address the fundamental question of whether there are distinct functional regions in the cerebellum, or whether functional specialization is better described in terms of continuous gradients⁷. The approach is predicated on the idea that, if a boundary between two regions divides functionally heterogeneous regions, then the activation pattern for two voxels that lie within the same region should be more correlated than voxel pairs that span a boundary. Critically, a meaningful functional parcellation needs to be predictive of boundaries for the activation patterns elicited by a different set of tasks. Using this approach, we demonstrate that the cerebellum has discrete functional regions and that our multi-domain task battery (MDTB) parcellation is superior to alternatives in predicting functional boundaries. The new functional parcellation of the cerebellar cortex provides an important step toward understanding the role of the cerebellum across diverse functional domains.

Results

To obtain a comprehensive functional parcellation of the cerebellar cortex, we developed an MDTB of 26 tasks comprising 47 unique task conditions (Fig. 1a and Supplementary Table 1), selected to encompass a wide range of processes required for motor, cognitive and affective/social function. To avoid strong learning-related changes, 24 healthy individuals were trained on the task protocol (approximately 10 h) before scanning. During scanning, each task was performed once per imaging run for a 35 s block (Fig. 1b). This ensured that all tasks were measured against a common baseline, allowing for any between-task comparison. To make this approach feasible, the tasks were split into two sets (Fig. 1a), and each task set was tested in two separate fMRI scanning sessions, resulting in a total of approximately 5.5 h of functional data per participant.

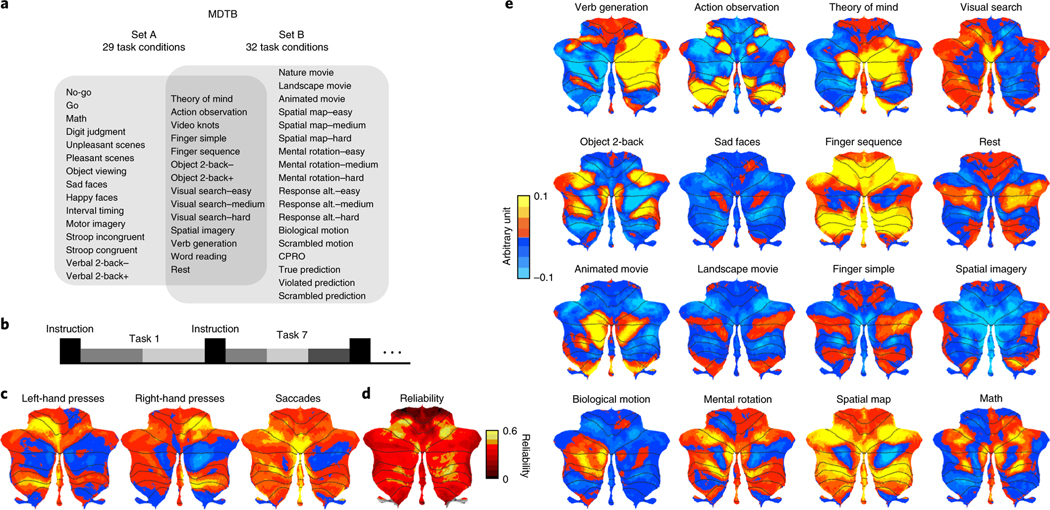
Fig. 1 |. MDtB.

a, Experimental design. A total of four fMRI scanning sessions were collected on the same set of participants using two tasks sets. Each set consisted of 17 tasks, with 8 tasks in common. The tasks were modeled as 29 task conditions in set A and as 32 in set B, with 14 task conditions common across both task sets. b, Timing of each task: 5 s instruction period followed by 30 s of task execution. Tasks consisted of a different number of task conditions (gray bars, range 1–3). c, Unthresholded, group-averaged motor feature maps, displayed on a surface-based representation of the cerebellar cortex¹⁴. d, Across-session reliability of activation patterns for each voxel. e, Group-averaged activation maps for selected tasks, corrected for motor features. The red-to-yellow colors indicate increases and the blue colors denote decreases in activation, relative to the mean activation across all conditions. Activity is normalized by the root-mean-square error of the time series fit for each voxel. CPRO, concrete permuted rules operations.

Identification of motor features from the MDTB.

As a first step, we sought to identify cerebellar regions where the hemodynamic response was closely tied to motor function, specifically hand and eye movements. Our experimental design did not include specific contrasts that isolated each motor component. Instead, we varied the motor demands across task conditions; for example, the motor sequence task involved approximately 40 left and right finger responses, the theory of mind tasks two left-hand responses and the movie tasks no responses. We then generated a motor feature model, which included the number of left- and right-hand responses and the number of saccadic eye movements made per task (see Methods). Using regularized regression, we could then estimate the activation across tasks attributable to motor involvement.

Left- and right-hand movements were associated with activation increases in the two hand motor areas of the cerebellum (Fig. 1c), the anterior hand region located on the boundary of lobules V and VI, and the inferior region in lobules VIIIb (ref. ¹⁰). Saccadic eye movements elicited activation in vermis VI, consistent with the location of the oculomotor vermis in the macaque monkey¹¹. Compared to previous contrast-based human fMRI studies¹², which have yielded relatively inconsistent results, our feature-based mapping approach resulted in an extraordinarily clear localization of eye movement activation to the oculomotor vermis. While these results mainly confirm the well-known functional localization within the cerebellum for movement, they demonstrate that a broad task-based approach without tightly matched control conditions provides a powerful means of revealing functional organization.

MDTB elicits varied activation patterns across the cerebellum.

We then characterized the task-related activation patterns that could not be explained by basic motor features. Overall, we could elicit strong and distinguishable patterns of activation (Fig. 1e and Supplementary Fig. 1) across the cerebellar cortex. To determine the reliability of the activation patterns, we calculated the correlation of the individual, unsmoothed task activation profiles for each voxel across the two sessions of each set. On average, these task activation profiles were reliable (set A: r = 0.43, 95% confidence interval (CI) = 0.39–0.46; set B: r = 0.42, 95% CI = 0.37–0.46; see Supplementary Fig. 2 for individual participants). The resulting voxel-wise reliability map (Fig. 1d) confirmed that this was the case for the entire cerebellar cortex, with the exception of lobules I–IV. These lobules are associated with foot movements^10,13, a feature absent from our tasks.

Qualitatively, the activation patterns elicited by our task sets replicated numerous results obtained in previous neuroimaging studies. For example, right-lateralized activation throughout Crus I, Crus II and VIIb was observed with the verb generation task⁸ while left-lateralized activation throughout Crus I and Crus II was demonstrated with the biological motion task. Consistent with previous working memory studies¹⁴, the n-back tasks activated two distinct lateral regions of lobules VII. Recent evidence for medial Crus I and Crus II activation during movie tasks was also corroborated¹⁵.

The task activation maps also demonstrated some insights that have not been (or not as clearly) reported in the previous literature. The rest condition (contrasted against the mean of all the other conditions) was associated with bilateral activation in a mid-hemispheric region in Crus I and II, effectively forming the cerebellar component of the default mode network⁵. Similar cerebellar regions were strongly activated during the theory of mind¹⁴ and movie tasks¹⁵. The finger sequence and visual search tasks led to strong activation in cerebellar hand and eye movement-related areas, respectively. Given that these activation maps were corrected for movement-related activity, these results indicate that these areas are especially activated during movements with high attentional demands. Finally, the action observation task elicited activation in a distinct set of areas surrounding the motor areas of the cerebellum, especially in the posterior motor representation. When using a dissimilarity measure to construct a representational space for all tasks (Supplementary Fig. 4), the action observation condition emerged as one of the most unique activity patterns.

The passive picture viewing tasks (that is, sad faces) did not elicit much activation in the cerebellum. This is generally consistent with the notion that the cerebellum does not receive cortico-pontine projections from the inferior temporal cortex, a pathway involved in visual object and scene recognition. To quantify this observation, we tested the activation patterns of all possible task conditions against each other. While over 95% of the pairwise comparisons were significant (uncorrected P < 0.001), the most notable exceptions were pairs of the picture viewing tasks (Supplementary Fig. 4a). In contrast, passively watching engaging movie snippets (nature movie, animated movie) resulted in reliable and specific activity patterns (Fig. 1e and Supplementary Fig. 1), probably related to processes required for action perception and social cognition.

Cerebellar lobules do not reflect functional subdivisions.

One way to summarize these activation patterns is to subdivide the cerebellum into functionally distinct regions. However, this approach is only meaningful if there are stable functional subdivisions in the cerebellum that generalize across tasks. To address this fundamental question, we developed an evaluation metric, which we refer to as the distance-controlled boundary coefficient (DCBC). If a boundary divides two functionally heterogeneous regions, then any equidistant pair of voxels within a region should have activation profiles that are more correlated with each other than two voxels that are separated by the boundary (Fig. 2a; see Methods). Specifically, we calculated correlations between voxel pairs using a range of spatial bins (4–35 mm). The difference between the within- and between-region correlations for each spatial bin then served as our evaluation criterion. This method extends standard clustering metrics (that is, silhouette coefficient) to account for spatial distance. Given that the spatial resolution of fMRI is insufficient to cleanly resolve individual folia, the spatial distance was measured in the volume (see Methods for details).

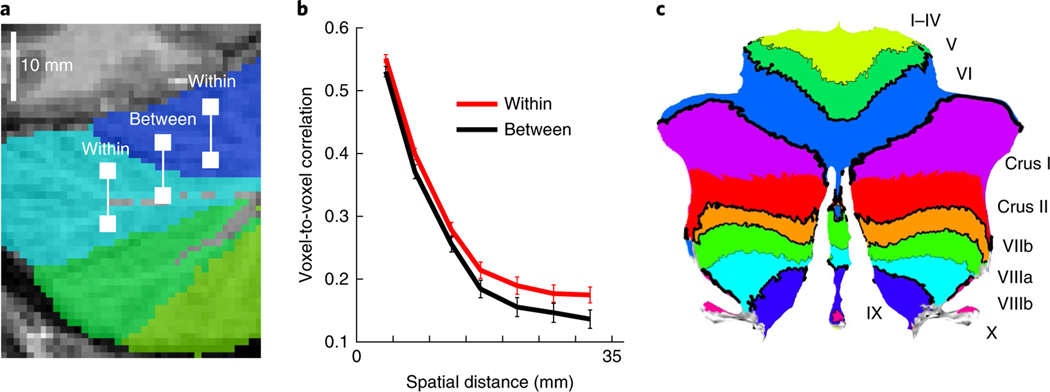
Fig. 2 |. DCBC.

a, Correlations between all pairs of voxels with the same distance were calculated and averaged depending on whether they were ‘within’ or ‘between’ regions. Voxel pairs were then binned according to spatial distance in the volume (4–35 mm in steps of 5 mm). b, Average cross-validated correlation (see Methods) as a function of spatial distance for lobular boundaries. The DCBC is defined as the difference in correlation (within-between) within each distance bin. The error bars show between-participant s.e.m. for n = 24 participants. c, Strength of the boundaries for lobular parcellation, with the thickness of the black lines indicating the DCBC value.

We first employed this evaluation method to determine the degree to which functional boundaries follow the major lobular subdivisions⁵. This is a question of high practical importance given that lobular boundaries are commonly used to define regions of interest for interpreting functional activations in the cerebellum. Notably, the correlation between voxels within a lobule was not much greater than the correlation between voxels that spanned a lobular boundary (Fig. 2b). The correlations, averaged over distances of 4–35 mm, were r = 0.28 (95% CI, 0.26–0.30) within lobules and r = 0.25 (95% CI, 0.05–0.46) between lobules. While statistically significant (t₂₃ = 4.62, P < .01), the difference was very small (DCBC = 0.03). Thus, lobular boundaries do not reflect strong functional subdivisions in the cerebellum.

The DCBC can also be used to evaluate the strength of individual boundaries (Fig. 2c). For example, the superior posterior fissure separating lobule VI from VII was the strongest lobular boundary (DCBC = 0.152), while the primary fissure, which serves as the first principal subdivision of the cerebellum, was relatively weak (DCBC = 0.068). The boundary separating Crus I and Crus II did not predict any functional specialization (DCBC = 0). In sum, many cerebellar fissures did not demarcate a change in function.

MDTB parcellation uncovers strong functional boundaries.

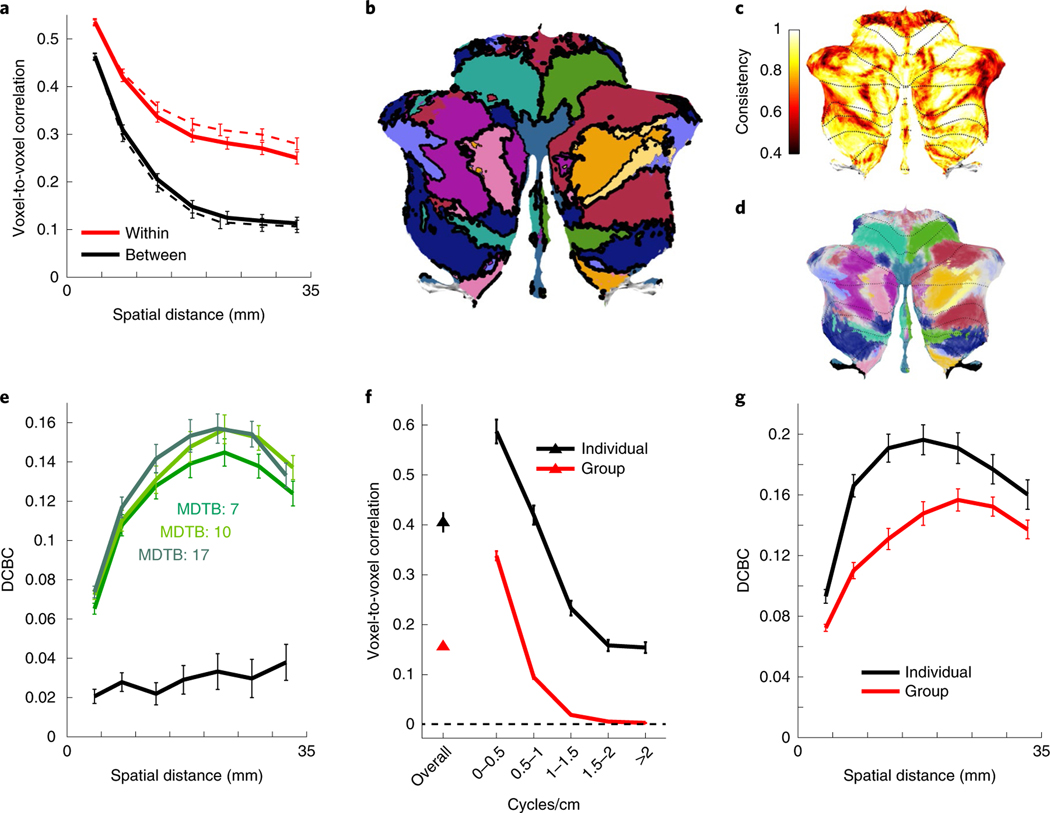
Next, we asked whether a parcellation based on the MDTB data would more clearly identify functional boundaries. We first estimated a group-based parcellation using all of the MDTB data. Using convex semi-non-negative vector factorization, we decomposed the N (tasks) × P (voxels) data matrix into a product of an N × Q (regions) matrix of task profiles and a Q × P matrix of voxel weights. The voxel weights, but not the task profiles, were constrained to be non-negative. Using a winner-takes-all approach, we then assigned each voxel to the region with the highest weight. Figure 3b shows the resulting parcellation using ten regions. For this parcellation, the average DCBC was 0.159 (Fig. 3a, dashed line, t₂₃ = 31.85, P < 1 × 10⁻¹⁰), a value higher than that obtained for the strongest lobular boundary.

Fig. 3 |. MDtB parcellation reveals functional boundaries in the cerebellar cortex.

a, Average cross-validated correlations (see Methods) for ‘within’ (red) and ‘between’ (black) voxel pairs for MDTB parcellation (10 regions). The solid lines indicate the values for the cross-validated estimates; the dashed lines are the estimates for the full parcellation. b, Ten-region MDTB parcellation. The DCBC for each boundary is visualized by the thickness of the black lines. c, Proportion of samples in the bootstrapped analysis (participants) where the voxel was assigned to the same compartment as in the original parcellation. Most voxels had a consistency of assignment >0.6. d, Visualization of boundary uncertainty, using the color scheme in b, but adjusted so that the degree of transparency is indicative of the uncertainty of the assignment. Voxels that were assigned to a single compartment on less than 50% of the cases are shown in gray. e, DCBC as a function of the spatial distance for the lower bound of the three MDTB parcellations (colored lines) and lobular parcellation (black line). f, Within-subject (black) and between-subject (red) reliability of activation patterns overall and across different spatial frequencies. g, DCBC as a function of voxel distance for the ten-region group parcellation (red) and the average of the ten-region individual parcellations (black). Only the cross-validated estimates of the prediction performance for novel tasks are shown. In all panels, the error bars show the between-participant s.e.m. for n = 24 participants.

However, functional parcellations will invariably yield boundaries for a given task set, since training and evaluation data overlap. Critically, a good parcellation should be able to predict boundaries for a new set of tasks. Therefore, we determined the parcellation based on all task conditions from set A and evaluated the boundaries using the unique tasks from set B. We repeated this out-of-sample generalization test in the other direction and averaged the two values. Using this approach, the average DCBC was 0.130, only slightly lower that the non-cross-validated estimate (Fig. 3a; t₂₃ = 24.232, P < 1 × 10⁻¹⁰). The cross-validated DCBC will underestimate the true predictive power of the full parcellation, with true performance on a novel task probably falling between the cross-validated and non-cross-validated DCBC. To remain conservative, we only report the cross-validated DCBC estimates for the remainder of the article.

The exact form of a parcellation depends on the specified number of regions. We also derived a parcellation with 7 (Supplementary Fig. 5d) or 17 regions (Supplementary Fig. 5f). While the 7-region parcellation performed slightly worse than the 10-region parcellation (DCBC = 0.121, t₂₃ = −4.18, P = 0.00036), the 17- and 10-region parcellations performed comparably (DCBC = 0.133, t₂₃ = 1.57, P = 0.131; Fig. 3e). While there was reasonable agreement across the different MDTB parcellations (Supplementary Fig. 5h), some differences in the functional subdivisions for the different parcellations emerged. While our results clearly show that the MDTB parcellations reflect true functional boundaries in the cerebellum, they also make clear that there are a number of equivalent ways to subdivide the cerebellum. Thus, the exact choice of a ‘final’ parcellation is constrained by practical considerations. In this study, we focus on the ten-region parcellation because it provides a useful level of resolution for a full functional characterization.

To assess the stability of the parcellation, we conducted a bootstrap analysis, across both participants and task conditions (for the details, see Methods). The mean Rand coefficient between each of the new parcellations and the original parcellation was 0.646 (95% CI = 0.55–0.73) for the bootstrap across participants and 0.654 (95% CI = 0.58–0.73) across task conditions. To quantify the uncertainty of specific boundaries, we calculated the proportion of bootstrap samples for which each voxel was assigned to the same compartment as in the original parcellation (Fig. 3c). Overall, consistency was good for most of the cerebellum (Fig. 3d). Lobules I–IV had higher uncertainty, probably a consequence of a lack of foot movements in our task battery.

The parcellations described earlier were based on group data. To quantify the variability in functional organization across individuals, we compared the correlation between the task activation maps across participants to the within-participant reliability across the two sessions (Fig. 3f). Overall, 27.7% of the pattern variance was shared between individuals, whereas 72.3% reflected idiosyncratic patterns. A spatial frequency decomposition of the patterns (see Methods) revealed that commonalities across participants were restricted to the low spatial frequencies (<1 cycle cm⁻²; activations of more than 5 mm in size), while the fine-grained patterns were purely idiosyncratic to the participant. Indeed, a parcellation derived from the functional data from the individual significantly outperformed group parcellation in predicting functional boundaries for new tasks for that same individual (Fig. 3g; t₂₃ = 5.88, P < 1 × 10⁻⁵).

In summary, using the MDTB data, we were able for the first time to quantitatively demonstrate the existence of distinct functional regions in the human cerebellum. Our results clearly advocate the adoption of a functional parcellation to replace lobular subdivisions as a tool to summarize functional cerebellar data.

Task-free parcellations identify overlapping but weaker boundaries.

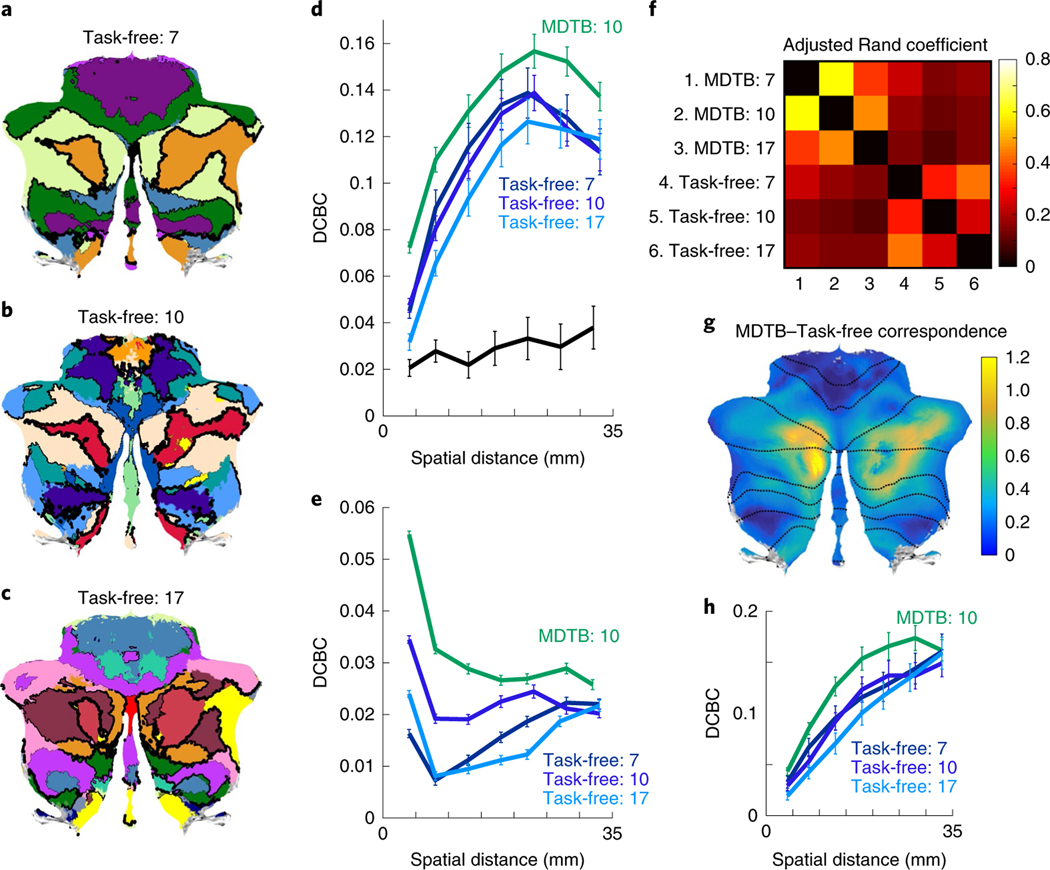
Prior work has leveraged the correlational structure of task-free (or ‘resting state’) fMRI data to derive various parcellations of the cerebellum, using 7⁵, 10⁶ or 17⁵ regions (Fig. 4a–c). These parcellations were only moderately consistent with each other (Fig. 4f), with an average adjusted Rand index of 0.33 (0 = no communality; 1 = perfect match). Correspondence between the different MDTB parcellations was slightly higher (adjusted Rand index = 0.47), indicating more stability across the MDTB parcellations. The average adjusted Rand index between the MDTB and task-free parcellations was 0.15, indicating that there are systematic differences between the two approaches. To determine where task-free and MDTB parcellations diverge, we conducted a searchlight analysis, computing the adjusted Rand index locally using a 1-cm radius sphere for each pair of parcellations. The results demonstrated that task-free and MDTB parcellations corresponded most tightly in the mid-lateral areas of lobule VII. In these ‘default mode’ regions, the agreement between the MDTB and task-free maps (Fig. 4g) was similar to the agreement between MDTB maps (Supplementary Fig. 5h). In contrast, in more lateral aspects of lobule VII, and especially areas engaged in motor control or action observation, the correspondence between task-free and MDTB parcellations was much weaker. This is probably due to the relatively low consistency among the task-free parcellations (Supplementary Fig. 5g).

Fig. 4 |. Comparison of MDtB and task-free parcellations of the cerebellum.

a–c, Cerebellar parcellations based on task-free data with 7, 10 and 17 regions⁶. Thickness of the black lines indicates the DCBC for the corresponding boundary. d, DCBC for different spatial distances for lobular (black), task-free (dark and light blue) and MDTB (green) parcellations. MDTB parcellation was evaluated in a cross-validated fashion (see text). e, Evaluation of the same parcellations on task-based data from 186 HCP participants. f, Matrix of adjusted Rand coefficients between three versions of the MDTB parcellations (7, 10, 17) and the three task-free parcellations (7, 10, 17). g, Correspondence between MDTB and task-free parcellations. A value of 1 (yellow-green) indicates that the adjusted Rand coefficient between task-free and MDTB parcellations is the same size as the adjusted Rand coefficient between MDTB parcellations. Lower values (blue-green) indicate weaker agreement between task-free and MDTB parcellations compared to MDTB on its own. h, Evaluation of MDTB parcellation (derived only from set A) and the task-free parcellations on the three movie tasks from set B. d,e,h, The error bars show the between-participant s.e.m. for n = 24 or n = 186 (e) participants.

We then evaluated whether task-free parcellations could predict functional boundaries in our MDTB data. The average DCBC for the task-free 7-, 10- and 17-region parcellations was 0.109, 0.106 and 0.097 respectively, substantially higher than the lobular parcellation (t₂₃ = 16.849, P < 1 × 10⁻¹⁰; Fig. 4d). Thus, all of the task-free parcellations are, to some degree, able to predict functional boundaries. However, the average task-free DCBC was significantly lower than the ‘lower bound’ for our MDTB 10-region parcellation (t₂₃ = 5.585, P < 1 × 10⁻⁵). This indicates that the MDTB parcellation outperformed the task-free parcellations in predicting functional boundaries on a novel set of task conditions.

Although the task conditions used for evaluation did not overlap with the tasks used for deriving the MDTB parcellation (see also Supplementary Fig. 6), we wanted to ensure that the superior performance of the MDTB parcellation would generalize to a completely separate data set. To this end, we evaluated the MDTB and task-free parcellations using data from 186 participants from the task-based Human Connectome Project (HCP; Fig. 4e) (ref. ¹⁶). Again, the MDTB 10-region parcellation significantly outperformed the three task-free parcellations (7-region: t₁₈₅ = 22.671, P < 1 × 10⁻¹⁰; 10-region: t₁₈₅ = 13.266, P < 1 × 10⁻¹⁰; 17-region: t₁₈₅ = 28.09, P < 1 × 10⁻¹⁰).

To ensure that the higher predictive power of the MDTB parcellation was not solely driven by regions associated with motor control, we reevaluated the DCBC using only the three movie tasks (Fig. 4h). Even though these conditions did not demand any overt movement, the advantage of the MDTB over the 7-region (t₂₃ = 2.7, P = 0.01), 10-region (t₂₃ = 5.3, P < 1 × 10⁻⁵) and 17-region (t₂₃ = 5.1, P < 1 × 10⁻⁵) task-free parcellation remained significant. Overall, these results demonstrate that the advantage of the MDTB over task-free parcellations extends to new data sets and to conditions that do not involve active tasks.

Characterizing activation by cognitive features.

An important advantage of a task-based approach is that we can make inferences about the processes that activate the cerebellar cortex. To characterize the functional profiles in each of the regions across tasks, we used predefined and non-orthogonal features¹⁷. We already successfully applied this approach when characterizing the activation patterns elicited by motor features (Fig. 1c), which could be directly operationalized as the number of finger and eye movements. To extend this approach, we needed to describe each task condition in terms of its underlying cognitive features. Therefore, we turned to the Cognitive Atlas, an online cognitive ontology¹⁸, which summarizes the current consensus in cognitive science of the processes associated with a large array of tasks. To construct a feature space, each of the task conditions was rated on each of the cognitive concepts (see Methods). We then estimated the feature weights for each region using non-negative regression. For visualization purposes, we depicted the top three feature weights for each region (Fig. 5).

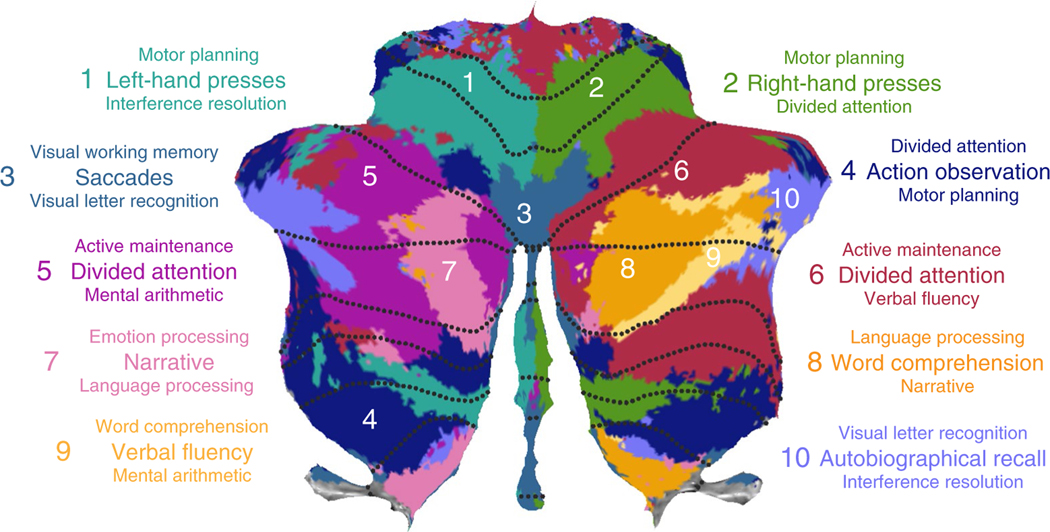
Fig. 5 |. Cognitive descriptors for the ten functional regions in the MDtB parcellation.

The three features that best characterize each region are listed. The font size indicates the strength of these feature weights.

The dominant features describing the three motor regions (regions 1, 2 and 3) were left-hand, right-hand and saccadic eye movements, respectively. The posterior associative motor region (region 4) was driven predominantly by action observation. For the remaining regions, the dominant features related to a range of cognitive processes. Regions 5 and 6 in the mid-hemispheric aspects of Crus I/II, lateralized to the left and right hemisphere respectively, were associated with attention- and working memory-related features such as divided attention and active maintenance.

More medially in both hemispheres were regions 7 and 8, best described by features associated with narrative (region 7) and word comprehension (region 8). Activity in right-hemispheric region 9, lateral to region 8, was best explained by features related to language processing (for example, verbal fluency and word comprehension). Finally, region 10, encompassing the most lateral aspects of Crus I/II was dominated by autobiographical recall. This region shows strong task-free correlations with the frontal pole and other areas related to the default mode network⁵. Overall, activity in the larger proportion of the cerebellum was explained by features related to cognitive, rather than motor, processes¹⁹.

Discussion

Summary.

The aim of this study was to derive a comprehensive picture of the functional organization of the human cerebellum. To do this, a group of participants was scanned over the course of four fMRI sessions while performing a diverse MDTB. Task-evoked activation patterns were leveraged to derive a functional parcellation of the cerebellar cortex. Using a new technique to quantitatively evaluate functional boundaries, we showed that the MDTB parcellation successfully predicted functional boundaries when tested with a novel set of tasks, outperforming existing parcellation based either on task-free fMRI data or on lobular structure.

Parcellations of the cerebellar cortex.

The lobular architecture of the cerebellum has provided, both in neurophysiological and neuroimaging studies, the primary reference for defining subregions^4,20. The macroanatomical folding into ten lobules is well conserved across species⁴ and under strong genetic control²¹. While the results from electrophysiological²² and neuroimaging studies^5,7 have suggested that lobular boundaries do not demarcate functional subdivisions, we present in this study the first quantitative evaluation of this hypothesis. Indeed, lobular boundaries appear to constitute only very weak boundaries in terms of functional organization.

The identified functional regions often spanned multiple lobules, with many of the boundaries traversing the cerebellar cortex along the parasagittal axis. The clear dissociation of anatomical and functional organization of the cerebellum, as revealed in the present study, questions the value of summarizing functional and anatomical data in terms of lobular regions of interest.

As an alternative, we employed our task-related data to develop a parcellation that could comprehensively describe the functional organization of the cerebellar cortex. Critically, the group-based MDTB parcellation predicted functional boundaries for new tasks in the same data set, as well as for a completely separate data set (HCP task data). These findings provide a compelling demonstration of discontinuities in the functional specialization across the cerebellar cortex. Evidence from meta-analyses has suggested the existence of ‘motor’, ‘cognitive’ and ‘affective’ regions of the cerebellum⁸. However, it has also been suggested that functional variation across the cerebellar cortex may be best understood in terms of smooth gradients⁷, without definable boundaries. If this were the case, our DCBC measure, reflecting the difference of within-region to between-region correlations, would have been near zero when tested on a novel task set. Instead, the values were positive, providing a rigorous demonstration of functional boundaries in the cerebellar cortex.

An open question is whether the boundaries defined through our task-based approach relate systematically to anatomical features of the cerebellum identified by molecular techniques²². Specifically, studies investigating aldolase C (zebrin II) expression in Purkinje cells in the rodent²³ and primate brain²⁴ have revealed a series of parasagittal zones across the cerebellar cortex. Olivocerebellar projections respect this zonal organization, with single climbing fiber inputs synapsing onto Purkinje cells that lie within a zone²³. The organization of zebrin II zones remains to be established in the human cerebellar cortex. However, we suspect that the alignment with the organization observed in this study may not be very tight given that the cerebellar hemodynamic signal is primarily reflective of mossy fiber input²⁵. Relative to climbing fibers, mossy fiber innervation patterns are likely to be patchier and more diffuse, potentially spanning multiple zonal regions²⁶.

The boundaries identified from task-free fMRI data were also able to predict task-based discontinuities. This finding is in accord with similar analyses of the cerebral cortex, demonstrating that task-based activation patterns in the neocortex can be predicted to some degree by parcellations obtained from the spontaneous fluctuations in the fMRI signal during rest²⁷. However, our MDTB parcellation outperformed alternative task-free parcellations^5,6 in predicting functional boundaries for completely different tasks within the MDTB and HCP data sets. While the MDTB parcellation was based on fewer participants than the other parcellations (24 versus 1,000), our data set entailed considerably longer scanning time per participant. One notable difference between the task-free parcellations and our MDTB parcellation was that the latter assigned homologous areas in the left and right hemispheres to different regions. This was the case for regions associated with hand movements (regions 1 and 2), working memory (regions 5 and 6) and narrative comprehension (regions 7 and 8). While the parcellation suggests some degree of hemispheric asymmetry within the cerebellum, the task activity profiles between homologous regions also shared many similarities (Supplementary Fig. 7). Second, the MDTB parcellation also indicated that the areas correlated with the default mode network in task-free data could be subdivided into regions related to narrative comprehension (regions 7 and 8), language functions (regions 8 and 9) and autobiographical recall (region 10).

While our group-based map could predict functional boundaries in individual participants, the finer spatial details of the functional organization were idiosyncratic for each individual. Consistent with this, the individual parcellation outperformed the group parcellation in predicting functional boundaries in that individual. Of course, individual parcellations require data collection for each participant using at least a subset of our task battery. It is worth noting that each individual parcellation was obtained on almost 3 h of data per participant, an amount of scanning time that is usually not feasible or practical. In future studies, we aim to determine the required amount of data per participant, identify the best subset of tasks and explore the possibility of combining individual and group data to derive an optimal parcellation.

Insights about functional topography.

An additional advantage of a multi-domain task-based approach for mapping the cerebellum is that we can not only identify functional boundaries, but relate the activation patterns to the task requirements. For many of the tasks in our battery, the activation patterns were in accord with the results obtained in previous fMRI studies that have examined a single or limited set of task domains. Examples in the present study include working memory, hand movement, language and theory of mind tasks.

By using a rich MDTB, we also identified functional regions that had not been observed or well described in previous work. A large and extended region of the cerebellar cortex was activated during action observation (region 4), surrounding the anterior, but to a much larger extent, posterior hand motor region. Interestingly, the action observation region was also activated during complex movement, as shown by the sequence production task. Taken together, these results suggest that anterior motor regions are more related to primary action execution, whereas posterior motor regions are more akin to a ‘premotor’ area, perhaps associated more with action planning and action comprehension. Notably, lesions limited to the posterior cerebellum rarely lead to lasting symptoms of ataxia²⁸.

A second example comes from our motor feature model, which revealed a region around vermis VI that was strongly associated with saccadic eye movements (region 3). This finding is consistent with neurophysiological data from non-human primates showing that this region is associated with oculomotor control¹¹. However, prior neuroimaging studies of the cerebellum have proven controversial regarding this issue. Some studies have also linked this area with eye movements¹², but other studies have argued for a functional role of this region in more complex cognitive and/or affective processes⁷. Based on pilot work for this study and other unpublished observations, we have found it difficult to elicit any cerebellar activation with a simple saccadic eye movement task. In contrast, we observed robust activation in this area during the visual search task, even when accounting for the average number of saccades made during a 30 s block. Thus, our results offer a fresh perspective on the functional role of this region, indicating that the hemodynamic signal is driven by eye movements performed under high attentional demands.

The identification of this oculomotor region is also of interest given that prior studies have suggested that vermal activation in lobule VI is associated with emotional processing⁷. Conditions in our battery designed to engage emotional and affective processing (for example, static images of unpleasant and pleasant scenes, sad and happy faces) only weakly activated this region. Given the strong association of this region with eye movements, it may be that prior activations were more related to differences in saccadic eye movements between conditions, rather than the emotional and affective processing demands of the tasks. Further support for this hypothesis comes from task-free fMRI studies showing that the oculomotor vermis is functionally connected to visual regions of the cerebral cortex^5,7. An obvious challenge for future research is to explore how variation in eye movements, affective processing and attentional demands interact in driving activation within this region.

Conclusions

This article presents a comprehensive MDTB for the human cerebellum, which is unique in its functional diversity and amount of data per individual. The group and individual task contrast maps and the group parcellations can be viewed at diedrichsenlab.org/imaging/mdtb.htm. We anticipate this resource will be useful for two important applications. First, the data, combined with our evaluation criterion, provide a quantitative assessment of functionally defined boundaries, something that has been absent in prior studies. Given that our acquisition parameters covered the entire brain, the methods presented in this study can be used to evaluate parcellations of the neocortex and other brain structures. Second, the novel MDTB parcellations provide an important tool to define functional regions of the cerebellum. Our analyses clearly show that the MDTB parcellations predict functional boundaries in a novel set of tasks better than existing task-free parcellations. Moreover, each region can be characterized by a rich functional task profile, allowing for a characterization of the associated cognitive processes. For future research, the parcellation and associated features can provide a useful guide in designing studies to test specific functional hypotheses and provide a reference for interpreting the results. The MDTB functional parcellation should also be of considerable utility for translational work, given the hypothesized involvement of cerebellar dysfunction in a range of neurological and psychiatric disorders²⁹. A functionally defined parcellation can help reveal dysfunction in specific cerebellar regions and cerebro-cerebellar circuits³⁰, providing further insight into the interaction between the cerebellum and neocortex.

Online content

Any methods, additional references, Nature Research reporting summaries, source data, statements of code and data availability and associated accession codes are available at https://doi.org/10.1038/s41593-019-0436-x.

Methods

Participants.

All participants gave informed consent under an experimental protocol approved by the institutional review board at Western University. A total of 31 participants were scanned performing set A; 26 of this original cohort returned to perform set B (mean break between sessions = 166 d; s.d. = 153 d, with half returning about a year later and the other half having sessions separated by 2–3 weeks). The five participants who did not return for set B were not included in the analyses. Two additional participants were excluded from the analyses because they failed to complete all 32 scanning runs. Therefore, the final sample for the MDTB consisted of 24 healthy individuals (16 women, 8 men; mean age = 23.8 years, s.d. = 2.6) with no self-reported history of neurological or psychiatric illness. All participants self-reported as right-handed (Edinburgh Handedness Inventory > 40). The sample size was chosen to allow for an accurate assessment of inter-participant variability of the functional organization of the cerebellum (see also Life Science Reporting Summary).

Experimental tasks.

The experimental tasks included in set A were chosen to engage a wide range of processing domains (cognitive, motor, affective, social), in many cases drawing on tasks that had previously been shown to engage the cerebellum. While recognizing that our selection process was somewhat arbitrary and that the tasks would differ on a number of different dimensions, our main criterion was to use a large battery that broadly sampled different functional domains. A full description of the tasks, along with the accompanying references, is provided in Supplementary Table 1.

Set B included eight tasks that had been included in set A (shared tasks, for example, theory of mind, motor sequence) and nine unique tasks. The shared tasks provided a means to establish a common baseline across the two task sets. This enables between-task comparison across task sets, which is done by subtracting the mean activation pattern of the shared tasks from each task set. Only tasks that were successful at eliciting activation in the cerebellar cortex in set A were included as shared tasks in set B. For some of the novel tasks, we selected conditions that are thought to assay similar processing domains as in task set A. For example, both sets included working memory tasks, but the tasks involved different stimulus dimensions (for example, verbal working memory in set A and spatial mapping in set B). Other tasks (for example, the naturalistic movie-viewing tasks) were novel in task set B.

Experimental design.

Each set consisted of 17 tasks. In every imaging run, each task was performed once for 35 s. The 35 s block was divided into a 5 s instruction period, where the task name (for example, ‘theory of mind task’), the response effector (‘Use your LEFT hand’) and the button-to-response assignment (‘1 = false belief, 2 = true belief’) were presented on the screen. This was followed by a 30 s period of continuous task performance. In general, novel stimuli were introduced across imaging runs to prevent participants from learning specific stimulus–response associations. The one exception was the motor imagery task where participants were required to imagine playing a game of tennis. The number of trials within the 30 s block varied from 1 (for example, the movie-viewing and mentalizing tasks) to 30 (for example, go/no-go task). Most tasks involved 10–15 trials per block. The motivation for testing all tasks within a scanning run, as opposed to testing one task in each run, was to ensure a common baseline for all tasks, enabling between-task comparisons.

Three of the shared tasks (object 2-back, visual search, semantic retrieval) had a rapid, discrete trial structure (15 per block), whereby each unique stimulus (picture, letter, noun) was presented for 1.6 s, with the response required to be completed within this window, followed by an intertrial interval (ITI) of 400 ms. Three of the shared tasks had a slower discrete trial structure: motor sequence task (trials = 8; trial duration = 4.6 s; ITI = 400 ms); theory of mind (trials = 2; duration = 14.6 s; ITI = 400 ms); and action observation (trials = 2; duration = 14 s; ITI = 1 s). The remaining two shared tasks, spatial imagery and rest, did not have a discrete trial structure (duration = 30 s).

Of the nine unique tasks in set A, six had the rapid discrete trial structure (interval timing, International Affective Picture System (IAPS) affective, IAPS emotional, verbal 2-back, motor imagery, stroop, math, passive viewing: trial = 15, duration = 1.6 s, ITI = 400 ms; go/no-go: trials = 30; duration = 800 ms; ITI = 200 ms). The math task was comprised of 10 trials (duration = 2.6 s; ITI = 400 ms). The motor imagery task did not have a discrete trial structure (duration = 30 s).

Of the nine unique tasks in set B, six had a discrete trial structure: the prediction, spatial map, and response alternatives tasks entailed 6 trials per block (duration = 4.8 s; ITI = 200 ms), the mental rotation task 9 trials per block (duration = 3 s; ITI = 300 ms), the biological motion task 10 trials per block (duration = 3 s; ITI = 0 s) and the concrete permuted rules operations (CPRO) task 4 trials per block (duration = 7.3 s; ITI = 200 ms). The three movie-viewing tasks (landscape, animated and nature) did not have a discrete trial structure (duration = 30 s).

Hand assignment across tasks.

For each task requiring responses, the responses were made with either the left, right or both hands using four-key button boxes. Hand assignment was consistent for sets A and B for the shared tasks. For tasks requiring two-choice discrimination, responses were made with the index or middle finger of the assigned hand, while responses for tasks requiring four-choice discrimination were made with the index and middle fingers of both hands. By including a motor feature model in our analysis, we could account for the motor requirements across the tasks.

Behavioral training.

For each task set, participants completed 3 d of training before the first scanning session. Training included all of the tasks with the exception of the rest condition and the three movies (set B). For each set, the three training sessions took place over the course of 4–7 d (set A: mean number of days = 5.2, s.d. = 3.5; set B: mean number of days = 4.4, s.d. = 1.8).

The first day was used to familiarize participants with the requirements for each of the 17 tasks. Participants were instructed to carefully read the instructions. When ready, they initiated a 35 s training block. The number of training blocks differed depending on the perceived level of difficulty of the task. For example, the two-alternative forced choice picture-based tasks (IAPS affective, IAPS emotional) were practiced for three blocks, while the stroop task was practiced for seven blocks. During this training session, a run consisted of consecutive blocks of the same task. Online feedback was provided for response-dependent tasks (green or red squares to indicate correct or incorrect responses, respectively). At the end of each run, an overall accuracy score was provided concerning performance on the tasks requiring a button response.

On the second training day, switching between tasks was introduced. Participants were given 6 runs of training, with each run composed of 1 block for each of 11 tasks that required manual responses. As on day 1, the timing for the first four runs was self-paced, with the participants allowed to read the instructions at their own pace before initiating the 30 s block. For the final two practice runs, the instruction phase was limited to 5 s, thus introducing the protocol that would be used in the scanner. Training on this day only included tasks that required overt responses. On the third training day, participants practiced all 17 tasks in four 10-minute runs (35 s per task), emulating the protocol to be used in the scanner sessions.

This training program ensured that participants were familiar with the requirements for each task and had considerable experience in switching between tasks. In this manner, we sought to minimize the impact of learning during the scanning sessions. On the third training day, performance was asymptotic, with participants correct on at least 85% of the trials for all of the tasks (range = 85–98%; see Supplementary Fig. 3).

Eye tracking.

Eye tracking data were recorded on the third training session to obtain an estimate of saccadic eye movements for each of the tasks. An algorithm implemented in the Eyelink Toolbox (v. 1.5.0)³¹ identified saccadic eye movements as events where eye velocity briefly exceeded a threshold of 30 degrees s⁻¹. These data, tabulated as the mean number of eye movements per task, were included as a motor feature in the second-level feature model. Eye tracking data from two participants in set A and three participants in set B were not obtained due to technical problems. However, since eye movement behavior was consistent across participants, we used group-based estimates.

Scanning sessions.

Participants completed four scanning sessions in total, two with set A and two with set B. The first scanning session for each set was conducted within a few days of the final training session (set A: mean = 2.0 d, s.d. = 1.6 d; set B: mean = 2.2 d, s.d. = 1.7 d) and the second scanning session was completed no more than 7 d after the first scanning session (set A: mean = 3.1 d, s.d. = 2.5 d; set B: mean = 2.7 d, s.d. = 2.3 d). Each scanning session consisted of eight imaging runs (10 min per run). Each of the 17 tasks was presented once for 35 s in each imaging run, producing 16 independent measurements per task. The task order was randomized across runs. To reduce order effects within each set, no two tasks were presented in the same order in two different runs. The order within each run, as well as the order of the runs, was kept constant for all participants. This procedure was chosen to allow for across-participant analyses on the time series level (results not presented in this article). As noted earlier, when possible, novel stimuli were used in each run to reduce the recall of specific stimulus–response associations.

Image acquisition.

All fMRI data were acquired on a 3T Siemens Prisma at the Centre for Functional and Metabolic Mapping at Western University. Whole-brain functional images were acquired using an echo-planar imaging sequence with multi-band acceleration (factor 3, interleaved) and in-plane acceleration (factor 2), developed at the Center for Magnetic Resonance Research at the University of Minnesota. Imaging parameters were: repetition time = 1 s; field-of-view = 20.8 cm; phase encoding direction P to A; 48 slices; 3 mm thickness; in-plane resolution 2.5 × 2.5 mm². Gradient echo field maps were acquired for distortion correction of the echo-planar imaging images due to B₀ inhomogeneities (repetition time = 0.5 s, fieldof-view = 24 cm, 46 slices with in-plane resolution of 3 × 3 × 3 mm³). We also acquired online physiological recordings of both heart and respiration during each functional run. For anatomical localization and normalization, a 5 min high-resolution scan of the whole brain was acquired (magnetization-prepared rapid acquisition gradient echo; field-of-view = 15.6 × 24 × 24 cm³, at 1 × 1 × 1 mm³ voxel size).

Image preprocessing.

Data preprocessing was carried out using tools from SPM12 (ref. ³²), Caret (v. 5.65)³³ and spatially unbiased infratentorial template (SUIT v. 3.3)²⁰, as well as custom-written scripts written in MATLAB 2015b. For all participants, the anatomical image was acquired in the first scanning session. Functional data were realigned for head motion within each session, and for different head positions across sessions using the six-parameter rigid body transformation. The mean functional image was then co-registered to the anatomical image and this transformation was applied to all functional images. No smoothing or group normalization was applied.

General linear model (GLM).

A GLM was fitted to the time series of each voxel separately for each imaging run. The 5 s instruction phase for all tasks was modeled using a single regressor, but was not included in later analyses. Each task was modeled using a boxcar regressor of 30 s, or a combination of multiple regressors if the block contained sub-conditions. These regressors could be 2 boxcar regressors of 15 s each (for example, the verb generation task where one sub-condition is word reading and the other is verb generation), 3 boxcar regressors of 10 s each (for example, visual search, display sizes of 4, 8 or 12) or 2 event-related regressors (for example, the stroop task, where each trial was congruent or incongruent). The rest condition was not modeled explicitly, but rather used as an implicit baseline in the model.

The quality of the GLM in modeling the blood-oxygen-level dependent signal response was determined by measuring the consistency of the activation patterns in the cerebellum across runs. This measure indicated that it was advantageous to omit the traditional high-pass filtering operation before the linear model (default operation in SPM). Instead, we opted to rely on the high-dimensional temporal autocorrelation model (the FAST option in SPM) to determine the optimal filtering, implemented in the GLM estimation. The beta weights from the first-level GLM were univariately pre-whitened by dividing them by the square root of the residual mean-square image. To include rest as a task condition in all subsequent analyses, we added a zero as an estimate for the rest condition and then removed the mean for each voxel across all conditions. As such, the beta weights expressed the amount of activation elicited by each condition relative to the mean of all conditions.

To combine activation estimates across the two tasks sets, the mean of the shared tasks was removed separately for each set. Both sets were then combined, retaining the repeated estimates for the shared task. This resulted in a total of 61 estimates (set A = 29; set B = 32) for the 47 unique conditions. The activation patterns were re-centered by removing the overall mean across all 61 conditions.

Cerebellar spatial normalization.

The SUIT toolbox (v.3.3) in SPM12 was used to isolate the cerebellum from the rest of the brain and provide a normalization to a spatially unbiased template of the cerebellum³⁴. The resulting cerebellar isolation mask was hand-corrected to ensure that it did not contain any shared voxels between the superior cerebellum and the directly abutting cerebral cortical regions of the inferior temporal and occipital cortex.

The probabilistic maps for the cerebellum were normalized into SUIT space using the diffeomorphic anatomical registration through exponentiated lie algebra algorithm³⁵. This algorithm deforms the cerebellum to simultaneously fit the probability maps of cerebellar gray and white matter onto the SUIT atlas template. This non-linear deformation was applied to both anatomical and functional data. The activation estimates (that is, the beta weights) and residual mean-square images from the first-level GLM were resliced into SUIT space. All images were masked with the cerebellar mask to avoid activation influences from the inferior occipital cortex. All data were visualized on a surface-based, flat-map representation of the cerebellar cortex in the SUIT toolbox. The flat-map representation allows the spatial extent of task-evoked activation patterns to be fully visualized. Note that this flat map is not a true unfolding of the cerebellar cortex, but averages over a substantial number of folia. Therefore, it is meant for display purposes only¹⁴.

Motor feature model.

Our primary goal was to study task-evoked activation patterns in the cerebellum beyond the well-known domain of motor function. Although not designed explicitly to measure motor-related activation, the 61 task conditions differed in the number of manual responses, as well as eye movements. To account for these motor-related activations, we generated a motor feature model (task conditions × three motor features). For the hand movements, we entered the number of left- and right-hand presses for each task during the scanner runs. For eye movements, we used the group-averaged eye movement data from the third training day to estimate the number of saccades for each task condition. All motor features were encoded in terms of movements s⁻¹ and z-normalized.

To extract and remove the motor-related activation across tasks, the 3 motor features were combined with an indicator matrix that had a 1 for each of the 61 task conditions. To estimate and subsequently remove the influence of the motor features, we estimated the linear model with L2-norm regression (fixed λ of 0.01) from the beta estimates of each participant (task conditions × voxels × participant). The average of all task conditions was used as a baseline measure and subtracted from the motor-corrected activation estimates. The activation estimates for the shared tasks were first averaged; then a group average was computed for the purposes of visualization on the cerebellar flat map¹⁴.

Reliability of activation patterns.

To determine intra-participant reliability across the entire cerebellar cortex, we calculated the correlation between the average activation estimates for the first and second session for each task set, separately for each participant. To obtain an overall reliability, we stacked the 29 (A) or 32 (B) activation estimates for all cerebellar voxels into a single vector and calculated the Pearson correlation between the two estimates. For Fig. 1e, this analysis was also performed for each voxel separately. The group-averaged correlations were then visualized on the cerebellar flat map.

Spatial frequency of activation patterns.

To determine how much of the variance of the activation patterns was common to the group relative to how much was idiosyncratic to the individual participants, we calculated two correlations, one between task-activity maps between two sessions for the same participant (as for reliability) and the second between sessions of different participants. Correlations were computed on all gray matter voxels in SUIT space. To determine the spatial scale of these common activation patterns, we decomposed the volume image for each task condition into five spatial frequency bands ranging from 0 to 5 cycles cm⁻². This decomposition was done separately for each participant, study, session and task condition. The within- and between-participant correlations were then computed for each spatial frequency band.

Evaluating functional boundaries.

We developed a method to evaluate functional boundaries from fMRI data. The rationale of the method is that, if a boundary is dividing two functionally heterogeneous regions, then two voxels that lie within the same region should have more similar functional profiles than two voxels that are in different regions (Fig. 2a; equation (1)). Because functional organization tends to be smooth, the correlation between two voxels will be higher for two adjacent voxels and fall off as the spatial distance increases¹⁰. To control for distance, we calculated the activation pattern correlations for all pairs of voxels separated by a specific Euclidean distance, using spatial bins ranging from 4 to 35 mm. Of course, it would have been preferable to measure the distance on the cerebellar cortical sheet, rather than in the volume. However, a veridical surface reconstruction of the cerebellar folia is only possible for resolutions higher than 0.2 mm³⁶. The use of volumetric distances will slightly favor lobular boundaries, since two voxels within the same lobule will tend to be closer on the cerebellar cortex than two voxels separated by a fissure, even if their distance in the volume is matched. To exclude spatial correlations that were driven by noise, we used a cross-validated correlation. Using u_i,1 to represent the functional profile (zero-meaned) of voxel i from one session, and u_j,2 the functional profile of voxel j from the other session, the correlation was calculated as:

$$r=\frac{\frac{1}{2}{\sum }_{i,j}\left(u_{i,1}^{\text{T}}{u}_{j,2}+u_{i,2}^{\text{T}}{u}_{j,1}\right)}{\sqrt{{\sum }_{i,j}\left(u_{i,1}^{\text{T}}{u}_{i,2}\right){\sum }_{i,j}\left(u_{j,1}^{\text{T}}{u}_{j,2}\right)}}$$ (1)

where the sum was done on all voxel pairs i,j in the corresponding 5 mm bin. Separate correlations were calculated for voxel pairs from the same region (within) and those where the voxel pairs came from different regions (between). We excluded voxels where the term u_i^T_,1u_i,2 was negative, since it indicated the absence of any reliable tuning across the two sessions. The difference between the within-region and between-region correlations defined the DCBC. A positive DCBC value indicates that voxel pairs originating from the same region are more functionally related than voxel pairs that lie across boundaries. The DCBC was calculated for each participant and spatial bin separately, and then averaged.

The DCBC can serve not only as a global measure of a parcellation (averaging across the cerebellum and spatial bins), but also as a measure to evaluate the strength of individual boundaries. For the latter, we first identified boundaries using an edge-based connectivity scheme³⁷. The strength of a given boundary is defined by the DCBC calculated only on the voxel pairs from the two regions that are separated by that boundary. To visualize boundary strength, the thickness of the boundary on the flat map was based on its DCBC value.

We applied this boundary evaluation procedure to MDTB parcellations, as well as parcellations based on lobular boundaries or task-free fMRI data. The lobular parcellation was obtained from a probabilistic atlas of the human cerebellum²⁰ that includes regions for lobules I–IV, V, VI, Crus I, Crus II, VIIb, VIIIa, VIIIa, IX and X. To ensure that that poor performance of the lobular parcellation was not due to inaccuracies in detecting the lobular boundaries, we repeated the analysis using a manual lobular parcellation in five participants. The parcellation from this sample predicted functional boundaries about as well as the one derived from the probabilistic atlas (DCBC: 0.022 versus 0.025; t₅ = 1.441, P = 0.209). The task-free 10-region parcellation⁶ was based on data archived as part of the HCP, while the other two were based on a large 1,000-person data set collected at Harvard and Massachusetts General Hospital⁵. All parcellations were sampled into SUIT space and evaluated using our MDTB.

MDTB data set parcellation.

To derive a parcellation from the MDTB, we used the activation profiles of gray-matter voxels averaged in SUIT volumetric space across participants. We used convex non-negative matrix factorization³⁸ to decompose the N (tasks) × P (voxels) data matrix into a product of an N × Q (regions) matrix of task profiles and a Q × P matrix of voxel weights. The voxel weights, but not the task profiles, are constrained to be non-negative. Furthermore, the task profiles are convex combinations of the raw data. Compared to other decomposition methods, such as independent component analysis, this method has the advantage that voxels cannot be explained by an inverted or negative regional task profile. This constraint is also reasonable given that mossy fiber input, the main neural signal driving the blood-oxygen-level dependent signal response in the cerebellum, is excitatory²⁵. To ensure convergence, we started the decomposition with random initializations and selected the iteration with the best reconstruction of the original data. A winner-takes-all approach was adopted to assign each voxel to the region with the highest weight.

To allow for a direct comparison with existing task-free parcellations^5,6, we used parcellations with 7, 10 and 17 regions (Supplementary Fig. 5d–f). Parcellations involving regions within this range achieved similar reconstruction accuracy and quality of functional boundaries.

We also derived separate parcellations for each participant to determine whether boundaries could be predicted better using an individual approach. An advantage of the individual parcellation is that idiosyncrasies of within-participant organization are captured. The disadvantage is that individual parcellations are derived on substantially fewer data than the group.

Bootstrap analysis.

To obtain a measure of boundary uncertainty, we performed bootstrap analyses across both participants and task conditions. For participants, we repeatedly drew 24 participants (with replacement) from our sample, averaged the data and derived a new functional parcellation. To be able to relate the parcellations to each other, each parcellation used the original solution as a starting value. For the task conditions, we repeatedly drew 47 task conditions (with replacement) from our data, again deriving a new parcellation each time. For each analysis, we repeated this process 100 times.

To evaluate the consistency of the parcellations globally, we calculated the adjusted Rand index, which measures the correspondence between two parcellations (0 = overlap not different from chance, 1 = perfect overlap). For a regionally specific analysis, we counted the number of times that each voxel was assigned to the same (most frequent) region. For visual display (Fig. 3d), we then used this assignment certainty to determine the transparency of the region coloring (<50% = fully transparent, 100% = fully opaque).

Evaluation of functional parcellations.

To evaluate the group and individual MDTB parcellations, we wanted to know how well functional boundaries could be predicted for each participant using a completely novel set of tasks. Because we did not acquire data with a third, independent task set, we used the existing data to estimate lower and upper bounds of predictability. For the lower bound, we derived the parcellation using the data from set A and evaluated it with the data from set B, using the unique tasks only. This procedure was then repeated with the task sets reversed and the results were averaged across the two cross-validation folds. Note that the outcome of this analysis will probably result in a lower value than would be obtained with the final segmentation, since each parcellation is based on half of the available data. As such, we used this estimate as an approximate lower bound. We also evaluated a parcellation derived from both sets A and B. We evaluated this parcellation as before, excluding the shared tasks from both task sets to make the estimate consistent with the lower-bound estimate. Because there is overlap between the data used for training and evaluation, the performance measure is overfitted and, therefore, was taken as an approximate upper bound. The true performance of the full parcellation, if applied to a completely new task set, would probably fall between these lower and upper bounds.

The anatomical and task-free parcellations could be directly evaluated on the MDTB data since each parcellation was derived from independent data. For consistency, we excluded the data from the shared tasks in the evaluation set.

To evaluate the degree to which the results depended on the similarity of the tasks in the training and test sets, we repeated the analysis, this time selecting the seven most distinct task conditions in each test set (Supplementary Fig. 6). The conditions were selected by computing the distance between activity patterns for each test condition to each training condition (Supplementary Fig. 4a). Then, we identified for each test condition the closest match in the training set and selected the seven test conditions for which this closest match was most dissimilar.

To further validate our results, we evaluated the MDTB and task-free parcellations on the task-based data from the HCP data set (https://db.humanconnectome.org)¹⁶. We used data from the 214 most recently added participants (scanned at 3T). Of the 214, 186 participants had complete data sets and these constituted our final sample. For each participant, we evaluated the parcellations on a set of 22 contrast maps from 7 tasks (all against rest).

Representational structure of task-related activation patterns.

Representational similarity analysis¹⁷ was used to investigate the representational structure of task-related activation patterns from the MDTB cerebellar data. The dissimilarity between the motor-corrected activation patterns was measured for each pair of task conditions using the cross-validated Mahalanobis distance, using the imaging runs as independent partitions³⁹. To calculate the distances between conditions across the sets, we first subtracted the mean of the shared task conditions from each imaging run. Cross-validation ensures that the average (expected) value of the dissimilarity measure is 0 if the two activation patterns only differ by noise. This allowed us to test for significant differences between activation patterns using a one-sample t-test against 0.

Classical multidimensional scaling was employed to visualize the distances between all possible pairs of task conditions. For the purposes of visualization, the pairwise distances for the shared tasks were averaged so that there were 47 (rather than 61) task conditions in the representational dissimilarity matrix. Multidimensional scaling projects the N-dimensional representational dissimilarity matrix into a lower-dimensional space so that distances from the higher space are preserved with as much integrity as possible. Multidimensional scaling was performed on the group-averaged representational dissimilarity matrix and the first three dimensions were visualized in a three-dimensional space.

Feature-based approach.

The power of our task-based approach in studying the cerebellum is that we can identify the involvement of each region across functional domains and different task variations. To summarize the task activation profiles for each region, we used a feature-based encoding model. The features included the three motor features (see earlier) and cognitive features, selected to capture the hypothetical mental processes involved in each task. To derive these features, we used an online cognitive ontology¹⁸, an atlas of tasks and the concepts associated with those tasks. Of the 815 concepts currently included in the atlas, 46 were judged to provide an appropriate and sufficient characterization of the tasks in our battery, creating a feature matrix (47 task conditions × 46 features). For example, features such as semantic knowledge and lexical processing were associated with tasks such as verb generation and semantic prediction; emotion recognition was associated with the IAPS emotional processing task and the biological motion task. As with the motor feature model, each feature was z-standardized and feature weights for each region were estimated with non-negative regression. For visualization purposes, the three highest weights for each region were computed.

Statistical analysis and inference.

Unless otherwise noted, all statistical tests were based on the n = 24 participants of our sample, considering participant as a random effect. Therefore, all t-tests were repeated measures with 23 d.f. Only the analysis presented in Fig. 4e is based on the HCP task data and was therefore based on n = 186 participants. All t-tests were two-sided. Data distribution was assumed to be normal, but this was not formally tested.

Reporting Summary.

Further information on research design is available in the Nature Research Reporting Summary linked to this article.