Modularity and robustness of frontal cortical networks

Guang Chen; Byungwoo Kang; Jack Lindsey; Shaul Druckmann; Nuo Li

doi:10.1016/j.cell.2021.05.026

. Author manuscript; available in PMC: 2022 Jul 8.

Published in final edited form as: Cell. 2021 Jul 1;184(14):3717–3730.e24. doi: 10.1016/j.cell.2021.05.026

Modularity and robustness of frontal cortical networks

Guang Chen ^1,⁴, Byungwoo Kang ^2,^3,⁴, Jack Lindsey ², Shaul Druckmann ^2,^5,^*, Nuo Li ^1,^5,^6,^*

PMCID: PMC8312479 NIHMSID: NIHMS1707554 PMID: 34214471

Summary

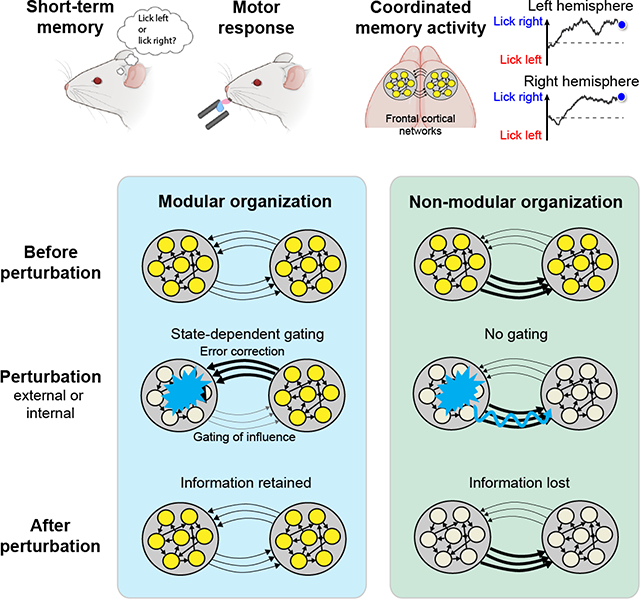
Neural activity underlying short-term memory is maintained by interconnected networks of brain regions. It remains unknown how brain regions interact to maintain persistent activity while exhibiting robustness to corrupt information in parts of the network. We simultaneously measured activity in large neuronal populations across mouse frontal hemispheres to probe interactions between brain regions. Activity across hemispheres was coordinated to maintain coherent short-term memory. Across mice, we uncovered individual variability in the organization of frontal cortical networks. A modular organization was required for the robustness of persistent activity to perturbations: each hemisphere retained persistent activity during perturbations of the other hemisphere, thus preventing local perturbations from spreading. A dynamic gating mechanism allowed hemispheres to coordinate coherent information while gating out corrupt information. Our results show that robust short-term memory is mediated by redundant modular representations across brain regions. Redundant modular representations naturally emerge in neural network models that learned robust dynamics.

Graphical Abstract

graphic file with name nihms-1707554-f0001.jpg

Introduction

Persistent neural activity bridges past and future events and underlies cognitive functions such as short-term memory (Barak et al., 2013; Funahashi et al., 1989; Fuster and Alexander, 1971; Romo et al., 1999). Persistent activity is distributed across interconnected brain regions (Chafee and Goldman-Rakic, 1998; Hernandez et al., 2010; Kopec et al., 2015; Svoboda and Li, 2018), and it is thought that interactions between brain regions maintain persistent activity and coordinate behavior-related information (Christophel et al., 2017; Svoboda and Li, 2018; Wang, 2001). At the same time, a widely held assumption is that distributed information produces robustness to internal and external perturbations, whereby corrupt information in one brain region can be compensated for by redundant information in other regions (Barrett et al., 2016; Christophel et al., 2017; Fornito et al., 2015). To mediate robustness through distributed information, multiple parallel representations must be compartmentalized such that perturbations in one representation do not propagate into another (Fornito et al., 2015; Kitano, 2004; Sporns and Betzel, 2016). Within interconnected networks, corrupt information can spread and degrade connected representations (Brummitt et al., 2012). It remains poorly understood how interconnected brain regions interact to coordinate coherent information that supports behavior while maintaining their integrity when parts of the network are perturbed.

Neurons in mouse anterior lateral motor cortex (ALM) exhibit persistent activity that instructs future choice (Allen et al., 2017; Chabrol et al., 2019; Chen et al., 2017b; Gao et al., 2018; Guo et al., 2014a; Li et al., 2015; Wu et al., 2020; Zatka-Haas et al., 2020). The two cortical hemispheres are strongly coupled through the corpus callosum (Harris et al., 2019; Oh et al., 2014; Winnubst et al., 2019) and both hemispheres work together to maintain choice information (Li et al., 2016). Choice information is robust to transient perturbations of ALM activity in one hemisphere and the recovery of choice information is dependent on input from the contralateral hemisphere (Inagaki et al., 2019; Li et al., 2016).

We examined how ALM hemispheres interact to maintain robust persistent activity by simultaneously recording population activity in both hemispheres. We found highly coordinated activity across hemispheres that maintained coherent parallel representations of choice information. Perturbation revealed unexpected variability in the organization of frontal cortical networks across a population of mice. In some mice, unilateral perturbations did not spread and each hemisphere maintained choice information during perturbation of the other hemisphere, thus exhibiting a modular organization across hemispheres. Such modular organization was required for the robustness of persistent activity to perturbations. In mice lacking modular organization, unilateral perturbations corrupted information in both hemispheres and these mice were less able to maintain choice information after perturbations.

Conceptually, the two hemispheres must be independent to retain choice information during unilateral perturbations. At the same time, the hemispheres must communicate to coordinate coherent information and recover information after perturbations. Theoretical analysis of the neural data and modeling suggest that the interhemispheric interaction was dynamically gated by activity state to simultaneously meet these two conflicting requirements. State-dependent gating organized the two hemispheres into modular representations that limited corrupt information from spreading while permitting coordination between hemispheres. Mice with more potent gating showed superior short-term memory behavior even in absence of external perturbations. Our results show that robust persistent activity is maintained by redundant modular representations distributed across multiple brain regions.

Results

Coordinated parallel representations distributed across cortical hemispheres

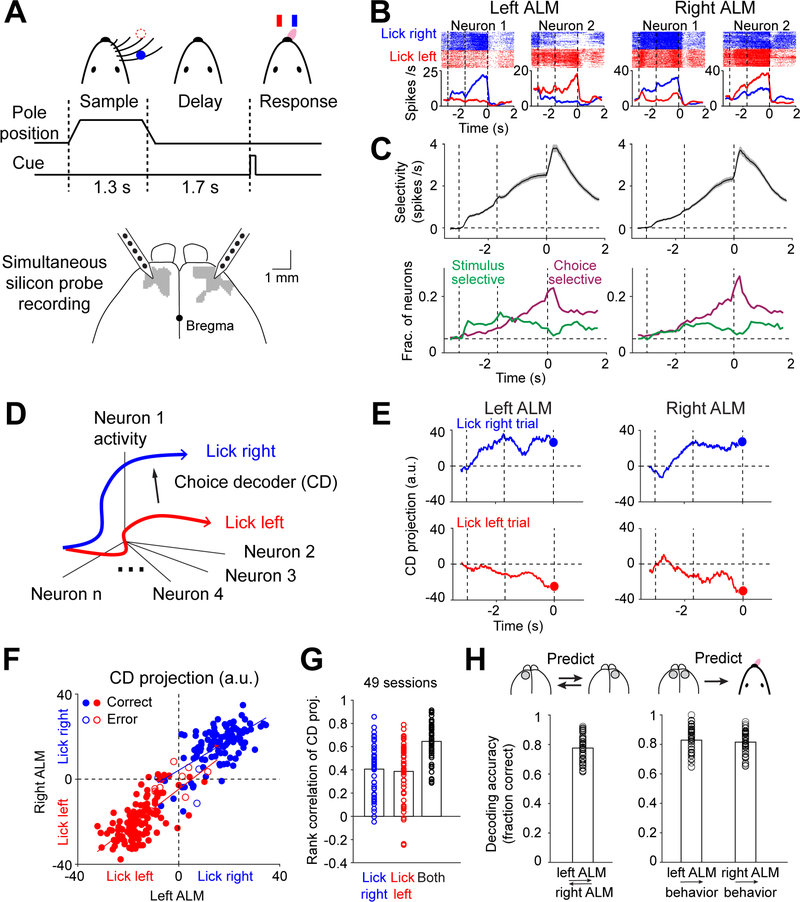
Mice performed a delayed response task in which they discriminated the location of a tactile stimulus (anterior or posterior) using their whiskers and reported the object location using directional licking (“lick left” or “lick right”) to obtain a water reward. A delay epoch (1.7 s) separated the sensory instruction and the behavioral response. This required mice to use short-term memory to produce correct choice responses (Figure 1A, Methods).

Anterior lateral motor cortex (ALM) is critical for this short-term memory (Chen et al., 2017b; Guo et al., 2014a; Li et al., 2015) (Figure 1A). To examine how information is maintained across two ALM hemispheres, we simultaneously recorded populations of neurons from both hemispheres (21–159 neurons in each hemisphere, average 71, Methods). A similar fraction of pyramidal neurons in each hemisphere distinguished trial type (left ALM, 1328/3189, right ALM, 1318/3160, Wilcoxon rank sum test, p<0.05, corrected for multiple comparisons; Figures 1B). In each hemisphere, spatially intermingled neurons were selective for either “lick left” or “lick right” trials (Figures S1A–C; left ALM, 51% “lick left”, 49% “lick right”; right ALM, 53%, 47%).

We examined what information is maintained by ALM activity. Trials differed in object location (‘stimulus’, anterior vs. posterior), lick direction (‘choice’, left vs. right), and reward (‘outcome’, rewarded vs. unrewarded). We separately computed neuronal selectivity for stimulus, choice, and outcome (Methods) (Chen et al., 2017b; Zatka-Haas et al., 2020). Selectivity during the sample epoch mostly reflected stimulus (Figures 1C and S1D). Stronger stimulus selectivity was observed in the left ALM (Figures 1C and S1E; p<10⁻⁴, paired two-tailed t-test), contralateral to the tactile stimulus (Figure 1A). Choice selectivity arose during the late sample epoch, ramped up through the delay, and reached a maximum during movement initiation (Figure 1C). Choice selectivity was similar in both hemispheres (Figures 1C and S1F; p=0.26, paired two-tailed t-test). Outcome selectivity was limited to the response epoch in both hemispheres (Figure S1D). These results show that the two ALM hemispheres have parallel representations of choice information during the delay epoch.

To examine the coordination of choice representations across hemispheres, we projected the population activity onto a linear choice decoder (CD) (Kaufman et al., 2015; Kiani et al., 2014; Li et al., 2016). Since the delay epoch activity mostly reflected upcoming choice (Figures 1C and S1D), we built linear decoders that were weighted sums of the neurons’ delay activity to best predict the future lick direction, with separate decoders for the left and right hemispheres (Methods, Figure 1D). This allowed us to monitor choice encoding in a neuronal population by looking at the decoder activity. The trajectory of choice encoding was highly correlated between hemispheres. On single trials, when the left hemisphere signaled “lick left” or “lick right”, the right hemisphere almost always signaled the same direction (Figures 1E and S1G). Correlation developed during the late sample epoch, reaching a maximum during the late delay epoch (Figure S1H).

To quantify this correlated choice encoding across hemispheres, we examined the trajectory values at the end of the delay epoch (before the ‘go’ cue). Trajectory endpoints were highly correlated across trials (Figure 1F–G). Choice encoding (lick left or lick right) in each hemisphere could be reliably read out from the decoder activity of the other hemisphere (Figure 1H, Methods). Similarly, the mouse’s lick direction could be predicted from the decoder activity of either hemisphere (Figure 1H). Thus, the two hemispheres have coherent choice encoding and each hemisphere contains redundant choice information.

The correlated ALM choice activity could reflect interactions between the two hemispheres or a common external input (Figure S2A). Widespread cortical activity correlates with movements (Musall et al., 2019; Salkoff et al., 2020; Stringer et al., 2019). To examine whether the correlated ALM delay activity could be explained by ongoing movements during the delay epoch, we measured orofacial movements using highspeed cameras and related movements to ALM activity using a convolutional neural network model (Figure S2B–C, Methods). The model predicted a substantial fraction of ALM activity in each hemisphere based on movements (Figure S2D). Subtracting the movement-related activity still left considerable correlation between the two hemispheres (Figure S2E), suggesting that activity reflecting ongoing movements was not the primary driver of the correlation between hemispheres.

Finally, we directly examined whether the correlated activity arose from external input by optogenetically photoinhibiting ALM (Methods). We silenced activity in both hemispheres during the early delay epoch, using 4 laser spots on each hemisphere that covered the entire ALM and surrounding regions (Figure S2F, Methods). After bilateral photoinhibition, trial-type selectivity in both hemispheres was abolished (Figures S2G). Importantly, activity trajectories of the two hemispheres also became significantly less correlated after photoinhibition (Figures S2H–I). Video analysis showed that ongoing movements were not sufficient to explain the decorrelated ALM activity after photoinhibition (Figure S2J–K). This suggests that the correlated activity across hemispheres during the delay epoch could not be fully explained by external input and likely reflected interactions between the two hemispheres.

These results show that the two ALM hemispheres contained parallel representations of choice during short-term memory and the two hemispheres interact to coordinate coherent choice information to support behavior.

Distinct interhemispheric interactions underlie parallel representations

To directly probe interactions between the two ALM hemispheres, we photoinhibited activity in one hemisphere and measured the impact on the other hemisphere (Methods). We performed simultaneous bilateral recording and photoinhibition in a large population of mice (135 sessions, 39 mice).

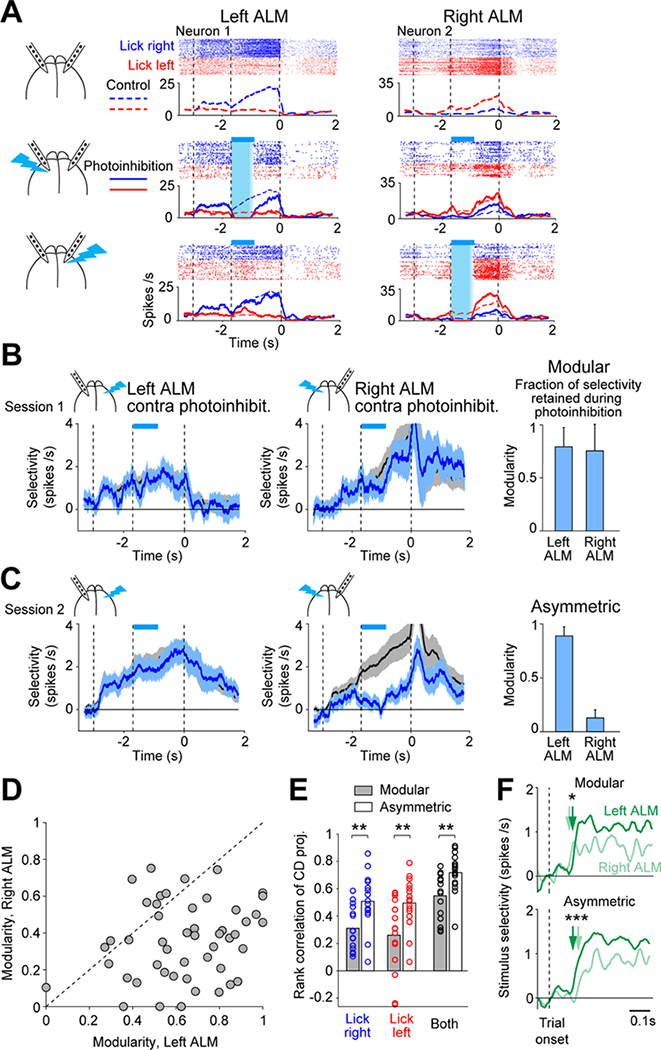
In many mice, neurons in each hemisphere maintained trial-type selectivity while the other hemisphere was silenced (Figure 2A). An example session is shown in Figure 2B. When the right ALM was silenced, selectivity in the left ALM was largely retained. Similarly, selectivity in the right ALM was maintained when the left ALM was silenced. Thus, the two hemispheres exhibited a modular organization, where each hemisphere compartmentalized its representation during perturbations of the other hemisphere.

Interestingly, other mice exhibited different interhemispheric interactions. Figure 2C shows an example session from a different mouse. When the left ALM was silenced, selectivity in the right ALM was abolished. In contrast, when the right ALM was silenced, selectivity in the left ALM was little affected. Thus, the interaction was asymmetric, where the left ALM appeared to drive selectivity in the right ALM and the right ALM could not maintain its representation while a perturbation was applied to the left ALM.

To quantify the degree to which each hemisphere could maintain its representation during perturbations to the other hemisphere, we calculated the ‘modularity’ of each hemisphere as the fraction of selectivity retained during the epoch when the other hemisphere was silenced (Figures 2B–C, Methods). The modularity of each hemisphere varied along a continuum across individual sessions (Figures 2D and S3A–E).

The variability in modularity was not due to heterogeneous sampling of neurons (Figures S3F–G), variability in photoinhibition (Figures S3H–I), or arousal state (Figures S3J). In sessions exhibiting modular organization, choice information was also less correlated between hemispheres in control trials (Figures 2E and S4A–F). In asymmetric sessions where one hemisphere drove the other, cross correlation analysis of activity trajectories between the left and right ALM showed congruent direction of activity flow in control trials (Figures S4G–H). These results show that differences in modularity reflect distinct interhemispheric interactions.

Modularity varied across individual mice, and also varied to a smaller degree within mouse across sessions (Figures S5A–E). Strain, gender, or age did not explain inter-subject variability (Figures S5F–G). We considered the possibility that distinct interhemispheric interactions reflected differences in mice behavior induced by the task. In asymmetric sessions, the left ALM always drove the right ALM (Figure 2D). In the standard task, mice used the right whiskers to discriminate object location, which could result in stronger tactile input to the left hemisphere. Consistent with this idea, stronger stimulus selectivity was observed in the left ALM (Figures 1C and S1E). Additionally, stimulus selectivity emerged earlier in the left ALM in asymmetric sessions (Figure 2F). The timing difference may reflect an imbalance of stimulus input to the two hemispheres, where the left ALM received stimulus input and in turn drove selectivity in the right ALM.

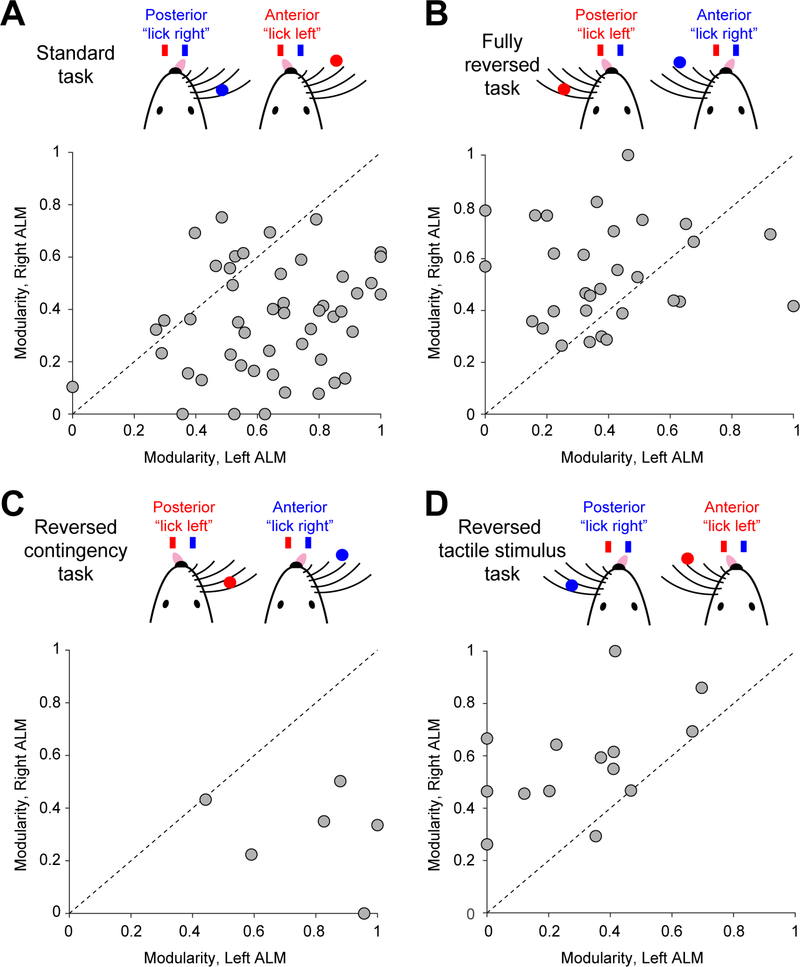
To test these notions, we trained a different group of mice on a task in which the tactile stimulus was placed on the left side of the mouse. In addition, the sensorimotor contingency was reversed, i.e., the posterior object location corresponded to “lick left” (Figure 3B). In this fully reversed task, the asymmetry of interhemispheric interactions was reversed such that the right ALM drove the left ALM (Figure 3B). Further systematic task manipulations showed that the side of the tactile stimulus, rather than the sensorimotor contingency, drove the shift in interhemispheric asymmetry (Figures 3C–D).

Figure 3. — (A) Modularity of left ALM versus right ALM in the standard task. Dots, sessions. 49 sessions, 17 mice. Data from Figure 2D.

(B) Fully reversed task. 30 sessions, 10 mice.

(C) Reversed contingency task. 6 sessions, 5 mice.

(D) Reversed tactile stimulus task. 14 sessions, 6 mice.

See also Figure S5.

These results reveal distinct organizations of frontal hemispheres across individual mice. The interhemispheric interactions could be shaped by task, suggesting that distinct organizations were not hardwired. An imbalance of stimulus input to the two hemispheres may shape the asymmetry of interhemispheric interactions.

Modular organization increases the robustness of choice information to perturbations

Taking advantage of this individual variability, we examined the relationship between distinct organizations across hemispheres and robustness of choice information to unilateral perturbations.

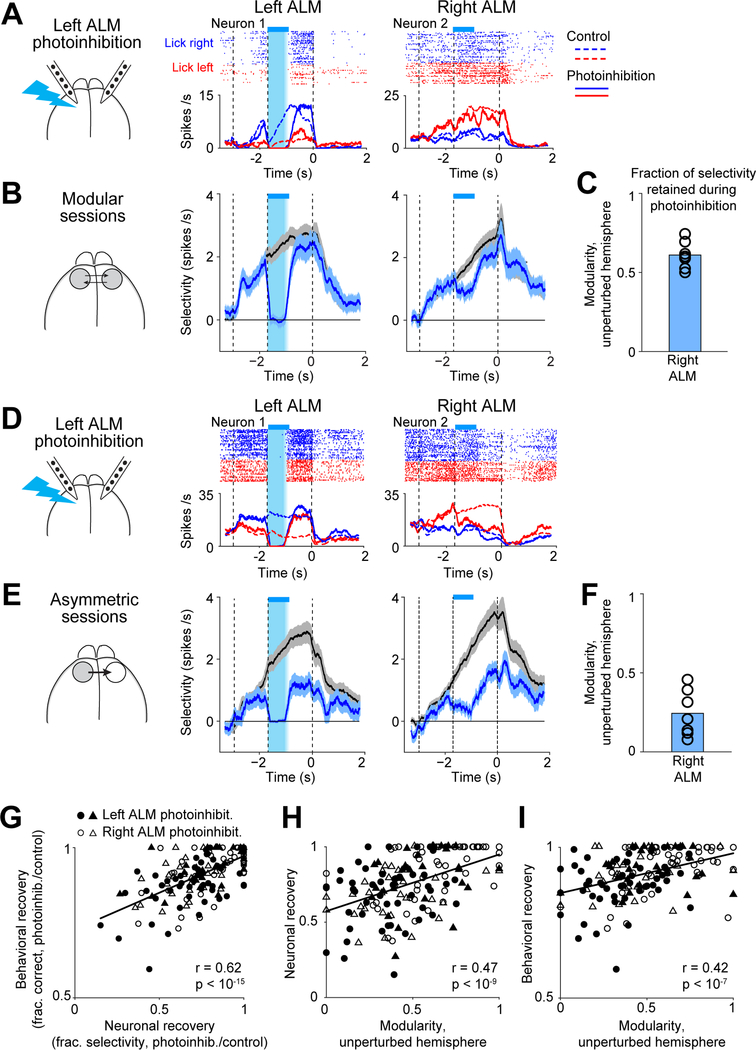
We measured the maintenance of trial-type selectivity following transient unilateral photoinhibition (Figure 4A, Methods). Selectivity recovered on average at the end of the delay epoch (control trial selectivity, 2.87 spikes/s; photoinhibition, 2.24 spikes/s), and behavioral choice was only slightly affected (control, 83.9% correct, photoinhibition 77.3%, n=79 sessions, 27 mice). However, recovery was variable across sessions (Figures 4A–F). The recovery of selectivity was correlated with the behavioral performance after photoinhibition (Figure 4G). Thus, different sessions exhibited different degrees of robustness to perturbations.

Modularity of the unperturbed hemisphere strongly predicted the recovery of selectivity and behavioral performance following unilateral photoinhibition (Figures 4H–I). In sessions where both hemispheres exhibited high modularity, the recovery was the strongest (Figures 4B–C). In asymmetric sessions where the driven hemisphere could not maintain selectivity during perturbations of the driver hemisphere, selectivity did not recover after the perturbation (Figures 4E–F). Recovery of selectivity was coordinated across hemispheres where selectivity recovered to the same degree in both hemispheres (Figures 4B and 4E). The degree of recovery in both hemispheres was predicted by the modularity of the unperturbed hemisphere (Figure 4H).

Thus, despite redundant choice information across the hemispheres (Figure 1), modular organization was required for maintenance of choice information after unilateral perturbations.

Analysis of interhemispheric interactions reveals state-dependent gating

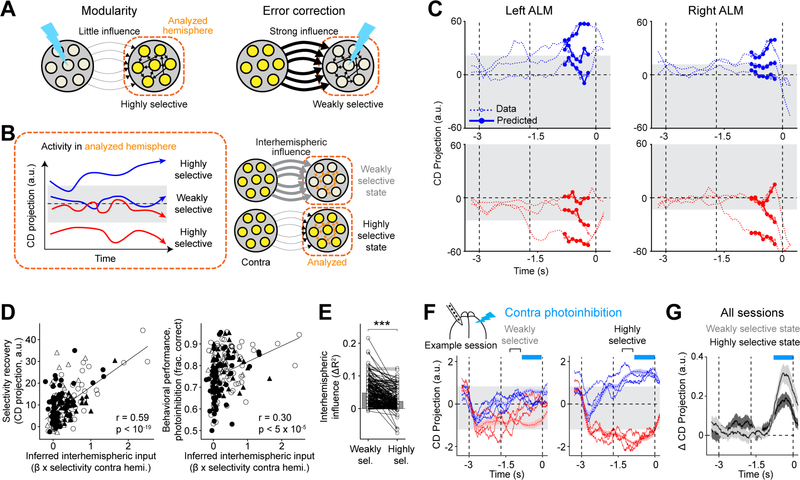
We sought to understand how hemispheres maintain modular representations and recover choice information after perturbations. At an algorithmic level, the unperturbed hemisphere needs to gate out the influence of the perturbed hemisphere (Figure 5A). At the same time, interhemispheric input is needed to recover the perturbed hemisphere (Figure 5A). To have both properties at the same time, interaction strength between the hemispheres needs to be modulated in a state-dependent way.

Figure 5. — (A) Modulation of interhemispheric interactions necessary for modularity and error correction in a hemisphere (‘analyzed hemisphere’).

(B) Key elements of the predictive model of ALM activity. *Left*, the analyzed hemisphere is in the highly selective state or weakly selective state depending on the strength of activity projection on the choice decoder (CD). *Right*, the strength of interhemispheric influence is modulated depending on the state of the analyzed hemisphere.

(C) 3 example “lick right” trials (*top*) and 3 example “lick left” trials (*bottom*). Model prediction is restricted to the late delay epoch (Methods). Gray, weakly selective state. Time bin, 400 ms; time step, 100 ms.

(D) *Left,* interhemispheric input inferred from control trials versus selectivity recovery in photoinhibition trials. The interhemispheric input is the selectivity in the unperturbed hemisphere multiplied with the interhemispheric coefficient (β₀ in the weakly selective state, Methods). *Right,* the inferred interhemispheric input versus behavioral performance in photoinhibition trials. Circles, sessions from the standard task; triangle, fully reversed task. Filled symbols, left ALM photoinhibition; open symbols, right ALM photoinhibition. Line, linear regression and Pearson’s correlation. 98 sessions, 28 mice.

(E) The strength of interhemispheric influence when the analyzed hemisphere is in the weakly versus highly selective state. The interhemispheric influence is the improvement of model prediction by incorporating interhemispheric influence on top of within-hemisphere influence (ΔR², Methods). Circles, single hemispheres in individual sessions. Bar, mean. 98 sessions. ***, p<0.001, two-tailed t-test.

(F) Example session showing effects of contralateral photoinhibition when the analyzed hemisphere is in the weakly versus highly selective state. Dashed lines, activity in control trials (mean ± s.e.m.); solid lines, example photoinhibition trials. Trials are sorted into highly selective or weakly selective (gray area) based on the CD projection before photoinhibition (Methods). Blue, “lick right”; red, “lick left”. Cyan bars, photoinhibition period.

(G) Activity change caused by photoinhibition relative to control trials (Methods). Data from all sessions and both ALM hemispheres (n=20). Mean ± s.e.m. across sessions.

See also Figure S6.

We inferred interhemispheric interactions from simultaneous recordings of both hemispheres in control trials. The large single-trial variability of ALM delay activity (Figure 1E–F) allowed us to observe each hemisphere across different states of activity and examine how interhemispheric interactions might differ across states. To quantify interhemispheric interactions, we constructed a model that predicted ALM single-trial dynamics from the activity within the hemisphere (‘analyzed hemisphere’) and the activity from the other hemisphere (‘contra hemisphere’). To test for state-dependence, we allowed the model to have two different states with potentially different influences from the contra hemisphere. We fit the model parameters to best predict ALM activity. This approach did not necessitate finding state-dependent difference in interhemispheric influence. If having state-dependent influence did not improve predictions of ALM activity, the model would infer the same interhemispheric influence in the two states. For each hemisphere, the model equations take the following form:

X_{t + 1}^{a n a l y z e d h e m i s p h e r e} = α X_{t}^{a n a l y z e d h e m i s p h e r e} + β (z_{t}) X_{t}^{c o n t r a h e m i s p h e r e},

β (z_{t}) = {\begin{array}{l} β_{0} & i f z_{t} = "weakly selective" state \\ β_{1} & i f z_{t} = "highly selective" state \end{array}

where X represents the activity of each hemisphere. We predicted activity projections on the choice decoder, instead of the full activity of each hemisphere. α is a scalar coefficient tying past within-hemisphere activity to future activity. β(z_t) is a coefficient that scales the influence of the other hemisphere, which takes on one of two values depending on a binary state variable z_t. Switching between the two states was dependent on the strength of choice encoding in the analyzed hemisphere (Methods). Specifically, z_t was in the “highly selective” state when the choice decoder activity was above a threshold and in the “weakly selective” state when below (Figure 5B–C).

We first validated the model. The model accurately predicted ALM activity on held out control trials (Figures 5C and S6A). Importantly, for nearly every session, adding the influence of the other hemisphere significantly improved model prediction (Figure S6B, p<5×10⁻³⁸, two-tailed t-test). The magnitude of the improvement was moderate because the activities of the two hemispheres were highly correlated, thus a large fraction of ALM activity could already be predicted from a hemisphere’s own past activity. Scrambling the trial identity of the simultaneous recording data abolished the improvement in model prediction (Figure S6B). Thus, the model consistently captured interhemispheric interactions.

We then analyzed the model-inferred interhemispheric interactions. The strength of interhemispheric influence inferred from control trials predicted the recovery of neuronal selectivity and behavioral performance following unilateral photoinhibition (Figure 5D). The model also captured the asymmetry of interhemispheric organization that was revealed by photoinhibition. In the standard task, the left ALM exhibited a larger influence over the right ALM (Figure S6C, p<5×10⁻³, paired two-tailed t-test), but the right ALM exhibited a larger influence over the left ALM in the fully reversed task (Figure S6C, p<10⁻²; c.f. Figure 3). Thus, the model captured session-to-session differences in the strength of interhemispheric interactions.

Finally, we examined the state-dependence of interhemispheric interactions. Although we did not constrain the values of the two coefficients β(z_t), the model-inferred coefficients were consistently different in nearly all sessions, indicating state-dependence (Figure S6D, p<0.001, paired two-tailed t-test). Importantly, the modulation was consistent with a state-dependent gating mechanism: the influence of the other hemisphere was weaker when choice encoding was strong within a hemisphere (Figure 5E, p<10⁻¹⁹, paired two-tailed t-test). This state-dependent gating could potentially explain how ALM hemispheres maintained choice information during unilateral perturbations and recovered choice information after the perturbation (Figure 5A): during photoinhibition the unperturbed hemisphere is in a highly selective state and thus is weakly influenced by the perturbed hemisphere (producing modularity), whereas the perturbed hemisphere is rendered to a weakly selective state and is therefore strongly influenced by the intact hemisphere (generating error correction).

We directly tested for state-dependent gating using perturbation experiments. The strength of choice encoding during the delay epoch differed substantially across trials (Figure 5C). We unilaterally photoinhibited ALM activity during the late delay epoch and examined whether selectivity state of the unperturbed hemisphere could modulate the influence of the perturbation (Figure 5F). In trials where the unperturbed hemisphere exhibited weak choice encoding, its selectivity was strongly affected by contralateral photoinhibition (Figure 5G). In contrast, when the unperturbed hemisphere exhibited strong choice encoding, its selectivity was less affected (Figure 5G, p<0.05, one-tailed t-test).

In summary, our analysis of ALM interhemispheric interactions revealed state-dependent gating of influence between the two hemispheres.

State-dependent gating could explain modular organization and behavioral performance

Can the state-dependent gating inferred from control trials explain modular organization and robustness of frontal cortical networks to perturbations?

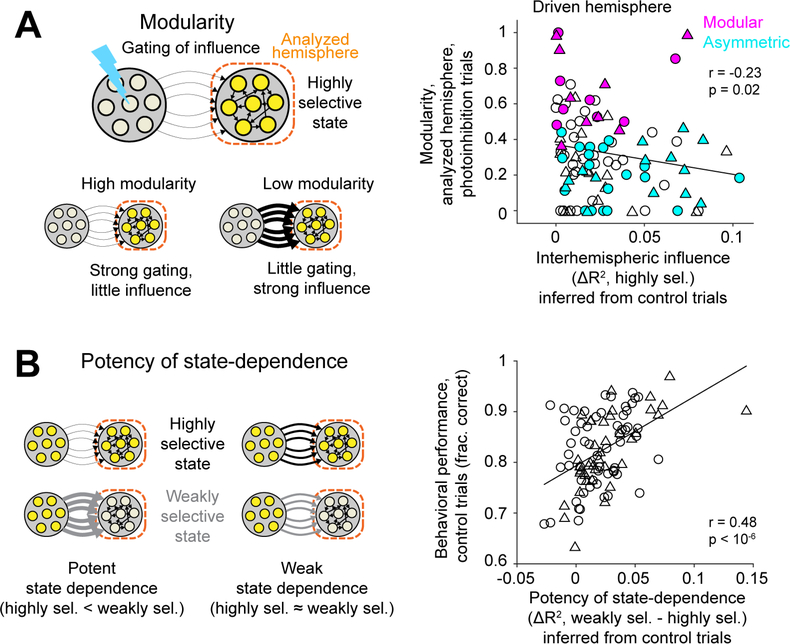
In state-dependent gating, gating of interhemispheric influence occurs when a hemisphere is in a highly selective state, which potentially produces modularity (Figure 6A). We examined the strength of interhemispheric influence in the highly selective state (from Figure 5E). In asymmetric sessions, the hemisphere with low modularity (driven hemisphere) showed strong influence from the other hemisphere (little gating, Figure 6A). In modular sessions, the same hemisphere showed little influence from the other hemisphere (strong gating, Figure 6A; modular vs. asymmetric sessions, p<0.01, one-sided Wilcoxon rank sum test). Modularity of the hemisphere was inversely correlated with the strength of interhemispheric influence (Figure 6A). These results show that modularity of a hemisphere (revealed by photoinhibition) could be explained by the gating of interhemispheric influence inferred from control trials.

Figure 6. — (A) *Left*, a hemisphere in a highly selective state gates out the influence of the other hemisphere to produce modularity. *Right*, interhemispheric influence in the highly selective state (ΔR² from Figure 5E) versus modularity of the analyzed hemisphere. Circles, right ALM in the standard task. Triangles, left ALM in the fully reversed task. Magenta, modular sessions. Cyan, asymmetric sessions.

(B) *Left*, the difference in interhemispheric influence between the weakly and highly selective states reflects the potency of state-dependence. *Right*, potency of state-dependence (based on ΔR² from Figure 5E, averaged across the two hemispheres) versus behavioral performance in control trials. Circles, standard task; triangle, fully reversed task. Line, linear regression and Pearson’s correlation. 98 sessions, 28 mice.

However, a hemisphere with strong gating is not completely decoupled from the other hemisphere. In state-dependent gating, the same hemisphere in a weakly selective state can still be strongly influenced by the other hemisphere to produce error correction (Figure 5A). Supporting this idea, the strength of interhemispheric influence in the weakly selective state predicted the recovery of choice information following photoinhibition (Figure 5D). Together, these results suggest that robustness to perturbations is jointly mediated by little influence in the highly selective state (producing modularity) and strong influence in the weakly selective state (generating error correction).

Finally, the potency of state-dependent gating, i.e., how different the influence was between states, predicted differences in behavioral performance across sessions. We quantified the potency of state-dependence as the difference in interhemispheric influence between the weakly and highly selective states (Figure 5E, Methods). The potency of state-dependence was significantly correlated with behavioral performance in control trials (Figure 6B). This suggests that the ability of the two hemispheres to dynamically gate influence and maintain modular representations might help better maintain choice information during normal behavior, possibly by increasing robustness to internal perturbations such as noise.

Together, these results suggest that state-dependent gating is closely related to the mechanism for modular organization and robustness of frontal cortical networks to external and internal perturbations.

Modeling identifies conditions in which interhemispheric interactions become modular or asymmetric

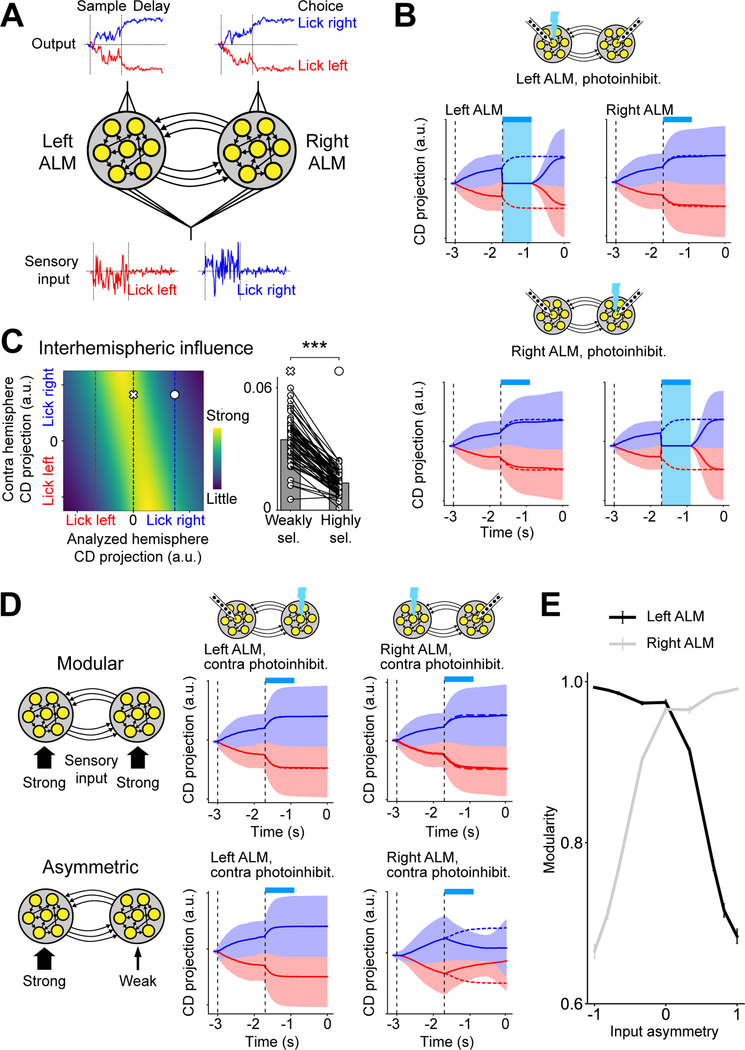
We next examined more generally what interhemispheric interactions might arise in highly connected networks required to perform the delayed response task with minimal additional assumptions. We chose recurrent neural networks (RNNs) due to their ability to generate models that are constrained to solve a task without enforcing their solutions (Sussillo and Abbott, 2009). Our goal was not to build a faithful model of ALM dynamics but to use RNNs as a tool to explore solutions to robust dynamics.

RNNs learned to perform the delayed response task and generated delay activity similar to those observed in the data (Figure 7A–B). Learned networks were robust to perturbations without experiencing perturbations during training when three conditions were met (Figure S7A–B). (1) Modular initialization: networks were partitioned into modules before training, in which the initial between-module connection weights were smaller than the within-module connection weights. (2) Modular training: the internal weights of each module were trained while keeping the between-module weights frozen. (3) Nonlinearity: units within the RNN had nonlinear input-output functions (Methods). Without these conditions, some learned networks exhibited discrete attractor dynamics but without modular organization, and these networks did not exhibit the robustness to perturbations we observe (Figure S7C).

We examined the mechanism by which RNN modules interact to maintain information during perturbations. Since the connectivity and activity of all units is known in simulations, we can directly calculate how a change of activity in one module influences the activity of the other module by calculating activity gradients (Methods). Remarkably, even though we did not build in any state-dependent gating mechanism, the interhemispheric influences of the robust RNNs were modulated such that the influence of the other hemisphere was smaller when a hemisphere was highly selective, and greater when it was weakly selective (Figure 7C, n=30 models). Like the neural data, state-dependent gating in RNNs could explain the robustness of RNNs to perturbations: little influence in the highly selective state predicted higher modularity in a hemisphere (Figure S7F); strong influence in the weakly selective state predicted better recovery of choice information in the perturbed hemisphere (Figure S7G). These results show that RNNs achieved robustness to perturbations by a similar state-dependent gating mechanism as observed in the neural data (Figures 5–6).

RNN modeling also provided insight regarding the asymmetry of interhemispheric interactions in ALM. Based on the findings that the asymmetry of interhemispheric influence can be flipped by reversing the side of the tactile stimulus (Figure 3), we hypothesized that it arises from asymmetric strength of sensory input to each hemisphere (Figure 2F). We trained RNNs that received unequal input to the two hemispheres (Methods). Consistent with our hypothesis, interhemispheric influence in these RNNs developed an asymmetry that was dependent on the relative strength of sensory input to each hemisphere (Figures 7D–E and S7D–E).

In summary, robust RNNs showed both state-dependent gating and modular dynamics even though we did not enforce such solutions. Moreover, asymmetric interhemispheric interactions might emerge when sensory inputs to each hemisphere are asymmetric.

Discussion

Our study provides evidence for modular organization in frontal cortical networks that maintain persistent activity. Redundant modular representations distributed across hemispheres coordinate coherent information (Figure 1) while maintaining their integrity when parts of the network are perturbed (Figure 2). Modular organization is required for the robustness of persistent activity to perturbations (Figure 4). A state-dependent gating mechanism allows connected hemispheres to limit corrupt information from spreading while still permitting coordination between hemispheres (Figures 5). State-dependent gating could explain the robustness of frontal cortical networks to external and internal perturbations (Figure 6).

Our results also reveal unexpected individual differences in frontal network organization, which could be shaped by task (Figure 3). Interhemispheric interactions were asymmetric in some mice, in which the hemisphere contralateral to the tactile stimulus drove selectivity in the other hemisphere. Our results suggest that an imbalance of stimulus input to the two hemispheres shapes the asymmetry of interhemispheric interactions (Figure 2F). This interpretation is supported by our findings in learned RNNs where the hemisphere receiving stronger sensory input became the driver hemisphere (Fig 7D–E). Future experiments tracking the activity of both hemispheres in the same animal across learning will shed light on the underlying mechanisms.

Our electrophysiology measured dynamics of neuronal populations from each hemisphere, but modular organization may exist at multiple spatial scales (Svoboda and Li, 2018). Multiple modular representations could be maintained by interdigitated neuronal populations within each hemisphere (Daie et al., 2021). Modular representations may extend beyond single brain regions, where groups of neurons in thalamo-cortical loops maintain a single modular representation (Guo et al., 2017). The fact that recording from a few dozen randomly sampled neurons in each hemisphere could reveal distinct interhemispheric interactions suggests that ALM activity encoding choice is low dimensional and multiple modular representations within a hemisphere are correlated with each other. Future experiments combining two-photon imaging and cellular resolution perturbations hold the promise for fine scale dissections of modular representations within each hemisphere (Daie et al., 2021).

Our analysis of interhemispheric interactions revealed a state-dependent gating: a hemisphere is little influenced by the other hemisphere (and perhaps by other brain regions (Finkelstein et al., 2021; Kopec et al., 2015)) when it is in a highly selective state, but when it is in a weakly selective state it allows strong influence from its inputs. This type of modulation makes sense from a normative point of view: if a representation has accurate information, then receiving outside influence could be detrimental, but a representation that has poor information would likely benefit from influence. We found similar state-dependent gating emerges in robust RNN models trained to solve the task, even though we did not enforce such solutions.

Redundant modular representations may support other cognitive processes, including working memory (Chafee and Goldman-Rakic, 1998; Romo et al., 1999), episodic memory (Zugaro et al., 2005), and perceptual decision-making (Brody and Hanks, 2016; Gold and Shadlen, 2001). Modular organization increases resiliency of networks (Brummitt et al., 2012; Variano et al., 2004). Redundant modular representations could suppress effects of perturbation, which suggests a potential explanation for lack of behavioral effects during certain acute experimental manipulations (Fetsch et al., 2018; Kopec et al., 2015; Li et al., 2016; Liu and Pack, 2017). Along similar lines, acute insults such as lesions or strokes often lead to neuron loss with subtle deficits on behavior (Fanning et al., 2014; Fisher, 1965; Leary and Saver, 2003). Redundant modular representations distributed across multiple brain regions could allow for resiliency of cognitive functions following certain chronic and acute perturbations to parts of the brain (Fornito et al., 2015; Palop et al., 2006).

Limitations of the study

How neural circuits implement state-dependent gating remains to be determined. Attractor models could produce dynamics that are little influenced by external input (Amit and Brunel, 1997; Barak et al., 2013; Brody et al., 2003; Finkelstein et al., 2021; Hopfield, 1982; Inagaki et al., 2019; Peixoto et al., 2019; Seung, 1996; Shenoy et al., 2013; Wang, 2001). Some learned RNNs exploited a gating mechanism where network dynamics in each RNN module self-reinforce activity states encoding specific choices, with no obvious neurons dedicated to suppressing interhemispheric influence. However, other models could also implement gating such as communication by coherence (Fries, 2005) or interactions along specific subspaces (Druckmann and Chklovskii, 2012; Kaufman et al., 2014; Semedo et al., 2019), which can be extended to include state-dependence. Future large-scale recordings from multiple brain regions (Jun et al., 2017; Sofroniew et al., 2016) are required to understand its mechanisms. Finally, we found that modularity varied across mice and sessions. The source of this variability and to what extent it reflects changes in the underlying circuits remain to be explored. Such exploration requires recording from the same neuronal populations across days, e.g., by calcium imaging.

STAR★METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Nuo Li (nuol@bcm.edu)

Materials availability

This study did not generate new unique reagents.

Data and code availability

The electrophysiology data and analysis code supporting the current study has not been deposited in a public repository because it is in a non-standard format, but will be made available in the near future. Modeling and simulation code can be found at https://github.com/druckmann-lab/Dual_ALM_RNN. All data and analysis code are available from the lead contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

This study is based on data from 43 mice (age > postnatal day 60, both male and female mice). 11 VGAT-ChR2-EYFP mice (Jackson laboratory, JAX Stock#014548) and 32 PV-IRES-Cre (JAX 008069) (Hippenmeyer et al., 2005) crossed to R26-CAG-LSL-ReaChR-mCitrine mice (JAX 024846) (Hooks et al., 2015) were used for simultaneous electrophysiology and photoinhibition during behavior.

All procedures were in accordance with protocols approved by the Institutional Animal Care and Use Committees at Baylor College of Medicine. Mice were housed in a 12:12 reverse light:dark cycle and tested during the dark phase. On days not tested, mice received 0.5–1 mL of water. On other days, mice were tested in experimental sessions lasting 1 to 2 hours where they received all their water (0.3 to 2 mL). If mice did not maintain a stable body weight, they received supplementary water (Guo et al., 2014b). All surgical procedures were carried out aseptically under 1–2 % isoflurane anesthesia. Buprenorphine Sustained Release (1 mg/kg) and Meloxicam Sustained Release (4mg/kg) were used for pre- and post-operative analgesia. After the surgery, mice were allowed to recover for at least three days with free access to water before water restriction.

METHOD DETAILS

Surgery

Mice were prepared for photoinhibition and electrophysiology with a clear-skull cap and a headpost (Guo et al., 2014a; Guo et al., 2014b). The scalp and periosteum over the dorsal surface of the skull were removed. A layer of cyanoacrylate adhesive (Krazy glue, Elmer’s Products Inc) was directly applied to the intact skull. A custom made headpost was placed on the skull (approximately over the visual cortex, where a stainless-steel pin was also implanted as a ground reference for electrophysiology) and cemented in place with clear dental acrylic (Lang Dental Jet Repair Acrylic; Part# 1223-clear). A thin layer of clear dental acrylic was applied over the cyanoacrylate adhesive covering the entire exposed skull, followed by a thin layer of clear nail polish (Electron Microscopy Sciences, Part# 72180).

Behavioral task

The behavioral task and training have been described (Guo et al., 2014a; Guo et al., 2014b). The stimulus was a metal pin (0.9 mm in diameter), presented at one of two possible positions (Figure 1A). The two pole positions were 5 mm apart along the anterior-posterior axis and were constant across sessions. The posterior pole position was 5 mm from the whisker pad. A two-spout lickport (4.5 mm between spouts) was used to deliver water rewards and record answer licks.

At the beginning of each trial, the vertical pole moved into reach of the whiskers (0.2 s travel time), where it remained for 1 second, after which it was retracted (retraction time 0.2 s). The sample epoch was defined as the time between the pole movement onset to 0.1 s after the pole retraction onset (sample epoch, 1.3 s, Figure 1A). Mice touched the object at both pole positions, typically with a different set of whiskers. The delay epoch (duration, 1.7 s) followed the sample epoch. An auditory ‘go’ cue indicated the end of the delay epoch (pure tone, 3.4 kHz, 0.1 s duration). Licking early during the trial was punished by a loud alarm sound (siren buzzer, 0.05 s duration), followed by a brief timeout (1–1.2 s). Licking the correct lickport after the ‘go’ cue led to a liquid reward (2–3 μL). Licking the incorrect lickport triggered a timeout (2–6 s). Trials in which mice did not lick within a 1.5 second window after the ‘go’ cue (‘no lick’) were rare and typically occurred at the end of a session.

Different groups of mice were tested in 4 variants of the task that systematically varied the sensorimotor contingency (the mapping between pole position and directional licking) and the side of tactile stimulus relative to the mouse (stimulating the right or left whisker pad) (Figure 3).

In the standard task (n=18 mice, 59 sessions for primary experiments with early delay photoinhibition; 4 additional mice were later tested for late delay photoinhibition experiments), the pole stimulated the right whisker pad. Posterior pole position corresponded to “lick right” and anterior pole position corresponded to “lick left”.

In the reversed contingency task (n=5 mice, 14 sessions), the pole stimulated the right whisker pad. But sensorimotor contingency was reversed where posterior pole position corresponded to “lick left” and anterior pole position corresponded to “lick right”.

In the reversed tactile stimulus task (n=6 mice, 21 sessions), the pole stimulated the left whisker pad. The sensorimotor contingency was the same as the standard task.

In the fully reversed task (n=10 mice, 41 sessions), the pole stimulated the left whisker pad and the sensorimotor contingency was also reversed from the standard task.

The standard task and fully reversed task were tested first, and most of the data were collected in these two tasks. The reversed contingency task and reversed tactile stimulus task were tested later to examine the effects of task parameters on interhemispheric organization (Figure 3).

Videography

Two CMOS cameras (CM3-U3–13Y3M, FLIR) were used to measure orofacial movements of the mouse under IR illumination (940 nm, Roithner Laser, LED940–66-60). One camera acquired the bottom view of the mouse with a 4–12 mm focal length lens (12VM412ASIR, Tamron) and pixel resolution of 0.065 mm/pixel. The second camera acquired the side view of the mouse with a 4–12 mm focal length lens (12VM412ASIR, Tamron) and pixel resolution of 0.07 mm/pixel. Videos were acquired at 200 Hz framerate using FlyCapture (FLIR).

Photoinhibition

Light from a 473 nm laser (UltraLasers, MBL-FN-473–300mW) or a 593.5 nm laser (UltraLasers, MGL-N-593.5–200mW) was controlled by an acousto-optical modulator (AOM; Quanta Tech, MTS110-A3-VIS). Photostimulation was performed by directing a focused laser beam over the surface of the brain through a craniotomy (beam diameter: 400 μm at 4σ). To prevent the mice from distinguishing photostimulation trials from control trials using visual cues, a ‘masking flash’ was delivered using 470 nm or 591 nm LEDs (Luxeon Star) near the eyes of the mice. The masking flash began as the pole started to move and continued through the end of the epoch in which photostimulation could occur.

For photoinhibition of ALM, we photostimulated cortical GABAergic neurons in VGAT-ChR2-EYFP mice or parvalbumin-positive interneurons in PV-IRES-Cre x R26-CAG-LSL-ReaChR-mCitrine mice (Hooks et al., 2015). The two methods resulted in similar photoinhibition: a single laser spot silenced 90% of spikes in a cortical area of 1 mm radius (at half-max) through all cortical layers (Li et al., 2019). At 80% activity reduction, photoinhibition with one laser spot covered 58% of ALM in one hemisphere (Li et al., 2016). This estimate was based on the boundaries of ALM derieved using photoinhibition behavioral data from (Guo et al., 2014a). ALM was defined as the area where photoinhibition over the entire delay epoch produced significant behavioral effects. ALM boundaries were derived by deconvolving the area producing significant behavioral effects with the point-spread function of the photoinhibition method (Li et al., 2019; Li et al., 2016). During electrophysiology, photoinhibition was deployed on 40% of the trials to obtain a large number of trials per condition.

We photoinhibited for 0.8 s, including a 200 ms linear ramp during offset to reduce rebound neuronal activity (Guo et al., 2014a; Li et al., 2019). In most experiments, photoinhibition started at the beginning of the delay epoch and ended 0.9 s before the onset of the ‘go’ cue. Three photoinhibition conditions were tested on randomly interleaved trials: photoinhibition of the left ALM, the right ALM, or both hemispheres. To photoinhibit single ALM hemispheres (e.g. Figure 2), we used one laser spot and a 40 Hz photostimulus with a sinusoidal temporal profile (1.5 mW average power). A scanning galvo (GVSM002, Thorlabs) positioned the laser spot on either the left or right ALM (anterior 2.5 mm and lateral 1.5 mm from bregma). To photoinhibit both hemispheres (Figures S2F–K), we used a constant photostimulus and the scanning galvo stepped the laser beam sequentially through 8 photoinhibition sites at the rate of 1 step per 5ms (step time: 0.2 ms; dwell time: 4.8 ms; measured using a photodiode). 8 photoinhibition sites were spaced in 1 mm at anterior 2–3mm and lateral 1–2 mm from bregma, covering ALM and surrounding cortical regions. Peak power was adjusted based on the number of photoinhibition sites to achieve 1.5 mW average power per site. The photoinhibition during scanning was similar to the single laser spot photoinhibition.

In experiments to directly test for state-dependent gating, we unilaterally photoinhibited ALM activity during the late delay epoch (Figure 5F–G). This allowed us to estimate the state of ALM hemispheres based on the delay activity prior to photoinhibition and examine their responses to photoinhibition of the contralateral hemisphere. In these sessions, photoinhibition started 0.9 s after the beginning of the delay epoch and ended right before the onset of the ‘go’ cue. Either the left or right ALM were photoinhibited on a subset (50%) of randomly interleaved trials (average power, 0.1–0.5 mW). Since selectivity cannot decrease below 0, we chose to use less power than the standard experiments to avoid driving selectivity to the floor in the weakly selective trials (Figure 5F). The fraction of spike rate decrease was < 50% in the photoinhibited hemisphere.

Electrophysiology

Extracellular spikes were recorded using 64-channel Cambridge NeuroTech silicon probes (H2 acute probe, 25 μm spacing, 2 shanks). The voltage signals were amplified and digitized on an Intan RHD2164 64-Channel Amplifier Board (Intan Technology) at 16 bit, recorded on an Intan RHD2000-Series Amplifier Evaluation System (sampling at 20,000 Hz), and stored for offline analysis.

One day prior to the recording session, two small craniotomies (diameter, <1 mm) were made over the left and right ALM (2.5 mm anterior, 1.5 mm lateral from bregma) (Guo et al., 2014a). Two silicon probes were acutely inserted 0.9–1.1 mm below the brain surface prior to the start of each recording session. To minimize brain movement, a drop of silicone gel (3–4680, Dow Corning, Midland, MI) was applied over the craniotomies after the electrodes were in the tissue. The tissue was allowed to settle for several minutes before the recording started. 2 to 8 recordings were made from each craniotomy. The silicon probe was painted with DiI (ThermoFisher scientific, D282), DiR (ThermoFisher scientific, D12731), or DiO (Sigma-Aldrich, D4292) to label the recording tracks. All recording locations within a craniotomy were reconstructed post-hoc. Recording depths were inferred from manipulator readings and verified based on histology.

Behavioral data analysis

Performance was computed as the fraction of correct choices, excluding early lick trials and no lick trials (Figures 4–6 and S2, S5). The “lick right” and “lick left” trials were combined to compute performance. Chance performance was 50%. Behavioral effects of photoinhibition were quantified by comparing the performance under photoinhibition with control performance using paired two-tailed t-test (Figure S2F).

To quantify the robustness of behavioral performance to unilateral photoinhibition (Figures 4 and S5), for each session we divided the behavioral performance (fraction correct) in photoinhibition trials by the control trial performance to calculate a relative behavioral performance (photoinhibition/control), or ‘behavioral recovery’. In each session, behavioral recovery was calculated separately for left ALM photoinhibition and right ALM photoinhibition. In Figure 4I, the behavioral recovery of each unilateral photoinhibition condition was correlated with modularity of the unperturbed hemisphere (each session contributed two data points, left ALM photoinhibition and right ALM photoinhibition).

Electrophysiology data analysis

Local field potential (LFP)

Previous studies found gamma band increased LFP coherence during communications between brain regions (Fries, 2005). We analyzed LFP power spectrum and coherence spectrum between the two ALM hemispheres. The extracellular recording traces were downsampled at 1000 Hz and band-pass filtered (1–100 Hz). Mice contacts with the electrical lickport produced large electrical artifact during licking in the response epoch. We therefore limited the analysis to the sample and delay epochs. Trials in which mice licked early were also excluded. LED masking flash also introduced photoelectric artifact. However, photoelectric artifact was absent in a limited number of sessions. We therefore limited to the analysis to those sessions (n= 7 from 2 mice).

The power spectrum of LFP signals typically falls off proportional to 1/frequency. To reduce the dynamic range and reduce the power leakage from the lower frequencies into the higher frequencies during spectral estimation, we whitened the LFP signals. In the pre-whitening process, a low-order (order = 3) autoregressive (AR) spectrum estimation was used, which could reduce the dynamic range but without fitting specific structural features of the data (Chen et al., 2017a). We used the Levinson Durbin recursion method to fit the AR model, and the coefficients (Ak) of this process were then used to filter the original time series data (Xt). The residuals:

Δ X t = X t - \sum_{k = 1}^{3} X (t - k) A k

were subject to the later spectral analysis.

We first normalized the filtered LFP signals (1–100 Hz) by calculating the z-score and performing the pre-whitening as described above. The power spectrum of the LFP was computed by using the multi-taper estimation method in MATLAB with the chronux package (http://chronux.org), using 0.8 s data segments (sample and delay epochs) and 3–5 tapers (TW = 3, K = 5). Then, we smoothed the spectrum after removing the 60 Hz line noise. Finally, the power at each frequency was divided by the mean power across all frequency bands (Figure S1I). Power spectrum was average across channels and trials for each session. LFP coherence spectrum (Figure S1I) between left and right ALM hemispheres was calculated using the “coherency” function in the chronux package http://chronux.org.

Spiking activity

The extracellular recording traces were band-pass filtered (300–6 kHz). Events that exceeded an amplitude threshold (4 standard deviations of the background) were subjected to spike sorting to extract single units. Spike sorting was either manual (Guo et al., 2014b) or using Kilosort2 (www.github.com/MouseLand/Kilosort2) (Pachitariu et al., 2016) followed by manually curated with the Phy 2.0 beta 1 GUI (https://github.com/cortex-lab/phy) (Rossant et al., 2016) and manual inspection (Guo et al., 2014a).

19736 single units were recorded across 135 recording sessions, of which 59 sessions were in the standard task and 41 sessions were in the fully reversed task. Spike widths were computed as the trough-to-peak interval in the mean spike waveform (Guo et al., 2014a). Units with spike width < 0.35 ms were defined as fast-spiking (FS) neurons (1073/19736) and units with spike widths > 0.45 ms as putative pyramidal neurons (17949/19736). Units with intermediate values (0.35 – 0.45 ms, 714/19736) were excluded. This classification was previously verified by optogenetic tagging of GABAergic neurons (Guo et al., 2014a). We concentrated our analyses on the putative pyramidal neurons.

Neuronal selectivity

Neurons were tested for significant trial-type selectivity during the sample, delay, or response epochs, using the spike counts from the “lick left” and “lick right” trials (Wilcoxon rank sum test, p<0.05, corrected by Bonferroni-Holm correction for multiple comparisons). Neurons that significantly differentiated trial types during any one of the trial epochs were deemed “selective” (7256/19736). In Figure S1A–C specifically, we used a looser significance criterion (two-tailed t-test, p<0.05, uncorrected for multiple comparison) to enable direct comparisons with previous studies of ALM activity, which used the looser criterion (Li et al., 2015; Li et al., 2016). This resulted more neurons included in Figure S1A–C (~75% of ALM neurons were deemed selective by this looser criterion).

To compute trial-type selectivity (Figures 1, 2, 4, and S2–3), we first determined each neuron’s preferred trial type using spike counts from a subset of the control trials (a random split half of the control trials, 30–200 trials, correct trials only), selectivity was calculated as the spike rate difference between preferred over non-preferred trial type on the remaining data (both correct and incorrect trials). Because different splitting of control trials may not always result in consistent preferred trial type, for each neuron the selectivity calculation was performed 30 times (using different splitting of control trials that determined preferred trial type) to obtain an averaged selectivity estimate for each neuron.

Trial types differed in object location (‘stimulus’, anterior vs. posterior), lick direction (‘choice’, left vs. right), and reward (‘outcome’, rewarded vs. unrewarded). We separately computed neuronal selectivity for each variable (Chen et al., 2017b; Zatka-Haas et al., 2020). For each cell, the spike counts within analysis windows were grouped according to trial types (“lick right” correct trials, CR; “lick left” correct trials, CL; “lick right” error trials, ER; “lick left” error trials, EL). The selectivity is calculated from the average spike counts (〈•〉) in each group:

S t i m u l u s s e l e c t i v i t y = \frac{(〈 C R 〉 - 〈 E L 〉) + (〈 E R 〉 - 〈 C L 〉)}{2}

C h o i c e s e l e c t i v i t y = \frac{(〈 C R 〉 - 〈 E R 〉) + (〈 E L 〉 - 〈 C L 〉)}{2}

O u t c o m e s e l e c t i v i t y = \frac{(〈 C R 〉 - 〈 E R 〉) + (〈 C L 〉 - 〈 E L 〉)}{2}

Stimulus selectivity represents the object location-selective response of the posterior trials (CR, ER) relative to the anterior trials (CL, EL). Choice selectivity represents the lick direction-selective response present in trials when the mouse licked right (CR, EL) compared to trials when the mouse licked left (CL, ER). Outcome selectivity represents the response present in the correct trials (CR, CL) relative to the error trials (ER, EL) (Figures 1, 2, and S1). This selectivity calculation was performed in analysis windows of 200ms during different times of the task (in 1 ms steps). For each neuron, its preferred and non-preferred trial type for each variable was determined using spike counts from a subset of the control trials. Selectivity was calculated as the spike rate difference between preferred over non-preferred trial type on the remaining data.

For each neuron, we also quantified the significance of selectivity based on the spike counts of individual trials at each time bins (Figure 1C)(Steinmetz et al., 2019; Zatka-Haas et al., 2020). Trial types were grouped as the following: stimulus selective, CR compared to EL and ER compared to CL; choice selective, CR compared to ER and EL compared to CL; outcome selective, CR compared to ER and CL compared to EL. For each group, the probability that spike counts in the preferred trial type is larger than the non-preferred trial type was calculated across all possible trial pairs. The statistical significance was calculated from shuffle test, in which the trial types were randomly permuted 1000 times. The p value is the fraction of times in which the probability (preferred > non-preferred trial type) in the shuffling dataset was larger than the actual dataset.

Modularity

To quantify the modularity of each ALM hemisphere (Figures 2–4 and S3, S5), we calculated the fraction of trial-type selectivity retained in a hemisphere during photoinhibition of the other hemisphere (the first 0.8 s of the delay epoch). Selectivity during the photoinhibition epoch was divided by the control trial selectivity during the same epoch. Sessions in which recording in one of the hemispheres had poor yield (n<5 delay selective single units, 6 sessions) or poor control trial selectivity (average selectivity <0.5 spikes/s during the early delay epoch or <1 spikes/s during the late delay epoch, 15 sessions) were not included in the analysis. Poor selectivity and poor yield produced noisy estimates of modularity. However, including these sessions did not qualitatively change the results. The modularity values were capped between 0 and 1, where a few sessions that had modularity values below 0 or above 1 were set to 0 and 1 to bound the outlier sessions in the plots (Figures 2–4). All the key results remain the same without this bound.

Modularity of each hemisphere varied across individual sessions (Figures 2–4 and S3, S5). To examine whether the variability in modularity was due to variable sampling of neurons in silicon probe recordings, we estimated the variability of modularity arising from neurons sampling using bootstrap (Figure S3F). For each round of bootstrap, we generated a resampled dataset in which we resampled (with replacement) the neurons within each session, while keeping the same number of neurons in each session. We then computed the modularity of each session in the resampled dataset. This procedure was repeated 10,000 times. The sampling variability for each session was calculated as the standard deviation in modularity across the 10,000 rounds of bootstrap. Finally, the sampling variability was averaged across sessions. The variability of modularity across sessions was significantly larger than the sampling variability (Figure S3G, p<0.001). This p value was the probability of observing a smaller across-sessions variability than the average sampling variability in the bootstrap resampled dataset. Using this p-value calculation, we performed power analysis on neuron sampling. We repeated the bootstrap procedure while reducing the number of neurons resampled per session. We found that 10 or more delay selective neurons per session had enough statistical power (at a significance criterion of p<0.01) to detect differences in modularity across sessions. Our actual dataset contained 26 or more delay selective neurons per session from each hemisphere.

Recovery of selectivity after photoinhibition

To quantify recovery of neuronal selectivity from photoinhibition (Figures 4 and S5), we calculated trial-type selectivity during the last time bin before the ‘go’ cue (last 200 ms of the delay epoch). For each session, the selectivity in photoinhibition trials were averaged across all delay selective neurons (see criteria above), and divided by the control trial selectivity to quantify the fraction of selectivity recovered. Because the recovery of the left ALM and right ALM after photoinhibition was coordinated (e.g. Figures 4B–C, both hemispheres always recovered similar fraction of selectivity), for each session we averaged the fraction of selectivity recovered in both hemispheres. We calculated the fraction of selectivity recovered separately for left ALM photoinhibition and right ALM photoinhibition conditions. In Figures 4 and S5, the fraction of selectivity recovered after unilateral photoinhibition was correlated with modularity of the unperturbed hemisphere (each session contributed two data points, left ALM photoinhibition and right ALM photoinhibition).

Choice decoder (CD) and population choice encoding

To examine choice encoding by a population of ALM neurons, we built linear choice decoders that were weighted sums of ALM neuron activity to best predict future lick direction, with separate choice decoders for the left and right ALM. On single trials, each choice decoder summed the underlying neuron activities to signal “lick right” or “lick left” (Figure 1D). We restricted the analysis to the recording sessions with > 5 neurons recorded simultaneously in each hemispheres and for > 5 trials per condition (135/135 sessions).

To build the choice decoder for a population of n ALM neurons, we found a n × 1 vector CD in the n dimensional activity space that maximally separates the response vectors in “lick right” trials and “lick left” trials based on the activity during the delay epoch. To estimate CD, we first esimated CD_t at different time points during the delay epoch (in 10 ms steps) using part of control trials (correct trials only). Average spike counts were computed in 400-ms windows in 10-ms steps. For each trial type (“lick right” and “lick left”) we computed the average spike counts ${\bar{x}}_{l i c k r i g h t}$ and ${\bar{x}}_{l i c k l e f t}$ , n × 1 response vectors that described the population response at each time point, t. CD_t is the difference in the mean response vectors:

C D_{t} = {\bar{x}}_{l i c k r i g h t} - {\bar{x}}_{l i c k l e f t}

During the delay epoch, the direction of CD_t was stable (correlation of CD_t’s between the early delay epoch vs. late delay epoch, 0.80 ± 0.01, mean ± s.e.m.). We averaged the CD_t’s from the delay epoch to obtain one CD. This fixed CD was used for activity projections in all relevant analysis.

The projection along CD captured 74.6±1.1% of the population selectivity for “lick left” and “lick right” trials over the sample and delay epoch (root mean square, RMS, of the spike rate difference between “lick right” trials and “lick left” trials), and 26.1±1.4% of the total variance in ALM task-related activity. Activity variance was quantified as the RMS of the baseline subtracted activity over the sample and delay epoch. We also considered other linear decoders, such as linear discriminant analysis (LDA), logistic regression, or support vector machine, and found them to be similar in decoding performance. Decoders that consider within-group covariance (e.g. LDA) did not substantially improve decoding performance likely because the number of trials is relatively small compared to the number of neurons (average 71 neurons in each hemisphere), leading to noisy estimates of the covariance.

Next, we projected ALM activity on the choice decoder CD. For each trial we computed the spike counts for individual neurons, x (n × 1 response vector), at each time point. The projected trajectories were obtained as CD^Tx (Figure 1E). To examine correlated choice encoding between ALM hemispheres (Figures 1F–G), for each session we took the single trial trajectory values at the last time bin before the ‘go’ cue (last 400 ms of the delay epoch) and calculated Spearman’s rank correlation between the left ALM trajectory values and right ALM trajectory values. We calculated rank correlation using trials from the same trial type (Figure 1G, “lick right” or “lick left” trials) or using both trial types of the session (Figure 1G, ‘both’). For shuffled control, we randomized the trial identity of activity data in each hemisphere and calculated Spearman’s rank correlation on the shuffled data.

To average CD trajectories changes across multiple sessions (Figure 5F), we first offset and normalized the trajectories for a particular session by subtracting the mean CD^Tx across all trials and time points in that session and then divided by the standard deviation of the CD^Tx. This removed fluctuations of mean activity level from session to session.

To predict upcoming lick direction using the choice decoder CD (Figure 1H), we calculated ALM activity projection on the choice decoder, CD^Tx, from the last time bin before the ‘go’ cue (last 400 ms of the delay epoch). For each session we computed a decsion boundary to best separate the “lick right” and “lick left” trials:

D e c i s i o n b o u n d a r y = \frac{〈 C D^{T} x_{l i c k r i g h t} 〉 / σ_{l i c k r i g h t}^{2} + 〈 C D^{T} x_{l i c k l e f t} 〉 / σ_{l i c k l e f t}^{2}}{1 / σ_{l i c k r i g h t}^{2} + 1 / σ_{l i c k l e f t}^{2}}

σ² is the variance of the projection values CD^Tx across multiple “lick right” or “lick left” trials. Both the CD and decision boundary were computed using independent control trials (correct trials only). Separate control trials were used to predict mice’s lick direction (Figure 1H, right, both correct and incorrect trials). To read out the choice encoding in one hemisphere from the other hemisphere (Figure 1H, left), we calculated the fraction of trials in which both hemispheres predicted the same lick direction.

Analysis of interhemispheric interactions

Predictive model of ALM activity

To infer the strength of interhemispheric influence in control trials, we devised a model of ALM delay activity. The model predicted single-trial activity in a particular time bin from past activity of the same hemisphere and activity in the other hemisphere. To improve signal-to-noise ratio, we used the model to predict the projection of ALM population activity on the choice decoder in each hemisphere. Although the model output was prediction of the activity projection on the choice decoder, the input for the model was not limited to the activity projection on the choice decoder but also included activity projections on the top three principal components of population activity that were orthogonal to the choice decoder (see Modeling training below). The choice decoder and principle components were estimated based on population activity during the delay epoch (see Population choice encoding above). Including more principal components did not significantly improve the prediction performance.

For each hemisphere, our predictive model was defined by the following equation:

X_{t + 1, 0}^{a n a l y z e d} = \sum_{p = 0}^{l_{a n a l y z e d}} \sum_{i = 0}^{n_{a n a l y z e d}} α_{p, i} X_{t - p, i}^{a n a l y z e d} + \sum_{q = - 1}^{l_{c o n t r a}} \sum_{j = 0}^{n_{c o n t r a}} β_{q, j} (z_{t}) X_{t - q, j}^{c o n t r a} + b,

where the ‘analyzed hemisphere’ refers to the hemisphere in which the model predicts activity, and the ‘contra hemisphere’ refers to the other hemisphere. $X_{t, 0}^{a n a l y z e d}$ , refers to the activity projection on the choice decoder at time t in the analyzed hemisphere. $X_{t, i}^{a n a l y z e d}$ , for i = 1, 2, or 3, refers to the activity projection on the i-th principal component, and similarly $X_{t, i}^{c o n t r a}$ refers to the activity in the contra hemisphere. l_analyzed and l_contra are the number of time steps in past activity that were used to predict current activity. n_analyzed and n_contra are the number of activity components used to predict choice encoding activity. Importantly, α_p,i and β_p,i denote the regression coefficients for i-th activity component at time lag p. The values of β_p,i(z_t) depend on a state variable z_t (see State-dependent gating below). Finally, b is a bias term. We computed firing rates using 400ms wide bins with a 100ms bin stride, i.e., the size of the timestep in the equation above was 100ms. Using different bin width or stride did not qualitatively change our results.

State dependent gating

To infer state-dependence of interhemispheric influence, we allowed β_q,j at each time point t to take one of two values depending on the binary state of a variable z_t, but without enforcing the values of β_q,j. The β_q,j values were obtained by training the model on neural data to best predict ALM activity (see Model training). In this model setup, β_q,j could take on any value across states to provide the best prediction of ALM activity. We then examined the β_q,j values and the interhemispheric influence the model inferred (see Interhemispheric influence).

The state variable z_t corresponded to the strength of choice encoding activity within the analyzed hemisphere. For “lick right” trials, z_t was in the “highly selective” state if the activity projection on the choice decoder at time point t was greater than a positive threshold, and otherwise in the “weakly selective” state (Figures 5B–C). For “lick left” trials, choice encoding is stronger when the activity projection on the choice decoder takes large negative values. Thus, z_t was in the “highly selective” state if the activity projection was smaller than a negative threshold (Figures 5B–C). In other words, z_t was in the “highly selective” state only if the activity projection was far from the decision boundary that separated “lick left” and “lick right” and also on the correct side of the decision boundary for a given trial type. Our choice of the state variable z_t was based on the observation that choice encoding was normally strong during the delay epoch in control trials (the presumed “highly selective” state) and rendered weak in photoinhibition trials (the presumed ”weakly selective” state). The threshold for each trial type was the median of the activity projection on the choice decoder during the late delay epoch. The thresholds were estimated using trials that were used to train other model parameters (training data).

Modeling training

The model was trained using 5-fold cross-validated ridge regression, with a regularization strength that achieved the best validation performance. We first trained a within-hemisphere model, which did not include input from the contra hemisphere. We then subtracted the prediction of the within-hemisphere model from ALM activity and predicted the residuals using input from the contra hemisphere. To train the switching linear coefficients β_q,j(z_t), we divided training samples into 2 groups based on their values of z_t, and performed ridge regression separately for each group.

However, due to strong autocorrelation in single-trial activity (e.g. Figures 1E and 5C), the input variables $X_{t - p, i}^{a n a l y z e d}$ and $X_{t - q, j}^{c o n t r a}$ tended to be highly correlated across time lags, which may render ridge regression less effective. Therefore, to reduce the correlation across the input variables, we made a change of variables such that the resulting input variables were the temporal difference of the original input variables: $X_{t - p, i}^{a n a l y z e d} \to X_{t - p, i}^{a n a l y z e d} - X_{t - (p + 1), i}^{a n a l y z e d}$ for p < l_analyzed, and $X_{t - q, i}^{c o n t r a} \to X_{t - q, i}^{c o n t r a} - X_{t - (q + 1), i}^{c o n t r a}$ for q < l_contra. For the same reason, we predicted the temporal change in activity $V_{t}^{a n a l y z e d}$ instead of $X_{t + 1, 0}^{a n a l y z e d}$ . These steps were taken in order to better predict the part of future activity that cannot be trivially predicted due to autocorrelation with past activity. After the change of variables, the model was described by the following equation:

\begin{array}{l} V_{t}^{a n a l y z e d} \equiv X_{t + 1, 0}^{a n a l y z e d} - X_{t, 0}^{a n a l y z e d} \\ = \sum_{p = 0}^{l_{a n a l y z e d}} \sum_{i = 0}^{n_{a n a l y z e d}} α_{p, i} {\tilde{X}}_{t - p, i}^{a n a l y z e d} + \sum_{q = - 1}^{l_{c o n t r a}} \sum_{j = 0}^{n_{c o n t r a}} β_{q, j} (z_{t}) {\tilde{X}}_{t - q, j}^{c o n t r a} + b, \end{array}

{\tilde{X}}_{t - p, i}^{a n a l y z e d} = {\begin{array}{l} X_{t - p, i}^{a n a l y z e d} - X_{t - (p + 1), i}^{a n a l y z e d} & p < l_{a n a l y z e d} \\ X_{t - p, i}^{a n a l y z e d} & p = l_{a n a l y z e d} \end{array}

{\tilde{X}}_{t - q, i}^{c o n t r a} = {\begin{array}{l} X_{t - q, i}^{c o n t r a} - X_{t - (q + 1), i}^{c o n t r a} & q < l_{c o n t r a} \\ X_{t - q, i}^{c o n t r a} & q = l_{c o n t r a} \end{array}

We found that using past activity from multiple time lags in the analyzed hemisphere (l_{analyzed = 7)} and to a lesser extent, in the contra hemisphere (l_{contra = 2)} improved the prediction performance. We restricted the model analysis to ALM delay activity. To allow for a sufficient number of time lags within the delay epoch, we chose to predict activity $(V_{t}^{a n a l y z e d})$ during the late delay epoch (from −0.9s to the last time bin before the ‘go’ cue, −0.2s). To account for the possibility that the timescale of interhemispheric interactions may be faster than the size of the timestep, we also included the contra-hemisphere activity at the same time step as the analyzed-hemisphere activity that we predicted (note that in $\sum_{q = - 1}^{l_{c o n t r a}} \sum_{j = 0}^{n_{c o n t r a}} β_{q, j} (z_{t}) {\tilde{X}}_{t - q, j}^{c o n t r a}$ , q starts from −1 instead of 0). This indeed moderately improved the prediction performance. We used the activity projections on the choice decoder and three principal components as input in the contra hemisphere (n_contra = 3), while using only the choice decoder activity as input in the analyzed hemisphere (n_analyzed = 0) to minimize overfitting. Excluding the three principal components from the contra hemisphere’s input and varying the number of input time lags or activity components used for activity prediction did not qualitatively change the results. To avoid potential confounds due to temporal correlations of activity, training and test samples were taken from separate sets of trials.

Interhemispheric influence

To infer the strength of interhemispheric influence, we tested how much model predictions improved if the model included the other hemisphere’s activity as input. To measure the model’s prediction performance, we computed the 5-fold cross-validated R². The predicted and actual activity $(V_{t}^{a n a l y z e d})$ was aggregated across time for each trial type to compute a R². The R² values from the two trial types and 5-fold train-test splits were then averaged. Our measure of influence from the contra to analyzed hemisphere was the difference in R² (“ΔR²”) between the within-hemisphere model (without input from the contra hemisphere) and the full model (incorporates input from the contra hemisphere). In a few analyzed hemispheres, calculating ΔR2 resulted in negative values, which likely resulted from overfitting and low signal-to-noise ratios. In those cases, the ΔR2 was set to 0. All the key results remain the same without this clipping. For comparison of ΔR² in the weakly and highly selective states (Figures 5E and 6A), we evaluated ΔR² separately for test samples in the two states. To examine whether ΔR² captured the influence from the other hemisphere, we shuffled the trial identity of the left and right ALM recording data. ΔR² vanished when shuffling trials of the contra hemisphere’s activity (Figure S6B). The potency of state-dependent gating (Figure 6B) was defined as the difference of ΔR² between the weakly and highly selective states for each analyzed hemisphere and averaged over the two hemispheres. This measured how much interhemispheric influence was modulated by states.

In Figure 5D, we used the interhemispheric input inferred using the coefficients β of the model (β was inferred from control trials) to predict neuronal and behavioral recovery after photoinhibition. The interhemispheric input to the perturbed hemisphere after a photoinhibition (Figure 5D) was computed by multiplying the remaining selectivity in the unperturbed hemisphere with the interhemispheric coefficients β. The β values in the weakly selective state of the model were used, as the analyzed hemisphere was rendered weakly selective by ipsilateral photoinhibition. β’s at different time lags were averaged. The remaining selectivity was the activity difference between the “lick left” and “lick right” trials, averaged over the photoinhibition epoch. The product of activity difference with the interhemispheric coefficient for each activity component was summed over all components to yield the inferred interhemispheric input. The selectivity recovery was the activity difference between “lick left” and “lick right” trials on the choice decoder in the first time bin (400ms) after photoinhibition.

In Figure S6C, we examined the asymmetry of interhemispheric input inferred from control trials. We limited this analysis to the first 0.8 s of the delay epoch. This was matched to the epoch of photoinhibition by which the asymmetry of modularity was measured in the experiment (Figure 2). The interhemispheric input to each hemisphere (analyzed hemisphere) was the product of the interhemispheric coefficients β in the model and the control-trial selectivity in the contra hemisphere. The β values in the weakly and highly selective states in the model were averaged for this analysis to obtain an average interhemispheric input strength. β’s at different time lags were also averaged. This inferred interhemispheric input was normalized to the control-trial selectivity of the analyzed hemisphere during the same epoch. The normalized interhemispheric input (Figure S6C) quantified the contribution from the other hemisphere relative to the total selectivity in the analyzed hemisphere. The larger the normalized interhemispheric input was to an analyzed hemisphere, the smaller the modularity of the analyzed hemisphere was. In Figure S6C, we found a larger normalized interhemispheric input from the left ALM to right ALM in the standard task, but the opposite in the fully reversed task. This pattern of asymmetry is consistent with the asymmetry of modularity measured from photoinhibition (Figure 3).

In Figure S6D, we compared the magnitude of interhemispheric coefficient β in the weakly and highly selective states. Because the interhemispheric coefficient β_q,j was a vector coefficient that span several activity components, the magnitude of interhemispheric coefficient was calculated as the L1 norm of β_q,j (the sum of the absolute value of β_q,j over q and j) for each state.

Photoinhibition experiments to test state-dependent gating

To directly test for state-dependent gating, we unilaterally photoinhibited ALM activity during the late delay epoch (Figure 5F–G). This allowed us to estimate the state of ALM hemispheres based on the delay activity prior to photoinhibition and examine their responses to contralateral photoinhibition.

In each trial, we computed the CD projections using spike counts in a 0.5s window before the onset of photoinhibition. Trials were then classified as “weakly selective” or “highly selective” based on the strength of CD projections. We set a threshold for each trial type (“lick right” and “lick left”) as the median of CD projections during the 0.5s window before photoinhibition onset (similar to Figure 5C). The trials with CD projections far away from the decision boundary and exceeding the median threshold were classified as “highly selective”. Trials on the correct side of the decision boundary but below the median threshold were classified as “weakly selective” (Figure 5F). A small minority of trials with CD projections on the wrong side of the decision boundary were discarded from the analysis because there was little selectivity to test for the effect of contralateral photoinhibition, though including these trials did not qualitatively change the results.

We quantified the effect of contralateral photoinhibition as the difference in CD projections between photoinhibition and control trials. The change in CD projections was averaged across all “weakly selective” trials (both “lick left” and “lick right” trials) or “highly selective” trials (Figure 5G).

Recurrent neural network modeling

We explored conditions in which modular and asymmetric interhemispheric interactions arise through learning by training recurrent neural networks (RNNs) to perform the delayed response task. The RNNs were defined by the equation:

τ \frac{d r}{d t} = - r + f (W^{r e c} r + W^{i n} u + b + ξ)

In this equation, τ is the unit time constant, r represents the population activity of N units, f(·) is the unit nonlinearity, u is an external input to these units, b is the bias or background input, and ξ represents an i.i.d. Gaussian noise to individual units. The N units were divided into two modules, which simulated the left and right hemispheres of ALM. W^rec is an N × N matrix representing the recurrent connectivity weights, which include both within-module and between-module weights, and Wⁱⁿ an N × 1 vector representing the input weights.

Mirroring the delayed response task mice performed, the RNNs received a trial type selective input during a sample epoch of 1.3s, and had to wait for a delay epoch of 1.7s before reporting their choice through a linear readout in each module (Figure 7A).

The trial type input u at each time point during the sample epoch was generated by sampling from an i.i.d. Gaussian distribution N(μ, σ) with μ = 0.15, σ = 1 for “lick right” trials and μ = −0.15, σ = 1 for “lick left” trials. An i.i.d. Gaussian noise with zero mean and a standard deviation of 0.2 (distinct from ξ delivered to individual units) was then added to the input throughout the sample and delay epochs. Note that even though the distributions of the input for the two trial types significantly overlap at any single time point, integrating the input over time renders the two trial types distinguishable. The values of μ and σ for each trial type and the strength of the input noise were chosen to approximately match the task performance of mice.

For results reported in the paper, the RNNs contained N=256 units with the Tanh nonlinearity and τ = 50 ms. The Gaussian noise ξ had zero mean with a standard deviation of 0.2. But the results were largely insensitive to the number of units, strength of noise, or exact shape of the neuronal nonlinearity, as long as its slope decreases for larger inputs (e.g. as in nonlinear functions of the form f(x) ~ x^1/n). The continuous RNN equation above was discretized with the 25ms step size for simulation.

The RNNs were trained by backpropagation through time. We minimized the binary cross entropy loss function between a sigmoid function applied to the linear readout of each module and the binary trial type label using gradient descent. To facilitate the training (in particular to mitigate the vanishing gradient problem), the binary cross entropy loss function was minimized not just at the end of the delay epoch but throughout the delay epoch. In addition, we only trained the recurrent weights W^rec and bias b while keeping all other weights such as Wⁱⁿ and the linear readouts frozen. Wⁱⁿ was randomly initialized with an i.i.d. Gaussian distribution N(0,1) and the linear readout in each module with $N (0, \frac{1}{\sqrt{N / 2}})$ (the initialization of W^rec is explained below, see Conditions for robust RNNs). We did not find that the training of Wⁱⁿ and the linear readouts substantially changed our results. Importantly, no perturbations were applied during training. The RNNs and their training were implemented in Pytorch (Paszke et al., 2019).

The trained RNNs exhibited qualitatively similar dynamics to the neuronal data (Figure 7B). To examine their choice-selective activity, we trained a linear choice decoder for each module in the same manner as for the neuronal data. Specifically, we computed the trial-average difference of population activity between the two trial types (only using correct trials in the training set) and normalized it at each time point during the delay epoch and averaged these directions across the delay epoch. The resulting choice decoders generally did not coincide with the linear readouts, but they had positive inner products. Most of variance in RNN activity was explained by the choice decoders (95.4 ± 1.0% variance explained, n=30 models).

To probe the modularity and robustness of the trained RNNs to perturbations, we applied perturbations that mimicked the optogenetic photoinhibition of ALM. The activity of all units in the perturbed module was clamped to zero to simulate photoinhibition. The photoinhibition period lasted for 0.8s after the onset of the delay epoch. Consistent with the neuronal data, the RNNs did not recover their trial-type selectivity after bilateral photoinhibition. However, trained RNNs were robust to unilateral photoinhibition of their activity when three conditions were met (Figures 7B and S7A–B): modular initialization, modular training, nonlinearity.

Conditions for robust RNNs

Modular initialization refers to initializing the between-module connections weaker than the within-module connections. Concretely, we randomly initialized the within-module weights with an i.i.d. Gaussian distribution $N (0, \frac{1}{\sqrt{N}})$ , and the between-module weights with $N (0, \frac{p}{\sqrt{N}})$ , where p < 1. Modular training refers to training the within-module weights first while keeping the between-module weights frozen. For the results reported in the paper, we kept the between-module weights frozen throughout the training, but we found that training the between-module weights after the within-module weights has been stabilized did not make much difference. Lastly, the condition of nonlinearity requires that the neuronal input-output function be nonlinear, as in the Tanh function. For visualization of the activity projections on the choice decoder in Figure 7B, we used the RNNs that were modular-trained with the modular-initialization parameter p = 0.2 and the Tanh nonlinearity. Qualitatively similar results were obtained when using a power-law nonlinearity that does not have a bounded dynamic range like the Tanh nonlinearity.

The various model and training parameters explored are shown in Figure S7B. To evaluate the trained models, we computed a robustness index that measured each model’s modular organization and its robustness to perturbations. Robustness index was defined as (modularity + selectivity recovery)/2 for each module within a model and averaged across modules. The modularity of a module was the fraction of selectivity (i.e., activity difference between trials types on the choice decoder) retained during photoinhibition of the other module, as for the neuronal data. Unless specified otherwise, the selectivity recovery of a module was the fraction of selectivity recovered after photoinhibition of that module up until the end of the delay epoch. The normalized initial interhemispheric connection strength in Figure S7B refers to the modular-initialization parameter p. For each value of model and training parameters, 30 randomly initialized RNNs were trained.

State-dependent interhemispheric influence in RNNs

We examined whether the robust RNNs gate between-module influences in a state-dependent manner as observed in the neuronal data. Since we knew the precise recurrent weights W^rec, we could directly compute how activity in one module is affected by change in activity in the other module. This corresponds to the gradient of activity in one module with respect to activity in the other module, which can be evaluated from the RNN equation. To focus on choice encoding activity, we projected this gradient on the choice decoder in each module. The projected gradient is given by the equation:

g (x, y) = \frac{\partial}{\partial y} (c d_{a n a l y z e d}^{T} f (W^{r e c} (c d_{a n a l y z e d} x + c d_{c o n t r a} y + {\bar{r}}_{n o n - c h o i c e}) + b))

In this equation, cd_analyzed and cd_contra refer to the choice decoders in the analyzed and contra modules respectively, x and y are the activity projections on the choice decoders in the analyzed and contra module respectively, and ${\bar{r}}_{n o n - c h o i c e}$ is the average population activity after projecting out the choice decoders. We did not include the external input in calculating the gradient since it was absent during the delay epoch. The interhemispheric influence, g(x, y), was evaluated in Pytorch for a grid of x and y values and visualized in Figure 7C.

To compare the interhemispheric influence in highly selective and weakly selective state in the analyzed hemisphere (Figures 7C and S7F–G), we calculated g(x, y) at the average CD projection of correct “lick left” or “lick right” trials in the analyzed hemisphere (see Figure 7C, highly selective state) or at the decision boundary between “lick left” and “lick right” trials (see Figure 7C, weakly selective state).

Asymmetric interhemispheric interactions in RNNs

For the experiments described above, the strength of input to each module was equal. We found that trained RNNs developed an asymmetry of between-module influences when the strength of the input to each module was asymmetric during training (Figure 7D). To modulate the relative strength of the input delivered to each module, we multiplied the components of Wⁱⁿ, the input weights to the left and right modules, with asymmetric gain factors, g_L and g_R:

W^{i n} = (\begin{matrix} W_{L}^{i n} \\ W_{R}^{i n} \end{matrix}) \Rightarrow (\begin{array}{l} W_{L}^{i n} g_{L} \\ W_{R}^{i n} g_{R} \end{array})

For analysis of the asymmetry of between-module influences (Figures 7D–E and S7D–E), the RNNs were always modular-trained with the modular-initialization parameter p = 0.1 and the Tanh nonlinearity. The input asymmetry (Figures 7E and S7D–E) was defined as (g_R − g_L)/(g_L + g_R) and the RNNs were trained with (g_L, g_R) = (1, 0), (1, 0.1), (1, 0.2), (1, 0.5), (1, 1), (0.5, 1), (0.2, 1), (0.1, 1), (0, 1). 50 randomly initialized RNNs were trained for each value of the input asymmetry. The fraction of correct trials was evaluated for each module separately and then averaged over the two modules (Figures S7D). The modularity of a module (Figure 7E) was the fraction of selectivity (i.e., activity difference between trials types on the choice decoder) retained during photoinhibition of the other module. The selectivity recovery of a module (Figure S7E) was the fraction of selectivity recovered after photoinhibition of that module up until the end of the delay epoch.

Neural activity prediction from videos of task-performing mice

To examine if the correlated delay activity across the two hemispheres of ALM could be explained by ongoing movements, we trained convolutional neural networks (CNNs) to predict ALM activity from videos of task-performing mice (Figure S2C). Our goal was to build models that related ALM activity to ongoing movements, then subtract this component of ALM activity from each hemisphere and examine if any correlated activity remains in the residual activity. The CNNs were chosen over linear models because of their superior prediction performance.

The CNNs were trained to predict the activity projections on the choice decoder and the top 3 principal components orthogonal to the choice decoder in the left and right ALM. The firing rates were computed using 400ms wide bins with a 100ms bin stride. The inputs to the CNNs were bottom- and side-view videos of mice during the delay epoch (see Videography). The video frames were temporally downsampled by a factor of 10 (down to 20 Hz) and spatially downsampled by a factor of roughly 3 (down to 130 × 104 pixels for the bottom view; 130 × 86 pixels, side view) to reduce the computational cost and overfitting. The CNNs predicted neural activity at each time point from all video frames within a 400ms time window that was matched to the time bin used to calculate the firing rates. All video frames from the time window were concatenated and fed into the networks. The same CNNs were used for prediction across all time points within the delay epoch.

CNN Architecture

The CNNs had 6 convolutional layers and 1 fully connected layer shared across sessions (512 units), followed by another fully connected layer specific to each session (128 units). To predict ALM activity projections on the choice decoder and the 3 principle components, 2 additional fully connected layers were used (64 units and 1 final readout unit), and these layers were specific to each session and each activity component. The first seven layers were shared across sessions in order to increase the number of training samples and avoid overfitting. The layers following them were session-specific to account for differences in appearance of mice. The bottom- and side-view video frames were fed into separate 6-layered convolutional networks of identical architecture, whose output activations were concatenated and fed into the session-independent fully connected layer. All convolutional layers had 64 output feature maps and a kernel size of 5 × 5, and a 2 ×2 max pooling was applied after the third and fifth convolutional layers. Units in each layer had a nonlinear activation function (ReLU, rectified linear units (Nair and Hinton, 2010)). Batch normalization was applied after each convolutional layer to facilitate training (Ioffe and Szegedy, 2015). To reduce overfitting, dropout was applied before the session-independent fully connected layer and the session-dependent fully connected layer with a drop probability of 0.3 (Hinton et al., 2012). The networks were trained by gradient descent to minimize the mean squared error between the predicted and target activity. The CNNs and their training were implemented in Pytorch (Paszke et al., 2019).

ALM activity prediction by CNNs

We used the networks to predict activity projections on the choice decoder (CD) and top 3 principal components of ALM activity in each hemisphere. The 4 components explained 40.9±9.4% of the single-trial activity variance during the delay epoch. The CNNs’ prediction performance was evaluated by 5-fold cross-validation (Figure S2D). For each trial type and time point, we computed variance explained (R²) across trials within each trial type:

R^{2} = 1 - \frac{\sum_{n t r i a l s} \sum_{i} {(x_{a c t u a l} - x_{p r e d i c t e d})}^{2}}{\sum_{n t r i a l s} \sum_{i} {(x_{a c t u a l} - 〈 x_{a c t u a l} 〉)}^{2}}

where x is the activity projection on the i^th activity component (CD or top 3 principle component). The R² was averaged across two trial types and all time points. This was done to ensure that R² measured how well the networks predicted variability of neural activity across trials, rather than an average change of neural activity across trial types or time.

To examine the extent to which ongoing movement may explain the correlated activity in ALM, we computed the interhemispheric correlation of the residual activity projection on the CD after subtracting the prediction by the CNNs (Figure S2E). The correlation was separately calculated for each trial type and time point on test data aggregated over the 5-fold cross-validation.

To examine whether the reduced interhemispheric correlation in bilateral photoinhibition trials was due to change in ongoing movements, we also predicted ALM activity from videos of mice in photoinhibition trials using CNNs. We used video frames from the late delay epoch, well after photoinhibition. CNNs produced poor predictions of ALM activity from the videos after bilateral photoinhibition (Figure S2J). However, the CNN-predicted ALM activity tended to have a higher interhemispheric correlation than the actual ALM activity (Figure S2K). The results in Figure S2J–K were based on the same CNNs above that were fine-tuned to bilateral photoinhibition trials. Specifically, we combined the videos of control trials and photoinhibition trials to fit the CNNs. In addition, we used a binary mask that excluded the regions where the photoinhibition laser was applied. The binary mask was carefully drawn to cover only the implant region but not part of the mouse’s face or body. The results were qualitatively unchanged when the CNNs were fine-tuned without the binary mask.

QUANTIFICATION AND STATISTICAL ANALYSIS

The sample sizes were similar to sample sizes used in the field: for behavior, 5 mice or more per condition; for electrophysiology, more than 20 (71±3.6, mean ± s.e.m.) units per brain region and per session. No statistical methods were used to determine sample size. All key results were replicated in multiple mice. Mice were randomly pre-allocated into experimental groups. Unless stated otherwise, the investigators were not blinded to allocation during experiments and outcome assessment. Trial types were randomly determined by a computer program. During spike sorting, experimenters cannot tell the trial type, so experimenters were blind to conditions. Statistical tests and bootstrap are described in detail in sections above. Error bars indicate mean ± s.e.m. unless otherwise noted.

Supplementary Material

SF2

Figure S2. Common input does not explain correlated choice encoding activity across two ALM hemispheres, Related to Figure 1

(A) Left, correlated choice encoding activity across hemispheres during the delay epoch. Right, two alternative hypotheses that explain the correlated activity.

(B) Measuring orofacial movements using highspeed cameras to examine whether the correlated ALM delay activity could be explained by ongoing movements.

(C) A schematic of neural activity prediction from videos of task-performing mice. We trained convolutional neural networks to predict single-trial activity in each hemisphere of ALM from bottom- and side-view videos of mice during the delay epoch (Methods). Left, frames from example “lick right” and “lick left” trials. Right, ALM activity projections on the choice decoder (CD) from the example trials. Dashed line, neuronal data; solid line, model prediction.

(D) Cross-validated R² of activity prediction by the convolutional neural networks (Methods). The networks predicted the activity projections on the CD and top 3 principal components of ALM activity in each hemisphere. The 4 components explain 40.9±9.4% of the single-trial activity variance during the delay epoch. Bar, mean across sessions; circles, individual sessions (n=69).

(E) Rank correlation of single trial CD projections across two hemispheres. Rank correlations are quantified within the same trial type. Black line, correlation of actual ALM activity; green line, correlation of predicted ALM activity; blue line, correlation of residual activity after subtracting the predicted activity from the actual activity; black dotted line, the critical correlation corresponding to the one-tailed p-value of 0.05. Error bar, s.e.m. over sessions.

(F) Left, bilateral ALM photoinhibition (Methods). Right, behavioral performance was significantly reduced after bilateral ALM photoinhibition during the early delay epoch. Bar, mean. Symbols, individual mice (mean ± s.e.m., bootstrap). ***P < 0.001, paired two-tailed t-test, control vs. photoinhibition.

(G) Selectivity of both ALM hemispheres. Black, control; cyan, photoinhibition trials.

(H) Projection of ALM activity on the CD at the end of the delay epoch. 2 example sessions. Top, control trials; bottom, photoinhibition trials. Blue, “lick right” trials according to object location; red, “lick left” trials. Solid circles, correct trials; open circles, error trials. Lines show best line fits to trials within each trial type.

(I) Left, rank correlation of single trial CD projections across hemispheres in control and photoinhibition trials. Rank correlations are quantified across both trial types. Right, fraction of trials the CD projections from both hemispheres show the same choice prediction. “Lick right” and “lick left” trials are pooled. Bar, mean; lines and circles, individual sessions (n=79). ***P < 0.001, paired two-tailed t-test.

(J) Top, neural activity prediction from videos of mice after bilateral photoinhibition. Bottom, ALM activity projections on the CD from example trials. Dashed line, neuronal data; solid line, model prediction.

(K) Rank correlation of single trial CD projections across hemispheres for actual neuronal data and predicted activity from videos of mice. Bar, mean across sessions; circles, individual sessions (n=57). ALM activity was more decorrelated after bilateral photoinhibition than predicted from videos. ***P < 0.001, two-tailed t-test.

NIHMS1707554-supplement-SF2.jpg^{(1.9MB, jpg)}

SF1

Figure S1. Neuronal selectivity and correlated choice encoding across two ALM hemispheres, Related to Figure 1

(A) ALM population selectivity across the two hemispheres. Selectivity is the difference in spike rate between the preferred and non-preferred trial type (Methods), normalized to the peak selectivity. Only putative pyramidal neurons with significant trial type selectivity are shown (left ALM, n=2467 neurons; right ALM, n=2444). Dashed lines, behavioral epochs. Data from the standard task (n=49 sessions, 17 mice).

(B) Proportion of ALM neurons with preparatory vs. peri-movement activity and proportion of ALM neurons with preference for “lick right” vs. “lick left”. Preparatory activity is defined as significant trial type selectivity during the sample or delay epoch. Peri-movement activity is significant trial type selectivity during the response epoch. Error bars, s.e.m. across mice. Left, selective pyramidal neurons from the left ALM; Right, selective pyramidal neurons from the right ALM.

(C) ALM population response during the “lick right” trials (blue) and “lick left” trials (red). Neurons are sorted by their preferred trial type. Left, selective pyramidal neurons from the left ALM; Right, selective pyramidal neurons from the right ALM. Mean ± s.e.m across neurons.

(D) Population selectivity for stimulus, choice, and outcome as a function of time. Selectivity is the difference in spike rate between the preferred and non-preferred trial type (Methods). Mean ± s.e.m across neurons.

(E) Comparison of stimulus selectivity across hemispheres. Selectivity of pyramidal neurons during specific epochs are averaged within individual sessions. Circles, individual sessions (n=49).

(F) Comparison of choice selectivity across hemispheres. Circles, individual sessions.

(G) Projection of ALM activity on the choice decoder (CD) at the end of the delay epoch, left ALM vs. right ALM. Data from 8 example sessions. Circles show individual trials from the sessions. Blue, “lick right” trials according to object location; red, “lick left” trials. Solid circles, correct trials; open circles, error trials. Lines show best line fits to trials within each trial type. Figure 1F shows data from session 8.

(H) Rank correlation of single trial CD projections across two hemispheres. Rank correlations are computed in 400ms time bins. Rank correlations are quantified within the same trial type (e.g. line fits in (G); blue, “lick right”; red, “lick left”) or across both trial types (black). Mean ± s.e.m. across sessions (n=49).

(I) Analysis of the local field potential (LFP) and LFP-LFP coherence between the two hemispheres during the delay epoch. Left, LFP power as a function of frequency. Mean ± s.e.m. across sessions. Data from the left and right ALM from multiple sessions are pooled (n=7 sessions). Right, LFP-LFP coherence between the left and right ALM. A trend of increase in coherence was observed in the gamma band (around 40 Hz) during the delay epoch relative to the sample epoch. Increased coherence suggests increased communication between the two hemispheres during the delay epoch (Fries, 2005).

NIHMS1707554-supplement-SF1.jpg^{(3.5MB, jpg)}

SF4

Figure S4. Distinct interhemispheric interactions inferred from photoinhibition are reflected in the interhemispheric dynamics in control trials, Related to Figure 2

(A) Standard task.

(B) Top row, an example session in which both ALM hemispheres appear modular. Left, bars show modularity of the left and right ALM. Right, projection of ALM activity on the choice decoder (CD) at the end of the delay epoch, left ALM vs. right ALM. Circles, individual control trials from the sessions. Blue, “lick right” trials; red, “lick left” trials. Bottom row, an example asymmetric session in which the left ALM appears to drive selectivity in the right ALM. In modular sessions, choice encoding activity was less correlated across hemispheres.

(C) Asymmetry across the two hemispheres predicts the rank correlation of CD projections in control trials. Rank correlations are quantified across both trial types. Asymmetry is the difference in modularity (left ALM – right LAM). Circles, individual sessions (n=49). Line, linear regression. Pearson’s correlation, r= 0.37, p<0.01.

(D) Fully reversed task.

(E) Same as (B) for two example sessions in the fully reversed task.

(F) Same as (C) for sessions in the fully reversed task (n=30). Pearson’s correlation, r= −0.33, p=0.07.

(G) Cross correlation analysis of ALM control trial activity across hemispheres. Left, ALM delay activity from an example trial projected on the CD (time bin size = 10 ms). Data from an asymmetric session in which the left ALM appears to drive selectivity in the right ALM. Note the trajectory in the left ALM (black) leads the trajectory from the right ALM (gray). Right, cross correlation of delay epoch trajectories across hemispheres. The plot shows average cross correlation of all control trials from the session. Circle, time lag of maximum correlation (peak time). Negative peak time indicates the left ALM leading the right ALM.

(H) Asymmetry across hemispheres predicts the time lag of control trial activity trajectories. A negative relationship (Pearson’s correlation, r= −0.25, p=0.03) suggests congruent direction of activity flow. For example, in sessions where photoinhibition suggests that the left ALM drives selectivity in the right ALM (positive asymmetry), the left ALM activity trajectories tend to lead the right ALM in control trials (negative peak time). 7 out of 79 sessions had peak time of 100 ms or longer were excluded.

NIHMS1707554-supplement-SF4.jpg^{(1.8MB, jpg)}

SF3

Figure S3. Distinct organizations of frontal cortical hemispheres across sessions, Related to Figure 2

(A) Left, schematic of the tasks. Right, modularity of the left ALM versus the right ALM. Data from 49 sessions in the standard task and 30 sessions from the fully reversed task are combined, (the same data as in Figures 3A–B).

(B) Modularity of the right ALM. Green, top 1/4 of the sessions with the highest modularity (n=20); Blue, bottom 1/4 of the sessions with the lowest modularity (n=18).

(C) Top, sessions with high modularity. Left, bar shows mean modularity. Circles, individual sessions. Right, selectivity of both ALM hemispheres in control (black) and left ALM photoinhibition trials (cyan). Mean ± s.e.m. across neurons. Bottom, sessions with low modularity.

(D) Same as (B) for modularity of the left ALM.

(E) Same as (C) for right ALM photoinhibition.

(F) Schematic of bootstrap analysis to quantify the variability of modularity across neuron sampling. For each recording session, the neurons from the session are resampled with replacement. Different colors and shades indicate sessions and neurons. The bootstrap resampling is repeated 10,000 times (see methods). The variability of modularity across multiple rounds of bootstrap quantifies the sampling variability.

(G) Standard deviation of modularity across sessions and across neuron resampling (sampling variability). Error bars show s.e.m. ***p < 0.001, bootstrap (Methods). Data from the standard task (n = 49 sessions).

(H) Effect of left ALM photoinhibition on spike rate across sessions with different modularity. Normalized spike rate is the average spike rate of putative pyramidal neurons during photoinhibition normalized to spike rate in control trials. Circles, individual sessions (n=79). Neurons with mean spike rate of <1 spikes/s were excluded. Left, spike rates in the left ALM. Right, spike rates in the right ALM.

(I) Same as (H) for right ALM photoinhibition.

(J) Neural activity measures of arousal did not distinguish sessions with different modularity. Low frequency band (2–8 Hz) LFP power (left) and population mean firing rate (right) of sessions with high or low modularity. Session groupings are from (C) and (E). Data from the standard task.

NIHMS1707554-supplement-SF3.jpg^{(2.1MB, jpg)}

SF5

Figure S5. Variability of modularity across mice, strain, gender, and age, Related to Figures 2 and 3

(A) Left, modularity of the left ALM versus the right ALM across all session in the standard task (the same data as Figure 2D). Right, variability of modularity within mouse across sessions. ΔModularity, changes in modularity across individual sessions relative to the average modularity for each mouse. Only mice with two or more sessions are included.

(B) Variability in modularity predicts robustness to perturbations across mice. Left, neuronal recovery vs. modularity of the unperturbed hemisphere (Pearson’s correlation, r= 0.71, p<10⁻⁵). Right, behavioral recovery vs. modularity of the unperturbed hemisphere (r=0.59, p<0.001). Circles, individual mice. Neuronal recovery and modularity of each mouse are averaged across sessions.

(C) Variability in asymmetry across hemispheres predicts the correlation of ALM choice encoding activity (Pearson’s correlation, r= 0.6, p=0.01). Asymmetry is the difference in modularity between the left and right ALM (left ALM – right ALM). Circles, individual mice. Asymmetry and rank correlation of each mouse are averaged across sessions.

(D) Variability in modularity predicts robustness to perturbations within mouse across sessions. Left, neuronal recovery vs. modularity of the unperturbed hemisphere (Pearson’s correlation r= 0.21, p<0.05). Right, behavioral recovery vs. modularity of the unperturbed hemisphere (r=0.54, p<0.01). Circles, individual sessions. Δ is relative to the across-session-average for each mouse.

(E) Variability in asymmetry across hemispheres predicts the correlation of ALM choice encoding activity within mouse across sessions (Pearson’s correlation, r= 0.41, p=0.03). Circles, individual sessions. Δ is relative to the across-session-average for each mouse.

(F) Modularity of the left ALM across mouse strain, gender, age, and days of behavioral training to reach a criterion performance (70% correct). **, p<0.01; n.s., p>0.05, two tailed t-test.

(G) Same as (F) for the right ALM.

NIHMS1707554-supplement-SF5.jpg^{(1.7MB, jpg)}

SF6

Figure S6. Predictive models of ALM activity capture asymmetry and state-dependent gating of interhemispheric interactions, Related to Figure 5

(A) The model prediction (cross-validated R²) of control trial activity in the left and right ALM (Methods). Bar, mean; circles, individual sessions. n=98 sessions from 28 mice.

(B) Top, the improvement of model prediction (ΔR², where R² is based on cross-validated model prediction, Methods) when including influence from the other hemisphere (Methods). The left and right ALM in each session are counted separately in the histogram. For each hemisphere, we first trained a within-hemisphere model that predicted future activity using the past activity within the hemisphere (Figure 5B, ‘analyzed hemisphere’). For nearly every session, the model prediction was improved by additionally incorporating input from the other hemisphere (Figure 5B, input from the ‘contra hemisphere’). Bottom, the improvement of model prediction (ΔR²) computed from the same data after shuffling the trial identity of the left and right ALM (Methods).

(C) The strength of interhemispheric influence inferred by the predictive models from ALM control trial activity (Methods). The influence of the left ALM over the right ALM is stronger in the standard task (left; n=58 sessions from 18 mice). The influence of the right ALM is stronger in the fully reversed task (right; n=40 sessions from 10 mice). **P < 0.01, paired two-tailed t-test.

(D) The magnitude of interhemispheric coefficient β in the weakly selective state and highly selective state (Methods). The interhemispheric coefficient is smaller when the analyzed hemisphere is in the highly selective state. Bar, mean; circles, individual sessions. n=98 sessions from 28 mice. ***P < 0.001, paired two-tailed t-test.

NIHMS1707554-supplement-SF6.jpg^{(1.1MB, jpg)}

SF7

Figure S7. Conditions for modularity, robustness, and asymmetric interhemispheric interactions to arise in recurrent neural networks, Related to Figure 7

(A) Top, a schematic of 3 conditions in which modular and robust neural dynamics arise in recurrent neural networks (RNNs) trained to perform the delayed response task (Methods). Modular initialization, the interhemispheric weights are initialized with smaller values than the within-hemisphere weights. Modular training, the within-hemisphere weights are trained first while keeping the interhemispheric weights frozen. Nonlinear units, RNN units have Tanh (or other nonlinear) activation functions. Middle, an example 256 × 256 weight matrix. The color indicates weight values. Bottom, example weight changes during training.

(B) Network robustness as a function of various model and training parameters. We measured the network robustness to unilateral ‘photoinhibition’ (transiently setting units’ activity to 0, Figure 7B). The robustness index measured network modularity and recovery following photoinhibition (as in Figures 2 and 4). A completely modular RNN with perfect recovery has an index of 1 (Methods). The x-axis shows the relative strength of the interhemispheric connection compared to within-hemisphere connection strength (Methods). When it is 1, the interhemispheric weights are initialized with equally large values as the within-hemisphere weights. When it is 0, the interhemispheric weights are all initialized to 0. All networks become more robust when the interhemispheric weights are small. RNNs with linear input-output units (dotted curves) are less robust than RNNs with nonlinear units (solid curves). Finally, all networks become more robust after modular training (dark green) than uniform training in which all weights are trained simultaneously (yellow green). In particular, the nonlinear RNNs (solid dark green curve) that are modular-trained and modular-initialized to a moderate degree exhibit the most robustness. Error bar, standard error across randomly initialized RNNs. n = 30 RNNs for each condition.

(C) An example non-modular RNN that is a discrete attractor network. The training parameters are highlighted in (B), red circle. Left, RNN state space and velocity vector field. In this network, choices are encoded by two fixed points (blue “lick right; red, “lick left”). The bold arrows illustrate the effect of left ALM photoinhibition in “lick right” trial. Photoinhibition clamps left ALM activity to zero (cyan arrow). This causes relaxation of network activity in right ALM (along the directions of the small arrows indicating velocity or state evolution by the RNN dynamics). The effect on the right ALM is therefore not gated, resulting in a complete collapse of network activity (gray arrow). Right, network activity during left ALM photoinhibition.

(D) Asymmetry of trained RNNs as a function of input asymmetry across hemispheres. The plot shows RNN task performance (fraction of correct choice) in control trials (dashed line) and after unilateral photoinhibition during the early delay epoch (solid lines). The input asymmetry is the difference in input magnitude between the left and right hemisphere (1 or −1 indicates input only to the right or left hemisphere respectively). RNN task performance significantly drops when the hemisphere receiving stronger input is perturbed. Error bar, standard error across randomly initialized RNNs. n = 50 RNNs for each condition.

(E) Same as (C) for selectivity recovery after unilateral photoinhibition (Methods).

(F) The strength of interhemispheric influence in RNNs in the highly selective state (from Figure 7C) versus modularity in the driven hemisphere. Line, linear regression. Circles, individual RNNs (n= 250 RNNs). See Figure 6A for comparison to neuronal data.

(G) The strength of interhemispheric influence in RNNs in the weakly selective state (from Figure 7C) versus selectivity recovery after unilateral photoinhibition. Selectivity recovery is the selectivity of the perturbed hemisphere in the first 400ms after photoinhibition. Line, linear regression. Circles, individual hemispheres from n=250 RNNs. See Figure 5D for comparison to neuronal data.

NIHMS1707554-supplement-SF7.jpg^{(2.5MB, jpg)}

Highlights.

Correlated and redundant representations of choice across frontal cortical networks
Individual variability shows modular organization is required for robustness
Dynamic gating allows communication and compartmentalization between brain regions
Redundant modular representations naturally emerge in robust network models

Acknowledgements:

We thank K.V. Shenoy, K. Daie, H. Inagaki, S. Ohmae, Z.V. Guo, T. Wang, H. Hou, M. Economo, S. Romani for comments on the manuscript, Sri Laasya Tipparaju for animal training. This work was funded by the Robert and Janice McNair Foundation (NL), Whitehall Foundation (NL), Alfred P. Sloan Foundation (NL), Searle Scholars Program (NL), Pew Scholars Program (NL), McKnight Foundation (NL), NIH NS112312 (NL), NS104781 (NL, SD), NS113110 (NL, SD), EB02871 (SD), and Simons Collaboration on the Global Brain (NL, SD).

Footnotes

Declaration of interests:

Authors declare no competing interests.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References:

Allen WE, Kauvar IV, Chen MZ, Richman EB, Yang SJ, Chan K, Gradinaru V, Deverman BE, Luo L, and Deisseroth K (2017). Global Representations of Goal-Directed Behavior in Distinct Cell Types of Mouse Neocortex. Neuron 94, 891–907 e896. [DOI] [PMC free article] [PubMed] [Google Scholar]
Amit DJ, and Brunel N (1997). Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb Cortex 7, 237–252. [DOI] [PubMed] [Google Scholar]
Barak O, Sussillo D, Romo R, Tsodyks M, and Abbott LF (2013). From fixed points to chaos: three models of delayed discrimination. Progress in neurobiology 103, 214–222. [DOI] [PMC free article] [PubMed] [Google Scholar]
Barrett DG, Deneve S, and Machens CK (2016). Optimal compensation for neuron loss. eLife 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brody CD, and Hanks TD (2016). Neural underpinnings of the evidence accumulator. Current opinion in neurobiology 37, 149–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brody CD, Romo R, and Kepecs A (2003). Basic mechanisms for graded persistent activity: discrete attractors, continuous attractors, and dynamic representations. Current opinion in neurobiology 13, 204–211. [DOI] [PubMed] [Google Scholar]
Brummitt CD, D’Souza RM, and Leicht EA (2012). Suppressing cascades of load in interdependent networks. Proc Natl Acad Sci U S A 109, E680–689. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chabrol FP, Blot A, and Mrsic-Flogel TD (2019). Cerebellar Contribution to Preparatory Activity in Motor Neocortex. Neuron 103, 506–519 e504. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chafee MV, and Goldman-Rakic PS (1998). Matching patterns of activity in primate prefrontal area 8a and parietal area 7ip neurons during a spatial working memory task. Journal of neurophysiology 79, 2919–2940. [DOI] [PubMed] [Google Scholar]
Chen G, Zhang Y, Li X, Zhao X, Ye Q, Lin Y, Tao HW, Rasch MJ, and Zhang X (2017a). Distinct Inhibitory Circuits Orchestrate Cortical beta and gamma Band Oscillations. Neuron 96, 1403–1418 e1406. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chen TW, Li N, Daie K, and Svoboda K (2017b). A Map of Anticipatory Activity in Mouse Motor Cortex. Neuron 94, 866–879 e864. [DOI] [PubMed] [Google Scholar]
Christophel TB, Klink PC, Spitzer B, Roelfsema PR, and Haynes JD (2017). The Distributed Nature of Working Memory. Trends Cogn Sci 21, 111–124. [DOI] [PubMed] [Google Scholar]
Daie K, Svoboda K, and Druckmann S (2021). Targeted photostimulation uncovers circuit motifs supporting short-term memory. Nature neuroscience 24, 259–265. [DOI] [PubMed] [Google Scholar]
Druckmann S, and Chklovskii DB (2012). Neuronal circuits underlying persistent representations despite time varying activity. Current biology : CB 22, 2095–2103. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fanning JP, Wong AA, and Fraser JF (2014). The epidemiology of silent brain infarction: a systematic review of population-based cohorts. BMC Med 12, 119. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fetsch CR, Odean NN, Jeurissen D, El-Shamayleh Y, Horwitz GD, and Shadlen MN (2018). Focal optogenetic suppression in macaque area MT biases direction discrimination and decision confidence, but only transiently. eLife 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Finkelstein A, Fontolan L, Economo MN, Li N, Romani S, and Svoboda K (2021). Attractor dynamics gate cortical information flow during decision-making. Nature neuroscience. doi: 10.1038/s41593-021-00840-6. [DOI] [PubMed] [Google Scholar]
Fisher CM (1965). Lacunes: Small, Deep Cerebral Infarcts. Neurology 15, 774–784. [DOI] [PubMed] [Google Scholar]
Fornito A, Zalesky A, and Breakspear M (2015). The connectomics of brain disorders. Nature reviews Neuroscience 16, 159–172. [DOI] [PubMed] [Google Scholar]
Fries P (2005). A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn Sci 9, 474–480. [DOI] [PubMed] [Google Scholar]
Funahashi S, Bruce CJ, and Goldman-Rakic PS (1989). Mnemonic coding of visual space in the monkey’s dorsolateral prefrontal cortex. Journal of neurophysiology 61, 331–349. [DOI] [PubMed] [Google Scholar]
Fuster JM, and Alexander GE (1971). Neuron activity related to short-term memory. Science 173, 652–654. [DOI] [PubMed] [Google Scholar]
Gao Z, Davis C, Thomas AM, Economo MN, Abrego AM, Svoboda K, De Zeeuw CI, and Li N (2018). A cortico-cerebellar loop for motor planning. Nature 563, 113–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gold JI, and Shadlen MN (2001). Neural computations that underlie decisions about sensory stimuli. Trends Cogn Sci 5, 10–16. [DOI] [PubMed] [Google Scholar]
Guo ZV, Inagaki HK, Daie K, Druckmann S, Gerfen CR, and Svoboda K (2017). Maintenance of persistent activity in a frontal thalamocortical loop. Nature 545, 181–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
Guo ZV, Li N, Huber D, Ophir E, Gutnisky DA, Ting JT, Feng G, and Svoboda K (2014a). Flow of cortical activity underlying a tactile decision in mice. Neuron 81, 179–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
Guo ZV, Hires SA, Li N, O’Connor DH, Komiyama T, Ophir E, Huber D, Bonardi C, Morandell K, Gutnisky D, et al. (2014b). Procedures for behavioral experiments in head-fixed mice. PloS one 9, e88678. [DOI] [PMC free article] [PubMed] [Google Scholar]
Harris JA, Mihalas S, Hirokawa KE, Whitesell JD, Choi H, Bernard A, Bohn P, Caldejon S, Casal L, Cho A, et al. (2019). Hierarchical organization of cortical and thalamic connectivity. Nature 575, 195–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hernandez A, Nacher V, Luna R, Zainos A, Lemus L, Alvarez M, Vazquez Y, Camarillo L, and Romo R (2010). Decoding a perceptual decision process across cortex. Neuron 66, 300–314. [DOI] [PubMed] [Google Scholar]
Hinton G, Srivastava N, Krizhevsky A, Sutskever I, and Salakhutdinov RR (2012). Improving neural networks by preventing co-adaptation of feature detectors. arXiv arXiv:1207.0580. [Google Scholar]
Hippenmeyer S, Vrieseling E, Sigrist M, Portmann T, Laengle C, Ladle DR, and Arber S (2005). A developmental switch in the response of DRG neurons to ETS transcription factor signaling. PLoS Biol 3, e159. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hooks BM, Lin JY, Guo C, and Svoboda K (2015). Dual-channel circuit mapping reveals sensorimotor convergence in the primary motor cortex. The Journal of neuroscience : the official journal of the Society for Neuroscience 35, 4418–4426. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hopfield JJ (1982). Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci U S A 79, 2554–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
Inagaki HK, Fontolan L, Romani S, and Svoboda K (2019). Discrete attractor dynamics underlies persistent activity in the frontal cortex. Nature 566, 212–217. [DOI] [PubMed] [Google Scholar]
Ioffe S, and Szegedy C (2015). Batch Normalization: Accelerating Deep Network Training byReducing Internal Covariate Shift. arXiv arXiv:1502.03167. [Google Scholar]
Jun JJ, Steinmetz NA, Siegle JH, Denman DJ, Bauza M, Barbarits B, Lee AK, Anastassiou CA, Andrei A, Aydin C, et al. (2017). Fully integrated silicon probes for high-density recording of neural activity. Nature 551, 232–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kaufman MT, Churchland MM, Ryu SI, and Shenoy KV (2014). Cortical activity in the null space: permitting preparation without movement. Nature neuroscience 17, 440–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kaufman MT, Churchland MM, Ryu SI, and Shenoy KV (2015). Vacillation, indecision and hesitation in moment-by-moment decoding of monkey motor cortex. eLife 4, e04677. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kiani R, Cueva CJ, Reppas JB, and Newsome WT (2014). Dynamics of neural population responses in prefrontal cortex indicate changes of mind on single trials. Curr Biol 24, 1542–1547. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kitano H (2004). Biological robustness. Nat Rev Genet 5, 826–837. [DOI] [PubMed] [Google Scholar]
Kopec CD, Erlich JC, Brunton BW, Deisseroth K, and Brody CD (2015). Cortical and Subcortical Contributions to Short-Term Memory for Orienting Movements. Neuron 88, 367–377 [DOI] [PMC free article] [PubMed] [Google Scholar]
Leary MC, and Saver JL (2003). Annual incidence of first silent stroke in the United States: a preliminary estimate. Cerebrovasc Dis 16, 280–285. [DOI] [PubMed] [Google Scholar]
Li N, Chen TW, Guo ZV, Gerfen CR, and Svoboda K (2015). A motor cortex circuit for motor planning and movement. Nature 519, 51–56. [DOI] [PubMed] [Google Scholar]
Li N, Daie K, Svoboda K, and Druckmann S (2016). Robust neuronal dynamics in premotor cortex during motor planning. Nature 532, 459–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
Li N, Chen S, Guo ZV, Chen H, Huo Y, Inagaki HK, Chen G, Davis C, Hansel D, Guo C, et al. (2019). Spatiotemporal constraints on optogenetic inactivation in cortical circuits. eLife 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Liu LD, and Pack CC (2017). The Contribution of Area MT to Visual Motion Perception Depends on Training. Neuron 95, 436–446 e433. [DOI] [PubMed] [Google Scholar]
Musall S, Kaufman MT, Juavinett AL, Gluf S, and Churchland AK (2019). Single-trial neural dynamics are dominated by richly varied movements. Nature neuroscience 22, 1677–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nair V, and Hinton G (2010). Rectified Linear Units Improve Restricted Boltzmann Machines. Paper presented at: Proceedings of the 27th International Confer-ence on Machine Learning (Haifa, Israel). [Google Scholar]
Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, Wang Q, Lau C, Kuan L, Henry AM, et al. (2014). A mesoscale connectome of the mouse brain. Nature 508, 207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pachitariu M, Steinmetz N, Kadir S, Carandini M, and Harris KD (2016). Kilosort: realtime spike-sorting for extracellular electrophysiology with hundreds of channels. Advances in Neural Information Processing Systems, 061481. [Google Scholar]
Palop JJ, Chin J, and Mucke L (2006). A network dysfunction perspective on neurodegenerative diseases. Nature 443, 768–773. [DOI] [PubMed] [Google Scholar]
Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, Killeen T, Lin Z, Gimelshein N, Antiga L, et al. (2019). PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32, Wallach H, Larochelle H, Beygelzimer A, d’Alché-Buc F, Fox E, and Garnett R, eds. (Curran Associates, Inc.), pp. 8024–8035. [Google Scholar]
Peixoto D, Verhein JR, Kiani R, Kao JC, Nuyujukian P, Chandrasekaran C, Brown J, Fong S, Ryu SI, Shenoy KV, et al. (2019). Decoding and perturbing decision states in real time. June 24, 2019. BioRxiv. doi: 10.1101/681783 [DOI] [PubMed] [Google Scholar]
Romo R, Brody CD, Hernandez A, and Lemus L (1999). Neuronal correlates of parametric working memory in the prefrontal cortex. Nature 399, 470–473. [DOI] [PubMed] [Google Scholar]
Rossant C, Kadir SN, Goodman DFM, Schulman J, Hunter MLD, Saleem AB, Grosmark A, Belluscio M, Denfield GH, Ecker AS, et al. (2016). Spike sorting for large, dense electrode arrays. Nature neuroscience 19, 634–641. [DOI] [PMC free article] [PubMed] [Google Scholar]
Salkoff DB, Zagha E, McCarthy E, and McCormick DA (2020). Movement and Performance Explain Widespread Cortical Activity in a Visual Detection Task. Cereb Cortex 30, 421–437. [DOI] [PMC free article] [PubMed] [Google Scholar]
Semedo JD, Zandvakili A, Machens CK, Yu BM, and Kohn A (2019). Cortical Areas Interact through a Communication Subspace. Neuron 102, 249–259 e244. [DOI] [PMC free article] [PubMed] [Google Scholar]
Seung HS (1996). How the brain keeps the eyes still. Proc Natl Acad Sci U S A 93, 13339–13344. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shenoy KV, Sahani M, and Churchland MM (2013). Cortical control of arm movements: a dynamical systems perspective. Annual review of neuroscience 36, 337–359. [DOI] [PubMed] [Google Scholar]
Sofroniew NJ, Flickinger D, King J, and Svoboda K (2016). A large field of view two-photon mesoscope with subcellular resolution for in vivo imaging. eLife 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sporns O, and Betzel RF (2016). Modular Brain Networks. Annu Rev Psychol 67, 613–640. [DOI] [PMC free article] [PubMed] [Google Scholar]
Steinmetz NA, Zatka-Haas P, Carandini M, and Harris KD (2019). Distributed coding of choice, action and engagement across the mouse brain. Nature 576, 266–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M, and Harris KD (2019). Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, 255. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sussillo D, and Abbott LF (2009). Generating coherent patterns of activity from chaotic neural networks. Neuron 63, 544–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
Svoboda K, and Li N (2018). Neural mechanisms of movement planning: motor cortex and beyond. Current opinion in neurobiology 49, 33–41. [DOI] [PubMed] [Google Scholar]
Variano EA, McCoy JH, and Lipson H (2004). Networks, dynamics, and modularity. Phys Rev Lett 92, 188701. [DOI] [PubMed] [Google Scholar]
Wang XJ (2001). Synaptic reverberation underlying mnemonic persistent activity. Trends Neurosci 24, 455–463. [DOI] [PubMed] [Google Scholar]
Winnubst J, Bas E, Ferreira TA, Wu Z, Economo MN, Edson P, Arthur BJ, Bruns C, Rokicki K, Schauder D, et al. (2019). Reconstruction of 1,000 Projection Neurons Reveals New Cell Types and Organization of Long-Range Connectivity in the Mouse Brain. Cell 179, 268–281 e213. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wu Z, Litwin-Kumar A, Shamash P, Taylor A, Axel R, and Shadlen MN (2020). Context-Dependent Decision Making in a Premotor Circuit. Neuron 106, 316–328.e6 [DOI] [PubMed] [Google Scholar]
Zatka-Haas P, Steinmetz N, Carandini M, and Harris KD (2020). A perceptual decision requires sensory but not action coding in mouse cortex. BioRxiv. September 16, 2020. doi: 10.1101/501627 [DOI] [Google Scholar]
Zugaro MB, Monconduit L, and Buzsaki G (2005). Spike phase precession persists after transient intrahippocampal perturbation. Nature neuroscience 8, 67–71. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SF2

Figure S2. Common input does not explain correlated choice encoding activity across two ALM hemispheres, Related to Figure 1

(A) Left, correlated choice encoding activity across hemispheres during the delay epoch. Right, two alternative hypotheses that explain the correlated activity.

(B) Measuring orofacial movements using highspeed cameras to examine whether the correlated ALM delay activity could be explained by ongoing movements.

(G) Selectivity of both ALM hemispheres. Black, control; cyan, photoinhibition trials.

NIHMS1707554-supplement-SF2.jpg^{(1.9MB, jpg)}

SF1

Figure S1. Neuronal selectivity and correlated choice encoding across two ALM hemispheres, Related to Figure 1

(E) Comparison of stimulus selectivity across hemispheres. Selectivity of pyramidal neurons during specific epochs are averaged within individual sessions. Circles, individual sessions (n=49).

(F) Comparison of choice selectivity across hemispheres. Circles, individual sessions.

NIHMS1707554-supplement-SF1.jpg^{(3.5MB, jpg)}

SF4

Figure S4. Distinct interhemispheric interactions inferred from photoinhibition are reflected in the interhemispheric dynamics in control trials, Related to Figure 2

(A) Standard task.

(D) Fully reversed task.

(E) Same as (B) for two example sessions in the fully reversed task.

(F) Same as (C) for sessions in the fully reversed task (n=30). Pearson’s correlation, r= −0.33, p=0.07.

NIHMS1707554-supplement-SF4.jpg^{(1.8MB, jpg)}

SF3

Figure S3. Distinct organizations of frontal cortical hemispheres across sessions, Related to Figure 2

(B) Modularity of the right ALM. Green, top 1/4 of the sessions with the highest modularity (n=20); Blue, bottom 1/4 of the sessions with the lowest modularity (n=18).

(D) Same as (B) for modularity of the left ALM.

(E) Same as (C) for right ALM photoinhibition.

(I) Same as (H) for right ALM photoinhibition.

NIHMS1707554-supplement-SF3.jpg^{(2.1MB, jpg)}

SF5

Figure S5. Variability of modularity across mice, strain, gender, and age, Related to Figures 2 and 3

(F) Modularity of the left ALM across mouse strain, gender, age, and days of behavioral training to reach a criterion performance (70% correct). **, p<0.01; n.s., p>0.05, two tailed t-test.

(G) Same as (F) for the right ALM.

NIHMS1707554-supplement-SF5.jpg^{(1.7MB, jpg)}

SF6

Figure S6. Predictive models of ALM activity capture asymmetry and state-dependent gating of interhemispheric interactions, Related to Figure 5

(A) The model prediction (cross-validated R²) of control trial activity in the left and right ALM (Methods). Bar, mean; circles, individual sessions. n=98 sessions from 28 mice.

NIHMS1707554-supplement-SF6.jpg^{(1.1MB, jpg)}

SF7

Figure S7. Conditions for modularity, robustness, and asymmetric interhemispheric interactions to arise in recurrent neural networks, Related to Figure 7

(E) Same as (C) for selectivity recovery after unilateral photoinhibition (Methods).

NIHMS1707554-supplement-SF7.jpg^{(2.5MB, jpg)}

Data Availability Statement

[R1] Allen WE, Kauvar IV, Chen MZ, Richman EB, Yang SJ, Chan K, Gradinaru V, Deverman BE, Luo L, and Deisseroth K (2017). Global Representations of Goal-Directed Behavior in Distinct Cell Types of Mouse Neocortex. Neuron 94, 891–907 e896. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R2] Amit DJ, and Brunel N (1997). Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb Cortex 7, 237–252. [DOI] [PubMed] [Google Scholar]

[R3] Barak O, Sussillo D, Romo R, Tsodyks M, and Abbott LF (2013). From fixed points to chaos: three models of delayed discrimination. Progress in neurobiology 103, 214–222. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] Barrett DG, Deneve S, and Machens CK (2016). Optimal compensation for neuron loss. eLife 5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] Brody CD, and Hanks TD (2016). Neural underpinnings of the evidence accumulator. Current opinion in neurobiology 37, 149–157. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R6] Brody CD, Romo R, and Kepecs A (2003). Basic mechanisms for graded persistent activity: discrete attractors, continuous attractors, and dynamic representations. Current opinion in neurobiology 13, 204–211. [DOI] [PubMed] [Google Scholar]

[R7] Brummitt CD, D’Souza RM, and Leicht EA (2012). Suppressing cascades of load in interdependent networks. Proc Natl Acad Sci U S A 109, E680–689. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] Chabrol FP, Blot A, and Mrsic-Flogel TD (2019). Cerebellar Contribution to Preparatory Activity in Motor Neocortex. Neuron 103, 506–519 e504. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R9] Chafee MV, and Goldman-Rakic PS (1998). Matching patterns of activity in primate prefrontal area 8a and parietal area 7ip neurons during a spatial working memory task. Journal of neurophysiology 79, 2919–2940. [DOI] [PubMed] [Google Scholar]

[R10] Chen G, Zhang Y, Li X, Zhao X, Ye Q, Lin Y, Tao HW, Rasch MJ, and Zhang X (2017a). Distinct Inhibitory Circuits Orchestrate Cortical beta and gamma Band Oscillations. Neuron 96, 1403–1418 e1406. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R11] Chen TW, Li N, Daie K, and Svoboda K (2017b). A Map of Anticipatory Activity in Mouse Motor Cortex. Neuron 94, 866–879 e864. [DOI] [PubMed] [Google Scholar]

[R12] Christophel TB, Klink PC, Spitzer B, Roelfsema PR, and Haynes JD (2017). The Distributed Nature of Working Memory. Trends Cogn Sci 21, 111–124. [DOI] [PubMed] [Google Scholar]

[R13] Daie K, Svoboda K, and Druckmann S (2021). Targeted photostimulation uncovers circuit motifs supporting short-term memory. Nature neuroscience 24, 259–265. [DOI] [PubMed] [Google Scholar]

[R14] Druckmann S, and Chklovskii DB (2012). Neuronal circuits underlying persistent representations despite time varying activity. Current biology : CB 22, 2095–2103. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R15] Fanning JP, Wong AA, and Fraser JF (2014). The epidemiology of silent brain infarction: a systematic review of population-based cohorts. BMC Med 12, 119. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] Fetsch CR, Odean NN, Jeurissen D, El-Shamayleh Y, Horwitz GD, and Shadlen MN (2018). Focal optogenetic suppression in macaque area MT biases direction discrimination and decision confidence, but only transiently. eLife 7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R17] Finkelstein A, Fontolan L, Economo MN, Li N, Romani S, and Svoboda K (2021). Attractor dynamics gate cortical information flow during decision-making. Nature neuroscience. doi: 10.1038/s41593-021-00840-6. [DOI] [PubMed] [Google Scholar]

[R18] Fisher CM (1965). Lacunes: Small, Deep Cerebral Infarcts. Neurology 15, 774–784. [DOI] [PubMed] [Google Scholar]

[R19] Fornito A, Zalesky A, and Breakspear M (2015). The connectomics of brain disorders. Nature reviews Neuroscience 16, 159–172. [DOI] [PubMed] [Google Scholar]

[R20] Fries P (2005). A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn Sci 9, 474–480. [DOI] [PubMed] [Google Scholar]

[R21] Funahashi S, Bruce CJ, and Goldman-Rakic PS (1989). Mnemonic coding of visual space in the monkey’s dorsolateral prefrontal cortex. Journal of neurophysiology 61, 331–349. [DOI] [PubMed] [Google Scholar]

[R22] Fuster JM, and Alexander GE (1971). Neuron activity related to short-term memory. Science 173, 652–654. [DOI] [PubMed] [Google Scholar]

[R23] Gao Z, Davis C, Thomas AM, Economo MN, Abrego AM, Svoboda K, De Zeeuw CI, and Li N (2018). A cortico-cerebellar loop for motor planning. Nature 563, 113–116. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R24] Gold JI, and Shadlen MN (2001). Neural computations that underlie decisions about sensory stimuli. Trends Cogn Sci 5, 10–16. [DOI] [PubMed] [Google Scholar]

[R25] Guo ZV, Inagaki HK, Daie K, Druckmann S, Gerfen CR, and Svoboda K (2017). Maintenance of persistent activity in a frontal thalamocortical loop. Nature 545, 181–186. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R26] Guo ZV, Li N, Huber D, Ophir E, Gutnisky DA, Ting JT, Feng G, and Svoboda K (2014a). Flow of cortical activity underlying a tactile decision in mice. Neuron 81, 179–194. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] Guo ZV, Hires SA, Li N, O’Connor DH, Komiyama T, Ophir E, Huber D, Bonardi C, Morandell K, Gutnisky D, et al. (2014b). Procedures for behavioral experiments in head-fixed mice. PloS one 9, e88678. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] Harris JA, Mihalas S, Hirokawa KE, Whitesell JD, Choi H, Bernard A, Bohn P, Caldejon S, Casal L, Cho A, et al. (2019). Hierarchical organization of cortical and thalamic connectivity. Nature 575, 195–202. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R29] Hernandez A, Nacher V, Luna R, Zainos A, Lemus L, Alvarez M, Vazquez Y, Camarillo L, and Romo R (2010). Decoding a perceptual decision process across cortex. Neuron 66, 300–314. [DOI] [PubMed] [Google Scholar]

[R30] Hinton G, Srivastava N, Krizhevsky A, Sutskever I, and Salakhutdinov RR (2012). Improving neural networks by preventing co-adaptation of feature detectors. arXiv arXiv:1207.0580. [Google Scholar]

[R31] Hippenmeyer S, Vrieseling E, Sigrist M, Portmann T, Laengle C, Ladle DR, and Arber S (2005). A developmental switch in the response of DRG neurons to ETS transcription factor signaling. PLoS Biol 3, e159. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R32] Hooks BM, Lin JY, Guo C, and Svoboda K (2015). Dual-channel circuit mapping reveals sensorimotor convergence in the primary motor cortex. The Journal of neuroscience : the official journal of the Society for Neuroscience 35, 4418–4426. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] Hopfield JJ (1982). Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci U S A 79, 2554–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] Inagaki HK, Fontolan L, Romani S, and Svoboda K (2019). Discrete attractor dynamics underlies persistent activity in the frontal cortex. Nature 566, 212–217. [DOI] [PubMed] [Google Scholar]

[R35] Ioffe S, and Szegedy C (2015). Batch Normalization: Accelerating Deep Network Training byReducing Internal Covariate Shift. arXiv arXiv:1502.03167. [Google Scholar]

[R36] Jun JJ, Steinmetz NA, Siegle JH, Denman DJ, Bauza M, Barbarits B, Lee AK, Anastassiou CA, Andrei A, Aydin C, et al. (2017). Fully integrated silicon probes for high-density recording of neural activity. Nature 551, 232–236. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R37] Kaufman MT, Churchland MM, Ryu SI, and Shenoy KV (2014). Cortical activity in the null space: permitting preparation without movement. Nature neuroscience 17, 440–448. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] Kaufman MT, Churchland MM, Ryu SI, and Shenoy KV (2015). Vacillation, indecision and hesitation in moment-by-moment decoding of monkey motor cortex. eLife 4, e04677. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R39] Kiani R, Cueva CJ, Reppas JB, and Newsome WT (2014). Dynamics of neural population responses in prefrontal cortex indicate changes of mind on single trials. Curr Biol 24, 1542–1547. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R40] Kitano H (2004). Biological robustness. Nat Rev Genet 5, 826–837. [DOI] [PubMed] [Google Scholar]

[R41] Kopec CD, Erlich JC, Brunton BW, Deisseroth K, and Brody CD (2015). Cortical and Subcortical Contributions to Short-Term Memory for Orienting Movements. Neuron 88, 367–377 [DOI] [PMC free article] [PubMed] [Google Scholar]

[R42] Leary MC, and Saver JL (2003). Annual incidence of first silent stroke in the United States: a preliminary estimate. Cerebrovasc Dis 16, 280–285. [DOI] [PubMed] [Google Scholar]

[R43] Li N, Chen TW, Guo ZV, Gerfen CR, and Svoboda K (2015). A motor cortex circuit for motor planning and movement. Nature 519, 51–56. [DOI] [PubMed] [Google Scholar]

[R44] Li N, Daie K, Svoboda K, and Druckmann S (2016). Robust neuronal dynamics in premotor cortex during motor planning. Nature 532, 459–464. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R45] Li N, Chen S, Guo ZV, Chen H, Huo Y, Inagaki HK, Chen G, Davis C, Hansel D, Guo C, et al. (2019). Spatiotemporal constraints on optogenetic inactivation in cortical circuits. eLife 8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R46] Liu LD, and Pack CC (2017). The Contribution of Area MT to Visual Motion Perception Depends on Training. Neuron 95, 436–446 e433. [DOI] [PubMed] [Google Scholar]

[R47] Musall S, Kaufman MT, Juavinett AL, Gluf S, and Churchland AK (2019). Single-trial neural dynamics are dominated by richly varied movements. Nature neuroscience 22, 1677–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R48] Nair V, and Hinton G (2010). Rectified Linear Units Improve Restricted Boltzmann Machines. Paper presented at: Proceedings of the 27th International Confer-ence on Machine Learning (Haifa, Israel). [Google Scholar]

[R49] Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, Wang Q, Lau C, Kuan L, Henry AM, et al. (2014). A mesoscale connectome of the mouse brain. Nature 508, 207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R50] Pachitariu M, Steinmetz N, Kadir S, Carandini M, and Harris KD (2016). Kilosort: realtime spike-sorting for extracellular electrophysiology with hundreds of channels. Advances in Neural Information Processing Systems, 061481. [Google Scholar]

[R51] Palop JJ, Chin J, and Mucke L (2006). A network dysfunction perspective on neurodegenerative diseases. Nature 443, 768–773. [DOI] [PubMed] [Google Scholar]

[R52] Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, Killeen T, Lin Z, Gimelshein N, Antiga L, et al. (2019). PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32, Wallach H, Larochelle H, Beygelzimer A, d’Alché-Buc F, Fox E, and Garnett R, eds. (Curran Associates, Inc.), pp. 8024–8035. [Google Scholar]

[R53] Peixoto D, Verhein JR, Kiani R, Kao JC, Nuyujukian P, Chandrasekaran C, Brown J, Fong S, Ryu SI, Shenoy KV, et al. (2019). Decoding and perturbing decision states in real time. June 24, 2019. BioRxiv. doi: 10.1101/681783 [DOI] [PubMed] [Google Scholar]

[R54] Romo R, Brody CD, Hernandez A, and Lemus L (1999). Neuronal correlates of parametric working memory in the prefrontal cortex. Nature 399, 470–473. [DOI] [PubMed] [Google Scholar]

[R55] Rossant C, Kadir SN, Goodman DFM, Schulman J, Hunter MLD, Saleem AB, Grosmark A, Belluscio M, Denfield GH, Ecker AS, et al. (2016). Spike sorting for large, dense electrode arrays. Nature neuroscience 19, 634–641. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R56] Salkoff DB, Zagha E, McCarthy E, and McCormick DA (2020). Movement and Performance Explain Widespread Cortical Activity in a Visual Detection Task. Cereb Cortex 30, 421–437. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R57] Semedo JD, Zandvakili A, Machens CK, Yu BM, and Kohn A (2019). Cortical Areas Interact through a Communication Subspace. Neuron 102, 249–259 e244. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R58] Seung HS (1996). How the brain keeps the eyes still. Proc Natl Acad Sci U S A 93, 13339–13344. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R59] Shenoy KV, Sahani M, and Churchland MM (2013). Cortical control of arm movements: a dynamical systems perspective. Annual review of neuroscience 36, 337–359. [DOI] [PubMed] [Google Scholar]

[R60] Sofroniew NJ, Flickinger D, King J, and Svoboda K (2016). A large field of view two-photon mesoscope with subcellular resolution for in vivo imaging. eLife 5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R61] Sporns O, and Betzel RF (2016). Modular Brain Networks. Annu Rev Psychol 67, 613–640. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R62] Steinmetz NA, Zatka-Haas P, Carandini M, and Harris KD (2019). Distributed coding of choice, action and engagement across the mouse brain. Nature 576, 266–273. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R63] Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M, and Harris KD (2019). Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, 255. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R64] Sussillo D, and Abbott LF (2009). Generating coherent patterns of activity from chaotic neural networks. Neuron 63, 544–557. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R65] Svoboda K, and Li N (2018). Neural mechanisms of movement planning: motor cortex and beyond. Current opinion in neurobiology 49, 33–41. [DOI] [PubMed] [Google Scholar]

[R66] Variano EA, McCoy JH, and Lipson H (2004). Networks, dynamics, and modularity. Phys Rev Lett 92, 188701. [DOI] [PubMed] [Google Scholar]

[R67] Wang XJ (2001). Synaptic reverberation underlying mnemonic persistent activity. Trends Neurosci 24, 455–463. [DOI] [PubMed] [Google Scholar]

[R68] Winnubst J, Bas E, Ferreira TA, Wu Z, Economo MN, Edson P, Arthur BJ, Bruns C, Rokicki K, Schauder D, et al. (2019). Reconstruction of 1,000 Projection Neurons Reveals New Cell Types and Organization of Long-Range Connectivity in the Mouse Brain. Cell 179, 268–281 e213. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R69] Wu Z, Litwin-Kumar A, Shamash P, Taylor A, Axel R, and Shadlen MN (2020). Context-Dependent Decision Making in a Premotor Circuit. Neuron 106, 316–328.e6 [DOI] [PubMed] [Google Scholar]

[R70] Zatka-Haas P, Steinmetz N, Carandini M, and Harris KD (2020). A perceptual decision requires sensory but not action coding in mouse cortex. BioRxiv. September 16, 2020. doi: 10.1101/501627 [DOI] [Google Scholar]

[R71] Zugaro MB, Monconduit L, and Buzsaki G (2005). Spike phase precession persists after transient intrahippocampal perturbation. Nature neuroscience 8, 67–71. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Modularity and robustness of frontal cortical networks

Guang Chen

Byungwoo Kang

Jack Lindsey

Shaul Druckmann

Nuo Li

Summary

Graphical Abstract

Introduction

Results

Coordinated parallel representations distributed across cortical hemispheres

Figure 1. Parallel representations of choice across frontal cortical hemispheres.

Distinct interhemispheric interactions underlie parallel representations

Figure 2. Distinct organizations of frontal cortical hemispheres.

Figure 3. Organization of frontal cortical hemispheres can be shaped by task.

Modular organization increases the robustness of choice information to perturbations

Figure 4. Modular organization predicts robustness to perturbations.

Analysis of interhemispheric interactions reveals state-dependent gating

Figure 5. Analysis of single-trial activity reveals state-dependent gating of interhemispheric interactions.

State-dependent gating could explain modular organization and behavioral performance

Figure 6. State-dependent gating could explain modular organization and behavioral performance.

Modeling identifies conditions in which interhemispheric interactions become modular or asymmetric

Figure 7. Network models of ALM interhemispheric interactions.

Discussion

Limitations of the study

STAR★METHODS

RESOURCE AVAILABILITY

Lead Contact

Materials availability

Data and code availability

EXPERIMENTAL MODEL AND SUBJECT DETAILS

METHOD DETAILS

Surgery

Behavioral task

Videography

Photoinhibition

Electrophysiology

Behavioral data analysis

Electrophysiology data analysis

Local field potential (LFP)

Spiking activity

Neuronal selectivity

Modularity

Recovery of selectivity after photoinhibition

Choice decoder (CD) and population choice encoding

Analysis of interhemispheric interactions

Predictive model of ALM activity

State dependent gating

Modeling training

Interhemispheric influence

Photoinhibition experiments to test state-dependent gating

Recurrent neural network modeling

Conditions for robust RNNs

State-dependent interhemispheric influence in RNNs

Asymmetric interhemispheric interactions in RNNs

Neural activity prediction from videos of task-performing mice

CNN Architecture

ALM activity prediction by CNNs

QUANTIFICATION AND STATISTICAL ANALYSIS

Supplementary Material

Highlights.

Acknowledgements:

Footnotes

References:

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases