Systematic review of predictive mathematical models of COVID-19 epidemic

Abstract

Background

Various mathematical models were published to predict the epidemiological consequences of the COVID-19 pandemic. This systematic review has studied the initial epidemiological models.

Methods

Articles published from January to June 2020 were extracted from databases using search strings and those peer-reviewed with full text in English were included in the study. They were analysed as to whether they made definite predictions in terms of time and numbers, or contained only mathematical assumptions and open-ended predictions. Factors such as early vs. late prediction models, long-term vs. curve-fitting models and comparisons based on modelling techniques were analysed in detail.

Results

Among 56,922 hits in 05 databases, screening yielded 434 abstracts, of which 72 articles were included. Predictive models comprised over 70% (51/72) of the articles, with susceptible, exposed, infectious and recovered (SEIR) being the commonest type (mean duration of prediction being 3 months). Common predictions were regarding cumulative cases (44/72, 61.1%), time to reach total numbers (41/72, 56.9%), peak numbers (22/72, 30.5%), time to peak (24/72, 33.3%), hospital utilisation (7/72, 9.7%) and effect of lockdown and NPIs (50/72, 69.4%). The commonest countries for which models were predicted were China followed by USA, South Korea, Japan and India. Models were published by various professionals including Engineers (12.5%), Mathematicians (9.7%), Epidemiologists (11.1%) and Physicians (9.7%) with a third (32.9%) being the result of collaborative efforts between two or more professions.

Conclusion

There was a wide diversity in the type of models, duration of prediction and the variable that they predicted, with SEIR model being the commonest type.

Introduction

The first case of COVID-19 was detected in Wuhan on 17 November 2019.¹ On 11 Mar 2020, the WHO declared COVID-19 as a pandemic.² This pandemic is the defining global health crisis of our time and the greatest challenge we have faced since World War II. Since its emergence in Asia late last year, the virus has spread to every continent except Antarctica.³ The total number of cases worldwide on 14 April 2021 was 138,297,267 with 2,976,297 deaths and 111,208,976 recoveries.³

The seminal paper of Kermack et al. in 1927 introduced the Susceptible, Infectious and Recovered (SIR) model for infectious diseases.⁴ Since then, with advances in information technology and fast computing methods, many variants of the SIR model have been developed. Mathematical models predicting the impact of COVID-19 have burgeoned since the onset of pandemic at a global level, with publications on models doubling almost every 20 days.⁵ Published predictive models have looked at various aspects of the pandemic. The models have used specific modelling techniques, assumptions and data gathered from real cases. The predicted outcomes depend on these variables. Models developed early in the epidemic might have had greater impact in planning and allocation of healthcare resources than the later ones.

Numerous mathematical models with varied techniques and predictions often leave the readers confused. This systematic review was carried out to analyse the initial epidemiological predictive models of the COVID-19 pandemic.

Materials and methods

The protocol for this systematic review was registered at www.osf.io on 30/07/2020.⁶ The population for the review comprised all studies on mathematical modelling of the COVID-19 epidemic. The outcomes of interest were epidemiological predictions of the model including the techniques used for mathematical predictions. Only those mathematical models that were published in peer-reviewed journals were included in the study. Studies without explicit mathematical modelling, reviewing COVID-19 with guesstimates, with no full text freely available, with only model description but no predictions and pre-print articles, were excluded. Narrative reviews and commentaries, perspective articles too were excluded, unless they provided novel modelling analyses or outcomes. Publication date range included in our review was from January to June 2020, in the predefined databases to ensure that we considered the initial models.

A detailed literature search was carried out and the following databases were searched; Medline through PubMed, Web of Science, medRxiv, bioRxiv and arXiv. Key words used were mathematical modelling, predictive modelling, COVID-19, SARS-CoV-2, peak infected cases and total deaths. The search strategy followed a two-stage approach. In the first stage, databases were searched using the keywords, and in the second stage, a manual search of articles from the references of the selected article was carried out. The literature search was conducted by two researchers independently. The searches were then reviewed by two other authors.

A data extraction form was designed for the study. Two authors independently extracted the data from all the studies and then compared them. In case of any disagreement, a designated third author again extracted the data separately and the discrepancy was resolved through mutual consultation.

Models were assessed for various prediction characteristics such as peak numbers, total infections, point of time where the pandemic was predicted to peak at a particular location, time to end of pandemic, effectiveness of nonpharmaceutical interventions (NPIs) and hospital admissions. The models were classified as ‘early’ if they had made their predictions before cases reached 2000 at their respective geographical location. Others were classified as ‘late’ models. Short-term models were those that predicted up to two weeks while long-term models predicted beyond this period.

Risk of bias in mathematical model is difficult to assess including with the use of PROBAST checklist for predictive models in medical science, as there is no selection and measurement bias in mathematical models, only the approach and type of models may differ.⁷ Quality assessment of the study articles was carried out based on five questions adapted from Holmdahl et al. published in June 2020.⁸ Narrative synthesis was performed as per the synthesis without meta-analysis guideline.⁹

Results

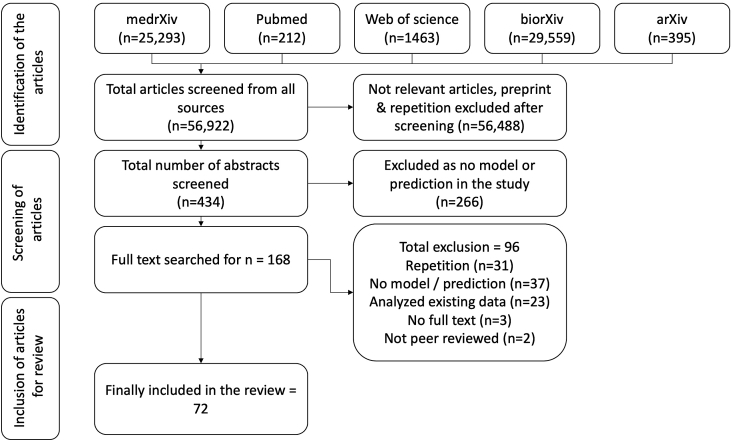
The chosen search strings yielded 56,922 hits in the five databases. The screening of titles yielded 434 abstracts, of which 266 did not contain predictive models. Another 96 were excluded due to other reasons listed in the PRISMA chart (Fig. 1). Finally, 72 articles were included in the systematic review.^{10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81}

Fig. 1.

PRISMA: Selection of articles.

Over 70% (51/72) of the articles contained predictive mathematical models, with susceptible, exposed, infectious and recovered (SEIR) being the commonest one (41/72, 56.9%). The common predictions were regarding cumulative cases (44/72, 61.1%), time to reach total numbers (41/72, 56.9%), peak numbers (22/72, 30.5%), time to peak (24/72, 33.3%), hospital utilisation (7/72, 9.7%) and impact of lockdown and NPIs (50/72, 69.4%). Prediction characteristics studied are listed in Supplementary Table 1. It was found that of the 72 articles, 20 articles were based on hypothetical scenarios which predicted outcomes in numbers, but these outcomes (number of asymptomatic cases and effect of screening, etc) could not be compared with real data. Among those which did (n = 52), the median duration of prediction was 3 months (interquartile range, 2–4 months; range: 10 days–48 months). Curve-fitting models invariably made short-term predictions.

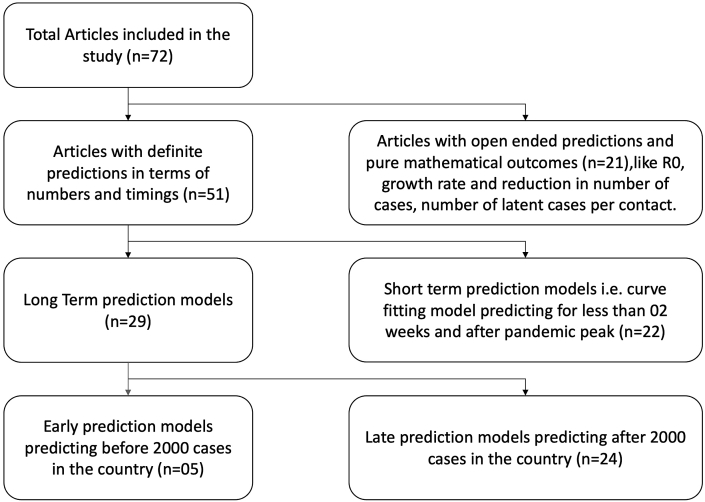
While certain models predicted definite outcomes in terms of time and numbers (51/72, 71%), others were pure mathematical models (21/72, 29%) which studied the impact of various parameters on the pandemic such as basic reproduction number (R₀), variable contact rates of infectious individuals, time spent in crowded zones and population density.^{22,28,31,34,35,43}

Of the 51 models which predicted definite outcomes, models were divided into long-term (n = 29) and short-term (n = 22) models. Furthermore, the long-term models were classified into early predictor models (n = 5) and late predictor models (n = 24) (Fig. 3). Among articles with definite predictions in terms of numbers or time, 22 were curve-fitting models with short-term outcomes, which modelled the epidemiological characteristics around the peak in their region.^{11,13,14,20,22,23,25,26,34,37,40,42,48, 49, 50,53,57,60, 61, 62,64,74}

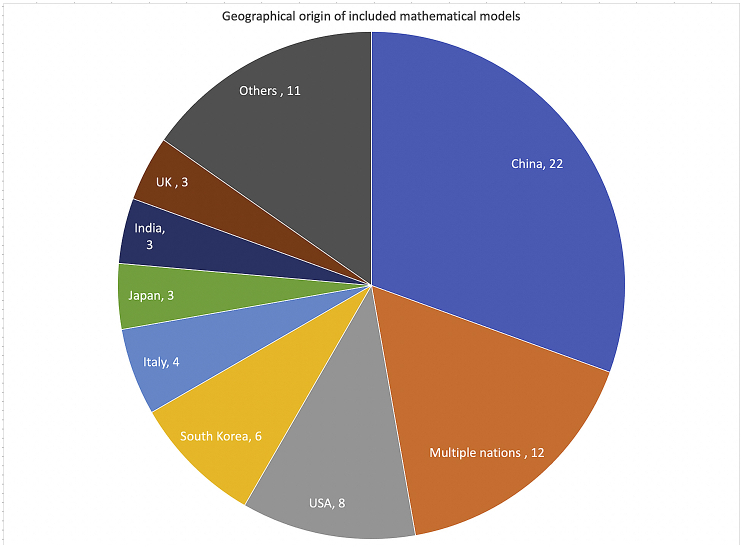
Fig. 3.

Geographical origin of included mathematical models.

While one model looked into the effects of lockdown and other NPIs like screening at airports another looked at specific impact of lockdown in India at 21, 42 and 60 days.^39,44 Many models predicted the estimated burden on health care system and utilisation.^{10,23,30,38,51,52,74}

The countrywise distribution of the studies is shown in Fig. 2. Most of the models predicted outcomes for China (22/71, 31%) followed by USA, South Korea, Japan, India, Iran, UK and Canada (Fig. 2). While most models predicted for a single country or city, there were 12 models that predicted outcomes for more than one country and 3 models that made worldwide predictions. Predictions were also made for the following regions—Hubei Province in China, California, Michigan and Utah in USA, Ontario in Canada, cities such as New York, London and Wuhan and cities in India such as New Delhi, Kolkata, Mumbai and Bangalore. Most studies were published in March (26/72, 36.1%), followed by April (21/72, 29.2%).

Fig. 2.

Characteristics of included mathematical models.

Mathematical models were published by various professionals including Engineers (12.5%), Mathematicians (9.7%), Epidemiologists (11.1%), Physicians (9.7%), Biostatisticians (5.5%) and others (18%). A third of the articles (32.9%) were collaborative efforts between two professions (e.g., Mathematicians and Physicians).

Quality assessment of the models is depicted in Table 1. All the models have clearly defined the purpose in their study. Only 11 (15.27%) considered the population density in the region studied.

Table 1.

Qualitative analysis of mathematical models.⁸

S No	Question	Yes (%)
1	Has the purpose of model been clearly depicted in the study?	72 (100%)
2	Has immunity been taken into account In the model?	54 (75%)
3	Has asymptomatic transmission been taken into account into the model?	37 (52%)
4	Has contact transmission been taken into account in the model?	72 (100%)
5	Has the statistical model displayed confidence intervals? (n = 22)	22 (100%)
6	Has the mechanistic model depicted various parameters, ranges? (n = 50)	50 (100%)
7	Has the prediction been made for a defined geographical region?	58 (81%)
8	Is population density taken into account in the model?	11 (16%)

A table of narrative synthesis of all the articles is provided depicting authors, title, geographical area of predictions, mathematical modelling technique and outcomes evaluated (Suppl Table 1). The characteristics of early and late predictors are also shown (Suppl Table 1).

Discussion

“All models are wrong, but some are useful” said George Fox.⁸² In a situation like the COVID-19 epidemic where uncertainty is rife, predictions from epidemiological models are one of the key tools available for early decision-making.

This review of all the published initial peer-reviewed mathematical models of COVID-19 attempts to summarise and synthesise their findings. The question of prediction arises in the initial stages of any situation (especially a pandemic like COVID-19) that is fraught with ambiguity, chaos and uncertainty. With the passage of time, most situations become clearer and hard data become available for computation. Hence, we did not consider subsequent models from July 2020 onwards. Our review showed that of the large numbers of models published, only a few were both predictive and peer reviewed. Because we studied only the peer-reviewed models, it is likely that models which were published largely for planning purposes by governments or models from news or social media are not included. It is also possible that some authors chose to forgo peer review and submitted their articles directly to various databases.

Systematic review of mathematical models has earlier been carried out in the context of other infectious diseases. Prieto et al. performed a systematic review to identify areas of enhancement of pandemic simulation models of Influenza epidemics for operational use at provincial and local levels.⁸³ A study by Harris et al. has reviewed mathematical models exploring the epidemiological impact of future TB vaccines.⁸⁴

There was a wide heterogeneity seen in the mathematical models evaluating epidemiology of the COVID epidemic (Table 2). The commonest one was SIR model and its variant. The model divided the population into different compartments and the movement of population from one compartment to another is predicted by differential equations. The approach is flexible as more number of compartments may be added. Both stochastic and deterministic model are possible. There were many non–SEIR-based models based on regression models and techniques such as ARIMA (based on time series). However, the model used depends on the aim of the researcher and data available. None of the methods is established as superior to another.⁸⁵

Table 2.

Types of mathematical models.

Model types	Characteristics	Strengths	Weaknesses
Epidemiological models (n = 41)	Compartmental models divide the population into different compartments. Movement from one compartment to another is predicted by differential equations. Can be stochastic or deterministic. Approach is flexible as number of compartments can be varied. e.g, SEIR or variations (SIR, SIRD etc).	Take into account dynamics of spread of infectious disease in a population. Ability to model numerous variables affecting spread like quarantine, isolation, vaccination, re-infection etc. Good for predicting worst-case scenarios and aggregate effect of interventions.	Highly dependent on estimation of parameters. Do not, usually, take into account variability of parameters during the course of the epidemic.
Data-driven models (n = 31)	Usually curve-fitting in nature. Can be predictive or pure mathematical (Open-ended). Used to evaluate concepts for validation or preparedness e.g. Regression model, ARIMA, Log logistic model etc.	Generally have a good fit to retrospective data. Good for short-term projections based on current estimated parameters.	Do not take into account dynamics of disease spread. Lack reliability for long-term predictions.

While short-term models that predicted over just two weeks were more accurate, they were not particularly useful due to the short prediction horizon. These curve-fitting models predicted close to actual outcomes, but with minimal preparedness benefits. However, in special situations where short-term predictions are desired, these might still have a role. These models can be used for validating a new set of assumptions or a new modelling technique.

A few long-term models were constructed early in the epidemic. What they lacked in precision, they made up in usefulness.⁸⁶ Later models were more precise due to larger data sets of more cases, but their usefulness progressively declined. Pure mathematical models (open-ended models) were used to evaluate concepts for validation or preparedness, without predicting any particular quantifiable outcome.

Mathematical modelling was done by a variety of professionals from engineers and mathematicians to doctors and biologists. Epidemiologists comprised about a tenth of all modellers. This demonstrated the interest that the epidemic had generated among various scientists traversing traditional professional silos. Even more interesting was the fact that almost a third of all models were collaborations between multiple professions.

Our study is one of the first systematic reviews of mathematical models of COVID-19 and seeks to synthesise the key characteristics. A limitation of our study was that we were unable to combine the various modelling results into a common numerical estimate. We attempted to estimate the Mean Absolute Percentage Error (MAPE) of the models with real-time data but were constrained by the predicted numbers not being available for different time-points. Another possible limitation was that we have not included articles whose free full text was not available.

An ideal model would be one which factors in the maximum number of relevant variables which could possibly affect study outcomes and predicts with closest proximity to the real outcomes. In this systematic review, the chosen mathematical models had different modelling and prediction characteristics, precluding such an analysis.

There was a wide range of variation in the outcomes predicted in various studies. Which is the model that a country should follow remains an unresolved question till date. It would be ideal for a model to have inputs from mathematicians, epidemiologists, and health care workers (involved in dealing with COVID). Inputs from varied professions help ensure the widest range of reasonable assumptions and make the model more robust. This epidemic is an opportunity for those interested in mathematical modelling (mathematicians, epidemiologists, HCWs and others) to collaborate and improve the models for their regions, considering various parameters based on their specific experience and training. It is also an opportunity for planners and administrators to utilise comprehensive models for informing the planning and preparedness for their regions.

The advent of newer technologies has made mathematical calculation relatively easy. Many free software such as ‘R’, ‘PYTHON’ etc. are now available for mathematical modelling. In the future, the use of more advanced and refined technologies such as artificial intelligence will allow more accurate real-time predictions.

Mathematical models have used varied assumptions and have predicted various outcomes. Actual data for comparisons remains dynamic as the pandemic is still evolving. Data are changing rapidly depending on time, place and effects of NPIs. Hence, it remains difficult to compare predictions with actual outcomes and also to compare all available models at a single platform. A similar review may require to be carried out after some time, when more epidemic data are available and more models are published.

Conclusion

This systematic review analyses all the initial epidemiological models of the COVID-19 pandemic from January to June 2020. The analysis of mathematical models was constrained by varied prediction parameters of different models and differing time horizons of predictions among different models. There was a wide range of assumptions and implications. Thus, no particular model was substantially superior to others.

This review revealed that majority of the mathematical models studied the effect of NPIs, which helped administrators to plan preventive measures. Early predictor models were possibly of greatest utility to administrators in taking planning decisions. SEIR variants were the commonest modelling technique. This systematic review has utility in helping future modellers choose among assumptions to incorporate in their models and also decide on preferred prediction parameters for a particular location or region.

Disclosure of competing interest

Four of the authors have previously authored a mathematical model for the COVID epidemic.

Appendix A. Supplementary data

The following is the Supplementary data to this article:

Multimedia component 1

Characteristics of mathematical models included in the study