Types of potentials in a mitotic spindle

Abstract

The dynamics of a mitotic spindle is very important to understand if the functioning of mitosis has to be understood and defined very accurately. There are a number of forces involved in such a process. Despite of the fact that there have been numerous studies done on the functioning of a mitotic spindle, there is still not a very precise understanding of this system and how it behaves. This study aims at understanding and expressing all the possible potentials which might be responsible in a mitotic spindle and its mechanism.

1. Introduction

Mitosis is defined as a process by which identical sets of genetic instructions are delivered to the product cells. Pico-Newton scale forces are involved in essential mitotic movements. The forces are generated by dynamic microtubules and mitotic motors that are essential in chromosome segregation and alignment. When the cell successfully undergoes the stages of prophase and metaphase, the mitotic cycle continues and the sister chromatids are pulled toward centromeres in the direction of opposite poles of the cell by disassembling kinetochore fibers during anaphase. The motors residing at the kinetochores have several significant responsibilities. One such responsibility is the protein removal from the microtubule attached kinetochores which silences the spindle assembly checkpoint. This process allows the transition from the stage metaphase to anaphase. With time the separation of homologous chromosomes that occurs during meiosis becomes less efficient, which means that extra chromosomes may be carried over into the gametes. This phenomenon is called nondisjunction [1], [2].

The spindle checkpoint is an important arresting point which is activated even when the single chromosome is not properly attached. The arresting of chromosome is immediately activated whenever the mistake is sensed. Furthermore, the cell should undergo arrest and eventually result in apoptosis. To ensure the arrest, spindle assembly checkpoint requires an attachment of misplaced kinetochores to the proteins that have different level of importance. However, the activation of all of the proteins such as Bub1 (budding uninhibited by benomyl 1), Bub3, Bub1-related 1 (BubR1), mitotic arrest deficiency 1 (Mad1), mitotic arrest deficiency (Mad2), monopolar spindle 1 (Mps1), and Aurora B should occur for the division to be prevented [3].

There have been studies on this aspect and most of the research focus on analysis of the cell after it undergoes mitosis and cytokinesis. This study focuses on studying and analyzing the potential terms which may be involved in pulling the sister chromatids apart after metaphase and insuring the proper chromosomal division. These potential terms are very important to understand because the forces which govern the functioning of the mitotic spindle are a result of these potentials. By measuring the forces we can estimate and evaluate the possible outcomes of cell division before the cell actually divides.

Spindle fibers guide the chromosomes towards the poles to ensure a single copy of each sister chromatids at different poles of the cell. When division occurs properly, the spindle assembly checkpoint is deactivated and $\mathbf{Cdc20}$ protein is activated. A principle target of the checkpoint is $\mathbf{Cdc20}$, a protein required for cell-cycle progression [4], when the further outcome of the cell is determined.

The paper [5] focused on forces that must be overcome to establish chromosomal attachment at different poles [5]. Almost every conceivable misarrangement of kinetochore microtubules has been seen at the beginning of prometaphase when chromosomes first interact with the spindle. The faulty arrangements may lead to unequal chromosome distribution if they persisted [5]. Therefore, the calculations in this article will focus on evaluating the state of chromosomes before the cell divides and uncontrolled growth proceeds. Civelekoglu-Scholey, Gul and Scholey, Jonathan M. [6] have studied this process and have expressed that the net force driving the movement of the chromosome is proportional to its velocity and its viscous drag coefficient [6]. Furthermore, it was determined that the viscosity of the cytoplasm may be determined if the shape of the cell is estimated correctly, hence the drag coefficient may be calculated with a good approximation. Another study points towards applying the concept of Young’s modulus to compute the force pulling on the kinetochore in anaphase [7].

In this paper we study the system of a mitotic spindle and express all the possible potentials that might be acting in this system and might govern this system. These potential terms are very important in describing this process because the forces which are involved in the cell division process are a direct result from these potentials.

2. Vibrational self-consistent fields (VSCF)

In our model of the potential fields which are present in the mitotic spindle, we assume that it behaves similarly to how molecules behave in terms of vibrations. The mitotic spindle can have anharmonic vibrations, just as molecules do, because of its structure. Anharmonic vibrations are defined as vibrations which follow the harmonic vibrations but with deviations from the simple harmonic motion. In harmonic oscillator vibrations, the modes of vibrations are independent of each other. Anharmonic vibrations behave in an exactly opposite way where the normal modes of vibrations are not independent of each other. These effects can be easily seen in molecular dynamics.

The main method that has been used so far in anharmonic vibrational spectroscopy calculations for biological molecules [9], small and large, is the vibrational self-consistent field method, including its extensions such as the correlation-corrected VSCF [10]. Applications to molecules where an analytic force field is applied are very effective for monosaccharides, peptides and even proteins [11], [12]. Based on these studies this field can be thought of being one of the potential functions which may play a significant part in describing the functioning of a mitotic spindle. The theoretical methodology can be described by the constructing a Schrodinger equation as follows [9],

$$\left[-\frac{1}{2}\sum _{j=1}^N\frac{{\partial }^2}{\partial Q^2}+V(Q_1,\dots ,Q_N)\right]{\psi }_N(Q_1,\dots ,Q_N)=E_N{\psi }_N(Q_1,\dots ,Q_N)$$ (2.1)

where V is the potential function and N is the number of normal modes. Eq. (2.1) rejects vibration–rotation coupling which can be significant for $J=0$ [13] but for large molecules (even the smallest biological molecules) this can be neglected. The ansatz made by VSCF is given by’

$${\psi }_N^{\left(n\right)}(Q_1,\dots ,Q_N)=\prod _{j=1}^N{\psi }_j^{\left(n\right)}\left(Q_j\right)$$ (2.2)

The harmonic vibration case is neglected here. For situations which do not deviate too much from harmonicity, normal mode coordinates are used as a good approximation for low lying vibrational states [9]. This gives the VSCF equations as,

$$\left[-\frac{1}{2}\frac{{\partial }^2}{\partial Q^2}+{\overline{V}}_j^{\left(n\right)}\left(Q_j\right)\right]={ϵ}_j^{\left(n\right)}{\psi }_j^{\left(n\right)}\left(Q_j\right)$$ (2.3)

where the effective potential ${\overline{V}}_j^{\left(n\right)}\left(Q_j\right)$ for the mode $Q_j$ is given as,

$${\overline{V}}_j^{\left(n\right)}\left(Q_j\right)=\langle \prod _{l\ne j}^N{\psi }_l^{\left(n\right)}\left(Q_l\right)|V(Q_1,\dots ...,Q_N)|\prod _{l\ne j}^N{\psi }_l^{\left(n\right)}\left(Q_l\right)\rangle$$ (2.4)

The VSCF approximation for the total energies is given as [9],

$$E_n=\sum _{j=1}^N{ϵ}_j^{\left(n\right)}-(N-1)\langle \prod _{j=1}^N{\psi }_j^{\left(n\right)}\left(Q_j\right)|V(Q_1,\dots ...,Q_N)|\prod _{j=1}^N{\psi }_j^{\left(n\right)}\left(Q_j\right)\rangle$$ (2.5)

This expression of VSCF may not be very accurate as defined in molecular dynamics. The same level of accuracy may be observed in the case of mitotic spindle vibration effects. More accuracy can be obtained by including various correlation effects between different vibration modes in the total vibrational wavefunction.

3. Potential term due to mechanical effects of molecule motions

In this section we include all the potentials related with mechanical molecular effects, namely bending, stretching and torsion, which might affect the functioning of a mitotic spindle. It is well known that the progression of molecular motion can be observed at the atomic level [14], [15], [16]. The possible mechanical motion of a mitotic spindle can be stretching, bending and twisting/torsional effect. The potential energy at any given time for such spatial motions can be given as a function of the atomic positions by,

$$V(r_1,r_2,\dots ,r_N)=\sum _{i<j}{V}_{bonds}\left(r_{ij}\right)+\sum _{i<j<k}{V}_{angles}\left({\theta }_{ijk}\right)+\sum _{i<j<k<h}{V}_{dihedral}\left({\varphi }_{ijkh}\right)$$ (3.1)

where $V_{bonds}\left(r_{ij}\right)$, $V_{angles}\left({\theta }_{ijk}\right)$ and $V_{dihedral}\left({\varphi }_{ijkh}\right)$ refer to the potential energy associated with bond-stretching, angle-bending, and dihedral angle rotations, respectively. The definition of valence interactions, modeled in most biomolecular force fields by bond-stretching, angle-bending and dihedral terms, requires the determination of force constants and equilibrium values for the distances and angles [15]. These are given by

$$V_{bonds}\left(r_{ij}\right)=\frac{1}{2}{k}_{ij}^b{(r_{ij}-r_{ij}^0)}^2$$ (3.2)

where $k_{ij}^b$ and $r_{ij}^0$ indicate the bond-stretching constant and the equilibrium distance, respectively.

$$V_{angles}\left({\theta }_{ijk}\right)=\frac{1}{2}{k}_{ijk}^{\theta }{({\theta }_{ijk}-{\theta }_{ijk}^0)}^2$$ (3.3)

where $k_{ijk}^{\theta }$ and ${\theta }_{ijk}^0$ indicate the angle-bending constant and the equilibrium angle, respectively. The important aspect to mention here is that the equilibrium values are not necessarily the values observed experimentally but are adjusted to achieve the best overall reproduction of the experimental (or theoretical) values for discrete molecules.

$$V_{dihedral}\left({\varphi }_{ijkh}\right)=\frac{1}{2}{k}_{\varphi }[1+cos(n\varphi +\gamma )]$$ (3.4)

where $k_{\varphi }$, $n$ and $\gamma$ are the torsion constant, multiplicity and phase angle, respectively. The torsion terms are corrections to the computed rotational energy profiles to ensure agreement with observed values (most often from quantum mechanics calculations) and in a well-tuned force field represent principal contributions only from non-classical through H-bond interactions, such as hyperconjugation, electron delocalization and polarization [15], [17].

4. Chemical potential

Chemical potential is a thermodynamics concept used in physics, chemistry, chemical engineering, and biology. It is an important concept because all of the thermodynamic properties of a material at a given temperature and pressure can be obtained from the knowledge of its chemical potential. Under the thermodynamic condition of constant temperature and pressure, chemical potential determines the stability of substances, such as chemical species, compounds, and solutions, and their tendency to chemically react to form new substances, to transform to new physical states, or to migrate from one spatial location to another [18].

In our model of the mitotic spindle we also consider the chemical potential as one of the factors which might come into play as to how the mitotic spindle functions. We can define chemical potentials for any individual cluster $\alpha$, irrespective of equilibrium [19], [20], [21]

$${\mu }_{\alpha }=E_{0\alpha }-kTln\frac{N_s}{C_{\alpha }}$$ (4.1)

where $C_{\alpha }$ is the areal concentration, $E_{0\alpha }$ is the energy of the cluster on the surface relative to the isolated constituent atoms, energy, $N_s$ is the number of sites per area that can hold the cluster (which, for simplicity, has been assumed to be much larger than the number of clusters), k is the Boltzmann constant and T is the temperature.

If we consider a binary AB system, where $\alpha =A_s{B}_t$, the effective chemical equilibrium $\overline{\mu }$ can be given as,

$${\overline{\mu }}_A\left[\sum _{s}s\left(\sum _t{C}_{A_s{B}_t}\right)\right]+{\overline{\mu }}_B\left[\sum _{t}t\left(\sum _s{C}_{A_s{B}_t}\right)\right]=\sum _{s,t}{C}_{A_s{B}_t}{\mu }_{A_s{B}_t}$$ (4.2)

where the sum s and t are over all the possible AB clusters. Since the concentrations of the clusters depend on kinetics of the system, the average $\overline{\mu }$ incorporates both energetics and kinetics. When the system contains only a single element, Eq. (4.2) reduces to,

$${\overline{\mu }}_{A0}=\frac{\sum _s{C}_{A_s}{\mu }_{A_{s}0}}{\sum _{s}s{C}_{A_s}}$$ (4.3)

where the subscript 0 denotes the single-element quantity.

The chemical potential may not be the most dominant potential on which the functions of a mitotic spindle depends upon, but it is still very important when taking into account all the specific potentials responsible in a mitotic spindle.

5. Lennard-Jones potential & Gay–Berne potential

Our model of the mitotic spindle also takes into account the potentials due to the molecular interaction effects. In this section we have discussed why we consider the Gay–Berne Potential instead of the more common Lennard-Jones Potential.

5.1. Lennard-Jones Potential (LJ)

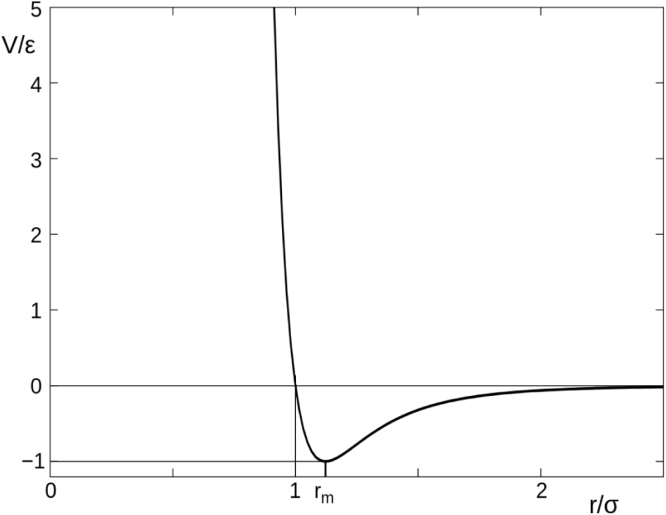
The Lennard-Jones potential (LJ) is a simple pair potential that can accurately model weak van der Waals bonds, yielding reliable bond energies and bond lengths [22]. The LJ has the form,

$$V\left(r\right)=4ϵ\left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right]$$ (5.1)

or is also expressed as,

$$V\left(r\right)=\left[\frac{A}{r^{12}}-\frac{B}{r^6}\right]$$ (5.2)

where,

V is the intermolecular potential between the two atoms or molecules

$ϵ$ is the well depth and a measure of how strongly the two particles attract each other

$\sigma$ is the distance at which the intermolecular potential between the two particles is zero as shown in Fig. 1.

Fig. 1.

Mitotic Spindle [8].

$r$ is the distance of separation between both particles (measured from the center of one particle to the center of the other particle)

$A=4ϵ{\sigma }^{12}$, $B=4ϵ{\sigma }^6$

The first part of the Eq. (3.1) describes the repulsive forces between particles while the latter part of the denotes attraction (see Fig. 2, Fig. 3, Fig. 4).

Fig. 2.

Lennard-Jones Potential. $r_m$ is the minimum r.

Fig. 3.

Typical molecular structure displaying Lennard-Jones Potential.

Fig. 4.

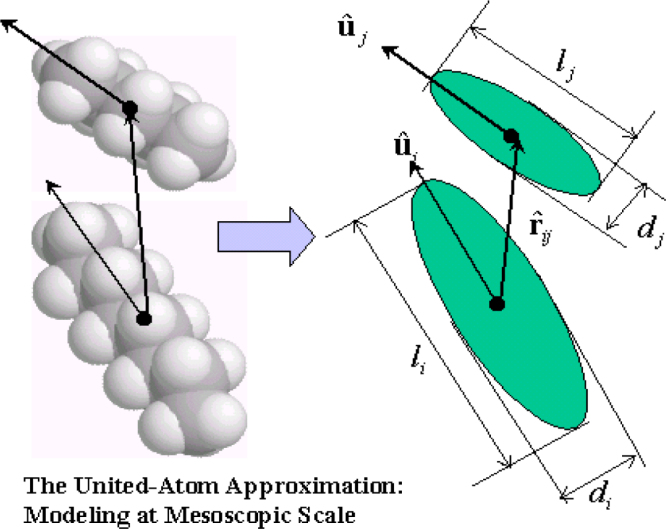
Typical molecular structure displaying Gay–Berne Potential [23].

The force equation related with the Lennard-Jones potential is given by,

$$F=-\frac{dV}{dr},$$ (5.3)

$$F=\frac{12A}{r^{13}}-\frac{6B}{r^7}$$ (5.4)

5.2. Gay–Berne potential (GB model)

There are limitations with the LJ potential. The LJ particles do not have a rotational degree of freedom, they cannot show order–disorder transition of orientation, which is a typical phenomenon observed in liquid crystals [23]. The GB model was proposed to model such phenomena. Gay–Berne potential has been widely used to evaluate the non-bonded interactions between coarse-grained particles being described as elliptical rigid bodies [24]. The commonly used GB model applies only to systems consisting of elliptic particles with identical sizes. Cleaver, Care, Allen, and Neal (CCAN) generalized the GB model to systems composed of elliptical particles of different sizes [25]. This generalization enlarges the scope of systems that the GB model can be used to simulate. Many processes in which the internal structures of the molecules are not modified and do not play an important role, for example, nanoscale self-assembly of stable chemical compounds which is primarily caused by electrostatic interactions rather than covalent bonding, can therefore be modeled based on the generalized GB potential [23]. Another reason for using the GB model is to reduce the computational cost which is an advantage over using other well known model such as the all atom force field [26] which requires a higher computational cost.

$$V_{GB}=\sum _i\sum _{j>i}4ϵ({\hat{\mathbf{u}}}_i,{\hat{\mathbf{u}}}_j,{\hat{\mathbf{u}}}_{ij})\{{\left[\frac{{\sigma }_0}{r_{ij}-\sigma ({\hat{\mathbf{u}}}_i,{\hat{\mathbf{u}}}_j,{\hat{\mathbf{u}}}_{ij})+{\sigma }_0}\right]}^{12}-{\left[\frac{{\sigma }_0}{r_{ij}-\sigma ({\hat{\mathbf{u}}}_i,{\hat{\mathbf{u}}}_j,{\hat{\mathbf{u}}}_{ij})+{\sigma }_0}\right]}^6\}+\sum _i\sum _{j>i}\frac{q_i{q}_j}{r_{ij}}+\sum _i\sum _{j>i}\frac{q_i{q}_j}{r_{ij}^2}\left(q_j{p}_i{\hat{\mathbf{u}}}_i\cdot {\hat{\mathbf{r}}}_{ij}+q_i{p}_j{\hat{\mathbf{u}}}_j\cdot {\hat{\mathbf{r}}}_{ij}\right)+\sum _i\sum _{j>i}\frac{p_i{p}_j}{r_{ij}^3}\left[{\hat{\mathbf{u}}}_i\cdot {\hat{\mathbf{u}}}_j-3\left({\hat{\mathbf{u}}}_i\cdot {\hat{\mathbf{r}}}_{ij}\right)\left({\hat{\mathbf{u}}}_j\cdot {\hat{\mathbf{r}}}_{ij}\right)\right]$$ (5.5)

where

$$\sigma ({\hat{\mathbf{u}}}_i,{\hat{\mathbf{u}}}_j,{\hat{\mathbf{u}}}_{ij})={\sigma }_{ij}^0\{1-\frac{\chi }{2}[\frac{{(\alpha {\hat{\mathbf{r}}}_{ij}\cdot {\hat{\mathbf{u}}}_i+{\alpha }^{-1}{\hat{\mathbf{r}}}_{ij}\cdot {\hat{\mathbf{u}}}_j)}^2}{1+\chi {\hat{\mathbf{u}}}_i\cdot {\hat{\mathbf{u}}}_j}{+\frac{{(\alpha {\hat{\mathbf{r}}}_{ij}\cdot {\hat{\mathbf{u}}}_i-{\alpha }^{-1}{\hat{\mathbf{r}}}_{ij}\cdot {\hat{\mathbf{u}}}_j)}^2}{1-\chi {\hat{\mathbf{u}}}_i\cdot {\hat{\mathbf{u}}}_j}]\}}^{-\frac{1}{2}}$$ (5.6)

is the orientation-dependent range parameter derived from the equi-density surface of the electron cloud of the uniaxially distributed Gaussian distribution,

$q_i$ and $p_i$ shows the charge on the $i$th particle and the $i$th dipole respectively,

$\widehat{{\mathbf{r}}_{ij}}$ is the distance unit vector between the particles $i\&j$

${\sigma }_{ij}^0$ is the contact parameter set as the quadratic means as the breadths of the two interacting particles: $\frac{\sqrt{d_i^2+d_j^2}}{2}$

$\chi$ and $\alpha$ are two parameters defined as,

$$\chi ={\left[\frac{(l_i^2-d_i^2)(l_j^2-d_j^2)}{(l_i^2+d_j^2)(l_j^2+d_i^2)}\right]}^{\frac{1}{2}}$$ (5.7)

and

$$\alpha ={\left[\frac{(l_i^2-d_i^2)(l_j^2+d_i^2)}{(l_j^2-d_j^2)(l_i^2+d_j^2)}\right]}^{\frac{1}{4}}$$ (5.8)

where $l_i>d_i$ and $l_j>d_j$

$\sigma ({\hat{\mathbf{u}}}_i,{\hat{\mathbf{u}}}_j,{\hat{\mathbf{u}}}_{ij})$ is the well depth of the interaction potential where,

$$\sigma ({\hat{\mathbf{u}}}_i,{\hat{\mathbf{u}}}_j,{\hat{\mathbf{u}}}_{ij})=\sqrt{{ϵ}_{0,i}{ϵ}_{0,j}}{\sigma }_1^{\nu }({\hat{\mathbf{u}}}_i,{\hat{\mathbf{u}}}_j){\sigma }_2^{\mu }({\hat{\mathbf{u}}}_i,{\hat{\mathbf{u}}}_j,{\hat{\mathbf{u}}}_{ij})$$ (5.9)

where ${ϵ}_{0,i},{ϵ}_{0,j},\mu$ and $\nu$ are adjustable parameters. The first function is dependent on the relative orientation of the two particles but independent of the distance between them,

$${ϵ}_1^{\nu }({\hat{\mathbf{u}}}_i,{\hat{\mathbf{u}}}_j)={\left[1-{\chi }^2{\left({\hat{\mathbf{u}}}_i\cdot {\hat{\mathbf{u}}}_j\right)}^2\right]}^{-\frac{1}{2}}$$ (5.10)

and

$${ϵ}_2^{\mu }({\hat{\mathbf{u}}}_i,{\hat{\mathbf{u}}}_j,{\hat{\mathbf{u}}}_{ij})=1-\frac{{\chi }_{ij}^{\prime }}{2}[\frac{{({\alpha }_{ij}^{\prime }{\hat{\mathbf{r}}}_{ij}\cdot {\hat{\mathbf{u}}}_i+{\alpha }_{ij}^{\prime -1}{\hat{\mathbf{r}}}_{ij}\cdot {\hat{\mathbf{u}}}_j)}^2}{1+{\chi }_{ij}^{\prime }{\hat{\mathbf{u}}}_i\cdot {\hat{\mathbf{u}}}_j}+\frac{{({\alpha }_{ij}^{\prime }{\hat{\mathbf{r}}}_{ij}\cdot {\hat{\mathbf{u}}}_i-{\alpha }_{ij}^{\prime -1}{\hat{\mathbf{r}}}_{ij}\cdot {\hat{\mathbf{u}}}_j)}^2}{1-{\chi }_{ij}^{\prime }{\hat{\mathbf{u}}}_i\cdot {\hat{\mathbf{u}}}_j}]$$ (5.11)

where the anisotropy parameters of interaction energy for this pair of particles are defined as,

$${\chi }_{ij}^{\prime }=\frac{1-{\left[\left(\frac{{ϵ}_E^i}{{ϵ}_S^i}\right)\left(\frac{{ϵ}_E^j}{{ϵ}_S^j}\right)\right]}^{\frac{1}{2\mu }}}{1+{\left[\left(\frac{{ϵ}_E^i}{{ϵ}_S^i}\right)\left(\frac{{ϵ}_E^j}{{ϵ}_S^j}\right)\right]}^{\frac{1}{2\mu }}}$$ (5.12)

and

$${\alpha }_{ij}^{\prime }=\sqrt{\frac{1}{1+{\left[\left(\frac{{ϵ}_E^i}{{ϵ}_S^i}\right)\left(\frac{{ϵ}_E^j}{{ϵ}_S^j}\right)\right]}^{\frac{1}{2\mu }}}}$$ (5.13)

In the above equations ${ϵ}_S^i$ and ${ϵ}_S^j$ are the well depths corresponding to the side-by-side arrangement for a pair of particles of the same type, and ${ϵ}_E^i$ and ${ϵ}_E^j$ are those corresponding to the end-to-end arrangement.

The GB potential tends to the LJ potential when the particles become spherical, i.e. when $l_i=d_i$, ${\hat{\mathbf{u}}}_i=0$ and/or $p_i=0$.

6. Conclusion

In this paper we have generalized the potentials and/or potential energies which might be responsible for the functioning of a mitotic spindle. The dynamics which govern the mitotic spindle depends on the forces which in turn depend on the potentials. The dynamics of a mitotic spindle is very challenging to understand and we have attempted to understand this considering all the factors that might affect its functioning. Our aim is to understand the mitotic spindle in a very precise way and this can only be possible if we understand the forces and potentials involved. Our next step is to extend this understanding into studying other physical and chemical properties of the mitotic spindle so that we can express the mechanism of a mitotic spindle in a more accurate way. These physical and chemical quantities can be calculated and compared with experimental results giving us a better understanding of our model.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data Availability

Data sharing is not applicable to this article as no new data were created or analyzed in this study.