MICROHEART:A MICROFLUIDIC PUMP FOR FUNCTIONAL VASCULAR CULTURE IN MICROPHYSIOLOGICAL SYSTEMS

Abstract

Advances in microphysiological systems have prompted the need for long-term cell culture under physiological flow conditions. Conventional laboratory pumps typically lack the ability to deliver cell culture media at the low flow rates required to meet the physiological ranges of fluid flow, and are often pulsatile or require flow reversal. Here, a microfluidic-based pump is presented, which allows for the controlled delivery of media for vascular microphysiological applications. The performance of the pump was characterized in a range of microfluidic systems, including straight channels of varying dimensions and self-assembled microvascular networks. A theoretical framework was developed based on lumped element analysis to predict the performance of the pump for different fluidic configurations and a finite element model of the included check-valves. The use of the pump for microvascular physiological studies demonstrated the utility of this system to recapitulate vascular fluid transport phenomena in microphysiological systems, which may find applications in disease models and drug screening.

1. INTRODUCTION

Microphysiological systems can transform the field of pre-clinical in vitro models by providing novel platforms for drug testing and therapeutic target discovery (Offeddu et al., 2020a; Wang et al., 2020). These systems present enhanced physiological relevance compared to 2D cultures through the assembly of multiple cell types into 3D morphologies that mimic specific tissues and organs (Truskey, 2018). Microfluidic channels in these systems act as access points for cell culture media, thus ensuring sufficient supply of nutrients. Additionally, control over fluid transport can be leveraged to impart mechanical stimuli, including fluid pressure gradients and flow-mediated shear stress (Serrano et al., 2021). Thus, these microfluidic channels recapitulate key roles of the vascular system in vivo. On the path to increasing physiological relevance of microphysiological systems, new ways to culture these models under functional fluid flow conditions are required.

Of particular interest, flow profiles through the vasculature vary depending on the hierarchical vessel location. In the microvasculature, the main site of nutrient exchange, flow velocities vary from ~5 mm s⁻¹ in arterioles to ~3 mm s⁻¹ in venules and 0.3 – 1 mm s⁻¹ in capillaries (Yuan and Rigor, 2011). Pulsatility of the flow due to the pumping of the heart takes place in large blood vessels down to arterioles, but is highly damped before reaching the capillaries. These flow profiles result in mechanical stimuli on the endothelium, such as shear stress on endothelial cells in the microcirculation with a typical magnitude of approximately 1 Pa (Roux et al., 2020). A normal component of stress is simultaneously produced by fluid pressure, which results in transmural flow across the endothelium and subsequent interstitial flow in the surrounding extra-cellular matrix (Shi and Tarbell, 2011). The application of fluid flow profiles that mimic these key aspects of blood flow in microphysiological systems offers the potential to exert physiological mechanical cues on the cells within.

Microfluidic channels in microphysiological systems can reproduce the typical dimensions of arterioles and venules, approximately 100–300 μm (Miller et al., 2012; Zhang et al., 2016). Advanced biofabrication techniques involving endothelial cell self-assembly into microvascular networks (Whisler et al., 2013) and hydrogel templating (Heintz et al., 2016), have also made it possible to form smaller channels down to the size of capillaries, < 10 μm (Yuan and Rigor, 2011). Existing pumping methodologies include syringe pumps, which are cumbersome, expensive, and typically cannot supply the low flow rates (< 100 μl min⁻¹) necessary for microphysiological flows, and hydrostatic fluid pressure sources, which are limited to short-term applications and lack consistent flow rates (Jeong et al., 2014). Importantly, these methods do not usually allow for physiological recirculation of cells and media through the system. Here, a new microfluidic pump, termed the ‘MicroHeart’, is presented, which draws upon existing technologies (Byun et al., 2014), but meets the specific criteria of low cost, ease of fabrication and the capability of producing recirculating flow within microphysiological systems with physiological profiles and tailored velocity and pulsatility.

2. MATERIALS AND METHODS

2.1. MicroHeart fabrication

The MicroHeart pump was assembled from two layers of polydimethylsiloxane (PDMS, Dow Corning Sylgard 184, Ellsworth Adhesives, US), which sandwich a 300 μm-thick silicone membrane (Laimeisi, China). The three layers were bonded together through plasma treatment (Fig. 1a,b) after cutting, punching, and sterilization by autoclaving. A 3D-printed inverse mold for the PDMS layers was supplied by Protolabs, US. The CAD file is available upon request. A channel 1× 1 mm runs through the bottom layer of the MicroHeart from an inlet to an outlet, encountering, in order:

• fluid capacitor (9 mm diameter), which stores fluid through deflection of the membrane.

• membrane-based check-valve based on the design in (Mosadegh et al., 2010), dimensions 5 mm (maximum width) by 5 mm (length).

• pressure chamber (6 mm diameter), where air pressure is applied to deflect the membrane and displace fluid.

• another check-valve and fluid capacitor with the same dimensions as their counterparts on the opposite side of the pressure chamber.

Figure 1.

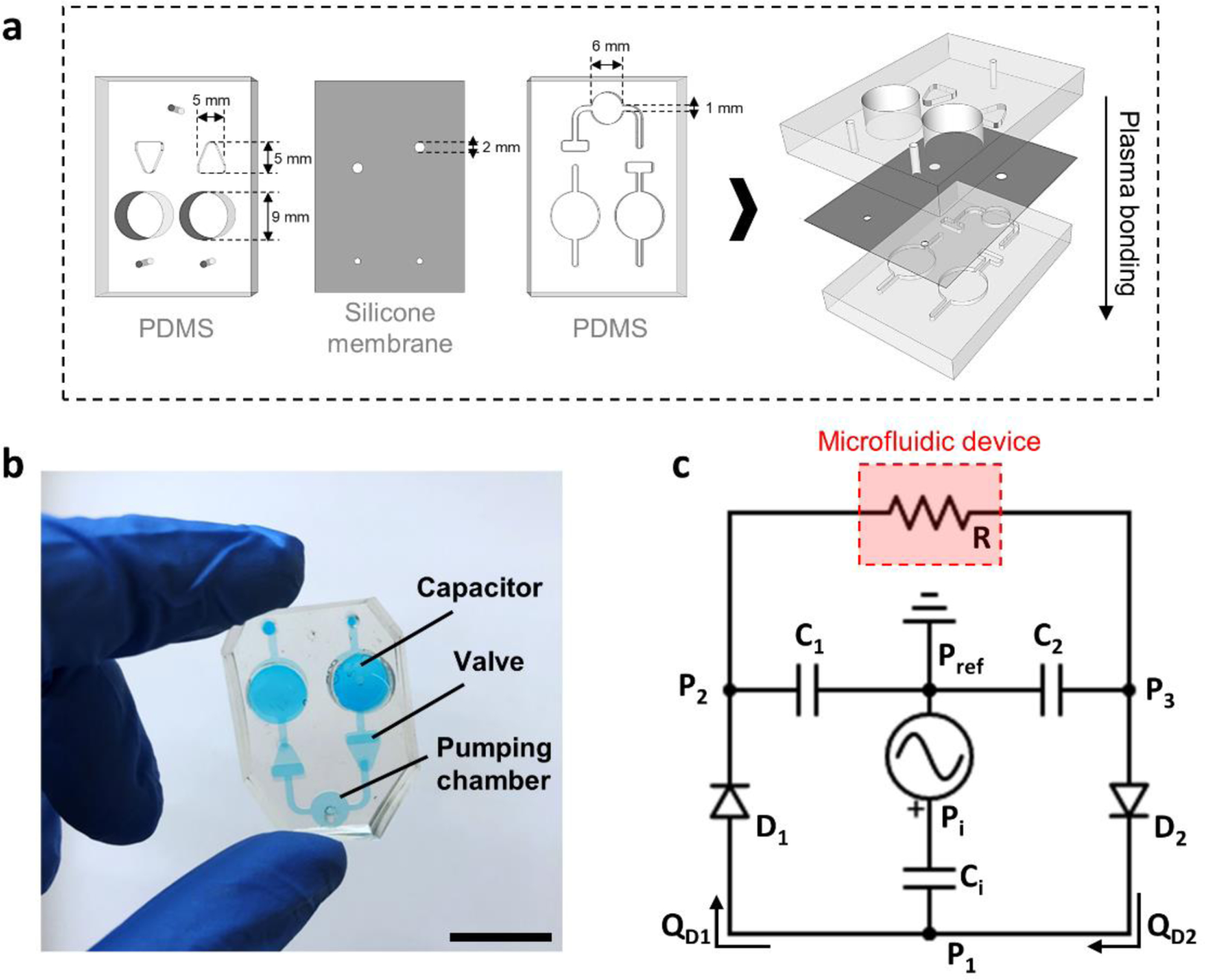
(a) Schematic representation of the MicroHeart fabrication and (b) photograph of the fully assembled MicroHeart. The scale bar is 1 cm. (c) Analogous electrical circuit used for lumped element modeling of flow in the MicroHeart. Pressures across the systems are denoted by P_1–3, and P_ref corresponds to atmospheric, reference pressure. Individual check-valves modelled as diodes are indicated as D_1–2, with their corresponding flow rate described as Q_D1–D2. C_i,1–2 correspond to the capacitance of each capacitor, while R denotes the resistance imposed by the connected microfluidic device.

Here, the inlet and outlet of the pump are connected to a microfluidic device through tubing (internal diameter 1 mm, McMaster-Carr, US). Positive pressure from a regulator (FlowEZ, Fluigent, US) connected to the lab air supply is applied in the pressure chamber periodically through a solenoid (S070C-6CG-32, SMC pneumatics, US). During the ON phase of a cycle, the applied pressure displaces fluid through the forward valve and into the fluid capacitor upstream of the device. During the OFF phase, pressure in the chamber is relieved and the membrane recovers its deformation as fluid flows from the downstream capacitor to the pressure chamber. The pressure difference between the two capacitors drives fluid through the microfluidic device, and is maintained by periodic pressurization of the MicroHeart, resulting in fluid re-circulation. During perfusion, the MicroHeart and connected device are enclosed in small chambers (autoclavable pipette tip boxes) to minimize evaporation.

2.2. Lumped and finite element computational modelling

To develop a predictive understanding of MicroHeart function for different microphysiological systems, a computational model based on a combined lumped-element and finite-element analyses was developed. The design of the pump was reduced to a series of discrete elements that dictate the temporal distribution of pressures and flow rates across the system (Bourouina and Grandchamp, 1996) (Fig. 1c). The pressure regulator acts as a source that imposes a pressure input (P_i) to the closed system. The resulting displacement of the membrane in the pumping chamber depends on its capacitance (C_i), defined through an analytical solution for the deflection of a circular membrane under a distributed pressure load (Eaton et al., 1999):

$$C_i=\frac{\pi a^6\left(1-v^2\right)}{16E{t}^3}$$ (1)

where a and t are the membrane radius and thickness, respectively, while E and υ are its elastic modulus and Poisson’s ratio. The linear relationship holds for the range of operating volume displacements (Fig. S1). Similarly, this relationship applies to the downstream capacitors with capacitances C₁ and C₂.

Stokes flow was assumed within the microfluidic channels, as viscous stresses dominate over convective inertial effects. In this context, an analytical approximation to the hydraulic resistance of the channel can be implemented (Bahrami et al., 2006):

$$R_C=\frac{12\mu L}{w{h}^3}{\left[1-\frac{192h}{{\pi }^{5}w}\mathit{\text{tanh}}\left(\frac{\pi w}{2h}\right)\right]}^{-1}$$ (2)

where μ is the liquid viscosity, and L, w, and h are the length, width, and height of the channel, respectively. For the microvascular networks, a framework was developed to characterize the multiple connecting segments and branches as a series of parallel and serial hydraulic resistances (Fig. S2). Each continuous segment has a corresponding hydraulic resistance given by the Hagen-Poiseuille equation:

$$R_N=\frac{8\mu L}{\pi r^4}$$ (3)

where L and r correspond to the vessel length and radius, respectively. The resistance contributions of all segments were lumped into a single, equivalent hydraulic resistor. Note that while the channels within the MicroHeart and connecting tubes also contribute flow resistance, their dimensions lead to resistances that are 2 – 3 orders of magnitude lower than the resistances of microfluidic systems, and were thus neglected. The effects of transient inertial forces, which translate to fluidic inductors, were also neglected on the basis of scaling arguments.

Each check-valve was considered a diode having two operational regimes: where the flow rate is permitted in the forward direction (P₁>P₂); and an ideal diode configuration where flow is assumed to be fully suppressed in the reverse direction (P₁<P₂). Additionally, a threshold pressure differential (P_th) was defined, below which the valve remains closed regardless of the flow direction. This opening threshold pressure was previously characterized (Mosadegh et al., 2010) and extrapolated in the present case to be approximately 400 Pa. In summary, the flow dynamics of the valve can be defined as:

$$Q_{D1}=\{\begin{array}{cc}\frac{P_1-P_2}{R_D},& P_1-P_2>P_{th}\\ 0,& P_1-P_2\le P_{th}\end{array}$$ (4)

where P₁ and P₂ are the upstream and downstream pressures of the first diode (D₁), respectively, and R_D is the hydraulic resistance imposed by the valve; similarly, for the second diode (D₂) the upstream and downstream pressures correspond to P₃ and P₁. A finite element model with COMSOL Multiphysics was developed to obtain an expression for R_D (Fig. S3). In a series of simulations, the membrane deformation was characterized according to the pressure differential across the valve, yielding the inverse plate stiffness parameter (λ), which relates to the average fluid gap height (δ) through:

$$\delta =\lambda \Delta P.$$ (5)

This relationship remained linear for the range of differential pressures considered in the operation of the pump. Finally, the flow rate across the valve was obtained by considering a rectangular duct geometry, under the assumption that the membrane fluid gap (~0.1 mm) is at least an order of magnitude lower than the valve width (2 mm). Thus, the previous hydraulic resistance parameter was implemented considering the pressure dependent height:

$$R_c=\frac{12\mu L}{w{\delta }^3}{\left[1-\frac{192\delta }{{\pi }^{5}w}\mathit{\text{tanh}}\left(\frac{\pi w}{2\delta }\right)\right]}^{-1}$$ (6)

where L and w correspond to the length and width of the valve that leads to the downstream channel. From this derivation, a power law relationship between the flow rate and pressure emerges, Q~ΔP⁴, which is in agreement with the analytical derivation provided by (Seker et al., 2009) for a similar microfluidic valve design. The finite element model was also used to ascertain the absence of backflow through the valve at pressures as low as 100 Pa (Fig. S3e,f).

Kirchhoff’s Law was applied to each node of the circuit to yield the following equations for mass conservation:

$$\frac{d{P}_1}{dt}=\frac{Q_{D2}-Q_{D1}}{C_i}+\frac{d{P}_i}{dt}$$ (7)

$$\frac{d{P}_2}{dt}=\frac{Q_{D1}-\frac{P_2-P_3}{R}}{C_1}$$ (8)

$$\frac{d{P}_3}{dt}=\frac{\frac{P_2-P_3}{R}-Q_{D2}}{C_2}$$ (9)

The system of equations and lumped element parameters were solved in MATLAB using the ode23s numerical solver. All initial conditions (pressures and flow rates) were set to zero and the independent input variables were the operational settings of the pump: applied pressure (P_i) and pumping frequency (f). These parameters were numerically compiled into a trapezoid step function with a linear pressure rise and fall occurring in 0.1 s, repeating every cycle. The model outputs the time varying pressures throughout the system, which are then used to calculate the flow rate and average velocity in the microfluidic system connected to the MicroHeart (Fig. S4).

2.3. Flow analysis in microfluidic channels and microvascular networks

Straight, rectangular cross-section microfluidic channels with dimensions 0.5 mm × 0.1 mm × 10 mm (w × h × L) (small channel), and 2 mm × 0.1 mm × 20 mm (large channel), were cast in PDMS using inverse molds fabricated through photolithography on SU-8 coated silicon wafers. Three-channel devices, previously described (Haase et al., 2019; Offeddu et al., 2019a), were also assembled from PDMS. After cutting, punching, and sterilization by autoclaving, all devices were bonded through air plasma treatment to #1 glass coverslips.

Microvascular networks formed within the central channel of the three-channel devices as previously described (Offeddu et al., 2019a). Briefly, human umbilical vein endothelial cells expressing green fluorescent protein (HUVECs-GFP, 6 mil mL⁻¹, Angio-Proteomie, US) and human lung fibroblasts (2 mil mL⁻¹, Lonza, US) were injected in the devices within a gelling fibrin solution. Over 7 days of static culture with Vasculife cell culture medium (Lifeline, US), changed daily, the HUVECs self-assembled into perfusable microvessels that bridged the side channels filled with media.

The flow velocities produced by the MicroHeart in the microfluidic channels and microvascular networks were measured through displacement analysis of 2 μm-diameter fluorescent beads (F13083, ThermoFisher), as described previously (Offeddu et al., 2019b). Only the central 2/3 of the projected area of the microfluidic channels were analyzed to minimize edge effects. The applied pressure in the MicroHeart was varied in the range 0.5 – 2.5 kPa (the maximum pressure allowed by the pressure regulator used), and the solenoid frequency was varied in the range 0.5 – 4 Hz. The imparted wall shear stress in the microvascular networks was estimated assuming the Hagen-Poiseuille equation to be roughly applicable:

$${\tau }_w=\frac{4\mu \overline{V}}{r}$$ (10)

where r is the vessel radius and $\overline{V}$ is the average fluid velocity obtained from experimental measurements or computational simulations.

2.4. Immune cell circulation, microvascular network perfusion, and permeability assay

The Jurkat T cell leukemia line was used to model immune cell circulation using the MicroHeart. Jurkat, clone E6–1 T cells (American Type Culture Center, Manassas, US) were cultured in RPMI-1640 medium with 10% fetal bovine serum and 1% penicillin/streptomycin (ThermoFisher, Waltham, US). Jurkat T cells were made fluorescent by incubating them with 10 μM CellTracker Red CMTPX Dye or 1 μM CellTracker Deep Red Dye (ThermoFisher, Waltham, US) for 30 minutes in Dulbecco’s phosphate buffered saline (DPBS). Excess dye was removed by centrifugation, and the Jurkat cells were resuspended at a density of 0.2 M cells mL⁻¹, in Vasculife medium for circulation with the MicroHeart.

The permeability of Texas Red-conjugated 70 kDa dextran (0.1 mg mL⁻¹, D1864, ThermoFisher) in the microvascular networks was measured as previously described (Offeddu et al., 2019a) on an Olympus FV1000 confocal microscope with temperature and atmosphere control. Samples subjected to MicroHeart flow over 24 hours (2.5 kPa and 1 Hz) were compared to static controls. Immunostaining of the samples used for the permeability assay was performed using a rabbit antibody against ZO-1 (61–7300, ThermoFisher, US) and a mouse antibody against heparin sulfate (HS, 370255-S, Amsbio, US). Longer-term perfusion of the microvascular networks up to 7 days was achieved by closing the gel seeding ports of the device with custom stoppers (pipette tips filled with cured PDMS) to prevent fluid leakage and evaporation.

2.4. Statistical analysis and data representation

Statistical significance was assessed by student’s t-tests using OriginPro2019 software. Probability values p < 0.05 were deemed significant (*, p < 0.01 **, p < 0.001 ***). All data representation details are provided in the figure captions.

3. RESULTS

3.1. Flow in microfluidic channels and computational model validation

The functionality of the MicroHeart was first characterized in straight microfluidic channels with different dimensions. In these experiments, fluorescent beads were circulated through the small or large channels at increasing applied pressures and a constant pumping frequency of 1 Hz. The average bead velocity progressively increased with higher applied pressures, up to 1.59 mm s⁻¹ in the large channel and 7.2 mm s⁻¹ in the small channel for a 2.5 kPa applied pressure (Fig. 2a,c). The relatively large variation in experimentally measured flow rates is likely attributable to inaccuracies associated with combined effects of (i) beads settling under gravity, and (ii) bead interactions with the channel walls.

Figure 2.

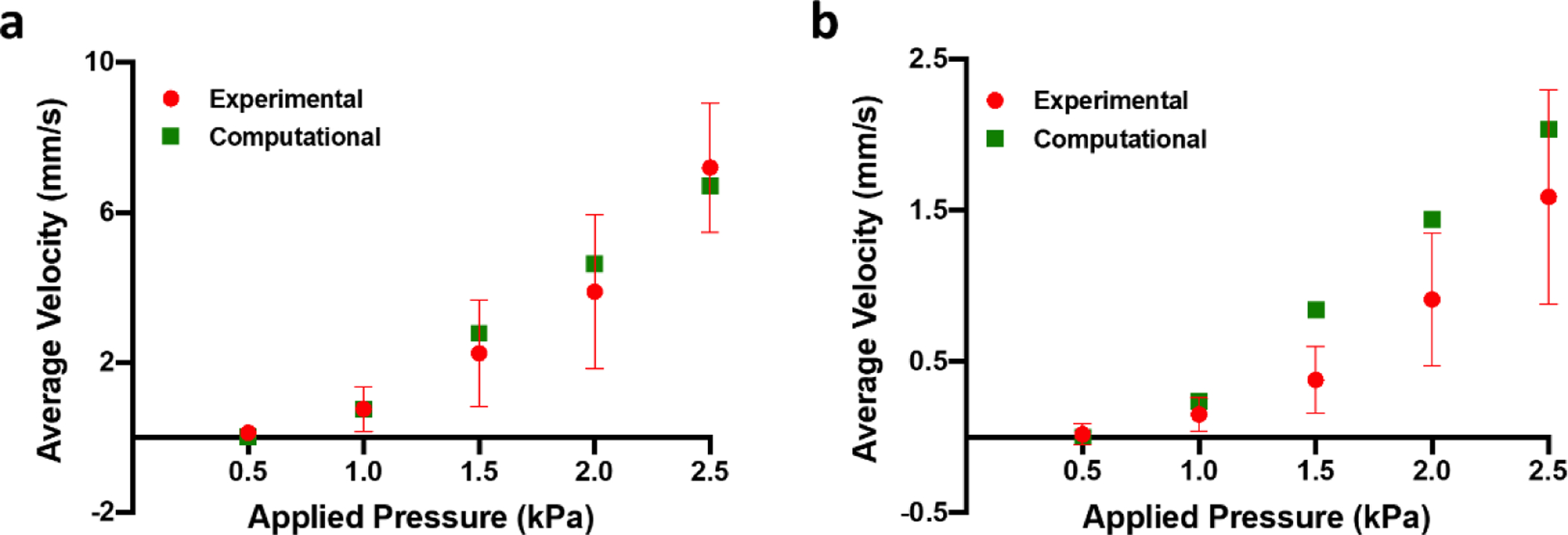
Experimental characterization and computational prediction of flow velocity in the small (a) and large (b) microfluidic channels. Data are represented as average and standard deviation between 3 locations per microfluidic channel, each of which contained more than 150 single bead track measurements.

Pulsatility of the flow produced by the MicroHeart in both the large and small channels was observed as a function of applied pressure. Minimum (v_L) and maximum (v_H) bead velocities per cycle were measured, and the pulsatility of the flow was defined as their ratio (Fig. S5). While both v_L and v_H increased with applied pressure, their ratio also increased, i.e. the flow became less pulsatile, up to a value of ~0.5 in the large channel and ~1 in the small channel for a 2.5 kPa applied pressure. The net flow rate can be calculated based on these bead velocities, and it was found to increase up to 19.06 μL min⁻¹ for the large channel and 21.61 μL min⁻¹ for the small channel for 2.5 kPa applied pressure.

The average bead velocity experimental values were used to validate the lumped element computational results, in which the particular flow resistance of each microfluidic channel was considered according to its ascribed geometry. From the model output, the average fluid velocity can be obtained for a given system once it reaches steady state operation, within a few seconds (Fig. S4). Comparison between the average fluid velocity results for the small channel shows excellent agreement with the computational model (Fig. 2a), while slightly less overlap was observed with the experimental values for the large channel (Fig. 2b). Deviations in the agreement between experimental and computational results could be attributed to the factors mentioned above regarding limitations in measuring flow using beads.

3.2. Flow in microvascular networks

Beads flowing in the microvascular networks followed multiple paths and were often observed to adhere to the endothelium (Fig. 3a, Suppl. Video S1). Similar to the microfluidic channels, bead velocity increased with pressure applied to the MicroHeart with a frequency of 1 Hz (Fig. 3b), from 0.59 mm s⁻¹ at 0.5 kPa to 3.34 mm s⁻¹ at 2.5 kPa. Contrary to the microfluidic channels, however, pulsatility of the flow could be not be observed in the microvascular networks for any pressures, as likely small compared to the variability in bead velocity (Fig. S6a). Bead velocity in the microvascular networks was also found to increase with applied frequency, (Figure 3c), from 1.12 mm s⁻¹ at 0.5 Hz to 2.23 mm s⁻¹ at 4 Hz when pressure was kept constant at 1.5 kPa. This is likely a result of longer idle times between pumping cycles for lower frequencies, which allows for additional time for the capacitors to equilibrate and a drop in differential pressure across the device.

Figure 3.

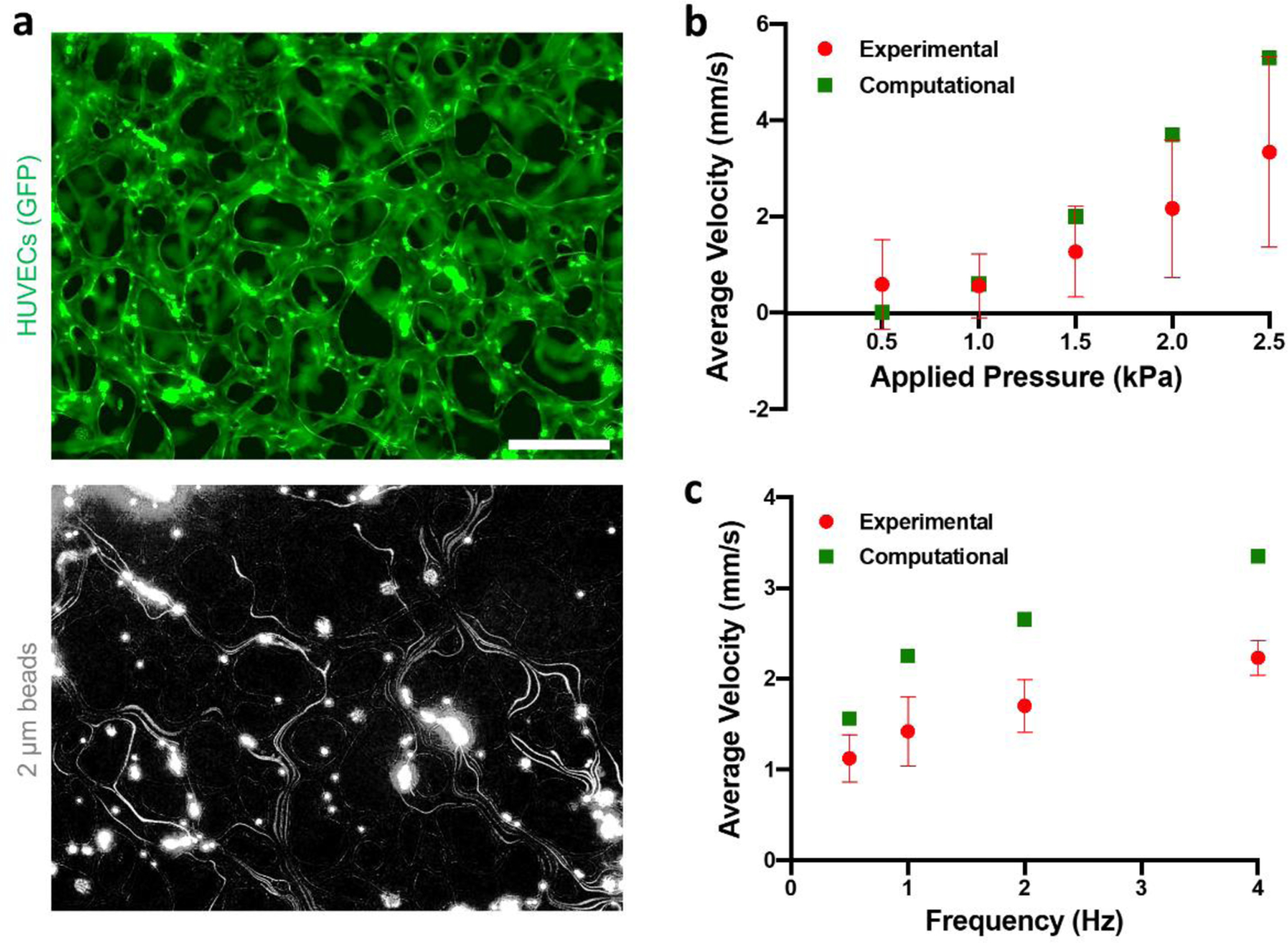
(a) MicroHeart flow in the microvascular networks (top) as visualized by fluorescent beads (bottom). The bead signal was projected over time, yielding the paths followed by the beads in the networks. The scale bar is 200 μm. (b) Experimental results and computational prediction of average flow velocity in the networks as a function of applied pressure for a frequency of 1 Hz, and (c) corresponding values as a function of frequency for an applied pressure of 1.5 kPa. Data are represented as average and standard deviation of 3 devices, for which all beads passing in the field of view at a single time (range: 5–14) were analyzed over 25 time points.

The computational model captured both the pressure and frequency trends well, although it predicted marginally higher fluid velocities in all cases. This, again, could be attributed to errors in the experimental measurements due to adhesive interactions between the beads and the microvascular wall. Based on these predictions, the model yielded flow rates in the microvascular networks in the range 0 – 30 μL s⁻¹ for the pressures and frequencies applied (Figure S4c–d, S6b). The computational model was used to extend this experimental range to capture the broader pressure/frequency parameters window in which the MicroHeart produces a physiological endothelial shear stress of ~ 1 Pa (Figure S6c,d). This prediction was done for microvascular networks in both the current device used (3 mm central channel width) and in a smaller device (1.2 mm central channel width, e.g. AIM chips, AIM Biotech, US). It found that, the shorter the width of the device central channel, the lower the applied MicroHeart pressure or frequency required to impart a physiological shear stress on the endothelium.

3.3. Applications to vascular biology studies

Culture under MicroHeart flow for 24 hours (2.5 kPa, 1 Hz) produced significant changes in the microvascular networks. Permeability of 70 kDa dextran decreased by a factor of 1.64 to 2.81 × 10⁻⁸ cm s⁻¹ after flow, from 4.59 × 10⁻⁸ cm s⁻¹ for static controls (Figure 4a). This increase in barrier function was accompanied by a qualitative increase in heparin sulfate produced in the networks. The proteoglycan, which is the most prevalent component of the endothelial glycocalyx (Weinbaum et al., 2007), was observed in higher density both as co-localized with the endothelium and in the surrounding matrix (Figure 4c). In addition to luminal flow along the endothelium, such changes may have also been produced by flow across the endothelium: During the 24 hours of MicroHeart flow, fluid was seen accumulating at the gel ports of the microfluidic device, consistent with transmural flow produced by pressurized media in the microvascular networks (Offeddu et al., 2019b).

Figure 4.

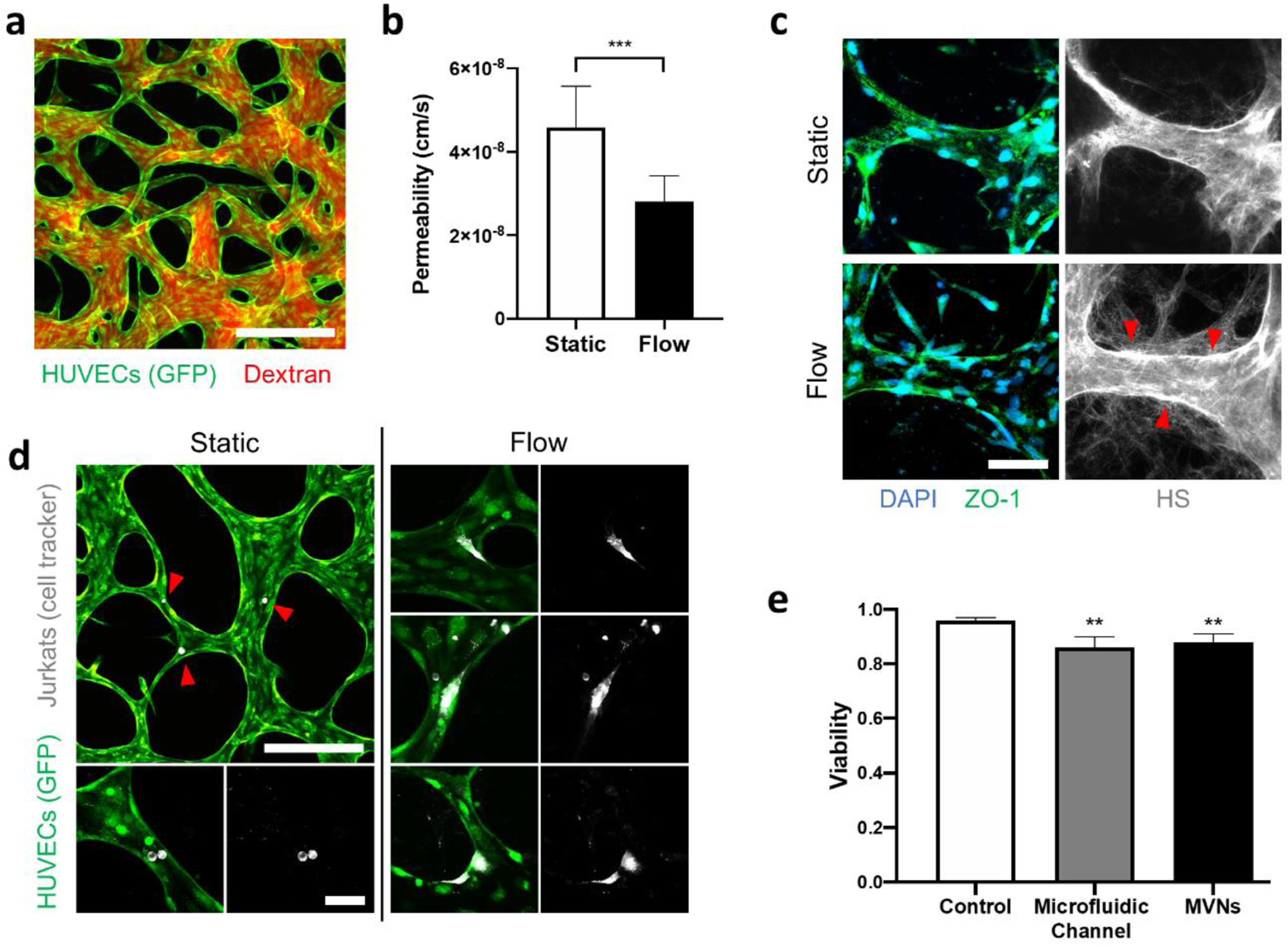
(a) Microvascular networks perfused with fluorescent dextran. The scale bar is 200 μm. (b) Endothelial permeability to 70 kDa dextran for static and MicroHeart flow samples. Data are represented as average and standard deviation between 3 regions from 3 samples. (c) Immunostaining of heparin sulfate (HS) in the microvascular networks. The red arrows point to endothelial regions of increased concentration of HS after MicroHeart flow. The scale bar is 50 μm. (d) Jurkat cells within the microvascular networks for static and MicroHeart flow samples. The red arrows point to single Jurkat cells arrested in the networks. The scale bars are 200 μm (top left) and 50 μm (bottom and all flow images). (e) Viability of Jurkat cells after 48 hours flow in microfluidic channels or microvascular networks, compared to static well plate controls. Data represented as average and standard deviation between 4 repeats.

MicroHeart flow also affected immune cells circulated over 48 hours in the microvascular networks (same pressure and frequency as above). Within static controls, which were only subjected to a transient (i.e. minutes) flow to perfuse cells, Jurkats were seldom found adhered to the endothelium and always maintained a round morphology (Figure 4c). In microvascular networks subjected to MicroHeart flow over the same time, Jurkats also rarely arrested on the endothelium. However, in these samples, the adhered Jurkats often showed actively migratory morphologies, as the cells spread on the endothelium through long extensions (Figure 4d). Viability of Jurkats under such flow conditions was found to be approximately 88 %, moderately lower than static controls (96 % viability in well plates over the same time), and comparable to the value measured for flow of the cells in the large microfluidic channels (Figure 4e). No accumulation of the circulating cells was observed in the MicroHeart, as cell concentrations sampled from different regions (media channels in the device, connecting tubes, and capacitors) were comparable at approximately 1 M cells mL⁻¹.

Longer-term (7 days) perfusion of the microvascular networks under MicroHeart flow was demonstrated (Figure S7). The networks remained viable without the need for replenishing cell culture media circulating through the system; they also showed improved stability compared to networks where media was replenished daily under static conditions. Throughout the time of MicroHeart flow, neither evaporation of the fluid was observed in the system, nor formation of bubbles, attesting to the capability of the system to produce longer-term flow.

4. DISCUSSION

The MicroHeart pump presented here can produce circulating fluid flow within microphysiological systems with relatively small flow rates, in the range of several to tens of microliters per minute. As such, the MicroHeart brings together the media re-circulating capabilities of gravity-driven perfusion methodologies based on rocking (Van Duinen et al., 2017) with the uni-directional flow capabilities of systems that utilize larger volumes of media (Jang et al., 2019). This is achieved through a simple design that produces fluid circulation without the need for multiple positive pressure inlets (Chen et al., 2017) or negative pressure inlets (Sin et al., 2004). However, key drawbacks of the current design are the need to stop flow to change or sample cell culture media, as well as the use of connector tubing, which introduces a risk of fluid leakage and bubble formation. Potential improvements on the current design are shown in Fig. S8, where direct assembly of the MicroHeart on top of microphysiological systems can replace tubing. Similarly, the use of a new capacitor design based on air springs with removable plugs can allow media change and sampling without flow stopping.

The flow produced by the MicroHeart presents several similarities to vascular flow in vivo: Flow velocities produced within both microfluidic channels and microvascular networks are in the range of several mm s⁻¹, which is comparable to the values expected in the microcirculation (Yuan and Rigor, 2011). Pulsatile flow can be produced in microfluidic channels with height of 100 μm, comparable to the size of arterioles, where blood flow pulsatility is expected. At the same time, pulsatility is not produced by the MicroHeart in microvascular networks, with vessel sizes comparable to capillaries, where blood flow is not pulsatile. Modulation of the applied pressure and frequency in the MicroHeart allows for the production of a tailored fluid flow profile for different microphysiological systems.

As an application example, the flow generated by the MicroHeart within microvascular networks can exert a physiological shear stress on the endothelium and adhered cells, affecting both. The increased barrier function observed after 24 hours of MicroHeart flow may be explained by an increased expression of the endothelial glycocalyx with flow, expected in vivo (Tarbell and Cancel, 2016), and previously observed to modulate microvascular network permeability (Offeddu et al., 2020b). Changes in morphology of Jurkat cells with flow were comparable to those observed for tumor cells in the microvascular networks (Hajal et al., 2020), explained through a mechanotransducive effect of vascular flow on cells adhered to the endothelium. As such, the MicroHeart pump offers the possibility to culture microphysiological systems under flow conditions that mimic blood flow and its characteristic effects on the cells within.

A lumped element-based model was implemented to capture the fundamental fluid and solid mechanics phenomena that dictate the functionality of the MicroHeart pump. The model is capable of predicting the fluid flow characteristics produced by the MicroHeart for microfluidic channels and microvascular networks. The theoretical framework of the computational model can be extended to predict and optimize the operation of the MicroHeart for other microphysiological systems. Possible MicroHeart applications are many, such as inducing physiological interstitial flow towards a microfluidic-engineered lymphatic vasculature, or re-circulating cells and paracrine factors through interconnected organotypic models.