Interrater sleep stage scoring reliability between manual scoring from two European sleep centers and automatic scoring performed by the artificial intelligence–based Stanford-STAGES algorithm

Abstract

Study Objectives:

The objective of this study was to evaluate interrater reliability between manual sleep stage scoring performed in 2 European sleep centers and automatic sleep stage scoring performed by the previously validated artificial intelligence–based Stanford-STAGES algorithm.

Methods:

Full night polysomnographies of 1,066 participants were included. Sleep stages were manually scored in Berlin and Innsbruck sleep centers and automatically scored with the Stanford-STAGES algorithm. For each participant, we compared (1) Innsbruck to Berlin scorings (INN vs BER); (2) Innsbruck to automatic scorings (INN vs AUTO); (3) Berlin to automatic scorings (BER vs AUTO); (4) epochs where scorers from Innsbruck and Berlin had consensus to automatic scoring (CONS vs AUTO); and (5) both Innsbruck and Berlin manual scorings (MAN) to the automatic ones (MAN vs AUTO). Interrater reliability was evaluated with several measures, including overall and sleep stage-specific Cohen’s κ.

Results:

Overall agreement across participants was substantial for INN vs BER (κ = 0.66 ± 0.13), INN vs AUTO (κ = 0.68 ± 0.14), CONS vs AUTO (κ = 0.73 ± 0.14), and MAN vs AUTO (κ = 0.61 ± 0.14), and moderate for BER vs AUTO (κ = 0.55 ± 0.15). Human scorers had the highest disagreement for N1 sleep (κ_N1 = 0.40 ± 0.16 for INN vs BER). Automatic scoring had lowest agreement with manual scorings for N1 and N3 sleep (κ_N1 = 0.25 ± 0.14 and κ_N3 = 0.42 ± 0.32 for MAN vs AUTO).

Conclusions:

Interrater reliability for sleep stage scoring between human scorers was in line with previous findings, and the algorithm achieved an overall substantial agreement with manual scoring. In this cohort, the Stanford-STAGES algorithm showed similar performances to the ones achieved in the original study, suggesting that it is generalizable to new cohorts. Before its integration in clinical practice, future independent studies should further evaluate it in other cohorts.

Citation:

Cesari M, Stefani A, Penzel T, et al. Interrater sleep stage scoring reliability between manual scoring from two European sleep centers and automatic scoring performed by the artificial intelligence–based Stanford-STAGES algorithm. J Clin Sleep Med. 2021;17(6):1237–1247.

BRIEF SUMMARY

Current Knowledge/Study Rationale: Recent years have seen an increasing number of automatic methods based on artificial intelligence to perform sleep stage scoring. Generalizability to new datasets constitutes a key factor for integration of these algorithms in clinical practice. Here, we independently investigate generalizability of the previously validated Stanford-STAGES algorithm to a new cohort of more than 1,000 participants.

Study Impact: To our knowledge, this is the first study proposing a large-scale and independent evaluation of a previously validated algorithm for sleep stage scoring. The Stanford-STAGES algorithm seems to be generalizable to new unseen cohorts, but other studies should further validate it in new cohorts with different patient groups, with the perspective of integrating it in clinical practice.

INTRODUCTION

According to international standards redacted by the American Academy of Sleep Medicine (AASM),¹ sleep evaluation is performed by recording of video polysomnography (PSG) and sleep epochs lasting 30 seconds are manually scored by human sleep experts as either wakefulness (W), rapid eye movement (REM) sleep, non–REM sleep stage 1 (N1) sleep, non–REM sleep stage 2 (N2) sleep, or non–REM sleep stage 3 (N3) sleep. Manual sleep stage scoring has some important drawbacks, including time consumption and the requirement of highly trained personnel. Furthermore, as AASM rules to score sleep are prone to a degree of subjective interpretation, sleep staging is prone to interrater variability.^2–7

Automatic sleep staging methods would significantly reduce the time needed for analysis of video PSGs and would also overcome the problem of interrater variability.⁸ Starting from the late 1960s,⁹ hundreds of different methods for automated sleep stage scoring have been proposed (see Penzel et al,¹⁰ Boostani et al,¹¹ Lajnef et al,¹² and Fiorillo et al¹³ for comprehensive reviews). However, such methods are still not used in clinical routine. This is because of many reasons, which include (1) the fact that most methods were validated only in cohorts with young healthy controls and are thus unreliable when applied to patients with sleep disorders; and (2) the lack of validation of these methods in different cohorts, thus not ensuring their generalizability to different populations.^13,14

Because of the increase of computational power and the availability of large datasets, the last years saw the increasing development of automatic methods that use artificial intelligence techniques (ie, based on deep neural networks). Compared with automated methods based on other techniques, algorithms based on artificial intelligence can easily deal with large amount of data and can directly learn patterns from data, without the need of humans to define relevant features for correct sleep stage classification. These methods have shown promising performances in terms of agreement with manual sleep stage scoring.¹³

Among these methods, the Stanford-STAGES algorithm¹⁵ (a software program written in Python performing both automated sleep stage scoring as well as automatic identification of narcolepsy patients based on automatic analysis of PSG signals; available at https://github.com/stanford-stages/stanford-stages, accessed March 5, 2020) seems to be a promising tool to be introduced in clinical sleep practice,¹⁶ mainly for 2 reasons. First, it showed good agreement with manual sleep stage scoring in 4 different databases including healthy controls and patients.¹⁵ Second, the algorithm describes sleep as a dynamic process, where each sleep epoch is represented as a mixture of W, N1, N2, N3, and REM sleep. Such a dynamic way of representing sleep has been shown to hold relevant physiologic information to identify patients with narcolepsy type 1¹⁵ and might also help to identify and diagnose other sleep disorders.

However, the Stanford-STAGES algorithm has only been tested in 1 study, and thus does not guarantee its generalizability to other cohorts and populations. The aim of this study is to evaluate interrater reliability (IRR) for sleep stage scoring between human scorers from 2 European sleep centers and the automatic Stanford-STAGES algorithm in a cohort of more than 1,000 participants.

METHODS

Study participants

The participants included in this study were part of Study of Health in Pomerania-TREND, which is 1 of the 2 cohorts within the framework of the Study of Health in Pomerania¹⁷ in northeastern Germany. Of the 4,420 participants included in the Study of Health in Pomerania-TREND baseline examinations, 1,249 underwent an optional 1-night full PSG. Because 183 participants were excluded for technical issues, our final study population included 1,066 participants. The population-based study was approved by the ethical committee of the University of Greifswald, Germany. The presented analysis was additionally approved by the ethical committee of the Medical University of Innsbruck, Austria.

PSG recordings and manual sleep scoring

Specific details concerning PSG recordings have been previously described.¹⁸ Briefly, PSGs were recorded according to the AASM 2007 standards¹⁹ with ALICE 5 devices (Philips Respironics, Eindhoven, The Netherlands), and the recordings included electroencephalogram (EEG; 6 derivations: F4A1, C4A1, O2A1, F3A2, C3A2, and O1A2), 2 electrooculographic channels, electromyogram recorded at chin and both anterior tibialis muscles, 1 electrocardiogram channel, pulse oximetry, nasal pressure, inductive plethysmography detecting respiratory effort, tracheal microphone, and body position sensor. EEG, electrooculographic, and electromyogram signals were sampled at 200 Hz. PSG recordings were digitally transferred in European Data Format (EDF) to the University Hospital Charité, Center of Sleep Medicine Berlin, Germany, where 30-second sleep epochs were manually scored by certified sleep technicians according to the AASM 2007 criteria.^18,19 Scoring of respiratory events was also performed according to AASM 2007,^18,19 and the apnea-hypopnea index (AHI) was calculated for each participant. As part of a research collaboration, the EDF files were also transferred to the Sleep Laboratory of the Department of Neurology, Medical University of Innsbruck (Austria), where the same sleep 30-second epochs were manually scored by 1 experienced sleep technician according to AASM 2012 criteria.^20,21 Furthermore, limb and periodic limb movements (PLMS) were scored and the PLMS index calculated for each participant.²¹

Automatic sleep stage scoring

To automatically score PSGs, the Python code of the Stanford-STAGES algorithm was retrieved from the repositories indicated in the original publication¹⁵ (https://github.com/stanford-stages/stanford-stages, accessed March 5, 2020), and the provided instructions for installation and setup of the code were carefully followed to ensure correct implementation.

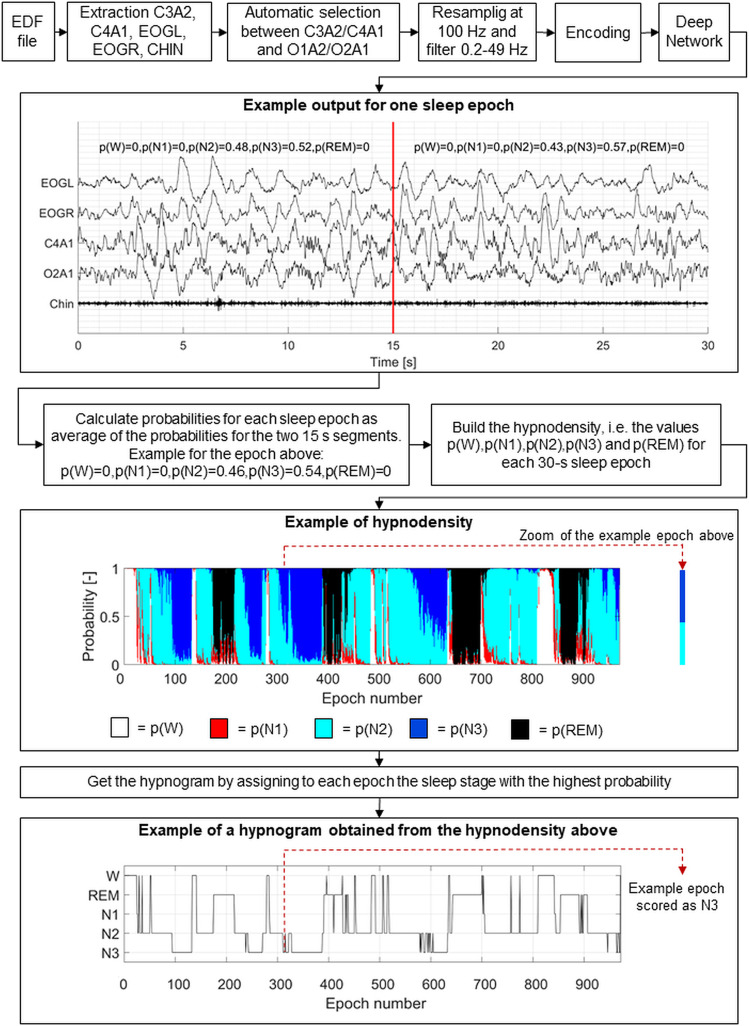
Figure 1 shows an overview of the steps of the automatic scoring. EDF files were given as input to the algorithm, which automatically performed the following steps. First, chin electromyogram, left and right electrooculographic signals, and 1 central (C3 or C4) and 1 occipital (O1 or O2) EEG signals referencing to the contralateral mastoid (A2 or A1, respectively) were extracted from the EDF file. The algorithm automatically selected whether to use the left or right EEG channels by choosing the less noisy ones following the procedure described in the original work.¹⁵ Afterward, the signals were resampled at 100 Hz, band-pass filtered between 0.2 and 49 Hz, and encoded with cross-correlation. The encoded signals were given as input to 16 already trained long short-term memory deep networks. For each 15-second segment of the EDF file, the algorithm returned the probabilities that that segment was W, N1, N2, N3, and REM sleep.

Figure 1. Schematic overview of the automatic sleep stage scoring with the Stanford-STAGES algorithm.

From the EDF files, the C3A2, C4A1, O2A1, and O1A2 electroencephalographic channels were extracted, as well as the electromyographic chin channel and the left and right electrooculographic channels. The algorithm automatically selected which of the 2 central and occipital channels to use. Then, the signals were resampled at 100 Hz, filtered between 0.2 and 49 Hz, and encoded with cross-correlation. The encoded signals were given in input to the deep neural network. For each 15-second segment, the network returned the probabilities that such segment was wakefulness (p(W)), N1 sleep (p(N1)), N2 sleep (p(N2)), N3 sleep (p(N3)), and rapid eye movement sleep (p(REM)). The figure reports an example epoch for which the obtained probability values are shown. For each 30-second sleep epoch, the average values of probabilities across the two 15-second segments were calculated, thus obtaining the values of probabilities for each sleep epoch. The hypnodensity was obtained as the graphical representation of the sleep stage probabilities for each sleep epoch. From the hypnodensity, the hypnogram was built by scoring each sleep epoch as the sleep stage with the highest probability. EDF = European data format; EOGL = electrooculogram left; EOGR = electrooculogram right; N1 = non-REM stage 1 sleep; N2 = non-REM stage 2 sleep; N3 = non-REM stage 3 sleep; REM = rapid eye movement sleep; W = wakefulness.

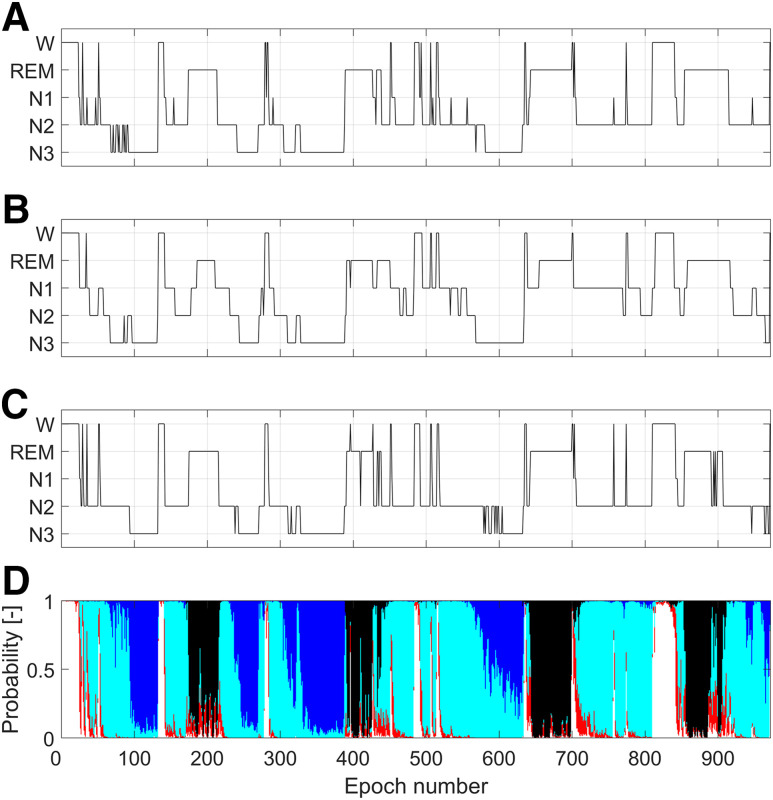
To allow comparison of the automatic sleep stage scorings to the manual ones, we averaged the probabilities of W, N1, N2, N3, and REM sleep over the two 15-second segments included in a 30-second epoch. The values of sleep stages probabilities for each epoch allowed us to generate a hypnodensity graph. The hypnogram was obtained by assigning to each epoch the sleep stage with the highest probability. Figure 2, C and D, shows the automatic hypnogram and hypnodensity obtained for 1 participant in comparison to the manual hypnograms scored in Innsbruck (Figure 2A) and in Berlin (Figure 2B).

Figure 2. Visual comparison of hypnograms and hypnodensity for the same polysomnographic recording.

(A) Manual hypnogram scored in Innsbruck. (B) Manual hypnogram scored in Berlin. (C) Hypnogram obtained by applying the automatic Stanford-STAGES algorithm. For each epoch, the sleep stage assigned was the one having the highest probability in the hypnodensity (D). Color codes for probabilities in the hypnodensity: white, W; red, N1; light blue, N2; dark blue, N3; black, REM. W = wakefulness, REM = rapid eye movement sleep, N1 = non-REM stage 1 sleep, N2 = non-REM stage 2 sleep, N3 = non-REM stage 3 sleep.

Further details concerning the methodology of the Stanford-STAGES algorithm can be found in the original publication.¹⁵

IRR evaluation

To evaluate IRR for sleep stage scoring, we built 5 confusion matrices (CMs) for each participant:

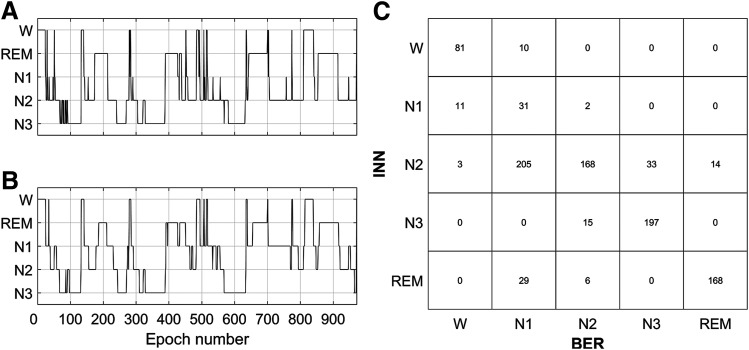
• The first CM was obtained bycomparing the hypnogram manually scored in Innsbruck to the one manually scored in Berlin (INN vs BER), as shown in Figure 3. The CM summarizes the relationship between the 2 hypnograms. The diagonal elements correspond to the number of epochs where the scorers were in agreement (ie, number of epoch that both scorers scored as W, N1, N2, N3, and REM sleep). The off-diagonal elements correspond to the number of epochs for which the scorers were not in agreement and indicate also the type of disagreement (eg, in Figure 3C, the element in {row 1, column 2} implies that 10 epochs were scored as W by the scorer in Innsbruck, but as N1 by the scorer in Berlin).

• The second CM was derived by comparing the hypnogram obtained from manual scoring in Innsbruck to the one obtained from the automatic scoring (INN vs AUTO). This CM was built similarly to the one in INN vs BER.

• The third CM was made by comparing the manual hypnogram from Berlin to the automatic one (BER vs AUTO). This CM was built similarly to the one in INN vs BER.

• The fourth CM was obtained by comparing the sleep epochs for which manual scorers from Innsbruck and Berlin agreed (ie, consensus epochs) to the respective sleep epochs automatically scored (CONS vs AUTO), as shown in Figure S1 ^{(804.8KB, pdf)} in the supplemental material.

• The fifth CM was derived by comparing both manual hypnograms to the automatic one (MAN vs AUTO). In case of disagreement between the 2 manual scorings for 1 sleep epoch, an epoch was counted equally in the 2 sleep stages that were manually assigned (Figure S2 ^{(804.8KB, pdf)} in the supplemental material). This is the same approach presented in the original publication of the Stanford-STAGES algorithm.¹⁵

Each CM was used to compute several IRR measures. More specifically, the overall Cohen’s κ and the overall accuracy (A; ie, the percentage of sleep epochs included in the diagonal of the CM) were calculated from each CM. Stage-specific Cohen’s κ (κ_W, κ_N1, κ_N2, κ_N3, κ_REM), accuracies (A_W, A_N1, A_N2, A_N3, A_REM), and F1 scores (F1_W, F1_N1, F1_N2, F1_N3, F1_REM) were also obtained. Finally, the overall F1 score (F1) was calculated as average across the stage-specific F1 scores. Figure S3 ^{(804.8KB, pdf)} in the supplemental material provides the equations that were used to compute all the IRR measures. We decided to calculate all these different measures to provide a complete and comprehensive overview of the agreement, as each of them considers different aspects of the agreement.²² In particular, accuracy gives higher importance to true positives and true negatives, F1 score to false negatives and false positives, and Cohen’s κ corrects accuracy for possible random agreement.²² The values of Cohen’s κ were interpreted according to Landis and Koch²³: κ < 0 indicating no agreement, 0 ≤ κ < 0.20 indicating slight agreement, 0.20 ≤ κ < 0.40 indicating fair agreement, 0.40 ≤ κ < 0.60 indicating moderate agreement, 0.60 ≤ κ < 0.80 indicating substantial agreement, and κ ≥ 0.80 indicating almost perfect agreement.

Figure 3. Hypnograms and relative confusion matrix.

(Left) Hypnograms for the same PSG recording scored by human scorers in Innsbruck (A) and Berlin (B) are shown. The confusion matrix (C) reports in the diagonal the number of epochs for which the scorers were in agreement and out of the diagonal the number of epochs for which there was disagreement and the type of disagreement (eg, the element in {row 1, column 2} indicates that 10 epochs were scored as W in the INN hypnogram but as N1 in the BER hypnogram). BER = Berlin, INN = Innsbruck, PSG = polysomnography, W = wakefulness, REM = rapid eye movement sleep, N1 = non-REM stage 1 sleep, N2 = non-REM stage 2 sleep, N3 = non-REM stage 3 sleep.

Sleep and demographic factors influencing IRR

The effects of age, sex, body mass index (BMI), PLMS index, and AHI on the overall κ, A, and F1 score values were evaluated by means of multiple linear regression analysis. All predictors (except for sex, which was included as a categorical predictor) and κ, A, and F1 score values were Z-score transformed. Noncollinearity of predictors was ensured by checking that the variation inflation factors were less than 10.²⁴ Normality of the residuals was checked by visual inspection of Q-Q plots. In case of not normal residuals, we applied cubic transformation to κ, A, and F1 score values.

RESULTS

Out of the 1,066 participants included in the study, 570 were men (53.47%). The median age of the participants was 54 years (5th–95th percentiles: 26–74 years), the median BMI was 28.0 kg/m² (5th–95th percentiles: 21.1–37.1 kg/m²), the median AHI was 3.9 events/h (5th–95th percentiles: 0.1–40.0 events/h), and the median PLMS index was 6.4 (5th–95th percentiles: 0–66.4). The distributions of sleep stages scored by the human scorers and the automatic algorithm across the participants are shown in Table 1. No significant difference was found in the percentage of manually scored W, whereas significant differences were present between the percentage of all other sleep stages scored by sleep experts in Innsbruck and Berlin and by the algorithm.

Table 1.

Sleep stages distributions in the hypnograms scored in Innsbruck, Berlin, and by the algorithm.

Sleep Stages	Measure	INN	BER	AUTO	P
					INN vs BER	INN vs AUTO	BER vs AUTO
W (% of TIB)	µ ± σ	18.80 ± 12.05	18.95 ± 12.39	24.57 ± 15.01	n.s.	< .001	< .001
	m [5th–95th]	16.49 [4.40–42.49]	16.62 [4.13–42.58]	21.71 [6.61–53.8]
N1 (% TIB)	µ ± σ	11.44 ± 6.61	20.43 ± 10.12	4.49 ± 3.05	< .001	< .001	< .001
	m [5th–95th]	9.88 [4.48–23.86]	18.55 [7.54–39.83]	3.76 [0.89–10.02]
N2 (% TIB)	µ ± σ	40.85 ± 9.47	31.41 ± 10.67	47.68 ± 11.44	< .001	< .001	< .001
	m [5th–95th]	41.57 [24.36–55.23]	31.20 [13.65–48.65]	48.59 [27.05–64.20]
N3 (% TIB)	µ ± σ	10.92 ± 7.01	14.71 ± 7.23	6.10 ± 6.23	< .001	< .001	< .001
	m [5th–95th]	10.85 [0.00–22.99]	14.29 [3.19–26.94]	4.50 [0.00–18.19]
REM (% TIB)	µ ± σ	14.34 ± 5.78	10.86 ± 5.54	11.91 ± 6.13	< .001	< .001	.001
	m [5th–95th]	14.21 [5.12–23.85]	10.80 [1.45–20.61]	11.90 [2.00–22.43]

The distributions are calculated as percentage of time in bed (TIB) and shown as mean (µ) ± 1 standard deviation (σ), median (m), and 5th–95th percentiles across the participants. Statistical analyses were performed with Mann-Whitney U tests corrected with Bonferroni procedure. Statistical significance was set at the value of .05. AUTO = automatic algorithm, BER = Berlin, INN = Innsbruck, N1 = non-REM stage 1 sleep, N2 = non-REM stage 2 sleep, N3 = non-REM stage 3 sleep, n.s. = nonsignificant; REM = rapid eye movement, W = wakefulness.

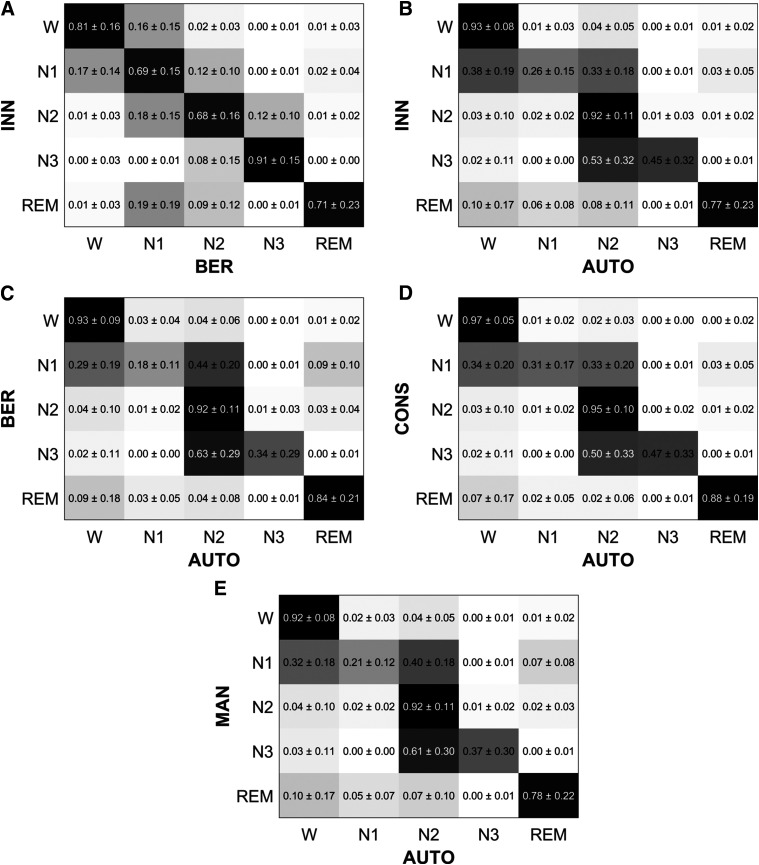
To have an overview of the obtained CMs across the participants, each CM was row-wise normalized (ie, for each row, the elements were divided by their sum). Figure 4 shows the mean and standard deviation values of the normalized CMs across the participants. As an example to interpret the row-wise normalized CMs, in Figure 4A, the element in {row 1, column 1} indicates that 81 ± 16% of the epochs scored as W in Innsbruck were also scored as W in Berlin. Similarly, the element in {row 1, column 2} indicates that 16 ± 15% of the epochs scored as W in Innsbruck were scored as N1 in Berlin.

Figure 4. Row-wise normalized confusion matrices across all participants.

The values are shown as mean and standard deviation across the participants. For each matrix element, a darker color represents a higher agreement. (A) INN vs BER: comparison of manual hypnograms scored in Innsbruck and Berlin. (B) INN vs AUTO: comparison of manual hypnograms scored in Innsbruck to the automatic ones. (C) BER vs AUTO: comparison of manual hypnograms scored in Berlin to the automatic ones. (D) CONS vs AUTO: comparison of the epochs where manual scorers from Innsbruck and Berlin were in consensus to the respective epochs automatically scored. (E) MAN vs AUTO: comparison of both manual hypnograms to the automatic one (in case of disagreement between manual scorers, an epoch was equally weighted between the 2 manually scored stages). As an example to interpret these row-wise CMs, in A, the element in {row 1, column 1} indicates that 81 ± 16% of the epochs scored as W in Innsbruck were also scored as W in Berlin. Similarly, the element in {row 1, column 2} indicates that 16 ± 15% of the epochs scored as W in Innsbruck were scored as N1 in Berlin. W = wakefulness, REM = rapid eye movement sleep, N1 = non-REM stage 1 sleep, N2 = non-REM stage 2 sleep, N3 = non-REM stage 3 sleep.

Table 2 shows the average, standard deviation, median, and 5th and 95th percentiles of the overall κ and stage-specific κ for all comparison across the participants. The values for overall and stage-specific accuracies and F1 scores are reported in Table S1 ^{(804.8KB, pdf)} and Table S2 ^{(804.8KB, pdf)} .

Table 2.

Overall and stage-specific values of Cohen’s κ for the different comparisons.

Parameter	Measures	Comparison
		INN vs BER	INN vs AUTO		BER vs AUTO		CONS vs AUTO		MAN vs AUTO
κ	µ ± σ	0.66 ± 0.13	0.68 ± 0.14		0.55 ± 0.15		0.73 ± 0.14		0.61 ± 0.14
	m [5th–95th]	0.67 [0.43–0.83]	0.70 [0.41–0.84]		0.56 [0.30–0.77]		0.76 [0.47–0.90]		0.62 [0.36–0.79]
κW	µ ± σ	0.78 ± 0.14	0.74 ± 0.17		0.70 ± 0.19		0.80 ± 0.17		0.72 ± 0.17
	m [5th–95th]	0.81 [0.48–0.94]	0.78 [0.38–0.92]		0.75 [0.31–0.92]		0.86 [0.43–0.96]		0.76 [0.39–0.91]
κN1	µ ± σ	0.40 ± 0.16	0.30 ± 0.16		0.22 ± 0.14		0.39 ± 0.20		0.25 ± 0.14
	m [5th–95th]	0.40 [0.13–0.66]	0.30 [0.04–0.57]		0.21 [0.02–0.47]		0.40 [0.05–0.70]		0.24 [0.04–0.48]
κN2	µ ± σ	0.62 ± 0.16	0.71 ± 0.14		0.53 ± 0.17		0.74 ± 0.15		0.62 ± 0.14
	m [5th–95th]	0.65 [0.34–0.84]	0.73 [0.46–0.87]		0.55 [0.24–0.79]		0.77 [0.46–0.92]		0.63 [0.37–0.81]
κN3	µ ± σ	0.66 ± 0.28	0.49 ± 0.33		0.40 ± 0.31		0.53 ± 0.34		0.42 ± 0.32
	m [5th–95th]	0.77 [0.00–0.93]	0.57 [0.00–0.91]		0.41 [0.00–0.88]		0.64 [0.00–0.94]		0.46 [0.00–0.87]
κREM	µ ± σ	0.75 ± 0.21	0.79 ± 0.21		0.74 ± 0.23		0.86 ± 0.21		0.76 ± 0.20
	m [5th–95th]	0.82 [0.26–0.96]	0.86 [0.30–0.96]		0.81 [0.15–0.95]		0.94 [0.36–0.99]		0.82 [0.30–0.95]

The values are shown as mean (µ) ± 1 standard deviation (σ), median (m), and 5th– 95th percentiles across the participants. INN vs BER: comparison of manual hypnograms scored in Innsbruck and Berlin; INN vs AUTO: comparison of manual hypnograms scored in Innsbruck to the automatic ones; BER vs AUTO: comparison of manual hypnograms scored in Berlin to the automatic ones; CONS vs AUTO: comparison of the epochs where manual scorers from Innsbruck and Berlin were in consensus to the respective epochs automatically scored; MAN vs AUTO: comparison of both manual hypnograms to the automatic one (in case of disagreement between manual scorers, an epoch was equally weighted between the two manually scored stages). AUTO = automatic algorithm, BER = Berlin, CONS = consensus, INN = Innsbruck, MAN = manual, N1 = non-REM stage 1 sleep, N2 = non-REM stage 2 sleep, N3 = non-REM stage 3 sleep, REM = rapid eye movement, W = wakefulness.

The results reported in Figure 4, Table 2, Table S1 ^{(804.8KB, pdf)} , and Table S2 ^{(804.8KB, pdf)} show that there was an average overall substantial agreement between the manual scorers (κ = 0.66 ± 0.13, A = 0.75 ± 0.10, F1 = 0.70 ± 0.10) and the automatic sleep staging algorithm agreed significantly more (P < .001 with Mann-Whitney U tests for all overall performances) with the scorings performed in Innsbruck (κ = 0.68 ± 0.14, A = 0.78 ± 0.10, F1 = 0.65 ± 0.13) than to the ones performed in Berlin (κ = 0.55 ± 0.15, A = 0.67 ± 0.12, F1 = 0.59 ± 0.12).

When the automatic scoring was compared with the epochs where there was an agreement between manual scorers (ie, CONS vs AUTO), substantial values of overall agreement were obtained (κ = 0.73 ± 0.14, A = 0.82 ± 0.10, F1 = 0.70 ± 0.13), indicating that the automatic scoring overall correctly classified the sleep epochs with clearer patterns. When both manual scorings were compared with the automatic ones (ie, MAN vs AUTO), the overall average performances (κ = 0.61 ± 0.14, A = 0.72 ± 0.01, F1 = 0.62 ± 0.12) ranged between to the ones obtained for INN vs AUTO and BER vs AUTO.

Concerning the single sleep stage performances, the accuracy values (Table S2 ^{(804.8KB, pdf)} ) were always high because of imbalanced classes; therefore, a meaningful analysis of the agreements can be performed only considering κ and F1 score values. The manual scorers from Innsbruck and Berlin tended to disagree mostly for scoring of N1 sleep (κ_N1 = 0.40 ± 0.16, F1_N1 = 0.49 ± 0.15), whereas the agreement was substantial for all the other sleep stages.

Compared with the 2 manual scorings, the automatic scoring had an average fair agreement for N1 (κ_N1 = 0.30 ± 0.16, F1_N1 = 0.34 ± 0.16 for INN vs AUTO and κ_N1 = 0.22 ± 0.14, F1_N1 = 0.28 ± 0.15 for BER vs AUTO). For N3 sleep, the average agreement between the human scorers and the algorithm was moderate (κ_N3 = 0.49 ± 0.33, F1_N3 = 0.48 ± 0.35 for INN vs AUTO and κ_N3 = 0.40 ± 0.31, F_N3 = 0.43 ± 0.33 for BER vs AUTO). The agreement was, on average, substantial for all the other sleep stages, except for N2 sleep for BER vs AUTO (moderate agreement).

The stage-specific performances for the comparison MAN vs AUTO ranged between the ones obtained for INN vs AUTO and BER vs AUTO. Concerning the comparison CONS vs AUTO, there was an average substantial agreement for W, N2 and REM sleep (κ_W = 0.80 ± 0.17, F1_W = 0.85 ± 0.14, κ_N2 = 0.74 ± 0.15, F1_N2 = 0.84 ± 0.11, κ_REM = 0.86 ± 0.21, F1_REM = 0.86 ± 0.23), whereas only a fair average agreement was obtained for N1 sleep (κ_N1 = 0.39 ± 0.20, F1_N1 = 0.42 ± 0.19) and a moderate one for N3 sleep (κ_N3 = 0.53 ± 0.34, F1_N3 = 0.50 ± 0.37).

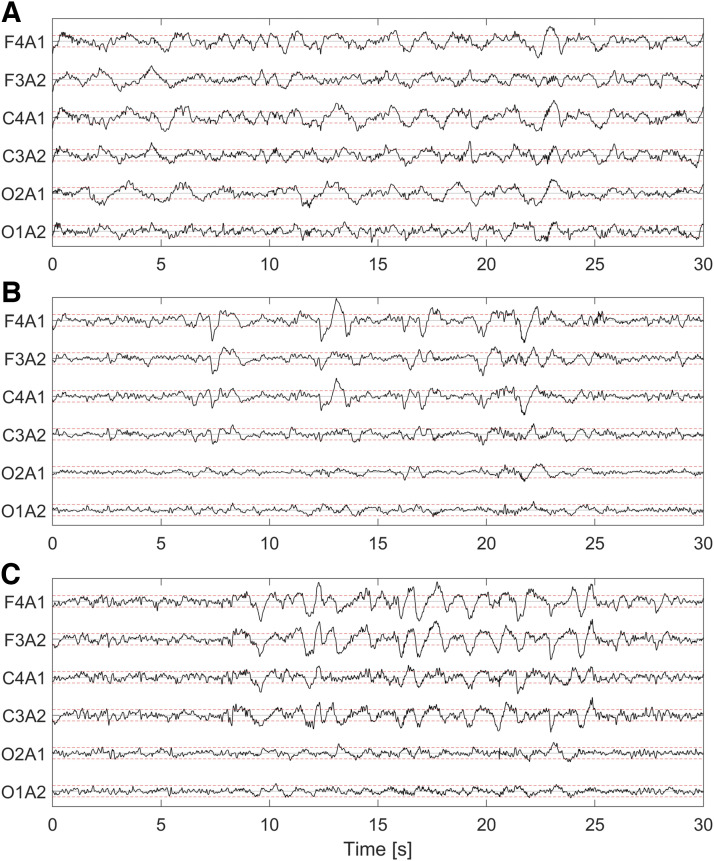
It can be noticed that the performances obtained for N3 sleep have median values of κ_N3 and F1_N3 for CONS vs AUTO around 0.10 higher than the average ones. This is because the automatic algorithm did not score any epoch as N3 sleep for 193 participants, whereas no N3 sleep was scored for 105 participants in Innsbruck and for 5 participants in Berlin. In general, we observed that the automatic algorithm scored significantly less N3 sleep compared with the human scorers (Table 1). To better understand the possible cause of disagreement between manual and automatic scoring, Figure 5 shows (A) an epoch in which the scorer correctly scored N3 sleep (as 24% of the epoch contains slow wave activity) but the algorithm scored N2 sleep; (B) an epoch in which the human scorers wrongly scored N3 sleep (as only 17% of the epoch contains slow wave activity), but the algorithm correctly scored N2 sleep; and (C) an epoch where human scorers and the algorithm correctly scored N3 sleep (slow wave activity present in 42% of the epoch). The percentages of slow wave activity in these epochs were manually counted by an independent scorer.

Figure 5. Example of sleep epochs where manual scorers agreed to score N3 sleep.

(A) Epoch that was correctly manually scored in both centers as N3 sleep (slow wave activity covers 24% of the epoch), but was scored as N2 by the algorithm. (B) Epoch that was wrongly scored as N3 by human scorers in the 2 sleep centers (17% of the epoch contains slow wave activity) but correctly scored as N2 by the algorithm. (C) Epoch correctly scored by the algorithm and the human scorers as N3 sleep (42% of the epoch has slow wave activity). For each electroencephalographic channel, the red lines are drawn at −37.5 and +37.5 µV to highlight the amplitude of 75-µV peak-to-peak amplitude of slow waves. N2 = non–rapid eye movement (NREM) stage 2 sleep, N3 = NREM stage 3 sleep.

Table 3 shows the results of the multiple regression analyses for the overall κ values, and Table S3 ^{(804.8KB, pdf)} and Table S4 ^{(804.8KB, pdf)} show the ones for accuracy and F1 score values. A higher disagreement for sleep stage scoring was observed for men and older participants with higher AHI and BMI.

Table 3.

Results of the multiple regression linear analyses for overall Cohen’s κ.

Predictors	INN vs BER		INN vs AUTO*		BER vs AUTO		CONS vs AUTO*		MAN vs AUTO*
	b	P	b	P	b	P	b	P	b	P
Intercept	−0.118	.003	−0.145	< .001	−0.188	< .001	−0.192	< .001	−0.208	< .001
Age	−0.106	< .001	−0.060	.053	−0.145	< .001	−0.097	.002	−0.132	< .001
Sex (F)	0.251	< .001	0.308	< .001	0.399	< .001	0.407	< .001	0.441	< .001
PLMS index	−0.023	.443	−0.047	.114	−0.033	.272	−0.057	.054	−0.042	.152
AHI	−0.227	< .001	−0.238	< .001	−0.175	<.001	−0.185	< .001	−0.200	< .001
BMI	−0.041	.189	−0.087	.005	−0.066	.031	−0.077	.012	−0.080	.008
Overall P	< .001		< .001		< .001		< .001		< .001

For each analysis, the overall Cohen’s κ was the outcome variable and age, sex (categorical), PLMS index, AHI, and BMI the predictors. Z-score transformations were applied to both outcome variable and predictors (except sex). For each model, the overall P value is reported, as well as the slope estimate (b) and the P value of each predictor. Statistical significance was set at the value of .05. INN vs BER: comparison of manual hypnograms scored in Innsbruck and Berlin; INN vs AUTO: comparison of manual hypnograms scored in Innsbruck to the automatic ones; BER vs AUTO: comparison of manual hypnograms scored in Berlin to the automatic ones; CONS vs AUTO: comparison of the epochs where manual scorers from Innsbruck and Berlin were in consensus to the respective epochs automatically scored; MAN vs AUTO: comparison of both manual hypnograms to the automatic one (in case of disagreement between manual scorers, an epoch was equally weighted between the 2 manually scored stages). AHI = apnea-hypopnea index, AUTO = automatic algorithm, BER = Berlin, BMI = body mass index, CONS = consensus, INN = Innsbruck. MAN = manual, PLMS = periodic limb movement during sleep. ^*Cubic transformation was applied to Cohen’s κ in the highlighted comparisons to meet the normality assumption of the model residuals.

DISCUSSION

We evaluated IRR for sleep stage scoring performed by human scorers in 2 European sleep centers and by the artificial intelligence–based Stanford-STAGES algorithm on a population-based study in 1,066 participants, who were part of the Study of Health in Pomerania-TREND baseline examination. The results showed an overall substantial agreement for sleep stage scoring between the 2 sleep centers and between human and automatic scoring. The human scorers disagreed mostly for N1 sleep and the automatic scoring had the lowest agreement with the manual scoring for N1 and N3 sleep. Furthermore, we assessed that sleep stage scoring disagreement is higher for older participants, for men, and for participants with higher AHI and BMI.

The overall agreement between scorers in Innsbruck and Berlin is in the range reported in previous studies.^2–7 There was substantial agreement for all sleep stages, except for N1 sleep. The lower agreement for scoring N1 sleep matches previous literature results^3–5,7 and substantiates the difficulties in scoring this stage, because of its transitory nature between wakefulness and deeper sleep¹ and to the lack of specific electrophysiologic elements (eg, as sleep spindles, K-complexes, delta waves, or rapid eye movements). All the stage-specific κ values lay in the range of the values reported in previous studies.^3–5,7 Therefore, our findings confirm the rates of IRR for sleep stage scoring between human scorers previously presented in literature.^3–5,7

The automatic scoring agreed more with the manual scoring performed in Innsbruck than the one carried out in Berlin. Sleep recordings from Innsbruck were included in the original work where the Stanford-STAGES algorithm was presented.¹⁵ However, they were not used to train the algorithm, thus ensuring no bias in our results. As the algorithm mostly disagreed with the human scorers for N1 and N3 sleep, a possible reason for the lower overall agreement for BER vs AUTO compared with INN vs AUTO might be the higher number of epochs scored as N1 and N3 sleep in Berlin.

The Stanford-STAGES algorithm has been originally tested on the Inter-Scorer Reliability Cohort, a cohort of 70 PSGs scored by 6 sleep experts,²⁵ where it achieved an average accuracy of 0.78 compared with manual sleep scoring.¹⁵ Because the Inter-Scorer Reliability Cohort includes only women²⁵ and male sex significantly decreases IRR, such accuracy should be compared with the average one we obtained when considering only women from our cohort (ie, 0.75 for MAN vs AUTO). This comparison shows that, in our cohort, the algorithm performed only slightly worse than in the Inter-Scorer Reliability Cohort. In the original study, the Stanford-STAGES algorithm has also been tested in 3 other cohorts,^26–29 all scored only by 1 single scorer, achieving average accuracy between 0.77 and 0.86.¹⁵ In our cohort, the automatic scoring had an average overall accuracy between 0.67 (for BER vs AUTO) and 0.78 (for INN vs AUTO). Therefore, when considering the performances obtained for INN vs AUTO, the Stanford-STAGES algorithm showed similar performances to the ones reported in the original study. This suggests an overall good generalizability of the algorithm to a new unseen cohort.

The statistical analyses revealed that increased age, male sex, and higher AHI and BMI are related to higher disagreement in sleep stage scoring. This is likely because of the increased sleep fragmentation and sleep structure changes seen in the elderly,^30,31 the lower sleep quality in men compared with women,³² the increased sleep fragmentation caused by increased end-apneic arousals,³³ and the increased sleep disruption associated with higher BMI.³⁴

Concerning single sleep stage performances, the biggest discrepancies compared with the manual hypnograms were found in the automatic scoring of N1 and N3 sleep. Previous studies have reported agreements (measured by κ) in the range of 0.16–0.57 for N1 sleep^3–5,7 between human scorers. The agreement values we found between automatic and manual scoring lay in this range.

For N3 sleep, previous studies have reported agreements (measured by κ) between human scorers in the range of 0.49–0.79.^3–5,7 On average, we found that the agreement between the Stanford STAGES-algorithm and the human scorers in Berlin and Innsbruck was lower, because the algorithm tended to score less epochs as N3 sleep. This could be because of several reasons. First, the automatic algorithm used only central and occipital EEG derivations, whereas the human scorers evaluated also the frontal EEG electrodes while scoring. As the slow waves characterizing N3 sleep are most prominent in the frontal derivations¹ and as AASM recommends using the frontal derivations to measure slow wave amplitudes,^19,20 the human scorers might have been more sensitive for recognizing slow wave activity (Figure 5A). Second, the underscoring of N3 sleep by the algorithm could be the consequence of the training process of the algorithm, where very few epochs scored as N3 sleep might have been included and no strategy to overcome class imbalance might have been used.¹⁵ Third, this discrepancy might also be caused by the human scorers being too sensitive to visual identification of slow wave activity (Figure 5B). Previous findings showed that some human raters tend to score N3 even in presence less than 20% of the epoch covered by slow wave activity.³⁵ An in-depth analysis of the causes of the discrepancies for scoring N3 sleep is not the main aim of this work. However, the results indicate possible issues of the Stanford-STAGE algorithm in scoring N3 sleep. Future independent studies should further investigate this.

Improvements for the generalizability of the Stanford-STAGES algorithm could be achieved by applying transfer learning, a technique that allows adaptation of a pretrained algorithm to unseen data to improve the classification performances. Some studies have already shown promising results in adapting a pretrained artificial intelligence algorithm for sleep stage scoring in new cohorts.^36–38 However, current transfer learning techniques still require expert knowledge in manual fine-tuning of the algorithms, making their implementation in a clinical environment impractical. Future studies should evaluate automatic procedures to apply transfer learning in the context of automatic sleep stage scoring.

Our results suggest that the Stanford-STAGES algorithm is overall generalizable to a new cohort and therefore potentially applicable in clinical practice; further validations in different cohorts are needed before its integration in clinical routine. In a first step, the algorithm could be used for semiautomatic sleep stage scoring. In particular, the hypnodensity could be used as a useful tool for this purpose, as a sleep expert could perform just a fast check for the epochs where a stage has a clearly higher probability than the other stages, whereas a more careful check would be required only for the remaining epochs. Previous studies showed that manual edit of an automatic sleep stage scoring substantially reduces the interrater variability^6,8,39 and that a semiautomatic approach is less time consuming than a complete manual analysis.⁴⁰ Future research should investigate the usefulness of the Stanford-STAGES algorithm in the context of semiautomated sleep stage scoring.

The main limitation of this work is that our study population belongs to a population-based cohort and thus does not represent the population usually admitted in a sleep center. Therefore, our results might be not representative of the performances of sleep stage scoring in a clinical environment, where current scoring rules are particularly challenging to apply to patients (eg, with neurodegeneration).⁴¹ Furthermore, as previously outlined, 2 different versions of the AASM manual for scoring sleep were used in the 2 different European centers^19,20 (these criteria slightly differ for the definitions of transitions N1-N2 and for the definition of REM sleep⁴²), thus the results might have a bias. Another potential limitation is that sleep stages were scored in Berlin by different sleep experts, whereas in Innsbruck it was only by one expert. Despite interrater variability between scorers in Berlin was minimized,¹⁸ the inclusion of different experts in Berlin might constitute a bias for the evaluation of IRR, which could not be considered in our analysis. Furthermore, different years of experience in sleep stage scoring of the different experts might have influenced our results. Finally, when we compared the performances achieved in this cohort to the ones obtained in the cohorts where the Stanford-STAGES algorithm was originally validated, we could not take into account possible difference in age, sex distribution, AHI, and BMI between the cohorts. These factors might be the cause of the slightly lower agreements seen in our cohort.

In conclusion, our study evaluated IRR for sleep stage scoring between 2 European sleep centers and the automatic artificial intelligence–based Stanford-STAGES algorithm. Our results show that IRR between human scorers is similar to previously reported results. Furthermore, we found that the Stanford-STAGES algorithm had an overall good agreement with manual scoring and that it performed similarly in this cohort as the in ones where it has been originally tested, thus suggesting that it is generalizable to new unseen cohorts. Future studies should further confirm our findings in new independent cohorts. Future research should also evaluate the integration of automatized transfer learning techniques for better adaptation of the Stanford-STAGES algorithm to new cohorts and the integration of the algorithm for semiautomated sleep stage scoring for clinical purposes.

DISCLOSURE STATEMENT

All authors have seen this manuscript and approved its submission. Work for this study was performed at the Department of Neurology, Medical University of Innsbruck. Study of Health in Pomerania is part of the Community Medicine Research Network of the University Medicine Greifswald, which is supported by the German Federal State of Mecklenburg-West Pomerania. Polysomnography assessment was in part supported by the German RLS organization (Deutsche Restless Legs Vereinigung). The authors report no conflicts of interest.

ABBREVIATIONS

A

accuracy

AASM

American Academy of Sleep Medicine

AHI

apnea-hypopnea index

AUTO

Automatic

BER

Berlin

BMI

body mass index

CM

confusion matrix

CONS

Consensus

EEG

electroencephalogram

EDF

European data format

INN

Innsbruck

IRR

interrater reliability

MAN

Manual

N1

non–rapid eye movement sleep stage 1

N2

non–rapid eye movement sleep stage 2

N3

non–rapid eye movement sleep stage 3

PLMS

periodic limb movements during sleep

PSG

polysomnography

REM

rapid eye movement

W

wakefulness