Abstract
We present a deep learning framework for wide-field, content-aware estimation of absorption and scattering coefficients of tissues, called Generative Adversarial Network Prediction of Optical Properties (GANPOP). Spatial frequency domain imaging is used to obtain ground-truth optical properties at 660 nm from in vivo human hands and feet, freshly resected human esophagectomy samples, and homogeneous tissue phantoms. Images of objects with either flat-field or structured illumination are paired with registered optical property maps and are used to train conditional generative adversarial networks that estimate optical properties from a single input image. We benchmark this approach by comparing GANPOP to a single-snapshot optical property (SSOP) technique, using a normalized mean absolute error (NMAE) metric. In human gastrointestinal specimens, GANPOP with a single structured-light input image estimates the reduced scattering and absorption coefficients with 60% higher accuracy than SSOP while GANPOP with a single flat-field illumination image achieves similar accuracy to SSOP. When applied to both in vivo and ex vivo swine tissues, a GANPOP model trained solely on structured-illumination images of human specimens and phantoms estimates optical properties with approximately 46% improvement over SSOP, indicating adaptability to new, unseen tissue types. Given a training set that appropriately spans the target domain, GANPOP has the potential to enable rapid and accurate wide-field measurements of optical properties.
Keywords: Optical imaging, tissue optical properties, neural networks, machine learning, spatial frequency domain imaging
I. INTRODUCTION
THE optical properties of tissues, including the absorption (μa) and reduced scattering coefficients, can be useful clinical biomarkers for measuring trends and detecting abnormalities in tissue metabolism, tissue oxygenation, and cellular proliferation [1]–[5]. Optical properties can also be used for contrast in functional or structural imaging [6], [7]. Thus, quantitative imaging of tissue optical properties can facilitate more objective, precise, and optimized management of patients.
To measure optical properties, it is generally necessary to decouple the effects of scattering and absorption, which both influence the measured intensity of remitted light. Separation of these parameters can be achieved with temporally or spatially resolved techniques, which can each be performed with measurements in the real or frequency domains. Spatial Frequency Domain Imaging (SFDI) decouples absorption from scattering by characterizing the tissue modulation transfer function to spatially modulated light [8], [9]. This approach has significant advantages in that it can easily be implemented with a consumer grade camera and projector, and achieve rapid, non-contact mapping of optical properties. These advantages make SFDI well-suited for applications that benefit from wide-field characterization of tissues, such as image-guided surgery [10], [11], tissue perfusion measurement [12], and wound characterization [13], [14]. Additionally, recent work has explored the use of SFDI for improving endoscopic procedures [15], [16].
Although SFDI is finding a growing number of clinical applications, there are remaining technical challenges that limit its adoption. First, SFDI requires structured light projection with carefully-controlled working distance and calibration, which is especially challenging in an endoscopic setting. Second, it is difficult to achieve real-time measurements. Conventional SFDI requires a minimum of six images per wavelength (three distinct spatial phases at two spatial frequencies) to generate a single optical property map. A lookup table (LUT) search is then performed for optical property fitting. The recent development of real-time single snapshot imaging of optical properties (SSOP) has reduced the number of images required per wavelength from 6 to 1, considerably shortening acquisition time [17]. However, SSOP introduces image artifacts arising from single-phase projection and frequency filtering, which corrupt the optical property estimations. To reduce barriers to clinical translation, there is a need for optical property mapping approaches that are simultaneously fast and accurate while requiring minimal modifications to conventional camera systems.
Here, we introduce a deep learning framework to predict optical properties directly from single images. Deep networks, especially convolutional neural networks (CNNs), are growing in popularity for medical imaging tasks, including computer-aided detection, segmentation, and image analysis [18]–[20]. We pose the optical property estimation challenge as an image-to-image translation task and employ generative adversarial networks (GANs) to efficiently learn a transformation that is robust to input variety. First proposed in [21], GANs have improved upon the performance of CNNs in image generation by including both a generator and a discriminator. The former is trained to produce realistic output, while the latter is tasked to classify generator output as real or fake. The two components are trained simultaneously to outperform each other, and the discriminator is discarded once the generator has been trained. When both components observe the same type of data, such as text labels or input images, the GAN model becomes conditional. Conditional GANs (cGANs) are capable of making structured predictions by incorporating non-local, high-level information. Moreover, because they can automatically learn a loss function instead of using a handcrafted one, cGANs have the potential to be an effective and generalizable solution to various image-to-image translation tasks [22], [23]. In medical imaging, cGANs have been proven successful in many applications, such as image synthesis [24], noise reduction [25], and sparse reconstruction [26]. In this study, we train cGAN networks on a series of structured (AC GANPOP) or flat-field illumination images (DC GANPOP) paired with corresponding optical property maps (Fig. 1). We demonstrate that the GANPOP approach produces rapid and accurate estimation from input images from a wide variety of tissues using a relatively small set of training data.
Fig. 1.
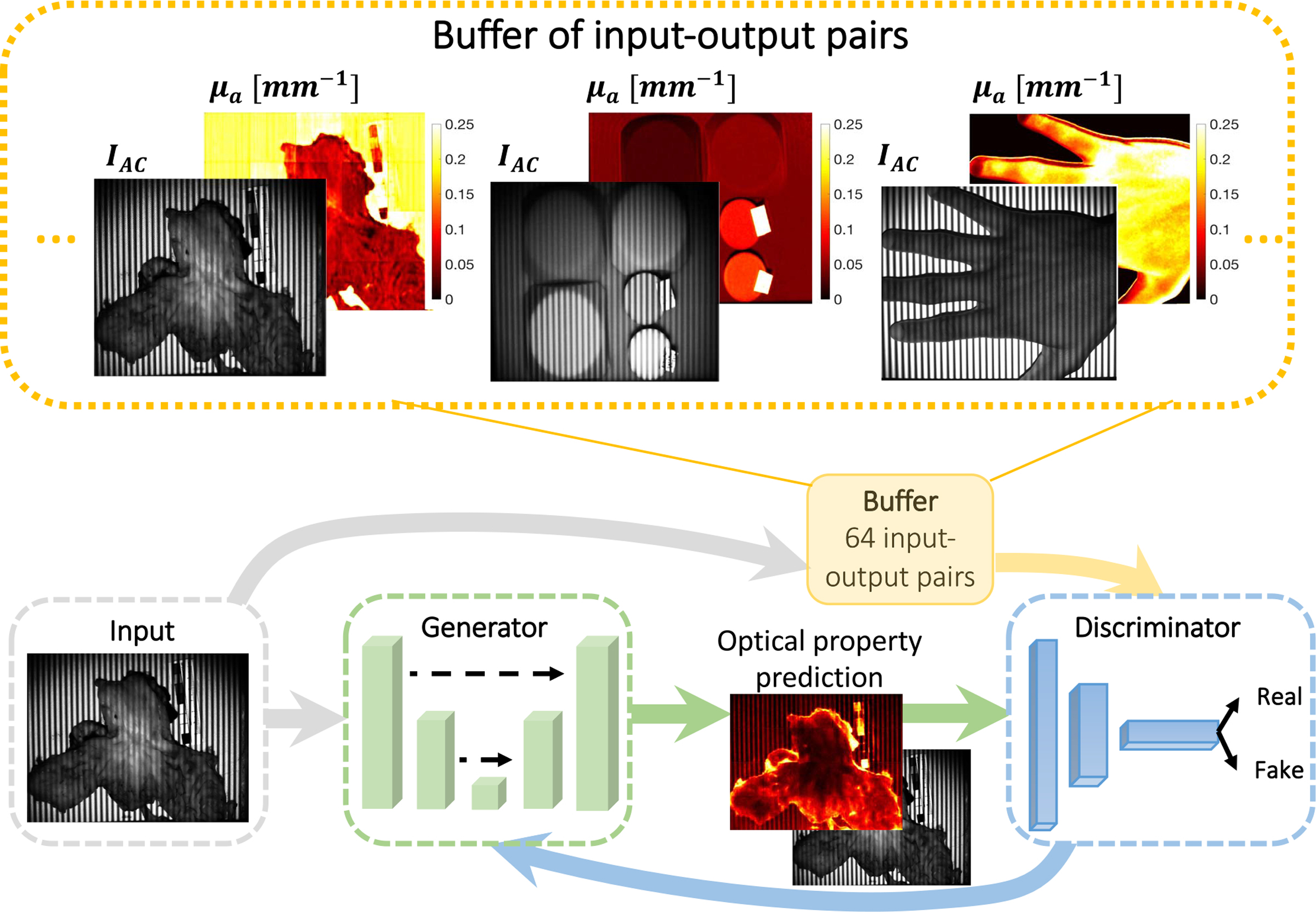
Proposed conditional Generative Adversarial Network (cGAN) architecture. The generator is a combination of ResNet and U-Net and is trained to produce optical property maps that closely resemble SFDI output. The discriminator is a three-layer classifier that operates on a patch level and is trained to classify the output of the generator as ground truth (real) or generated (fake). The discriminator is updated using a history of 64 previously-generated image pairs.
II. RELATED WORK
A. Diffuse Reflectance Imaging
Optical absorption and reduced scattering coefficients can be measured using temporally or spatially resolved diffuse reflectance imaging. Approaches that rely on point illumination inherently have a limited field of view [27], [28]. Non-contact, hyperspectral imaging techniques measure the attenuation of light at different wavelengths, from which the concentrations of tissue chromophores, such as oxy- and deoxy-hemoglobin, water, and lipids, can be quantified [29]. A recent study has also proposed using a Bayesian framework to infer tissue oxygen concentration by recovering intrinsic multispectral measurements from RGB images [30]. However, these methods fail to unambiguously separate absorption and scattering coefficients, which poses a challenge for precise chromophore measurements. Moreover, accurate determination of both parameters is critical for the detection and diagnosis of diseases [1], [5].
B. Single Snapshot Imaging of Optical Properties
SSOP achieves optical property mapping from a single structured light image. Using Fourier domain filtering, this method separates DC (planar) and AC (spatially modulated) components from a single-phase structured illumination image [17]. A grid pattern can also be applied to simultaneously extract optical properties and three-dimensional profile measurements [31]. When tested on homogeneous tissue-mimicking phantoms, this method is able to recover optical properties within 12% for absorption and 6% for reduced scattering using conventional profilometry-corrected SFDI as ground truth.
C. Machine Learning in Optical Property Estimation
Despite its prevalence and increasing importance in the field of medical imaging, machine learning has only recently been explored for optical property mapping. This includes a random forest regressor to replace the nonlinear model inversion [32], and using deep neural networks to reconstruct optical properties from multifrequency measurements [33]. Both of these approaches aim to bypass the time-consuming LUT step in SFDI. However, they require diffuse reflectance measurements from multiple images to achieve accurate results and process each pixel independently without considering the content of surrounding pixels.
III. CONTRIBUTIONS
We propose an adversarial framework for learning a content-aware transformation from single illumination images to optical property maps. In this work, we:
develop a data-driven model to estimate optical properties directly from a single input reflectance image;
demonstrate advantages of structured (AC) versus flat-field (DC) illumination to determine optical properties via an adversarial learning approach;
perform cross-validated experiments, comparing our technique with model-based SSOP and other deep learning-based methods; and
acquire and make publicly-available a dataset of registered flat-field-illumination images, structured-illumination images, and ground-truth optical properties of a variety of ex vivo and in vivo tissues.
IV. METHODS
For training and testing of the GANPOP model, single structured or flat-field illumination images were used, paired with registered optical property maps. Ground truth optical properties were obtained by conventional six-image SFDI. GANPOP performance was analyzed and compared to other techniques both in unseen tissues of the same type as the training data (human ex vivo esophagus images from a new patient) and in different tissue types (in vivo and ex vivo swine gastrointestinal tissues).
A. Hardware
In this study, all images were captured using a commercial SFDI system (Reflect RS™, Modulated Imaging Inc.). A schematic of the system is shown in Fig. 2. Cross polarizers were utilized to reduce the effect of specular reflections, and images were acquired in a custom-built light enclosure to minimize ambient light. Raw images, after 2×2 pixel hardware binning, were 520×696 pixels, with a pixels size of 0.278 mm in the object space.
Fig. 2.
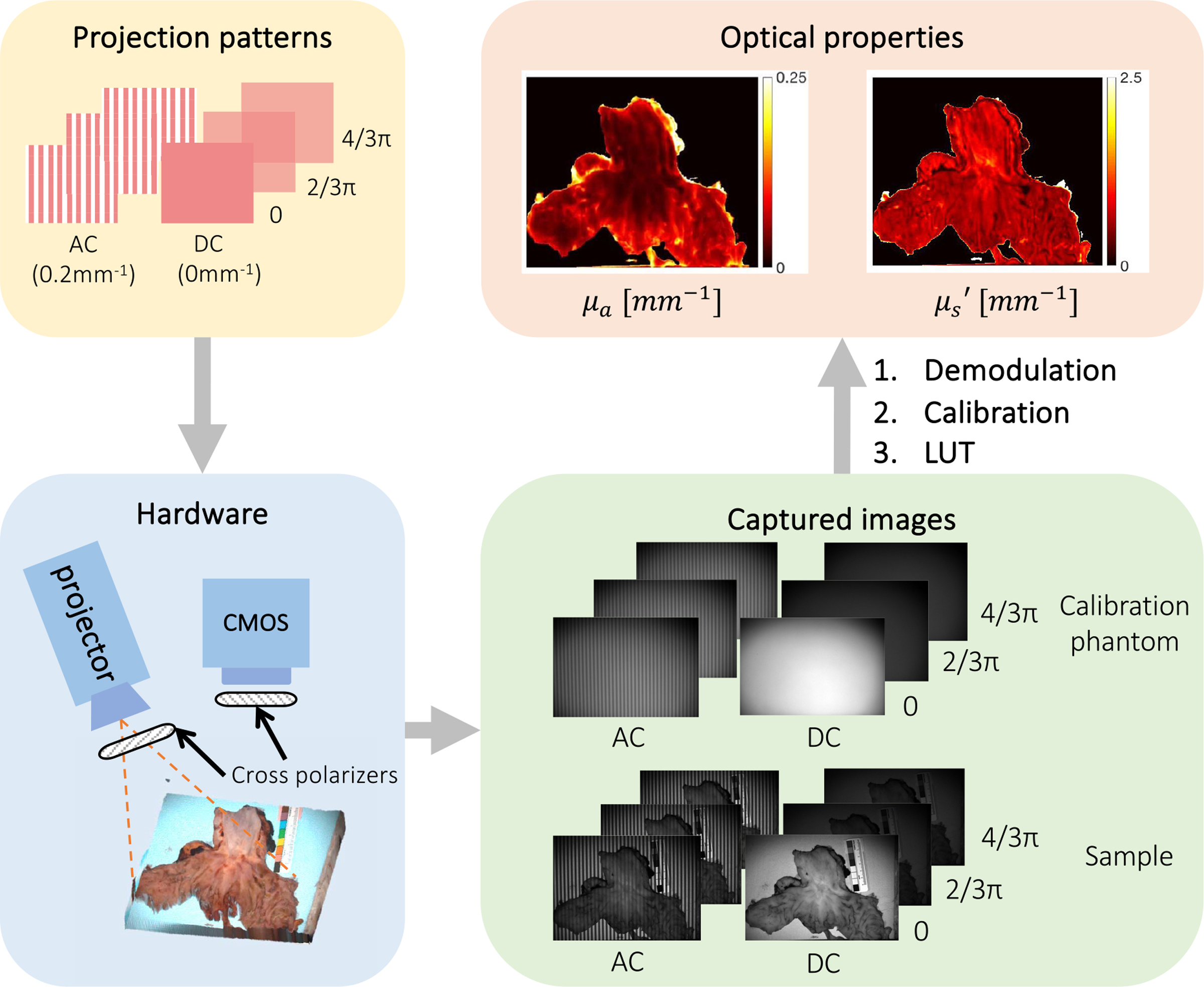
Overview of conventional SFDI illumination patterns, hardware, and processing flow. SFDI captures six frames (three phase offsets at two different spatial frequencies) to generate an absorption and reduced scattering map. DC indicates planar illumination images and AC indicates spatially modulated images. To calculate optical properties, acquired images are demodulated, calibrated against a reference phantom, and inverted using a lookup table.
B. SFDI Ground Truth Optical Properties
Ground truth optical property maps were generated using conventional SFDI with 660 nm light following the method from Cuccia et al. [9]. First, images of a calibration phantom with homogeneous optical properties and the tissue of interest are captured under spatially modulated light. We used a flat polydimethylsiloxane-titanium dioxide (PDMS-TiO2) phantom with reduced scattering coefficient of 0.957 mm−1 and absorption coefficient of 0.0239 mm−1 at 660 nm. We project spatial frequencies of 0 mm−1 (DC) and 0.2 mm−1 (AC), each at three different phase offsets (0, , and ) for this study. AC images are demodulated at each pixel x using:
| (1) |
where I1, I2, and I3 represent images at the two phase offsets. The spatially varying DC amplitude is calculated as the average of the three DC images. Diffuse reflectance at each pixel x is then computed as:
| (2) |
Here, MAC,ref denotes the demodulated AC amplitude of the reference phantom, and Rd,predicted is the diffuse reflectance predicted by Monte Carlo models. Where indicated, we corrected for height and surface angle variation of each pixel from depth maps measured via profilometry. Profilometry measurements were obtained by projecting a spatial frequency of 0.15 mm−1 and calculating depth at each pixel [34]. A k value of 0.8 and 0.4 was used at DC and AC in order to minimize error in angle correction [35]. Finally, μa and are estimated by fitting and into an LUT previously created using Monte Carlo simulations [36].
C. Single Snapshot Optical Properties (SSOP)
SSOP was implemented as the model-based alternative of AC GANPOP. This method separates DC and AC components from a single-phase structured-light image by frequency filtering with a 2D band-stop filter and a high-pass filter [17]. Both filters are rectangular windows that isolate the frequency range of interest while preserving high-frequency content of the image. In this study, cutoff frequencies fDC = [0.16 mm−1, 0.24 mm−1] and fAC = [0, 0.16 mm−1] were selected [31]. MDC can subsequently be recovered through a 2D inverse Fourier transform, and the AC component is obtained using an additional Hilbert transform.
D. GANPOP Architecture
The GANPOP architecture is based on an adversarial training framework. When used in a conditional GAN-based image-to-image translation setup, this framework has the ability to learn a loss function while avoiding the uncertainty inherent in using handcrafted loss functions [23], [37]. The generator is tasked with predicting pixel-wise optical properties from SFDI images while the discriminator classifies pairs of SFDI images and optical property maps as being real or fake (Fig. 1). The discriminator additionally gives feedback to the generator over the course of training. The generator employs a modified U-Net consisting of an encoder and a decoder with skip connections [38]. However, unlike the original U-Net, the GANPOP network includes properties of a ResNet, including short skip connections within each level [39] (Fig. 3). Each residual block is a 3-layer building block with an additional convolutional layer on both sides. This ensures that the number of input features matches that of the residual block and that the network is symmetric [40]. Moreover, GANPOP generator replaces the U-Net concatenation step with feature addition, making it a fully residual network. Using n as the total number of layers in the encoder-decoder network and i as the current layer, long skip connections are added between the ith and the (n − i)th layer in order to sum features from the two levels. After the last layer in the decoder, a final convolution is applied to shrink the number of output channels and is followed by a Tanh function. Regular ReLUs are used for the decoder and leaky ReLUs (slope = 0.2) for the encoder. We chose a receptive field of 70 × 70 pixels for our discriminator because this window captures two periods of AC illumination in each direction. This discriminator is a three-layer classifier with leaky ReLUs (slope = 0.2), as discussed in [23]. The discriminator makes classification decisions based on the current batch as well as a batch randomly sampled from 64 previously generated image pairs. Both networks are trained iteratively and the training process is stabilized by incorporating spectral normalization in both the generator and the discriminator [41]. The conditional GAN objective for generating optical property maps from input images (G : X → Y) is:
| (3) |
where G is the generator, D the discriminator, and pdata is the optimal distribution of the data. We empirically found that a least squares GAN (LSGAN) objective [42] produced slightly better performance in predicting optical properties than a traditional GAN objective [21], and so we utilize LSGAN in the networks presented here. An additional loss term was added to the GAN loss to further minimize the distance from the ground truth distribution and stabilize adversarial training:
| (4) |
Fig. 3.
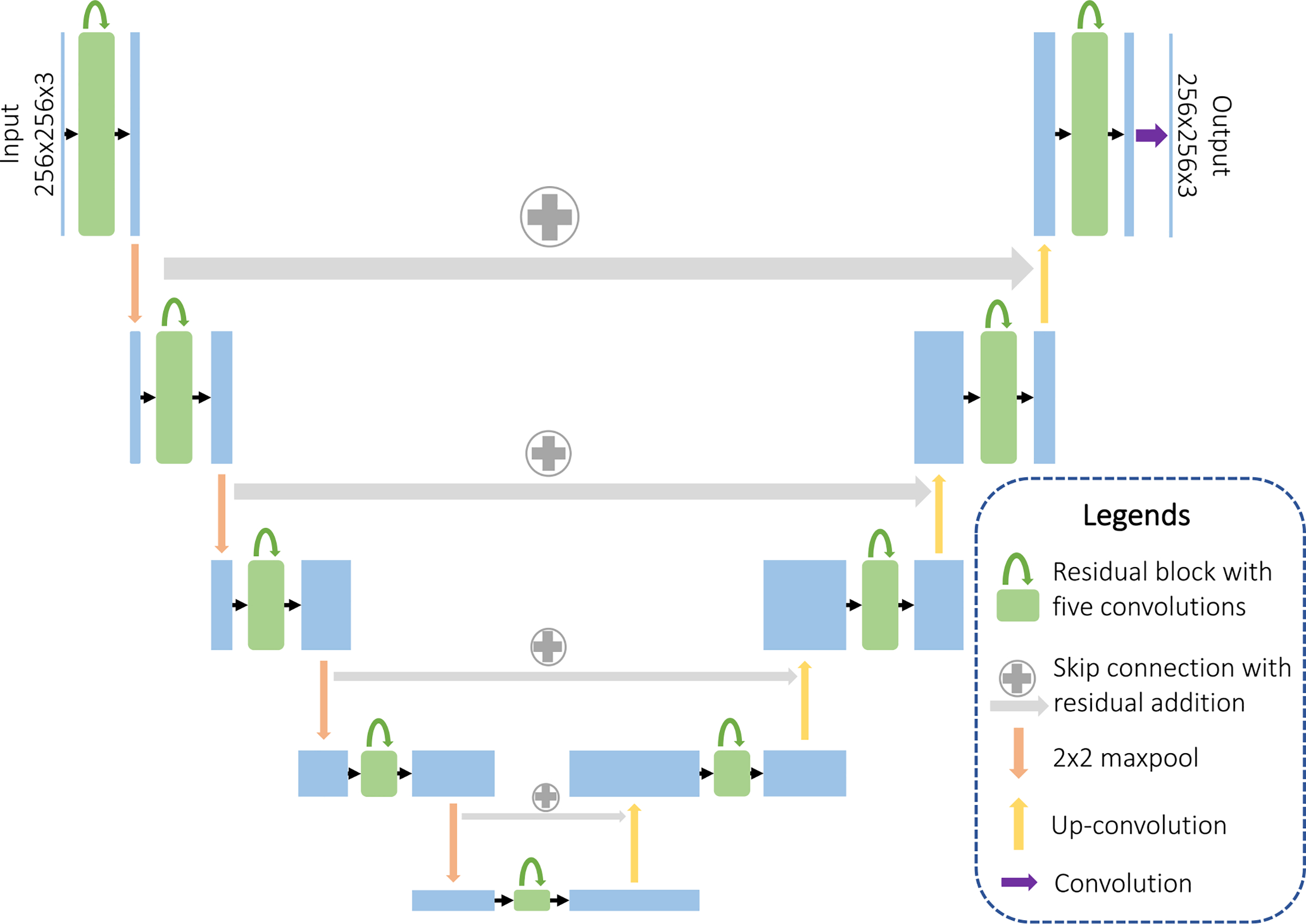
Detailed architecture of the proposed generator. We use a fusion network that combines properties from ResNet and U-Net, including both short and long skip connections in the form of feature addition. Each residual block contains five convolution layers, with short skips between the first and the fifth layer.
The full objective can be expressed as:
| (5) |
where λ is the regularization parameter of the loss term. This optimization problem was solved using an Adam solver with a batch size of 1 [43]. The training code was implemented using Pytorch 1.0 on Ubuntu 16.04 with Google Cloud. A single NVIDIA Tesla P100 GPU was used for both training and testing. For all experiments, λ was set to 60. A total of 200 epochs was used with a learning rate of 0.0002 for half of the epochs and the learning rate was linearly decayed for the remaining half. Both networks were initialized from a Gaussian distribution with a mean and standard deviation of 0 and 0.02, respectively. In addition, we performed comparative analyses of our proposed network against other commonly-used architectures for image-to-image translation, including ResNet and U-Net, both standalone and incorporated into a GAN structure.
Conventional neural networks typically operate on three-channel (or RGB) images as input and output. In this study, four separate networks (N1 to N4) were trained for image-to-image translation with a variety of input and output parameters, summarized in Table I.
Table I:
SUMMARY OF NETWORKS TRAINED IN THIS STUDY
| Input | Output | |||
| Ni | Channel 1 | Channel 2 | Channel 1 | Channel 2 |
| N1 | μa | |||
| N2 | μa | |||
| N3 | μa,corr | |||
| N4 | μa,corr | |||
For input, IAC and IDC represent single-phase raw images at 0.2 mm−1 and 0 spatial frequency, respectively. MDC,ref and MAC,ref are the demodulated DC and AC amplitude of the calibration phantom. Channel 3 is left as zeros in all cases. It is important to note that MAC,ref and MDC,ref are measured only once during calibration before the imaging experiment and thus do not add to the total acquisition time. The purpose of these two terms is to account for drift of the system over time and correct for non-uniform illumination, making the patch used in the network origin-independent. These two calibration images are also required by traditional SFDI and the SSOP approaches. A network without calibration was empirically trained, and it produced 230% and 58% larger error than with calibration in absorption and scattering coefficients, respectively. A single output image contains both μa and in different channels. Two dedicated networks were empirically trained for estimating μa and independently, but no accuracy benefits were observed. Optical property maps calculated by non-profile-corrected SFDI were used as ground truth for N1 and N2. We also assessed the ability of GANPOP networks (N3 and N4) to learn both optical property estimation and sample height and surface normal correction by training and testing with profilometry-corrected data (μa,corr and ).
All optical property maps for training and testing were normalized to have a consistent representation in the 8-bit images commonly used in CNNs. We defined the maximum value of 255 to be 0.25 mm−1 for μa and 2.5 mm−1 for . Additionally, each image of size 520 × 696 was segmented at a random stride size into multiple patches of 256 × 256 pixels and paired with a registered optical property patch for training, as shown in Fig. 4.
Fig. 4.

Example input-output pair used in N1 showing each individual channel as well as the combined RGB images. Channel 1 and 2 of the output contain μa and , respectively. Thus, a high absorption appears red while a high scattering appears green.
E. Tissue Samples
1). Ex Vivo Human Esophagus:
Eight ex vivo human esophagectomy samples were imaged at Johns Hopkins Hospital for training and testing of our networks. All patients were diagnosed with esophageal adenocarcinoma and were scheduled for an esophagectomy. The research protocol was approved by the Johns Hopkins Institutional Review Board and consents were acquired from all patients prior to each study. All samples were handled by a trained pathologist and imaged within one hour after resection [44].
Example raw images of a specimen captured by the SFDI system are shown in Fig. 2, 4, and 12(a). All samples consisted of the distal esophagus, the gastroesophageal junction, and the proximal stomach. The samples contain complex topography and a relatively wide range of optical properties (0.02–0.15 mm−1 for μa and 0.1–1.5 mm−1 for at λ = 660 nm), making it suitable for training a generalizable model that can be applied to other tissues with non-uniform surface profiles. An illumination wavelength of 660 nm was chosen because it is close to the optimal wavelength for accurate tissue oxygenation measurements [45].
Fig. 12.
Example results for AC input to non-profilometry-corrected optical properties (N1). From left to right: RGB image and raw structured illumination image, SFDI ground truth, SSOP output, AC GANPOP output, absolute percent error map between SSOP and ground truth, and absolute percent error map between AC GANPOP and ground truth. From top to bottom: (a) ex vivo human esophagus, (b) ex vivo pig stomach and esophagus, (c) in vivo pig colon, and (d) in vivo human foot. Optical properties are measured in mm−1.
In this study, six ex vivo human esophagus samples were used for training of the GANPOP model and two used for testing. A leave-two-out cross validation method was implemented, resulting in four iterations of training for each network. Performance results reported here are from an average of these four iterations.
2). Homogeneous Phantoms:
The four GANPOP networks were also trained on a set of tissue-mimicking silicone phantoms made from PDMS-TiO2 (P4, Eager Plastics Inc.) mixed with India ink as absorbing agent [46]. To ensure homogeneous optical properties, the mixture was thoroughly combined and poured into a flat mold for curing. In total, 18 phantoms with unique combinations of μa and were fabricated, and their optical properties are summarized in Fig. 5.
Fig. 5.
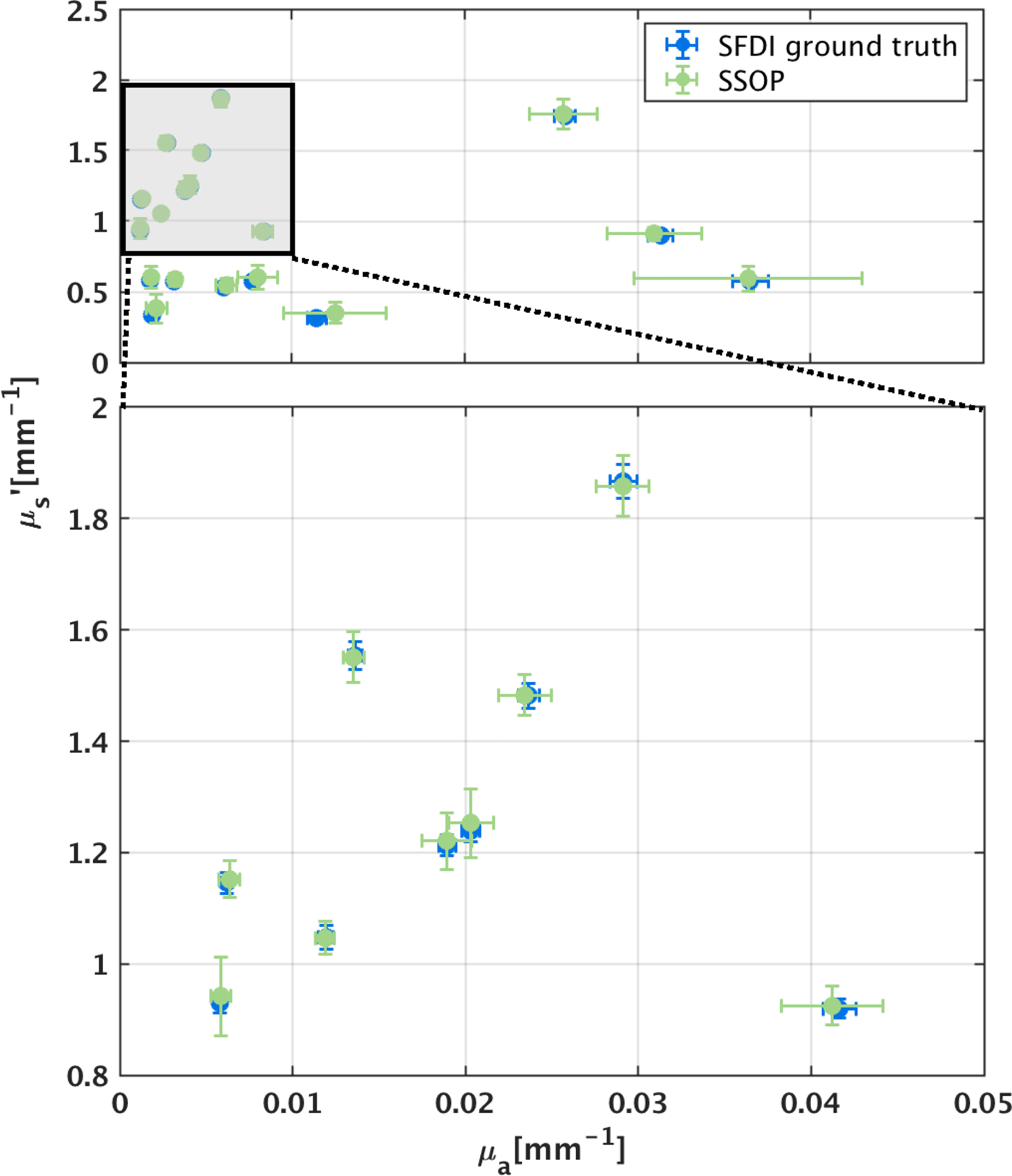
Validation of SSOP model-based prediction of optical properties with 18 homogeneous tissue phantoms. SSOP prediction from a single input image demonstrates close agreement with SFDI prediction from six input images.
In this study, six tissue-mimicking phantoms were used for training and twelve for testing. We intentionally selected phantoms for training that had optical properties not spanned by the human training samples (highlighted by green ellipses in Fig. 6), in order to develop GANPOP networks capable of estimating the widest range of optical properties.
Fig. 6.
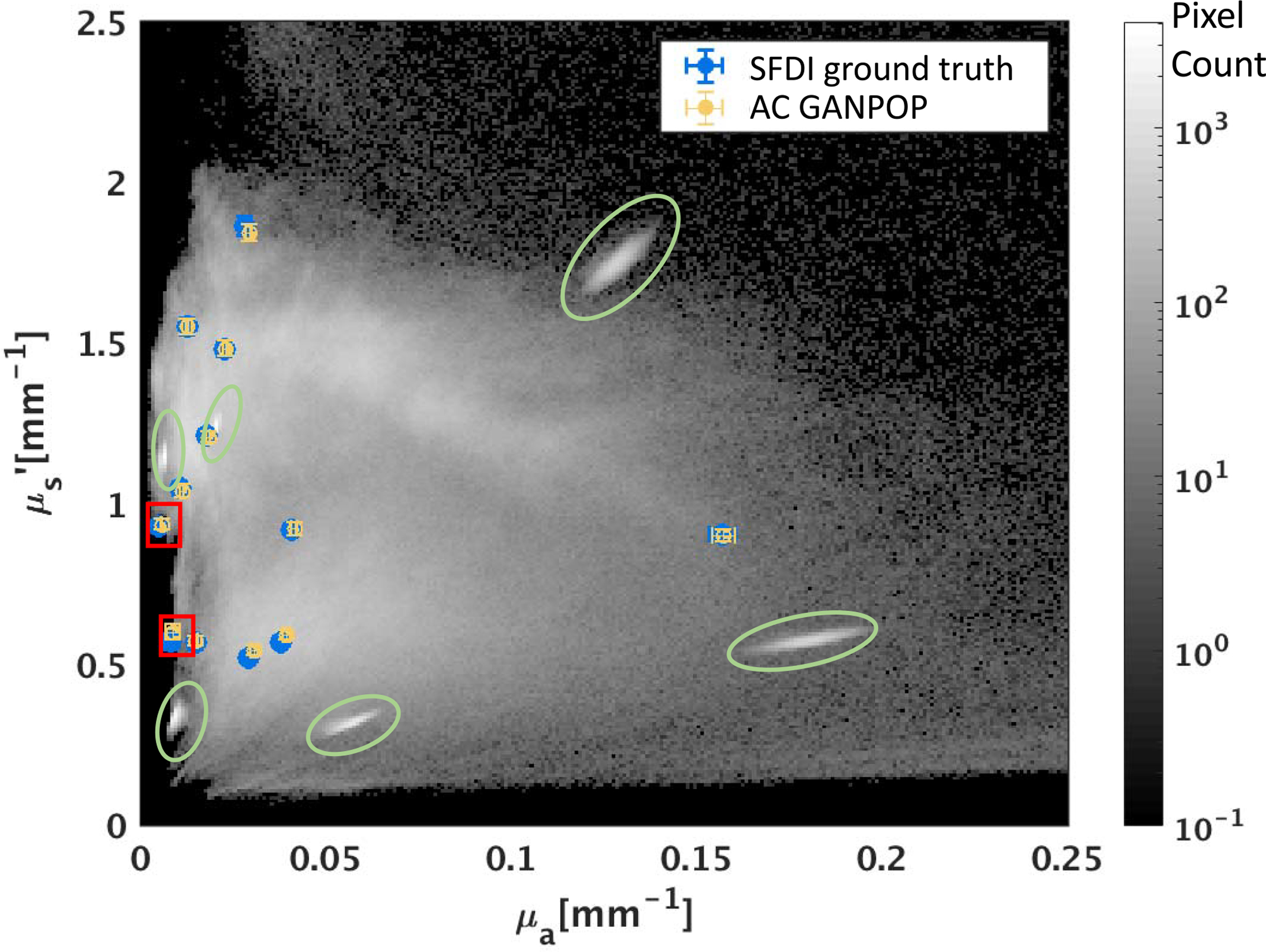
Scatter plot showing optical property pairs estimated by AC GANPOP compared to ground truth from conventional SFDI on 12 tissue phantoms. The 2D histogram in the background illustrates the distribution of training pixels among all optical property pairs, determined by SFDI. Green ellipses indicate dense pixel counts due to homogeneous phantoms used in training. Testing samples in the red box fell outside of the training range but were accurately predicted by AC GANPOP.
3). In Vivo Samples:
To provide the network with in vivo samples that were perfused and oxygenated, eight human hands and feet with different levels of pigmentation (Fitzpatrick skin types 1–6) were imaged with SFDI. This protocol was approved by the Johns Hopkins Institutional Review Board and consent was acquired from each participant prior to imaging. Six hands and feet were used for training and two for testing. Similar to human esophagus samples, leave-two-out cross validations were used for each network.
4). Swine Tissue:
Four specimens of upper gastrointestinal tracts that included stomach and esophagus were harvested from four different pigs for ex vivo imaging with SFDI. Optical properties of these samples are summarized in Fig. 7. Additionally, we imaged a pig colon in vivo during a surgery. The live study was performed with approval from Johns Hopkins University Animal Care and Use Committee (ACUC). All swine tissue images were excluded from training and used only for testing optical property prediction.
Fig. 7.
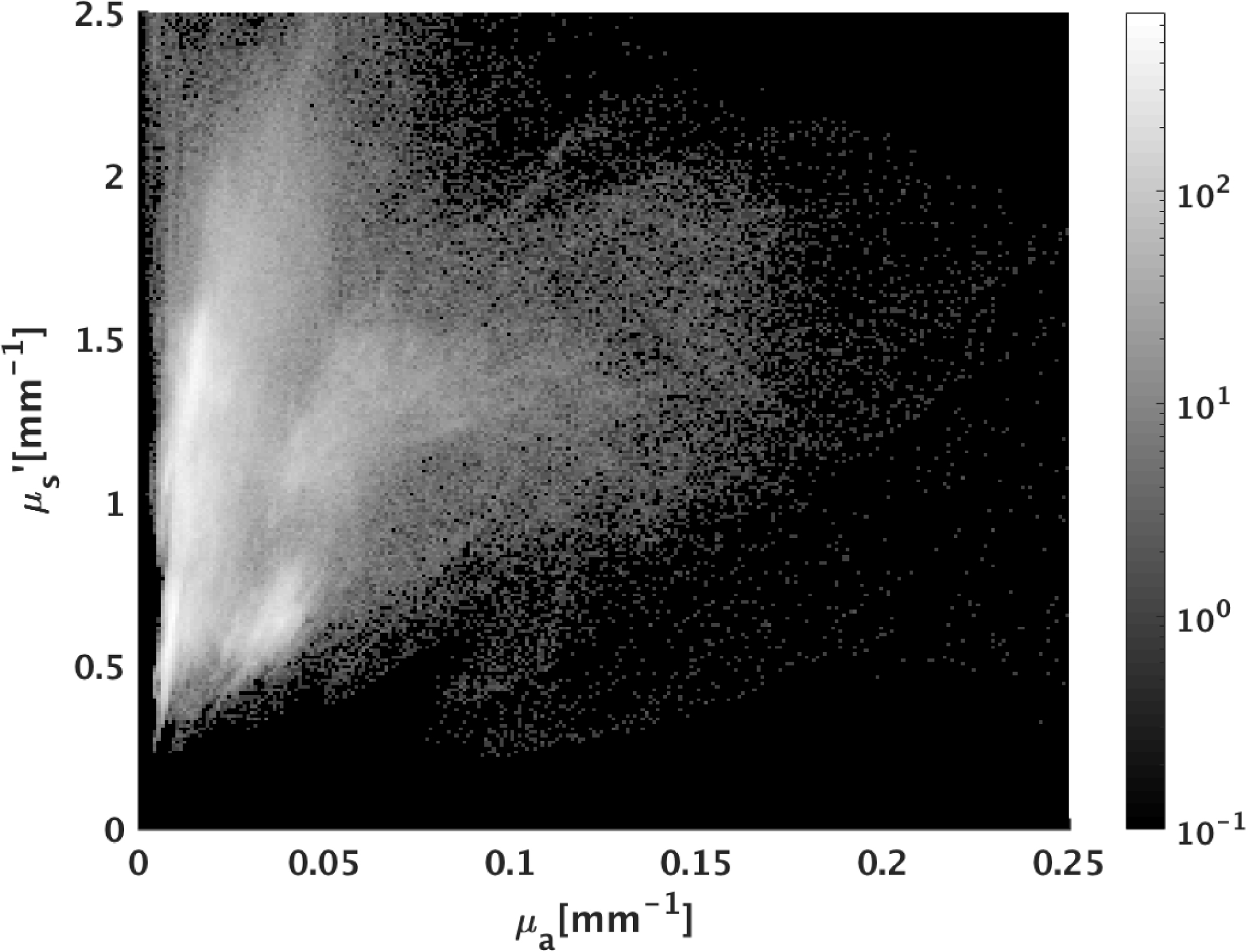
Histogram of optical property distribution of testing pixels from pig samples. Compared to training samples, pig tissues tested in this study had, on average, lower absorption coefficients and higher scattering coefficients.
F. Performance Metric
Normalized Mean Absolute Error (NMAE) was used to evaluate the performance of different methods, which was calculated using:
| (6) |
pi and pi,ref are pixel values of predicted and ground-truth data, and T is the total number of pixels. The metric was calculated using SFDI output as ground truth. A smaller NMAE value indicates better performance.
Additional metrics were used to assess pixel accuracy at constant reflectance values, including normalized error:
| (7) |
and average optical property (OP) deviation:
| (8) |
V. RESULTS
A. SSOP Validation
For benchmarking, SSOP was implemented as a model-based counterpart of GANPOP. For independent validation, we applied SSOP to 18 homogeneous tissue phantoms (Fig. 5). Each value was calculated as the mean of a 100 × 100-pixel region of interest (ROI) from the center of the phantom, with error bars showing standard deviations. SSOP demonstrates high accuracy in predicting optical properties of the phantoms, with an average percentage error of 2.35% for absorption and 2.69% for reduced scattering.
B. AC GANPOP Test in Homogeneous Phantoms
Phantom optical properties predicted by N1 are plotted with ground truth in Fig. 6. Each optical property reported is the average value of a 100 × 100 ROI of a homogeneous phantom, with error bars showing standard deviations. On average, AC GANPOP produced 4.50% error for absorption and 1.46% for scattering. The scatter plot in Fig. 6 is overlaid on a 2D histogram of pixel counts for each (μa,) pair used in an example training iteration. Green ellipses indicate training samples from homogeneous phantoms. The two testing results enclosed by red boxes have optical properties outside of the range spanned by the training data but were still reasonably estimated by the AC GANPOP network.
C. GANPOP Test on Ex Vivo Human Esophagus
GANPOP and SSOP were tested on the ex vivo human esophagus samples. NMAE scores were calculated for the two testing samples from each of four-fold cross validation iterations, and the average values from the four networks tested on a total of eight samples are reported in Fig. 8. Results from N3, N4, and SSOP are also compared to profilometry-corrected ground truth and shown in the same bar chart. On average, AC GANPOP produced approximately 60% higher accuracy than SSOP. Example optical property maps of a testing sample generated by N1 are shown in Fig. 12(a).
Fig. 8.
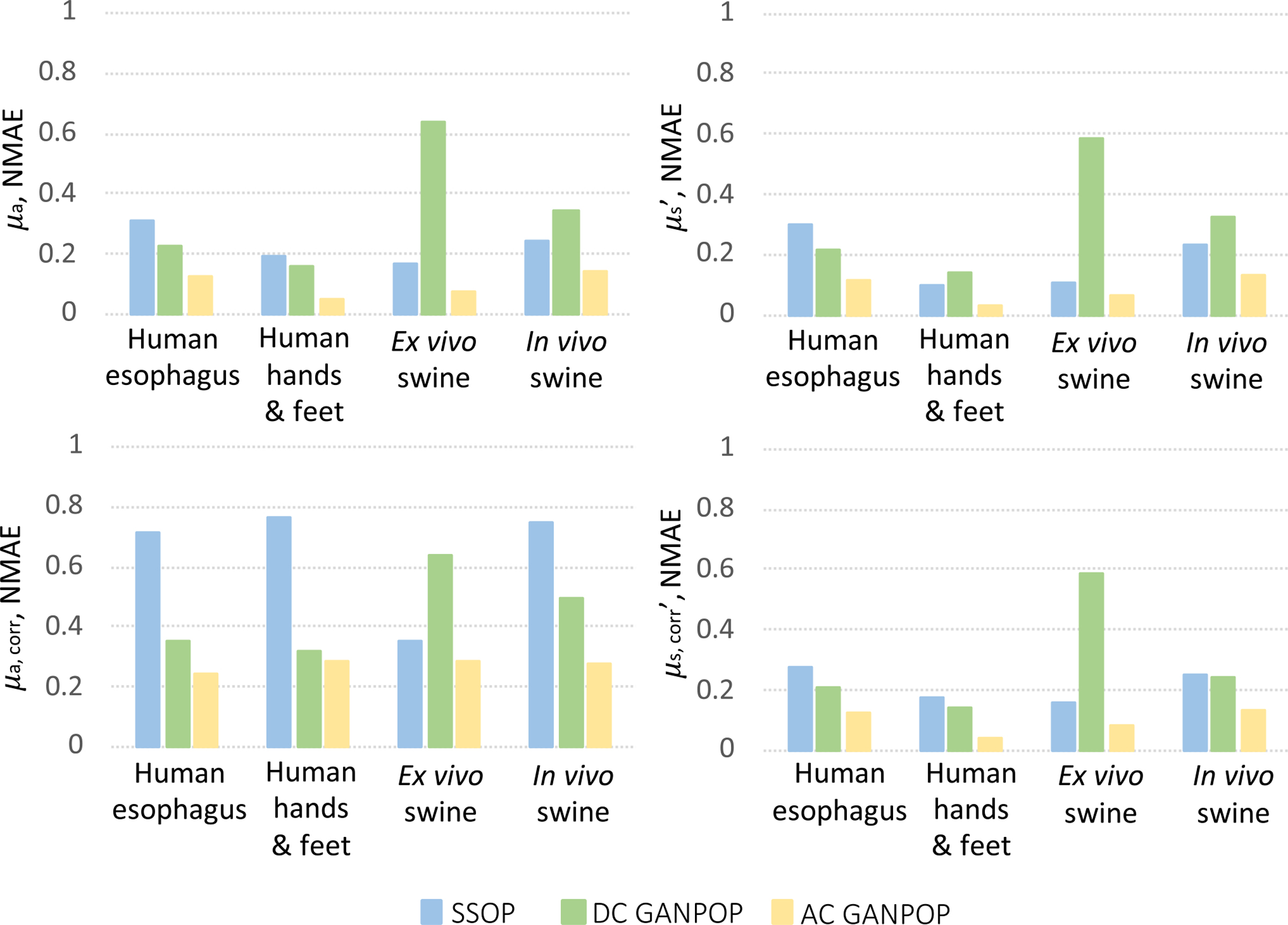
Accuracy of SSOP (blue), DC GANPOP (green) and AC GANPOP (yellow) in predicting optical properties of various types of samples. Average NMAE for absorption (left column) and scattering coefficients (right column) are reported. Top row shows the accuracy as compared to profile-uncorrected SFDI ground truth, and bottom row is against corrected ground truth. The same uncorrected SSOP data is used in both cases.
D. GANPOP Test on Pig Samples
Each of the four GANPOP networks were tested on ex vivo esophagus and stomach samples from four pigs. Average NMAE scores for GANPOP and SSOP method were calculated for all eight pig tissue specimens (four esophagi and four stomachs) and are summarized in Fig. 8. Background regions, which were absorbing paper, were manually masked in the calculation, and the reported scores are the average values of 779,101 tissue pixels. Despite the fact that some testing samples had optical properties not covered by the training set (Fig. 7), AC GANPOP outperforms SSOP in terms of average accuracy and image quality (Fig. 12).
The networks were additionally tested on an in vivo pig colon. Average NMAE scores for GANPOP and SSOP are reported in Fig. 8 as average values of 118,594 pixels. The generated maps are shown in Fig. 12(c). AC GANPOP produces more accurate results than SSOP when compared to both uncorrected and profile-corrected ground truth data.
E. GANPOP Test on Hemisphere Phantoms
To prove that AC GANPOP has the potential to infer profilometry correction from a single image, N3 was additionally tested on a hemisphere phantom with expected μa = 0.013mm−1 and . Shown in Fig. 9, AC GANPOP produces smaller errors than uncorrected SFDI, especially for angles greater than 30 degrees. Moreover, AC GANPOP results follow a similar error profile to the corrected ground truth. With a more sophisticated profilometry correction scheme, this error can be further minimized.
Fig. 9.
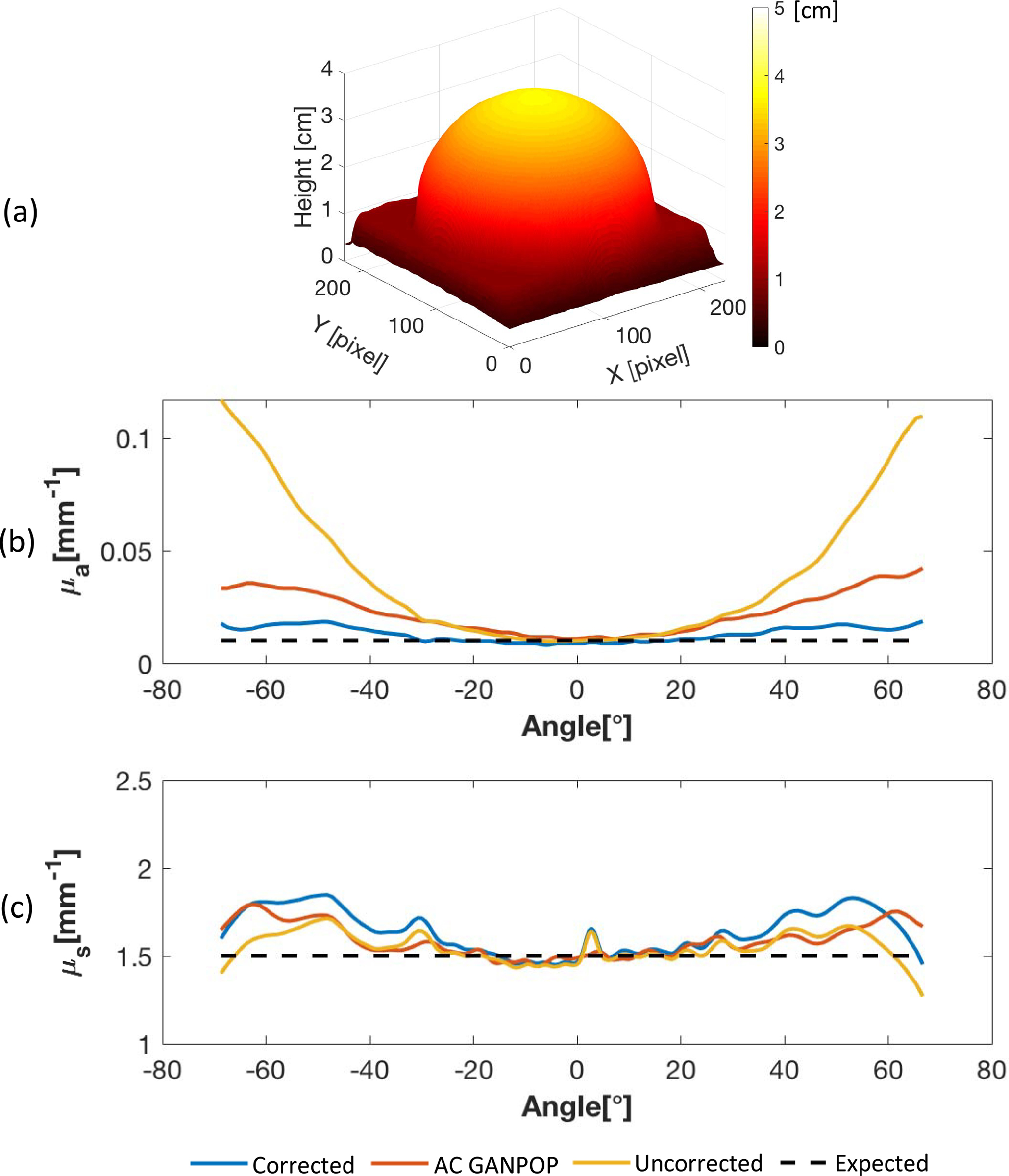
(a): Height map of a hemisphere phantom measured by SFDI profilometry; (b) and (c): Absorption and scattering coefficients measured by AC GANPOP (N3), profile-corrected (ground truth) and uncorrected SFDI compared to expected values.
F. GANPOP Test on In Vivo Human Hands
To further demonstrate that GANPOP is able to accurately compute optical properties of inhomogeneous media, we segmented hand images into vessels and background tissue and calculated the respective NMAE (Table II). Fig. 10 shows optical property maps of a representative human hand from SFDI, SSOP, and AC GANPOP, with vessels clearly visible in the absorption maps.
Table II:
PERFORMANCE COMPARISON OF SSOP, DC GANPOP, AND AC GANPOP FOR FULL HAND IMAGES, VESSELS, AND BACKGROUND TISSUES
| SSOP | DC GANPOP | AC GANPOP | ||||
|
μa NMAE |
NMAE |
μa NMAE |
NMAE |
μa NMAE |
||
| Vessels | 0.1069 | 0.0600 | 0.1007 | 0.0968 | 0.0305 | 0.0206 |
| Background | 0.2311 | 0.1307 | 0.1345 | 0.1203 | 0.0407 | 0.0321 |
| Hand overall | 0.2262 | 0.1284 | 0.1339 | 0.1199 | 0.0404 | 0.0320 |
Fig. 10.

Absorption (top) and reduced scattering (bottom) maps of the back of a hand generated by (a) SFDI ground truth, (b) SSOP, and (c) AC GANPOP. GANPOP result closely resembles the ground truth in terms of pixel accuracy and image quality, even for fine vascular structures.
G. Decoupling Absorption and Scattering
To explore the capability of GANPOP to decouple the contributions of scattering and absorption to reflectance measurements, we compare SSOP, DC GANPOP, and AC GANPOP to a baseline predictor that outputs the average scattering and absorption coefficients from training pixels with equal diffuse reflectance. For the human esophagus, examining all pixels with an , we find that the ground truth SFDI optical property measurements show a standard deviation of 26.7% for absorption and 25.0% for reduced scattering. The baseline change in optical properties between and 0.205 is much smaller–approximately 3.7% in absorption and 1.2% in reduced scattering. The normalized errors show that absorption and scattering errors are correlated for all methods (Fig. 11(e)-(h)). To assess the overall ability of each method to decouple optical properties, Fig. 11(i) shows the average optical property deviation of all optical property pairs for each reflectance value in the human esophagus testing samples. The SSOP error decreases with larger Rd, likely due to increased signal-to-noise ratios resulting from more detected photons. The baseline exhibits an improvement in accuracy that is generally correlated with the number of training pixels. DC GANPOP outperforms the baseline error at almost all values, indicating that its wide distribution of optical property estimates is consistently better than a constant pair prediction, and that it is effectively incorporating information about image content into each pixel prediction. AC GANPOP achieves the lowest error for all reflectances with more than 20 training pixels.
Fig. 11.
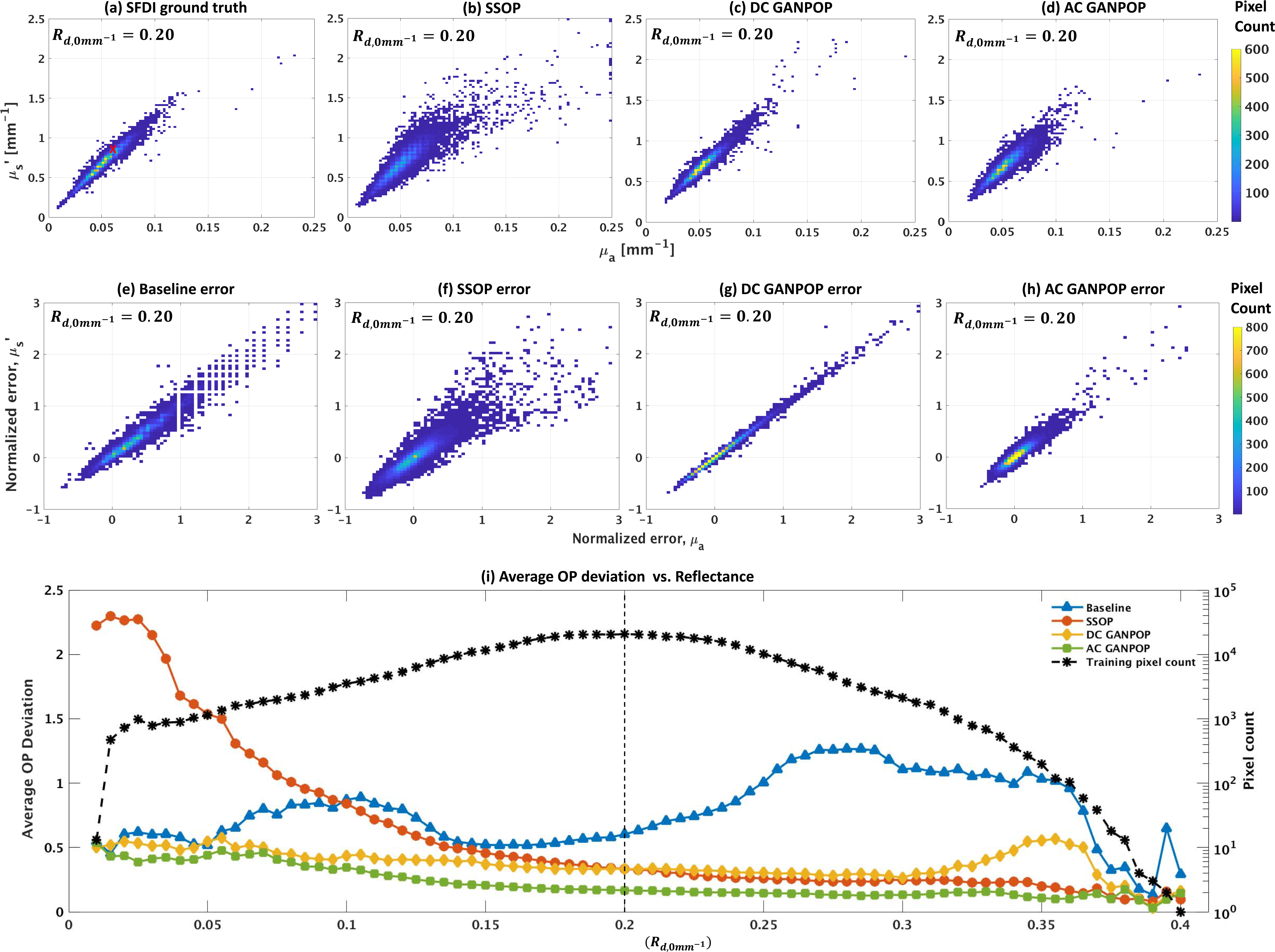
Top row: optical property distributions of esophagus test samples estimated by: (a) SFDI ground truth, (b) SSOP, (c) DC GANPOP, and (d) AC GANPOP, at a constant reflectance of . Red cross in (a) marks the baseline measurement, which is the average value of all training optical property pairs. Middle row: corresponding error histograms from (e) baseline, (f) SSOP, (g) DC GANPOP, and (h) AC GANPOP. Bottom row: (i) plot of average average optical property (OP) deviation of all optical property pairs for a given DC reflectance. Each average OP deviation is calculated as the average distance of all test points from ground truth at the corresponding reflectance level. Dotted line in (i) indicates where (a)-(h) are sampled.
H. Comparative Analysis of Existing Deep Networks
Several deep learning architectures were explored for the purpose of optical property mapping, including conventional U-Net [38] and ResNet [39], both stand-alone and integrated in a cGAN framework [23], [40]. The NMAE performance of each architecture was compared to AC GANPOP. All the networks were four-fold cross-validated, and the testing dataset included eight ex vivo human esophagi, four ex vivo pig GI samples, one in vivo pig colon, and eight in vivo hands and feet (Table III).
Table III:
PERFORMANCE COMPARISON OF THE PROPOSED FRAMEWORK AGAINST MODEL-BASED SSOP AND OTHER DEEP LEARNING ARCHITECTURES WHEN TESTED ON PROFILE-UNCORRECTED DATA (N1). PERFORMANCE IS MEASURED IN TERMS OF NORMALIZED MEAN ABSOLUTE ERROR (NMAE)
| Data type | SSOP | ResNet | UNet | ResNet-UNet | ResNet GAN | UNet GAN | Proposed (ResNet-UNet GAN) | |||||||
| μa | μa | μa | μa | μa | μa | μa | ||||||||
| Human esophagus | 0.312 | 0.298 | 0.192 | 0.136 | 0.144 | 0.136 | 0.185 | 0.129 | 0.201 | 0.140 | 0.148 | 0.143 | 0.124 | 0.121 |
| In vivo pig colon | 0.171 | 0.112 | 2.032 | 0.145 | 0.251 | 0.186 | 1.533 | 0.145 | 1.953 | 0.133 | 0.190 | 0.152 | 0.074 | 0.067 |
| Ex vivo pig GI tissue | 0.246 | 0.235 | 0.516 | 0.415 | 0.208 | 0.187 | 0.392 | 0.337 | 0.511 | 0.564 | 0.187 | 0.171 | 0.143 | 0.133 |
| In vivo hands and feet | 0.194 | 0.101 | 0.337 | 0.070 | 0.100 | 0.066 | 0.250 | 0.068 | 0.643 | 0.162 | 0.089 | 0.056 | 0.048 | 0.030 |
| Overall | 0.231 | 0.187 | 0.769 | 0.192 | 0.176 | 0.144 | 0.590 | 0.170 | 0.827 | 0.250 | 0.154 | 0.131 | 0.097 | 0.088 |
VI. DISCUSSION
In this study, we have described a GAN-based technique for end-to-end optical property mapping from single structured (AC) and flat-field (DC) illumination images. Compared to the original pix2pix paradigm [23], the generator of our model adopted a fusion of U-Net and ResNet architectures for several reasons. First, a fully residual network effectively resolved the issue of vanishing gradients, allowing us to stably train a relatively deep neural network [40]. Second, the use of both long and short skip connections enables the network to learn from the structure of the images while preserving both low and high frequency details. The information flow both within and between levels is important for the prediction of optical properties, as demonstrated by the improved performance over a U-Net or ResNet approach. To further demonstrate the importance of skip connections in the network, we conducted an experiment with all skip connections removed and the network failed to converge. We also varied the number of convolutional layers by adding two additional layers in both the generator and the discriminator. Without skip connections, the deeper network did not converge. With skip connections, the network produced similar accuracy to the original GANPOP architecture. However, adding more layers means a higher computational cost and a longer time to train as it makes the model significantly larger (300 million parameters, as compared to 78 million in the original model).
As shown in Table III, the inclusion of a discriminator significantly improved the performance of the fusion generator. This was especially apparent in the case for pig data, likely due to this testing tissue differing considerably from the training samples. We hypothesize that the cGAN architecture enforced the similarity between generated images and ground truth while preventing the generator from depending too much on the context of the image. Overall, the AC GANPOP method outperformed the other deep networks by a significant margin on all data types (Table III). We additionally conducted ablation studies by isolating the and loss in (5). With only , the network became a standalone fusion generator, which performed poorly compared to using the proposed objective (ResNet-UNet versus ResNet-UNet GAN in Table III). With only loss, the network failed to converge. This is because loss guides the training of the network after initialization, when there are large differences between predictions and ground truth. As the predictions become more accurate, contributes more to the overall loss function. Additionally, we empirically found that a least squares GAN outperformed a conventional GAN when trained for 200 epochs. However, as discussed in [47], this improvement could potentially be matched by a conventional GAN with more training.
The training set used in this study is relatively small, including 6 human esophagi, 6 hands and feet, and 6 homogeneous phantoms. Effective training is achieved in this small dataset through several strategies. First, the incorporation of spectral normalization stabilizes training and prevents mode collapse [41]. Second, we utilized patch-wise training and applied random stride sizes when extracting patches. This served to augment the dataset and provided random jitter. Moreover, training samples had heterogeneous optical properties, covering a wide range for both absorption and scattering (Fig. 6). We believe that this also helped with data efficiency as every pixel was used in learning the transformation from reflectance images to optical properties.
Compared to phantom ground truth in Fig. 6, AC GANPOP estimated optical properties with standard deviations on the same order of magnitude as conventional SFDI. Additionally, the AC GANPOP networks exhibited potential to extrapolate phantom optical properties that were not present in the training samples (highlighted by the red boxes in Fig. 6). This provides evidence that these networks have successfully learned the relationship between diffuse reflectance and optical properties, and are able to infer beyond the range of training data.
Fig. 8 shows that AC GANPOP consistently outperformed SSOP when tested on these types of data. From Fig. 7, it is evident that optical properties of the pig samples differed considerably from those of human esophagi used for training. Nevertheless, AC GANPOP exhibited more accurate estimation than the model-based SSOP benchmark. Moreover, a single network was trained for estimating both μa and due to its lower computational cost and potential benefits in learning the relationships between the two parameters in tissues.
Table II displays the accuracy of AC GANPOP compared to SSOP on different regions a representative hand image, including vessels and background tissues. The NMAE values of these subtypes have a similar trend to those of the full images. Combined with the qualitative results shown in Fig. 10, this indicates that GANPOP is capable of not only accurately inferring optical properties of relatively homogeneous media, but also capturing subtle changes caused by transitions in tissue types.
Compared to SSOP, AC GANPOP optical property maps contain fewer artifacts caused by frequency filtering (Fig. 10 and 12). For both GANPOP and SSOP optical property estimation, a relatively large error is present on the edge of the sample. This is caused by the transition between tissue and the background, which poses problems for SFDI ground truth, and would be less significant for in vivo imaging. Artifacts caused by patched input are visible in GANPOP images, which can be reduced by using a larger patch size. However, this was not implemented in our study due to the size and the number of the specimens available for training. In our benchmarking with SSOP, we implemented the first version of the technique, which does not correct for sample height and surface angle variations. This allowed comparing identical input images for both SSOP and AC GANPOP.
In addition to training GANPOP models to estimate optical properties from objects assumed to be flat (N1 and N2), we trained networks that directly estimate profilometry-corrected optical properties (N3 and N4). For the same AC input, these models generated improved results over SSOP when tested on human and pig data. When compared against profile-corrected ground truth, they produced 47.3% less error for μa and 29.1% for than did uncorrected output from N1. Combined with results shown in Fig. 9, this demonstrates that AC GANPOP is capable of inferring surface profile from a single fringe image and adjusting measured diffuse reflectance accordingly.
In experiment N2 and N4, when trained on DC illumination images, the GANPOP model became less accurate. It is important to note that any model that only considers DC reflectance values from pixels individually would be inherently limited in predicting the correct optical property pair among the infinite possibilities that would give the same reflectance measurement. However, since GANPOP is a content-aware framework that incorporates information from surrounding pixels in its prediction, it is possible to estimate optical properties from a more representative distribution than an approach that considers pixels in isolation. This hypothesis is supported by Fig. 11, which shows that DC GANPOP produces a wide range of estimates for a single diffuse reflectance and a lower average error than a baseline approach that gives a single optical property pair that minimizes errors for each reflectance in a training set. Therefore, we hypothesize that, when sufficiently trained on a certain tissue type, GANPOP has the potential to enable fairly rapid and accurate wide-field measurements of optical properties from conventional camera systems. This could be useful for applications such as endoscopic imaging of the GI tract, where the range of tissue optical properties is limited and modification of the hardware system is challenging.
The generator models trained in this study were 600MB in size with 78 million parameters. Each iteration was trained on approximately 500 patches, and this process took 3 hours on an NVIDIA Tesla P100 GPU. In terms of speed, GANPOP requires capturing one sample image instead of six, thus significantly shortening data acquisition time while avoiding image artifacts due to motion or change in ambient light. For optical property extraction, the model developed here without optimization takes approximately 0.04 s to process a 256 × 256 image on an NVIDIA Tesla a P100 GPU. Therefore, this technique has the potential to be applied in real time for fast and accurate optical property mapping. In terms of adaptability, random cropping ensures that our trained models work on any 256 × 256 patches within the field of view. Additionally, while the models were trained on the same calibration phantom at 660 nm, they could theoretically be applied to other references or wavelengths by scaling the average MDC,ref and MAC,ref.
For future work, a more generalizable model that would work on a range of imaging systems could be trained using domain adaptation techniques. A wider range of optical properties could also be incorporated into the training set, though this would inevitably incur a higher computational cost and necessitate a much larger dataset for training. Another future direction is to explore the applications of GANPOP in situations where SFDI data is difficult to acquire. Findings from this study indicate that training on a relatively small set of images can enable a GANPOP generator that is accurate and robust. Thus, in cases where acquiring training data is expensive or laborious, we hypothesize that a small dataset containing relatively few samples would be sufficient for enabling accurate predictions. Moreover, although all input images used here were acquired at an approximately-constant working distance, GANPOP could be modified to work for a variety of imaging geometries. Incorporating monocular depth estimates into the prediction may enable GANPOP to account for large differences in working distance [48], [49]. This could be particularly useful for endoscopic screening where constant imaging geometries are difficult to achieve. Having a model trained on images at multiple wavelengths, this technique can be modified to provide critical information in real time, such as tissue oxygenation and metabolism biomarkers. Accuracy in this application may also benefit from training adversarial networks to directly estimate these biomarkers rather than using optical properties as intermediate representations. By similar extension, future research may develop networks to directly estimate disease diagnosis and localization from structured light images.
VII. CONCLUSION
We have proposed a deep learning-based approach to optical property mapping (GANPOP) from single snapshot wide-field images. This model utilizes a conditional Generative Adversarial Network consisting of a generator and a discriminator that are iteratively trained in concert with one another. Using SFDI-determined optical properties as ground truth, AC GANPOP produces significantly more accurate optical property maps than a model-based SSOP benchmark. Moreover, we have demonstrated that DC GANPOP can estimate optical properties with conventional flat-field illumination, potentially enabling optical property mapping in endoscopy without modifications for structured illumination. This method lays the foundation for future work in incorporating real-time, high-fidelity optical property mapping and quantitative biomarker imaging into endoscopy and image-guided surgery applications.
ACKNOWLEDGMENT
The authors would like to thank Dr. Darren Roblyer’s Group, Boston University for sharing SFDI software.
This work was supported in part by the NIH Trailblazer Award under Grant R21 EB024700.
Contributor Information
Mason T. Chen, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA.
Faisal Mahmood, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA.; Harvard Medical School, Boston, MA 02115, USA
Jordan A. Sweer, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA. Triple Ring Technologies, Newark, CA 94560, USA
Nicholas J. Durr, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA.
REFERENCES
- [1].Richards-Kortum R and Sevick-Muraca E, “Quantitative optical spectroscopy for tissue diagnosis,” Annu. Rev. Phys. Chem, vol. 47, no. 1, pp. 555–606, 1996. [DOI] [PubMed] [Google Scholar]
- [2].Drezek RA et al. , “Light scattering from cervical cells throughout neoplastic progression: Influence of nuclear morphology, dna content, and chromatin texture,” J. Biomed. Opt, vol. 8, no. 1, pp. 7–17, 2003. [DOI] [PubMed] [Google Scholar]
- [3].Maloney BW, McClatchy DM, Pogue BW, Paulsen KD, Wells WA, and Barth RJ, “Review of methods for intraoperative margin detection for breast conserving surgery,” J. Biomed. Opt, vol. 23, no. 10, 2018, Art. no. 100901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Mourant JR et al. , “Light scattering from cells: The contribution of the nucleus and the effects of proliferative status,” J. Biomed. Opt, vol. 5, no. 2, pp. 131–138, 2000. [DOI] [PubMed] [Google Scholar]
- [5].Steelman ZA, Ho DS, Chu KK, and Wax A, “Light-scattering methods for tissue diagnosis,” Optica, vol. 6, no. 4, pp. 479–489, April. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Lin AJ et al. , “Spatial frequency domain imaging of intrinsic optical property contrast in a mouse model of alzheimer’s disease,” Ann. Biomed. Eng, vol. 39, no. 4, pp. 1349–1357, April. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Shah N et al. , “Noninvasive functional optical spectroscopy of human breast tissue,” Proc. Nat. Acad. Sci. USA, vol. 98, no. 8, pp. 4420–4425, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Dögnitz N and Wagnières G, “Determination of tissue optical properties by steady-state spatial frequency-domain reflectometry,” Lasers Med. Sci, vol. 13, no. 1, pp. 55–65, 1998. [Google Scholar]
- [9].Cuccia DJ, Bevilacqua F, Durkin AJ, Ayers FR, and Tromberg BJ, “Quantitation and mapping of tissue optical properties using modulated imaging,” J. Biomed. Opt, vol. 14, no. 2, April. 2009, Art. no. 024012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Pharaon MR et al. , “Early detection of complete vascular occlusion in a pedicle flap model using quantitative [corrected] spectral imaging,” Plastic Reconstructive Surgery, vol. 126, no. 6, pp. 1924–1935, February. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Gioux S et al. , “First-in-human pilot study of a spatial frequency domain oxygenation imaging system,” J. Biomed. Opt, vol. 16, no. 8, 2011, Art. no. 086015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Weinkauf C, Mazhar A, Vaishnav K, Hamadani AA, Cuccia DJ, and Armstrong DG, “Near-instant noninvasive optical imaging of tissue perfusion for vascular assessment,” J. Vascular Surgery, vol. 69, no. 2, pp. 555–562, February. 2019. [DOI] [PubMed] [Google Scholar]
- [13].Kaiser M, Yafi A, Cinat M, Choi B, and Durkin AJ, “Noninvasive assessment of burn wound severity using optical technology: A review of current and future modalities,” Burns, vol. 37, no. 3, pp. 377–386, May 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Yafi A et al. , “Quantitative skin assessment using spatial frequency domain imaging (SFDI) in patients with or at high risk for pressure ulcers,” Lasers Surg. Med, vol. 49, no. 9, pp. 827–834, November. 2017. [DOI] [PubMed] [Google Scholar]
- [15].Angelo JP, Van De Giessen M, and Gioux S, “Real-time endoscopic optical properties imaging,” Biomed. Opt. Express, vol. 8, no. 11, pp. 5113–5126, November. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Nandy S et al. , “Label-free quantitative optical assessment of human colon tissue using spatial frequency domain imaging,” Tech Coloproctol, vol. 22, no. 8, pp. 617–621, August. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Vervandier J and Gioux S, “Single snapshot imaging of optical properties,” Biomed. Opt. Express, vol. 4, no. 12, pp. 2938–2944, December. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Suzuki K, “Overview of deep learning in medical imaging,” Radiol. Phys. Technol, vol. 10, no. 3, pp. 257–273, September. 2017. [DOI] [PubMed] [Google Scholar]
- [19].Shin H-C et al. , “Deep convolutional neural networks for computer–aided detection: CNN architectures, dataset characteristics and transfer learning,” IEEE Trans. Med. Imag, vol. 35, no. 5, pp. 1285–1298, May 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Tajbakhsh N et al. , “Convolutional neural networks for medical image analysis: Full training or fine tuning?” IEEE Trans. Med. Imag, vol. 35, no. 5, pp. 1299–1312, May 2016. [DOI] [PubMed] [Google Scholar]
- [21].Goodfellow I et al. , “Generative adversarial nets,” in Advances in Neural Information Processing Systems, Ghahramani Z, Welling M, Cortes C, Lawrence ND, and Weinberger KQ, Eds. New York, NY, USA: Curran Associates, 2014, pp. 2672–2680. [Google Scholar]
- [22].Mirza M and Osindero S, “Conditional generative adversarial nets,” 2014, arXiv:1411.1784. [Online]. Available: https://arxiv.org/abs/1411.1784 [Google Scholar]
- [23].Isola P, Zhu J-Y, Zhou T, and Efros AA, “Image-to-image translation with conditional adversarial networks,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jul. 2017. [Google Scholar]
- [24].Diaz-Pinto A, Colomer A, Naranjo V, Morales S, Xu Y, and Frangi AF, “Retinal image synthesis and semi–supervised learning for glaucoma assessment,” IEEE Trans. Med. Imag, vol. 38, no. 9, pp. 2211–2218, September. 2019. [DOI] [PubMed] [Google Scholar]
- [25].Yang Q et al. , “Low–dose CT image denoising using a generative adversarial network with wasserstein distance and perceptual loss,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1348–1357, June. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Yang G et al. , “DAGAN: Deep de–aliasing generative adversarial networks for fast compressed sensing MRI reconstruction,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1310–1321, June. 2018. [DOI] [PubMed] [Google Scholar]
- [27].Swartling J, Dam JS, and Andersson-Engels S, “Comparison of spatially and temporally resolved diffuse-reflectance measurement systems for determination of biomedical optical properties,” Appl. Opt, vol. 42, no. 22, pp. 4612–4620, August. 2003. [DOI] [PubMed] [Google Scholar]
- [28].Weber JR, Cuccia DJ, Durkin AJ, and Tromberg BJ, “Noncontact imaging of absorption and scattering in layered tissue using spatially modulated structured light,” J. Appl. Phys, vol. 105, no. 10, May 2009, Art. no. 102028. [Google Scholar]
- [29].Palmer GM, Viola RJ, Schroeder T, Yarmolenko PS, Dewhirst MW, and Ramanujam N, “Quantitative diffuse reflectance and fluorescence spectroscopy: Tool to monitor tumor physiology in vivo,” J. Biomed. Opt, vol. 14, no. 2, 2009, Art. no. 024010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Jones G, Clancy NT, Helo Y, Arridge S, Elson DS, and Stoyanov D, “Bayesian estimation of intrinsic tissue oxygenation and perfusion from RGB images,” IEEE Trans. Med. Imag, vol. 36, no. 7, pp. 1491–1501, July. 2017. [DOI] [PubMed] [Google Scholar]
- [31].Van De Giessen M, Angelo JP, and Gioux S, “Real-time, profile-corrected single snapshot imaging of optical properties,” Biomed. Opt. Express, vol. 6, no. 10, pp. 4051–4062, October. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Swapnesh Panigrahi SG, “Machine learning approach for rapid and accurate estimation of optical properties using spatial frequency domain imaging,” J. Biomed. Opt, vol. 24, no. 7, pp. 1–6, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Zhao Y, Deng Y, Bao F, Peterson H, Istfan R, and Roblyer D, “Deep learning model for ultrafast multifrequency optical property extractions for spatial frequency domain imaging,” Opt. Lett, vol. 43, no. 22, pp. 5669–5672, November. 2018. [DOI] [PubMed] [Google Scholar]
- [34].Gioux S, Mazhar A, Cuccia DJ, Durkin AJ, Tromberg BJ, and Frangioni JV, “Three-dimensional surface profile intensity correction for spatially modulated imaging,” J. Biomed. Opt, vol. 14, no. 3, 2009, Art. no. 034045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Zhao Y, Tabassum S, Piracha S, Nandhu MS, Viapiano M, and Roblyer D, “Angle correction for small animal tumor imaging with spatial frequency domain imaging (SFDI),” Biomed. Opt. Express, vol. 7, no. 6, pp. 2373–2384, June. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Martinelli M, Gardner A, Cuccia D, Hayakawa C, Spanier J, and Venugopalan V, “Analysis of single Monte Carlo methods for prediction of reflectance from turbid media,” Opt. Express, vol. 19, no. 20, pp. 19627–19642, September. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Chen R, Mahmood F, Yuille A, and Durr NJ, “Rethinking monocular depth estimation with adversarial training,” 2018, arXiv:1808.07528. [Online]. Available: https://arxiv.org/abs/1808.07528 [Google Scholar]
- [38].Ronneberger O, Fischer P, and Brox T, “U-net: Convolutional networks for biomedical image segmentation,” in Medical Image Computing and Computer-Assisted Intervention—MICCAI. Cham, Switzerland: Springer, 2015, pp. 234–241. [Online]. Available: https://link.springer.com/chapter/10.1007%2F978-3-319-24574-4_28 [Google Scholar]
- [39].He K, Zhang X, Ren S, and Sun J, “Deep residual learning for image recognition,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2016. [Google Scholar]
- [40].Quan TM, Hildebrand DGC, and Jeong W-K, “FusionNet: A deep fully residual convolutional neural network for image segmentation in connectomics,” 2016, arXiv:1612.05360. [Online]. Available: https://arxiv.org/abs/1612.05360 [Google Scholar]
- [41].Miyato T and Koyama M, “cGANS with projection discriminator,” 2018, arXiv:1802.05637. [Online]. Available: https://arxiv.org/abs/1802.05637 [Google Scholar]
- [42].Mao X, Li Q, Xie H, Lau RY, Wang Z, and Smolley SP, “Least squares generative adversarial networks,” in Proc. IEEE Int. Conf. Comput. Vis. (ICCV), Oct. 2017. [DOI] [PubMed] [Google Scholar]
- [43].Kingma DP and Ba J, “Adam: A method for stochastic optimization,” 2014, arXiv:1412.6980. [Online]. Available: https://arxiv.org/abs/1412.6980 [Google Scholar]
- [44].Sweer JA, Chen MT, Salimian KJ, Battafarano RJ, and Durr NJ, “Wide-field optical property mapping and structured light imaging of the esophagus with spatial frequency domain imaging,” J. Biophotonics, vol. 12, no. 9, September. 2019, Art. no. e201900005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Mazhar A et al. , “Wavelength optimization for rapid chromophore mapping using spatial frequency domain imaging,” J. Biomed. Opt, vol. 15, no. 6, 2010, Art. no. 061716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Ayers F, Grant A, Kuo D, Cuccia DJ, and Durkin AJ, “Fabrication and characterization of silicone-based tissue phantoms with tunable optical properties in the visible and near infrared domain,” Des. Perform. Validation Phantoms Conjunct. Opt. Meas. Tissue, Int. Soc. Opt. Photon, vol. 6870, February. 2008, Art. no. 687007. [Google Scholar]
- [47].Lucic M, Kurach K, Michalski M, Gelly S, and Bousquet O, “Are GANs created equal? A large-scale study,” in Proc. Adv. Neural Inf. Process. Syst, 2018, pp. 700–709. [Google Scholar]
- [48].Mahmood F, Chen R, and Durr NJ, “Unsupervised reverse domain adaptation for synthetic medical images via adversarial training,” IEEE Trans. Med. Imag, vol. 37, no. 12, pp. 2572–2581, December. 2018. [DOI] [PubMed] [Google Scholar]
- [49].Mahmood F, Chen R, Sudarsky S, Yu D, and Durr NJ, “Deep learning with cinematic rendering: Fine-tuning deep neural networks using photorealistic medical images,” Phys. Med. Biol, vol. 63, no. 18, August. 2018, Art. no. 185012. [DOI] [PubMed] [Google Scholar]


