The misunderstanding of vaccine efficacy

Abstract

Although the efficacies of vaccines against SARS-CoV-2, i.e., the virus that causes Covid-19, have been publicized and praised, and although they are assumed to encourage vaccine compliance, little is known about how well these figures are understood by the general public. Our study aims to fill this gap by investigating whether laypeople have an adequate grasp of what vaccine efficacy means and, if not, which misconceptions and consequences are the most common. To this end, we carried out three online behavioral experiments involving 1800 participants overall. The first, exploratory experiment, with a sample of 600 UK participants, allowed us to document, by means of both an open-ended question and a multiple-choice question, a common misinterpretation of the efficacy of SARS-CoV-2 vaccines as the non-incidence rate among the vaccinated. We formally demonstrated that this error leads to a systematic overestimation of the probability of individuals who are vaccinated developing Covid-19. The second experiment confirmed the prevalence of this misinterpretation in a new sample of 600 UK and Italian participants, by means of a slightly different multiple-choice question that included more response options. Finally, in a third experiment, involving another 600 UK and Italian participants, we investigated the behavioral implications of the documented error and showed that it might undermine the general positive attitude toward vaccines as well as the intention to get vaccinated. On the whole, the results of this study reveal a general misunderstanding of vaccine efficacy that may have serious consequences for the perceived benefits of SARS-CoV-2 vaccines and, thus, the willingness to be vaccinated.

1. Introduction: the (non-obvious) concept of vaccine efficacy

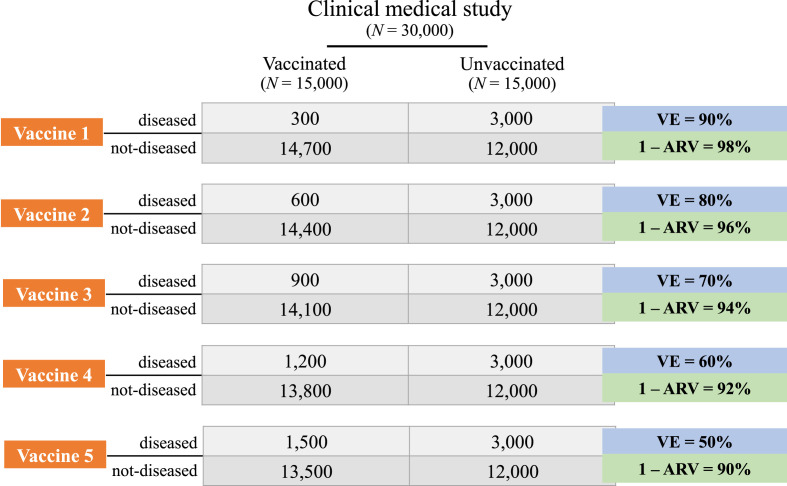
The protective effect of a vaccine is typically expressed in both scientific and popular dissemination contexts as vaccine efficacy (VE). VE is computed based on the results of a double-blind, randomized, controlled trial in which half the subjects receive the vaccine, while the other half receive a placebo. Both groups are followed prospectively to determine their attack rates, and VE is then defined as the percentage reduction in the attack rate among vaccinated compared to unvaccinated individuals under these ideal circumstances, which corresponds to the relative risk reduction among the vaccinated as compared to the unvaccinated (Orenstein et al., 1985; Weinberg and Szilagyi, 2010):

$$\text{VE}=\frac{\left(\text{ARU}-\text{ARV}\right)}{\text{ARU}}\text{x}100=\left(1-\text{RR}\right)\text{ x }100$$

where ARU and ARV indicate the attack rates among unvaccinated and vaccinated groups, respectively, while RR is the relative risk of developing the disease for vaccinated compared to unvaccinated subjects. The VE ranges from 0% (when ARV = ARU, indicating the vaccine is completely ineffective) to 100% (when ARV = 0, indicating that the vaccine eliminates the risk entirely). For example, the efficacy of the Moderna vaccine, VE_mRNA1273, has been reported to be 94.05% (obtained from 11 Covid-19 cases out of the 15,210 vaccinated individuals and 185 Covid-19 cases out of the 15,210 non-vaccinated individuals, Baden et al., 2020) and the efficacy of the Pfizer vaccine, VE_BNT162b2, has been reported to be 95.03% (obtained from 8 Covid-19 cases out of the 18,198 vaccinated individuals and 162 Covid-19 cases out of the 18,325 non-vaccinated individuals, Polack et al., 2020). These figures are much greater than the FDA's stated acceptable threshold (FDA Center for Biologics, 2020) and received enthusiastic scientific (Science, 2020) and popular media coverage (BBC, 2020; N.Y. Times, 2020).

The main questions of our study are whether the information conveyed by VE is well-understood by the general public and, if not, what the implications of possible errors are. Our concerns regarding the comprehension of VE stem from the consideration that its non-obvious meaning has often been misrepresented in mainstream and trade media, as illustrated in the following examples from Reuters and Vox (but see also ABC News, 2021; The Conversation, 2020):

“If a vaccine has an efficacy of, say, 80%, it means that if 100 people who have not previously been infected by the coronavirus are given the vaccine, on average 80 of them will not get the disease that the virus causes: COVID-19” (Reuters, 2020).

“Pfizer and BioNTech say their vaccine had an efficacy of 95 percent against Covid-19, meaning 95 percent of people who received the vaccine were protected against the disease” (Vox, 2020).

The problem does not appear to be confined to popular outlets since, as pointed out by Olliaro (2021), incorrect interpretation of the significance of VE can also be found in prestigious scientific journals, including an editorial in Lancet Infectious Diseases:

“The rationale is that if 95% of people are protected from disease after two doses (as determined in the phase 3 trial of the PfizerBioNTech vaccine) …” (The Lancet Infectious Diseases, 2021).

A closer inspection of these examples suggests a misinterpretation of VE that may assume one of two slightly different variants. To detail them, let us call D the statement “to develop the disease,” V the statement “to be vaccinated,” and E the statement “to be exposed to the virus.” From now on, in order not to overload the notation, VE will refer to the fractional version of the above formula (i.e., without the multiplication by 100). In the first statement above, VE is clearly confused with the non-incidence rate among the vaccinated, i.e., the probability of not having the disease if vaccinated, P(not-D|V), which corresponds to 1 – ARV. The subsequent examples are more ambiguous since they leave unspecified what it means for a person to be “protected against the disease.” If it means that a protected person will not develop Covid-19, while an unprotected person will, then, just as in the previous example, VE is confused with P(not-D|V). If it is meant, instead, that, in addition to vaccination status, it is relevant whether the person will or will not be exposed to the SARS-CoV-2 virus, then VE is confused with P(not-D|V&E). These two variants of the error converge for increasing values of P(E) and coincide if it is assumed that, sooner or later, everyone will be exposed to the virus. It is important to note though that, while P(not-D|V) can be easily computed, P(not-D|V&E) is a less-defined concept, since it would require quantifying the risk of exposure, a piece of information that strongly depends on various individual factors (including a person's job, living conditions and practice of preventive measures) and that goes far beyond the purview of a phase 3 clinical trial. The two variants of misinterpretation of VE are nevertheless similar in one important respect: as formally demonstrated in the following section, they both imply a systematic underestimation of the benefits provided by vaccination.

2. The mathematical relationship between VE and the non-incidence rate among vaccinees

To appreciate the implication of misunderstanding VE as P(not-D|V) (i.e., 1 – ARV), first consider the available data on mRNA-1273 and BNT162b2 vaccines. As stated, their VEs have been reported as 94.05% and 95.03%, respectively, while P(not-D|V) is 99.93% for the mRNA-1273 vaccine and 99.96% for the BNT162b2 vaccine. These values indicate that, if VE is confused with the non-incidence rate among vaccinees, the attack rate of the vaccinated is overestimated by an order of magnitude: from less than 0.1% to 5–6%. Importantly, such an overestimation is not a peculiarity of the two vaccines considered. Here, we demonstrate that VE is always smaller than P(not-D|V), except for two (vanishingly rare) limit cases, in which they are equal.

• Proposition

• VE = 1 – ARV (i.e., P(not-D|V)) if either ARU = 1 (i.e., all unvaccinated individuals develop the disease) or ARV = 0 (i.e., no vaccinated individual develops the disease). In all remaining cases (i.e., ARU < 1 and ARV > 0), VE < 1 – ARV.

• Proof

• 1.If ARU = 1, VE = (ARU – ARV)/ARU = (1 – ARV)/1 = 1 – ARV;
• 2.If ARV = 0, VE = (ARU – ARV)/ARU = (ARU – 0)/ARU = 1;
• 3.If ARU < 1 and ARV > 0, then ARV/ARU > ARV, from which it follows that VE = (ARU – ARV)/ARU = 1 – ARV/ARU < 1 – ARV.

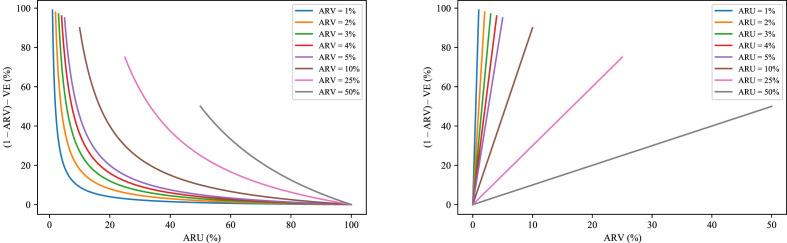
Figure 1 allows an appreciation of the relationship between 1 – ARV and VE by plotting their difference as a function of ARU for different values of ARV (left) and as a function of ARV for different values of ARU (right). As illustrated, the gap between 1 – ARV and VE is maximal for small values of ARU, that is, in all (common) situations in which the incidence of a condition is rather low. Moreover, for any fixed value of ARU, the difference increases with greater ARV, that is, the less efficacious the vaccine, the greater the difference.

Let us now consider the possible confusion of VE with P(not-D|V&E). In what follows, we show that P(not-D|V&E), even if it is always smaller than 1 – ARV (except for one limit case, in which they are equal), is always larger than VE (again, except for one limit case, in which they are equal).

• Proposition

• If everybody is exposed to the virus (i.e., P(E) = 1), then P(not-D|V&E) = 1 – ARV, otherwise (i.e., P(E) < 1), P(not-D|V&E) < 1 – ARV. If all unvaccinated individuals exposed to the virus develop the disease (i.e., P(E) = ARU), then P(not-D|V&E) = VE, otherwise (i.e., P(E) > ARU), P(not-D|V&E) > VE.

• Proof

• 1.P(not-D|V&E) = 1 – P(D|V&E) by additivity;
• 2.1 – P(D|V&E) = 1 – P(D&E|V)/P(E|V) by the chain rule of probability;
• 3.P(D&E|V) = P(D|V) since exposure to the virus is a necessary condition for developing the disease;
• 4.P(E|V) = P(E) given the assumption of comparability of groups in double blind placebo-controlled trials;
• 5.From 1, 2, 3, 4, it follows that P(not-D|V&E) = 1 – P(D|V)/P(E);
• 6.
  From 5, it follows that:

  • 6.1
    If P(E) = 1, P(not-D|V&E) = 1 – P(D|V) = 1 – ARV;
  • 6.2
    If P(E) < 1, P(not-D|V&E) < 1 – ARV;
  • 6.3
    If P(E) = ARU, P(not-D|V&E) = 1 – P(D|V)/ARU = 1 – ARV/ARU = VE;
  • 6.4
    If P(E) > ARU, P(not-D|V&E) > 1 – ARV/ARU = VE.

Therefore, the misunderstanding of VE as P(not-D|V&E) is simply a less-extreme version of the error of misunderstanding VE as P(not-D|V), in that both imply a systematic overestimation of the probability of developing Covid-19 among vaccinated individuals.

3. Confusion of VE with the non-incidence rate among vaccinees: empirical evidence

In this section, we report the details of two behavioral experiments, which, in both UK and Italian samples, confirmed a pervasive confusion of VE with the rate of individuals who do not develop Covid-19 among those vaccinated.

3.1. Experiment 1

3.1.1. Setting

Online data collection was carried out December 10–18, 2020, through Prolific Academic (http://prolific.ac), one of the most popular and reliable crowdsourcing platforms for behavioral research (Palan and Schitter, 2018). There were no time limits on task completion, and the average response time was less than 2 min. Participants received 0.63 British pounds, which guarantees an hourly rate in line with the Prolific compensation policy.

3.1.2. Participants

We recruited 600 UK residents, all native speakers of English. This sample was well-suited to the study due to their native language and their residence in one of the only countries that had begun mass vaccination at the time, as well as because the UK contingent on Prolific constitutes a particularly representative cross-section of the population, as compared to the cohorts of other countries on the platform (e.g. Italy or the USA). The mean age of participants was 37 years (SD = 13.8), ranging from 18 to 80 years (5 participants did not declare their ages). Females made up 64%; 52% of participants had either an undergraduate or graduate degree, and 5% declared that they had participated in a medical trial.

3.1.3. Design and stimuli

Participants were randomly assigned to one of two groups: the first received an open-ended question (N = 300); the second, a multiple-choice question (N = 300).

Participants in both groups were presented with the following prompt:

In a rigorous clinical study, scientists find that a vaccine for Covid-19 has an efficacy of 90%.

Then, participants in the first group were asked the following open-ended question (virtually unlimited space was available for the response):

In your understanding, what does this 90% mean?

(Please give your own interpretation based on what you know right now, without asking anyone else or searching online. Be as specific as you can.)

Participants in the second group were asked instead the following multiple-choice question (bolded as in the presented text; the order of response options was randomized):

In your understanding, what does this 90% indicate?

(Please select the alternative which reflects your own interpretation based on what you know right now, without asking anyone else or searching online.)

• □ The percentage of individuals who do not develop Covid-19 among those vaccinated

• □ The percentage of individuals who do not develop Covid-19 among those vaccinated minus the percentage of individuals who do develop Covid-19 among those vaccinated

• □ The percentage of individuals who do develop Covid-19 among those not vaccinated minus the percentage of individuals who do develop Covid-19 among those vaccinated, divided by the former percentage

• □ The percentage of individuals who do not develop Covid-19 among those vaccinated minus the percentage of individuals who do not develop Covid-19 among those not vaccinated, divided by the latter percentage

• □ The difference between the percentages of individuals who do not and who do develop Covid-19 among those vaccinated minus the difference between the percentages of individuals who do not and who do develop Covid-19 among those not vaccinated

• □ Other (if you select this option, you will be asked to specify your answer)

In this first, exploratory experiment, we posed the same question with two different response formats to pursue two information objectives. On the one hand, we were interested in participants’ spontaneous definitions of VE, which only an open-ended question could reveal. On the other hand, we wanted to exclude the possibility that incorrect answers to the open-ended question were due to the difficulty of reporting a complex definition such as that of VE. Therefore, to see whether participants were at least able to recognize the correct definition when they encountered it, we presented half with a list of response options, including a concise, though precise, formal definition of VE (i.e., the third option in the above list). The response options comprised our target error — in the variant that could be quantified and, therefore, that could reasonably be the outcome of a clinical trial (i.e., VE as 1 – ARV) — as well as three other incorrect alternatives (for their formalizations, see Table 2). Notably, two of the incorrect options (four and five in the above list) refer to a comparison between experimental (“the vaccinated individuals”) and control (“the unvaccinated individuals”) groups, which served as a check as to whether a reference to this prerequisite of a controlled clinical trial would draw more responses that included this key component of the correct answer.

Table 2.

Frequencies and percentages for the multiple-choice options of Experiment 1 (bolded as in the presented text), with corresponding formulas (not included in the presented text).

Response	N	%
The percentage of individuals who do not develop Covid-19 among those vaccinated  1 – ARV [Target error]	192	64
The percentage of individuals who do not develop Covid-19 among those vaccinated minus the percentage of individuals who do develop Covid-19 among those vaccinated  (1 – ARV) – ARV	49	16
The difference between the percentages of individuals who do not and who do develop Covid-19 among those vaccinated minus the difference between the percentages of individuals who do not and who do develop Covid-19 among those not vaccinated  ((1 – ARV) – ARV) – ((1 – ARU) – ARU)	28	9
The percentage of individuals who do not develop Covid-19 among those vaccinated minus the percentage of individuals who do not develop Covid-19 among those not vaccinated, divided by the latter percentage  ((1 – ARV) – (1 – ARU))/(1 – ARU) = (ARU – ARV)/(1 – ARU)	15	5
The percentage of individuals who do develop Covid-19 among those not vaccinated minus the percentage of individuals who do develop Covid-19 among those vaccinated, divided by the former percentage  (ARU – ARV)/ARU [Correct response]	8	3
Other	8	3
Total	300	100

3.1.4. Results – open-ended question

Four independent judges reviewed and coded each response to the open-ended question. Agreement was above 95%, and disagreements were solved via discussion (they concerned only a few incorrect answers, and whenever the evaluation was not unanimous, the statement was classified as “other error”). The results of classification are reported in Table 1 ; an example for each class of answer and additional classification criteria are outlined in the Appendix. Overall, the amount of correct answers or answers that expressed at least a correct intuition (even if not fully detailed) was notably low: 1% (95% CI, 0%–2%). Another 1% (95% CI, 0%–2%) of answers were classified as “mixed,” because they contained a correct intuition (e.g., a reference to risk reduction with respect to a control group) but were nevertheless vague and/or included one or more errors. As expected, the great majority of wrong answers (77%; 95% CI, 72%–82%) perpetrated the target error. More specifically, out of these answers, 79% (95% CI, 74%–84%) were compatible with both variants of the error detailed in the previous section; 12% (95% CI, 8%–16%) indicated a misinterpretation of VE as P(not-D|V), i.e., 1 – ARV; while the remaining 9% (95% CI, 5%–13%), a misinterpretation of VE as P(not-D|V&E); for examples, see the Appendix. Errors other than the target error did not match any of the options from the multiple-choice task; they amounted to 5% (95% CI, 3%–7%) of responses and did not form any identifiable patterns. The remaining answers were classified as reiterations (13%; 95% CI, 9%–17%) or generic comments (3%; 95% CI, 1%–5%). Of the 17 participants who had participated in a medical trial, two provided an answer that was classified as “mixed,” one as a “comment,” and the remaining 14 as the target error. A different distribution of responses was observed among participants with a higher (i.e., graduate degree and above) versus lower education level (i.e., less than a graduate degree), ꭓ²(7, N = 300) = 21.11, p = .004. Specifically, participants with a lower education level provided a greater number of answers that were classified as “reiteration or vague,” compared to participants with a higher education level (21% vs. 5%, respectively, p < .001), but no difference was observed in either the number of “correct” answers (1% vs. 2%, respectively, p > .05) or target errors (72% vs. 77%, respectively, p > .05). No significant difference was observed between males and females (p > .05).

Table 1.

Frequencies and percentages for the open-ended response classes of Experiment 1 (for specific examples, see the Appendix).

Response	N	%
Non-incidence rate among vaccinated individuals  (i.e., the two variants of the target error)	231a	77a
Reiterations or vague answers  (i.e., responses that re-state the question or that address only a quality or capacity of the vaccine without implying an effect on people)	37	13
Comments  (i.e., responses that express opinions rather than answer the question)	9	3
Other errors  (i.e., incorrect responses that differ from the error above and/or are confused)	15	5
Mixed answers  (i.e., responses that suggest a correct intuition but are imprecise and/or contain additional errors)	4	1
Correct responses  (i.e., responses aligned with the correct definition, even if not fully detailed)	4	1
Total	300	100

^aOf the 231 answers classified as the target error, 27 clearly mentioned P(not-D|V); 22 clearly indicated P(not-D|V&E); while for the remaining 182 answers, both interpretations were possible.

3.1.5. Results – multiple-choice question

The results of the multiple-choice question are reported in Table 2. The correct option was the least-popular choice (3% of the total; 95% CI, 1%–5%), while the most popular (64% of the total; 95% CI, 59%–69%; significantly greater than chance, z = 19.05, p < .001) was the target error, that is, the percentage of individuals who do not develop Covid-19 among those vaccinated (i.e., 1 – ARV), a result that fully confirmed the misinterpretation of VE as revealed by the open-ended question. (Note that chance level was set at 20% to account for five alternatives, i.e., by discarding the “Other” option; of course, if this sixth, non-detailed option were included, it would lower chance level to 1/6, thus increasing the distance of the most-popular selection above chance.) The second-most-selected incorrect option (16%; 95% CI, 12%–21%) was the one indicating the difference between the rate of individuals who do not develop and who do develop Covid-19 among those vaccinated. The option outlining the difference between the difference in the rates of vaccinated individuals who do not and who do develop Covid-19 and the difference in the rates of unvaccinated individuals who do not and who do develop Covid-19 was chosen by 9% (95% CI, 6%–13%) of participants (i.e., three times more often than the correct option). Another 5% (95% CI, 3%–7%) of respondents selected the option whose formalization mirrors the correct definition of VE while incorrectly focusing on individuals who do not develop Covid-19. Finally, 3% (95% CI, 1%–5%) of participants chose the “Other” option, none of whom went on to furnish the correct answer.

Of the 14 participants who had participated in a medical trial, eight chose the target error; two, the option that indicated the difference between the rate of individuals who do not develop and who do develop Covid-19 among those vaccinated; and four, one each of the remaining four classes. No statistical difference in the distribution of choices was observed between lower- and higher-educated participants, ꭓ²(5, N = 300) = 8.39, p = .136, nor between males and females, ꭓ²(5, N = 300) = 3.81, p = .577.

3.2. Experiment 2

The second experiment was designed to replicate and extend the results of the first by polling a different population of participants, as well as by excluding the possibility that selections of the target error option in the multiple-choice question of Experiment 1 were boosted by the fact that it was the shortest-available option.

3.2.1. Setting

Online data collection was carried out April 29 – May 4, 2021, through Prolific Academic (http://prolific.ac). As with previous experiments, there were no time limits on task completion, and participants received 0.63 British pounds compensation. The average response time was 3 minutes.

3.2.2. Participants

We recruited a new sample of 600 participants: 300 UK residents, and 300 Italian residents, all native speakers of English or Italian, respectively. The mean age of participants was 32 years (SD = 12.1), ranging from 18 to 74 years (2 participants did not declare their ages). The UK sample was found to be significantly older than the Italian sample (M _age = 37, SD = 13.6 vs. M _age = 27, SD = 7.9, t(596) = 10.89, p < .001). Across countries, females constituted 51.5% (53% and 47% in the UK and Italian samples, respectively), and 55% of participants had either an undergraduate or graduate degree (56% and 55% in the UK and Italian samples, respectively). As reported in Table 3 , the two samples differed with respect to their SARS-CoV-2 vaccination status: 42% of UK participants had already received at least one dose of vaccine versus 13% of Italian participants. In both samples, the greatest number had not yet been vaccinated but intended to receive it (47% and 76% of the UK and Italian participants, respectively), while less than 6% of respondents indicated one of the following: undecided, unable or unwilling to receive the vaccine. Overall, 13% of participants (11 UK participants and 64 Italian participants) reported that they had participated in a medical trial.

Table 3.

SARS-CoV-2 vaccination status of participants of Experiments 2 and 3.

Vaccination status	Experiment 2			Experiment 3
	UK	Italy	Overall	UK	Italy	Overall
	N (%)	N (%)	N (%)	N (%)	N (%)	N (%)
Already received	127 (42)	38 (13)	165 (27)	153 (52)	33 (11)	186 (31)
Intend to receive	141 (47)	229 (76)	370 (62)	109 (37)	242 (80)	351 (59)
Still deciding	16 (6)	18 (6)	34 (6)	19 (6)	15 (5)	34 (6)
Cannot receive	4 (1)	7 (2)	11 (2)	3 (1)	7 (2)	10 (2)
Do not intend to receive	12 (4)	8 (3)	20 (3)	12 (4)	7 (2)	19 (2)

3.2.3. Design and stimuli

Participants were presented with the following prompt:

In a rigorous clinical study, scientists found that a vaccine for Covid-19 has an efficacy of 90%.

Please think about how you believe scientists arrived at this figure until the next page appears.

After 30s, the following multiple-choice question appeared (bolded as in the presented text; the order of the response options was randomized):

In my understanding, the scientists arrived at this 90% figure by computing:

(Please select the alternative which reflects your own interpretation based on what you know right now, without asking anyone else or searching online.)

• □ The percentage of individuals who did not develop Covid-19 among those vaccinated

• □ The percentage of individuals who did not develop Covid-19 among those vaccinated minus the percentage of individuals who did develop Covid-19 among those vaccinated

• □ The percentage of individuals who did develop Covid-19 among those not vaccinated minus the percentage of individuals who did develop Covid-19 among those vaccinated, divided by the former percentage

• □ The percentage of individuals who did not develop Covid-19 among those vaccinated minus the percentage of individuals who did not develop Covid-19 among those not vaccinated, divided by the latter percentage

• □ The difference between the percentages of individuals who did not and who did develop Covid-19 among those vaccinated minus the difference between the percentages of individuals who did not and who did develop Covid-19 among those not vaccinated

• □ The percentage of individuals who were vaccinated among those who did not develop Covid-19

• □ The percentage of individuals who were not vaccinated among those who did develop Covid-19

• □ Other (if you select this option, you will be asked to specify your answer)

Compared to the multiple-choice task of Experiment 1, three changes were introduced. First, an interval of 30s was imposed between the appearance of the initial statement about the VE and the subsequent question and response options. This was intended to allow participants to independently consider the meaning of VE before seeing the response options. Second, the question and the response options were rephrased from the present tense, using the past instead, in order to emphasize that the efficacy figure described was the result of a clinical trial. Finally, and most importantly, two new incorrect options were added to the six previously employed. This was designed to check for, and possibly to eliminate, a potential response bias in the multiple-choice task of Experiment 1, in which the target error was also the shortest statement. The two new options (the second and third from the bottom in the above list) had lengths comparable to that of the target error and, as with all the other options in the list, could technically be computed from the data of a phase 3 clinical trial (in that they are directly quantifiable from ARU and ARV).

3.2.4. Results

The results of Experiment 2 are reported in Table 4 . Overall, the correct option was selected by 8% (95% CI, 6%–10%) of participants. Yet again, the most-popular choice (32%; 95% CI, 28%–36%; significantly greater than chance, z = 12.4, p < .001) was the percentage of individuals who did not develop Covid-19 among those vaccinated (i.e., the target error, 1 – ARV). (Chance was set at 14% to account for seven detailed, alternative options.) As in Experiment 1, the second- (23%; 95% CI, 20%–26%) and the third-most-frequent (20%; 95% CI, 17%–23%) errors comprised, respectively, the option that outlines the difference between the rate of individuals who did not develop and who did develop Covid-19 among those vaccinated (the second option in the above list), and the option detailing the difference between the difference in the rates of vaccinated individuals who did not and who did develop Covid-19 and the difference in the rates of unvaccinated individuals who did not and who did develop Covid-19 (the fifth and longest option in the above list). The proportion of selection of each of these two options was also greater than chance (z = 6.1, p < .001, and z = 4, p < .001, for the second- and third-most-frequent errors, respectively); nevertheless, they were both selected less often than the target error (z = −2.85, p < .01 and z = −4.2, p < .001, respectively). The two new options referring to the percentage of individuals who were vaccinated among those who did not develop Covid-19, and to the percentage of individuals who were not vaccinated among those who did develop Covid-19 were selected by 8% (95% CI, 6%–10%) and 1% (95% CI, 1%–2%) of participants, respectively.

Table 4.

Frequencies and percentages for the multiple-choice options of Experiment 2 (bolded as in the presented text), with corresponding formulas (not included in the presented text).

Response	UK	Italy	Overall
	N (%)	N (%)	N (%)
The percentage of individuals who do not develop Covid-19 among those vaccinated  1 – ARV [Target error]	96 (32)	96 (32)	192 (32)
The percentage of individuals who did not develop Covid-19 among those vaccinated minus the percentage of individuals who did develop Covid-19 among those vaccinated  (1 – ARV) – ARV	64 (21)	76 (25)	140 (23)
The difference between the percentages of individuals who did not and who did develop Covid-19 among those vaccinated minus the difference between the percentages of individuals who did not and who did develop Covid-19 among those not vaccinated  ((1 – ARV) – ARV) – ((1 – ARU) – ARU)	57 (19)	63 (21)	120 (20)
The percentage of individuals who did develop Covid-19 among those not vaccinated minus the percentage of individuals who did develop Covid-19 among those vaccinated, divided by the former percentage  (ARU – ARV) /ARU [Correct response]	20 (7)	29 (10)	49 (8)
The percentage of individuals who were vaccinated among those who did not develop Covid-19  (1 – ARV) / ((1 – ARV) + (1 – ARU))	31 (10)	14 (5)	45 (8)
The percentage of individuals who did not develop Covid-19 among those vaccinated minus the percentage of individuals who did not develop Covid-19 among those not vaccinated, divided by the latter percentage  ((1 – ARV) – (1 – ARU)) / (1 – ARU) = (ARU – ARV) / (1 – ARU)	26 (9)	15 (5)	41 (7)
The percentage of individuals who were not vaccinated among those who did develop Covid-19  (ARU) / (ARU + ARV)	3 (1)	4 (1)	7 (1)
Other	3 (1)	3 (1)	6 (1)
Total	300 (100)	300 (100)	600 (100)

No significant difference in the distribution of responses was observed between UK and Italian participants, ꭓ²(7, N = 600) = 12.50, p = .085, among participants with a different vaccination status, ꭓ²(28, N = 600) = 32.73, p = .246, between participants with higher and lower education levels, ꭓ²(7, N = 600) = 4.28, p = .747, between participants who had participated in a medical trial and those who had not, ꭓ²(7, N = 600) = 6.10, p = .528, nor between males and females, ꭓ²(7, N = 600) = 7.10, p = .419.

Overall, the results of our first two experiments converge in indicating that a significant portion of laypeople misunderstands VE as 1 – ARV. This error appears to be genuine and not a consequence of the relative complexity of the correct answer. Indeed, the results of the open-ended question were confirmed by those of the two multiple-choice questions, in which the correct answer emerged as one of the two least-popular options, even when compared to longer and more-convoluted alternatives.

4. Confusion of vaccine efficacy with the non-incidence rate among vaccinees: behavioral implications

In this section, we present the results of a third empirical investigation, which illustrates, in terms of vaccine acceptance, the potential implications of the misinterpretation of VE documented in Experiments 1 and 2. Specifically, we compared, in samples of UK and Italian participants, the behavioral intention to receive a vaccine for a hypothetical new variant of the SARS-CoV-2 virus, as well as the attitude toward such a vaccine, when vaccine benefits were conveyed either with VE or with the corresponding non-incidence rate among vaccinees, i.e., 1 – ARV. For an illustration, see Fig. 2 .

Fig. 2.

VE and corresponding 1 – ARV values for fixed values of ARU (20%) and different values of ARV (from 2% to 10%).

Based on the results of Experiments 1 and 2, our prediction was that, by misinterpreting VE as 1 – ARV, participants would underestimate vaccine benefits (at least for non-negligible values of ARV), and that, consequently, the presentation of the benefits in terms of VE rather than 1 – ARV would be associated with a weaker intention to receive the vaccine, as well as with a less-positive attitude toward the vaccine.

4.1. Experiment 3

4.1.1. Setting

Online data collection was carried out April 30 – May 5, 2021, through Prolific Academic (http://prolific.ac). Again, there were no time limits on task completion, and participants received 0.63 British pounds compensation. The average response time was 2 minutes.

4.1.2. Participants

We recruited a new sample of 600 participants: 296 UK residents and 304 Italian residents, all native speakers of English or Italian, respectively. The mean age of participants was 34 years (SD = 12.9), ranging from 18 to 77 years (2 participants did not declare their ages). As in Experiment 2, the UK sample was found to be significantly older than the Italian sample (M _age = 40, SD = 13.5 vs. M _age = 27, SD = 8.1, t(596) = 14.48, p < .001). Across countries, females constituted 47% (50% and 44% in the UK and Italian samples, respectively), and 51% of participants had either an undergraduate or graduate degree (54% and 47% in the UK and Italian samples, respectively). As in Experiment 2, the samples recruited in the two countries differed in SARS-CoV-2 vaccination status: 52% of UK participants versus 11% of Italian participants had already received at least one dose of the vaccine, while the percentages of those unvaccinated who intended to receive the vaccine were 37% and 80%, respectively, with less than 6% of participants selecting each of the following responses: undecided, unable or unwilling to receive the vaccine.

4.1.3. Design and stimuli

This experiment employed a 2 × 2 (information type: VE vs. 1 – ARV; ARV level: 2% vs. 8%) between-subjects design. All participants were presented with the following scenario:

Imagine that a new variant of the virus that causes Covid-19 has emerged.

This variant spreads more easily than previous variants of the virus and is estimated to afflict approximately 20% of people in your region by the end of the summer.

Studies indicate that the antibodies generated by current vaccines or prior infections with Covid-19 are ineffective against the new variant.

However, scientists have developed a new vaccine to address the new variant.

This vaccine meets regulatory safety standards and it does not negatively interact with previous vaccinations.

We employed an extremely high incidence rate (ARU = 20%) to encourage participants to think of this hypothetical variant of SARS-CoV-2 as a major threat. As a consequence, for the difference between VE and 1 – ARV to span a wide-enough range, ARV also had to be unusually high (from 2% to 8%). Note, however, that as shown in Fig. 1, similar differences can be found for lower values of ARU and, consequently, ARV.

Fig. 1.

Depicted is the difference between 1 – ARV and VE. The left plot reports the difference between 1 – ARV and VE as a function of ARU, with each curve representing a different value of ARV (from 1% to 50%). The right plot reports the difference between 1 – ARV and VE as a function of ARV, with each curve representing a different value of ARU (again from 1% to 50%). In all cases ARV is assumed never to exceed ARU.

In accordance with the experimental condition, participants were then presented with one of the following messages:

[Type of information: VE]

In a rigorous clinical study carried out in your region, scientists found that the new vaccine has an efficacy of 90% [60%].

[Type of information: 1 – ARV]

In a rigorous clinical study carried out in your region, scientists found that 98% [92%] of individuals vaccinated with the new vaccine do not develop Covid-19.

After reading one of the statements above, participants’ intentions to receive the vaccine were measured, along with their attitudes toward the vaccine. For intention to receive the vaccine, the question (adapted from Nan et al., 2012) read:

If this vaccine against the hypothetical new variant of the Covid-19 virus were available and offered to you, would you choose to receive it?

Participants responded on an 11-point scale anchored by “definitely no” (0) and “definitely yes” (10), so that higher scores indicated greater intention to receive the vaccine. The middle point was labelled as “unsure” (6).

Participants’ attitudes toward the vaccine were assessed by asking them to rate the following statement

“If you were to accept this vaccination against the hypothetical new variant of the Covid-19 virus, it would be”

on three 0–5 semantic differential items: foolish/wise, harmful/beneficial, bad/good (a measure adapted from Abhyankar et al., 2008). The scores were then averaged to form an index for the general attitude toward the new vaccine (Cronbach's α = 0.93, M = 8.55, SD = 2.03), where higher scores indicate a more favorable attitude. After data collection, a final screen reminded participants that the variant of the virus described in the scenario was hypothetical.

4.1.4. Results

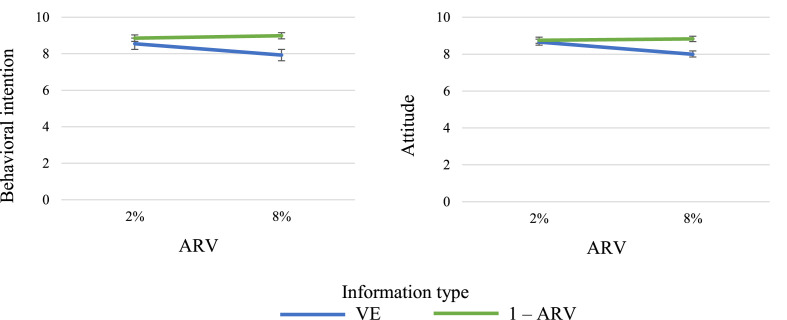
To test the hypothesis that information type and ARV level affected participants' behavioral intentions, we ran an ANOVA including the two factors as independent variables, with age, gender, education level, vaccination status (codified as 1 = yes or intend to receive; 2 = undecided; 3 = cannot receive; 4 = do not intend to receive), country, and having participated in a clinical trial as covariates. Results showed a significant main effect of information type, F(1, 585) = 15.82, p < .001, η_p ² = 0.03, a main effect of ARV level, F(1, 585) = 4.85, p < .028, η_p ² = 0.01, and an interaction effect between information type and ARV level, F(1, 585) = 6.66, p = .010, η_p ² = 0.01. Participants' intentions to vaccinate were, not surprisingly, greater when ARV was 2% than when 8% (M = 8.70, SD = 2.3 vs. M = 8.45, SD = 2.4), and, as predicted, greater when the information about the benefits of the vaccine was presented in terms of 1 – ARV, rather than when presented in terms of VE (M = 8.92, SD = 2.1 vs. M = 8.24, SD = 2.4). As can be observed in Fig. 3 , the significant interaction indicates that the information type was crucial for only the higher value of ARV. The sole covariate that significantly affected participants' intentions to receive the vaccine was their vaccination status (p < .001), in the plausible direction of a greater intention among those who had already received or intended to receive an existing SARS-CoV-2 vaccine. The same analysis was performed on participants’ attitudes toward the vaccine, and the results hewed closely to those obtained for intention. In particular, participants showed more favorable attitudes toward the vaccine when the ARV level was 2% than when it was 8% (M = 8.70, SD = 2.0 vs. M = 8.40, SD = 2.1, F(1, 585) = 6.33, p = .012, η_p ² = 0.01), and more favorable when they were provided with 1 – ARV information than VE information (M = 8.79, SD = 1.9 vs. M = 8.21, SD = 2.1, F(1, 585) = 7.27, p = .007, η_p ² = 0.01). As revealed by the significant interaction effect (F(1, 585) = 6.53, p = .011, η_p ² = 0.01), again, the difference between the two information types was relevant when ARV was 8% but not when it was 2% (see Fig. 3).

Fig. 3.

Results of Experiment 3. Mean behavioral intention to receive the vaccine (left panel) and mean attitude toward it (right panel) in the four conditions of Experiment 3 (ARU = 20%). Error bars represent standard errors of mean (± SEM).

Overall, the results of Experiment 3 indicated that, for both the UK and the Italian participants, vaccine benefits presented in terms of 1 – ARV rather than VE were associated with a greater intention to receive the vaccine and a more-positive attitude toward it when the ARV level was 8% but not when it was 2%. Because ARU = 20% in our scenarios, these two cases correspond to a difference between 1 – ARV and VE of 32% and 8%, respectively. As shown in the left panel of Fig. 1, appreciable differences between 1 – ARV and VE can also be obtained with lower values of ARV whenever they are associated with lower values of ARU. For example, in a more likely scenario in which ARU = 5%, then an ARV = 2% would mean a difference between 1 – ARV and VE of 38%.

5. General discussion

Scientists and health authorities agree that mass vaccination against Covid-19 offers the most promising strategy by which to reduce deaths and, ultimately, to bring the pandemic under control (Yamey et al., 2020; UNICEF, 2021). Yet they also warn that incidence of the disease will be lowered only if a substantial portion of the population is inoculated (Liu et al., 2020; Peretti-Watel et al., 2020; WHO, 2020). With this objective in mind, serious concerns have emerged from a number of recent studies (Paul et al., 2020; Reiter et al., 2020; Sherman et al., 2020; Troiano and Nardi, 2021) that indicate a vaccine acceptance rate far too low to achieve herd immunity. Vaccine hesitancy is a complex phenomenon that depends on various factors, including socio-cultural, political, and economic considerations (Larson et al., 2014, 2018; MacDonald, 2015). In the case of SARS-CoV-2 vaccination, the major determinants of uncertainty or unwillingness to vaccinate have been reported to belong to the confidence domain, that is, a lack of trust in the safety and benefits of vaccines (Sherman et al., 2020; Troiano and Nardi, 2021; Pogue et al., 2020; Taylor et al., 2020; Wong et al., 2020). In our study, we considered only the perception of benefits and, more specifically, the public's understanding of VE, and we did not explore concerns about vaccine safety, itself a multifaceted issue that might well both interact with the perceived efficacy and heavily affect vaccine uptake.

Our results highlight a major problem in the communication of VE information: despite a worldwide campaign that aims to present nearly every person with the choice of whether or not to accept a SARS-CoV-2 vaccination, almost all participants in Experiments 1 and 2 were unaware of the meaning of VE, often confusing it with the non-incidence rate among the vaccinated (i.e., 1 – ARV). A generic accounting of this error as arising from the complexity of the definition of VE appears to be disconfirmed by the limited number of vague responses to an open-ended question and, above all, by the non-random distribution of incorrect responses in two multiple-choice questions. Misinterpretation of VE was, on the contrary, systematic and aligned with our expectations based on misreports in the media: it proved robust across gender, education level, and previous experience with medical trials; across the open-ended question and both multiple-choice questions, which differed slightly in wording and number of alternatives; as well as across countries, whose participants differed at least in native language, vaccination status and mean age. We also formally demonstrated that the misunderstanding of VE as 1 – ARV leads to a systematic undervaluation of the personal safety benefits of the vaccine. Accordingly, in Experiment 3, we showed that this may significantly undermine the general positive attitude toward new vaccines, as well as the intention to get vaccinated — even in individuals who have already accepted or have decided to accept a current SARS-CoV-2 vaccination, as have some participants in our experiment. It is worth highlighting that Experiment 3 data collection was carried out in a moment in which, in both the UK and Italy, vaccination campaigns were leading to a significant decrease in the infection rate, and authorities were contemplating loosening social-distancing restrictions. These circumstances might have decreased vaccine skepticism and, consequently, the impact of the documented error on the perceived benefits of vaccines. More studies are needed to quantify the role of this error in vaccine hesitancy in non-hypothetical scenarios involving real choices, possibly across different periods of time.

The finding that people routinely misunderstand statistical information about the benefits of various screening tests and treatments, including vaccination, is not new. In particular, it is well-known that laypeople, and even health professionals, tend to evaluate more favorably benefits expressed in terms of relative, rather than absolute, risk reductions, since they appear to be larger (Akl et al., 2011; Bodemer et al., 2014; Gigerenzer, 2014). This effect has been shown to depend on the size, availability and intelligibility of the baseline risk (e.g., Bodemer et al., 2014; Sorensen et al., 2008), and can be considered an expression of a more general tendency to discount prior probability information (base rate fallacy, Kahneman and Tversky, 1973; Pighin and Tentori, 2020). The error documented in this study, however, is of a different, more substantial stripe. Indeed, when asked to interpret a relative risk reduction (VE), our participants not only failed to normalize the difference between the incidence in the control and treatment groups by the baseline risk, but, as noted in the Results section, they disregarded the incidence in the control group entirely. In this respect, the persistence of the error in the multiple-choice context is particularly striking, given that the corresponding option was one of few available that did not mention unvaccinated individuals. Also remarkable is that the second-most-frequent error in both Experiments 1 and 2, was the selection of the other option that referred exclusively to vaccinated individuals.

The result that laypeople tend to ignore the role and importance of a control group in vaccine testing — even those who have participated in a controlled clinical trial and would presumably be more mindful of this factor — is a noteworthy result unto itself. By focusing on the experimental group (i.e. vaccinees) alone, laypeople appear to disregard the importance of having a term of comparison (i.e. non-vaccinees) in order to draw any reliable conclusion about the intervention (i.e. the vaccination). Such neglect of a prerequisite for a rigorous medical investigation may well affect the perceived reliability of its conclusions. Indeed, the apparent lack of basic understanding of how interventions are related to health outcomes precludes distinguishing causal evidence from other categories of empirical evidence, or even non-scientific opinions. Future research might explore in greater depth this hypothesis and investigate whether and to what extent neglect of a control group plays a role in the perceived reliability of VE figures and, ultimately, in the persistence of low confidence in the safety and benefits of vaccines in spite of scientific data supporting them.

Importantly, we are left with the question of why laypeople confuse VE with the non-incidence rate among the vaccinated. An exhaustive explanation of this error is beyond the scope of this paper, in which we limit deliberation to a general consideration and a suggestion. Although there is no doubt that such confusion is an error, the interest in 1 – ARV is not altogether misplaced, in that it represents a piece of information about individual risk that is not expressed by VE alone. Consider, for illustrative purposes, two vaccines that reduce, with the same efficacy VE₁ = VE₂ = 60%, the incidence of two syndromic diseases, which have broadly different incidences ARU₁ = 0.25% and ARU₂ = 25%. These values would correspond to 1 – ARV₁ = 99.9% and 1 – ARV₂ = 90%, respectively. It would appear entirely rational for an individual, in pursuit of precautionary behavior, to be interested in discriminating between these two cases, i.e., in knowing whether her probability of developing the disease when vaccinated is on the order of 0.1% or 10%. Providing both values corresponding to 1 – ARV and VE, alongside lay explanations of how they are obtained, would improve comprehension and retention of critical information about vaccines and would facilitate broad adoption. This could indeed serve two purposes: preventing the public from confusing them and helping the public to correctly evaluate (rather than overestimate) the risk of developing a target condition when vaccinated. To what extent the confusion between these two variables may discourage real vaccine compliance remains to be empirically explored, as does the question of whether people would trust vaccines more if they were to recognize the role of a control group in vaccine testing. We contend that some segment of the population will always accept a vaccination, while another portion will always refuse. But, as suggested by various studies (Pogue et al., 2020; Taylor et al., 2020; Wong et al., 2020; Orenstein et al., 1985), as well as by the results of our Experiment 3, some number among the persuadable segment between these two extremes may well be swayed by clearer and more complete information on the benefits of accepting the vaccine.

Data availability statement

Data are available upon request. The authors support data sharing and queries in this regard can be addressed to the corresponding author.

Credit author statement

Katya Tentori: Conceptualization, Methodology, Investigation, Writing-Original draft preparation Writing-Reviewing and Editing. Andrea Passerini: Methodology, Visualization, Writing-Reviewing and Editing. Benjamin Timberlake: Investigation, Writing-Reviewing and Editing. Stefania Pighin: Conceptualization, Methodology, Investigation, Data curation, Writing-Reviewing and Editing.

Declaration of competing interest

None declared.

Appendix.

Examples of answers (open-ended question, Experiment 1)

Class of answer		Examples
Target error
	Compatible with both interpretations	“It will work for 90% of the people that are vaccinated”
	P(not-D|V)	“90% of people vaccinated do not show symptoms of Covid-19″
	P(not-D|V&E)	“Out of 100 vaccinated people exposed to Covid-19, 90 people will not contract the disease”
Reiterations or vague answers		“It is mostly successful”
Comments		“90 isn't good enough, medicine needs to be 99.9″
Other errors		“It stops 90% from dying”
Mixed answers		“90% of the people that receive the vaccine will be protected from contracting coronavirus compared to a group that is not vaccinated”
Correct responses		“The number of people diagnosed with Covid-19 is reduced by 90% in the vaccinated group compared to the control group”

Additional criteria (open-ended question, Experiment 1)

No distinction was made between numerically equivalent expressions articulating:

• - single-case (e.g., “There is a 90% chance of the vaccine working”) or frequency (e.g., “The vaccine works on 90 out of 100 people”) formats;

• - complementary outcomes (e.g., “The vaccine works in 90% of cases, it doesn't work in 10% of people”), a single positive outcome type (e.g., “The vaccine works on 90% of people”), or a negative outcome type (e.g., “The vaccine won't work for 10% of people”);

• - the understanding of the action of the vaccine as generic (e.g., “The vaccine works on 90 out of 100 people”) or as targeting infection, disease, or transmission (e.g., “The vaccine is effective in preventing the virus in 90% of people treated with it” or “In 90% of cases tested, the vaccine successfully prevented Covid-19”);

• - in the past tense the understanding of the efficacy of the vaccine, which apparently referred to the controlled study (e.g., “90% of people who received the vaccine did not get Covid-19”), or in present/future tenses the effectiveness of the vaccine, which presumably referred to the real world (e.g., “90% of people who receive the vaccine will not develop Covid-19”).