Gene-Based Association Testing of Dichotomous Traits With Generalized Functional Linear Mixed Models Using Extended Pedigrees: Applications to Age-Related Macular Degeneration

Abstract

Genetics plays a role in age-related macular degeneration (AMD), a common cause of blindness in the elderly. There is a need for powerful methods for carrying out region-based association tests between a dichotomous trait like AMD and genetic variants on family data. Here, we apply our new generalized functional linear mixed models (GFLMM) developed to test for gene-based association in a set of AMD families. Using common and rare variants, we observe significant association with two known AMD genes: CFH and ARMS2. Using rare variants, we find suggestive signals in four genes: ASAH1, CLEC6A, TMEM63C, and SGSM1. Intriguingly, ASAH1 is down-regulated in AMD aqueous humor, and ASAH1 deficiency leads to retinal inflammation and increased vulnerability to oxidative stress. These findings were made possible by our GFLMM which model the effect of a major gene as a fixed mean, the polygenic contributions as a random variation, and the correlation of pedigree members by kinship coefficients. Simulations indicate that the GFLMM likelihood ratio tests (LRTs) accurately control the Type I error rates. The LRTs have similar or higher power than existing retrospective kernel and burden statistics. Our GFLMM-based statistics provide a new tool for conducting family-based genetic studies of complex diseases. Supplementary materials for this article, including a standardized description of the materials available for reproducing the work, are available as an online supplement.

1. Introduction

Age-related macular degeneration (AMD) is a common complex disease that leads to irreversible vision loss in the elderly and afflicts almost 10 million individuals in the United States (Friedman et al. 2004). AMD is caused by an interaction of aging, genetics, and environmental/nutritional factors (Fritsche et al. 2014). Family-based linkage studies detected major susceptibility loci for AMD on chromosomes 1 and 10 (Fisher et al. 2005). Using population data, dozens of disease-causing genes and hundred of mutations have been discovered by genome-wide association studies (Age-Related Eye Disease Study Research Group 1999; Seddon et al. 2007; Chen et al. 2010; Neale et al. 2010; Fritsche et al. 2013, 2016). However, no gene-based association studies have been performed to dissect AMD using family data so far, although next-generation sequencing technologies provide massive data resources, such as those of whole genome sequencing (WGS) and whole exome sequencing (WES) which are rich resources to search for causal genetic variants of complex disorders (Abecasis et al. 2012; Tennessen et al. 2012; Lek et al. 2016). To accommodate family data, we develop generalized functional linear mixed models (GFLMM) and related software in this work to analyze a dichotomous trait for sequencing data. We apply the GFLMM to a real exome chip dataset to identify AMD associated susceptibility genes (Weeks et al. 2000, 2004).

Although rich data resources are available and a data-intensive and data-driven analysis era is coming, powerful and computationally efficient statistical methods and related software are needed to test for association between complex traits and variants, to screen for causal variants and to reduce false positives and to properly deal with high dimensionality (Bansal et al. 2010; Kiezun et al. 2012). Few statistical methods are available to analyze extended pedigrees for sequencing studies. For family data, one needs to take pedigree structure into account to model correlations of pedigree members. To control for population structure and familial or cryptic relatedness in genome-wide association studies (GWAS) while analyzing common variants, mixed models were developed for association studies and gained popularity due to their ability to control false positive rates and their good power performance (Henderson 1984; Price et al. 2006; Yu et al. 2006; Aulchenko, De Koning, and Haley 2007; Zhao et al. 2007; Kang et al. 2008; Astle and Balding 2009; Kang et al. 2010; Zhang et al. 2010; Lippert et al. 2011; Yang, Lee, et al. 2011; Yang, Weedon, et al. 2011; Korte et al. 2012; Listgarten et al. 2012; Segura et al. 2012; Svishcheva et al. 2012; Zhou and Stephens 2012; Listgarten, Lippert, and Heckerman 2013; Pirinen, Donnelly, and Spencer 2013; Yang et al. 2014; Zhou and Stephens 2014; Hayeck et al. 2015; Loh et al. 2015; Song, Hao, and Storey 2015; Chen et al. 2016). To our knowledge, the mixed models developed so far cannot be directly applied to the analysis of rare variants or a combination of rare and common variants. Here, a variant is considered rare if its minor allele frequency (MAF) is less than or equal to 0.03 (the cutoff can be different in certain circumstances). There is a need to develop statistical methods to analyze next-generation sequencing data which may contain rare and common variants for familial data and may correct for population stratification.

In recent years, a class of fixed effect models has been developed for unrelated samples to test for region-based or gene-based association between a quantitative/dichotomous/survival trait and genetic variants in a region or within a gene (Cordell and Clayton 2002; Luo, Boerwinkle, and Xiong 2011; Luo, Zhu, and Xiong 2012, 2013; Fan et al. 2013, 2014, 2015; Vsevolozhskaya et al. 2014, 2016; Zhang, Boerwinkle, and Xiong 2014; Svishcheva, Belonogova, and Axenovich 2015; Wang et al. 2015; Fan, Chiu, et al. 2016; Fan, Wang, Chiu, et al. 2016; Fan, Wang, Yan, et al. 2016; Zhao, Zhu, and Xiong 2016). Since gene boundaries can be defined at the transcript level, gene-based can be changed to transcript-based. To simplify our presentation, we only use terminology gene-based hereafter and one may change it to region-based or transcript-based. The fixed effect models can be functional regression models or traditional additive models. In functional regression models, genotyping data are viewed as a realization of a stochastic process that varies along a chromosome region (Ross 1996). Using functional data analysis techniques, it is natural to summarize an individual’s genetic information as a stochastic function (de Boor 2001; Ramsay and Silverman 2005; Ramsay, Hooker, and Graves 2009; Ferraty and Romain 2010; Horvath and Kokoszka 2012). An individual’s discrete genotypes can be used to estimate his/her genetic variant function (GVF) using a collection of smooth basis functions. The trait variable is related to the GVF while adjusting for covariates to build theoretical functional regression models. By using functional data analysis techniques, the theoretical functional regression models are revised to be ordinary regression models which can be used to test for association between the traits and the genetic variants. One advantage of the functional regression models is that they can properly reduce the high dimensionality of the sequencing data to draw useful information. In short, functional models turn the curse of dimensionality of sequencing data to be a blessing.

In genetics, a “major” gene has a relatively large effect on the trait. In contrast, a polygene means a gene where the effects of variants within the gene are small and the effects are likely in a similar scale across the gene region (Lange 2002). When genetic effects are relatively large (i.e., a major gene), the effects of variants are unlikely to be constant across the gene region, and it is reasonable to model genetic effects as a fixed function as in functional regression models (Luo, Boerwinkle, and Xiong 2011; Luo, Zhu, and Xiong 2012, 2013; Fan et al. 2013, 2014, 2015; Vsevolozhskaya et al. 2014, 2016; Svishcheva, Belonogova, and Axenovich 2015; Wang et al. 2015; Fan, Wang, Chiu, et al. 2016; Fan, Wang, Yan, et al. 2016). For polygenic effects, it is reasonable to model the genetic effects as a random variable with a mean of zero and a constant variance as is done by the sequence kernel association tests (SKAT), its optimal unified tests (SKAT-O), and a combined sum test of rare and common variants (SKAT-C) (Wu et al. 2011; Lee et al. 2012; Ionita-Laza et al. 2013a). The fixed effect models have similar or higher power than SKAT procedure to analyze major genes while SKAT procedure performs better in analysis of polygenes (Fan, Chiu, et al. 2016).

In association analysis, we mainly search for major genes. We argue that the regression models which treat major gene’s contribution as fixed effects are more appropriate in association analysis. In addition to major genes, geneticists have long known of the existence of polygenes. The functional models and SKAT procedure are complimentary to each other. Moreover, the functional models are well-suited for analyzing next-generation sequencing data since they can be used to analyze: (1) rare variants; (2) common variants, and (3) a combination of the two. This motivates us to extend the unrelated population-based fixed models to analyze related pedigree data.

In the literature, the research to analyze rare variants on general extended families for dichotomous traits focuses on kernel and collapsing/burden tests (De et al. 2013; Ionita-Laza et al. 2013b; Schaid et al. 2013; Wang et al. 2013; Svishcheva, Belonogova, and Axenovich 2014; Yan et al. 2015; Fernandez et al. 2018). The kernel and collapsing/burden tests are good to analyze polygenes but less powerful to analyze major genes which have relatively large effects on the traits (Fan, Chiu, et al. 2016).

Motivated by the need to analyze family AMD data, we develop gene-based GFLMM by extending the generalized functional linear models previously discussed for population data (Cordell and Clayton 2002; Fan et al. 2014). The GFLMM model the major gene effect as a fixed mean, the polygenic contributions as a random variation, and the correlations between pedigree members by kinship coefficients. We then test for association between the dichotomous trait and the genetic variants by testing if the fixed mean is zero using likelihood ratio test (LRT) statistics. To assess the behavior of our GFLMM LRT statistics and to make sure the methods can be used to analyze AMD family data, we conduct simulation studies to evaluate Type I error rates and power, and compare our statistics with prominent statistical methods from the literature (Schaid et al. 2013).

2. Applications to AMD Pedigree Data

Our goal is to analyze real exome chip data from the UCLA/Pittsburgh family-based study of AMD which include extended pedigrees (Weeks et al. 2000, 2004). To analyze the AMD pedigree data, we use GFLMM and build related LRT statistics (Section 3).

2.1. AMD Pedigree Data

In the AMD studies, an individual was considered affected with AMD according to the “C” diagnostic scheme previously defined (Weeks et al. 2000, 2004); an individual was considered unaffected if they were unaffected and at least 65 years old at last exam. After sample quality checks using a thorough and rigorous data cleaning pipeline (Laurie et al. 2010), which included checks for chromosomal aberrations, gender, Hardy–Weinberg equilibrium, relatedness, duplicates, and genotype quality, 976 genotyped individuals of European ancestry were available for analysis. To completely connect pedigrees, we included non-genotyped individuals who shared the same family with those 976 genotyped individuals. The connected pedigrees contained 2727 pedigree members, 1275 with a known AMD trait (1031 affected and 244 unaffected). A total number of 111,547 autosomal variants were included in the study; 30,096 were common (MAF > 0.05), and 81,451 were rare (MAF ≤ 0.05). In the analysis, we adjusted for gender since it is significantly associated with AMD in the null model (p-value = 0.00197).

2.2. Application to AMD Data

As we were interested in the possibility that different transcripts might convey different risk for AMD, we carried out transcript-based tests to investigate AMD susceptibility genes on autosomes using the LRT statistics, the retrospective kernel-based and burden tests (Schaid et al. 2013). Gene boundaries were defined at the transcript level and sets of transcripts that shared identical boundaries were only tested once. Tests were conducted in two different ways. First we considered a combination of common and rare variants, and tested a total number of 16,913 autosomal transcripts at a genome-wide significance threshold of 2.96 × 10⁻⁶ after Bonferroni correction. We next excluded all common variants, and focused on the genes having at least two polymorphic rare variants. A total number of 14,961 transcripts were tested, associated with a significance threshold of 3.34 × 10⁻⁶ after Bonferroni correction.

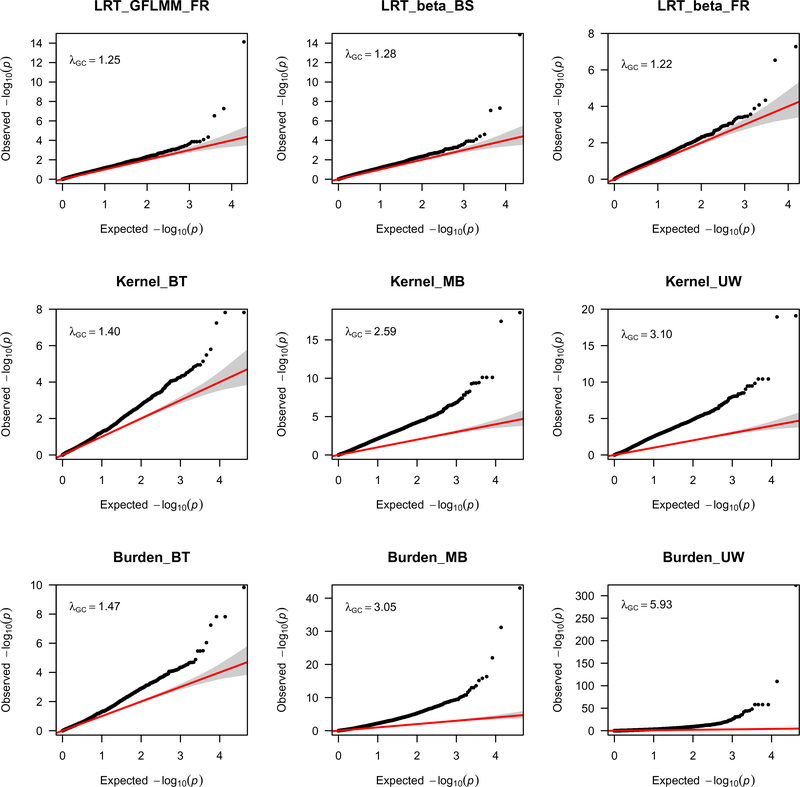
Table 1 showed significant and suggestive significant signals for the AMD data. Only the results of the LRT GFLMM statistics (6) were shown (as these converged more often than LRT GFLMM statistics (5) did). For the analysis of the common and rare variants, we confirmed that strong association was detected between AMD and CFH and ARMS2, two known AMD susceptibility genes (Table 1). The kernel and burden tests except kernel_BT and burden_BT reached genome-wide significance (see the p-values in bold associated with CFH and ARMS2 in Table 1).

Table 1.

Results of association analysis of age-related macular degeneration data.

Rare and common variants

LRT statistics of mixed models

Schaid’s methods

Chr

Gene

Start

End

Number of variants

GFLMM (6)

Kernel-based tests

Burden tests

B-sp basis

Fourier basis

kernel_BT

kernel_MB

kernel_UW

burden_BT

burden_MB

burden_UW

1

CFH

196621007

196716634

15

8.30 × 10−8

2.94 × 10−7

2.86 × 10−2

2.76 × 10−19

1.16× 10−19

1.53 × l0−1

7.02 × 10−16

1.07 × 10−19

196621007

196670695

3

4.84 × 10−8

5.30 × 10−8

3.65 × l−1

3.81 × 10−18

8.09 × 10−20

5.35 × l0−1

2.67 × 10−14

4.87 × 10−19

10

ARMS2

124214178

124216868

2

1.32 × 10−15

NA

1.94 × 10−1

9.74 × 10−8

3.82 × 10−9

1.91 × 10−1

8.13 × 10−5

2.01 × 10−7

Rare variants

LRT statistics of mixed models

Schaid’s methods

Chr

Gene

Start

End

Number of variants

GFLMM (6)

Kernel-based tests

Burden tests

B-sp basis

Fourier basis

kernel_BT

kernel_MB

kernel_UW

burden_BT

burden_MB

burden_UW

8

ASAH1

17913924

17941879

6

5.95 × 10−3

9.94 × 10−6

4.25 × 10−4

1.41 × 10−3

3.29 × 10−5

7.18 × l0−1

9.25 × l0−1

1.64 × 10−2

12

CLEC6A

8608590

8630926

3

3.78 × 10−5

4.71 × 10−3

1.56 × 10−2

1.67 × 10−2

1.61 × 10−2

5.34 × 10−2

5.30 × l0−1

3.67 × 10−2

14

TMEM63C

77648101

77725838

5

5.30 × 10−2

1.93 × 10−5

1.49 × 10−5

9.46 × 10−6

2.15 × 10−5

3.07 × 10−2

2.16 × 10−2

3.51 × 10−2

22

SGSM1

25202135

25322813

10

1.56 × 10−5

NA

6.40 × 10−3

7.03 × 10−3

3.37 × 10−2

1.39 × 10−1

6.58 × l0−1

3.42 × 10−1

NOTE: The association with a significant p — value < 2.96 × 10 ⁻⁶ were highlighted in bold. The results of suggestive association were included if a p-value is less than 10 ⁻⁵. Abbreviations: chr. chromosome: NA. did not converae

For gene CFH, two transcripts reached genome-wide significance (Table 1). The larger 96 kb region with 15 variants contained the other smaller one with only 3 variants, which indicated that the primary CFH variants associated with AMD might be located within the smaller region between 196,621,007 and 196,670,695 bp on chromosome 1. For gene ARMS2, both of the variants in our exome chip data were common variants with MAF = 0.39 and 0.10, respectively, so they were not included in the rare variant analysis. For CFH, the 96 kb region contained 7 rare variants (MAF ≤ 0.05, Table A.1 of Supplementary Materials I); the models failed to reach the significance threshold using the 7 rare variants, indicating that the common variants within CFH might play a pivotal role in the significant association signal.

In Table A.1 of Supplementary Materials I, we listed all variants within CFH and ARMS2, and examined their association on an individual variant level by conducting the W_QLS test suggested by Thornton and McPeek (2007) and the LRT GLMM statistic (3). For the gene ARMS2, a single nucleotide polymorphism (SNP) rs10490924 is strongly associated with AMD. For the gene CFH, 7 SNPs are strongly associated with AMD and each of them is a common variant. Hence, it makes sense to perform a gene-based associated analysis for the gene CFH for a unified analysis.

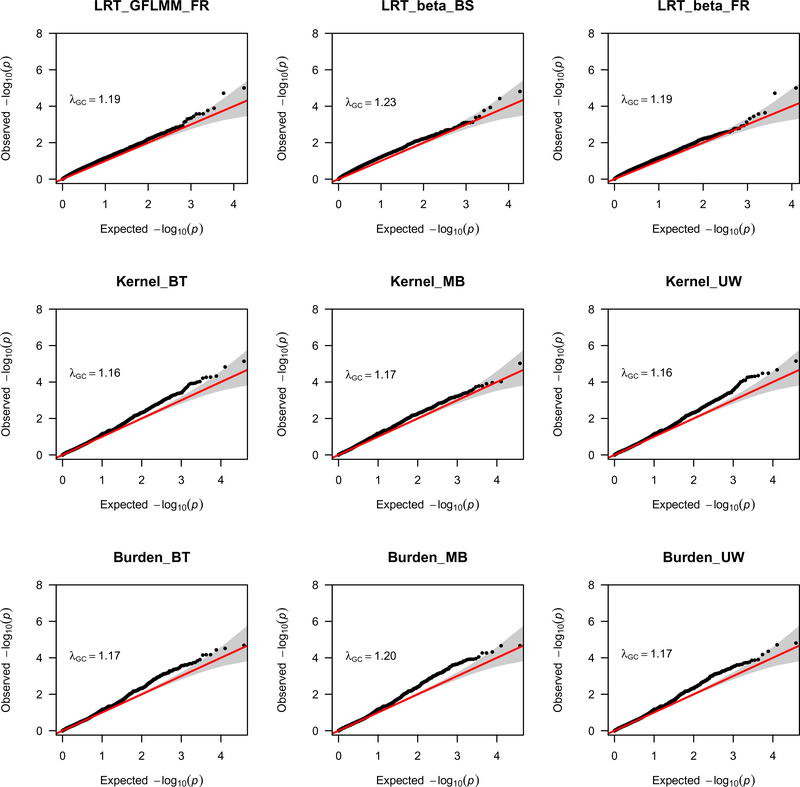
Quantile-quantile (Q-Q) plots of the gene-based statistics in Figure 1 show that, while the LRT statistics had lower λ_GC values, the kernel and burden test statistics had quite elevated λ_GC values to analyze both common and rare variants. Thus, when analyzing common and rare variants, the kernel and burden test statistics are not appropriate because they have high false positive rates. For the analysis of the rare variants with MAF ≤ 0.05, which is expected to be less powerful, only suggestive association were found. In the Q-Q plots in Figure 2, the LRT statistics and the kernel and burden test statistics had similar λ_GC values when only rare variants were analyzed.

Figure 1.

Q-Q plots for the LRT GFLMM statistics (5) and (6), and the retrospective kernel and burden tests when all common and rare variants are analyzed for AMD data.

Figure 2.

Q-Q plots for the LRT GFLMM statistics (5) and (6), and the retrospective kernel and burden tests when only rare variants are analyzed for AMD data.

By using rare variants, the LRT statistics show suggestive association signal with AMD for four genes, ASAH1, CLEC6A, TMEM63C, and SGSM1, since they provide p-values slightly larger than the threshold of 3.34 × 10⁻⁶ (Table 1). For the four genes, the kernel and burden test statistics also provide some suggestive association signals. Since both the LRT statistics and the kernel and burden test statistics had similar λ_GC values around 1.0 in Figure 2, the suggestive signals are useful for further investigation when more data are available. The suggestive signal at ASAH1 is especially interesting because, as we explain more fully in Section 5, ASAH1 may play a role in AMD (Petrov et al. 2019; Qu et al. 2019; Sugano et al. 2019).

3. Methods: Generalized Functional Linear Mixed Models

3.1. Generalized Functional Linear Mixed Models

Consider a single pedigree from a family-based study. The pedigree includes n participants with a dichotomous trait of interest coded as 1 and 0 denoting affected and unaffected, respectively. In addition, the n participants are genotyped within a chromosome region. Let i denote the ith individual with m genetic variants in the region. The physical locations of the m variants, denoted by 0 ≤ u₁ ≤ u₂ ≤ · · · u_m, are normalized on the unit region [0, 1]. For the ith individual, let y_i denote his/her disease status, and Z_i = (z_i1, …, z_ic)′ denote a c × 1 vector of fixed effect covariates. In addition, let X_i = (x_i(u₁), …, x_i(u_m))′ denote the genotypes at the m variants, where x_i(u_j) (= 0, 1, 2) is the number of minor alleles of individual i at the jth variant. For the n individuals who are phenotyped and genotyped, let Ω be a n × n matrix containing diagonal elements Ω_ii = 1 + h_i, where h_i is the inbreeding coefficient for individual i, and off-diagonal elements Ω_ik = 2ϕ_ik. The parameter ϕ_ik is the kinship coefficient between individuals i and k, the probability that a randomly chosen allele at a given locus from individual i is identical by descent (IBD) to a randomly chosen allele from individual k conditional on their ancestral relationship (Lange 2002). In practice, the pedigree may include members who are not genotyped or phenotyped and they can be used to calculate relationships between the pedigree members, that is, kinship and inbreeding coefficients.

Let us denote the ith individual’s GVF as X_i(u), u ∈ [0, 1]. Using the observed discrete genotypes X_i, we may estimate the related GVF X_i(u), which will be discussed below. To relate the GVF to the trait status adjusting for covariates, we consider the following GFLMM

$$\mathrm{logit}\left({\pi }_i\right)={\alpha }_0+Z_i^{\prime }\alpha +{\int }_0^1{X}_i(u)\beta (u)du+G_i,$$ (1)

where π_i = P(y_i = 1|Z_i, X_i, G_i) is the disease probability of the dichotomous trait for subject i, conditional on the covariates Z_i, genotype vector X_i, and polygenic variation G_i, α₀ is a regression intercept, α is a c × 1 vector of fixed regression coefficients of covariates, β(u) is the genetic effect of GVF X_i(u) at position u, and G = (G₁, …, G_n)′ is a multivariate normal random polygenic vector with mean 0 and covariance matrix ${\sigma }_G^2\mathrm{\Omega }$. Here ${\sigma }_G^2$ is a polygenic variance component. In the GFLMM (1), the GVF X_i(u) is assumed to be smooth. This assumption can be relaxed by considering the following beta-smooth only GFLMM

$$\mathrm{logit}\left({\pi }_i\right)={\alpha }_0+Z_i^{\prime }\alpha +\sum _{j=1}^m{x}_i\left(u_j\right)\beta \left(u_j\right)+G_i,$$ (2)

where the genetic effect function β(u) is assumed to be continuous/smooth and so it is called beta-smooth only GFLMM. In the above model (2), the integration term ${\int }_0^1{X}_i(u)\beta (u)du$ in GFLMM (1) is replaced by a summation term ${\sum }_{j=1}^m{x}_i\left(u_j\right)\beta \left(u_j\right)$, and we make no assumption about smoothness of the GVF X_i(u). We use the raw genotype data X_i = (x_i(u₁), …, x_i(u_m))′ directly in the beta-smooth only GFLMM (2).

Fan et al. (2014) proposed generalized functional linear models for analyzing case control association studies for unrelated population data. There were no random terms G_i in the models of Fan et al. (2014). In this article, the GFLMM (1) and (2) are developed to analyze pedigree data. In addition to the fixed effect terms, the random terms (G₁, …, G_n)′ are utilized to model polygenic variation ${\sigma }_G^2$ and correlation among the pedigree members.

The trait correlation of related individuals or family members is modeled as being partly due to genetic influences, that is, the sharing of alleles IBD contributes to the correlation of the traits of related individuals (Lange 2002). In this article, we assume the correlation is from polygenes. This is a typical approach used in association analysis of familial data (Thornton and McPeek 2007). At one gene locus, there are three possible scenarios of allele sharing IBD. For one polygene, it is impossible to know which scenario it is for two related individuals unless the two individuals are from an identical twin (and so they share two genes IBD for sure). Hence, the three scenarios cannot be separately treated. The random variation G_i in GLMM (3) collectively models all effects of polygenes and the number of polygenes is usually very large. We have to use kinship coefficients to measure the correlation.

3.2. Additive Generalized Linear Mixed Models (GLMM)

By using the genotype data directly, we may relate the m genetic variants to the trait status while adjusting for covariates by the following additive generalized linear mixed model (GLMM)

$$\mathrm{logit}\left({\pi }_i\right)={\alpha }_0+Z_i^{\prime }\alpha +\sum _{j=1}^m{x}_i\left(u_j\right){\beta }_j+G_i,$$ (3)

where β_j is the genetic effect of variant x_i(u_j) and the other terms are the same as those in the GFLMM (1). There is only one difference between model (2) and model (3). The genetic effect coefficients β_j in GLMM (3) are each individually estimated and so are “free” and not forced to lie on a continuous function of the position u. In contrast, in model (2) we assume that the genetic effect function β(u) is a continuous function of the position u. Therefore, β(u_j), j 1, 2, …, m, are the values of function β(u) at each of the m physical positions. The GLMM (3) hardly ever converges when the number of genetic variants is large which leads to a large number of parameters. Hence, the GLMM (3) is not useful for analyzing sequence data.

3.3. Revised Generalized Functional Linear Mixed Models

The genetic effect function β(u) in GFLMM (1) and GFLMM (2) is assumed to be a continuous function of physical position u. One may expand it using B-spline or Fourier basis functions. Formally, let us expand the genetic effect function β(u) using a series of K_β basis functions ${\psi }_1(u),\dots ,{\psi }_{K_{\beta }}(u)$ as $\beta (u)=\left({\psi }_1(u),\dots ,{\psi }_{K_{\beta }}(u)\right)$ ${\left({\beta }_1,\dots ,{\beta }_{K_{\beta }}\right)}^{\prime }=\psi {(u)}^{\prime }\beta$, where $\beta ={\left({\beta }_1,\dots ,{\beta }_{K_{\beta }}\right)}^{\prime }$ as K_β × 1 vector of coefficients and $\psi (u)={\left({\psi }_1(u),\dots ,{\psi }_{K_{\beta }}(u)\right)}^{\prime }$. We consider two types of basis functions: (1) the B-spline basis: ψ_k(u) = B_k(u), k = 1, …, K_β; and (2) the Fourier basis: ψ₁(u) = 1, ψ_2r+1(u) = sin(2πru), and ψ_2r(u) = cos(2πru), r = 1, …, (K_β – 1)/2. Here for Fourier basis, K_β is taken as a positive odd integer (de Boor 2001; Ramsay and Silverman 2005; Ramsay, Hooker, and Graves 2009; Ferraty and Romain 2010; Horvath and Kokoszka 2012).

To estimate the GVF X_i(u) from the genotypes X_i, we use an ordinary linear square smoother (Ramsay and Silverman 2005; Ramsay, Hooker, and Graves 2009; Luo, Boerwinkle, and Xiong 2011; Luo, Zhu, and Xiong 2012, 2013; Fan et al. 2013, 2014, 2015; Vsevolozhskaya et al. 2014, 2016; Zhang, Boerwinkle, and Xiong 2014; Svishcheva, Belonogova, and Axenovich 2015; Wang et al. 2015; Fan, Chiu, et al. 2016; Fan, Wang, Chiu, et al. 2016; Fan, Wang, Yan, et al. 2016; Zhao, Zhu, and Xiong 2016). Let ϕ_k(u), k = 1, …, K, be a series of K basis functions. Let Φ denote the m × K matrix containing the values ϕ_k(u_j), and we let ϕ(u) = (ϕ₁(u), …, ϕ_K(u))′. Using the discrete realizations X_i = (x_i(u₁), …, x_i(u_m))′, we estimate the GVF X_i(u) using an ordinary linear square smoother as follows

$${\widehat{X}}_i(u)=\left(x_i\left(u_1\right),\dots ,x_i\left(u_m\right)\right)\mathrm{\Phi }{\left[{\mathrm{\Phi }}^{\prime }\mathrm{\Phi }\right]}^{-1}\varphi (u).$$ (4)

Assume that the genetic effect function β(u) is expanded by a series of basis functions ψ_k(u), k = 1, …, K_β, as β(u) = ψ(u)′β. Replacing X_i(u) in the GFLMM (1) with ${\widehat{X}}_i(u)$ in (4) and β(u) with the expansion, we have the following revised GFLMM

$$\begin{gathered} \mathrm{logit}\left({\pi }_i\right)={\alpha }_0+Z_i^{\prime }\alpha +\left(x_i\left(u_1\right),\dots ,x_i\left(u_m\right)\right)\mathrm{\Phi }{\left[{\mathrm{\Phi }}^{\prime }\mathrm{\Phi }\right]}^{-1} \\ \times {\int }_0^1\varphi (u){\psi }^{\prime }(u)du\beta +G_i \\ ={\alpha }_0+Z_i^{\prime }\alpha +W_i^{\prime }\beta +G_i, \end{gathered}$$ (5)

where $W_i^{\prime }=\left(x_i\left(u_1\right),\dots ,x_i\left(u_m\right)\right)$ $\mathrm{\Phi }{\left[{\mathrm{\Phi }}^{\prime }\mathrm{\Phi }\right]}^{-1}{\int }_0^1\varphi (u){\psi }^{\prime }(u)du$. In the statistical packages R or Matlab, codes to calculate Φ[Φ′Φ]⁻¹ and ${\int }_0^1\varphi (u){\psi }^{\prime }(u)du$ are readily available (Ramsay, Hooker, and Graves 2009).

Denote $W_i^{\prime }={\sum }_{j=1}^m{x}_i\left(u_j\right)\left({\psi }_1\left(u_j\right),\dots ,{\psi }_{K_{\beta }}\left(u_j\right)\right)$. For the beta-smooth only GFLMM (2), β(u_j) is introduced as the genetic effect at the position u_j. Expanding β(u_j) by B-spline or Fourier basis functions as above, the GFLMM (2) can be revised as

$$\begin{gathered} \mathrm{logit}\left({\pi }_i\right)={\alpha }_0+Z_i^{\prime }\alpha +\left[\sum _{j=1}^m{x}_i\left(u_j\right)\left({\psi }_1\left(u_j\right),\dots ,{\psi }_{K_{\beta }}\left(u_j\right)\right)\right] \\ \times {\left({\beta }_1,\dots ,{\beta }_{K_{\beta }}\right)}^{\prime }+G_i \\ ={\alpha }_0+Z_i^{\prime }\alpha +W_i^{\prime }\beta +G_i. \end{gathered}$$ (6)

3.4. Handling Missing Genotype Data

Missing genotypes, which are invariably encountered in analyses of real data, can be handled by modifying (4) so that each individual’s GVF is estimated using only the available genotype data. For example, suppose the genotype information is missing at the first variant for individual i, so we have X_i = (?, x_i(u₂), …, x_i(u_m))′. Then let Φ₁ be the (m − 1) × K matrix containing the values ϕ_k(u_j) where j ∈ (2, …, m). Then we can estimate the GVF using the available genotype data as

$${\widehat{X}}_i(u)=\left(x_i\left(u_2\right),\dots ,x_i\left(u_m\right)\right){\mathrm{\Phi }}_1{\left[{\mathrm{\Phi }}_1^{\prime }{\mathrm{\Phi }}_1\right]}^{-1}\varphi (u).$$ (7)

Furthermore, in addition to modifying the calculation of the GVF, the summations over the m variants need to be appropriately adjusted. For example, in our case where the genotype at the first variant is missing, model (6) becomes

$$\begin{gathered} \mathrm{logit}\left({\pi }_i\right)={\alpha }_0+Z_i^{\prime }\alpha +\left[\sum _{j=2}^m{x}_i\left(u_j\right)\left({\psi }_1\left(u_j\right),\dots ,{\psi }_{K_{\beta }}\left(u_j\right)\right)\right] \\ \times {\left({\beta }_1,\dots ,{\beta }_{K_{\beta }}\right)}^{\prime }+G_i. \end{gathered}$$

3.5. Likelihood Functions

For subject i, assume that his/her likelihood L_i depends only on (Z_i, X_i, G_i) and is independent of (Z_j, X_j, G_j), j ≠ i. Given the covariates Z_i, genotypes X_i, and random polygenic variation G_i, the likelihood of GLMM (3) or GFLMM (5) or (6) of subject i is $L_i\left(y_i\mid Z_i,X_i,G_i\right)={\pi }_i^{y_i}{\left(1-{\pi }_i\right)}^{1-y_i}$. Given the covariates Z = (Z₁, …, Z_n)′, genotypes X = (X₁, …, X_n)′, and random polygenic variations G = (G₁, …, G_n)′, the likelihood of GLMM (3) or GFLMM (5) or (6) is

$$L(y\mid \mathbf{Z},\mathbf{X},\mathbf{G})={\mathrm{\Pi }}_{i=1}^n{L}_i\left(y_i\mid Z_i,X_i,G_i\right)={\mathrm{\Pi }}_{i=1}^n{\pi }_i^{y_i}{\left(1-{\pi }_i\right)}^{1-y_i}.$$

The integrated likelihood function of (α₀, α, β, ${\sigma }_G^2$) is

$$\begin{gathered} L(y\mid \mathbf{Z},\mathbf{X})={\left(2\pi \right)}^{-n/2}\det {\left({\sigma }_G^2\mathrm{\Omega }\right)}^{-1/2}\int {\mathrm{\Pi }}_{i=1}^n{\pi }_i^{y_i}{\left(1-{\pi }_i\right)}^{1-y_i} \\ \times \exp \left(-\frac{{\mathbf{G}}^{\prime }{\left({\sigma }_G^2\mathrm{\Omega }\right)}^{-1}\mathbf{G}}{2}\right)d\mathbf{G}. \end{gathered}$$ (8)

The likelihood (8) is built in a traditional way where random effects are integrated out and has been used in genetic studies before (Chen et al. 2016). Then, LRT can be calculated based on the integrated likelihood function (8). Our models can analyze rare variants and a combination of rare and common variants, while the approach of Chen et al. (2016) handles only single individual variants.

3.6. Parameter Estimation

In the proposed models (5) and (6), the contributions of a random vector (G₁, …, G_n)′ are correlated according to the pedigree structure with a covariance matrix ${\sigma }_G^2\mathrm{\Omega }$. The covariance matrix differs from pedigree to pedigree. Routines for mixed models in standard packages cannot be used for parameter estimation. For linear mixed models for quantitative traits under normal assumptions, the marginal likelihood has a closed form and maximum likelihood estimation can be performed conveniently. However, in models (5) and (6), the marginal likelihood does not have a closed form and must be approximated using, for example, a Laplacian approximation (Gilmour, Anderson, and Rae 1985; Schall 1991; Breslow and Clayton 1993; Vazquez et al. 2010). In this article, we use the R package pedigreemm which is an extension of the lme4 R package (Bates and Vazquez 2014; Bates et al. 2015). The pedigreemm package uses the capabilities of lme4 while allowing for correlations between pedigree members by applying Cholesky decomposition of the covariance structure of the random effects (G₁, …, G_n)′. Briefly, let Ω = CC′ and ${\left(G_1^{*},\dots ,G_n^{*}\right)}^{\prime }=C^{-1}{\left(G_1,\dots ,G_n\right)}^{\prime }$, where C is the Cholesky factor (Harvillel and Callanan 1989). Then, we have

$$\mathrm{var}\left({\left(G_1^{*},\dots ,G_n^{*}\right)}^{\prime }\right)=C^{-1}\mathrm{\Omega }{\left(C^{\prime }\right)}^{-1}{\sigma }_G^2=I_n{\sigma }_G^2,$$

where I_n is an n × n identity matrix. Thus, the elements of ${\left(G_1^{*},\dots ,G_n^{*}\right)}^{\prime }$ are mutually independent, and lme4 procedure can be applied because the random effects are now independent (Bates 2009).

3.7. LRT Statistics

To test for association between the dichotomous trait and the m genetic variants, the null hypothesis is $H_0:\beta ={\left({\beta }_1,\dots ,{\beta }_{K_{\beta }}\right)}^{\prime }=0$. Under the null, the GFLMM (5) and (6) are simplified as

$$\mathrm{logit}\left({\pi }_i\right)={\alpha }_0+Z_i^{\prime }\alpha +G_i.$$ (9)

The GFLMM (5) or (6) and the null model (9) are nested. By fitting the GFLMM (5) or (6) and the null model (9), we may test the null H₀ : β = 0 by a χ²-distributed LRT statistic with K_β degrees of freedom using the pedigreemm R package (Vazquez et al. 2010).

In total, these combinations define three different LRT statistics, as outlined in Table 2. In addition to evaluating their Type I error rates via simulation (as described below), we also evaluated their power as well as the power of six different kernel and burden tests developed by Schaid et al. (2013); these are also listed in Table 2.

Table 2.

Notation used in the figures.

Notation	Description and interpretation
LRT GFLMM FR	LRT of GFLMM (5) with the Fourier basis vs. null model (9)
LRT_beta_BS	LRT of GFLMM (6) with the B-Spline basis vs. null model (9)
LRT_beta_FR	LRT of GFLMM (6) with the Fourier basis vs. null model (9)
kernel BT	Kernel test with weights based on Beta distribution
kernel MB	Kernel test with Madsen-Browning weights
kernel UW	Kernel test with equal weights
burden BT	Burden test with weights based on Beta distribution
burden MB	Burden test with Madsen-Browning weights
burden UW	Burden test with equal weights

4. Simulation Studies

To evaluate the performance of the proposed GFLMM and LRT statistics, we simulated data to estimate empirical Type I error rates and power levels. In our simulations, a variant is considered to be rare if its MAF is ≤ 0.03. Two scenarios were considered: (1) some variants are common and the rest are rare; (2) all variants are rare.

4.1. Simulation Design

4.1.1. Pedigree Template of 25 Families

We first simulated 25 families including 11 two-generation nuclear pedigrees and 14 three-generation extended pedigrees by randomly choosing progeny sizes from a negative binomial distribution (Cavalli-Sforza and Bodmer 1999). We assumed that each child within the second generation has a 25% chance of having offspring. The pedigree structures included 228 individuals (119 males and 109 females; 70 founders and 158 nonfounders) within 25 families. The pedigree size ranged from 4 to 24 with an average value of 9.12.

4.1.2. Pedigree Template of 50 Families

By doubling the 25 families, the pedigree structures included 456 individuals (238 males and 218 females; 140 founders and 316 nonfounders) within 50 families.

4.1.3. Genetic Variants

The sequence data are of European ancestry from 10,000 chromosomes covering a 1 Mb region, simulated by Yun Li at the University of North Carolina, Chapel Hill using the calibrated coalescent model as programmed in COSI (Schaffner et al. 2005). The sequence data were generated using COSI’s calibrated best-fit models, and the generated European haplotypes mimic CEPH Utah individuals with ancestry from northern and western Europe in terms of site frequency spectrum and linkage disequilibrium (LD) patterns (Schaffner et al. 2005; The International HapMap Consortium 2007). To evaluate empirical Type I error and power levels, we randomly sampled two haplotypes for each founder. For each nonfounder, we chose one haplotype at random from his or her parents. Genotypes were constructed by summing up two haplotypes for each individual to determine the number of minor alleles.

4.1.4. Type I Error Simulations

To evaluate Type I error rates of our LRT statistics, we utilized the 50 two- or three-generation families with a total of 456 related individuals as a template as well as the 25 families with 228 individuals as another template. For each pedigree, we generated phenotype datasets using the model

$$\mathrm{logit}\left({\pi }_i\right)={\alpha }_0+z_{i1}+z_{i2}+G_i,$$ (10)

where α₀ = −4.60, z_i1 is a dichotomous covariate taking values 0 and 1 with a probability of 0.5, z_i2 is a continuous covariate from a standard normal distribution N(0, 1), and (G₁, …, G_n)′ is generated as a normal vector sampled from a multivariate normal with mean 0 and covariance matrix ${\sigma }_G^2\mathrm{\Omega }$ with σ_G = 0.2. After assigning the phenotype for each individual, pedigrees were ascertained if they contained at least one pair of affected siblings, either in the second or third generation, or both. Through the ascertainment, we effectively sampled cases enriched for the dichotomous trait, thus weakening the influence of the polygenic effect.

Genotypes were selected from variants in 6, 9, 12, 15, 18, and 21 kb subregions randomly selected from the 1 Mb region. Note that the trait values are not related to the genotypes, and so the null hypothesis holds. For each simulation scenario, 3 × 10⁶ phenotype-genotype datasets were generated to fit the models and to calculate the test statistics and related p-values. Then, an empirical Type I error rate was calculated as the proportion of p-values of the convergent models in the 3 × 10⁶ datasets which were smaller than a given α level.

4.1.5. Empirical Power Simulations

To evaluate the power of our LRT statistics, trait status was determined for each individual based upon the genotypes. To do this, we considered a mixed effect logistic regression genetic model to compute the probability of being affected for an individual. We simulated datasets under the alternative hypothesis by randomly selecting subregions to obtain causal variants. First, we generated genotypes of m variants in a selected subregion, similar to the Type I error simulations. Then, M of the m variants were randomly selected to be causal, yielding causal genotypes (x_i(u₁), …, x_i(u_M)). For each dataset, the causal variants are the same for all the individuals in the dataset, but we allow the causal variants to be different from dataset to dataset. Then, we generated the dichotomous disease traits by

$$\mathrm{logit}\left(p_i\right)={\alpha }_0+z_{i1}+z_{i2}+{\beta }_1{x}_i\left(u_1\right)+\cdots +{\beta }_M{x}_i\left(u_M\right)+G_i,$$ (11)

where α₀, z_i1, z_i2, (G₁, …, G_n)′ were the same as in the Type I error model (10), (x_i(u₁), …, x_i(u_M))′ were genotypes of the ith individual at the causal variants, and the β’s are additive effects for the causal variants defined as follows. Modeled as the approach of Wu et al. (2011), we used |β_j| = c|log₁₀(MAF_j)|, where MAF_j was the MAF of the jth variant. Three different settings were considered: 5%, 10%, and 15% of variants in the subregions are chosen as causal variants. When 5%, 10%, and 15% of the variants were causal, c = log(90)/k, log(70)/k, and log(50)/k, respectively. For the template of 50 two- or three-generation families with a total of 456 related individuals, the constants k and genetic effect sizes decrease as region sizes increase

$$k=\{\begin{array}{ll}3.5\hfill & \text{if}\text{region}\text{size}=6\text{kb,}\hfill \\ 4.0\hfill & \text{if}\text{region}\text{size}=9\text{kb,}\hfill \\ 4.5\hfill & \text{if}\text{region}\text{size}=12\text{kb,}\hfill \\ 5.0\hfill & \text{if}\text{region}\text{size}=15\text{kb,}\hfill \\ 5.5\hfill & \text{if}\text{region}\text{size}=18\text{kb,}\hfill \\ 6.0\hfill & \text{if}\text{region}\text{size}=21\text{kb.}\hfill \end{array}$$ (12)

In addition to varying the percentage of causal variants in the subregion, we also varied the direction of effect. We considered situations where (i) all causal variants have positive effects; (ii) 20%/80% causal variants have negative/positive effects; and (iii) 50%/50% causal variants have negative/positive effects. Burden tests are expected to be most powerful when all causal variants have effects in the same direction (e.g., under scenario (i)). For each setting, 3000 datasets were simulated to calculate the empirical power as the proportion of p-values which are from the convergent models and smaller than a given α level.

4.2. Functional Data Analysis Parameters and Dynamic Rule

In the data analysis and simulations described above, we used functions from the fda R package to create the basis functions (Ramsay et al. 2014). In the simulations presented in the main text, we implement a dynamic rule to handle the genotype data to make sure that the results are stable. The order of the B-spline basis was 4, the upper limit of B-spline basis functions was K = K_β = 16, and the upper limit of Fourier basis functions was K = K_β = 17. First, we perform a principal component analysis to evaluate the effective dimension of the genotype data M_gao (Gao, Starmer, and Martin 2008). Then,

1. if M_gao ≤ 18, the number of B-spline basis functions was K = K_β = 6, and the number of Fourier basis functions was K = K_β = 7;

2. if 18 < M_gao ≤ 24, the number of B-spline basis functions was K = K_β = 8, and the number of Fourier basis functions was K = K_β = 9;

3. if 24 < M_gao ≤ 30, the number of B-spline basis functions was K = K_β = 10, and the number of Fourier basis functions was K = K_β = 11;

4. if 30 < M_gao ≤ 36, the number of B-spline basis functions was K = K_β = 12, and the number of Fourier basis functions was K = K_β = 13;

5. if 36 < M_gao ≤ 42, the number of B-spline basis functions was K = K_β = 14, and the number of Fourier basis functions was K = K_β = 15;

6. if M_gao > 42, the number of B-spline basis functions was K = K_β = 16, and the number of Fourier basis functions was K = K_β = 17;

In Supplementary Materials II, Appendix B, we present additional simulation results when the order of the B-spline basis was 4, the number of B-spline basis functions was K = K_β = 6, and the number of Fourier basis functions was K = K_β = 7 for the 50 family template.

In Supplementary Materials III, Appendix C, we present additional simulation results when the order of the B-spline basis was 4, the number of B-spline basis functions was K = K_β = 16, and the number of Fourier basis functions was K = K_β = 17 for the small 25 family template. In Supplementary Materials IIII, Appendix D, additional simulation results are shown when the order of the B-spline basis was 4, the number of B-spline basis functions was K = K_β = 6, and the number of Fourier basis functions was K = K_β = 7 for the small 25 family template.

In the data analysis, the order of the B-spline basis was ≤4. As these data were more sparsely genotyped than the simulated data, to improve convergence rates, we used the modified dynamic rule as defined in Appendix E, since 15,099 out of 16,913 gene regions contain less than 12 variants.

4.3. Simulation Results

In this subsection, we present simulation results for the Type I error rates and power levels using bar plots for the templates of 50 and 25 two- or three- generation families, where the statistics evaluated are referred to using the notation defined in Table 2. In the table, three LRT statistics, three kernel tests and three burden tests are presented. The three LRT statistics are based on the GFLMM (5) and (6). The kernel and burden tests are from Schaid et al. (2013). Extensive simulations were carried out, comparing the Type I error rates at three nominal significance levels of the three different LRT statistics (listed in Table 2), varying the region size from 6 to 21 kb.

4.3.1. Empirical Type I Error Rates of 50 Family Template

The empirical Type I error rates are reported in Table 3 at four nominal significance levels α = 0.01, 0.001, 0.0001, and 0.00001. In the table, the results of three LRT statistics were reported for the GFLMM (5) and (6). The LRT statistics control the Type I error rates correctly, no matter whether the genotype data are smoothed or not and which basis functions are used to smooth the GVF and β(t) (Table 3). When the number of B-spline basis functions was K = K_β = 6 and the number of Fourier basis functions was K = K_β = 7, the results are reported in Table B.1 in Supplementary Materials II, Appendix B and the LRT statistics control the Type I error rates correctly.

Table 3.

Empirical type I error rates of the LRT statistics at nominal levels α 0.01,0.001,0.0001, and 0.00001, using the 50 two- or three-generation families with a total of 456 related individuals as a template.

			Type I error rates of LRT statistics
Variant type	Region size (mean # of variants)	Nominal level α	GFLMM (5)	GFLMM (6)
			Fourier basis	B-sp basis	Fourier basis
Rare and common	6 kb	0.01	0.005152	0.005236	0.005283
	(117)	0.001	0.000382	0.000392	0.000406
		0.0001	3.06E-05	3.07E-05	3.46E—05
		0.00001	2.35E—06	7.88E—07	3.22E—06
	9 kb	0.01	0.004816	0.004837	0.004919
	(176)	0.001	0.000380	0.000371	0.000404
		0.0001	2.93E—05	2.39E—05	3.16E—05
		0.00001	2.44E—06	1.65E—06	1.71E—06
	12 kb	0.01	0.004656	0.004818	0.004711
	(235)	0.001	0.000359	0.000375	0.000362
		0.0001	2.52E—05	3.33E—05	2.73E—05
		0.00001	0.000000	1.71E—06	0.000000
	15 kb	0.01	0.004773	0.004740	0.004774
	(293)	0.001	0.000392	0.000369	0.000398
		0.0001	3.00E—05	2.61E—05	2.80E—05
		0.00001	2.57E—06	2.61E—06	1.93E—06
	18 kb	0.01	0.004581	0.004658	0.004607
	(352)	0.001	0.000322	0.000338	0.000337
		0.0001	2.33E—05	2.72E—05	2.53E—05
		0.00001	1.73E—06	1.76E—06	1.01E—06
	21 kb	0.01	0.004463	0.004561	0.004410
	(410)	0.001	0.000306	0.000334	0.000317
		0.0001	2.86E—05	2.47E—05	2.81E—05
		0.00001	1.74E—06	3.53E—06	1.04E—06
Rare	6 kb	0.01	0.005798	0.006236	0.007339
	(106)	0.001	0.000422	0.000491	0.000600
		0.0001	2.60E—05	3.09E—05	4.42E—05
		0.00001	8.13E—07	1.58E—06	7.75E—07
	9 kb	0.01	0.006217	0.006364	0.007704
	(159)	0.001	0.000469	0.000563	0.000659
		0.0001	2.95E—05	2.91E—05	5.44E—05
		0.00001	3.99E—06	2.42E—06	9.97E—06
	12 kb	0.01	0.006041	0.006157	0.007316
	(212)	0.001	0.000476	0.000493	0.000643
		0.0001	3.77E—05	5.10E—05	6.05E—05
		0.00001	3.27E—06	3.34E—06	6.28E—06
	15 kb	0.01	0.006008	0.006378	0.007259
	(265)	0.001	0.000435	0.000511	0.000624
		0.0001	3.27E—05	4.11E—05	5.78E—05
		0.00001	2.51E—06	8.57E—07	5.62E—06
	18 kb	0.01	0.005957	0.006306	0.007044
	(318)	0.001	0.000525	0.000503	0.000672
		0.0001	4.69E—05	4.17E—05	6.71E—05
		0.00001	5.97E—06	5.21E—06	8.18E—06
	21 kb	0.01	0.005937	0.006204	0.006781
	(371)	0.001	0.000480	0.000498	0.000599
		0.0001	4.73E—05	3.89E—05	6.54E—05
		0.00001	3.44E—06	4.32E—06	5.80E—06

NOTE: The order of B-spline basis was 4, and the number of basis functions of B-spline was K = K_β = 16; the number of Fourier basis functions was K = K_β = 17.

4.3.2. Empirical Type I Error Rates of 25 Family Template

When the number of B-spline basis functions was K = K_β = 16 and the number of Fourier basis functions was K = K_β = 17, the results are reported in Table C.1 in Supplementary Materials III, Appendix C. In Table D.1 of Supplementary Materials IIII, Appendix D, we present simulation results when the order of the B-spline basis was 4, the number of B-spline basis functions was K = K_β = 6, and the number of Fourier basis functions was K = K_β = 7. In Tables C.1 and D.1, we find that the LRT statistics control Type I error rates accurately.

4.3.3. Empirical Power Simulations of 50 Family Template

Based on the simulated data, the power of the LRT statistics was compared with the power of the retrospective kernel and burden statistics developed by Schaid et al. (2013): three different weighting schemes were considered for both the kernel and burden statistics (Table 2). The results are reported in Figures A.1–A.12 in Supplementary Materials I. In Figures A.1–A.6, some variants are common and the rest are rare. In Figures A.7–A.12, the variants are all rare. In plots (a1)–(a3) of each figure, all causal variants have positive effects; when 20%/80% causal variants have negative/positive effects, we present the results in plots (b1), (b2), and (b3) for each figure; when 50%/50% causal variants have negative/positive effects, the results are presented in plots (c1), (c2), and (c3).

When the region sizes are between 6 and 15 kb, the LRT GFLMM (5) and (6) statistics have higher power than the kernel and burden tests in Figures A.1–A.4 and A.7–A.10. When the region sizes are 18 and 21 kb, the power levels of kernel and burden tests are lower or similar to those of LRT GFLMM (5) and (6) in Figures A.5, A.6, A.11, and A.12. The choice of the B-spline or the Fourier basis has little effect on power. The three LRT GFLMM statistics (5) and (6) control Type I error rates well and have similar good power levels as shown in Figures A.1–A.12. The power levels of the LRT beta-smooth only GFLMM (6) statistics are almost identical to those of the LRT GFLMM statistics (5) which smooth both the GVFs X_i(u) and the genetic effect function β(t), regardless of basis choice. Hence, the three LRT GFLMM statistics (5) and (6) are very stable in terms of power performance and they do not strongly depend on whether the genotype data are smoothed or not, or which basis functions are used.

When some variants are common and the rest are rare, the kernel-based approach with Madsen–Browning weights performs the best among the kernel and burden statistics in Figures A.1–A.6. When all variants are rare, the kernel-based approach with weights based on the beta distribution performs the best (Figures A.7–A.12). As noted in Schaid et al. (2013), the kernel statistics have higher power than burden ones.

In Supplementary Materials II, Appendix B, we present simulation results when the order of the B-spline basis was 4, the number of B-spline basis functions was K = K_β = 6, and the number of Fourier basis functions was K = K_β = 7. The power levels of LRT GFLMM statistics (5) and (6) in Figures B.1–B.12 can be low.

4.3.4. More Simulation Results of 25 Family Template

In Supplementary Materials III, Appendix C, we present simulation results when the order of the B-spline basis was 4, the number of B-spline basis functions was K = K_β = 16, and the number of Fourier basis functions was K = K_β = 17. The power levels of LRT GFLMM statistics (5) and (6) are presented in Figures C.1–C.12. In Supplementary Materials IIII, Appendix D, we present simulation results when the order of the B-spline basis was 4, the number of B-spline basis functions was K = K_β = 6, and the number of Fourier basis functions was K = K_β = 7. Compared with the results of Supplementary Materials III, Appendix C, the power levels of LRT GFLMM statistics (5) and (6) in Figures D.1–D.12 are lower.

5. Discussion

AMD is a common complex disease and is caused by an interplay of aging, genetics, and environmental factors. While AMD family data has been collected (Ratnapriya et al. 2020), most AMD association studies have mainly focused on using population data to identify genes and variants which are associated with AMD, partly because of a dearth of powerful methods for carrying out region-based association tests of a dichotomous trait like AMD on family data. Here we apply GFLMM we developed to test for association between the dichotomous AMD trait and genetic variants in each gene region in our AMD family dataset. Using common and rare variants, we observe strong association between AMD and two known AMD susceptibility genes: CFH and ARMS2. Gene-based rare variant burden analyses were carried out by the International AMD Genomics Consortium in a large dataset of 16,144 advanced AMD cases versus 17,832 controls (Fritsche et al. 2016); the analyses ignored family structure—for example, the dataset included a set of unrelated individuals extracted from the family dataset we analyze here. When testing was restricted to the 703 genes, CFH attains significance, but ARMS2 and the other genes listed in our Table 1 are not among their top hits. However, note that they used only rare protein-altering variants, while our analysis that gives a signal for ARMS2 used both common and rare variants.

By using rare variants, we find suggestive association signals in four gene regions, ASAH1, CLEC6A, TMEM63C, and SGSM1. The Consortium did not see significant burden test signals at these genes in Fritsche et al. (2016). The suggestive signal at ASAH1 is especially interesting because ASAH1 deficiency leads to retinal inflammation (Petrov et al. 2019) and underexpression of ASAH1 makes retinal cells more vulnerable to oxidative stress (Sugano et al. 2019). Consistently, in the aqueous humor, ASAH1 is identified as a down-regulated protein in AMD as compared to controls (Qu et al. 2019). Thus, several lines of congruent evidence complement our suggestive gene-based association of ASAH1 with AMD to suggest that ASAH1 may play a role in AMD.

In this article, we analyzed the AMD family data in two different ways: (1) all genetic variants and (2) rare variants only. From the results, we can see that it is a good strategy to analyze all variants in addition to only analyzing rare variants. It is reasonable to assume that a combination of rare and common variants affects the risk of many complex disorders. After all, we are searching for causal variants, not rare or common variants.

To analyze the related pedigrees and high dimensional sequencing data, we developed GFLMM for analyzing familial dichotomous trait data. In these models, the effect of a major gene is modeled as a fixed mean, the polygenic contributions is modeled as a random variation, and the correlation of pedigree members is modeled by inbreeding and kinship coefficients. LRT statistics based on the GFLMM are built to test for association between a dichotomous trait and the genetic variants. Simulation results indicate that the LRT statistics accurately control the Type I error rates for a pedigree dataset of moderate sample size (i.e., 456 individuals in 50 pedigrees), as well as for a small sample size dataset (228 individuals in 25 pedigrees). In our analysis of the AMD data, the kernel and burden tests have high false positive rates while the GFLMM control the Type I errors well. In addition to properly controlling Type I error rates, GFLMM can handle both common and rare variants, avoiding arbitrary MAF threshold-based filtering of variants. Functional models are very flexible since they can analyze: (1) rare variants, (2) common variants, and (3) a combination of the two. This elegant feature deserves further utilization in dissecting complex disorders.

It can be challenging to get linear mixed models to converge. To improve convergence rates, in addition to selecting a better optimizer and increasing the number of function evaluations, we added the dynamic rule defined above to better match the statistical model to the underlying dimensionality of the data. This improved the convergence rate. For example, for the GFLMM (6) power simulation results in Figure A.6(a1), the LRT of GFLMM (6) using the B-spline basis converged 97.1% of the time; the convergence rate using the Fourier basis of 93.7% was poorer, suggesting the B-spline basis version should be preferentially used for GFLMM (6). In these power results about 63% of the time a warning was generated about a boundary fit, likely indicating that the random component is not needed. For the simulations presented here, we conservatively evaluated each statistic on replicates with no errors or warnings.

While the dynamic rule presented above worked reasonably well on the simulated data, when applied to the real AMD data, it did not work as well, likely because these data are more sparsely genotyped than the simulated data. To improve convergence rates, we used the adjusted dynamic rule presented in Appendix E. While we have shown that our statistics are promising, future work is needed into choosing an optimal dynamic rule for one’s particular data to improve convergence rates and to reduce errors and warnings when fitting these models.

In major gene analysis, the LRT statistics of GFLMM have higher power than the kernel-based and burden tests proposed by Schaid et al. (2013). The kernel-based tests proposed in Schaid et al. (2013) perform better than burden tests. In the previous work, it was shown that the tests of fixed effect regression models have higher power than SKAT for population data in major gene association studies (Fan, Chiu, et al. 2016). Therefore, the proposed models provide an alternative competitive method for carrying out gene-based association tests.

One major difference between our statistics and the kernel-based tests is that we model the major gene contribution by a fixed effect mean while kernel-based tests model the gene contribution as a random term with a zero mean and a constant variance. In the previous work and the current article, it is shown that our models have higher power in major gene association analysis and kernel-based tests perform better for polygenic analysis (Fan, Chiu, et al. 2016). If the number of causal genetic variants at a locus is very large and each causal variant contributes a small amount to the traits, the kernel-based test assumption of means of zero is likely to be satisfied and kernel-based tests could perform better. However, assuming means of zero for regression coefficients is unlikely to be valid. For instance, if some of the causal variants’ contributions to the traits are relatively large, it is unlikely that regression coefficients of genetic variants are around zero. In major gene association studies, we argue that our LRT statistics perform better than kernel-based tests in most cases.

The GFLMM (5) and (6) are designed to analyze familial data from one population. Comparing with previous fixed models which were designed to analyze unrelated population samples, one random term G_i is added to model the polygenic variation and familial correlation for pedigree members (Cordell and Clayton 2002; Fan et al. 2013, 2014, 2015; Fan, Chiu, et al. 2016; Fan, Wang, Chiu, et al. 2016; Fan, Wang, Yan, et al. 2016). The models can be extended to accommodate population structure and cryptic relatedness by adding extra random terms to the models (Chen et al. 2016). For cryptically related individuals, one may replace the kinship coefficients with empirical genetic relationship matrix (GRM). The empirical GRM can be calculated based on marker data to account for population structure and cryptic relatedness (Yang et al. 2010; Gianola et al. 2016; Wang 2016). For individuals i and j from different pedigrees, the kinship coefficient ϕ_ij = 0. However, the empirical genetic relationship coefficient of i and j can be different from 0 since they can be cryptically related to each other. More research is needed to characterize the properties of models which accommodate population structure and cryptic relatedness as well as adding variance component at the major gene to the models.