Abstract
Brain age estimated by machine learning from T1-weighted magnetic resonance images (T1w MRIs) can reveal how brain disorders alter brain aging and can help in the early detection of such disorders. A fundamental step is to build an accurate age estimator from healthy brain MRIs. We focus on this step, and propose a framework to improve the accuracy, generality, and interpretation of age estimation in healthy brain MRIs. For accuracy, we used one of the largest sample sizes (N=16,705 samples). For each subject, our proposed algorithm first explicitly splits the T1w image, which has been commonly treated as a single-channel 3D image in other studies, into two 3D image channels representing contrast and morphometry information. We further proposed a “fusion-with-attention” deep learning convolutional neural network (FiA-Net) to learn how to best fuse the contrast and morphometry image channels. FiA-Net recognizes varying contributions across image channels at different brain anatomy and different feature layers. In contrast, multi-channel fusion does not exist for brain age estimation, and is mostly attention-free in other medical image analysis tasks (e.g., image synthesis, or segmentation), where treating channels equally may not be optimal. For generality, we used truly lifespan data 0–97 years of age for real-world utility; and we thoroughly tested FiA-Net for multi-site and multi-scanner generality by two phases of cross-validations in discovery and replication data, compared to most other studies with only one phase of cross-validation. For interpretation, we directly measured each artificial neuron’s correlation with the chronological age, compared to other studies looking at the saliency of features where salient features may or may not predict age. Overall, FiA-Net achieved a mean absolute error (MAE) of 3.00 years and Pearson correlation r=0.9840 with known chronological ages in healthy brain MRIs 0–97 years of age, comparing favorably with state-of-the-art algorithms and studies for accuracy and generality across sites and datasets. We also provide interpretations on how different artificial neurons and real neuroanatomy contribute to the age estimation.
Keywords: Multi-channel Fusion, Attention network, lifespan brain MRI, age prediction, deep learning
1. Introduction
Estimating brain age based on MRIs provides an important biomarker for brain health (Gaser and Franke, 2019). A common practice is a two-stage process known as “built on normal, applied to abnormal”. The accuracy of age estimation is decided in the first stage, which starts from healthy brain MRIs. This first stage builds a machine learning model to predict the brain age as close as possible to the actual chronological age in healthy brain MRI. The model is then applied, in the second stage, to estimate the brain age in abnormal brain MRIs, which usually appear normal but indeed are subtly altered by neuropsychiatric or neurological diseases. The difference between the predicted age and the actual chronological age, often referred to as the “brain age gap (BAG)”, can reveal accelerated or delayed aging. In recent examples, studies in this fashion have found abnormal aging associated with psychosis (Chung et al., 2018), HIV (Cole et al., 2017b), Alzheimer’s Disease (Franke and Gaser, 2012; Gaser et al., 2013), schizophrenia (Koutsouleris et al., 2014; Schnack et al., 2016), epilepsy (Pardoe et al., 2016), traumatic brain injury (Cole et al., 2015) and other brain diseases (Gaser and Franke, 2019; Cole and Franke, 2017). Machine-learning-powered age estimation also revealed subtle early changes in brain health as a result of certain environmental exposures (Steffener et al., 2016). Comprehensive surveys can be found in works (Cole and Franke, 2017; Sajedi and Pardakhti, 2019; Gaser and Franke, 2019).
This paper focuses on the first stage – building an age estimator from healthy brain MRIs. This is because that increasing the accuracy of age estimation in healthy MRI (i.e., the first stage) can improve the algorithm’s sensitivity to detect subtle abnormal aging in diseased populations (i.e., the second stage). Recent studies focusing on the first stage are summarized in Table 1. Compared to them, we aimed to improve (a) accuracy; (b) generality; and (c) interpretation of age estimation in healthy MRIs. We developed a novel algorithm and designed a novel study with several features toward each of these three criteria.
Table 1:
A list of machine learning studies about estimating brain age using healthy brain MRIs. Light gray rows are studies that included subjects spanning from youth (15 years) up to 97 years old. Dark gray rows are studies with ages spanning from pre-schoolers (3–5 years) up to 97 years old, or, in the current proposed work, from 0 to 97 years old. (Abbreviations: MAE - mean absolute error; WM - White matter; GM - Gray matter; CSF - Cerebrospinal fluid; ROI - regions of interest; CNN - Convolutional Neural network; ResNet - Residual neural network; LSTM - Long-short Term Memory;. Fus-CNN - our proposed attention-modulated multi-channel fusion CNN.)
| Study | Algorithm | #Subjects | Ages (years) | MAE (years) | Channels/feature |
|---|---|---|---|---|---|
| Part I. Studies using traditional machine learning | |||||
| Cole et al. (2017b) | Gaussian process regression | 2,001 | 18–90 | 5.01 | T1w WM/GM/CSF maps |
| Chung et al. (2018) | Ridge regressionR | 1,373 | 3–21 | 1.41 | T1w ROI features |
| Kwaket al. (2018) | Partial least square regression | 666 | 40–94 | 6.795 *% | Tiw ROI features |
| Lewis et al. (2018) | Linear regression | 1,592 | 3–22 | 1.52 | T1w GM image |
| Aycheh et al. (2018) | Gaussian process regression | 2,911 | 45–91 | 4.05 | T1w ROI features |
| Becker et al. (2018) | Gaussian process regression | 6,362 | 5–90 | 3.86 | T1w ROI features |
| Pomponio et al. (2020) | Generalized additive model | 10,477 | 3–96 | 5.35 | T1w ROI features |
| Hu et al. (2020) | Logistic regression | 251 | 0–2 | 0.09 † | T1w ROI features |
| Part II. Studies using deep learning | |||||
| Cole et al. (2017a) | 3D CNN | 2,001 | 18–90 | 4.16 | T1w image |
| Jónsson et al. (2019) | 3D ResNet | 1,264 | 15–80 | 3.63 | T1w image |
| Feng et al. (2020) | 3D CNN | 10,158 | 18–97 | 4.06 | T1w image |
| Jiang et al. (2020) | 3D CNN | 1,454 | 18–90 | 5.55 | T1w image |
| Bashyam et al. (2020) | 2D ResNet | 11,729 | 3–95 | 3.702 | T1w image |
| Peng et al. (2020) | 3D CNN | 14,503 | 42–82 | 2.14 | T1w image |
| He et al. (2020) | 2D ResNet+LSTM | 1,640 | 0–20 | 0.96 | T1w image |
| Proposed | 3D Fus-CNN | 16,705 | 0–97 | T1w split into contrast and morphometry images | |
: This study reported root mean square error (RMSE) instead of mean absolute error (MAE).
: While all other studies used cross-sectional data (MRI from only 1 visit), this study used longitudinal data, where each subject had 7 MRIs, scanned every 3 months until 1 year old and every 6 months until 2 years old.
Accuracy, the first criterion, refers to how algorithm-estimated brain ages approach the actual chronological ages in healthy subjects. An algorithm is more accurate if it scores a lower mean absolute error (MAE) than other algorithms in a common dataset. In studies that spanned ages from youth (15 years) up to 97 years (light gray rows in Table 1) or studies that spanned ages from preschoolers (3–5 years) up to 97 years (dark gray rows in Table 1), the current MAE is around 3.5–5.5 years. In these studies, the errors (MAEs) from traditional or deep learning algorithms are surprisingly comparable (Part I versus Part II of Table 1). Nevertheless, deep convolutional neural networks (CNNs) have led to significantly better results than traditional machine learning methods in many other analysis tasks on natural images (Krizhevsky et al., 2012; He et al., 2016) and medical images (Shen et al., 2017; Litjens et al., 2017). This motivated us to further improve the accuracy of deep learning CNN for age prediction, with three contributions toward accuracy in this paper.
We used a larger sample size to fuel deep learning toward higher accuracy. Studies in 2017–2018 typically used one to two thousand healthy subjects. Very recently, the sample size has increased to close to, or over, ten thousand. This is done by merging many publicly-available datasets on healthy brain MRIs. As shown in the third column of Table 1, our study used one of the largest sample sizes (N=16,705 by merging 11 datasets).
We explicitly split one 3D T1-weighted (T1w) image into contrast and morphometry channels (two 3D images) to improve age estimation accuracy. Some studies used diffusion or functional MRI in addition to T1w for age estimation. However, diffusion or functional MRI sequences are usually available for only hundreds to lower thousands of healthy subjects (Richard et al., 2018; Niu et al., 2020; Li et al., 2018). As recent studies mentioned, when the sample size increases to over ten thousand, T1w is usually the only MRI sequence available to all subjects (Feng et al., 2020; Pomponio et al., 2020). While T1w MRI is the only image used at this sample size, T1w MRI offers not just contrast information, as other studies used. Morphometry information, for example, can be extracted from segmented regions of interest (ROI) or tissue types and is highly related to age (Sowell et al., 2003; Pomponio et al., 2020; Gilmore et al., 2018). Explicit segmentation is more often used in age estimation studies using non-deep learning models (Cole et al., 2017b; Aycheh et al., 2018; Becker et al., 2018; Chung et al., 2018; Kwak et al., 2018; Lewis et al., 2018; Hu et al., 2020). It may not fit a 3D CNN framework as the handcrafted features often reduce the power of deep features. One novelty of our work is that we derived a 3D RAVENS image, characterizing voxel-wise morphometry in addition to the 3D intensity contrast image. The RAVENS value (regional analysis of volumes examined in normalized space) at a voxel quantifies volumetric expansion or shrinkage ratio compared to the corresponding anatomy in a common atlas, and is suitable to study brain development (Erus et al., 2015). In other words, we explicitly split the single 3D T1w image into two 3D images representing contrast and morphometry channels of information. We will show that using the T1w image as two channels with two 3D images, as we proposed, reduces errors of age estimation compared to existing studies treating the T1w image as only one 3D image, for two motivations. One motivation is that intensity/contrast information is relative in T1w, does not carry physical meanings, and can be arbitrary. In contrast, a morphometry channel with RAVENS maps is naturally normalized, has a physical meaning (voxel-wise expansion/shrinkage ratio), and is relatively stable when intensities change. The second motivation is the potential to avoid deep neural networks from being dominated by the salient information in the contrast channel while overlooking more implicit information in the morphometry channel.
We designed attention fusion networks to further improve the accuracy over current attention-free fusion algorithms. Explicitly splitting the T1w image into two 3D image channels opened up the opportunity to fuse them at the image and feature levels. Multi-channel fusion has not yet been used for brain age estimation. The state-of-the-art multi-channel MRI fusion algorithms were proposed for medical image synthesis (Zhou et al., 2020) or segmentation (Zhou et al., 2019). However, they treated different channels equally, which may not be optimal. To address this, we proposed attention mechanisms and hence a Fusion-with-Attention neural network (FiA-Net) to fuse multi-channel information. The proposed FiA-Net included hard and soft attention and mutual attention, and their combinations, to recognize and learn how different channels could contribute differently at different anatomic locations and different feature levels. This is important because attention mechanisms allow the fusion network to perform feature recalibration (Hu et al., 2019) and encourage the aggregation of multi-channel information in the presence of useless or redundant information from two channels (Li et al., 2019b). Attention has been widely used in machine translation (Vaswani et al., 2017), image classification (Wang et al., 2017; Hu et al., 2019) and medical image segmentation (Schlemper et al., 2019), but not yet for multi-modal MRI fusion, especially for brain age estimation.
Generality, the second criterion, refers to how an algorithm can be applied to data from different imaging sites, imaging scanners, and different age groups, while still achieving a consistent accuracy. We proposed two modules to promote generality.
We built our algorithm on truly lifespan data (0–97 years) for age generality and real-world utility. As Table 1 shows, those studies that constrained themselves to a narrow age range usually have a lower estimation error. For example, knowing that a healthy brain is 0–2 years of age, the estimated age would be bounded in this age range and the error of estimation will be no more than 2 years. However, in real-world applications, this assumption does not always hold. Indeed, the age estimator built from healthy MRIs will be ultimately used to quantify how brain disorders accelerate or delay brain aging in patients. For patients, we do not know the boundary of their brain ages even though the chronological ages are known. For example, a 2-year-old patient’s brain may look like a 3–5 or even 5–10-year-old brain, and vice versa. Therefore, we cannot just build a model from healthy subjects 0–2 years of age and apply it to patients 0–2 years of age. Lifespan studies that do not pose an arbitrary constraint on the range of the estimated ages are highly preferable (Pomponio et al., 2020; Becker et al., 2018; Bashyam et al., 2020). Lifespan studies emerged very recently with data in 5–90 (Becker et al., 2018) or 3–96 years of age (Pomponio et al., 2020; Bashyam et al., 2020) (see Table 1). We used subjects 0–97 years of age, so far the widest age range, which also covered 0–3 years of age when the brain develops most rapidly (Ou et al., 2017; Sotardi et al., 2021). This will largely increase the across-age generality and real-world utility of our algorithm.
We designed two phases of cross-validations, thoroughly testing the multi-site/scanner generality. The first phase of cross-validation was in the discovery cohort (N=6,049). In this phase, the training and testing data were not overlapping but some of them came from the same datasets with the same imaging site and scanners. This phase is the same as other age estimation studies (Feng et al., 2020; Peng et al., 2020). The new second phase used completely unseen data from completely different datasets, with different imaging sites, scanners, or protocols. This second phase has been rarely done in other studies, but may thoroughly reflect the multi-site/scanner generality of our algorithm.
Interpretation, the third goal, is also important for real-world utility. It is non-trivial, though, and thus not studied in many deep learning age estimation studies (Cole and Franke, 2017; Jónsson et al., 2019; Bashyam et al., 2020; Peng et al., 2020; He et al., 2020). Very few deep learning age estimation studies included interpretation. They computed the age activation map (Feng et al., 2020; Shi et al., 2020) on the brain MRIs on test subjects. An activation map is an indirect interpretation that may be useful for classification since the decision is made by maximizing the class probability (Zhou et al., 2016). However, an arbitrary testing subject may or may not represent the average response map in healthy subjects of the same age. Moreover, features with high activation/response, also known as salient features, may not necessarily possess a high predictive power. Saliency could indirectly imply predictive power but not always (Rudin, 2019). Motivated by very recent progress indirectly interpreting each artificial neuron’s role in CNNs recognizing objects in natural images (Bau et al., 2020), we used a different interpretation strategy.
We directly measured the predictive power of hidden neurons in our deep neural network model by its correlation with age. For the brain age CNN, the last artificial neuron usually represents the predicted age, which is highly correlated to the chronological age on the test set. Thus, the correlation between the last neuron’s activation and the chronological age in a cohort can be used to understand the performance of the artificial neuron in the algorithm (Hu et al., 2020; Peng et al., 2020). Similarly, this strategy can be generalized to understand every hidden neuron in the CNN, by computing the correlation between the artificial neuron’s response and the chronological ages on the evaluated cohort. The advantage of this interpreting method is that it evaluated an artificial neuron’s ability to extract age-related features over a cohort with different ages, instead of an arbitrary subject’s response (Shi et al., 2020). We used this method to measure the importance of different neurons in different layers and different attention methods. Further, it can be used to understand how the learned features in different layers correlated to the target task (e.g. age prediction). Besides, the salient regions in the brain related to normal aging could be captured by the CNN for each anatomic position, shedding light on the neuroanatomic interpretation.
Overall, we assumed that amassing one of the largest cohorts of lifespan healthy brain MRI data (Section 2 for Data), coupled with the proposed attention-driven multi-channel fusion neural network (Section 3 for Methods, Section 4), as well as comprehensive and thorough validation designs (Section 5 for Study Design), could help promote (a) accuracy, (b) generality, and (c) interpretation in brain age estimation among healthy brain MRIs (Section 6 for Results).
2. Data
2.1. Gathering lifespan healthy MRIs from 16,705 samples in 11 datasets
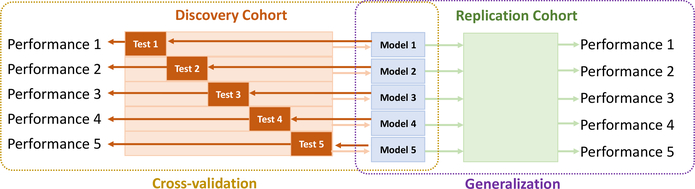
Our data includes a discovery cohort for the first phase of cross-validation and a replication cohort for the second phase of validation (see the two-phase validation in Fig. 5). As Table 2 shows, our discovery cohort included 8 datasets containing T1w MRIs from 6,049 healthy scans aged 0–97 years (47.7% males). Seven of these datasets are publicly available, and we supplemented them with a proprietary normal cohort (the MGHBCH dataset (He et al., 2020; Ou et al., 2017; Weiss et al., 2019) in Table 2) to add more subjects in the 0–6 years age range. This way, our data spans 0–97 years of age whereas other lifespan studies only used data 3–96 years of age (Pomponio et al., 2020; Bashyam et al., 2020) or 5–97 years of age (Becker et al., 2018). The discovery cohort was used for the first phase 5-fold cross-validation. Our replication cohort included 3 other independent and publicly-available datasets, with T1w MRI from 10,656 healthy samples 5–60 years of age (54.2% males). The replication cohort was used as additional but completely-unseen data for the second phase of validation of our algorithm (Fig. 2). The median age and the detailed sex ratio in each dataset and in the overall discovery and replication cohorts are all listed in Table 2.
Figure 5:
Our two-phase validation strategy. The first cross-validation happened in the discovery cohort, which was split in five folds of equal sample sizes (Test i) for five cross-validations. In each cross validation, the set ”Test i” (dark orange box) was used for evaluation and the rest four folds (light orange box) were used for training ”Model i” (blue boxes). In the second phase of validation, each trained ”Model i” (blue box) was applied on the completely-unseen replication cohort (green box) to evaluate accuracy and generality.
Table 2:
Demographics of datasets used in this paper, sorted by median age (years).
| Dataset | Nsamples | Age range [Median] | Male/Female | Scanners | |
|---|---|---|---|---|---|
| Discovery Cohort | MGHBCH (He et al., 2020) | 428 | 0–6 [1.7] | 226/202 | 3T Siemens |
| NIH-PD (Evans et al., 2006) | 1,211 | 0–22.3 [9.8] | 585/626 | 1.5T Siemens,GE | |
| ABIDE-I (Di Martino et al., 2014) | 567 | 6.47–56.2 [14.8] | 469/98 | 3T Siemens,Philips, GE | |
| BGSP (Holmes et al.,2015) | 1,570 | 19–53 [21] | 665/905 | 3T Siemens | |
| BeijingEN 1 | 180 | 17–28 [21] | 73/107 | 3T Siemens | |
| IXI 2 | 556 | 20.0–86.3 [48.6] | 247/309 | 1.5T/3T Philips,GE | |
| DLBS (Parket al.,2012) | 315 | 20–89 [54] | 117/198 | 3T Philips | |
| OASIS-3 (LaMontagne et al., 2018) | 1,222 | 42–97 [69] | 750/472 | 1.5T/3T Siemens | |
| Total | 6,049 | 0–97 [22.8] | 3,132/2,917 | - | |
| Replication Cohort | ABCD (Volkow et al., 2018) | 8,639 | 9–11 [9.91] | 4,508/4,131 | 3T Siemens,Philips, GE |
| CMI (Alexander et al., 2017) | 1,765 | 5–21.9 [10.1] | 1,117/648 | 1.5T/3T Siemens | |
| CoRR (Zuo et al., 2014) | 252 | 6–60 [20.4] | 148/104 | 3T Siemens,Philips, GE | |
| Total | 10,656 | 5–60 [12] | 5,773/4,883 | - | |
| All | 16,705 | 0–97 years | 8,905/7,800 | - | |
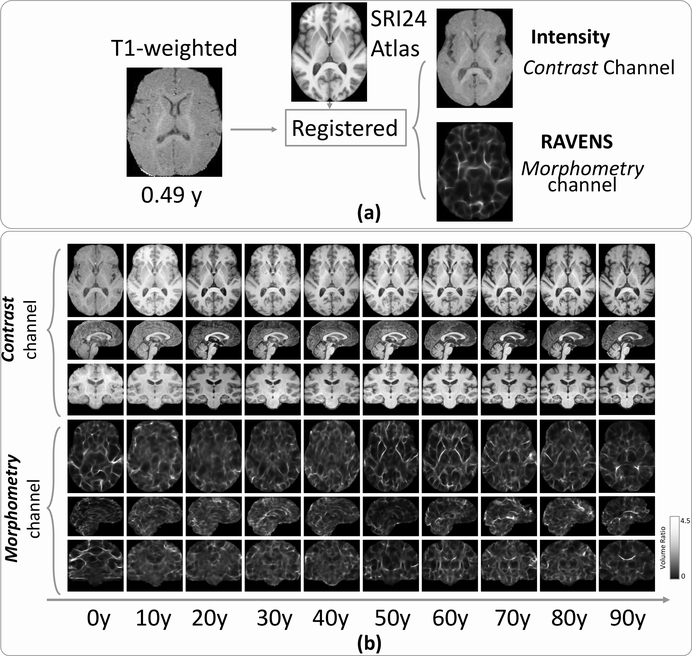
Figure 2:
Explicit split of a 3D T1w image into two 3D images representing two channels of information (contrast and morphometry). (a) A subject’s T1w image was registered to the SRI24 atlas, leading to a 3D registered intensity image (the first channel, contrast information) and a 3D RAVENS image (the second channel, morphometry information), both residing in the SRI24 atlas space. (b) Randomly-chosen subjects in every ten years of the age range for their two channels of images. Each column shows the MRI slices in the axial (top row), sagittal (middle row), and coronal (bottom row) planes. All images resided in the SRI24 atlas space.
T1w MRIs were scanned in different sites and on different scanners (1.5T or 3T, Siemens, Philips, or GE MRI scanners). Details can be found in the cited references or webpages for each dataset. Please see the next sub-section for pre-processing and harmonization. Some of these datasets also contain MRIs of diseased brains, but we only included subjects with healthy brains. These strategies were commonly adopted in other brain age estimation studies that merged multiple datasets for larger sample sizes (Cole et al., 2017a; Pomponio et al., 2020; Bashyam et al., 2020; Feng et al., 2020).
2.2. Minimum pre-processing and harmonization
Each T1w MRI underwent N4 bias correction (Tustison et al., 2010), field of view normalization (Ou et al., 2018), and Multi-Atlas Skull Stripping (MASS) (Doshi et al., 2013; Ou et al., 2015). The pipeline has been extensively validated in children as young as newborns (Zöllei et al., 2020; Morton et al., 2020) and adults as old as 100 years of age (Pomponio et al., 2020). No regional segmentation, tissue segmentation, or surface construction was used, because deep learning could receive as input the whole image and does not require these hand-crafted regional or surface features (Cole and Franke, 2017; Bashyam et al., 2020; He et al., 2020). Keeping the pre-processing minimum could also reduce the accumulations of errors, and could encourage the generality of the developed algorithm.
For the same token, harmonization of multi-site data was also kept minimum, similar to other age estimation studies using deep learning (He et al., 2020; Cole and Franke, 2017; Feng et al., 2020; Jiang et al., 2020; Bashyam et al., 2020). Specifically, the histogram of each skull-stripped T1w image was matched to the histogram of the SRI24 T1w atlas (Rohlfing et al., 2010). This atlas was used to split the T1w image into two channels, as the next section will describe. Then, the intensities in each skull-stripped and histogram-matched T1w image were normalized into 0–1, by subtracting the mean intensity and dividing the standard deviation intensity in each brain. The histogram matching and intensity normalization steps served as harmonization across datasets. More sophisticated scanner- or site-specific harmonization could be used but were not used. This was similar to other age estimation studies, because the purpose was for the algorithm to generalize well to other datasets with unforeseen sites, scanners, or imaging protocols, not just for the algorithm to have a super good performance in our dataset (Cole and Franke, 2017; Feng et al., 2020; Bashyam et al., 2020).
3. Methods
3.1. Overview of the proposed network architecture
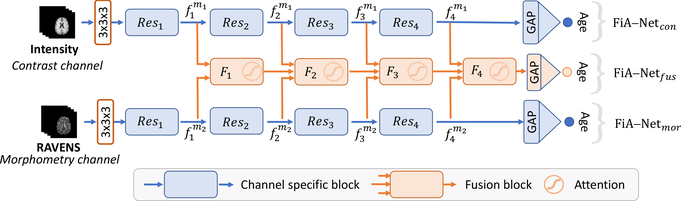
Fig. 1 shows the overall architecture of our proposed attention-driven multi-channel fusion neural network (FiA-Net). Two channel-specific networks FiA-Netcon and FiA-Netmor, shown as the two blue paths in Fig. 1, provide intermediate results. They learn from the contrast and morphometry channels independently. One attention-driven fusion network FiA-Netfus, shown in the orange middle path in Fig. 1, offers the final brain age estimation results.
Figure 1:
Overview of the proposed network architecture. It has three branches: two channel-specific networks (FiA-Netcon and FiA-Netmor, top and bottom paths in blue colors) provide channel-specific age estimation results, and one attention-driven fusion network (FiA-Netfus, middle path in orange) provides the final age estimation results. In channel-specific branches, the Resi(i = 1, 2, 3, 4) boxes are residual network blocks, and are the intermediate deep features of channel image mi after the ith residual block. In the fusion branch, the Fi boxes are the fusion blocks. GAP is the global average pooling.
The following sub-sections detail our algorithm. Splitting a 3D T1w image into two 3D images, the first novelty of our framework, will be described in Section 3.2. It led to channel-specific neural networks in Section 3.3 and multi-channel fusion. Our proposed multi-channel fusion is a layer-level fusion (Section 3.4) driven by the proposed attention mechanisms (Section 3.5).
3.2. Splitting T1w into two channels
The skull-stripped and harmonized 3D T1w image was non-rigidly registered to the SRI24 atlas (Rohlfing et al., 2010) by the Deformable Registration via Attribute-Matching and Mutual-Saliency weighting (DRAMMS) algorithm (Ou et al., 2011), which has been extensively validated for across-subject registration over the lifespan (Ou et al., 2014). The publicly-available SRI24 atlas has a voxel size of 1×1×1mm, and was constructed from T1w of 24 healthy brains (12 young subjects 25.5±4.3 (19–33) years of age and 12 old subjects 77.7±4.9 (67–84) years of age).
As shown in Fig. 2a, registering to the SRI24 atlas space led to the split of a single 3D T1w image into two 3D images representing two channels of information. One channel is the 3D registered intensity image, having the same anatomy as the SRI24 atlas and representing the contrast information (top row in Fig. 2a). The other channel is the 3D RAVENS map (regional analysis of volumes examined in normalized space (Davatzikos et al., 2001)), also in the SRI24 atlas space. The 3D RAVEN image encoded the density, or relative volume ratio, at each voxel of this subject with regard to its corresponding voxel in the atlas space (bottom row in Fig. 2a). This channel quantified voxel-wise morphological information. RAVENS map was used because it preserves the whole-brain volume (Davatzikos et al., 2001), because of its extensive use as a 3D quantitative morphometric map in brain development studies related to cognition and aging (Erus et al., 2014; Da et al., 2014; Truelove-Hill et al., 2020), and because RAVENS map is a by-produce of the registration step (hence no additional pre-processing is needed).
We chose the SRI24 atlas for two reasons. One, in our previous work with a smaller sample size (N=1,640, ages 0–22 years) (He et al., 2020), we found that the age estimation errors were statistically equivalent using the SRI24 or using a 6-year-old pediatric brain atlas (Ou et al., 2017). A second reason was to encourage real-world utility. Using a fixed SRI24 atlas, our framework could be applied to subjects of all ages without needing to know a rough age range beforehand.
3.3. Channel-specific network
For each channel, we used a 3D version of the residual network (He et al., 2016) to extract deep features. ResNet is a widely used neural network architecture for many computer vision and medical image analysis tasks. A typical residual network has four stages, in which the small convolutional kernels with a size of 3×3×3 is typically used in the convolutional layers, and another kernel with a size of 1×1×1 is used in the shortcut paths. Our residual block Resi as shown in Fig. 1 contained two 3D convolutional layers with a short connection. This was the same as the ResNet in He et al. (2016). The spatial resolution was reduced to half after each stage, by a convolutional layer with a stride of 2, while the number of features was doubled. Therefore, the Resi+1 block in Fig. 1 had a half of the resolution and doubled feature size than the Resi block. This way, the spatial information was converted gradually to the semantic information of brain age from Res1 to Res4.
In this paper, we used ResNet-18 as the backbone and we removed the first max-pooling layer to keep the spatial resolution at the beginning. The number of channels on each block was the same as the number of channels on the ResNet. Thus, each Resi block in Fig. 1 contained two residual blocks. The kernel size of the convolutional layer was 3×3×3 with a padding of 1. After each convolutional layer, instance normalization (Ulyanov et al., 2016) was used to remove instance-specific contrast information, followed by a Rectified Linear Unit (ReLU) layer.
3.4. Layer-level fusion without attention - current state-of-the-art
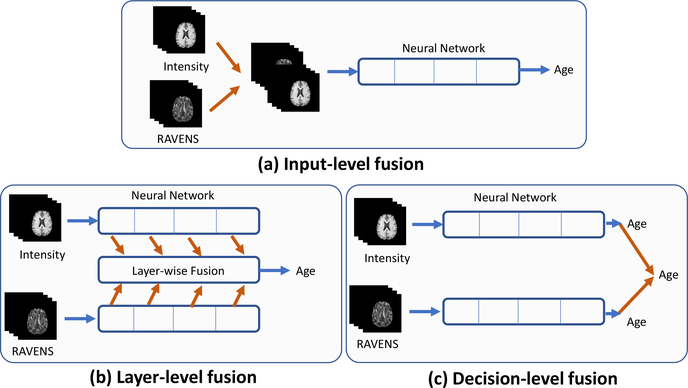
There are three strategies to fuse information from multiple channels. Input-level fusion concatenates input images from different channels (Fig. 3a). layer-level fusion merges deep features from different channels (Fig. 3b). Decision-level fusion makes a collective decision from multiple decisions independently drawn from different channels (Fig. 3c). Among them, layer-level fusion often outperforms the other two fusions strategies, although at a cost of higher computational burdens (Zhou et al., 2019; Feichtenhofer et al., 2016; Zhou et al., 2020). Therefore, our multi-channel fusion was a layer-level fusion, for each of the four layers as shown in Fig 1.
Figure 3:
Three different fusion strategies. Orange arrows represent the fusion.
Let us use to denote the deep features extracted by the residual block Resi at ith resolution level (i.e., ith layer) from the contrast channel image . Similarly, let us use to denote the deep features extracted by the residual block Resi at the ith layer from the morphometry channel image . Here, four levels are used, i.e., i = 1,2,3,4, following the standard ResNet settings (He et al., 2016). The state-of-the-art layer-level fusion algorithm used in medical image analysis (primarily for medical image synthesis (Zhou et al., 2020) and medical image segmentation Zhou et al. (2019)) is to fuse these intermediate feature maps without the attention mechanism. That is, they treated deep features and from two channels equally, by taking the maximum of them with equal weights (hence the fused maximum deep feature ) or by adding them with equal weights (hence the fused additive deep feature ), or by multiplying them with equal weights (hence the fused multiplicative deep feature ).
| (1) |
where , and are three fusion outputs (maximum, additive and multiplicative operations). This layer-level fusion algorithm does not consider the relative importance between the two-channel inputs (Zhou et al., 2020, 2019). We will use this attention-free layer-level fusion algorithm as a baseline algorithm later in our algorithm validation.
3.5. Fusion with attention - our proposed algorithm
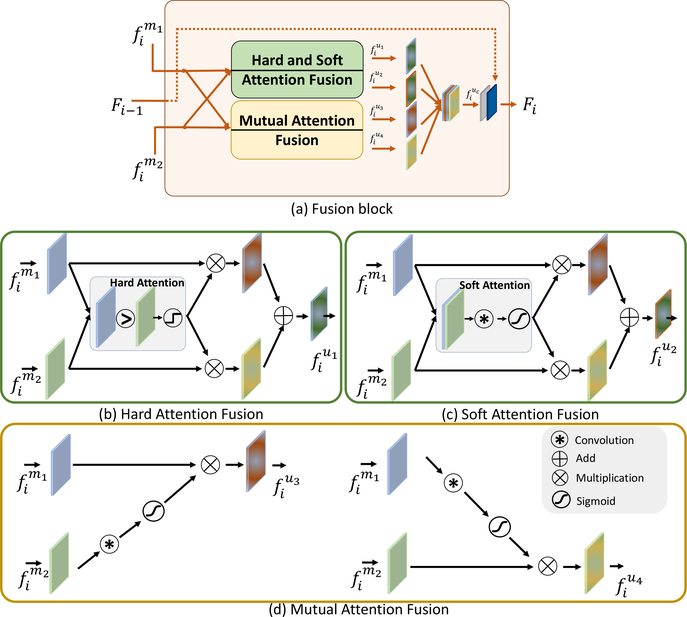
We proposed to add attention mechanisms into Eq. 1. Specifically, we proposed to introduce “hard attention” into the maximum fusion , turning it to ; we introduced “soft attention” into the additive fusion , turning it into ; and, we introduced “mutual attention” into the multiplication fusion , turning it into and . Fig. 4a shows the overview of these four attention mechanisms. Then Fig. 4b–c show each one of them.
Figure 4:
The proposed attention-driven fusion block in the ith layer. (a) Overview of the fusion block, which contains four attention mechanisms: hard attention, illustrated in (b) and the output features are denoted as ; soft attention, illustrated in (c) and the output features are denoted as ; and two mutual attentions, illustrated in (d) and the output features are denoted as and .
Hard attention kept features from only channel at a specific location and feature element. This is shown in Fig. 4(b). The weights of the hard attention was binarized to 1 or 0, controlled by the max operation by:
| (2) |
where and were deep features from different channels m1 and m2 in the ith residual block in Fig. 1. λ was a binarized weight of the two channels. ⨂ was the element-wise multiplication, “C” was the convolutional layer with a kernel size of 3 × 3 × 3 and were the fused features of the hard attention.
Soft attention combined features from different channels with learnable weights (Schlemper et al., 2019; Hu et al., 2019). The weights were continuously valued between 0 and 1, and had a sum equal to 1. It is shown in Fig. 4(c) and formulated as follows:
| (3) |
where σ(x) = 1/(1 + e−x) was the Sigmoid function with the output λ [0, 1], “[.,.]” was the concatenate operation and i ϵ [1, 4] was the index of the block.
Mutual-attention fusion applied the attention mechanism cross different channels. It assumed that deep features from one channel should be emphasized if the feature responses in the other channel were strong. In other words, it mutually emphasized the important features and suppressed the irrelevant features (Xu et al., 2018). Mutual-attention fusion is sketched in Fig. 4(d) and defined as:
| (4) |
where was the attention computed from the deep feature and the same strategy applied to . The definitions of σ and C were the same as in above.
Finally, these four fusion outputs were combined by:
| (5) |
where the outputs were concatenated as , followed by a convolutional layer C, a normalization layer and an activation layer. We obtained the fused features Fi on the ith block shown in Fig. 1. Note that when i = 1, there was no previous input, and the output of the first convolutional layer was simply fed into the second convolutional layer. If i > 1, the previous output Fi−1 was concatenated, followed by another set of convolutional, normalization, and activation layers.
| (6) |
4. Algorithm implementation
We used the global average pooling at the end of the convolutional layers, followed by a fully-connected layer for brain age regression. For network training, we used the mean absolution error (MAE) as the loss function, which was defined by:
| (7) |
where N was the number of samples, pi was the known chronological age of the subject and was the estimated brain age from the neural network. Since there were three outputs of the proposed fusion network: FiA-Netint, FiA-NetRAV, FiA-Netfus (as shown in Fig. 1), the total training loss was defined as:
| (8) |
The network was trained from a random weight initialization using the Adam optimizer with β1 = 0.9, β2 = 0.999. The learning rate was set to 0.0001 and the total training epochs was 20. The training of the 3D neural network required a large memory, thus the batch size was set to 1 for saving the GPU memory and the instance normalization is applied. The network was trained on a single NVIDIA Titan V GPU with 24G memory, using the PyTorch deep learning libraries. The source code is available: https://github.com/shengfly/FiAnet.
5. Experimental setup
In this section, we first present our experiments to understand the effects of the key modules in our algorithm (Section 5.1). Then, we describe our experimental settings to (a) evaluate accuracy (Section 5.2); (b) assess generality (Section 5.3); and (c) visually interpret the proposed framework (Section 5.4).
5.1. Experiments to understand our algorithm
We used 5-fold cross-validation in the discovery cohort to quantify the effects of three major modules in our algorithm. The accuracy metrics include mean absolute error (MAE) and cumulative score (CS), which can be found in a later Section 5.2.
The first key module in our algorithm is splitting the 3D T1w image into two channels for multi-channel fusion, as detailed in Section 3.2 and Fig. 2. We compared the cross-validation accuracy in the discovery cohort, for (i) using the contrast channel alone; (ii) using the morphometry channel alone; and (iii) fusion of two channels at the simplest form: input-level fusion (see Fig. 3). For each of these three branches, we computed the mean and standard deviation values of the mean MAE and CS in the 5-fold cross-validation. We expected that two channels, even in the simplest form of fusion (namely, the input-level fusion), would lead to a smaller error than each channel alone. This would justify the explicit split of T1w into two image channels in our algorithm.
The second key module in our algorithm is the layer-level fusion of two channels, as described in Section 3.4 and Fig. 3. Given two input channels, we compared (i) input-level; (ii) layer-level (without attention yet); and (iii) decision-level fusions. We recorded the mean and standard deviation values of the mean MAE and CS in the 5-folder cross-validations in the discovery cohort. We expected that layer-level fusion, even without attention, would have a lower error than the other fusion strategies. This would justify the use of layer-level fusion in our algorithm.
The third key module in our algorithm is the attention mechanisms to drive the layer-level fusion, as described in Section 3.5 and Fig. 4. We compared (i) layer-level fusion without attention, which is the state-of-the-art multi-channel medical image fusion strategy (Zhou et al., 2020); and (ii) layer-level fusion with attention, which is the proposed FiA-Netfus. We expected that attention mechanisms would further reduce the errors in age estimation.
One other question would also help better understand our algorithm. Question: given the four proposed attention models (hard attention in Eq. 2, soft attention in Eq. 3, and two mutual attention models and in Eq. 4, and their concatenation in Eq. 5, which attention model played a more important role? For this, we computed the Pearson correlation coefficients between features after each of the attention model (in the 4th layer) and the known chronological ages across subjects in the discovery cohort. An attention mechanism was considered more effective if the features after that attention mechanism had an overall higher level of correlation with the age information.
5.2. Experiments to evaluate the accuracy of our algorithm
Before we describe the experiment setup for evaluating accuracy, let us first define two accuracy metrics: the mean absolute error (MAE) (defined in Eq. 7) and the cumulative score (CS) (Geng et al., 2007). The MAE is a widely used measurement for brain age estimation (Feng et al., 2020; Pomponio et al., 2020) and CS is used to evaluate the performance of the system with different error levels (Geng et al., 2007; He et al., 2020; Chen et al., 2013). In our work, the CS was defined as:
| (9) |
where Ne≤α was the number of test MRI samples on which the age estimation made an absolute error e no higher than the error threshold α years. A higher CS(α) meant better performance. The CS was a function of the error threshold α, thus, results with this metric were given as curves, as α increased. We also recorded the performance of CS with certain error thresholds, such as α = 2 and α = 5 years.
We designed two experiments to evaluate the accuracy of our algorithm.
(a). Validate accuracy among state-of-the-art algorithms in the same data.
Using the 5-fold cross-validation strategy in the discovery cohort, we evaluated the accuracy of our algorithm (FiA-Netfus) with two state-of-the-art algorithms. The whole discovery cohort was randomly split into 5 folds of equal sample size. Each time, 4 folds were used for training and the left-out one fold was used for testing, until each fold had been used once and only once. The average and standard deviation of MAEs in cross-validations are reported in this paper. One algorithm we compared against was the widely-used 3D CNN single-channel (T1w image) for age estimation (Cole and Franke, 2017). Splitting the T1w image into two or more channels does not exist for age estimation, but using multi-channel MRI exists for MRI synthesis in an algorithm named Hi-Net (Zhou et al., 2020). It is a layer-level fusion method, but without attention (i.e., equal weights across channels). Hi-Net (Zhou et al., 2020) with two of our input channels (contrast and morphometry) was therefore used as the second competing algorithm in our validation.
(b). Validate accuracy among other studies that used different datasets.
Various brain age estimation studies exist, with the growing sample sizes and wider age ranges in recent studies (see Table 1). Different studies used different datasets, different pre-processing, different algorithms, and different cross-validation schemes. We know that the error of age estimation is largely dependent on the age range of the datasets. For example, building an estimator for subjects ages 0–2 years would have bounded the error to be within 2 years. Therefore, we could only list studies for their age ranges and reported MAEs. Among them, we closely compared our MAE with MAEs in other studies with similar age ranges.
5.3. Experiments to assess the generality of our algorithm
We designed two experiments to assess the generality of algorithms.
(a). Evaluate generality across different datasets.
An ideal algorithm should be generally applicable to various datasets and should score low MAEs across datasets, despite datasets coming from different sites, scanners, and imaging protocols. From this perspective, we recorded the MAEs in all 11 datasets in our data, to compare three algorithms ResNetfus (He et al., 2016), Hi-Netfus (Zhou et al., 2020), and our proposed FiA-Netfus. Of those 11 datasets (see Table 2), 8 were used in the discovery cohort for cross-validation, and the other 3 were used as completely-unseen replication cohort for the second-phase more challenging validation (see Fig. 5). An algorithm was considered more general if it scored lower MAEs in more datasets, especially among those 3 datasets in the replication cohort.
(b). Evaluate generality when the training samples changed.
As the red blocks in Fig. 5 show, we had 5-fold cross-validations in the discovery cohort. They let us build five age estimators, each using 80% of the samples in the discovery cohort. The five age estimators are shown as the blue boxes in the middle of Fig. 5. We obtained five predicted ages, from the five age estimators, for each subject in the replication cohort (green box in Fig. 5). By this setting, we not only had an average among the five absolute errors (AE) for a subject n in the replication cohort, denoted as μAE(n), but also a standard deviation among the five absolute errors for this subject, termed as σAE(n). Indeed, the MAE of an algorithm was , where N is the total number of subjects. Here, σAE(n) quantified how general or stable the algorithm was when the training samples changed. Or, in short, it reflected the uncertainty of the age estimation on this subject n in the replication cohort. Therefore, we could quantitatively compare the generality among ResNetfus (He et al., 2016), Hi-Netfus (Zhou et al., 2020), and our proposed FiA-Netfus. An algorithm was considered more general/stable when training samples changed, if its uncertainties across subjects in the replication cohort, i.e., , were lower than those by other algorithms.
5.4. Experiments to visually interpret our algorithms
Currently, one widely-used method to interpret deep neural network is through the class activation map (CAM) (Zhou et al., 2016). CAM localizes the salient features on the last layer of the deep neural network and maps them back to the original input image. Here, salient features are defined as those with higher magnitudes of responses from convolutions than other features. Grad-CAM (Selvaraju et al., 2017) can further map the salient features on any target layers of the neural network for visualization in the input image. Along this line, recent age estimation studies created age activation maps (Feng et al., 2020; Shi et al., 2020) on brain MRIs. However, features with high responses may not always be those features that predict age. Conversely, features strongly correlated with age may not always have strong responses to convolutions, and may not always be salient features. This is very similar to the situations in medical image segmentation, registration, and prediction tasks, where the salient features may not always the best features for classifying voxels (Sharif et al., 2020), finding voxel correspondences (Ou et al., 2011), or predicting outcomes (Sun et al., 2019).
To address this issue, we explicitly quantified the correlations between features from each artificial neuron in the deep neural network and the chronological ages. A neuron in the deep neural network with a high correlation with age was considered of a higher predictive value. This way, features that may not be salient but were strongly correlated with age could be identified. This was also similar to very recent progress in interpreting neurons in deep neural networks for natural image recognition (Bau et al., 2020).
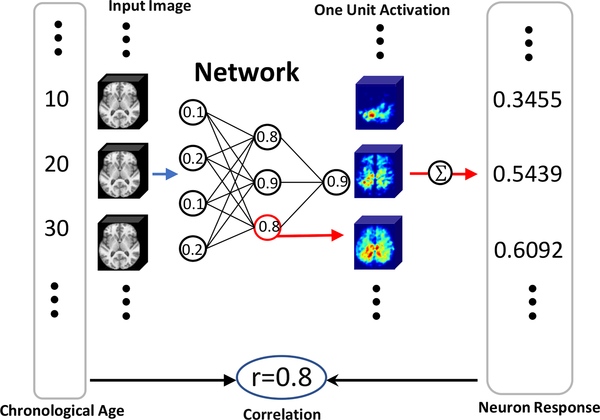
Our interpretation strategy is illustrated in Fig. 6. Once the age estimation model was trained (shown as the ”Network” in Fig. 6), the predictive value ri of every voxel uin the ith neuron was computed using a forward pass
| (10) |
where was the vector of chronological age across subjects (the big vertical box containing chronological ages at the left side of Fig. 6), was the vector of features in at voxel u of the ith neuron (the big vertical box containing neuron response features at the right side of Fig. 6). was the calculated Pearson correlation (the circled correlation number in the bottom middle of Fig. 6).
Figure 6:
Strategy to interpret the predictive value of each neuron in the deep neural network.
The calculation was done at every voxel in every neuron, but due to space limitations, we could not display them all. We will show in the Results Section 6.4, the voxel-wise correlation with chronological ages for four neurons with the largest weights in the last layer of FiA-Netfus. These were the four most heavily used neurons in FiA-Netfus. Besides visualization, we also segmented the SRI24 into 62 regions (Doshi et al., 2016; Sotardi et al., 2021; Morton et al., 2020), and calculated the average correlation coefficients in each ROI for each of those four highest-ranked neurons. This would quantify which neuroanatomic regions were more involved in the age estimation in FiA-Netfus.
6. Experimental results
Here we report the results corresponding to each of these sub-sections in Experimental setup (Section 5). Results to understand three key modules and two key choices in our algorithm are in Section 6.1, and then results for accuracy, generality, and interpretation are in Sections 6.2, 6.3, and 6.4, respectively.
6.1. Results to understand our algorithm
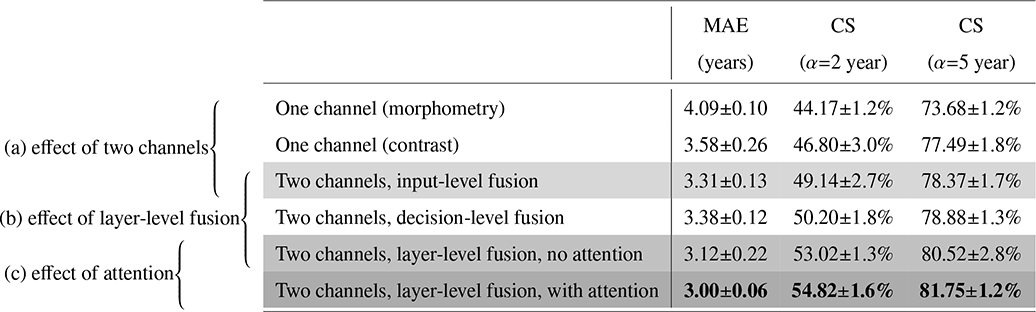
Parts a,b,c in Table 3 show the effect of the three key modules in our algorithm.
Table 3:
Quantification of the effects of the three key modules in our algorithm. Results are obtained by 5-fold cross-validations in the discovery cohort.
 |
(a). Effect of splitting the T1w image into two channels.
The first three rows (Part a) in Table 3 show that explicitly splitting the T1s image into two channels and fusing the two channels provided better results than each channel alone.
(b). Effect of layer-level multi-channel fusion.
The third to the fifth rows (Part b) in Table 3 show the results of different fusion strategies. Layer-level fusion, even without attention mechanisms, provided better performance than the input-level and decision-level fusion strategies.
(c). Effect of attention mechanisms.
The fifth and sixth rows (Part c) in Table 3 show that the proposed attention mechanisms further improved the accuracy of layer-level fusion compared with the one without attentions.
Overall, results in Table 3 help us better understand the three key modules in our algorithm. Splitting the T1w image into two channels reduced the average MAE from 4.09 to 3.31 years. On top of that, layer-level fusion further reduced the average MAE to 3.12 years. Then on top of that, attention mechanisms reduced the average MAE even further to 3.00 years. These three modules in our algorithm also led to more subjects having errors less than 2 years (from the initial 44.2% to 49.1%, then to 53.0%, and finally to 54.8%), and more subjects having errors less than 5 years (from the initial 73.7% to 78.4%, then to 80.5%, and finally to 81.8%). Therefore, the three key modules in our algorithm were all necessary and effective.
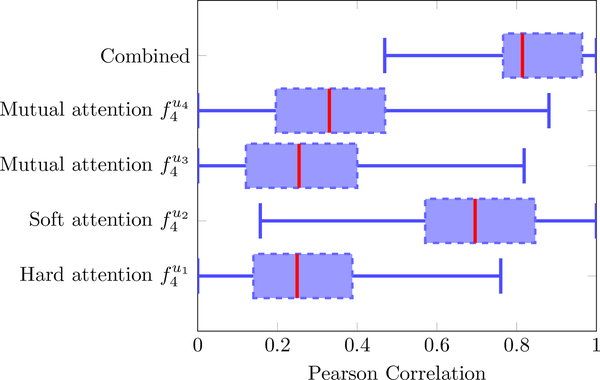
When it came to which of the four proposed attention mechanisms was more effective, Fig. 7 shows such a comparison in the last layer. The soft attention was more informative of age, while the other three attention models all contributed, and the concatenation of all features was most informative than each attention mechanism alone. Therefore, the proposed hard, soft, and mutual mechanisms (sketched in Fig 4a and defined in Eq. 5) were all needed and their concatenation outperformed every single mechanism.
Figure 7:
Further understanding of the important choices in our algorithm. The predictive value of the four attention mechanisms and their concatenations (, , , , and ) at the last layer of the fusion branch FiA-Netfus.
With the justification of these major modules and choices in our algorithms, the next subsections will present results for the accuracy, generality, and interpretation of FiA-Netfus.
6.2. Results for accuracy
Section 5.2 introduced two experiments to validate the accuracy of our algorithm. The results of these two experiments are shown below.
(a). Accuracy compared to state-of-the-art algorithms in the same data.
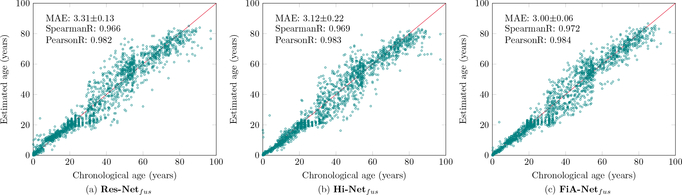
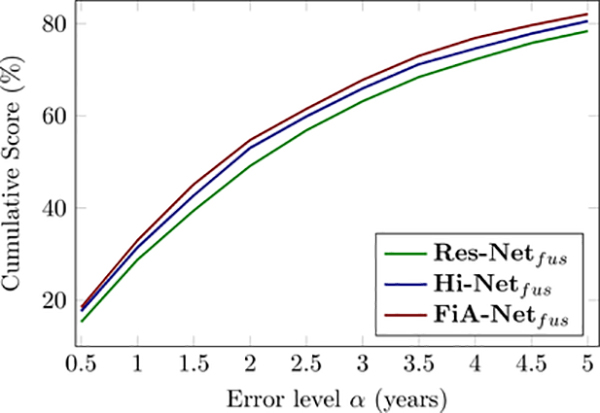
Fig. 8 compares the accuracy of three algorithms on the same data, by the same 5-fold cross-validation in our discovery cohort. FiA-Netfus had the lowest MAE, the highest Pearson and Spearman correlations between the predicted and actual chronological ages than the other two algorithms (ResNetcon (He et al., 2016) and Hi-Netfus (Zhou et al., 2020)). Similarly, when we measured the accuracy by CS(α) values at different thresholds of α, Fig. 9 shows that FiA-Netfus led to a larger percentage of subjects having errors lower than a certain error level α, for all possible error levels. By both metrics, FiA-Netfus scored the highest accuracy among the three algorithms in the same data (our discovery cohort) and by the same cross-validation strategy.
Figure 8:
Accuracy comparisons among three algorithms using the same data and the same 5-fold cross-validation strategies, using MAE as the accuracy metric. The solid red line in each panel describes the ideal predictions where the predicted ages are identical to the chronological ages. Each green dot represent a subject.
Figure 9:
Accuracy comparisons among three algorithms using the same data and the same 5-fold cross-validation strategies, using CS as the accuracy metric. The CS curve of brain age estimation using the different networks in cross validation.
(b). Accuracy compared to other studies that used different datasets.
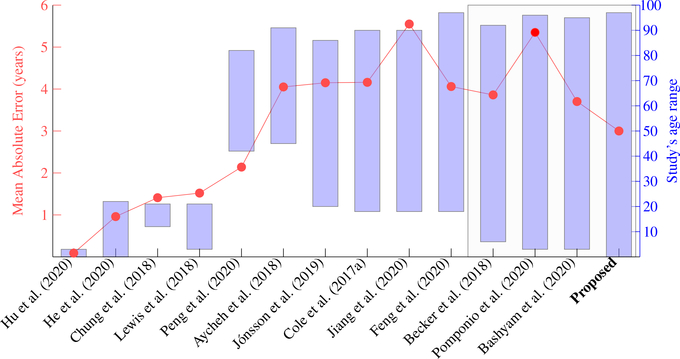
Fig. 10 shows 14 studies conducted in 2018–2020. The red dots show the MAEs in each study and follow the red scale on the left side of the figure. The blue boxes show the age ranges of the study and follow the blue scale on the right side of the Figure. The first observation is that errors are highly related to the age ranges in studies. For example, Hu et al. (2020) reported an MAE at 0.09 years for 251 healthy brains scanned during 0–2 years of age. Plus, unlike other studies that used cross-sectional images (MRI at a visit), Hu et al. (2020) used longitudinal brain MRIs of the same subjects scanned repeatedly at 1, 3, 6, 9, 12, 18, and 24 months of age. In other studies with age ranges 3–22 years (Chung et al., 2018; Lewis et al., 2018), the MAEs were around 1.5 years. But, that does not necessarily mean their algorithm was more accurate because the effect of age ranges should be considered (Jiang et al., 2020). A more fair comparison is in studies of roughly the same range. For this purpose, we highlight four studies on the rightmost of the figure, as within a black box. These four studies were: Becker et al. (2018) with MAE=3.86 years using 6,362 healthy brains 5–90 years of age; Pomponio et al. (2020) and Bashyam et al. (2020) with MAEs at 5.35 and 3.702 years using 10,477 and 11,729 healthy brains 3–96 years of age, and ours with MAE=3.00 years using 16,705 healthy brains 0–97 years of age. Among these four studies using very similar age ranges and similar sample sizes, our study had the lowest MAE. Although, it is difficult to conclude whether our lower MAE came from the algorithm, the sample size, or the dataset themselves. Therefore, comparison in this figure is just a reference, and the most rigorous comparison excluding the effect of sample size, age range, and data samples should be those results using the same data, as we presented in the previous paragraph and in Fig. 8.
Figure 10:
Accuracy comparison among different studies that used different datasets. Each column is one study. They used different datasets and had different age ranges. Red dots, following the red scale bar on the left, are the Mean Absolution Error (MAE) in each study. Blue bars, following the blue scale bar on the right, are the age ranges in each study. Our proposed study is represented by the blue bar on the most right part of the figure. The gray rectangle box highlights four studies, in the right part of the figure, which used > 6,000 subjects and lifespan data. Therefore, these studies in the gray rectangle box are more comparable, and among them, our study had the lowest MAE.
6.3. Results for generality
Section 5.3 introduced two experiments to evaluate the generality of our algorithm. Below, we show the results of these two experiments.
(a). Generality across datasets.
Table 4 shows the MAE and CS values for each dataset in the discovery and replication cohorts. The proposed FiA-Netfus had the lowest MAE and the highest CS values in 6 out of 8 datasets in the discovery cohort where 5-fold cross-validation was done. When the model that was trained in the discovery cohort was applied to the completely-unseen replication cohort, FiA-Netfus scored the lowest MAE and the highest CS values among three algorithms in all three replication datasets. More importantly, the margins between the MAEs of FiA-Netfus and the MAEs of the other two competing algorithms were wider in the replication cohort than in the discovery cohort. Overall, the results in Table 4 clearly show that the proposed FiA-Netfus algorithm could not only generalize among the discovery datasets in cross-validations, but even more generalizable than the other two algorithms in completely-unseen replication data. This suggests that the proposed FiA-Netfus could better capture the true age information from brain MRI and less contaminated by imaging sites, scanners, or parameters. In other words, the model resulted from FiA-Netfus was found more generalizable to different datasets.
Table 4:
Generality comparisons among three algorithms across datasets. Here, the generality as measured by the MAEs in each dataset in the discovery and replication data, as mentioned in Section 5.3(a).
| ResNetfus (He et al., 2016) |
Hi-Netfus (Zhou et al., 2020) |
FiA-Netfus |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | Nsubjects | Age range (years) | MAE (years) | CS (α=2 years) | CS (α=5 years) | MAE | CS (α=2 years) | CS(α=5 years) | MAE | CS (α=2 years) | CS (α=5 years) | ||||
| Discovery Data | BeijingEN | 180 | 17–28 | 2.14 | 59.4% | 91.7% | 1.86 | 68.3% | 95.0% | 1.73 | 65.0% | 96.7% | |||
| DLBS | 315 | 20–89 | 5.95 | 22.5% | 50.8% | 6.29 | 20.3% | 47.9% | 5.58 | 23.8% | 54.6% | ||||
| MGHBCH | 428 | 0–6 | 1.81 | 72.7% | 92.8% | 0.90 | 91.8% | 98.4% | 0.99 | 90.0% | 98.4% | ||||
| IXI | 556 | 20–86 | 6.10 | 24.3% | 51.4% | 6.28 | 22.3% | 47.7% | 6.3 | 20.5% | 46.3% | ||||
| ABIDE-I | 567 | 6–56 | 3.51 | 42.0% | 79.9% | 3.22 | 49.0% | 82.2% | 3.07 | 49.9% | 84.6% | ||||
| NIH-PD | 1,211 | 0–22 | 1.59 | 69.3% | 96.6% | 1.44 | 75.1% | 97.6% | 1.31 | 80.9% | 97.8% | ||||
| BGSP | 1,570 | 19–53 | 2.03 | 64.3% | 91.4% | 1.93 | 65.9% | 93.5% | 1.88 | 66.8% | 93.7% | ||||
| OASIS-3 | 1,222 | 42–97 | 4.70 | 29.9% | 62.3% | 4.42 | 32.2% | 67.0% | 4.22 | 35.0% | 70.4% | ||||
| All | 6,049 | 0–97 | 3.31 | 49.1% | 49.4% | 3.12 | 53.0% | 80.5% | 3.00 | 54.8% | 82.1% | ||||
| Replication Datal | ABCD | 8,639 | 9–12 | 3.17 | 34.8% | 81.7% | 3.55 | 37.0% | 76.4% | 2.86 | 48.8% | 92.3% | |||
| CMI | 1,765 | 5–22 | 3.29 | 38.7% | 80.4% | 3.79 | 37.4% | 74.1% | 2.97 | 44.1% | 83.8% | ||||
| CoRR | 252 | 6–60 | 6.43 | 32.6% | 60.6% | 5.47 | 37.5% | 66.7% | 5.35 | 41.0% | 66.6% | ||||
| All | 10,656 | 5–60 | 4.29 | 35.4% | 74.3% | 4.27 | 37.3% | 72.4% | 3.72 | 44.6% | 80.9% | ||||
(b). Generality when the training samples changed.
In the second experiment (See Section 6.3 for more detail), the five age estimators, each trained using 80% of the discovery data, led to five estimated ages and hence five errors for each of the subjects in the replication cohort. These five estimated ages should be ideally identical (i.e., zero standard deviation among these five estimated ages for each replication subject). In reality, a standard deviation closer to zero is preferred. Table 5 shows the mean of the standard deviations among the five estimated ages for each subject in the replication cohort. The proposed FiA-Netfus algorithm had the lowest standard deviation overall, suggesting the highest stability/generality when the training samples varied.
Table 5:
Generality comparisons among three algorithms when the training samples vary. Here, generality was measured by the mean of the standard deviations among the 5 estimated ages for each subject in the three replication datasets, as detailed in Section 5.3(b).
| mean of stdev among 5 models | ResNetfus (Heetal., 2016) | Hi-Netfus (Zhou et al., 2020) | FiA-Netfus (Proposed) |
|---|---|---|---|
| ABCD | 1.66 | 2.11 | 1.75 |
| CMI | 1.83 | 1.82 | 1.52 |
| CoRR | 2.84 | 2.56 | 2.34 |
| Average | 2.11 | 2.17 | 1.86 |
6.4. Results for interpretation
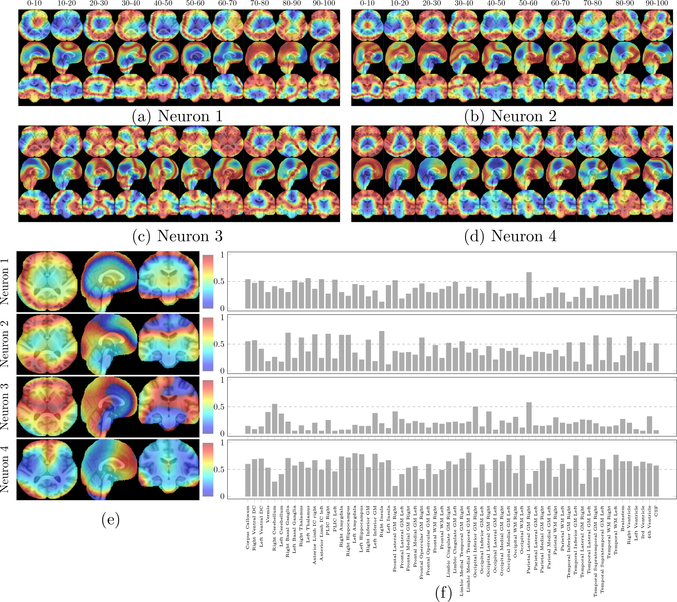
We computed the Pearson correlation coefficients between chronological age and feature responses at every voxel in every neuron on the last layer of FiA-Netfus. Note that a neuron contains features at every voxel in the brain, therefore the correlation or the predictive value was calculated at each voxel in a neuron. The correlation map for a neuron was then resized to the space of the original image (SRI24 space) by the 3D trilinear interpolation. Fig. 11 shows the voxel-wise correlation maps for four neurons with the largest weights (in absolute values) among all neurons in the last layer of our deep neural network. In other words, these four neurons were the most important driving forces in the last layer of FiA-Netfus. Fig. 11(a)–(d) show voxel-wise correlations with chronological ages in these four neurons on different age groups (with 10-year interval) and Fig. 11(e) shows the voxel-wise correlation with chronological ages in these four neurons over 0–97 years. Visual observation from these figures shows that the occipital, parietal, and frontal lobes were all driving forces for age estimation. ROI analyses, in Fig. 11(f), found that the neuroanatomic regions mostly involved age estimation in FiA-Netfus were: occipital and temporal white matter, parietal lateral, temporal inferior, and temporal lateral gray matter, insula, basal ganglia, ventricle, amygdala, hippocampus, and cerebellum. Deep features from these anatomic regions in the last layer of FiA-Netfus had an average 0.55–0.75 Pearson correlation coefficients with the chronological ages.
Figure 11:
Interpretation of four most-weighted neurons in the last layer of FiA-Netfus. (a)-(d): voxel-wise correlations with chronological ages in the four neurons on different age groups. (e): voxel-wise correlations with chronological ages in each neuron over 0–97 years. The neurons were ranked by their weights in the last layer of FiA-Netfus in descending order. (f): average correlations in 62 auto-segmented brain structures.
Besides, the saliency maps in Fig 11 show a central-to-peripheral and posterior-to-anterior pattern of “activated” brain regions transitioning from 0–10 to 10–20 and 20–30 years. This echoes our recent findings of myelination maturation in a similar neuro-development pattern but on a larger age scale (Sotardi et al., 2021). Neuroanatomy for age estimation stayed relatively stable during 30–40, 40–50 and 50–60 years of age intervals. The activated regions in later adulthood were almost inverse of those in early childhood. Our future study will dive into a higher spatiotemporal granularity of such patterns and statistically compare how this agrees with computational neuroscience findings across the lifespan.
7. Discussion and Conclusion
Machine-learning-based brain age estimation from T1-weighted MRI has gained growing attention. Key to the sensitivity and utility of such age estimation is how to build an accurate, generalizable and interpretable age estimator from healthy brain MRIs before it can be applied to abnormal cases. To this end, we present in this paper an attention-driven multi-channel fusion algorithm named FiA-Net. Specifically, we gathered data with one of largest scales and widest age ranges (Table 2), we proposed a novel algorithm that split T1w into two channels (Section 3.2) and that conducted layer-level fusion (Section 3.4) with attentions (Section 3.5), and, we used direct interpretation at neurons in the deep neural network (Section 5.4).
The higher performance of our algorithm was rooted in our algorithm designs. The explicit split of the T1-weighted intensity image into two channels (contrast and morphometry) opened up the opportunity for multi-channel fusion. Existing studies just used the T1w image as an intensity image, or just extracted features from segmented regions or reconstructed surfaces, where the hand-crafted features are not optimal for 3D CNN (see Table 1). Another key module was the proposed attention mechanisms for multi-channel fusion at the layer levels. Existing multi-channel fusion in medical image analysis was primarily for MRI synthesis (Zhou et al., 2020) or MRI segmentation (Zhou et al., 2019). Table 3 clearly showed the contributions of these three modules in our algorithm (splitting T1w into two channels, having layer-level fusions, and designing attention mechanisms). Fig. 7 further confirmed that the concatenation of the four proposed attentions mechanisms in the last layer of FiA-Netfus led to better results than no attention or each attention alone.
We showed the accuracy and generality of the proposed algorithm. For accuracy, our algorithm achieved a lower error than two other state-of-the-art algorithms for multi-channel fusion: ResNetfus (He et al., 2016) and Hi-Netfus (Zhou et al., 2020). The higher accuracy reflected when using the same data (Figs. 8 and 9), and when comparing across studies using different data (Fig. 10). For generality, showed the generality across datasets (Table 4) and when training samples changed (Table 5).
For neuroanatomic interpretation, Fig. 11 showed a few anatomic regions that match with neuroscience findings on typical brain development (Sotardi et al., 2021; Gilmore et al., 2018). However, we would like to emphasize that these regions were informative regions used in the proposed FiA-Netfus. When the algorithms, datasets, and even the age range change, the informative anatomic regions may be found differently. Therefore, it is difficult to compare the informative anatomic regions across studies. Adding to this difficulty is the lack of ground truth on which set of anatomic regions really determines age. Perhaps the anatomic regions informative of age will also change as the brain grows from infancy to later life. This should be further studied, in the context of sex and race/ethnicity. Another future work is in the interpretation of the neural network itself. We studied neurons, and voxels in the neurons, that correlated with age, which we think is an extension of reporting salient neuroanatomic regions. However, it is not completely clear how the features across neurons and features across different voxels in the same neurons interact to jointly drive the combinatorial decision. Interpreting neural networks is, in itself, an actively studied topic that is non-trivial and is within our future work. Recent progress includes regression activation map (Wang and Yang, 2017) and network dissection (Bau et al., 2020).
Many of the algorithm and study designs in our work were toward real-world utility. We used the T1w image as it is usually the only MRI sequence available to every subject when thousands of subjects are used (Feng et al., 2020; Peng et al., 2020; Pomponio et al., 2020). Second, we used lifespan data, also aiming for real-world utility. A patient’s brain age may be quite different from the chronological age. Therefore, we cannot assume a narrow range of brain age. From this angle, our algorithm capable of predicting lifespan age should be more practical than many studies in Table 1 that constrain the predicted ages in a narrow age range. Besides, we kept the pre-processing and data harmonization minimum (Section 2), because it would reduce the risk of accumulations of failures or errors in pre-processing steps. Despite that, the data came from very different sites and scanners, and our results show generality in two phases of cross-validations.
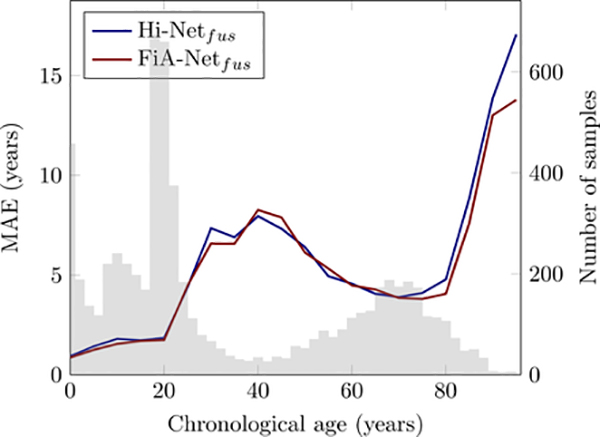
Brain age estimation studies have several common limitations, and they can also be seen in our study. First, this paper does not use the age estimators in patients. Developing an accurate age estimator is a critically important first step before it can be used in patients. We focused on this step, just like others (Cole and Franke, 2017; He et al., 2020; Pomponio et al., 2020; Feng et al., 2020; Hu et al., 2020). Our next step is to apply the model in various diseased populations. Second, our data distribution was unbalanced. Fig. 12 shows that the errors of age estimation increased in ages where sample sizes were relatively smaller. This trend was the same for different algorithms. Balancing sample distribution across ages could further improve the accuracy of age estimation Feng et al. (2020), and is one of our future efforts. Third, we did not use sex or race information. Sex differences may exist on normal brain aging (Goyal et al., 2019), but the findings are being debated in the literature (Tu et al., 2019; Biskup et al., 2019). So far, sex and race have rarely been used as covariates in brain age estimation studies (e.g., these studies in Table 1). Yet, our future work can add them as additional features to the neural network. Fourth, we only used T1w MRI as it is almost the only MRI sequence available at this scale of sample size. Other studies have combined T1w with diffusion or functional MRI for age estimation, although often on smaller sample sizes (Richard et al., 2018; Niu et al., 2020; Li et al., 2018). Our multi-channel attention-driven fusion network can be used to integrate structural, diffusion, and functional MRI channels. Fifth, while we compared the overall accuracies across studies (Fig. 10, where algorithms vary and database vary), and we compared the overall and dataset-specific accuracies across algorithms (Table 4, where only the algorithms vary), future work should ideally compare different studies on each dataset they have used in common. This will highlight how different algorithms generalize across datasets. Currently it is difficult as studies typically did not report their accuracy in each constituting dataset. We reported our errors in each of our datasets in Table 4, so future studies can compare. Sixth, while interpretations were provided in our study and in other age estimation studies (Shi et al., 2020; Lewis et al., 2018; Kwak et al., 2018), a comparison is difficult. Ages vary among studies (fetal (Shi et al., 2020), elderly (Kwak et al., 2018), and ours on lifespan). Datasets vary, and algorithms and features in studies also vary. The interpretation methods also vary. Worse, ground truth is largely unknown. Seventh, using lifespan data, despite its real-world utility, may introduce larger errors in healthy brains. For example, as Table 1 shows, when constraining the estimated age of subjects 3–22 years old to be within 3 and 22 years, the errors can be as lows as around 1.5 years (Chung et al., 2018; Lewis et al., 2018). However, having such constraints limit the algorithm’s use to be only in healthy subjects but not in patients, because patients aged 3–22 years may exhibit a brain age beyond this range. One future direction is to further reduce the errors in narrow age ranges using the currently estimated age to initialize a refined search in nearby ages. This strategy has been done in age estimation studies using facial image (Guo et al., 2008; Lai et al., 2017; Li et al., 2019a).
Figure 12:
Age estimation errors (MAE) as a function of sample size at each age. The color curves are the MAEs of different algorithms, and they comply with the scales in the left y axis. The gray bars are the numbers of samples at each age, and they follow the scales in the right y axis.
Explicitly splitting the T1w images into two channels is technically feasible and has potential clinical usage. Technically, almost all MRI-based age estimation studies in Table 1 used some pre-processing steps, including at least three steps (bias correction, skull stripping, and registration to the atlas (either affine or deformable)), some even including additional pre-processing steps such as structural segmentation or cortical surface reconstruction, etc. Our work only included the three minimum pre-processing steps, no segmentation or cortical surface reconstruction was needed. The RAVENS map in the morphometry channel was a byproduct of deformable registration in this minimum pre-processing pipeline. It was based on our open-source and publicly-released DRAMMS registration algorithm with a validated high accuracy in a fully-automated fashion. Therefore, our pre-processing was minimum compared to those in Table 1, and was based on automated, validated, and public software tools. Clinically, splitting T1w into contrast and morphometry channels is to increase the specificity of age estimation biomarkers. When age estimators are used to quantifying accelerated or delayed aging in diseases, the specificity issue arises – how to differentiate among diseases that are associated with similar levels of abnormal aging (Cole and Franke, 2017; Kaufmann et al., 2019). While some brain disorders change MRI contrast (e.g., multiple sclerosis), others change morphometry (e.g., hydrocephalus). Therefore, splitting T1w into contrast and morphometry opens opportunities to quantify which channel is the source of abnormal aging, and thereby has the potential to increase the specificity of age estimation biomarkers, which we leave for future studies to verify.
In conclusion, we have studied the brain age estimation on a large cohort using our proposed 3D attention-driven multi-channel fusion convolutional neural network. We showed accuracy, generality, and interpretation. Future work includes using larger-scale, multi-site, more balanced data; using demographics as covariates; developing hierarchical estimation strategies (lifspan as the initialization and piecewise narrower age groups as refinement); and applying the model in various diseased cohorts.
Highlights.
A “fusion-with-attention” convolutional neural network (FiA-Net) is proposed to fuse the contrast and morphometry image channels split from T1-weighted MRI for brain age estimation.
The proposed method is evaluated on a large cohort with 16,705 healthy MRI scans over lifespan (0–97), achieving the mean absolution error of 3.00 years.
We evaluate the proposed method based on accuracy, Generality, and Interpretation.
8. Acknowledgement
This work was funded, in part, by the Harvard Medical School and Boston Children’s Hospital Faculty Development Award (YO), St Baldrick Foundation Scholar Award Grace Fund (YO), and Charles A. King Trust Research Fellowship (SH).
Footnotes
Conflict of Interest
This piece of the submission is being sent via mail.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alexander LM, Escalera J, Ai L, Andreotti C, Febre K, Mangone A, Vega-Potler N, Langer N, Alexander A, Kovacs M, et al. , 2017. An open resource for transdiagnostic research in pediatric mental health and learning disorders. Scientific data 4, 170181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aycheh HM, Seong JK, Shin JH, Na DL, Kang B, Seo SW, Sohn KA, 2018. Biological brain age prediction using cortical thickness data: a large scale cohort study. Frontiers in aging neuroscience 10, 252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bashyam VM, Erus G, Doshi J, Habes M, Nasralah I, Truelove-Hill M, Srinivasan D, Mamourian L, Pomponio R, Fan Y, et al. , 2020. MRI signatures of brain age and disease over the lifespan based on a deep brain network and 14 468 individuals worldwide. Brain 143, 2312–2324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bau D, Zhu JY, Strobelt H, Lapedriza A, Zhou B, Torralba A, 2020. Understanding the role of individual units in a deep neural network. Proceedings of the National Academy of Sciences 117, 30071–30078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker BG, Klein T, Wachinger C, Initiative ADN, et al. , 2018. Gaussian process uncertainty in age estimation as a measure of brain abnormality. NeuroImage 175, 246–258. [DOI] [PubMed] [Google Scholar]
- Biskup E, Quevenco FC, Ferretti MT, Santuccione-Chadha A, 2019. Sex differences in brain metabolic activity: Beyond the concept of brain age. Proceedings of the National Academy of Sciences of the United States of America 116, 10630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen K, Gong S, Xiang T, Change Loy C, 2013. Cumulative attribute space for age and crowd density estimation, in: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 2467–2474. [Google Scholar]
- Chung Y, Addington J, Bearden CE, Cadenhead K, Cornblatt B, Mathalon DH, McGlashan T, Perkins D, Seidman LJ, Tsuang M, et al. , 2018. Use of machine learning to determine deviance in neuroanatomical maturity associated with future psychosis in youths at clinically high risk. JAMA psychiatry 75, 960–968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole JH, Franke K, 2017. Predicting age using neuroimaging: innovative brain ageing biomarkers. Trends in neurosciences 40, 681–690. [DOI] [PubMed] [Google Scholar]
- Cole JH, Leech R, Sharp DJ, Initiative ADN, 2015. Prediction of brain age suggests accelerated atrophy after traumatic brain injury. Annals of neurology 77, 571–581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole JH, Poudel RP, Tsagkrasoulis D, Caan MW, Steves C, Spector TD, Montana G, 2017a. Predicting brain age with deep learning from raw imaging data results in a reliable and heritable biomarker. NeuroImage 163, 115–124. [DOI] [PubMed] [Google Scholar]
- Cole JH, Underwood J, Caan MW, De Francesco D, van Zoest RA, Leech R, Wit FW, Portegies P, Geurtsen GJ, Schmand BA, et al. , 2017b. Increased brain-predicted aging in treated hiv disease. Neurology 88, 1349–1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Da X, Toledo JB, Zee J, Wolk DA, Xie SX, Ou Y, Shacklett A, Parmpi P, Shaw L, Trojanowski JQ, et al. , 2014. Integration and relative value of biomarkers for prediction of mci to ad progression: spatial patterns of brain atrophy, cognitive scores, apoe genotype and csf biomarkers. NeuroImage: Clinical 4, 164–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davatzikos C, Genc A, Xu D, Resnick SM, 2001. Voxel-based morphometry using the ravens maps: methods and validation using simulated longitudinal atrophy. NeuroImage 14, 1361–1369. [DOI] [PubMed] [Google Scholar]
- Di Martino A, Yan CG, Li Q, Denio E, Castellanos FX, Alaerts K, Anderson JS, Assaf M, Bookheimer SY, Dapretto M, et al. , 2014. The autism brain imaging data exchange: towards a large-scale evaluation of the intrinsic brain architecture in autism. Molecular psychiatry 19, 659–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doshi J, Erus G, Ou Y, Gaonkar B, Davatzikos C, 2013. Multi-atlas skull-stripping. Academic radiology 20, 1566–1576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doshi J, Erus G, Ou Y, Resnick SM, Gur RC, Gur RE, Satterthwaite TD, Furth S, Davatzikos C, Initiative AN, et al. , 2016. Muse: Multi-atlas region segmentation utilizing ensembles of registration algorithms and parameters, and locally optimal atlas selection. Neuroimage 127, 186–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erus G, Battapady H, Satterthwaite TD, Hakonarson H, Gur RE, Davatzikos C, Gur RC, 2014. Imaging patterns of brain development and their relationship to cognition. Cerebral Cortex 25, 1676–1684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erus G, Battapady H, Satterthwaite TD, Hakonarson H, Gur RE, Davatzikos C, Gur RC, 2015. Imaging patterns of brain development and their relationship to cognition. Cerebral cortex 25, 1676–1684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans AC, Group BDC, et al. , 2006. The NIH MRI study of normal brain development. Neuroimage 30, 184–202. [DOI] [PubMed] [Google Scholar]
- Feichtenhofer C, Pinz A, Zisserman A, 2016. Convolutional two-stream network fusion for video action recognition, in: conference on computer vision and pattern recognition, pp. 1933–1941. [Google Scholar]
- Feng X, Lipton ZC, Yang J, Small SA, Provenzano FA, Initiative ADN, Initiative FLDN, et al. , 2020. Estimating brain age based on a uniform healthy population with deep learning and structural mri. Neurobiology of Aging 91, 15–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franke K, Gaser C, 2012. Longitudinal changes in individual brainage in healthy aging, mild cognitive impairment, and alzheimer’s disease. GeroPsych: The Journal of Gerontopsychology and Geriatric Psychiatry 25, 235. [Google Scholar]
- Gaser C, Franke K, 2019. Ten years of BrainAGE as an neuroimaging biomarker of brain aging: What insights did we gain? Frontiers in Neurology 10, 789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaser C, Franke K, Klöppel S, Koutsouleris N, Sauer H, 2013. Brainage in mild cognitive impaired patients: predicting the conversion to alzheimer’s disease. PloS one 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geng X, Zhou ZH, Smith-Miles K, 2007. Automatic age estimation based on facial aging patterns. IEEE Transactions on pattern analysis and machine intelligence 29, 2234–2240. [DOI] [PubMed] [Google Scholar]
- Gilmore JH, Knickmeyer RC, Gao W, 2018. Imaging structural and functional brain development in early childhood. Nature Reviews Neuroscience 19, 123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goyal MS, Blazey TM, Su Y, Couture LE, Durbin TJ, Bateman RJ, Benzinger TLS, Morris JC, Raichle ME, Vlassenko AG, 2019. Persistent metabolic youth in the aging female brain. Proceedings of the National Academy of Sciences 116, 3251–3255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo G, Fu Y, Dyer CR, Huang TS, 2008. Image-based human age estimation by manifold learning and locally adjusted robust regression. IEEE Transactions on Image Processing 17, 1178–1188. [DOI] [PubMed] [Google Scholar]
- He K, Zhang X, Ren S, Sun J, 2016. Deep residual learning for image recognition, in: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 770–778. [Google Scholar]
- He S, Gollub RL, Murphy SN, Perez JD, Prabhu S, Pienaar R, Robertson RL, Grant PE, Ou Y, 2020. Brain age estimation using LSTM on children’s brain MRI. ISBI 2020, 420–423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes AJ, Hollinshead MO, O’keefe TM, Petrov VI, Fariello GR, Wald LL, Fischl B, Rosen BR, Mair RW, Roffman JL, et al. , 2015. Brain genomics superstruct project initial data release with structural, functional, and behavioral measures. Scientific data 2, 150031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu D, Wu Z, Lin W, Li G, Shen D, 2020. Hierarchical rough-to-fine model for infant age prediction based on cortical features. IEEE journal of biomedical and health informatics 24, 214–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu J, Shen L, Albanie S, Sun G, Wu E, 2019. Squeeze-and-excitation networks. IEEE transactions on pattern analysis and machine intelligence 42, 2011–2023. [DOI] [PubMed] [Google Scholar]
- Jiang H, Lu N, Chen K, Yao L, Li K, Zhang J, Guo X, 2020. Predicting brain age of healthy adults based on structural mri parcellation using convolutional neural networks. Frontiers in neurology 10, 1346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jónsson BA, Bjornsdottir G, Thorgeirsson T, Ellingsen LM, Walters GB, Gud-bjartsson D, Stefansson H, Stefansson K, Ulfarsson M, 2019. Brain age prediction using deep learning uncovers associated sequence variants. Nature communications 10, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufmann T, van der Meer D, Doan NT, Schwarz E, Lund MJ, Agartz I, Alnæs D, Barch DM, Baur-Streubel R, Bertolino A, et al. , 2019. Common brain disorders are associated with heritable patterns of apparent aging of the brain. Nature neuroscience 22, 1617–1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koutsouleris N, Davatzikos C, Borgwardt S, Gaser C, Bottlender R, Frodl T, Falkai P, Riecher-Rössler A, Möller HJ, Reiser M, et al. , 2014. Accelerated brain aging in schizophrenia and beyond: a neuroanatomical marker of psychiatric disorders. Schizophrenia bulletin 40, 1140–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krizhevsky A, Sutskever I, Hinton GE, 2012. Imagenet classification with deep convolutional neural networks, in: Advances in neural information processing systems, pp. 1097–1105. [Google Scholar]
- Kwak S, Kim H, Chey J, Youm Y, 2018. Feeling how old i am: subjective age is associated with estimated brain age. Frontiers in aging neuroscience 10, 168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai D, Chen Y, Luo X, Du J, Wang T, 2017. Age estimation with dynamic age range. Multimedia Tools and Applications 76, 6551–6573. [Google Scholar]
- LaMontagne PJ, Keefe S, Lauren W, Xiong C, Grant EA, Moulder KL, Morris JC, Benzinger TL, Marcus DS, 2018. Oasis-3: Longitudinal neuroimaging, clinical, and cognitive dataset for normal aging and alzheimer’s disease. Alzheimer’s & Dementia: The Journal of the Alzheimer’s Association 14, P1097. [Google Scholar]
- Lewis JD, Evans AC, Tohka J, Group BDC, et al. , 2018. T1 white/gray contrast as a predictor of chronological age, and an index of cognitive performance. Neuroimage 173, 341–350. [DOI] [PubMed] [Google Scholar]
- Li H, Satterthwaite TD, Fan Y, 2018. Brain age prediction based on resting-state functional connectivity patterns using convolutional neural networks, in: 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), IEEE. pp. 101–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Lu J, Feng J, Xu C, Zhou J, Tian Q, 2019a. Bridgenet: A continuity-aware probabilistic network for age estimation, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 1145–1154. [Google Scholar]
- Li X, Zhao H, Han L, Tong Y, Yang K, 2019b. Gff: Gated fully fusion for semantic segmentation. arXiv preprint arXiv:1904.01803. [Google Scholar]
- Litjens G, Kooi T, Bejnordi BE, Setio AAA, Ciompi F, Ghafoorian M, Van Der Laak JA, Van Ginneken B, Sánchez CI, 2017. A survey on deep learning in medical image analysis. Medical image analysis 42, 60–88. [DOI] [PubMed] [Google Scholar]
- Morton SU, Vyas R, Gagoski B, Vu C, Litt J, Larsen RJ, Kuchan MJ, Lasekan JB, Sutton BP, Grant PE, et al. , 2020. Maternal dietary intake of omega-3 fatty acids correlates positively with regional brain volumes in 1-month-old term infants. Cerebral Cortex 30, 2057–2069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu X, Zhang F, Kounios J, Liang H, 2020. Improved prediction of brain age using multimodal neuroimaging data. Human Brain Mapping 41, 1626–1643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou Y, Akbari H, Bilello M, Da X, Davatzikos C, 2014. Comparative evaluation of registration algorithms in different brain databases with varying difficulty: results and insights. IEEE transactions on medical imaging 33, 2039–2065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou Y, Gollub RL, Retzepi K, Reynolds N, Pienaar R, Pieper S, Murphy SN, Grant PE, Zöllei L, 2015. Brain extraction in pediatric adc maps, toward charac terizing neuro-development in multi-platform and multi-institution clinical images. NeuroImage 122, 246–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou Y, Sotiras A, Paragios N, Davatzikos C, 2011. DRAMMS: Deformable registration via attribute matching and mutual-saliency weighting. Medical image analysis 15, 622–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou Y, Zöllei L, Da X, Retzepi K, Murphy SN, Gerstner ER, Rosen BR, Grant PE, Kalpathy-Cramer J, Gollub RL, 2018. Field of view normalization in multi-site brain mri. Neuroinformatics 16, 431–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou Y, Zöllei L, Retzepi K, Castro V, Bates SV, Pieper S, Andriole KP, Murphy SN, Gollub RL, Grant PE, 2017. Using clinically acquired mri to construct age-specific adc atlases: Quantifying spatiotemporal adc changes from birth to 6-year old. Human brain mapping 38, 3052–3068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pardoe HR, Hiess RK, Kuzniecky R, 2016. Motion and morphometry in clinical and nonclinical populations. Neuroimage 135, 177–185. [DOI] [PubMed] [Google Scholar]
- Park J, Carp J, Kennedy KM, Rodrigue KM, Bischof GN, Huang CM, Rieck JR, Polk TA, Park DC, 2012. Neural broadening or neural attenuation? investigating age-related dedifferentiation in the face network in a large lifespan sample. Journal of Neuroscience 32, 2154–2158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng H, Gong W, Beckmann CF, Vedaldi A, Smith SM, 2020. Accurate brain age prediction with lightweight deep neural networks. Medical Image Analysis, 101871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pomponio R, Erus G, Habes M, Doshi J, Srinivasan D, Mamourian E, Bashyam V, Nasrallah IM, Satterthwaite TD, Fan Y, et al. , 2020. Harmonization of large mri datasets for the analysis of brain imaging patterns throughout the lifespan. NeuroImage 208, 116450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richard G, Kolskår K, Sanders AM, Kaufmann T, Petersen A, Doan NT, Sánchez JM, Alnæs D, Ulrichsen KM, Dørum ES, et al. , 2018. Assessing distinct patterns of cognitive aging using tissue-specific brain age prediction based on diffusion tensor imaging and brain morphometry. PeerJ 6, e5908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohlfing T, Zahr NM, Sullivan EV, Pfefferbaum A, 2010. The sri24 multichannel atlas of normal adult human brain structure. Human brain mapping 31, 798–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudin C, 2019. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nature Machine Intelligence 1, 206–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sajedi H, Pardakhti N, 2019. Age prediction based on brain MRI image: a survey. Journal of medical systems 43, 279. [DOI] [PubMed] [Google Scholar]
- Schlemper J, Oktay O, Schaap M, Heinrich M, Kainz B, Glocker B, Rueckert D, 2019. Attention gated networks: Learning to leverage salient regions in medical images. Medical image analysis 53, 197–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnack HG, Van Haren NE, Nieuwenhuis M, Hulshoff Pol HE, Cahn W, Kahn RS, 2016. Accelerated brain aging in schizophrenia: a longitudinal pattern recognition study. American Journal of Psychiatry 173, 607–616. [DOI] [PubMed] [Google Scholar]
- Selvaraju RR, Cogswell M, Das A, Vedantam R, Parikh D, Batra D, 2017. Grad-cam: Visual explanations from deep networks via gradient-based localization, in: Proceedings of the IEEE international conference on computer vision, pp. 618–626. [Google Scholar]
- Sharif MI, Li JP, Khan MA, Saleem MA, 2020. Active deep neural network features selection for segmentation and recognition of brain tumors using mri images. Pattern Recognition Letters 129, 181–189. [Google Scholar]
- Shen D, Wu G, Suk HI, 2017. Deep learning in medical image analysis. Annual review of biomedical engineering 19, 221–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi W, Yan G, Li Y, Li H, Liu T, Sun C, Wang G, Zhang Y, Zou Y, Wu D, 2020. Fetal brain age estimation and anomaly detection using attention-based deep ensembles with uncertainty. NeuroImage 223, 117316. [DOI] [PubMed] [Google Scholar]
- Sotardi S, Gollub RL, Bates SV, Weiss R, Murphy SN, Grant PE, Ou Y, 2021. Voxelwise and regional brain apparent diffusion coefficient changes on mri from birth to 6 years of age. Radiology 298, 415–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sowell ER, Peterson BS, Thompson PM, Welcome SE, Henkenius AL, Toga AW, 2003. Mapping cortical change across the human life span. Nature neuroscience 6, 309–315. [DOI] [PubMed] [Google Scholar]
- Steffener J, Habeck C, O’Shea D, Razlighi Q, Bherer L, Stern Y, 2016. Differences between chronological and brain age are related to education and self-reported physical activity. Neurobiology of aging 40, 138–144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun P, Wang D, Mok VC, Shi L, 2019. Comparison of feature selection methods and machine learning classifiers for radiomics analysis in glioma grading. IEEE Access 7, 102010–102020. [Google Scholar]
- Truelove-Hill M, Erus G, Bashyam V, Varol E, Sako C, Gur RC, Gur RE, Koutsouleris N, Zhuo C, Fan Y, et al. , 2020. A multidimensional neural maturation index reveals reproducible developmental patterns in children and adolescents. Journal of Neuroscience 40, 1265–1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu Y, Fu Z, Maleki N, 2019. When does the youthfulness of the female brain emerge? Proceedings of the National Academy of Sciences 116, 10632–10633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, Gee JC, 2010. N4itk: improved n3 bias correction. IEEE transactions on medical imaging 29, 1310–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulyanov D, Vedaldi A, Lempitsky V, 2016. Instance normalization: The missing ingredient for fast stylization. arXiv preprint arXiv:1607.08022. [Google Scholar]
- Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, Kaiser Ł, Polosukhin I, 2017. Attention is all you need, in: Advances in neural information processing systems, pp. 5998–6008. [Google Scholar]
- Volkow ND, Koob GF, Croyle RT, Bianchi DW, Gordon JA, Koroshetz WJ, Pérez-Stable EJ, Riley WT, Bloch MH, Conway K, et al. , 2018. The conception of the ABCD study: From substance use to a broad NIH collaboration. Developmental cognitive neuroscience 32, 4–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang F, Jiang M, Qian C, Yang S, Li C, Zhang H, Wang X, Tang X, 2017. Residual attention network for image classification, in: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 3156–3164. [Google Scholar]
- Wang Z, Yang J, 2017. Diabetic retinopathy detection via deep convolutional networks for discriminative localization and visual explanation. arXiv preprint arXiv:1703.10757. [Google Scholar]
- Weiss RJ, Bates SV, Song Y, Zhang Y, Herzberg EM, Chen YC, Gong M, Chien I, Zhang L, Murphy SN, et al. , 2019. Mining multi-site clinical data to develop machine learning mri biomarkers: application to neonatal hypoxic ischemic encephalopathy. Journal of translational medicine 17, 1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu D, Ouyang W, Wang X, Sebe N, 2018. Pad-net: Multi-tasks guided predictionand-distillation network for simultaneous depth estimation and scene parsing, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 675–684. [Google Scholar]
- Zhou B, Khosla A, Lapedriza A, Oliva A, Torralba A, 2016. Learning deep features for discriminative localization, in: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 2921–2929. [Google Scholar]
- Zhou T, Fu H, Chen G, Shen J, Shao L, 2020. Hi-net: hybrid-fusion network for multi-modal mr image synthesis. IEEE transactions on medical imaging 39, 2772–2781. [DOI] [PubMed] [Google Scholar]
- Zhou T, Ruan S, Canu S, 2019. A review: Deep learning for medical image segmentation using multi-modality fusion. Array 3, 100004. [Google Scholar]
- Zölei L, Iglesias JE, Ou Y, Grant PE, Fischl B, 2020. Infant freesurfer: An automated segmentation and surface extraction pipeline for t1-weighted neuroimaging data of infants 0–2 years. Neuroimage, 116946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo XN, Anderson JS, Bellec P, Birn RM, Biswal BB, Blautzik J, Breitner JC, Buckner RL, Calhoun VD, Castellanos FX, et al. , 2014. An open science resource for establishing reliability and reproducibility in functional connectomics. Scientific data 1, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]