A novel incremental simulation of facial changes following orthognathic surgery using FEM with realistic lip sliding effect

Abstract

Accurate prediction of facial soft-tissue changes following orthognathic surgery is crucial for surgical outcome improvement. We developed a novel incremental simulation approach using finite element method (FEM) with a realistic lip sliding effect to improve the prediction accuracy in the lip region.

First, a lip-detailed mesh is generated based on accurately digitized lip surface points. Second, an improved facial soft-tissue change simulation method is developed by applying a lip sliding effect along with the mucosa sliding effect. Finally, the orthognathic surgery initiated soft-tissue change is simulated incrementally to facilitate a natural transition of the facial change and improve the effectiveness of the sliding effects.

Our method was quantitatively validated using 35 retrospective clinical data sets by comparing it to the traditional FEM simulation method and the FEM simulation method with mucosa sliding effect only. The surface deviation error of our method showed significant improvement in the upper and lower lips over the other two prior methods. In addition, the evaluation results using our lip-shape analysis, which reflects clinician’s qualitative evaluation, also proved significant improvement of the lip prediction accuracy of our method for the lower lip and both upper and lower lips as a whole compared to the other two methods.

In conclusion, the prediction accuracy in the clinically critical region, i.e., the lips, significantly improved after applying incremental simulation with realistic lip sliding effect compared with the FEM simulation methods without the lip sliding effect.

1. Introduction

Orthognathic surgery involves osteotomy of the jaw bones to correct jaw deformities and restore normal facial appearance and function. It is completed by cutting the jaws into pieces and repositioning them individually to a desired position. Although facial soft tissue is not directly operated on, it naturally changes following the underlying bony movements. Due to the complex nature of facial anatomy, orthognathic surgery requires extensive surgical planning for both bone and soft tissue. While surgeons can accurately plan the bony surgeries by virtually simulating osteotomies on three-dimensional patient models to reconstruct a normal skeleton (Bobek et al., 2015; McCormick and Drew, 2011; Xia et al., 2015), they are still unable to accurately predict facial changes following bony surgery because of the complex physical interaction between the facial structures. Therefore, the current practice is to normalize the skeleton, hoping optimal facial appearance is automatically achieved by the normalized skeleton. However, this approach is not reliable due to significant intra-patient variations in thickness and contour of the soft-tissue envelope. The problem is even bigger in patients with composite defects of both skeleton and soft tissues. For example, in the scenario of a patient with a skeletal deformity and a mild soft-tissue defect, a surgeon would have to know, before surgery, how to overcorrect the skeleton to camouflage the soft-tissue defect. This information can only be attained by having a planning-system that accurately simulates soft-tissue changes after skeletal reconstruction, thereby providing feedback driven adjustments to the surgical planning tools.

Various methods have been developed to predict three-dimensional (3D) facial change according to the bony movements (Chabanas et al., 2003; Cotin et al., 2000; Keeve et al., 1998; Kim et al., 2010a; Kim et al., 2010b; Koch et al., 1996; Mollemans et al., 2006; Mollemans et al., 2007; Zachow et al., 2004). Among them, finite element method (FEM) is reported to be the most common and accurate simulation method, in which patient’s specific anatomy and biomechanical tissue properties are incorporated(Pan et al., 2012). However, modeling capabilities are still limited and prediction accuracy around the clinically critical regions, e.g., the lips, is still beyond the clinically acceptable range (Nadjmi et al., 2014). The prediction accuracy in the lips, especially the lower lip, is critical due to their distinctive geometry. Patients with jaw deformities often suffer severely deformed (strained) lower lips preoperatively. During the surgery, the shape and position of the upper and lower lips change independently according to the corresponding bony movements, and the strained lower lip is automatically restored to its relaxed status. In our previous projects, we significantly improved the facial change prediction accuracy in clinically critical regions, including the lips, by developing a FEM simulation method with an enhanced intraoral mucosa sliding effect. However, even with the mucosa sliding effect, the movement of the upper and the lower lips was not simulated individually because the upper and lower lips were still treated as a whole in the FE mesh (Kim et al., 2017; Knoops et al., 2018a; Knoops et al., 2018b; Zhang et al., 2018; Zhang et al., 2016). Consequently, the accuracy of the prediction result was still less than ideal around the lips (Knoops et al., 2018a; Nadjmi et al., 2014). This is especially prominent for patients with severe jaw deformities and asymmetry in which the lips are significantly deformed (Kim et al., 2017).

3D modeling of the lip movement was actively studied in the field of computer graphics (Badin et al., 2002; Badin et al., 1998; Guiard-marigny et al., 1996; King et al., 2000; Kuratate and Riley, 2010; Ouni and Gris, 2018; Revéret and Benoît, 1998). Their studies are mainly focused on developing a numerical lip model to generate a realistic animation for audiovisual speech synthesis, not for simulating surgical change considering biomechanical characteristics. Sliding movement of the lips was also studied for the simulation of facial expression and speech where the lip shape change driven by active muscle activity was one of the major interests (Eskes et al., 2017a; Eskes et al., 2017b; Groleau et al., 2007; Nazari et al., 2010; Nazari et al., 2011). These studies are more focused on accurate implementation of muscle structure and activity than the accuracy of the mesh modeling. Some studies used non-patient-specific generic mesh model (Eskes et al., 2017a; Eskes et al., 2017b) and others used only one case of a patient-specific mesh model (Groleau et al., 2007; Nazari et al., 2010; Nazari et al., 2011). The studies that used a patient-specific mesh model referred to the previously developed mesh modeling method (Chabanas et al., 2003). In the referred study, a manually generated generic FE mesh was adapted to the patient data by separately transforming the skin surface and internal surface (Chabanas et al., 2003). However, no details on the method to achieve accurate lip geometry was presented, especially for the contacting surface between the upper and lower lips. To our best knowledge, accurate modeling and sliding of the lips were not implemented in the facial change simulation following orthognathic surgery.

In this study, we hypothesize that the application of the lip sliding effect is a key factor for improving the facial change prediction accuracy in the lip region. To test our hypothesis, we propose the following improvements: 1) a lip-detailed patient-specific FE mesh generation, and 2) an incremental FEM simulation method that incorporates the realistic lip sliding effect along with the mucosa sliding effect. Finally, our new facial change prediction method was quantitatively validated using clinical datasets of 35 patients. The contribution of our study is the advancement in FE mesh modeling and prediction methods to improve facial change prediction accuracy based on the insight into the interaction between the facial structures. The developed prediction method can innovate the current surgical planning procedure for orthognathic surgery by enabling adjustment of bony surgical plan based on the predicted facial change to eventually achieve optimal surgical outcome. A preliminary version of this approach was first reported at 2019 Medical Image Computing and Computer-assisted Intervention (Kim et al., 2019). In this manuscript, both methodology and validation have been significantly improved.

2. Materials and methods

Our new facial change prediction approach consists of two stages. In the first stage, a patient specific lip-detailed FE mesh is generated by improving the lip geometry of our previously developed patient-specific anatomically-detailed FE mesh. In the second stage, facial change according to the surgical plan is predicted using an incremental FEM simulation along with the implementation of the sliding effect of the lip and the mucosa.

2.1. Generation of initial patient-specific FE mesh using eFTP-VP method

The initial patient-specific hexahedral FE mesh is generated using our previously developed method, eFTP-VP, which has been proven efficient and accurate (Zhang et al., 2018; Zhang et al., 2016). Our eFTP-VP method generates quality anatomically-detailed patient FE mesh using a generic facial model without having to segment individual patient data, significantly reducing the required time and labor compared to the traditional method. First, patient- specific facial soft-tissue models are generated by deforming a generic facial model, eFace template, to the patient’s facial geometry using a hybrid landmark-based morphing with thin-plate spline (TPS) technique (Haili and Rangarajan, 2000). The geometrical accuracy of the acquired facial soft-tissue model is further improved by applying a dense surface fitting method. Finally, a patient-specific FE mesh is generated from the facial soft-tissue model using volumetric parameterization (Li et al., 2011; Xia et al., 2010; Zhang et al., 2018). The resulted FE mesh (a total of approximately 40,000 elements and 50,000 nodes) is composed of 6 layers; the outermost layer represents the skin surface, and the innermost layer represents the bony and intraoral mucosa surface. Generating a FE mesh with accurate lip geometry directly from a generic facial model is practically impossible without post improvement due to the limited quality of CT images. The generated anatomically-detailed FE mesh, which lacks geometrical accuracy only in the lip region, served as a solid foundation for the following lip geometry improvement. More details of eFTP-VP is described in our previous study (Zhang et al., 2018).

2.2. Lip-detailed patient-specific FE mesh generation

The patient-specific FE mesh is further refined by separately modeling the accurate geometry of the upper and lower lips using the following steps: 1) digitization of lip surface points and 2) generation of detailed lip mesh.

2.2.1. Digitization of lip surface points

For lip-detailed FE mesh generation, it is necessary to separate: 1) upper and lower lip surfaces from each other and 2) lip inner surfaces from the labial surface of the teeth. To achieve this, manual digitization of the lip surface by surgeons or trained professionals is required because the quality of the CT images around the lip region is often poor due to low soft-tissue differentiability and artifacts caused by orthodontic appliances and amalgam fillings. Even without artifacts, acquisition of clear lip surface separated from the teeth surface with orthodontic appliances is practically impossible without manual intervention. Separation of the upper and lower lip surface for closed lip case is another challenging task.

For the convenience of the manual digitization, the lip surface points are digitized on CT parasagittal planes. CT parasagittal planes are generated along the dental arch between the labial commissures (where the upper and lower lips meet and the lip-end points are located) (Fig. 1). First, occlusal plane is defined as a fitting plane of the average points of corresponding upper and lower teeth landmarks on cusps using principal component analysis (PCA). Then, dental arch is approximated by a fitting curve of the projected teeth landmarks on the occlusal plane. Finally, the parasagittal images are regularly generated along and orthogonal to the dental arch by interpolating original CT images. We believe parasagittal plane orthogonal to the dental arch is optimal for visualization of the cross-section view of the teeth and the lip surface together.

Fig. 1.

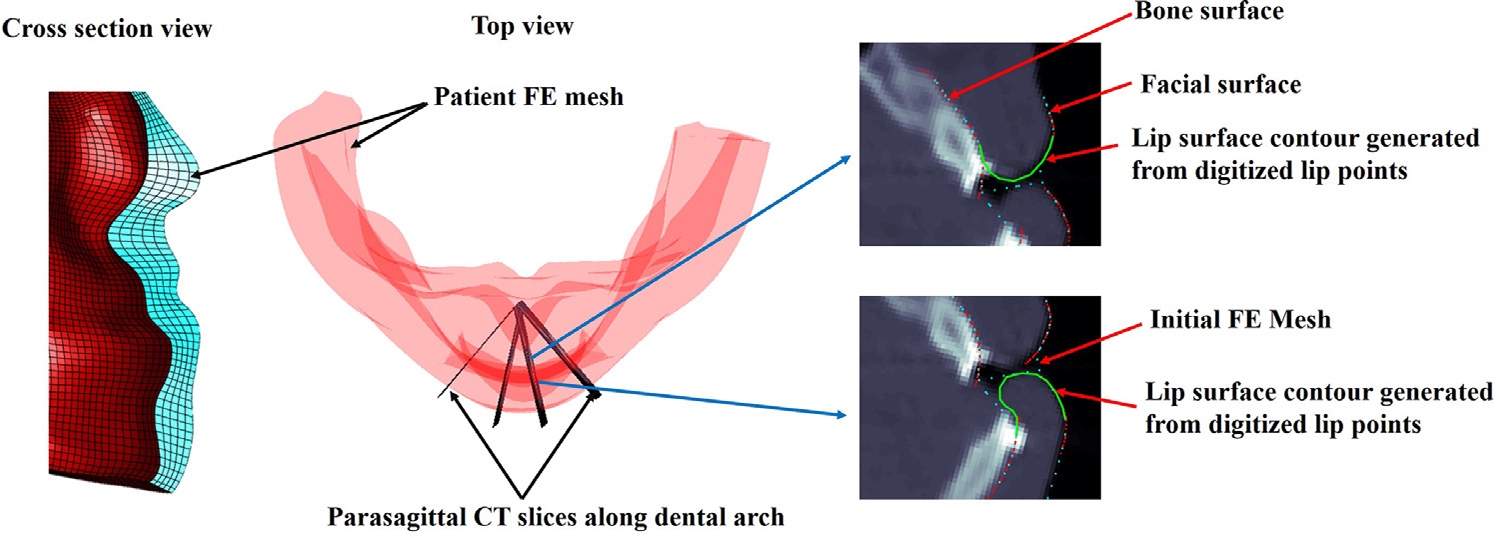
Digitization of the lip surface points on the parasagittal CT slices. Contours for upper and lower lip surfaces generated based on the digitized lip surface points (green).

During the digitization, both bony and facial soft tissue contours are displayed on the parasagittal planes to help the surgeon recognize the outer and inner surface of the lip on each parasagittal image (Fig. 1). Cross-section of the existing mesh is also overlaid on the parasagittal slices to help recognize the existing mesh. A series of points along the lip surface is then sequentially digitized from the outer to inner lip surface (or the other way) to form a contour of the upper and lower lip profiles, respectively (Fig. 1). Clinicians are allowed to digitize as many points as they want to achieve accurate and smooth lip contours. The effect of the orthodontic braces on the simulation is empirically assumed negligible. Thus, the lip inner surface is digitized following the teeth surface when the patient is under orthodontic treatment. Clinicians are instructed to follow the following rules to improve the continuity and smoothness between the existing mesh and the lip part which will be changed according to the digitization; 1) digitization on the first and the last parasagittal slices, which placed at the both labial commissures, should not apply too much difference from the existing mesh. 2) the first and the last digitized lip surface points, e.g., for the upper lip, the most superior digitized points on the inner and outer lip surfaces, should lie on the existing mesh.

2.2.2. Generation of lip-detailed mesh

The lip-detailed mesh is generated by modifying the lip nodes of the initial FE mesh using the digitized lip surface points. The initial patient-specific FE mesh is a structured hexahedral mesh.(Zhang et al., 2018) However, the digitized lip points are unstructured random points that are unrelated to the existing mesh structure. Therefore, it is necessary to interpolate the digitized lip points in order to prevent invalid elements and generate a mesh which matches with the existing FE mesh structure. This interpolation can be efficiently achieved using a surface parameterization technique. The lip detailed mesh is generated as follows: 1) 2D parameterization of 3D coordinates of the lip surface nodes. 3) 2D parameterization of 3D coordinates of the digitized lip points. 4) calculating 3D coordinates of the new lip nodes (detailed lip nodes) corresponding to the mesh grid of the initial mesh. 5) replacing the lip nodes inside of the digitized lip points boundary with the newly acquired detailed lip nodes. 6) modifying the internal mesh nodes of the lip region accordingly.

The nodes of the initial mesh corresponding to the upper and lower lip surfaces are selected (Fig. 2a). Each lip mesh node represented with a coordinate triplet $(x,y,z)\in {ℝ}^3$ can be parameterized by two variables u and v, (u, v) ∈ [0, n_c], [0, n_r], where n_c and n_r are the number of the selected elements along each axis (Fig. 2d); x = x(u, v), y = y(u, v) and z = z(u, v). The two variables, u and v, represent 2D grid coordinates of the lip mesh nodes (Fig. 2d).

Fig. 2.

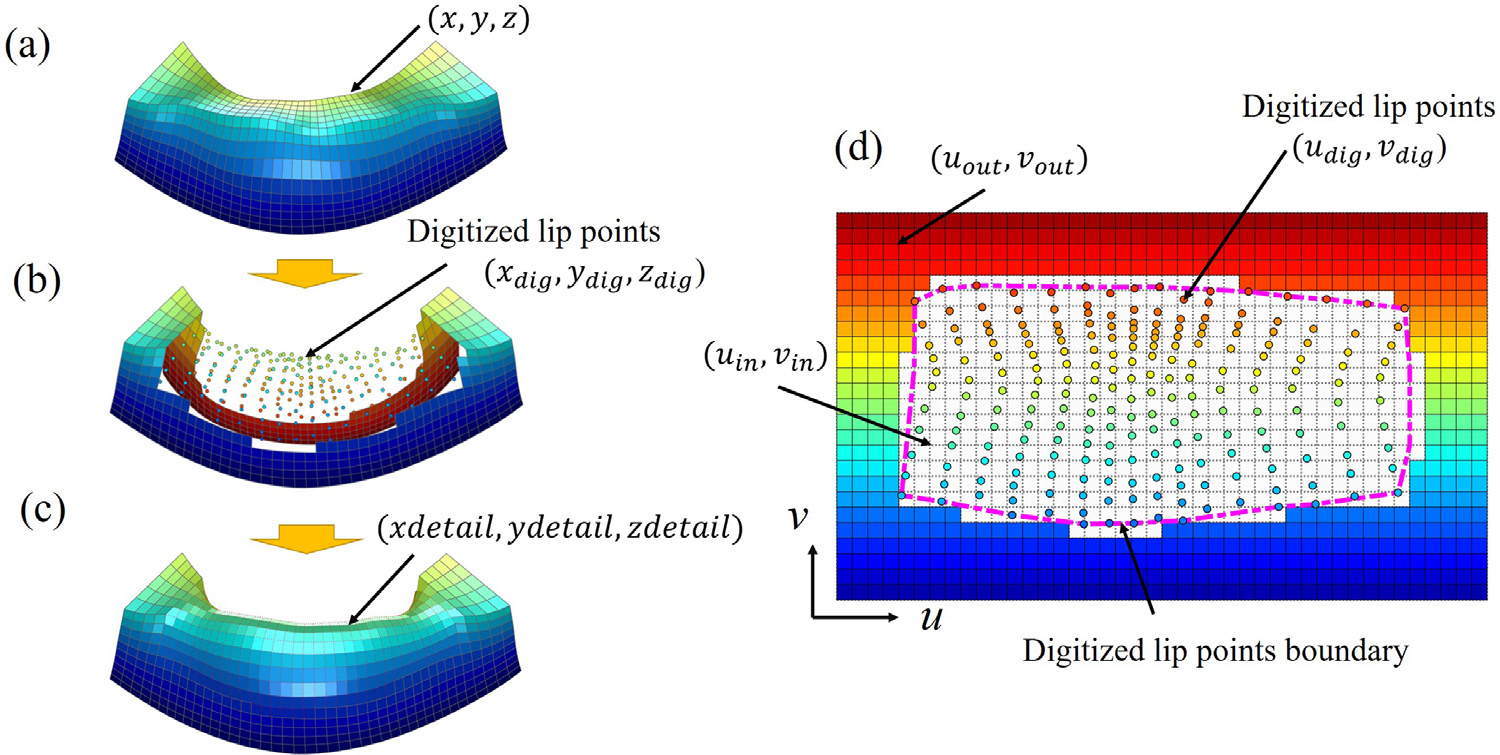
Lip surface mesh generation based on the digitized landmarks. Lower lip for illustration. (a) Lip surface extracted ‘nm the initial FE mesh. (b) Lip surface and digitized lip points represented in Cartesian coordinate system. (c) Final lip-detailed mesh surface (d) Parametric domain of the lip nodes represented in grid coordinate system. Digitized lip surface points in circles. Boundary of the digitized lip points in dotted line (magenta).

The lip nodes are divided into two groups using the digitized lip points boundary (magenta dotted line in Fig. 2d): The nodes inside of the boundary ((x_in, y_in, z_in ) and (u_in, v_in)) and outside of the boundary ((x_out, y_out, z_out) and (u_out, v_out)). 2D grid coordinates of the digitized lip points (u_dig, v_dig) are interpolated using the nodes outside of the boundary ((x_out, y_out, z_out) and (u_out, v_out)) and the 3D coordinates of the digitized lip points ((x_dig, y_dig, z_dig)). The nodes inside of the boundary are not used for the interpolation because they are deemed wrong. Please note that the calculated 2D grid coordinates of the digitized lip points ((u_dig, v_dig)) are random in both number and location and not aligned with the regular grid pattern ((u_{i n}, v_{i n})) of the initial mesh as shown in Fig. 2d. To achieve valid mesh structure, the 3D coordinates of the lip nodes corresponding to the grid pattern of the initial mesh need to be calculated.

New 3D coordinates of the lip nodes (x_detail, y_detail, z_detail) corresponding to the regular 2D grid of the initial mesh (u_{i n}, v_{i n}) are estimated by interpolating the information (3D and 2D coordinates) acquired above using TPS. The interpolation is performed for each 3D axis (x, y and z ), respectively. The achieved 3D coordinate (x_detail, y_detail, z_detail) represents the detailed lip nodes that follow the structure of the initial mesh. The lip nodes inside of the digitized lip boundary (x _in, y_in, z_in) are then replaced with the detailed lip nodes (x_detail, y_detail, z_detail) (Fig. 2c) to achieve detailed lip surfaces. The detailed lip nodes only consist the nodes on the lip surfaces. Therefore, the internal lip nodes corresponding to the lip region are modified accordingly using the detailed lip nodes using TPS to complete the lip-detailed mesh generation.

2.3. Facial changes prediction using incremental simulation method with realistic sliding effect

Postoperative change of facial soft-tissue is predicted using incremental FEM simulation with the realistic sliding effect of the lips and the mucosa. First, simulation conditions for FEM simulation including material property and boundary condition are defined. Second, facial change according to the surgical plan is simulated using incremental simulation method.

2.3.1. Material Property and Boundary Condition for FEM Simulation

The lip-detailed patient-specific FE mesh is assigned with nearly incompressible linear non-homogeneous material properties. The lip muscle elements are defined inside of the upper and lower lip regions, which is equivalent to the Orbicularis Oris muscle. We assumed the lip muscle acts as a frame of the lips that determines the intrinsic shape of the lips and maintain its shape against the force applied by the interaction between the lips. Transversely isotropic property is applied to the lip muscle elements to mimic the characteristics of the lip muscle and to maintain the unique shape of the lip, preventing undesirable deformation the lips caused from the lip interaction during the incremental simulation. Higher stiffness is applied along superior-inferior direction (Young’s modulus for longitudinal direction: 9,000 Pa, Young’s modulus for transverse direction: 3,000 Pa, Poisson’s ratio for both direction: 0.47). Our internal study identified a ratio between the longitudinal and transversal material properties of the lip muscle to best capture the lip change. The rest of the mesh elements, except the lip muscle elements, are assigned with isotropic linear material properties (Young’s modulus: 3000 Pa, Poisson’s ratio: 0.47).

Patient-specific boundary conditions are assigned to three types of the mesh nodes: fixed, moving and sliding. The fixed nodes are defined in the regions that are not changed during the surgery (red in Fig. 3). Their nodal displacement is set to zero during the FEM simulation. The moving nodes are the ones assumed to be attached to the bone and move in sync with the osteotomized bony segments (sky-blue in Fig. 3). They are defined along the superior part of the maxillary segment and the inferior part of the mandibular distal segment. For genioplasty case, the region corresponding to the chin segment is additionally defined as moving nodes. The sliding nodes are further classified into lip sliding nodes and mucosa sliding nodes. The lip sliding nodes are defined on the contacting surface between the upper and lower lips. The mucosa sliding nodes are defined in the areas that are assumed to slide along the bony surface, i.e., the intraoral mucosa not including the lip surface (green in Fig. 3). All the boundary nodes are patient-specific and manually defined on the innermost surface of the FE mesh except for the lip sliding nodes. Finally, the rest of the mesh nodes are free nodes that are spatially unconstrained during the simulation (green-blue in Fig. 3). Our study focuses on the transition between two static equilibria, preoperative and postoperative, assuming that the postoperative facial tissue is fully relaxed and under no stress (or force). All the mesh elements, including the muscle elements, are considered to be passive. Therefore, all the free nodes are assumed to have zero nodal force postoperatively and their movement is determined by solving FEM based on the above boundary condition. (Kim et al., 2017)

Fig. 3.

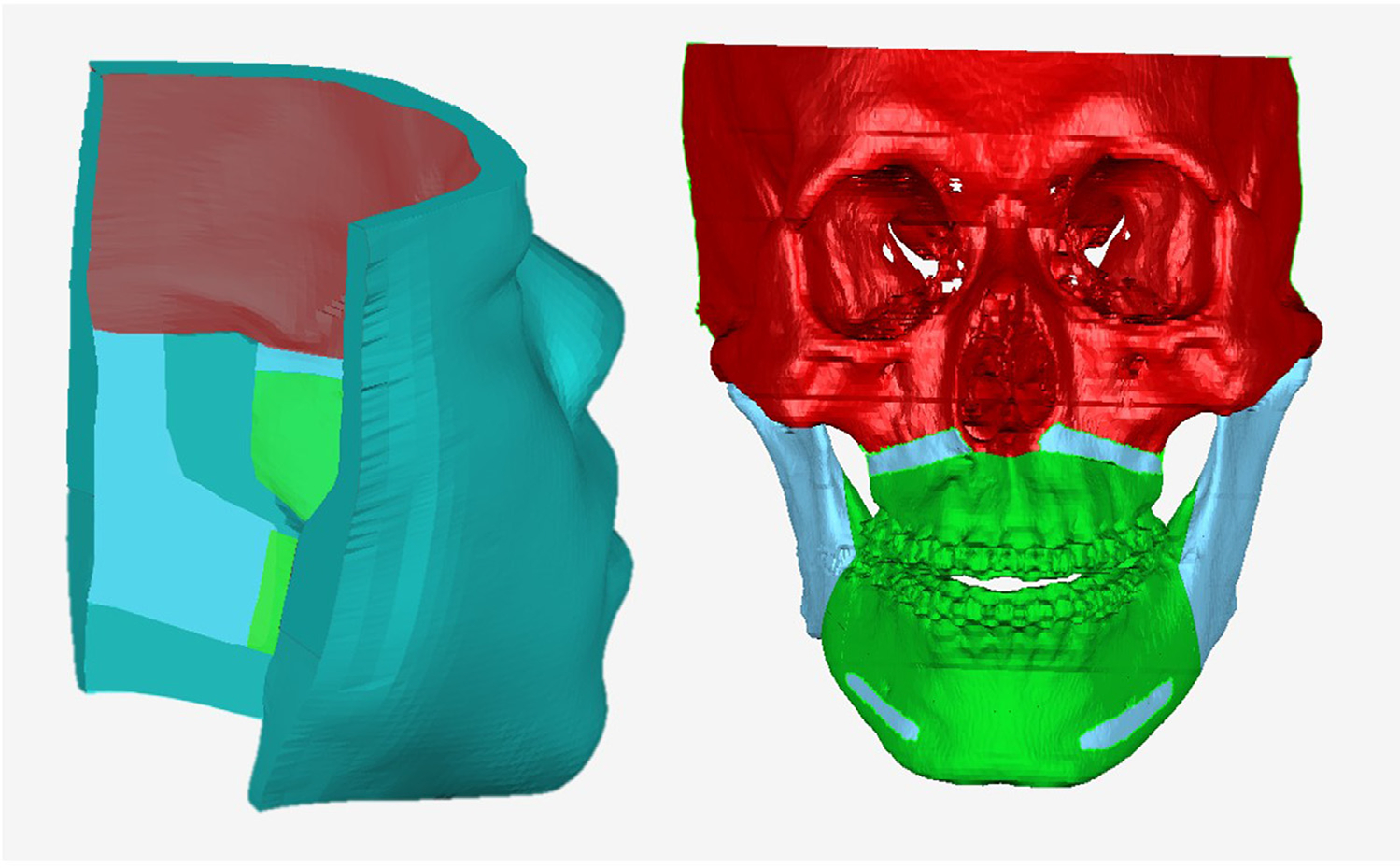
Boundary condition for FEM simulation represented on FE mesh and the bony surface for illustration. Color coding of fixed nodes: red; Moving nodes: sky-blue; Sliding nodes: green; Free nodes: green-blue.

2.3.2. Incremental simulation of facial changes with realistic sliding effect

Facial changes are incrementally simulated along with the realistic lip and mucosa siding effect using FEM. Each incremental simulation is implemented by following steps. 1) Regulate the FE mesh to improve simulation stability. 2) Facial change simulation with the realistic sliding effect by applying incremental bony movements.

2.3.2.1. To regulate FE mesh according to the occlusal plane to prevent invalid elements.

At the beginning of each incremental simulation, the patient FE mesh is regulated to minimize mesh distortion and mitigate numerical instability during the iterative incremental simulation. The mesh regulation was performed by remeshing the mesh grid and aligning the horizontal grid of the innermost mesh surface (layer) with the occlusal plane (Fig. 4b). The occlusal plane is an imaginary plane that separates the maxilla and mandible. The occlusal plane is an important reference for orthognathic surgery because malocclusion is corrected by changing the relationship between the maxilla and the mandible on the occlusal plane. During the simulation, the mesh nodes corresponding to each of the maxilla and mandible follows the underlying bony movements. The relative difference in the nodal displacement between the maxillary and mandibular nodes may result in severe mesh distortion along and parallel with the occlusal plane depending on the severity of the malocclusion. Moreover, the orientation of the innermost mesh grid pattern is arbitrary at the beginning of each incremental simulation, and the occlusal plane can cross multiple horizontal grids of the mesh, which is especially obvious for the initial preoperative mesh as shown in Fig. 4a. Therefore, without mesh regularization, large amount of elements distortion can occur along the occlusal plane at arbitrary angle. This uncontrolled mesh distortion can accumulate during the repeated incremental simulation and result in numerical instability or even failure of the simulation. The mesh regulation limits the area of mesh distortion within the certain horizontal levels of the grid by aligning the mesh innermost grid with the occlusal plane. The mesh regulation further eliminates the element distortion by remeshing the whole mesh according to the adjusted inner mesh and eventually improving the quality of the mesh at each iteration.

Fig. 4.

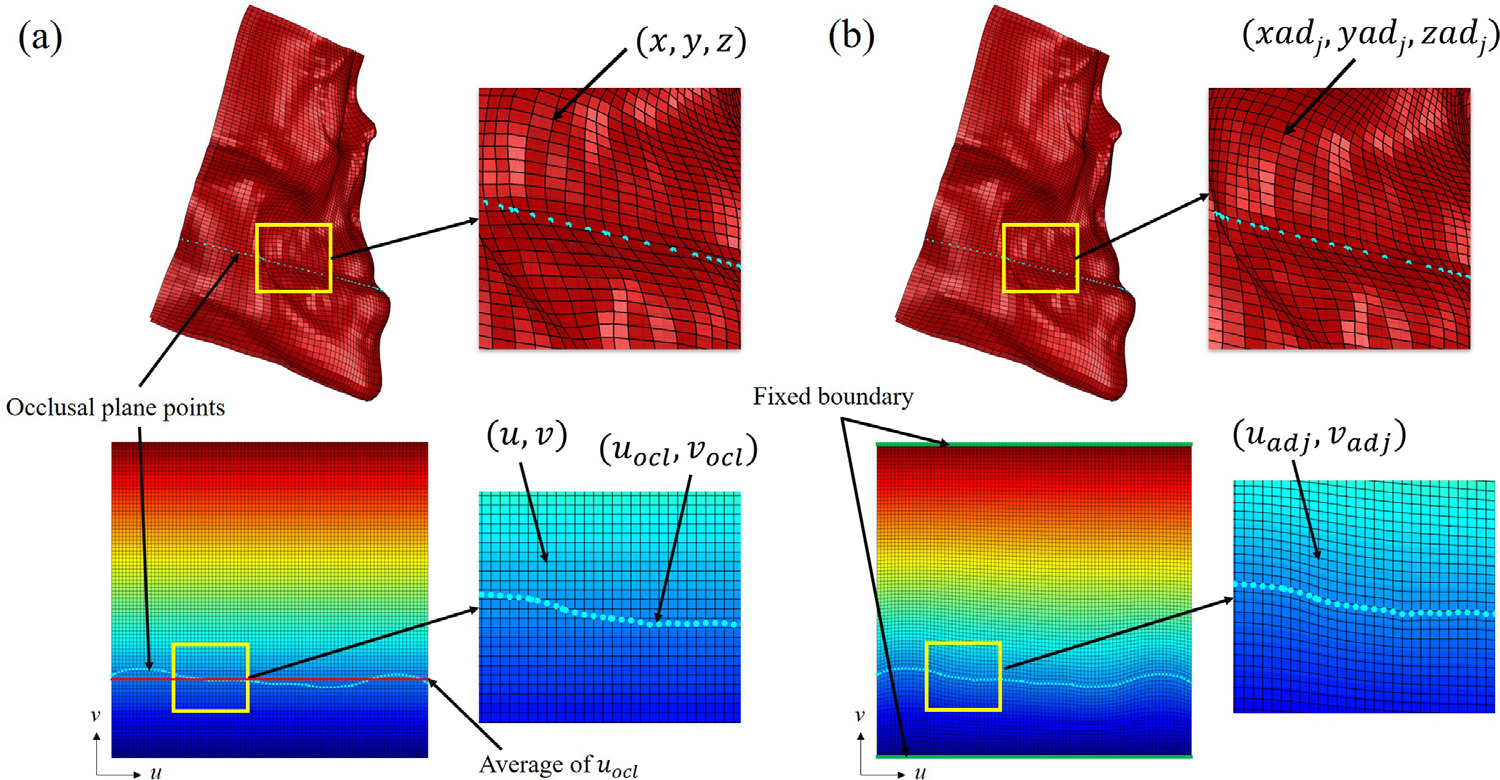
Mesh regulation according to the occlusal plane. Mesh innermost surface represented in 3D Cartesian and 2D grid coordinate system. (a) mesh innermost grid(black) and occlusal plane(sky-blue) before regulation. (b) mesh innermost grid after regulation.

FE Mesh regulation is performed using a surface parameterization technique. Each node on the innermost surface of the mesh $(x,y,z)\in {ℝ}^3$ is parameterized by two variables u and v, (u, v) ∈ [0, n_c], [0, n_r], where n_c and n_r are the total number of elements along each axis (Fig. 4); x = x(u, v), y = y(u, v) and z = z(u, v), The two variables, u and v, represent 2D grid coordinates of the innermost surface of the mesh (Fig. 4a). The occlusal plane is estimated as the best fitting plane for all upper and lower teeth landmarks defined in (Zhang et al., 2016). The occlusal plane points $\left(x_{ocl},y_{ocl},z_{ocl}\right)\in {ℝ}^3$ are then calculated by finding intersections between the estimated occlusal plane and the innermost surface of the mesh (Fig. 4a). The 2D grid coordinates of the occlusal plane points (u_ocl, v_ocl) are also calculated by interpolating the grid coordinates of the neighboring nodes (Fig. 4a). Fig. 4a clearly demonstrates the misalignment between the mesh grid and the occlusal plane points. To solve this misalignment, first, the horizontal grid line corresponding to the average of v_ocl is selected. Then, the transformation T_ocl which align the selected horizontal grid line to the occlusal plane points (u_ocl, v_ocl) is calculated. All of the rest of the grid nodes are then adjusted according to the acquired transformation T_ocl using TPS (Fig. 4b). The top and bottom of the mesh grid is fixed during the adjustment. As a result, new adjusted 2D coordinates of the mesh (u_adj, v_adj) are acquired. Finally, the 3D Cartesian coordinates of the adjusted mesh nodes (x_adj, y_adj, z_adj) are interpolated using the known coordinates of the original mesh nodes ((x, y, z) and (u, v)) and 2D grid coordinates of the adjusted nodes (u_adj, v_adj). To complete the mesh alignment, the mesh layers between the outermost surface (facial surface) and innermost surface (bone surface) are also adjusted accordingly. The adjusted mesh grid on the innermost surface matches with the estimated occlusal plane (Fig. 4b).

2.3.2.2. Incremental simulation with realistic sliding effect.

Incremental simulation with the realistic sliding effect is implemented in 2 steps. First, facial change simulation with the realistic sliding effect is performed by applying the surgical bony movements in 3 increments. Second, the FE mesh resulted from the first step is adjusted to ensure a geometrical match with the bony surface. As a result, the realistic sliding effect acts as ‘no-separation’ sliding which allows the soft tissue surface slides on the bony surface without penetration and separation as well.

In the first step, the facial change is simulated by applying incremental bony movements to the moving nodes. Three incremental steps of bony movements between pre- and post-operative bone position are acquired by calculating two additional intermediate bone positions using linear interpolation of translation and rotation represented with quaternions (Maker, 1995; Shoemake, 1985), which results in total of four bone positions. The mucosa sliding effect is implemented by applying a nodal force constraint on the mucosa sliding nodes and forcing them to move along the bony surface (Kim et al., 2017). The lip sliding effect is also applied along with the mucosa sliding effect. The lip sliding nodes are found using a point-wise collision detection algorithm (threshold: 0.2 mm) to detect the contacting nodes between the upper and lower lips. The lip sliding effect is achieved by applying a master-slave approach (Muñoz and Jelenic, 2004) to constrain degrees-of- freedom (DOF) of the lip sliding nodes. Thereby, the upper and lower lip sliding nodes are not allowed to further collide with each other in a vertical direction (craniocaudal direction) while the movements in other directions are unconstrained. As a result, the upper and lower lip sliding nodes slide against each other without penetrating each other and move independently according to the underlying bony change.

In the second step, nodal displacement boundary condition is applied to the mucosa sliding nodes to resolve any potential geometrical mismatch between the bony surface and the mucosa sliding nodes (Kim et al., 2017). The required nodal displacement is calculated by finding the closest point from each mucosa sliding node to the current bony surface updated with the incremental movement (Kim et al., 2017). The lip sliding effect is also applied during the second step. The resulted FE mesh of each incremental simulation is fed as the input FE mesh for the next incremental simulation until all 3 increments are completed. During the simulation, FEM is performed with our in-house code using Matlab.

3. Experiments and result

3.1. Patient subjects and data acquisition

Our facial change prediction method was evaluated using 35 randomly selected patients (17 females and 18 males with 23.0 ± 4.0 years old) using a random table. The inclusion criteria were: 1) diagnosed with jaw deformities, 2) already undergone an orthognathic surgery, and 3) had complete sets of pre- and postoperative CT and 3D photographs (3dMD) data in our digital archive [IRB0413–0045] (Table 1). The patients who were diagnosed with a syndromic deformity or underwent secondary revision surgery were excluded from the study. The CT scans were acquired following our routine clinical protocol: 512×512 of scanning matrix, 1.25 mm of slice thickness, and 250 mm of field of view. The postoperative CT scans were acquired within the first six weeks from the surgery, while the postoperative 3D photographs were captured at least six months after the surgery in order to avoid post-surgical swelling (Hsu et al., 2013).

Table 1.

The classification of jaw deformities and the surgery.

	Mandibular surgery	Double-Jaw Surgery	Genioplasty
Classification of Deformity	Yes	Yes	Yes	No
Skeletal Class I	0	5	0	5
Skeletal Class II	0	5	2	3
Skeletal Class III	1	24	7	18
Subtotal	1	34	9	26

The bony structures were segmented from the pre- and post-operative CT scans using thresholding (226 Hounsfield Unit) and manual editing when applicable. Postoperative CT scans were registered to preoperative ones based on surgically unchanged regions, i.e., cranium and midface, using our previously proven surface-best-fit method (accuracy: 0.12 mm ± 0.19 mm) (Xia et al., 2007). The registered postoperative CT scans served as a “blueprint” for actual bony movements. Then, virtual osteotomies were performed on the preoperative CT models, and the movement vector of each bony segment was acquired by registering each preoperative bony segment to the blueprint of the postoperative models. The translational and rotational movements were ranged from 0.0 to 6.3 mm and 0.0 to 9.8° for the maxillary Le Fort I segment, and from 2.1 to 11.5 mm and from 0.5 to 13.3° for the mandibular distal segment. Finally, the acquired movement vector of each bony segment was applied to the corresponding moving nodes as boundary condition to simulate the facial change following the bony change.

3.2. Lip-detailed patient-specific FE mesh generation

Lip-detailed patient-specific FE meshes were generated using our new mesh generation method. Lip surface digitization was performed typically on around 15 to 20 parasagittal slices for each lip to generate detailed and smooth lip surfaces. Depending on the complexity of lip geometry, approximately 10 to 20 points were digitized on each parasagittal slice. The patient’s preoperative facial 3D photograph, which includes both 3D facial surface and color texture, was used to replace the 3D CT soft tissues. This was to add the color texture onto the facial model and compensate the unnatural facial deformation during the CT scanning, e.g., strained lips or undesired facial expressions (Kim et al., 2017). The preoperative facial surface of the 3D photograph was registered to that of preoperative CT based on the rigid facial regions, i.e., forehead and nasal bridge. For the evaluation of prediction accuracy, postoperative facial surface of the 3D photograph was also registered to the preoperative CT soft-tissue using the same technique. The initial patient-specific mesh was then generated based on the facial surface of the 3D photograph using the previously developed anatomically-detailed FE mesh generation method (Zhang et al., 2018). Finally, the initial FE mesh was further improved using the above lip-detailed patient-specific mesh generation method to improve lip geometry. During the lip points digitization, the facial surface of the 3D photographs was overlaid on the parasagittal plane of the CT image to accurately and efficiently digitize the actual lip outer surface. An example of the resulted lip-detailed patient-specific mesh is shown in Fig. 5. The upper and lower lip were open when the patients had preoperative open-mouth. Otherwise, the upper and lower lip surfaces touched each other. As a result, the geometrical accuracy in the lip region was improved while the global geometry of the initial FE mesh, which was already accurate (Zhang et al., 2018), was preserved. The absolute surface deviation between the meshes before and after the lip improvement was 0.06±0.04 (Mean±SD, mm) with maximum absolute difference of 0.24 mm.

Fig. 5.

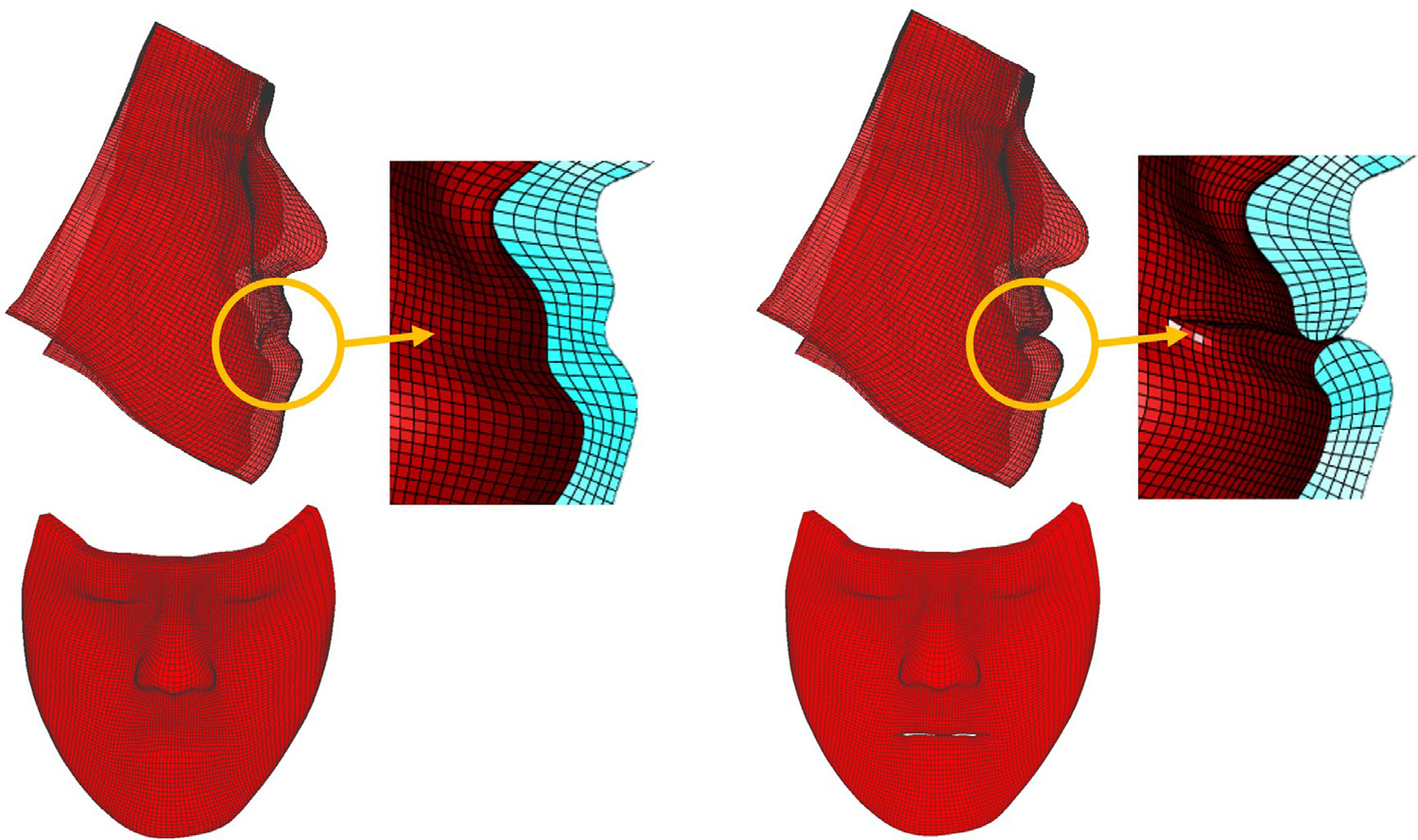
An example of the lip-detailed mesh. (left) initial mesh without lip-detailed geometry (right) lip-detailed mesh with lip opening.

We also measured the required time for the lip-detailed mesh generation. The initial patient-specific mesh was generated within 2–3 hours using our previously developed eFTP-VP method, which is a significant reduction in time compared to 24–48 hours of work for the traditional mesh generation method. However, improvement for the detailed-lip mesh requires additional 3–4 hours, especially due to the manual digitization.

3.3. Facial soft-tissue change prediction using three different methods

We predicted the facial soft-tissue change using our incremental simulation method and two other simulation methods for comparison. Method #1 was the traditional FEM simulation approach without applying any sliding effect (Kim et al., 2017; Koch et al., 1996). All FE mesh nodes contacting the bony surface were assumed to be attached to the corresponding bony segment without sliding. Method #2 was our previously developed three-stage FEM simulation with the mucosa sliding effect (Kim et al., 2017). Sliding effect was applied only to the intraoral mucosa region. The sliding effect between the upper and lower lips was not considered. In both methods, patient FE meshes were generated using our previous method (Zhang et al., 2018), and therefore the upper and lower lips were not separated and treated as a whole during the simulation in both methods. Method #3 was our incremental simulation method with the realistic sliding effect of the lip and the mucosa using the lip-detailed FE mesh as described above.

3.4. Prediction result evaluations for validation

The prediction accuracy was evaluated using two different methods; 1) surface deviation and 2) lip-shape analysis. Standard surface deviation error was used to evaluate the average value of the absolute Euclidean distances between the predicted and the postoperative facial surface along the surface normal vectors of the postoperative outcome. While the purpose of new simulation method is to improve the prediction accuracy in the lips, we nonetheless evaluated the accuracy of the entire face that was divided into 6 regions based on the facial landmarks (palpebrale inferius, alar, subnasale, cheilion, and labiomental fold) to ensure our new method would not affect the other regions.

The lip-shape analysis was used for qualitative evaluation of the prediction result by analyzing the geometrical difference of the two-dimensional lip profiles between the predicted result and the postoperative outcome (Fig. 6). Facial profile was acquired along the midline of the facial surface. A lip profile was defined as a convex part of each lip (blue in Fig. 6.a,b,c and d). The difference was quantified by the combination of 1) the required displacement to match two lip profiles and 2) the difference in the size and center of the best fitting circle for each lip profile. The required displacement between two lip profiles was calculated using Procrustes analysis which can be used to match two different shapes. The difference between the center of the fitting circles represented the difference in the lip position, and the difference between the fitting circles size represented the difference in the lip shape (size and curvature). The lip-shape analysis evaluated the upper and lower lips and both upper and lower lips as a whole, separately. The initial unpublished data showed a statistically significant correlation between the clinician’s qualitative evaluation and the outcome value of the lip-shape analysis. The goal of the lip-shape analysis was to provide quantitative value that can directly reflect clinician’s qualitative clinical evaluation of the prediction result. In one of our internal studies, we identified the quantitative criteria that maximizes the correlation between the value of the lip shape analysis and the qualitative evaluation performed by our experienced clinician. The qualitative evaluation divided the results into two groups (1. clinically acceptable prediction and 2. clinically unacceptable prediction). For single lip, either upper or lower, values of the lip shape analysis less than 0.55 were considered clinically acceptable and the values equal or greater than 0.55 were clinically unacceptable. For both upper and lower lips evaluated as a whole, the threshold value was 0.7.

Fig. 6.

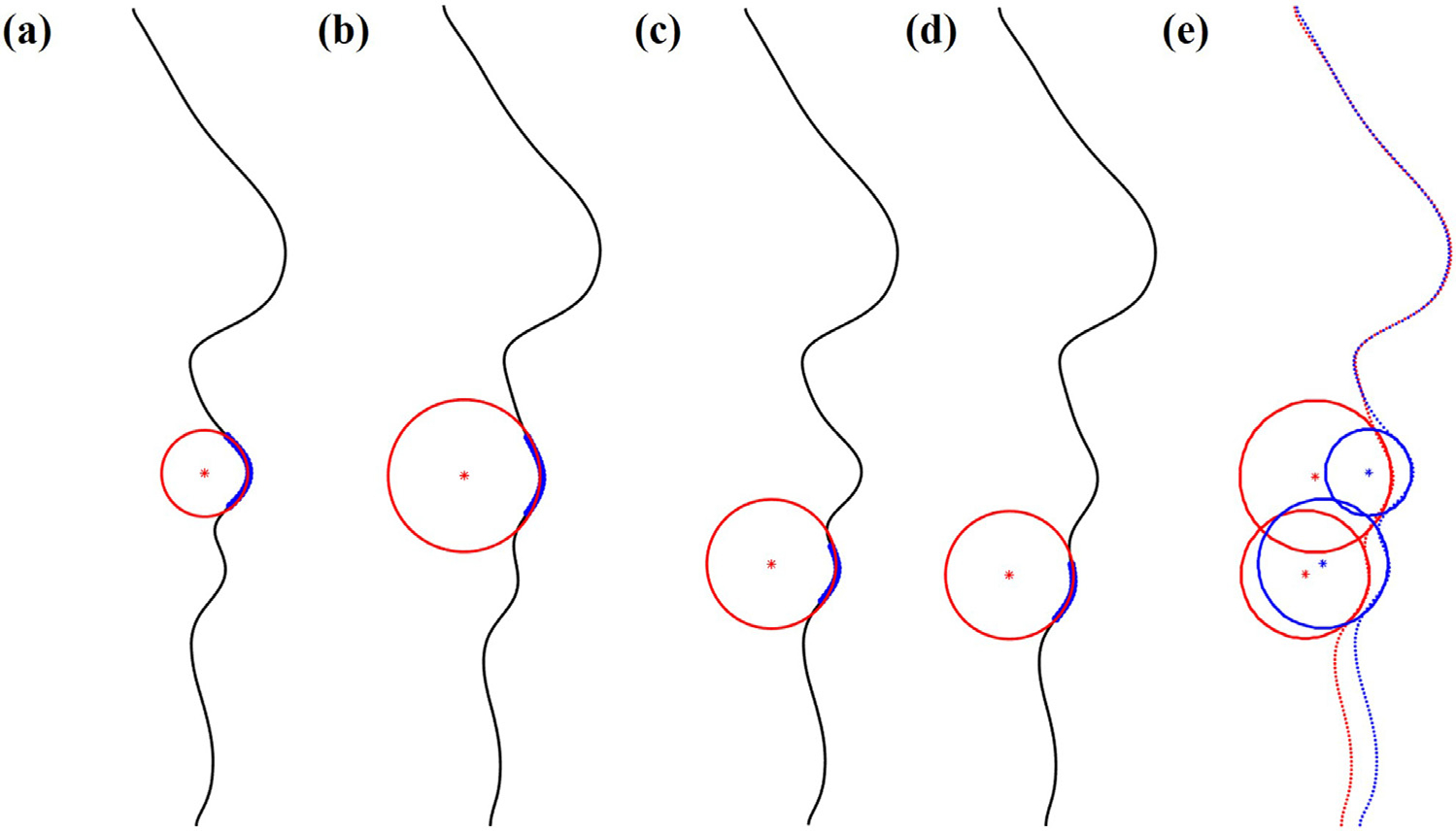
An example illustrating the lip-shape analysis method. (a) best fitting circle of the upper lip for the predicted facial result (b) best fitting circle of the upper lip for the postoperative outcome (c) best fitting circle of the lower lip for the predicted facial result (d) best fitting circle of the lower lip for the postoperative outcome (e) best fitting circles of the upper and lower lip for the predicted result (blue) and the postoperative outcome (red).

Repeated measures analysis of variance (ANOVA) was performed to detect statistically significant differences among prediction accuracy of the three methods. The Bonferroni method was used as post hoc test. Student’s t-test was also performed to further analyze the surface deviation error. The Wilcoxon signed-rank test was performed to analyze the qualitative improvement of the prediction accuracy evaluated by the lip-shape analysis.

3.5. Evaluation results

We predicted facial soft-tissue changes for all 35 subjects using three different prediction methods. Randomly selected examples of the predicted results with color texture are shown in Fig. 7. For the same cases, color-coded surface deviation error maps of the predicted results using different methods compared with the postoperative outcomes are shown in Fig. 8. Fig. 9 shows the improvements of Method #3 (our method) compared with other methods. Case #4 was additionally added in Fig. 9 as an example showing minor improvement. The result of each method was compared with the actual postoperative soft-tissue (Table 2).

Fig. 7.

Randomly selected examples of the simulated results with color texture. The top row shows the frontal view while the bottom row shows the right view of example patient. (a) Preoperative soft tissue. (b) Predicted facial soft-tissue using Method #1. (c) Predicted facial soft-tissue using Method #2. (d) Predicted facial soft-tissue using Method #3, our incremental FEM simulation with the realistic sliding effect. (e) The actual postoperative soft tissue.

Fig. 8.

Color-coded maps of the surface deviation error of the predicted results compared with the postoperative outcomes for the same cases in Fig. 7. From left to right: predicted result using Method #1, predicted result using Method #2 and predicted result using Method #3 (our method)

Fig. 9.

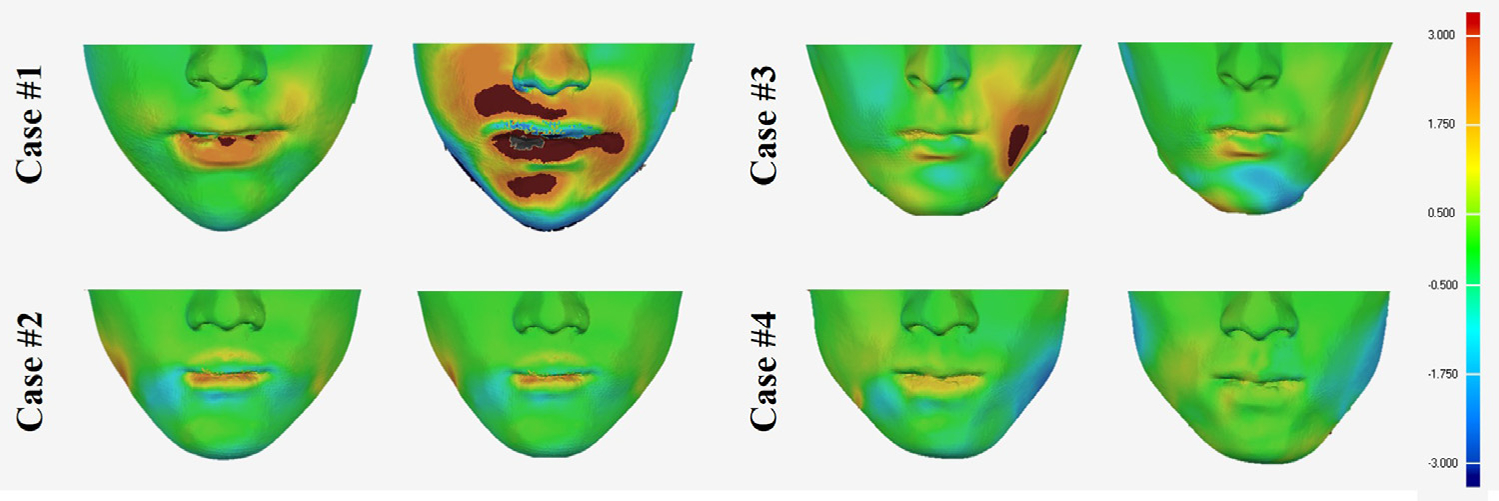
Color-coded maps of the improvements of the predicted results using Method #3 (our method) compared with the results of Method #1 (left) and Method #2 (right) represented with surface deviation. The same case as in Fig 7 for case #1, case #2 and case #3. Case #4 as an example showing minor improvement.

Table 2.

Prediction accuracy evaluation of three different simulation methods using surface deviation.

	Surface Deviation Error (Mean ± SD, mm) Prediction method			Improvement over Method #2 (%)
Region	Method #1	Method #2	Our Method	Our Method
Entire face	1.08 ± 0.28	1.08 ± 0.32	1.03 ± 0.30	5
1. Nose	1.04 ± 0.49	0.93 ± 0.39	0.91 ± 0.35	14
2. Upper lip	1.09 ± 0.55	1.06 ± 0.46	0.86 ± 0.36**	22**
3. Lower lip	1.50 ± 0.52*	1.41 ± 0.56*	1.10 ± 0.41**	29**
4. Chin	1.07 ± 0.52	1.17 ± 0.61	1.08 ± 0.51	0
5. Right cheek	0.89 ± 0.38	0.87 ± 0.40	0.86 ± 0.39	3
6. Left cheek	1.17 ± 0.47*	1.16 ± 0.47	1.01 ± 0.45	14

^*Significantly greater than 1 mm.

^**Significant improvement compared with Method #1 and #2. (P<0.05).

The results showed that our method improved the prediction accuracy in the lip region compared to other two methods. The result of the ANOVA test showed that the surface deviation error of our method was statistically significantly improved in the lower lip (P<0.05). Our method achieved a 29% of the prediction accuracy improvement over Method #2 (Table 2 and Fig. 7). In addition, the lower lip prediction achieved millimeter accuracy (not significantly different from 1mm), while the other two methods showed error significantly greater than 1 mm (Method #1: 1.50 mm; Method #2: 1.41 mm) according to Student’s t-test (P<0.05). The prediction accuracy of the upper lip also showed significant improvement with our method (0.86mm; 22% improvement compared to method #2) compared to the other two methods (Method #1: 1.09 mm; Method #2: 1.06 mm). Except in the lips, there was no significant difference among the 3 simulation methods in other regions. Our method (Method #3) also showed improvement in the lip region regardless of skeletal deformity types except for the upper lip of skeletal Class III cases (Table 3). The results of the lip shape analysis also proved that using our method, the prediction accuracy showed statistically significant quantitative and qualitative improvement in the lower lip and both lips as a whole compared with Method #1 and #2. (P<0.05) (Table 4 and 5).

Table 3.

Prediction accuracy improvement according to the types of jaw deformities.

	Upper Lip		Lower Lip
Improvement compared with Method #1 (%)	Method #2	Method #3	Method #2	Method #3
Skeletal Class I	17	31	35	43*
Skeletal Class II	−18	11	8	16
Skeletal Class III	2	0	20	26**

^*Significant improvement compared with Method #1 (P<0.05).

^**Significant improvement compared with Method #1 and Method #2 (P<0.05).

Table 4.

Quantitative prediction accuracy evaluation of three different simulation methods using lip-shape analysis.

Region	Method #1	Method #2	Method #3
Upper Lip	0.5 ± 0.4	0.4 ± 0.3	0.4 ± 0.2
Lower Lip	0.7 ± 0.3	0.6 ± 0.3	0.4 ± 0.2
Both Lips (as a whole)	0.9 ± 0.5	0.8 ± 0.3	0.6 ± 0.2*

^*Significant improvement compared with Method #1 and #2. (P<0.05).

Table 5.

Qualitative prediction accuracy evaluation of three different simulation methods using lip-shape analysis.

	Method #1		Method #2		Method #3
Region	Acceptable	Un-acceptable	Acceptable	Un-acceptable	Acceptable	Un-acceptable
Upper Lip	26	9	26	9	29	6
Lower Lip	13	22	15	20	26*	9
Both Lips (as a whole)	12	23	14	21	26*	9

^*Significant improvement compared with Method #1 and #2. (P<0.05).

4. Discussion

We have developed and validated an incremental FEM simulation method with the realistic sliding effect to predict facial soft-tissue change following orthognathic surgery. The developed method significantly improved the prediction accuracy in the lip region quantitatively and qualitatively with the addition of the realistic lip sliding effect compared with the previously developed methods.

The accuracy improvement in lip regions is contributed to two factors: the realistic lip sliding effect and the incremental simulation. The upper and lower lips not only slide over the teeth and bones, they also slide against each other. Although our previous method with the sliding effect of the intraoral mucosa has improved the accuracy in the clinically critical regions including the lips (Kim et al., 2017), the simulation in lip region is still unrealistic (Kim et al., 2017). This is because the upper and lower lips are treated as a whole and do not move separately. In this study, the lip sliding effect combined with the lip-detailed FE mesh allows independent and natural movement of the upper and lower lips, thus significantly improving the prediction accuracy in the lip region. In addition, transversely isotropic material property is applied to the lip region to maintain the intrinsic lip shape during the simulation and to even further improve the accuracy. However, the effect of inhomogeneity in the lip region is limited and challenging to prove because it is applied only to the small region of the lips. In this study, the region of the sliding nodes was also further extended to enhance the effect of sliding. Degloving of the soft tissue during the surgery may justify the use of the extended sliding region. Degloving is to separate the periosteum from the bone during the orthognathic surgery. After bony segments are repositioned, the periosteum and any soft tissue attached to the periosteum is reattached to the bone automatically. However, after the reattachment, the correspondence between the soft-tissue and the bony segment may change and does not remain the same as the preoperative relationship. This condition cannot be accurately achieved by the moving nodes, which is assumed to be attached to the bone, and may be better simulated by the sliding nodes. Our new method also solves the mouth-opening problem. In extreme cases, patient’s mouth is open preoperatively due to their deformities. After the surgery, the mouth is “automatically” closed following the bony movements. Our realistic lip sliding effect along with incremental simulation allows such simulation smoothly and naturally.

The effectiveness of the sliding effect was further enhanced by incremental simulation of facial change. In a real clinical situation, the bony movement and its corresponding facial change are a continuous transition from pre- to postoperative status. However, in the previously published studies, bony movements are applied in a one-step fashion from pre- to postoperative position. Due to the complexity of the soft tissue deformation and the soft tissue-to-bone interaction, this may cause inaccurate simulation of the sliding effect especially for the lips. Incremental simulation solved this problem by simulating the transitional state between the pre- and postoperative bone and face, which enabled natural change in the relationship between the lips and, consequently, the lip shape. The total steps of increment were fixed at 3 to balance the accuracy improvement and the required computational power. The incremental facial change simulation takes about 30 minutes to complete on a regular office computer while the other methods, which does not require repeated simulation, takes about 10 minutes. In addition, a mesh regulation method was implemented to prevent a potential instability of mesh element during the repeated FEM simulation for our incremental simulation. As a result of the incremental simulation with the realistic sliding effect, the prediction accuracy in the lip region is significantly improved without affecting other regions.

We evaluated the accuracy of the facial change prediction quantitatively and qualitatively using surface deviation error and our new lip-shape analysis. Surface deviation has been widely used as a standard error evaluation method for facial change prediction because it is represented by a unit of distance. While it may be intuitive, surface deviation error does not well represent anatomical correspondence and the clinician’s qualitative evaluation (Khambay and Ullah, 2015; Kim et al., 2017). The lip-shape analysis of measuring geometrical difference between the upper and lower lips was meant to overcome the limitation associated with the surface deviation error, thus directly reflecting the clinician’s qualitative evaluation. The actual emphasis of the lip-shape method was on the geometry of the lip rather on the overall surface deviation. Although they are connected in some aspect, the lip shape algorithm does better predict the clinical outcome than a pure mathematical distance measure. It is also important to note that the results of lip-shape analysis are less intuitive and not directly comparable to other measurements, e.g., surface deviation error.

The developed prediction method has a limitation. It requires extra time and effort for the lip-detailed mesh generation and the incremental simulation. The required time for surgical planning using our method can tremendously increase because it is not uncommon to take 6–8 iterations for surgeons to revise the surgical plan to achieve the optimal surgical plan, which prevents clinicians from adopting it for daily clinical routine. Therefore, a more efficient approach is required for the complete integration of the facial change prediction into a clinical environment. We are currently working on implementing automized landmark digitization using machine-learning technique to reduce the data processing time. We are also planning to improve the efficiency of assembling process of the global stiffness matrix because it consumes most of time for the incremental simulation. The real challenge ahead is reducing the time clinicians spend on manipulating the surgical planning tool to adjust and improve the planning. We envision a process where the surgical planning simulation tool provides the surgeon with a series of planning options already acquired based on the predicted outcomes and the surgeon selects the optimal planning among them.

5. Conclusion

Prediction accuracy in the lip region is crucial because the lip plays a critical role in facial aesthetics. We have significantly improved the facial change prediction accuracy in the lip region by developing a novel incremental FEM simulation method with the realistic sliding effect of the lip and mucosa. The significant achievement of our approach is the generation of the lip-detailed FE mesh and the application of the realistic lip sliding effect in addition to the mucosa sliding effect. Our method successfully simulated independent movement of each lip and, thus, achieved the natural and realistic postoperative lip shape. However, accurate modeling of the lip geometry and the incremental simulation requires extra work and computational time. In the future, a more efficient prediction approach is necessary for integration of the facial soft-tissue change prediction into daily clinical protocol.