The distance between g-tensors of nitroxide biradicals governs MAS-DNP performance: the case of the bTurea family

Abstract

Bis-nitroxide radicals are common polarizing agents (PA), used to enhance the sensitivity of solid-state NMR experiments via Magic Angle Spinning Dynamic Nuclear Polarization (MAS-DNP). These biradicals can increase the proton spin polarization through the Cross-Effect (CE) mechanism, which requires PAs with at least two unpaired electrons. The relative orientation of the bis-nitroxide moieties is critical to ensure efficient polarization transfer. Recently, we have defined a new quantity, the distance between g-tensors, that correlates the relative orientation of the nitroxides with the ability to polarize the surrounding nuclei. Here we analyse experimentally and theoretically a series of biradicals belonging to the bTurea family, namely bcTol, AMUPol and bcTol-M. They differ by the degree of substitution on the urea bridge that connects the two nitroxides. Using quantitative simulations developed for moderate MAS frequencies, we show that these modifications mostly affect the relative orientations of the nitroxide, i.e. the length and distribution of the distance between the g-tensors, that in turn impacts both the steady state nuclear polarization/depolarization as well as the build-up times. The doubly substituted urea bridge favours a large distance between the g-tensors, which enables bcTol-M to provide ϵ_on/off > 200 at 14.1 T/600 MHz/395 GHz with build-up times of 3.8 s using a standard homogenous solution. The methodology described herein was used to show how the conformation of the spirocyclic rings flanking the nitroxide function in the recently described c- and o-HydrOPol affects the distance between the g-tensors and thereby polarization performance.

Graphical Abstract

Introduction

Sensitivity, or signal to noise ratio per square root of time unit, has always been the Achilles heel of solid-state Nuclear Magnetic Resonance (ssNMR). While ssNMR is one of the most potent ways to access atomic scale information on solids, its application to samples that contain a low concentration of NMR active nuclei is hindered by a lack of sensitivity. This lack of sensitivity primarily arises from the low polarization of nuclear spins, even under high magnetic fields.

Unlike nuclear spins, electron spins have a large gyromagnetic ratio and thus a larger spin polarization; unpaired electrons have ^~658 times higher polarization than protons at a given magnetic field. Interactions between electrons and nuclei can be utilized to increase the nuclear polarization through a process called Dynamic Nuclear Polarization (DNP) [1,2], which uses microwave (μw) irradiation while collecting the NMR spectra. In the past two decades, DNP, combined with Magic Angle Spinning (MAS), high magnetic fields and high power μw sources, has yielded high resolution ssNMR data with high sensitivity [3–9]. This development has facilitated a plethora of ssNMR applications, both in structural biology and material science [5–11].

MAS-DNP is most often carried out using biradicals as polarizing agents (PA) [12–15], usually bis-nitroxides, for which the solubility, the electron-electron coupling, the relaxation times of the electron spins and relative orientations of the two radicals have been finely tuned [13,15–20]. Such PAs facilitate an increase in nuclear spin polarization in a short timescale that is characteristic of each polarizing agent (called build-up time). The geometrical properties of the bis-nitroxides have significant implications on the MAS-DNP [21–25]. For instance, it has been demonstrated theoretically and experimentally that strong electron-electron dipolar/exchange interaction, yield faster build-up times [19] and can determine the final polarization levels both with and without μw irradiation [18,19,23,26,27].

From a theoretical point of view, the Cross Effect (CE) under MAS is time dependent and involves magnetic interactions via “rotor events” [5,28–33]. Simulations revealed early on the role of the electron relaxation time, the μw nutation, the electron-electron and electron-nuclear interactions [24,25,28,29,34,35]. However, analysis was more complex when trying to understand the role of relative orientation of the two nitroxide radicals. For a given biradical, the relative orientation can be quantified via its three Euler angles [α, β, γ) leading to a difficult interpretation [25,36]. Attempts to scan these Euler angles provided some insight on the role of the β angle [25], but missed some important aspects such as the relative orientations’ effects on the MAS-DNP field profile [37–39] as well as the build-up times [39].

To overcome this complexity, we explored the role of the relative orientation between two nitroxides in MAS-DNP in terms of the distance between their g-tensors, also referred to as the g-tensors’ distance [39]. In this approach, the relative orientation is quantified by taking the norm of the difference between the matrices of the two g-tensors. When the two nitroxides have the same orientation, this norm is zero and it increases as the two nitroxide’s g-tensors become non-colinear. Simulations revealed that a larger distance between the g-tensors generates more overall CE rotor events and larger electron polarization differences [39]. In turn, they create higher nuclear spin polarization, faster build-up rates [39], while lowering the depolarization effect [23,34,39].

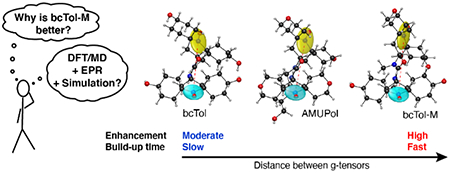
In this article we demonstrate experimentally the importance of the distance between the g-tensors on MAS-DNP enhancement, using one of the best performing family of polarizing agents, the bTureas. In particular, we focused on three members, all of which are water-soluble: AMUPol [14], bcTol [40] and bcTol-M [41] (Fig 1). We have also improved previous simulation models [42] to the point that it enables prediction of MAS-DNP properties of biradicals that are closely related, a hallmark of accurate simulations. Moreover, we show for the first time that the relative orientation between g-tensors is the main driving force of the improved performance, from bcTol [40] to AMUPol [14] to bcTol-M [41].

Fig. 1:

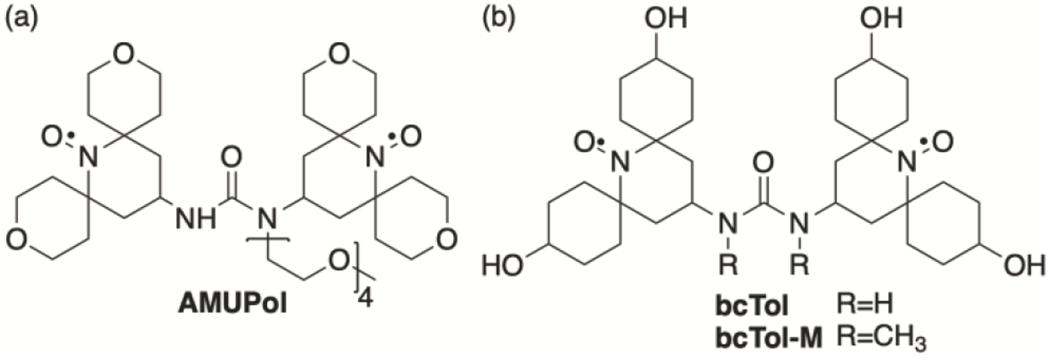
Structures of AMUPol, bcTol and bcTol-M.

In the first section of this manuscript, we explain the experimental and theoretical considerations. In the second section, the structure of the biradicals is solved by combining DFT, Molecular Dynamics and EPR at two frequencies, 9.6 and 240 GHz. The MAS-DNP field profiles were used to confirm the validity of the determined structures. Finally, MAS-DNP simulations predict the build-up times, polarization, depolarization and enhancement. The simulations tool served to discriminate which of the exchange interaction/dipolar coupling or the g-tensors’ distance most influences the MAS-DNP properties. Finally, the results are discussed in the context of biradical design and we explore how these findings can provide an alternative/complementary explanation for the efficiency of recently introduced HydrOPol from the bTurea family [20].

Experimental and Simulations

Experimental

Sample preparation.

10 ± 0.5 mM solution of bcTol, AMUPol and bcTol-M (see Fig. 1) in d8-glycerol/D₂O/H₂O (6/3/1 v/v/v) with 250 ± 10 mM ¹³C-¹⁵N-Proline. d8-Glycerol and ¹³C-¹⁵N uniformly labelled proline was purchased from Cambridge Isotopes, AMUPol was purchased form Cortecnet, bcTol and bcTol-M were prepared as previously described [40,41].

Electron Paramagnetic Resonance (EPR) experiments.

Continuous wave (CW) EPR measurements were carried out at 100 K at 9.6 and 240 GHz. At 9.6 GHz, samples were measured inside the sapphire rotor on an EMX-Nano using a N₂ cooled Dewar. The field modulation was set to 0.1 mT and the μw power to 1 μW in order to avoid signal saturation. The 240 GHz spectra were measured under the same conditions as previously described [38]. The field modulation was set to 0.3 mT and the power kept low enough to avoid passage effects. Two 90-degree out-of-phase signal components are measured simultaneously in an IQ mixing scheme, which allows to obtain pure absorptive and dispersive components via a simple normalized linear combination between the two measured phase components. The calibration of the magnetic field allows the determination of the g-values with a global uncertainty of 2e-4 [38,43].

MAS-DNP experiments.

Samples were packed into a 3.2 mm sapphire rotor using Vespel caps. The samples were placed into liquid N₂ and thawed, a process that was repeated three times to remove bubbles and to improve glass formation. The experiments were carried out at the NHMFL (Tallahassee, FL, USA) on the 14.1 T / 600 MHz / 395 GHz MAS-DNP setups [44]. This instrument is equipped with a quasi-optical table which enables accurate control of the μw beam which is distributed between an Overhauser and a MAS-DNP setup. In particular it has been upgraded with a Martin-Puplett (MP) interferometer [45,46], that can theoretically lead to an increase in the μw field by up to a factor √2. This interferometer provides an additional 10-15 % improvement in enhancements. For each sample the μw power and MP setting were optimized. Sample temperature in absence of μw was 95 K (VT / Drive / Bearing = 91 / 98 / 100 K) for a spinning speed of 8 kHz. The build-up times were measured by saturation recovery. The depolarization measurements were carried out using a previously published method [19,38].

MAS-DNP field profiles (or enhancement as a function of the magnetic field) were obtained by sweeping the magnetic field close to the EPR transition while maintaining the μw frequency fixed. The MAS-DNP field profile of AMUPol was recorded with a 2 M ¹³C-urea instead of proline and has been previously reported [38]. Since the high field EPR spectra of the AMUPol sample with proline and the one with urea where identical, the measurement of the MAS-DNP field profile was not repeated.

Simulations

Definitions.

The nuclear polarization at thermal equilibrium, in the presence and absence of μw irradiation, are defined as P_n,Boltzman, P_n,on, and P_n,off, respectively. The resulting polarization gain ϵ_B and the depolarization ϵ_Depo are defined as:

$${ϵ}_B=P_{n,\mathrm{on}}/P_{n,\mathrm{Boltzman}},$$

$${ϵ}_{\mathrm{Depo}}=P_{n,\text{off}}/P_{n,\mathrm{Boltzman}}.$$

Experimentally, the ratio ϵ_on/off corresponds to the ratio of the NMR signal in presence and absence of μw irradiation:

$${ϵ}_{\text{on}/\text{off}}=P_{n,\text{on}}/P_{n,\text{off}}.$$

This last ratio is routinely reported when quantifying the efficiency of nitroxide biradicals, although it has been demonstrated in general that ϵ_B ≠ ϵ_on/off [18,23,30,34].

The distance between the g-tensors, L_a,b, is an essential parameter for the CE mechanism [39]. It correlates the polarization performance with the two nitroxides’ g-tensor relative orientation. For two tensors, a and b, with respective Euler angles (0,0,0) and Ω = (α,β,γ), L_a,b is defined as the Frobenius norm of the difference of the tensors:

$$\begin{gathered} L_{a,b}(\mathrm{\Omega })={\Vert ({\widehat{g}}_a-{\widehat{g}}_b(\mathrm{\Omega }))\Vert }_{\text{Fro}} \\ =\surd \text{Tr}\left[{({\widehat{g}}_a-{\widehat{g}}_b(\mathrm{\Omega }))}^{†}({\widehat{g}}_a-{\widehat{g}}_b(\mathrm{\Omega }))\right]. \end{gathered}$$

Where ${\widehat{g}}_a$ and ${\widehat{g}}_b(\mathrm{\Omega })$ represents the g tensors matrices for the relative orientation $\mathrm{\Omega }=(\alpha ,\beta ,\gamma ).$ The norm quantifies how two g-tensors relate as both the effect of the relative orientations and the anisotropy of the g-tensors are accounted for. For a bis-nitroxide with g values [g_x, g_y, g_z] = [2.00924, 2.006082, 2.00204], L_a,b ∈ [0, 10.18 × 10⁻³]. The trivial case L_a,b(0,0,0) = 0 only generates SE [24,29]. Except otherwise specified, all angles are in degrees.

Numerical simulations.

The MAS-DNP simulations were performed via the latest implementation of a previously published method [38,42], improved to take into account larger dipolar/exchange interactions (see SI). The “box” model uses N copies of a three-spin system (2 electrons, 1 proton) distributed in a box. These copies can be isolated or interacting with one another. The “multi-nuclei” model simulates an isolated biradical in interaction with many protons. The powder averaging is achieved using 1200 REPULSION [47] crystal orientations for the box model, and 600 for the multi-nuclei.

Except as otherwise specified, the temperature was set to 100 K, the MAS frequency was 8 kHz, the μw frequency was 395.175 GHz and the μw nutation frequency was 0.4 MHz. To obtain a better agreement, in particular with bcTol-M, the μw nutation frequency was set 1.15 times higher than 0.35 MHz, used in a previous publication [38]. This was justified by the use of a Martin-Puplett interferometer that converts the μw polarization from linear to elliptic [44,46].

The electron relaxation time, T_1,e, was assumed to be anisotropic with and T_2,e = 2.5 μs [38,41,48,49], and identical for all three biradicals [41]. The nuclear relaxation time of the bulk nuclei was set to T_1,n = 80 s, in agreement with the T_1,n measured on the undoped sample. The protons closer to the electrons have a relaxation that inversely depends on the square of the hyperfine coupling, with the condition that if the nucleus has a dipolar hyperfine coupling of 3 MHz, its relaxation time is 0.04 s (see SI for a detailed explanation).

The concentration of the biradicals was assumed to be 10 mM. Each box contained 40 biradicals randomly distributed. The minimal distance between the two nitroxides, each belonging to different biradical molecules, was set to 1.8 nm. Only one nucleus per biradical was considered, located close to the electron spin a and only coupled to a with a dipolar hyperfine coupling of 3 MHz with a dipolar angle (ϕ,θ) of (30°, 75°). Its relaxation time was assumed to be short (T_1n = 0.04 s).

The multi-nuclei model uses as input MD simulations carried out in explicit water. Thus, it accounts for the presences of the protons on the biradical as well as their isotropic and anisotropic hyperfine couplings (obtained from DFT). For each crystal orientation in the MAS-DNP simulations protons have been randomly removed in order to match the experimental [¹H] concentration. As each nucleus is connected to two electron spins, the mathematical model has been revamped. The polarization exchange of close protons was treated using Landau Zener (LZ) approximations and Froissart–Stora formula, while those further away were treated using a classical polarization exchange. The expression accounts for the fact that each proton is now connected to two electron spins. This new model is designed for moderate MAS frequencies and allows a smooth transition between the LZ and rate equation approach. All the details related to the model are given in the SI.

The model can become more quantitative by combining the box model and multi-nuclei model to allow the prediction of ϵ_on/off, ϵ_B and ϵ_Depo [38]. The multi-nuclei model assesses the effect of polarizing many nuclei, notably on the build-up times in the final polarization. The box model accounts for the biradical-biradical interactions (see SI for details). Assuming that both effects are independent, i.e. the “inter-molecular” CE is negligible, the models can be extrapolated to predict a multi-nuclei-multi-electron model via:

$$ϵ={ϵ}_{\text{Multi}-\text{nuclei}}\times \frac{{ϵ}_{\text{Box}}^{\text{Interacting}}}{{ϵ}_{\text{Box}}^{\text{Isolated}}}.$$

The hypothesis is reasonable for biradicals as inter-molecular CE rotor events are particularly weak, for homogenously distributed biradicals at high magnetic field [24,34,42].

DFT simulations

Except otherwise specified, the DFT computation were carried out via Orca 4.2 [50]. The preliminary structures were generated and optimized using Avogadro v1.2 [51]. The structures were optimized using BP86 [52,53] and def2-TZVP [54]. All DFT simulations used a Polarizable Continuum Model Ethanol as it has close dielectric properties with the glycerol used in the samples (PCM(Ethanol)) [55].

The dipolar interaction and the hyperfine couplings were computed using PBE0 [56] and EPR-III [57]. The hyperfine coupling to either electron 1 or 2 were computed, bearing in mind that accurate determination is beyond the scope of this article [58]. The g-tensors were calculated via the basis IGLO-II [59] and PBE0 [56]. To reach more accurate g-tensor values, the gauge origin was chosen to be at the centre of the spin density (option “Ori CenterOfSpinDens” in Orca“)..

The exchange interaction was computed using the range-separated functional CAM-B3LYP [60] with the def2-SVP basis and a very tight convergence (10⁻¹¹ Hartrees) [61].

EPR simulations.

The EPR spectra were computed using Easyspin 5.2.20 [62] via the Hamiltonian diagonalization method (“matrix”). The line broadening used, corresponding to a g-strain proportional to [2(g_x - 2), g_y - 2, g_z - 2] × 4.5%, and a mixture of Gaussian Lorentzian, 0.5 and 0.3 mT.

The EPR spectra were fitted using the DFT-predicted parameters as starting points. The g-values were adjusted first, then the exchange interaction was estimated. Finally, g-tensors’ Euler angles and exchange were refined together. The dipolar Euler angles were left unchanged as they have very little impact on the fits.

In the fitting procedure, a weighting function was applied to the EPR spectra: 1 for the 9.6 GHz (X-band) and 2 for the 240 GHz. As a consequence, the contribution of the high field EPR spectra to the least-square sum was higher, forcing a better agreement with the high field than the low field. The rational for this approach is simple: the low field EPR spectra are heavily influenced by the dipolar/exchange interaction and the ¹⁴N hyperfine coupling strains, which make an optimal fit nearly impossible. However, when multiple good fits were found, the chosen one had a match to the low field features (resonant position and relative intensity).

The uncertainty for the parameters that were obtained are listed in Table 1 (SI). Those uncertainties were obtained by manually testing and evaluating the quality of the fits. While this is rather primitive, the least square map approach is not reliable enough to quantify the agreement between the simulated and experimental spectra, in particular the agreement with the resonant position.

Table 1:

List of the calculated (DFT) and experimental geometric parameters (after fitting) for the bcTol, AMUPol and bcTol-M biradicals. Euler angles are given in degrees with respect to the first g-tensor, using the rotation convention (active rotation) of Easyspin, v5.2

Biradical	g-tensor [gx, gy, gz]	g-tensor relative orientation (α,β,γ) (degrees)	14N hyperfine coupling (MHz)	Dipolar coupling / J- exchange interaction (MHz)	Dipolar orientation (ϕ,θ) (degrees)	La,b (× 103)
bcTol (DFT)	[2.00923, 2.00625, 2.0022]	[57, 46.6,118]	-	34.5 / −12	[170, 81]	5.2
(exp)	[2.00915, 2.0061, 2.00216] ±2.10−4	[67, 56,120] ±[10,10,5]	[20 18 103] ±2	34 ± 1 / −14 ±1.5	[170, 81]	5.8
AMUPol (DFT)	[2.00923 2.00626 2.00214]	[48, 59, 120]	n.c.	35.1 / −11	[167, 78]	6.5
(exp)	[2.00925,2.00619,2.00212] ±2.10−4	[58, 57, 126] ±[5,10,5]	[20 18 103] ±2	35 ± 2 / −16 ± 2	[167, 78]	6.4
bcTol-M (DFT)	[2.00923,2.00625, 2.0022]	[59, 79, 120]	n.c.	35.5 / −14	[169, 73]	7.2
(exp)	[2.00925, 2.00618, 2.00218] ±2.10−4	[58, 81,134] ±[5,10,10]	[20 18 103] ±2	36 ± 2 / −21 ± 2	[169, 73]	7.2-7.8

Molecular Dynamics (MD) Simulations.

MD simulations were carried out using OpenMM [63] and the AMBER (ffsb99) force field [64]. For the nitroxide, the force field was derived by Barone’s group [65] and the urea bridge force field by Özpınar et al. [66]. Lone pairs were added to the nitroxide in order to faithfully represent the hydrogen bonding occurring in the solvent [65].

The charges were obtained from the DFT structures, using the two steps RESP fitting procedure with Multiwfn [67], in order to provide reliable MD structures. The MD simulations were carried out in TIP3P water [68]. The input of MAS-DNP simulation was obtained with the MD simulations that were first minimized, then equilibrated for 20 ps and propagated for 100 ps in steps of 1 fs, under a pressure of 1 bar and a temperature of 298 K. The structure was then minimized to mimic freezing. The obtained biradical in water overlays accurately with the DFT prediction (see Fig. S3 for details). The major difference was found in a small variation in the conformations of the rings, due to the presence of hydrogen bonding with the water.

The biradical’s flexibility was assessed with MD simulations were carried out for 100 ns in water at 298 K and the structures was extracted every 500 ps.

Results

Determination of the geometry of the biradicals

In this section, the structure of a given biradical in frozen solution is elucidated. More specifically, the most important geometric features for MAS-DNP, namely the relative orientation between the nitroxides as well as the strength of the dipolar and exchange interaction, are determined by a combined approach of DFT and EPR.

DFT simulations.

The first step in determining the geometry of the biradicals involves computing their structures with DFT. For these simulations, we assumed that the hydroxyl groups on bcTol and bcTol-M were in an equatorial position, and that the rings of AMUPol were in the more stable “open” conformation [20,69]. Fig. 2 shows the lowest energy structure of bcTol (a), AMUPol (b) and bcTol-M (c). The g-tensors are depicted as ellipsoids with principal axis proportional to the g-tensor’s principal axis frame values to illustrate their relative orientation. The dipolar vector is represented as a dotted line that bridges the two nitroxide functional groups.

Fig. 2:

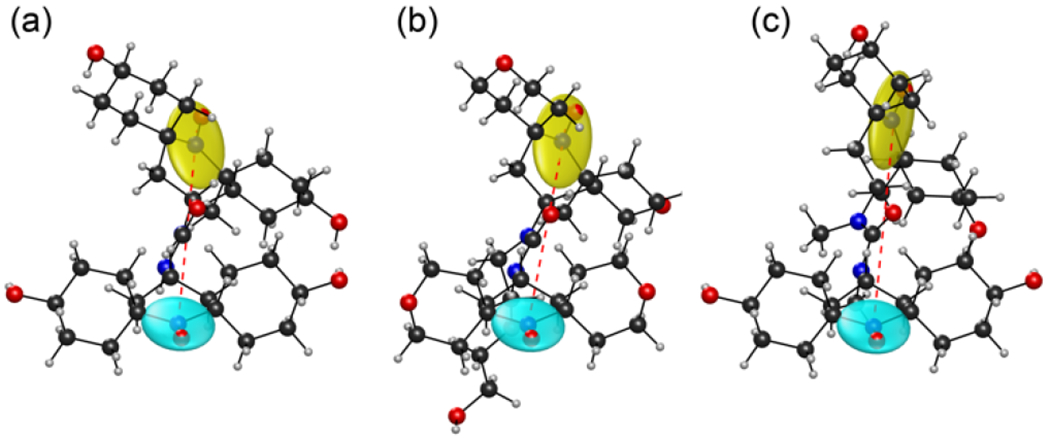
3D representation of bcTol (a), AMUPol (b) and bcTol-M (c). Ellipsoids in blue and yellow represent the g-tensors on each nitroxide, the red dotted line depicts the dipolar vector.

Fig. 1 illustrates the effect of substituents on the nitrogens of the urea bridge; bcTol contains no substituent, AMUPol contains one PEG chain, bcTol-M contains two methyl groups. It is noteworthy that the PEG chain on AMUPol forms a hydrogen bond with the N-H of the urea bridge, in effect “locking” the urea bridge.

The substituents on the urea bridge generate a steric hindrance that affects the global geometry of the biradical, changing the orientation of the six-membered nitroxides moieties and thereby the g-tensors’ distance L_a,b. The change in angles between the nitroxides was quantified in terms of the Euler angles of the g-tensors and the corresponding L_a,b, in addition to the predicted dipolar coupling vector and the exchange interaction (Table 1, SI). As the number of substituents increases, L_a,b increases. This may only be attributed in part to an increase in the β angle [16].

EPR measurements and fitting.

Solid state continuous wave (CW) EPR spectra, in particular high field CW-EPR spectra, are very sensitive to the relative orientation of the g-tensors. They are thus used to check and refine the DFT predictions. To improve the accuracy of the parameters, the solid state spectra at two frequencies [36,70–72], 9.6 and 240 GHz were fitted (Fig. 3).

Fig. 3:

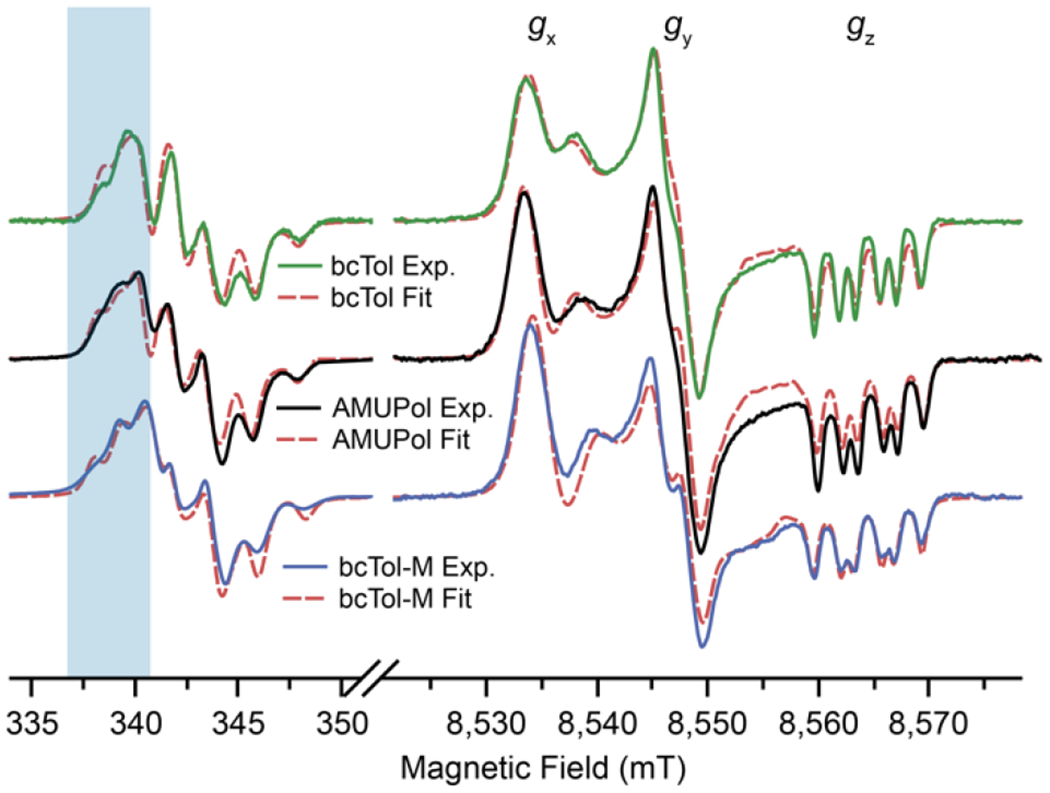
EPR spectra at 9.6 GHz and 240 GHz for bcTol (green), AMUPol (black), bcTol-M (blue). The red dashed lines overlayed on the EPR spectra correspond to the fitted EPR spectra for each biradical. The blue overlay represents the low field region of the X-band EPR spectra highlighting significant differences.

At 9.6 GHz, the three biradicals have slightly different EPR spectra. In particular, one transition located in the low field region (around 338 mT, blue overlay), shifts from bcTol to bcTol-M, toward lower field. This reflects stronger exchange interaction and allows ranking of the exchange interaction for the biradicals: $|J_{a,b}^{\text{bcTol-M}}|>|J_{a,b}^{\text{AMUPol}}|>|J_{a,b}^{\text{bcTol}}|$.

The high-frequency EPR spectra display greater changes. They are similar to those reported by Geiger et al. [41], but differ from the fact that they are not pseudo-modulated but collected in CW mode. At the right-hand side of the high-field spectra, the splittings are different in the g_z region. The g_y region shows a clear splitting for bcTol-M, less pronounced for AMUPol, and only a shoulder for bcTol. Finally, the relative signal amplitude between the g_x and g_y region is different for all three biradicals: g_x is less intense than g_y for bcTol, nearly equal for AMUPol, and more intense for bcTol-M.

The best fits of the EPR spectra are shown as dotted lines (Fig. 3). The DFT predictions generate EPR spectra that are in good agreement with the high field EPR spectra but is not ideal for the low magnetic field ones. After fitting, the agreement between simulations and experiments is very good for all three biradicals. The corresponding parameters are shown in Table 1. The Euler angles that were predicted by DFT and the ones extracted from the EPR fits are slightly different. A small adjustment (within ^~15 degrees) is sufficient to obtain an excellent agreement, which confirms the capability of DFT to predict the structure of the biradicals in the frozen state. The Euler angles change upon introduction of substituents on the urea, especially the β angle which increases from 56 degrees for bcTol to a maximum for bcTol-M (β ≈ 81 degrees). These Euler angle modifications result in a different distance between the g-tensors, increasing from ~5.8 × 10 ⁻³ to ~7.8 × 10 ⁻³.

The exchange interaction plays a significant role in the low field EPR spectra and is in particular responsible for the “shoulder” in the above-mentioned 338 mT region (blue overlay), and the splitting in the g_z region of the high-field EPR spectra. The EPR fits reveal a trend with increasing substitution on the urea bridge; the exchange interaction decreases from bcTol to bcTol-M from −13 MHz for bcTol to −16 MHz for AMUPol to −21 MHz for bcTol-M. The DFT predicted the correct sign, relative intensity and order of magnitude for each biradical, but needed adjustments: bcTol (−12 vs −14 MHz), AMUPol (−11 vs −16 MHz) and bcTol-M (−14 vs −21 MHz). Predicting such low coupling remains challenging by DFT as it is sensitive to the relative orientation [61].

To improve the agreement between experiment and simulations, intrinsic line-broadening and g-strain are necessary [36,38]. Those line broadening effects do not account for the true nature of the conformation distributions. The correct line broadening may very well be reproduced by a distribution of exchange interactions [41,61], but also slight variations in the geometrical structure (vide infra). Here we chose not to overfit the data and reduced the number of parameters that were adjusted by assuming a single biradical conformation for each biradical.

Flexibility analysis.

The good but imperfect agreement of the experimental and theoretical EPR spectra as well as the necessity of using g-strain to obtain matching, may reflect the existence of a distribution of conformations for the biradicals. To assess the flexibility of the biradicals, MD simulations were carried out to obtain trajectories over 100 ns. Fig. 4 shows the distribution of the distance between the g-tensors for the three biradicals. For bcTol, MD simulations predict an average L_a,b = 4.2 × 10 ⁻³, for AMUPol L_a,b = 5.6 × 10 ⁻³, L_a,b = 7.2 × 10 ⁻³. From the histogram spread, it is clear that bcTol and AMUPol are far more flexible than bcTol-M at 298 K. In contrast, bcTol-M seems to be fairly rigid as the g-tensors’ distance is narrow but still spans a significant range. The broad distribution of conformations for bcTol and AMUPol seems to be narrower at low temperature in glycerol/water as indicated by the resolved EPR transitions for high field, particularly in the g_z region.

Fig. 4:

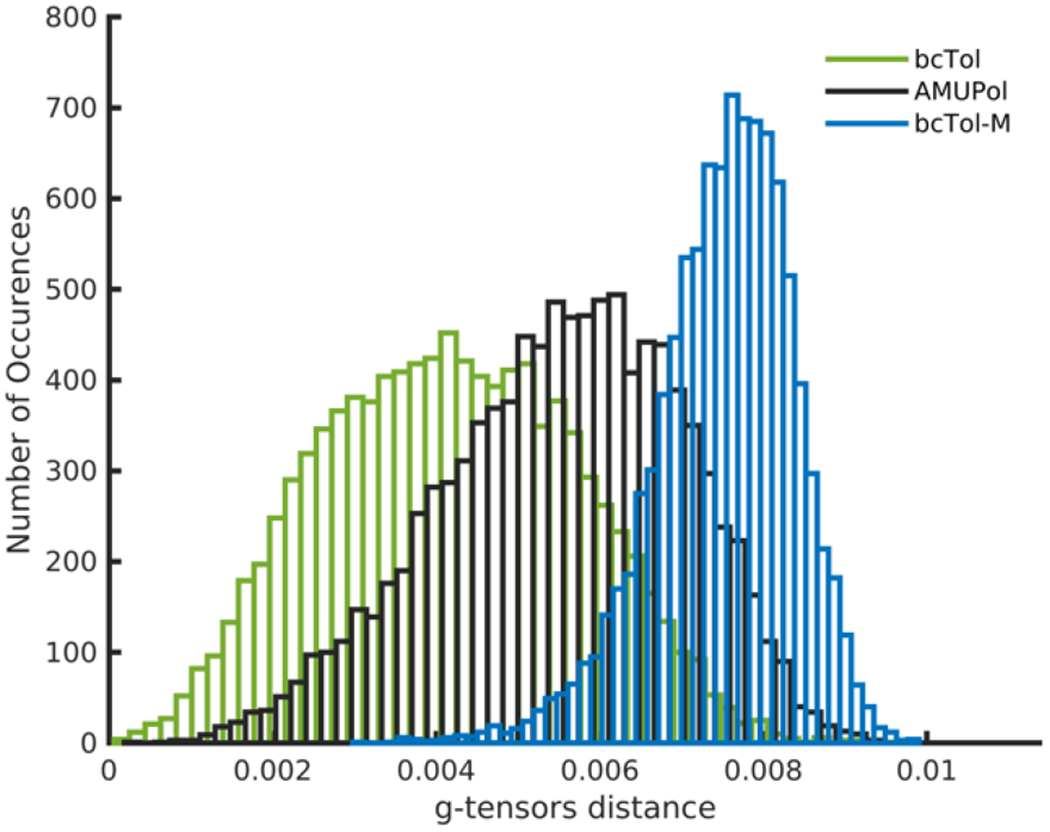
Histograms of the g-tensors’ distance for bcTol (green), AMUPol (black) and bcTol-M (blue) at 298 K in water

As these simulations are carried out in water (not glycerol-water), and at room temperature (and not 100 K), they may under-estimate the average L_a,b and over-estimate the flexibility. They cannot be used to safely extract the Euler angle distribution from the g-tensors. However, they confirm the “rigidifying” role of the substitution on the urea ring, as well as the shift in the g-tensors’ distance with increased substitution, and they justify the existence of conformation distribution.

Impact of the biradical’s geometry on the MAS-DNP properties: MAS-DNP field profile, polarization, depolarization and build-up

The geometrical properties of the bis-nitroxides modify the MAS-DNP properties. In this section, we correlate the biradical’s structure with the MAS-DNP field profile, and polarization/depolarization properties as well as the build-up times for all three biradicals.

MAS-DNP field profiles.

For bis-nitroxides with moderate electron-electron interactions, the MAS-DNP field profiles shape shows a positive and negative lobe. The relative intensity and symmetry of these lobes depend on the relative orientations of the nitroxides. For a large distance between the g-tensors, the MAS-DNP field profile tend to be symmetric, with lobes of similar shape and intensity [39]. A gyrotron operating at ^~ 395 GHz offers a high “resolution” on the MAS-DNP field profiles, as a high magnetic field emphasizes the effect of the g-tensors’ distance.

The three MAS-DNP field profiles are shown in Fig. 4. They share obvious similarities: the MAS-DNP field profiles are asymmetric, and the maximum enhancement is on the positive lobe. However, there are noticeable differences in the field profiles for the three radicals. First, the maximum of the positive lobes shifts toward the lower field in the following order: bcTol, AMUPol, bcTol-M. Second, the opposite order is observed for the minimum, which shifts toward higher field, most notably for bcTol-M. Third, the absolute ratio of maximum/minimum enhancement is ^~0.52 for bcTol, ^~0.73 for AMUPol and ^~0.8 for bcTol-M. The MAS-DNP field profile is more symmetric for bcTol-M than for AMUPol or bcTol, in line with the expected g-tensors’ distance in the order: bcTol, AMUPol, bcTol-M. This corroborates the impact of the substitution on the urea bridge, as shown in Table 1.

The theoretical MAS-DNP field profiles are computed from the geometrical and magnetic parameters determined by EPR spectroscopy: g-values, Euler angles, exchange interaction, dipolar coupling and relaxation times. The field profiles are depicted as open symbols with dashed lines in Fig. 5 for each biradical. The agreement between experiments and simulations for bcTol and AMUPol is very good. Notably, the overall shape, the relative intensity and the position of the maxima/minima are well reproduced. For bcTol-M the agreement is moderate. The relative intensity for the positive and negative lobes as well as their positions are all reproduced, but the agreement is imperfect in the middle of the field profile.

Fig. 5:

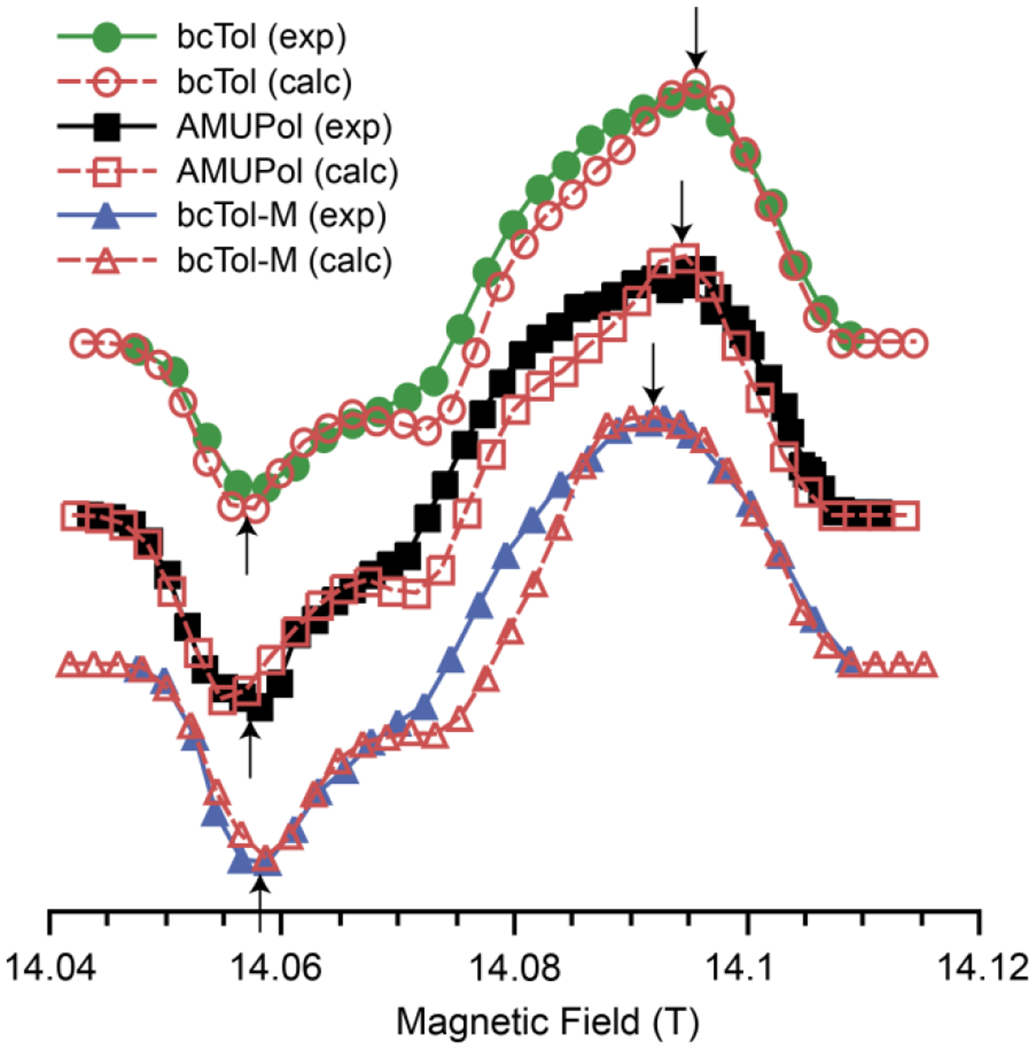
Experimental (full line) and calculated (red dashed line) DNP field profile of bcTol (circles), AMUPol (squares), bcTol-M (triangles). Arrows show the location of the maxima and minima of the enhancements.

Impact of the distance between the g-tensors on polarization gain, depolarization and build-up.

The exchange interaction and the relative orientation are two properties that change the most in-between the biradicals from the bTurea family in homogeneous solutions (see DFT and EPR section). They both impact the MAS-DNP quantities measured (T_B, ϵ_on/off, ϵ_B and ϵ_Depo). To determine which one most influences the performance we proceeded in two steps. In the first step, we checked the simulations’ abilities to predict T_B, ϵ_on/off, ϵ_B and ϵ_Depo, when using the EPR determined parameters. In the second step, the simulations enable quantifying the effect of relative g-tensor orientations on the MAS-DNP performance, by assuming that all parameters are constant, except the g-tensors’ relative orientation.

The experimental values T_B, ϵ_on/off, ϵ_B and ϵ_Depo are listed in Table 2 for all three biradicals. The build-up time gets shorter as the urea bridge is substituted, from 6.5 s down to 3.8 s. Additionally, the enhancement ϵ_on/off increases from bcTol to bcTol-M, starting at 140 and ending at 205. The depolarization is nearly identical within the experimental uncertainty at ca. 0.5, thus ϵ_B increases with the distance between the g-tensors, i.e. from bcTol to bcTol-M from ^~75 to ^~102. The simulated data is also listed in Table 2. The predicted build-up times are in very good agreement with the experiments for AMUPol and bcTol-M (within 5%). For bcTol, the simulations tend to underestimate it by ^~14%, a difference that may originate from the sample preparation. Indeed, assuming a concentration of 9.5 mM for bcTol (5% error on bcTol concentration) leads to a predicted build-up of 6.0 s, which is closer to the experiments. Lastly, the multi-nuclei model also predicts accurately the build-up times of AMUPol at 9.4 T with 3.6 s [14] and 18.8 T [73] proving the model’s robustness.

Table 2:

Experimental and calculated ϵ_Depo,ϵ_B,ϵ_on/off and T_B for bcTol, AMUPol and bcTol-M at 14.1 T

Biradical	Experiments		Theory from EPR fitted parameters		Theory assuming identical Ja,b = −16 MHz/ Da,b = 35 MHz
	ϵDepo/ϵB/ϵon/off	TB(s) (μw on)	ϵDepo/ϵB/ϵon/off	TB(s) (μw on)	ϵDepo/ϵB/ϵon/off	TB(s) (μw on)
bcTol	0.5 ± 0.1/ 75 ± 13 / 150 ± 10	6.5 ± 0.5 s	0.57/83/145.7	5.6 s	0.58/84.5/146.2	5.4 s
AMUPol	0.5 ± 0.1 / 85 ± 14 / 170 ± 10	4.8 ± 0.2 s	0.52/91/176	4.6 s	-	-
bcTol-M	0.5 ± 0.1/ 103 ± 6 /205 ± 10	3.8 ± 0.1 s	0.49/121/245	3.8 s	0.49/117/237	4 s
AMUPol at 9.4 T and 18.8 T		3.5 s @ 9.4 T* 5.1 s @ 18.8 T**		3.6 s @9.4T 5 s @ 18.8 T

^*see refs [14] for 9.4 T

^**see ref [73] for 18.8 T

When combining the box and multi-nuclei model, the simulations of ϵDepo/ϵ_B/ϵ_on/off lead to values within 15% of the experimental ones for each biradical. The largest error is observed for the ϵ_on/off of bcTol-M which exceeds the experimental one by 19%. Overall, simulations and experiments are in very good agreement one-another, confirming the models’ abilities to predict the MAS-DNP properties under these conditions.

To separate the influence of the dipolar/exchange interaction and the distance between the g-tensors on the MAS-DNP performance, another set of simulations was carried out for bcTol and bcTol-M. In that case the dipolar coupling and exchange interaction were set to 35 and −16 MHz, respectively. The dipolar vector was also kept identical to match the one for AMUPol. While this situation is not physically accurate, it effectively isolates the role of the g-tensors’ distance for these two biradicals. The results are reported in the last columns of Table 2. The build-up times obey strictly the same trends, increasing from bcTol to bcTol-M.

Comparison of these simulations with the simulation that is based on the accurate parameters of the biradicals allows identification of the role of the relative orientation. The build-up is ^~5% faster for bcTol and ^~5% slower for bcTol-M while the simulations generate nearly identical ϵ_Depo/ϵ_B/ϵ_on/off. This demonstrates that the variations in the MAS-DNP properties is mostly due to the increase in the distance between the g-tensors rather than a change in the electron-electron interactions: as the g-tensors’ distance increases, the build-up times become shorter, and the polarization gain higher.

Discussion

Effect of the distance between the g-tensors on the MAS-DNP properties

The concept of g-tensors’ distance was introduced to give a correlation of the MAS-DNP performance with the three Euler angles describing the relative orientation of the two tensors in biradicals [39]. This concept was based on theoretical consideration of previous work but remained unproven experimentally. Here we compare theory with experiments using three members of the bTurea family [14,40,41]. The three biradicals were chosen because of their high solubility in water and similar molecular weight, thus eliminating possible complications that could arise from aggregation of the sample or variations in different relaxation times. Although these compounds belong to the same biradical family, they have different MAS-DNP properties, thus offering a robust way to provide a quantitative analysis of the role of the dipolar/exchange interaction and the g-tensors’ relative orientation. The variation of the distance between the g-tensors explains why bcTol-M is superior to AMUPol and AMUPol is superior to bcTol at 14.1 T. bcTol-M not only gave the highest ϵ_on/off ~205 but also one of the fastest polarization build-up times reported thus far for biradicals in the context of MAS-DNP at 14.1 T.

The data and analysis presented here shows that DFT/EPR can be used to accurately extract the geometrical features of the biradicals, even if their structures are similar. The DFT/EPR data demonstrates that the biradicals can be ranked with respect to the distance between the g-tensors in the following order: bcTol, AMUPol, bcTol-M. The experimental EPR spectra could be reliably fitted and some of the results can be compared to previously reported data. The fit confirms that bcTol has a lower exchange interaction than AMUPol and bcTol-M has the largest, in agreement with a previous study [36]. The Euler angles for AMUPol obtained here fall within the uncertainty of previously published result [38] ([123.1, 129.8, −46] = [56.9, 50.2, 134]), with slightly lower β angle and higher γ angle. They also are in good agreement with the Euler angles found by Soetbeer et al. [36]. However, the relative orientations obtained for bcTol and bcTol-M are not equivalent to the values obtained by the same group for PyPol and PyPolDiMe [36], but these two biradicals have a close structure to bcTol and bcTol-M, respectively. This may be explained by variation in the fitting procedure and the fact that the uncertainties are larger in this previous work, but may also be attributed to different structures [36]. The β angles of bcTol and bcTol-M are more in line with the predictions of Sauvée et al. for PyPol and PyPolDiMe ([16], Fig. S4).

The MD simulations confirm the trend in the distances between the g-tensors, even at room temperature in water: bcTol-M is more rigid than AMUPol and AMUPol is more rigid than bcTol. This result seems to be in contradiction with the previous bcTol/AMUPol/bcTol-M study where bcTol-M was found the most flexible [41]. However, the method used in the previous study (random conformation search, different force field, implicit water) [41] differs from the one used here (time propagation, specific force field, explicit water). The different approach used to predict the flexibility may likely explain the different outcomes. The results obtained here correlate well with the expectation that the steric hindrance introduced by the substituents on the urea linker can “lock” the conformation of bcTol-M.

The geometrical and magnetic parameters, extracted from the DFT/EPR fits, lead to quantitative MAS-DNP simulations in a homogeneous solution. In this work, the main MAS-DNP properties such as the field profile, the build-up T_B and the routinely measured ϵ_on/off are all predicted with <20% error. This is the first time that such level of accuracy has been reached on multiple biradicals that have very close structures.

The MAS-DNP field profile simulations are in good agreement with the experimental one. This fact confirms that DFT calculations and EPR spectroscopy can be combined to precisely determine the average conformation of the biradicals. The agreement remain imperfect for all biradicals as there seems to be a systematic “error” close to where the enhancement changes sign. The reason for this discrepancy is not clear but it is not a consequence of the reduced number of nuclei; one or many nuclei generate the same MAS-DNP field profile (see Fig. S4). Besides the biradical’s geometry, the factors that have the greatest impact on the MAS-DNP field profile are the anisotropic parameters given to T_1e [38,41,48,74,75], the μw nutation frequency ([38], SI) and the g-tensors’ relative orientation. For nitroxides, the exact orientation dependence of T_1e is unknown due to the lack of a theoretical mode for this solution [74,75]. Thus, the T_1e dependence on the g-value is phenomenological [38]. In addition, the μw B₁ field is notoriously heterogenous [76–79]. It may be optimistic to expect a perfect fit with a single μw nutation frequency as well as the temperature distribution. It should be noted that the MAS-DNP field profile of bcTol-M turned out to be more sensitive to the relative orientation of the g-tensors than those of bcTol and AMUPol. A better agreement may be obtained if a distribution of the Euler angles of the g-tensors is used. Determining all these parameter variations (μw field intensity and distribution, g-tensor’s distribution, anisotropic T_1e values, temperature gradient, etc.) remains beyond the scope of this study.

Obtaining the correct T_B required nearly no adjustment but accurate ϵ_on/off values required two parameters to be adjusted: the μw nutation and the nuclear relaxation of the close protons. These two values are difficult to extract experimentally; only two ENDOR experiments have been able to determine accurately the T_1,n/T_1,x of the close protons. However the application of these pulse ENDOR experiments at high field, in glassy matrices, remains challenging [80,81]. In absence of experimental data, we assumed that paramagnetic relaxation was mediated by the hyperfine coupling and the chosen value enabled a better agreement for ϵ_on/off. To complicate matters further, the exact μw field intensity is unknown as indicated earlier; not only it remains highly inhomogeneous, but it should manifest in different ϵ_on/off for different parts of the sample [77]. Inhomogeneous μw fields generate inhomogeneous sample temperature, which should be accounted for in ideal simulations. We used a value that enables good reproduction of the DNP field profile while not being too different from previous simulations [38]. All in all, this level of accuracy required adjustments of the μw field and the close proton relaxation times. Future experiments may require that these factors be revisited.

Irrespective of these considerations, the most important fact is that as the urea bridge gets substituted, the distance between the g-tensors increases. The direct consequence is that most of the performance improvements (shorter build-up times, higher polarization gains) observed between bcTol, AMUPol and bcTol-M arise from the increased g-tensors’ distance. Surprisingly, the overall impact of the exchange interaction on the performance of the biradicals is negligible. Despite a 50% increase in the exchange interaction from bcTol to bcTol-M, it marginally contributes to the polarization gains or the build-up as it remains relatively small. That is not to say that large exchange interactions (>40 MHz) have no impact on the DNP performance of biradicals [17–19,26], but in the case of the bTurea family in a partially deuterated and homogenous solution, the distance between g-tensors is the dominating factor that affects the performance of the biradicals.

Open or closed biradicals?

The analysis carried out in this manuscript could provide new insights on the recently reported members of the bTureas family of biradicals, namely the HydrOPols [20]. Their structures are based on PyPolPEG2OH, a good MAS-DNP performer [16]. Two diastereoisomers were reported; one favours an “open conformation” of the spirocycles adjacent to the nitroxide (o-HydrOPol) and the other “closed conformation” (c-HydrOPol) [20] (see Fig. S5 for 2D representations). The open and closed HydrOPols showed very different MAS-DNP properties; the open one generated a much larger DNP enhancement (about. x10) than the closed one. The fact that these conformational changes dramatically affected the MAS-DNP performance was unexpected. The authors hypothesized that the open and closed conformations affected the solvent accessibility of the nitroxide and thereby the DNP performance [20], along with a change in molecular weight, which slows the electron relaxation rates [16]. Both factors seemed important for explaining the improved performance of o-HydrOPol.

Given the strong correlation of the distance between the g-tensors with MAS-DNP properties of bTurea derivatives reported in this paper, a hypothesis, not explored in the aforementioned paper [20], can be proposed: the conformations of the rings flanking the nitroxides modify the distance between the g-tensors. Using the same DFT approach as reported in this paper, the structures of the two HydrOPol diastereomers were computed (Fig. 6; for the corresponding geometrical properties, see Table S1). The relative orientations of the two g-tensors varies significantly between the open and the closed diastereomers, due to the strain induced by the conformation of the ring. The distance between the g-tensors for the “open” conformer is very similar to that of AMUPol, while it is significantly lower for the “closed” conformer (L_a,b = 6.6 × 10 ⁻³, vs 4.1 × 10 ⁻³). Assuming all other parameters equal, a MAS-DNP simulation predict a ratio of enhancement at the optimal field position of

$$\frac{{ϵ}_{\text{on}/\text{off}}^{\text{c}-\text{HydrOPol}}}{{ϵ}_{\text{on}/\text{off}}^{\text{o}-\text{HydrOPol}}}\approx 0.2,$$

Fig. 6:

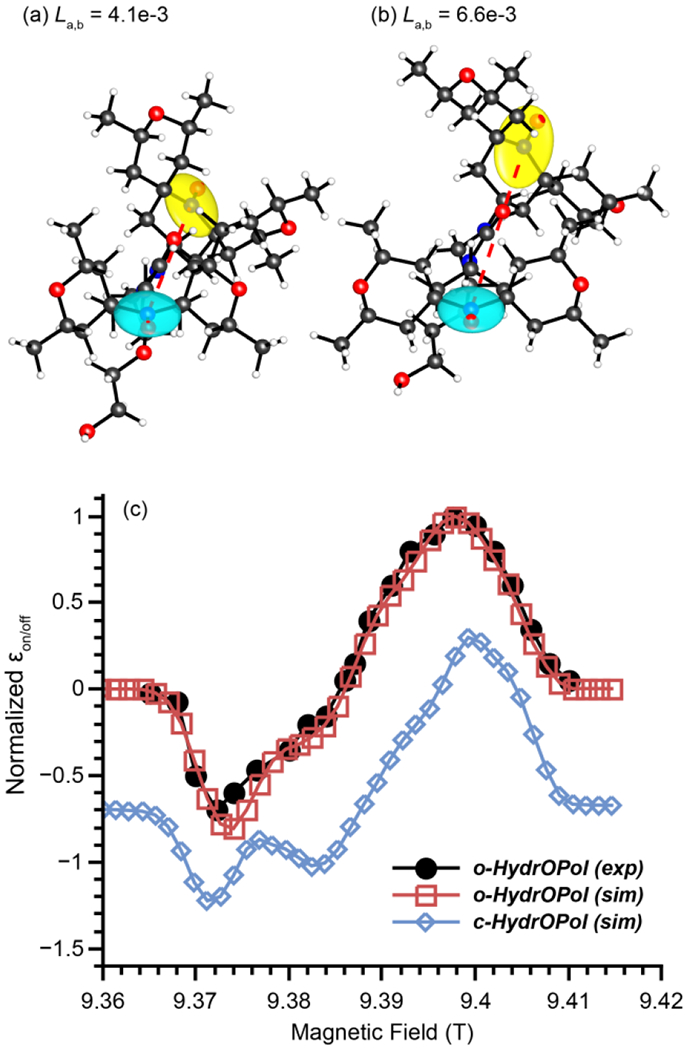
3D representation of c-HydrOPol (a) and o-HydrOPol (b). Ellipsoids in blue and yellow represent the g-tensors on each nitroxide, the red dotted line, the dipolar vector. (c) Experimental o-HydrOPol MAS-DNP field profile extracted from Figure S29 in [20] (black circles), calculated MAS-DNP field profile from DFT simulations for o-HydrOPol (red squares), and c-HydrOPol (blue diamonds)

which is close to the experimental data reported (^~0.1) [20]. This shows that the open conformation may perform much better than the closed one mostly because of the change in the distance between the g-tensors. This could be verified by comparing the experimental MAS-DNP field profiles of the two diastereomers. The calculated field profiles for o-HydrOPol and c-HydrOPol differ significantly (Fig. 6). At 9.4 T, the MAS-DNP field profile for o-HydrOPol is relatively symmetric with an absolute ratio between the maximum and minimum enhancement of 0.75. For c-HydrOPol, the MAS-DNP field profile is very asymmetric with an absolute ratio of 0.5 and the negative region showing “features”. The field profile for o-HydrOPol has been reported [20] (see extracted data in Fig. 6 (c)), which shows an excellent agreement with the simulations. However, the MAS-DNP field profile of c-HydrOPol is not reported and thus, our hypothesis cannot be entirely validated. The authors pointed out that c-HydrOPol may also tend to form clusters which would further explain why it performs poorly, adding to the already poor relative orientations.

Perspectives.

The results obtained in this manuscript lead to the obvious question: is it possible to find derivatives of bTurea that have even better DNP properties? Answering this question is difficult. In 2016, Sauvée et al. [16] published an extensive analysis of bTurea derivatives, where different substituents were incorporated into the urea bridge. PyPolPEG2OH had the highest enhancement and potentially highest polarization gain, if the depolarization is assumed constant for all biradicals. Thanks to a structure similar to AMUPol and longer electron relaxation times, it gave an enhancement of ^~300 at 9.4 T, which is close to the value of 330 ± 60 of o-HydrOPol. Considering all the biradicals that were tested, it is noteworthy that at 14.1 T, PyPolC6OPEG4, PyPolPEG10 and PyPolDiMe gave the best performance, in particular PyPolDiMe, which gave fast build-ups at 5 mM concentration. An important conclusion of this extensive work is that solubility is equally important as the geometrical properties.

In light of the results obtained here, bcTol-M outperforms most of the biradicals in the bTurea family that have been published to date. In particular, the high solubility of bcTol-M makes it superior to PyPolDiMe and, in absence of comparison, one can safely assume that it is a challenger to PyPolPEG2OH, PyPolC6OPEG4 and PyPolPEG10. Judging from the available data, an optimal bTurea should have two methyl groups on the urea bridge (PyPolDiMe, bcTol-M), have an open conformer (o-HydrOPol), and have high solubility to avoid aggregation (bcTol, bcTol-M, AsymPolPOK) [19,40,41]. While the open and close conformation have a huge consequence on the relative orientation of these HydrOPols (and bcTol), they modestly change the relative orientations of bcTol-M (see SI). As the closed conformations are less prone to reduction [20], a closed version of bcTol-M/PyPol-DiMe could potentially be used for in-cell studies.

It is not clear whether it is still worth developing new compounds in the bTurea family. In recent years, new generations of biradicals have been designed, both homo-biradicals (e.g. bis-nitroxides) and hetero-biradicals (e.g. Trityl-TEMPO [17,82] / BDPA-TEMPO [83,84]). Members of the new generation of bis-nitroxide biradicals that have much larger exchange interaction than the bTureas, such as AsymPolPOK [19] and TinyPol [26], are efficient DNP performers even at high field. For example, AsymPolPOK has reduced depolarization effects and very fast build-up, which seems to arise from its very large exchange interaction, significantly reduces the experimental time [19,30,42]. The development of this new generation of bis-nitroxides has focussed on increasing the dipolar/exchange interaction while targeting the (90°, 90°, 90°) Euler angles. The work described in this paper shows that further development of bis-nitroxides for MAS-DNP will need include a larger distance between the g-tensors.

Conclusions

In this work we investigated the influence of the distance between g-tensors on the MAS-DNP performance of three highly water-soluble biradicals belonging to the bTurea family. These biradicals, bcTol, AMUPol and bcTol-M, mainly differ by the substitution on the urea bridge. At 14.1 T, bcTol offers the lowest enhancement ϵ_on/off ≈ 150 and longest build-up time (6.5 s), while bcTol-M provide the largest ϵ_on/off ≈ 205 and shortest build-up time (3.8 s). AMUPol sits in between the two (ϵ_on/off ≈ 170, 4.8 s). Since these biradicals lead to similar nuclear depolarization levels, bcTol-M thus generates the highest polarization level at 14.1 T.

DFT calculations and high-field EPR spectroscopy revealed that as substituents are introduced into the urea bridge, the relative orientation of two nitroxides changes. This g-tensors’ distance is minimal for bcTol (no substitution), larger for AMUPol (one substituent), and maximal for bcTol-M (two substituents). The structures determined in this manner were verified by comparing experimental MAS-DNP data with simulated data. The simulations accurately reproduced the MAS-DNP field profile, as well as the build-up times, polarization gain, depolarization and enhancements (T_B, ϵ_B, ϵ_Depo and ϵ_on/off), with an average error of 9%. The theoretical analysis showed that the performance improvement in the order bcTol < AMUPol < bcTol-M at 14.1 T can be, for the most part, attributed to the change in the relative orientation of the two nitroxides, while the variation in the exchange interaction had a modest impact. This is the first quantitative demonstration of the g-tensors’ distance role on a biradical MAS-DNP performance, confirming past theoretical considerations [39].

Using the approach developed in this work, we evaluated some recent members of the bTurea family, specifically the role of the spirocycles flanking the nitroxide functional groups. The conformation of these rings have been analysed recently and it was suggested that water accessibility may be responsible for the changes in performance between c-HydrOPol and o-HydrOPol [20]. We suggest an alternative, may be complementary, explanation: the rings influence the g-tensors’ distance, with the open conformation favouring better MAS-DNP performance.

Overall, this work provides experimental proof that, while long electron relaxation times, significant dipolar/exchange interactions are needed and desirable for improved biradical performance, future bisnitroxide design for MAS-DNP must aim at larger distance between g-tensors.

• Substituents on the “bTurea” bridge change the relative orientation of the nitroxides

• The “distance” between g-tensors determines the MAS-DNP polarization performance

• Model predicts experimental enhancements and build-up times within 10%

• Conformation of spirocycles flanking the nitroxides affects the relative orientation