Abstract
A novel approach of preprocessing EEG signals by generating spectrum image for effective Convolutional Neural Network (CNN) based classification for Motor Imaginary (MI) recognition is proposed. The approach involves extracting the Variational Mode Decomposition (VMD) modes of EEG signals, from which the Short Time Fourier Transform (STFT) of all the modes are arranged to form EEG spectrum images. The EEG spectrum images generated are provided as input image to CNN. The two generic CNN architectures for MI classification (EEGNet and DeepConvNet) and the architectures for pattern recognition (AlexNet and LeNet) are used in this study. Among the four architectures, EEGNet provides average accuracies of 91.37%, 94.41%, 85.67% and 90.21% for the four datasets used to validate the proposed approach. Consistently better results in comparison with results in recent literature demonstrate that the EEG spectrum image generation using VMD-STFT is a promising method for the time frequency analysis of EEG signals.
Introduction
MI based Brain Computer Interface (BCI) systems have recently seen many breakthrough research in attaining higher classification accuracies. However, a system for decoding the thought process of a person is still an evolving challenge in the age of automation. These systems mostly rely on the EEG signals, which are electrical readings of the brain activity captured by placing electrodes on the scalp. The first step towards a system for thought process recognition is motor imaginary identification, where the subject’s imagination of moving a body part is identified based on the features extracted from EEG signals. For discriminating the activity imagined by a subject, EEG signals are analysed in time, frequency or in time-frequency domains. The information extracted are either spontaneous signal or evoked potential which appear in EEG [23]. In the category of spontaneous signals, Event Related Desynchronisation (ERD) activity observed in the Sensorimotor cortex region of the brain represents suppression of the mu band of EEG signals during the imagination of an activity in response to stimuli. The suppression is possible due to imaginary movement, actual movement or due to some memory tasks. In the case of imaginary movement, after suppression of mu-beta band, a synchronisation activity (Event Related Synchronisation,ERS) appears which results in power increase in mu beta-rhythm [26]. The ERD and ERS activities appear in the contralateral side of the brain, which then spread to the ipsilateral side. This can be harnessed for controlling devices [39]. Numerous methods for feature extraction and classification of EEG signals in the context of MI identification are proposed in literature among which work utilising the image form of EEG signals are described below.
The EEG feature extraction methods demonstrated as effective include Common Spatial Pattern (CSP) [22], band power features [13] and autoregressive (AR) parameters [15]. Besides extracting features from EEG signals, features from image representation of EEG signals have also been explored. A method involving two-dimensional image form of EEG from which, Harris corner detector and scale-invariant feature transform was combined to form feature vector. The feature vector when classified using k- nearest neighbour algorithm [12] provided an accuracy of 96.21% for BCI Dataset Ia and 78.99% for BCI Dataset III. Image form of EEG signals classified with CNN resulted in better classification accuracy [5]. Representation of spectrum of EEG signals in the form of multi dimensional tensor, and classification using deep recurrent convolutional network has demonstrated significant improvements in the classification accuracy [3].
Features in the form of image were extracted using STFT of Intrinsic Mode Function (IMF), obtained by decomposing EEG signals using Empirical Mode Decomposition(EMD) [24]. However, EMD has short comings like sensitivity to noise and mode mixing. The VMD resolved the shortcomings in EMD by having a strong mathematical theory [10], and thus find applications in diverse fields like speech enhancement [11], hyperspectral images [21], digital forensic [28] and heart sound segmentation [35]. VMD decomposes the real valued multi component signal into subsignals adaptively using the calculus of variation. This iterative process of decomposition provides number of band limited modes of the input signals along with a center frequency for each mode [10]. In order to perceive the frequency variations within a mode, STFT of EEG signal are also helpful. STFT provides time-frequency distributions without cross-terms along with higher resolutions in both time and frequency domains [29, 37].
Several classifiers are being explored for the classification of extracted features from EEG signals. Among the various classifiers, deep learning networks like CNN, Deep Belief network (DBF), Restricted Boltzmann Machines (RBM) and Hybrid CNN remain outstanding [8]. Classifiers such as Linear Discriminant Analysis (LDA), Fisher Discriminant analysis (FDA) and Support Vector Machine (SVM) are also found to be effective for classification of EEG signals [1]. Deep learning models have hierarchical multistage learning structure for extracting the information from data. This property makes deep networks capable of analysing big data. The deep learning models especially CNN, finds application in EEG feature extraction, in spite of concerns regarding local minima, lower performance and higher computational costs [14]. CNN has been successful in image classification problems with numerous architectures, and has exhibited superior results in EEG classification in the case of seizure detection, emotion detection and in BCI paradigms [9, 32]. CNN with the multiple layers of processing decomposes the complex structure of image into less complex structures, which account for the superiority of CNN in image classification [32]. The representation of EEG signals as image and feeding it to CNN network have yielded promising results [3, 5]. Training of CNN from scratch requires lot of data which are deprived of in many situations especially in the case of EEG signals. In this case, transfer learning enables the utilisation of pre-trained network for classification by fine tuning with new data. The transfer learning has provided remarkable progress in utilisation of CNN in physiological signal processing, by eliminating the requirement of training a new network [33, 43].
Even though CNN provides promising results in extracting features and classifying EEG signals for developing BCI systems, there lack a method which can be reliably applied to different datasets as the datasets vary in EEG capturing protocols and equipment. This maybe due to the fact that, availability of multiple datasets collected from different labs remain sparse, and do not provide promising results in implementing hardware for assisting technologies for people with movement restrictions. Hence, in this work a novel method of preprocessing and classifying EEG signals using CNN is proposed. The preprocessing involves, transforming EEG signals into spectrum image which is generated from the VMD modes of EEG signals. EEG signals from three electrodes C3, Cz and C4 which are placed at the sensorimotor cortex area of the brain are decomposed into four VMD modes. In order to visualise time frequency variation in each VMD mode, STFT of the VMD modes are perceived as images. For identifying the imagined activity, viz. left hand, right hand, feet or tongue movement, the spectrum images of four different classes are classified using CNN classifiers. The CNN architectures considered for this work are models for MI based EEG signal classification and pattern recognition which are fine tuned for each subject using EEG spectrum image. The four datasets used are Dataset I [6], Dataset II [36], Dataset III [7], Dataset IV [16] which are available in public domain. The paper is structured as follows. Details of dataset are provided in section 2 followed by methods adopted is briefly discussed in section 3. The section 4 depicts results and discussion and finally section 5 is provided with conclusions.
Description of EEG dataset
Dataset I consists of EEG signals of three subjects during the imaginary movement execution of left hand, right hand, foot or tongue. The imagination started at 3 sec with an arrow appearing on the screen in one of the four directions corresponding to each task, before which the subject is alerted with an acoustic stimulus at 3 sec. The subject imagined the movement till the arrow disappeared at 7 sec. In this study, EEG signals during the time interval from 2 sec to 7 sec was extracted. The EEG signals monitored were sampled at 250 HZ and filtered between 1 and 50 HZ.
Dataset II is from BCI Competition 2008 Graz dataset A which consists of EEG data from nine subjects during imaginary movement execution of left hand, right hand, foot or tongue. In this cue-based BCI paradigm similar to the dataset I the motor imagination started from 3 seconds and extends up to . The EEG signals used in this study was of duration of starting from to . The EEG signals are sampled at a rate of and were filtered between and .
In Dataset III each subject was asked to move each fingers before the MI experiment began. Each trial was of duration during which instruction for left/right hand movement imagination appeared on the screen. Before the imagination a preparation time of () was provided. The interval extracted for this study is . After each run, the subject was given feedback based on the classification accuracy of the trial. The sampling rate of the EEG signals were and the signals were bandpass filtered between and .
Dataset IV consists of four different paradigms wherein paradigm two consists of 5 classes of MI tasks correspondingly imaginary movement of left/right hand, left/right feet or tongue was utilised in this work. The other paradigm consists of left/right movement, 5 finger movement and keyboard entry. Each trial was of duration which was used in this work. Each trial began with an action signal which appeared for . The time during which the action signal remained, the participants implemented the selected motor imagery once. EEG data recorded at sampling rate were band-pass filtered between . Additionally, a notch filter was present.
The description regarding number of subjects, number of channels, number of total trials, number of rejected trials, number of classes and epoch duration in each of the four datasets utilised in this work are provided in Table 1. The unlabeled as well as corrupted trials are rejected from all 4 datasets.
Table 1.
Details regarding number of subjects, number of channels ,total number of trials, number of rejected trials, number of classes and epoch duration in seconds for the four publicly available datasets which are utilised in the proposed method
Methods
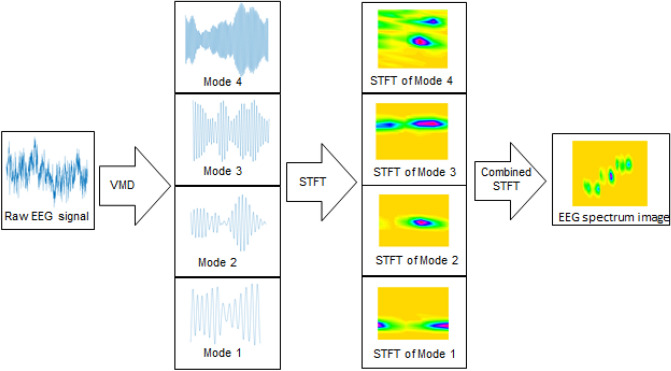
The EEG spectrum image is generated using STFT of VMD modes of EEG signals corresponding to the electrodes in sensorimotor cortex area of the brain. The preprocessing methods adopted are depicted in Fig. 1. The EEG signal is decomposed into 4 VMD modes with centre frequency around the EEG frequency bands. The STFT of each of the VMD modes are combined by stacking to form EEG signal image spectrum. The VMD and STFT methods are detailed in subsequent sections.
Fig. 1.
Proposed process flow for generating the EEG spectrum image based on VMD and STFT
Variational mode decomposition
VMD adaptively decomposes a real valued multicomponent signal, x(t) into number of discrete sub signals, or modes, iteratively. The decomposed L number of modes are compact around a center frequency, . The IMF and center frequencies of these IMF are computed using optimization methodology. The method tries to minimize the sum of the bandwidths of L modes, subject to the condition that, sum of the L modes is equal to the original signal using the alternate direction method of multipliers (ADMM) [10]. Mathematically, the procedure is expressed as
| 1 |
where, is the mode with center frequency . is the Dirac delta, t is time, and denotes the convolution. Above formulation is obtained using the following steps.
Compute unilateral frequency spectrum of signal x(t) by means of Hilbert transform.
Shift the frequency spectrum to the base-band by multiplying with an exponential signal with estimated center frequency
Estimate the bandwidth through the H1 Gaussian smoothness of the demodulated signal, which being the squared L2-norm of the gradient
The above constrained optimization problem in Eq.(1) is modified as unconstrained along with the quadratic penalty term. [10]. The corresponding modified equation is written as
| 2 |
where, is the augmented Lagrangian, is the balancing parameter of data fidelity constraint, and is the Lagrangian multiplier. Eq. (2) is then solved with the ADMM and the solutions in the spectral domain are written as in Eq. (3) and Eq.(4)
| 3 |
| 4 |
where, and represent the Fourier transforms of , x(t), and respectively. The mode in the time domain is obtained as the real part of the inverse Fourier transform of this filtered analytic signal .
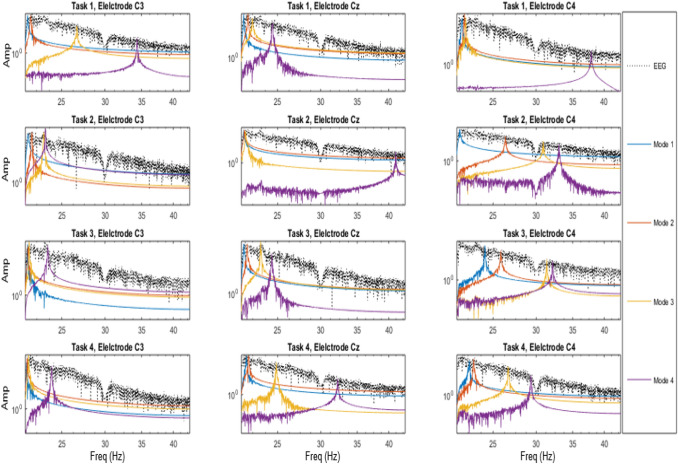
Each EEG epoch for the four different tasks of imaginary movement of left hand, right hand, tongue and foot were of 5 seconds duration for the dataset I and II, 4 seconds for dataset III and 1 seconds duration for dataset IV. The EEG signals from the electrodes C3, Cz and C4 in sensorimotor cortex area were decomposed using VMD. Empirically the number of modes was fixed as four, where each mode center frequency corresponds to the estimation of EEG frequency bands namely Delta, Theta, Alpha and Beta. The modes were arranged according to the increasing frequencies, viz. Delta, Theta , Alpha and Beta. The power in each of the four modes for the four tasks, and the three electrodes (C3, Cz, C4) for the subject S02 of dataset II are plotted in Fig. 2. Each subplot in the figure shows the power variation for all the modes for a duration of 5 seconds. Left most figure in each column represents power in the 4 VMD modes for C3 electrode, middle one for Cz and the right most for C4 electrode whereas, each row corresponds to each task, imaginary movement of left hand, right hand, feet and tongue respectively.
Fig. 2.
The power in each of the four VMD modes of EEG signals for S02 of dataset II is plotted for the three electrodes and for the four tasks. The x-axis represents frequency in Hz and y-axis represents power in modes
Short time Fourier Transform
The STFT is a method in which Fast Fourier Transform (FFT) of each of the data frames are computed. The data frames are obtained from a signal, by dividing signal into small sequential or overlapping data frames. The computed FFT of successive data frames can be arranged to provide time-frequency representation of the signal. To obtain the data frames, the signal is multiplied with a window function, h(n) of length, K. The length of the window function decides the frequency resolution, and time resolution of the signal in the spectrum. A large window provides less resolution in time and more resolution in frequency. Along with the window length, window type decides the time frequency distribution, since the strong time-variable signal causes frequency aliasing. The formulation of STFT is given as
| 5 |
where, x(n) is input signal at time n, h(n) is window function of length K and is DTFT of windowed signal centered around mR.
In order to detect the onset of ERD/ERS activity, a window length of 200 ms with an overlap of is provided. The Gabor, which uses a Gaussian window is used as the window function.
EEG spectrum image
The EEG signal from an electrode of length N was decomposed into 4 VMD modes, where l represents modes from 1 to 4. The STFT of mode, was converted into a color image of size M × L × 3, to emphasize the distribution of magnitude of the spectrum. M and L are given as in Eqs. (6) and (7)
| 6 |
where, p represents the number of zero padding
| 7 |
where, w represents the window size and o represents overlapping window.
By stacking the 4 spectrum corresponding to 4 modes, the image size was 4M × L × 3. The window size of 50 with zero padding of 10 was chosen for all datasets. The overlapping window size was of 35 points for 75% overlap. In the case of dataset I and II for interval of 5 seconds have 1250 points, where the EEG spectrum image has size 124 × 31 × 3, while for dataset III and IV has size 124 × 134 × 3 and 124 × 37 × 3 respectively.
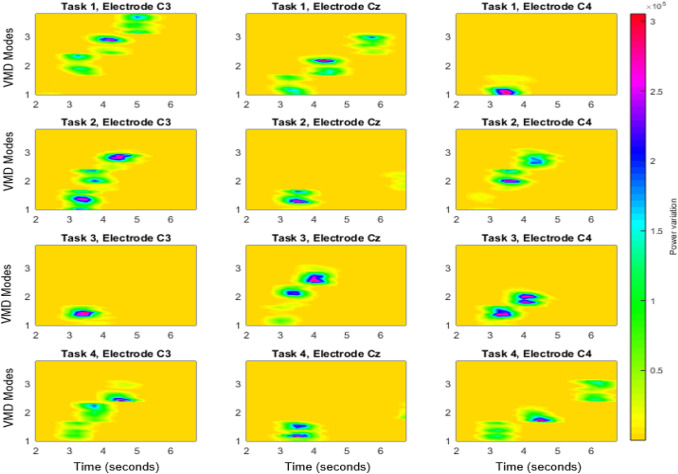
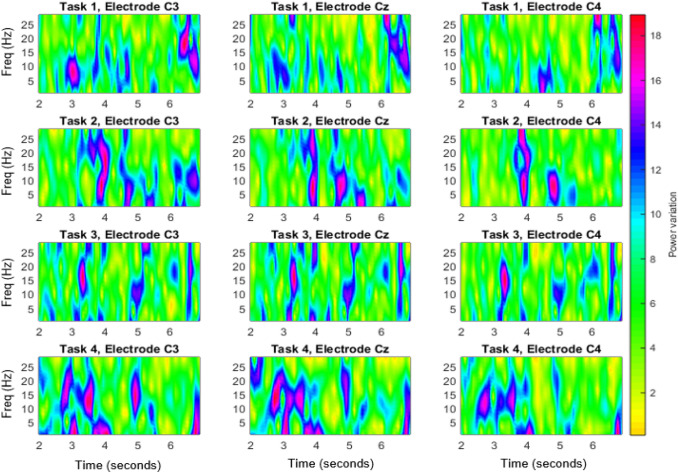
The EEG spectrum images thus generated for the four different tasks and for the 3 electrodes for subject, S02 of dataset II are shown in Fig. 3. Correspondingly Fig. 4 shows the image generated with STFT of EEG signals without modal decomposition. It is evident from Fig. 3 and Fig. 4, that the power variation due to the imaginary movement is more detectable in VMD-STFT spectrum image, than in the STFT spectrum image. In each plot, X represents time from 2 to 7 sec and Y axes represents modes respectively. Each subplot in the figure shows the power variation for all the modes for a duration of 5 sec. Left figure in each column represents the power for C3 electrode, middle one for Cz and the right for C4 electrode whereas each row corresponds to each task.
Fig. 3.
The EEG spectrum image based on VMD-STFT for S02 of dataset II for the three electrodes and for the four tasks. The x-axis of each plot represents time from 2 seconds to 7 seconds and y axis represents the VMD modes
Fig. 4.
STFT of EEG signals of S02 of dataset II for the three electrodes and for the four tasks. The x-axis of each plot represents time from 2 seconds to 7 seconds and y axis represents frequency in Hz
CNN classifications
The CNN architectures consist of a multilayer structure with an input layer being the first layer, and the following layers have number of convolutional and max-pooling or average pooling layers. Dropout layers were provided in between the different convolutional layers to avoid over fitting. The last layer designed for classification have fully connected layer and a dense layer followed by softmax layer. The first layer of CNN learns basic features by filtering, while the deeper layers were designed to learn higher level features by decomposing the input into complex structures. The last layer, fully connected layer assembles the learned features from the previous layers for classification. The CNN incorporates forward propagation algorithms to find the output, and backward propagation algorithms to optimize the error.
EEGNet consists of a 2D convolutional layer followed by depthwise convolution, and a seperable convolution layer with each layer having batch normalisation, dropout and average pooling. DeepConvNet architecture was developed so as to have a standard Convolutional network which meets the purpose of generic tool for brain signal decoding tasks. The architecture has four convolution-max-pooling blocks and a dense softmax classification layer. For further details regarding EEGNet and DeepConvNet reader is referred to [18] and [32] respectively.
The two architectures for pattern recognition, AlexNet [17] and LeNet [19], were fine tuned for EEG spectrum image input wherein the architectures were adopted without modification in layers. The different layers of the four models adopted in this work are given in Table 2. The layers of ConvNet and EEGNet are modified with 3 channel layer as the EEG spectrum image is RGB image.
Table 2.
CNN layers for the four architectures
| LeNet-5 ([19]) | EEGNet ([18]) | DeepConvNet(EEG) ([32]) | AlexNet ([17]) |
|---|---|---|---|
| Input | Input | Input | Input |
| Conv2D | Conv2D | Conv2D | Conv2D |
| AveragePooling2D | BatchNorm | Conv2D | MaxPooling2D |
| Conv2D | DepthwiseConv2D | BatchNorm | BatchNorm |
| AveragePooling2D | BatchNorm | MaxPooling2D | Conv2D |
| Flatten | AveragePool2D | Dropout | MaxPooling2D |
| Dense | Dropout | Conv2D | BatchNorm |
| Dense | SeparableConv2D | BatchNorm | Conv2D |
| Dense | BatchNorm | MaxPooling2D | MaxPooling2D |
| AveragePool2D | Dropout | BatchNorm | |
| Dropout | Conv2D | Conv2D | |
| Flatten | BatchNorm | BatchNorm | |
| Dense | MaxPooling2D | Conv2D | |
| Dropout | BatchNorm | ||
| Conv2D | Conv2D | ||
| BatchNorm | MaxPooling2D | ||
| MaxPooling2D | BatchNorm | ||
| Dropout | Flatten | ||
| Flatten | Dense | ||
| Dense | Dropout | ||
| BatchNorm | |||
| Dense | |||
| Dropout | |||
| BatchNorm | |||
| Dense | |||
| Dropout | |||
| BatchNorm | |||
| Dense |
The EEG spectrum image as discussed in Sect. 3.3 without rescaling were provided as input to each of the architecture by modifying the input layer so that information in EEG spectrum image is not disrupted. The size of the input layer is 4M x L x 3 which is of size 124 x 81 x 3 for dataset I and dataset II, while for dataset III and dataset IV are 124 x 134 x 3 and 124 x 37 x 3 respectively. Each of the network was trained and tested for a single subject by dividing total trials of the subjects into 70% and 30% respectively with 10 fold cross validation. The trained model is fine tuned and tested with 70% and 30% of the trials separately for each subject.
The kernel size for each network are 5x5, 7x7, 5x5 and 9x9 for LeNet, EEGNet, ConvNet and AlexNet respectively. Activation function for the networks are RELU for LeNet, ConvNet and AlexNet while ELU for EEGNet.
Results and discussion
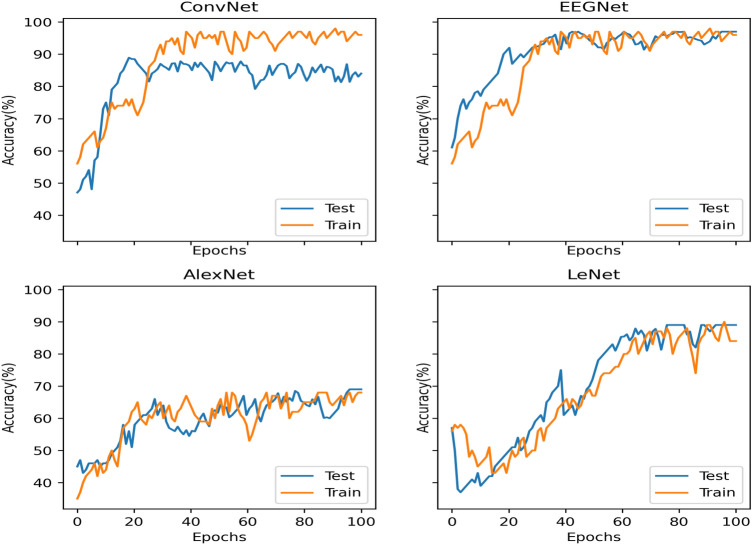
An extensive comparison of classification accuracies of the EEG spectrum image for MI classification are implemented with four CNN architectures ConvNet, EEGNet , AlexNet and LeNet. A comparison on EEG spectrum image from STFT of EEG signals are also performed. Among the four networks, two CNN architectures are generic architectures for EEG analysis while, two other models are for the pattern recognition. The classification accuracies for the methods of EEG spectrum image generated using STFT and VMD –STFT respectively for all subjects in each of the dataset are summarised in Tables 3, 4, 5, 6. The maximum accuracy obtained for each subject in the dataset for 100 epoch is reported. The performance curve for S02 of dataset II is plotted in Fig. 5 for epoch size of 100. Figure 5 includes four subplots, each corresponding to each CNN architecture. In each subplot, training and testing performance curves are plotted. From the figure it is observed that EEGNet and ConvNet learn at a faster rate. The training and testing accuracies stabilise with an epoch of 20 for EEGNet and ConvNet and 40 for AlexNet and LeNet respectively.
Table 3.
Classification accuracy for subjects in dataset I for the four CNN architectures
| Subjects | EEGNet | DeepConvNet | EEGNet | AlexNet | LeNet |
|---|---|---|---|---|---|
| STFT | VMD+STFT | VMD+STFT | VMD+STFT | VMD+STFT | |
| S01 | 55.31 | 81.68 | 93.17 | 63.27 | 78.4 |
| S02 | 60.22 | 85.49 | 89.03 | 60.57 | 60.28 |
| S03 | 57.73 | 73.52 | 91.92 | 53.98 | 66.66 |
| Avg | 57.75 | 80.23 | 91.37 | 59.27 | 68.45 |
| STD | 2.46 | 6.12 | 2.12 | 4.78 | 9.19 |
Table 4.
Classification accuracy for subjects in dataset II for the four CNN architectures
| Subjects | EEGNet | DeepConvNet | EEGNet | AlexNet | LeNet |
|---|---|---|---|---|---|
| STFT | VMD+STFT | VMD+STFT | VMD+STFT | VMD+STFT | |
| S01 | 70.13 | 68.45 | 93.57 | 61.91 | 80.41 |
| S02 | 84.27 | 87.61 | 97.74 | 68.38 | 89.18 |
| S03 | 65.58 | 78.03 | 93.68 | 55.2 | 67.93 |
| S04 | 57.92 | 75.6 | 91.04 | 60.72 | 76.49 |
| S05 | 58.33 | 71 | 94.87 | 50.38 | 75.21 |
| S06 | 79.37 | 69.98 | 95.28 | 65 | 52.85 |
| S07 | 66.49 | 71.45 | 96.48 | 62.28 | 81.29 |
| S08 | 55.78 | 82.63 | 89.41 | 71.66 | 73.92 |
| S09 | 69.29 | 65.11 | 97.65 | 59.04 | 78.38 |
| AVG | 67.46 | 74.43 | 94.41 | 61.49 | 75.07 |
| STD | 10.32 | 6.76 | 2.74 | 7.22 | 10.77 |
Table 5.
Classification accuracy for subjects in dataset III for the four CNN architectures
| Subjects | EEGNet | DeepConvNet | EEGNet | AlexNet | LeNet |
|---|---|---|---|---|---|
| STFT | VMD+STFT | VMD+STFT | VMD+STFT | VMD+STFT | |
| S01 | 72.91 | 68.22 | 89.38 | 61.32 | 66.41 |
| S02 | 80.39 | 94.81 | 86.2 | 59.84 | 69.75 |
| S03 | 77.66 | 84.92 | 94.5 | 79.04 | 58.2 |
| S04 | 56.02 | 60.33 | 73.04 | 50.74 | 68.33 |
| S05 | 78.29 | 92.37 | 91.72 | 70.82 | 73.02 |
| S06 | 72.17 | 79.23 | 88.31 | 79.78 | 68.63 |
| S07 | 58.24 | 71.03 | 85.34 | 68.82 | 71.88 |
| S08 | 76.49 | 70 | 91.2 | 58.91 | 60.34 |
| S09 | 54.95 | 79.37 | 80.62 | 61.84 | 74.13 |
| S10 | 81.23 | 96.49 | 69.2 | 95.91 | 73.39 |
| S11 | 66.94 | 88.23 | 91.9 | 92.31 | 83.45 |
| S12 | 69.24 | 96.12 | 94.32 | 78.39 | 60.24 |
| S13 | 80.73 | 75.32 | 87.41 | 56.91 | 68.29 |
| S14 | 81.3 | 94.47 | 93.26 | 87.55 | 73.45 |
| S15 | 58.05 | 93.94 | 80.94 | 61.39 | 59.25 |
| S16 | 68.3 | 92.35 | 91.03 | 49.35 | 55.04 |
| S17 | 79.84 | 86.4 | 85.3 | 87.25 | 74.31 |
| S18 | 81.27 | 95.25 | 77.59 | 68.3 | 82.23 |
| S19 | 58.24 | 86.95 | 96.42 | 75.32 | 68.39 |
| S20 | 73.39 | 97.66 | 81.42 | 77.94 | 78.28 |
| S21 | 83.28 | 87.93 | 83.33 | 61.49 | 68.73 |
| S22 | 80.36 | 97.02 | 79.23 | 92.44 | 71.89 |
| S23 | 68.34 | 96.26 | 85.5 | 97.6 | 84.18 |
| S24 | 57.17 | 97.33 | 89.52 | 78.69 | 66.15 |
| S25 | 64.48 | 96.59 | 69.16 | 58.94 | 69.32 |
| S26 | 89.74 | 92.51 | 88.03 | 91.55 | 74.88 |
| S27 | 77.77 | 95.15 | 81.44 | 69.69 | 60.87 |
| S28 | 68.36 | 97.87 | 85.72 | 87.27 | 74.22 |
| S29 | 80.27 | 93.67 | 85.24 | 69.8 | 81.16 |
| S30 | 69.59 | 79.95 | 96.19 | 79.59 | 83.2 |
| S31 | 86.45 | 98.15 | 78.06 | 49.24 | 58.43 |
| S32 | 68.04 | 86.36 | 91.92 | 96.34 | 77.07 |
| S33 | 55.2 | 95.05 | 89.41 | 61.37 | 66.53 |
| S34 | 61.04 | 96.84 | 72.58 | 67.93 | 68.6 |
| S35 | 62.5 | 77.47 | 88.62 | 61.48 | 74.35 |
| S36 | 91.94 | 98.28 | 94.14 | 72.38 | 77.63 |
| S37 | 77.4 | 53.24 | 85.56 | 68.73 | 58.29 |
| S38 | 67.82 | 94.2 | 93.39 | 70.3 | 62.26 |
| S39 | 89.14 | 88.11 | 91.74 | 80.39 | 73.22 |
| S40 | 76.47 | 69.95 | 75 | 59.29 | 88.94 |
| S41 | 54.69 | 89.5 | 88.26 | 71.41 | 74.57 |
| S42 | 76.76 | 97.4 | 87.49 | 86.74 | 82.89 |
| S43 | 78.44 | 89.82 | 94.27 | 77.74 | 64.32 |
| S44 | 80.62 | 94.18 | 94.63 | 49.38 | 58.27 |
| S45 | 68.02 | 86.83 | 85.49 | 87.93 | 74.38 |
| S46 | 66.47 | 90.33 | 70.84 | 50.84 | 68.92 |
| S47 | 57.83 | 98.78 | 89.53 | 61.3 | 66.55 |
| S48 | 78.92 | 96.16 | 71.1 | 60.19 | 73.29 |
| S49 | 88.19 | 93.2 | 79.39 | 80.46 | 74.38 |
| S50 | 80.83 | 94.28 | 89.43 | 69.04 | 71.64 |
| Avg | 72.63 | 88.51 | 85.66 | 71.82 | 70.72 |
| STD | 10.27 | 10.64 | 7.49 | 13.55 | 7.88 |
Table 6.
Classification accuracy for subjects in dataset IV for the four CNN architectures
| Subjects | EEGNet | DeepConvNet | EEGNet | AlexNet | LeNet |
|---|---|---|---|---|---|
| STFT | VMD+STFT | VMD+STFT | VMD+STFT | VMD+STFT | |
| S01 | 57.83 | 81.75 | 86.74 | 82.18 | 78.31 |
| S02 | 68.48 | 95.64 | 97.42 | 78.04 | 70.26 |
| S03 | 73.19 | 86.32 | 82.93 | 66.91 | 82.42 |
| S04 | 67.29 | 88.48 | 91.84 | 50.75 | 59.27 |
| S05 | 58.93 | 88.03 | 94.27 | 68.94 | 69.54 |
| S06 | 62.49 | 92.99 | 89.02 | 61.38 | 85.35 |
| S07 | 77.55 | 76.19 | 87.25 | 74.28 | 75.22 |
| S08 | 84.28 | 79.84 | 90.18 | 62.39 | 81.02 |
| S09 | 58.1 | 69.78 | 88.55 | 77.21 | 74.93 |
| S10 | 71.63 | 78.66 | 85.76 | 71.05 | 83.49 |
| S11 | 76.37 | 88.47 | 92.49 | 67.3 | 77.2 |
| S12 | 65.28 | 94.59 | 96.01 | 69.29 | 87.23 |
| AVG | 68.45 | 85.06 | 90.20 | 69.14 | 77.02 |
| STD | 8.45 | 7.92 | 4.34 | 8.51 | 7.90 |
Fig. 5.
Testing and training performance curve for 100 epochs for subject 2 of dataset II
Highest average accuracy of 91.37% with a standard deviation (STD) of for the three subjects are achieved for the dataset I for the EEG spectrum image classified with EEGNet as indicated in Table 3. For Dataset II with 9 subjects, highest average accuracy of 94.41% is obtained for EEGNet classifier with STD of . The other networks show less accuracies with higher STD among subjects. In the case of dataset III, highest average accuracy of 89.51% is obtained for ConvNet but the STD is . For EEGNet, an average accuracy of 86% with reduced STD of is obtained. An average accuracy of 85.66% with least STD of is obtained for EEGNet for dataset IV. The average accuracy for each dataset are shown in Table 7 for comparison. Recent prominent results for various methods and classifiers for MI classification of the four datasets are shown in Table 8. Among the enormous results available for the first two datasets, only state of the art results are included, which indicate superiority of deep learning networks. The accuracies vary from 85% to 98% for dataset I, 74% to 96% for dataset II, 66 to 73% for dataset III and 54 to 86% for dataset IV. The proposed method has resulted in an average accuracy within the range of 85.67 to 94.41% for all the four datasets. The results for STFT image remain inferior to VMD-STFT EEG spectrum image. Since the modal decomposition of EEG using VMD is based on power in the frequency bands, further STFT of the decomposed modes help in acquiring superior EEG image spectrum.
Table 7.
The average classification accuracy for the four datasets with four CNN architectures
| EEGNet | DeepConvNet | EEGNet | AlexNet | LeNet | |
|---|---|---|---|---|---|
| STFT | VMD+STFT | VMD+STFT | VMD+STFT | VMD+STFT | |
| Dataset I | 57.75 | 80.23 | 91.37 | 59.27 | 68.44 |
| Dataset II | 67.46 | 74.42 | 94.41 | 61.49 | 75.07 |
| Dataset III | 72.64 | 88.52 | 85.67 | 71.83 | 70.72 |
| Dataset IV | 68.45 | 85.06 | 90.21 | 69.14 | 77.02 |
Table 8.
Classification performance for existing methodologies with same dataset
| Paper | Feature | Classifier | Accuracy(%) | |
|---|---|---|---|---|
| Dataset I | [34] | Wavelet energy | Sparse representation-based classifier | 92.23 |
| [42] | AAT ,Scale Invariant Feature Transform | k-NN | 97.99 | |
| [45] | Temporally constrained sparse group spatial pattern | SVM | ||
| [25] | PSD(welch method) | CNN | 98 | |
| [44] | Local temporal common spatial patterns,Phase locking value | LDA | 90.56 | |
| Dataset II | [20] | PSD+DWT | VGGNet-CNN | 96.2 |
| [38] | Reformulated Common spatial pattern | FDA+transfer learning | 80.17 | |
| [44] | Local temporal common spatial patterns,Phase locking value | LDA | 83.26 | |
| [31] | Common spatial patterns,Temporal representation | CNN | 74.46 | |
| [4] | Time frequency series based RFB estimation | SVM | 82.01 | |
| Dataset III | [7] | Common spatial patterns | FLDA | |
| [40] | Riemannian tangent space | SVM | ||
| [30] | Riemannian Procrustes Analysis | MDM | 66 | |
| [41] | NIL | CNN-EEGNet | 66 | |
| Dataset IV | [2] | Common spatial pattern | Random forest | 54 |
| [27] | Time- and frequency-domain connectivities | SVM |
Conclusions
This work proposes an approach for transforming EEG signals to the image form by applying STFT on VMD modes of EEG signals. The image manifests spectrum of the EEG signals which were distinctively captured around the frequency bands of EEG signal. Signals from three electrodes in the SMR region of the brain were considered for the four classes of MI movements. The EEG spectrum image for the four classes of MI movements from four different publicly available data sets were classified using CNN. The widely accepted architectures for MI based EEG signal classification and pattern recognition were fine tuned for the EEG spectrum image input. The approach with EEGNet CNN classifier provides superior accuracies consistent for the four datasets utilised for validating the approach. Thus the EEG spectrum image generation opens up a new approach for the time-frequency analysis of EEG for MI classification.
Declarations
Conflict of interest
All authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
K. Keerthi Krishnan, Email: keerthi.ack@gmail.com
K. P. Soman, Email: kp_soman@amrita.edu
References
- 1.Abiri R, Borhani S, Sellers EW, Jiang Y, Zhao X. A comprehensive review of eeg-based brain-computer interface paradigms. J Neural Eng. 2019;16(1):011001. doi: 10.1088/1741-2552/aaf12e. [DOI] [PubMed] [Google Scholar]
- 2.Anam K, Nuh M, Al-Jumaily A. Comparison of eeg pattern recognition of motor imagery for finger movement classification. In: 2019 6th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI), pp. 24–27. IEEE 2019
- 3.Bashivan P, Rish I, Yeasin M, Codella N. Learning representations from eeg with deep recurrent-convolutional neural networks. arXiv preprint arXiv:1511.06448 2015
- 4.Bhattacharyya S, Mukul M.K. Reactive frequency band based movement imagery classification. Journal of Ambient Intelligence and Humanized Computing 2018;pp. 1–14
- 5.Bizopoulos P, Lambrou G.I, Koutsouris D.: Signal2image modules in deep neural networks for eeg classification. In: 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), pp. 702–705. IEEE 2019 [DOI] [PubMed]
- 6.Blankertz B, Muller KR, Krusienski DJ, Schalk G, Wolpaw JR, Schlogl A, Pfurtscheller G, Millan JR, Schroder M, Birbaumer N. The bci competition iii: validating alternative approaches to actual bci problems. IEEE Trans Neural Syst Rehabil Eng. 2006;14(2):153–159. doi: 10.1109/TNSRE.2006.875642. [DOI] [PubMed] [Google Scholar]
- 7.Cho H, Ahn M, Ahn S, Kwon M, Jun S.C. Eeg datasets for motor imagery brain–computer interface. GigaScience. 2017;6(7):gix034. doi: 10.1093/gigascience/gix034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Craik A, He Y, Contreras-Vidal JL. Deep learning for electroencephalogram (eeg) classification tasks: a review. J Neural Eng. 2019;16(3):031001. doi: 10.1088/1741-2552/ab0ab5. [DOI] [PubMed] [Google Scholar]
- 9.Dose H, Møller J.S, Puthusserypady S, Iversen H.K. A deep learning mi-eeg classification model for bcis. In: 2018 26th European Signal Processing Conference, 2018;pp. 1690–93. IEEE
- 10.Dragomiretskiy K, Zosso D. Variational mode decomposition. IEEE Trans Signal Process. 2014;62(3):531–544. doi: 10.1109/TSP.2013.2288675. [DOI] [Google Scholar]
- 11.Gowri B.G, Kumar S.S, Mohan N, Soman K, P. A vmd based approach for speech enhancement. In: Advances in Signal Processing and Intelligent Recognition Systems, 2016;pp. 309–321. Springer
- 12.Hatipoglu B, Yilmaz CM, Kose C. A signal-to-image transformation approach for eeg and meg signal classification. Signal, Image Video Process. 2019;13(3):483–490. doi: 10.1007/s11760-018-1373-y. [DOI] [Google Scholar]
- 13.Herman P, Prasad G, McGinnity TM, Coyle D. Comparative analysis of spectral approaches to feature extraction for eeg-based motor imagery classification. IEEE Trans Neural Syst Rehabil Eng. 2008;16(4):317–326. doi: 10.1109/TNSRE.2008.926694. [DOI] [PubMed] [Google Scholar]
- 14.Hosseini MP, Pompili D, Elisevich K, Soltanian-Zadeh H. Optimized deep learning for eeg big data and seizure prediction bci via internet of things. IEEE Trans Big Data. 2017;3(4):392–404. doi: 10.1109/TBDATA.2017.2769670. [DOI] [Google Scholar]
- 15.Huan NJ, Palaniappan R. Neural network classification of autoregressive features from electroencephalogram signals for brain-computer interface design. J Neural Eng. 2004;1(3):142. doi: 10.1088/1741-2560/1/3/003. [DOI] [PubMed] [Google Scholar]
- 16.Kaya M, Binli MK, Ozbay E, Yanar H, Mishchenko Y. A large electroencephalographic motor imagery dataset for electroencephalographic brain computer interfaces. Sci Data. 2018;5:180211. doi: 10.1038/sdata.2018.211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Krizhevsky A, Sutskever I, Hinton G.E. Imagenet classification with deep convolutional neural networks. In: Advances in neural information processing systems, 2012;pp. 1097–1105
- 18.Lawhern VJ, Solon AJ, Waytowich NR, Gordon SM, Hung CP, Lance BJ. Eegnet: a compact convolutional neural network for eeg-based brain-computer interfaces. J Neural Eng. 2018;15(5):056013. doi: 10.1088/1741-2552/aace8c. [DOI] [PubMed] [Google Scholar]
- 19.LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE. 1998;86(11):2278–324.
- 20.Ma X, Wang D, Liu D, Yang J. Dwt and cnn based multi-class motor imagery electroencephalographic signal recognition. J Neural Eng. 2020;17(1):016073. doi: 10.1088/1741-2552/ab6f15. [DOI] [PubMed] [Google Scholar]
- 21.Mol PG, Sowmya V, Soman K. Performance enhancement of minimum volume based hyper spectral unmixing algorithms by variational mode decomposition. Indian Journal of Science and Technology. 2015;8(24).
- 22.Müller-Gerking J, Pfurtscheller G, Flyvbjerg H. Designing optimal spatial filters for single-trial eeg classification in a movement task. Clin Neurophysiol. 1999;110(5):787–798. doi: 10.1016/S1388-2457(98)00038-8. [DOI] [PubMed] [Google Scholar]
- 23.Padfield N, Zabalza J, Zhao H, Masero V, Ren J. Eeg-based brain-computer interfaces using motor-imagery: techniques and challenges. Sensors. 2019;19(6):1423. doi: 10.3390/s19061423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Park C, Looney D, ur Rehman N, Ahrabian A, Mandic D.P. Classification of motor imagery bci using multivariate empirical mode decomposition. IEEE Transactions on neural systems and rehabilitation engineering 2012; 21(1), 10–22 [DOI] [PubMed]
- 25.Pérez Zapata A.F, et al. Classification of motor imagery eeg signals using a cnn architecture and a meta-heuristic optimization algorithm for selecting training parameters 2019.
- 26.Pfurtscheller G, Da Silva FL. Event-related eeg/meg synchronization and desynchronization: basic principles. Clin Neurophysiol. 1999;110(11):1842–1857. doi: 10.1016/S1388-2457(99)00141-8. [DOI] [PubMed] [Google Scholar]
- 27.Phang CR, Ko LW. Global cortical network distinguishes motor imagination of the left and right foot. IEEE Access. 2020;8:103734–103745. doi: 10.1109/ACCESS.2020.2999133. [DOI] [Google Scholar]
- 28.Premjith B, Mohan N, Poornachandran P, Soman K, P. Audio data authentication with pmu data and ewt. Procedia Technol. 2015;21:596–603. doi: 10.1016/j.protcy.2015.10.066. [DOI] [Google Scholar]
- 29.Ramos-Aguilar R, Olvera-López JA, Olmos-Pineda I. Analysis of eeg signal processing techniques based on spectrograms. Res Comput Sci. 2017;145:151–162. doi: 10.13053/rcs-145-1-12. [DOI] [Google Scholar]
- 30.Rodrigues PLC, Jutten C, Congedo M. Riemannian procrustes analysis: transfer learning for brain-computer interfaces. IEEE Trans Biomed Eng. 2018;66(8):2390–2401. doi: 10.1109/TBME.2018.2889705. [DOI] [PubMed] [Google Scholar]
- 31.Sakhavi S, Guan C, Yan S. Learning temporal information for brain-computer interface using convolutional neural networks. IEEE Trans Neural Net Learn Syst. 2018;29(11):5619–5629. doi: 10.1109/TNNLS.2018.2789927. [DOI] [PubMed] [Google Scholar]
- 32.Schirrmeister RT, Springenberg JT, Fiederer LDJ, Glasstetter M, Eggensperger K, Tangermann M, Hutter F, Burgard W, Ball T. Deep learning with convolutional neural networks for eeg decoding and visualization. Human Brain Map. 2017;38(11):5391–5420. doi: 10.1002/hbm.23730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shin HC, Roth HR, Gao M, Lu L, Xu Z, Nogues I, Yao J, Mollura D, Summers RM. Deep convolutional neural networks for computer-aided detection: Cnn architectures, dataset characteristics and transfer learning. IEEE Trans Med Imag. 2016;35(5):1285–1298. doi: 10.1109/TMI.2016.2528162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sreeja S, Samanta D, et al. Distance-based weighted sparse representation to classify motor imagery eeg signals for bci applications. Multimedia Tools and Applications 2020; pp. 1–19 .
- 35.Sujadevi V, Mohan N, Kumar SS, Akshay S, Soman K. A hybrid method for fundamental heart sound segmentation using group-sparsity denoising and variational mode decomposition. Biomed Eng Lett. 2019;9(4):413–424. doi: 10.1007/s13534-019-00121-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tangermann M, Müller KR, Aertsen A, Birbaumer N, Braun C, Brunner C, Leeb R, Mehring C, Miller KJ, Mueller-Putz G, et al. Review of the bci competition iv. Front Neurosci. 2012;6:55. doi: 10.3389/fnins.2012.00055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Uyulan C, Erguzel TT. Analysis of time-frequency eeg feature extraction methods for mental task classification. Int J Comput Intell Syst. 2017;10(1):1280–1288. doi: 10.2991/ijcis.10.1.87. [DOI] [Google Scholar]
- 38.Wang B, Wong C.M, Kang Z, Liu F, Shui C, Wan F, Chen C.P. Common spatial pattern reformulated for regularizations in brain-computer interfaces. IEEE Transactions on Cybernetics 2020. [DOI] [PubMed]
- 39.Wolpaw JR, McFarland DJ. Multichannel eeg-based brain-computer communication. Electroencephalogr Clin Neurophysiol. 1994;90(6):444–449. doi: 10.1016/0013-4694(94)90135-X. [DOI] [PubMed] [Google Scholar]
- 40.Xu J, Grosse-Wentrup M, Jayaram V. Tangent space spatial filters for interpretable and efficient riemannian classification. J Neural Eng. 2020;17(2):026043. doi: 10.1088/1741-2552/ab839e. [DOI] [PubMed] [Google Scholar]
- 41.Xu L, Xu M, Ke Y, An X, Liu S, Ming D. Cross-dataset variability problem in eeg decoding with deep learning. Frontiers in Human Neuroscience. 2020;14. [DOI] [PMC free article] [PubMed]
- 42.Yilmaz BH, Yilmaz CM, Kose C. Diversity in a signal-to-image transformation approach for eeg-based motor imagery task classification. Med Biol Eng Comput. 2020;58(2):443–459. doi: 10.1007/s11517-019-02075-x. [DOI] [PubMed] [Google Scholar]
- 43.Yosinski J, Clune J, Bengio Y, Lipson H. How transferable are features in deep neural networks? In: Advances in neural information processing systems, 2014;pp. 3320–3328.
- 44.Yu Z, Ma T, Fang N, Wang H, Li Z, Fan H. Local temporal common spatial patterns modulated with phase locking value. Biomed Signal Process Control. 2020;59:101882. doi: 10.1016/j.bspc.2020.101882. [DOI] [Google Scholar]
- 45.Zhang Y, Nam CS, Zhou G, Jin J, Wang X, Cichocki A. Temporally constrained sparse group spatial patterns for motor imagery bci. IEEE Trans Cybern. 2018;49(9):3322–3332. doi: 10.1109/TCYB.2018.2841847. [DOI] [PubMed] [Google Scholar]