A 4-year longitudinal neuroimaging study of cognitive control using latent growth modeling: developmental changes and brain-behavior associations

Abstract

Despite theoretical models suggesting developmental changes in neural substrates of cognitive control in adolescence, empirical research has rarely examined intraindividual changes in cognitive control-related brain activation using multi-wave multivariate longitudinal data. We used longitudinal repeated measures of brain activation and behavioral performance during the multi-source interference task (MSIT) from 167 adolescents (53% male) who were assessed annually over four years from ages 13 to 17 years. We applied latent growth modeling to delineate the pattern of brain activation changes over time and to examine longitudinal associations between brain activation and behavioral performance. We identified brain regions that showed differential change patterns: (1) the fronto-parietal regions that involved bilateral insula, bilateral middle frontal gyrus, left pre-supplementary motor area, left inferior parietal lobule, and right precuneus; and (2) the rostral anterior cingulate cortex (rACC) region. Longitudinal confirmatory factor analyses of the fronto-parietal regions revealed strong measurement invariance across time implying that multivariate functional magnetic resonance imaging data during cognitive control can be measured reliably over time. Latent basis growth models indicated that fronto-parietal activation decreased over time, whereas rACC activation increased over time. In addition, behavioral performance data, age-related improvement was indicated by a decreasing trajectory of intraindividual variability in response time across four years. Testing longitudinal brain-behavior associations using multivariate growth models revealed that better behavioral cognitive control was associated with lower fronto-parietal activation, but the change in behavioral performance was not related to the change in brain activation. The current findings suggest that reduced effects of cognitive interference indicated by fronto-parietal recruitment may be a marker of a maturing brain that underlies better cognitive control performance during adolescence.

1. Introduction

In developmental neuroscience research, it is necessary to examine relationships between brain function and behavior over time and across ages (Crone and Elzinga, 2015; (Madhyastha et al., 2018)Madhyastha et al., 2019). Only longitudinal research examining within-person temporal changes as trajectories (as opposed to a cross-sectional snapshot at a single time) is able to reveal developmental pathways of adaptive and maladaptive brain functioning. However, challenges arise with respect to the measurement reliability of neuroimaging data in longitudinal designs (Herting et al., 2018). The present study employs a latent variable modeling approach using structural equation modeling (SEM) to tackle measurement challenges while studying individual differences in within-person changes in brain activation and behavior during cognitive control. Most prior developmental neuroscience research on cognitive control has examined differences in the magnitude of brain activation across different age-cohorts, thus limiting inferences regarding true developmental changes on the individual-level. Here, we used longitudinal functional magnetic resonance imaging (fMRI) data to investigate developmental changes in brain activation during cognitive control across adolescence, and further examined longitudinal brain-behavior associations. The current approach attempts to shed light on within-person developmental trajectories of cognitive control-related brain function, while simultaneously considering age-related behavioral change, which may facilitate new conceptualizations of systematic brain development, and improve existing neural systems models of cognitive control.

Although there have been theoretical models regarding developmental changes in neural substrates of cognitive control in adolescence, empirical research has rarely examined intraindividual changes in cognitive control-related brain activation using multi-wave multivariate longitudinal data. In the present study, we focused on cognitive control development during adolescence, observed by brain activation and behavioral performance during the multi-source interference task (MSIT; Bush et al., 2003). The MSIT measures detection and response to conflict associated with both flanker conflict and motor spatial conflict, and it was developed by combining multiple dimensions of cognitive interference (that are measured by Stroop-like tasks, Eriksen Flanker-type tasks, and Simon effect tasks) with decision making (Bush et al., 2003). Throughout adolescence, prefrontal cortex regions—known to be critical in cognitive control—undergo maturation, including increased myelination, experience-dependent synaptogenesis and pruning, as well as strengthening of connections within prefrontal circuitry (Liston et al., 2006; Luna et al., 2015; Paus, 2005). Indeed, the remarkable development and specialization of prefrontal cortex regions that support higher-order cognition during adolescence marks adolescence as a neurobiological critical period (Larsen and Luna, 2018). The proposed rapid development of neurobiology related to cognitive control during this critical period can be best tested by examining within-person developmental trajectories.

Prior research has identified brain regions, particularly within the prefrontal cortex, that appear crucial for cognitive control during childhood and adolescence (Crone and Steinbeis, 2017 for review). Yet, there remains a dearth of research as to how activation in different brain regions involved in cognitive control change across development (i.e., within-person change) and whether there are between-person differences in such within-person change. Currently, within cognitive control research, neuroimaging studies using longitudinal data measured at three or more time points are extremely rare, with one notable exception of a cohort-sequential longitudinal study of inhibitory control (Ordaz et al., 2013). Specifically, Ordaz et al. (2013) examined longitudinal trajectories of brain activation observed during an antisaccade task across ages 9 to 26 years (participants contributing between one to six time points). The results indicated no changes in motor response control regions (e.g., pre-supplementary motor area), decreases in activation in executive control regions (e.g., dorsolateral prefrontal cortex), and increases in activation in error-processing regions (e.g., dorsal anterior cingulate cortex; dACC) with age. Among these regions, only error-processing activation in the dACC was significantly predictive of behavioral performance. One of the significant contributions of this study is the demonstration of longitudinal trajectories of cognitive control-related brain activation which varied across different regions of the brain.

To understand differential developmental changes across brain regions engaged in cognitive control, we utilized latent growth modeling because of several methodological advantages that are germane to this approach. The latent growth model is well suited for delineating patterns of changes (e.g., linear versus non-linear), and it estimates not only within-person change, but also between-person differences in within-person change. In latent growth modeling, the measure should capture the same construct in the same metric across time so that scores obtained from the measure can be compared quantitatively to track intraindividual changes (see Kim-Spoon and Grimm, 2016 for review). For multivariate longitudinal data, measurement invariance (Meredith, 1993)—i.e., whether the same construct was measured in the same metric—can be statistically tested through longitudinal confirmatory factor analysis. After confirming that constructs are measured in a consistent way across measurement occasions (factorial invariance), those factors can be used in a second-order growth model. This model involves a theoretically error-free construct, instead of using error laden variables and composite scores, thereby improving measurement reliability and validity (Grimm et al., 2017; Hancock et al., 2001; McNeish & Wolf, 2020).

Brain activation is often used to understand cognitive constructs or processes but such inferences are fraught with challenges (Poldrack, 2006). For example, researchers have raised concerns regarding the reliability of regions of interest (ROI)-based analyses for testing individual difference inferences in fMRI (Elliott et al., 2020; Fröhner et al., 2019; Kragel et al., 2020; Lebreton et al., 2019). We believe that latent variable modeling can be used to improve reliability of neuroimaging data, thereby improving between-subjects inferences. In theory and in practice, psychometric approaches have shown that aggregating covarying indicators (i.e., latent variables) produces scores that are more reliable and have better predictive validity compared to separate indicators when examined alone (Nunnally and Bernstein, 1994). Specifically, confirmatory factor analysis using latent variable modeling is a powerful data reduction technique, as it extracts a small number of latent variables based on the covariations among a set of observed variables. In neuroimaging studies, confirmatory factor analysis can be applied to test a construct validity hypothesis, evaluating whether the correlations among the observed variables—e.g., eigenvariate values of ROIs—can be patterned according to the mathematical expectations of a single latent construct. Nevertheless, there have been only a few functional neuroimaging studies using confirmatory factor analyses to consider latent constructs based on multiple brain regions (e.g., Bolt et al., 2018; Kim-Spoon et al., 2016; Moore et al., 2018; Nees et al., 2012).

As such, latent variable modeling offers several key advantages: First, it optimizes power and reduces type-1 error by reducing the number of statistical parameters that are estimated while maximizing sample size. Second, it improves reliability by enhancing effect size and predictive validity (Cooper et al., 2019; Kragel et al., 2020; Poldrack et al., 2017). Third, for repeated measures fMRI data, longitudinal confirmatory factor analysis can be used to ascertain reliability of measured constructs, because it allows a quantitative test of whether the construct/process is robustly and reliably associated with its manifest indicators (i.e., neural activation of multiple ROIs) over time. In developmental neuroscience research, there is a particular challenge to assessing reliability in longitudinal fMRI data from children and adolescents, because test-retest reliability (defined as the consistency in producing stable results at each instance; Khoo et al., 2006) of fMRI data with longer scan intervals is expected to reflect not only consistency of the fMRI measurement itself but also the meaningful changes due to age-related development (Herting et al., 2018). For example, researchers have interpreted lower reliability values (represented by intraclass correlation coefficient) as indicating greater developmental changes (Koolschijn et al., 2011). Unlike the intraclass correlation approach, testing measurement invariance in longitudinal confirmatory factor analysis offers an alternative and more rigorous way to determine whether fMRI data yield individual-level measures that are consistent in their construct validity across time (e.g., equivalent latent factor loadings and intercept means across time) while also allowing for estimation of developmental changes (e.g., latent factor means freely estimated) that are not due to unreliability of measurement.

The primary goal of the present study was to fill in gaps in the developmental neuroscience literature by investigating intraindividual changes in cognitive control related-brain activation specific to the developmental period of adolescence and examining how such changes are related to behavioral performance during cognitive control (brain-behavior associations). We applied latent variable modeling to multivariate repeated measures data of brain activation (neural cognitive control) and behavioral performance (behavioral cognitive control) to investigate: 1) measurement models of brain activation patterns during cognitive control, using longitudinal confirmatory factor analyses; 2) patterns of and individual differences in developmental trajectories of brain activation and behavioral performance during cognitive control, using univariate growth models; and 3) longitudinal brain-behavior associations of cognitive control, using multivariate growth models. Specifically, with respect to brain-behavior associations, we examined how levels and changes in brain activation were related to levels and changes in behavioral performance across four yearly assessments.

2. Methods and materials

2.1. Participants

The sample included 167 adolescents (53% males) from a southeastern state in the United States, who participated in annual assessments across four years. Adolescents were 13 to 14 years of age at Time 1 (M = 14.07, SD = 0.54 for Time 1, M = 15.05, SD = 0.54 for Time 2, M = 16.07, SD = 0.56 for Time 3, and M = 17.01, SD = 0.55 for Time 4). About 78% of adolescents identified as White, 14% Black or African-American, 6% as more than one race, 1% as American Indian or Alaska Native, and 1% Asian. Median annual family income was in the $35,000-$50,000 range, with varying levels of family economic status (50% “poor/near poor” and 50% “non-poor” according to income-to-needs ratio). Among the primary caregivers (137 mothers, 21 fathers, and 9 others), 34% had a high school degree or less, 24% some college education, 24% bachelor’s degree, and 18% graduate degree. Inclusion criteria included being age 13 to 14 at Time 1 with vision corrected to be able to see the computer display clearly. Exclusion criteria were claustrophobia, history of head injury resulting in loss of consciousness for >10 min, orthodontia impairing image acquisition, severe psychopathology (e.g., psychosis), and other contraindications to magnetic resonance imaging (MRI).

At Time 1, 157 adolescents participated. At Time 2, 10 adolescents were added (to offset annual attrition) for a final sample of 167 (150 at Time 2, 147 at Time 3, and 150 at Time 4). Across all four years, 24 adolescents did not participate at all four time points for reasons including: ineligibility for tasks (n = 2), declined participation (n = 17), and lost contact (n = 5) during the follow-up assessments. Rate of participation was not significantly predicted by income, sex, race or study variables (ps > 0.08). The only exception was the effect of behavioral cognitive control at Time 3, but the effect size was small (η ² = 0.08).

2.2. Procedures

Data included in the present study were collected as part of a larger project. Adolescent participants and their primary caregivers were recruited via email announcements, newspaper advertisements, postcards, and flyers. Data collection was administered at university offices where participants completed self-report questionnaires, behavioral and neuroimaging tasks, and were interviewed by trained research assistants. The study duration was on average five hours long and participants were compensated monetarily for their time. All procedures were approved by the institutional review board of the university and written informed consent or assent was received from all participants.

2.3. Task

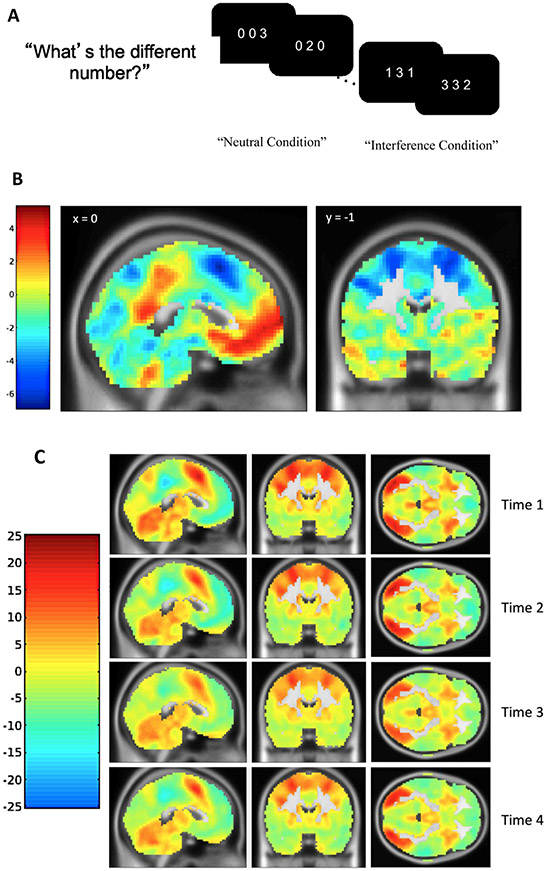
We measured detection and response to conflict associated with both flanker and spatial interference using the MSIT (Bush et al., 2003) in an MRI scanner. In the MSIT, on each trial, the participant was presented with three digits and asked to identify the digit that was different from the others by pressing the button corresponding to the digit. For trials in the neutral condition, the target’s identity was congruent with the target’s relative position on the screen, but in the interference condition, the target’s identity did not match its relative position (see Fig. 1A). Four blocks of 24 interference trials and 4 blocks of 24 neutral trials were interleaved with an interstimulus interval of 1.75 s. To assess behavioral cognitive control, we used intraindividual variability in response time, indexed as intraindividual standard deviations (ISD; MacDonald et al., 2012) for correct responses in the interference condition. Lower ISD scores represented better cognitive control. Accordingly, we found a significant positive effect of MSIT interference on ISD response time scores, such that intraindividual variability in response time was higher for interference trials compared to neutral trials [t(153) = 14.66 at Time 1, t(148) = 9.92 at Time 2, t(142) = 9.75 at Time 3, and t(141) = 8.88 at Time 4, all ps < 0.001].

Fig. 1. Schematic Display of the Multi-Source Interference Task (MSIT) and Activation Maps Showing Significant Activation for the Interference-Neutral Contrast.

Note: A) Adolescents were instructed to identify the different digit while ignoring its position. B) Statistical T map showing regions of positive and negative linear change in the interference effect on BOLD responses with time point using the Sandwich Estimator Toolbox after applying a gray matter mask. C) Statistical T maps showing regions of positive (interference > neutral) and negative (neutral > interference) interference effect for each time point after applying a gray matter mask.

2.4. Pubertal development

Pubertal developmental status was assessed annually using adolescent self-reports on a five-item scale (Petersen et al., 1988). Boys and girls answered the same three questions regarding growth spurt in height, pubic hair, and skin changes. Additionally, boys were asked about facial hair growth and voice change, and girls were asked about breast development and menarche. The mean scores across the five items were used to indicate stage-normative pubertal timing.

2.5. fMRI acquisition and preprocessing

Neuroimaging data were obtained on a 3T Siemens Tim Trio scanner using a 12-channel head matrix coil. Functional images were obtained with TR = 2 s, slice thickness = 4 mm, 34 axial slices, FoV = 220 × 220 mm, TE = 30 ms, flip angel = 90°, voxel size = 3.4 × 3.4 × 4 mm, 64 × 64 grid, and slices were hyperangulated at 30° from anterior-posterior commissure. Anatomical images with a 1mm³ isotropic voxel resolution were acquired using a rapid acquisition gradient echo sequence with repetition time (TR) = 1200 ms, field of view (FoV) = 245 × 245 mm, echo time (TE) = 2.66 ms and 192 slices. SPM8 (Wellcome Trust Neuroimaging Center) was used to preprocess the MRI data at all time-points. After correcting the functional scans for motion using a six-parameter rigid body transformation, the mean functional image was co-registered to the corresponding anatomical image using a rigid-body transformation estimated to maximize the normalized mutual information between the anatomical and mean functional image. Next the anatomical image was segmented to produce spatial normalization parameters which were then used to normalize the functional images to MNI-152 template. Normalization produced images resliced to an isotropic voxel size of 3 mm³. Finally, the normalized functional images were smoothed using a 6 mm full-width-half-maximum Gaussian kernel.

A GLM was fit in SPM8 to the preprocessed imaging data acquired from each participant at each time point. The interference and neutral task conditions were modeled as alternating boxcars convolved with a canonical double-gamma haemodynamic response function (HRF) using SPM8′s default parametrization of the gamma functions. The six realignment parameters obtained during preprocessing were used to model the effect of head motion. Framewise displacement (FD) was obtained using the realignment parameters, with rotational displacement replaced with millimeter equivalents assuming displacement along the surface of a sphere with a 100 mm diameter (Power et al., 2012; Siegel et al., 2014). High motion volumes with FD greater than 0.9 mm were censored non-destructively by adding a regressor for each censored volume in the design matrix of the GLM. A high-pass filter with cutoff of 0.006 Hz was used to remove low-frequency noise. Finally, for each participant at each time point, a contrast map was constructed by subtracting the neutral condition beta map from the interference condition beta map.

Interference minus neutral contrast maps were entered into four second-level GLMs in SPM8, one for each longitudinal time-point, using root mean square frame displacement as a regressor of no interest. To assess how the interference effect on blood-oxygen-level dependent (BOLD) responses changed with time-point, the first-level interference contrasts across all four time points were entered into a longitudinal group-level model using the Sandwich Estimator Toolbox, version 2.1.0 (SwE; Guillaume et al., 2014), while controlling for age-correlated changes in in-scanner head motion using root mean square frame displacement as a no-interest regressor (Satterthwaite et al., 2012). This SwE method combines ordinary least squares estimates of parameters of interest with estimates of variance/covariance based on a sandwich estimator (Eicker, 1963) and thus accounts for within-subject correlations across time. It has been shown that this method is asymptotically robust against misspecification of the covariance model and does not depend on the SPM assumption of common longitudinal variance structure of the whole brain. We used the SwE whole brain map as a guide to select ROIs within each wave so that we could evaluate developmental changes in these ROIs over time.

At each time point, the SPM GLM showed a significant interference effect on BOLD responses, consistent with that observed in prior literature (see Fig. 1B; Kim-Spoon et al., 2019). Our longitudinal model showed significant linear increases and decreases in the interference effect on BOLD responses in cognitive control regions identified by the MSIT. The SwE derived map of time-related changes in BOLD was used to identify nine clusters of interest for an ROI analysis, including bilateral insula, bilateral middle frontal gyrus (MFG), left pre-supplementary motor area (SMA), left rostral anterior cingulate cortex (rACC), left inferior parietal lobule (IPL), right precuneus, and left middle occipital gyrus (see Fig. 1C and Supplementary Table S1; for coordinates for peak regions within each time point, see Supplementary Tables S2-5). From each time point, the first eigenvariate values in the interference minus neutral contrast was obtained, after adjusting for an F-contrast of the effect of interest. Data and code are available upon request given a formal sharing agreement.

2.6. Data analytic approaches and model fitting preparation

Prior to analysis, statistical outliers (n = 20 across all variables and all time points) were winsorized to the next value that was not an outlier (i.e., within 3.29 SD; Tabachnick and Fidell, 2001), resulting in all variables with acceptable skewness and kurtosis (< 3 and < 10, respectively). We performed multivariate GLM analyses to evaluate possible effects of demographic covariates on neural and behavioral measures of cognitive control (eight ROI variables and one behavioral performance scores) at each time point. Predictors included the main effects of age, pubertal development, sex, race, and family income, as well as the interaction effects of sex by age and sex by pubertal development (testing whether age or pubertal development effects on cognitive control may vary between boys and girls). Across all four time points, these demographic covariates were not significant predictors of cognitive control variables (p = .07 - 0.89) and thus were not included in the main analyses. Table 1 depicts descriptive statistics and correlations for the study variables.

Table 1.

Descriptive statistics and bivariate correlations of study variables.

	1	2	3	4	5	6	7	8	9	10	11	M	SD	Min	Max
Fronto parietal regions T1	–											−0.000	0.895	−2.709	2.189
Fronto parietal regions T2	.340*	–										−0.623	0.742	−3.132	2.308
Fronto parietal regions T3	.261*	.222*	–									−0.808	0.769	−3.041	1.424
Fronto parietal regions T4	.443*	.394*	.312*	–								−0.888	0.652	−2.580	1.308
rACC T1	−0.036	−0.065	.011	−0.184*	–							−0.507	0.424	−1.676	0.812
rACC T2	−0.139	−0.006	−0.135	−0.092	.251*	–						−0.430	0.343	−1.262	0.632
rACC T3	−0.066	−0.195*	−0.176	−0.241*	.055	.186	–					−0.262	0.361	−1.427	0.695
rACC T4	−0.054	−0.015	.024	−0.151	.048	0.208*	0.281*	–				−0.314	0.351	−1.426	0.463
Behavioral CC T1	.153	.172*	.109	.180*	−0.176*	−0.039	−0.082	−0.106	–			0.240	0.040	0.150	0.347
Behavioral CC T2	.115	.086	.076	.167*	−0.224*	−0.082	−0.108	−0.177	.491*	–		0.206	0.041	0.112	0.301
Behavioral CC T3	.036	.090	.162	.107	−0.157	−0.052	−0.061	−0.079	.451*	.587*	–	0.192	0.042	0.105	0.377
Behavioral CC T4	.005	.184*	.006	.137	−0.242*	.014	−0.062	−0.165	.391*	.595*	.506*	0.181	0.044	0.095	0.315

Note. rACC = the rostral anterior cingulate cortex; CC = Cognitive Control; T1 = Time 1; T2 = Time 2; T3 = Time 3; T4 = Time 4. Although we used the latent factors of fronto-parietal regions, manifest variable factor scores were used for descriptive purposes.

^*p < .05.

Models were tested using Structural Equation Modeling (SEM) in Mplus statistical software version 8.4 (Muthén and Muthén, 1998–2018). Model fit was assessed by χ² value, degrees of freedom, corresponding p-value, Root Mean Square Error of Approximation (RMSEA) and its 90% Confidence Intervals (CI), and Confirmatory Fit Index (CFI). RMSEA values less than 0.08 and CFI values greater than 0.90 were taken to reflect acceptable fits (Little, 2013). For nested model comparisons, we used χ² difference tests (Bollen, 1989). We ensured that fit values for all the models that we interpreted were acceptable and focused on nested model fit comparisons, as all of these fit indices have been shown to be more effective at identifying differences in misspecification based on a comparison of nested model, in contrast to decisions based on comparisons with a priori cutoff values (Marsh et al., 2004).

We used full information maximum likelihood (FIML) estimation to handle missing data (Arbuckle, 1996; Little and Rubin, 2003). The FIML method relies on the assumption that missing values are missing at random. Missing at random requires that missing data are either missing completely at random, or that the missing information depends on variables that are included in the model. In longitudinal models of repeated measures data, those variables are the previous measurements of the same variable (Ghisletta and Lindenberger, 2005). Little’s MCAR test indicated that the missing data pattern for all neural cognitive control variables resembled a Completely at Random pattern (χ² = 49.39, df = 54, p = .65), whereas the missing data pattern for all behavioral cognitive control variables did not (χ² = 49.92, df = 19, p < .001). Given the superiority of FIML estimation to those obtained with listwise deletion or other ad hoc methods (Schafer and Graham, 2002) and that all our longitudinal models involved repeated measures of data, thus satisfying at least missing at random, we used the FIML estimation procedure to address missing data.

We first performed longitudinal confirmatory factor analyses to examine whether the same construct was measured in the same metric at each time point. We compared two alternative models testing weak (metric) versus strong (scalar) invariance (Grimm et al., 2017). The model testing weak invariance constrained factor loadings to be equal over time, implying that the same ROIs contributed in the same way to the latent factor. The model testing strong invariance additionally constrained individual ROI intercepts to be equal over time, implying that the scale of the factor does not change across time, which makes it possible to compare mean factor scores over time.

Next, we tested univariate growth models to examine developmental trajectories of neural and behavioral cognitive control. The growth models allowed us to appreciate (1) patterns of longitudinal changes (linear growth versus non-linear, latent basis growth), (2) statistical significance of the change rates (i.e., mean of the shape factor) as well as individual differences in the change rates (i.e., variance of the shape factor), and (3) statistical significance of the average level and individual differences of the initial levels (i.e., mean and variance of the intercept factor). Linear and nonlinear models were tested to fit the baseline model for the observed data patterns across the four time points. The first latent factor was the intercept, with all factor loadings fixed to one. The second latent factor was the shape, indicating growth of the function and change over time. The two growth factors were allowed to covary. Nested model comparisons were used to determine the shape of the trajectories. Two models were tested as nested models. First, in the linear growth model, a linear pattern of change was assumed and factor loadings for the linear slope factor were fixed to 0, 1, 2, and 3. Next, the latent basis growth model allowed the data to estimate the shape of growth by fixing the factor loadings to the first and last time points to 0 and 1, respectively, and freely estimating the second and third time points.

Finally, we tested multivariate growth models examining longitudinal brain-behavior associations of cognitive control to determine whether changes in brain activation were associated with changes in behavioral performance during cognitive control. The latent growth factors of brain activation and behavioral performance were estimated along with the covariances among the intercept and shape factors both within and across brain and behavior.

3. Results

3.1. Longitudinal confirmatory factor analysis of neural cognitive control

Prior to examining developmental changes in neural cognitive control, we examined whether the same construct was measured consistently at each time point by testing longitudinal measurement invariance using longitudinal confirmatory factor analyses. We first considered eight ROIs while excluding the left middle occipital gyrus given that it is generally involved in performing tasks that require visual processing, rather than directly engaged in cognitive control functioning per se. In this model, the left rACC was not significantly loaded on the common latent factor as the other seven ROIs, thus it was not included in the longitudinal confirmatory factor analyses. Additionally, modification indices suggested correlating the residual of right insula with the residual of left insula within each time point, thus these residual correlations were included. As suggested by Grimm et al. (2017), these longitudinal confirmatory factor analyses models included correlations between residuals for the same variable measured at different time points.

Constraining individual ROI intercepts to be equal across time in addition to factor loadings did not result in a significant deterioration in model fit (Δχ² = 10.031, Δdf = 18, p = .931). Thus, the model comparison result indicated that the model with strong invariance was more parsimonious version of the model (χ² = 534.303, df = 334, p < .001, RMSEA = 0.061, 90% CI [.051, 0.071], CFI = 0.924), compared to the model with weak invariance (χ² = 524.272, df = 316, p < .001, RMSEA = 0.064, 90% CI [.054, 0.074], CFI = 0.921). As reported in Fig. 2, in the strong invariance model, the seven factor loadings were all substantial, statistically significant, and the range was relatively narrow (standardized λ = 0.526 - 0.861, all ps < 0.05). Factor means decreased over time and all factor variances were significant. The strong invariance finding provides evidence of construct comparability suggesting that any observed changes in the construct can be seen as true construct differences rather than due to measurement artifacts.

Fig. 2. Longitudinal Confirmatory Factor Analysis with Strong Invariance for the Fronto-Parietal Regions.

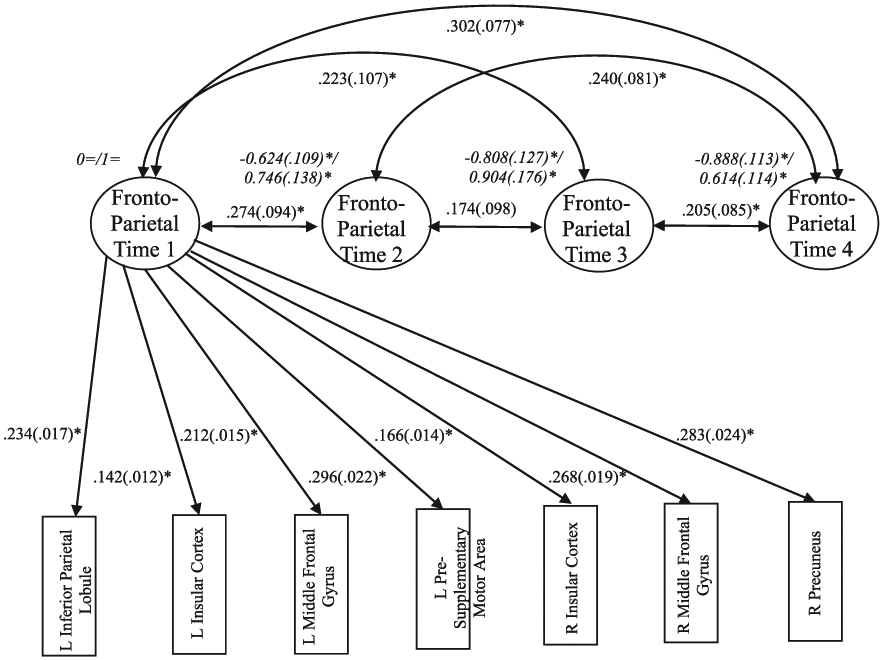
Note. Factor mean/variance are presented in italics. For clarity of presentation, factor loadings are presented for Time 1 only (factor loadings were equal across time), and residual correlations across time for the same variable and between left and right insula within the same time point are not presented. L = left; R = right; “=” fixed parameters; *p < .05.

Following construct validation through longitudinal confirmatory factor analysis of neural cognitive control variables, we labeled the common latent factor that encompasses seven ROI indicators (left and right insula, left and right MFG, left pSMA, left IPL, and right precuneus) as “fronto-parietal” because those seven ROIs were located in the fronto-parietal network previously identified as involved in cognitive control (Dosenbach et al., 2008; Sebastian et al., 2013). We clarify that this was a label for the regions that load onto a common latent factor, but there was no evidence of functional connectivity or this activity actually reflecting FPN. Further analyses involving neural cognitive control were conducted separately for the fronto-parietal regions and for the left rACC which was not significantly loaded on the same latent factor as the other seven ROIs.

3.2. Developmental trajectories of neural and behavioral cognitive control: univariate growth models

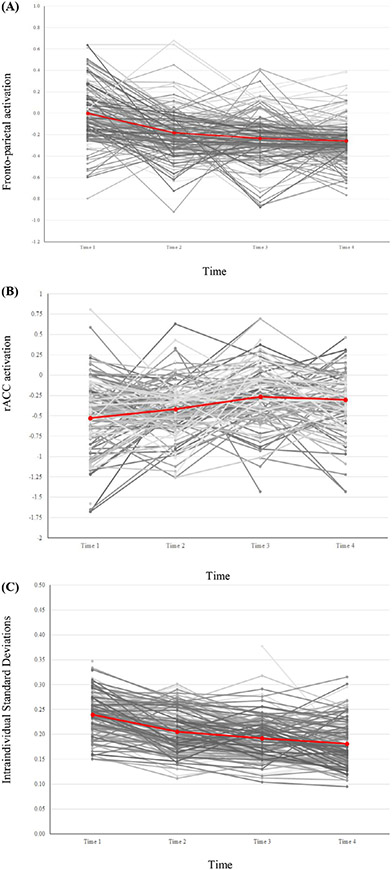
To examine developmental trajectories of cognitive control, we tested univariate growth models separately for fronto-parietal activation, rACC activation, and ISD response time scores. As shown in Table 2, for the fronto-parietal regions, second-order growth modeling was used. In these second-order growth models, the factors for the measurement model (as in longitudinal confirmatory factor analysis models) were first-order factors and the growth factors were second-order factors, so that the second-order growth factors (i.e., intercept and shape) accounted for the developmental changes of the first-order factors (i.e., the fronto-parietal regions) across time. For the fronto-parietal regions, the latent basis growth model provided the better fit to the data compared to the linear growth model (see Table 2). The results from the fronto-parietal second-order latent basis growth model are reported in Table 3. The mean of the shape factor was significant but the variance was not. This result indicated significant decreases in fronto-parietal activation over time with non-significant individual differences in change rates. There were significant individual differences in initial levels while the mean of the intercept factor was fixed at zero for identification (Grimm et al., 2017). The intercept and shape factors did not significantly covary with each other. The mean growth curve trajectory (based on estimated means) is presented along with the longitudinal plot of fronto-parietal activation factor scores across the four times in Fig. 4-a.

Table 2.

Model fit for univariate growth models of neural and behavioral cognitive control.

Model Label	χ2	df	p(exact)	RMSEA [90% CI]	CFI	Δχ2	Δdf	p(d)
Fronto-parietal regions
a. Linear growth model	555.501	339	<0.001	0.063 [0.054, 0.073]	0.918
b. Latent basis growth model rACC	541.413	337	<0.001	0.062 [0.052, 0.071]	0.923	14.088	2	<0.001
a. Linear growth model	16.581	8	0.034	0.082 [.021, 0.138]	0.494
b. Latent basis growth model	2.545	6	0.863	0.009 [.000, 0.054]	1.000	14.036	2	<0.001
Intraindividual standard deviations
a. Linear growth model	30.407	8	<0.001	0.130 [.083, 0.180]	0.860
b. Latent basis growth model	4.913	6	0.555	0.000 [.000, 0.090]	1.000	25.494	2	<0.001

Note. rACC = the rostral anterior cingulate cortex; RMSEA = root mean square error of approximation; CI = confidence interval; CFI = comparative fit index; Δχ² = difference in likelihood ratio tests; Δdf = difference in df; p(d) = probability of the difference tests. Best-fitting model in boldface.

Table 3.

Parameter estimates for Univariate growth models of neural and behavioral cognitive control.

	Fronto-parietal regions			rACC			Intraindividual SD
	Est	S.E.	Est/S.E	Est.	S.E.	Est/S.E	Est.	S.E.	Est/S.E
Shape factor loadings
Time 1	0=			0=			0=
Time 2	0.715*	.102	7.010	0.476*	.111	4.289	0.576*	.048	11.976
Time 3	0.912*	.123	7.402	1.160*	.147	7.889	0.806*	.052	15.431
Time 4	1=			1=			1=
Means
Intercept factor	0=			−0.526*	.034	−15.558	0.240*	.003	75.556
Shape factor	−0.258*	.033	−7.802	0.223*	.042	5.306	−0.059*	.004	−15.896
Factor Variances
Intercept factor	0.036*	.013	2.878	0.087*	.023	3.787	0.001*	.000	4.267
Shape factor	0.009	.016	0.547	0.092*	.034	2.686	0.000	.000	1.375
Factor Covariance
Intercept↔Shape	−0.015	.012	−1.189	−0.074*	.025	−2.931	0.000	.000	0.072

Note. rACC = the rostral anterior cingulate cortex; Est. = Estimate; S.E. = standard error; “=” fixed parameters. The ratio Est/S.E. can be viewed as a Z value.

^*p < .05.

Fig. 4. Mean growth curve with individual values across four times.

Note. A. Fronto-parietal activation factor scores. B. Rostral anterior cingulate cortex (rACC) activation C. Intraindividual variability behavioral performance scores.

For rACC, the latent basis growth model provided a better fit to the data compared to the linear growth model (see Table 2). The results from the latent basis growth model for rACC are reported in Table 3. The mean and the variance of the shape factor were significant, indicating significant increases in rACC activation over time with significant individual differences in change rates. The mean of the intercept factor was significantly different from zero, and there were significant individual differences in initial levels. The intercept and shape factors significantly covaried with each other, indicating that higher initial levels were associated with smaller increases in change rates. The mean growth curve trajectory (based on estimated means) is presented along with the longitudinal plot of rACC activation raw scores across the four times in Fig. 4-b.

For behavioral performance data (ISD scores), the latent basis growth model provided a better fit to the data compared to the linear growth model (see Table 2). The results from the latent basis growth model for behavioral cognitive control are reported in Table 3. The mean of the shape factor was significant but the variance was not. The result indicated significant decreases in intraindividual variability in response time with non-significant individual differences in change rates. The mean of the intercept factor was significantly different from zero, and there were significant individual differences in initial levels. The intercept and shape factors did not significantly covary with each other. The mean growth curve trajectory (based on estimated means) is presented along with the longitudinal plot of ISD raw scores across the four times in Fig. 4-c.

3.3. Longitudinal brain-behavior associations: bivariate growth models of brain activation and behavioral performance

To examine longitudinal brain-behavior associations of cognitive control, we used bivariate growth models to estimate dynamic associations among growth factors (intercept and shape factors) of brain activation and behavioral performance (see Fig. 3). For fronto-parietal activation, the overall fit of the bivariate growth model was acceptable (χ² = 688.279, df = 451, p < .001, RMSEA = 0.056, 90% CI [.048, 0.065], CFI = 0.917). As reported in Table 4, the initial level of behavioral performance was significantly related to the initial level of fronto-parietal activation, indicating that better behavioral performance (i.e., lower ISD scores) was related to lower fronto-parietal activation at Time 1 when adolescents were 13–14 years. In order to examine whether the significant association between the level of neural activation and the level of behavioral performance persisted over time, we reran the bivariate growth model with the intercept rescaled at Time 4 (i.e., intercept factor loadings fixed to −1 at Time 1 and 0 at Time 4 with Times 2 and 3 freely estimated). The result revealed that better behavioral performance was significantly associated with lower fronto-parietal activation at Time 4 when adolescents were 16–17 years (Est. = 0.002, SE. = 0.001, p = .036). Changes in fronto-parietal activation were not associated with changes in behavioral performance. The level of fronto-parietal activation (at Time 4) was not related to changes in behavioral performance, and the level of behavioral performance (at Time 4) was not related to changes in fronto-parietal activation.

Fig. 3. Bivariate Growth Model for Neural and Behavioral Cognitive Control.

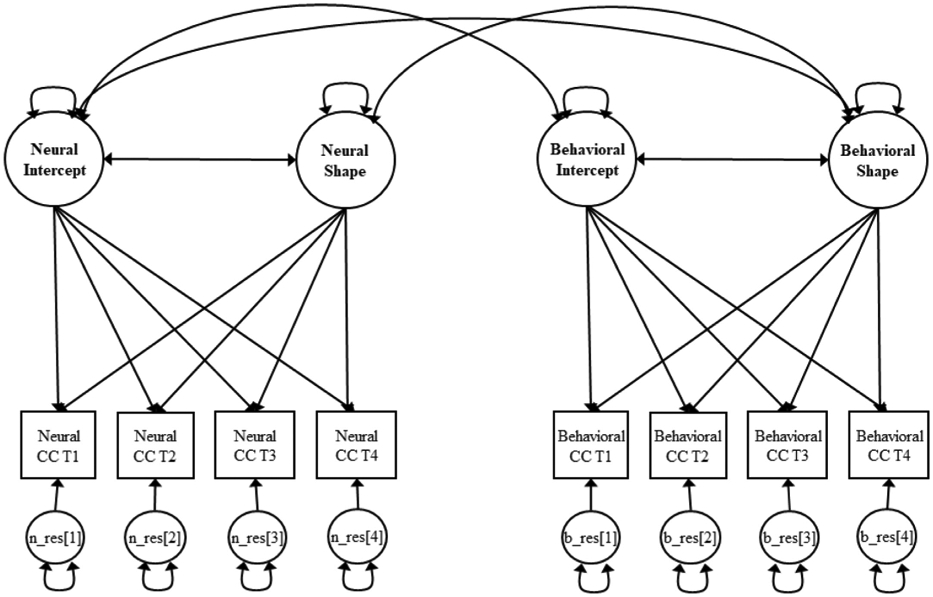
Note. The model was estimated separately for the fronto-parietal regions and the rostral anterior cingulate cortex (neural cognitive control). For the fronto-parietal regions, latent factors were used instead of manifest variables (as shown in Fig. 2). CC = cognitive control; T1 = Time 1; T2 = Time 2; T3 = Time 3; T4 = Time 4; n_res = neural residual; b_res = behavioral residual.

Table 4.

Parameter estimates for bivariate growth models of neural and behavioral cognitive control.

	Fronto-parietal regions			rACC
	Est	S.E.	Est/S.E.	Est.	S.E.	Est/S.E.
Shape factor loadings
NCC T1	0=			0=
NCC T2	0.718*	0.102	7.067	0.513*	.115	4.421
NCC T3	0.899*	.121	7.422	1.189*	.156	7.607
NCC T4	1=			1=
BCC T1	0=			0=
BCC T2	0.576*	.048	12.006	0.575*	.048	11.996
BCC T3	0.805*	.052	15.474	0.805*	.052	15.450
BCC T4	1=			1=
Factor Means
NCC Intercept	0=			−0.528*	0.034	−15.629
NCC Shape	−0.259*	.033	−7.898	0.217*	0.043	5.096
BCC Intercept	0.240*	.003	76.566	0.240*	.003	76.601
BCC Shape	−0.059*	.004	−15.919	−0.059*	.004	−15.902
Factor Variances
NCC Intercept	0.036*	.013	2.867	0.083*	0.023	3.655
NCC Shape	0.008	.016	0.471	0.093*	0.035	2.652
BCC Intercept	0.001*	.000	4.273	0.001*	.000	4.267
BCC Shape	0.000	.000	1.380	0.000	.000	1.409
Factor Covariance
NCC Intercept ↔ BCC Intercept	0.002*	.001	2.032	−0.003	0.001	−1.868
NCC Shape ↔ BCC Shape	0.000	0.000	0.068	0.000	0.002	0.158
NCC Intercept ↔ BCC Shape	−0.001	0.001	−1.126	0.000	0.001	−0.292
BCC Intercept ↔ NCC Shape	0.000	0.001	−0.367	0.001	0.002	0.801
NCC Intercept ↔ NCC Shape	−0.014	.012	−1.114	−0.072*	.025	−2.857
BCC Intercept ↔ BCC Shape	0.000	.000	0.068	0.000	.000	0.044

Note. rACC = the rostral anterior cingulate cortex; NCC = neural cognitive control; BCC = behavioral cognitive control, measured by intraindividual standard deviations in response time; T1 = Time 1; T2 = Time 2; T3 = Time 3; T4 = Time 4; Est. = Estimate; S.E. = standard error; “=” fixed parameters. The ratio Est/S.E. can be viewed as a Z value.

^*p < .05.

For rACC, the overall fit of the bivariate growth model was acceptable (χ² = 16.909, df = 24, p = .853, RMSEA = 0.000, 90% CI [.000, 0.036], CFI = 1.000). As reported in Table 4, the association between the initial level of behavioral performance and the initial level of rACC activation indicated a trend towards poor performance (i.e., higher ISD scores) among adolescents with lower rACC activation (p = .062). Similar to fronto-parietal activation, changes in rACC activation were not associated with changes in behavioral performance. The initial level of rACC activation was not related to changes in behavioral performance, and the initial level of behavioral performance was not related to changes in rACC activation.

4. Discussion

We aimed to examine intraindividual changes in brain activation during cognitive control and further examine how changes in brain activation may be associated with changes in behaviors using multivariate repeated measures data of adolescents. The current study is the first study using longitudinal data from a large sample in a single cohort assessed annually over four years from 13 years to 17 years; it is also the first to estimate these neurodevelopmental trajectory patterns within adolescence, a developmental period critical to establishing adult-level stability of cognitive control processing (Luna et al., 2015). Our univariate growth modeling results suggested nonlinear patterns of developmental changes in neural activation implicated in cognitive control. Specifically, we found a decreasing trajectory with non-significant variation in fronto-parietal regions and an increasing trajectory with significant variation in rACC. In addition, our bivariate growth modeling results suggested that lower activation in fronto-parietal regions was related to better cognitive control behavioral performance.

In processing our longitudinal fMRI data measured repeatedly over four years, we identified brain regions activated for the interference minus neutral contrast that showed recognizable changes over time using the SwE method (Guillaume et al., 2014). The multiple ROIs that we identified were consistent with prior findings regarding brain regions generally involved in cognitive control (Sebastian et al., 2013; Spielberg et al., 2015). In particular, a meta-analysis of fMRI studies using MSIT reported two reliable activation clusters including the dACC/medial prefrontal cortex/SMA cluster and the right insula/right IFG/right putamen cluster (Deng et al., 2018). Our longitudinal confirmatory factor analysis model with strong factorial invariance revealed that multiple fronto-parietal regions (including seven ROIs of bilateral insula, bilateral MFG, left pSMA, left IPL, right precuneus) were consistently loaded on the same latent factor and activated in a concerted pattern across four years. Those ROIs in the fronto-parietal regions are known to be involved in attention to salience (insula), motor control (MFG and pSMA), and spatial attention and visuomotor processing (IPL and precuneus) (Sebastian et al., 2013; Spielberg et al., 2015). In contrast, the left rACC was not loaded on the same latent factor as the fronto-parietal regions. The peak of this region fell in Brodmann area 11 (BA 11) which is known to engage in decision making that involves conflict processing (Taylor et al., 2006; Rogers et al., 1999; Sebastian et al., 2013).

As has been shown in many fMRI studies, a single region can be involved in a broad range of tasks (Kanai and Rees, 2011). Furthermore, brains regions do not function in isolation, but rather as parts of larger collections of interacting brain regions (Bullmore and Sporns, 2009; Fox et al., 2005). Therefore, the use of latent factor modeling in analyzing multiple ROIs that are related to a particular function during a behavioral task is a promising way to address correlations between ROIs that reflect neural substrates of a common latent construct. Indeed, our findings of longitudinal confirmatory factor analysis based on multiple fronto-parietal regions illustrate that latent variable modeling using SEM is a feasible way of representing associations of functionally related brain regions, which complements other functional approaches used in the field to assess brain systems and networks (e.g., Woo et al., 2017). Furthermore, testing for longitudinal measurement invariance enabled us to use the repeated measures fMRI data to be compared quantitatively, so that reliable variance in intraindividual changes can be examined.

The longitudinal trajectory of decreasing fronto-parietal activation indicated that positive interference effects (i.e., interference > neutral) became smaller across adolescence. We found no significant variance in change rates for fronto-parietal activation, suggesting relatively homogeneous decreasing trajectories. The observed decreases in the fronto-parietal activation are consistent with prior research demonstrating age-related decreases in brain activation during cognitive control, reflecting more refined and more efficient neural functioning with development (Crone and Steinbeis, 2017; Luna et al., 2010; Tamm et al., 2002). We note that our longitudinal data revealed significant intraindividual changes in fronto-parietal activation to task-specific interference processing, whereas a cross-sectional study of 8- to 19-year-olds who performed the MSIT found no age differences in brain activation to interference processing (i.e., interference versus neutral conditions) (Liu et al., 2016). Instead, Liu et al. (2016) found that older youths showed lower pre-SMA activation to overall task processing (i.e., interference plus neutral conditions against implicit baseline). As such, the discrepancy in the findings highlight the importance of examining within-person changes over time, as opposed to comparing individuals of different ages.

The decreasing trajectory of fronto-parietal activation across adolescence observed in the current study appears to be inconsistent with the findings from a longitudinal study by Ordaz et al. (2013), who reported no significant changes in growth curves with regard to activation in motor response control regions including pre-SMA, bilateral posterior parietal cortex, and putamen. One possibility for the inconsistent findings may be differences in specific neuroimaging paradigms, such as the use of cognitive interference (in our study) versus response inhibition (in Ordaz et al.). Another possibility for the discrepancy in the findings may be the age range of the samples. Our single-cohort sample had a narrow age range within each time point and the whole sample was assessed annually over four years within the developmental period of adolescence, ages 13 through 17 years. In contrast, the sample used by Ordaz et al. included participants aged 9 years to 26 years, with participants contributing between one to six time points across yearly assessments. Given such sample differences, it is plausible that the current study could capture the adolescence-specific changes more sensitively than the study by Ordaz et al. Further replications are needed for clarifying potentially differential developmental trajectory patterns of task-specific neural activation (e.g., cognitive interference versus response inhibition) during adolescence.

The longitudinal trajectory of increasing rACC activation indicated that in general negative interference effects (i.e., neutral > interference) became smaller across adolescence. In addition, there was significant variation in change rates for the rACC growth trajectories. The negative interference effects shown in rACC activation is consistent with prior research using the MSIT that showed decreased rACC activation with demanding cognitive activity (i.e., task-induced deactivation; Bush et al., 2000). Prior research also suggested that rACC activation may play a critical role in dynamic regulation of cognitive control via performance optimization and error evaluation (Braver et al., 2001; Polli et al., 2005). Our finding of increasing rACC activation across adolescence, implying decreases in reduced rACC recruitment during the interference condition compared to the neutral condition, aligns with the prior finding by Ordaz et al. (2013), who reported age-related increases in dACC activation for error monitoring during the corrected error trials compared to the fixation baseline. Taken together, the findings corroborate the theorized ACC involvement in cognitive control (Botvinick et al., 2001) by clarifying that increases in ACC recruitment with development may reflect the maturation of neural cognitive control, particularly in conflict and error processing.

Turning to behavioral performance data, age-related improvement was indicated by a decreasing trajectory of intraindividual variability in response time across four years. The current finding presents the first evidence of within-person developmental changes in cognitive control performance based on the MSIT, and the result is in line with prior cross-sectional research reporting larger reaction time differences between the neutral versus the interference condition among adolescents compared to adults during the MSIT (Fitzgerald et al., 2010).

Overall, we found differential change patterns and individual differences in the developmental trajectories of neural activation and behavioral performance during MSIT. In our examination of developmental trajectories of fronto-parietal activation, rACC activation, and MSIT behavioral performance, rACC activation was the only construct that showed significant variance in change across four years. This finding suggested greater individual differences in the developmental trajectory of rACC in contrast to the trajectories of fronto-parietal activation and behavioral performance. With respect to the pattern of the developmental trajectory, all three constructs (i.e., fronto-parietal, rACC, and behavioral) fit non-linear patterns of growth better than a linear pattern. For fronto-parietal activation and behavioral performance, the largest change (decrease) occurred between Time 1 and Time 2, suggesting most rapid change in early adolescence. For rACC activation, the developmental trajectory showed a peak around Time 3, with the largest change (increase) occurring between Time 2 and Time 3 and thus suggesting most rapid change during middle adolescence.

Within the neuroscience literature, correlations between neural and behavioral indicators have been frequently used to evaluate brain-behavior associations. However, correlations can have problems, especially when the goal is to examine longitudinal changes in brain-behavior associations (Cooper et al., 2019; Rousselet and Pernet, 2012). For example, Pearson correlations are affected by many factors that are likely to vary across repeated measurements, including the slope around which points are clustered, the magnitude of the residuals, restriction of range, heteroscedasticity, and sensitivity to outliers (Wilcox, 2012). Instead of using the conventional approach with correlations, we evaluated longitudinal brain-behavior associations by testing bivariate growth models to estimate joint development between neural and behavioral cognitive control processes to better understand the way their changes are related over time. We found a significant association between the level of behavioral performance and the level of fronto-parietal activation, indicating that adolescents with lower fronto-parietal activation showed better cognitive control performance. Thus, greater cognitive interference demands placed on fronto-parietal regions in developing adolescent brains may be related to poor behavioral performance. The association between the level of behavioral performance and the level of rACC activation was weaker and not statistically significant, suggesting that individual differences in behavioral performance were better accounted for by the magnitude of fronto-parietal activation than rACC activation. Finally, the individual differences in changes in fronto-parietal and rACC activation were not significantly associated with the individual differences in changes in ISD scores, indicating that the changes in neural activation and the changes in behavioral performance are not dynamically linked across adolescence. However, the non-significant associations between brain changes and behavior changes are likely due in part to the non-significant variance in change rates shown in behavioral cognitive control as well as fronto-parietal activation.

Recent concerns have been raised about the temporal reliability of individual differences in brain activation, especially because reliability is important for examining brain activation as a biomarker of health risk or endophenotypes of clinical outcomes (Elliott et al., 2020; Kragel et al., 2020). In the present study, longitudinal confirmatory factor analyses revealed robust measurement models of neural cognitive control based on multiple ROIs in the fronto-parietal regions (insula, MFG, pSMA, IPL, and precuneus) across four years during adolescence. Thus, our findings demonstrated that multiple ROI indicators during the MSIT task could be reliably measured across time as shown by longitudinal measurement invariance. Longitudinal confirmatory factor analysis has a clear advantage over intraclass correlation coefficients to measure reliability of fMRI data due to the ability to formally test temporal equivalence in the measurement structure. With measurement equivalence tested and supported, it is then feasible to more directly interpret longitudinal changes in factor means as real developmental change that is not attributable to developmental changes in reliability of measurement.

Limitations of the current study suggest directions for future research. First, longitudinal neuroimaging research that uncovers developmental changes in the connections between the rACC and the fronto-parietal regions (such as functional or structural connectivity) is needed to advance our understanding of how those brain regions work together to contribute to intraindividual changes in cognitive control development. Second, we used a latent basis growth model to discover the best-fitting shape of non-linear change. Although this somewhat exploratory approach is deemed to be useful because the growth function of neural activation during cognitive control is not clearly known, we note that the estimated parameters from the latent basis growth model can be difficult to map onto theoretical notions of particular patterns of developmental processes, and that the model does not make predictions outside the observation period (Grimm et al., 2011). Third, we used cut-offs of RMSEA ⟨ 0.08 and CFI ⟩ 0.90 based on Little (2013) who provided model fit evaluation guidelines for longitudinal SEM considering unique features of longitudinal models (e.g., requiring both covariance and mean structures as opposed to models used for SEM fit assessment recommendations that model only covariance). Nevertheless, these were less stringent than the commonly used cut-off criteria that have been recommended based on simulations of single-occasion covariance structure models (e.g., RMSEA ≤ 0.06 and CFI ≥ 0.95; see Hu and Bentler, 1999). All of our models satisfied RMSEA ≤ 0.06 and the models involving rACC models satisfied CFI ≥ 0.95. However, the models involving fronto-parietal indicators had CFIs ranging from 0.91 to 0.92, pointing out a need for replication to improve the model and identify misspecification. We speculate that the worse CFI fit of the models involving fronto-parietal indicators may reflect the ‘model size’ effect, demonstrating a worsening of CFI as the number of observed variables increased (Shi et al., 2018). Finally, replication of our findings is needed given that we used the same data set for selecting brain regions and for testing our statistical models. As an initial inferential step in testing a latent growth modeling approach to analyzing multi-wave multivariate neuroimaging data, we used functionally defined ROIs defined from the SwE procedure which may be susceptible to inflated effect sizes (Vul et al., 2009), although perspectives on how inflated and the extent to which nonindependent ROIs are useful are mixed (Lieberman et al., 2009). We recommend that future studies ideally use independent datasets for selection and analyses to ensure independence of the results while preventing circularity (Kriegeskorte et al., 2009).

5. Conclusion

Consistent with neurodevelopmental models of adolescent motivated behavior that emphasize the regulating role of prefrontal cortex functioning over limbic functioning, the development of cognitive control has implications for risky decision making and health risk behaviors during adolescence (Casey et al., 2008; Kim-Spoon et al., 2017). As adolescents age, the decreasing activation trajectory of the fronto-parietal regions together with the increasing activation trajectory of rACC may reflect maturing neural substrates of cognitive control that improve the top-down control by the prefrontal cortex over limbic reward and emotional processing—top-down control that ultimately drives the decline of impulsive decision making from adolescence to adulthood. Given that the magnitude of fronto-parietal activation (but not rACC activation) was a significant predictor of behavioral performance during cognitive control, reduced effects of cognitive interference indicated by fronto-parietal recruitment may be a marker of a maturing brain that underlies better cognitive control performance during adolescence. Methodologically, our work illustrates that latent variable modeling can facilitate multivariate repeated measures of fMRI data to be used in complex longitudinal models to critically inform our understanding of the neurobehavioral development of cognitive control and many other functions.