Generalizing Treatment Effect Estimates from Sample to Population: A case study in the difficulties of finding sufficient data

Abstract

Background:

Given increasing concerns about the relevance of research to policy and practice, there is growing interest in assessing and enhancing the external validity of randomized trials: determining how useful a given randomized trial is for informing a policy question for a specific target population.

Objectives:

This paper highlights recent advances in assessing and enhancing external validity, with a focus on the data needed to make ex post statistical adjustments to enhance the applicability of experimental findings to populations potentially different from their study sample.

Research design:

We use a case study to illustrate how to generalize treatment effect estimates from a randomized trial sample to a target population, in particular comparing the sample of children in a randomized trial of a supplemental program for Head Start centers (the REDI study) to the national population of children eligible for Head Start, as represented in the Head Start Impact Study.

Results:

For this case study, common data elements between the trial sample and population were limited, making reliable generalization from the trial sample to the population challenging.

Conclusions:

To answer important questions about external validity, more publicly available data are needed. In addition, future studies should make an effort to collect measures similar to those in other datasets. Measure comparability between population datasets and randomized trials that use samples of convenience will greatly enhance the range of research and policy relevant questions that can be answered.

1. Introduction

Randomized controlled trials remain the “gold standard” for research designs to estimate the effects of interventions. However, a shortcoming of nearly all randomized trials across a variety of fields (including medicine, public health, education, and social program evaluation) is that their measured effects are formally only generalizable to the subjects (e.g., students, patients, service providers) within the trial itself, leaving open the question of whether the intervention would be effective in a different target population. Important policy questions regarding program implementation may involve populations quite different from those in the trial, in which case practitioners and stakeholders must evaluate how well an existing trial can inform a particular policy decision. This issue is of particular relevance given increasing concerns about gaps between research and practice. Recent evidence across a number of fields has indicated that the subjects in a trial are often quite different from the individuals of policy or practice interest (e.g., Humphreys, Weingardt, & Harris, 2007; Rothwell, 2005; Stirman et al., 2005; Westen, Stirman, & DeRubeis, 2006). The topic has received particular attention in mental health. For example, Braslow et al. (2005) found that minorities were often under-represented in studies of psychiatric treatment and Susukida et al. (in press) found that, on average, individuals who participate in randomized trials of drug abuse treatment have higher levels of education and are more likely to be employed than are individuals seeking drug abuse treatment nationwide. In education, Bell et al. (in press) have shown that these differences can translate into bias when estimating population effects.

More formally, randomized trials offer internal validity: unbiased estimation of treatment effects in the sample of individuals in the trial, but do not necessarily offer external validity: “whether the causal relationship holds over variation in persons, settings, treatment, and measurement variables” (Shadish, Cook, & Campbell, 2002, p. 20). Bareinboim and Pearl (2013) define a closely related term, “transportability,” as “a license to transfer causal effects learned in experimental studies to a new population, in which only observational studies can be conducted.” (Bareinboim & Pearl, 2013, p. 107). Cook (2014) gives a broad overview of the challenges in generalizing from one sample to another, including discussion of extrapolation to new settings and contexts. What we are concerned with in this paper is how we can estimate the average treatment effect in a target population of interest, given data from a randomized trial. In other words, how can policy makers and practitioners who want to implement best practices in their programs, schools, and clinics use existing randomized control trial evidence to evaluate the effects of an intervention in their target population? How feasible for practitioners are methods for evaluating the effects of existing randomized control trials in different populations of interest?

In this process, defining the target population is a crucial step, and the choice of target population will depend on the specific policy or practice question of interest; for some questions the appropriate target population may be a national population, for others it may be a more narrow sub-population, such as participants in a federal program in a particular state. (And in fact the same randomized trial may be used to generalize effects to multiple target populations). Throughout this paper we assume that the target population is well-defined and appropriate for the question of interest.

Fundamentally, problems of external validity arise when there are factors that moderate treatment effects and that differ between the trial and the population (Cole & Stuart, 2010; Olsen et al., 2013). If the composition of subjects in the trial differs from that in the population of interest on effect moderators, then the average effect in the trial may not reflect the average that would be observed in the population. Given increasing concerns about external validity (see, e.g., Orr, 2015), statisticians and methodologists have begun to develop statistical methods to assess and enhance external validity. An ideal research process for improving external validity is to begin by formally defining a target population and then carrying out a randomized trial in a sample selected to be representative of that population. However, this sample selection process is generally difficult to carry out and quite rare; Olsen et al. (2013) document that only 7 of the 273 studies in the Digest of Social Experiments (Greenburg & Schroder, 2004) were conducted in random samples from the population of interest. (And in fact in many cases the target population itself is also not well defined). Additional approaches for assessing and enhancing external validity utilize multiple studies on the same intervention (e.g., individual patient meta-analysis that combines multiple randomized trials, or cross-design synthesis, which combines experimental and non-experimental evidence). See Stuart, Bradshaw, and Leaf (2014) for an overview of these design and analysis approaches.

The turn towards an emphasis on external validity is driven by an interest in using the results of internally valid randomized controlled trials to inform practice in other settings and with different target populations. Other papers (as cited above) introduce and illustrate statistical methods for assessing and enhancing generalizability; the current paper examines the practical issues that arise in the process of employing one of the proposed methods for estimating target population treatment effects using a randomized trial sample and population data. In this paper we focus on settings where a single randomized trial has been conducted, and where there is interest in generalizing the results of that trial to a specific target population, but where we do not have information in the population about possible treatment receipt (only covariates and possibly outcomes are available). Some recent work (e.g., Cole & Stuart, 2010; Stuart et al., 2011; O’Muircheartaigh & Hedges, 2014) has proposed reweighting approaches that weight the trial sample to look like the target population on a set of key characteristics. However, there has been relatively little use of those methods and little investigation of how well they perform, or how feasible they are in practice. This paper focuses on the assumptions and data needed to utilize a reweighting method to estimate treatment effects in target populations, and highlights recommendations for the design of future studies and datasets to help facilitate such estimation.

2. Methods

2.1. Formal setting for external validity

We first clearly define the quantity of interest using the concept of potential outcomes (Rubin, 1974). Consider a setting where we are interested in estimating the effect of a supplemental enrichment program for children in Head Start. After identifying the treatment and comparison conditions of interest, the next step is clearly defining the target population of interest. For our case study, detailed further below, the target population is the entire population of students affected by Head Start policies: all children in Head Start programs across the U.S. Each individual in the population of interest has two potential outcomes: their outcome (e.g., a measure of emergent literacy skill scores) if they receive the intervention of interest (e.g., the supplemental enrichment program), denoted Y_1i, and their outcome (emergent literacy skill scores) if they receive the comparison condition of interest (e.g., standard instruction), denoted Y_0i. The treatment effect for individual i is defined as the difference between these two potential outcomes: Δ_i = Y_1i - Y_0i. In this paper, our interest is in estimating the population average treatment effect (PATE), denoted Δ: the average Δ_i across all N individuals in the target population: $\Delta =\frac{1}{N}\sum _{i=1}^N{\Delta }_i$.

In this case study, we utilize data from an existing randomized trial of a supplemental enrichment program, the REDI program, in which children in Head Start centers were randomized to receive the supplemental program or not. Let P_i denote membership in the population of interest (P_i=1 for children in the population and P_i=0 for those in the trial sample). We assume that the same specific individuals are not in both the sample and the population, although a slight modification of the weights defined below allows for the individuals in the sample to be a subset of the individuals in the population dataset, as in Stuart et al. (2011). Let T_i denote treatment assignment in the trial (T_i=1 for intervention, T_i=0 for control). If treatment assignment is randomized, the difference in potential outcomes between the observed treatment and control groups in the trial sample (those for whom P_i=0), $\widehat{\mathrm{\Delta }}={\overline{Y}}_{P=0,T=1}-{\overline{Y}}_{P=0,T=0}$ (where ${\overline{Y}}_{P=p,T=t}$ denotes the sample mean of Y for individuals in population p and treatment condition t), provides an unbiased estimate of the treatment effect in the trial sample, but may not provide a good estimate of the PATE. We define the external validity bias as the difference between the impact estimated in the evaluation sample and the true population impact, $\widehat{\Delta }-\Delta$.

Imai, King, and Stuart (2008) provide a framework for thinking about this bias, decomposing the overall bias when estimating a population treatment effect using an experimental or non-experimental study sample into four pieces: internal validity bias due to observed characteristics, internal validity bias due to unobserved characteristics, external validity bias due to observed characteristics, and external validity bias due to unobserved characteristics. When interest is in estimating the PATE, standard beliefs about a randomized trial being the gold standard design may not hold, if, for example, the external validity bias is larger than the internal validity bias of a small, non-representative randomized trial. This paper focuses on trying to reduce the bias due to observed differences between the sample and population. Cole and Stuart (2010) and Olsen et al. (2013) provide analytic expressions for external validity bias as a function of the extent of treatment effect heterogeneity, and the differences between a trial sample and the target population of interest.

2.2. Measures for assessing external validity

Stuart et al. (2011) and Tipton (2014) propose indices that summarize the similarity between a randomized sample and a population. The Stuart et al. (2011) index is based on the mean difference between the predicted probabilities of participating in the trial, compared between the units in the trial and those in the target population (similar to the idea of assessing propensity score overlap in a non-experimental study). The Tipton (2014) index is based on the Bhattacharyya coefficient (1943), which measures the similarity of the densities of predicted logit probabilities between the trial and population. Tipton (2014) provides some rules of thumb for interpreting the index as a measure of the similarity between the trial sample and the population, and for when the trial is sufficiently similar to the population to enable generalization. In Section 3.2 we illustrate the calculation of these metrics in the case study for this paper.

2.3. Reweighting approach to estimate population treatment effects

In this paper we consider a reweighting approach for equating a randomized trial sample and a target population, with the goal of estimating the target population average treatment effect. It is useful for settings where there is interest in generalizing from a trial to a target population, and the only available data are data from a single trial and covariate data on the population. (If there are multiple trials conducted, other approaches, such as cross-design synthesis, may be more useful). While in this paper we focus on the reweighting approach, other model-based approaches, such as Bayesian Additive Regression Trees (BART; Kern et al., 2016) could be used instead, and would generally have the same data needs as the reweighting approach.

The reweighting approach is related to inverse probability of treatment weighting (IPTW) for estimating causal effects in non-experimental studies, and non-response weighting adjustments for handling survey non-response. The main idea is to weight the randomized trial sample to look like the population of interest on a set of key covariates. The specific procedure is as follows:

1. Create a combined (stacked) data set with the randomized trial sample and the population dataset, with a set of covariates X observed in both groups.

2. Create an indicator variable for being in the target population (P).

3. Estimate a model of membership in the population (P) as a function of the covariates X, e.g., using logistic regression.

4. Create weights for individuals in the trial sample, defined as $w_i=\frac{p_i}{1-p_i}$, where $p_i=P(P_i=1|X_i)$

5. Estimate treatment effects using the individuals in the randomized trial by running a weighted regression of outcome as a function of treatment status and the covariates, with the weights calculated in Step 4.

Details of this process using the case study are provided below.

There are three structural assumptions underlying the reweighting approach investigated (see Stuart et al., 2011, for more details):

(A-1) Given the observed covariates X, every subject in the population has a non-zero probability of participating in the randomized trial. If this were not true, there would be some set of individuals in the population who would not be represented at all in the trial; generalizing to them would require extrapolating outside the range of the data in the trial.

(A-2) Unconfounded sample selection: there are no unobserved variables related to selection into the trial and treatment effects, given the observed covariates X. The implication of this assumption is that we need to observe and adjust for all factors that drive selection into the trial and moderate treatment effects. However, we do not need to adjust for factors that relate to only one of these mechanisms (e.g., a factor that is related to inclusion in the trial but that does not moderate treatment effects).

(A-3) Treatment assignment is random in the trial.

These are important assumptions to consider in any empirical example, and are discussed further in the context of the case study below.

2.4. Data needs for using these approaches

In order to utilize the reweighting approach one must have data on both the randomized trial of an intervention of interest and a specific target population. The necessary data elements from the randomized trial sample include a treatment indicator (treatment vs. control), covariates, and the outcome(s) of interest. In the target population dataset one needs covariate information. Although some approaches, such as BART, can utilize outcome data from the population, the reweighting approach focused on in this paper does not use such data; it only requires covariate data in the population. (And in fact if outcome data on the population is available, methods using BART may be preferable; Kern et al., 2016). If outcome data under the control condition is available in the population (e.g., if the control condition in the trial was “usual care” and no one in the population received the treatment of interest), that data can also be useful as a check on the similarity between the weighted trial sample and the population (Stuart et al., 2011).

For the reweighting approach, covariates within the sample and population datasets must possess sufficient overlap to allow for the generation of a group of “common” covariates that can be used to estimate membership in the target population and that will plausibly satisfy Assumption A-2 above; in particular, the reweighting approach can only adjust the randomized trial to look like the population with respect to observed characteristics. If the trial and population differ on an unobserved variable (or variables) that moderates treatment effects (a violation of Assumption A-2), the estimated PATE will be biased (except in pathological cases where biases caused by different variables may cancel each other out). Because of this, it is generally appropriate to include as many covariates in the set of covariates X as possible; this is similar to the advice in the propensity score literature that it is generally better to err on the side of including covariates rather than excluding them when using propensity scores to estimate treatment effects in non-experimental studies (Stuart, 2010; Myers et al., 2011). It is especially crucial to include likely effect moderators, either based on data analysis of the randomized trial data (e.g., subgroup analyses or other methods for assessing treatment effect heterogeneity) or through a conceptual model of impacts (e.g., which factors program developers think may moderate treatment effects; that conceptual model would also presumably influence the potential moderators measured and examined in the trial). For example, a particular intervention may be hypothesized (or observed in the trial) to be more effective for individuals with particularly low baseline levels of achievement, in which case it would be important to observe those baseline achievement levels in the trial and population.

2.5. Background and selection of the case study

The overall goal of this paper, and thus the selection of a motivating case study, is to illustrate the feasibility of using these newly developed statistical methods for estimating population treatment effects using existing data. A clean and “well-behaved” case study would be one that has a randomized trial conducted with a clear and well-defined target population, and a comprehensive set of covariates available for both the trial and the target population; this is the type of case study often used in papers describing new statistical methods. In contrast, the case study detailed below was not selected because it is particularly “well-behaved” or ideal for the statistical method, but rather to focus on the practical implications and challenges in using the generalizability method in the real world. The growing focus on external validity (Orr, 2015) demands practical examples to illustrate the weaknesses and strengths of our current methods of data collection and statistical methodologies for the purposes of evaluating external validity and estimating treatment effects in populations outside trial-specific samples.

To illustrate the use of these methods for estimating population treatment effects, and their complications in practice, we chose to select a case study in the area of early childhood education. This choice was driven by a growing interest in methods to assess and enhance generalizability in that field (e.g., as exemplified by a 2014 meeting on external validity organized by the Office of Planning, Research, and Evaluation within the Administration for Children & Families of the US Department of Health and Human Services), and the lack of examples of their use in that area. Within the broad field of early childhood education, we chose to focus on interventions that evaluated academic outcomes in order to identify a randomized trial and a target population to illustrate the statistical methods.

Even though significant resources have been invested in making information from randomized control trials in education available to practitioners through resources such as the What Works Clearinghouse and Institute for Education Sciences websites, a search of these and other online sources (detailed in the Appendix), produced few available options for access to randomized trial sample and target population data. The appendix details the process we used, and some of the challenges we encountered in identifying a case study, particularly a lack of public use data from randomized trials and a lack of comparable measures across data sources.

The randomized trial we ultimately identified for our case study was of the Head Start REDI intervention, which involved an enrichment program that included lessons, extension activities, teaching strategies and teacher support. The enrichment was randomly assigned to Head Start classrooms: 44 classrooms were assigned to the intervention or to a control group that consisted of maintaining “usual practice.” The intervention took place over the course of one year in Head Start for 356 four-year-olds. The Head Start classrooms that participated in the REDI study are all located in three counties in Pennsylvania. The outcomes of interest for the REDI study were language development, emergent literacy, and social-emotional competencies. The battery of assessments included child assessments, teacher ratings, parent ratings, and direct classroom observations (Bierman et al., 2008). The study found significant effects of the intervention on 7 of 11 language, emergent literacy, emotional understanding, and social problem-solving skill measures. For our case study we chose to focus on a single academic outcome, the Elision test, a measure of phonological awareness and an indicator of emergent literacy skills, which showed significant positive effects in the REDI trial.

2.6. Selection of the Target Population

In a practical application of the reweighting method, a practitioner or policymaker will have a target population in mind, for which she is interested in evaluating the potential impact of a given intervention. For our case study, we are interested in determining how well the REDI intervention would work for Head Start students across the country. To evaluate the impact of the intervention in a target population, one must obtain data on that population of interest. For the REDI case study two main datasets provide the potential for population level, early childhood data: the Early Childhood Longitudinal Birth Cohort (ECLS-B) study and the Head Start Impact Study (HSIS). Since the REDI trial was conducted in Head Start centers, we chose the Head Start Impact Study as our target population dataset to illustrate the reweighting method. The positive impact from the REDI trial raises the question of whether similar effects would be observed if the intervention were more broadly implemented in Head Start classrooms nationally. The program evaluators argue that their findings of a positive effect of the intervention on students’ literacy skills suggest that, “it is possible to integrate empirically validated strategies for promoting these critical emergent literacy skills in ways that are consistent with Head Start practices” (Bierman et al., 2008, p. 1813). We thus used the nationally representative HSIS dataset available through ICPSR² to evaluate the impact of integrating the REDI intervention in the national Head Start population.

The HSIS is a nationally representative sample of Head Start programs and children (U.S. Department of Health and Human Services, 2010). In fact, the HSIS is itself a randomized controlled trial designed to evaluate the effects of Head Start; it was carried out among centers with waiting lists (to facilitate random assignment) and thus results are formally representative of the population of children in centers with waiting lists. Children who applied for Head Start were randomly assigned, in separate three-year-old and four-year-old cohorts, to the treatment group, which was allowed to enroll in Head Start, or a control group, which could not enroll in Head Start that year. Using the Head Start Impact Study data allows us to evaluate the impacts of REDI in the target population of Head Start eligible students; however, other policy makers or practitioners might be interested in the effects of the REDI program in a different target population. For example, there may be interest in the effects of the REDI intervention on all four-year-olds, including a more socioeconomically diverse population of children than those eligible for Head Start, in which case a nationally representative dataset of children in the U.S., such as the Early Childhood Longitudinal Study - Birth Cohort, would be a more appropriate population dataset.³

3. Results

This section details the use of the REDI and HSIS data to evaluate the generalizability of the REDI program to Head Start-eligible children nationwide, as represented by the HSIS. Given the HSIS sampling, we work from the specific motivating question, “What would the impacts of the REDI intervention have been for children in all Head Start centers in the nation (with waiting lists) in approximately 2002?”

For our analyses we use both the REDI randomized controlled trial sample of four-year-olds enrolled in Head Start centers in Pennsylvania (N=352), and the nationally representative sample of Head Start eligible four-year-olds in the Head Start Impact Study (N=1,983)⁴. For the analyses we utilize the HSIS child base weight, which weights the HSIS sample to be nationally representative. For simplicity in this illustrative case study we will treat the children as the units of analysis (rather than Head Start classrooms or centers); calculation of standard errors accounts for clustering at the center level. To address missing data on covariates and outcomes, we ran a single imputation in each dataset separately (REDI and HSIS), and then appended the datasets to generate the common covariates (detailed below). The largest missing values in the REDI dataset were for mother’s education and mother’s marital status, both with 11% missing values. The Elision outcome variable had 6% missing values, while other common covariates had less than 3% missing values in the REDI dataset.

3.1. Measures

3.1.1. Outcomes

The outcome of interest examined was the Elision assessment of phonological processing from the Test of Preschool Early Literacy (TOPEL).⁵ The Elision test measures the ability to remove phonological segments from spoken words to form other words.⁶ Preschoolers who possess this and other early phonological awareness skills are more proficient in reading skills during first and second grade, even after controlling for vocabulary skills and student IQ (Bryant et al., 1990; Catts et al., 1999). The Elision test showed a significant intervention effect in the REDI program evaluation.

3.1.2. Common covariate measures

In addition to the outcome measure, we were able to create a total of 7 covariates measured comparably across the two datasets: male, race/ethnicity (Black, Hispanic, and White/Other), household size, mother’s marital status, mother’s education level, a baseline measure of the Applied Problems mathematics test from the Woodcock Johnson III, and a baseline measure of the Elision test score.⁷ Some were easily defined, such as child gender, while others we were able to make comparable by combining or altering existing variables in the appropriate datasets; full details on how they were made comparable across the two datasets is provided in Appendix B.

As detailed in Appendix B, 3 covariates required significant editing to generate variable structures that could be applied to both REDI and HSIS, including race, mother’s marital status, and mother’s education. The difficulty in generating common variables for such simple demographic measures demonstrates the importance of survey data collection processes for future applications of the proposed reweighting method and other post-hoc analyses to assess generalizability. When survey items are designed differently, or when surveys collect different types of demographic information, generating common variables can be difficult.

Additionally, some similar constructs in both the REDI and HSIS datasets were measured using different tests or assessments, such that they could not be used to generate common covariates. For example, the HSIS used the Peabody Picture Vocabulary Test (PPVT), while REDI used the Expressive One-Word Picture Vocabulary Test (EOWPVT). Although both assess an ability to use words to describe pictures, the use of different tests made it difficult to make these variables comparable, and ultimately they were excluded from the model.

3.2. Estimation of Weights and Covariate Diagnostics

As a reminder, the generalizability method illustrated in this paper aims to reweight the trial (REDI) sample to look like the target population (HSIS) in order to equate the two samples with respect to a set of observed covariates. To do this, the reweighting method begins with a logistic regression model to estimate the probability of membership in the HSIS target population. The dependent variable is membership in the HSIS population (P_i=1 for individuals in the HSIS target population; P_i=0 for individuals in the REDI trial sample); the model is weighted by the HSIS base weight to reflect the population. Predictors in the model were variables for gender, race, family size, mother’s marital status, mother’s highest level of education, a baseline measure of the Applied Problems mathematics test, and a baseline measure of the Elision test score. The predicted probabilities from this logistic regression model were then used to calculate the weights for the REDI sample, using the equation in Section 2. This weight is used to weight the REDI subjects to resemble the nationally representative HSIS target population; see Kern et al. (2016) and Hirano, Imbens, and Ridder (2003) for more details on this weighting, which is analogous to “weighting by the odds” when estimating the average treatment effect on the treated in non-experimental studies.

Before describing the weights themselves we present the Tipton (2014) and Stuart et al. (2011) measures of similarity between the REDI randomized trial sample and the population of Head Start eligible students. In this case study the Tipton metric was 0.93, a value that implies “very high” generalizability according to Tipton (2014). This interpretation indicates that the REDI sample is like a random sample drawn from the broader Head Start population, at least with respect to the observed covariates. The Stuart et al. (2011) metric produces a less optimistic evaluation of the overlap between the sample and target population, producing an absolute standardized difference in means between the propensity scores for the sample and population of 0.73. This indicates that differences between the sample and population may be large enough to result in unreliable estimates due to extrapolation. The difference between the Tipton and Stuart metrics is potentially consistent with results in Tipton et al. (under review) showing that simply by chance the standardized mean difference can be large in small and moderate random samples. Another explanation could potentially be that given the small size of the study sample relative to the size of the population the average propensity scores are all quite large and clustered around 1 (Figure 1). However, the different results for the two metrics indicate the need for more work to understand the differences between these metrics, and the implications for our conceptualization of external validity.

Figure 1:

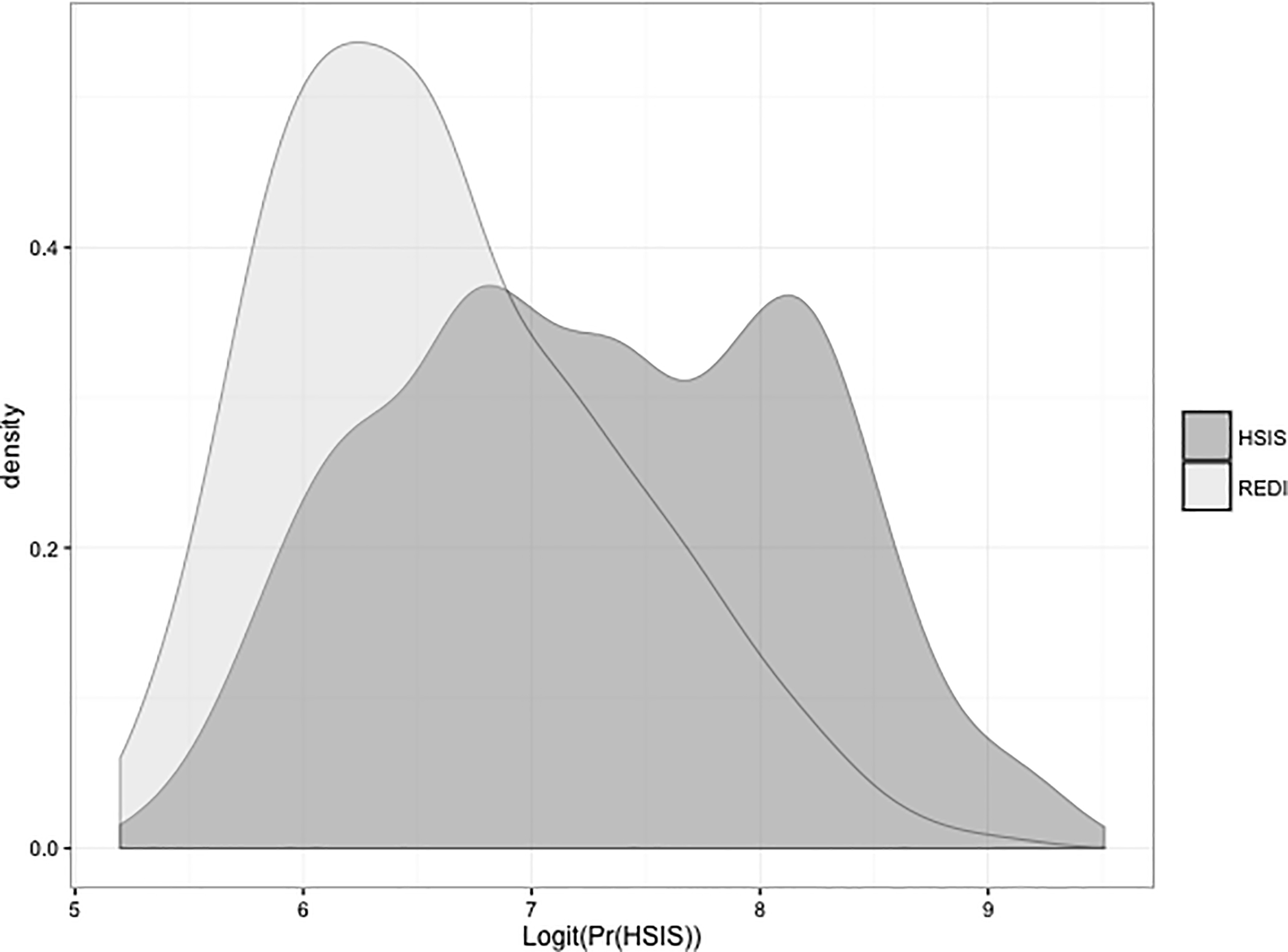
Distribution of logit propensity scores in the REDI sample and HSIS population

The resulting weight included some large values, as can happen with inverse weighting (Schafer & Kang, 2008). To limit the influence of extreme weights, the weights were trimmed at the 95^th percentile, with all values above the 95^th percentile set equal to the value at the 95^th percentile (as in Lee, Lessler, & Stuart, 2011). In particular, 18 cases had their weights truncated to approximately 3000 (the 95^th percentile); the largest weight before trimming was approximately 8000 but most trimmed weights were closer to 4500 before trimming. (Note that the mean of the weights is also large, due to the large size of the HSIS population relative to the REDI sample). It is important to note that a set of individuals with large outlying weights could indicate large differences between the trial sample and the target population, and possibly segments of the population that are not well represented in the trial. This can also be identified through density plots of the propensity scores themselves, as shown in Figure 1. If large areas of non-overlap are found, researchers may need to refine the definition of the target population to reflect a subset for which more reliable generalizations can be obtained; see Tipton et al. (in press) for a strategy for doing so.

In addition to examining the weights, another diagnostic, the standardized mean difference (SMD), can be used to compare unweighted and weighted covariate means between the trial sample and population. The standardized mean difference is calculated as the difference in means between groups (e.g., unweighted REDI sample and HSIS population) divided by the standard deviation of the pooled values; if the weighting is successful the samples should look more similar after the weights are applied. Table 1 compares the REDI and HSIS samples with respect to the 7 commonly measured covariates, before and after the propensity score weighting. In Table 1 “REDI unwt.” refers to the original REDI sample, without the propensity score weights. “REDI wtd.” refers to the REDI sample, but with the propensity score weights applied. Similarly, the SMD columns indicate “unwtd.” and “wtd.” to reflect without and with the propensity score weights, respectively. All HSIS calculations (e.g., the HSIS mean column) use the HSIS base weights to ensure national representativeness, as denoted by the “base wt.” notation.

Table 1:

Comparison of REDI and HSIS samples

Variables	REDI unwtd. Mean	HSIS base wt. Mean	REDI wtd. Mean	Std. Mean Difference unwtd.	Std. Mean Difference wtd.
Male	0.46	0.51	0.44	0.1	0.13
White/Other	0.66	0.32	0.38	−0.71	−0.12
Black	0.16	0.18	0.21	0.06	−0.06
Hispanic	0.19	0.5	0.42	0.63	0.16
Family size	4.59	4.93	4.69	0.19	0.14
Mother married	0.36	0.5	0.42	0.29	0.16
Mother High School Ed.	0.42	0.32	0.31	−0.22	0.02
Mother Postsecondary Ed.	0.28	0.26	0.29	−0.07	−0.09
Applied Standard Score Pre-test	94.88	87.04	89.44	−0.48	−0.15
Elision Pre-Test	8	6.79	7.23	−0.34	−0.12

^*The column labeled “base wt.” use the Head Start Impact Study weight that ensures the mean is nationally representative. “unwtd.” refers to no weighting. The “std. mean Difference wtd.” column refers to weighting by the generalizability population weights defined in Section 2.

The SMD calculations shown in Table 1 generally indicate that there is improved covariate balance after the weighting; most variables show a smaller standardized mean difference following the weighting indicating that the REDI sample looks more similar to the HSIS population. There are a few exceptions, including gender, mother having some postsecondary education, and Black that had mean values after weighting that were slightly further from the HSIS mean as compared with their unweighted means. Although propensity score theory says that in large samples all covariates should see more similarity following the weighting (Rubin & Thomas, 1996), in real data (especially small samples) it is not uncommon for some variables to become more different following the propensity score adjustment. This is particularly common for variables that did not show large differences before the weighting, as we see in Table 1; gender, black, and mother having some postsecondary education had the smallest SMDs before the weighting (and still relatively small SMDs following the weighting). This pattern occurs because the variables showing large differences between the sample and population are the ones that drive the propensity score model; for further discussion of this see Stuart, Lee, and Leacy (2013).

3.3. Estimating the SATE and PATE

In the full evaluation of the REDI intervention, the Elision test was positively and significantly affected by the intervention, with an effect size of $0.35,p=0.001$. In the program evaluation, the intervention effect was modeled using a hierarchical linear model, with child race, child gender, and a pre-intervention score as Level 1 covariates, and site (central or Southeastern Pennsylvania), cohort, and intervention status as Level 2 covariates (Bierman et al., 2008).

For our case study, we can only replicate the REDI evaluation model to a certain extent. We use the common covariates we were able to generate to run a simple regression, using the covariates that were also in level 1 of their hierarchical model: child gender, child race, and the pre-test score for the Elision test. For the analysis, we run two models. First, an unweighted model, to estimate the SATE: the effect of the intervention on the Elision test in the randomized controlled trial sample. Second, a weighted model that uses the weights defined above to estimate the PATE: the effect of the REDI intervention in the target population, the nationally representative population of Head Start eligible 4-year-olds. The standard error calculations use survey methods (Taylor series linearization) to account for the weighting and clustering (see, e.g., McCaffrey et al., 2004).

As a reminder, interpreting the results of the weighted model as an estimate of the PATE requires the three assumptions detailed above:

(A-1) Given the observed covariates X, every subject in the population has a non-zero probability of participating in the randomized trial. The density plot and SMD diagnostics make this assumption seem reasonable in this data, in that generally good covariate balance is obtained, and there is overlap across the range of propensity scores.

(A-2) Unconfounded sample selection: there are no unobserved variables related to selection into the trial and treatment effects, given the observed covariates X. This assumption is likely more questionable in this example, especially given the difficulty in finding common measures. For example, it is plausible that family income would moderate the effects of the program, but this measure is not available for adjustment. Similarly, effects could vary across levels of cognition or other measures of reading or other skills not captured by the Applied Problems standard score pre-test or the Elision pre-test.

(A-3) Treatment assignment is random in the trial. This assumption is satisfied given the conduct of the HSIS.

Table 2 shows the estimates of the SATE and PATE. The SATE estimate is not statistically significant at the alpha = 0.05 level. However, the PATE estimate is larger and marginally significant with a p-value=0.05. This indicates that the REDI intervention, if implemented for the entire target population of Head Start eligible 4-year-olds would have a positive and marginally significant effect on students’ Elision test, an indicator of phonological awareness, if Assumptions A-1 to A-3 are met in this analysis. It should be noted that the more sophisticated estimation techniques used in the original evaluation of the REDI sample do find significant effects for the treatment on students’ outcomes in the randomized controlled trial sample. The more simplistic case study analysis provides some evidence that these positive findings would be replicated if the intervention was scaled up and expanded to all Head Start centers nationally. While in this case study similar conclusions are obtained with respect to the SATE and PATE, this is not guaranteed and other examples may see large differences between the SATE and PATE.

Table 2:

Estimates of the Sample Average Treatment Effect (SATE) and Population Average Treatment Effect (PATE)

Variables	SATE (Std. Error)	p-value	PATE (Std. Error)	p-value
Treatment	0.66 (0.45)	0.16	1.11 (0.54)	0.05
Constant	9.34 (0.70)	0.00	9.56 (0.89)	0.00
N	352		352

One note is that the standard errors of the PATE estimate are larger than those of the SATE estimate, which is common when trying to generalize results from sample to population, in part because of the extrapolation (and thus uncertainty) inherent in doing that generalization. Larger weights, indicating more extrapolation, will make the increase in standard errors even greater.

It is important to note that although the common covariates we generated allow for an estimation of the treatment effect on the Elision post-test score in some capacity, the number of common covariates we were able to produce remains small, limiting our ability to develop the best possible model for generating a weight for the REDI sample to use in these analyses, as discussed further below. However, our model serves as a basic illustration of the reweighting methodology for assessing the generalizability of the effect estimate for the Elision test in the REDI randomized controlled trial, and we find the potential for a positive effect of the REDI intervention in a broader target population.

3.4. Evaluating Effect Heterogeneity

As discussed above, the reason why the SATE and PATE may differ is if there are variables that moderate treatment effects and that differ between the sample and population. Thus, methods to detect treatment effect heterogeneity are inherently related to methods that assess generalizability. To develop a greater understanding of why the PATE estimate may be larger than the SATE estimate in the motivating example, we (post-hoc) examine whether the variables with large differences between the REDI sample and HSIS target population moderate treatment effects. In particular, we investigated whether there is evidence of any effect heterogeneity across racial and ethnic subgroups (White, Black, Hispanic) or across levels of the Applied Problems standard score. The Applied Problems test is a math test that assesses students’ quantitative reasoning and math knowledge. Completing this test requires students to construct mental math models through the use of their language comprehension, calculation, and math skills (Wendling, Schrank, & Schmitt 2007). This was one variable that showed the largest standardized mean differences between the trial sample and the population (Table 1).

To investigate potential effect heterogeneity across these variables we estimated impacts in the (unweighted) REDI sample using three separate models to include interaction terms for Black, Hispanic, and the Applied Problems standard score. The models also included the same covariates from the SATE and PATE estimates: child gender, child race, and pre-test score for the Elision test. For the Applied Problems standard score, we included the Applied Problems pre-test in the model as well as the interaction term of Applied Problems with treatment. We test for effect heterogeneity because we might hypothesize for example, that due to lower scores on the Applied Problems pre-test in the HSIS population (mean=87.0), on average, than in the REDI sample (mean=94.9), weighting the REDI sample to look like the HSIS population could make the impact go up, since individuals with higher impacts (lower applied problems test scores) are more represented in the HSIS population than in the REDI sample.

These analyses, however, demonstrated no evidence of effect heterogeneity across the Applied Problems score or the racial and ethnic categories (Table 3); none of the interaction terms reach statistical significance.

Table 3.

Interaction Terms from 3 Models Predicting Elision scores and examining effect moderation

Interaction Term	Coefficient (Std. Error)	P-value
Treatment * Black	0.14 (1.06)	0.894
Treatment * Hispanic	0.87 (1.00)	0.395
Treatment * Applied Problems Standard Score	−0.06 (0.03)	0.099

Conclusions drawn from subgroup analyses should be interpreted cautiously given that these analyses are beset by the challenges in all randomized trials (Supplee et al., 2013), in particular worries about multiple comparisons and concerns about limited power to detect effect moderators. However, evaluating the possibility of effect heterogeneity is an important step in the analysis process because these analyses may help explain differences between PATE and SATE estimates.

4. Discussion

This paper has provided a case study of using an existing randomized controlled trial, combined with data from a target population of interest, to estimate the population average treatment effect of a treatment condition of interest. Although new statistical methods are promising for estimating population treatment effects using existing data, this paper shows that the feasibility of these methods in more general practice depends on 1) generating relevant population datasets, and 2) ensuring measure comparability between trials and population datasets.

Data availability is crucial for answering questions about generalizability. In particular, data are needed on randomized trials and on target populations for all the important moderators of intervention impact. The data gathering process for this case study involved multiple steps, including evaluating studies for high quality randomized controlled trials and accessing restricted data through license applications or contacting investigators. The small number of publicly available high quality randomized controlled trials with individual level data available is a significant limiting factor to generalizability assessments for policy makers and practitioners. There are many high quality trials that have evaluated interventions in early childhood education, and the results of these studies are collected and made available to researchers and practitioners through tools such as the What Works Clearinghouse and the Institute for Education Sciences websites. As a result, practitioners generally only have access to results valid for the participants in the randomized controlled trial, without the tools necessary to evaluate the external validity of these results and the tools to evaluate the effects of these trials in their particular population of interest. Some data are available through restricted access, including the Head Start Impact Study used in our case study, and in these cases the data licensing step serves as an important component of the data procedures to protecting respondent confidentiality. However, many studies (even those funded through federal grants which frequently include policies for making data publicly available) do not have procedures in place that would allow practitioners or researchers to apply for access to these datasets. Greater access to individual level data from these studies would enhance our abilities to use them to answer questions that may go somewhat beyond the specific aims of the original studies. We note that in K-12 education there is often school level data available (e.g., through the Common Core of Data), which can be used to establish populations of interest, but such data are still often limited in terms of the measures available, which could reduce confidence in Assumption A-2 (no unmeasured effect moderators).

In addition, even when datasets exist and are accessible, many are extremely limited in terms of the overlap of key measures. The key underlying assumption of many of the existing methods for generalizing treatment effect estimates is that the variables that differ between the sample and population and that moderate treatment effects are observed. We had difficulty finding randomized trials and population data that had enough common covariates to make that assumption plausible. In the REDI and HSIS case study we were able to utilize only 7 commonly measured covariates, even though over 75 variables were available in the REDI dataset and several hundred available in the HSIS dataset. This allows us to demonstrate the reweighting method, but the set of covariates is insufficient to avoid concerns about the potential for bias in the PATE estimate. As a result of these concerns, the REDI case study presented here faces the problem of inadequate data to ensure reliable generalization from the sample to the population. The potential for evaluating the effects of local randomized controlled trials in population datasets in the future, depends heavily on establishing common measures across population and trial datasets. Thus, in addition to making data more easily available, researchers should endeavor to collect standard (and standardized) measures in their studies, to help facilitate combining such data with other sources.

Of course the measurement goals of a researcher carrying out a randomized trial are often quite different from the measurement goals of the designers of large population datasets; individuals carrying out an evaluation are often interested in whether impacts are seen on a measure specific to the core components and goals of the intervention. However, we encourage researchers and survey designers to consider the inclusion of a battery of common measures to facilitate the combining of datasets to answer more complex and nuanced research questions. There is increasing interest in such integrative data analysis and data harmonization, and although there is some progress in developing methods that allow the combining of somewhat different measures (e.g., Bauer & Hussong, 2009), a set of common measures can go a long way in making the data more usable. As one model, some fields are moving towards a “common data model,” including initiatives such as the NIH Toolbox (NIH Toolbox CB, 2013), PROMIS (Cella et al., 2007), and PhenX (Hamilton et al., 2011). Orr (2015) argues that evaluators should adopt a two stage model, with Stage 1 used to conduct a streamlined experimental evaluation, with a larger more complete evaluation at Stage 2 for those interventions that show particular promise in Stage 1. For studies that show promise in Stage 1, the inclusion of common measures in Stage 2 may help generate sufficient data for additional analyses of the generalizability of the effect estimates, expanding the potential use of the outcomes of a single trial for practitioners in different settings or serving different populations.

This key underlying assumption that we can adjust for all of the effect moderators (Assumption A-2) also points to the need for more empirical and theoretical work understanding treatment effect heterogeneity. Our confidence in whether or not we can generalize results from a trial to a target population depends on whether we are confident that we have measured the relevant effect moderators. Although there have been recent advances in detecting effect heterogeneity (e.g., Kent et al., 2010; Schochet, Puma, & Deke, 2014; Weiss, Bloom & Brock, 2013), many studies are underpowered to detect effect heterogeneity and more work is needed in this area.

We also highlight that the reweighting approach for equating a randomized trial sample and a target population that we illustrate was developed only recently, and more work is needed to determine when this and other similar approaches work well, and how sensitive the results are to the underlying assumptions. Results in Kern et al. (2016) indicate that when the assumption of no unmeasured effect moderators is satisfied, flexible modeling approaches such as BART or reweighting approaches can work well, but when that assumption is not satisfied neither of the methods performs well. Further work should also consider how to extend these methods to multilevel settings to better account for the clustering of children within sites or schools. Additional work is also needed to evaluate the best methods for analyzing external validity and estimating generalizability under different conditions related to the underlying assumptions. To make these models useful to policy makers and practitioners, clear guidelines about the best-practice models under different conditions will be necessary.

Finally, a premise of the methods discussed here is that there is a well-defined target population. Any discussion of “generalizability” needs to be couched within the question “generalizability to whom?” In addition, a particular randomized trial may be used to generalize effects to multiple target populations (e.g., to individual states, for state-level decision making, or to the nation as a while), and a study may be generalizable to one population but not to another (see, e.g., Tipton, 2014).

In conclusion, as research studies in fields such as early childhood education become more and more rigorous in terms of their internal validity, there is growing interest in also assessing their potential external validity or generalizability. Researchers and policymakers would like to be able to answer more questions from existing data, e.g., whether a policymaker can use the results from a given randomized trial to inform their decision-making for their population of interest (e.g., the Head Start director of a particular state). Statistical methods are beginning to be developed to estimate population treatment effects, but the data to use those methods appropriately are still lacking. That work is important and should continue. However, this paper highlights, in the context of a very real-world example, that even with improving statistical methods, the research field is still far away from being able to confidently generalize results from randomized trials to target populations. And existing data limitations make it difficult to utilize these methods for practical evaluations of the effects of randomized controlled trials in populations of interest. Given the growing interest in generalizability, researchers conducting trials, and entities generating population data, need to incorporate considerations of external validity as part of their decision-making process about study design and data collection. Increased coordination within research fields, to move towards the collection of common measures, will greatly improve the potential for assessing external validity and generalizability, enhancing our ability to make informed decisions about the value of interventions in different settings and with different populations.

APPENDIX A: Identification of case study

To choose a recent randomized controlled trial for the case study, we established our area of interest as studies of early childhood education with an academic outcome measure for literacy or math skills. To locate population data and a randomized trial, we utilized three main websites: the What Works Clearinghouse (WWC)⁸, Inter-university Consortium for Political and Social Research (ICPSR)⁹, and Childcare & Early Education Research Connections¹⁰, with a final check for additional data sources using the Institute for Education Sciences website¹¹. We additionally limited our search to high quality randomized controlled trials, considering only studies in the What Works Clearinghouse that “meet evidence standards without reservations,” and we applied the same type of strict criteria for the design of randomized controlled trials when evaluating other potential study options on the additional websites.

The search for a recent randomized controlled trial study of early childhood education resulted in a list of 16 potential studies. However, several issues narrowed this list. First, some randomized controlled trials evaluated childcare subsidies or funding for pre-school programs. Although these interventions included academic outcome measures, they are less likely to be interventions existing practitioners could easily implement in a different setting. Second, a number of studies focused on non-academic outcomes such as social-emotional development. We chose to turn our attention to studies that included academically oriented intervention programs. Among these studies, a number were focused on subgroups of students, such as students with specific disabilities. Population data on students with specific disabilities can be more difficult to locate (although the Pre-Elementary Education Longitudinal Study (PEELS) does provide a nationally representative sample of children with disabilities.)

In the end, we narrowed our list to approximately six studies that fit our criteria of high quality randomized controlled trials of early childhood academic interventions focused on literacy or mathematics. Of these six studies only one, Project Upgrade, had open access, publicly available data.

Project Upgrade, a two-year randomized controlled trial, tested the effectiveness of three different language and literacy interventions in childcare centers in Miami-Dade County, Florida. We first examined this dataset as a potential case study. The success of the reweighting approach relies on being able to adjust for a relatively large set of covariates that may differ between the trial sample and population and that moderate treatment effects. However, it proved difficult to identify many such covariates between Project Upgrade and a target population dataset. We compared Project Upgrade to the Head Start Impact Study (HSIS; U.S. Department of Health and Human Services, 2002–2006), since both target low-income student populations. However, we found that although on the surface HSIS and Project Upgrade measured similar covariates for children, the studies utilize different specific measures of these covariates at both the classroom level and the individual level. For example, the HSIS classroom observation tool includes the Early Childhood Environment Rating Scale—Revised (ECERS-R), a rating scale that measures the quality of the classroom environment. In comparison, Project Upgrade utilizes a measure called Observation Measures of Language and Literacy Instruction in Early Childhood Education Classrooms (OMLIT). This battery of measures includes a series of questions related to the classroom environment, but the variables are measured differently than those included in the ECERS-R scale. In fact, Project Upgrade documentation includes a footnote indicating that they considered using the ECERS-R and rejected it in favor of the OMLIT, which they perceive to be a better measure of classroom environment and time use related to early childhood literacy. As a result, the two studies have topically similar assessments but a very limited number of common covariates. The two datasets did contain one identical scale, the Arnett Caregiver Rating Scale. However, even though the measure was the same, the Project Upgrade open access data file had the scale score variables already generated, rather than including the individual items. These variables were standardized to have a mean of 0 and a standard deviation of 1, but we believe this standardization used the mean for the Project Upgrade sample, rather than a national mean. As a result, when we generated a standardized score within the HSIS, the two standardized variables were not comparable, regardless of the fact that they had the same standardized mean and standard deviation.

Given the lack of sufficient covariate overlap between the Project Upgrade data and the Head Start Impact Study we turned back to the results of our initial search for early childhood randomized controlled trials, examining the five remaining randomized controlled trial studies of early childhood literacy or math. None of these studies had data that were readily available to researchers, so we contacted the principal investigator for the evaluation of the Research-Based, Developmentally Informed (REDI) intervention in Head Start centers to request data access. We were given permission to use requested parts of the data for a generalizability assessment and coordinated with the principal investigator to receive the necessary data files.

APPENDIX B: Covariate definitions and comparability

This appendix details the creation of the 8 common covariates between the REDI and HSIS samples and how the variables in each dataset were made comparable.

• Male – This variable was generated from a single variable for child’s gender in each of the two datasets.

• Race Dummy Variables – We created common race dummy variables by using multiple race variables in REDI to match the mutually exclusive categorical child’s race variable that was already generated in the HSIS. The HSIS variable was broken into three categories: white/other, Black, and Hispanic. The REDI data contained survey responses that were not mutually exclusive categories; instead, the parents “marked all that apply” when indicating their child’s race. We created a common set of race dummy variables by generating REDI variables to match the HSIS variables. All the white and Black respondents who indicated that they were Hispanic and Latino in the REDI data were coded as Hispanic. All non-Hispanic Black respondents were categorized as Black, and finally, all non-Hispanic white, Asian, and Other respondents were grouped in a white/other category.

• Spanish Speaking – Both surveys ask the parent whether the student spoke Spanish at home, however the REDI survey asks the more general question of whether Spanish is a language used at home, while the HSIS survey asks the more specific question of which language is the primary language spoken at home. Thus, there may be students who speak Spanish in the HSIS dataset, but if they do not use it as their primary language at home they may not be captured as Spanish speaking in this variable. Although this variable was generated as a potential covariate, the variable was ultimately not used in the propensity score model because of its collinearity with the Hispanic race/ethnicity dummy variable.

• Household Size – This common variable was created from two variables in each dataset, a variable counting children living in the household and a variable counting adults living in the household. In both datasets the variables included the focal child and the survey respondent.

• Mother’s Marital Status – The HSIS survey includes a question about maternal marital status. The REDI dataset asked about the respondent’s marital status. In most instances the REDI respondent was the child’s mother, but this was not universally true. So, to generate an equivalent measure in the REDI data we combined several variables. The adult respondent was asked about their marital status, so if the respondent to the REDI survey was female, related to the child as a parent, and indicated that she was married we combined those three variables to indicate that the child’s mother was married.

• Mother’s education – The HSIS data had a specific measure of child’s mother’s highest level of education. In the REDI dataset, we used the highest level of education indicated by the respondent if she was female and related to the child as a parent to generate mother’s highest level of education.

• Applied Standard Score – This is the Applied Problems mathematics test from the Woodcock Johnson III that assesses quantitative reasoning, but the test relies on language comprehension. Both datasets included this measure as a single variable in both the baseline data and post-intervention wave of data collection. We utilize the baseline measure for both datasets.

• Elision Score – Both datasets include a raw score for the Elision measure as a pre- and post-test.