Abstract
As of March 24, 2020, the Food and Drug Administration (FDA) authorized to bleed the newly recovered from Coronavirus Disease 2019 (COVID-19), i.e., the ones whose lives were at risk, separate Plasma from their blood and inject it to COVID-19 patients. In many cases, as observed the plasma antibodies have cured the disease. Therefore, a four-echelon supply chain has been designed in this study to locate the blood collection centers, to find out how the collection centers are allocated to the temporary or permanent plasma-processing facilities, how the temporary facilities are allocated to the permanent ones, along with determining the allocation of the temporary and permanent facilities to hospitals. A simulation approach has been employed to investigate the structure of COVID-19 outbreak and to simulate the quantity of plasma demand. The proposed bi-objective model has been solved in small and medium scales using -constraint method, Strength Pareto Evolutionary Algorithm II (SPEA-II), Non-dominated Sorting Genetic Algorithm II (NSGA-II), Multi-Objective Grey Wolf Optimizer (MOGWO) and Multi Objective Invasive Weed Optimization algorithm (MOIWO) approaches. One of the novelties of this research is to study the system dynamic structure of COVID-19’s prevalence so that to estimate the required plasma level by simulation. Besides, this paper has focused on blood substitutability which is becoming increasingly important for timely access to blood. Due to shorter computational time and higher solution quality, MOIWO is selected to solve the proposed model for a large-scale case study in Iran. The achieved results indicated that as the plasma demand increases, the amount of total system costs and flow time rise, too. The proposed simulation model has also been able to calculate the required plasma demand with 95% confidence interval.
Keywords: Bi-objective stochastic model, Simulation–optimization model, Blood supply chain, COVID-19
1. Introduction
Nowadays we are challenging with the daily increase in natural and man-made diseases. Disease diagnosis is one of the most critical medical issues. Each patient has his or her own course of treatment. In addition to medical treatment, many diseases require humanitarian help such as blood supply. Blood or its components are vitally essential for many patients such as thalassemia suffering individuals, car accident victims and those seriously suffering from Coronavirus Disease 2019 (COVID-19) [1]. The recently discovered coronavirus causes an infectious disease called COVID-19 [2]. This newly-emerged virus and its resulting disease were unknown until the recent outbreak in December 2019 in Wuhan, China [3]. The body immune system works as its defense force. When a virus attacks a human’s body, an army of defense cells including white blood cells are dispatched to fight the virus [4]. To fight against the virus, these blood cells secrete antibodies which remain in the part of blood called plasma forever [5].
The amber yellow liquid part of box, i.e., plasma is composed of water, salts, hormones, clotting factors, etc. and makes up 55% of the blood volume. The most abundant solute in plasma is a group of plasma proteins, including albumins and globulins. Albumins help to increase blood clotting, while globulins protect your body against infections and the same antibodies make your body resistant to COVID-19 [6]. When a person with COVID-19 recovers, a large amount of this antibody is probably in their blood [7]. The promising idea is to take plasma from the recovered people and inject it into the patients with a severe illness. These antibodies stimulate the patient’s immune system to spot and kill the virus [8]. This is not the first time this method has been used to treat patients. In fact, this solution was used many times before to treat diseases such as Severe Acute Respiratory Syndrome (SARS), Middle East Respiratory Syndrome (MERS), and Hemagglutinin Type 1 and Neuraminidase Type 1 (H1N1) pandemic [9].
A report published by [10] revealed that this treatment could be effective in treating SARS and COVID-19 diseases, too. In the blood plasma of the disease recovered patients, some permanent antibodies are produced by the immune system [11]. To isolate the protective antibodies, plasma is tested and filtered and then the resulted liquid is converted into a drug. When injected into a new patient, this derived plasma, or so-called the refined plasma, provide passive immunity until the patient’s own immune system produces antibodies [12]. With the incidence of COVID-19, the request for this product has grown. In addition, some factors like the vitality of the product, its short life cycle and high processing costs besides the problems of collecting, storing and distributing it among hospitals demonstrate the importance of designing an efficient supply chain for blood [13].
Blood is a perishable product playing a vital role in the survival of human beings, especially during the prevalence of COVID-19 [14]. The demand for blood varies in different periods and may increase or decrease. One effective way to tackle this issue is to develop a supply chain which requires an accurate information system and smart planning [15]. If the appropriate amount and type of blood is not available when required, an inadequate blood supply may expose the patients’ lives to danger. Postponing the treatment process due to lack of the suitable blood can also prolong the patient’s hospitalization time [16]. This in turn increases the costs and risks for the patients. On the other hand, an excess blood supply results in blood loss and higher costs. It also raises this question now as to whether we have mistakenly selected the donors by taking inappropriate and unnecessary blood.
Due to being afraid of Coronavirus and the consequent implementation of social distancing and the low level of donor participation, blood donation has unfortunately dropped dramatically during the COVID-19 epidemic. Furthermore, various challenges have hindered voluntary blood donation in this period. Firstly, donors are not going to proactively attend the blood banks or hospitals because of fearing to contact Coronavirus in case of being exposed to the infected patients. Secondly, the staff’s movement at the blood collection centers and the donors getting restricted due to the lockdown has exacerbated the situation. Under such circumstances, it has become necessary to design a coherent supply chain with the potential to monitor the blood centers’ plasma donation and the plasma inventory. Locating the blood collection centers can reduce the supply chain costs and minimize the blood flow time [17]. Thus, to optimally locate the collection centers and allocate them to hospitals can result in providing plasma at the right time and the right place. Of the most significant motivations for doing this research is to save more patients’ lives which can happen by controlling the collected plasma inventory and optimally distributing the plasma.
The demand is considered uncertain at the time of COVID-19 outbreak. Therefore, supply and demand are changing in different time periods. Hence, it is better to divide the planning horizon into smaller time periods. In addition, taking the multi-commodity mode into account makes the planning of plasma supply chain more accurate and closer to the real world. So, investigating the multi-commodity and multi-period mode is another contribution of this research study. In this study, a simulation–optimization model is presented pursuing the goal to design an efficient supply chain for collecting the recovered patients’ plasma and distributing the appropriate amount of plasma at a minimum cost and flow time among the hospitals. The proposed supply chain includes the collection centers, the permanent and temporary centers and the hospitals.
If red blood cells contain an antigen that its antibody exists in a COVID-19 sufferer’s plasma, the red blood cells will clump together and die right after the injection. The red blood cells of blood type “O” lack antigens. As a result, blood type “O” can be injected into all other blood groups. However, a patient of blood type “AB” can receive plasma from all blood groups if needed because the plasma of blood type “AB” has no antibody against other blood types [18]. Therefore, in this study, a priority matrix has been defined so that only the blood compatible with the blood type of a COVID-19 patient is sent to the relevant hospital. This prevents blood shortage and makes the proposed model more flexible [19]. Thus, one of the research contributions is the possibility of substituting different blood types.
The optimum temperature for transporting plasma products is −20 °C or colder [20]. To maintain this temperature during transportation, the proper refrigerator equipped vehicles are required to be selected for transportation. Training the individuals involved in plasma transportation is a must. They need to be trained how to carry and pack and how to deal with some unpredictable events such as cold store failure. Therefore, transportation capacity is limited due to the limited number of the suitable cold refrigerators and trained people during the ongoing prevalent pandemic known as COVID-19. So, one of the novel ideas considered in the present study is the transportation capacity with special conditions of COVID-19 outbreak. Plasma can also be decomposed at any stage, then it is sent to the due disposal center. These innovations allow the models to represent plasma supply chain costs more accurately and optimally design the network. It is also necessary to predict the amount of demand required in the context of COVID-19, that is when the quantity of blood demand is increasing. Predicting the required demand quantity for different blood types can prevent shortage and help obtain the proper amount of blood at the right time.
Moreover, identifying the factors affecting COVID-19 outbreak and examining their interactions can help to unveil the weak and strong points of COVID-19 prevention programs. This structure can be considered as a model for decision makers to prevent the outbreak of COVID-19. Therefore, one of the study novel ideas is to investigate the system dynamic structure of COVID-19 incidence and to estimate the required demand quantity using the simulation approach. The estimated demand is incorporated into the mathematical model as an uncertain parameter and the proposed mathematical model minimizes the plasma flow time and supply chain costs. Therefore, using this approach is a contribution of this paper.
The proposed model has been solved in small and medium scales using -constraint, Strength Pareto Evolutionary Algorithm II (SPEA-II), Non-dominated Sorting Genetic Algorithm II (NSGA-II), Multi-Objective Grey Wolf Optimizer (MOGWO) and Multi-Objective Invasive Weed Optimization algorithm (MOIWO) approaches. As MOIWO outperforms compared with other approaches, it is used for solving the case study of large scale. Among the advantages of using the proposed meta-heuristic algorithms are the following [21], [22]: 1. These algorithms only use the values of the objective function to perform the optimization process and do not require additional information such as the function derivative. 2. Due to the simplicity of the search process, they work very quickly and efficiently. 3. The proposed algorithms are very flexible and well suited for handling all kinds of objective functions and constraints.
The research questions are as it follows:
1. Where are the best locations of the collection centers during COVID-19 pandemic?
2. How are different collection centers’ blood groups allocated, distributed and stored during the outbreak of COVID-19?
3. How can the required amount of plasma be predicted for the patients with COVID-19?
Accordingly, the research objectives include the following:
-
1.
To minimize the total costs of the plasma supply chain during the COVID-19 prevalence, including the total costs of establishing collection centers, processing, transportation and storing blood across the whole supply chain.
-
2.
To minimize blood flow time during COVID-19 outbreak: Blood flow time has a direct impact on the infected ones’ health. Minimizing blood flow time can reduce the incurred loss.
-
3.
To estimate the amount of demand for different required blood types: One of the objectives of this research is to study the system dynamic structure of COVID-19 in order to estimate the required plasma quantity using simulation.
This research has been compiled in 7 sections. In Sections 1, 2, the introduction and literature review are stated, respectively. In Section 3, problem description is presented. In Section 4, the research method, simulation model and mathematical model are dealt with. Furthermore, the solution methods are given in Section 5. The computational results are presented in Section 6. The discussion is presented in Section 7. Finally, the concluding remarks are covered in Section 8.
2. Literature review
The studies about blood products were first introduced by [23]. Nahmias [24] and Sirelson and Brodheim [25] are also among the leading researchers working in this field. Yongming [26] described the blood bank and blood donation service in a small hospital in the earthquake-prone rural area of Indonesia. His objective function was to improve customer satisfaction. He considered the time-window constraint for the transportation of blood as a perishable product.
Hosseini-Motlagh et al. [27] presented a robust mathematical model for managing blood supply chain under uncertainty, the study whose contribution was undertaking motivational initiatives of governments to encourage donors to donate blood. Locating blood distribution centers accompanied with their allocating capacity was one of the objectives of their research. The possibilistic–stochastic optimization was used to solve the proposed model. The results exhibited the presented approach performing satisfactorily. Compared with the research done by Hosseini-Motlagh et al. [27], the advantages of our study are considering different blood types and their substitution priority, and allocating the centers to demand points and examining the flow among the centers. In addition, Hosseini-Motlagh et al. [27] considered deterministic demand, while in our research, demand is estimated by a simulation approach. Goodarzian et al. [28] designed a multi-objective, multi-product, and multi-period medical supply chain model for the distribution, location, allocation, and inventory control problems of required medicine during the outbreak of COVID-19. Also, they considered sustainability as one of their contributions. Medicine demand was also estimated by simulation. They used four meta-heuristic algorithms including ant colony optimization, fish swarm algorithm, firefly algorithm, and variable neighborhood search algorithm as well as developed hybrid meta-heuristic algorithms. Then, the case study was considered in Tehran/Iran. The results indicated that with increasing demand, the amount of released carbon dioxide (CO2) increases sharply. Nagurney [29] proposed a mathematical model to manage the blood supply chain in the COVID-19 pandemic condition. They investigated fixed and elastic demand along with the availability of personnel. Their main aim was to maximize profits in their proposed supply chain. They considered the scenario-based on the inclusion of labor. One of the advantages of our research over Nagurney [29] is the estimation of blood demand by the simulation approach and considering blood substitutability. Rastegar et al. [30] formulated a mathematical model for location and inventory controlling of the influenza vaccine in the outbreak of the COVID-19 pandemic. They considered justice in the distribution of vaccines among high-risk people. Therefore, priority was given to the distribution of vaccines with priority to the elderly. Their main goal was to maximize the minimum delivery-to-demand ratio. Their case study was investigated in thirty provinces of Iran. Liu et al. [31] proposed a mathematical model for distribution management in blood supply chain. The routing of blood transport vehicles plus the management of the blood distribution centers’ inventory were the most important decisions of their research. It is worth mentioning that considering the quality of donated blood was one of the contributions of their model. Minimizing the shortage and loss costs can be viewed as the most critical objective of their research. They employed decomposition-based algorithm to solve the proposed model. In comparison with the study of Liu et al. [31], the merits of our study are locating, allocating and examining blood flow along with substitution priority of different blood groups. Estimating stimulation-based plasma demand is another benefit of our study. Hamdan and Diabat [32] provided a two-level multi-objective model for resilient blood chain design in disaster situations. The destruction of collection centers and transportation routes were among the innovations of their proposed model. They pursued the objectives as minimizing the delivery time of the donated blood and minimizing the supply chain costs. The model was solved by the Lagrangian relaxation-based approach for a case study in Jordan. One of the advantages of our study over Hamdan and Diabat [32] is taking transportation capacity and substitution priority into account. Also, of other merits of our research are minimizing the flow time, allocating centers to hospitals, and estimating the required demand. Dehghani et al. [33] proposed a stochastic mathematical model for blood supply chain management. Considering proactive transshipment and order quantities simultaneously was one of the key novelties in their research. They aimed to minimize loss and shortage costs. The Quasi-Monte Carlo approach was also applied to generate the scenarios. According to the results, the total supply chain costs’ reduction was reported for a case study done in Australian hospitals. Compared with the research carried out by Dehghani et al. [33], our research took the advantage to investigate the transportation capacity and substitution priority accompanied with a real case study. Besides, locating collection centers and allocating centers to hospitals are considered of other study advantages. Araújo et al. [34] provided a two-level model for minimizing costs in blood supply chain. In the presented multi-commodity and multi-period model, strategic decisions were made at the first level and operational decisions at the second level. They simultaneously paid attention to the purchase, shortage and instantaneous perishing of blood were viewed as the novel ideas of their model. The case study was related to a region located in the south of Portugal and the results indicated that as the demand increases, the total supply chain costs significantly increase, too. Relative to the research done by Araújo et al. [34], our study focused on the transportation capacity and substitution priority and estimating plasma demand using simulation. Haeri et al. [35] proposed a multi-objective resilient model for blood supply chain management. One of their model’s objectives was to locate and allocate blood collection centers. The data envelopment analysis was provided to evaluate the efficacy of the designed model. The involved uncertainty was defined by fuzzy numbers and their innovation was to consider the supply chain related resilience. Pursuant to the results, the model performed appropriately for a case study in Iran. Compared with the study done by Haeri et al. [35], the merits of our research are multi-echelon supply chain, plasma inventory control and focusing on substitution priority. Haghjoo et al. [1] designed a reliable blood supply chain. A multi-period robust mathematical model was presented at the time of disaster. Their model’s main objective functions were to locate and allocate blood distribution facilities. The possibility of facilities getting destroyed after the occurrence of a disaster was one of their innovations. The model was solved using self-adaptive imperialist competitive algorithm and invasive weed optimization approaches and the results were compared. Among the differences between our study and that of Haghjoo et al. [1], we can point out plasma inventory control, multi-commodity model, and plasma demand estimation using simulation. Rajendran and Ravindran [36] proposed a stochastic model for managing platelet inventory in blood supply chain. The major goal this study pursued was to minimize blood losses and shortages while dealing with uncertain demand and it involved simultaneously considering scenario-based and stochastic uncertainties. Another novelty of their model was using the Modified Stochastic Genetic Algorithm (MSGA). Hosseinifard et al. [37] investigated the inventory in a two-echelon blood network. They made decision about the location of the temporary care centers requiring to be covered by the blood bases every day. Considering the uncertainty for hospitals’ blood demand, they determined the amount of the daily required blood for each hospital. With respect to the proposed chain’s sustainability being their most important innovation. The main difference between our study and that of Hosseinifard et al. [37] refers to the proposed model being of a multi-period and multi-commodity type accompanied with the collection centers’ location. In addition, our research dealt with substitution priority and transportation capacity. Zahiri et al. [38] proposed a three-level supply chain model for blood network management when disasters occur, where patient satisfaction and transportation capacity were mostly involved as the innovation. The proposed model was tested for a potential earthquake in Iran using NSGA-II algorithm. The simulation of demand amount, the possibility of substituting blood and locating and controlling the collection centers’ inventory are among the differences between our study and their research. Samani et al. [39] presented an integrated blood network model for the situations when disasters happen, in which demand was considered uncertain. The intended objectives were minimizing the transportation costs and minimizing the maximum unmet demand. Finally, a heuristic algorithm was used to solve the stochastic and possibilistic mathematical model. Simulating the amount of plasma demand regarding different types of plasma and the transportation capacity are some of the differences between the research cases we have done and that of Samani et al. [39]. Habibi et al. [40] presented a mathematical approach to manage the relief chain associated perishable products. Their network included blood donors and the temporary, mobile and permanent blood transfusion facilities and they targeted to determine the amount of the accumulated blood and the optimal location of blood transfusion facilities in various scenarios. The objective function was cost minimizing and shortage level. It is worth mentioning that different budget estimation and allocation strategies were their main contribution. Salehi et al. [41] proposed a novel approach for planning how to allocate relief products under disaster occurrence where decisions were related to logistics under the uncertainty of cost. The model was examined for an earthquake in Tehran. The possibility of similar blood substitution, inventory control and distribution of plasma are among the differences between our research and that of Salehi et al. [41]. Ramezanian et al. [42] presented a blood platelets network under uncertainty, in which a model of blood transfusion centers’ location and allocation was formulated. Considering the advertisement cost and experience factor on donors were the innovations of their study. The results revealed the system performance improvement after implementing the model. Masoumi et al. [43] investigated a model of supply chain to minimize blood deterioration and operational costs. The novel idea in their study was examining the synergy of a merger/acquisition in the blood banks. For this purpose, a time window was viewed for the time when blood perishes. Furthermore, demand uncertainty was considered. A large-scale case study suggested that expanding the problem’s dimensions would increase the costs exponentially. Simulating the quantity of the required demand, the possibility of substituting compatible blood types and locating collection centers periodically are some of the differences between our research and that of Masoumi et al. [43]. Fahimnia et al. [17] investigated a model for disaster related circumstances, in which the objective functions were formulated to minimize the blood supply time and the network costs. Using a combined approach of Lagrangian relaxation and -constraint, the model was solved. Examining supply chain utility using new indicators and balancing between time and cost were the fundamental novel ideas of the research. Finally, the model’s performance was measured by a numerical example. Simulating the amount of plasma demand, considering different types of plasma and the transportation capacity are among the differences between our study and that of Fahimnia et al. [17]. Dillon et al. [44] made decision about selecting hospitals in blood supply chain. Considering the uncertainty of blood demand, they identified the amount of daily required blood for each hospital. In their study, the demand was random and several approaches were presented to meet the demand in emergency wards. Considering this point that periodic review policy, blood perishability and lead times, were their basic contributions. Fereiduni and Shahanaghi [45] provided a model for distributing and locating hospitals and blood distribution centers. One of the novelties of their research was to take the uncertainty of demand into account. Meanwhile, comparing the proposed model by the p-robust optimization approach and the robust optimization was another innovation of their study. Inventory control in multi-commodity mode, the due transportation capacity, the possibility of substituting similar blood types, and estimating the demand using simulation are some of the advantages of our study compared to that of Fereiduni and Shahanaghi [45]. Nahofti et al. [46] provided a model for allocating the temporary blood centers for the potential disasters occurring in Tehran. The proposed model was an integer model and the parameters were defined as fuzzy numbers, which was designed to deal with earthquake conditions. The considered contribution involves interactive planning among the supply chain levels. The results reported the model’s performance as appropriate with high reliability. In terms of the differences, we can mention controlling different blood products’ inventory in multi-period mode, considering the transportation capacity and the possibility of substituting similar blood products between our study and that of Nahofti et al. [46]. Arvan et al. [47] studied the blood donation centers’ location. Their model included blood test centers, demand points and blood labs. Their study objective function was to lower the transportation costs and to establish blood centers. Their novel idea was taking the multi-commodity and multi-period mode along with cost uncertainty into account. Since the model was multi-objective, -constraint method was employed for optimization. Numerical examples with small scales were used to validate the model. Simulating the quantity of demand, the possibility of substituting similar blood, and controlling the inventory of blood products are the key differences between our study and that of Arvan et al. [47]. Zahraee et al. [48] examined an algorithm to locate the blood centers involving blood perishing time. The objective was to minimize cost and blood shortage. The case study was associated with Tehran. Based on the results, the model’s efficiency increases as the number of distribution centers rises provided that the problem assumptions are observed. Zahiri et al. [48] investigated a model for allocating the blood network facilities and managing its flow. The proposed model required two planning levels where the first one included technical planning and the second one covered operational planning. Their innovation involved presenting a novel hybrid multi-objective self-adaptive differential evolution algorithm and comparing it with the NSGA-II approach. A probabilistic optimization approach was utilized to solve a randomly-generated example to prove the model’s efficiency. Compared to the research of Zahraee et al. [48], our study related benefits are considering transportation capacity and the possibility of substituting blood types.
It is vividly perceived from the literature that so far no study has been conducted to deal with the plasma supply chain during the outbreak of COVID-19. Also, no efficient method was employed for predicting the blood demand in the previous studies. The reason for this is lack of a study addressing the structure of the system dynamic affecting plasma demand. This issue can lead to better understanding the system and getting to investigate COVID-19 related factors’ interactions. Besides, most of the performed studies have not investigated the transportation capacity, multi-period and multi-commodity model. It has become necessary to pay attention to transportation capacity due to the special conditions of plasma transportation. Moreover, the multi-period nature of the model leads to properly programming for the entire planning horizon which is divided into in shorter periods. The possibility of blood type substitution as a critical issue has not been surveyed in most studies. Ignoring this issue makes the problem unrealistic. Simultaneously integrating the location and allocation of blood facilities, and distribution, inventory control, and plasma flow can bring the problem closer to the real world not being addressed in the previous studies. Table 1 summarizes the detailed characteristics of recent research on the blood supply chain.
Table 1.
A review of literature on blood supply chain.
| Author | Type of model |
Solution procedure |
Model nature |
Decision level |
Commodity |
Objective function |
Period |
Number of echelon |
Constraint |
Application type |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimization | Simulation | Exact | Heuristic | Meta Heuristic | Deterministic | Uncertainty | Location | Inventory | Routing | Allocation | Flow | Distribution | Single | Multi | Coverage | Cost | Distance | time | Single | Multi | Single | Multi | Transportation Capacity | Substitution priority | Numerical Example | Original case study | |
| [41] | x | x | x | x | x | x | x | x | x | x | x | x | |||||||||||||||
| [39] | x | x | x | x | x | x | x | x | x | x | x | x | |||||||||||||||
| [38] | x | x | x | x | x | x | x | x | x | x | x | x | |||||||||||||||
| [37] | x | x | x | x | x | x | x | x | x | x | |||||||||||||||||
| [36] | x | x | x | x | x | x | x | x | x | x | |||||||||||||||||
| [35] | x | x | x | x | x | x | x | x | x | x | x | x | |||||||||||||||
| [33] | x | x | x | x | x | x | x | x | x | x | |||||||||||||||||
| [32] | x | x | x | x | x | x | x | x | x | x | x | x | |||||||||||||||
| [31] | x | x | x | x | x | x | x | x | x | x | x | x | |||||||||||||||
| [30] | x | x | x | x | x | x | x | x | x | x | |||||||||||||||||
| [29] | x | x | x | x | x | x | x | x | |||||||||||||||||||
| [28] | x | x | x | x | x | x | x | x | x | x | |||||||||||||||||
| [27] | x | x | x | x | x | x | x | x | x | x | x | x | |||||||||||||||
| [1] | x | x | x | x | x | x | x | x | x | x | x | ||||||||||||||||
| Current research | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||||||||
According to the literature review, the following items can be considered as the research gaps:
-
1.
The dynamic structure of COVID-19 outbreak and the interactions of influential elements. Defining the structure of COVID-19 pandemic outbreak can help realize the strengths and weaknesses of this disease outbreak control. Also, defining the interactions among the influential elements is the simulation input and estimating the demand for relief supplies requires this structure to be defined.
-
2.
Accurately estimating the stochastic demand by simulation approaches. In most studies, no exact approach is at hand for estimating the demand. And most of the performed studies identified demand as a deterministic or probabilistic parameter by the decision makers based on the historical data. However, in this paper the simulation approach is used to accurately estimate the demand. The proposed simulation can obtain the required plasma demand with high accuracy. Validating the simulation based on the real-world results can prove this claim.
-
3.
Designing a multi-echelon, multi-period, multi-commodity and multi-objective model to minimize costs and blood delivery time for the COVID-19 patients. The demand is considered uncertain at the time of COVID-19 outbreak. Since supply and demand change in different time periods, thus it is better to divide the planning horizon into smaller time periods.
-
4.
Simultaneously making decisions about the location and allocation of blood facilities besides blood inventory control and distribution when COVID-19 breaks out. Proper and optimal location of plasma collection centers can reduce the time period providing service for the patients. Plasma inventory control can also minimize the amount of the perished plasma. Properly distributing plasma can also prevent the shortage of this vital commodity at demand points.
-
5.
The possibility of substituting the donated blood for those suffering from COVID-19. This issue ensures the timely blood units’ availability. Substitution priority can also make the model more flexible and closer to the real world.
Therefore, it can be concluded that the main contributions of this paper are as it follows:
-
1.
Investigating the system dynamic structure of COVID-19 outbreak and the elements’ interactions: Therefore, first off, the indicators affecting the outbreak of COVID-19 are identified and then, the interactions of these indicators are drawn.
-
2.
Estimating the required amount of plasma for COVID-19 patients using simulation, which is performed by Enterprise Dynamic software. One atom is considered for each blood type. Finally, the stochastic demand quantity is estimated as a probability distribution function.
-
3.
Designing a four-echelon, multi-period, multi commodity and bi-objective mathematical model under uncertainty to minimize plasma flow time and supply chain costs: The proposed supply chain levels: (1) Blood collection centers, (2) Temporary blood facilities, (3) Permanent blood centers, and (4) Hospitals (i.e., Demand points).
-
4.
Locating, allocating, inventory controlling, and investigating the plasma flow within the Blood Supply Chain (BSC). Simultaneously focusing on these features can make the model more flexible and closer to the real world. The intended location problem is categorized as discrete. The procedure is as it follows: the optimal locations are selected out of the candidate locations. Also, allocating the collection centers to the temporary centers, the temporary ones to the permanent centers, the permanent centers to the demand points, and the amount of inventory stored in each of these centers are performed. Finally, the amount of plasma flow dispatched to these centers is calculated according to the demand quantity and blood perishability.
-
5.
Validating the simulation–optimization model through a real-world case study, which is the plasma supply chain during the outbreak of COVID-19 in Mazandaran/Iran. The simulation model derived results are compared with those of the real world at a certain confidence interval level.
-
6.
Considering blood substitutability in an optimization model with inventory management: Blood substitution is based on the blood type prioritization Matrix. The blood of the donors with positive types cannot be transferred to those with negative types, but the opposite is possible. For example, someone with blood type “A+” cannot give blood to others with type “A-”, but he/she can receive it.
3. Problem statement
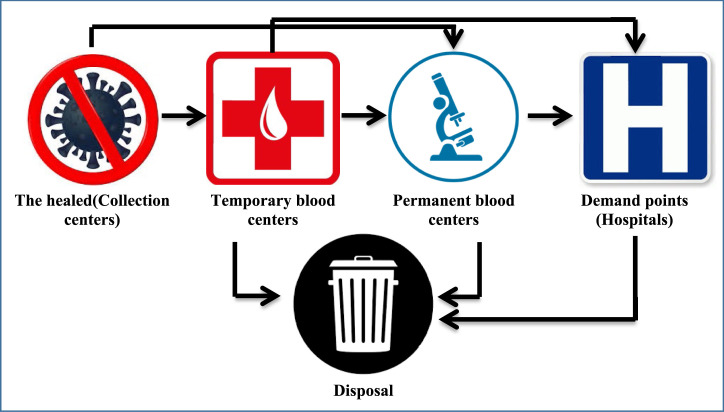
The study blood supply chain network is made up of diverse layers, namely: (1) The blood collection centers, (2) The temporary blood facilities, (3) The permanent blood centers and (4) The Hospitals (i.e., Demand points). The recovered patients can donate their plasma to either the collection centers or the temporary facilities. Blood can be processed both in the temporary and permanent blood centers. The permanent blood centers have more accurate and advance testing equipment and better transfusion technology than the temporary ones. There may be no need for more advanced tests after the initial tests in the temporary blood centers. Therefore, the received blood may directly go from the temporary centers to the intended hospital. However, the blood received by the temporary centers may be transferred to the permanent centers for further tests. In some cases, due to lack of sufficient plasma in the received blood, it is rejected and disposed. Due to the insignificant rate of rejection it has been considered negligible in our model. The blood may also be disposed due to its expiration, so the FIFO (First In, First Out) method is used as the inventory policy to reduce the disposal level (See Fig. 1).
Fig. 1.
Blood supply chain structure during COVID-19 outbreak.
If the collection center’s donated blood has the desired plasma, it is sent to a permanent center. Otherwise, the received blood will be dispatched to the temporary centers for additional tests. If the required plasma is available at this stage, it is sent to the intended hospital; otherwise one of the two following conditions occurs. If no useful plasma is found, it is disposed, and if some plasma is achieved, it is dispatched to a permanent center for further testing. The initial inventory in this center is zero based on the nature of the problem.
If the accepted plasma is accessible in the permanent center, the plasma is sent to the hospital; otherwise, it gets disposed. The objective of this problem is to determine the location and the number of blood collection centers as well as the amount of plasma collected in the collection centers, the temporary and permanent ones. The allocation of collection centers to the temporary and permanent centers and the allocation of permanent and temporary centers to the hospitals are also other objectives of this research. Finally, determining the expired blood quantity is another important goal of the proposed model.
4. Research methods
The research method consists of 6 sections including the research type, the data collection method, the data analysis method and the research steps. This section also describes the simulation model and the mathematical model.
4.1. Research type
This research is applied in terms of purpose, a field research with a case study in terms of method, quantitative in mathematical and simulation model in terms of data. The present research purpose is applied, its method is a field research with a case study and the data are qualitative in the mathematical model and blended in the simulation model.
4.2. Collecting data method
The research data were collected from 7.01.2020 to 7.08.2020. The research area is Mazandaran province of Iran. The required data were obtained from some reliable sources, Google Map, the historical data and the interviews with the authorities of the hospitals and the blood transfusion organization, etc.
4.2.1. Qualitative vs. quantitative data
The data used in the mathematical model are quantitative. The data include information on holding costs, the initial blood inventory of the centers, the transportation time and costs, the centers’ capacity, blood lifespan, and the maximum number of the established collection centers. The data used in the simulation are blended (qualitative and quantitative). The data such as the COVID-19 outbreak relevant risks are qualitative and the data including the hospital capacity, loss rate and transmission rate are qualitative.
4.3. Data analysis method
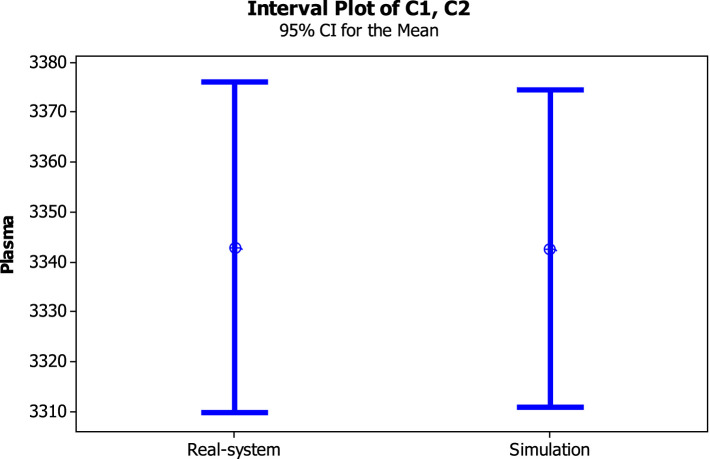
Enterprise Dynamic 8 software was employed for computer based simulation and BARON solver of GAMS 25.1.2 software was used to solve the problems in small and medium scales. Furthermore, the NSGA-II, SPEA-II, MOGWO and MOIWO approaches were applied to solve the numerical examples and the MOIWO was employed to solve the case study in MATLAB R2020b v9.9.0.1495850 software. All tests were run on a computer with an Intel Core i5-8250U 1.60 GHz CPU and 8 GB RAM. The sensitivity analysis was used to analyze the mathematical model. In the sensitivity analysis of the model parameters, the effect of changing the model parameters on the problem outputs was investigated. Also, to analyze the simulation model, the simulation results were compared with the real-world data under a certain confidence interval.
4.4. Research steps
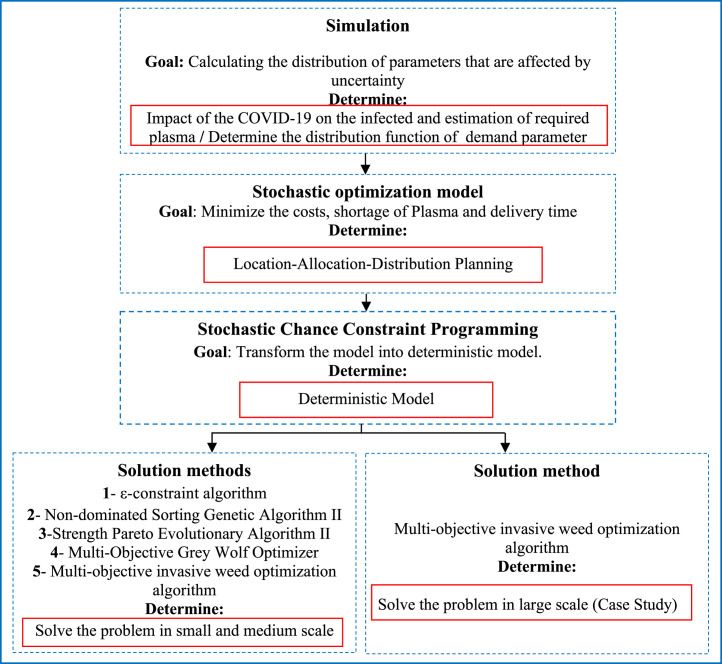
Fig. 2 depicts the research framework. In the first step, the conceptual model was drawn for estimating the number of people infected with COVID-19, and the plasma demand distribution function was estimated using a simulation approach and Enterprise Dynamic software. It should be noted that the demand distribution function enters the mathematical model as a parameter. In the second step, the stochastic mathematical model was presented in order to minimize the logistics costs and delivery time of plasma to hospitals. The main goal of the mathematical model by locating plasma collection centers is to plan the distribution of the collected plasma. In the third step, a stochastic chance constraint programming approach is used to convert the proposed stochastic model into a deterministic counterpart. Finally, in the fourth step, the problem is solved in small and medium scales using -constraint, NSGA-II, SPEA-II, MOGWO and MOIWO approaches, which were compared using the performance evaluation indicators of multi-objective models. In the fifth step, the outperformed algorithm was selected to solve the case study.
Fig. 2.
Research Framework.
4.5. Simulation model
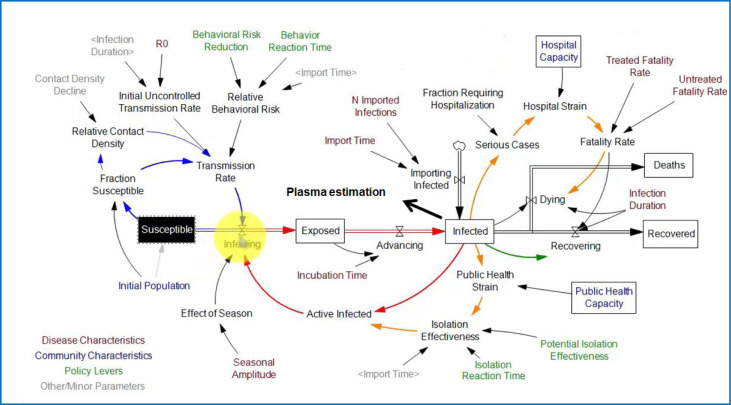
In Fig. 3, the conceptual model for COVID-19 epidemic based on the Systems Dynamics approach is observed [49]. Accordingly, four types of stock variables were used, which include “deaths, the infected, susceptible and recovered”. The auxiliary variables include “Hospital capacity strain index”, “Fatality rate” and “Contacts rate”. The parameters include “Serious cases”, “Disease duration”, “Infectivity”, “Incubation time”, “Hospital capacity”, “Fraction requiring hospitalization”, “Isolation effectivity”, “Post-Isolation effectivity” and “Smart Isolation effectivity”.
Fig. 3.
The framework of simulation model using Enterprise Dynamic software for COVID-19 outbreak.
Enterprise Dynamic (ED) software is a powerful computer simulation software reported to have many successful applications in solving various problems. This software can customize a variety of complex models using atom module and 4DScript codes. 4DScript is the programming language of ED software which uses 4DScript codes written inside each atom to simulate various problems [50]. Fig. 4 displays the simulation model of the designed system dynamic structure using Enterprise Dynamic software for COVID-19 pandemic. The considered Performance Measures (PFM) include AvgContent (cs) and output (cs), which calculate the output entity of the system. The output entity shows the amount of distribution functions of the required plasma demand. The simulation approach is a separate run and the warm-up period is 100,000 h. The warm up period is the time that the simulation will run before starting to collect results [51]. This allows the Queues (and other aspects in the simulation) to get into conditions that are typical of normal running conditions in the simulated system [52]. Separate run is a type of simulation run that performs a different number of runs simultaneously and reports the results on average. The observation period is considered as 1,000,000 h.
Fig. 4.
System dynamic model for COVID-19 epidemic.
As shown in Fig. 3, 28 server atoms, one source and one sink were to simulate the structure of COVID-19 outbreak. It is worth mentioning that the plasma server calculates the quantity of the required plasma based on the number of the infected people.
The 4D Script code corresponding to this atom is as it follows. In this code, one plasma unit stands for each of the infected people.
The proposed 4DScript code counts the average number of the entities inside an “infected” atom. One plasma unit is considered for each entity. Therefore, the simulation model estimates the (demand for blood type in hospital in period ) parameter. Then this parameter enters into the mathematical model as an input.
4.6. Mathematical model
The sources of the indices, parameters and variables viewed in this research are based on the study assumptions and some previous studies. For example, the inventory control parameters and variables are defined based on the studies performed by [37] and [9]. Also, the allocation related parameters and variables are derived from the research conducted by [37]. The idea for the flow related parameters and variables are taken from the model proposed by [35]. The remaining indices, parameters and variables are considered based on the current research assumptions and COVID-19 situations to make the proposed model more realistic. Table 2 includes the sources of the variables, parameters and indices.
Table 2.
Sources of variables, parameters and indices.
In this subsection, the model assumptions are described as the following:
-
1.
There are some candidate locations where the blood collection centers () could be established by imposing a fixed cost ().
-
2.
Different blood groups () are considered. There is also the possibility to substitute the usage of a specific blood type with other ones based on the predetermined priority ().
-
3.
Storing blood among the periods at the permanent (), the temporary blood centers () and the hospitals () is allowed and costly. However, the inventory level is not permitted to surpass the storage capacity (, , ).
-
4.
At the beginning of the planning horizon (), some blood inventory is available in the collection centers () and the temporary blood centers ().
-
5.
Travel time (, , , ) and transportation cost (, , , , ) between the representative points of the blood centers and hospitals are estimated based on the geographical distance.
-
6.
It is possible to substitute blood types in the hospital if needed ().
-
7.
The process time (, , ) and cost (, , ) of each blood unit vary in different centers and hospitals.
-
8.
Transportation of blood between the centers and hospitals (, , ) is subjected to the identical transportation capacity () among all centers. The number of the temporary () and permanent centers () and hospitals () are constant during successive periods.
-
9.
Each collection center is represented by the point located in the center of the corresponding area. Also the maximum number of the collection centers is limited ().
-
10.
The demand quantity for plasma () is taken as stochastic. Plasma demand is the output of the simulation model that is entered into the mathematical model as a parameter.
4.6.1. Indices, parameters and decision variables
| Indices | |
| Blood types | |
| The candidate location for establishing blood collection centers | |
| Hospitals | |
| Permanent blood centers | |
| Temporary blood centers | |
| Time periods | |
| Parameters | |
| Blood holding cost at permanent blood center i | |
| Blood holding cost at temporary blood center | |
| Blood holding cost at hospital | |
| Demand for blood type in hospital at period ood holding cost at h | |
| Available inventory of blood type in collection center | |
| Available inventory of blood type in temporary blood center | |
| Travel time from collection centers to temporary blood center | |
| Travel time from temporary blood center to hospital | |
| Travel time from collection centers to permanent blood center i | |
| Travel time from permanent blood center i to hospital | |
| Travel time from temporary blood center to permanent blood center i | |
| Transportation cost from temporary blood center to hospital | |
| Transportation cost from collection center to temporary blood center | |
| Transportation cost from permanent blood center i to hospital | |
| Transportation cost from collection center to permanent blood center i | |
| Transportation cost from temporary blood center to permanent blood center i | |
| The operation cost of a unit of blood in a temporary blood center | |
| The operation cost of a unit of blood in a permanent blood center i | |
| Operation time per unit of blood in all collection centers | |
| Fixed cost for establishing a collection center | |
| Rate at which process is redirected from temporary blood centers to permanent centers | |
| The time required to substitute a unit of blood type with blood type at hospital | |
| Maximum capacity for transportation between centers | |
| Operation cost of a unit of blood in a collection center | |
| Operation time per unit of blood at temporary blood center | |
| Operation time per unit of blood at permanent blood center i | |
| Blood storage capacity of temporary blood center | |
| Blood storage capacity of permanent blood center i | |
| Blood storage capacity of hospital | |
| Maximum number of collection centers to be opened | |
| Substitution priority for using blood type b instead of blood type | |
| 1 if blood type can substituted by blood type , 0 otherwise | |
| A big number | |
| Blood lifespan | |
| Decision Variables | |
| Amount of blood type expired in hospital at period | |
| Amount of blood type expired in temporary center at period | |
| Amount of blood type expired in permanent center i at period | |
| Amount of blood type transferred from temporary center to permanent center i at period | |
| Amount of blood type transferred from temporary center to hospital at period | |
| Amount of blood type transferred from permanent center i to hospital at period | |
| Amount of blood type processed at temporary center at period | |
| Amount of blood type tested at permanent center i at period | |
| Amount of blood type stored at permanent center i at period | |
| Amount of blood type stored at temporary center at period | |
| Amount of blood type stored at hospital at period | |
| Amount of blood type substituted with blood type at hospital at period | |
| 1 if blood transfer is opened from permanent center i to hospital at period , 0 otherwise | |
| 1 if collection center is allocated to temporary center at period , 0 otherwise | |
| 1 if collection center is allocated to permanent center i at period , 0 otherwise | |
| 1 if a collection center is opened in location at period , 0 otherwise | |
| 1 if blood transfer is opened from temporary center to hospital at period , 0 otherwise | |
| 1 if blood transfer is opened from temporary center to permanent center i at period , 0 otherwise | |
4.6.2. Mathematical model
According to the presented assumptions and notations, the model is formulated as it follows. The proposed model is able to determine the allocation of the blood donor groups (i.e., blood collection centers) to the temporary or permanent blood facilities, the allocation of the temporary centers to the permanent blood centers, the allocation of the permanent blood centers to the hospitals, and the location of the blood collection centers. Furthermore, the inventory levels of blood products kept by the collection centers, temporary centers, permanent centers and hospitals during each period are identified (See Box I).
| (1) |
| (2) |
Box I.
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
The first objective function minimizes the total costs. The first part minimizes the collection centers’ establishment costs, the second part minimizes operation cost, the third part minimizes transportation costs and the fourth part minimizes blood holding costs. Whereas the second objective function minimizes blood flow time to COVID-19 patients. The intended time includes operation time and travel time.
Constraints (3), (4) determine the amount of blood processed and tested in the temporary centers and permanent centers. Also, constraints (3), (4) relate the flow variable and the allocation variable. Constraint (5) specifies the number of the opened collection centers in each period and limits it to a maximum number. Constraints (6)–(8) determine the amount of blood expired in the permanent centers, temporary centers, and hospitals, respectively. These constraints calculate the quantity of blood stored at each permanent center, temporary center, and hospital at exactly L periods back minus the amount of consumption in that period minus the amount of the blood sent to the hospitals. This is to ensure that the FIFO (First In, First Out) policy is assigned to minimize the expired blood. Constraints (9), (10) ensure that each collection center can be assigned to only one center, either temporary or permanent, respectively. Constraint (11) calculates the amount of blood dispatched from the temporary centers to the permanent centers. Constraints (12)–(14) calculate the amount of blood of each type stored in the hospitals, temporary centers, and permanent centers at each period, respectively. Constraint (15) indicates that each blood collection center can simultaneously supply blood to only one temporary center or permanent center. Hence, controlling the collected plasma inventory and the optimal plasma distribution can save many patients’ lives, which is one of the key motivations for this research. Thus, Constraint (15) relates the location variables to the allocation variable. Constraints (16)–(18) restrict the amount of blood transferred among the centers to the maximum capacity of transportation. Also, Constraints (16)–(18) associate the flow variables with the location ones. Constraints (19)–(21) indicate that the amount of blood stored in the temporary centers, permanent centers and hospitals should not exceed their storage capacity. Constraint (22) ensures that enough blood is supplied to the hospitals to satisfy the demand of COVID-19 patients. Constraints (23)–(24) specify the type of decision variables.
5. Solution methods
Stochastic Chance Constraint Programming, -constraint, NSGA-II, MOGWO and MOIWO approaches deployed to solve the mathematical model are described in this section.
5.1. Stochastic chance constraint programming
Stochastic Chance Constraint Programming is utilized to convert a stochastic mathematical model into a deterministic counterpart [53]. This approach is a well-known widely used method introduced by Charnes and Cooper [54]. A successful application of this method can be seen in [55]. Consider the following minimization model with the parameters , , and , where the symbol indicates uncertainty of the related parameter. In general, the probability of a constraint’s occurrence is defined as implied in constraint (25) [56]:
| (25) |
Therefore, the model is rewritten as follows:
| (26) |
| (27) |
| (28) |
| (29) |
A summary of the results of Chance Constraint Programming for minimization and maximization problems is as Eqs. (30)–(32).
| (30) |
| (31) |
| (32) |
Based on the Constraints (30)–(32), the multi-objective chance constraint model at % confidence level for the Constraint (12) is defined as Eq. (33):
| (33) |
Therefore, due to the uncertainty of parameter () in constraint (12), Constraint (33) is replaced by Constraint (12).
5.2. -constraint Method
-constraint is a broadly applied method to get the exact solutions for multi-objective problems [57]. Plenty of successful applications have been reported to solve various problems for this method [58]. The general form of this algorithm is as defined by Eqs. (34), where X is the feasible set of the mathematical model [59]:
| (34) |
5.3. Design of the NSGA-II algorithm
The main features of the Genetic Algorithm are multi directionality and global search by maintaining a population of the appropriate solutions from one generation to the next generation [60]. Generation-by-generation approaches are useful when considering Pareto solutions [61]. In the following, the main mechanism behind the NSGA-II algorithm similar to that employed by [62] is described in detail.
5.3.1. Chromosome structure
In the proposed chromosome structure, there are h (h 1,…,H) hospitals, j (j 1,…,J) candidate locations for the establishment of collection centers, t (t 1, …,T) periods, i (i 1,…,I) permanent centers and k (k 1,…,K) temporary centers. Due to the presence of 13 segments in the structure of the defined chromosome, only 3 segments are explained in detail and the rest is described similarly. Thirteen chromosome segments are defined separately for the variables (1) , (2) , (3) , (4) , (5) , (6) , (7) , (8) , (9) , (10) , (11) , 12) , and 13) .
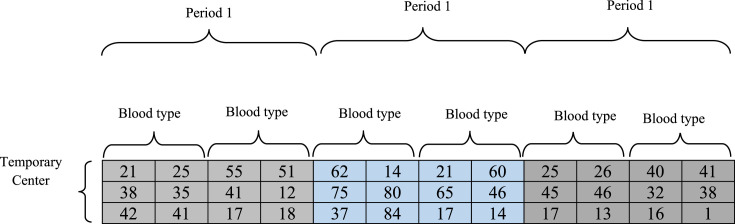
The first segment consists of two sections. The right section shows the variable . The numbers inside each gene are also equal to the amount of the expired blood units of type in hospital at period . The left section shows the variable . The numbers inside each gene also indicate the inventory level of blood type at hospital in period (See Fig. 5).
Fig. 5.
Chromosome segment 1 representation.
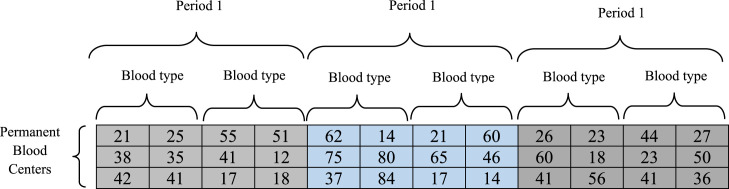
The second chromosome segment consists of three sections. The right, middle and left sections show variables , and , respectively. Accordingly, the numbers inside each gene related to the temporary center at period indicate the amount of the expired blood units of type , the amount of the processed blood type and the inventory level of blood type , respectively (See Fig. 6).
Fig. 6.
Chromosome segment 2 representation.
The third chromosome segment consists of three sections. The right section shows the variable . The numbers inside each gene are equal to the amount of the expired blood units of type in the permanent center i at period t. The middle section represents the variable .The numbers inside each gene indicate the quantity of blood type tested at the permanent center i in period t. The left section demonstrates the variable . The numbers inside each gene are equal to the inventory level of blood type at the permanent center i in period t (See Fig. 7).
Fig. 7.
Chromosome 3 Representation.
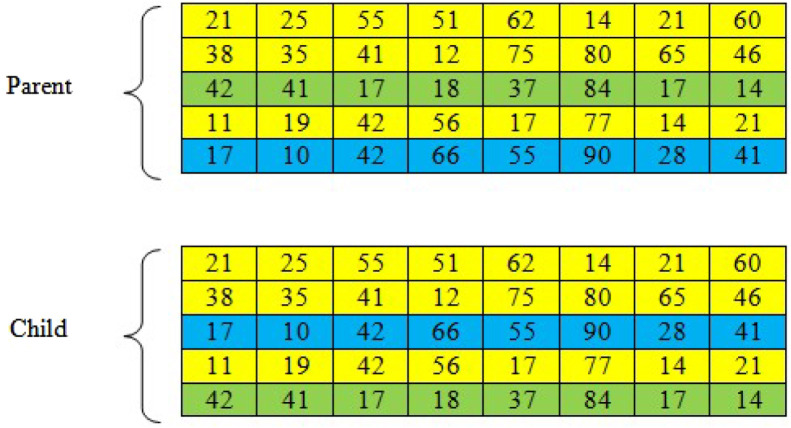
5.3.2. Reproduction operators
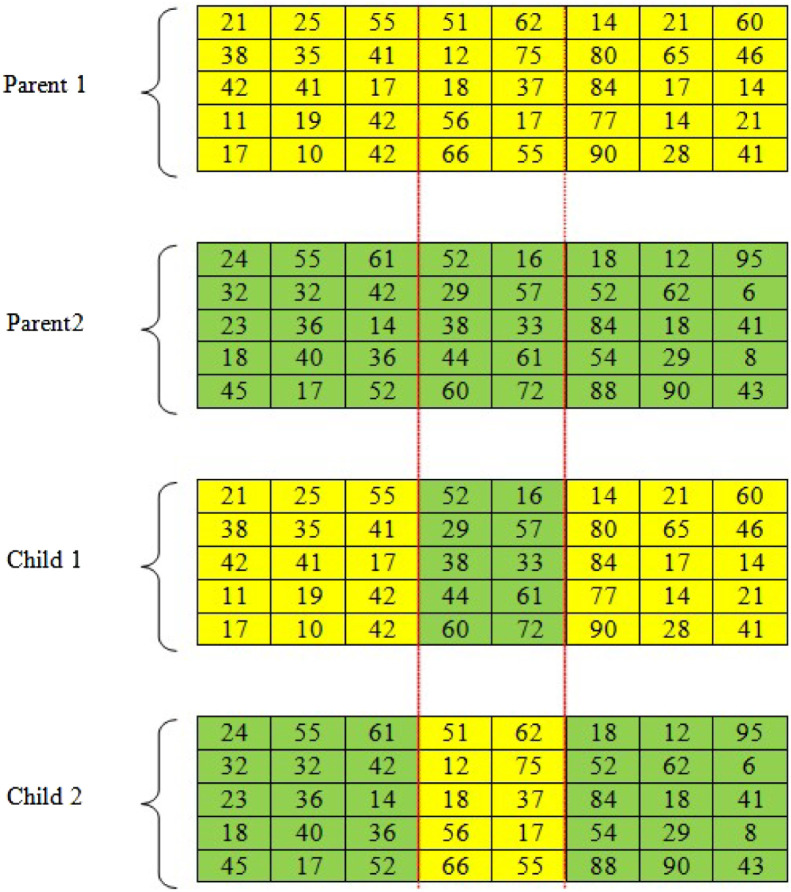
The initial solution in the genetic algorithm is generated randomly. A double-point crossover operator is designed for generating off-springs based on a crossover probability. Fig. 8 illustrates the proposed crossover operator’s schematic.
Fig. 8.
Double-point crossover.
As seen in Fig. 9, the mutation operator is used according to the mutation rate. Two rows are randomly selected in the chromosome. Then, a swap operator changes the alleles.
Fig. 9.
Mutation Operator.
The tuned configurations of the parameters for NSGA-II are listed in Table 3.
Table 3.
The parameters of NSGA-II algorithm.
| Population size | Crossover rate | Mutation rate | Max iteration |
|---|---|---|---|
| 100 | 0.4 | 0.04 | 100 |
5.3.3. Constraint handling strategy
Some of the model constraints including the constraints (1)–(19), (21)–(24) are satisfied regarding the corresponding chromosome structure, but for the rest of the constraints, the penalty strategy is used in case of the constraint violation. For example, the calculation of the violation penalty for the constraints (19)–(21) is formulated as it follows. The index p is the number of the objective functions.
| (35) |
| (36) |
| (37) |
The total value of the violation penalty for a specific designed chromosome is equal to the sum of the violation penalties for all violated constraints. According to Eq. (38), the value of the violation penalty is dynamic and varies according to the iteration value. The iteration number increase results in the value of the violation penalty raise [62].
| (38) |
And at last, the final value of the objective function for a penalized chromosome is calculated as given by Eq. (39).
| (39) |
Therefore, as perceived Equation (39) is dynamic. The objective function does not get worse if the penalty amount is zero; but if an amount of penalty is imposed, according to its value, the objective function exacerbates during successive iterations and the corresponding solution will have less chance to be selected for the next populations.
5.4. SPEA -II Algorithm (Strengthen Pareto Evolutionary Algorithm-II)
The SPEA algorithm, initially introduced by [63], is an evolution of the SPEA-II algorithm approach proposed by [64]. This algorithm uses two internal and external population archives. The external archive is empty at the beginning. After evaluating the objective functions of the internal population, all non-dominated solutions of the current population of the internal archive are transferred to the external archive. The external archive is moved to the next iteration. In each iteration, if the number of the members of the external archive is less than the predetermined size, the non-dominated solutions of the internal archive of that iteration and the external archive of the previous iteration are hired to complete the rest of the population. There are lots of reports supporting the successful applications of this method in solving various industrial and non-industrial problems [65]. This method consists of some steps as the following:
Step 1: Generate the initial population , then generate a population of size N, and a null eternal file , then set the generation count as .
Step2: Define the individual fitness of population and external file .
Step 3: Define ; if the archived Pareto size of is over the max limit , cut the size to ; but if the size of is less than , join the dominated Pareto in the and to the until the size of gets equal to .
Step 4: If , output the external file as the final Pareto frontier, and stop the search; otherwise, turn to step 5.
Step 5: Select the individuals from for the mating pool.
Step 6: Run crossover and mutation for the individuals of the mating pool and the population , let , turn to step 3.
5.4.1. Chromosome representation
In this step, each chromosome is represented by the length , where H indicates the number of the hospitals and I represents the number of the permanent centers. The first string of the numbers is composed of H+I non-repeating random natural numbers. The second string also consists of I random numbers demonstrating the locations of the permanent centers. The following figure presents the SPEA-II algorithm’s chromosome structure for a network with 2 permanent centers and 5 hospitals.
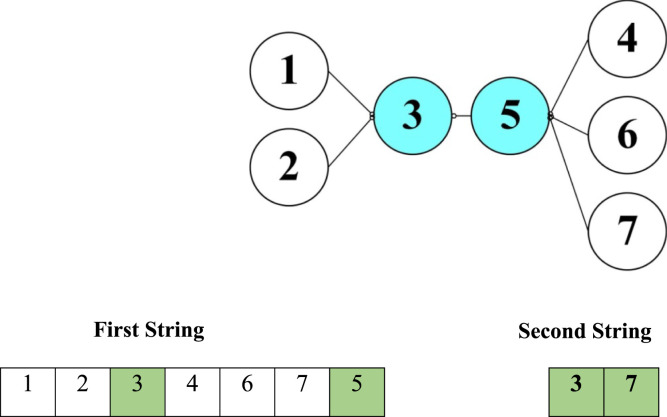
In Fig. 10, the sequence of the first string’s numbers is between 1 and 7. To display this chromosome, two points 3 and 7 were randomly selected as the permanent centers. Areas 3 and 5 which are inside cells 3 and 7 are then identified as the permanent centers of the first string. In the first string, each permanent center is allocated to the genes on the right side. For example, permanent center 3 is allocated to hospitals 1 and 2 and permanent center 5 is allocated to hospitals 4, 6 and 7. One of the advantages of this method is that the probability of infeasible solution is reduced. A similar chromosome is also drawn for the temporary centers and collection centers, of course not described here. In this algorithm, the same crossover and mutation operators considered for NSGA-II method are also used. The tuned configurations of parameters for SPEA-II are listed in Table 4.
Fig. 10.
Coding structure of SPEA-II.
Table 4.
The parameters of SPEA-II algorithm.
| Population size | Crossover rate | Mutation rate | Max iteration | External file |
|---|---|---|---|---|
| 100 | 0.3 | 0.03 | 100 | 50 |
5.5. Multi-objective Grey Wolf Optimizer
Multi-Objective Grey Wolf Optimizer inspired by social life and gray wolf hunting as a novel swarm intelligence algorithm proposed by [66], employs four types of wolves to simulate leadership hierarchies. The leaders of the group, namely, a male and a female called Alpha are in charge of making decisions about hunting, sleeping location, waking time, and so on. Alpha decisions are dictated to the group. Interestingly, Alpha is not necessarily the strongest member of the group but it is the best member in terms of group management. The second level in the gray wolf hierarchy is Beta. Beta Wolf acts as the consultant of Alpha and the group organizer. Beta executes Alpha’s commands in the group and refers its feedback to Alpha. Omega has the lowest rank among the gray wolves. Omega is the last group of the wolves allowed to eat. If a wolf is not Alpha, Beta or Omega, it is called Delta. Delta Wolf is responsible to report to Alpha and Beta, but dominates Omega. Gray wolf hunting has three stages of tracking, chasing and approaching the prey.
5.5.1. Encircling prey
To model the social hierarchy of wolves, the best solution is considered as alpha and the second and the third best solutions are considered as beta and delta. The rest of the candidate solutions are considered as omega. The optimization is driven by Alpha, Beta and Delta, and the fourth group follows these three groups. To model the encircling behavior of wolves, Eqs. (40)–(41) are utilized.
| (40) |
| (41) |
| (42) |
| (43) |
where t refers to the number of the current iterations, and are the coefficient vectors, is the hunting position vector and is the position vector of a wolf. Eqs. (42), (43) are used to calculate the vectors. Vector “a” decreases linearly from 2 to 0 during the iteration period in both the exploration and exploitation phases. is a random vector between 0 and 1. Due to vectors and being random, the wolves can randomly change their position inside the space encircling the prey using Eqs. (42), (43).
5.5.2. Hunting
The wolves update their position using the following equations.
| (44) |
| (45) |
| (46) |
| (47) |
| (48) |
| (49) |
| (50) |
5.5.3. Attacking prey
The attack or exploitation phase, which occurs when the prey stops, is done by reducing the value of variable “a” from 2 to 1. The value of is also dependent on “”, so it decreases. As the value of decreases, wolves are forced to attack the prey. The value of is also a random numerical vector in the range [0,2]. This random value strengthens () or weakens the effect of the prey position in determining the distance. This vector is the effect induced by the obstacles that prevent approaching the prey in nature.
5.5.4. Constraint handling
Penalty strategy is used for constraint handling. The penalty considered for constraints (51)–(53) is formulated as it follows. “P” is the number of the objective functions.
| (51) |
| (52) |
| (53) |
Eq. (58) is used to calculate the amount of total penalty:
| (54) |
5.5.5. The parameters of MOGWO
The results of parameter setting are presented in Table 5:
Table 5.
The parameters of MOGWO.
| Parameters | Value |
|---|---|
| Initial value of | 0.5 |
| Number of search agents (NSA) | 80 |
| Maximum number of iterations (MaxIt) | 1000 |
The initial value of is 0.5, the number of search agents is 80 and the maximum number of the iterations is 1000.
5.6. Multi-objective Invasive Weed Optimization algorithm
The Invasive Weed Algorithm was primarily introduced by [67]. Kundu et al. [68] modified this algorithm and introduced Multi-Objective Invasive Weed Optimization algorithm. Weeds are some plants whose invasive growth is a major threat to crops. Weeds are very stable and adaptable to changes in the environment. As a result, this algorithm tries to be inspired by the power of adaptability and randomness of weed populations. The steps of the Multi-Objective Invasive Weed Optimization algorithm are as the following:
5.6.1. Generating initial population
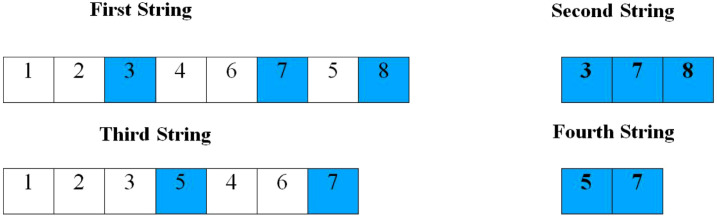
For this purpose, a string with the length of is defined for the temporary and collection centers. Index j indicates the number of collection centers and k indicates the number of temporary centers. Three points 3, 7 and 8 have been selected as temporary centers. Each temporary center is allocated to its left-side box, the collection centers. For example, in string 1, temporary center 7 is allocated to the collection centers 4 and 6. The way the cells of the collection centers are filled is ascending which reduces the possibility of infeasible solutions. String 2 identifies the allocated temporary centers. The third string has the length of . Index i indicates the number of permanent centers and h shows the number of hospitals. In string 3, the hospital 5 is allocated to permanent centers 1, 2, 3 and the hospital 7 is allocated to permanent centers 4 and 6. String 4 also identifies the allocated hospitals. Fig. 11 shows the coding structure of MOIWO.
Fig. 11.
Coding the structure of MOIWO.
5.6.2. Seed propagation based on the fitness value (reproduction)
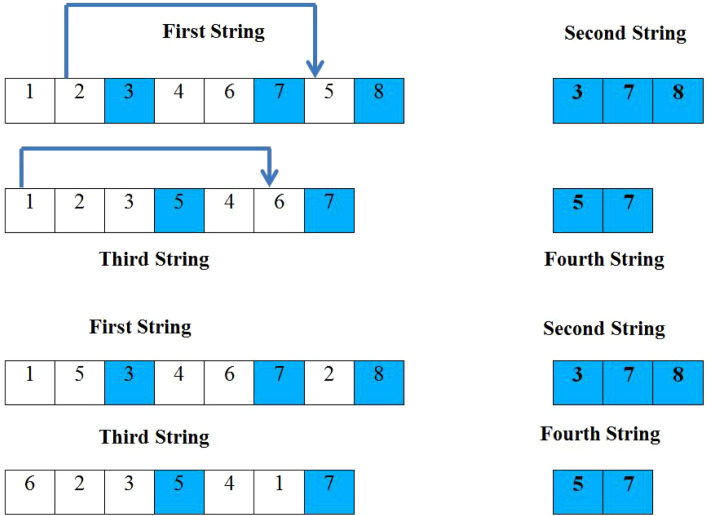
All produced weeds should be evaluated and ranked based on their fitness values. The higher the weed’s fitness, the more seeds it produces. For reproduction, two points are randomly chosen and then their corresponding cells are replaced. Fig. 12 depicts the reproduction process.
Fig. 12.
Reproduction process.
5.6.3. Constraint handling strategy
Penalty strategy is used for constraint handling. The penalty Constraint (55) as follows.
| (55) |
5.6.4. Calculating the number of producible seeds
| (56) |
where
5.6.5. Competitive exclusion
If the total number of plants reaches , all of them are sorted and the extra plants (with less fitness) are removed. Finally, by returning to step seed propagation, entire procedure is repeated until the stopping criterion is satisfied.
5.6.6. Stopping criterion and tuning of parameters
In this study, the MOIWO algorithm will stop if one of the following conditions occurs:
-
•
Reaching a certain number of iterations (Max Iteration)
-
•
A certain number of iterations in which no improvement occurs in the objective functions value.
The results of parameter setting are presented in Table 6:
Table 6.
The parameters of MOIWO.
| Parameter | Value |
|---|---|
| Initial numbers of populations (n-pop) | 100 |
| Maximum number of seeds (S-max) | 3 |
| Minimum number of seeds (S-min) | 0 |
| Initial value of standard deviation () | 0.4*n |
| Final value of standard deviation () | 2 |
| Nonlinear modulation index (n) | 4 |
6. Computational results
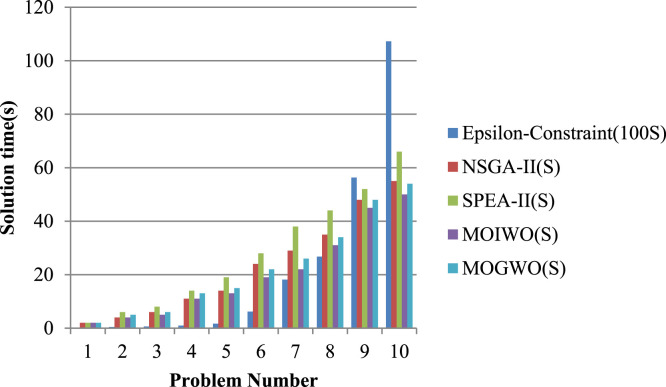
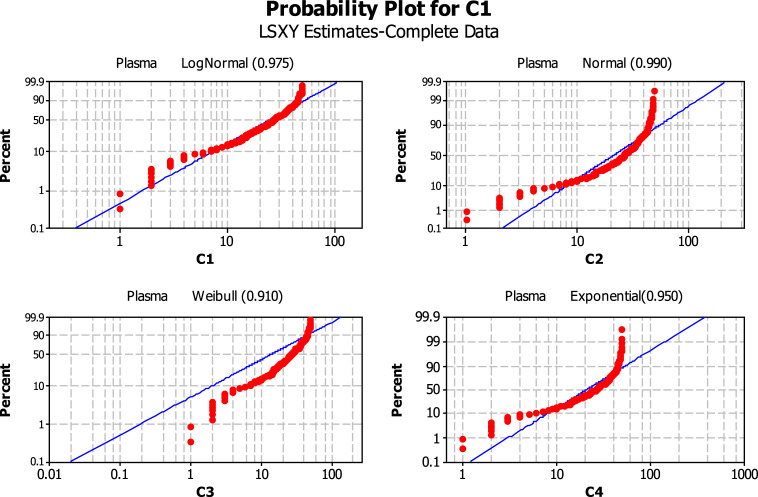
Firstly, the effectiveness of the NSGA-II, SPEA-II, MOGWO and MOIWO algorithms is compared to that of -constraint and is discussed in this section. Secondly, the Pareto solutions obtained by solving a real world case study are presented.
6.1. Investigation of the solution approaches efficiency
In this section, NSGA-II, SPEA-II, MOGWO, MOIWO and -constraint approaches are compared with each other for small and medium scale problems. The dimensions of 10 test problems used for comparing two approaches are given in Table 7. Instances 1 to 5 are small-scale problems and instances 6 to 10 are medium-scale ones.
Table 7.
The problem instances for comparing approaches.
| Problem number | Collection centers | Temporary centers | Permanent centers | Hospital |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 2 |
| 2 | 2 | 1 | 1 | 3 |
| 3 | 1 | 2 | 1 | 3 |
| 4 | 1 | 2 | 2 | 2 |
| 5 | 2 | 2 | 2 | 2 |
| 6 | 3 | 2 | 2 | 3 |
| 7 | 4 | 2 | 2 | 4 |
| 8 | 3 | 1 | 3 | 3 |
| 9 | 4 | 3 | 2 | 5 |
| 10 | 4 | 3 | 3 | 6 |
Table 8 shows the range of sampling data for solving small and medium-scale samples.
Table 8.
The range of sampling data ($ dollars, S seconds, L Liter).
| Parameters | Range | Parameters | Range | Parameters | Range | |
|---|---|---|---|---|---|---|
| U(5,10) $ | U(100, 200) $ | U(2000, 3000)S | ||||
| U(300, 400)L | U(5,10)$ | U(700,800)L | ||||
| U(10, 20)L | U(5, 10)$ | U(800,99)L | ||||
| U(2000, 3000)S | U(2000,3000)S | U(600,700)L | ||||
| U(1500,2500)S | U(5000, 6000) $ | U(4, 10) | ||||
| U(2000,3000)S | U(0.2,0.3) | U(2000, 3000)S | ||||
| U(200, 300) $ | U(300, 400)S | U(250, 350) $ | ||||
| U(300, 400) $ | U(100,150)L | |||||
| U(200, 300) $ | U(5, 10)$ |
Table 9 shows the average values for two objective functions (i.e., columns and ) of 10 Pareto solutions obtained by solving the considered instances. The relative gap column represents the gap between the values of each of the objective functions yielded by NSGA-II, SPEA-II, MOGWO, MOIWO and the optimal ones achieved by -constraint method.
Table 9.
Pareto solutions and corresponding values of objective functions.
| No |
-constraint |
NSGA-II |
SPEA-II |
Relative gap % (NSGA-II) |
Relative gap % (SPEA-II) |
||||||||
| Time (s) | Time (s) | Time (s) | |||||||||||
| 1 | 16615.3 | 40.3 | 2 | 16615.3 | 40.3 | 2 | 16615.3 | 40.3 | 2 | 0 | 0 | 0 | 0 |
| 2 | 16621.1 | 44.8 | 45 | 16630.2 | 44.8 | 4 | 16640.6 | 44.9 | 6 | 0.05 | 0 | 0.09 | 0.22 |
| 3 | 16711.2 | 46.6 | 63 | 16719.8 | 46.8 | 6 | 16731.25 | 46.9 | 8 | 0.05 | 0.4 | 0.08 | 0.63 |
| 4 | 16719.0 | 50.1 | 96 | 16724.3 | 50.9 | 11 | 16731.14 | 51.2 | 14 | 0.03 | 0.7 | 0.07 | 0.58 |
| 5 | 16808.6 | 52.1 | 164 | 16842.4 | 52.2 | 14 | 16848.84 | 52.4 | 19 | 0.2 | 0.1 | 0.23 | 0.57 |
| 6 | 29462.2 | 68.9 | 617 | 29470.6 | 70.9 | 24 | 29484.24 | 71.0 | 28 | 0.02 | 2.8 | 0.07 | 2.95 |
| 7 | 29479.8 | 70.8 | 1814 | 29486.6 | 71.7 | 29 | 29496.24 | 70.9 | 38 | 0.02 | 1.2 | 0.05 | 0.14 |
| 8 | 29540.6 | 73.3 | 2674 | 29543.6 | 73.5 | 35 | 29550.25 | 73.7 | 44 | 0.01 | 0.2 | 0.03 | 0.54 |
| 9 | 29570.3 | 73.5 | 5629 | 29581.2 | 73.9 | 48 | 29593.41 | 74.1 | 52 | 0.03 | 0.5 | 0.07 | 0.80 |
| 10 | 29608.3 | 74.1 | 10725 | 29634.4 | 74.5 | 55 | 29661.87 | 74.8 | 66 | 0.08 | 0.5 | 0.18 | 0.93 |
| Ave | 23113.6 | 59.4 | 2182.9 | 23124.8 | 59.95 | 22.8 | 23135.31 | 60.0 | 27.7 | 0.049 | 0.64 | 0.087 | 0.73 |
| No | MOIWO |
MOGWO |
Relative gap % (MOIWO) |
Relative gap % (MOGWO) |
||||||
| Time (s) | Time (s) | |||||||||
| 1 | 16615.3 | 40.3 | 2 | 16615.3 | 40.3 | 2 | 0 | 0 | 0 | 0 |
| 2 | 16625.6 | 44.8 | 4 | 16628.7 | 44.8 | 5 | 0.027 | 0 | 0.045 | 0 |
| 3 | 16714.5 | 46.7 | 5 | 16716.8 | 46.7 | 6 | 0.019 | 0.214 | 0.033 | 0.214 |
| 4 | 16722.0 | 50.5 | 11 | 16724.1 | 50.8 | 13 | 0.017 | 0.314 | 0.030 | 0.436 |
| 5 | 16831.1 | 52.2 | 13 | 16838.3 | 52.3 | 15 | 0.133 | 0.191 | 0.176 | 0.682 |
| 6 | 29466.7 | 69.4 | 19 | 29468.5 | 69.8 | 22 | 0.015 | 0.720 | 0.021 | 1.289 |
| 7 | 29484.3 | 70.9 | 22 | 29484.9 | 71.0 | 26 | 0.015 | 0.561 | 0.017 | 0.281 |
| 8 | 29543.2 | 73.4 | 31 | 29543.5 | 73.5 | 34 | 0.008 | 0.136 | 0.009 | 0.272 |
| 9 | 29576.9 | 73.7 | 45 | 29578.8 | 73.8 | 48 | 0.022 | 0.271 | 0.028 | 0.406 |
| 10 | 29619.5 | 74.3 | 50 | 29628.4 | 74.5 | 54 | 0.037 | 0.269 | 0.067 | 0.536 |
| Ave | 23119.9 | 59.6 | 20.2 | 23122.7 | 59.7 | 22.5 | 0.0293 | 0.267 | 0.0426 | 0.411 |
As seen, the average relative gap for the NSGA-II, SPEA-II, MOIWO and MOGWO algorithms is less than 1%, revealing the proper performance of these approaches. The solution time for NSGA-II, SPEA-II, MOIWO and MOGWO algorithms is less than that of the -constraint approach in all cases. Comparing the results of NSGA-II, SPEA-II, MOIWO and MOGWO algorithms demonstrated the relative gap value for MOIWO algorithm being lower than that for NSGA-II, MOGWO and SPEA-II in all cases. Also, the average solving time in MOIWO algorithm is less than that of other algorithms in all cases. So it is concluded that the MOIWO approach performed better than SPEA-II, NSGA-II, and MOGWO and can be used to solve a case study of large scale.
Fig. 13 shows the solution time in small and medium-scale problems. As given, the solution time of -constraint method as an exact algorithm increases remarkably as the problem scale increases. Also, the solution time of NSGA-II, SPEA-II, MOGWO and MOIWO algorithms is less than that of the -constraint. Comparing the solution time of MOIWO and other algorithms revealed the outperformance of MOIWO approach, therefore this algorithm is picked as the superior one.
Fig. 13.
Computational times.
6.2. Comparing algorithms’ performance
In this study, two criteria known as Spacing Metrics (SM) and Mean Ideal Distance (MID) are applied in order to compare the performance of the applied algorithms.
Spacing Metric (SM): This metric is used to investigate the non-dominated solutions’ uniformity [69]. Eq. (57) formulates this metric:
| (57) |
where is the Euclidean distance of two Pareto points, is the mean Euclidean distance and n is the total number of the points. It is obvious that the lower the value of this metric, the better the performance of the algorithm.
Mean ideal distance (MID): MID refers to the distance between the Pareto points and the ideal points [63]. This metric is calculated by Eq. (58).
| (58) |
where n is the total number of Pareto points and is the j-th value of the objective function for the th Pareto point. Also, and are the maximum and minimum Pareto values of the th objective function. Obviously, the lower the value of this metric, the better the performance of the algorithm.
In Table 10, the results produced by solving the problems in small and medium scale for 10 Pareto points are given. This table shows two metrics MID and SM plus the solution times. As seen, the mean values of MID and SM for the MOIWO approach are 5.181 and 0.561, respectively and those of MID and SM for the SPEA-II and NSGA-II approaches are 5.802, 0.747 and 5.211, 0.577, respectively and those of MID and SM for the MOGWO approach are 5.197 and 0.567 respectively. Therefore, the MOIWO method outperformed other approaches in terms of MID and SM metrics for all Pareto solutions. Consequently, the MOIWO algorithm was chosen to solve the real case study of large scale.
Table 10.
The results of performance metrics.
| No | NSGA-II |
SPEA-II |
MOIWO |
MOGWO |
||||
|---|---|---|---|---|---|---|---|---|
| MID | SM | MID | SM | MID | SM | MID | SM | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 5.57 | 0.64 | 6.28 | 0.70 | 5.53 | 0.62 | 5.55 | 0.61 |
| 3 | 5.63 | 0.67 | 6.28 | 0.71 | 5.59 | 0.63 | 5.61 | 0.65 |
| 4 | 5.72 | 0.61 | 6.34 | 0.75 | 5.70 | 0.61 | 5.71 | 0.61 |
| 5 | 5.76 | 0.62 | 6.37 | 0.78 | 5.73 | 0.60 | 5.74 | 0.61 |
| 6 | 5.79 | 0.64 | 6.45 | 0.84 | 5.74 | 0.62 | 5.77 | 0.64 |
| 7 | 5.86 | 0.64 | 6.50 | 0.88 | 5.83 | 0.63 | 5.83 | 0.63 |
| 8 | 5.88 | 0.64 | 6.58 | 0.90 | 5.85 | 0.61 | 5.88 | 0.62 |
| 9 | 5.92 | 0.65 | 6.60 | 0.93 | 5.89 | 0.64 | 5.91 | 0.64 |
| 10 | 5.98 | 0.66 | 6.62 | 0.98 | 5.95 | 0.65 | 5.97 | 0.66 |
| Mean | 5.211 | 0.577 | 5.802 | 0.747 | 5.181 | 0.561 | 5.197 | 0.567 |
6.3. Blood supply chain case study
Mazandaran is a northern bound province in Iran, which is made up of 21 cities consisting of nearly 60 counties with a population of more than 3 million [40], [75]. Nowadays, Mazandaran province consists of 17 permanent centers, 3 of which are considered as the base centers of blood transfusion. In addition, Mazandaran province has 6 blood transfusion buses serving as the collection centers carrying out blood transfusion operations in 14 cities. The number of the ones recovered from Coronavirus in this province is reported as 1300 until 7.1.2020, and the main goal is to receive blood plasma from the recovered ones and inject it into the suffering patients. As demand points, the Province Blood Transfusion Organization is responsible for receiving, testing and storing blood to meet the demands of the care centers and hospitals at the time of COVID-19 pandemic. There are 47 hospitals and care centers in Mazandaran province and the Blood Transfusion Organization should supply their blood needs. In order to cover the demand in a timely manner, the Blood Transfusion Organization plans how to select and establish new blood centers in the candidate cities, namely, Behshahr and Babolsar.
It is worth noting that not all plasma types are decent for every COVID-19 patient. The Plasma Priority Matrix is used to determine the Plasma substitution priorities as represented in Table 11 which describes the types of plasma with the potential to be substituted with a certain plasma type. When considering plasma substitution, additional cross-matching tests need to be performed.
Table 11.
Prioritization Matrix.
| Blood type | Priorities |
||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| A+ | A+ | A- | O+ | O- | |||
| A- | A- | O- | |||||
| B+ | B+ | B- | O+ | O- | |||
| B- | B- | O- | |||||
| AB+ | AB+ | A+ | B+ | A- | B- | O+ | O- |
| AB- | AB- | A- | B- | O- | |||
| O+ | O+ | O- | |||||
| O- | O- | None | |||||
Table 12 lists the simulation parameters and variables. Some parameters are assumed by the decision makers based on the case study scale, and the rest is derived from other mentioned sources. For instance, the population of Mazandaran is 3,100,000 and the contact rate is assumed to be 60 contacts/person.
Table 12.
Simulation parameters and variables.
| Name | Definition | Initial value | Units | Reference |
|---|---|---|---|---|
| Hospital capacity | Maximum number of beds in a hospital | 28000 | Beds | [70] |
| Contacts rate | Number of people a person who is infected and not quarantined can meet (only two ways of physical contact and transmission through sneezing and coughing are considered) | 60 | Contacts/person | Assumed |
| Susceptible | The number of susceptible people who are more likely to be infected | 3’100’000 | People | [70] |
| Fatality rate | The ratio of people who die to the total number of infected | 4 | % | [71] |
| Disease duration | The time when the first symptoms of the disease appear | 14 | Days | [72] |
| Fraction requiring hospitalization | The ratio of people hospitalized to the total number of infected | 20 | % | [71] |
| Infectivity | The possibility of engaging the lungs during disease | 0.025 | % | [73] |
| Incubation time | Duration of disease latency | 7 | Days | [74] |
Table 13, Table 14, Table 15 presents the capacity of the collection centers, temporary centers, and the permanent centers, respectively. Table 16 displays transportation cost between the collection centers and the temporary centers. Table 17 demonstrates the transportation cost among the blood centers and hospitals, the capacity of each hospital and blood holding cost.
Table 13.
Collection centers capacity (Liter).
| Babolsar | Babol | Juybar | Sari | Neka | Behshahr | |
|---|---|---|---|---|---|---|
| Period 1 | 160 | 170 | 200 | 160 | 190 | 180 |
| Period 2 | 200 | 160 | 140 | 200 | 100 | 160 |
Table 14.
Capacity of the temporary centers.
| Babolsar | Juybar | Behshahr |
|---|---|---|
| 60 | 50 | 45 |
Table 15.
Capacity of the permanent blood centers.
| Babol | Sari | Neka |
|---|---|---|
| 1000 | 1000 | 800 |
Table 16.
Transportation cost between the collection centers and temporary centers ($).
| Temporary center | Collection center |
|||||
|---|---|---|---|---|---|---|
| Babolsar | Babol | Juybar | Sari | Neka | Behshahr | |
| Behshahr | 78 | 72 | 48 | 28 | 17 | 4 |
| Juybar | 36 | 32 | 4 | 22 | 52 | 74 |
| Babolsar | 4 | 24 | 36 | 50 | 78 | 80 |
Table 17.
Transportation cost, capacity of each hospital and inventory holding cost.
| No | Hospitals | Blood Centers Transportation cost ($) |
Hospital capacity | Inventory holding cost ($) | |||
|---|---|---|---|---|---|---|---|
| Babolsar | Babol | Sari | Behshahr | ||||
| 1 | Imam Khomeini Behshahr | 2000 | 1500 | 1000 | 500 | 400 | 3 |
| 2 | Shohada Behshahr | 2000 | 1500 | 1200 | 500 | 400 | 5 |
| 3 | Mehr Behshahr | 1500 | 1000 | 800 | 400 | 400 | 5 |
| 4 | Amiri Behshahr | 2000 | 1500 | 1200 | 500 | 400 | 3 |
| 5 | Bo Ali Neka | 1200 | 900 | 500 | 200 | 400 | 4 |
| 6 | Imam HosseinNeka | 1500 | 1000 | 500 | 300 | 400 | 5 |
| 7 | Imam Khomeini Sari | 1000 | 500 | 200 | 500 | 400 | 5 |
| 8 | Bo Ali Sari | 600 | 200 | 100 | 300 | 400 | 5 |
| 9 | Hazrat Fatemeh Sari | 1000 | 500 | 200 | 400 | 400 | 2 |
| 10 | Zare Sari | 800 | 600 | 200 | 300 | 400 | 6 |
| 11 | Shafa Sari | 600 | 250 | 50 | 150 | 400 | 3 |
| 12 | Nime Shaban Sari | 800 | 600 | 300 | 600 | 300 | 4 |
| 13 | Amir Mzandarani Sari | 450 | 350 | 250 | 400 | 400 | 6 |
| 14 | Hekmat Sari | 600 | 500 | 200 | 600 | 400 | 6 |
| 15 | Velayat Sari | 400 | 200 | 100 | 300 | 400 | 6 |
| 16 | Haj Azizi Juybar | 1000 | 500 | 300 | 500 | 200 | 8 |
| 17 | Kudakan Babol | 500 | 300 | 1000 | 1500 | 300 | 4 |
| 18 | Shahid Beheshti Babol | 800 | 200 | 800 | 1500 | 300 | 4 |
| 19 | 17 Sahrivar Babol | 700 | 300 | 1500 | 2000 | 300 | 4 |
| 20 | Mehregan Babol | 250 | 100 | 350 | 500 | 300 | 4 |
| 21 | YahyaNejad Babol | 800 | 200 | 1500 | 2000 | 300 | 3 |
| 22 | Clinic Babol | 450 | 250 | 600 | 1000 | 400 | 3 |
| 23 | Hazrat Zeinab Babolsar | 200 | 400 | 1000 | 2000 | 400 | 7 |
| 24 | Shafa Babolsar | 200 | 600 | 1500 | 2000 | 400 | 7 |
Due to the NP-hardness of the designed model, the described MOIWO is employed to find Pareto solutions for the question case as a large-scale problem. During successive periods, the model identifies these: (1) how to allocate plasma donors to temporary and permanent facilities, temporary facilities to permanent ones, and permanent facilities to hospitals, (2) the location of collection facility, and (3) the blood inventory level.
6.4. Case study results
Fig. 14 depicts the results of the discussed simulation model analyzing the effect of COVID-19 on plasma demand. As observed, the plasma demand distribution function follows the normal distribution with a correlation coefficient of 0.990.
Fig. 14.
Simulation results.
To validate the proposed simulation model, its results were compared with those of the real system. Therefore, to evaluate validation, the simulation model was run 100 times for 1,000,000 h and the average value of the estimated plasma demand was considered as the output. The data used for real system performance included the official statistics from Iran Ministry of Health. Fig. 15 compares the output of the proposed simulation model with that of the real system. The vertical axis is the estimated plasma level.
Fig. 15.
Comparison of simulation results with real system.
Thus, regarding the closeness of the estimated plasma level and the required amount obtained by the real system, with 95% confidence interval, it can be conclude that the simulation model can estimate the real system properly and acceptably.
Table 18 gives the blood flow from the temporary to the permanent blood centers in terms of liters. The max volume of blood is supplied from Behshahr center to Neka unit in period 1 and the min quantity is supplied from Babolsar center to Babol unit in period 1.
Table 18.
The blood flow from the temporary centers to the permanent centers.
| Permanent centers | Temporary centers |
|||||
|---|---|---|---|---|---|---|
| Behshahr |
Juybar |
Babolsar |
||||
| Periods | ||||||
| Neka | 75 | 26 | 44 | 38 | 60 | 63 |
| Sari | 52 | 50 | 43 | 57 | 66 | 45 |
| Babol | 33 | 35 | 32 | 30 | 30 | 38 |
Similarly, Table 19 shows the amount of blood donated from the collection centers to the temporary ones. As clearly perceived, the highest amount of blood transfusion from Behshahr donor to Babolsar temporary center in the first period is 80 L and the lowest amount of that from Neka donor to Behshahr temporary center is 15 L. The stored blood quantity at hospitals and permanent blood centers in terms of liters is presented in Table 20, Table 21, respectively.
Table 19.
The amount of blood transferred from the collection centers to the temporary centers.
| Temporary center | Collection center |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Babolsar |
Babol |
Juybar |
Sari |
Neka |
Behshahr |
|||||||
| Period | ||||||||||||
| Behshahr | 78 | 54 | 73 | 51 | 45 | 42 | 28 | 30 | 15 | 25 | 55 | 52 |
| Juybar | 35 | 47 | 30 | 41 | 42 | 45 | 20 | 28 | 52 | 38 | 75 | 56 |
| Babolsar | 32 | 50 | 26 | 35 | 34 | 45 | 50 | 42 | 79 | 55 | 80 | 56 |
Table 20.
Amount of blood inventory at the hospitals.
| No | Hospitals | Blood expired (L) | Amount of Blood held at hospital (L) |
|---|---|---|---|
| 1 | Imam Khomeini Behshahr | 0 | 27 |
| 2 | Shohada Behshahr | 2 | 30 |
| 3 | Mehr Behshahr | 1 | 28 |
| 4 | Amiri Behshahr | 0 | 34 |
| 5 | Bo Ali Neka | 2 | 28 |
| 6 | Imam HosseinNeka | 1 | 32 |
| 7 | Imam Khomeini Sari | 0 | 45 |
| 8 | Bo Ali Sari | 5 | 36 |
| 9 | Hazrat Fatemeh Sari | 4 | 40 |
| 10 | Zare Sari | 3 | 32 |
| 11 | Shafa Sari | 3 | 29 |
| 12 | Nime Shaban Sari | 2 | 32 |
| 13 | Amir Mzandarani Sari | 2 | 42 |
| 14 | Hekmat Sari | 5 | 45 |
| 15 | Velayat Sari | 3 | 33 |
| 16 | Haj Azizi Juybar | 0 | 35 |
| 17 | KudakanBabol | 0 | 28 |
| 18 | Shahid Beheshti Babol | 3 | 47 |
| 19 | 17 Sahrivar Babol | 4 | 32 |
| 20 | Mehregan Babol | 2 | 59 |
| 21 | YahyaNejad Babol | 4 | 35 |
| 22 | Clinic Babol | 2 | 29 |
| 23 | HazratZeinab Babolsar | 0 | 38 |
| 24 | Shafa Babolsar | 0 | 44 |
Table 21.
The amount of inventory held at the permanent blood centers.
| Period | Neka |
Sari |
Babol |
|||
|---|---|---|---|---|---|---|
| 32 | 38 | 20 | 24 | 25 | 30 | |
| 25 | 41 | 26 | 30 | 30 | 25 | |
| 20 | 35 | 20 | 20 | 27 | 28 | |
To solve the case study, 100 Pareto solutions have been generated in each iteration considering the problem being of bi-objective type (see Fig. 16).
Fig. 16.
Convergence of solutions in the case study.
The following two conditions considered to stop the algorithm:
-
•
Stop after a hundred iterations (max iteration 100)
-
•
Stop when a determined number of iterations is performed without any improvement.
The average values for the first and second objective functions in Pareto solutions are 390022.72 and 21441.6, respectively. The average time spent for solving the case study is 86.4 s. According to the case study, the convergence of the Pareto solutions resulting from the MOIWO algorithm is depicted for the first and second objective functions.
In Fig. 17, the flow of blood transfusion to different locations in the first period is seen, where 6 collection centers, 3 temporary facilities, 3 permanent blood centers and 24 hospitals are represented by yellow, green, blue, and gray points, respectively.
Fig. 17.
The amount of blood transfusion between different locations in the first period.
As it is clear, the received blood flows from the donors to the temporary facilities and permanent centers, from the temporary centers to the permanent centers and ultimately from the permanent blood centers to the hospitals. For example, blood transfusion flow amount from Babolsar donor to Juybar temporary center is 35 L, from Behshahr donor to Neka center is 35 L, from Juybar temporary center to Neka permanent center is 44 L, and from Sari center to hospital number 1 is 27 L.
6.5. Sensitivity analysis
In this section, the sensitivity analysis of some proposed mathematical model’s parameters is discussed. Fig. 18 depicts the relationship between the first objective function’s changes in terms of demand variation. As seen, as the blood demand gets higher, the total cost of the system increases, and as the demand gets lower, the system’s cost gets down. For instance, the amount of blood demand increase by 30% leads to system’s costs by 462003.1 units (15% raise) and the demand drop by 20% results in system’s cost decrease by 315529 units (19% drop).
Fig. 18.
Sensitivity analysis of demand changes on the total costs.
As shown in Fig. 19, the demand changes’ impact on the second objective function (i.e., blood flow time) is indicated. As it is obvious, the flow time increases as the demand rises and decreases as the demand decreases. For example, a 20% demand increase brings about the flow time increase by 31625.1 units (32% raise). Also, a 30% demand decrease leads to the flow time drop by 11711.98 units (45% drop).
Fig. 19.
Sensitivity analysis of demand changes on the second objective function.
Fig. 20 illustrates the centers’ storage capacity changes influencing the total system costs. As understood, the centers’ capacity increase will reduce the total costs. For example, the centers’ capacity increase by 30% will reduce the total costs by 296667.29 units (23% drop) and the capacity reduction by 30% will increase the total cost by 566819.81 units (31% raise). The reason for this trend is the huge difference between the holding costs and the cost of establishing a new center. Due to the higher cost of establishing a new center compared to the holding cost, increasing the centers’ capacity will reduce the need to establish new centers. As a result, fewer centers are established and the supply chain costs get reduced.
Fig. 20.
Sensitivity analysis of the capacity of centers.
Fig. 21 demonstrates the transportation capacity changes’ impact on the total costs of the system and the total expired blood quantity in the centers. As seen, increasing the transportation capacity will reduce the total costs along with the expired blood amount. This relationship is predictable as by increasing the transportation capacity, a smaller number of transportation will be required, and less transportation cost will be imposed on the blood supply chain. Moreover, increasing the transportation capacity will reduce the blood flow time which results in lower quantity of the expired blood. According to this figure, the transportation capacity increase by 30% will reduce the total costs to 294506.54 units (24% drop) and the transportation capacity decrease by 20% will increase the total costs to 469474.71 units (16% raise). It can be concluded from the results that with a 30% increase in the transportation capacity, the amount of the expired blood declines to 22 L (54% drop).
Fig. 21.
Sensitivity analysis of the capacity of transportation.
7. Discussion
The practical implications of the current research derived results can be useful for hospitals, blood transfusion organizations, permanent and temporary medical centers, and finally, for all patients. For example, hospitals can be prepared to deal with large volumes of plasma demand during the outbreak of COVID-19 by knowing the estimated demand. Considering blood substitutability in hospitals can guarantee timely blood units’ availability during the outbreak of COVID-19.
As the sensitivity analysis results indicate, demand increase brings about total system cost and flow time increase. As it was explained, plasma demand is estimated using a simulation model. Consequently, it seems imperative to conduct a more detailed study about the simulation model to be able to manage demand. In the simulation model, the parameter “hospital capacity” has an inverse effect on “deaths”. Also, the parameter “relative behavioral risks” has a direct effect on “transmission rate”. So, the managers and decision makers are advised to increase the hospitals’ capacity so that to be able to hospitalize the patients as much as possible. To reduce the behavioral risks, it is also recommended to set strict rules such as maintaining social distance that reduces transmission rate. And ultimately, it is perceived that “isolation effectiveness“ increase leads to higher ”public health“ and its decrease results in higher ”serious cases“, ”hospital strain“ and ”deaths”. Therefore, improving the isolated patients’ performance lowers the contact rate and thus, reduces the death rate.
Moreover, the total system cost will decrease by increasing the established centers’ capacity which is due to lower holding costs compared with establishment costs. Therefore, the managers and decision makers in charge are recommended to establish the centers with higher capacity in order to minimize the total system costs since the centers’ capacity increase will also reduce the number of the established centers.
The transportation capacity increase will reduce the total supply chain related cost. Besides, by increasing the transportation capacity, it seems necessary to open a smaller number of blood transfers. Thus, managers and decision makers need to increase the transportation capacity so that to come up with reduced supply chain costs. In addition, the transportation capacity increase results in lower total quantity of the expired blood, which can be due to this fact that increasing the transportation capacity lowers the required transports’ number. Because of the limited number of blood carrying vehicles, by increasing their transportation capacity, the donated blood will wait less time to be sent to the hospitals. As a result, the possibility of blood deterioration is reduced.
To determine the research strategy, the research questions are answered as it follows:
1. How are the allocation, distribution, and inventory level of different types of blood? 2. Where is the optimal location of collection centers during COVID-19 outbreak? 3. How can the amount of plasma required for COVID-19 patients be predicted to prevent shortage? Table 18, Table 19, Table 20, Table 21 give the results of the location, allocation, distribution and inventory control of the required plasma types. For example, in Table 18, the permanent centers in Neka, Sari and Babol are assigned to all three temporary centers of Behshahr, Juybar and Babolsar. Table 19 also depicts the required plasma distribution. In addition, the results indicate that all potential centers have reopened. The amount of the blood stored and expired in each hospital and the permanent center is also reported in Table 20, Table 21.
Demand has been estimated using system dynamic structure simulation of COVID-19 outbreak (Fig. 4). The desired demand with 95% reliability follows normal distribution with a correlation coefficient of 0.990 (Fig. 14). Also, to prevent shortage, the possibility of compatible blood replacement has been incorporated in the model’s assumptions (Table 11).
Due to the fact that this research is a “case study” in terms of strategy, the required data and parameters have been extracted from reliable references, Google Map, the information about the hospitals, blood transfusion organization, and etc.
In order to compare this research with the previous studies, two recent studies of [38] and [1] have been considered.
Zahiri et al. [38] compared meta-heuristic algorithms to solve the stochastic blood supply chain problem in Mazandaran Province/Iran. The proposed model was solved with MOICA (Multi-Objective Imperialist Competitive Algorithm) and NSGA-II algorithms. According to their results, the MOICA algorithm performed better than other algorithms. Compared to the study done by Zahiri et al. [38], the merit behind our research is the multi-commodity of the proposed model and the possibility of blood groups’ substitution () during the outbreak of COVID-19.
Also in the current study, location and inventory decisions have been considered, which was taken into account by Zahiri et al. [38]. Meanwhile, simulation based plasma demand estimation is of the key benefits of our study during COVID-19 outbreak compared to that of Zahiri et al. [38].
In another similar study, Haghjoo et al. [1] considered the distribution centers’ location and such centers being allocated to the hospitals in the blood supply chain in Mazandaran province. The proposed multi-period and single-commodity model was solved using Self-Adaptive Imperialist Competitive Algorithm (SAICA) and Invasive Weed Optimization (IWO) approaches. In the current study, like that of Haghjoo et al. [1], the multi-echelon mathematical model was solved using four metaheuristic methods. Considering the multi-commodity feature in the proposed model, the substitution possibility of the blood groups and transport capacity are the advantages of this study compared with the one done by Haghjoo et al. [1].
Of the benefits behind using the proposed meta-heuristic algorithms, we can point out the following [21], [22], [76]:
1. The NSGA-II and SPEA-II algorithms use only the values of the objective function to perform the optimization process and do not require additional information such as the function derivative; 2. Due to the simplicity of the search process of MOIWO and MOGWO, they work very quickly and efficiently; 3. The proposed algorithms (NSGA-II, SPEA-II, MOIWO, and MOGWO) are very flexible and work with all kinds of objective functions and constraints in the search space.
Regarding the proposed simulation approach, it possesses the following merits [77]:
-
–
The simulation is presented as a separate run, which paves the ground for the simulation to be run several times and to report the average of the obtained results. This minimizes simulation errors as much as possible.
-
–
Enterprise Dynamic software has a high convergence speed and a programming language called 4DScript making it possible to simulate all problems, both industrial and non-industrial cases.
-
–
The open source structure of the ED allows users to generate special atoms to simulate their problem.
The disadvantages of using the simulation approach are as follows [50]:
-
–
Usually, numerous runs are required for each simulation model, and this can lead to high costs for using a computer. Simulation also requires access to a computer system equipped with features such as high RAM and CPU.
-
–
Due to the large number of runs for computer simulation, most simulations are time consuming.
Also, the disadvantages of the proposed meta-heuristic algorithms are the following [78], [79]:
-
–
Meta-heuristic algorithms are not able to calculate the global optimum and calculate the local optimum.
-
–
The final solution in NSGA-II, SPEA-II, MOIWO and MOGWO algorithms depends on the coder’s skill in defining chromosomes and the initial value of its parameters.
8. Conclusion
In this research, a blood supply chain in case of COVID-19 outbreak has been discussed. In order to deliver the plasma of the recovered sufferers to the patients, a four-echelon multi-objective supply chain minimizing plasma delivery time and supply chain costs has been proposed. The chain includes collection centers, temporary centers, permanent centers and hospitals. The amount of blood plasma the patients require is viewed as uncertain parameters and is estimated using a simulation approach.
In the present study, the system dynamic structure of COVID-19 outbreak has been designed for the first time, which has the potential to estimate the number of COVID-19 patients. This structure also pursues the goal to estimate the amount of plasma the patients require for the first time. Simulating the structure of COVID-19 outbreak was not studied in detail in the previous studies. For example, the season induced effect on the required plasma quantity is dealt with in the simulation. Examining this factor can lead the managers to be carefully prepared and exactly plan for all seasons. It should be mentioned that the subject known as logistics in plasma therapy during COVID-19 pandemic has not been investigated in any study so far. Also concurrently addressing location, inventory control, allocation, distribution, and plasma flow has not been surveyed in multi-period and multi-commodity model at the time of this pandemic. Considering time is very important in this outbreak, too. Therefore, minimizing plasma flow time can lead to the patients’ satisfaction and survival. Substitution of similar blood types is essential due to lack of plasma in critical situations. Substitution of similar plasmas during COVID-19 prevalence also increases the patients’ satisfaction and reduces human losses. With this technique, COVID-19 patients can be served faster and easier. Transportation during the outbreak also needs special equipment and trained personnel. Therefore, plasma transportation capacity is limited, which has been addressed in this study.
Consequently, first, the system dynamic structure of COVID-19 outbreak was developed and implemented using the simulation model. The simulation model extracted results for the observation period of 1,000,000 h indicated that the plasma demand distribution function follows the normal distribution with a correlation coefficient of 0.990. With 95% confidence interval, the simulation model could yield a good estimate of the real world. Then, the demand distribution function was entered into the mathematical model and the stochastic model was converted into the deterministic counterpart by the chance constraint approach.
The proposed model was solved in small and medium scales using -constraint, NSGA-II, SPEA-II, MOIWO and MOGWO approaches. The mean values of the MID and SM metrics for MOIWO algorithm were 5.181 and 0.561, respectively, revealing the proposed algorithm’s outperformance. The mean values of the MID and SM for the SPEA-II, NSGA-II and MOGWO approach were (5.802, 0.747), (5.211, 0.577) and (5.197, 0.567), respectively. Also, the solution time for MOIWO was shorter than that for other algorithms in all cases. Therefore, the MOIWO algorithm was selected to solve the case study defined for Mazandaran province in Iran.
The results revealed that all the collection centers considered for the case study have been established. The amount of blood stored and transferred among the centers was also determined.
The sensitivity analysis derived results demonstrated that increasing the demand leads to total system costs and flow time increase. For instance, a 30% increase in the demand results in the total cost of the system and the amount of flow time increase by 15% and 41%, respectively. Also, the centers’ capacity increase reduces the number of the established centers. As a result, the established centers’ capacity increase leads to increasing the total costs of the system. Therefore, in order to lower the system costs, the managers and decision makers in charge are recommended to establish some centers with higher capacity. Besides, reducing the simulation related transmission decreases the plasma demand. Therefore, the responsible managers and decision makers are recommended to impose some strict rules for social distancing.
This research, like other cases, has its own limitations and assumptions, which are expressed as it follows:
-
–
As there was no official database for some parts of cost elements, the driver’s estimations and blood transfusion center officers were asked to help. The questions about the transportation costs for each route have been categorized and the estimated costs have been entered into the mathematical model.
-
–
In addition, the recent high inflation rate and the rising transportation costs in Iran make it more difficult to estimate the relevant costs.
-
–
Due to several ways of COVID-19 transmission, in the system dynamic structure of the simulation model, only two ways of physical contact and transmission through sneezing and coughing are discussed. Therefore, other ways of transmission such as eating food contaminated with the virus or touching contaminated objects have been neglected.
-
–
Due to the instability of COVID-19 incidence rate and despite the fact that the incidence rate among Iranians is higher than that of the world, in the simulation part of this study, only the information reported by the World Health Organization (WHO) has been used for the incidence rate and fatality rate.
The following directions are proposed for the would-be research:
-
–
The routing of the transportation vehicles along with the location of depots that plays a significant role in blood chain. The cooperation of the members of the distribution supply chain can also be considered with the routing vehicles. So that due to the limited transportation capacity, vehicles can use the capacity of other vehicles to transfer plasma. Thus, if a vehicle reaches its maximum capacity, it can deliver the excess plasma to a vehicle with sufficient capacity to carry that plasma.
-
–
Considering other objectives including maximizing coverage and minimizing plasma shortage. Maximizing coverage and minimizing shortages can satisfy more patients and save more lives.
-
–
Dealing with other simulation model parameters such as the incidence rate in pregnant women and heart problem suffering patients as the mortality rate is higher among these groups. Also other parameters such as lockdown can be considered in the simulation as a parameter reducing the transmission rate.
-
–
Surveying resilience and sustainability in the blood supply chain during the outbreak of COVID-19. In order to study sustainability, it is recommended to simultaneously pay attention to the environmental, social (such as employment in collection centers) and the economic factors. There is also the possibility of the failure of the plasma cold stores. Considering this fact that the support system can make plasma supply chain resilient.
-
–
Since it is necessary to maintain social distance and reduce the collection centers’ capacity, donors can reserve time to donate blood. Reserving blood donation time can be taken as “office hours” and “non-office hours”.
-
–
Addressing the government’s advertisements to attract donors in the mathematical model. The government conducts local advertising to attract more recovered people to donate plasma. They advertise using social networks, TV commercials, and banners in the city.
-
–
Involving other approaches such as robust optimization instead of chance constraint programming for solving uncertain problems.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Haghjoo N., Tavakkoli-Moghaddam R., Shahmoradi-Moghadam H., Rahimi Y. Reliable blood supply chain network design with facility disruption: A real-world application. Eng. Appl. Artif. Intell. 2020;90 [Google Scholar]
- 2.Nilashi M., Asadi S., Abumalloh R.A., Samad S., Ibrahim O. Intelligent recommender systems in the COVID-19 outbreak: The case of wearable healthcare devices. J. Soft Comput. Decis. Support Syst. 2020;7:8–12. [Google Scholar]
- 3.Kairon P., Bhattacharyya S. 2020. Comparative study of variational quantum circuit and quantum backpropagation for COVID-19 outbreak predictions. arXiv preprint arXiv:2008.07617. [Google Scholar]
- 4.Chen J., Qi T., Liu L., Ling Y., Qian Z., Li T., Lu H. Clinical progression of patients with COVID-19 in Shanghai, China. J. Infect. 2020;80:1–6. doi: 10.1016/j.jinf.2020.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shen C., Wang Z., Zhao F., Yang Y., Li J., Yuan J., Wei J. Treatment of 5 critically ill patients with COVID-19 with convalescent Plasma. JAMA. 2020;323:1582–1589. doi: 10.1001/jama.2020.4783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Krebs H.A. Chemical composition of blood Plasma and serum. Annu. Rev. Biochem. 1950;19:409–430. doi: 10.1146/annurev.bi.19.070150.002205. [DOI] [PubMed] [Google Scholar]
- 7.Duan K., Liu B., Li C., Zhang H., Yu T., Qu J., Peng C. Effectiveness of convalescent Plasma therapy in severe COVID-19 patients. Proc. Natl. Acad. Sci. 2020;117:9490–9496. doi: 10.1073/pnas.2004168117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bloch E.M., Shoham S., Casadevall A., Sachais B.S., Shaz B., Winters J.L., Pekosz A. Deployment of convalescent Plasma for the prevention and treatment of COVID-19. J. Clin. Invest. 2020;130:2757–2765. doi: 10.1172/JCI138745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liu Y., Gayle A.A., Wilder-Smith A., Rocklöv J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J. Travel Med. 2020 doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Roback J.D., Guarner J. Convalescent Plasma to treat COVID-19: possibilities and challenges. JAMA. 2020;323:1561–1562. doi: 10.1001/jama.2020.4940. [DOI] [PubMed] [Google Scholar]
- 11.Tanne J.H. Covid-19: FDA approves use of convalescent Plasma to treat critically ill patients. BMJ. 2020;368:m1256. doi: 10.1136/bmj.m1256. [DOI] [PubMed] [Google Scholar]
- 12.Y J., Sohn Y., Lee S.H., Cho Y., Hyun J.H., Baek Y.J., Roh J. Use of convalescent Plasma therapy in two COVID-19 patients with acute respiratory distress syndrome in Korea. J. Korean Med. Sci. 2020 doi: 10.3346/jkms.2020.35.e149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ivanov D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp. Res. E Logist. Transp. Rev. 2020:136. doi: 10.1016/j.tre.2020.101922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ranney M.L., Griffeth V., Jha A.K. Critical supply shortages—the need for ventilators and personal protective equipment during the Covid-19 pandemic. N. Engl. J. Med. 2020;382 doi: 10.1056/NEJMp2006141. [DOI] [PubMed] [Google Scholar]
- 15.Zabihi F., Khakzar Bafruei M. Price discount determination in pricing and inventory control of perishable good with time and price demand. Int. J. Supply Oper. Manag. 2017;4:263–273. [Google Scholar]
- 16.Rani P., Mishra A.R., Mardani A. An extended pythagorean fuzzy complex proportional assessment approach with new entropy and score function: Application in pharmacological therapy selection for type 2 diabetes. Appl. Soft Comput. 2020 doi: 10.1016/j.asoc.2020.106441. [DOI] [Google Scholar]
- 17.Fahimnia B., Jabbarzadeh A., Ghavamifar A., Bell M. Supply chain design for efficient and effective blood supply in disasters. Int. J. Prod. Econ. 2017;183:700–709. [Google Scholar]
- 18.Samani M.R., Torabi A., Hosseini-Motlagh M. Integrated blood supply chain planning for disaster relief. Int. J. Disaster Risk Reduct. 2018;27:168–188. [Google Scholar]
- 19.Pirabán A., Guerrero W.J., Labadie N. Survey on blood supply chain management: Models and methods. Comput. Oper. Res. 2019;112 [Google Scholar]
- 20.Varchanis S., Dimakopoulos Y., Wagner C., Tsamopoulos J. How viscoelastic is human blood Plasma? Soft Matter. 2018;14:4238–4251. doi: 10.1039/C8SM00061A. [DOI] [PubMed] [Google Scholar]
- 21.Tavana M., Abtahi A.R., Di Caprio D., Hashemi R., Yousefi-Zenouz R. An integrated location-inventory-routing humanitarian supply chain network with pre-and post-disaster management considerations. Socio-Econ. Plan. Sci. 2018;64:21–37. [Google Scholar]
- 22.Larraín S., Pradenas L., Pulkkinen I., Santander F. Multiobjective optimization of a continuous kraft pulp digester using SPEA2. Comput. Chem. Eng. 2020;143 [Google Scholar]
- 23.Zyl V. University of North Carolina at Chapel Hill; 1963. Inventory Control for Perishable Commodities. [Google Scholar]
- 24.Nahmias S. Perishable inventory theory: A review. Oper. Res. 1982;30:680–708. doi: 10.1287/opre.30.4.680. [DOI] [PubMed] [Google Scholar]
- 25.Sirelson V., Brodheim E. A computer planning model for blood platelet production and distribution. Comput. Methods Programs Biomed. 1991;35:279–291. doi: 10.1016/0169-2607(91)90006-f. [DOI] [PubMed] [Google Scholar]
- 26.Yongming Z. A brief introduction to American blood taking system. Clin. Transfus. Insp. 1999:1–3. [Google Scholar]
- 27.Hosseini-Motlagh S.M., Samani M.R.G., Cheraghi S. Robust and stable flexible blood supply chain network design under motivational initiatives. Socio-Econ. Plan. Sci. 2020;70 [Google Scholar]
- 28.Goodarzian F., Taleizadeh A.A., Ghasemi P., Abraham A. An integrated sustainable medical supply chain network during COVID-19. Eng. Appl. Artif. Intell. 2021;100 doi: 10.1016/j.engappai.2021.104188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nagurney A. Optimization of supply chain networks with inclusion of labor: Applications to Covid-19 pandemic disruptions. Int. J. Prod. Econ. 2021 doi: 10.1016/j.ijpe.2021.108080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rastegar M., Tavana M., Meraj A., Mina H. An inventory-location optimization model for equitable influenza vaccine distribution in developing countries during the COVID-19 pandemic. Vaccine. 2021;39:495–504. doi: 10.1016/j.vaccine.2020.12.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Liu W., Ke G.Y., Chen J., Zhang L. Scheduling the distribution of blood products: A vendor-managed inventory routing approach. Transp. Res. E Logist. Transp. Rev. 2020;140 [Google Scholar]
- 32.Hamdan B., Diabat A. Robust design of blood supply chains under risk of disruptions using Lagrangian relaxation. Transp. Res. E Logist. Transp. Rev. 2020;134 [Google Scholar]
- 33.Dehghani M., Abbasi B., Oliveira F. Proactive transshipment in the blood supply chain: A stochastic programming approach. Omega. 2020 [Google Scholar]
- 34.Araújo A.M., Santos D., Marques I., Barbosa-Povoa A. Blood supply chain: a two-stage approach for tactical and operational planning. OR Spectrum. 2020;42:1023–1053. [Google Scholar]
- 35.Haeri A., Hosseini-Motlagh S.M., Ghatreh Samani M.R., Rezaei M. A mixed resilient-efficient approach toward blood supply chain network design. Int. Trans. Oper. Res. 2020;27:1962–2001. [Google Scholar]
- 36.Rajendran S., Ravindran A.R. Inventory management of platelets along blood supply chain to minimize wastage and shortage. Comput. Ind. Eng. 2019;130:714–730. [Google Scholar]
- 37.Hosseinifard Z., Abbasi B. The inventory centralization impacts on sustainability of the blood supply chain. Comput. Oper. Res. 2018;89:206–212. [Google Scholar]
- 38.Zahiri B., Torabi A., Mohammadi M., Aghabegloo M. A multi-stage stochastic programming approach for blood supply chain planning. Comput. Ind. Eng. 2018;122:1–14. [Google Scholar]
- 39.Samani M.R.G., Hosseini-Motlagh S.M. An enhanced procedure for managing blood supply chain under disruptions and uncertainties. Ann. Oper. Res. 2019;283:1413–1462. [Google Scholar]
- 40.Habibi M., Paydar M.M., AsadiGangraj E. Designing a bi-objective multi-echelon robust blood supply chain in disaster. Appl. Math. Model. 2018;55:583–599. [Google Scholar]
- 41.Salehi F., Mahootchi M., Moattar Husseini S.M. Developing a robust stochastic model for designing a blood supply chain network in a crisis: a possible earthquake in Tehran. Ann. Oper. Res. 2017:1–25. [Google Scholar]
- 42.Ramezanian R., Behboodi Z. Blood supply chain network design under uncertainties in supply and demand considering social aspects. Transp. Res. E Logist. Transp. Rev. 2017;104:69–82. [Google Scholar]
- 43.Masoumi A., Yu M., Nagurney A. Mergers and acquisitions in blood banking systems: A supply chain network approach. Int. J. Prod. Econ. 2017;193:406–421. [Google Scholar]
- 44.Dillon M., Oliveira F., Abbasi B. A two-stage stochastic programming model for inventory management in the blood supply chain. Int. J. Prod. Econ. 2017;187:27–41. [Google Scholar]
- 45.Fereiduni M., Shahanaghi K. A robust optimization model for blood supply chain in emergency situations. Int. J. Ind. Eng. Comput. 2016;7:535–554. [Google Scholar]
- 46.Nahofti J., Teymoury E., Pishvaee S. Blood products supply chain design considering disaster circumstances (Case study: earthquake disaster in Tehran) J. Ind. Syst. Eng. 2016;9:51–72. [Google Scholar]
- 47.Arvan M., Tavakkoli-Moghaddam R., Abdollahi M. Designing a bi-objective and multi-product supply chain network for the supply of blood. Uncertain Supply Chain Manag. 2015;3:57–68. [Google Scholar]
- 48.Zahraee M., Jafri R., Firouzi A. Efficiency improvement of blood supply chain system using Taguchi method and dynamic simulation. Procedia Manuf. 2015;2:1–5. [Google Scholar]
- 49.Vega D.I. Lockdown, one, two, none, or smart. Modeling containing COVID-19 infection, A conceptual model. Sci. Total Environ. 2020 doi: 10.1016/j.scitotenv.2020.138917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Shahabi A., Raissi S., Khalili-Damghani K., Rafei M. Designing a resilient skip-stop schedule in rapid rail transit using a simulation-based optimization methodology. Oper. Res. 2019:1–31. [Google Scholar]
- 51.Ghasemi P., Khalili-Damghani K. A robust simulation–optimization approach for pre-disaster multi-period location–allocation–inventory planning. Math. Comput. Simulation. 2021;179:69–95. [Google Scholar]
- 52.Ghasemi P., Babaeinesami A. Simulation of fire stations resources considering the downtime of machines: A case study. J. Ind. Eng. Manag. Stud. 2020;7:161–176. [Google Scholar]
- 53.Ma R., Li X., Gao W., Lu P., Wang T. Random-fuzzy chance-constrained programming optimal power flow of wind integrated power considering voltage stability. IEEE Access. 2020;8 [Google Scholar]
- 54.Thore S. Chance-constrained activity analysis. European J. Oper. Res. 1987;30:267–269. [Google Scholar]
- 55.Buakum D., Wisittipanich W. Stochastic internal task scheduling in cross docking using chance-constrained programming. Int. J. Manag. Sci. Eng. Manag. 2020:1–7. [Google Scholar]
- 56.Rout P.K., Nanda S., Acharya S. Computation of multi-choice multi-objective fuzzy probabilistic two stage programming problem. Int. J. Comput. Sci. Math. 2020;11:168–191. [Google Scholar]
- 57.Pérez Cañedo B., Verdegay J.L., Miranda Pérez R. An epsilon-constraint method for fully fuzzy multiobjective linear programming. Int. J. Intell. Syst. 2020;35:600–624. [Google Scholar]
- 58.Cooper K., Hunter S.R., Nagaraj K. Biobjective simulation optimization on integer lattices using the epsilon-constraint method in a retrospective approximation framework. INFORMS J. Comput. 2020;32:1080–1100. [Google Scholar]
- 59.Laumanns M., Thiele L., Zitzler E. An efficient, adaptive parameter variation scheme for metaheuristics based on the epsilon-constraint method. European J. Oper. Res. 2006;169:932–942. [Google Scholar]
- 60.Deb K., Pratap A., Agarwal S., Meyarivan T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002;6:182–197. [Google Scholar]
- 61.Yi J.H., Xing L.N., Wang G.G., Dong J., Vasilakos A.V., Alavi A.H., Wang L. Behavior of crossover operators in NSGA-III for large-scale optimization problems. Inform. Sci. 2020;509:470–487. [Google Scholar]
- 62.Khalili-Damghani K., Abtahi A., Ghasemi A. A new bi-objective location-routing problem for distribution of perishable products: Evolutionary computation approach. J. Math. Model. Algorithms Oper. Res. 2015;14:287–312. [Google Scholar]
- 63.Zitzler E., Thiele L. International Conference on Parallel Problem Solving from Nature. Springer; Berlin, Heidelberg: 1998. Multiobjective optimization using evolutionary algorithms—a comparative case study; pp. 292–301. [Google Scholar]
- 64.Zitzler E., Laumanns M., Thiele L. Computer Engineering and Networks Laboratory (TIK); ETH Zurich, Zurich, Switzerland: 2001. SPEA 2: Improving the Strength Pareto Evolutionary Algorithm: TIK Report 103; p. 236. [Google Scholar]
- 65.Hasani A., Mokhtari H., Fattahi M. A multi-objective optimization approach for green and resilient supply chain network design: a real-life case study. J. Cleaner Prod. 2021;278 [Google Scholar]
- 66.Mirjalili S., Mirjalili S.M., Lewis A. Grey wolf optimizer. Adv. Eng. Softw. 2014;69:46–61. [Google Scholar]
- 67.Mehrabian A.R., Lucas C. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inform. 2006;1:355–366. [Google Scholar]
- 68.Kundu D., Suresh K., Ghosh S., Das S., Panigrahi B.K., Das S. Multi-objective optimization with artificial weed colonies. Inform. Sci. 2011;181:2441–2454. [Google Scholar]
- 69.Zitzler E. Shaker; Ithaca: 1999. Evolutionary Algorithms for Multiobjective Optimization: Methods and Applications; p. 63. [Google Scholar]
- 70.Gholipoor Z., Khazan H., Azargashb E., Youssefi M.R., Rostami A. Prevalence and risk factors of intestinal parasite infections in Mazandaran province, North of Iran. Clin. Epidemiology Glob. Health. 2019 [Google Scholar]
- 71.World Health Organization Z. 2020. p. 72. [Google Scholar]
- 72.Lauer S.A., Grantz K.H., Bi Q., Jones F.K., Zheng Q., Meredith H.R., Lessler J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann. Internal Med. 2019;172(2020):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Chen L., Xiong J., Bao L., Shi Y. Convalescent Plasma as a potential therapy for COVID-19. Lancet Infect. Dis. 2020;20:398–400. doi: 10.1016/S1473-3099(20)30141-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Briscese G., Lacetera N., Macis M., Tonin M. National Bureau of Economic Research; 2020. Compliance with Covid-19 Social-Distancing Measures in Italy: The Role of Expectations and Duration. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Alizadeh-Navaei R., Saeedi M., Valadan R., Roozbeh F., Amjadi O., Zaboli E., Assadi T. Laboratory abnormalities in patients with COVID-19 in Mazandaran Province, Iran. Iran. Red Crescent Med. J. 2020;22 [Google Scholar]
- 76.Tirkolaee E.B., Aydın N.S., Ranjbar-Bourani M., Weber G.W. A robust bi-objective mathematical model for disaster rescue units allocation and scheduling with learning effect. Comput. Ind. Eng. 2020;149 [Google Scholar]
- 77.Attar A., Raissi S., Khalili-Damghani K. Simulation–optimization approach for a continuous-review, base-stock inventory model with general compound demands, random lead times, and lost sales. Simulation. 2016;92:547–564. [Google Scholar]
- 78.Fathollahi-Fard A.M., A S., Ahmadi K., Goodarzian F., Cheikhrouhou N. A bi-objective home healthcare routing and scheduling problem considering patients’ satisfaction in a fuzzy environment. Appl. Soft Comput. 2020 doi: 10.1016/j.asoc.2020.106385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Goodarzian F., Hosseini-Nasab H., Muñuzuri J., Fakhrzad M.B. A multi-objective pharmaceutical supply chain network based on a robust fuzzy model: A comparison of meta-heuristics. Appl. Soft Comput. 2020 [Google Scholar]