Abstract
Functional connectome “fingerprint” is a highly characterized brain pattern that distinguishes one individual from others. Although its existence has been demonstrated in adults, an unanswered but fundamental question is whether such individualized pattern emerges since infancy. This problem is barely investigated despites its importance in identifying the origin of the intrinsic connectome patterns that mirror distinct behavioral phenotypes. However, addressing this knowledge gap is challenging because the conventional methods are only applicable to developed brains with subtle longitudinal changes and typically fail on the dramatically developing infant brains. To tackle this challenge, we invent a novel model, namely, disentangled intensive triplet autoencoder (DI-TAE). First, we introduce the triplet autoencoder to embed the original connectivity into a latent space with higher discriminative capability among infant individuals. Then, a disentanglement strategy is proposed to separate the latent variables into identity-code, age-code, and noise-code, which not only restrains the interference from age-related developmental variance, but also captures the identity-related invariance. Next, a cross-reconstruction loss and an intensive triplet loss are designed to guarantee the effectiveness of the disentanglement and enhance the inter-subject dissimilarity for better discrimination. Finally, a variance-guided bootstrap aggregating is developed for DI-TAE to further improve the performance of identification. DI-TAE is validated on three longitudinal resting-state fMRI datasets with 394 infant scans aged 16 to 874 days. Our proposed model outperforms other state-of-the-art methods by increasing the identification rate by more than 50%, and for the first time suggests the plausible existence of brain functional connectome “fingerprint” since early infancy.
Keywords: Infant Functional Connectome, Rs-fMRI, Triplet Autoencoder
1. Introduction
Using brain functional connectivity profiles to establish individual uniqueness among a cohort is important for individualized characterization of disease and health [1], understanding intrinsic patterns of brain organization [2] and their relationship with distinct behavioral phenotypes [3]. To date, it has been shown that the brains of adults [1-4] and adolescents [5] exhibit highly individualized functional connectome patterns, which is unique enough to be taken as “fingerprint” for distinguishing an individual from others. Of note, most of the functional connectome fingerprinting studies focus on adults, in which the brain function is relatively stable across different scans. Only a few studies involved the developing brains from adolescent cohorts [4, 5]. To the best of our knowledge, there is no study on the brain functional connectome fingerprinting in infants, whose brains are undergoing dramatic development, although brain folding fingerprinting in infants has been investigated [22]. However, studying the fingerprinting capability of the infant functional connectivity is of great neuroscientific significance with the examination of: 1) Whether such individualized functional connectome pattern emerges early during infancy, which features the most critical and dynamic postnatal brain development [6, 7, 18, 19]; 2) Which functional connection(s) and network(s) manifest more individualized uniqueness during the early brain development. Addressing these questions is challenging because the intrinsic patterns for identifying an individual infant from their peers are overwhelmed by the rapid brain development. Conventional methods designed for adults only suite the scenario with subtle longitudinal brain change and are thus typically fail on infant data.
To fill this knowledge gap, we develop a novel model called disentangled intensive triplet autoencoder (DI-TAE). It restrains the overwhelming interference from brain development by separating the invariance of the individualized brain connectome from the variance of the dramatic brain development. Specifically, at first, triplet autoencoder [8, 9] is chosen as the basic model to enhance the discrimination capability of function connectivity for its potential on capturing high-order discriminative information from comparison within triplet sample. Then, the latent variables of the autoencoder are disentangled into identity-code, age-code, and noise-code, representing the individualized information, developmental information, and unconcerned noise, respectively. This new strategy helps to not only effectively extract the discriminative information for identification but also simultaneously model the variance and invariance in the brain connectome by unifying age prediction and individual identification in a single framework. A cross-reconstruction loss is further designed requiring the identity codes obtained from the same subjects are replaceable with each other in the reconstruction process, so as to guarantee the effectiveness of the disentanglement. Next, equipping with a new defined intensive triplet loss, the inter-subject dissimilarity is deeply emphasized to learn a more discriminative feature variable. Finally, since the high dimension of the whole brain functional connectivity features poses a significant challenge for efficient learning, a variance-guided bootstrap aggregating is designed, only including a small portion of features at each time, to boost the accuracy while preventing overfitting.
In experiments based on a longitudinal infant dataset, the high identification accuracy obtained by DI-TAE not only validates the superiority of our proposed model but also, for the first time, proves that brain functional connectome “fingerprint” emerges since infancy. With further analysis, networks that manifest more on individualized uniqueness during the early brain development were also identified for revealing the developmental trajectory of brain connectome fingerprint from infants to adults.
2. Method
2.1. Disentangled intensive triplet autoencoder
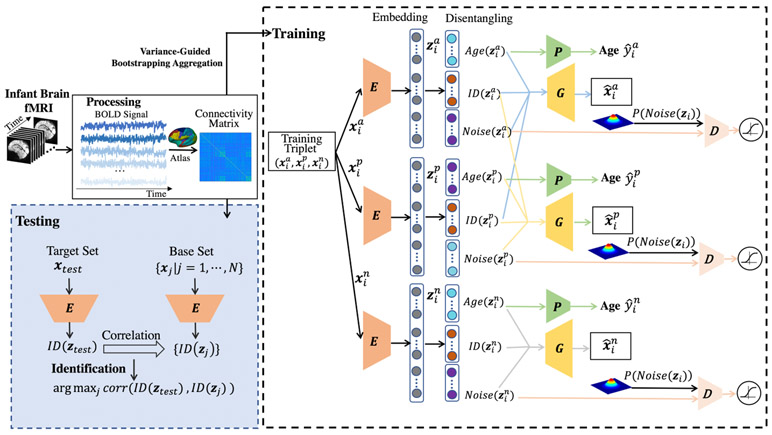
Unifying disentanglement, age prediction, and individual identification into a triplet autoencoder, the disentangled intensive triplet autoencoder (DI-TAE) is trained with specifically defined losses and dedicatedly designed for infant functional connectome fingerprinting. The framework of DI-TAE is depicted in Fig. 1 and detailed below.
Fig. 1.
The framework of our proposed DI-TAE model.
The individual infant identification test is performed across paired of scans consisting of one “target” and one “base” data, with the requirement that the target and base sessions are acquired from different ages. That is, each subject has two longitudinal fMRI scans from two different sessions. In the process of identification, one scan will be selected from the target set iteratively with the goal of determining the corresponding scan obtained from the same subject in the base set. The proposed model uses triplet examples to train the network. Denoted by (, , ), the three input functional connectomes form the i-th triplet, where (anchor) and (positive) are of the same subject and from the target set and the base set, respectively, while (negative) belongs to a different subject and is from the base set. Herein, i = 1, ⋯, M and M is the total number of the triplets.
Encoding.
The three inputs , , and employ a neural network, denoted as E, as their shared encoder. The outputs of the encoder are called the latent variables, which denoted as , , and . Indices a, p, and n will be omitted unless otherwise specified when we are referring to a common process for , , and .
Latent variable disentanglement.
Since the age-related dramatic developmental variance highly interfere identifying the same subject’s functional connectome from the base set, we should separate the age-related variance and identity-related invariance in functional connectome. Here, zi is disentangled into three parts: Age(zi), ID(zi), and Noise(zi). They are called age-code, identity-code, and noise-code, which represent the developmental information, individualized information, and unconcerned noise, respectively. The basic requirements of the disentanglement are:
(1) The concatenation of Age(zi), ID(zi), and Noise(zi) equals zi;
(2) and should be as similar as possible, while differs from and also differs from as much as possible.
(3) Age(zi) is capable of age prediction;
(4) Noise(zi) obeys a Gaussian distribution.
Cross reconstruction requirements.
The elements in the triplet employ a neural network, denoted as G, as their shared decoder. Conventionally, since zi = [Age(zi), ID(zi), Noise(zi)] is the latent variable encoded from xi, a direct requirement is the reconstruction of xi from zi, which signifies the similarity between xi and . On the other side, since ID(zi) represents the identity-related invariance, and should be capable of replacing each other in reconstructing and . Therefore, to further ensure the effectiveness of the disentanglement, we introduce the cross reconstruction requirements: the similarity between and G([, , ]), and the similarity between and G([, , ]).
Age predictor and adversarial discriminator.
To ensure that the Age(zi) learns the age-related information, a neural network is designed as the regressor P to predict age from Age(zi). Furthermore, a discriminator D is designed to impose the adversarial regularization on Noise(zi), which tries to ensure Noise(zi) follows a Gaussian distribution through adversarial learning [16].
E, G, P, and D are all parameterized and learned together with the following losses.
Intensive triplet loss.
Ordinary triplet loss merely focuses on the relative distance between the (Anchor, Positive) and (Anchor, Negative) pairs. Considering that (Positive, Negative) is also a pair of different labels, as shown in Fig. 2, the inter-subject dissimilarity can be deeply enhanced if the relative distance between (Anchor, Positive) and (Positive, Negative) is also measured as a new constraint. Thus, a new intensive triplet loss is defined as follows, where corr is the Pearson correlation:
| (1) |
| (2) |
| (3) |
Fig. 2.
Compared with the triplet loss (a), intensive triplet loss (b) maximizes not only the distance between anchor and negative but also the distance between positive and negative.
Reconstruction loss.
The reconstruction loss is defined based on the cross-reconstruction requirements described above. It consists of ordinary reconstruction and cross reconstruction from the triplet samples. is the expectation operator.
| (4) |
| (5) |
| (6) |
Age prediction loss.
L2 norm is adopted as our regression loss for age prediction:
| (7) |
Where is the real age corresponding to .
Adversarial loss.
Let be the prior distribution of Noise(zi), Prob(xi) be the distribution of the data, and q(Noise(zi)∣xi) be the encoding distribution. The distribution requirement on Noise(zi), defined by the disentanglement, requires the aggregated posterior distribution q(Noise(zi)) = ∫xi q(Noise(zi)∣xi)Prob(xi)dxi matches the predefined prior Prob(Noise(zi)). This regularization on Noise(zi) is realized by an adversarial procedure with the discriminator D, which leads to a problem, where
| (8) |
Full Objective.
The objective functions to optimize E, G, P, and D are written as:
| (9) |
| (10) |
where , λ1, λ2, and λ3 are trade off parameters. The model alternatively updates E, G, P, and D with and .
2.2. Variance-guided bootstrap aggregating
Brain functional connectome can be represented by the upper triangle of the functional connectivity matrix. However, the whole-brain functional connectivity matrix is a high dimensional vector that is inefficient for training or trends to overfit. It has been proved that the “thin slice” of the functional connectome may still lead to comparable accuracy for individual identification [12]; therefore, bootstrap aggregating with randomly chosen partial connectivity links from the full connectome is introduced to promote the learning efficiency and effectiveness. Specifically, 1) the discriminative capability (DC) of a connection e is measured by DC(e) = σ{Ci(e)∣i = 1, ⋯, N}, where Ci is the functional connectome of the i-th scan, σ is the standard deviation operator, and N is the number of scans in the base set; 2) K connectivity links with a dimensionality far smaller than that of the original connectome are randomly chosen out of the full connectome with the probability of {P_e = DC(e)/Σe DC(e)}. By applying the chosen indices to all connectomes repetitively, we generate bootstrap samples; 3) T models are fitted by T bootstrap samples before the final identification result can be obtained by majority voting. We set K = 5000 and T = 50 in our experiment after several empirical tests.
3. Experiments
3.1. Data description
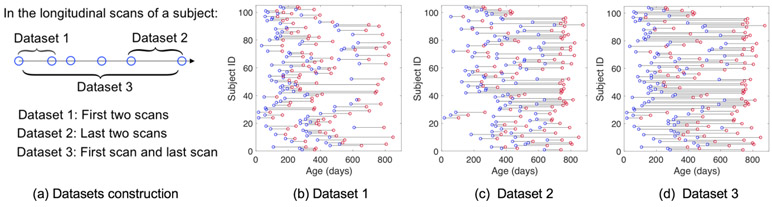
We verified the effectiveness of the proposed DI-TAE model and study the infant brain connectome fingerprinting on a high-resolution resting-state fMRI (rs-fMRI) data including 104 subjects (53 females/51 males) with 394 longitudinal scans acquired at different ages ranging from 16 to 874 days in the UNC/UMN Baby Connectome Project [23]. All infant MR images were acquired during natural sleeping on a 3T Siemens Prisma MRI scanner using a Siemens 32 channel head coil. T1-weighted and T2-weighted MR images were obtained with the resolution = 0.8×0.8×0.8 mm3. The rs-fMRIs scans were acquired with TR/TE = 800/37 ms, FA = 80°, FOV = 220 mm, resolution = 2×2×2 mm3, and total volume = 421 (5 min 47 sec). All structural and functional MR images were preprocessed following a state-of-the-art infant-tailored pipeline [21, 24-27]. Cortical surfaces were reconstructed and aligned onto a public 4D infant surface atlases [20, 28, 29]. At each cortical vertex on the middle cortical surface, its representative fMRI time-series were extracted [17]. An infant-specific functional parcellation template with 420 cortical ROIs were then constructed and warped onto each individual cortical surface. The time series within each ROI were averaged and further correlated with those from all others. The functional connectivity matrix was derived by calculating the Pearson correlation coefficient between time series of each pair of ROIs. Fishers r-to-z transformation was conducted to improve the normality of the functional connectivity. To validate our model based on data sets with different distributions of age and inter-session time gap, three datasets (i.e., Dataset 1, Dataset 2, and Dataset 3) were generated from the 394 longitudinal rs-fMRI scans. Fig. 3. illustrates how the datasets were generated and the distribution of each dataset.
Fig. 3.
Experimental datasets description. (a) The way that the three datasets constructed from the longitudinal scans; (b-d) The age distributions of the three datasets. Each line indicates a subject and each circle indicates a scan.
3.2. Validation of DI-TAE
We compare the proposed DI-TAE model with following seven methods: four state-of-the-art methods in brain connectome fingerprinting study including (1) Euclidean distance based 1-nearest neighbors algorithm (1-NN) [10]; (2) the Pearson correlation-based identification (P-Corr) [3, 4]; (3) PCA-reconstruction based identification (PCA-based) [11]; and (4) dynamic functional connectivity strength-based identification (DFC-Str) [1]. Three models derived from our DI-TAE for validating each of our proposed strategies, including: (5) taking differential power measure (DP) [3] as the contribution index to replace the discriminative capability measure, DC, defined in our model; (6) applying random selection [12] to replace the variance-guidance in the bootstrap aggregating in our model; and (7) taking the ordinary triplet loss to replace the intensive triplet loss in our model.
The encoder E and decoder G in DI-TAE were all designed as a two-layer perception neural networks. The predictor P constitutes of 6 densely connected layers of dimension (300, 500, 100, 100, 20, 1) with ReLU as the activation function. The discriminator D constitutes of 5 densely connected layers of dimension (300, 30, 30, 10, 1) with ReLU as the activation function of the first 4 layers and Sigmoid as the activation function of the last layer. DI-TAE was implemented with Pytorch and optimized with Adam by a fixed learning rate as 0.001. The batch size was set as 200. The dimension of the latent variable was 2000, while the dimensions of age code, identity code, and noise code were set as 300, 1400, and 300, respectively. λ1 = 0.1, λ2 = 0.8, and λ3 = 0.1. Except the dedicated different parts for comparison, methods (5)-(7) share the same architecture with DI-TAE for the fairness of the comparison. For DFC-Str based identification, the sliding window has a width of 125 TR (i.e., 100 s) and slide on time with a time step of 1 TR (i.e., 800 ms). The PCA components number was set to 80 in PCA-based identification.
The identification rate was measured as the percentage of subjects whose identity was correctly predicted out of the total number of subjects. The predicted identity of the scan is correct means the corresponding scan obtained from the same subject in the base set is determined. The comparison results are shown in Table 1. Without training required, the identification tests of methods (1)-(4) were implemented directly. With training and testing required, our model and methods (5)-(7) were assessed by 10 times of 10-fold cross validation. The means and standard deviations of the 10 identification accuracies are reported. Our DI-TAE model outperformed the four state-of-the-art methods by increasing their identification accuracy by more than 50%. On Dataset 2, although the age gap between the two sessions are in average 191 days, the identification accuracy still reaches 81.7%. When changing the DC in our model to DP (or random selection) or changing the intensive triplet loss proposed by us to the ordinary triplet loss, the accuracy of the model was significantly reduced, further validating the effectiveness of the proposed strategies.
Table 1.
The comparison of DI-TAE with other seven methods with identification rate (%). The scans in Session 2 were acquired later than those in Session 1.
| Target set-Base set | Session 2- Session 1 | Session 1- Session 2 | ||||
|---|---|---|---|---|---|---|
| Dataset 1 | Dataset 2 | Dataset 3 | Dataset 1 | Dataset 2 | Dataset 3 | |
| 1-NN [10] | 21.12 | 33.64 | 20.19 | 23.08 | 34.62 | 16.35 |
| P-Corr [3] | 39.42 | 50.96 | 32.69 | 42.31 | 58.65 | 33.65 |
| PCA-based [11] | 38.46 | 52.88 | 28.85 | 37.50 | 55.77 | 29.81 |
| DFC-Str [1] | 39.42 | 53.85 | 31.73 | 38.46 | 56.73 | 31.73 |
| DP [1] + ours | 49.1 ± 1.3 | 62.5 ± 0.9 | 42.6 ± 1.1 | 47.5 ± 0.7 | 61.4 ± 1.5 | 42.6 ± 1.4 |
| Random [12] + ours | 50.2 ± 3.8 | 65.2 ± 2.6 | 42.3 ± 3.5 | 46.2 ± 3.6 | 59.7 ± 2.8 | 38.9 ± 2.7 |
| Triplet loss [8] + ours | 59.2 ± 1.3 | 77.6 ± 1.7 | 57.3 ± 1.3 | 58.8 ± 1.4 | 75.3 ± 1.8 | 57.1 ± 1.5 |
| DI-TAE (proposed) | 65.6 ± 1.3 | 81.7 ± 1.5 | 63.5 ± 1.3 | 66.5 ± 1.5 | 80.1 ± 1.7 | 62.7 ± 1.3 |
3.3. Infant functional connectome fingerprinting
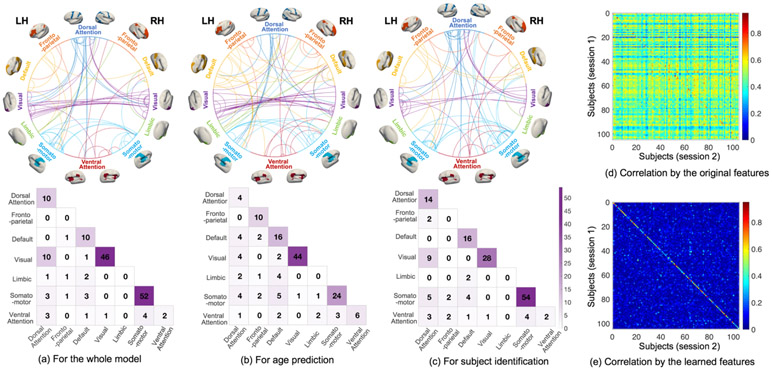
Based on our proposed model DI-TAE, the identification rate of infants on the three data sets are over 70% on average, suggesting the plausible existence of brain functional “fingerprint” during early infancy. The most contributive connections for infant fingerprinting were further analyzed by the weights of the learned encoder in DI-TAE and shown in Fig. 4. It seems that the visual and somatomotor networks manifest more individualized uniqueness during the early brain development. Compared to our findings, the connections in the frontoparietal network are more important in adult functional fingerprinting [3, 14, 15], which shows that there may be difference between the developing infant brains and the stably developed adult brains. Moreover, since better identification performance were always obtained on Dataset 2 with all the methods, we can see that it is easier to identify the identity of the scan with more developed brains and smaller age difference between the two scan sessions.
Fig. 4.
The most contributive connections for the whole identification model (a), for age prediction (b), and for subject identification (c). The most contributive connections were obtained by thresholding the whole connectome at the 99.9 percentile of weights. In the circle plots, the ROIs are organized into 7 networks [13] and lines represent connections. The numbers in the colored matrices are the number of contributive connections within and between each pair of networks. The correlation matrix between the scans of two sessions based on the original features and that based on the learned features by DI-TAE are shown in (d) and (e), respectively. Figure (e) shows that the correlation between the scans of the same subject is much larger than that of different subjects, indicating the significantly increased discriminative capability of the learned features.
4. Conclusion
In this paper, we proposed a disentangled intensive triplet autoencoder to address the absence of effective methods in studying functional connectome fingerprinting of infant brains. Disentangling the age-related variance from subject identity-related invariance, our model successfully captures individualized patterns of infant brain functional connectivity out of the overwhelming dramatic brain development. With a high identification rate for infants, for the first time, our results suggest that the brain functional “fingerprint” may exist from early infancy. Our proposed DI-TAE model serves as a potentially powerful method for studying individualized brain connectome pattern and its development, even such connectome is undergoing dramatic changes.
Acknowledgments.
This work was partially supported by NIH grants (MH116225, MH117943, MH104324, MH109773). This work also utilizes approaches developed by an NIH grant (1U01MH110274) and the efforts of the UNC/UMN Baby Connectome Project Consortium.
References
- 1.Liu J, Liao X, Xia M, et al. : Chronnectome fingerprinting: Identifying individuals and predicting higher cognitive functions using dynamic brain connectivity patterns. Human brain mapping, 39(2), pp.902–915 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Miranda-Dominguez O, Feczko E, Grayson DS, et al. : Heritability of the human connectome: A connectotyping study. Network Neuroscience, 2(02), pp.175–199 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Finn ES, Shen X, Scheinost D, et al. : Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity. Nature neuroscience, 18(11), p.1664–1674 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Horien C, Shen X, Scheinost D, et al. : The individual functional connectome is unique and stable over months to years. Neuroimage, 189, pp.676–687 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kaufmann T, Alnæs D, Doan NT, et al. : Delayed stabilization and individualization in connectome development are related to psychiatric disorders. Nature neuroscience, 20(4), pp.513–515 (2017). [DOI] [PubMed] [Google Scholar]
- 6.Gilmore JH, Knickmeyer RC and Gao W: Imaging structural and functional brain development in early childhood. Nature Reviews Neuroscience, 19(3), p.123 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhang H, Shen D and Lin W: Resting-state functional MRI studies on infant brains: A decade of gap-filling efforts. NeuroImage, 185, pp.664–684 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hoffer E and Ailon N: Deep metric learning using triplet network. In International Workshop on Similarity-Based Pattern Recognition, pp. 84–92. Springer, Cham: (2015). [Google Scholar]
- 9.Yang Y, Chen H and Shao J: Triplet enhanced autoencoder: model-free discriminative network embedding. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, pp. 5363–5369. AAAI Press; (2019). [Google Scholar]
- 10.Bishop CM: Pattern Recognition and Machine Learning (Information Science and Statistics), Springer-Verlag New York, Inc., Secaucus, NJ, USA, 2006 [Google Scholar]
- 11.Amico E and Goñi J, The quest for identifiability in human functional connectomes. Scientific reports, 8(1), pp.1–14 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Byrge L and Kennedy DP: High-accuracy individual identification using a “thin slice” of the functional connectome. Network Neuroscience, 3(2), pp.363–383 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thomas Yeo BT, Krienen FM, Sepulcre J, et al. : The organization of the human cerebral cortex estimated by intrinsic functional connectivity. Journal of neurophysiology, 106(3), pp.1125–1165 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Demeter DV, Engelhardt LE, Mallett R, et al. : Functional Connectivity Fingerprints at Rest Are Similar across Youths and Adults and Vary with Genetic Similarity. iScience, 23(1), p.100801 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vanderwal T, Eilbott J, Finn ES, et al. : Individual differences in functional connectivity during naturalistic viewing conditions. Neuroimage, 157, pp.521–530 (2017). [DOI] [PubMed] [Google Scholar]
- 16.Makhzani A, Shlens J, Jaitly N, Goodfellow I and Frey B, 2015. Adversarial autoencoders. arXiv preprint arXiv:1511.05644 (2015). [Google Scholar]
- 17.Glasser MF, Sotiropoulos SN, Wilson JA, et al. : The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage, 80, pp.105–124 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang H, Stanley N, Mucha PJ, et al. : Multi-layer Large-Scale functional connectome reveals infant brain developmental patterns. In International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer, Cham, pp. 136–144 (2018). [Google Scholar]
- 19.Stoecklein S, Hilgendorff A, Li M, et al. : Variable functional connectivity architecture of the preterm human brain: Impact of developmental cortical expansion and maturation. Proceedings of the National Academy of Sciences, 117(2), pp.1201–1206 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. https://www.nitrc.org/projects/infantsurfatlas.
- 21.Li G, Wang L, Yap P-T, et al. : Computational neuroanatomy of baby brains: A review. Neuroimage, 185, 906–925 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Duan D, Xia S, Rekik I, et al. : Individual Identification and Individual Variability Analysis Based on Cortical Folding Features in Developing Infant Singletons and Twins. Human Brain Mapping, 41(8), 1985–2003, (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Howell BR, Styner MA, Gao W, et al. : The UNC/UMN baby connectome project (BCP): an overview of the study design and protocol development. NeuroImage, 185, 891–905 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang L, Li G, Shi F, et al. : Volume-based analysis of 6-month-old infant brain MRI for autism biomarker identification and early diagnosis. in International Conference on Medical Image Computing and Computer-Assisted Intervention, 411–419 (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Li G, Nie J, Wang L, Shi F, et al. : Measuring the dynamic longitudinal cortex development in infants by reconstruction of temporally consistent cortical surfaces. NeuroImage, 90, 266–279 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li G, Wang L, Shi F, Lin W, Shen D, Simultaneous and consistent labeling of longitudinal dynamic developing cortical surfaces in infants. Medical Image Analysis, 18(8): 1274–1289 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sun L, Zhang D, Lian C, Wang L, et al. : Topological correction of infant white matter surfaces using anatomically constrained convolutional neural network. NeuroImage, 198, 114–124 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li G, Wang L, Shi F, Gilmore JH, Lin W, Shen D: Construction of 4D high-definition cortical surface atlases of infants: Methods and applications. Medical Image Analysis, 25(1), 22–36 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wu Z, Wang L, Lin W, Gilmore J H, Li G, Shen D: Construction of 4D Infant Cortical Surface Atlases with Sharp Folding Patterns via Spherical Patch-based Group-wise Sparse Representation. Human Brain Mapping, 40 (13), 3860–3880 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]