Combining mechanistic modeling and machine learning, a multivariable sudden cardiac death predictor outperforms clinical metrics.
Abstract
Cardiac sarcoidosis (CS), an inflammatory disease characterized by formation of granulomas in the heart, is associated with high risk of sudden cardiac death (SCD) from ventricular arrhythmias. Current “one-size-fits-all” guidelines for SCD risk assessment in CS result in insufficient appropriate primary prevention. Here, we present a two-step precision risk prediction technology for patients with CS. First, a patient’s arrhythmogenic propensity arising from heterogeneous CS-induced ventricular remodeling is assessed using a novel personalized magnetic-resonance imaging and positron-emission tomography fusion mechanistic model. The resulting simulations of arrhythmogenesis are fed, together with a set of imaging and clinical biomarkers, into a supervised classifier. In a retrospective study of 45 patients, the technology achieved testing results of 60% sensitivity [95% confidence interval (CI): 57-63%], 72% specificity [95% CI: 70-74%], and 0.754 area under the receiver operating characteristic curve [95% CI: 0.710-0.797]. It outperformed clinical metrics, highlighting its potential to transform CS risk stratification.
INTRODUCTION
Cardiac sarcoidosis (CS), an inflammatory heart disease characterized by the formation of noncaseating granulomas in the heart, results in substantial morbidity and decreased quality of life (1). Patients with CS are at high risk of sudden cardiac death (SCD) due to abnormal uncoordinated heart rhythms or ventricular arrhythmias. In CS, ventricular arrhythmias arise from disease-induced remodeling in the heart, including active inflammation and subsequent fibrosis proliferation (2). Prophylactic implantable cardioverter defibrillator (ICD) therapy can reduce mortality (3–5); however, it comes with a notable risk of adverse events (3, 4), necessitating precise SCD risk assessment (5). The current “one-size-fits-all” clinical criterion for SCD risk assessment, left ventricular ejection fraction (LVEF) of <35%, does not provide adequate guidance for ICD implantation in patients with CS (5). The presence of myocardial fibrosis on contrast-enhanced magnetic resonance imaging (MRI) [i.e., late gadolinium enhanced MRI (LGE-MRI)] furnishes a somewhat improved SCD risk stratification in CS (6). Modest improvement has also been achieved by visualizing active inflammation on 18F-fludeoxyglucose (FDG) positron emission tomography (PET) scans (7). Despite these efforts, a recent meta-analysis found that the level of appropriate ICD therapy in CS is only 22 to 36%, while 11 to 25% of patients receive inappropriate therapy (8).
Our team has demonstrated that mechanistic computational modeling of cardiac electrical function outperforms clinical metrics in assessing arrhythmia risk in patients with ischemic cardiomyopathy (9) and repaired tetralogy of Fallot (10). These personalized heart models incorporated the distribution of focal scar in the ventricles, an important determinant of arrhythmia propensity in these diseases (11). In CS, the spatial distributions of inflammation and fibrosis within the ventricular myocardium are believed to be key factors underlying arrhythmogenesis (12–14), in addition to other phenotypic biomarkers (15). This suggests that accurate risk stratification in CS might be achieved by developing a new generation of multiscale (i.e., from cellular to the whole heart) mechanistic models that account for arrhythmogenesis from fibrosis and inflammation and then creating a risk predictor that considers both the mechanistic assessment of arrhythmogenicity and various phenotypic biomarkers.
Here, we develop a novel two-step precision technology to assess SCD risk due to ventricular arrhythmia in patients with CS. First, multimodality imaging–based mechanistic simulations of the patient’s heart rhythm disorder are performed. Each personalized digital heart is a novel MRI-PET fusion model that assesses the patient’s arrhythmogenic propensity arising from heterogeneous CS-specific remodeling in the ventricles. Next, a supervised multivariable classifier learns from the results of mechanistic modeling and clinical and imaging biomarkers to predict the risk of SCD. We term this integrated personalized risk assessment approach the Computational Heart and Artificial Intelligence (CHAI) Risk Predictor.
In a proof-of-concept retrospective study, we demonstrate that the robust and generalizable CHAI Risk Predictor outperforms clinical metrics in forecasting arrhythmic events in patients with CS. The results showcase the potential for CHAI to radically shift the paradigm of clinical SCD risk assessment and patient selection for prophylactic ICD deployment in the CS population, resulting in prevention of arrhythmic death and avoidance of unnecessary ICD implantations.
RESULTS
CHAI Risk Prediction overview
Figure 1 presents an overview of the two-step CHAI Risk Prediction technology. In the first step, the patient’s ventricular arrhythmia propensity is noninvasively assessed in a personalized MRI-PET mechanistic heart model. This three-dimensional (3D) multiscale model incorporates the individual patient’s heart geometry and the unique arrhythmia substrate in CS, composed of heterogeneously distributed regions of fibrosis and inflammation. Regions of disease-induced remodeling are segmented from the corresponding clinical images of the patient’s heart: LGE-MRI for fibrosis and FDG-PET for inflammation. Following image fusion, regions of fibrosis and inflammation within the resulting 3D model are assigned disease-specific regional cell and tissue electrophysiological properties (Fig. 2, A to C). This manifests at the whole-heart level as regional slowing of conduction velocity, altered tissue anisotropy, and regional changes in refractoriness (14, 16, 17). Simulations of each personalized heart model’s responses to rapid pacing delivered from multiple biventricular sites reveal all potential ventricular arrhythmias [ventricular tachycardias (VTs), typical in CS] that could arise from the patient’s CS-remodeled substrate.
Fig. 1. The multivariable CHAI Risk Predictor synergistically combines mechanistic modeling and ML.
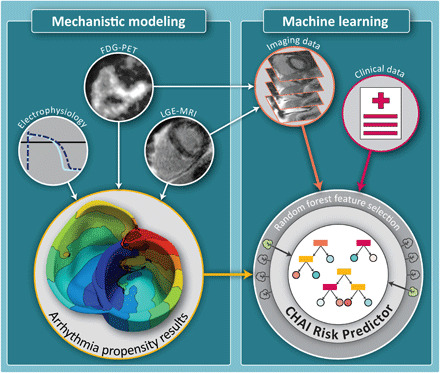
In the first step (left), LGE-MRI and FDG-PET images are used, together with electrophysiological data, to create personalized MRI-PET fusion models. Mechanistic computational modeling of cardiac electrical function is performed to investigate the arrhythmia propensity of the CS patient’s heart. In the second step (right), a supervised ML algorithm is trained and optimized to predict the risk of SCD due to ventricular arrhythmia using features selected by a random forest algorithm from three types of inputs: (i) features characterizing the patient’s arrhythmogenic propensity extracted from the results of mechanistic simulations (yellow arrow), (ii) features extracted from clinical images characterizing heterogeneity in disease remodeling in the patient’s ventricles (orange arrow), and (iii) baseline patient data (red arrow).
Fig. 2. MRI-PET fusion mechanistic heart models represent the unique arrhythmia substrate in CS.
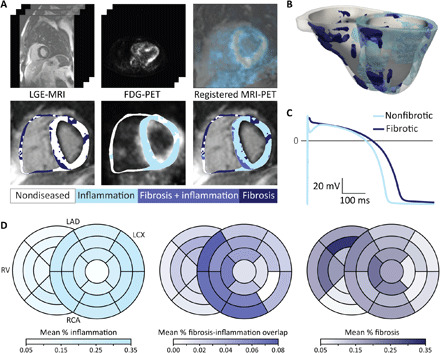
(A) LGE-MRI (top left) and FDG-PET (top middle) images are rigidly registered on the basis of mutual information and anatomical landmarks (top right). Typical LGE-MRI resolution is 1.75 mm by 1.75 mm by 10 mm, and typical FDG-PET resolution is 4.7 mm by 4.7 mm by 3.3 mm. Intensity-based thresholding is used to identify fibrosis and inflammation on LGE-MRI (bottom left) and FDG-PET (bottom middle), respectively, then regions of overlap are identified from the overlaid fibrosis and inflammation segmentations (bottom right). (B) Reconstructed heart model for the patient whose LGE-MRI and FDG-PET images are shown in (A). (C) Action potential traces for nonfibrotic and fibrotic myocardium. Figure S2 shows the methodology for mechanistic simulations of arrhythmogenesis in each MRI-PET fusion heart model. (D) Mean proportion of each type of disease-induced remodeling present in each of the 26 American Heart Association (AHA) segments for the 45 patients, the reconstructed models of which are presented in fig. S1. Darker colors indicate that remodeling is relatively more common in that location compared with other locations. LAD; left anterior descending artery, LCX; left circumflex, RCA; right coronary artery.
In the second step, a supervised machine learning (ML) algorithm uses features extracted from the results of the mechanistic simulations of VT induction (450 mechanistic modeling runs, each resulting in millions of transmembrane voltage data points over time, reduced to multiple arrhythmia propensity quantifiers), combined with additional patient data, to complete VT risk prediction for each patient with CS. Additional features include baseline clinical data that could predispose to SCD risk and features extracted from the patient’s LGE-MRI and FDG-PET images—a complete list is provided in table S2. Although LGE-MRI and FDG-PET are used to construct each MRI-PET fusion model, the modeling process can be thought of as dimensionality reduction of the images (binary thresholding of fibrosis and inflammation, myocardium segmentation). The MRI-PET fusion model does not explicitly represent heterogeneities in the degree of fibrosis and inflammation in each region of remodeling; previous work has suggested that these heterogeneities may be associated with VT risk (18). Thus, variables that quantified these heterogeneities were made available to the classifier in feature selection. Among all features, only the most important ones, as determined by a random forest algorithm, are included in the final VT risk classifier.
A full description of the CHAI methodology—including the construction of the MRI-PET fusion multiscale models; simulation protocol to assess VT inducibility; feature extraction; and training, optimization, and testing of the ML algorithm—is provided in Materials and Methods. Where applicable, we have prepared this manuscript according to the transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD) guidelines (table S1) (19).
CHAI proof-of-concept study: Patient cohort and clinical SCD risk prediction
To evaluate the ability of the CHAI Risk Predictor to correctly assess each patient’s clinical VT risk, we performed a retrospective proof-of-concept study of 45 patients with adjudicated CS from a single center. The study was approved by the Johns Hopkins University Institutional Review Board. Table 1 provides clinical and imaging characteristics for all patients in the study. Median follow-up was 1.71 years [interquartile range (IQR): 0.67 to 2.53 years]; 16 patients (36%) experienced clinical VT during follow-up. There were no statistically significant differences in any demographic or clinical characteristics between patients who did and did not experience clinical VT. Patients who experienced clinical VT had statistically significantly higher burdens of disease remodeling (fibrosis, inflammation, and fibrosis-inflammation overlap).
Table 1. Clinical and imaging characteristics for retrospective CS cohort.
Values are provided as means (SD), n (%), or median [Q1, Q3] as appropriate. P values were calculated with two-sided two-sample t test, chi-square test, Fisher’s exact test, or Kruskal-Wallis test.
| Missing | Overall | No clinical VT | Clinical VT | P | |
| n | 45 | 29 | 16 | ||
| Demographic and clinical characteristics | |||||
| Age (years) | 0 | 54 (11) | 54 (9) | 53 (14) | 0.674 |
| Female sex | 0 | 20 (44%) | 16 (55%) | 4 (25%) | 0.102 |
| Weight (kg) | 1 | 91.8 (22.2) | 89.2 (20.9) | 96.6 (24.4) | 0.327 |
| Enhancement present on LGE-MRI |
0 | 32 (71%) | 18 (62%) | 14 (88%) | 0.094 |
| Abnormal uptake on FDG-PET |
0 | 32 (71%) | 18 (62%) | 14 (88%) | 0.094 |
| LVEF | 0 | 50.6 (14.7) | 52.0 (15.4) | 48.1 (13.5) | 0.376 |
| QRS duration (ms) | 3 | 114 (31) | 107 (29) | 126 (33) | 0.079 |
| Follow-up and clinical events | |||||
| Time between MRI and PET (days) |
4* | 53 [28, 158] | 55 [29, 161] | 53 [18, 138] | 0.808 |
| Follow-up duration (days) | 0 | 624 [244, 925] | 600 [322, 847] | 677 [100, 1071] | 0.713 |
| ICD implantation | 0 | 16 (36%) | 5 (17%) | 11 (69%) | 0.002 |
| Appropriate shock | 0 | 5 (11%) | 0 (0%) | 5 (31%) | 0.004 |
| Burden of disease remodeling (as % of myocardial volume) | |||||
| Nondiseased | 0 | 0.652 (0.251) | 0.718 (0.235) | 0.532 (0.241) | 0.018 |
| Fibrosis | 0 | 0.153 (0.034) | 0.144 (0.029) | 0.170 (0.035) | 0.019 |
| Inflammation | 0 | 0.236 (0.297) | 0.163 (0.275) | 0.368 (0.298) | 0.031 |
| Fibrosis-inflammation overlap |
0 | 0.041 (0.054) | 0.025 (0.044) | 0.070 (0.058) | 0.013 |
| Fibrosis, excluding overlap with inflammation |
0 | 0.112 (0.056) | 0.119 (0.049) | 0.100 (0.066) | 0.328 |
| Inflammation, excluding overlap with fibrosis |
0 | 0.195 (0.248) | 0.138 (0.233) | 0.298 (0.248) | 0.043 |
*Exact dates for both MRI and PET are unavailable for four patients because of heterogeneous deidentification procedures, but patients were only included in the study if it could be determined that their MRI and PET were acquired less than 1 year apart. No patients in the cohort experienced inappropriate shocks during follow-up.
To establish a baseline level of clinical risk prediction accuracy for this cohort, we applied three SCD risk prediction metrics, each currently used in clinical practice, to the dataset: LVEF of <35% (5), qualitative assessment by a radiologist of the presence of fibrosis on LGE-MRI (6), and qualitative assessment by a radiologist of the presence of inflammation (abnormal FDG uptake) of FDG-PET (7). No method achieved sensitivity and specificity greater than 40% (Table 2). These results are in line with previous studies of VT risk prediction in CS (5–7) and support the need for a risk prediction methodology for patients with CS that achieves high sensitivity and specificity.
Table 2. Results of clinical SCD risk prediction methods applied to CS cohort.
While MRI-based and PET-based risk prediction achieved the same numeric results, the group of patients with fibrosis on LGE-MRI was not found to be the same as the group with abnormal uptake on FDG-PET, although there was an overlap between the groups. PPV, positive predictive value; NPV, negative predictive value.
| Clinical risk prediction method | Sensitivity | Specificity | PPV | NPV | Accuracy |
| LVEF <35% | 0.125 | 0.828 | 0.286 | 0.632 | 0.555 |
| Fibrosis on LGE-MRI | 0.875 | 0.379 | 0.438 | 0.846 | 0.555 |
| Abnormal uptake on FDG-PET | 0.875 | 0.379 | 0.438 | 0.846 | 0.555 |
CHAI proof-of-concept study: MRI-PET mechanistic modeling
3D MRI-PET fusion electrophysiological models were developed for the 45 patients in the cohort, as presented in Fig. 2 (A to C) and described in Materials and Methods. Geometrical models for all patients are presented in fig. S1, highlighting the differences in the distribution of disease remodeling in the patient population; Fig. 2D illustrates the most frequent anatomical locations of disease remodeling. MRI-PET mechanistic modeling was validated with clinical ablation data (Fig. 3), demonstrating correspondence between predicted VT circuits and clinical ablation targets, as detailed in Materials and Methods. Simulations of VT induction via rapid pacing were performed in each personalized MRI-PET model to assess propensity to VT.
Fig. 3. Validation of MRI-PET fusion models by correspondence of induced VTs with clinical ablation lesions.

(A) Multiple views of two patients’ reconstructed MRI-PET fusion heart models. White stars indicate pacing locations from which each VT (shown in the corresponding row of the center column) was induced in the model following rapid pacing. (B) Activation maps of the VTs induced in each patient’s heart (numbered). White arrows indicate pathways of reentrant propagation. White dashed arrows indicate that the pathway passes through myocardium that is not visible in the displayed orientation. Isochrone line spacing is 22.5 ms. (C) Right: Clinical ablation lesions (red) and endocardial volume exported from the electroanatomical mapping system (EAM, Ensite, St. Jude Medical) (dark gray) shown registered to the reconstructed heart model (green). For patient 1, lesions were made on the RV endocardium. For patient 2, lesions were executed on both the RV and LV endocardium. Inset: Lesions and endocardial volume exported from the EAM overlaid on activation maps from (B) to illustrate correspondence between reentry pathways and clinical ablation lesions. Further detail on MRI-PET model validation is presented in Materials and Methods.
Figure 4 illustrates the mechanisms of VTs induced in the heart models of patients with CS. As Fig. 4 (A and B) shows, areas of fibrosis and fibrosis-inflammation overlap often serve as obstacles around which a VT reentrant pathway forms. Depending on its spatial distribution, fibrosis can also be part of the reentrant pathway (Fig. 4, C and D), as it sustains slow conduction. Regions of inflammation also often comprise part or all of the reentrant pathway due to the slowed transverse conduction there. Figure 4E presents the proportion of reentry pathways through each AHA (American Heart Association) segment; these can be compared to the regional occurrences of diseased-induced remodeling (Fig. 2D). Inflammation was most often found in the left ventricle (LV), while fibrotic remodeling was most frequently located on the septum, anterior wall of the right ventricle (RV), and left ventricular outflow tract. Reentry was most often located on the septum, consistent with clinical studies (17). In Fig. 4E, a total of 1170 AHA segments were assessed (26 per patient); it was found that at least 1 reentry pathway was partially or completely located in 135 of these segments across 78 unique reentry pathways induced in 28 patients’ MRI-PET fusion models. Regions with high proportions of fibrosis-inflammation overlap or fibrosis were most likely to sustain reentry (Fig. 4F). The probability of reentry decreased with the proportion of nondiseased tissue: Regions with 80 to 100% nondiseased tissue had only a 6% chance of sustaining reentry. These results indicate that the spatial distribution of disease-induced remodeling is a major determinant of reentry location; the tissue composition alone does not entirely predict whether a reentry will pass through a given region.
Fig. 4. Disease-induced remodeling leads to reentrant VT in MRI-PET fusion models.
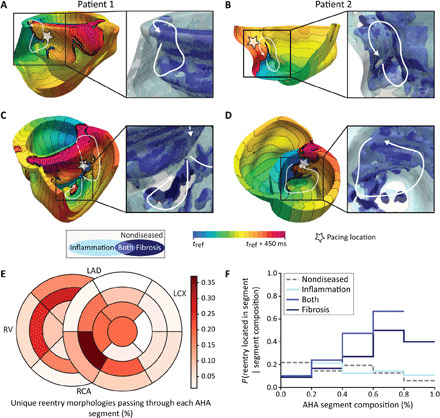
(A to D) Electrical activation maps showing reentrant VT induced in the MRI-PET fusion models in the same two patients as in Fig. 3 [patient 1 in (A) and (C) and patient 2 in (B) and (D)]. A total of 450 ms of electrical activity are shown as isochrones of electrical activation in each model; isochrone line spacing is 22.5 ms. White arrows mark the reentry pathways. White star indicates pacing location. Inset (right side of each panel): Zoomed-in view of substrate heterogeneity near the induced VT. (A) and (B) show that regions of fibrosis can be part of the reentry pathway, slowing conduction enough to create an excitable gap that allows reentry to be sustained. Areas of fibrosis and fibrosis-inflammation overlap can also serve as obstacles around which a reentrant pathway forms, as in (C) and (D). This occurs if the propagating wavefront cannot pass through these regions faster (due to significantly slowed conduction and decreased anisotropy) than it can travel around them through regions of nondiseased myocardium or inflammation. Regions of inflammation characterized with slowed transverse conduction (and thus decreased wavelength) often make up part or all of the reentry pathway. (E) Percent of unique reentry pathways in all patients’ models (78 total) passing through each AHA segment. (F) Probability of ≥1 reentry pathway(s) passing through an AHA segment given the segment’s tissue composition. This can be read as, “If the AHA segment is made up of 60 to 80% fibrosis-inflammation overlap, there is a 67% chance that ≥1 reentry morphology will pass through that segment.”
CHAI proof-of-concept study: Mechanistic simulation-only VT risk prediction
We first predicted VT risk using only the results of mechanistic simulations, before proceeding with the AI part of the technology. Following previous studies (9, 10, 20), a patient was deemed at risk for VT if sustained VT was induced in the personalized model from at least one pacing site; we termed this simulation-only risk prediction methodology SimVT (Fig. 5A). Like the clinical risk prediction methodologies, SimVT was applied to the entire dataset at once since it did not require training. SimVT achieved 88% sensitivity and 52% specificity (Fig. 5B). It provided improvement over clinical risk prediction methodologies but resulted in an imbalance of sensitivity and specificity due to its heuristic nature. However, there was a significantly higher level of arrhythmogenic propensity in the models of patients who experienced VT (Fig. 5C). This suggests that there may be additional predictive information embedded in the VT induction simulation results that was not harnessed by SimVT.
Fig. 5. Simulation-only risk prediction methodology and results.

(A) Binary simulation-only risk prediction methodology (SimVT) as proposed by Arevalo et al. (9). (B) Results of SimVT when applied to the entire CS cohort of 45 patients. (C) The number of pacing sites, out of 10 sites in total, from which VT was induced, is statistically significantly higher (***P < 0.001) in the models of patients who experienced clinical VT (red) versus patients who did not (blue). Sensitivity, Sens; specificity, Spec; positive predictive value, PPV; negative predictive value, NPV; accuracy, Acc.
CHAI proof-of-concept study: Multivariable ML risk predictor development
The full CHAI Risk Predictor was next implemented. It consisted of feature extraction from the VT inducibility simulation results (450 mechanistic model runs), preprocessing of features extracted from all data sources (simulations results, clinical data, and imaging), random forest feature selection, and a random forest classifier. Hyperparameters of the ML pipeline were optimized with a Bayesian Gaussian Process optimizer, which decreased computation time and increased the likelihood of convergence compared to a random search or grid search. The absence of knowledge of which features from the VT inducibility simulation results could be most predictive necessitated the use of supervised ML algorithm to extract features from the mechanistic simulation results (referred to as “fit-from-training” features in the remainder of the results). Details are provided in Materials and Methods. Because of the small dataset size, data from all patients were used to train, optimize, and estimate the validation and testing performance of the risk predictor.
CHAI proof-of-concept study: Classifier performance
To estimate the expected performance of the CHAI Risk Predictor on previously unseen patients, we performed 560 iterations of nested stratified cross-validation, resulting in a total of 560 outer test sets and 2800 inner cross-validation sets. This allowed us to calculate 95% confidence intervals (CIs) for each performance metric. The test sets were made up of 20% of the total dataset, selected in a controlled random fashion so that all unique combinations of three patients who experienced VT were held out in exactly one test set each [ = 560]. Patients in each test set who did not experience VT were selected via random repeated fivefold cross-validation splitting. Overfitting and lack of generalizability (ability to accurately predict risk of previously unseen patients) are common pitfalls of ML classifiers trained with few input samples, so this allowed us to examine whether the CHAI Risk Predictor was generalizable given the small dataset.
The CHAI Risk Predictor achieved a testing sensitivity of 60% (95% CI: 57 to 63%) and specificity of 72% (95% CI: 70 to 74%). In comparison to the other metrics evaluated here (LVEF, LGE-MRI, FDG-PET, and SimVT), the CHAI Risk Predictor achieved a balance of sensitivity and specificity in testing (Fig. 6A), while the other four metrics had either high sensitivity or specificity (Table 2 and Fig. 5B). It achieved a cross-validation area under the receiver operating characteristic curve (AUROC) of 0.856 (95% CI: 0.849, 0.862) and a testing AUROC of 0.754 (95% CI: 0.710, 0.797) (Fig. 6B). The nonoverlapping CIs imply that some overfitting occurred, but this is expected in classifiers trained with data from a small cohort. The test results indicate strong generalizability despite mild overfitting.
Fig. 6. CHAI Risk Predictor cross-validation and testing results.
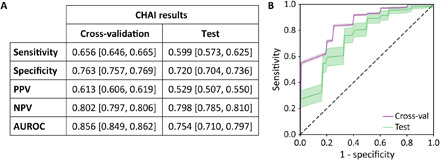
(A) Cross-validation and testing performance metrics presented as mean (95% CI). CIs (95%) are calculated by aggregating the results over 560 iterations of nested cross-validation. (B) Receiver operating characteristic curves for cross-validation (purple) and testing (green). Shaded regions represent 95% CIs, calculated via nested cross-validation with 2800 inner-loop cross-validation sets and 560 outer-loop test sets.
Table 3 lists the 20 features most often selected for inclusion in the final optimized classifier in each iteration of nested cross-validation, in order of mean importance in the trained classifier after selection. Up to five features were selected in each iteration. Most of the frequently selected features were derived from imaging (discussion of that is found in Materials and Methods), but simulation features had high importance when selected and tended to be more different between the groups of patients with and without clinical VT, suggesting that they are highly predictive. Clinical data features were rarely selected. Despite the poor performance of the LGE-MRI and FDG-PET clinical risk assessments, burdens of disease remodeling (i.e., total amounts of total amounts and proportions of varying degrees of fibrosis, fibrosis-inflammation overlap, and inflammation) were frequently selected—this exemplifies the ability of the CHAI Risk Predictor to integrate predictive information from the fused MRI-PET images.
Table 3. The 20 most frequently selected features and their mean importance over 560 iterations of nested cross-validation.
Mean importance refers to the importance in the trained random forest classifier after the feature has been selected. Values are provided as median [Q1, Q3] for patients in the entire dataset who did and did not experience clinical VT. P values are calculated with the Kruskal-Wallis test. Note that these are not the only features selected over 560 optimized ML classifiers with 560 different development sets. Optimal hyperparameters for calculation of fit-during-training simulation features are determined via fivefold stratified cross-validation on the entire dataset. Proportion of pacing locations from which sustained reentry is induced, Psus; SDs above the mean of normal myocardium, SD; VT inducibility score, weighted, VTIw; importance, imp; simulation results, simu.
| Feature name | Source |
Mean imp. when selected |
Selection frequency |
No VT (n = 29) | VT (n = 16) | P |
|
Psus, 4 extra stimuli, fit from training |
Simu | 0.374 | 0.045 | 0.000 [0.000, 1.000] | 1.500 [1.000, 2.000] | <0.001 |
| Fractal ratio, ≥5 SD | MRI | 0.362 | 0.029 | 0.035 [0.032, 0.038] | 0.030 [0.027, 0.032] | 0.001 |
| LV inflammation (%) | PET | 0.354 | 0.023 | 0.017 [0.000, 0.280] | 0.530 [0.171, 2.025] | 0.002 |
| Fractal ratio, ≥6 SD | MRI | 0.349 | 0.041 | 0.040 [0.037, 0.045] | 0.032 [0.029, 0.039] | 0.004 |
| Fractal dimension, ≥6 SD, 0.28 cm3 box |
MRI | 0.324 | 0.021 | 0.729 [0.697, 0.764] | 0.791 [0.755, 0.805] | 0.008 |
| Whole heart, fibrosis-inflammation overlap (%) |
MRI-PET | 0.309 | 0.705 | 0.000 [0.000, 0.027] | 0.055 [0.022, 0.118] | <0.001 |
| Whole heart, ratio: Inflamed fibrosis to all fibrosis (%) |
MRI-PET | 0.295 | 0.066 | 0.000 [0.000, 0.187] | 0.289 [0.131, 0.759] | 0.001 |
| Whole heart, nondiseased (%) |
MRI-PET | 0.295 | 0.809 | 0.813 [0.731, 0.871] | 0.621 [0.360, 0.701] | 0.002 |
| VTIw, 4 extra stimuli, fit from training |
Simu | 0.294 | 0.043 | 0.000 [0.000, 0.250] | 0.500 [0.250, 1.000] | <0.001 |
| Fractal ratio, ≥4 SD | MRI | 0.279 | 0.027 | 0.032 [0.030, 0.034] | 0.029 [0.025, 0.029] | 0.001 |
| Fractal dimension, ≥6 SD, 0.14 cm3 box |
MRI | 0.278 | 0.021 | 0.876 [0.866, 0.888] | 0.907 [0.879, 0.921] | 0.003 |
| Ratio: Diffuse fibrosis to all fibrosis |
MRI | 0.273 | 0.021 | 0.851 [0.781, 0.891] | 0.767 [0.682, 0.830] | 0.008 |
| Whole heart, ≥4 SD (%) |
MRI | 0.269 | 0.020 | 0.064 [0.045, 0.071] | 0.077 [0.068, 0.101] | 0.001 |
| Ratio: Diffuse fibrosis to dense fibrosis |
MRI | 0.253 | 0.025 | 5.724 [3.560, 8.188] | 3.309 [2.148, 4.900] | 0.008 |
| Whole heart, diseased (%) |
MRI-PET | 0.250 | 0.023 | 0.187 [0.129, 0.269] | 0.379 [0.299, 0.640] | 0.002 |
| VTIw, 4 extra stimuli, RV pacing |
Simu | 0.249 | 0.020 | 0.000 [0.000, 0.000] | 0.250 [0.250, 0.500] | 0.001 |
| Fractal dimension (≥4 SD, 0.14 cm3 box) |
MRI | 0.239 | 0.025 | 0.906 [0.898, 0.913] | 0.918 [0.911, 0.934] | 0.001 |
| Whole heart, inflammation only (%) |
MRI-PET | 0.219 | 0.714 | 0.031 [0.000, 0.120] | 0.244 [0.087, 0.464] | 0.003 |
| Whole heart, all fibrosis (%) |
MRI | 0.184 | 0.521 | 0.133 [0.124, 0.159] | 0.170 [0.144, 0.182] | 0.015 |
| Whole heart, fibrosis only (%) |
MRI-PET | 0.108 | 0.698 | 0.126 [0.115, 0.143] | 0.115 [0.039, 0.144] | 0.227 |
DISCUSSION
This study presents a multivariable classifier technology to assess the risk of SCD due to arrhythmia in the CS patient population: the CHAI Risk Predictor. In a proof-of-concept study of 45 patients with CS, CHAI was found to be appreciably superior in predicting arrhythmic events compared to current clinical risk metrics. The four current risk metrics evaluated are binary and thus have a fixed level of sensitivity and specificity. In contrast, the CHAI Risk Predictor can be trained to target different trade-offs between sensitivity and specificity depending on the algorithm used to select the binary “cut point” from the continuous predicted risk scores. In this study, the cut point was selected automatically to balance sensitivity and specificity for the training data before being applied to predict risk for the validation or testing data. When trained with this methodology, the CHAI Risk Predictor achieved high sensitivity and specificity in testing, in contrast to the severe imbalance of sensitivity and specificity in current clinical risk prediction metrics.
Assessment of SCD risk in patients with CS, a complex cardiac disease, has been traditionally very difficult (2). As a result, many patients with CS undergo unnecessary ICD implantations, while others who would benefit from an ICD do not receive one (5), often perishing in the prime of their life. Should the superior risk prediction capability of CHAI be confirmed in larger prospective clinical studies, it could transform the management of patients with CS, a population for whom there is currently no reliable arrhythmia risk prediction approach. The CHAI Risk Predictor could eliminate many unnecessary ICD implantations and their associated complications (infections, device malfunctions, and inappropriate shocks) while ensuring that patients with CS at high risk for lethal arrhythmias are adequately protected. The risk assessment could be repeated at follow-ups when patients are reimaged to account for changes in arrhythmia susceptibility over time if the diseased substrate remodels.
The CHAI Risk Predictor incorporates a novel digital heart methodology to assess the arrhythmogenic propensity of the CS-remodeled substrate. Personalized biophysically detailed heart models are reconstructed from both LGE-MRI and FDG-PET images, each representing different aspects of electrophysiological disease remodeling, and used to evaluate VT inducibility. These are the first personalized heart models created with data from multiple imaging modalities. Further, the combined electrophysiological effects of inflammation and fibrosis have never been previously represented in heart models. The approach presented here thus charts a previously unexplored path in the development and utilization of patient-specific mechanistic simulations in diagnosis and treatment of heart rhythm disorders. Similar to the methodology here, MRI techniques such as native T1 mapping and extracellular volume mapping could be incorporated in biophysically detailed modeling of complex heart diseases. Last, this is one of the very few studies to develop and use a large number of personalized mechanistic heart models and apply them to address a clinical need. As a matter of fact, the cohort of 45 patients is the largest cohort in any patient-specific biophysically detailed computational ventricular modeling study to date. Previous such efforts have been limited to small sample sizes and had been used predominantly to explore arrhythmia mechanisms, rarely considering the potential translational utility of cardiac computational modeling.
Mechanistic cardiac modeling is based on the foundation of well-established biophysical principles such as ion transport kinetics across membranes and the laws of electrical current flow in connected cells. While simulations can predict how remodeling in the diseased heart can disrupt normal electrical current propagation and cause arrhythmias, they cannot determine how such arrhythmogenic conditions may be inadvertently altered by other real-world patient-specific variables (which are represented by the clinical data) and cannot determine the level of arrhythmia risk on their own. Furthermore, dimensionality reduction of imaging data takes place in mechanistic model construction—a model is created via image segmentation and binary thresholding, but heterogeneities in the degree and distribution of disease-induced remodeling, which may be predictive of clinical outcomes, are lost in the process. The multivariable ML classifier developed here addresses these issues by learning from the combination of arrhythmogenesis simulation results and other patient-specific data. The use of deterministic simulation results in the ML predictor reduces the complexity of the learning process by contributing features that explicitly reflect arrhythmogenesis arising from disease-induced remodeling, thus ensuring excellent test performance and generalizability despite the potential limitation of the small patient cohort.
ML and mechanistic modeling have historically been distinct approaches. The CHAI Risk Predictor illustrates how they can be used synergistically and suggests how to overcome concerns over clinical decisions being informed by “black-box” algorithms that lack explainability. The technology developed here paves the way for the use of integrative approaches in precision medicine that predict adverse events in complex diseases with a high degree of accuracy and mechanistic underpinning. The merging of computational modeling and data science with medicine, as exemplified by the CHAI technology, is poised to lead to major advances in the improvement of patient care.
MATERIALS AND METHODS
Study design and participants
The CHAI Risk Predictor was developed and assessed using retrospective data from 45 patients with adjudicated CS evaluated at the Johns Hopkins Hospital. The sample size was determined by the availability of retrospective data that met the inclusion and exclusion criteria for the study, as described below. Personalized MRI-PET mechanistic heart models were developed for all patients, and simulations of VT inducibility were performed in each model. Simulation result data from 450 simulation runs were used for VT inducibility feature extraction by a supervised algorithm. These features were combined with a set of imaging features and patient clinical biomarkers and used in a multivariable ML classifier. The risk predictor was trained, optimized, and evaluated with nested stratified cross-validation to calculate 95% CIs for all cross-validation and testing performance metrics. Researchers performing manual or semimanual steps (segmentation and analysis of VT morphologies) in the model construction and ML feature extraction processes were blinded to clinical outcomes.
Criteria for inclusion were adjudicated CS, clinical assessment including LGE-MRI and FDG-PET imaging, and clinical follow-up including assessment of arrhythmia outcomes. Patients were excluded from the study if their LGE-MRI and FDG-PET scans were acquired more than 1 year apart, if either scan was not of high enough quality for model reconstruction (due to motion artifact, poor preparation for FDG-PET, or ICD artifact), or if they had a comorbid heart condition (such as arrhythmogenic right ventricular cardiomyopathy) that could confound their arrhythmia risk. These criteria were established before searching the Johns Hopkins retrospective sarcoid database. A total of 57 patients met the inclusion criteria for the study, and 12 were excluded for these reasons. For the 45 patients included in the study, LGE-MRI and FDG-PET imaging data were acquired at a median of 53 days (and a maximum of 10 months) apart (IQR: 28 to 158 days). Images were acquired between 2008 and 2018. Clinical data (age, weight, sex, and QRS duration) were collected at the same time as imaging data for each patient.
The median follow-up period was 1.71 years (IQR: 0.67 to 2.53 years); patients were followed clinically for assessment of CS progression and/or follow-up post-ICD implantation. The outcome of interest, clinical VT, was defined as multiple episodes of nonsustained VT or any episodes of sustained VT. Of the 16 (36%) patients in the cohort who experienced clinical VT, 11 (69%) received ICDs, and 5 (31%) had appropriate shocks. Inappropriate shock data were not available. Of the 29 (64%) patients in the cohort who did not experience clinical VT, 5 (17%) received ICDs.
LGE-MRI and PET imaging data acquisition
Cardiac LGE-MRI imaging visualizes myocardial fibrosis. LGE-MRI imaging data used retrospectively in this study were acquired on 1.5-T scanners (GE Medical Systems, Waukesha, WI or Avanto, Siemens, Erlangen, Germany) using electrocardiographic gating and breath holding as previously described (21). LGE imaging was performed 10 to 18 min after an injection of gadolinium (0.2 mmol/kg; gadopentetate dimeglumine; Bayer Healthcare Pharmaceuticals, Montville, NJ, USA). Phase-sensitive inversion recovery gradient recall echo sequences (repetition time of 2.5 to 5.5 ms, echo time of 1.52 ms, flip angle at 10°, in-plane resolution of 1.3 mm by 1.3 mm, slice thickness of 10.0 mm, and inversion time selected for maximal myocardial nulling, typically 240 to 290 ms) were used for the assessment of myocardial fibrosis.
FDG-PET imaging assesses myocardial inflammation. Before acquisition of the FDG-PET imaging data used retrospectively in this study, patients were instructed to follow a high-fat, low-carbohydrate diet for 1 day followed by 12 hours of fasting (22) to shift myocardial metabolism to fatty acid utilization and suppress the uptake of FDG by the normal myocardium. Myocardial metabolic imaging was performed with cardiac PET/computed tomography (CT; Discovery Rx VCT PET/CT, GE Healthcare, Waukesha, WI). Cardiac and whole-body FDG PET/CT scans were performed 60 min after intravenous administration of FDG at a dose of 0.135 mCi/kg as previously described (23).
Generating personalized MRI-PET fusion heart models
Figure 2 presents an overview of the methodology for constructing personalized MRI-PET fusion heart models. Figure S2 presents additional detail about the approach, with a flowchart of the modeling process shown in fig. S2A. The various steps in geometric model construction, assigning of electrophysiological properties to the different CS-remodeled regions in the ventricular myocardium, and the simulation protocol to assess the arrhythmogenic propensity of the disease-induced substrate by rapid pacing in each personalized model are described below.
Geometrical model construction
Geometrical model construction began with registration of 3D stacks of LGE-MRI and FDG-PET images in 3D Slicer (24). Rigid automatic initialization to maximize mutual information between the 3D image stacks was performed, followed by semimanual rigid landmark-based adjustment. The FDG-PET images were interpolated to the resolution of the LGE-MRI. The ventricular myocardium was segmented from LGE-MRI in CardioViz3D using a validated semiautomatic method (25), which has been used in previous virtual heart projects by our team (9, 10, 20, 26).
Next, fibrotic tissue was segmented on each slice of the LGE-MRI scan using the signal threshold to reference mean method (27). First, Otsu thresholding was used to binarize the myocardium regions of high and low intensity as we have done previously, with separate thresholds calculated for the RV and LV to account for differing intensity of nonfibrotic myocardium (10). The mean of the lower-intensity region was then chosen as the reference mean of normal myocardium. A threshold of ≥3 SD was used for fibrotic tissue because it has been shown to accurately capture diffuse fibrosis in other cardiomyopathies (27, 28); there have not been studies of the optimal threshold to identify fibrosis specifically in CS. The myocardial segmentation was projected onto the interpolated FDG-PET scan using the rigid transformation matrix calculated in the registration step, and then areas of active granulomatous inflammation within the myocardium were identified from FDG-PET using a body weight standardized uptake value (SUVBW) threshold of 4. In the absence of previously published experimental data that correlated SUVBW with local electrophysiological changes or suggested a cutoff value of SUVBW to define acute inflammation, the threshold was based on the minimum value for standardized uptake value maximum for the CS cohort in the 2014 clinical study by Osborne et al. (29). Figure 2A shows the registration, segmentation, and thresholding process for LGE-MRI and PET images.
A 3D mesh with a mean edge length of 350 μm was created from the segmented images using Synopsys’ Simpleware ScanIP software. Segmented regions of fibrosis and inflammation were interpolated to 350-μm3 voxel resolution and mapped onto the mesh using a previously described method (9, 26). Fiber orientations in the mesh were assigned on a per-element basis using a validated approach (30) used in a number of previous publications (9, 10, 20, 26). Briefly, the Laplace-Dirichlet method was used to define transmural and apicobasal directions at every point in the ventricles, and then bidirectional spherical linear interpolation was applied to assign fiber orientations based on a set of rules.
Modeling the electrophysiology of the CS ventricles
The methodology for computational modeling of the electrophysiology of the CS ventricles implemented here involved assigning different electrophysiological properties in regions of active granulomatous inflammation and fibrosis that had progressively replaced inflammation. Four tissue regions were defined in the geometrical models reconstructed from the LGE-MRI and FDG-PET images: nondiseased myocardium, inflamed myocardium, fibrotic myocardium, and areas of overlap between inflamed and fibrotic myocardium, each with different electrophysiological properties at the cell and tissue levels (Fig. 2C and fig. S2B). Below, we describe the electrophysiological properties assigned to each region and provide justification for each modeling choice.
Modeling the ion channel kinetics of the CS ventricles
The 3D ventricular models incorporated human ventricular myocyte action potential dynamics. To represent nondiseased myocardium, the ten Tusscher human ventricular membrane kinetic model was used, with added representation of INaL from the O’Hara-Rudy ionic model (31, 32), as we have done in a previous modeling study (10). In areas of fibrosis, changes were made to ion channel kinetics based on experimental data from human hypertrophic cardiomyopathy (HCM) cardiomyocytes reported by Coppini et al. (33). These measurements were made with cardiomyocytes collected during myectomy from regions of hypertrophy, which have been shown to contain substantial amounts of diffuse fibrosis (34). In the absence of measurements of ionic current remodeling in areas of fibrosis in patients with CS, the similarities in fibrosis histology between HCM and CS (12, 13, 34) justified this modeling choice. This cell model has previously been used to represent areas of diffuse fibrosis in patient-specific organ-scale models of repaired tetralogy of Fallot (10), another type of nonischemic cardiomyopathy. Specific changes included 107% increase of INaL maximal conductance, 19% increase of ICaL maximal conductance, 34% decrease of IKr maximal conductance, 27% decrease of IKs maximal conductance, 85% decrease of Ito maximal conductance, 15% decrease of IK1 maximal conductance, 34% increase of sodium-calcium exchanger (NCX) activity, and 43% reduction of Sarcoplasmic/Endoplasmic Reticulum Calcium Atpase (SERCA) activity. The net results of the changes to the cell model in areas of fibrosis include increased action potential duration at 90% repolarization from 280 to 330 ms (18% increase) and abatement of the notch after depolarization. Figure 2C shows action potential traces for regions of fibrotic and nonfibrotic myocardium.
Unlike fibrotic remodeling, inflammation has not previously been represented in patient-specific heart models. Recent data suggest that certain inflammatory cytokines modulate ion channel kinetics, specifically that interleukin-1 (IL-1) and IL-6 may alter the transient outward K+ and L-type Ca++ currents (35). However, this has only been observed in inherited and acquired channelopathies (i.e. Brugada syndrome and long and short QT syndromes) and has not been reported in CS (35). Further, the typical granulomatous inflammation in CS mainly implicates interferon-γ, tumor necrosis factor–α (TNFα), transforming growth factor, IL-2, and IL-12 (2). As there is a lack of quantitative data on how these cytokines might alter specific ionic currents, we did not make any assumptions about how inflammation may alter ion channel kinetics in CS and instead modeled the ion channel kinetics within inflamed regions according to whether they were also fibrotic. Regions of inflammation only, without fibrosis, were assigned the same ion channel kinetics as nondiseased (nonfibrotic) myocardium, while regions of overlap between fibrosis and inflammation were assigned the same ion channel kinetics as fibrotic myocardium (fig. S2B).
Modeling cell-to-cell conduction within the CS ventricles
In fibrosis-only and nondiseased tissue regions, conduction velocities were the same as in our previous simulation studies (10, 20). Specifically, in nondiseased regions, tissue conductivities were 0.136 and 0.0536 S/m in the longitudinal and transverse directions, respectively, resulting in conduction velocities of 54.4 and 33.5 cm/s. Areas of fibrotic myocardium were assigned conductivities of 0.0925 and 0.0209 S/m in the longitudinal and transverse directions, respectively, resulting in conduction velocities of 43.2 and 17.9 cm/s (fig. S2B). These choices are supported by the finding that monomorphic reentrant VTs are often recorded in CS patients with late-stage nonactive disease, which is dominated by fibrosis rather than active inflammation, suggesting that slowed conduction and resultant functional conduction block occur in areas of established fibrosis (36).
Myocardial inflammation in CS correlates with abnormal unipolar voltage regions associated with VT on electroanatomic maps (16, 37) and has been shown to increase the arrhythmogenic propensity of the heart (38, 39). VT has been recorded in CS patients with active inflammation, suggesting that arrhythmogenic changes to conduction may occur in areas of active granulomatous inflammation, especially those in which fibrogenesis processes have begun (36). Tselentakis et al. (38) demonstrated that myocardial inflammation causes conduction velocity to decrease by approximately 40% in the transverse direction only. Recent work also demonstrated that TNFα, which is implicated in CS, may result in slowed conduction as it induces gap junction (connexin-40 and connexin-43) dysfunction. George et al. (39) observed a statistically significant decrease in transverse conduction velocity following exposure of guinea pig hearts to TNFα and a decrease in longitudinal conduction velocity, but this was not statistically significant. Accordingly, we represented areas of inflammation with electrophysiological properties reflecting these limited data regarding the quantitative effects of inflammation on cell-to-cell conduction. The conductivities assigned to areas of inflammation (fig. S2B) were 0.136 and 0.02515 S/m in the longitudinal and transverse directions, resulting in conduction velocities of 54.4 and 20.1 cm/s (or a 40% decrease in transverse conduction velocity and no change in longitudinal conduction velocity compared to regions of nondiseased myocardium).
Areas of overlap between fibrosis and inflammation were considered areas of “in-progress” fibrotic remodeling because inflammation precedes fibrotic remodeling in CS and then diminishes as fibrosis becomes more extensive (2). Although there are limited data on the electrophysiological properties of this region in CS, there is evidence that inflammation also precedes fibrotic remodeling in myocardial infarction (MI) healing (40) and that areas of newly formed fibrosis, which are presumably still inflamed, exhibit slowed conduction and decreased anisotropy in addition to ionic changes, but these changes are not as extensive as those in areas of older established fibrosis (41). Although the fibrogenic pathways are different in CS and MI (2, 40), in the absence of data on the electrophysiologic properties of this region in CS, we assumed that it might exhibit similarly slowed conduction and decreased anisotropy. In support of this assumption, we note that gap junction lateralization, which results in slowed conduction and decreased anisotropy, has been observed histologically in fibrotic regions of human heart tissue from patients with CS (42). In addition, Muser et al. (16) observed that areas of both fibrosis and inflammation in CS typically have abnormal unipolar voltage and either normal or abnormal bipolar voltage on electroanatomic maps, which further supports our assumption. Thus, we assigned to this region conductivity values between those of inflammation-only (less severe) and fibrosis-only (more severe) regions (41), with conductivities of 0.0925 and 0.02515 S/m in the longitudinal and transverse directions, respectively, resulting in conduction velocities of 43.2 and 20.1 cm/s. The longitudinal conductivity was decreased to match that of the fibrosis-only region to represent that fibrotic remodeling has begun to occur in the overlap region. However, the transverse conductivity was kept the same as in the inflammation-only region, which is slightly higher than that of the fibrosis-only region, to represent that the fibrotic remodeling in the overlap region is not complete (fig. S2B).
Simulation of 3D propagation of electrical activity within the CS ventricles
Computational simulations of the 3D propagation of electrical activity in the personalized MRI-PET fusion models consisted of solving a reaction-diffusion partial differential equation representing the spread of current in the ventricular myocardium together with ordinary differential and algebraic equations representing myocyte membrane dynamics at each node in the mesh. The mathematical description of electrical conduction in cardiac tissue was based on the monodomain representation (41). Simulations were performed using the software package CARP on a high-performance computing system. A free version of this software is available for academic use (https://carp.medunigraz.at/carputils/). Full detail regarding the mathematical simulations of electrical activity is found in our previous publications (9, 26).
VT inducibility testing in personalized MRI-PET fusion models
To examine the propensity of each patient’s CS substrate to sustain VT, endocardial rapid pacing was delivered sequentially from each of 10 biventricular sites: 3 on the RV and 7 on the LV. Figure S2C shows the myocardial segments in which stimuli were delivered. The stimulus train consisted of six beats (S1) at a cycle length of 450 ms followed by a premature stimulus (S2) initially given at 300 ms. The timing between S1 and S2 was progressively shortened until VT was induced. If VT was not induced, then up to three (S3, S4, and S5) additional premature stimuli were delivered 250 ms after the previous stimulus. Two seconds of VT was simulated. The pacing protocol was similar to those used clinically (43) and has been used in our previous studies (9, 10, 20). The most extensive protocol with four premature stimuli was termed Protocol VT-S5 (extra stimuli S1 to S5). Protocols VT-SX were also tested, where SX indicates the number of extra stimuli (S3 to S5). The least extensive protocol, VT-S3, did not induce reentry in any of the patients’ models.
MRI-PET fusion model validation
Once the MRI-PET fusion modeling methodology was developed, we undertook a validation study with retrospective clinical data. We hypothesized that the personalized models would correctly predict the VT locations by comparison with clinical ablation lesions, the typical invasive data available for patients with CS.
Figure 3 presents comparison of induced VTs with clinical ablation lesions for two patients with sarcoidosis who underwent ablation procedures. As shown in Fig. 3 (A and B), for one of the patients, two VTs were induced following rapid pacing from the locations indicated: one at the anterior LV-RV junction near the base of the heart and one on the RV free wall and septum on the posterior side of the RV apex. Clinical ablation lesions were consistent with these VT morphologies, as evident from Fig. 3C. Extensive endocardial RV ablation was performed along the anterior LV-RV junction, which corresponds with VT morphology 1 in the figure, and on the RV apex and RV outflow tract, which corresponds with VT morphology 2 in the figure. For the other patient, two VTs were induced: one on the mid LV side of the septum and one on the RV endocardium at the anterior LV-RV junction. These VT morphologies correspond well with the two separate clusters of clinical ablation lesions: one on the LV endocardium at the mid septum and one on the RV endocardium near the mid anterior LV-RV junction. In addition to being consistent with the clinical ablation lesions, the locations of the observed VT morphologies in both patients’ biventricular models are consistent with Muser et al.’s (16) finding that, in patients with CS, abnormal electrograms are frequently located on the septum and near the base of the RV and LV.
CHAI Risk Predictor training and optimization
As described in the Results, the CHAI Risk Predictor technology consists of two steps. First, mechanistic computational modeling of cardiac electrical function in personalized MRI-PET fusion models is performed to investigate the arrhythmia propensity of each patient’s heart. Second, a supervised ML classification algorithm predicts the risk of VT, using features selected via random forest from three types of inputs: (i) features characterizing the patient’s arrhythmogenic propensity extracted from the results of mechanistic simulations of VT induction in each MRI-PET fusion heart model, (ii) features from LGE-MRI and FDG-PET imaging that are eliminated in the process of heart model creation (binary thresholding) but might be independent predictors of SCD risk, and (iii) baseline patient data that may predispose to SCD risk.
Feature extraction from the three types of inputs
A complete list of features extracted for each patient is provided in table S2. Some features were extracted by a supervised algorithm from the results of mechanistic simulations of arrhythmogenesis in the classifier training process. They follow common “feature types” but could be unique for each training dataset.
Extraction of features from VT inducibility simulation results in MRI-PET mechanistic models
Feature extraction from VT inducibility simulation result data began with calculation of 21 predefined features. These were based on previously published studies of ventricular arrhythmia risk prediction and of arrhythmogenic propensity in CS. For example, one study reported that RV remodeling is associated with increased risk of VT in CS (44), so we included features that quantified the inducibility of the heart following pacing from the three sites on the RV.
As discussed in the Results, to extract predictive information embedded in the simulation result data, we developed a supervised feature extraction algorithm that was integrated in the ML classifier pipeline. It was implemented by extending scikit-learn’s BaseEstimator and TransformerMixin classes. This approach was designed to minimize data leakage and bias that could be introduced by manually crafting such features with knowledge of the simulation results.
A single mechanistic simulation run output consists of millions of transmembrane voltage measurements over thousands of time steps for each personalized heart model. To decrease the dimensionality of the simulation result data and extract features for input to the ML classifier, sequential steps were undertaken (fig. S3). The simulations result data were first preprocessed. For each of the 10 pacing locations, we recorded whether reentry was induced, how many extra stimuli were required to induce reentry, and the AHA segments in which the reentry pathway was located. Reentry induction and number of extra stimuli were extracted automatically, but identification of reentry pathways required manual analysis. The researcher analyzing the reentry pathways was blinded to clinical outcomes to avoid bias.
The simulation results feature extractor was fitted with the training data and then used (as a pipeline step, before prediction) to transform the simulation result data into features, which followed a set of rules that we devised on the basis of the mechanistic understanding of arrhythmogenesis following rapid pacing. Figure S3 illustrates the simulation feature extractor fitting and transformation process. The following four metrics (features) quantified inducibility:
1) A proportion of pacing sites, Psus, from which sustained VTs were induced in the heart models.
2) A proportion of pacing sites, Pany, from which any VT (sustained or unsustained) was induced. The rationale for choosing to impose this rule is the same as that in item 1 above, with the addition that even unsustained VT induced in the models could be predictive of clinical outcome.
3) VT inducibility score
where M is the number of unique sustained VT morphologies induced in each MRI-PET heart model.
4) Weighted VT inducibility score
where i is the number of extra stimuli (after S1) required to induce each VT.
Feature types 1 and 2 quantified inducibility, without considering the number of reentry morphologies or the number of extra stimuli required to induce VT. Feature types 3 and 4 above progressively incorporated more potentially predictive information to increase the resulting candidate features’ capacity, i.e., the complexity of problems that they can represent.
During fitting of the feature extraction and classification pipeline, the number of pacing locations used to calculate these features (N) was selected as a hyperparameter. The optimal combination of N pacing locations (corresponding to those shown in fig. S2C) resulting in the greatest difference in inducibility between patients who did and did not experience clinical VT was selected for each pacing protocol (VT-S4 and VT-S5) (fig. S3). To avoid overfitting, one set of N pacing locations was selected for each pacing protocol during fitting of the pipeline, although inducibility was quantified with up to four metrics (features) for each pacing protocol. Psus was used in optimizing the combination of pacing locations for each pacing protocol, and then the optimal pacing locations for each pacing protocol were used to calculate all feature types in the next step.
The rationale for choosing to impose this rule is that, as shown in Fig. 5, the number of pacing locations from which VT is induced in the models could be predictive of clinical outcome. Furthermore, some pacing locations or combinations of pacing locations might be more predictive of clinical VT because (i) VTs in CS are often found in specific regions (particularly the septum and RV) due to the pathophysiology of the disease (45), and (ii) as shown in Fig. 2D, some regions were more likely to contain disease-induced remodeling. This feature extraction approach may reduce computational costs for future patients: If all features selected for inclusion in the classifier entailed pacing from fewer than 10 locations, fewer than 10 simulations would be required to apply the risk predictor to previously unseen patients.
During feature transformation (after fitting), the inducibility of each patient’s MRI-PET fusion model from the selected N lettered pacing locations was used to calculate the four feature types for each pacing protocol. The VT inducibility score and its weighted version were perfectly correlated for VT-S4, so only the VTI inducibility score was included. This resulted in seven features, which could be different each time the classifier was fit, since they were defined by learning from the training data.
The process of dimensionality reduction of the simulation result data described here maintained the mechanistic rules for feature selection set forth deductively ahead of time while allowing the training data to inductively inform the final choice of features. It was repeated in each inner loop of cross-validation and each outer loop of nested cross-validation. This approach reduced the chance of bias or data leakage that could be introduced if we had entirely predefined all simulation features. The protocol used to calculate a small number of features that contained maximum predictive information was dictated by the desire to not overfit the training data. This process leveraged the potential of ML to discover previously unexplored predictive patterns in the mechanistic simulation data.
Extraction of features from the clinical record
In this study, features extracted from the clinical record for each patient included the patient’s age, weight, sex, QRS duration, and LVEF. In addition, we included an expert radiologist’s assessment of the presence of inflammation on FDG-PET and the presence of fibrosis on LGE-MRI as binary values, since these are sometimes used clinically as independent risk prediction metrics for patients with CS. All features extracted from the clinical record are listed in table S2.
Extraction of features from LGE-MRI and FDG-PET imaging data
Although clinical images are the basis of the personalized MRI-PET models, features extracted from raw imaging data were included as separate inputs in the ML risk classifier because MRI-PET model generation is based on segmented images (i.e., binary thresholding of imaging data resulting in image dimensionality reduction). Thus, we hypothesized that features extracted from raw (unprocessed) images might provide additional prognostic information. A list of imaging data features is presented in table S2. These features were predefined by the researchers based on literature review.
Among the imaging data features, a subset was related to the entropy of LGE-MRI signal intensity, which quantifies the intensity heterogeneity in the ventricular wall. Entropy has previously been used to predict SCD risk in ischemic cardiomyopathy (18). Entropy was computed according to the following formula (46) using the normalized histogram of image intensity
where k is the number of gray levels in the image, and pk is the probability associated with each gray level.
Another subset of imaging data features resulted from fractal analysis of LGE-MRI images. Fractal dimension can quantify the complexity of the fibrosis border and has previously been used to characterize cardiac fibrosis in a rabbit model of ischemic cardiomyopathy (47) but has not been used for arrhythmia risk stratification. We used a 3D variation of the fractal dimension–based feature “N2” defined and used by Beheshti et al. (48) to analyze tumor complexity. It quantified how quickly the complexity of the 3D surface of the fibrosis volume decreases as imaging resolution decreases.
CHAI Risk Predictor specification, training, optimization, and testing
The CHAI Risk Predictor was developed as a scikit-learn Pipeline that joined together the simulation feature extraction methods described in the preceding section, preprocessing of all features, feature selection, and a random forest classifier. Here, we discuss the specifications of the model, training and optimization procedures, and details of the nested cross-validation methodology used to estimate CIs for cross-validation and testing performance metrics. The Pipeline was used for three reasons: (i) It ensures no data leakage between training and testing sets, (ii) it is highly customizable for handling simulation data but is built entirely on open-source libraries, and (iii) it is easy to interpret.
CHAI Risk Predictor pipeline
The CHAI Risk Predictor pipeline began with three different feature preprocessors (transformers). Each transformer was wrapped into a pipeline to avoid data leakage—all transformers were configured with the training data and then applied to the test data (within the classifier pipeline) before risk prediction. A numeric transformer was applied to predefined simulation features, continuous-valued imaging feature, and continuous or near-continuous clinical features (weight, age, QRS duration, and LVEF). It included mean value imputation and minimum-maximum scaling of numeric features. A categorical transformer was applied to categorical features (sex and qualitative clinical assessments of LGE and PET images). It included constant imputation of missing values with an “unknown” string and one-hot encoding with the first column dropped for each feature. There were no missing categorical features in this dataset, so this resulted in three binary feature columns.
The final transformer was the simulation inducibility feature extractor described in the preceding section. This was fit using the training simulation result data and then used to transform both the training and validation (or testing) simulation result data into a set of seven fit-from-training simulation features. It also included mean value imputation if simulation results were missing for any patients, although there were no missing simulation results for any of the patients in this study.
Feature extraction resulted in 141 features for each patient: 3 categorical clinical features, 4 continuous clinical features, 21 predefined simulation features, 7 fit-from-training simulation features, and 106 features extracted from MRI and PET images. A random forest was then used in the next step of the pipeline to select features by ranking them in order of importance; a maximum of five features could be selected because of the very small dataset size. Importance is a quantitative measure of how well a feature can stratify patients in the training set with respect to an output variable. When used in a feature selection algorithm, it reduces multicollinearity: If two features describe the same aspect of the data and both are predictive, only the more predictive one will be selected. As importance is affected by how many times a feature can be used to split groups of patients, it tends to favor continuous variables over variables with few discrete values. Of note, the random forest algorithm, used here because of its superior performance on small datasets, tends to favor continuous imaging features over simulation feature results. These continuous imaging features from FDG-PET and LGE-MRI are not as different between patients who did and did not experience clinical VT. The number of selected features and hyperparameters of the selection algorithm were optimized as described in the following section.
The last step of the pipeline was a random forest classifier. This classification methodology allows for calculation of feature importance, which determines the relative contribution of each feature to the predicted output, thus providing interpretability. Once trained, the random forest classifier predicted the probability of VT occurrence for each patient, then each patient was classified as high or low risk by thresholding the resultant probabilities with an optimal threshold determined from the training data.
CHAI Risk Predictor hyperparameter optimization
Bayesian optimization with Gaussian processes was used to optimize hyperparameters of the classification algorithm. Briefly, this algorithm attempted to minimize the cross-validation score (−1 * AUROC) by approximating the cost function with a Gaussian process or a multivariate Gaussian. This allowed us to optimize 16 different hyperparameters, with each following a uniform probability distribution from some minimum to maximum value, in only 50 iterations. A full cycle of optimization, training, and testing took less than 2 min to complete. The same optimization cycle with random search took almost 2 hours and did not always reach the optimal score found by the Bayesian optimization.
Hyperparameters included the number of pacing sites (N) used to calculate dynamically extracted simulation features, the maximum number of feature selection for inclusion in the random forest classifier, and various parameters used to control the degree of overfitting of both the feature selection algorithm and the classifier (number of estimators, maximum leaf nodes, minimum samples per leaf, maximum depth, maximum samples and features considered for each tree in the random forest, and the cost complexity pruning parameter).
Nested cross-validation of CHAI Risk Predictor
CHAI Risk Predictor training, optimization, and testing were performed with nested cross-validation to calculate 95% CIs for each cross-validation and testing performance metric and to estimate the generalization accuracy over many test sets. The dataset in this study is smaller than is typical for ML approaches, so we designed the nested cross-validation procedure to maximize the insight into the CHAI Risk Predictor’s out-of-sample performance.
Five hundred sixty iterations of nested cross-validation were performed. Each test set included three patients from the dataset who experienced clinical VT and five to six who did not. Patients who did and did not experience clinical VT were assigned to test sets separately. For patients who experienced clinical VT (16 patients), we controlled the test set composition such that each test set included a unique combination of 3 patients who experienced clinical VT. There were 560 such combinations [], and the order of combinations was randomly shuffled. Then, patients who did not experience clinical VT were assigned to test sets via repeated fivefold cross-validation. Each repetition of fivefold cross-validation resulted in four sets of six patients and one set of five patients, selected without replacement. These were matched with the randomly shuffled combinations of patients who did experience clinical VT, resulting in a total of 560 test sets with eight to nine patients each. For each test set, hyperparameter optimization and classification pipeline fitting were performed as described via fivefold stratified cross-validation with data from the remaining 36 to 37 patients.
Hyperparameters were optimized to maximize AUROC as discussed in the preceding section. To assess classifier performance, we also calculated the sensitivity, specificity, positive predictive value, and negative predictive value using binary outcome predictions by the classifier. Comparison of the CHAI Risk Predictor with the clinical risk metrics was not straightforward—the other four metrics assessed in this study were static predetermined binary scores rather than trainable ML classifiers that output a continuous risk score like the CHAI Risk Prediction. Thus, they were applied to the entire dataset at once. We believe that it is appropriate to compare the testing results with the entire dataset results for the clinical risk metrics: Since the clinical metrics and SimVT do not require training, applying them on the entire dataset at once will result in the same performance metrics as applying them on each test set and then aggregating the results, if each patient is held out in the same proportion of test sets.
Acknowledgments
Funding: This work was supported by NIH grants R01HL142496 (to N.A.T.) and R01HL126802 (to N.A.T.), Lowenstein Foundation (to N.A.T.), Robert E. Meyerhoff Professorship (to J.C.), Johns Hopkins University Undergraduate Research Fellowship (to R.Y.), and NSF Graduate Research Fellowship DGE-1746891 (to J.K.S.). Author contributions: Conceptualization: J.K.S., A.P., D.M.P., N.A.T., and J.C. Data curation: J.C., D.R.O., and J.K.S. Formal analysis: J.K.S. Funding acquisition: N.A.T. Investigation: J.K.S. and R.Y. Methodology: J.K.S., A.P., and D.M.P. Project administration: N.A.T. and J.C. Resources: N.A.T., J.C., and D.R.O. Software: J.K.S. Supervision: N.A.T. and J.C. Validation: J.K.S., A.P., and D.M.P. Visualization: J.K.S. and R.Y. Writing—original draft: J.K.S. Writing—review and editing: J.K.S., A.P., D.M.P., R.Y., J.C., D.R.O., and N.A.T. Competing interests: The authors declare that they have no competing interests. Data and materials availability: The authors declare that all data supporting the findings of this study are available within the paper and the Supplementary Materials. The MRI images and patient clinical data can be provided by the authors pending Johns Hopkins University Institutional Review Board approval and a completed material transfer agreement. Requests for these data should be sent to N.A.T. The material transfer agreement form can be found at https://ventures.jhu.edu/faculty-inventors/forms-policies/material-transfer-agreement-request-form-for-outbound-material/. The image processing software CardioViz3D can be freely obtained from www-sop.inria.fr/asclepios/software/CardioViz3D/. The open-source software used for image registration and preprocessing can be freely obtained from www.slicer.org/. Computational meshes are generated using the software Simpleware ScanIP, available from Synopsys. Regarding the rule-based approach to assign fiber orientations in the computational mesh, the original publication (30) presents a set of algorithms and subroutines that can be easily implemented. Ionic models are freely available from the repository CellML (https://models.cellml.org/cellml); additional ion current modifications implemented here are described in Materials and Methods. The electrophysiology simulator CARPentry is freely available from https://carpentry.medunigraz.at/carputils/index.html and can be used to execute 3D ventricular simulations. Simulation results were visualized using Meshalyzer, which can be downloaded from https://github.com/cardiosolv/meshalyzer. The ML algorithms described in this manuscript were developed in Python using the following libraries and custom-built extension of these libraries: scikit-learn (https://scikit-learn.org/stable/), pandas (https://pandas.pydata.org/), scikit-optimize (https://scikit-optimize.github.io/stable/), and NumPy (https://numpy.org/). The ML code for data processing, simulation feature extraction, and model development will be made available.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/31/eabi8020/DC1
REFERENCES AND NOTES
- 1.Gerke A. K., Judson M. A., Cozier Y. C., Culver D. A., Koth L. L., Disease burden and variability in sarcoidosis. Ann. Am. Thorac. Soc. 14, S421–S428 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hamzeh N., Steckman D. A., Sauer W. H., Judson M. A., Pathophysiology and clinical management of cardiac sarcoidosis. Nat. Rev. Cardiol. 12, 278–288 (2015). [DOI] [PubMed] [Google Scholar]
- 3.Betensky B. P., Tschabrunn C. M., Zado E. S., Goldberg L. R., Marchlinski F. E., Garcia F. C., Cooper J. M., Long-term follow-up of patients with cardiac sarcoidosis and implantable cardioverter-defibrillators. Heart Rhythm 9, 884–891 (2012). [DOI] [PubMed] [Google Scholar]
- 4.Schuller J. L., Zipse M., Crawford T., Bogun F., Beshai J., Patel A. R., Sweiss N. J., Nguyen D. T., Aleong R. G., Varosy P. D., Weinberger H. D., Sauer W. H., Implantable cardioverter defibrillator therapy in patients with cardiac sarcoidosis. J. Cardiovasc. Electrophysiol. 23, 925–929 (2012). [DOI] [PubMed] [Google Scholar]
- 5.Birnie D. H., Sauer W. H., Bogun F., Cooper J. M., Culver D. A., Duvernoy C. S., Judson M. A., Kron J., Mehta D., Cosedis Nielsen J., Patel A. R., Ohe T., Raatikainen P., Soejima K., HRS expert consensus statement on the diagnosis and management of arrhythmias associated with cardiac sarcoidosis. Heart Rhythm 11, 1305–1323 (2014). [DOI] [PubMed] [Google Scholar]
- 6.Hulten E., Agarwal V., Cahill M., Cole G., Vita T., Parrish S., Bittencourt M. S., Murthy V. L., Kwong R., Di Carli M. F., Blankstein R., Presence of late gadolinium enhancement by cardiac magnetic resonance among patients with suspected cardiac sarcoidosis is associated with adverse cardiovascular prognosis: A systematic review and meta-analysis. Circ. Cardiovasc. Imaging 9, e005001 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Paz Y. E., Bokhari S., The role of F18-fluorodeoxyglucose positron emission tomography in identifying patients at high risk for lethal arrhythmias from cardiac sarcoidosis and the use of serial scanning to guide therapy. Int. J. Cardiovasc. Imaging 30, 431–438 (2014). [DOI] [PubMed] [Google Scholar]
- 8.Franke K. B., Marshall H., Kennewell P., Pham H. D., Tully P. J., Rattanakosit T., Mahadevan G., Mahajan R., Risk and predictors of sudden death in cardiac sarcoidosis: A systematic review and meta-analysis. Int. J. Cardiol. 328, 130–140 (2021). [DOI] [PubMed] [Google Scholar]
- 9.Arevalo H. J., Vadakkumpadan F., Guallar E., Jebb A., Malamas P., Wu K. C., Trayanova N. A., Arrhythmia risk stratification of patients after myocardial infarction using personalized heart models. Nat. Commun. 7, 11437 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shade J. K., Cartoski M. J., Nikolov P., Prakosa A., Doshi A., Binka E., Olivieri L., Boyle P. M., Spevak P. J., Trayanova N. A., Ventricular arrhythmia risk prediction in repaired tetralogy of fallot using personalized computational cardiac models. Heart Rhythm 17, 408–414 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Deng D., Prakosa A., Shade J., Nikolov P., Trayanova N. A., Sensitivity of ablation targets prediction to electrophysiological parameter variability in image-based computational models of ventricular tachycardia in post-infarction patients. Front. Physiol. 10, 628 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Riezzo I., Ventura F., D’Errico S., Neri M., Turillazzi E., Fineschi V., Arrhythmogenesis and diagnosis of cardiac sarcoidosis. An immunohistochemical study in a sudden cardiac death. Forensic Sci. Int. 183, e1–e5 (2009). [DOI] [PubMed] [Google Scholar]
- 13.Roberts W. C., McAllister H. A. Jr., Ferrans V. J., Sarcoidosis of the heart. A clinicopathologic study of 35 necropsy patients (group 1) and review of 78 previously described necropsy patients (group 11). Am. J. Med. 63, 86–108 (1977). [DOI] [PubMed] [Google Scholar]
- 14.Banba K., Kusano K. F., Nakamura K., Morita H., Ogawa A., Ohtsuka F., Ohta Ogo K., Nishii N., Watanabe A., Nagase S., Sakuragi S., Ohe T., Relationship between arrhythmogenesis and disease activity in cardiac sarcoidosis. Heart Rhythm 4, 1292–1299 (2007). [DOI] [PubMed] [Google Scholar]
- 15.Kiko T., Yoshihisa A., Kanno Y., Yokokawa T., Abe S., Miyata-Tatsumi M., Misaka T., Oikawa M., Kobayashi A., Ishida T., Takeishi Y., A multiple biomarker approach in patients with cardiac sarcoidosis. Int. Heart J. 59, 996–1001 (2018). [DOI] [PubMed] [Google Scholar]
- 16.Muser D., Santangeli P., Liang J. J., Castro S. A., Magnani S., Hayashi T., Garcia F. C., Frankel D. S., Dixit S., Zado E. S., Lin D., Desjardins B., Callans D. J., Alavi A., Marchlinski F. E., Characterization of the electroanatomic substrate in cardiac sarcoidosis: Correlation with imaging findings of scar and inflammation. JACC Clin. Electrophysiol. 4, 291–303 (2018). [DOI] [PubMed] [Google Scholar]
- 17.Okada D. R., Smith J., Derakhshan A., Gowani Z., Misra S., Berger R. D., Calkins H., Tandri H., Chrispin J., Ventricular arrhythmias in cardiac sarcoidosis. Circulation 138, 1253–1264 (2018). [DOI] [PubMed] [Google Scholar]
- 18.Androulakis A. F. A., Zeppenfeld K., Paiman E. H. M., Piers S. R. D., Wijnmaalen A. P., Siebelink H. M. J., Sramko M., Lamb H. J., van der Geest R. J., de Riva M., Tao Q., Entropy as a novel measure of myocardial tissue heterogeneity for prediction of ventricular arrhythmias and mortality in post-infarct patients. JACC Clin. Electrophysiol. 5, 480–489 (2019). [DOI] [PubMed] [Google Scholar]
- 19.Moons K. G. M., Altman D. G., Reitsma J. B., Ioannidis J. P. A., Macaskill P., Steyerberg E. W., Vickers A. J., Ransohoff D. F., Collins G. S., Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): Explanation and elaboration. Ann. Intern. Med. 162, W1–W73 (2015). [DOI] [PubMed] [Google Scholar]
- 20.Cartoski M. J., Nikolov P. P., Prakosa A., Boyle P. M., Spevak P. J., Trayanova N. A., Computational identification of ventricular arrhythmia risk in pediatric myocarditis. Pediatr. Cardiol. 40, 857–864 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kramer C. M., Barkhausen J., Flamm S. D., Kim R. J., Nagel E.; Society for Cardiovascular Magnetic Resonance Board of Trustees Task Force on Standardized Protocols , Standardized cardiovascular magnetic resonance (CMR) protocols 2013 update. J. Cardiovasc. Magn. Reson. 15, 91 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Okumura W., Iwasaki T., Toyama T., Iso T., Arai M., Oriuchi N., Endo K., Yokoyama T., Suzuki T., Kurabayashi M., Usefulness of fasting 18F-FDG PET in identification of cardiac sarcoidosis. J. Nucl. Med. 45, 1989–1998 (2004). [PubMed] [Google Scholar]
- 23.Skali H., Schulman A. R., Dorbala S., 18F-FDG PET/CT for the assessment of myocardial sarcoidosis. Curr. Cardiol. Rep. 15, 352 (2013). [PMC free article] [PubMed] [Google Scholar]
- 24.Fedorov A., Beichel R., Kalpathy-Cramer J., Finet J., Fillion-Robin J. C., Pujol S., Bauer C., Jennings D., Fennessy F., Sonka M., Buatti J., Aylward S., Miller J. V., Pieper S., Kikinis R., 3D slicer as an image computing platform for the quantitative imaging network. Magn. Reson. Imaging 30, 1323–1341 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.N. Toussaint, T. Mansi, H. Delingette, N. Ayache, M. Sermesant, Eurographics Workshop on Visual Computing for Biomedicine, in An Integrated Platform for Dynamic Cardiac Simulation and Image Processing: Application to Personalised Tetralogy of Fallot Simulation (The Eurographics Association, 2008).
- 26.Prakosa A., Arevalo H. J., Deng D., Boyle P. M., Nikolov P. P., Ashikaga H., Blauer J. J. E., Ghafoori E., Park C. J., Blake R. C., Han F. T., MacLeod R. S., Halperin H. R., Callans D. J., Ranjan R., Chrispin J., Nazarian S., Trayanova N. A., Personalized virtual-heart technology for guiding the ablation of infarct-related ventricular tachycardia. Nat. Biomed. Eng. 2, 732–740 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mikami Y., Kolman L., Joncas S. X., Stirrat J., Scholl D., Rajchl M., Lydell C. P., Weeks S. G., Howarth A. G., White J. A., Accuracy and reproducibility of semi-automated late gadolinium enhancement quantification techniques in patients with hypertrophic cardiomyopathy. J. Cardiovasc. Magn. Reson. 16, 85 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yan A. T., Shayne A. J., Brown K. A., Gupta S. N., Chan C. W., Luu T. M., Di Carli M. F., Reynolds H. G., Stevenson W. G., Kwong R. Y., Characterization of the peri-infarct zone by contrast-enhanced cardiac magnetic resonance imaging is a powerful predictor of post-myocardial infarction mortality. Circulation 114, 32–39 (2006). [DOI] [PubMed] [Google Scholar]
- 29.Osborne M. T., Hulten E. A., Singh A., Waller A. H., Bittencourt M. S., Stewart G. C., Hainer J., Murthy L., Skali H., Dorbala S., Di Carli M. F., Blankstein R., Reduction in 18F-fluorodeoxyglucose uptake on serial cardiac positron emission tomography is associated with improved left ventricular ejection fraction in patients with cardiac sarcoidosis. J. Nucl. Cardiol. 21, 166–174 (2014). [DOI] [PubMed] [Google Scholar]
- 30.Bayer J. D., Blake R. C., Plank G., Trayanova N. A., A novel rule-based algorithm for assigning myocardial fiber orientation to computational heart models. Ann. Biomed. Eng. 40, 2243–2254 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.O’Hara T., Virág L., Varró A., Rudy Y., Simulation of the undiseased human cardiac ventricular action potential: Model formulation and experimental validation. PLOS Comput. Biol. 7, e1002061 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.ten Tusscher K. H. W. J., Panfilov A. V., Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol. Circ. Physiol. 291, H1088–H1100 (2006). [DOI] [PubMed] [Google Scholar]
- 33.Coppini R., Ferrantini C., Yao L., Fan P., Del Lungo M., Stillitano F., Sartiani L., Tosi B., Suffredini S., Tesi C., Yacoub M., Olivotto I., Belardinelli L., Poggesi C., Cerbai E., Mugelli A., Late sodium current inhibition reverses electromechanical dysfunction in human hypertrophic cardiomyopathy. Circulation 127, 575–584 (2013). [DOI] [PubMed] [Google Scholar]
- 34.Galati G., Leone O., Pasquale F., Olivotto I., Biagini E., Grigioni F., Pilato E., Lorenzini M., Corti B., Foà A., Agostini V., Cecchi F., Rapezzi C., Histological and histometric characterization of myocardial fibrosis in end-stage hypertrophic cardiomyopathy. Circ. Heart Fail. 9, e003090 (2016). [DOI] [PubMed] [Google Scholar]
- 35.Lazzerini P. E., Laghi-Pasini F., Boutjdir M., Capecchi P. L., Cardioimmunology of arrhythmias: The role of autoimmune and inflammatory cardiac channelopathies. Nat. Rev. Immunol. 19, 63–64 (2019). [DOI] [PubMed] [Google Scholar]
- 36.Furushima H., Chinushi M., Sugiura H., Kasai H., Washizuka T., Aizawa Y., Ventricular tachyarrhythmia associated with cardiac sarcoidosis: Its mechanisms and outcome. Clin. Cardiol. 27, 217–222 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Siddiqi F. K., Paz Y. E., Olesnicky L., Bokhari S., Cheung J. W., Correlation of inflammation due to cardiac sarcoidosis by positron emission tomography-computed tomography imaging and endocardial voltage mapping in a patient with recurrent ventricular tachycardia. Europace 16, 907 (2014). [DOI] [PubMed] [Google Scholar]
- 38.Tselentakis E. V., Woodford E., Chandy J., Gaudette G. R., Saltman A. E., Inflammation effects on the electrical properties of atrial tissue and inducibility of postoperative atrial fibrillation. J. Surg. Res. 135, 68–75 (2006). [DOI] [PubMed] [Google Scholar]
- 39.George S. A., Calhoun P. J., Gourdie R. G., Smyth J. W., Poelzing S., TNFα modulates cardiac conduction by altering electrical coupling between myocytes. Front. Physiol. 8, 334 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Swirski F. K., Nahrendorf M., Cardioimmunology: The immune system in cardiac homeostasis and disease. Nat. Rev. Immunol. 18, 733–744 (2018). [DOI] [PubMed] [Google Scholar]
- 41.Costa C. M., Plank G., Rinaldi C. A., Niederer S. A., Bishop M. J., Modeling the electrophysiological properties of the infarct border zone. Front. Physiol. 9, 356 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Siqueira W. C., da Cruz S. G., Asimaki A., Saffitz J. E., da M., Moreira C. V., Brasileiro G., Rocha L. O. S., Cardiac sarcoidosis with severe involvement of the right ventricle: A case report. Autops. Case Reports. 5, 53–63 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Cheng A., Dalal D., Butcher B., Norgard S., Zhang Y., Dickfeld T., Eldadah Z. A., Ellenbogen K. A., Guallar E., Tomaselli G. F., Prospective observational study of implantable cardioverter-defibrillators in primary prevention of sudden cardiac death: Study design and cohort description. J. Am. Heart Assoc. 2, e000083 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yasuda M., Iwanaga Y., Kato T., Izumi T., Inuzuka Y., Nakamura T., Miyaji Y., Kawamura T., Ikeguchi S., Inoko M., Kurita T., Miyazaki S., Risk stratification for major adverse cardiac events and ventricular tachyarrhythmias by cardiac MRI in patients with cardiac sarcoidosis. Open Heart 3, e000437 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Naruse Y., Sekiguchi Y., Nogami A., Okada H., Yamauchi Y., MacHino T., Kuroki K., Ito Y., Yamasaki H., Igarashi M., Tada H., Nitta J., Xu D., Sato A., Aonuma K., Systematic treatment approach to ventricular tachycardia in cardiac sarcoidosis. Circ. Arrhythmia Electrophysiol. 7, 407–413 (2014). [DOI] [PubMed] [Google Scholar]
- 46.F. Orlhac, C. Nioche, I. Buvat, Texture — User Guide Local Image Features Extraction (2018).
- 47.McLachlan C. S., Jelinek H. F., Kummerfeld S. K., Rummery N., McLachlan P. D., Jusuf P., Driussi C., Yin J., A method to determine the fractal dimension of the cross-sectional jaggedness of the infarct scar edge. Redox Rep. 5, 119–121 (2000). [DOI] [PubMed] [Google Scholar]
- 48.Beheshti S. M. A., AhmadiNoubari H., Fatemizadeh E., Khalili M., An efficient fractal method for detection and diagnosis of breast masses in mammograms. J. Digit. Imaging 27, 661–669 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/31/eabi8020/DC1


