Evaluation of Recirculation During Venovenous Extracorporeal Membrane Oxygenation Using Computational Fluid Dynamics Incorporating Fluid-Structure Interaction

Supplemental Digital Content is available in the text.

Abstract

Recirculation in venovenous extracorporeal membrane oxygenation (VV ECMO) leads to reduction in gas transfer efficiency. Studies of the factors contributing have been performed using in vivo studies and computational models. The fixed geometry of previous computational models limits the accuracy of results. We have developed a finite element computational fluid dynamics model incorporating fluid-structure interaction (FSI) that incorporates atrial deformation during atrial filling and emptying, with fluid flow solved using large eddy simulation. With this model, we have evaluated an extensive number of factors that could influence recirculation during two-site VV ECMO, and characterized their impact on recirculation, including cannula construction, insertion depth and orientation, VV ECMO configuration, circuit blood flow, and changes in volume, venous return, heart rate, and blood viscosity. Simulations revealed that extracorporeal blood flow relative to cardiac output, ratio of superior vena caval (SVC) to inferior vena caval (IVC) blood flow, position of the SVC cannula relative to the cavo-atrial junction, and orientation of the return cannula relative to the tricuspid valve had major influences (>20%) on recirculation fraction. Factors with a moderate influence on recirculation fraction (5%–20%) include heart rate, return cannula diameter, and direction of extracorporeal flow. Minimal influence on recirculation (<5%) was associated with atrial volume, position of the IVC cannula relative to the cavo-atrial junction, the number of side holes in the return cannula, and blood viscosity.

Extracorporeal membrane oxygenation (ECMO) is used to provide gas exchange to support patients with severe acute respiratory failure who are not able to maintain oxygenation through the natural lungs. In the venovenous configuration (VV ECMO) used for respiratory support, blood is drained from the central venous system, pumped through an artificial membrane lung for gas exchange, and reinfused back into the venous system. Fully oxygenated reinfused blood passes into the right ventricle and on to the systemic circulation, mixing with venous return and increasing saturation. In practice, however, a variable amount of oxygenated reinfused blood is aspirated into the drainage limb of the circuit and recirculated through the membrane lung, reducing the efficiency of gas transfer. Understanding and minimizing recirculation is important to maximize oxygen delivery during VV ECMO. The degree of recirculation is dependent on multiple factors, including cannulation configuration, cannula positioning, extracorporeal circuit flow, native cardiac output,¹ and has been reported to vary from 2% to 57%.^2–4 Although these factors are known, the precise contribution of each to recirculation is less well known. Gas transfer efficiency is reduced in direct proportion to the amount of recirculation; therefore, an understanding of how these factors contribute is necessary to maximize extracorporeal support.

An understanding of recirculation can be obtained through the use of mathematical modeling and simulation.⁴ While the use of physical bench models is useful,⁵ these models provide static geometric approximations to vascular structures, while the use of computational fluid dynamics (CFD) has enabled high-fidelity simulation in anatomically accurate geometries.⁶ To date, CFD models of blood flow and recirculation have used static solid geometries that do not reflect the real-time changes in geometry that can affect flow patterns. The goal of this study was to develop a CFD model of the vascular structures that incorporated fluid-structure interaction (FSI) to more realistically model atrial expansion and contraction during the cardiac cycle and evaluate various operational parameters on recirculation during two-site VV ECMO. This FSI CFD model is based on human anatomy, allowing a more precise evaluation the main factors affecting VV ECMO recirculation. These factors include cannula construction, insertion depth, and orientation, VV ECMO configuration, circuit blood flow, and changes in volume, venous return, heart rate, and blood viscosity. The results provide the physician and engineer useful information to address the problem of recirculation.

METHODS

Model Geometry

A 3-dimensional (3D) model of the superior vena cava, inferior vena cava, and right atrium was constructed for the studies. The geometry was obtained from slices of a contrast computed tomogram (CT) scan of the chest from a deidentified adult. Use of images was approved through exemption by the Institutional Review Board (no. E11041) The contrast-containing atrium and superior (SVC) and inferior venae cavae (IVC) were segmented from surrounding tissue followed by 3D surface reconstruction using InVesalius (Renato Archer Information, Campinas SP, Brazil). A surface mesh was developed from the reconstructed surface and shelled with a 2 mm offset using MeshLab (ISTI-CNR, Pisa, Italy) to create the geometry consisting of atrial, SVC and IVC walls with an interior blood domain (see Image, Supplemental Digital Content 1, http://links.lww.com/ASAIO/A570). The surface mesh was imported and converted to a solid geometry in COMSOL Multiphysics v5.4 (COMSOL Inc., Burlington, MA) for solution using the finite element method. The imported geometry was further modified to segment an outlet boundary corresponding to the tricuspid valve opening,⁷ to create inlet boundaries on the inferior and superior vena cavae, and to add single-lumen intravascular cannulas that matched dimensions of commercially available devices used for ECMO (Figure 1). The surface mesh and a cross-section of the volume mesh are given in Supplemental Digital Content 2 (http://links.lww.com/ASAIO/A570). The IVC inlet boundary was extruded as needed to accommodate the side holes of the drainage cannula.

Figure 1.

Model geometry with components and boundary conditions labeled. The return and drainage cannulas are shown in the SVC and IVC. The inflow and outflow boundaries are also shown for the SVC, IVC, and tricuspid valve, with their boundary conditions described in the text. The fixed constraints represent the components of the structural mesh that are not allowed to deform with the moving mesh. The representative directions of the mainstream and recirculated extracorporeal flows are shown in red. ECMO, extracorporeal membrane oxygenation; SVC, superior vena cava; IVC, inferior vena cava.

Domain and Boundary Conditions

The atrial wall and cannulas were modeled as linear elastic materials. Blood was represented as a non-Newtonian fluid using the Carreau viscosity model⁸:

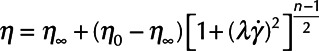(1)

where η, η₀, and η_∞ represent apparent, zero, and infinite shear rate viscosity values, respectively, λ is the relaxation time, n is the power index, and γ is the dependent variable shear rate.

FSI was incorporated into the model with a moving mesh using the Arbitrary Lagrangian-Eulerian (ALE) formulation, with the solid component represented by the atrial wall, the fluid component represented by blood, and two-way pressure and wall-normal velocity coupling defined at the inner atrial wall. A fixed constraint was applied to the SVC inlet wall boundary, IVC inlet wall boundary, and tricuspid valve ring. The atrial wall and cannulas were defined as frictionless contact pairs to constrain the cannulas within the atrial geometry. Material properties are given in Table 1.

Table 1.

Material Properties for Model Components

Boundary conditions were specified as time-varying flow at the vena cavae inlets and tricuspid valve outflow, with velocity profiles obtained from echocardiographic studies that included both passive and active phases of right atrial emptying (see Supplemental Digital Content 3, http://links.lww.com/ASAIO/A570; Animation, Supplemental Digital Content 4, http://links.lww.com/ASAIO/A571; and Legend, Supplemental Digital Content 4, http://links.lww.com/ASAIO/A572). Constant and equal volumetric flow was applied to the return cannula inlet and drainage cannula outlet. The external wall of the atrium was set to ambient pressure.

Meshing and Solution

A solution mesh was created on the geometry consisting of approximately 1.1 × 10⁶ tetrahedral fluid domain elements with 65,000 prism boundary elements on no-slip wall boundaries. The structural mesh of the atrial wall and vena cavae consists of triangular surface elements extruded into 2 layers of prism elements across the thickness of the structure, each 1 mm deep.

Element size at all no-slip wall boundaries maintained to respect the relationship required for turbulence modeling:

(2)

where y⁺ is dimensionless distance to the wall (wall units), y is the element size normal to the wall, u_τ is friction velocity, and ν is kinematic viscosity. This constraint was relaxed to a value of approximately 25 for near-wall azimuth dimensions, and 50 for elements further from the wall within the fluid domain.¹³ Mesh quality statistics based on both element skewness and maximum angle are provided and explained in Supplemental Digital Content 5 (http://links.lww.com/ASAIO/A570).

Fluid flow was solved using the large eddy simulation (LES) approach, which resolves larger eddies using the Navier-Stokes equations and models the small subscale eddies. Subscale eddies were modeled with the residual-based variational multiscale (RBVM) method,¹⁴ a method for consistent subscale modeling that is applicable to laminar and transitional flow as well as to turbulent flow, all of which would be expected under these operating conditions. The fluid flow field was two-way coupled to the mechanical properties of the atrial wall to model pressure-driven deformation from expansion and contraction of the right atrial chamber. One cardiac cycle was solved to establish initial conditions for the following cardiac cycles, which were used for calculations.

A fully coupled direct solver was used to solve all dependent flow and fluid-structure variables simultaneously. A second-order backward differentiation formula (BDF) solver was used with time-steps (Δt) chosen to meet the CFL (Courant-Friedrichs-Lewey) condition for all elements, necessary for LES:

(3)

where u, v, and w are the local blood flow velocities, and Δx, Δy, and Δz are the element sizes, in the x, y, and z directions, respectively. A convergency criteria of 0.001 was used.

Since oxygen transport under these flow rates is greatly dominated by convection (Péclet number approximately 10⁸), Lagrangian particle tracing was subsequently solved on the flow field for calculation of recirculation in place of Eulerian convection-diffusion, with 5,000 massless particles released into the inlet cannula over the first cardiac cycle. Particles traversing the drainage cannula and tricuspid valve were counted over subsequent cycles until >90% of the particles crossed the exit boundaries. Recirculation fraction was calculated as the particle transmission probability through the drainage cannula.

Recirculation Factors

We chose to study several factors that are known or suggested to contribute to recirculation.¹ We also included other factors that we considered could contribute to recirculation but not previously reported. Each are described in the sections below. These known factors and other geometric, material property, and operational factors were systematically examined through alterations in the model (Table 2). The baseline model operating parameters were chosen to reflect typical clinical conditions (Table 3) and were used except where modified for simulations. In describing the magnitude of effect on recirculation, a value <5% was considered minimal, 5%–20% moderate, and >20% major significance.

Table 2.

Parameter Values Used for Simulations

Test Parameter	Parameter Values
Extracorporeal blood flow	[0, .5, …, 5.0] L·min–1
Return cannula orientation	[0, 15, 30] degrees
Cannula insertion depth	[–2 cm, 0 cm, +2 cm]
Blood flow direction	Femoro-jugular and jugulo-femoral
Return cannula size	[22, 24, 26, 28] Fr
Blood viscosity (η∞)	[.0025, .003, .0035] Pa·s
Heart rate	[60, 90, 120] s–1
Atrial volume	[0, +15%, +30%]
Inferior vena caval flow fraction	[.68, .5, .32]

The same baseline configuration was used except for the parameter being varied.

Table 3.

Baseline Configuration Operating Parameters

Parameter	Value*
Blood viscosity (η∞)	0035 Pa·s
Cardiac output	5.0 L min–1
Extracorporeal blood flow	4.0 L min–1
Heart rate	60 min–1
SVC:IVC blood flow fraction	0.32:0.68
Systolic ejection interval	0.5
Cannula size	28 Fr drainage 24 Fr return
Flow direction (two-site)	Femoro-jugular
Cannula insertion depth	Tip at cavo-atrial junction
Cannula orientation	Coincident

*These constant values were used for all simulations except for any parameter under study which was varied.

Extracorporeal Circuit Flow Rate

The dependence of recirculation fraction on volumetric blood flow rate is well known in the clinical setting and has been previously demonstrated in dual-site single-lumen cannulation with in vitro studies.¹⁵ Using the current model, the relationship between circuit flow and recirculation fraction was examined by varying circuit flow from 10% to 100% of cardiac output, which was fixed at 5.0 L min^–1.

Atrial Volume

The volume of the atrial chamber due to changes in intravascular volume, with reduced volumes in hypovolemia and elevated volumes in hypervolemia, is another parameter that could influence mixing of blood in the atrium and thus affect recirculation fraction. To study this effect, simulations were performed with comparisons between the baseline atrial volume and increases by 15% and 30% above baseline. The cardiac output and heart rate were held constant.

Heart Rate

Heart rate has the potential to influence recirculation through an increase in velocity of atrial wall contraction leading that can affect mixing, and a reduction in atrial diastolic filling time. Using the current model, the effect of heart rate at a constant cardiac output and extracorporeal circuit flow was evaluated at rates of 60, 90, and 120 per minute.

Blood Viscosity

Blood viscosity is a fundamental determinant of fluid flow and has the potential to influence blood flow patterns. While the influence of viscosity on blood flow in simple geometries such as pipes is predictable, its effect on flow in complex geometries such as this model with FSI is uncertain. Simulations were performed at three viscosities, 0.0035, 0.0030, and 0.0025 Pa s representing viscosity at normal hematocrit (approximately 40%) and 2 lower values representing approximate hematocrits of 30% and 20%.

Cannula Inflow Orientation

The orientation of inflow from the SVC cannula following cannula insertion is typically a function of anatomy and not under full control of the surgeon or physician. This orientation, however, is presumed to have an influence on recirculation, with a direction targeting the tricuspid valve expected to result in a lower recirculation rate. Simulations were performed with the inflow cannula extended further into the atrium and directed along the insertion path (0°), directed toward the center of the tricuspid valve (30°), and an intermediate position directed toward the wall between the cavo-atrial junction and the tricuspid valve (15°).

Return Cannula Size

Cannula diameter determines blood flow velocity for a given volumetric flow. Since inflow velocity will influence the pattern of mixing of blood in the atrium, an assessment of this parameter was performed. Simulations were conducted for inflow cannula diameters of 22 Fr, 24 Fr, 26 Fr, and 28 Fr, which approximate the range of sizes used in adult extracorporeal support and represent a relative range of velocities from 1 m s^–1 (28 Fr) to 2.6 m s^–1 (22 Fr) at full support.

Cannula Insertion Depth

Cannula insertion depth is known to affect recirculation.¹ Overinsertion of the SVC inflow cannula past the cavo-atrial junction would presumably direct blood more directly toward the drainage cannula, reducing mixing, and increasing recirculation. Withdrawal of this cannula into the SVC may minimize these effects. Insertion depth of the IVC drainage cannula would likely affect recirculation as well. Overinsertion of the drainage cannula would reduce the amount of blood drained from the IVC and increase the amount of blood drained from the atrium containing reinfused blood.

Direction of Blood Flow

Clinical studies have demonstrated improved saturation when circuit flow is in the femoro-atrial direction, with drainage from the IVC and return into the SVC. The presumption is that this is due at least in part to reduced recirculation,¹ but recirculation has not been directly measured and compared in vivo. The model was used to address this question by comparing the typical configuration to two reverse flow configurations, having the return cannula tip located at both the cavo-atrial junction and at 5 cm below the cavo-atrial junction in the IVC.

Return Cannula Tip Design

Cannulas designed for blood return are manufactured with a variable number of side holes near the tip of the cannula. Straight tipped cannulae have no side holes and would eject blood following the axis of the cannula with minimal disturbance. Side holes can be expected to distribute some of the blood in an off-axis direction, increasing mixing with returning venous blood, potentially reducing recirculation. To characterize the extent to which side holes contribute to recirculation simulations were performed under baseline conditions using a straight cannula, a cannula with a pair of opposed side holes 1 cm from the tip, and a cannula with two pairs of opposed side holes at 1 cm and 2 cm from the tip, and rotated 90° relative to each other.

Vena Caval Blood Flow Distribution

Normal venous return is not distributed evenly between the venae cavae, but rather with about two-thirds derived from the IVC and the remaining third from the SVC.¹⁶ During shock states, IVC blood flow decreases relative to that of the SVC, reducing to about half of the cardiac output, presumably as a compensatory mechanism.¹⁷ Furthermore, conditions in critical illness such as intraabdominal hypertension can directly compress the IVC and independently reduce IVC blood flow.¹⁸ A reduction in IVC blood flow relative to SVC can influence recirculation. If circuit drainage is from the IVC, then a reduction in IVC flow would cause more SVC/atrial blood to enter the IVC, increasing recirculation. To evaluate this factor, simulations were run with varying SVC:IVC blood flow ratios.

Oxygen Transfer

Recirculation negatively affects oxygen transfer, with the degree of impact related to the interrelationship between extracorporeal blood flow, venous return, and recirculation fraction. A mass balance was used to calculate oxygen transfer:

(4)

where is the oxygen transfer provided by the circuit, is the total oxygen transfer delivered to the pulmonary artery, and are extracorporeal blood flow and cardiac output respectively, R is recirculation fraction, is mixed venous oxygen saturation (0.65), and Hb is hemoglobin (12 g dl^–1). The levels of extracorporeal flow and cardiac output are the same as used in Figure 1. In addition, two additional calculations at low values of cardiac output (4.0 and 3.0 L min^–1) at an extracorporeal flow of 5.0 L min^–1 were preformed to simulate higher ratios of extracorporeal flow fraction of 1.25 and 1.67, respectively.

Hemolysis Evaluation

Hemolysis is a problem complicating extracorporeal support. Under typical extracorporeal support conditions hemolysis rates are low and usually not clinically important. Under some conditions, however, hemolysis can impact support and may lead to adverse patient outcomes. An understanding of circuit factors contributing to hemolysis may provide useful insight.

A computational index of hemolysis was evaluated in the model, comparing return cannula diameter and return cannula side hole number. A narrower diameter and the presence of side holes can increase shear stresses leading to erythrocyte damage. The power law model for index of hemolysis is the most applied formulation, first introduced by Giersiepen et al¹⁹:

(5)

where τ is the deviatoric turbulent viscous stress tensor²⁰ and C, α, and β are experimentally determined constants with values of 3.63 × 10^–7, 2.416 and 0.785, respectively. A Lagrangian formulation of the power law was employed with the use of particle tracing. A total of 2,500 massless particles evenly distributed over the vena cavae inflow and the return cannula boundaries were released. The Giersiepen power law equation was integrated over each of the particle pathlines during their traversal from inlet to outlet. The hemolytic index was converted to the Normalized Index of Hemolysis (NIH)²¹:

(6)

The sum of NIH values of all pathlines was obtained to represent the overall normalized index. Since the site of highest shear rates occur in the return cannula, simulations were performed for the different diameters of return cannula, and the number of side holes on the return cannula, all at a circuit flow of 4 L/min.

RESULTS

Although the CFL condition is a necessary condition for convergence, a mesh dependence study was performed with two additional mesh refinements consisting a 15% and 30% increase in mesh size using the baseline parameters at an extracorporeal flow of 4 L/min. Recirculation fractions were 30.19%, 30.61%, and 30.27%, respectively, suggesting the chosen solution parameters were not influence by mesh density.

Extracorporeal Circuit Flow

Extracorporeal circuit blood flow rate relative to cardiac output during two-site VV ECMO had a major influence on recirculation fraction (Figure 2). Values were minimal at low-flow rates but increased with extracorporeal flow fraction. When extracorporeal flow reached cardiac output, recirculation fraction approached 40%. Values of this magnitude are consistent with clinically reported values.⁴

Figure 2.

Recirculation fraction as a function of extracorporeal circuit blood flow in typical two-site single lumen cannula configuration with femoro-jugular flow direction. Cannula sizes: 28 Fr drainage, 24 Fr return. CO, cardiac output; HR, heart rate.

Insight into this relationship can be gained from examining the flow streamlines associated with the return and drainage cannulas (see Image, Supplemental Digital Content 6, http://links.lww.com/ASAIO/A570). At low flow (Image, Supplemental Digital Content 6A and 6B, http://links.lww.com/ASAIO/A570) reinfused blood from the return cannula mixes in the upper atrium and does not reach the drainage cannula, leading to low recirculation. At high flow (Image, Supplemental Digital Content 6C and 6D, http://links.lww.com/ASAIO/A570) more infused blood reaches into the IVC and the drainage cannula in a more complex pattern, increasing recirculation.

Atrial Cavity Volume

Changes in right atrial volume at the beginning of atrial filling had a minor impact on recirculation rate, with a slight decrease in recirculation associated with increasing volume (Figure 3A). A larger atrial chamber size, as may occur with hypervolemia and atrial distension, may reduce recirculation by allowing more mixing than would occur in a smaller chamber.

Figure 3.

A: Effect of atrial volume on recirculation. Atrial volume increases of 15% and 30% above baseline had a small influence on reducing recirculation, presumably due to increased volume available for mixing. B: Recirculation fraction as a function of heart rate at a constant cardiac output and circuit flow. Recirculation fraction increases with increasing heart rate, conceivably due to greater atrial contraction as well as a smaller atrial volume expansion associated with shorter diastolic filling times. CO, cardiac output; HR, heart rate; Qcircuit, extracorporeal circuit flow.

Heart Rate

Changes in heart rate had a moderate impact on recirculation, with recirculation fraction increasing with increasing heart rate (Figure 3B). There are two potential explanations. A higher heart rate with more rapid atrial wall movement could alter the dynamics of blood flow within the atrium. Second, a higher heart rate at a constant cardiac output reduces diastolic filling time and atrial end-diastolic volume, leading to a smaller chamber and facilitating recirculation.

Blood Viscosity

Simulations performed with three blood viscosity values corresponding to a normal hematocrit (40%), mild anemia (30%), and moderate (20%) anemia (0.0035, 0.003, and 0.0025 Pa s, respectively) failed to show any clinically significant influence of viscosity on recirculation, with values differing by less than 1%.

Return Cannula Orientation

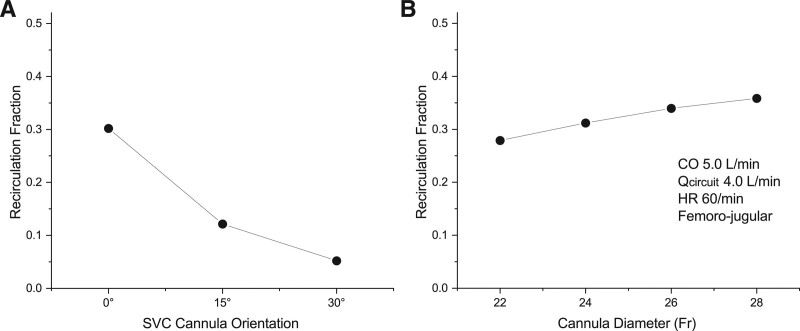
Orientation of the tip of the return cannula determines the direction of the return jet with respect to the drainage cannula and the tricuspid valve. Clinical experience indicates that orientation toward the tricuspid valve and away from the drainage cannula can reduce recirculation. The current simulation study supports this finding, with a major reduction of recirculation with the cannula extended further into the atrium and directed directly toward the tricuspid valve, and a lesser but significant reduction when directed between the two (Figure 4A).

Figure 4.

A: Impact on orientation of the inflow cannula tip on recirculation. The 0° orientation directs the return jet directly toward the drainage cannula. The 30° orientation directs the jet directly toward the center of the tricuspid valve, while the 15° orientation directs it intermediate between these two. B: Influence of inflow cannula diameter on recirculation fraction. Smaller diameter results in higher inflow velocity. A modest reduction in recirculation was associated with decreasing cannula size and increasing inflow velocity, possibly due to increased mixing within the atrium. CO, cardiac output; HR, heart rate; Qcircuit, circuit blood flow.

The reason for decreased recirculation is likely twofold. During tricuspid valve opening orientation of the return blood jet directly toward the valve reduces mixing of blood entering the right ventricle. During closure of the valve, orientation of the jet away from the drainage cannula increasing mixing of blood in the atrium before entering the drainage cannula, lowering its saturation, and thereby decreasing recirculation.

Return Cannula Diameter

Diameter of the return cannula (and the associated change inflow velocity) had a moderate effect on recirculation (Figure 4B). The smallest diameter studies (22 Fr) resulted in a lower recirculation. The reason for this finding is not clear since a higher inflow velocity is expected to direct more blood toward the drainage cannula. It is conceivable that the higher velocity resulted in improved mixing in the atrial chamber, with drainage of blood having a lower saturation.

Cannula Insertion Depth

Insertion depth of both the drainage cannula and the return inflow cannula affected recirculation. It is recognized clinically that over-insertion of either cannula will reduce the distance between cannulas and increase recirculation. A slight increase in recirculation is noted when the SVC return cannula is inserted deeper than the cavo-atrial junction (Figure 5A). Also appreciated is a notable reduction in recirculation when the return cannula is withdrawn into the SVC. In this position, there is more opportunity for greater mixing in the SVC leading to a reduced recirculation. Advancing the drainage cannula into the atrium also demonstrated a more pronounced increase in recirculation (Figure 5B). Withdrawing more distally into the IVC, however, had no major impact.

Figure 5.

A: Effect of SVC return cannula insertion depth on recirculation fraction. Simulations were carried out at a cardiac output of 5 L min^–1, heart rate 60, and circuit blood flow of 4 L min^–1. B: Effect if IVC drainage cannula insertion depth on recirculation fraction. Positioning the cannula tip 1.5 cm above the cavo-atrial junction resulted in a slight reduction in recirculation. Since the drainage cannula was multiholed, most drainage occurs more distal in the IVC and thus not affected significantly by the deeper insertion. Positioning the cannula tip more distally in the IVC had slight impact Simulations were carried out at a cardiac output of 5 L min^–1, heart rate 60, and circuit blood flow of 4 L min^–1.

Direction of Blood Flow

The direction of extracorporeal blood flow had a moderate influence on recirculation (Figure 6A). Flow in the femoro-jugular direction resulted a modestly lower recirculation than flow in the jugulo-femoral direction. This may be explained by fact that IVC blood flow is typically much higher than SVC flow, and that femoral drainage captures a greater percentage of desaturated venous blood.

Figure 6.

A: Effect of blood flow direction on recirculation during two-site VV ECMO. Flow in the femoro-jugular direction resulted in lower recirculation than flow in the jugulo-femoral direction. There was a slightly lower recirculation with the cannula tip positioned at the atrial-IVC junction compared with a more distal position of the tip in the IVC (5 cm below the junction). Simulations were carried out at a cardiac output of 5 L min^–1, heart rate 60, and circuit blood flow of 4 L min^–1. F→J, femoro-jugular direction; J→F, jugulo-femoral direction. B: Effect of return cannula tip design on recirculation. Three tip designs were studied: a straight tipped with no side holes, a design with a pair of opposed side holes 1 cm from the tip, and a design with two pairs of opposed side holes at 1 cm and 2 cm from the tip, rotated 90° with respect to each other.

Return Cannula Tip Design

The design of the return cannula tip had a minor impact on recirculation (Figure 6B). The straight tipped cannula ejected blood directly along the cannula axis, with minimal disturbance at the tip. The addition of a pair of side holes produced some flow disturbance at the tip resulting in a slightly lower recirculation (10% lower relative to baseline). The addition of two pairs of side holes did not appreciably affect recirculation relative to a single pair of side holes.

Venae Cavae Flow Distribution

Simulations confirmed a major relationship between SVC:IVC flow ratio and recirculation when flow direction is femoro-jugular. A lower ratio (higher relative IVC flow) (as observed in normal humans) was associated with a lower recirculation fraction (Figure 7). As IVC flow is decreased relative to SVC flow, recirculation increases. These findings can be explained by noting under usual operating conditions in the femoro-jugular configuration circuit drainage exceeds IVC flow, necessitating blood from the atrium (and return cannula) to enter the IVC and thus the drainage cannula. The lower the relative IVC flow, the greater amount of blood that enters from the atrium, resulting in a higher recirculation.

Figure 7.

Influence of ratio of venous return between the SVC and IVC on recirculation. A reduction in IVC flow relative to the SVC resulted in higher recirculation using the femoro-jugular configuration.

Oxygen Transfer

The impact of recirculation on oxygen transfer is given as a graph in Supplemental Digital Content 7 (http://links.lww.com/ASAIO/A570). The left set of curves represent the increasing oxygen transfer with increasing extracorporeal flow at a CO of 5 L min^–1. The filled circles represent total delivery to the pulmonary artery from the circuit and venous return. The filled squares represent the circuit delivery. The recirculation fraction curve is given with the open diamond as reference, reproduced from Figure 2. The right set of curves provide simulations for extracorporeal flow fraction greater than one achieved by reducing cardiac output to 4 and 3 L min^–1 at a fixed circuit flow of L min^–1. The drop in oxygen transfer represents marked increases in recirculation from the high extracorporeal flow fraction and demonstrates that excessive circuit flow can be detrimental by worsening oxygen delivery.

Hemolysis

The calculated normalized indices of hemolysis (NIH) for the cannula configurations studied are given in Supplemental Digital Content 8 (http://links.lww.com/ASAIO/A570). There was a slight inverse association between cannula size and NIH likely related to the increased turbulent shear stress introduced with greater flow velocity. The addition of two- and four-side holes introduced a greater increase in the calculated NIH through the addition of sites leading to increased shear forces and rate of hemolysis.

DISCUSSION

Recirculation of oxygenated blood returned from the ECMO circuit to the venous system is an important contributor to the loss of efficiency in oxygen transport during VV ECMO. While general contributors to recirculation are well recognized, they remain somewhat unpredictable, as several known variables can influence it. This study sought to systematically study the effect of known and potential variables using a dynamic computational model.

This study yielded information on recirculation that could provide insight into VV ECMO performance. Some of the results are expected and are consistent with reported experimental and clinical findings. Recirculation was nearly linearly related to extracorporeal blood flow over most of the range of flow studied. Studies using dual-lumen cannulas have confirmed this finding,^22,23 although studies using two-site cannulation are lacking. Flow in the femoro-jugular direction is associated with less recirculation. This finding was noted by Rich et al who compared flow directions in a series of patients.²⁴ Although recirculation in that study was not directly measured, a reduction in flow required to maintain saturation served as a proxy for reduced recirculation.

The finding of profound differences in recirculation associated with orientation of the inflow cannula deserves further comment. Reports by Lin²⁵ and Bonacchi²⁶ have demonstrated that recirculation can be largely eliminated by the use of inflow cannulas that are inserted deep, close to the tricuspid valve, and curved to direct flow directly at the valve. The current study suggests that deep insertion of the cannula may not necessary, but that only placement of the cannula in the superior portion of the atrium with orientation toward the valve may be all that is needed to achieve similar results. Use of this approach may reduce the difficulty and risk associated with more specially designed cannulas.

Other findings have not been previously studied. A change in atrial volume was found to slightly influence recirculation, with smaller volumes resulting in higher recirculation, presumably because less volume is available for mixing. In clinical practice, greater extremes in volume may be found, and thus changes in recirculation may be more pronounced. Increases in heart rate at constant cardiac output increased recirculation, which is conceivably due to alterations in atrial blood flow patterns as well as less atrial distension related to smaller stroke volume, resulting in less mixing. The fraction of cardiac output returning through the IVC was found to be a significant determinant of recirculation, with higher recirculation found when venous return through the IVC was diminished as can be found in critical illness.

No recommendation on the design of side holes in the return cannula has been put forth in the literature, and choice is often arbitrary. This simulation study demonstrated that the addition of 2- side holes resulted in a small reduction in recirculation, presumably due to diversion of flow away from the direction of the drainage cannula, but that an additional two-side holes did not confer any significant additional benefit. However, the addition of side holes has the risk of increased shear forces leading to hemolysis risk, but this study was not designed to address shear rates.

Reported in vivo recirculation fractions are limited and quite variable, and since not under controlled conditions, cannot be directly related to the findings of this study. However, our findings are within the ranges of recirculation reported for two-site VV ECMO. In a swine model of VV ECMO, Lee et al measured recirculation rates from 0% to 66%, but the operating conditions were not reported.²⁷ Broman et al measured recirculation in a small series of VV ECMO patients and noted a mean recirculation of 42% with a circuit blood flow of 4.1 L·min^–1 in the jugulo-femoral direction,⁴ comparable to our results in the same direction (Figure 6A). Our simulations included a study of high extracorporeal flow rates where circuit flow exceeded cardiac output, demonstrating a drop in oxygen delivery with increasing circuit flow. Although this study did not directly address it due to computational demands, an optimization procedure could be implemented to identify the optimal flow rate for any given cannulation configuration and cardiac physiology.

Hemolysis is a known complication of ECMO. It is expected that the smaller the return cannula, the higher the degree of turbulence and associate shear stresses, and the rate of hemolysis. Although no values for NIH have been reported for ECMO cannulas, the values from our simulations are lower than values measured in ECMO blood pumps and oxygenators. Meyer et al reported NIH values between .0032 and .0058 for roller and centrifugal pumps in a neonatal circuit.²⁸ Kawahito et al reported values of 0.007 to 0.0164 in a bench testing of ECMO oxygenators.²⁹ While our lower values may suggest less hemolysis, it is important to note that hemolysis prediction models are validated under specific operating conditions, and no validated mathematical model exists for ECMO circuit components. Given that limitation, a hemolysis computational model may still be helpful in comparing operating conditions using CFD. Our simulations showed only a minor increase in NIH with the use of smaller cannulas. Although no one has reported experimentally measured NIH as a function of cannula size, a study by Lehle et al³⁰ used plasma free hemoglobin (fHb) levels as a marker of hemolysis during VV ECMO, and reported values from 51 to 58 mg/L for cannulas ranging from 15 to 21 Fr, with no association between cannula size and fHb levels. However, cannula sizes may have been chosen appropriate for the flow. An association between flow rate and fHb was noted, suggesting that increasing flow rates through a cannula could increase hemolytic rate. Our findings support a slight association between cannula size at a constant flow rate and calculated hemolytic index but not to a degree of clinical concern. We also noted an increase in simulated NIH with the addition of side holes to the cannula, an expected behavior since cannula side holes are designed for manufacturing convenience and not for flow dynamics. However, the decrease in recirculation associated with the addition of side holes may outweigh the risk of hemolysis.

The advantage of 3D CFD modeling with FSI is to allow more precise evaluation of recirculation associated with cannula construction, insertion depth and orientation, as well as VV ECMO configuration, ECMO circuit blood flow, pathologic changes in heart anatomy, heart rate, and blood viscosity. Computational fluid dynamics (CFD) is playing an increasingly important role in the design and evaluation of medical devices and is being recognized by regulatory agencies as an important step in the development of medical devices.³¹ Computational capabilities of hardware and software have continued to improve, and the introduction of multiphysics capabilities such as FSI are becoming commonplace. This study is based on a 3D CFD model that incorporates FSI to model the dynamics of right atrial blood flow including atrial expansion and contraction, providing a better approximation to in vivo hemodynamics that is not possible with fixed-geometry or lumped parametric models. Solution using LES, although more computationally intensive, provides a more accurate solution than Reynolds-averaged Navier-Stokes methods, as the latter assumes fully developed turbulent flow, whereas this model has regions of laminar, transitional, and turbulent flow. The model is based on direct anatomic measurements of the right atrium and venae cavae obtained from a human contrast computed tomographic scan. With the introduction of vascular cannulae into the geometry, the ability to model the complex blood flow patterns that occur during VV ECMO is feasible and can provide insight into recirculation patterns during extracorporeal support.

The use of mathematical or computational models to study recirculation is limited, and this study represents the first use of FSI with computational fluid dynamics. Broman et al employed a comprehensive lumped parameter model³² to study recirculation related to blood flow under different cannulation conditions, but other model parameters were fixed. Jamil et al employed computational fluid dynamics in a right atrial geometry to evaluate recirculation in a dual-lumen cannula as a function of cannula position.⁶ Their study employed a geometry obtained from MRI, but the geometry was fixed, in contrast to our study which included atrial dynamics through a FSI model.

The major limitation of this study is the lack of full validation of the model. Simulations with fixed geometries are feasible to validate, as the design variables of the computational model can accurately replicate the bench model. In contrast, the dynamics of a complex FSI model are not precisely as reproducible on the bench as would be a fixed-geometry model. Despite this limitation, the performance of the model is consistent with observed clinical findings, for example, the dependence of recirculation on blood flow, and the findings associated with reversal of blood flow direction. In addition, CFD applications and the codes to execute them have matured and are becoming more widely accepted in the design and analysis of medical devices. In support of the utility of this model is the fact that this study is focused on the comparison of effects of parameter variation rather than absolute values of dependent variables in given scenarios.

The computational time required for these simulations limited the study to variation in a single variable at a time. It is possible that there are interactions that may be revealed by variation in two or more variables. The magnitude of these interactions is not likely to be dominant, and therefore the findings reported are expected to provide important insight.

CONCLUSIONS

In conclusion, the addition of FSI as well as other features of dynamic and static structural mechanics to computational fluid dynamics increases the potential for more accurate modeling of artificial organ performance. This study identified how variations in the application of venovenous cannulation and support can have marked effects on extracorporeal circuit performance, providing guidance for clinical application and future design. Our simulations revealed that extracorporeal blood flow relative to cardiac output, ratio of SVC to IVC blood flow, position of the SVC cannula relative to the cavo-atrial junction, and orientation of the return cannula relative to the tricuspid valve had major (> 20%) influences on recirculation fraction. Factors with a moderate (5%–20%) influence on recirculation fraction include heart rate, return cannula diameter, and direction of extracorporeal flow. Minimal (<5%) influence on recirculation was associated with atrial volume, position of the IVC cannula relative to the cavo-atrial junction, the number of side holes in the return cannula, and blood viscosity (as determined by hematocrit).