Serial dependence revealed in history-dependent perceptual templates

Summary

In any given perceptual task, the visual system selectively weighs or filters incoming information. The particular set of weights or filters form a kind of template, which reveals the regions or types of information that are particularly useful for a given perceptual decision.^1,2 Unfortunately, sensory input is noisy and ever-changing. To compensate for these fluctuations, the visual system could adopt a strategy of biasing the templates such that they reflect a temporal smoothing of input, which would be a form of serial dependence.^3–5 Here, we demonstrate that perceptual templates are, in fact, altered by serial dependence. Using a simple orientation detection task and classification-image technique, we found that perceptual templates are systematically biased toward previously seen, task-irrelevant orientations. The results of an orientation discrimination task suggest that this shift in perceptual template derives from a change in the perceptual appearance of orientation. Our study reveals how serial dependence biases internal templates of orientation and suggests that the sensitivity of classification-image techniques in general could be improved by taking into account history-dependent fluctuations in templates.

eTOC Blurb

Using an orientation detection task and classification-image technique, Murai and Whitney demonstrate that perceptual templates used by observers to make judgements about incoming information are biased by previously seen stimuli, indicating that some of the most basic perceptual representations are serially dependent on prior experiences.

Results

Our sensory input is susceptible to various sources of noise that could contaminate our perceptual interpretations. To stabilize perception, the visual system can leverage knowledge about the statistical structure of the external world.⁶ For example, the well-known “oblique effect” of orientation perception, in which oblique orientations are perceived less accurately than cardinal orientations, can be explained by the natural orientation statistics that exist in the environment.⁷

In addition to the spatial statistics of the world, the visual system could utilize temporal statistics as well. Some of the evidence that the visual system takes advantage of the temporal structure of the environment comes from work revealing serial dependencies in visual perception: the perception of objects is biased toward previous stimuli.^3,4 Serial dependencies have been found in many domains including the perception of numerosity,^4,8,9 object location,^10,11 face identity and expression,^5,12,13 and attractiveness.^14,15 It also generalizes across tasks, manifesting in everything from continuous report and discrimination^3,5,16,17 to magnitude estimation^14,18,19 and classification.²⁰ Sequential dependencies contribute to perceptual stability by taking the temporal redundancy of events into account in order to compensate for noisy sensory representations.²¹ An additional clear benefit of serial dependencies is that, by recycling previous representations, the visual system improves efficiency, speed, stability, and robustness to noise.^21–23

Despite all the evidence for serial dependencies in perception and decision, how, exactly, do prior visual stimuli alter the perception and decisions about subsequent stimuli? One possibility is that prior stimuli alter the sensitivity to or the weights assigned to different parts or features of a noisy image. If this is the case, then we should expect that serial dependencies should alter the perceptual templates that observers use to make judgments about subsequent stimuli. A perceptual template refers to how the visual system weighs or filters incoming information for a particular perceptual decision.^24–27 Perceptual templates are frequently revealed using the classification-image technique, which investigates how the trial-by-trial variation in stimulus noise affects observer perception.^1,2

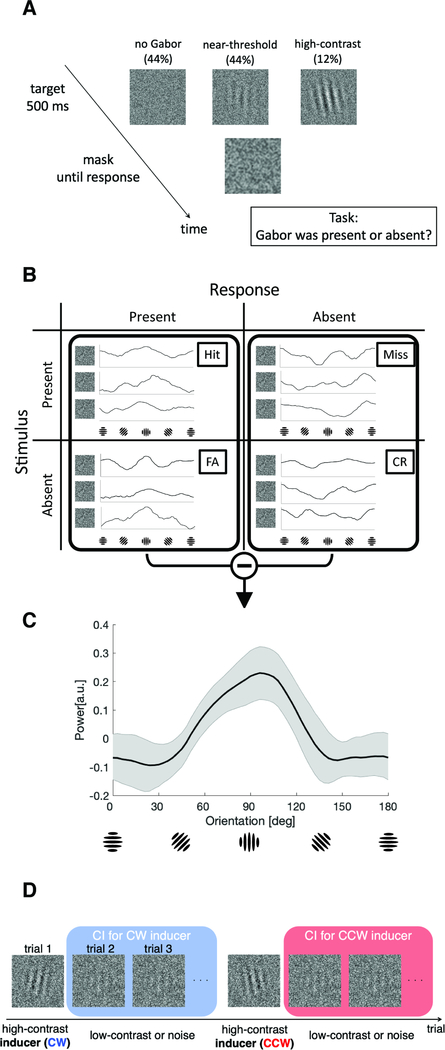
In Experiment 1, we tested whether perceptual templates are altered by the history of visual input using a classification-image approach. Participants judged whether a vertical Gabor (target) was present or absent in a white noise image (Figure 1A). Since the target Gabor was near-threshold and hard to detect, they had to make their responses based on the patterns of the noise images. To visualize their perceptual template of vertical orientation, we classified trials into one of four stimulus-response categories (Figure 1B). Each noise image (excluding the Gabor signal) was 2-D Fourier-transformed separately to analyze the power distribution of orientations, and then averaged for each of the four stimulus-response categories. The classification image was calculated by subtracting the distributions of orientation power for the noise images in absent response trials (Miss and Correct Rejection) from that for present response trials (Hit and False Alarm) (Figure 1C). Importantly, in both Hit and Miss trials, the target Gabor was removed from the original image and only the remaining noise was analyzed. To test for serial dependence—any effect of the previous stimulus on the subsequent perceptual template of orientation—a high-contrast Gabor tilted clockwise (CW) or counterclockwise (CCW) was presented occasionally as an inducer. We conducted the same classification image analysis separately for trials following CW and CCW inducers (Figure 1D). The inducer trials were excluded from all analyses.

Figure 1. Schematics of the first (detection) experiment.

(A) In each trial, the participants judged whether a Gabor stimulus was present or absent in a noisy image. In 44% of the trials, a near-threshold Gabor was embedded in a white noise stimulus. In another 44% of the trials, the white noise was presented on its own, without any Gabor. In the remaining 12% of the trials, a high-contrast Gabor was presented to induce serial dependence. (B) Trials were classified into 4 categories based on stimulus presence and the subject’s response. Each noise image (excluding all Gabor signal information) was Fourier-transformed and the power of each orientation was calculated. The orientation power is graphed here for twelve example noise stimuli: only the noise was included in this analysis; the signal Gabor orientation was removed. (C) The classification image (CI) was obtained by subtracting the mean power distribution for “absent” response trials (Miss and Correct Rejection [CR]) from the mean power distribution for “present” response trials (Hit and False Alarm [FA]). This group-averaged CI is tuned toward vertical orientations and has a vector average that is not significantly different from vertical (mean = 92.5, p = .75). (D) To estimate how the inducers might distort the classification image in subsequent trials, CIs were estimated separately for trials following clockwise (CW) and counterclockwise (CCW) inducers. The inter-inducer interval was 5–11 trials, roughly 8–20 seconds in time.

Participants accurately detected vertical orientation in the noise images (Figure 2A). If the participants detected vertical orientation in the noise images, the power of vertical orientation should be stronger in present-response trials, which is exactly what we found. The power of near-vertical orientations in the noise images was stronger when participants judged the target Gabor was present, compared to the trials when they judged the target was absent. The mean vector angle of the classification image was 92.5 deg (95% CI = [84.1 100.6] deg), which was close to the veridical vertical orientation.

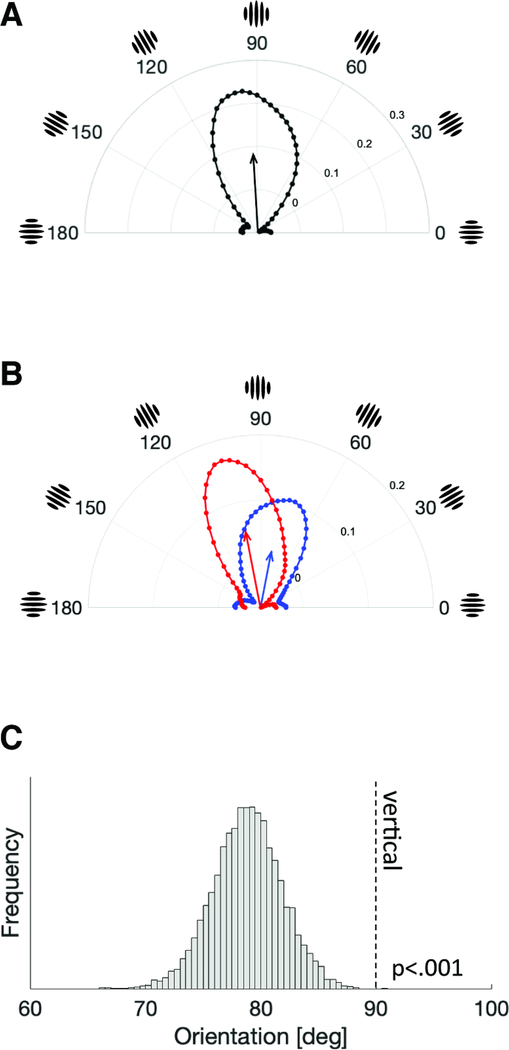
Figure 2. Perceptual template of orientation is biased toward prior orientation.

(A) The group-averaged classification image for all the trials, which is replotted from Figure 1c. The angle represents the orientation, and the radius represents the power of each orientation in the classification image (arbitrary unit). The black arrow indicates the mean vector of the orientation vectors in the classification image (approximately vertical). (B) The classification image for trials following CW (blue) and CCW (red) inducers. The arrows represent the mean vectors for each classification image. In the analysis, the CCW curve was flipped and merged with the CW curve, and the mean vector was calculated for this integrated classification image. (C) The histogram of the bootstrapped mean vector angles for the integrated classification image, indicating that the CI was biased toward previous inducer orientations (p<.001). See also Figure S1.

To quantify any serial dependency—how the inducer orientation impacts the classification image in following trials—we calculated the classification images separately for trials following CW and CCW inducers. As shown in Figure 2B, the classification images were skewed toward inducer orientations, which means that the orientations near the inducer orientation were more readily detected. Because the classification images are based exclusively on pure noise stimuli, with no signal included (see STAR Methods), there is no way for response bias to generate a coherent classification image (see also Discussion section). To increase the signal-to-noise ratio, we flipped the classification image that followed CCW inducers and merged it with the classification image that followed CW inducers. Thus, the integrated classification image can be regarded as the perceptual template of vertical orientation after a CW inducer was observed. The mean vector angle of this integrated classification image was 78.8 deg (95% CI = [72.8 84.8] deg), significantly skewed toward the inducer orientation, compared to either the veridical vertical orientation (90 deg; p < .001) or the mean vector angle of the classification image without the inducer orientation taken into account (92.5 deg; p < .001). To rule out the possibility that the afterimage of the inducer Gabor affected the obtained classification images, we calculated the classification images separately depending on their temporal distance from the inducer. The serial dependence in the classification image was comparable whether it was measured soon after the inducer (78.6 deg; 1–3 trials after the inducer) or was delayed (77.2 deg; 4–7 trials after the inducer), suggesting that the bias in the classification image toward the inducer orientation was not caused by an afterimage of the inducer (Supplementary Figure 1). This means the orientations around the inducer orientation were reported more readily by observers, suggesting that the inducer orientation facilitated nearby orientations in subsequent trials, consistent with the time course of serial dependency.^3,20

The shift in the perceptual template was caused by previous stimuli, but it does not tell us whether the perceptual appearance was altered by the preceding inducer stimuli. To address this, Experiment 2 used an orientation discrimination task where participants judged whether the Gabor was tilted CW or CCW relative to vertical (Figure 3; see STAR Methods). In doing this, we dissociated response repetition effects that are independent from the visual inputs and the perceptual shift. If the participants repeated the same responses irrespective of visual stimuli at some probability, it would affect the guess or lapse rate and the psychometric function should shift vertically; if the perceptual shift occurs, it should appear as a horizontal shift of the psychometric function (Figure 3C). In the group average, we found a moderate vertical shift (p = .044; bootstrap test) and a very strong horizontal shift (p < .001; bootstrap test) in the psychometric functions. The vertical shift revealed a difference of 4.1% in the asymptotes, meaning that the participants tended to repeat the same responses at this rate irrespective of visual stimuli. However, the magnitude of this effect was modest and its statistical significance would not survive a correction for multiple comparisons. A much stronger and more important effect was that the PSE for trials following CW trials was shifted 2.42 degrees compared to the PSE for CCW inducer trials. Thus, the Gabor stimulus appeared to be tilted toward the most recent inducer orientation (Figure 4).

Figure 3. Schematics of the second (discrimination) experiment.

(A) In a trial, the participants judged whether the Gabor was (1) absent, (2) present and tilted CW, or (3) present and tilted CCW. In 44% of the trials, a near-threshold Gabor was embedded in a white noise stimulus. In another 44% of the trials, the white noise was presented on its own, without any Gabor. In the remaining 12% of the trials, a high-contrast Gabor was presented to induce serial dependence. (B) Psychometric functions were estimated separately for trials following CW and CCW inducers. (C) A hypothetical visualization showing how the response bias and perceptual shift could affect psychometric functions differently.

Figure 4. Serial dependence attracts the current perception toward prior inputs.

(Left panel) The psychometric functions of a representative participant for trials following CW (blue) and CCW (red) inducers in the discrimination experiment. (Right panel) Group average of point of subjective equality (PSE) to vertical orientation. The significant difference between the PSEs (p<.001), indicates that prior orientation information attracted the observers’ percepts of what counted as vertical.

Discussion

In the present study, we used a classification image technique to demonstrate that serial dependence alters perceptual templates of orientation. Our results indicate that the serial dependence happens in a simple detection task, and that the perceptual template is altered by attracting the target’s appearance toward previous stimuli. These findings suggest that some of the most basic perceptual representations are serially dependent on previous visual input.

Perceptual templates have been thought to reflect the regions or features that are weighted or filtered by the visual system to perform a given task.¹ The biased perceptual template found in this study suggests that the inducer orientation facilitates nearby orientations in subsequent trials and that these orientations more readily reported. This effective facilitation could involve a change in sensitivity based on prior stimuli²¹ and/or an orientation-dependent modulation of criterion.²⁸ Previous classification image literature has assumed that the internal template is stable over time. As such, classification image experiments typically analyze each trial independently.^{26,27,29–32} In contrast to this assumption, the current finding reveals that perceptual templates can be flexible and contingent on prior information, consistent with serial dependency in perception and decision.^3,16,17,33 Furthermore, the discrimination experiment confirmed that what counts as perceptually vertical is shifted toward the inducer orientation. Although caution should be warranted in estimating vertical and horizontal shifts of psychometric functions separately, because these could be dependent on each other, this result suggests that the shift in the perceptual template may happen by attracting the target’s appearance due to the serial dependence. The classification image technique, in general, only captures a linear approximation of how observers use stimulus information. Further research will be needed regarding whether and how serial dependence alters our perceptual templates in a non-linear manner.

Recent studies have debated which stage or stages in the visual hierarchy are responsible for serial dependence. One of the predominant hypotheses assumes that this attractive sequential effect results from the proactive interference by previously activated information in working memory.^10,34–36 This model assumes that the working memory of the current stimulus is interfered with and biased by memory traces from prior stimuli, while maintaining and recalling the current stimulus information to perform complicated tasks such as reproduction or delayed comparison of orientations.^10,37 However, our results suggest that the serial dependence can occur even in a simple detection task that, unlike previous studies, requires no working memory—no maintenance, rehearsal, or retrieval of a previously seen orientation. Additionally, the particular tilt of the Gabor patch was task-irrelevant in the detection task in Experiment 1. Nevertheless, the perceptual template was distorted by the most recent inducer orientation, suggesting that the serial dependence here does not result from the proactive interference of task-related information in the previous trials.

Another hypothesis assumes that the serial dependence originates from the inertia of perceptual decisions or responses.^16,33,38 However, this cannot account for the classification images found here. First, the distortion in the classification image indicates that the serial dependence is not a mere repetition of the same responses. Even if the same present or absent responses tended to be repeated at any given probability, the orientation power would be cancelled out in the classification image for these repeated response trials because the noise stimuli used in our study were composed of uniform white noise. That is, repeated responses would wipe out any possible classification image. This is consistent with previous studies, which show that perceptual templates revealed by classification images are not affected by response biases.^39–41 Furthermore, the detection task in the first experiment required a present/absent judgement, thus the particular tilt of the Gabor stimulus was essentially irrelevant to the decisions. Nevertheless the perceptual template was altered by previously seen orientations, suggesting that the serial dependence may occur independent of task-related decision inertia.

Our results suggest that serial dependence can impact relatively early stages of sensory processing with a minimum involvement of working memory or perceptual decision-making. Our results are consistent with recent findings that serial dependence is strongest when the previous and current objects are located at the same retinal position⁴² and that the serial dependence occurs at an early-level sensory stage before the sensory information is integrated with spatial context such as perceptual tilt induced by surrounding stimuli.⁴³ Furthermore, an fMRI study showed that the orientation representation in the primary visual cortex is attracted toward previously seen orientations.⁴⁴ Consistent with these studies, the current findings support the view that the attractive sequential effects can emerge as early as sensory or perceptual processing.

It should be noted that the present results do not contradict the possibility of serial dependency in higher cognitive processes including decision and memory.³⁴ Although perceptual templates are usually understood to reveal early visual processes or sensory representations,^45,46 they may still be subject to decision weights.²⁵ Likewise, that serial dependence impacts templates for perceptual detection does not mean it is purely a low-level perceptual effect. On the contrary, it has been shown that serial dependence requires top-down processes, such as conscious awareness of prior stimuli in binocular rivalry,⁴⁷ or attention to previous stimuli.³ Consistent with these studies, our classification images were obtained under conditions that involved attended stimuli. Serial dependence can manifest in various ways including in perception, decision, and memory.³⁴ Furthermore, perceptual decisions can have subsequent effects on appearance.³³ Our task was a simple detection one, however, our results do not adjudicate between the role of decision and attention, or if there is any difference.

Our results reveal a positive serial dependency, but they do not rule out the presence of adaptation or negative aftereffects. Indeed, negative and positive serial effects could compete against each other or exist in parallel^{3,12,33,48,49} and which one appears phenomenologically dominant might depend on the reliability of current and prior information.^10,11,17,21 In general, positive serial dependence happens when prior information is reliable and current sensory evidence is impoverished, and the negative serial effect occurs in the opposite case. In the present study, the high-contrast inducers would be the most reliable source of information that attracts following noisy inputs. Further study will be needed to address how the top-down and bottom-up processes interact with each other to generate the serial dependence of visual perception and decision.

Serial dependency in perception has been observed across a wide range of visual attributes.^{3–5,8–12,16,23,50} From a broader perspective, such hysteretic effects are ubiquitous in higher cognitive processes as well, including attention,⁵¹ working memory,⁵² and decision-making.⁵³ This series of studies suggests that similar computational algorithms are implemented at multiple processing stages. Just as the distribution of orientation information in natural scenes accounts for the variation in orientation sensitivity,⁷ visual features could have unique forms of temporal stability and autocorrelations in the environment, and thus may have different (spatio)temporal operators within which the information is smoothed. These operators, or Continuity Fields as they were coined,³ could be object, feature, modality, or task-specific. Indeed, recent psychophysical studies have proposed that the magnitude of serial dependence for a given visual attribute is associated with the temporal stability of that attribute in the outer world, suggesting the presence of a content-specific process of temporal smoothing, rather than one central generator of serial dependence.^12,54 In line with this research, our results suggest a low-level processing mechanism that promotes perceptual stability of orientation representation over time.

STAR Methods

Resource availability

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Yuki Murai (ymurai@berkeley.edu)

Material Availability

This study did not generate any unique reagents.

Data and Code Availability

For data analysis, we used MATLAB (R2019b) and the Palamedes toolbox.⁵⁵ Experiment data are available at Open Science Framework (OSF) repository: https://osf.io/3df4q/

Experiment Model and Subject Details

We conducted two experiments. In Experiment 1, participants were asked to detect a vertical Gabor embedded in a noisy image. This experiment aimed to quantify the degree to which the perceptual template for a vertically oriented stimulus is biased by previously seen stimuli. In Experiment 2, we measured the illusory tilt of the Gabor induced by previous stimuli using an orientation discrimination task.

Participants

All participants reported to have normal or corrected-to-normal vision. The experiments were carried out in accordance with the recommendations of the institutional review boards of the University of California at Berkeley, with written informed consent obtained from all the participants.

Experiment 1.

Twenty-two healthy volunteers (10 males, 18–26 years old) participated in the experiment.

Experiment 2.

Twenty-two healthy volunteers (6 males, 18–23 years old) participated in the experiment. None of them participated in Experiment 1.

Method Details

Apparatus

The visual stimuli were presented on a CRT monitor (Sony Trinitron Multiscan G520, 1024*768 pixels, 100 Hz refresh rate). Participants were seated 57.3 cm from the monitor in a dark booth with their heads stabilized using a chin rest. The display was gamma-corrected using a luminance meter (Konica Minolta, LS-110).

Stimuli and Procedure

All the stimuli were generated using MATLAB (MathWorks, R2017a) and the Psychophysics Toolbox.^56,57

Experiment 1.

A schematic of the experimental procedure is shown in Figure 1A. In the experiment, a low-contrast near-vertical target Gabor (signal) embedded in static white noise was presented in 44% of the trials. In another 44% of the trials, static white noise was presented on its own (noise only, no signal). In the remaining 12% of the trials, a high-contrast Gabor (40% Michelson contrast) embedded in white noise was presented as an inducer. The inducer Gabor patch was oriented 10 degrees clockwise or counter-clockwise relative to vertical. The number of trials between any two sequential inducer trials was randomized between 4 to 10. The stimulus duration was 500 ms, and the maximum contrast of the white noise was approximately 60%. To reduce any possible luminance aftereffect across trials, the target stimulus was masked by low-pass filtered luminance contrast noise (~100% contrast) for 500 ms, and the Gabor phase was randomized across trials. The size of the visual stimulus was 14×14 degrees visual angle (d.v.a). The Gabor stimuli were confined to a Gaussian contrast envelope with a 3 d.v.a standard deviation. The Gabor patch spatial frequency was 0.5 cpd. The orientation of the low-contrast Gabor stimulus was randomized across trials within ± 3 degrees relative to vertical. Participants were asked to judge whether the near-vertical target Gabor was present or absent in the noisy image. The target contrast was adjusted for each individual participant so that d’ was around 1.5 in a preliminary experiment. Each experimental session consisted of 100 trials, and the inter-trial interval was randomized within 800–1200 ms. The participants completed 15–25 sessions in approximately 2 hours.

Experiment 2.

The stimulus parameters were the same with Experiment 1, with the exception of the Gabor orientation and the experimental task. The participants were asked to judge whether the Gabor was 1) absent or 2) present and tilted clockwise or 3) present and tilted counterclockwise (a simultaneous detection and discrimination task⁵⁸). The target Gabor orientation was randomized within the range of ±10 degrees relative to vertical.

Quantification and Statistical Analysis

Experiment 1: Classification image analysis

Since the Gabor stimulus was near-threshold and barely recognizable, the subjects actually had to make their responses based on the patterns of the noise images. They might answer “present” if a noise stimulus had stronger power in the vertical orientation compared to other orientations; or they might respond “absent” if other orientations had stronger power than vertical.

To estimate the pattern of the noise images when the subjects answered “present” and “absent” respectively, we sorted trials into one of four stimulus-response categories. For example, if the target was absent and the observer reported present, the trial was classified as a false alarm ([FA]; Figure 1B). Each orientation’s power at the Gabor patch’s spatial frequency was calculated for each noise image by fast-Fourier-transform. To focus on the orientation information that was at the spatial location of the Gabor stimulus, we first filtered each noise image by the same Gaussian window that enveloped the Gabor stimulus, and then 2-D Fourier-transformed each image separately. In Hit and Miss trials, when the target Gabor was present, only this noise image was analyzed; the signal (target Gabor) was subtracted from the original image (see Supplemental information). Furthermore, all the inducer trials were excluded from the analysis.

The power distributions of noise images were then averaged for each of four categories (Fig. 1B), and we subtracted the sum of the power distributions for Miss and Correct Rejection trials from the sum of the power distributions for Hit and False Alarm trials. It would be expected that the Hit and False Alarm trials should have stronger vertical power than Miss and Correct Rejection trials. This integrated power distribution (Figure 1C) represents the perceptual template of vertical orientation that the participants utilized to judge whether they perceived vertical orientation in the image. We hereafter refer to this integrated power distribution as the classification image.

To test for serial dependence—any effect of the previous inducers on the subsequent classification images—, this same analysis was conducted separately for trials following clockwise (CW) and counter-clockwise (CCW) inducers (Figure 1C). If the inducers introduce a positive sequential effect on subsequent trials, the classification image would skew toward the inducer orientation; if a negative aftereffect occurs from the inducers, the classification image would be repelled away from the inducer orientation. To increase the signal-to-noise ratio, the classification image for CCW inducer trials was flipped and merged with that for CW inducer trials as if all the inducers had CW orientations.

To rule out the possibility that the afterimage of the inducer Gabor affected the obtained classification images, we calculated the classification images separately for trials soon after the inducer (1–3 trials after the inducer, ~2–5 sec) and later trials (4–7 trials after the inducer, ~7–12 sec). Serial dependence was tested for each trial group using the same analysis: trials following CW and CCW inducers were separately analyzed, and the classification image for trials after CCW inducers was flipped and merged with that for trials after CW inducers (Figure S1). If an afterimage of the inducer Gabor biases classification images in following trials, its effect should be stronger in the earlier trials. In this analysis, we excluded one participant who had no FA trials in the late trial group.

The classification image was first calculated for each individual observer, and then averaged across participants for the group result. To quantify which orientation had relatively stronger power in the classification image, we calculated the mean vector of power distributions, which is identical to the centroid of a polygon composed of the end points of vectors in polar coordinates (Figure 2A).

Experiment 2: Perceptual shift of Gabor orientation

Experiment 2 measured the degree of serial dependence—the equivalent perceptual rotation of the Gabor orientation caused by the inducer trials. To do this, another group of participants performed a simultaneous detection and discrimination task using the same stimuli. In the analysis, the proportion of clockwise responses was plotted as a function of Gabor orientation, separately for trials following CW and CCW inducers. Here we analyzed only Hit trials, in which the participants successfully detected the Gabor stimulus. Then a cumulative normal distribution was fit to each curve. To dissociate the perceptual and decisional serial dependence, we estimated the lower and upper asymptotes in addition to the mean and standard deviation of the psychometric function. If the serial dependence is generated from repetitive responses, irrespective of sensory input, then the guess and lapse rates should be different between trials following CW and CCW inducers. That is, CW responses may be increased after the participants saw a CW inducer, irrespective of target Gabor orientation, and the psychometric function could be shifted upward. We estimated such a vertical shift in the psychometric function from the difference in asymptote values for trials following CW and CCW inducers. The point of subjective equality (PSE) was estimated as the Gabor orientation which gives the mean value of the best-fit cumulative normal distribution, which should be perceptually equivalent to the vertical orientation. Typically, the PSE is defined as the stimulus value which gives 50% response probability. However, since we estimated the vertical and horizontal shifts of psychometric functions separately, both shifts could affect the stimulus value corresponding to 50% response probability. Therefore, the mean value of the best-fit cumulative normal distribution was used as an index of horizontal location of psychometric functions. The perceptual shift was operationally defined as the difference in PSEs for CW and CCW inducer trials. The psychometric functions were fit separately to each participant’s data, and the significance of vertical and horizontal shifts in the group data was evaluated using bootstrap tests.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Open Science Framework	https://osf.io/	SCR_003238
Software and algorithms
MATLAB R2017a, R2019b	The MathWorks	SCR_001622
Psychophysics Toolbox 3	http://psychtoolbox.org/	SCR_002881
Palamedes Toolbox	http://www.palamedestoolbox.org/	SCR_006521

Highlights.

The visual system selectively weighs valued incoming information using “templates”

Perceptual templates are biased toward previously seen, task-irrelevant orientations

Templates incorporate serial dependence to smooth noisy visual input

Basic perceptual representations are serially dependent on previous visual input