Tensile properties of segmented block copolymers with monodisperse hard segments

Abstract

The tensile properties of segmented block copolymers with mono-disperse hard segments were studied with respect to the hard segment content (16–44 wt.%) and the temperature (20–110 °C). The copolymers were comprised of poly(tetramethylene oxide) segments with the molecular weights of 650–2,900 Da and of mono-disperse bisester-tetra-amide segments (T6A6T) based on adipic acid (A), terephthalic acid (T) and hexamethylene diamine (6). An increasing content of T6A6T gave rise to an increased modulus, yield stress and fracture stress. The modulus could be modeled by a composite model. Moreover, a strain-softening was observed well below the yield stress, due to the shearing of the T6A6T crystallites. At strains >200%, a strain-hardening of the PTMO segments took place and this even for PTMO segments that were amorphous in the isotropic state. The strain hardening increased the tensile properties. An increase in temperature had little effect on the modulus of the copolymers, but was found to lower the yield and fracture stresses. At temperatures above the melting temperature of the oriented PTMO, no strain-hardening took place. The yield stress as a function of temperature could be described by the Eyring relationship, but a modulus–yield stress relationship could not be established.

Introduction

Thermoplastic elastomers (TPEs) based on the segmented block copolymers display a two-phase morphology, with a continuous soft phase of low glass transition (T_g) and a phase-separated hard phase with a high transition temperature [1, 2]. The phase-separated hard phase is the physical cross-links of the low T_g soft phase segments and also acts as a filler for the soft phase [1–4]. Segmented block copolymers often have a hard phase consisting of crystallized segments with a high melting temperature. Generally, segmented block copolymers are soft materials with a relatively low yield stress, high fracture strain and high fracture stress. With the increasing temperature, the modulus, yield stress the fracture stress decrease whereas the fracture strain increases, as is usually the case for polymers [1, 5–9]. The tensile and elastic properties of TPEs are sensitive to the type, concentration and morphology of the hard phase [1, 2].

The hard segment (HS) crystallites have a nano-ribbon-like structure with a high aspect ratio [10–14], and these nano-ribbons reinforce the soft phase [3, 4, 15]. Upon stretching of such a copolymer, both the soft and the hard phases are deformed, and for a high enough strain, yielding of the hard phase occurs [13, 16–18]. During this yielding, the crystallites are sheared and their orientation changed (Fig. 1) [4, 13].

Fig. 1.

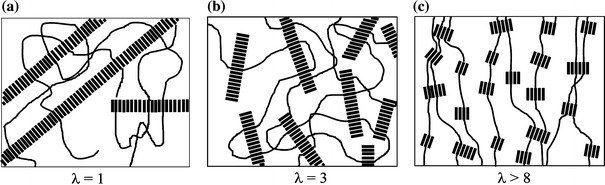
A schematic representation of the change in crystalline morphology of PTMO-TΦT copolymers during straining: (a) long, randomly oriented crystalline ribbons; (b) broken up ribbons oriented in the strain direction; and (c) very small ribbons with an orientation perpendicular to the strain [16]

Upon straining of these materials, a dramatic decrease in the initial E-modulus is observed which is said to be due to a lowering of the aspect ratio of the ribbon-like crystallites (Fig. 1b). At a strain of 200%, the E-modulus can be lowered as much as tenfold and moreover, the ribbons become oriented in the stretching direction. At even higher stains, the ribbons are further broken up into crystallites with small aspect ratios and now also the small ribbons turn perpendicular to the stretching direction (Fig. 1c).

If the HSs are mono-disperse in length the copolymer has a lower soft segment T_g, a sharper HS melting transition [2–4, 13–15, 18–25]. The mono-disperse segments crystallize fast and almost completely, and as a result, the soft phase contains very little dissolved HSs [3, 4, 14, 15, 17, 18]. The mono-disperse HSs have crystallites with nano-ribbon-like structures with high aspect ratios (i.e. 300–1,000) [2–4, 13–15, 18]. When the HSs are truly monodisperse the modulus is from room temperature to near the HS melting temperature, almost independent of temperature [2–4, 12–15, 18–25]. One can question whether this means that also the yield and fracture properties of these materials are also temperature independent.

Segmented copolymers with mono-disperse rigid segments have, at room temperature, a simple two-phase morphology. Interesting is to study the effect of the HS content and the temperature on the tensile properties of such a well-defined system. A PTMO_x-T6A6T system (Fig. 2), with an emphasis on PTMO₂₀₀₀-T6A6T [15], was chosen for this investigation.

Fig. 2.

The polymer structure of PTMO_x-T6A6T

PTMO_x-T6A6T segmented block copolymers have been defined as TPEs consisting of alternating soft (PTMO) and hard segments (T6A6T) [15]. The T6A6T segments have a symmetric structure with tetra-amide groups that can H-bond with both neighboring T6A6T units. The HSs crystallize into nano-ribbons that are dispersed in the continuous low T_g phase. These nano ribbons as observed with AFM have high aspect ratios. The crystallinity of the tetra-amide segment in the copolymers as measured by FT-IR was found to be very high, ~80–90% [15], and the T_m of the T6A6T segments in the copolymers was about 185 °C and slightly dependent on the content of PTMO segments. At room temperature the copolymers were elastic solids with an amorphous PTMO phase. The copolymer displayed, at room temperature, an excellent elastic behavior, which was probably due to the mono-disperse HS and particular at low HS contents. Moreover, the PTMO segments were at room temperature able to strain-crystallize as a result of their enhanced ultimate properties.

However, the tensile properties as a function of temperature of such segmented block copolymers with the well-defined mono-disperse HS have, until now, barely been studied. This paper thus describes the investigation of the tensile properties of PTMO_x-T6A6T polymers (Fig. 2) as a function of the PTMO length in the range of 650–2,900 Da as well as the influence of temperature on PTMO₂₀₀₀-T6A6T.

Experimental section

Materials

The PTMO_x-T6A6T copolymers were synthesized according to the solution/melt polymerization route described in a previous study [15]. Dumbbell-shaped test bars were prepared by injection molding of the copolymers in an Arburg Allrounder 221-55-250 injection molding machine.

Viscometry

The solution viscosities were measured at a concentration of 0.1 g/dL in a mixture of phenol/1,1,2,2-tetrachloroethane (1:1 molar ratio) at 25 °C using a capillary Ubbelohde type 1B. The inherent viscosities could then be calculated from these data. The value of the inherent viscosity was found to approach that of the intrinsic viscosity [26].

Dynamic mechanical thermal analyses

Samples (70  ×  9  ×  2 mm) for the dynamic mechanical thermal analyses (DMTA) measurements were prepared on an Arburg H manual injection molding machine, with a barrel temperature set  20°C higher than the melting temperature. The test samples were dried in vacuum at 50 °C for 24 h prior to analysis. DMTA thermograms were recorded with a Myrenne ATM3 torsion pendulum at a frequency of 1 Hz and 0.1% strain. The storage (G′) and loss (G′′) moduli were measured as functions of temperature. The samples were cooled to −100 °C and subsequently heated at a rate of 1 °C/min. The temperature at the maximum of the loss modulus peak was taken as the glass transition temperature (T_g). The flow temperature (T_flow) was defined as the temperature where the storage modulus reached 1 MPa. The start of the rubbery plateau, i.e., the intercept of the tangents, was denoted the flex temperature (T_flex).

Tensile tests

Stress–strain curves were obtained on injection molded dumbbells (ISO37 type 2), using a Zwick Z020 universal tensile machine equipped with a 500 N-load cell. The strain was measured with extensometers. The tensile tests were carried out at an initial strain rate of 0.4 s⁻¹ (test speed of 60 mm/min). For test temperatures other than room temperature, a temperature-controlled environment chamber was used. The E-moduli at each temperature were determined in eightfold at a strain of 0.1–0.25%. The standard deviation in the modulus was 5–8%. Also measured were the stress at 10% strain (σ_10%), the yield stress (σ_y), the yield strain (ɛ_y), the fracture stress (σ_b), the fracture strain (ɛ_b), and the true fracture stress (σ_true). The true fracture stress was obtained by multiplying σ_b by the straining factor (= 1 + (ɛ_b/100)).

Results and discussion

PTMO_x-T6A6T copolymers are transparent TPE materials with a well-defined morphology [15]. The PTMO_x length was varied from 650 to 2900 Da, and the mono-disperse bisester tetra-amide segment T6A6T readily crystallized into nano-ribbons with high aspect ratios [15]. The T6A6T crystallinity was found to be high and, as a result, only little of the HS was dissolved in the PTMO phase. At room temperature, the copolymers had a two-phase structure; a rather pure PTMO phase with nano-crystallites from mono-disperse T6A6T segments dispersed within it. However, if the PTMO was to undergo a strain-induced crystallization, the structure would become more complex. The copolymers all had high molecular weights and were processed by injection molding.

DMTA

The thermo-mechanical properties of the PTMO_x-T6A6T polymers were studied by DMTA. The storage and loss moduli were determined as functions of temperature (Fig. 3).

Fig. 3.

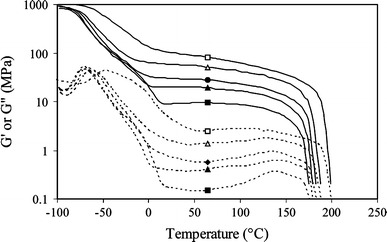
Storage and loss modulus curves as functions of temperature for PTMO_x-T6A6T with varying molecular weight of the PTMO segment: □, 650 g mol⁻¹; △, 1,000 g mol⁻¹; ●, 1,400 g mol⁻¹; ▲, 2,000 g mol⁻¹; ■, 2,900 g mol⁻¹

Three transitions were present in the graphs: the glass transition of the PTMO phase, the melting transition of the PTMO, and the melting transition of the T6A6T. A glass transition of the amorphous T6A6T phase, expected at a temperature of 125 °C, was not observed. The PTMO was found to be partly crystallized for PTMO lengths above 1,000 Da. The T_g of the soft phase of PTMO_x-T6A6T increased from −70 °C for PTMO₂₉₀₀ and PTMO₂₀₀₀ to −45 °C for PTMO₆₅₀ (Table 3). This increase in T_g was due to an increased density of physical cross-links [3]. The crystalline PTMO phase of the longer PTMO segments was expected to also contribute to the cross-link density. The low T_g values for the PTMO₂₉₀₀- and PTMO₂₀₀₀-based polymers indicated that the concentration of T6A6T segments in the polyether phase must be very low.

The melting temperature of the PTMO phase was identified as a shoulder on the G′ and G′′ curves in the DTMA graph (Fig. 3). A PTMO melting temperature was clearly present for samples with PTMO lengths of at least 1,400 Da and ranged between 5 and 10 °C. The flex temperature (T_flex), defined as the start of the rubber plateau, increased as a result of the crystalline PTMO phase melting temperature. The T_flex was influenced by the T_g and the T_m of the PTMO; the higher T_flex (0 °C) of PTMO₆₅₀-T6T6T was due to the relatively high T_g (−45 °C). Nevertheless, all the copolymers displayed T_flex values below room temperature. Thus in the isotropic state at room temperature the copolymer had a two phase structure.

The copolymers had above room temperature rubber moduli that were almost temperature-independent (about 0.4% change per degree C). This is typical for copolymers with crystallizable segments of mono-disperse length [2–4, 13–15, 18–25] The flow temperatures decreased with increasing PTMO length and corresponded well with the melting temperatures recorded with DSC [15]. The decrease in melting temperature (T_flow) of T6A6T with PTMO content has been explained as a result of the solvent effect of the PTMO on the HS crystals [3, 4, 13–15, 18].

The storage modulus at room temperature 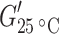for the copolymers decreased drastically with increasing length of the flexible segment and thus with decreasing amide content (Figs. 3 and 5). This significant change in modulus was partly due to the changing crosslink density but mainly a result of the decreasing HS content, which gave rise to a decrease in the reinforcing effect of the HS crystallites [3, 15]. The reinforcing effect of the crystallites was a function of the crystalline content as well as of the aspect ratio of these crystallites. The aspect ratio of the T6A6T crystallites in the copolymers was high [15].

Fig. 5.

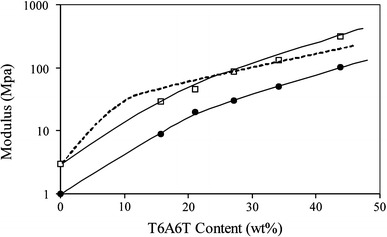
G′ and E moduli as functions of the T6A6T content: □, E-modulus; ●, G′-modulus. The Halpin–Tsai relationship for the E-modulus (dashed line) is also presented

Tensile properties at room temperature

Tensile properties of the segmented block copolymers were studied on injection molded dumbbell samples (ISO37 s2). The stress–strain curves were typical of thermoplastic elastomeric materials with crystalline HS which deform on yielding (Fig. 4, Table 1).

Fig. 4.

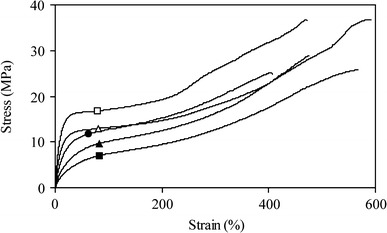
Stress–strain curves for PTMO_x-T6A6T at room temperature with varying molecular weight of the PTMO segment: □, 650 g mol⁻¹; △, 1,000 g mol⁻¹; ●, 1,400 g mol⁻¹; ▲, 2,000 g mol⁻¹; ■, 2,900 g mol⁻¹

Table 1.

Tensile properties of the PTMO_x-T6A6T copolymers

	T6A6T (wt.%)	ηinh (dL/g)	G′-modulus (MPa)	E-modulus (MPa)	E/G′ (−)	σ10% (MPa)	ɛy (%)	σy (MPa)	ɛb (%)	σb (MPa)
PTMO650	43.8	1.8	102	311	3.0	11.3	25	16	471	37
PTMO1,000	34.2	2.5	51	133	2.6	7.95	29	12	593	37
PTMO1,400	27.1	1.5	30	87	2.9	5.62	42	11	407	25
PTMO2,000	21.1	2.9	20	46	2.3	3.40	49	9	476	29
PTMO2,900	15.7	3.5	9	29	3.2	2.28	66	6	568	26

At small deformations, the stress increased fairly linearly with the strain (Hooke’s law) [5–9]. Above the yield strain, the stress gradually increased, and at strains higher than 200% strain-hardening took place.

The E-modulus increased strongly with the concentration of tetra-amide segment as was also the case for the storage G′-modulus (Fig. 5). The underlying explanation for this effect on the E-modulus was thus the same as that for the G′ modulus. For the PTMO copolymers with zero HS concentration the G′ and E moduli were approximately 1 and 3 MPa, respectively.

The Young (E) and storage (G′) moduli are related according to [5–9, 26]:

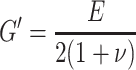1

where ν is the Poison ratio.

For an ideal elastomer the Poison constant has a value of 0.5 and corresponding E/G′ ratio is 3. An E/G′ ratio of 3 was obtained for the studied copolymers.

The reinforcing effect of the ribbon-like crystallites can be modeled. There are several mechanical models that describe the modulus of a composite as a function of filler content [27, 28]. The Halpin–Tsai model calculates the elastic modulus of a fiber composite with randomly oriented fibers as a function of fiber content and aspect ratio [27–30]. The Halpin–Tsai model has been applied to semi-crystalline polymers [31] as well as to segmented block copolymers [3, 15], and was chosen for modeling the modulus in the present study. In this calculation, it was assumed that the crystallinity of the amide segments was 88%. The following parameters were used for calculating the E-modulus according to the Halpin–Tsai relationship: the E-modulus of the matrix polymer (PTMO) was 3 MPa; the E-modulus of the reinforcing phase (crystalline amide) was 5,000 MPa; the aspect ratio of the crystallites was 1,000. A detailed description of the calculations can be found elsewhere [32].

The increase in E-modulus as described by the Halpin–Tsai model (dashed line) displayed a reasonable fit with the experimental results of the E-modulus (Fig. 5). Thus, the strong increase in modulus with amide content of the segmented block copolymers could be explained by the high amide crystallinity and the high aspect ratio of the crystallites.

As with very soft materials, the initial modulus is not always easy to measure accurately. Therefore, a stress at 10% strain is sometimes given. For a Hookean material, the initial modulus and the stress at 10% strain, a strain below the yield strain, should give similar values. The tensile tests for the PTMO copolymers with mono-disperse HS showed that the stresses at 10% strain were lower than expected from the initial modulus values (Table 1). This implies that plastic deformation had taken place well before the yield strain (at 25–66% strain). Segmented block copolymers often display significant strain-softening believed to be due to the break-up of the long crystalline ribbons [4, 10–13].

The yield strain increased with increasing PTMO length and thus also with decreasing T6A6T content (Table 1 and Fig. 6). A higher strain was therefore needed with decreasing T6A6T content before the crystals were sufficiently stressed to yield. The yield stress increased linearly with the T6A6T content (Fig. 6). As both the (log) modulus and the yield stress were directly related to the crystallinity, the yield stress–(log) modulus relationship should be simple [6, 18, 33–36]. The yield stress–(log) modulus relationship is often studied on polyethylene [33–35], however in these studies the PE crystallite thickness is frequently changed at the same time as the PE crystallinity and probably also the aspect ratio of the crystallites. Since the T6A6T segments of the studied segmented block copolymers were mono-disperse in length, the crystallite thickness in these copolymers was expected to be constant and also the crystallinity of the T6A6T segments was constant. The yield stress was found to increase linearly with the log modulus (Table 1). However, since the crystalline ribbons were broken up far before the yield stress was attained, the structure at the initial modulus differed from that at the yield point strain, and therefore a physical meaning for a yield stress–(log) modulus relationship for these materials was not present.

Fig. 6.

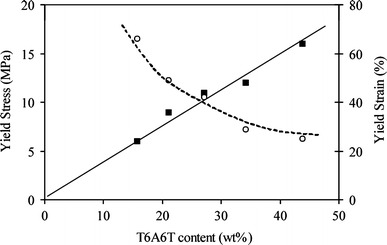
The yield stress, ■, and yield strain; ◯, as functions of the T6A6T content

At higher strains, there was an upsweep in the stress–strain curve due to strain-hardening. This effect was strong for all the studied segmented copolymers at room temperature, even those with lower PTMO_x length. The strain-hardening could result from strain crystallization of either the PTMO or the T6A6T segment, but seeing as the T6A6T segments were already highly crystalline, the strain-hardening was thought to be mainly caused by the PTMO segments. It was surprising to see that even copolymers with PTMO₆₅₀ and PTMO₁₀₀₀ that were amorphous in the unoriented state had a strong strain-hardening effect. Upon straining of the polymer, PTMO chains became aligned and were able to crystallize with a higher melting temperature (43 °C) than the unoriented PTMO (0 °C) [37].

The fracture strains and fracture stresses were found to be high. Spun fibers of similar segmented copolymers with smooth surfaces could easily reach strains at break of over 1,000% [36–38]. This is higher than the natural draw ratio of coiled chains (600–700%) [5–9].

Influence of temperature on tensile behavior

In general, the temperature has a strong effect on the tensile properties of multiphase segmented block copolymers. At sub-zero temperatures (below T_flex), the materials lose their typical elastomeric character. Above the T_flex, on the other hand, the stress levels in the tensile curve decrease with increasing temperature.

The tensile properties of PTMO₂₀₀₀-T6A6T as functions of temperature were studied in the temperature range 20–110 °C (Fig. 7 and Table 2). This temperature range was above the T_flex and well below the HS melting temperature of the copolymer (183 °C).

Fig. 7.

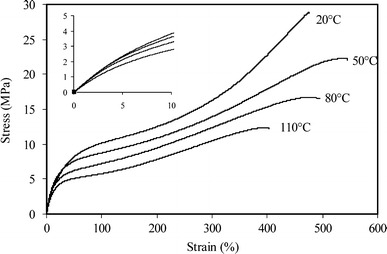
Stress–strain curves for PTMO₂₀₀₀-T6A6T at various temperatures

Table 2.

Tensile results for PTMO₂₀₀₀-T6A6T at various temperatures, η_inh = 2.2 dL/g

Temperature	G′ (MPa)	E-Modulus (MPa)	E/G′ (−)	σ10% (MPa)	σy (MPa)	ɛy (%)	σb (MPa)	ɛb (%)	σ atrue (MPa)
20 °C	20	53	2.7	4.5	8.7	49	29	480	165
50 °C	20	59	3.0	3.8	7.2	42	22	550	143
80 °C	18	56	3.1	3.4	5.8	37	17	490	98
110 °C	16	53	3.3	2.9	4.7	33	12	400	61

^a σ_true was obtained by multiplying σ_break with the straining factor (=1 +  (ɛ_break/100))

The initial E-modulus was found to be unchanged with increasing temperature, however, the stress at 10%, the yield stress, the yield strain and the fracture strain all decreased with increasing temperature. A clear strain-hardening effect was only observed at room temperature. Increasing the temperature the yield stress was found to decrease. Also the fracture strain did not increase and possibly even decreased.

E-modulus

The Young modulus (E) remained fairly constant with increasing temperature as did the shear storage modulus (G′). This is typical for segmented block copolymers with rigid segments of mono-disperse length [2–4, 13–15, 18–24]. The temperature-independency of the E- and G-modulus indicates that the HS crystallinity and the aspect ratio of the crystallites did not change upon heating. This is thought to be due to the fact that the mono-disperse segments crystallized over their full length. A fringed layer on the crystallites, which melts at lower temperatures, was not present. The crystallites melted over a narrow temperature range and not over a broad range. The ratio of E/G′ for these copolymers was ~3 and did not change with temperature (Table 2).

Stress at 10% strain

The stress at 10% strain decreased by 36% when the temperature was increased from 20 to 110 °C, while, the E-modulus remained unchanged (Table 2). The stress at 10% strain on other TPEs decreased even stronger [39]. Already at 10% strain a strain softening was taking place and with increasing temperature, a more significant strain-softening seemed to take place. This means that at higher temperature the crystallites deformed more easily.

Yield behavior

The yield point is generally seen as a point of onset for a substantial plastic deformation [5–9]. For many applications, a deformation beyond the yield point would be undesirable. For semi-crystalline polymers the yield stress decreases more or less linearly with temperature (Table 2 and Fig. 8). This again suggested a strain-softening, due to the break-up of the crystalline ribbons, which increased with temperature. The crystalline ribbons deformed at higher temperatures at lower stresses. The yield strain also deceased with temperature and this is unusual. The lowing of the yield strain with increasing temperature suggests that at higher temperatures the HS crystallites are more easily deformed.

Fig. 8.

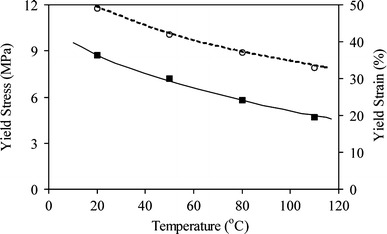
The tensile properties of PTMO₂₀₀₀-T6A6T as functions of temperature. ■, yield stress; ◯, yield strain

The yield stress as a function of strain rate and temperature can be described by the Eyring relationship [5, 6, 8]. For the studied copolymers with a constant modulus, this relationship describes the strain-softening behavior of the crystallites.

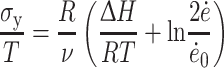2

Here, σ_y is the yield stress, ν the activation volume, ΔH the activation enthalpy, R the gas constant, T the temperature, 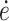the strain rate, and 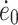is a constant. A linear relationship is obtained if σ_y/T is plotted as a function of the reciprocal temperature (σ_y/T vs. 1/T). Linearity is to be expected when one unique flow mechanism controls the yield stress. An Eyring plot was made for PTMO₂₀₀₀-T6A6T (σ_y/T vs. 1/T) and a linear relationship was obtained (Fig. 9). This indicates that the yield behavior can be described by this relationship.

Fig. 9.

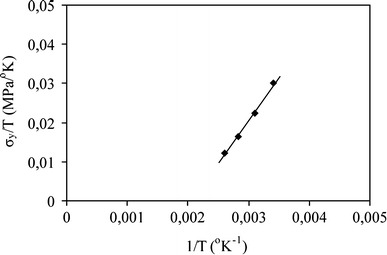
An Eyring plot σ_y/T vs 1/T for PTMO₂₀₀₀-T6A6T at 20, 50, 80, and 110 °C

After the yield point

At strains higher than the yield strain the engineering stresses increased steadily. Moreover, necking was absent during the tensile measurement indicating that no localization of stress took place. At room temperature and >200% strain, a significant strain-hardening effect was observed. This was believed to be the result of a strain-induced crystallization of the PTMO₂₀₀₀ segments [4]. The PTMO₂₀₀₀ segments at room temperature in the unoriented state are amorphous; however, on orientation the melting temperature of PTMO₂₀₀₀ increased to 43 °C and strain-induced crystallization can take place [37]. The fact that the strain crystallization of PTMO₂₀₀₀ at higher temperatures (> 50 °C) did not take place was probably due to the test temperature being higher than the melting temperature of the strained crystallized PTMO segments (43 °C).

Fracture behavior

The fracture properties are very sensitive to the molecular weight and strain-hardening of a copolymer. Normally, the fracture stress decreases with increasing temperature whereas the fracture strain increases [5–9, 25]. Moreover, the fracture stress is often less dependent on temperature than the yield stress. At room temperature the fracture stress was high (Fig. 7) as a result of the strain-induced crystallization of the PTMO segments. With increasing temperature to 110 °C, a decrease in both the stress and the strain at break was observed. A single parameter for the fracture stress and the fracture strain is the true fracture stress, and also this parameter displayed a strong decrease with temperature (Table 2). Strain hardening stabilizes the deformation and the absence of strain hardening at higher temperatures lowered both the fracture strain and the fractures stress.

Conclusions

The tensile properties of segmented copolymers comprised of PTMO flexible segments and mono-disperse segments were studied. The PTMO length was varied from 650 to 2,900 Da and the test temperature from 20 to 110 °C. The mono-disperse T6A6T segments had a very high crystallinity and the crystallites displayed a nano-ribbon structure with very high aspect ratios. Both the storage (G′) modulus and the Young modulus increased strongly with T6A6T content, and this significant increase in modulus could be modeled by a fiber composite model. Parameters in this modulus increase are the crystalline content and aspect ratio of the crystallites. The modulus also barely changed with temperature, suggesting that the properties of the polyether matrix, the properties of the T6A6T crystallite, the T6A6T crystallinity as well as the crystallite aspect ratio remained unchanged. The stress values at 10% strain, i.e., well below the yield strain, were lower than for a material with a Hookean behavior. This suggests that a certain amount of strain-softening took place at 10% strain, and this strain-softening we think was due a lowering of the aspect ratio of the crystallites (Fig. 1).

With increasing mono-disperse HS, the yield stress increased linearly whereas the yield strain displayed a linear decrease. The change in yield stress as a function of temperature could be modeled by the Eyring model. As at room temperature both the (log) modulus and the yield stress were linearly related to the T6A6T content (T6A6T crystallinity), it was deemed of interest to study the modulus-yield stress relationship. However, strain-softening already occurred prior to the yield point and the structure of the crystallites at the yield point must have been different from that at the point where the modulus was determined. Also the yield stress decreased with temperature while the modulus hardly changed. Thus it is not sensible to study a yield stress–(log) modulus relationship, a direct comparison was not meaningful.

At room temperature and strains >200% a strain-hardening was seen, and this even for PTMO₆₅₀ and PTMO₁₀₀₀ that were amorphous in the isotropic state. This strain-hardening effect for the copolymers was strong and was believed to be due to the PTMO segments and not T6A6T. This was confirmed by the result that the strain-hardening was absent when the temperature was increased above the melting temperature of the oriented PTMO.