Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2021 Jul 16;6(29):19233–19237. doi: 10.1021/acsomega.1c02684

Symmetry–Binding Correlations of Crown Ether Complexes with Li+ and Na+

Yaffa Shalit 1, Inbal Tuvi-Arad 1,*
PMCID: PMC8320112  PMID: 34337261

Abstract

graphic file with name ao1c02684_0007.jpg

The gas-phase structure of 18-crown-6 in the presence of Li+ and Na+ cations is highly flexible and generally distorted. Using density functional theory calculations, natural bond orbital analysis, and symmetry measures, we reveal the driving forces behind the structural and energy trends of 18-crown-6 and its phenyl substituents. We show that the structural deviation from C3-symmetry increases with the non-bonded interactions between the occupied spx orbitals of the crowns’ oxygen atoms and the unoccupied 2s orbital of the cation. These orbital interactions are strongly correlated with the overall host–guest interaction energy. Our approach highlights the role of non-bonded interactions and paves the way for deeper understanding of structure–reactivity relations of flexible host–guest systems.

Introduction

Host–guest supramolecular chemistry is a fast-growing field of modern chemistry, with many applications in catalysis, ion transport and separation, drug delivery, non-linear optics, and so on.1−3 Numerous experimental and theoretical studies show that the shape, symmetry, and flexibility of the hosts’ molecules serve as key factors in their function and their ability to capture different ions and neutral molecules within their cavities. One of the earliest and most important classes of hosts is crown ethers.4 Their ability to bind metal cations and small neutral molecules makes them useful for medical applications, chiral recognition, extracting hazardous materials, and more.1,5−9 Specific symmetric conformers of 18-crown-6 (18C6) with alkali cations were reported as belonging to specific point groups (e.g., Ci, C2, D2, C3v, and D3d).10−14 In the presence of Li+ and Na+, the host is highly folded.10,14,15 Several researchers suggested that non-bonded interactions are the stabilizing factors of alkali cations in crown ethers,16,17 but their effect was not quantified. Both experimental and theoretical studies stress the importance of crown ethers’ flexibility in forming stable complexes.10,15,18,19 This flexibility, along with the low barrier for transformation between conformers, poses a significant challenge to the theoretical description of the conformational manifold of these complexes. While many studies were performed in the presence of a solvent, it is interesting to note the structural similarity found by Choi et al.,15 between the gas-phase lowest-energy conformers of dibenzo-18C6 in the presence of alkali cations and their related structure in aqueous solution. In particular, they showed that the average distances of Li+ and Na+ to the oxygen atoms of dibenzo-18C6 are nearly the same in both phases and claimed that the folded structure of the crown hinders the interaction with the solvent molecules.

In this study, we hypothesize that when a flexible host binds a non-flexible guest, its symmetry is quantitatively influenced by the level of interaction with the guest. Particularly, for 18C6 and its phenyl derivatives, we theorize that the folding increases the direct effect of the cation on the host’s symmetry and focus on quantifying this effect for the gas-phase complexes of crown ethers with Li+ and Na+. Our perspective is statistical and is based on density functional theory calculations of conformational ensembles of 18C6 and its phenyl substituents in the gas phase. The natural bond orbital (NBO) methodology20 was used to uncover the driving forces that determine the binding of Li+ and Na+ cations, and the continuous symmetry measure (CSM)21,22 was used as a global structural descriptor. A total of 10 systems described in Figure 1 were studied. These are 18C6 (I), benzo-18C6 (II), ortho-dibenzo-18C6 (III), meta-dibenzo-18C6 (IV), and para-dibenzo-18C6 (V) with the alkali cations Li+ and Na+. Similar sets of conformers without guest cations were included for comparison.

Figure 1.

Figure 1

Open in a new tab

Studied 18C6 molecules. M+ = Li+ and Na+.

Results and Discussion

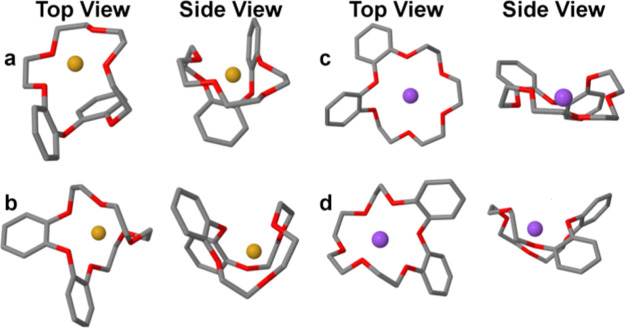
Figure 2a,b presents two conformers of III with Li+ that serve as examples of the general phenomenon. Our data set includes 42 conformers of III with Li+, separated from each other by an electronic energy gap of 0.2 kcal/mol on average. Among these, conformer a has the weakest interaction energy, Eint, of −113.70 kcal/mol, and conformer b has the strongest Eint (−123.32 kcal/mol). Eint measures the effect of separating the ion from the host–guest complex without altering the host’s geometry. Due to the low transformation barriers between conformers, Eint is a reasonable approximation to the overall binding energy of each conformer.

Figure 2.

Figure 2

Open in a new tab

Selected conformers of III in the gas phase with Li+ (left) and Na+ (right). Conformers a and c have the weakest Eint. Conformers b and d have the strongest Eint. Li+ and Na+ cations are marked in gold and purple, respectively.

As is evident from Figure 2, the crown cavities of conformers a and b are highly twisted, and the Li+ cations reside inside them but not exactly in the center, in accordance with earlier studies.10,18 The level of distortion of the crown can be quantified with S(C3)—the CSM with respect to the C3 point group, which is the highest-order rotational symmetry possible for an unsubstituted 18C6. Apparently, conformer b is much more distorted (S(C3) = 21.87) than conformer a (S(C3) = 14.31), but both have a CSM value which is far from zero. Figure 2c,d presents two conformers with the strongest and weakest Eint of III with Na+ in our data set (c: Eint = −93.69 kcal/mol, S(C3) = 3.45; d: Eint = −97.82 kcal/mol, S(C3) = 9.79). With both cations, the distortion increases as the binding becomes stronger.

In order to gain deeper understanding of the meaning of these CSM values, we display in Figure 3 a box and whisker plot of the deviation from C3 symmetry for our full set of conformers divided according to the type of the guest. Results for conformers optimized without any cation are shown for comparison. Unifying the data of different hosts with respect to the CSM is justified based on one-way ANOVA tests that showed that the statistical differences between the average CSM for the subsets of conformers of different hosts and the same guest are generally insignificant at the 0.05 level of confidence. We note that different hosts do show significant differences when it comes to energy, as will be discussed below. The conformers in each subset are not related to those in the other subsets since they were optimized through separate processes described in the Computational Methods section, which led to a slightly different number of conformers and energy ranges for each subset [see Table S1 of the Supporting Information (SI)]. Nevertheless, they can provide a general picture of the flexibility and distortion of these systems.

Figure 3.

Figure 3

Open in a new tab

Box and whisker plot of the deviation from C3 symmetry for all conformers, unified by the identity of the cation. The red line connects the median values.

Several interesting findings can be deduced from Figure 3. First, let us look at the leftmost box. While one conformer has a perfect C3 symmetry (the minimum-energy conformer of the unsubstituted crown), the rest of the conformers are distorted, and this distortion can be quite significant. No correlation was found between this distortion and the electronic energy of the molecules. Such a distortion range expresses the natural flexibility of the hosts and the interplay between energy and entropy. Comparing to the middle box in Figure 3, Li+ cations cause substantial distortion to the crowns’ skeleton, and the difference between the average distortions of the two groups of conformers is statistically significant. The rightmost box, of crown ethers with Na+ cations, displays distortion levels which are similar to those of the uncomplexed conformers. As is evident, Na+ also leads to a single perfectly symmetric conformer of host I with zero CSM. This conformer is not the minimum-energy conformer for the data set of I with Na+, and statistically, it is an outlier in Figure 3. Being larger than Li+, Na+ reduces the ability of the crown to fold and thus decreases the distortion levels back to the range found without a guest cation. However, as opposed to the uncomplexed conformers, the distortion in the presence of either of these cations is related to the binding processes, as will be demonstrated below.

In order to explore the sources of distortion and the binding trends, we applied the method of NBO analysis20 to our set of conformers. Several donor–acceptor non-bonded interactions exist between the crown and the cation. However, the strongest ones (by a factor of at least three from any other significant interactions) are orbital interactions (OI) between the occupied spx orbitals of the crown’s oxygen atoms (with x varying between 1.15 and 2.62) and the unoccupied 2s orbital of the cation. For each conformer, six such interactions exist, and they are naturally larger for the oxygen atoms, which are closer to the cation. We used their median value in each conformer as a representative descriptor (which generally also correlates with the sum of these interactions per conformer). The median OI of this type per conformer correlates with both the level of distortion of the crown and the overall Eint (Table 1). As the OI gets stronger, the crown cavity becomes less C3 symmetric, with a positive correlation between the two parameters. In addition, Eint becomes stronger (i.e., larger absolute value), demonstrating a negative correlation with the OI. We note that the conformer with the strongest Eint is not the conformer with the minimum electronic energy. Similarly, the conformer with the weakest Eint is not necessarily the one with the maximum electronic energy in our data set. Moreover, no correlation was found between the overall electronic energy and either Eint, OI, or S(C3), supporting the conclusion that the ability to create strong non-bonded interactions between the host and the guest ion is the driving force behind the reactivity and structure of these hosts.

Table 1. Pearson Correlation Coefficients between OIs, Distortion Levels, and the Eint for Hosts I–V with Li+ and Na+ (p < 0.005).

    host
guest parameter I II III IV V
Li+ number of Conformers 35 43 42 36 27
  OI–S(C3) correlation coefficient 0.80 0.81 0.64 0.74 0.62
  OI–Eint correlation coefficient –0.78 –0.70 –0.76 –0.88 –0.88
Na+ number of conformers 28 39 30 35 31
  OI–S(C3) correlation coefficient 0.81 0.79 0.76 0.63 0.51
  OI–Eint correlation coefficient –0.92 –0.91 –0.85 –0.87 –0.78
Open in a new tab

The correlations are plotted in Figure 4 for Li+ and in Figure S1 of the Supporting Information file for Na+. Results for dibenzo-18C6 were unified in these plots since ANOVA test showed that at the 0.001 level, there is no significant difference between the conformer sets with respect to the average Eint, S(C3), or the OI. Figure 4 shows that the Eint becomes weaker when phenyl groups are added (similarly for Na+, Figure S1). Furthermore, compared to Na+, the Eints of Li+ are stronger by 20–25 kcal/mol, and the distortion with respect to C3 is higher—ranging between 6 and 22 for Li+ and 0 and 15 for Na+. These trends are related to the size of the cations and their distance from the center of the crown. In the presence of Li+, the distortion of the crown is higher in order to support stronger binding through interactions with multiple oxygen atoms. The substituents on the other hand create a steric hindrance that limits the ability of the cation to reach the center of the crown and thus weaken the Eint. A box and whisker plot of the distance of Li+ from the center of the crown presented in Figure 5 (Figure S2 of the Supporting Information for Na+) shows that the last effect is maximized for III due to the proximity of the phenyl rings to each other. For IV and V, the steric effect on the distance is comparable to that of II. Finally, we note that out of 347 conformers with either Li+ or Na+ in our data set, perfect C3 symmetry was obtained only once for one conformer of I with Na+. As mentioned above, this is not the minimum-energy conformer. In fact, except for its symmetry, this conformer is intermediary in all other aspects: its electronic energy is higher by 3.6 kcal/mol relative to the most stable conformer and lower by 0.9 kcal/mol from the least-stable conformer in this data set. Its Eint value is −101.3 kcal/mol, which is 0.7 kcal/mol above the average Eint for this data set (see Figure S1d). These results indicate that while symmetry is not a driving force in the binding process, the deviation from C3 symmetry carries insightful information about the host–guest interaction energy.

Figure 4.

Figure 4

Open in a new tab

Overall interaction energy, median OI, and distortion trends of Li+ conformers. (a–c) Eint as a function of the OI for 18C6, B18C6, and DB18C6, respectively. (d–f) OI as a function of the deviation from C3 symmetry for 18C6, B18C6, and DB18C6, respectively. Correlation coefficients are presented in Table 1.

Figure 5.

Figure 5

Open in a new tab

Box and whisker plots of the distance of Li+ from the center of the crown for hosts I–V. The red line connects median values.

Conclusions

In this study, we showed that conformers of 18C6 and its phenyl substituents are generally distorted and lack the C3 symmetry, which is expected from perfectly symmetric crowns. In the presence of Li+ or Na+, this distortion is related to the strength of non-bonded interactions between the host and the guest, which in turn teaches us about the overall host–guest interaction energy. The theoretical challenge in describing such flexible systems stems from the wealth of parameters required to describe their energetic, geometric, and chemical characteristics and the ease by which these parameters change. Our approach reduces this number to only a few global descriptors that effectively explore structural and binding trends that were overlooked before. Such an approach contributes to deeper understanding of the reactivity of the studied systems and has the potential to shed light on the properties and design of other host–guest systems.

Computational Methods

Conformational analyses of hosts I–V (Figure 1) with and without the presence of Li+ and Na+ cations were performed in the gas phase using the LowModeMD23 algorithm in MOE24 with an energy window of 25 kcal/mol and the MMFF94X force field. Up to 100 conformers from each system were further optimized with Gaussian 1625 at the B3LYP26−28 level with the def2TZVP29 basis set and D3-dispersion corrections.30 For the conformers with cations, we calculated the distance of the cation from the center of mass of the host (excluding the hydrogen atoms) and the CSM (see below) with respect to the C3 point group based on the crown skeleton excluding the hydrogen atoms, the phenyl substituents, and the cations. Using the combined thresholds of 1 × 10–6 Hartree for the electronic energy and 5% difference for S(C3), conformers with similar energy and symmetry were excluded in order to prevent statistical bias. The process resulted with 27–66 unique conformers for each set within an energy range of 4–9.8 kcal/mol. Details are provided in Table S1 of the Supporting Information. For the conformers with cations, Eints were calculated as the difference between the complex electronic energy and the electronic energies of the isolated cation and the separated host (without reoptimization of its coordinates). In addition, natural bond orbital (NBO) analysis was performed as implemented in Gaussian 16, from which several OI parameters were extracted.

The CSM, S(G), represents the minimal distance of a molecular structure with N atoms from a structure with the same set of atoms and bonds that belongs to the point group G, according to eq 1

graphic file with name ao1c02684_m001.jpg 1

where {Qk} and {Pk} are the sets of coordinates of the atoms of the original and symmetric structures, respectively. The denominator is a normalization factor, and Q0 is the center of mass. The CSM scale is continuous between 0, which represents perfect symmetry, and 100, obtained when the nearest symmetric structure collapses to the center of mass. Our recently developed algorithm was used for these calculations.22

Acknowledgments

This study is supported by the Open University of Israel’s Research Fund, grants 504941 and 102128. A free online CSM calculator is available at http://csm.ouproj.org.il.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c02684.

  • Link to a repository with Cartesian coordinates and electronic energies for all conformers of the host–guest complexes in this study and additional tables and figures (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao1c02684_si_001.pdf (679.8KB, pdf)

References

  1. Gokel G. W.; Leevy W. M.; Weber M. E. Crown Ethers: Sensors for Ions and Molecular Scaffolds for Materials and Biological Models. Chem. Rev. 2004, 104, 2723–2750. 10.1021/cr020080k. [DOI] [PubMed] [Google Scholar]
  2. Ogoshi T.; Yamagishi T.-A.; Nakamoto Y. Pillar-Shaped Macrocyclic Hosts Pillar[n]Arenes: New Key Players for Supramolecular Chemistry. Chem. Rev. 2016, 116, 7937–8002. 10.1021/acs.chemrev.5b00765. [DOI] [PubMed] [Google Scholar]
  3. Liu Z.; Nalluri S. K. M.; Stoddart J. F. Surveying Macrocyclic Chemistry: From Flexible Crown Ethers to Rigid Cyclophanes. Chem. Soc. Rev. 2017, 46, 2459–2478. 10.1039/c7cs00185a. [DOI] [PubMed] [Google Scholar]
  4. Pedersen C. J. Cyclic Polyethers and Their Complexes with Metal Salts. J. Am. Chem. Soc. 1967, 89, 7017–7036. 10.1021/ja01002a035. [DOI] [Google Scholar]
  5. Avilés-Moreno J. R.; Quesada-Moreno M. M.; López-González J. J.; Martínez-Haya B. Chiral Recognition of Amino Acid Enantiomers by a Crown Ether: Chiroptical IR-VCD Response and Computational Study. J. Phys. Chem. B 2013, 117, 9362–9370. 10.1021/jp405027s. [DOI] [PubMed] [Google Scholar]
  6. Chehardoli G.; Bahmani A. The Role of Crown Ethers in Drug Delivery. Supramol. Chem. 2019, 31, 221–238. 10.1080/10610278.2019.1568432. [DOI] [Google Scholar]
  7. Móczár I.; Huszthy P. Optically Active Crown Ether-Based Fluorescent Sensor Molecules: A Mini-Review. Chirality 2018, 31, 97–109. 10.1002/chir.23031. [DOI] [PubMed] [Google Scholar]
  8. Liu Z.; Zhou Y.; Guo M.; Lv B.; Wu Z.; Zhou W. Experimental and Theoretical Investigations of Cs+ Adsorption on Crown Ethers Modified Magnetic Adsorbent. J. Hazard. Mater. 2019, 371, 712–720. 10.1016/j.jhazmat.2019.03.022. [DOI] [PubMed] [Google Scholar]
  9. Wang J.; Zhuang S. Cesium Separation from Radioactive Waste by Extraction and Adsorption Based on Crown Ethers and Calixarenes. Nucl. Eng. Technol. 2020, 52, 328–336. 10.1016/j.net.2019.08.001. [DOI] [Google Scholar]
  10. Martínez-Haya B.; Hurtado P.; Hortal A. R.; Hamad S.; Steill J. D.; Oomens J. Emergence of Symmetry and Chirality in Crown Ether Complexes with Alkali Metal Cations. J. Phys. Chem. A 2010, 114, 7048–7054. 10.1021/jp103389g. [DOI] [PubMed] [Google Scholar]
  11. Gámez F.; Hurtado P.; Martínez-Haya B.; Berden G.; Oomens J. Vibrational Study of Isolated 18-Crown-6 Ether Complexes with Alkaline-Earth Metal Cations. Int. J. Mass Spectrom. 2011, 308, 217–224. 10.1016/j.ijms.2011.06.015. [DOI] [Google Scholar]
  12. Al-Kahtani A. A.; Al-Jallal N. A.; El-Azhary A. A. Conformational and Vibrational Analysis of 18-Crown-6-Alkali Metal Cation Complexes. Spectrochim. Acta, Part A 2014, 132, 70–83. 10.1016/j.saa.2014.04.170. [DOI] [PubMed] [Google Scholar]
  13. Glendening E. D.; Feller D.; Thompson M. A. An Ab Initio Investigation of the Structure and Alkali Metal Cation Selectivity of 18-Crown-6. J. Am. Chem. Soc. 1994, 116, 10657–10669. 10.1021/ja00102a035. [DOI] [Google Scholar]
  14. Inokuchi Y.; Boyarkin O. V.; Kusaka R.; Haino T.; Ebata T.; Rizzo T. R. Ion Selectivity of Crown Ethers Investigated by UV and IR Spectroscopy in a Cold Ion Trap. J. Phys. Chem. A 2012, 116, 4057–4068. 10.1021/jp3011519. [DOI] [PubMed] [Google Scholar]
  15. Choi C. M.; Heo J.; Kim N. J. Binding Selectivity of Dibenzo-18-Crown-6 for Alkali Metal Cations in Aqueous Solution: A Density Functional Theory Study Using a Continuum Solvation Model. Chem. Cent. J. 2012, 6, 1–8. 10.1186/1752-153X-6-84. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Avilés-Moreno J. R.; Berden G.; Oomens J.; Martínez-Haya B. Complexes of Crown Ether Macrocycles with Methyl Guanidinium: Insights into the Capture of Charge in Peptides. ChemPhysChem 2018, 19, 2169–2175. 10.1002/cphc.201800596. [DOI] [PubMed] [Google Scholar]
  17. Gotoh K.; Kunimitsu S.; Zhang H.; Lerner M. M.; Miyakubo K.; Ueda T.; Kim H.-J.; Han Y.-K.; Ishida H. Structure and Dynamic Behavior of the Na–Crown Ether Complex in the Graphite Layers Studied by DFT and 1 H NMR. J. Phys. Chem. C 2018, 122, 10963–10970. 10.1021/acs.jpcc.8b02965. [DOI] [Google Scholar]
  18. Inokuchi Y.; Boyarkin O. V.; Kusaka R.; Haino T.; Ebata T.; Rizzo T. R. UV and IR Spectroscopic Studies of Cold Alkali Metal Ion-Crown Ether Complexes in the Gas Phase. J. Am. Chem. Soc. 2011, 133, 12256–12263. 10.1021/ja2046205. [DOI] [PubMed] [Google Scholar]
  19. Inokuchi Y.; Kusaka R.; Ebata T.; Boyarkin O. V.; Rizzo T. R. Laser Spectroscopic Study of Cold Host-Guest Complexes of Crown Ethers in the Gas Phase. ChemPhysChem 2013, 14, 649–660. 10.1002/cphc.201200746. [DOI] [PubMed] [Google Scholar]
  20. Weinhold F.; Landis C. R.; Glendening E. D. What Is NBO Analysis and How Is It Useful?. Int. Rev. Phys. Chem. 2016, 35, 399–440. 10.1080/0144235X.2016.1192262. [DOI] [Google Scholar]
  21. Zabrodsky H.; Peleg S.; Avnir D. Continuous Symmetry Measures. J. Am. Chem. Soc. 1992, 114, 7843–7851. 10.1021/ja00046a033. [DOI] [Google Scholar]
  22. Alon G.; Tuvi-Arad I. Improved Algorithms for Symmetry Analysis: Structure Preserving Permutations. J. Math. Chem. 2018, 56, 193–212. 10.1007/s10910-017-0788-y. [DOI] [Google Scholar]
  23. Labute P. LowModeMD-Implicit Low-Mode Velocity Filtering Applied to Conformational Search of Macrocycles and Protein Loops. J. Chem. Inf. Model. 2010, 50, 792–800. 10.1021/ci900508k. [DOI] [PubMed] [Google Scholar]
  24. Molecular Operating Environment (MOE) version 2019.12; Chemical Computing Group Inc.: 1010 Sherbooke St. West #910, Montreal, QC, Canada, H3A 2R7, 2019.
  25. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16 Rev. C.01, Wallingford, CT, 2016.
  26. Becke A. D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  27. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
  28. Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
  29. Weigend F.; Ahlrichs R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  30. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c02684_si_001.pdf (679.8KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES