Combining cross‐section images and modeling tools to create high‐resolution root system hydraulic atlases in Zea mays

Abstract

Root hydraulic properties play a central role in the global water cycle, in agricultural systems productivity, and in ecosystem survival as they impact the canopy water supply. However, the existing experimental methods to quantify root hydraulic conductivities, such as the root pressure probing, are particularly challenging, and their applicability to thin roots and small root segments is limited. Therefore, there is a gap in methods enabling easy estimations of root hydraulic conductivities in diverse root types. Here, we present a new pipeline to quickly estimate root hydraulic conductivities across different root types, at high resolution along root axes. Shortly, free‐hand root cross‐sections were used to extract a selected number of key anatomical traits. We used these traits to parametrize the Generator of Root Anatomy in R (GRANAR) model to simulate root anatomical networks. Finally, we used these generated anatomical networks within the Model of Explicit Cross‐section Hydraulic Anatomy (MECHA) to compute an estimation of the root axial and radial hydraulic conductivities (k _x and k _r , respectively). Using this combination of anatomical data and computational models, we were able to create a root hydraulic conductivity atlas at the root system level, for 14‐day‐old pot‐grown Zea mays (maize) plants of the var. B73. The altas highlights the significant functional variations along and between different root types. For instance, predicted variations of radial conductivity along the root axis were strongly dependent on the maturation stage of hydrophobic barriers. The same was also true for the maturation rates of the metaxylem vessels. Differences in anatomical traits along and across root types generated substantial variations in radial and axial conductivities estimated with our novel approach. Our methodological pipeline combines anatomical data and computational models to turn root cross‐section images into a detailed hydraulic atlas. It is an inexpensive, fast, and easily applicable investigation tool for root hydraulics that complements existing complex experimental methods. It opens the way to high‐throughput studies on the functional importance of root types in plant hydraulics, especially if combined with novel phenotyping techniques such as laser ablation tomography.

Abbreviations

k _AQP

contribution of aquaporins to the plasma membrane hydraulic conductivity

k _m

plasma membrane intrinsic hydraulic conductivity

K _PD

conductance of plasmodesmata per unit membrane surface

k _r

radial hydraulic conductivity

K _rs

root system hydraulic conductance

k _x

specific axial hydraulic conductance

L _pc

protoplast permeability

1. INTRODUCTION

Root hydraulic properties are part of the major functional plant properties influencing root water uptake dynamics. Among them, the radial hydraulic conductivity (k _r ) is a key component of the water absorption from the soil to the vasculature of the plant, and the axial hydraulic conductance (k _x ) defines the water transport along the root (Leitner et al., 2014). Changes in the local root hydraulic properties, at the cell and organ‐scale, are known to have overall repercussions on the plant hydraulic behavior (Meunier et al., 2020; Tardieu et al., 2018) and are considered as important breeding targets to create drought resilient varieties (Maurel & Nacry, 2020). Quantitative root hydraulic conductivity data along roots are therefore needed for a thorough understanding of root water uptake dynamics.

The root axial conductivity (k _x ) is a function of the xylem vessel area, maturation, and number (Martre et al., 2001; Sanderson et al., 1988). It can be approximated using Poiseuille–Hagen's law applied to xylem vessels area (Frensch & Steudle, 1989) or measured directly using a pressure probe attached to a root segment with cut ends (Meunier et al., 2018).

The root radial conductivity (k _r ) is influenced by different root anatomical traits and cell‐scale hydraulic properties. On the one hand, root anatomical traits define the baseline for the root radial conductivity as they delineate the structure of the network of root cells (Steudle, 2000). Rieger and Litvin (1999) showed that the radial conductivity is inversely related to the root radius and cortex width. Similarly, increasing the number of cell layers in the cortex (Chimungu et al., 2014), the size of cortex cells (Lynch et al., 2014), as well as the presence of aerenchyma (Fan et al., 2007) all seem to lower the radial hydraulic conductivity. On the other hand, the cell‐scale hydraulic properties, such as the contribution of aquaporins to the hydraulic conductivity of plasma membranes, can modulate the root radial conductivity (Javot & Maurel, 2002; Parent et al., 2009) on the short term. The hydraulic conductance of plasmodesmata may also have a crucial impact, especially after the formation of suberin lamellae locally blocking the transmembrane pathway (Couvreur et al., 2018). The development of such hydrophobic barriers (e.g., the lignified Casparian strip and suberin lamellae in cell walls of the endodermis and exodermis) drastically reduces the root radial conductivity on the long term (Enstone et al., 2002). The quantification of the radial hydraulic conductivity is challenging due to the complexity of the associated experimental procedures. It is even more complicated to assess it at different locations along the root axis and on different root types. The most direct way to estimate root radial conductivity is on roots grown in soil‐less environments using a root pressure probe (Frensch & Steudle, 1989). Other experimental techniques employ a pressure chamber to measure water flow through roots that were successively cut into smaller parts (Zwieniecki et al., 2002), or employ the high pressure flow meter device on whole root systems (Tyree et al., 1994). From a different perspective, modeling tools may connect the dots between complementary data available, possibly at different scales, to assist the estimation of root radial conductivity (Passot et al., 2019). In Heymans et al. (2020), we used this approach to connect root anatomical with cell hydraulic data using the root anatomy and hydraulic anatomy simulators GRANAR (Heymans et al., 2020) and MECHA (Couvreur et al., 2018). At larger scale, Doussan, Page, and Vercambre (1998) and Zarebanadkouki et al. (2016) connected the root hydraulic architecture model of Doussan, Vercambre, and Page (1998) to water tracer data using an inverse modeling method to derive profiles of hydraulic conductivity along roots.

Such estimations are so complex that many studies that simulate water uptake with functional–structural root models still rely on the root hydraulic conductivity profiles estimated more than 20 years ago by Doussan, Page, and Vercambre (1998) (e.g., R‐SWMS, Javaux et al., 2008; OpenSimRoot, Postma et al., 2017; or MARSHAL, Meunier et al., 2020). Today, we need new methods to rapidly quantify root hydraulic conductivities from more easily available data.

Here, we present a procedure to generate a high‐resolution hydraulic conductivity atlas from experimental data combined to recent modeling tools. In short, with free‐hand root cross‐sections and fluorescent microscopy, we were able to extract easily anatomical traits that can be used to run the Generator of Root Anatomy in R (GRANAR) (Heymans et al., 2020). Then, using the generated hydraulic anatomical networks with MECHA (Couvreur et al., 2018), we estimated the k _r and k _x along the root axis of each maize root type. The coupling of these models to multiple root cross‐section images creates a new way to generate a root hydraulic conductivity atlas that takes into account the impact of anatomical traits, the development of hydrophobic barriers and the cell hydraulic properties. The method that we developed is cheap, reproducible and adaptable to different environments than the one tested in this study.

2. MATERIAL AND METHODS

2.1. Plant materials and growth condition

Five Zea mays (maize cultivar B73) plants were grown in pots for 14 days. The PVC pot dimensions were 12 cm diameter, 25 cm deep, and filled with two soil layers for a total volume of 2 L after watering. The bottom soil layer was composed of 1.5 kg per pot of potting soil (80% sieved potting soil DCM [Grobbendonk, Belgium]: 20% sand) and the superficial soil layer was made of .1 kg per pot of sandy soil (50% sieved potting soil DCM [Grobbendonk, Belgium]: 50% sand). The soil was at field capacity when the germinated seeds were planted and not rewatered afterwards. The seeds were placed at 1 cm deep in the first soil layer. The germination of the seeds occurred in a petri dish maintained vertically in dark conditions between two wet filter papers. Ahead, the seeds were initially sterilized in a 50% bleach bath for 5 min then rinsed in water five times, interrupted by the sponging of the rinsing water. From the 15 seeds that were put under germination, five were selected based on the length of the tap root (0.5 to 1 cm long) in order to have a homogenous root growth. Each seed was planted in a different pot column. The pots were separated from each other over a grid pattern, where the cells are 20 cm long and 13 cm large with a total of 5 rows and 10 columns. The other pots that composed this experimental design were occupied by other maize genotypes following the same growth condition. All plants were grown in a greenhouse (Louvain‐la‐Neuve, Belgium, May 2018) with the environmental settings of the greenhouse set to 60% for the relative humidity and a temperature of 25°C (±3°C).

2.2. Processing of root cross‐sections

After 14 days of growth in the pots, the root systems were excavated and carefully washed. The root systems were scanned on a flatbed scanner (Medion 3600 DPI) customized in‐house in such a way that the light source and the sensor are positioned on both sides of a large water container (21 × 60 × 4 cm). Root samples were conserved in a FAA (95% ethanol : glacial acetic acid : 37% formaldehyde : water/50:5:10:35) (Ruzin, 1999) and kept at 4°C. Before staining the roots, they were rinsed in tap water for 15 min. The roots were stained with .1% (w/v) berberine hemi‐sulphate for 1 h and post‐stained with 0.5% (w/v) aniline blue for 30 min before making free‐hand root cross‐sections following the Brundrett et al. (1988) protocol. Three or more free‐hand root cross‐sections per root type were taken on minimum three different roots at every 5 cm or less to create an atlas of anatomical traits along each root type. Cross‐section images were acquired with a Leitz SM‐LUX (Germany) fluorescent microscope equipped with a Leica camera DFC320 (Cambridge, United Kingdom).

2.3. Root typology

The root types selected for this analysis are the taproot, the basal roots (embryonic roots), the shoot born roots on the first node and two types of lateral roots, the short ones and long ones (longer than 5 cm with second order lateral roots on it) (Passot et al., 2018). Because we were able to measure lateral root lengths but not their growth rates, we chose to have two classes of lateral roots instead of the three types characterized by Passot et al. (2018). We had to base the classification on root length instead of root growth rate. After a few days of growth, the length of individual lateral roots clearly discriminates between longer roots classified as type A by Passot et al. (2018) and the other two lateral types (B and C) that are shorter than the A type after a couple of days.

2.4. Root image analysis

2.4.1. From root cross‐section image to root anatomical traits

The images were analyzed with the ImageJ (version 1.47) software (Schneider et al., 2012). The anatomical traits that we measured manually are listed in Table 1. On each root cross‐section image, transects were drawn from one side to the other passing by the center, or two transects from two distinct side meeting in the center if the image did not cover the entire root cross‐section. The selection of the transects was also made in order to have the most intact cells crossing the lines. With the segmented lines tools of ImageJ, those lines were followed to measure the tissue width of the epidermis, the exodermis, the cortex, the endodermis, and pericycle cell layer, as well as the stele diameter. Following the same lines, the numbers of cells in the cortex and in the stele were counted. The specific cell diameter of the cortex and the stele was calculated by dividing the width of the root tissue by the number of cell layers within the root tissue. The metaxylem vessels' diameters were calculated from the surface area of all metaxylem vessels divided by their number. The surface area was measured with the polygon tool of ImageJ. The number of protoxylem elements was counted by addition of all lignify cells in the surroundings of metaxylem vessels. The staining procedure to spot the lignified cell walls is described in Section 2.4.3. An overview of the anatomical traits measurement protocol can be found in Figure S1.

TABLE 1.

List of the measured anatomical traits acquired with ImageJ on the root cross‐section images that have been used to get the GRANAR parameters

Measured anatomical traits on the root cross‐section image		GRANAR parameters
Traits	Description from traits to parameter	Tissue type	Properties	Unit
EpW	Epidermis cell radial width	epidermis	cell_diameter	μm
ExW	Exodermis cell radial width	exodermis	cell_diameter	μm
nCF	Number of cortex cell layer	cortex	n_layers	#
CoW	Cortex width (CoW) divided the number of cortex cell layer (CF)	cortex	cell_diameter	μm
EnW	Endodermis cell radial width	endodermis	cell_diameter	μm
PeW	Pericycle cell radial width	pericycle	cell_diameter	μm
SD	Global stele diameter	stele	layer_diameter	μm
nS SW	The number of stele cells on the stele diameter (nS) is used to divide the global stele diameter (SD) in order to obtain the stele cell radial width (SW)	stele	cell_diameter	μm
MXA MXW	The Metaxylem vessel area (MXA) is used to calculate the metaxylem vessel diameter (MXW) based on circular assumption	xylem	max_size	μm
nMX	Number of Metaxylem vessels	xylem	n_files	#
nPX	Number of Protoxylem vessels (nPX) divided by the number of Metaxylem vessels (nMX)	xylem	ratio	#

2.4.2. From anatomical traits to root cell network generation

We needed to capture anatomical descriptors that are ready‐to‐use for downstream computational models to create a series of functions that represent the evolution of the hydraulic conductivities as a function to the distance from the root tip. Therefore, such root hydraulic conductivity atlas along the different maize root types would take into account the development of the anatomical traits. With the gathered root cross‐section images, and the extracted root anatomical traits measured along the roots axes, we computed linear regressions of the different anatomical traits against the distance to the tip for each root type. The coefficients of the linear models were used to estimate the different GRANAR input parameters along the root type axes at every wanted location (the spatial resolution is described below). However, if the regression between the distance along the root and the anatomical traits did not significantly differ from the uniform model (p value > .05), the average value of the anatomical traits along the root axis was taken instead of the value predicted by the linear model.

An exception was made for the relation between the size of the stele and the one of the metaxylem. Instead of the regular regression methods to obtain the coefficients of the linear models, a Napierian logarithmic transformation was applied on the stele area and the xylem area, similarly as in Yang et al. (2019). The linear regression of the Napierian logarithm between those anatomical traits was used to set the metaxylem diameter parameter (GRANAR parameter: xylem max_size). The goal was to conserve the relationship between the size of the stele and that of the metaxylem. Nevertheless, the regular regression method was still used to set the number of metaxylem elements (GRANAR parameter: xylem n_files).

The chosen distances between the simulated root cross‐sections used to generate the atlas vary along three regions of the root. From 0 to 2 cm from the tip, the spatial resolution is 0.5 cm. From 2 to 15 cm from the tip, we selected a resolution of one cross‐section every centimeter, and between 15 and 40 cm from the tip, one every 5 cm. The number of technical replicates for each simulated root cross‐section is two, with small artificial stochasticity (GRANAR parameter randomness set to 1). This artificial stochasticity produces a small random shift in the center of every cell proportional to the distance from the center of the generated root cross‐section. We tested the generated root cross‐sections to validate that their simulated anatomical traits match the set of experimental values for those anatomies (Figure S2).

2.4.3. Estimation of k _r and k _x from generated root cell network

Radial and axial hydraulic conductivities (k _r and k _x ) were then estimated for each simulated anatomical network along the selected root types using MECHA (Couvreur et al., 2018) and with the maize cell hydraulic parameters described in the section below. To test the effect of the distance from the apex and the factor root type, each hydrophobic barrier scenario or xylem maturation was computed for every generated root cross‐section. To identify the type of hydrophobic barriers that were encountered on the cross‐section images, we used the berberine‐aniline blue fluorescent staining procedure for suberin, lignin, and callose in plant tissue (Brundrett et al., 1988). This procedure designed to highlight exodermal and endodermal Casparian strips and suberin lamellae also works to identify the lignification of the xylem cell walls. Metaxylem vessels with fully lignified cell walls were considered as mature vessels.

2.5. Description of MECHA hydraulic parameters

The simulation framework MECHA (Couvreur et al., 2018) can estimate root radial conductivities from the root anatomy generated with GRANAR from the subcellular‐scale hydraulic properties of cell walls, membranes, and plasmodesmata. The cell wall hydraulic conductivity was set to 2.8 × 10⁻⁹ m² s⁻¹ MPa⁻¹, as measured by Zhu and Steudle (1991) in maize. Lignified and suberized wall segments in the endodermis and exodermis were considered hydrophobic and attributed null hydraulic conductivities. The protoplast permeability (L _pc , 7.7 × 10⁻⁷ m s⁻¹ MPa⁻¹) measured by Ehlert et al. (2009) was partitioned into its three components: the plasma membrane intrinsic hydraulic conductivity (k _m ), the contribution of aquaporins to the plasma membrane hydraulic conductivity (k _AQP ), and the conductance of plasmodesmata per unit membrane surface (K _PD ). The latter parameter was estimated as 2.4 × 10⁻⁷ m s⁻¹ MPa⁻¹ (Couvreur et al., 2018), based on plasmodesmata frequency data from Ma and Peterson (2001), and the plasmodesmata conductance estimated by Bret‐Harte and Silk (1994). By blocking aquaporins with an acid‐load treatment, Ehlert et al. (2009) measured a k _AQP of 5.0 × 10⁻⁷ m s⁻¹ MPa⁻¹. The remaining value of km after subtraction of k _AQP and K _PD from L _pc was 0.3 × 10⁻⁷ m s⁻¹ MPa⁻¹. Each value of km, k _AQP , k _PD , and L _pc was set uniform across tissue types. For details on the computation of k _r , see Couvreur et al. (2018).

The specific root axial hydraulic conductance k _x (m⁴ s⁻¹ MPa⁻¹) is the sum of specific conductances of individual vessels k _xyl (m⁴ s⁻¹ MPa⁻¹), estimated using the Hagen–Poiseuille equation:

$$k_{\mathit{xyl}i}={A_i}^2/8\mathit{\pi \mu }$$ (1)

$$k_x={\sum }_i^N{k}_{\mathit{xyl}i}$$ (2)

where A (m⁴) is the transverse area of one xylem vessel, i is the xylem vessel number, N is the total number of xylem vessels in parallel within a cross‐section, and μ (MPa s) is the dynamic viscosity of the xylem sap. Xylem sap being essentially water, μ was assumed equal to 10⁻⁹ MPa s.

2.6. Root hydraulic conductivities benchmark

As the root hydraulic conductivities obtained in this study are compared, among other studies, with the ones estimated in Doussan, Page, and Vercambre (1998) and Doussan, Vercambre, and Page (1998), which refer to lateral root segment ages, we assumed that the lateral roots have an average growth rate of 1 cm per day (Passot et al., 2018) to turn root segment ages into distances from the apex.

The details about the GRANAR‐MECHA coupling are available in an online Jupyter NoteBook ( https://mybinder.org/v2/gh/HeymansAdrien/GranarMecha/main ). The complete procedure can be run online or locally after downloading the related gitHub repository (ht tps://github.com/HeymansAdrien/GranarMecha doi: https://doi.org/10.5281/zenodo.4316762). This complementary open‐source tool helps the users to change anatomical traits and cell hydraulic properties to personalize the exercise at will. The outputs of each generated root cross‐section can be visualized through different figures that show the proportion of the water fluxes in each compartment (apoplastic and symplastic fluxes) and a table with the estimated k _r and k _x for all maturation scenarios.

The whole script that was used to compute the root hydraulic atlas from the root anatomical measurement is presented as a Rmarkdown script stored in a GitHub repository (https://github.com/granar/B73_HydraulicMap doi: https://doi.org/10.5281/zenodo.4320861). All input and output data of this study are stored in the same repository.

2.7. Statistical analysis

The statistical analysis was conducted using R software (version 3.5.1, R Core Team, 2018). The R package that was used for the data manipulation was tidyverse (Wickham et al., 2019). All analyses of variance (ANOVAs) were conducted considering the full length of the roots (not restricted to the actual intervals where the roots show the features). The combination of distance from the apex and the factor root type was included in the performed two‐way ANOVAs. The function aov from the package stats was used for this purpose. Using these generalized linear models and the emtrends function from the package emmeans (Lenth et al., 2018), we were able to compare pairwise the change of the anatomical traits along their root type axes. Those tests were used to seek anatomical traits changes along root type axes. Other ANOVAs, used to parametrize GRANAR and benchmark the anatomical input with the output from the cross‐section generation procedure, were performed using the same function, but the dataset was split per root type factor, and the distance from the apex was the explicative variable. The Pearson correlation coefficients used in the comparison between the GRANAR output and the theoretical values from the input parameter were computed with the function ggpairs from the package GGally (Emerson et al., 2013).

3. RESULTS

3.1. Changes in anatomical traits

The first step of the procedure to create a root hydraulic atlas is to understand the change of anatomical traits along the different root type axes. The root cross‐section images gathered along the different root types show that some anatomical traits change along the root axis (Table 2). In general, the axial roots (Tap‐, Basal‐, and Shoot born‐ roots) are narrower at their tip than at their base. It is primarily due to a shrinkage of the stele (Figure 1). This shrinkage is linked to a smaller stele cell number. Only the long laterals do not present a significant decrease (p < .05). However, basal‐ and shoot‐born roots also have smaller diameter closer to the tip (p < .05). The change in the stele diameter also differs across root types. The change of stele diameter along the root axes for the shoot born roots is steeper than for the tap root (p < .05). The cortex width tends to be wider as we move away from the tip of the root. The change of cortex width along the root axis is also different between the long lateral and the basal‐ and shoot‐born roots (p < .05).

TABLE 2.

P value of the two‐way analysis of variance (ANOVA) models performed to test the hypothesis under which the cell tissue types are influenced by the distance from the apex and the root type

Variable: anatomical traits	Distance from apex	Root type	Distance * root type
	p value	p value	p value
Epidermis width (μm)	.01537	.00542	.04410
Exodermis width (μm)	.00281	7.31e‐10	.42145
Cortex width (μm)	4.11e‐07	<2e‐16	.00109
Cortex cell width (μm)	1.50e‐07	2.94e‐14	.033
Endodermis width (μm)	2.38e‐13	1.37e‐05	.912
Pericycle width (μm)	.000979	< 2e‐16	.000519
Stele diameter (μm)	6.16e‐16	< 2e‐16	1.07e‐08
Stele cell width (μm)	<2e‐16	<2e‐16	.276
Stele cell number (#)	5.56e‐09	< 2e‐16	6.85e‐05
Metaxylem number (#)	<2e‐16	<2e‐16	.475
Metaxylem vessel diameter (μm)	.030735	<2e‐16	.000502
Protoxylem number (#)	6.21e‐15	<2e‐16	.0493

FIGURE 1.

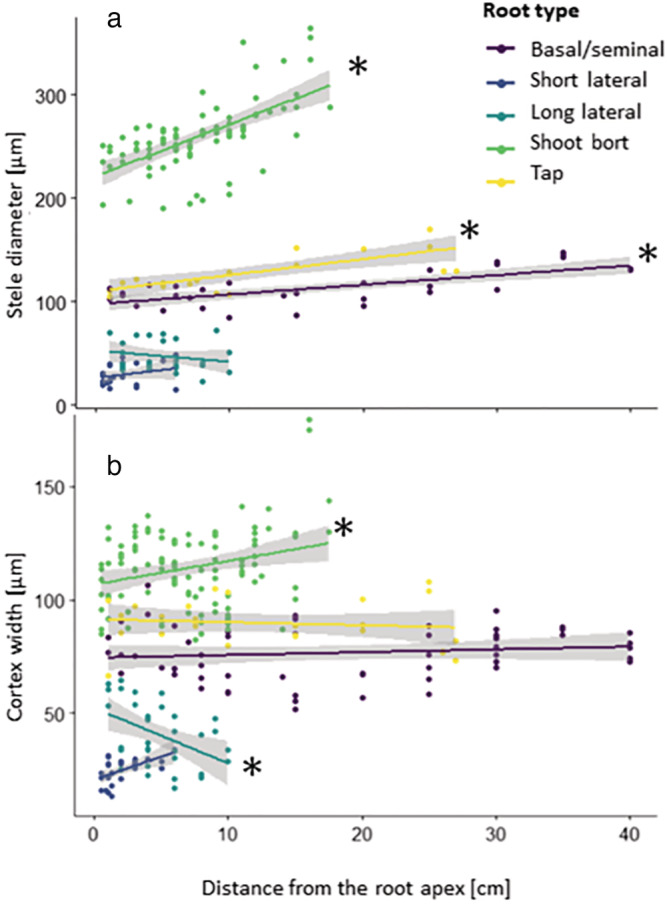
Relation between the distance from the apex and (a) the stele diameter, and (b) the cortex width for the different root types. Data show all experimental measures for the dedicated anatomical traits. The dark shadings show the 95% interval of confidence around the linear regression for each root type. (*): slope different than 0 (p < .05; generalized linear model: the anatomical layer width as a function of the distance, the root type and the combination of both)

Closer to the tip, as the stele area decreases, the number of xylem vessels is also reduced, whereas the size of the metaxylem vessels does not shrink significantly for most root types (p > .05). The relation between the stele and xylem areas is strong (R ² = .975), but it is not linear. However, when we look at the Napierian logarithm of those areas, similarly as in Yang et al. (2019), the linearity of this relationship is strong (R ² = .991, Figure 2). Due to the strong relationship between those anatomical traits, we used the Napierian relationship between the size of the stele and the metaxylem vessels into the GRANAR parametrization procedure instead of using the regular linear regression

FIGURE 2.

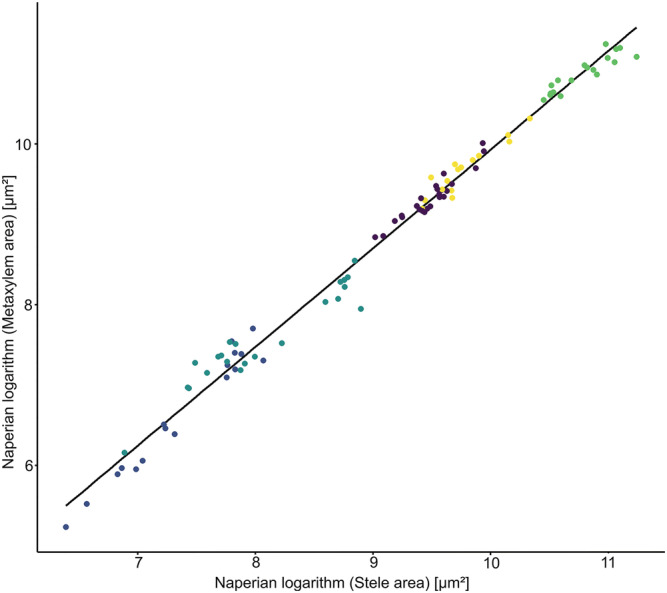
Allometric relationship between the Napierian logarithm of the metaxylem area and the one of the stele area. Data show experimental mean per root cross‐section image. R ² = .991

3.2. Building an atlas of root anatomies and hydrophobic barriers

Each input parameter for the model GRANAR is a function depending on the root type and the distance from its apex. With such information, we were able to simulate representative root cross‐sections along each root type, at any longitudinal position (Figure 3).

FIGURE 3.

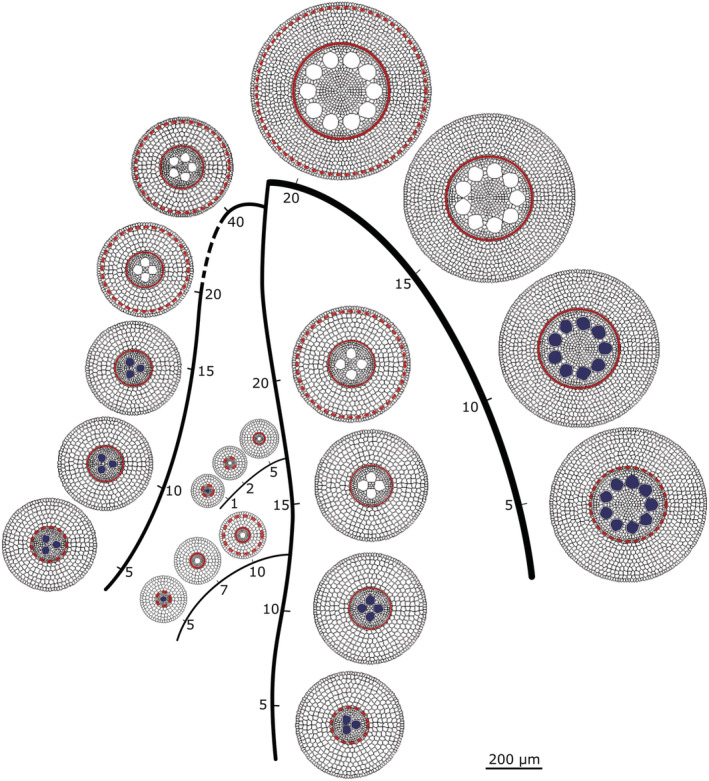
Schematic representation of a maize root system with five root types. Along each root type, the generated representative root cross‐sections pair with the nearby tick marks. The numbers along the roots describe the distance from the tip of the root in centimeters. The 200‐μm bar stands for the displayed root cross‐sections, though the scale is free in between in the rest of the figure. The filled metaxylem vessels are not mature yet. The dashed red circles stand for the Casparian strip. The continuous red circles stand for the fully suberized endodermis

In addition to the overview of the root cross‐section of the root system, we added the location of hydrophobic barriers and metaxylem maturation zone based on staining signals (Figure 4). The berberine‐aniline blue fluorescent staining procedure for suberin, lignin, and callose allowed us to estimate the position of the different maturation zones (Figure 5). On the main root axes, the taproot, the basal‐, and the shoot‐born roots had a fully suberized endodermis before the maturation of the metaxylem. In addition, the lignification of the metaxylem vessels usually occurred shortly after the complete suberization of the endodermis. On the opposite, in lateral roots, the metaxylem vessels were lignified before the complete suberization of the endodermis. Moreover, short lateral roots had lignified metaxylem vessels before the suberin lamellae started to deposit on the cell walls of the endodermis. For long lateral roots, lignified metaxylem vessels were found where some suberin had started to deposit as a lamellae against primary walls of the endodermis.

FIGURE 4.

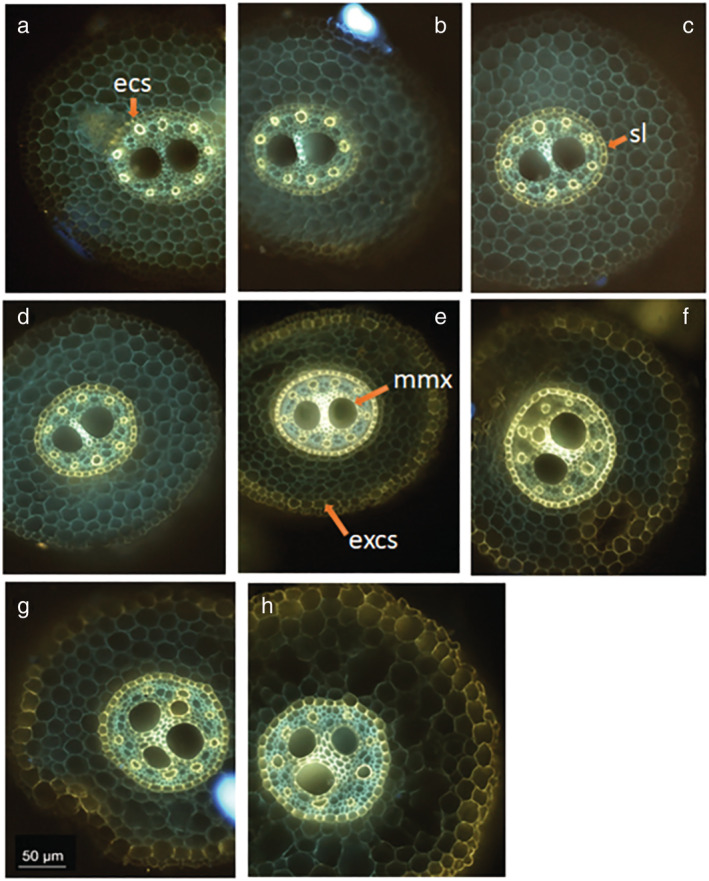
Basal root cross‐sections. (a) 3 cm from apex, the arrow point at the endodermal Casparian strip (“ecs”); (b) 5 cm from apex; (c) 8 cm from apex, the arrow point at the suberin lamellae that formed on the endodermis (“sl”); (d) 10 cm from apex; (e) 15 cm from apex, the “mmx” arrow points the lignify cell wall of the mature metaxylem vessels, the “excs” arrow points the exodermal Casparian strip; (f) 20 cm from apex; (g) 25 cm from apex; and (h) 30 cm from apex. Bar = 50 μm

FIGURE 5.

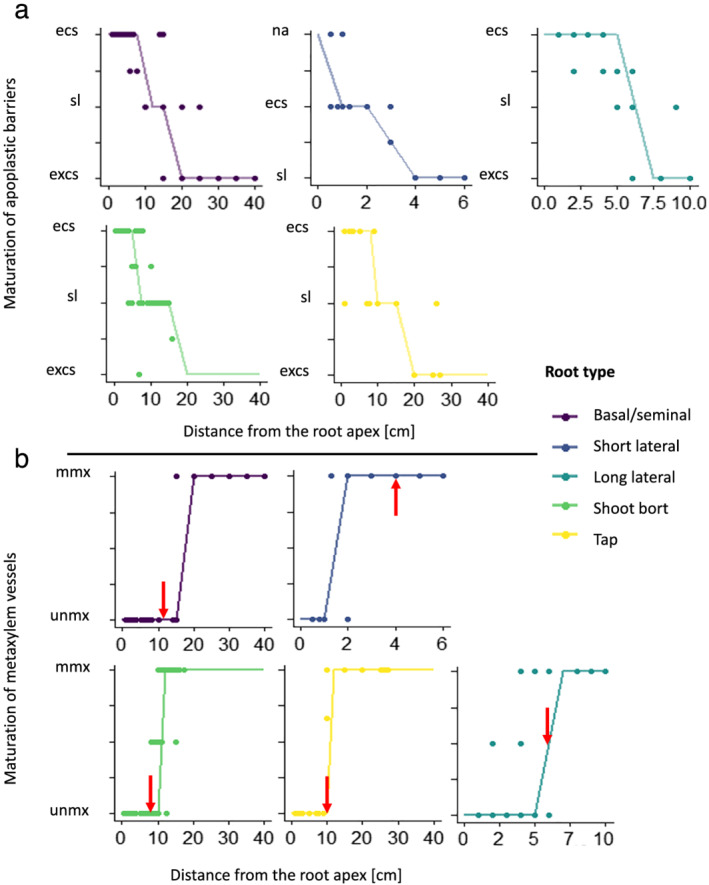
Development of the maturation for hydrophobic barriers (a) and for the metaxylem vessels (b) along the root axis for the different root types. Half values were applied when the transition between two maturations was observed. The lines are a discretization of the local weighted regressions of the scatter plots. (a) “na” = no hydrophobic barriers; “ecs” = endodermal Casparian strip; “sl” = fully suberized endodermis; “excs” = suberized endodermis and exodermal Casparian strip. (b) “unmx” = only the protoxylem vessels are lignified; “mmx” = all xylem vessels are lignified. The arrows point out where the endodermis is fully suberized for the specific root type

The time needed to generate root cross‐sections with GRANAR was around 1 to 20 s depending on the number of cells on the anatomical network.

3.3. Building an atlas of root hydraulic conductivities

The next step of the process to make high‐resolution atlases for the root hydraulic conductivity is to estimate the k _r and k _x of all the generated cross‐sections. To estimate the k _r of the generated root cross‐section, we used the MECHA model (Couvreur et al., 2018) (Figure 6).

FIGURE 6.

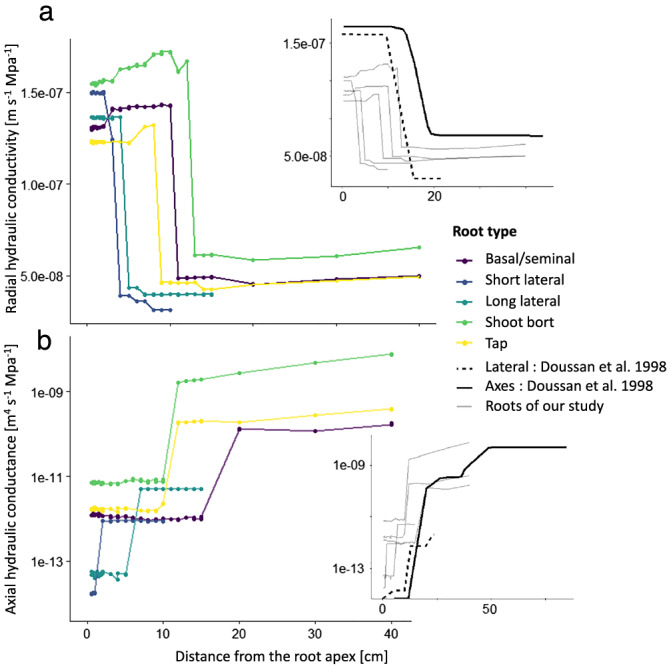
Hydraulic conductivity atlas along the different root types. (a) Estimation of the k _r for each generated root cross‐section along the different root. The side panel shows the two Doussan, Page, and Vercambre (1998) and Doussan, Vercambre, and Page (1998) estimations for k _r and our estimations in comparison. (b) Estimation of the axial hydraulic conductance for each generated root cross‐section along the different root. The side panel shows the two Doussan, Page, and Vercambre (1998) and Doussan, Vercambre, and Page (1998) estimations for k _x and our estimations in comparison

We adjusted the maturation scenario in MECHA to fit our experimental data of the maturation zone for the hydrophobic barriers and metaxylem lignification. The cell hydraulic parameters were kept the same for all cross‐sections. For the kx, we used the Hagen–Poiseuille laws as explained in Section 2 (Equations 1 and 2).

For each hydrophobic scenario, the radial hydraulic conductivity was significantly influenced by the distance from the apex, the root type factor, and the combination of both (Table S2). The axial hydraulic conductance, with only protoxylem or with all functioning xylem elements, was also highly dependent on the distance from the apex, the root type factor, and the combination of both (Table S2).

To estimate the k _r for the three scenarios, the model MECHA took around less than 1 to 5 min per root cross‐section.

4. DISCUSSION

We presented here a protocol to estimate root hydraulic properties that could be repeated in further studies (e.g., with different species, genotypes, or environment). Our method is quicker than root pressure probing (the established experimental procedure) to estimate the root radial conductivity of a root segment (Figure S3). This increase in throughput enabled the estimation of k _r on more root cross‐sections per experiment. In addition, as root traits can be interpolated along the root axis, hydraulic atlases with high spatial resolution can be created. It takes a total time of 30 min, on average, to link anatomical traits with hydraulic properties. This includes the free‐hand cross‐sections, the extraction of anatomical traits with ImageJ, the generation of root anatomical networks with GRANAR, and the estimation of three hydraulic scenarios with three different types of hydrophobic barriers. On the contrary, one estimation for the radial hydraulic conductivity from the root pressure probe takes at least 3 to 5 h, as steady root pressure has to be established after the connection between the root and the device (Liu et al., 2009). In both cases, making free‐hand root cross‐section takes around 10 to 20 min and is mandatory to link anatomical traits with hydraulic properties. One should keep in mind that the experimental procedure is likely to be more accurate, illustrating the usual tradeoff between precision and throughput.

Meunier et al. (2020) showed that modifying hydraulic properties changes the root system hydraulic architecture and thus affects the whole root system conductance (K _rs ). Tuning root hydraulic conductivity functions to match experimental data or test new hypotheses through simulation studies could therefore show the local impact of root anatomy or cell hydraulic properties on the whole root system conductance. A better understanding of the effect of local root traits on the global hydraulic behavior of the root system would enhance the breeding efforts towards more drought tolerant cultivars.

We expect our analysis pipeline will be of particular interest with new techniques such as the Laser Ablation Tomography (Strock et al., 2019) and root traits recognition algorithm (Sosa et al., 2014). Those techniques could drastically increase the number of root cross‐section images that can be taken on an experiment and the deep learning approach can speed up the process of root traits extraction procedure from those images. These are two limiting aspects in perspective of further improvements of the estimation of radial hydraulic conductivities along roots.

In comparison with the hydraulic conductivity atlas of Doussan, Page, and Vercambre (1998) and Doussan, Vercambre, and Page (1998), our data, for the different root types, show a drop in radial conductivity closer to the tip. Our result is close to the one of Zarebanadkouki et al. (2016), who estimated that the first drop of k _r occurred after four centimeters within the stepwise function with three transition zones due to the development of hydrophobic barriers. This early drop is due to the deposition of suberin lamellae in endodermal cell walls, which has been shown to be sensitive to environmental conditions (Tylová et al., 2017), so variability in its position along the root can be expected. The proportionally smaller second drop due to the addition of the exodermal Casparian strip is compensated further away by the expansion of the stele and the larger number of xylem vessels. Those anatomical effects on the radial conductivity follow the same trends as in Heymans et al. (2020). In our study, the estimated radial conductivities are within the range of Doussan, Page, and Vercambre (1998) and Doussan, Vercambre, and Page (1998), and in a slightly higher range relative to the estimations of Zarebanadkouki et al. (2016) and Meunier et al. (2018).

The use of the Hagen–Poiseuille equations to estimate the k _x is straightforward when the area of each xylem element is known. Our predicted range and trends both match direct measurements by Meunier et al. (2018) and estimations from Doussan, Page, and Vercambre (1998) and Doussan, Vercambre, and Page (1998). Uncertainties related to the application of the Hagen–Poiseuille law have been discussed in the literature. Frensch and Steudle (1989) have shown that it may overestimate experimental k _x values by a factor of two to five. This could be due to the presence of perforation plates (Brodersen et al., 2018; Shane et al., 2000) or persistent xylem cross‐walls (Sanderson et al., 1988). In this study, we did not divide the estimated k _x by a coefficient. The uncertainty of identification of mature xylem vessels by the used staining procedure could shift the transition zone shootward. Other staining procedures could lift those uncertainty, such as the one with the Fluorol yellow 088 (synonyms: 2,8‐dimethylnaphtho[3,2,1‐kl] xanthene; Solvent Green 4, CAS 81‐37‐8) and PEG 400 (PEG 400:glycerol:water = 10:9:1, v:v) allow intense staining of lipids and suberin lamellae (Kitin et al., 2020). We also assume that xylem sap has the same viscosity as water. This hypothesis could be discussed in relation to xylem sap temperature or solute concentration (Bruno & Sparapano, 2007).

The hydraulic conductivity atlas that we computed for this genotype in this precise environmental condition (Zea mays var. B73 in pots) is an example case. Our methodology allows the inclusion of the effect of root anatomical changes, the development of the hydrophobic barriers, and takes into account the selected cell hydraulic properties summarized in Section 2. This study is the first to our knowledge to propose a method to characterize a root hydraulic conductivity atlas with such a high spatial resolution along roots and across five different root types. We posit our approach will allow more realistic parametrizations of functional–structural plant models targeting root water uptake. Such a root hydraulic conductivity atlas can as well be connected to complementary modeling tools (e.g., Meunier et al., 2020) to estimate hydraulic parameters such as the root system conductance or the standard sink fraction for models working at larger scales (e.g., Agee et al., 2021; Cai et al., 2018; Sulis et al., 2019), as envisioned by Passot et al. (2019). Future modeling studies could reuse the anatomical networks and the root hydraulic conductivities that we built on their root system architecture. This modeling framework could as well be used inversely, to search for cell‐scale hydraulic conductivities that reproduce measured hydraulic properties at the root scale, as in Ding et al. (2020), or at the plant scale.

5. CONCLUSION

In this study, we showed how to use stained root cross‐section images and computational tools (organ‐scale root models: GRANAR and MECHA) to create a high‐resolution hydraulic atlas of a maize root system (var. B73 in our example). Our hydraulic atlas includes hydraulic information (radial and axial properties) and anatomical data along five root types (taproot, basal, shoot born, long laterals, and short laterals).

Anatomical differences along the root axes and between root types have an impact on the radial and axial hydraulic properties of the roots. The values and trends shown in this study are within the same range as the estimations that can be found in the literature.

Compared with measures from root pressure probing, our method has the advantages of being quick and produces high‐resolution results on any type of root. We expect our new methodology to be of great use for further root hydraulic studies as it streamlines the estimation of local root hydraulic properties from experimental data. These local root conductivities can be used in functional–structural root models to estimate macroscopic hydraulic properties. It opens the way to test or benchmark the local impact of local root traits on the global hydraulic behavior of a root system.

FUNDING INFORMATION

This work was supported by the Belgian Fonds de la Recherche Scientifique (FNRS Grant 1208619F to V.C. and MIS Grant F.4524.20. to H.A. and G.L.).

CONFLICT OF INTEREST

The Authors did not report any conflict of interest.

Supporting information

Figure S1: Overview of a maize root cross‐section and the measure taken with ImageJ to parametrize GRANAR in this study. From left to right: ExW) Exodermis width; CoW) Cortex width; EnW) Endodermis width; nS) number of stele cell along the transect; nMX) number of Metaxylem vessel; SD) Stele diameter; MXA) all Metaxylem area; nP) number of protoxylem element; PeW) Pericycle width; CF) number of Cortex layer; EpW) Epidermis width.

Figure S2: Comparison between GRANAR output and the theoretical values from the input parameter for four anatomical traits. A, Metaxylem area. B, stele radius (endodermis included). C, cortex width. D, Total root radius. The R² values convey the information about the variance from the linear regression between the theoretical values and the output values. PCC = Pearson Correlation Coefficient. Err = relative error.

Figure S3: Comparison between root pressure probe and model based methodology. In both cases, cross‐sections are needed to estimate the kr.. On the upper part of the figure, the estimation for the kr from the root pressure probe takes at least three to five hours. On the opposite, extracting the anatomical traits needed to run GRANAR with ImageJ takes around 10 minutes. GRANAR creates a root cellular network in a few seconds. MECHA takes around 5 minutes to estimate the kr.

Table S1: p‐value of the two‐way ANOVA models performed to test the hypothesis under which the kr is influenced by the distance from the apex and the factor root type.

Heymans, A. , Couvreur, V. , & Lobet, G. (2021). Combining cross‐section images and modeling tools to create high‐resolution root system hydraulic atlases in Zea mays . Plant Direct, 5(7), e334. 10.1002/pld3.334