Automatic quantification of lobular inflammation and hepatocyte ballooning in nonalcoholic fatty liver disease liver biopsies

Summary

Automatic quantification of cardinal histologic features of nonalcoholic fatty liver disease (NAFLD) may reduce human variability and allow continuous rather than semiquantitative assessment of injury. We recently developed an automated classifier that can detect and quantify macrosteatosis with greater than or equal to 95% precision and recall (sensitivity). Here, we report our early results on the classifier’s performance in detecting lobular inflammation and hepatocellular ballooning. Automatic quantification of lobular inflammation and ballooning was performed on digital images of hematoxylin and eosin–stained slides of liver biopsy samples from 59 individuals with normal liver histology and varying severity of NAFLD. Two expert hepatopathologists scored liver biopsies according the nonalcoholic steatohepatitis clinical research network scoring system and provided annotations of lobular inflammation and hepatocyte ballooning on the digital images. The classifier had precision and recall of 70% and 49% for lobular inflammation, and 91% and 54% for hepatocyte ballooning. In addition, the classifier had an area under the curve of 95% for lobular inflammation and 98% for hepatocyte ballooning. The Spearman rank correlation coefficient for comparison with pathologist grades was 45.2% for lobular inflammation and 46% for hepatocyte ballooning. Our novel observations demonstrate that automatic quantification of cardinal NAFLD histologic lesions is feasible and offer promise for further development of automatic quantification as a potential aid to pathologists evaluating NAFLD biopsies in clinical practice and clinical trials.

1. Introduction

Nonalcoholic fatty liver disease (NAFLD) is the most common liver disease in the United States affecting 1 in 3 adults and 1 in 8 children [1,2]. The most severe phenotype of the disease, nonalcoholic steatohepatitis (NASH), is estimated to affect 3% to 5% of the US population [3,4]. The spectrum of NAFLD begins with a mild phenotype, simple steatosis, where only steatosis is present in the liver and extends to NASH, where steatosis is present with hepatic necroinflammation and fibrosis [5]. Liver biopsy is the current “gold standard” diagnostic test for phenotyping NAFLD [5]. Accurate phenotyping of NAFLD is critical because simple steatosis rarely progresses, whereas NASH can progress to cirrhosis, liver failure, and hepatocellular carcinoma [6–9].

The NAFLD activity score (NAS), the state-of-the-art scoring system for liver biopsies, is based on the sum of 3 numerical grades determined by manual pathologist assessment and semiquantification of steatosis, lobular inflammation, and hepatocyte ballooning [10]. These 3 lesions were selected for inclusion in the NAS based on a multiple logistic regression analysis that showed these lesions were independently associated with diagnosis of NASH [10]. Because these lesions are potentially reversible in the short term, unlike fibrosis, they were chosen as end points for therapeutic trials for NASH. A recent expert panel report recommended the use of liver biopsy to define histologic outcomes in phase 2 and 3 clinical trials in NASH and also recommended the use of NAS to define and quantify NAFLD activity [11].

Semiquantitative assessment of steatosis, lobular inflammation, and hepatocyte ballooning has a couple important limitations stemming from the very nature of semiquantitative grading that forces continuous measures to be threshold into discrete grading bins. The first limitation is that semiquantitative grades may fail to accurately show improvements. For example, a steatosis grade 0 implies 0% to 4% steatosis, whereas grade 1 implies 5% to 33% steatosis. Consider patient A, who enters a study with 7% steatosis and improves by 3%. With this, patient A improves from steatosis grade 1 to 0. Now consider patient B who enters a study with 30% steatosis and improves 24%. Patient B is a steatosis grade 1 before and at the end of the study. Looking at study results, one may be led to believe patient A’s 3% improvement was more significant than patient B’s 24% improvement. The second limitation is that semiquantitative grading scale inevitably leads to interrater and intrarater variability [10,12–17]. Rater variability will be amplified for cases that lie near a grading cutoff (threshold) and may worsen based on the skills and/or training of the rater.

We hypothesize that automated decision support tools for pathologists, by offering a continuous rather than semiquantitative method for grading the histologic lesions of NAFLD, could increase the precision and accuracy of grading histologic activity. The aim of this initial study is to determine if an automated tool using supervised machine learning could be trained by pathologists to detect lobular inflammation and hepatocyte ballooning. Our group has previously published research demonstrating the feasibility of the accurate categorization of the white regions in liver biopsy images including macrosteatosis, central veins, portal veins, portal arteries, sinusoids, and bile ducts [18]. To date, no previous work has set out to automatically quantify lobular inflammation and hepatocyte ballooning.

2. Materials and methods

The analysis discussed herein is based on a data set of 59 unique liver biopsy scans. Of the 59 patients in the study, pathologist semiquantitative grading was available for 47 patients with the remaining image scans being used solely for annotations and machine learning. Two study pathologists (D.K. and R.K.) provided semiquantitative grades for each of the key histologic lesions comprising the NAS (steatosis, lobular inflammation, and hepatocyte ballooning). The patients in the study represented the full range of phenotypes from patients not having NAFLD, to those with various stages of NAFLD.

High-resolution digital images of the hematoxylin and eosin–stained slides of liver biopsy images in the study were generated using the NanoZoomer scanner manufactured by Hamamatsu (Hamamatsu City, Shizuoka, Japan) and housed in the Medical College of Wisconsin pathology department. The images were scanned at ×20 magnification and saved as RGB images in the lossless tiff file format. To create files small enough to efficiently work with given available hardware and computing resources, the files were reduced to 50% their original size. The smaller files are saved as red, green, blue JPEG images with an 80% compression factor. The size reduction was performed with bicubic interpolation and antialiasing to preserve as much of the original image detail as possible. This resulted in a resolution of 0.92 μm per pixel with respect to actual tissue size. The research protocol was reviewed and approved by the Internal Review Board of the Medical College of Wisconsin.

2.1. Quantification of lobular inflammation and hepatocyte ballooning in biopsy sections

Biopsy images are tiled into individual 25 pixel square sections. Tile size was selected by trial and error and by visual inspection of tile size appropriate with respect to lesion size. Although there may be a more optimal tile size, our intent here is to show feasibility rather than develop a model intended for any specific use. Once an image is tiled, each tile is then assigned a probability of containing lobular inflammation and then automatically classified using a probability threshold as either containing lobular inflammation or not. The area of tiles classified as lobular inflammation versus the total area of the biopsy section is then computed to approximate the overall percentage of lobular inflammation. An identical process is also performed for quantifying the incidence of hepatocyte ballooning. Fig. 1 pictorially demonstrates the process of classifying tiles for hepatocyte ballooning.

Fig. 1.

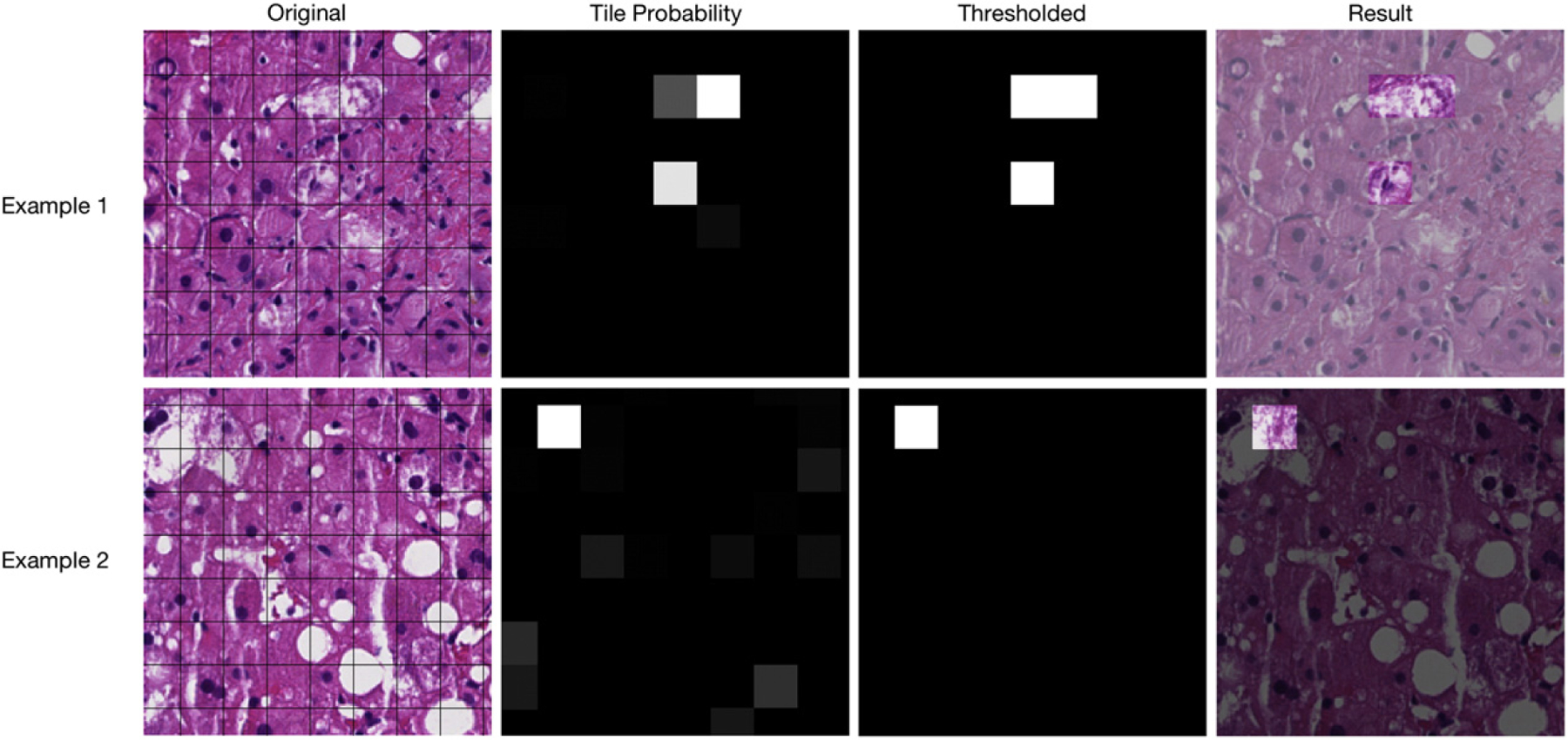
The process of identifying hepatocyte ballooning. Actual results and tiles are shown for 2 different biopsy sections. Original scanned images are first divided into tiles. Each tile is assigned a probability of containing hepatocyte ballooning (black is a probability of 0, middle gray is 50%, and white is 100%). Last, a threshold is determined for what probability is required for a tile to be automatically classified as hepatocyte ballooning.

Our study pathologists used a custom built Web-based Java (Oracle Corporation, Redwood City, CA) applet to manually annotate 138 areas of lobular inflammation and 48 areas of hepatocyte ballooning on biopsy images. In addition, study pathologists annotated 291 regions of fibrosis, 128 regions of portal inflammation, and 1969 types of white regions inclusive of macrosteatosis, central veins, portal veins, portal arteries, sinusoids, and bile ducts. Lobular inflammation and hepatocyte ballooning annotations are available as bounded polygons. These regions serve as the positive class for learning data in each of their respective learning tasks. It was also necessary to establish a negative class for learning. To accomplish this, 2 different types of negative regions were developed:

1. Regions, excluding the positive class of interest (ie, lobular inflammation or hepatocyte ballooning depending on the task). This includes macrosteatosis, central veins, portal veins, portal arteries, sinusoids and bile ducts, portal inflammation, fibrosis, and a generic “other” class.

2. Ten randomly selected tiles from each image. Although there is no guarantee that a randomly selected tile does not contain lobular inflammation (or hepatocyte ballooning), even in cases with high incidence of these lesions, there is a high probability that a randomly selected tile does not contain the lesion.

Because lobular inflammation and hepatocyte ballooning were annotated as bounded polygons, it was necessary to convert the polygon to a tile similar to what is used to quantify total incidence of lobular inflammation or hepatocyte ballooning. Fig. 2 shows the feature process with shaded areas representing that the tile image features are extracted for. The first is a tile centered on the polygon’s centroid (Fig. 2B). The second is a tile randomly offset from the polygon centroid (Fig. 2C). The motivation behind splitting polygon annotations into 2 different unique tiles is to first capture what a tile looks like should it fall directly on the lesion and second to capture what it looks like if only part of the feature falls within a tile.

Fig. 2.

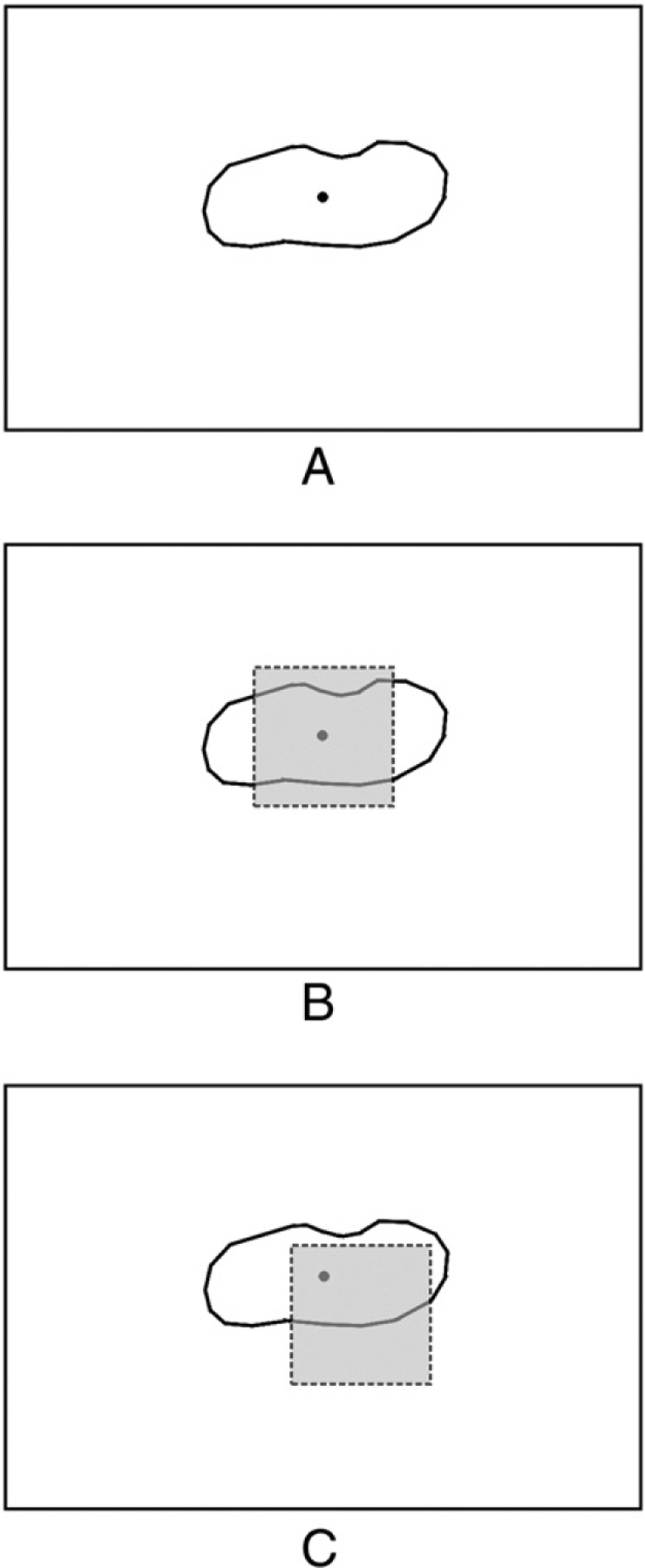
Features extracted for machine learning experiments to simulate the effects of image tiling for classification. A, A polygon annotation. B, Features are extracted for a tile centered on the polygon’s centroid. C, Features are extracted for a tile randomly offset from the polygon’s centroid.

For each positively and negatively labeled region, the types of features used by the classifier for learning are as follows:

• Texture — Texture and histogram statistics are computed for the gray scale region at each Σ level [19].

• Gray level co-occurrence matrix (GLCM) — The co-occurrence matrix is computed for pixels in each region [20].

• GLCM statistics — Statistical measures related to the GLCM, such as contrast and correlation.

• N-jet — For each Σ level in our scale representation, we compute the 2 jet of the region and extract related statistics [21].

• Nuclear density — For each region, the mean, min, max, and SD of nuclear density are used as features (see Discussion below).

Accuracy of the classifier is measured in 2 ways. First, a data set consisting of positive and negative learning tiles is analyzed using a 10-fold cross validation to gauge overall accuracy of the classifier [22]. Cross-fold validation entails taking our data set of positive and negative tiles and splitting the data set into 10 subsets and then running experiments, where a model is learned from data in 9 of the subsets and tested against data in the tenth. To reduce variability, the experiment is repeated 10 times with each subset serving as the “tenth” test subset exactly once. Results are then aggregated across all 10 experiments. Second, entire images are tiled into individual sections, and the total area of tiles classified as lobular inflammation or hepatocyte ballooning versus the total area of the biopsy section is computed and correlated with pathologists’ semiquantitative grades.

2.2. Nuclear density

Lobular inflammation is most visible by the presence of the nuclei of inflammatory cells. As inflammatory cells are smaller than other nearby cells, the number of nuclei in inflamed areas is higher. To quantify this, a measure was established called nuclear density. The nuclear density metric for a given pixel P is measured as the number of pixels within a fixed radius of P that is also part of a nucleus. We hypothesized this metric would serve as a good proxy for quantifying inflammation, as a higher concentration of inflammatory cells should yield a higher number of nuclei in a region and consequently a higher nuclear density.

The first step toward calculating nuclear density was to develop a process for isolating cell nuclei. Based on the hemotoxyphilic staining characteristics of nuclei, steps are taken to threshold nuclei from the biopsy images [23]. Once the nuclei are extracted, it is possible to compute nuclear density. Nuclear density for a pixel (x,y) and a surrounding radius r is defined as the following:

$$\text{Nuclear}\text{Density}\left(x,y,r\right)=\sum _{\left(i,r\right)\in R}f\left(i,j\right)$$

where R represents the set of pixels within radius r of (x, y) and f (i, j) = 1 if a pixel is identified as nuclar and 0 otherwise.

Using this equation for nuclear density, it is possible to calculate the nuclear density metric for all pixels in an image. Fig. 3 shows a pictorial representation of the nuclear density calculations for an image. The nuclear density image clearly shows a high concentration of nuclei in this case caused by portal inflammation, stromal cells, and other portal structures. Although nuclear density statistics for an entire tissue section correlates with pathologist lobular inflammation grades, better concordance is obtained using the nuclear density measure as a feature for supervised learning experiments.

Fig. 3.

Creation of a heat map representing the nuclear density.

2.3. Precision and recall

The model’s performance for detecting lobular inflammation and hepatocyte ballooning is measured by calculating the precision and recall (specificity) rates. Precision (also known as positive prediction rate) is a measure of the model’s positive predictive ability. Specifically, we are measuring what percentage of tiles classified as containing a given lesion type are correct. For both lobular inflammation and hepatocyte ballooning, precision is measured as the following:

$$\text{Precision}\text{=}\frac{\text{True-Positive}\text{Tile}\text{Classifications}}{\text{True-Positive}+\text{False-Positive}\text{Tile}\text{Classifications}}$$

Recall is the fraction of all positive tiles that are detected for each lesion type. For lobular inflammation, recall is the percentage of all tiles that actually contain lobular inflammation that is correctly identified. Mathematically, recall is measured as the following:

$$\text{Recall}\text{=}\frac{\text{True-Positive}\text{Tile}\text{Classifications}}{\text{True-Positive}+\text{False-Negative}\text{Tile}\text{Classifications}}$$

3. Results

3.1. Histologic characteristics of subjects

Pathologist scored hematoxylin and eosin liver biopsy slides from 47 (20 with normal liver histology and 27 with NAFLD of varying severity) of the 59 total patients in our data set according to the NAS scoring system [10]. The remaining 12 image scans were used only for annotations and machine learning. In the NAFLD group, 19 subjects had simple steatosis, and 8 had NASH. Fig. 4 shows the pathologist grading distribution of lobular inflammation and hepatocyte ballooning among the 47 patients. Across our data set, a total 138 areas of lobular inflammation and 48 areas of hepatocyte ballooning were annotated on biopsy images.

Fig. 4.

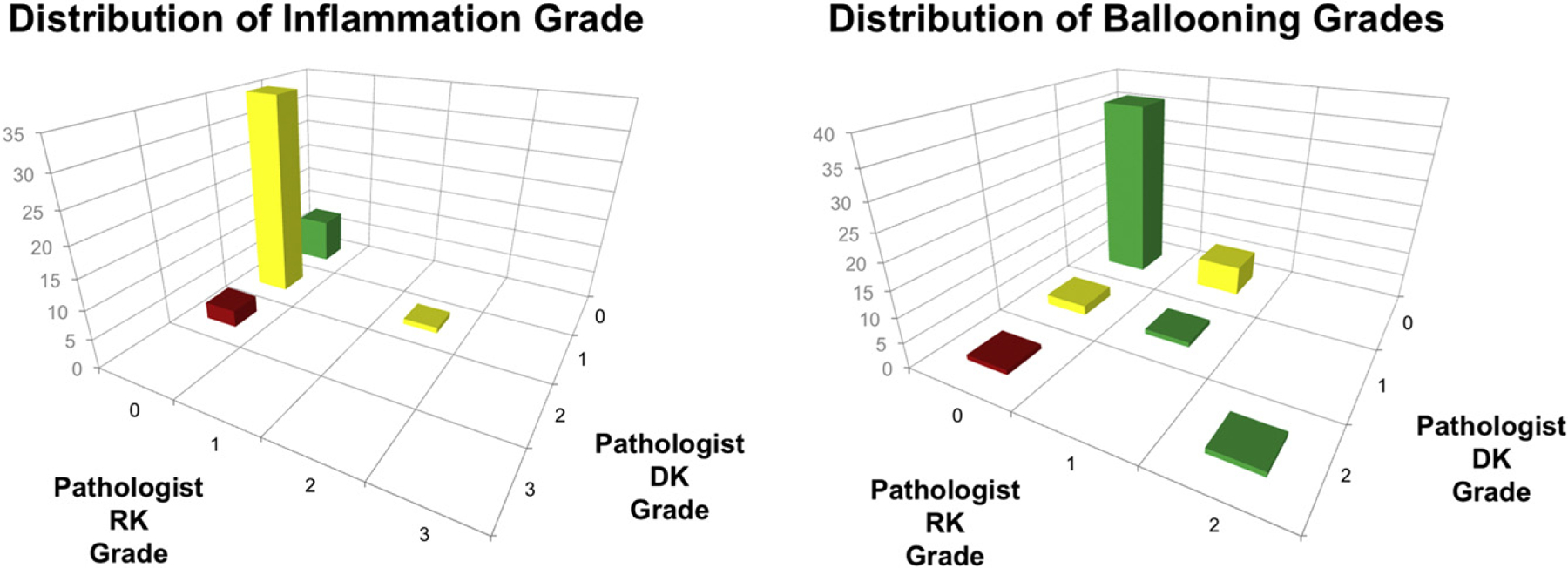
Distribution of pathologist grades for lobular inflammation and hepatocyte ballooning.

As shown in Fig. 4, our data set is skewed toward cases with minimal findings of lobular inflammation and hepatocyte ballooning. This does not present an immediate problem for our analysis, as our focus is on the precision and recall (sensitivity) of our model to correctly classify individual image tiles. Additional data would, however, be needed across the full spectrum of lobular inflammation and hepatocyte ballooning grades to draw more meaningful conclusions about the impact of false-positives and false-negatives on quantifying an entire tissue sample.

3.2. Automatic quantification of lobular inflammation

Evaluation of lobular inflammation classification was carried out using a 10-fold cross validation experiment.

It is important to point out that our data set of tiles is heavily skewed toward negative examples (tiles without lobular inflammation). Experiments were intentionally designed with a large skew toward tiles without lobular inflammation, as even in patients with high incidence of lobular inflammation, the number of tiles without lobular inflammation would significantly outnumber those with lobular inflammation. The model classifies lobular inflammation with a 0.70 precision and 0.49 recall (sensitivity).

In the cross validation experiment, 95.6% of tiles were classified correctly. This represents a statistically significant improvement over the baseline accuracy of 94.0% (P < .001) obtainable by always predicting not lobular inflammation. Although the accuracy metric is not a clinically meaningful, it demonstrates the improvements over naive baseline methods based on the predictive power of the model.

The recall-precision curve is shown in Fig. 5 along with the receiver operating characteristic (ROC) curve for the experiment. Examination of both of these curves to evaluate classifier performance is important, as our data set is largely skewed toward negative nonlobular inflammation examples [24]. Namely, with an ROC curve, the goal is to be toward the “upper left” of the curve, whereas with precision-recall curves, the goal is to be near the “upper right.” The ROC curve has a large area under the curve of 0.946 indicating the model has a strong ability to discriminate between tiles with lobular inflammation and those without.

Fig. 5.

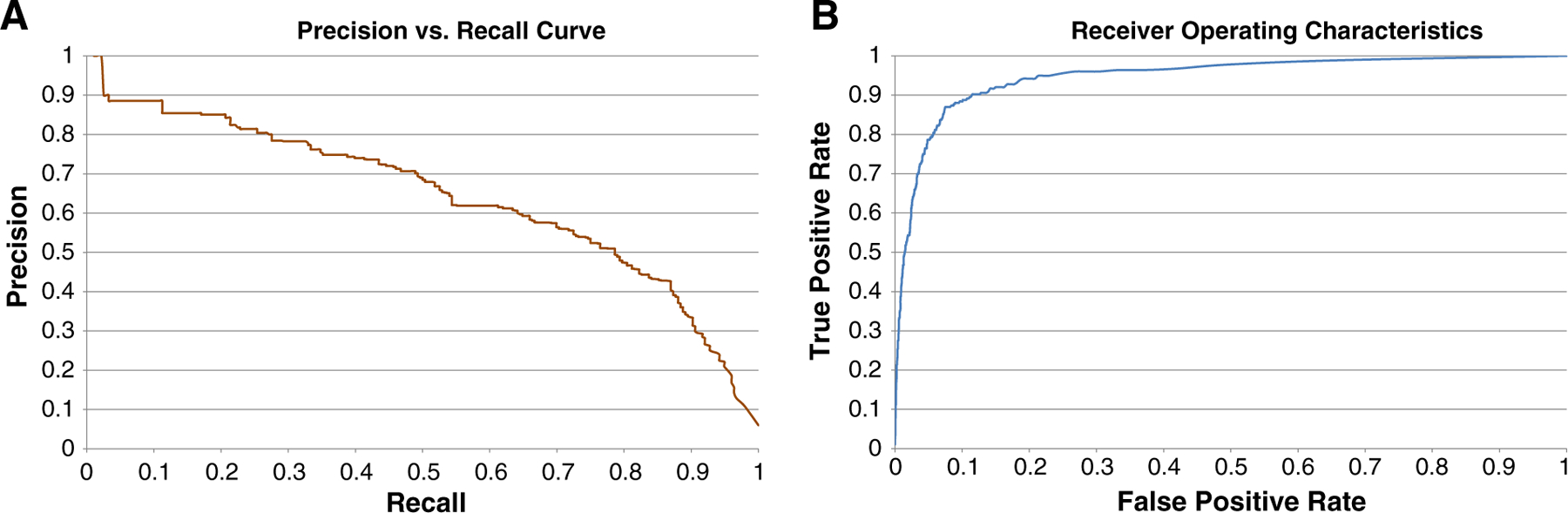
Precision versus recall (A) and ROC (B) curves for lobular inflammation.

Although the immediate focus of our research was the accurate identification of individual tiles of lobular inflammation, we also sought to gauge model performance by measuring how it compared with pathologist grades. For each patient, the overall percentage of tissue with lobular inflammation was calculated by taking the total area of tiles classified as having lobular inflammation and dividing by total tissue area. The motivation for this metric in our analysis is that tiles containing lobular inflammation would approximately represent 1 focus of lobular inflammation, and the metric would therefore be proportional to the number of lobular inflammation foci per unit area of tissue. To obtain percentage lobular inflammation, a different model was created for each patient using only training data from other patients, otherwise known as a leave-one-sample-out approach.

There is a general concordance between the modeled percent lobular inflammation and pathologist grade. The 4 patients who received the highest pathologist grades all rank near the top of the model. Conversely, those with the lowest grade score near the bottom (Fig. 6). Case FLE038 stands out as an outlier in the analysis. Examination of the case revealed that this tissue sample is considerably smaller by surface area compared with the other samples in our study. In fact, the FLE038 sample was approximately 75% smaller than the mean size of all samples. As evident in this case, a smaller tissue section would be far more susceptible to the impact of false-positive tiles. The overall Spearman rank correlation for the comparison between the model and average of the pathologists score is 0.452 with a P of 0.002.

Fig. 6.

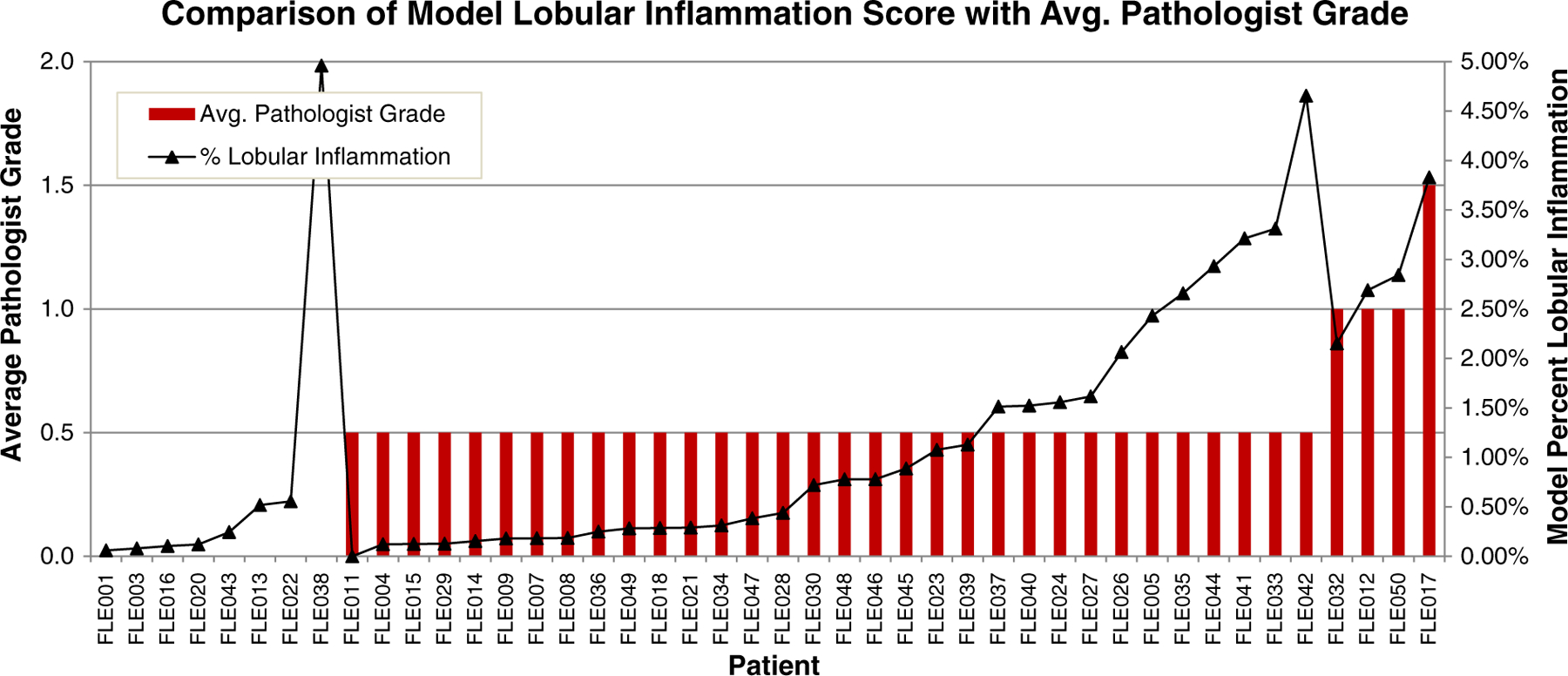
Comparison of average pathologist grade with model percentage for lobular inflammation.

3.3. Automatic quantification of hepatocyte ballooning

Similar to lobular inflammation, evaluation of the hepatocyte ballooning classifier was carried out using a 10-fold cross-validation experiment. The model classified hepatocyte ballooning with 0.91 precision and 0.54 recall. As with lobular inflammation, the data set is skewed heavily toward examples without hepatocyte ballooning. Based on this, a baseline accuracy of 97.9% would be obtainable simply by always predicting not hepatocyte ballooning for every tile. In our model, 98.9% of regions were correctly classified. This is a statistically significant (P < .001) improvement over the baseline method. As with lobular inflammation, the high level of accuracy has no clinical meaning, but it does demonstrate the predictive ability of the model and show a gain over a naive baseline method.

With the data set skewed heavily toward examples without hepatocyte ballooning, classifier performance must be evaluated through examination of both the recall-precision curve and the ROC curve (Fig. 7). The ROC curve shows that the model has a strong ability (area under the curve of 0.983) to discriminate between tiles as having or not having a ballooned hepatocytes. Similarly, the precision-recall curve shows a very high precision rate of 90% is obtainable while still recalling more than 50% of all tiles containing ballooned cells. This confirms that the model performs well despite the skew toward negative instances.

Fig. 7.

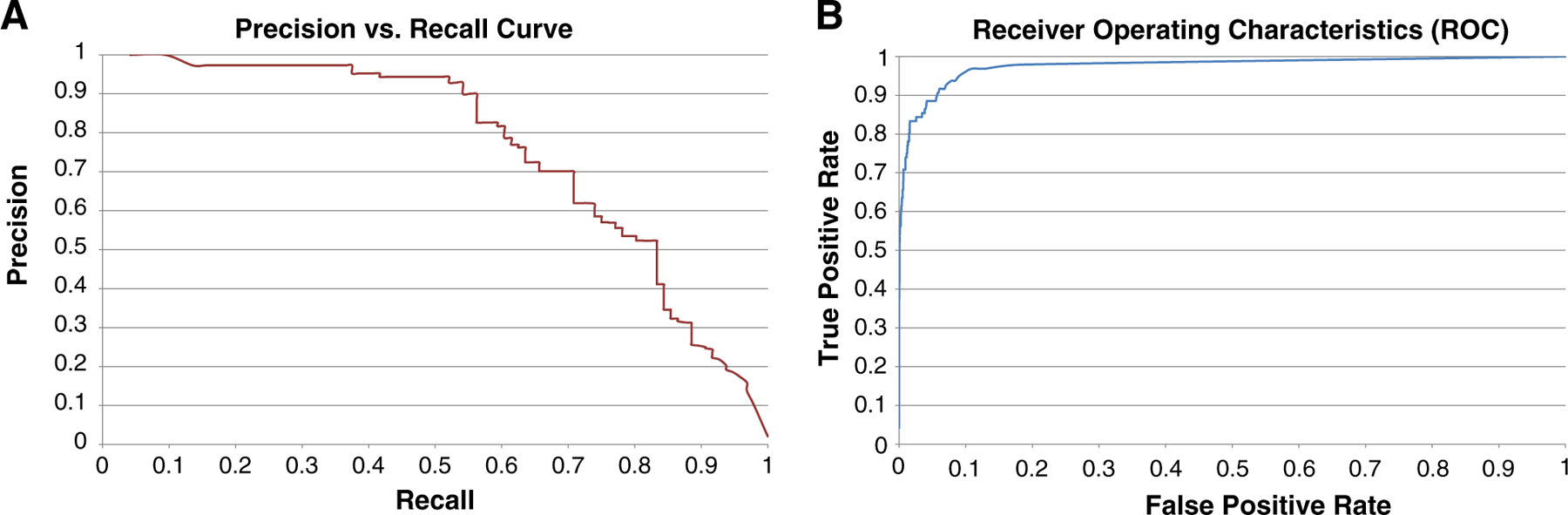
Precision versus recall (A) and ROC (B) curves for hepatocyte ballooning.

The next step in the analysis was to examine the concordance of a continuous metric derived from model predictions of hepatocyte ballooning with scores provided by our expert pathologists. For each patient, we took the surface area of tiles classified as containing hepatocyte ballooning and divided by total tissue area. This metric should be approximately equal to the percentage of tissue area containing hepatocyte ballooning if all tiles are correctly classified. The model obtained a Spearman rank correlation of 0.460 and a P = .001 with our pathologist grades.

Fig. 8 shows the results of each individual case. The chart shows a good relationship between the average pathologist grade and the computed percentage of ballooning with cases that received a higher pathologist grade typically receiving a higher computed percentage ballooning. This is particularly prevalent on the 2 cases that received the highest grades from study pathologists. FLE008 received a score of 2 from both R.K. and D.K., and FLE029 received a score of 0 and 2 from R.K. and D.K., respectively. These 2 patients received the second and third highest overall percentage ballooning from the model. Case FLE021 presents as an obvious outlier. Examination of the case more closely revealed the model was misclassifying glycogenosis as hepatocyte ballooning. There are several cases that received a grade 0 from both study pathologists but where the model detected some hepatocyte ballooning. These cases are all the result of 1 to 3 tiles in the entire image being false-positives. As the model had a far higher precision (positive predictive rate) than recall (sensitivity) of tiles, the impact of just a few false-positives is seen in these cases.

Fig. 8.

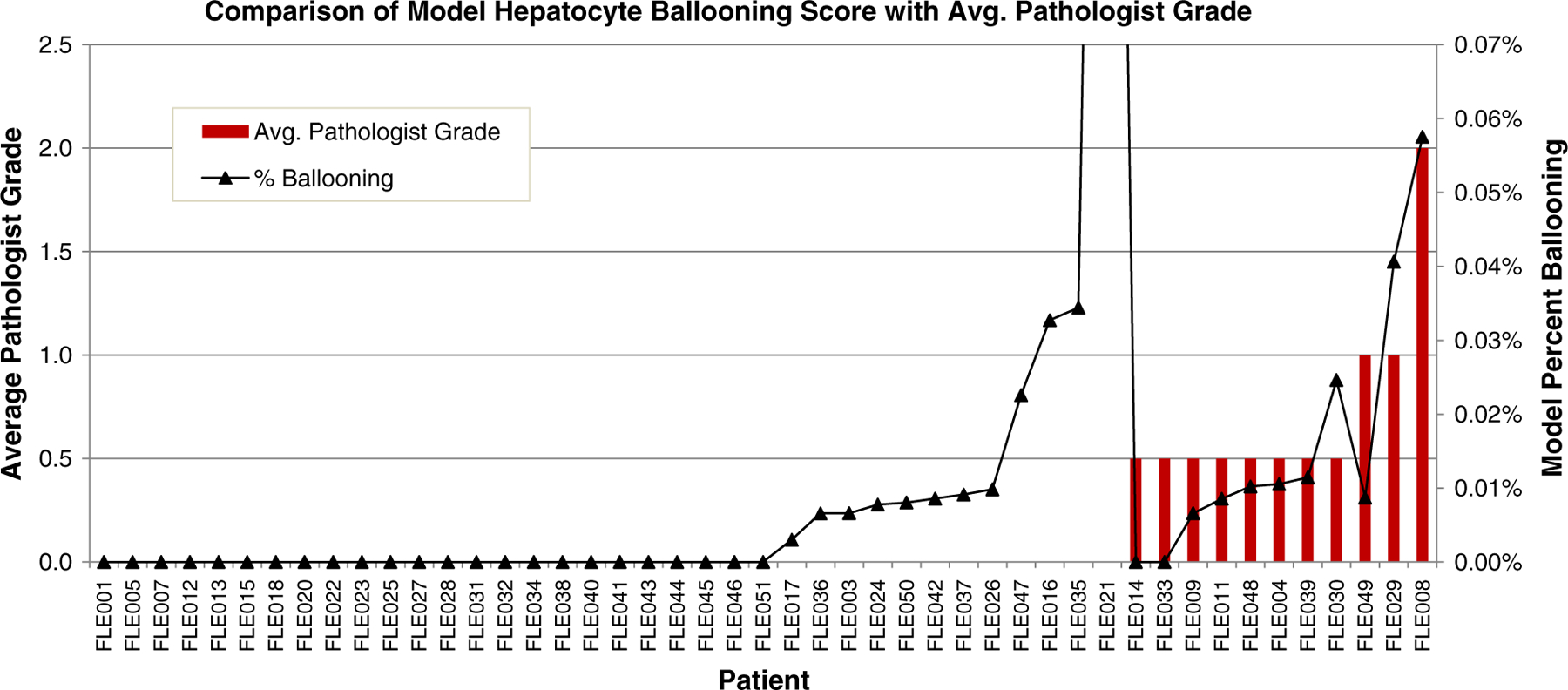
Comparison of average pathologist grade to model percentage for hepatocyte ballooning. Patient in FLE021 has glycogenosis, a condition similar in appearance to hepatocyte ballooning.

4. Discussion

The results of this study demonstrate that it is feasible to develop a system using supervised machine learning to automatically quantify 2 of the cardinal features needed to phenotype NAFLD, lobular inflammation, and hepatocyte ballooning. These findings are significant, as more accurate continuous measurements are more desirable than semiquantitative scores to measure NAFLD activity and quantify patient’s response to therapeutics used in trials or patient care.

Although the overall test statistics for correlation with pathologist grade is not as high as those our research group has shown for steatosis grading [12,18], it shows a general concordance between the model scores and pathologist grades and demonstrates the feasibility of such an approach. Although our ultimate goals are to replace discrete grades with continuous measures of lesions, we thought it important to show the general relationship between continuous measures and pathologist grade. It is important to note that the continuous metrics we used in our analysis are different than the metrics used by pathologists for semiquantitative grading. Both our continuous metric and pathologist grade should, however, increase with lesion prevalence. Correlation coefficients may also be of limited meaning, as we are correlating 47 continuous values to 4 discrete bins of average pathologist grade. Furthermore, our data set is skewed toward patients with minimal incidence of lobular inflammation and hepatocyte ballooning, so additional research is needed to examine model performance on more severe cases.

Because of the large skew in the data set of tiles without lobular inflammation or hepatocyte ballooning, a large increase in the number of false-positives (ie, incorrect predictions of lobular inflammation or hepatocyte ballooning) would have a minimal impact on the false-positive rate. This is because the metric is calculated as (false-positives)/(false-positives + true-negatives), and the true-negatives (correct predictions of not lobular inflammation or hepatocyte ballooning) in the denominator will dominate the metric. Based on this, one must also look at the recall-precision curve to evaluate the classifier. Specifically, the precision rate is not susceptible to the large skew of negative examples in the data set. Examination of the recall-precision curve shows predictions of lobular inflammation may be made with approximately 65% precision while still recalling 50%+ of all lobular inflammation. A decrease in recall rate should be an acceptable tradeoff for increased precision in this experiment, provided recall is consistent across patients from different laboratories, cutting and staining procedures, etc. In other words, if patient A has more lobular inflammation than patient B, identifying 50% of patients A’s lobular inflammation will still quantify to a higher score than recalling 50% of patient B’s.

Examination of the classifier results showed areas with glycogen and/or many fat droplets confusing the detection of hepatocyte ballooning. Example 2 of Fig. 1 shows such a case. In example 2, a ballooned cell adjacent to small fat droplets (upper left of Fig. 1, example 2) is correctly identified. However, another ballooned cell located in between the 3 steatotic cells with large fat droplets at the bottom right of the example is missed. The model assigned this tile a 23% chance of containing hepatocyte ballooning demonstrating that the model detected some ballooning activity; however, this fails to meet the threshold for being considered a positive detection of hepatocyte ballooning. Examination of the tile probabilities of example 2 also shows an overall increase in the probability of ballooning activity in tiles, where no ballooning exists presumably do to the appearance of the cytoplasm. Future models should include more training examples of both the positive and negative ballooning class in areas of glycogen or high steatotic cells incidence to afford the classifier a richer training set to make correct predictions in these areas. In practice, a tool could be developed that presorts tiles by probability allowing an interactive step, whereby a pathologist makes the final determination.

The continuous measures used herein are based on surface area of tiles with lesions divided by the total surface area of tissue. This metric can likely be improved by modifying the denominator. Specifically, rather than total surface area of tissue, it may be desirable to use total surface area of tissue excluding portal regions. This may more accurately reflect disease activity in the regions of primary interest for a given lesion.

No previous efforts have been published attempting to automatically quantify lobular inflammation and hepatocyte ballooning in images of scanned NAFLD liver biopsy sections. Automatic quantification of lobular inflammation and hepatocyte ballooning may provide a means for reducing the inherent human variability in semiquantitative assessment of NAFLD histology and provide pathologists a reliable tool for measuring NAFLD lesions on a continuum. Furthermore, continuous accurate measurement of NAFLD cardinal histologic features, such as steatosis, lobular inflammation, hepatocyte ballooning, and portal inflammation, is highly desirable in assessing NAFLD disease activity and monitoring response to therapeutic interventions in clinical trials.

In summary, this is the first study showing that automatic quantification of lobular inflammation and hepatocyte ballooning is feasible in digital images of liver biopsies from patients with NAFLD. We are currently conducting studies to optimize and validate the performance of our automated classifier and are also developing algorithms for automated quantification of hepatic fibrosis. These studies will include exhaustive annotation of unseen test cases, so the performance of our model may be reported on the ability to identify all lesions on a given tissue sample, rather than proxy metrics based on a subset of annotated tiles. These early findings offer promise for further development of automatic quantification as a potential aid to pathologists evaluating NAFLD biopsies in clinical practice and clinical trials.