TrajectoryNet: A Dynamic Optimal Transport Network for Modeling Cellular Dynamics

Abstract

It is increasingly common to encounter data from dynamic processes captured by static cross-sectional measurements over time, particularly in biomedical settings. Recent attempts to model individual trajectories from this data use optimal transport to create pairwise matchings between time points. However, these methods cannot model continuous dynamics and non-linear paths that entities can take in these systems. To address this issue, we establish a link between continuous normalizing flows and dynamic optimal transport, that allows us to model the expected paths of points over time. Continuous normalizing flows are generally under constrained, as they are allowed to take an arbitrary path from the source to the target distribution. We present TrajectoryNet, which controls the continuous paths taken between distributions to produce dynamic optimal transport. We show how this is particularly applicable for studying cellular dynamics in data from single-cell RNA sequencing (scRNA-seq) technologies, and that TrajectoryNet improves upon recently proposed static optimal transport-based models that can be used for interpolating cellular distributions.

1. Introduction

In data science we are often confronted with cross-sectional samples of time-varying phenomena, especially in biomedical data. Examples include health measurements of different age cohorts (Oeppen & Vaupel, 2002), or disease measurements at different stages of disease progression (Waddington, 1942). In these measurements we consider data that is sampled at multiple timepoints, but at each timepoint we have access only to a distribution (cross-section) of the population at that time. Extracting the longitudinal dynamics of development or disease from static snapshot measurements can be challenging as there are few methods of interpolation between distributions. Further exacerbating this problem is the fact that the same entities are often not measured at each time, resulting in a lack of point-to-point correspondences. Here, we propose to formulate this problem as one of unbalanced dynamic transport, where the goal is to transport entities from one cross sectional measurement to the next using efficient and smooth paths. Our main contribution is to establish a link between continuous normalizing flows (CNF) (Grathwohl et al., 2019) and dynamic optimal transport (Benamou & Brenier, 2000), allowing us to efficiently solve the transport problem using a Neural ODE framework (Chen et al., 2018a). To our knowledge, TrajectoryNet¹ is the first method to consider the specific paths taken by a CNF between distributions.

The continuous normalizing flow formulation allows us to generalize optimal transport to a series of distributions as in recent work (Chen et al., 2018b; Benamou et al., 2019). These works focus on the theoretical aspects of the problem, here focus on the computational aspects. This link allows us to smooth flows over multiple and possibly unevenly spaced distributions in high dimensions. This matches the setting of time series data from single-cell RNA sequencing.

Single-cell RNA sequencing (Macosko et al., 2015) is a relatively new technology that has made it possible for scientists to randomly sample the entire transcriptome, i.e., 20–30 thousand species of mRNA molecules representing transcribed genes of the cell. This technology can reveal detailed information about the identity of individual cells based on transcription factors, surface marker expression, cell cycle and many other facets of cellular behavior. In particular, this technology can be used to learn how cells differentiate from one state to another: for example, from embryonic stem cells to specified lineages such as neuronal or cardiac. However, hampering this understanding is the fact that scRNA-seq only offers static snapshots of data, since all cells are destroyed upon measurement. Thus it is impossible to monitor how an individual cell changes over time. Moreover, due to the expensive nature of this technology, generally only a handful of discrete timepoints are collected in measuring any transition process. TrajectoryNet is especially well suited to this data modality. Existing methods attempt to infer a trajectory within one timepoint (Haghverdi et al., 2016; Saelens et al., 2019; La Manno et al., 2018), or interpolate linearly between two timepoints (Yang & Uhler, 2019; Schiebinger et al., 2019), but TrajectoryNet can interpolate non-linearly using information from more than two timepoints. TrajectoryNet has advantages over existing methods in that it:

1. can interpolate by following the manifold of observed entities between measured timepoints, thereby solving the static-snapshot problem,

2. can create continuous-time trajectories of individual entities, giving researchers the ability to follow an entity in time,

3. forms a deep representational model of system dynamics, which can then be used to understand drivers of dynamics (gene logic in the cellular context), via perturbation of this deep model.

While our experiments apply this work specifically to cellular dynamics, these penalties can be used in many other situations where we would like to model dynamics based on cross-sectional population level data.

2. Background and Related Work

Optimal Transport.

Introduced originally by (Monge, 1781) and in modern form by (Kantorovich, 1942), the linear program formulation of static optimal transport (OT) has the relatively high cost of O(n³) for discrete measures. Recently, there have been a number of fast approximations using entropic regularization. Cuturi (2013) presented a parallel algorithm for the discrete case as an application of Sinkhorn’s algorithm (Sinkhorn, 1964). Recent effort approximates OT on subspaces (Muzellec & Cuturi, 2019) or even a single dimension (Kolouri et al., 2019). These efforts emphasis the importance to the field of obtaining fast OT algorithms. Another direction that has recently received increased attention is in unbalanced optimal transport where the goal is to relax the problem to add and remove mass (Benamou, 2003; Chizat et al., 2018; Liero et al., 2018; Schiebinger et al., 2019). While many efficient static optimal transport algorithms exist, and recently for the unbalanced case (Yang & Uhler, 2019), much less attention has focused on dynamic optimal transport, the focus of this work.

Dynamic Optimal Transport.

Another formulation of optimal transport is known as dynamic optimal transport. Benamou & Brenier (2000) showed how the addition of a natural time interpolation variable gives an alternative interpretation with links to fluid dynamics that surprisingly leads to a convex optimization problem. However, while solvers for the discretized dynamic OT problem are effective in low dimensions and for small problems they require a discretization of space into grids giving cost exponential in the dimension (See Peyré & Cuturi (2019) Chap. 7 for a good overview of this problem). One of our main contributions is to provide an approximate solver for high dimensional smooth problems using a neural network.

Single-cell Trajectories from a Static Snapshot.

Temporal interpolation in single-cell data started with solutions that attempt to infer an axis within one single time point of data cell “pseudotime” – used as a proxy for developmental progression – using known markers of development and the asynchronous nature of cell development (Trapnell et al., 2014; Bendall et al., 2014). An extensive comparison of 45 methods for this type of analysis gives method recommendations based on prior assumptions on the general structure of the data (Saelens et al., 2019). However, these methods can be biased and fail in a number of circumstances (Weinreb et al., 2018; Lederer & La Manno, 2020) and do not take into account experimental time.

Matching Populations from Multiple Time Points.

Recent methods get around some of these challenges using multiple timepoints (Hashimoto et al., 2016; Schiebinger et al., 2019; Yang & Uhler, 2019). However, these methods generally resort to matching populations between coarse-grained timepoints, but do not give much insight into how they move between measured timepoints. Often paths are assumed to minimize total Euclidean cost, which is not realistic in this setting. In contrast, the methods that estimate dynamics from single timepoints (La Manno et al., 2018; Bergen et al., 2019; Erhard et al., 2019; Hendriks et al., 2019) have the potential to give relatively accurate estimation of local direction, but cannot give accurate global estimation of distributional shift. A recent line of work on generalizing splines to distributions (Chen et al., 2018b; Benamou et al., 2019) investigates this problem from a theoretical perspective, but provides no efficient implementation.

With TrajectoryNet, we aim to unite these approaches into a single model combining in inferring continuous time trajectories from multiple timepoints, globally, while respecting local dynamics within a single timepoint.

3. Preliminaries

We provide an overview of static optimal transport, dynamic optimal transport (Benamou & Brenier, 2000), and continuous normalizing flows.

3.1. The Monge-Kantorovich Problem

We adopt notation from the standard text (Villani, 2008). For two probability measures μ, ν defined on $\mathcal{X}\subset {ℝ}^n$, let Π(μ, ν) denote the set of all joint probability measures on $\mathcal{X}\times \mathcal{X}$ whose marginals are μ and ν. Then the p-Kantorovich distance (or Wasserstein distance of order p)between μ and ν is

$$W{(\mu ,\nu )}_p≔{\left(\underset{\pi \in \Pi (\mu ,\nu )}{\text{inf}}{\int }_{\mathcal{X}\times \mathcal{Y}}d{(x,y)}^{p}d\pi (x,y)\right)}^{1/p},$$ (1)

where p ∈ [1, ∞). This formulation has led to many useful interpretations both in GANs and biological networks. For the entropy regularized problem, the Sinkhorn algorithm (Sinkhorn, 1964) provides a fast and parallelizable numerical solution in the discrete case. Recent work tackles computationally efficient solutions to the exact problem (Jambulapati et al., 2019) for the discrete case. However, for the continuous case solutions to the discrete problem in high dimensional spaces do not scale well. As the rate of convergence of the empirical Wasserstein metric between empirical measures $\widehat{\mu }$ and $\widehat{\nu }$ with bounded support is shown in (Dudley, 1969) to be

$$\mathbb{E}\left[\left|W_p\left({\widehat{\mu }}_n,{\widehat{\nu }}_n\right)-W_p(\mu ,\nu )\right|\right]=O(n^{-\frac{1}{d}})$$ (2)

where d is the ambient dimension. However, recent work shows that in high dimensions a more careful treatment that the rate depends on the intrinsic dimension not the ambient dimension (Weed & Bach, 2019). As long as data lies in a low dimensional manifold in ambient space, then we can reasonably approximate the Wasserstein distance. In this work we approximate the support of this manifold using a neural network.

3.2. Dynamic Optimal Transport

Benamou & Brenier (2000) defined and explored a dynamic version of Kantorovich distance. Their work linked optimal transport distances with dynamics and partial differential equations (PDEs). For a fixed time interval [t₀, t₁] with smooth enough, time dependent density and velocity fields, P(x, t) ≥ 0, $f(x,t)\in {ℝ}^d$, subject to the continuity equation

$${\partial }_{t}P+\nabla \cdot (Pf)=0$$ (3)

for t₀ < t < t₁ and $x\in {ℝ}^d$, and the conditions

$$P\left(\cdot ,t_0\right)=\mu ,P\left(\cdot ,t_1\right)=\nu$$ (4)

we can relate the squared L² Wasserstein distance to (P, f) in the following way

$$W{(\mu ,\nu )}_2^2=\underset{(P,f)}{\text{inf}}\left(t_1-t_0\right){\int }_{{ℝ}^d}{\int }_{t_0}^{t_1}P(x,t)|f(x,t){|}^2\mathit{\text{dtdx}}$$ (5)

In other words, a velocity field f(x, t) with minimum L² norm that transports mass at μ to mass at ν when integrated over the time interval is the optimal plan for an L² Wasserstein distance. The continuity equation is applied over all points of the field and asserts that no point is a source or sink for mass. The solution to this flow can be shown to follow a pressureless flow on a time-dependent potential function. Mass moves with constant velocity that linearly interpolates between the initial and final measures. For problems where interpolation of the density between two known densities is of interest, this formulation is very attractive. Existing computational methods for solving the dynamic formulation for continuous measures approximate the flow using a discretization of space-time (Papadakis et al., 2014). This works well in low dimensions, but scales poorly to high dimensions as the complexity is exponential in the input dimension d. We next give background on continuous normalizing flows, which we show can provide a solution with computational complexity polynomial in d.

3.3. Continuous Normalizing Flows

A normalizing flow (Rezende & Mohamed, 2015) transforms a parametric (usually simple) distribution to a more complicated one. Using an invertible transformation f applied to an initial latent random variable y with density P_y, We define x = f(y) as the output of the flow. Then by the change of variables formula, we can compute the density of the output x:

$$\text{log }{P}_x(\cdot )=\text{log }{P}_y(\cdot )-\text{log det}\frac{\partial f}{\partial y}$$ (6)

A large effort has gone into creating architectures where the log determinant of the Jacobian is efficient to compute (Rezende & Mohamed, 2015; Kingma et al., 2016; Papamakarios et al., 2017).

Now consider a continuous-time transformation, where the derivative of the transformation is parameterized by θ, thus at any timepoint t, $\frac{\partial x(t)}{\partial t}=f_{\theta }(x(t),t)$. At the initial time t₀, x(t₀) is drawn from a distribution P (x, t₀) which we also denote P_t0 (x) for clarity, and it’s continuously transformed to x(t₁) by following the differential equation f_θ(x(t), t):

$$\begin{gathered} x\left(t_1\right)=x\left(t_0\right)+{\int }_{t_0}^{t_1}{f}_{\theta }(x(t),t)dt,x\left(t_0\right)~P_{t_0}(x), \\ \text{log }{P}_{t_1}\left(x\left(t_1\right)\right)=\text{log }{P}_{t_0}\left(x\left(t_0\right)\right)-{\int }_{t_0}^{t_1}Tr\left(\frac{\partial f_{\theta }(x(t),t)}{\partial x(t)}\right)dt, \end{gathered}$$ (7)

where at any time t associated with every x through the flow can be found by following the inverse flow. This model is referred as continuous normalizing flows (CNFs) (Chen et al., 2018a). It can be likened to the dynamic version of optimal transport, where we model the measure over time rather than the mapping from $P_{t_0}$ to $P_{t_1}$

Unsurprisingly, there is a deep connection between CNFs and dynamic optimal transport. In the next section we exploit this connection and show how CNFs can be used to provide a high dimensional solution to the dynamic optimal transport problem with TrajectoryNet.

4. TrajectoryNet: Efficient Dynamic Optimal Transport

In this section, we first describe how to adapt continuous normalizing flows to approximate dynamic optimal transport in (Section 4.1). We then describe further adaptations for analysis of single-cell data in (Section 4.2) and finally provide training details in (Section 4.3).

4.1. Dynamic OT Approximation via Regularized CNF

Continuous normalizing flows use a maximum likelihood objective which can be equivalently expressed as a KL divergence. In TrajectoryNet we add an energy regularization to approximate dynamic OT. Dynamic OT is expressed with an optimization over flows with constraints at t₀ and t₁ (see eq. (4)). By relaxing this constraint to minimizing a divergence at t₁ CNFs can approximate dynamic OT.

For sufficiently large λ under constraint (3) this converges to the optimal solution in (5). This is encapsulated in the following theorem. See Appendix A.1 for proof.

Theorem 4.1. With time varying field $f(x,t):{ℝ}^d\times ℝ\to {ℝ}^d$ and density $P(x,t):{ℝ}^d\times ℝ\to {ℝ}^{+}$ such that ∫ P(x, t)dx = 1 for all t₀ ≤ t ≤ t₁ and subject to the continuity (3). There exists a sufficiently large λ such that

$$\begin{gathered} W{(\mu ,\nu )}_2^2=\left(t_1-t_0\right)\underset{(P,f)}{\text{inf}}\underset{x_0~\mu }{\mathbb{E}}\left[{\int }_{t_0}^{t_1}\Vert f(x(t),t){\Vert }^{2}dt\right] \\ +\lambda KL\left(P\left(\cdot ,t_1\right)\Vert \nu \right);s.t.P\left(\cdot ,t_0\right)=\mu \end{gathered}$$

Intuitively, a continuous normalizing flow with a correctly scaled penalty on the squared norm of f approximates the W₂ transport between μ and ν. Dynamic optimal transport can be thought of as finding a distribution over paths such that the beginnings of the paths match the source distribution, end of the path matches the target distribution, and the cost of the transport is measured by expected path length. Continuous normalizing flows relax the target distribution match with a KL-divergence penalty. When the KL-divergence is small then the constraint is satisfied. However, CNFs usually do not enforce the path length constraint, which we add using a penalty on the norm of f as defined by the Neural ODE. When we impose this penalty over uniformly sampled data, this is equivalent to penalizing the expected path length.

We can approximate the first part of this continuous time equation using a Riemann sum as ${\mathbb{E}}_{x_0~\mu }\left[{\int }_{t_0}^{t_1}\Vert f_{\theta }(x,t){\Vert }^{2}dt\right]={\sum }_{x~P_{t_0}}{\sum }_{i=t_0}^{t_1}\Delta t_i\Vert f_{\theta }(x,t){\Vert }^2$. This requires a forward integration using a standard ODE solver to compute as shown in Chen et al. (2018a). If we consider the case where the divergence is small, then this can be combined with the standard backwards pass for even less added computation. Instead of penalizing ||f_θ(x, t)||² on a forward pass, we penalize the same quantity on a backwards pass. Using the maximum likelihood and KL divergence equivalence, we obtain a loss

$$L(x)=-\text{log }p(x)+{\lambda }_e{\int }_t{\Vert f(x(t),t)\Vert }^2$$ (8)

Where the integral above is computed using an ODE solver. In practice, both a penalty on the Jacobian or additional training noise helped to get straight paths with a lower energy regularization λ_e. We found that a value of λ_e large enough to encourage straight paths, unsurprisingly also shortens the paths undershooting the target distribution. To counteract this, we add a penalty on the norm of the Jacobian of f as used in Vincent et al. (2010); Rifai et al. (2011). Since f represents the derivative of the path, this discourages paths with high local curvature, and can be thought of as penalizing the second derivative (acceleration) of the flow. Our energy loss is then

$$L_{\mathit{\text{energy}}}(x)={\lambda }_e{\int }_t{\Vert f(\tilde{x},t)\Vert }^2+{\lambda }_j{\int }_t{\Vert J_f(\tilde{x})\Vert }_F^2,$$ (9)

where ${\Vert J_f(x)\Vert }_F^2$ is the Frobenius norm of the Jacobian of f. Comparing Figure 2(e) to (d) we demonstrate the effect of this regularization. Without energy regularization TrajectoryNet paths follow the data. However, with energy regularization we approach the paths of the optimal map. TrajectoryNet solution biases towards undershooting the target distribution. Our energy loss gives control over how much to penalize indirect, high energy paths.

Figure 2.

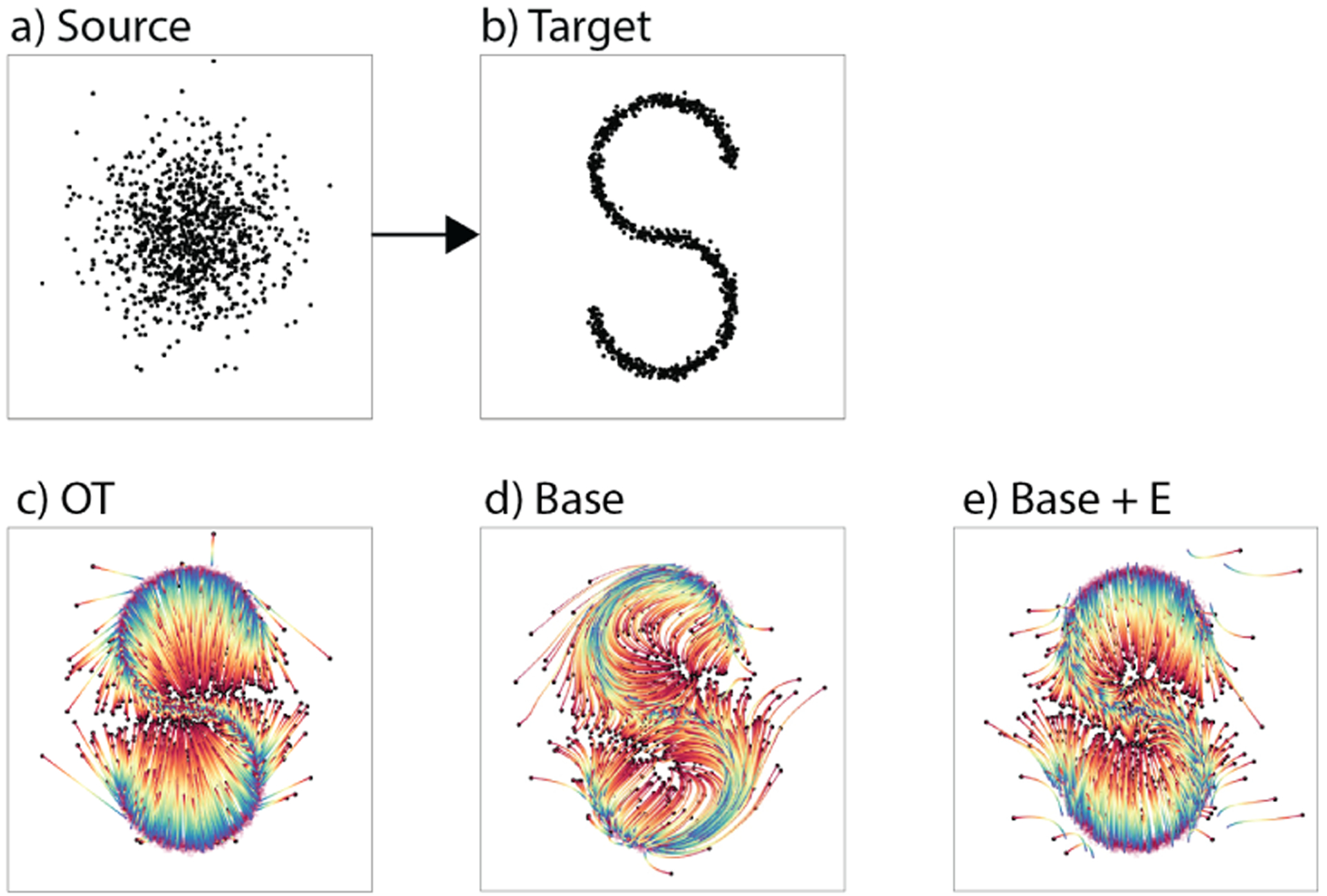
Transporting a Gaussian (a) to an S-curve (b) via (c) static optimal transport, (d) Base TrajectoryNet without regularization follows density (e) TrajectoryNet with energy regularization demonstrates more straight paths similar to OT.

Optimal transport is traditionally performed between a source and target distribution. Extensions to a series of distributions is normally done by performing optimal transport between successive pairs of distributions as in Schiebinger et al. (2019). This creates flows that have discontinuities at the sampled times, which may be undesirable when the underlying system is smooth in time as in biological systems. The dynamic model approximates dynamic OT for two timepoints, but by using a single smooth function to model the whole series the flow becomes the minimal cost smooth flow over time.

4.2. Further Adaptation for Single-Cell Trajectories

Up to this point we have shown how to perform dynamic optimal transport in high dimensions with a regularized CNF. We now introduce priors needed to mimic cellular systems that are characterized by growth/death rather than just transport, endowed with a manifold structure, and knowledge of local velocity arrows. Similar priors may also be applicable to other data types. For example in studying the dynamics of a disease, people may be newly infected or cured, we may have knowledge on acceptable transition states, indicating a density penalty, or visits may be clustered such as in a hospital stay so we may have estimates of near term patient trends, indicating the use of velocity priors. To enforce these priors we add corresponding regularizations listed below:

1. A growth rate regularization that accommodates unbalanced transport, described in Section 4.2.1.

2. A density-based penalty which encourages interpolations that lie on dense regions of the data. Often data lies on a low-dimensional manifold, and it is desirable for paths to follow this manifold at the cost of higher energy (See Section 4.2.2 for details).

3. A velocity regularization where we enforce local estimates of velocity at measured datapoints to match the first time derivative of cell state change. (See Section 4.2.3 for details).

These regularizations are summarized in a single loss function defined as

$$\begin{gathered} L_T=\underset{\text{Dynamic OT}}{\underbrace{\stackrel{\text{Normalizing Flow}}{\overbrace{\sum _{i=1}^k-\text{log }{P}_{t_i}(x_{t_i})}}+L_{\mathit{\text{energy}}}}} \\ +\underset{\text{Biological priors}}{\underbrace{L_{\mathit{\text{density}}}+L_{\mathit{\text{velocity}}}+L_{\mathit{\text{growth}}}}} \end{gathered}$$ (10)

4.2.1. Allowing Unbalanced Optimal Transport

We use a simple and computationally efficient method that adapts discrete static unbalanced optimal transport to our framework in the continuous setting. This is a necessary extension but is by no means a focus of our work. While we could also apply an adversarial framework, we choose to avoid the instabilities of adversarial training and use a simple network trained from the solution to the discrete problem. We train a network $G(x,t):{ℝ}^d\times [0,1]\to {ℝ}^{+}$, which takes as input a cell state and time pair and produces a growth rate of a cell at that time. This is trained to match the result from discrete optimal transport. For further specification see Appendix B. We then fix weights of this network and modify the way we integrate mass over time to

$$\begin{gathered} \text{log }{M}_{t_i}(x)=\text{log }{M}_{t_{i-1}}(x)-{\int }_{t_{i-1}}^{t_i}Tr\left(\frac{\partial f_{\theta }(x(t),t)}{\partial x(t)}\right)dt \\ +\text{log }G\left(x_{t_{i-1}},t_{i-1}\right) \end{gathered}$$ (11)

We note that adding growth rate regularization in this way does not guarantee conservation of mass. We could normalize M(x) to be a probability distribution during training, e.g., as $P(x)=M(x)/{\sum }_{x\in {ℝ}^d}M(x)$. However, this now requires an integration over ${ℝ}^d$, which is too computationally costly. Instead, we use the equivalence of the maximum likelihood formulation over a fixed growth function g and normalize it after the network is trained.

4.2.2. Enforcing Transport on a Manifold

Methods that display or perform computations on the cellular manifold often include an implicit or explicit way of normalizing for density and model data geometry. PHATE (Moon et al., 2019) uses scatter plots and adaptive kernels to display the geometry. SUGAR (Lindenbaum et al., 2018) explicitly models the data geometry. We would like to constrain our flows to the manifold geometry but not to its density. We penalize the flow such that it is always close to at least a few measured points across all timepoints.

$$L_{\mathit{\text{density}}}\left(x,t_d\right)=\sum _k\text{max}\left(0,\text{min}-\text{k}\left(\left\{\Vert x\left(t_d\right)-z\Vert :z\in \mathcal{X}\right\}\right)-h\right)$$ (12)

This can be thought of as a loss that penalizes points until they are within h Euclidean distance of their k nearest neighbors. We use h = 0.1 and k = 5 in all of our experiments. We evaluate L_density on an interpolated time t_d ∈ (t₀, t_k) every batch.

4.2.3. Conforming to known Velocity

Often it is the case where it is easy to measure direction of change in a short time horizon, but not have good predictive power at the scale of measured timesteps. In health data, we can often collect data from a few visits over a short time horizon estimating the direction of a single patient in the near future. In single-cell data, RNA-velocity (La Manno et al., 2018; Bergen et al., 2019) provides an estimates $\widehat{dx/dt}$ at every measured cell. We use these measurements to regularize the direction of flow at every measured point. Our regularization requires evaluating f(x, t) periodically at every measured cell adding the regularization:

$$\begin{gathered} L_{\mathit{\text{velocity}}}(x,t,\widehat{dx/dt})=\text{cosine-similarity}(f(x,t),\widehat{dx/dt}) \\ =\frac{f(x,t)\cdot \widehat{dx/dt}}{\Vert f(x,t)\Vert \widehat{dx/dt}} \end{gathered}$$ (13)

This encourages the direction of the flow at a measured point to be similar to the direction of local velocity. This ignores the magnitude of the estimate, and only heeds the direction. While RNA-velocity provides some estimate of relative speed, the vector length is considered not as informative, as it is unclear how to normalize these vectors in a system specific way (La Manno et al., 2018; Bergen et al., 2019). We note that while current estimates of velocity can only estimate direction, this does not preclude future methods that can give accurate magnitude estimates. L_velocity can easily be adapted to take magnitudes into account by considering L₂ similarity for instance.

4.3. Training

For simplicity, the neural network architecture of TrajectoryNet consists of three fully connected layers of 64 nodes with leaky ReLU activations. It takes as input a cell state and time and outputs the derivative of state with respect to time at that point. To train a continuous normalizing flow we need access to the density function of the source distribution. Since this is not accessible for an empirical distribution we use an additional Gaussian at t₀, defining $P_{t_0}(\cdot )=\mathcal{N}(0,1)$, the standard Gaussian distribution, where P_t(x) is the density function at time t.

For a training step we draw samples $x_{t_i}~{\mathcal{X}}_{t_i}$ for i ∈ {1, …, k} and calculate the loss with a single backwards integration of the ODE. In the following sections we will explain how adding the individual penalty terms achieve regularized trajectories. While there are a number of ways to computationally approximate these quantities, we use a parallel method to iteratively calculate the log $P_{t_i}$ based on log $P_{t_{i-1}}$. To make a backward pass through all timepoints we start at the final timepoint, integrate the batch to the second to last timepoint, concatenate these points to the samples from the second to last timepoint, and continue till t₀, where the density is known for each sample. We note that this can compound the error especially for later timepoints if k is large or if the learned system is stiff, but gives significant speedup during training.

To sample from $P_{t_i}$ we first sample ${\widehat{x}}_{t_0}~P_{t_0}$ then use the adjoint method to perform the integration ${\widehat{x}}_{t_i}={\widehat{x}}_{t_0}+{\int }_{t_0}^{t_i}{f}_{\theta }(x(t),t)dt;x(0)={\widehat{x}}_{t_0}$.

5. Experiments

All experiments were performed with the TrajectoryNet framework with a network of consisting of three layers with LeakyReLU activations. Optimization was performed on 10,000 iterations of batches of size 1,000 using the dopri5 solver (Dormand & Prince, 1980) with both absolute and relative tolerances set to 1 × 10⁻⁵ and the ADAM optimizer (Kingma & Ba, 2015) with learning rate 0.001, and weight decay 5 × 10⁻⁵ as in (Grathwohl et al., 2019). We evaluate using three TrajectoryNet models with different regularization terms. The Base model refers to a standard normalizing flow. +E adds L_energy, +D adds L_density,+V adds L_velocity, and +G adds L_growth.

Comparison to Existing Methods.

Since there are no ground truth methods to calculate the trajectory of a single cell we evaluate our model using interpolation of held-out timepoints. We leave out an intermediary timepoint and measure the Kantorovich-distance also known as the earth mover’s distance (EMD) between the predicted and held-out distributions. For EMD lower is more accurate. We compare the distribution interpolated by TrajectoryNet with four other distributions. The previous timepoint, the next timepoint, a random timepoint and the McCann interpolant in the discrete OT solution as used in (Schiebinger et al., 2019).

5.1. Artificial Data

For artificial data where we have known paths, we can measure the mean squared error (MSE) predicted by the model based on the first timepoint. Here we leave out the middle timepoint t_1/2 for training then calculate the MSE between the predicted point at time t_1/2 and the true point at t_1/2 for 5000 sampled trajectories. This gives a measure of how accurately we can model simple dynamical systems.

We first test TrajectoryNet on two datasets where points lie on a 1D manifold in 2D with Gaussian noise (See Figure 4). First two half Gaussians are sampled with means zero and one in one dimension. These progressions are then lifted onto curved manifolds in two dimensions either an arch or a tree mimicking a differentiating system where we have two sampled timepoints that have some overlap. Table 1 shows the Wasserstein distance (EMD) and the mean squared error for different interpolation methods between the interpolated distribution at t_1/2 and the true interpolated distribution at t_1/2. Because optimal transport considers the shortest Euclidean distance, the base model and OT methods follow the lowest energy path, which is straight across. With density regularization or velocity regularization TrajectoryNet learns paths that follow the density manifold. Figure 3 and Figure S2 demonstrate how TrajectoryNet with density or velocity regularization learns to follow the manifold.

Figure 4.

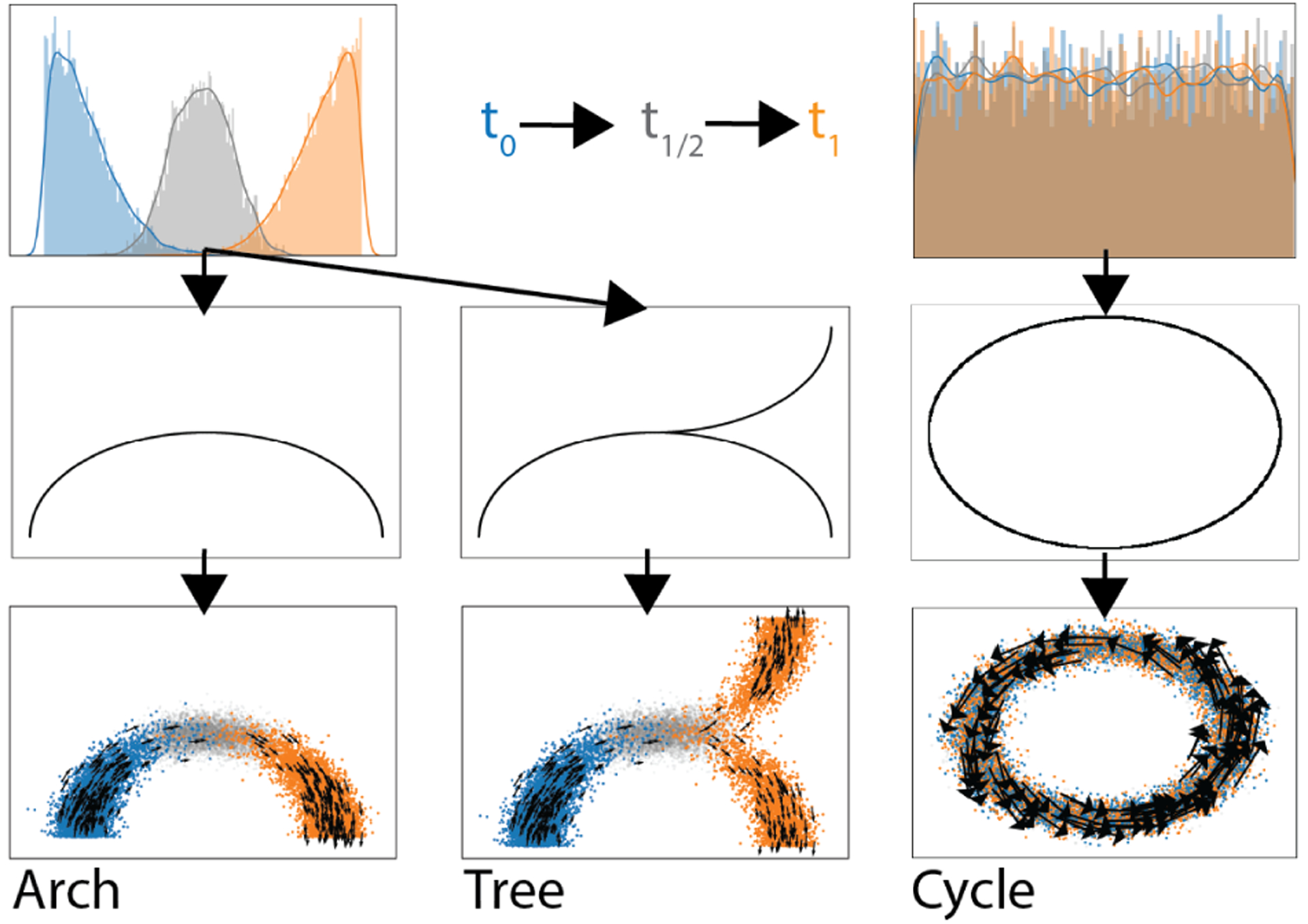
A 1D distribution of data over time embedded in two dimensions along a smooth manifold. On a single branch (left), with a tree structure (center), and circle (right).

Table 1.

Shows the Wasserstein distance EMD and MSE for artificial datasets between the left out timepoint and the predicted points for our two generated datasets. Mean over 3 seeds.

	EMD			MSE
	Arch	Cycle	Tree	Arch	Cycle	Tree
Base	0.691	0.037	0.490	0.300	0.190	0.218
Base + D	0.607	0.049	0.373	0.236	0.191	0.145
Base + V	0.243	0.033	0.143	0.107	0.068	0.098
Base + D + V	0.415	0.034	0.252	0.156	0.081	0.132
OT	0.644	0.032	0.492	0.252	0.192	0.196
prev	1.086	0.035	1.092	0.652	0.192	0.666
next	1.090	0.035	1.068	0.659	0.192	0.689
rand	0.622	0.406	0.420	0.243	0.346	0.161

Figure 3.

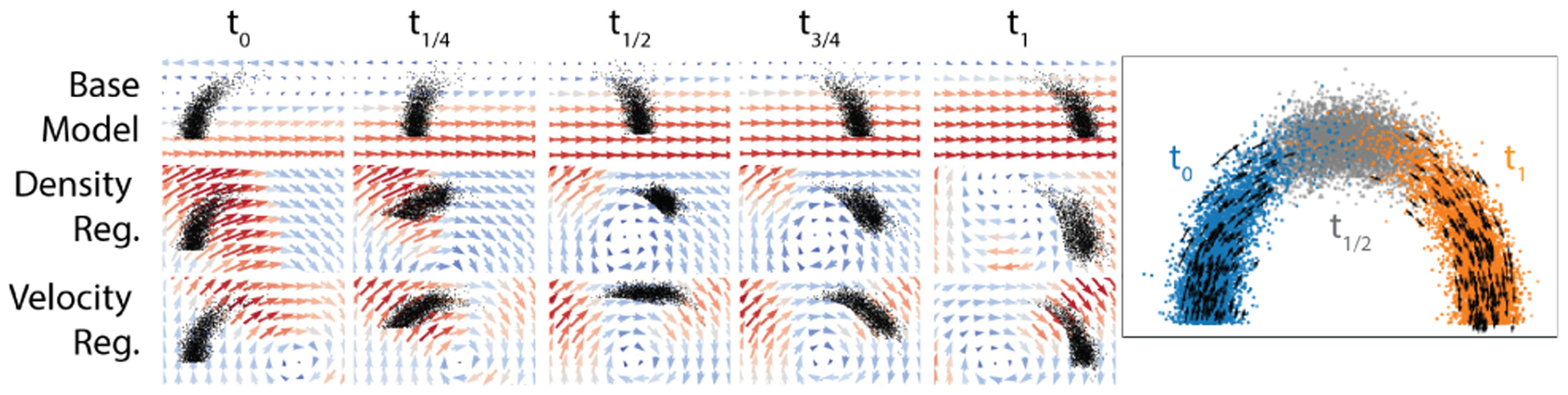
Density regularization or velocity regularization can be used to follow a 1D manifold in 2D.

A third artificial dataset shows the necessity of using velocity estimates for some data. Here we have an unchanging distribution of points distributed uniformly over the unit circle, but are traveling counterclockwise at π/5 radians per unit time. This is similar to the cell-cycle process in adult systems. Without velocity estimates it is impossible to pick up this type of dynamical system. This is illustrated by the MSE of the cycle dataset using velocity regularization in Table 1.

5.2. Single-Cell Data

We run our model on 5D PCA due to computational constraints, but note that computation time scales roughly linearly with dimension for our test cases (See Appendix C), which is consistent to what was found in Grathwohl et al. (2019). Since there are no ground truth trajectories in real data, we can only evaluate using distributional distances. We do leave-one-out validation, training the model on all but one of the intermediate timepoints then evaluating the EMD between the validation data and the model’s predicted distribution. We evaluate and compare our method on two single-cell RNA sequencing datasets.

Mouse Cortex Data.²

The first dataset has structure similar to the Arch toy dataset. It consists of cells collected from mouse embryos at days E12.5, E14.5, E16, and E17.5. In Figure 6(d) we can see at this time in development of the mouse cortex the distribution of cells moves from a mostly neural stem cell population at E12.5 to a fairly developed and differentiated neuronal population at E17.5 (Cotney et al., 2015; Katayama et al., 2016). The major axis of variation is neuron development. Over the 4 timepoints we have 2 biological replicates that we can use to evaluate variation between animals. In Table 2, we can see that TrajectoryNet outperforms baseline models, especially when adding density and velocity information. The curved manifold structure of this data, and gene expression data in general means that methods that interpolate with straight paths cannot fully capture the structure of the data. Since TrajectoryNet models full paths between timepoints, adding density and velocity information can bend the cell paths to follow the manifold utilizing all available data rather than two timepoints as in standard optimal transport.

Figure 6.

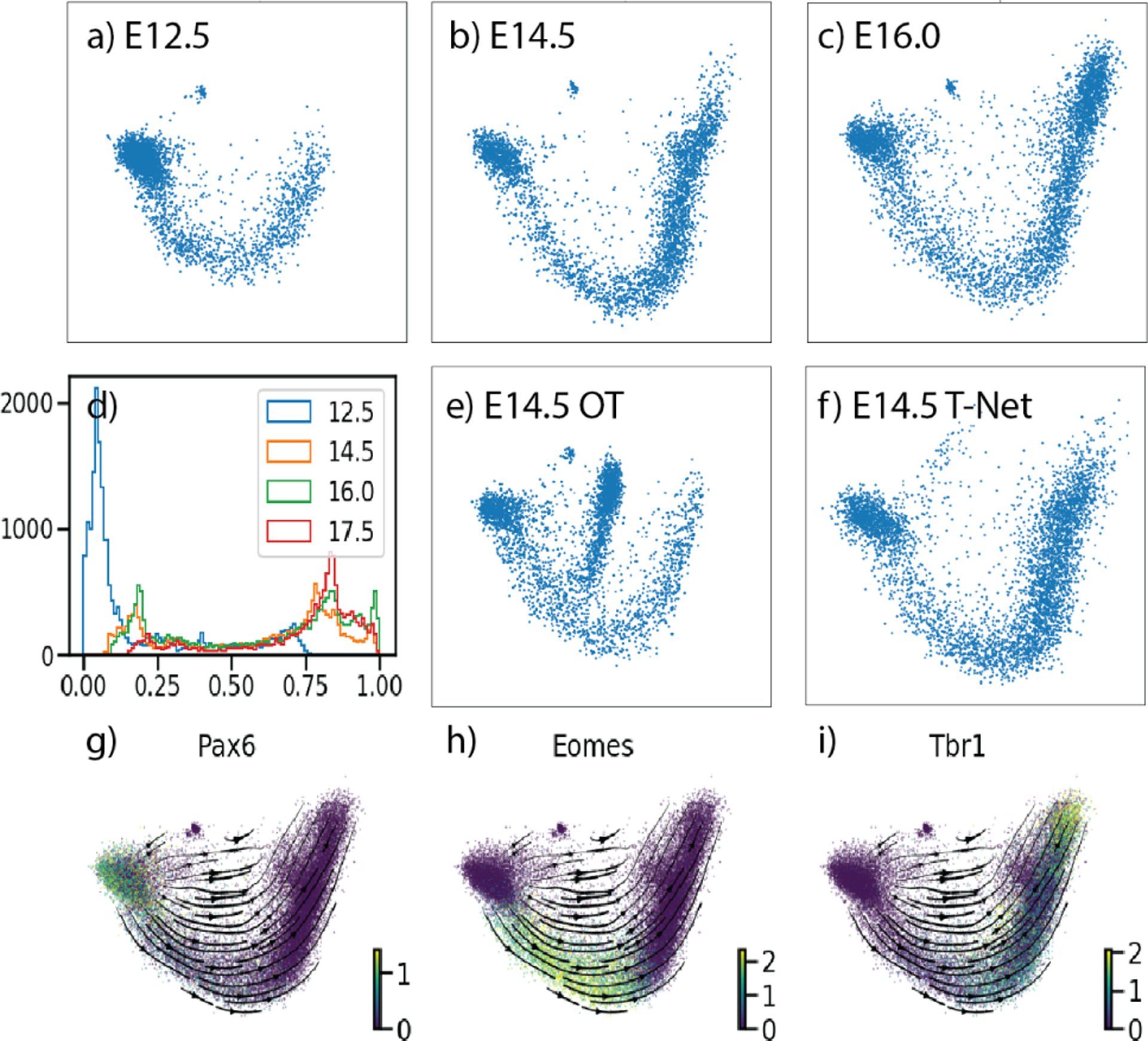
Shows the first 2 PCs of the mouse cortex dataset. (a-c) show the distributions for the first three timepoints. (d) shows the distribution of cells over PC1. the interpolated points for E14.5 using (e) static OT, and (f) TrajectoryNet with density regularization. (g-i) shows expression of three markers of early (Pax6) mid (Eomes) and late (Tbr1) stage neurons.

Table 2.

Shows the Wasserstein distance between the left out timepoint and the predicted distribution for various methods on a 4 timepoint mouse embryo cortex dataset. Mean and standard deviation over 3 seeds.

	rep1	rep2	mean
Base	0.888 ± 0.07	0.905 ± 0.06	0.897 ± 0.06
Base + D	0.882 ± 0.03	0.895 ± 0.03	0.888 ± 0.03
Base + V	0.900 ± 0.09	0.898 ± 0.10	0.899 ± 0.10
Base + D + V	0.851 ± 0.08	0.866 ± 0.07	0.859 ± 0.07
OT	1.098	1.095	1.096
prev	1.628	1.573	1.600
next	1.324	1.391	1.357
rand	1.333	1.288	1.311

Embryoid body Data.

Next, we evaluate on a differentiating Embryoid body scRNA-seq time course. Figure 7 shows this data projected into two dimensions using a non-linear dimensionality reduction method called PHATE (Moon et al., 2019). This data consists of 5 timepoints of single cell data collected in a developing human embryo system (Day 0-Day 24). See Figure 5 for a depiction of the growth rate. Initially, cells start as a single stem cell population, but differentiate into roughly 4 cell precursor types. This gives a branching structure similar to our artificial tree dataset. In Table 3 we show results when each of the three intermediate timepoints are left out. In this case velocity regularization does not seem to help, we hypothesis this has to do with the low unspliced RNA counts present in the data (See Figure S3). We find that energy regularization and growth rate regularization help only on the first timepoint, and that density regularization helps the most overall.

Figure 7.

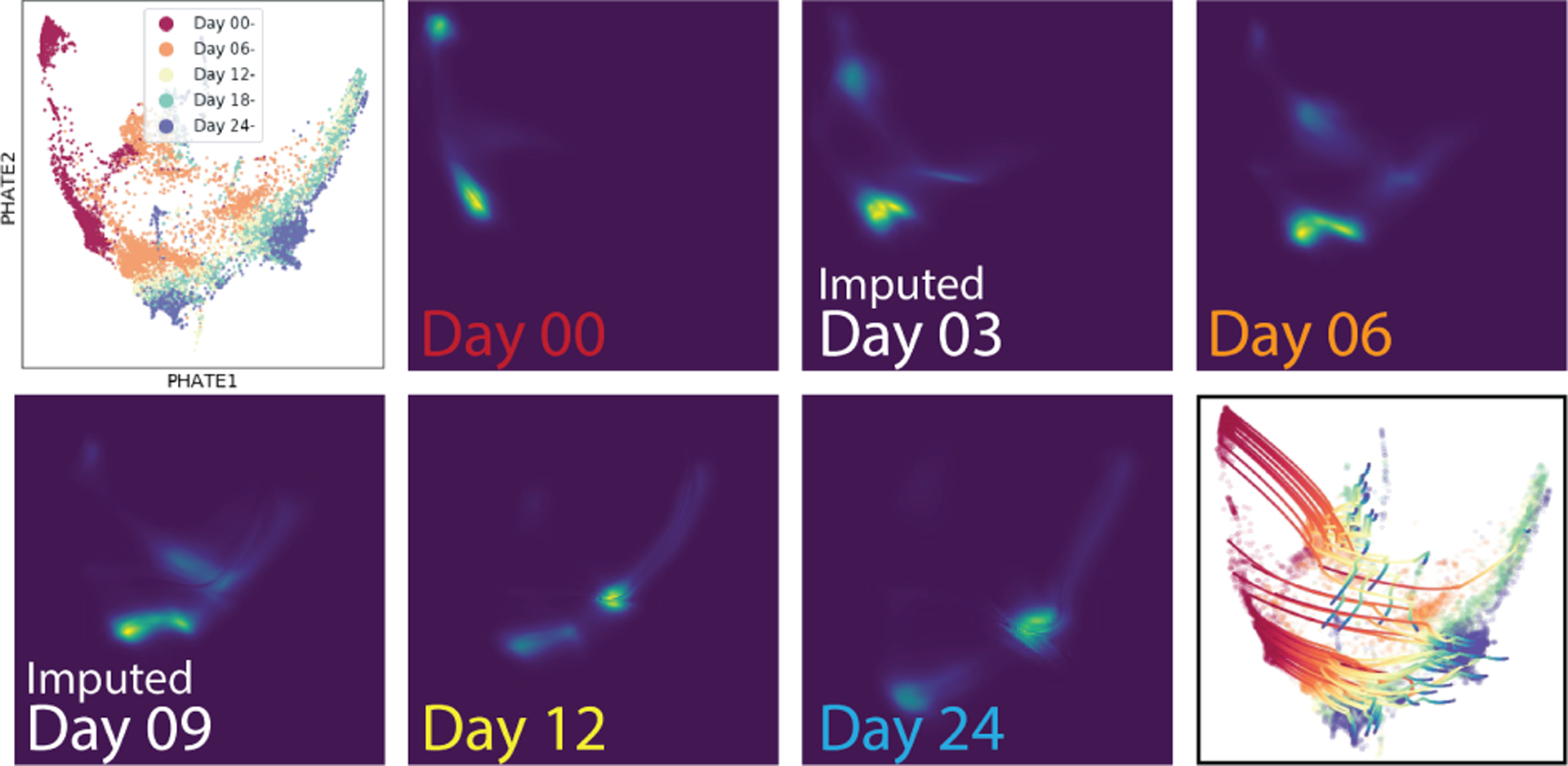
Shows the Embryoid body dataset projected into 2D with PHATE (Moon et al., 2019) with paths and densities imputed using TrajectoryNet.

Figure 5.

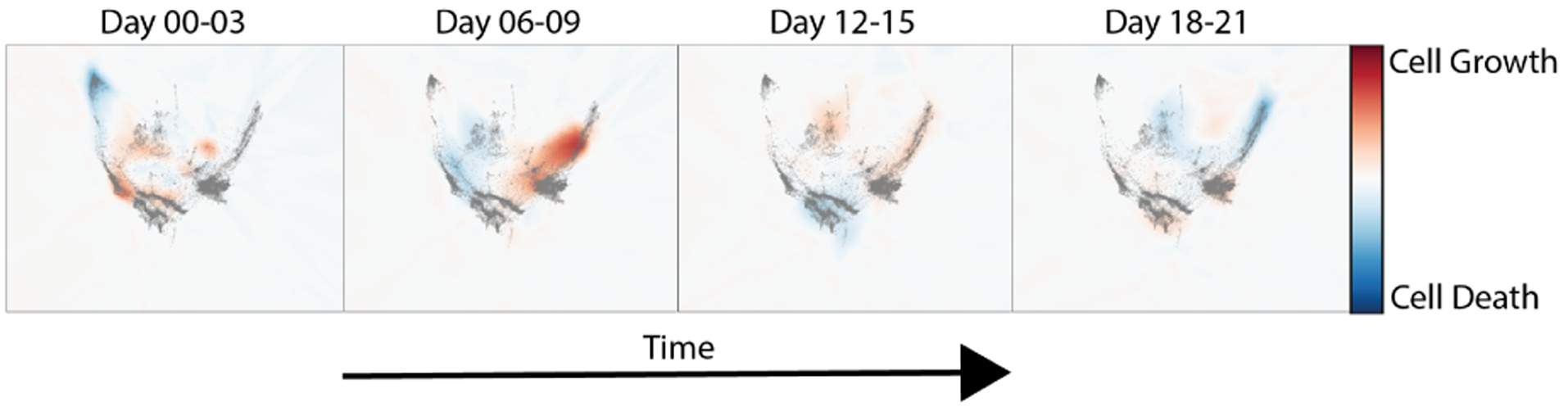
Cell growth model learned on Embryoid Body Data (Moon et al., 2019)

Table 3.

Shows the Wasserstein distance (EMD) between the left out timepoint and the predicted distribution for various methods on the 5 timepoint Embryoid body dataset.

	t=1	t=2	t=3	mean
Base	0.764	0.811	0.863	0.813
Base + D	0.759	0.783	0.811	0.784
Base + V	0.816	0.839	0.865	0.840
Base + D + V	0.930	0.806	0.810	0.848
Base + E	. 0.737	0.896	0.842	0.825
Base + G	0.700	0.913	0.829	0.814
OT	0.791	0.831	0.841	0.821
prev	1.715	1.400	0.814	1.309
next	1.400	0.814	1.694	1.302
rand	0.872	1.036	0.998	0.969

We can also project trajectories back to gene space. This gives insights into when populations might be distinguishable. In Figure 8, we demonstrate how TrajectoryNet can be projected back to the gene space. We sample cells from the end of the four main branches, then integrate TrajectoryNet backwards to get their paths through gene space. This recapitulates known biology in Moon et al. (2019). See appendix D for a more in-depth treatment.

Figure 8.

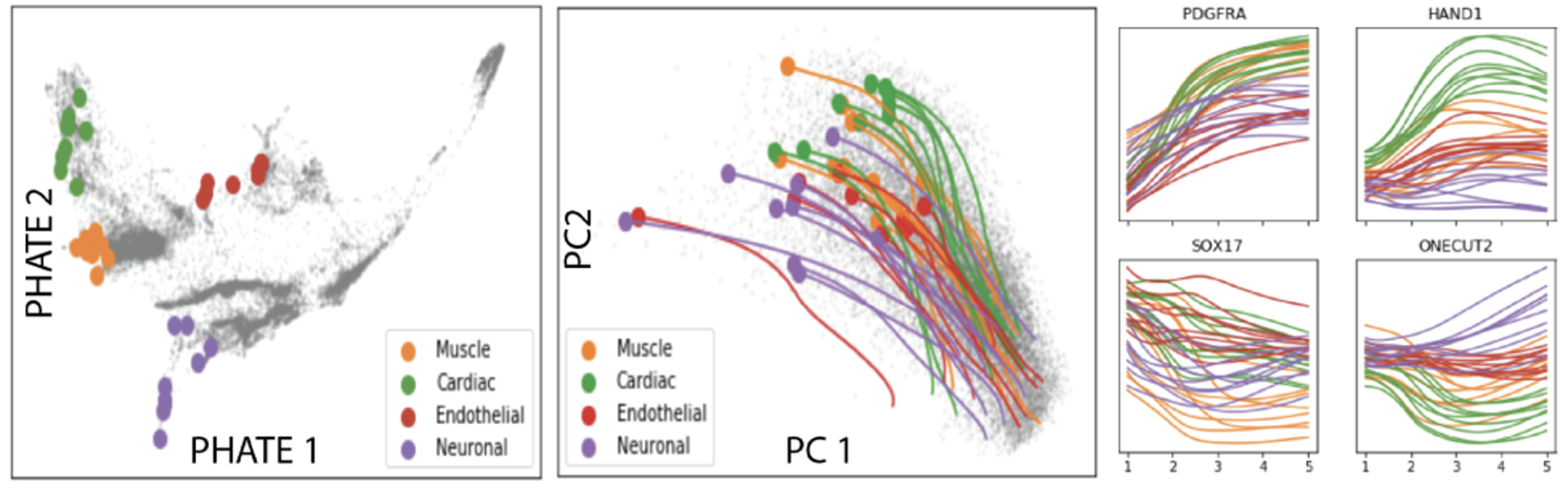
For curated endpoints, shows location on PHATE dimensions, TrajectoryNet paths projected into PCA space, and trajectories for 4 genes.

6. Conclusion

TrajectoryNet computes dynamic optimal transport between distributions of samples at discrete times to model realistic paths of samples continuously in time. In the single-cell case, TrajectoryNet ”reanimates,” cells which are destroyed by measurement to recreate a continuous-time trajectory. This is also relevant when modeling any underlying system that is high-dimensional, dynamic, and non-linear. In this case, existing static OT methods are under-powered and do not interpolate well to intermediate timepoints between measured ones. Existing dynamic OT methods (non-neural network based) are computationally infeasible for this task.

In this work we integrate multiple priors and assumptions into one model to bias TrajectoryNet towards more realistic dynamic optimal transport solutions. We demonstrated how this gives more power to discover hidden and time specific relationships between features. In future work, we would like to consider stochastic dynamics (Li et al., 2020) and learning the growth term together with the dynamics.

Figure 1.

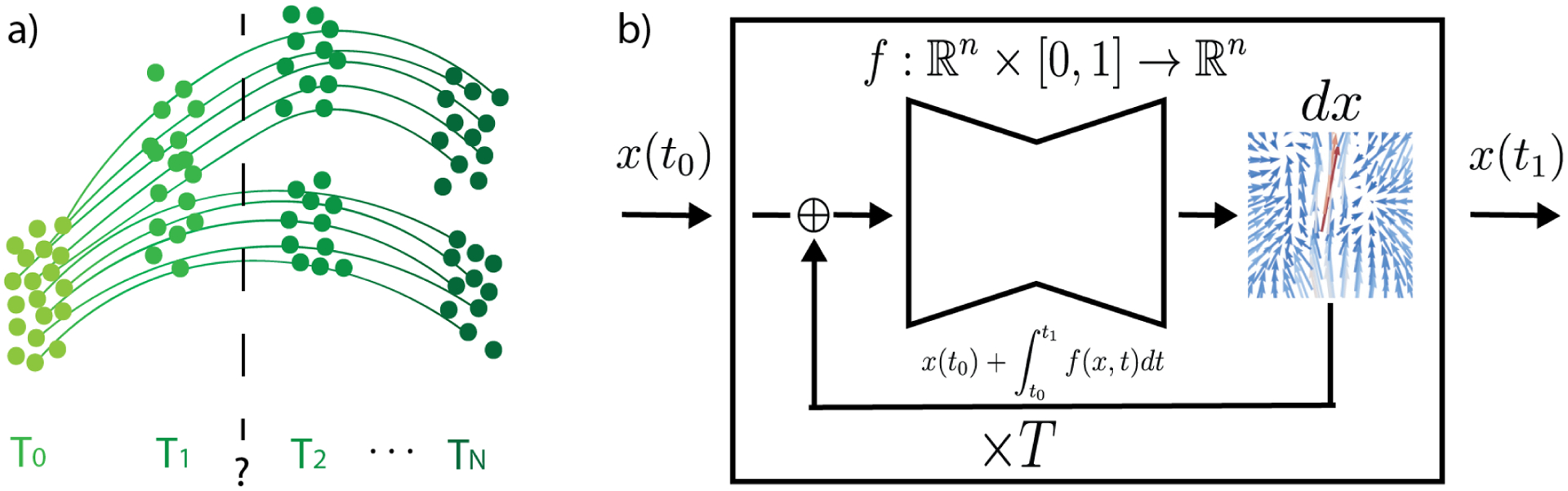
TrajectoryNet learns trajectories of particles from distributions sampled over time. We use a Neural ODE to learn the derivative of the dynamics function. To find the output at time t₁ for a given input at time t₀ we integrate T times letting the ODE solver choose the integration timepoints.