Predicting patient-specific response to adaptive therapy in metastatic castration-resistant prostate cancer using prostate-specific antigen dynamics

Abstract

Abiraterone acetate (AA) has been proven effective for metastatic castration-resistant prostate cancer (mCRPC), and it has been proposed that adaptive AA may reduce toxicity and prolong time to progression, when compared to continuous AA. We developed a simple quantitative model of prostate-specific antigen (PSA) dynamics to evaluate prostate cancer (PCa) stem cell enrichment as a plausible driver of AA treatment resistance. The model incorporated PCa stem cells, non-stem PCa cells and PSA dynamics during adaptive therapy. A leave-one-out analysis was used to calibrate and validate the model against longitudinal PSA data from 16 mCRPC patients receiving adaptive AA in a pilot clinical study. Early PSA treatment response dynamics were used to predict patient response to subsequent treatment. We extended the model to incorporate metastatic burden and also investigated the survival benefit of adding concurrent chemotherapy for patients predicted to become resistant. Model simulations demonstrated PCa stem cell self-renewal as a plausible driver of resistance to adaptive therapy. Evolutionary dynamics from individual treatment cycles combined with metastatic burden measurements predicted patient response with 81% accuracy (specificity=92%, sensitivity=50%). In those patients predicted to progress, simulations of the addition of concurrent chemotherapy suggest a benefit between 1% and 11% reduction in probability of progression when compared to adaptive AA alone. This study developed the first mCRPC patient-specific mathematical model to use early PSA treatment response dynamics to predict subsequent responses to adaptive AA, demonstrating the putative value of integrating mathematical modeling into clinical decision making.

Introduction

Prostate cancer (PCa) is the most prevalent cancer in men in the US. About 1 in 9 American men will be diagnosed with PCa in his lifetime (>248,000 estimated in 2021) and 1 in 41 will die from it. Consequently, PCa remains the second leading cause of death in American men [2]. Following surgery or radiation treatment, androgen deprivation therapy (ADT) has been the mainstay treatment for hormone sensitive PCa for over 70 years [3]. ADT suppresses the production of testicular androgen, which both the normal and cancerous prostate cells depend on for survival and proliferation [4]. Despite new strategies in “precision medicine” in which the specific therapy is guided by molecular biomarkers for individual patients, treatment protocols are typically based on the conventional strategy of “maximum tolerated dose until progression”. This often results in the competitive release of the resistant phenotype, leading to early treatment progression [5]. In an effort to delay progression, intermittent ADT has been shown to be a promising alternative that reduces toxicity and delays progression [6], [7], [8]. Despite this advance, patients inevitably develop castration-resistant prostate cancer, which often progresses to metastatic castration-resistant prostate cancer (mCRPC).

Second-line hormone therapy with abiraterone acetate (AA), which inhibits the production of androgens from other cells by blocking the protein CYP17⁹, has been shown to prolong overall survival when compared to prednisone or placebo [9], [10], [11], [12], [13]. In the COU-AA-302 trial evaluating AA with prednisone versus prednisone alone in mCRPC, AA was shown to improve median overall survival (35.3 with AA vs. 30.1 month without) and more than double median radiographic progression-free survival (16.5 vs. 8.2 months). While radiographic progression-free survival (rPFS) and overall survival (OS) were the primary endpoints, the study also evaluated prostate-specific antigen (PSA) progression. The PSA response rate (PSA decline $\ge$ 50%) to AA was 68%, compared to just 29% in the prednisone alone group, with a median time to PSA progression of 11.1 months versus 5.6 months with prednisone alone [13]. It has been proposed that adaptively administering AA in mCRPC, allowing for treatment holidays when a patient has sufficiently responded, may be able to increase overall response and delay progression [5]. However, maximizing the benefit of adaptive therapy requires understanding the dominant drivers of resistance, predicting individual patient responses, and identifying when and how to modulate treatment to maximize response time.

Many mathematical models have been developed to simulate the various biological mechanisms of clinical PCa treatment resistance [5,[14], [15], [16], [17], [18], [19]]. These studies have contributed significantly to our understanding of how the different mechanisms that may lead to resistance could be exploited for adaptive therapies, but most mathematical models have yet to be rigorously calibrated and validated with patient-specific disease dynamics, and to be evaluated for predictive power [20]. For predictive certainty, model complexity and uncertainty must be kept proportional to the available data. PSA has been used as a marker of PCa development and progression for many years, despite concerns regarding overdiagnosis and overtreatment. We have previously demonstrated how PSA dynamics, rather than measurements taken at single timepoints, can be used to predict individual patient responses to intermittent hormone therapy in castration-naïve PCa [1]. In more advanced PCa, such as in the case of mCRPC, alternative biomarkers such as cell-free DNA and circulating tumor DNA, have been shown to be correlated with PSA response rates [21], [22], [23], [24]. However, very few studies routinely collect such data, when compared to PSA. Here, we sought to investigate if PSA dynamics could be used to predict response to adaptive AA in mCRPC.

We extended our relatively simple model of PCa stem cell dynamics with previously demonstrated predictive power [1]. We calibrated and validated the model against longitudinal PSA data from 16 mCRPC patients receiving adaptive AA in a proof-of-principle prospective pilot trial (NCT02415621). We then used early treatment dynamics to predict how individual patient respond to subsequent treatment cycles. We further investigated how to integrate individual metastatic burden into the predictive modeling framework to increase patient-specific prediction accuracy. We also use the model to simulate the addition of concurrent chemotherapy in those patients predicted to progress during the second cycle of treatment.

Materials and Methods

Patient Data

Sixteen mCRPC patients received adaptive AA therapy as part of a pilot trial at Moffitt Cancer Center [5]. Prior to trial registration, patients received AA plus prednisone as standard of care. Patients who achieved a 50% or more decline of their PSA were eligible to enroll in the trial. Each patient's PSA immediately prior to beginning AA was considered as their baseline. Treatment with

AA was paused when PSA fell below 50% of the individual baseline PSA, and resumed when PSA rose above baseline levels. PSA was monitored every 4 to 6 weeks, with restaging bone scan, pelvic and abdominal CT scan performed every 12 weeks. Patients remained on the trial until radiographic progression based on PCWG2 criteria [25].

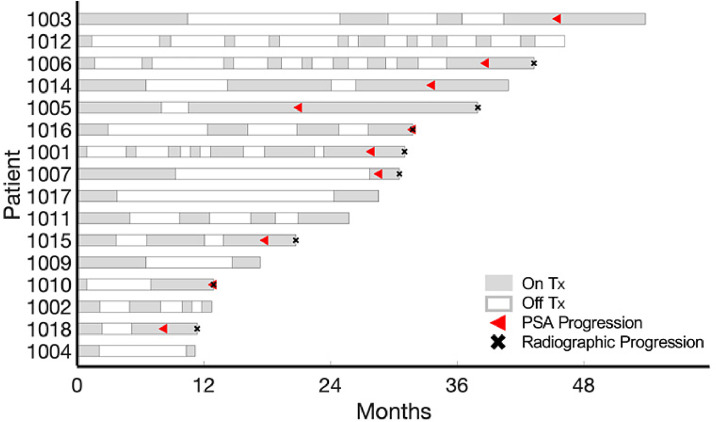
We analyzed longitudinal PSA data (collected every 4-6 weeks both whilst receiving AA and during AA holidays) for the patients enrolled in the trial (average number of data points per patient = 24, range = 9 – 41) to evaluate early PSA response dynamics as predictive biomarker of PSA progression. PSA progression is defined as PSA increasing $\ge 25\%$ and at least $2\text{ng}/\text{mL}$ above the nadir, confirmed by a second value 3 or more weeks later. Eight of the 16 patients developed PSA progression within the first four cycles of treatment, and eight patients were still responding after four cycles (one patient developed resistance after 9 cycles of treatment) (Fig. 1).

Fig. 1.

Treatment times for patients included in the study. Sixteen patients were included in the model analysis. Gray and white denote when treatment was on and off, respectively. Red triangles and black x's denote when patient developed PSA and radiographic progression, respectively. (Color version of figure is available online)

Mathematical Model

The mathematical model simulates the dynamics of prostate cancer stem-like cells (PCaSCs) ($S$), non-stem differentiated cells ($D$), and PSA ($P$). PCaSCs divide at rate $\lambda \left(\text{da}{\mathrm{y}}^{-1}\right)$ to produce either a PCaSC and non-stem PCa cell with probability $1-p_s$ (asymmetric division) or two PCaSCs with probability $p_s$ (symmetric division), with negative feedback from the differentiated cells. Non-stem PCa cells die at rate $\alpha \left(\text{da}{\mathrm{y}}^{-1}\right)$ in response to treatment, which is modulated by the parameter $T_x=1$ and $T_x=0$, denoting when treatment is on and off, respectively. PSA is produced by the non-stem PCa cells at rate $\rho \left(\mu g/L\text{da}{\mathrm{y}}^{-1}\right)$ and decays at rate $\phi \left(\text{da}{\mathrm{y}}^{-1}\right)$. The mathematical equations describing these interactions are given by

$$\begin{array}{ccc}\hfill \frac{\mathit{dS}}{\mathit{dt}}& =& \left(\frac{S}{S+D}\right)p_s\lambda S,\hfill \\ \hfill \frac{\mathit{dD}}{\mathit{dt}}& =& (1-\frac{S}{S+D}{p}_s)\lambda S-\alpha T_{x}D,\hfill \\ \hfill \frac{\mathit{dP}}{\mathit{dt}}& =& \rho D-\phi P.\hfill \end{array}$$ (1)

Model calibration and validation

Previous analysis has shown that the rate at which uninhibited PCaSCs divide can be approximated as once a day, i.e., $\lambda =\ln \left(2\right)$[26]. Sensitivity and correlation analysis showed that $\rho$ and $\phi$ could be uniform among all patients and $p_s$ and $\alpha$ be patient-specific without significantly changing the model results [1]. We deployed a Type 1b bootstrap internal validation leave-one-out analysis [27] to determine the uniform values for $\rho$ and $\phi ,$while allowing $p_s$ and $\alpha$ to be patient-specific. That is, for patient $j$, we used nested optimization to find the uniform values for ${\rho }_j$ and ${\phi }_j$and the patient-specific values for $p_s$ and $\alpha$ for all patients $n$, with $n\ne j$, in the training set, over each patient's treatment course. We then validated the model using ${\rho }_j$ and ${\phi }_j$ to determine the patient-specific $p_s$ and $\alpha$ for patient $j$. This process was repeated for all $N=16$ patients.

Treatment response prediction

For patient $j$, ${\rho }_j$ and ${\phi }_j$ were used to fit the model to each cycle individually for all patients in the training set. That is, finding the optimal value for $p_s$ and $\alpha$ while allowing ${\rho }_j$ and ${\phi }_j$ to remain fixed for each individual cycle (Fig. 2A). Given $p_s$ and $\alpha$ for cycle $i$ for patient $j$, we used the relative changes in $p_s$ for all patients in our training set to generate the cumulative probability distribution of relative changes in $p_s$ from cycle $i$ to cycle $i+1$ (Fig. 2B). We sampled from this distribution to determine 100 values of $p_s$ for cycle $i+1.$As $p_s$ and $\alpha$ are exponentially related [1], we sampled from the 95% confidence interval around the exponential curve relating $p_s$ and $\alpha$ (Fig. 2C) to find 100 values for ${\alpha }_{i+1}$. We used these values to simulate the distribution of patient $j$’s responses in cycle $i+1$.

Fig. 2.

Cycle by cycle parameter changes. (A) Parameter distributions of $p_s$for Cycles 1 through 4. (B) Cumulative probability distribution of relative changes in $p_s$ from Cycle 1 to Cycle 2. (C)$\alpha$ vs. $p_s$ fit (black curve) and 95% confidence interval (gray) for ($\alpha ,p_s$) pairs (black dots) for Cycle 2.

Each model simulation was determined to predict response or resistance based on the PSA progression criteria defined in the trial. That is, if PSA increased more than 25% and at least 2 $\text{ng}/\text{mL}$ above the nadir during treatment, then the simulation was classified as resistant. Of the 100 response simulations, we quantified the number of resistant simulations to derive a probability of resistance, $\mathrm{Pr}\left(\Omega \right)$. If $\mathrm{Pr}\left(\Omega \right)$ was greater than a given threshold, ${\kappa }_i$, obtained from the training set for each predicted treatment cycle $i$, then the prediction was considered resistant. Otherwise, it was classified as responsive. For each leave-one-out patient, an optimal cutoff value $k_i$ for cycle $i$was determined to be the threshold that maximized the accuracy within the training set. Model predictions correctly classifying clinically observed responders as responders ($\mathrm{Pr}\left(\Omega \right)<{\kappa }_i)$ were denoted true negative, while correctly classified clinically resistors ($\mathrm{Pr}\left(\Omega \right)>{\kappa }_i)$ were denoted as true positive.

Statistical analysis

The two-sample t-test was used to calculate the statistical significance of the difference between parameter distributions.

Results

Model accurately describes clinical data

The model is able to simulate longitudinal PSA data from mCRPC patients (Fig. 3A-B). In line with previous results of intermittent ADT [1], the model fits to the data demonstrate that continuous responders have a slowly increasing PCaSC population (Fig. 3A), while patients who progress have a rapidly increasing PCaSC population (Fig. 3B). This shows that prostate cancer stem cell enrichment is a plausible driver of resistance to AA therapy. A comparison of the stem cell self-renewal rate $p_s$ between responsive and resistant patients showed that resistant patients tend to have a larger $p_s$ value, though not significant in this small cohort (Fig. 3C). No difference in the uniform values for $\rho$ and $\phi$ for each leave-one-out analysis were found (Fig. 3D).

Fig. 3.

Leave-one-out analysis results. Model fits to PSA data and corresponding stem cell dynamics for a (A) continuous responder and (B) a patient who developed resistance in his third cycle of treatment. Parameter distributions for (C) patient-specific parameters $p_s$ and $\alpha$ and (D) uniform model parameters $\phi$ and $\rho$ determined via leave-one-out analysis.

Early treatment dynamics can predict subsequent response

Model predictions are classified as true positive, true negative, false positive and false negative in comparison to the clinical outcomes (Fig. 4A). Model predictions for a continuous responder and a patient who progressed in the third cycle are shown in Fig. 4B-C. The model was fit over the first treatment cycle using the $\rho$ and $\phi$ values obtained from the training set. Using the relative change in $p_s$ from cycle $i$ to cycle $i+1$ as well as the exponential relationship between $p_s$ and $\alpha$, we obtained 100 parameter pairs of ($p_{s_{i+1}},{\alpha }_{i+1}$) that were used to forecast the patient's response in the subsequent cycle. The model accurately predicted that Patient 1011 would continue to respond in both the second and third cycles (Fig. 4B). Patient 1014 progressed in his third cycle of treatment. Though $\mathrm{Pr}\left(\Omega \right)=0.49$ in cycle 2, this is below the threshold ${\kappa }_2$ and consequently the model correctly predicts that this patient will continue to respond. In cycle 3, $\mathrm{Pr}\left(\Omega \right)=0.70$ which is larger than ${\kappa }_3$. This is a correct prediction as Patient 1014 develops resistance in cycle 3. Overall, the model is able to correctly predict patient response with 78% accuracy (specificity = 92%, sensitivity = 38%).

Fig. 4.

Model prediction results. (A) Prediction classifier table. Model predictions for (B) Patient 1011 who was a continuous responder and (C) Patient 1014 who progressed in the third cycle. The model correctly predicted that Patient 1011 would continue to respond in both the second and third cycles and that Patient 1014 would continue to respond in the second cycle and develop resistance in the third cycle. Prediction classifications are determined using cycle- and patient-specific κ values. If the P(Ω) > κ, then the patient is predicted to develop resistance. Model predictions were compared to actual data to determine accuracy.

Incorporating metastatic burden

Despite treatment, several patients continued to develop metastases during the trial. Though rising PSA has been shown to be correlated with metastatic burden, it is not predictive of the development of new metastatic growths [28]. We sought to investigate whether correlating metastatic growth with the stem cell self-renewal rate, $p_s$, would improve the prediction accuracy of our model. That is, developing new metastatic growths during a cycle of treatment is likely the consequence of a larger number of anatomically distributed PCaSCs, whose dynamics are primarily driven by the self-renewal rate $p_s.$ Thus, we propose a novel way to correlate new metastatic growths with $p_s$.

As previously described, ($p_{s_{i+1}},{\alpha }_{i+1}$) pairs for cycle $i+1$were obtained by uniformly sampling from the cumulative probability distribution of relative changes in $p_s$ from cycle $i$ to $i+1$. Fig. 5A shows that in general, the relative change ranged between -75% and 150%, with about 30% of the patients experiencing larger relative changes in $p_s$. To incorporate the metastatic burden, we used a skewed sampling to sample from the cumulative probability distribution, with the degree of the skew dependent on the number of new metastatic growths. This resulted in larger relative increases in $p_s$ for patients with larger metastatic burden$.$ As shown in Fig. 3C, patients with larger $p_s$ developed resistance to adaptive AA faster in comparison to those with smaller $p_s$ values. Consequently, the skewed sampling results in a larger fraction of simulations that predict resistance, thereby increasing the $\mathrm{Pr}\left(\Omega \right).$ It should be noted that this also resulted in ${\kappa }_i$ changing in response to larger $\text{Pr}\left(\Omega \right)$ for particular patients within the training cohort.

Fig. 5.

Model prediction results when considering metastatic burden.(A) Parameter sampling with and without metastases. When a patient's metastatic burden is not considered, a uniform sampling is performed to determine $p_s$ value in next cycle. If a patient develops a new metastatic growth, the sampling is skewed such that the sampled stem cell self-renewal value is more likely to be larger in the next cycle. (B) Model predictions for Patient 1010 with and without incorporating metastatic burden. Patient 1010 developed on new metastatic growth during his first off-treatment cycle. Using PSA dynamics alone, the model incorrectly predicts that Patient 1010 will continue to respond. Using a skewed sampling results in a correct prediction that Patient 1010 will progress in cycle 2.

A comparison between the model predictions using a uniform and skewed sampling for an individual patient are shown in Fig. 5B. Patient 1010 developed a new metastatic growth during his first cycle of treatment. With a uniform sampling, the model predicted that the $\mathrm{Pr}\left(\Omega \right)=0.47.$As this was below the threshold ${\kappa }_2$, the model incorrectly predicted that this patient would continue to respond in the second cycle (false negative). Using a skewed sampling, the $\mathrm{Pr}\left(\Omega \right)$ increased to 0.53, which was larger than the new threshold ${\kappa }_2$ resulting in a correct resistant prediction (true positive). Overall, incorporating each patient's metastatic increased the accuracy to 81% (specificity = 92%, sensitivity = 50%).

Concurrent chemotherapy can improve time to progression

Concurrently administering the chemotherapeutic docetaxel with ADT has shown benefit in metastatic hormone-naïve prostate cancer patients [29], [30], [31]. In particular, the STAMPEDE trial conducted in 2016 showed a 10 month increase in overall survival in high-risk, locally advanced PCa patients receiving ADT with docetaxel compared to ADT alone [31]. Cabazitaxel is a second-line chemotherapeutic that has shown survival benefit after progression on docetaxel and is often given as standard of care after AA [32]. As previous studies have shown that chemotherapy provides more benefit when administered earlier in the disease course, we sought to investigate the effect of administering concurrent chemotherapy prior to progression on AA alone.

Unlike AA, chemotherapy can induce cell death in both PCaSCs and non-stem cells [33]. As such, we extended our model to include death terms (${\delta }_S,{\delta }_D$) on both cell populations in response to chemotherapy ($T_{xD}=1$). That is,

$$\begin{array}{ccc}\hfill \frac{\mathit{dS}}{\mathit{dt}}& =& \left(\frac{S}{S+D}\right)p_s\lambda S-{\delta }_S{T}_{\mathit{xD}}S,\hfill \\ \hfill \frac{\mathit{dD}}{\mathit{dt}}& =& (1-\frac{S}{S+D}{p}_s)\lambda S-\alpha T_{x}D-{\delta }_D{T}_{\mathit{xD}}D,\hfill \\ \hfill \frac{\mathit{dP}}{\mathit{dt}}& =& \rho D-\phi P.\hfill \end{array}$$ (2)

Due to the patients included in our study being chemotherapy-naïve, we did not have clinical data to calibrate the model to obtain values for ${\delta }_{\mathrm{S}}$ and ${\delta }_{\mathrm{D}}.$ Consequently, the values for these parameters were derived from literature, where it is said that approximately three times more non-stem cells die in response to chemotherapy than PCaSCs[33]. We chose ${\delta }_{\mathrm{S}}=0.0027\left(\text{da}{\mathrm{y}}^{-1}\right)$ and ${\delta }_{\mathrm{D}}=0.008\left(\text{da}{\mathrm{y}}^{-1}\right)$ such that model simulations would show a decline in each population when chemotherapy was given.

For the patients predicted to progress during their second cycle of adaptive therapy, we simulated adding up to 10 cycles of concurrent chemotherapy during cycle two and compared the responses with and without chemotherapy (Fig. 6). While some patients received minimal benefit (3% decrease in $P\left(\Omega \right),$ Patient 1015) from concurrent therapy, others received as much as an 11% decrease in $P\left(\Omega \right)$ with concurrent treatment (Patient 1005).

Fig. 6.

Model simulation comparison between adaptive abiraterone with and without concurrent chemotherapy. (A) Without concurrent chemotherapy, Patient 1015 is predicted to have a 58% probability of developing resistance in his second cycle of treatment (left). Concurrent chemotherapy (right) provides a minimal reduction (3%) in the probability of developing resistance. (B) Patient 1005 has a 79% probability of progressing during cycle 2 without concurrent chemotherapy (left). This can be reduced by 11% if chemotherapy is given concurrently during cycle 2 (right).

Discussion

In this study, we have analyzed a simple mathematical model of PCaSC and PSA dynamics to predict individual mCRPC patient responses to adaptive AA therapy. The model has been calibrated and validated against clinical data from 16 mCRPC patients from a pilot trial. With just two patient-specific parameters, our results show that the model is able to accurately describe individual patient dynamics. Similar to previous analyses of PCa stem cell dynamics underlying resistance to intermittent ADT, we found that stem cell enrichment is a likely driver of treatment resistance, despite AA working through an alternative pathway than ADT [9]. As these patients are advanced metastatic PCa patients, their PSA dynamics are likely also driven by multiple factors that the model may not be able to account for. Despite that, the model was able to use early treatment evolutionary PSA dynamics to predict subsequent responses with 78% accuracy.

Incorporating the metastatic burden improved the overall accuracy to 82%, with a specificity of 92% and a sensitivity of 50%. The lower sensitivity is due to the few progression events within this data cohort. While patients respond on average for 3.3 treatment cycles, the majority of progression events occurred within the second cycle. This limitation made it difficult to determine the optimal threshold value for cycle predictions where few patients progressed, resulting in a higher proportion of false negative results. We are confident that model accuracy, as well as sensitivity and specificity, would increase with a larger patient cohort. Nevertheless, the patients who were incorrectly predicted to develop resistance during the second cycle instead progressed during the third cycle. As such, the model may serve as an early indicator of treatment resistance for a subset of patients.

We also investigated the potential benefit of concurrent chemotherapy with AA prior to progression on AA alone. Model simulations showed a 3% to 11% decrease in the probability of resistance when compared to AA alone. While 3% may be dismissed mathematically, it may mean a difference for individual patients based on their individual risk-benefit situation; as such the model predicted probabilities may provide invaluable information for the clinician to discuss with each patient when deciding if, when and how to adapt treatment. Using the presented model, the oncologist can discuss different treatment routes with associated risk and likelihood of success to guide patients decide what is the best course of action for their individual treatment expectations. As such, we believe that this is an option that should be considered for patients and warrants critical evaluation in a prospective clinical trial setting. We do note that the concurrent chemotherapy simulations used chemotherapy sensitivity parameters (${\delta }_S$ and ${\delta }_D$) that were not previously calibrated to clinical data. Future studies will include calibrating the model to clinical data of patients receiving concurrent chemotherapy to determine the values for these parameters that can be used in further model simulations.

As previously mentioned, alternative biomarkers such as ctDNA, cfDNA, and PCa stem cell antigen (PSCA) and other stem cell markers have been shown to be correlated with advanced PCa and metastasis [[21], [22], [23], [24],34]. However, due to the lack of availability of data, we were not able to design our model based on these dynamics. Collecting and analyzing such biomarkers are promising future avenues for clinical studies and mathematical modeling.

Conclusions

This validation study demonstrates the utility of mathematical modeling in clinical decision making. Using a simple dynamic model of PCaSC, non-stem cells, and PSA, we are able to use early treatment dynamics to predict who may or may not respond to subsequent treatment in mCRPC. Despite PSA notoriously being considered a poor biomarker for treatment response, both in early- and advanced-stage prostate cancer, we showed that our model could use PSA dynamics – rather than absolute PSA values – to predict response with an 81% accuracy. Our model is the first of its kind to correlate PSA dynamics with metastatic burden to understand how an individual patient's disease is evolving. As this model predicts PSA, and not radiographic progression, this may provide sufficient lead-in time for clinicians to intercede with alternative treatment options prior to radiographic progression, potentially minimizing adverse events and toxicity and maximizing survival. After prospective validation, such integrated approach could equip clinicians with an additional decision support tool to use when deciding how to effectively treat patients.

Author Contributions

R.B.N., J.Z., R.A.G. and H.E. conceptualized the study. R.B.N. and H.

E. performed the modeling and statistical analyses. R.B.N., J.Z., T.Z., A.Z.W., R.B., R.A.G. and

H.E. wrote the manuscript.

Acknowledgements

We thank the participants of the clinical trial. This work was supported by NIH/NCI R21CA234787 “Predicting patient-specific responses to personalize ADT for prostate cancer”, and in part by NIH/NCI U54CA143970-05 (Physical Science Oncology Network) “Cancer as a complex adaptive system”, the Ocala Royal Dames for Cancer Research, Inc., and The JAYNE KOSKINAS TED GIOVANIS FOUNDATION FOR HEALTH AND POLICY, a Maryland private foundation dedicated to effecting change in health care for the public good. The opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and not necessarily represent the official views of the National Institutes of Health, the Ocala Royal Dames for Cancer Research, or the JAYNE KOSKINAS TED GIOVANIS FOUNDATION FOR HEALTH AND POLICY, its directors, officers, or staff.