Abstract
Background
In medical diagnosis and clinical practice, diagnosing a disease early is crucial for accurate treatment, lessening the stress on the healthcare system. In medical imaging research, image processing techniques tend to be vital in analyzing and resolving diseases with a high degree of accuracy. This paper establishes a new image classification and segmentation method through simulation techniques, conducted over images of COVID-19 patients in India, introducing the use of Quantum Machine Learning (QML) in medical practice.
Methods
This study establishes a prototype model for classifying COVID-19, comparing it with non-COVID pneumonia signals in Computed tomography (CT) images. The simulation work evaluates the usage of quantum machine learning algorithms, while assessing the efficacy for deep learning models for image classification problems, and thereby establishes performance quality that is required for improved prediction rate when dealing with complex clinical image data exhibiting high biases.
Results
The study considers a novel algorithmic implementation leveraging quantum neural network (QNN). The proposed model outperformed the conventional deep learning models for specific classification task. The performance was evident because of the efficiency of quantum simulation and faster convergence property solving for an optimization problem for network training particularly for large-scale biased image classification task. The model run-time observed on quantum optimized hardware was 52 min, while on K80 GPU hardware it was 1 h 30 min for similar sample size. The simulation shows that QNN outperforms DNN, CNN, 2D CNN by more than 2.92% in gain in accuracy measure with an average recall of around 97.7%.
Conclusion
The results suggest that quantum neural networks outperform in COVID-19 traits’ classification task, comparing to deep learning w.r.t model efficacy and training time. However, a further study needs to be conducted to evaluate implementation scenarios by integrating the model within medical devices.
Keywords: Medical imaging and analysis, Artificial intelligence, Quantum neural networks, Medical informatics
Background
In the clinical trial and drug discovery process, the role of statistical analytics and machine learning has been shown to be significant, especially in biological imaging and analysis, commonly used at various stages, from preclinical R&D to clinical trials, solving problems like sputum detection [1], image augmentation [2] and other applications, such as nucleus counting [3]. In the recent past, substantial research work have been proposed studying various classical machine learning and deep learning methods applied to an image that assists scientists and medical practitioners in analyzing and seeing inorganic growth or accumulation of tissues, cells, and subcellular components in CT scans, along with a more technology-oriented solution in the space of wearable technology [4] and tele-health care services to discover COVID-19 [5]. An example of detecting brain tumors through deep learning methods has been studied by researchers [6] and diverse COVID-19 diagnosis research work using deep learning and traditional machine learning methods as shown in Table 1. Currently, with evolving COVID-19 mutants it is now becoming extremely important to leverage faster and accurate solutions for clinical discovery, prompting therefore our study to understand the evolution in terms of offering medical imaging solutions for factor detection of mutant variants [7].
Table 1.
Empirical research for detecting COVID-19 using deep learninga
| Model proposed | Study | Dataset size | Training samples sufficiency | Model performance |
|---|---|---|---|---|
| MODE (Multi-objective differential evolution) based CNN | Singh et al. [47] | 1000 + CT images | + + + | Accuracy—90.6% |
| UNET + + | Chen et al. [44] | 46,000 + CT images | + + + |
Accuracy—95.24% Sensitivity—100% Specificity—93.55% |
| Stacked Two CNN three dimensional for classification and VNET for Segmentation | Xu et al. [43] | 19,000 + CT Images with COVID-19, 1175 healthy samples | + + + | Accuracy—86.70% |
| COVNet + ResNet 50 for classification and U-Net for segmentation | Li et al. [35] | 4000 + CT Samples | + + + |
Sensitivity—90.0% Specificity—96.0% |
| Transfer Learning + ResNet 50 for classification and UNet + + (3D) for segmentation | Jin et al. [10] | 1100 + total samples with 730 positive samples | + + |
AUC—0.991 Sensitivity—97.4% Specificity—92.2% |
| Inception with Transfer Learning technique | Wang et al. [32] | 450 + CT scans of confirmed COVID-19 | + |
Accuracy—82.9% Sensitivity—84.0% Specificity—80.5% |
| Neural Networks with ResNET 50, attention technique and Feature Pyramid Network | Song et al. [42] | 750 + Images | + |
Accuracy—86.0% F-Score—87.0% Sensitivity—93.0% |
| Deep Conv Net(2D) on ResNet-50 for classification and UNet for segmentation | Gozes et al. [41] | 50 + patients’ samples | + |
AUC—0.996 Sensitivity—98.2% Specificity—92.2% |
|
VBNet neural network to Segment COVID-19 infection regions in CT scans |
Shan et al. [13] | 200 + CT scan samples | + | Dice Coef.—91.6% |
| 2D CNN | Jin et al. [10] | 970 CT Scan samples | + |
Accuracy—94.0% AUC—0.979 |
| SVM + Wavelet transformation | Barstugan et al. [39] | 150 CT Scan Samples | + | Accuracy—99.68% |
| Deep CNN(3D) for classification and U-Net for segmentation | Zheng et al. [46] | 500 + Samples | + | AUC-ROC—0.959 |
| DCNN | Heinrich et al. [31] | 500 + Samples | + | Dice Coef.—71.0% |
| CNN-LSTM | Islam et al. [60] | 4000 + X-ray Samples | + + + |
AUC—0.992 Sensitivity—99.3% Specificity—98.9% |
| VGG-19-RNN | Zabirul Islam et al. [59] | 6000 + x-ray samples(sample with CoViD, pneumonia and normal cases) | + + + |
Accuracy—99.9% AUC—99.9% Recall -99.8% |
| Ensemble DCCNs | Singh [1] | 6000 + (sample with CoViD, tuberculosis, pneumonia) | + + + | Accuracy—99.2% |
aRefer to Abbreviations for detailed nomenclature
There has been active research in biomedical image analysis using deep learning methods, whereby deep learning seems to have outperformed most computer vision problems for instance [8]. Nevertheless, computer vision techniques have shown vast opportunities in numerous application areas, especially in medical research and healthcare [9]. Medical imaging does provide better visibility than standard medical records’ data assessment, such as solving for Diabetic Retinopathy [10]. High-resolution images analyzed can provide any growth details on actuals, on a day-to-day basis, helping a medical practitioner to evaluate the situation quickly and provide a better treatment. It is apparent to be mentioned that the success of leveraging deep learning over traditional machine learning methods have been studied along with wide area of application in the medical domain [11]. Moreover, recent developments of quantum computing, vis a vis its application of quantum algorithm in varied domains, has now opened up new research areas for further optimizing classical machine learning problems [12]. In fact, recently, researchers from Massachusetts Institute of Technology (MIT) created an algorithm to overcome the challenges of developing computationally efficient and performing algorithms in order to solve several medical imaging problems [13].
The domain of medical science needs significant development for making sense of an analysis generated from an image. Previous studies dealing with this topic, have discussed the varied applications of machine learning, deep learning, and quantum algorithms in drug discovery and screening process, thereby solving problems that include compound property and activity prediction, using multitask DNN on 12,000 compounds [14]. Importantly, Quantum is a new paradigm today, with multiple applications being evaluated to solve problems in the fields of optimizing deep learning or machine learning tasks, finance [15], drug discovery [16], along with helping in shedding light on various clinical research [17]. Table 2 enlists extant literature that has dealt with drug discovery.
Table 2.
Previously studied applications of machine learning in drug discovery and medical diagnosis
| Description of study | Author | Methodsa |
|---|---|---|
| Skin cancer detection | Kadampur and Al Riyaee [9] | DNN |
| Protein structure prediction | Torrisi et al. [18] | DL-CNN, DL-RNN |
| Cuneiform Dehydration Method for Medical Diagnosis | Baranov [50] | Image Filtering, thresholding, Gaussian blur |
| Quantitative structure–activity relationship analysis in drug discovery | Uesawa [51] | Deep learning |
| Quantum chemical properties analysis | Gilmer et al. [52] | Message passing neural network (MPNN) |
| Predicting compound property and activity | Mayr et al. [27] | Multitask DNN |
| Predicting pharmacological properties of drugs and for drug repurposing leveraging transcriptomic data from the LINCS project | Aliper et al. [53] | DNN |
| Automatic molecular structure learning |
Merkwirth and Lengauer [54] Lusci et al. [55] |
DNN and RNN |
| Method to model drug induced liver injury (DILI) | Xu et al. [56] | UGRNN |
| Neural fingerprints of the compound | Duvenaud et al. [57] | Graph CNN |
| Predicting the ligand–protein interactions | Gomes et al. [48] | CNN, DNN |
| Predicting the reactions and retrosynthetic analysis | Liu et al. [36] | Neural sequence to sequence model and Monte-Carlo tree search |
| Drug discovery with on short learning | Altae-Tran et al. [58] | LSTM |
| Visual Screening from protein–ligand complex | Pereira et al. [49] | DNN |
| Facilitating probe selection for gene-expression arrays | Tobler et al. [3] | Naïve Bayes, neural nets |
aRefer to Abbreviations for detailed nomenclature
Although, there have been other studies that have deliberated upon the success of employing deep learning in drug discovery [16] and MRI image analysis for brain tumors, and for detecting and segmenting pneumonia traces using classical machine learning models [6] or leveraging deep learning in biomedical image segmentation applications [18]. The core purpose of this paper is to evaluate and provide empirical evidence for applying Quantum algorithms in medical imaging and drug discovery problems.
Quantum machine learning
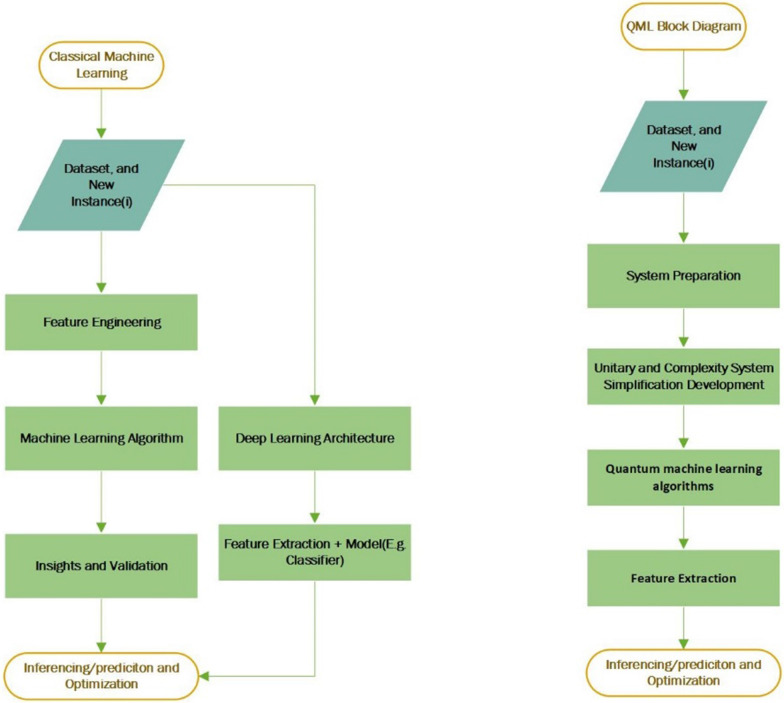
The recent developments of Quantum Enhanced Learning [19], fusing AI and ML to obtain significant optimal solutions for boosting algorithmic performance has given rise to a new area of research termed ‘Quantum Machine Learning’ (QML), which has effectively evolved from the theory of quantum computing. The concept behind leveraging quantum computing for machine learning tasks is to inherently achieve solution parallelism [20], achieved for optimal constraint solving, using Moore’s law [21]. Quantum algorithms are centered on the concept of Boolean algebra (e.g., OR, AND, and NOT gates) and quantum physics. The data storage layout is established from Quantum bit (Qb) or qubits1 that depends on theoretical foundations of electron spin [22]. Importantly, quantum methods in addition can translate other than 1’s or 0’s such as complex information or negative values. A typical model development flow diagram is demonstrated in Fig. 1, explaining the basic control flow difference of classical machine learning versus Quantum machine learning algorithms.
Fig. 1.
Execution block diagram of classical machine learning/deep learning versus quantum machine learning algorithm designing (refer to Table 4. for algorithmic details on QML)
The need for quantum algorithms
QML is considered as one of the future areas of research in deep learning algorithms. The two key tasks QML can better perform when compared to classical deep learning techniques include:
Enhance learning algorithms like Bayesian networks [25], Tensors, and search.
QML’s ability to deal with large-scale biased datasets yield faster complexity factors for major classical computing and machine learning tasks, consuming thereby less space and time. Effectively, it uses quantum annealers and tunneling for loss function minimization tasks, solving thereby complex problems of finding super-local minima, and a close approximation of global minima. In fact, multiple methods within the QML strategy are based on fast quantum algorithms for linear algebra, and semi-definitive or constraint-specific problems like optimization, as in the case of neural network models for weight adjustment, during both search and optimization tasks, similar to gradient descent-based optimizer. Assuming the task is to optimize a linear function of MxM matrix(X), over a parallel space with constraints(c), the solver has runtime complexity of O(c(c2 + nω + cns)logO(1)(cnR/ϵ)) [26]. Notably, herein, ϵ is denoted as an approximation factor, while s denotes sparsity, and R represents a range that is bound to yield an optimal matrix(X). Notably, these proven methods outperform classical optimization methods, yielding thereby complexity of O (ncs(Rr/ϵ)4 + ns(Rr/ϵ)7) as proposed by Arora and Kale [27]. The proposed optimizers in turn, tend to improve the overall solution convergence for any machine learning problems.
This paper looks to address two major research questions, while evaluating the application of QML in specific practice, specifically focusing upon medical image diagnostics and/or drug discovery,
RQ1
Are quantum algorithms suited for large-scale classification problems in medical image diagnostics dealing and industrial applications?
RQ2
Can quantum algorithms outperform classification or segmentation tasks in comparison with classical deep learning methods w.r.t model efficacy, biased training, and inferencing performance on high-resolution clinical image data?
The research questions would further provide support to exemplify the application of quantum theory in optimizing deep learning techniques to achieve superior performance in solution convergence and quality of the model. Another important aspect to emphasize on supporting production deployment is selecting appropriate quantum hardware for training, while deploying the model for real-time inferencing in health informatics applications, which is discussed later in this paper under the experiment section.
Application of quantum machine learning
The foundation of QML targets to solve research foundation problems in mathematical analysis to generalize quantum to improve classical learning tasks with potential optimization to speed of execution. Some of the task’s researchers are leveraging includes quantum techniques in Quantum Simulation [28], applied around nanotech, bio-medical imaging, physical chemistry, and with quantum systems tasks, such as search [29], which further provides polynomial speed, as compared to classical algorithms for other varied scenarios.
Method
The section discusses the methodology followed for building the model, provide details on overall data collection process followed, key modeling process imbibed for the study, and analysis performed with quantum networks.
Quantum neural network model
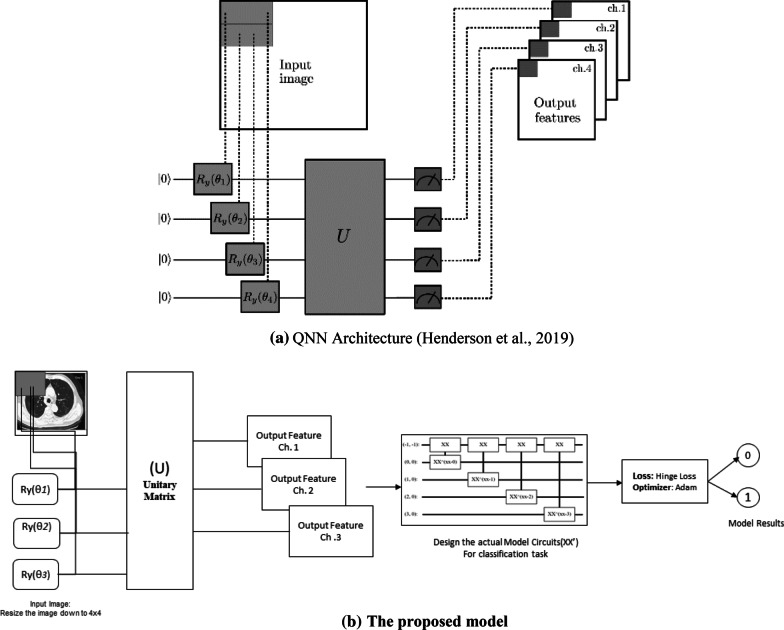
This study conducted an experimental analysis with a new variant of a learning model to further take advantage of quantum computing devices to perform learning tasks with quantum data [30]. We assumed that Quanvolutional neural network or Quantum neural network (QNN) would solve classical deep learning problems to be computationally faster from the design paradigm. Figure 2a illustrates the QNN architecture, which would help in understanding the Quantum network design methodology. Further, for simulation, we benchmarked the QNN model across other studies from extant literature. The rationale behind this exercise was to help in exploring varied application scenarios in the medical image analysis task that is presented in subsequent sections. Notably, the process of designing QNN has been described in Table 3 and has been elaborated upon in the subsequent sections.
Fig. 2.
a QNN Architecture [31]. b The proposed model
Table 3.
Algorithm design stages for quanvolutional neural network
| Stage 1: An input image with small region of interest is embedded into a quantum circuit. An example of a 2 × 22 × 2 square region |
| Stage 2: A quantum computation, associated with a unitary matrix(Ua) in Fig. 3, is performed on the system. A Cirq could generate the unitary, most quantum operations have a unitary matrix representation applied to the gate, operations and circuit that represents an object |
| Stage 3: The system is then quantified by obtaining the list of classical expected values |
| Stage 4: Similar to the classical convolution layer, each expected value is mapped to a different channel of a single output pixel |
| Stage 5: The process is iteratively executing across different regions of the image. A full input image scan is viable by re-positioning an output object positioned a multi-channel image |
| Stage 6: The quantum convolution layer would additionally abide to quantum or classical layers |
aRefer to Abbreviations for detailed nomenclature
The proposed system is illustrated below in Fig. 2b. From a practical implementation perspective, the model accepts input image rescaled to 4 × 4 size before being fed into the Unitary matrix to obtain features at different channel. Further the features were leveraged to create a quantum circuit model, thereafter, followed by compiling the model using a loss function and optimizer using TensorFlow Keras model utility library.
Data and pre-processing
This section discusses the data collection process and the pre-processing activities that were conducted during the experiments. Notably herein, the relative transformation measures were required for modeling a QML algorithm. Additionally, this section consists of two sub-sections; the first, describes the data collection process, along with the larger data schema, while the second, discusses the affirmative steps that are taken for pre-processing in pre-modeling stages.
Data collection
The model development and verification for quantum deep learning-based image classification would require a large sample set for the quantum machine to perform. As a pre-requisite step, learning models require a significant amount of training dataset for building an efficient model [32], thus a through process was followed for sampling the image files to eliminate any representational biases. Hereafter, this study combined data shared by semanticscholar.com, along with the research work done by Chen et al. [33], and Jin et al. [34].
The data collection process adopted a strategy to collect CT scan samples of varied age groups, ranging from 20–30, 30–45, 45–60, and above 60 years of age, with both positive and negative samples. Key sources were identified, based on represented data statistics (Table 4), along with other open dataset sources from Microsoft open research database, Google dataset search, Stanford, and MIT datasets. Notably, the data search process ensured that the data resolutions were consistent across all the sources. The preferred resolution range of images were chosen (256 × 256 and 448 × 448), because image resolution does play a vital role in deep learning space, and often, high-resolution images do go on to impact model training performance and efficacy to a great extent [35].
Table 4.
Dataset
| Dataset description | Data statistics | Source |
|---|---|---|
| CT scans for COVID-19 | 349 CT images of 216 patients | https://github.com/UCSD-AI4H/COVID-CT |
| SIRM COVID-19 database | Sample < 50 images | https://www.sirm.org/en/2020/03/31/COVID-19-case-4/ |
| Radiopedia COVID dataset | Sample < 50 images | https://radiopedia.com |
| Eurorad dataset | Sample < 50 images | https://www.eurorad.org/case/16689 |
| Center for artificial intelligence in medicine and imaging | More than 5000 + sample images of patients | https://aimi.stanford.edu/resources/COVID19#data |
| Total samples selected | ~ 10,000 + |
Figures 3a, b and 4, adopted from Shi et al. [36]; Li et al. [37]; and Hani et al. [38] represent classical CoViD-19 and non-COVID-19 (influenzas and virus pneumonia) scans. Based on this, we discuss the overall finding that was observed from CT scans taken through a specific time duration.
Fig. 3.
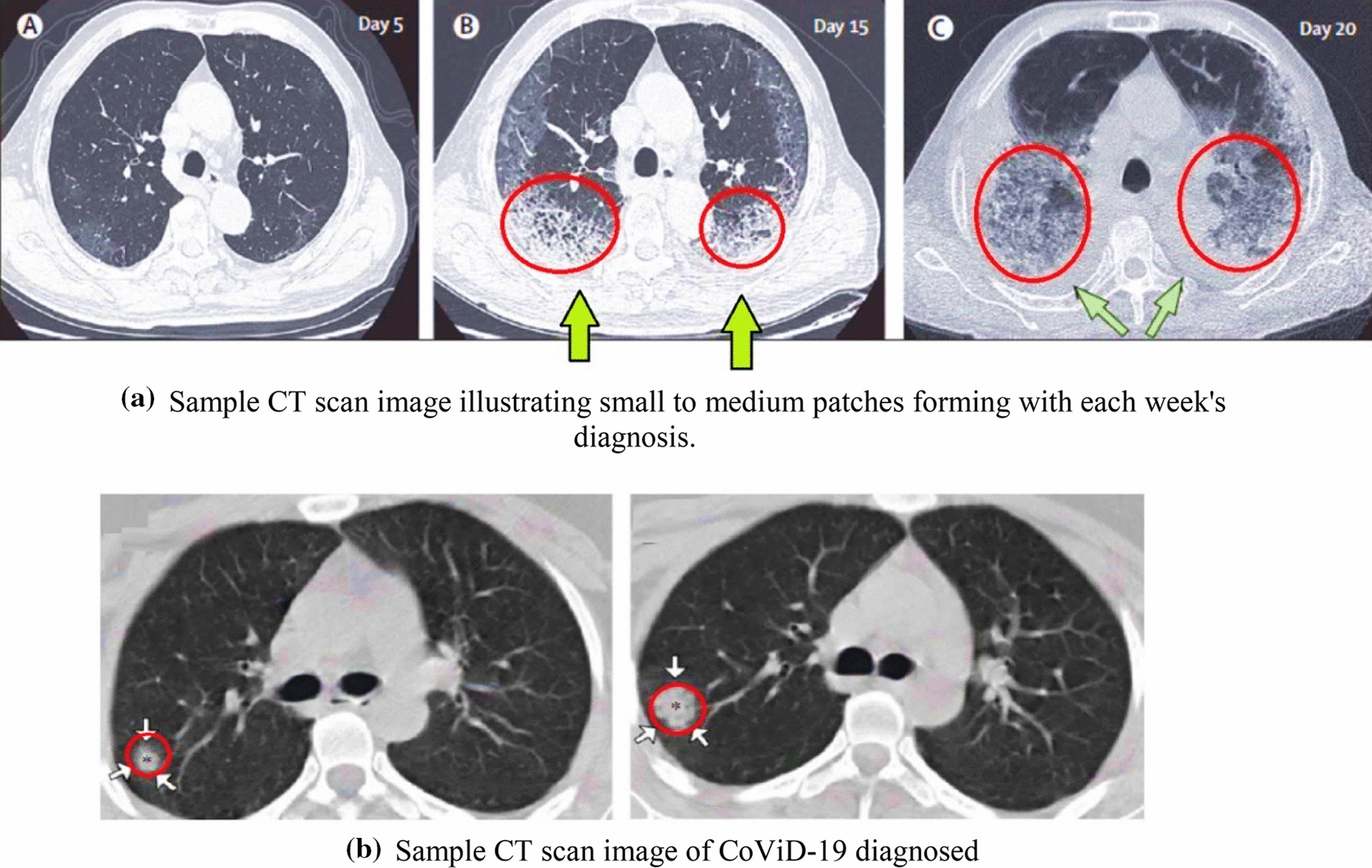
a Sample CT scan image illustrating small to medium patches forming with each week's diagnosis. b Sample CT scan image of CoViD-19 diagnosed
Fig. 4.
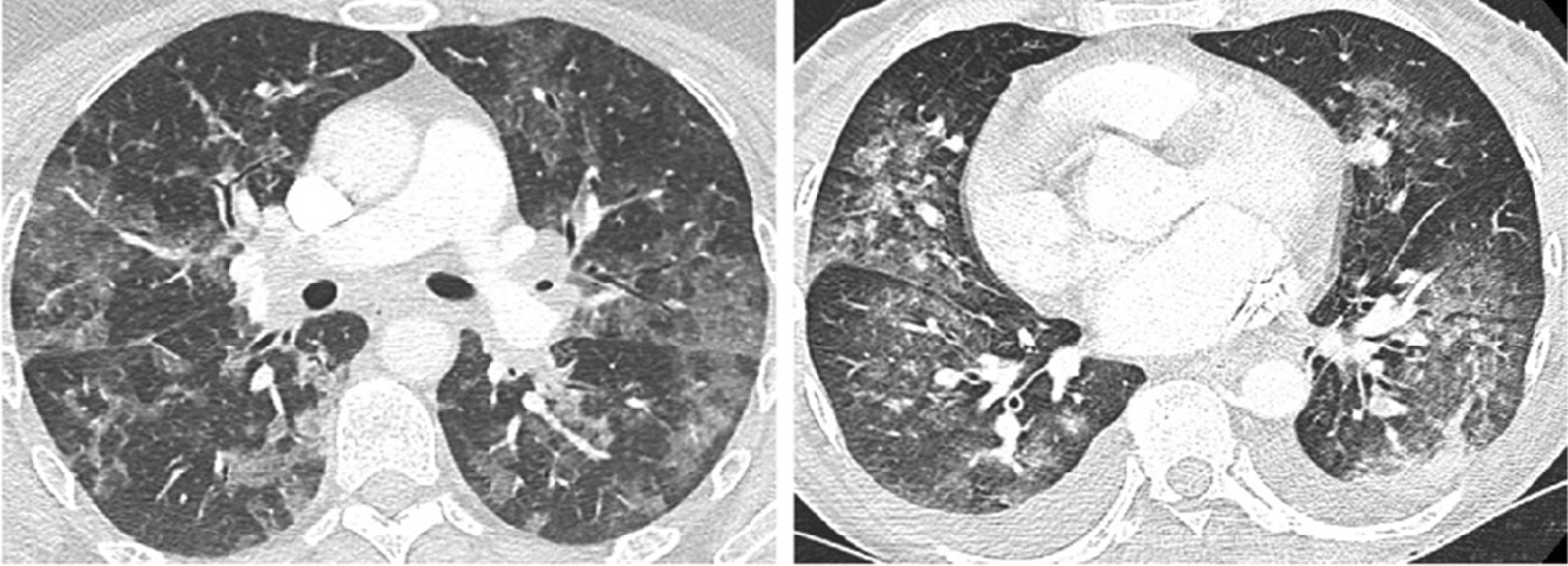
CT scan of two patients of 45-year and 48-years of age with influenza virus pneumonia and Goodpasture syndrome shows bilateral ground-glass opacities in contrast to COVD-19 patients (Hani et al. 2020)
The sample data illustrated in Fig. 3a is identified as CoViD-19 positive. A significant growth in building patches was observed in the lungs over 10 days during quarantine (day 5 and day 15 scan). The scan of day 20 showed the formation of a dense mucus that was concentrated across the lungs. Figure 3b illustrates mucus, segmented across a small patch growth across two weeks of supervision. An evaluation dataset of non-CoViD-19 suffering from pneumonia and influenza was also sourced for validation of the model results.
Pre-processing and normalization
Importantly, the datasets that were used come from multiple sources; the process of data normalization included comparing the homogeneity of data sources, while further calibrating the images to the required scale for modeling. The study leveraged upon color models of an abstract mathematical model, describing the way colors can effectively be represented as tuples of numbers that are useful in viewing conditions. Once the image was thoroughly analyzed, the dataset was normalized using erosion and dilation [39], leveraging upon OpenCV library, a morphological transformation method, primarily used for handling noise, or detecting intensity collisions. Further, image de-noising (Buades et al. 2011) and scaling was done, using Python-OpenCV library, which in turn, was implemented to the entire dataset for standardization, with the help of fast Nl Means Denoising function for colored images, where the source image input of 8-bit 3-channel images were provided with template window size of 7 pixels and 21-pixel, and hColor of 10 in order to remove the colored noise; post this, they were kept into consideration for the completion of the de-noising process. Notably herein, de-noising generally impacts the image segmentation process in the overall modeling situation.
Handling representation and measuring bias in image dataset
The section discusses the impact of measuring bias that depicts the systematic value distortion, which takes place when an issue with a specific device is utilized to visualize and observe an image quality from a training perspective. Importantly, this type of bias is hard to replicate with sampling technique, and thus requires a manual review of the colored images, being used for training [40]. This study further leverages upon bootstrapping resampling technique [41] with different ratios to assemble the required representation of the dataset for experiments.
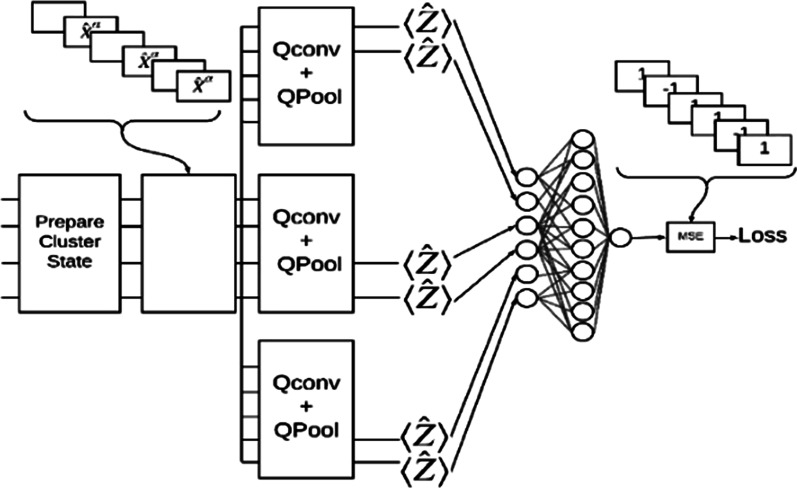
Experiments
In this section, the data pre-processing, model implementation, and evaluation methods have been explained. The experiment processes involved choosing a base model for initial trials and develop the same using the data collected. Based on various performance criteria compared between QNN, QCNN,2 Hybrid CNN with a single filter and Hybrid CNN with multiple filters (Fig. 5) from the simplicity of circuit design and performance measurement, QNN was chosen for remaining benchmarking during the trials. Furthermore, the experiments were performed using TensorFlow Quantum (TFQ), and a python framework for QML development. Notably, we leveraged upon D-wave Leap and TensorFlow Quantum Framework as a platform for training and evaluating the experimental setup. The estimated wait time for problem submission was 1–10 s on a 2041 qubits system, under 13.5 qubit temperature (mK). Detailed specifications of the platform may be referred from D-wave and TensorFlow.3
Fig. 5.
A quantum CNN: hybrid Convolution with multiple quantum filters
TFQ's core focus area is generally on quantum data, and a hybrid quantum-classical model. Various components that need to be followed to build a quantum circuit within the TensorFlow environment have been described below,
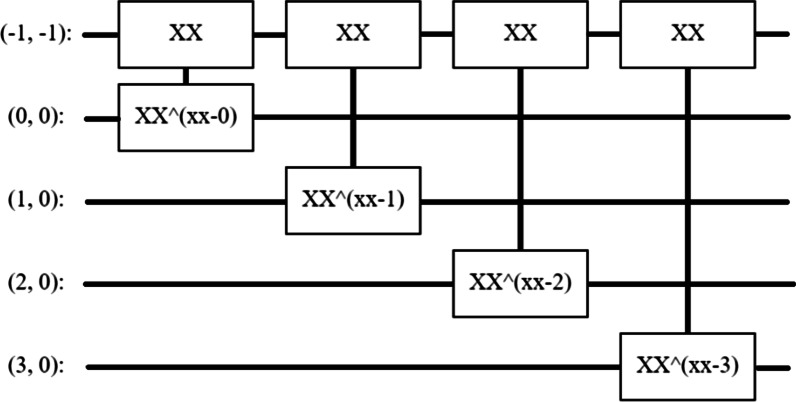
Circuit—Cirq is used to design the quantum circuit (Fig. 6). Cirq4 is a python framework for writing, optimizing quantum circuits executing in quantum hardware.
Pauli Sum—the linear combinations of tensor products of Pauli operators5 defined in Cirq is represented by Pauli sum, operations like circuits, create batches of operators of varying size are of such type.
Fig. 6.
A quantum circuit
The experiments performed, involved various feature engineering and transformation stages applied to design. Since the quantum machine cannot handle the large size of the image, we re-scaled it to 4 × 4 at the data processing stage. The overall image calibration steps performed are stated as below,
Input raw data using Keras
Filtering the dataset to only 3 s and 6 s
Downscales the images to fit in a quantum hardware.
Treating and removing contradictory examples
Convert binary images to Cirq circuits
Convert the Cirq circuits to a TensorFlow quantum circuits
In QML, a pixel is represented as a qubit, wherein each stage would actually depend on the pixel value. The process of encoding the data into the Quantum circuit was iterated at multiple threshold values, in the range [0.5, 0.6, 0.7]. A circuit at 0.5 threshold is represented in Fig. 7, and which effectively is a form of 2-layer circuit design for binary classification problems. In terms of model development, various iterations were performed to optimize the general performance of the model through a range of hyper-parametrization testing at various epochs.
Fig. 7.
The circuit from the training samples in the first iteration of the 2-layer circuit
Finally, the experiment encompassed creating a 2-layered model (Fig. 7) fitting the data-circuit size, including both preparation and readout operations. In fact, this method could possibly be compared to running a small recurring neural network across pixels. Notably herein, each layer uses n instances of the same gate, with each of the data qubits acting on the readout qubit. Additionally, the model building process further used hinge loss as a loss function, along with adaptive learning rate optimization (ADAM) optimizer instead of stochastic gradient descent-based optimizer, which was computationally inexpensive, and possibly even easier to implement. The experimentation process was conducted with different epoch and batch sizes, and the results are presented in the following sections; notably, the overall model parameters are shown in Table 5 below.
Table 5.
QNN parameter
| Parameter(s) | Value |
|---|---|
| Layer | PQC |
| Output shape | (None, 1) |
| Param | 32 |
| Model | Sequential |
| Loss function | Hinge |
| Optimizer | ADAM |
| Evaluation metrics | Hinge accuracy |
Evaluation criteria
This paper presents validation loss and validation accuracy as evaluation criteria for the QNN model, whereby the selected metric is ‘hinge loss’ for the experiment, as the problem formulation alludes to a binary classification problem [42]. Importantly, the ‘hinge loss’ represents the difference in prediction from actuals. Moreover, since validation loss is not used to update weights in general, it possibly serves as the right measure of any neural network model. A hinge loss6 i.e., l(y) is calculated by comparing prediction (y) with the actual target for prediction (t), followed by subtracting the value from 1, while computing thereafter the maximum value between 0 and the result of the earlier computation.
Results
To conclude the experimentation process and benchmarking with other relevant methods adopted for detecting COVID-19 patients, the model built, used a 9500-training dataset, encompassing an evaluation conducted over 1500 validation sample sets. The efficacy and the performance evaluation criteria are based on experiments performed with three, five and ten epochs and similar batch sizes. The key metrices taken into the consideration are loss and hinge accuracy shown in Table 6 and confusion matrix shown in Table 7.
Table 6.
Loss score and hinge accuracy
| Epoch | Loss | Hinge accuracy | Validation loss | Val hinge accuracy |
|---|---|---|---|---|
| 1/10 | 0.6566 | 0.7534 | 0.3870 | 0.8160 |
| 2/10 | 0.3568 | 0.8263 | 0.3348 | 0.8311 |
| 3/10 | 0.3281 | 0.8497 | 0.3269 | 0.8579 |
| 4/10 | 0.2994 | 0.9061 | 0.2894 | 0.8769 |
| 5/10 | 0.2707 | 0.9542 | 0.2594 | 0.8978 |
| 6/10 | 0.2707 | 0.9582 | 0.2293 | 0.9188 |
| 7/10 | 0.2133 | 0.9586 | 0.1993 | 0.9397 |
| 8/10 | 0.1872 | 0.9582 | 0.1692 | 0.9607 |
| 9/10 | 0.1872 | 0.9582 | 0.1692 | 0.9607 |
| 10/10 | 0.1821 | 0.9692 | 0.1691 | 0.9657 |
Table 7.
Confusion matrix
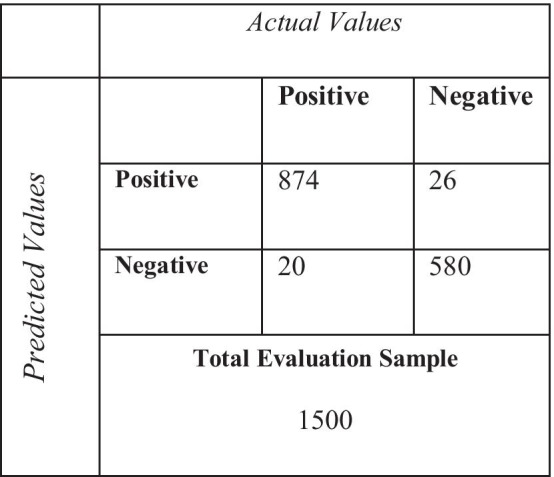
The change in epoch lowers the loss score, while improving the overall hinge accuracy. The change in accuracy score sees a significant lift after the third epoch, and gradually improves, reducing thereby the loss to 0.1559; notably, the percentage score of the change of loss is shown in the analysis in Fig. 8. The overall precision of the implemented model is 97.11%, whereas recall is 97.76% respectively.
Fig. 8.
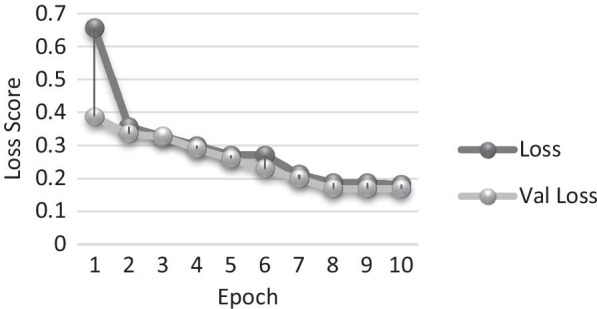
Change in loss per epoch (training and validation)
While comparing the traditional deep learning model with QNN (Fig. 9), the latter obtained a 2.92% lift from the 2D CNN model, trained for classification problems in the CT scan data set of COVID-19 patients. The analysis further describes the efficiency of the overall system to scale classification models, whereby the total time to train the model with 9500 images was observed to be 52 min on quantum optimized hardware, while compared to an experiment using CNN on K80 GPU Instance.
Fig. 9.
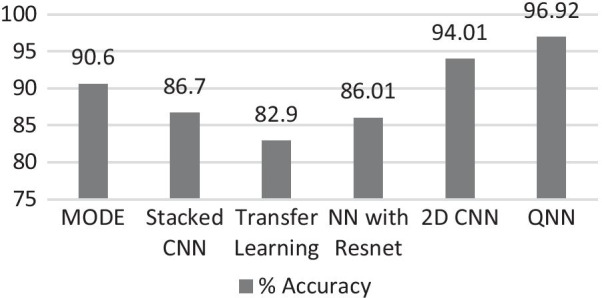
Comparison of various DL models versus QNN
Discussion
The study does entail certain limitations; for instance, the dataset and the training time comparison were limited to available samples. The images collected were limited to CT-Scan with a focus on identifying discoverable patches denoting COVID-19 infection. Further, a detailed study is required to incorporate signals that may occur in a CT-Scan image tending to non-COVID signals to make the model more robust on detection. Further, this study is limited to a minimum viable solution model that would possibly need additional research to take the present version of the model into readily deployable services mode, within the ambit of the biomedical device ecosystem from an end-to-end technology implementation standpoint, supporting thereby large-scale usage in clinical trials.
The crucial point of discussion from a future research standpoint would be around how to leverage the power of quantum algorithms on hardware and localize it to biomedical devices for seamless analysis. This study did demonstrate a substantial advantage to overall medical imaging problems, using quantum learning techniques, while also implementing classical learning models in the context for performance and efficacy in improved model implementations. The model demonstrates robustness while comparing the overall recall value, as any incorrect misclassification of CoViD-19 infected patient could lead to reduction in the overall significances of the predicted outcome further deferring accurate medical diagnosis when compared to a wrongly classified patient with pneumonia or other viral infection that may show similar strains.
While the study also discussed the aspects of hardware requirements for training and evaluation of such models, significant research is still under process, whereby there has been an attempt to launch an economical cloud platform for quantum hardware simulation and modeling. Further, this study provides scope for new development area of edge-quantum computing, and opens up research dialogues around faster diagnostics, and easy interpretation of quantum algorithms in the medical world.
Conclusion
In this study, we proposed a quantum neural learning model to classify patients with COVID-19 infection, leveraging upon computed tomography scan images in medical diagnosis. The suggested model attained optimal degree of model efficacy during an experimental comparison, yielding 96.92% of accuracy overall, leveraging 9500 + CT-Scan sample images. Additionally, the overall computation time for training the model recorded was 52 min, with the entire sample, along with the inferencing time recorded, which was a minute per image. This overall model training time was significantly less as compared to classical CNN model building with similar samples, using quantum hardware. Our results thereby yield not only a significant lift in the overall accuracy, but also optimizes upon the execution time. The model could be further deployed in clinical trials and medical diagnoses, which have a significant impact on overall decision support for treating patients with early symptoms. Moreover, a medical practitioner could also leverage upon our framework for quicker diagnostics, helping him/her to follow-up with the right treatment, and thereby save a life.
The impact of this paper not only quantifies the ability of QML, but also would help clinical scientists build diagnostic tools applied to drug discovery and disease identification problems with much faster analytical capability using quantum hardware. The study further provides prospects to evaluate quantum algorithms for more complex problems pertaining to image segmentation.
Acknowledgements
Not Applicable.
Abbreviations
- DL
Deep learning
- CNN
Convolutional neural network
- QNN
Quantum neural network
- QCNN
Quantum convolutional neural network
- ADAM
Adaptive learning rate optimization
- MODE
Multi-objective differential evolution
- RNN
Recurring neural networks
- AUC-ROC
Area under the curve-receiver operating curve
- DNN
Deep neural network
- LSTM
Long short-term memory
- CT
Computed tomography
- CXR
Chest x-ray
- Unitary Matrix(U)
In Quantum mechanics, the Hermitian adjoint of a matrix is denoted by a dagger (†) and the equation is represented by U†U = UU† = I, comparable with linear algebra equation U*U = UU* = I, when composite square matrix U is unitary, if conjugate transpose U* is inverse
- Pauli Sum
Calculate and simplify the sum of Pauli operators (I, X, Y, Z) according to Pauli algebra rules
- Circuit
It represents Quantum model, a sequence of quantum gates for performing a series of computations
- Hinge Loss Formula
L(y) l(y) = max(0,1 − t*y)
- Qubit
A qubit is a basic unit of quantum information representing information as 0 or 1
- CoViD-19
Coronavirus disease
Authors' contributions
KS staged the overall conceptualization of the problem, performed data collection and experimentation. Dr. PRS validated key metrics and revised the manuscript from a quality perspective. Both authors have read and approved the final manuscript.
Funding
Not Applicable.
Availability of data and materials
The datasets generated and/or analyzed during the current study are available in the GitHub repository, https://bit.ly/3xGUS8Q. The dataset does not consist of any confidential data.
Declarations
Ethics approval and consent to participate
Not Applicable. The data leveraged in the study were obtained from open-source databases, no additional approval is required.
Consent for publication
Not applicable.
Competing interests
KS is full-time Data Scientist at Microsoft Corporation India. All other authors declare they have no conflict of interest.
Footnotes
Refer to Abbreviations for detailed nomenclature.
Refer to Abbreviations.
Refer to Abbreviations for detailed nomenclature.
Refer to definition of pauli operators in nomenclature section.
Refer to Abbreviations for detailed nomenclature.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Kinshuk Sengupta, Email: efpm01.004@iimrohtak.ac.in.
Praveen Ranjan Srivastava, Email: praveen.ranjan@iimrohtak.ac.in.
References
- 1.Niu J, Shi Y, Cai M, Cao Z, Wang D, Zhang Z, Zhang X. Detection of sputum by interpreting the time-frequency distribution of respiratory sound signal using image processing techniques. Bioinformatics. 2017;34(5):820–827. doi: 10.1093/bioinformatics/btx652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bloice M, Roth P, Holzinger A. Biomedical image augmentation using Augmentor. Bioinformatics. 2019;35(21):4522–4524. doi: 10.1093/bioinformatics/btz259. [DOI] [PubMed] [Google Scholar]
- 3.Shu J, Liu J, Zhang Y, Fu H, Ilyas M, Faraci G, et al. Marker controlled superpixel nuclei segmentation and automatic counting on immunohistochemistry staining images. Bioinformatics. 2020;36(10):3225–3233. doi: 10.1093/bioinformatics/btaa107. [DOI] [PubMed] [Google Scholar]
- 4.Milon Islam Md, Saifuddin Mahmud LJ, Muhammad Md, Islam R, Nooruddin S, Ayon SI. Wearable technology to assist the patients infected with novel coronavirus (COVID-19) SN Comput Sci. 2020;1(6):320. doi: 10.1007/s42979-020-00335-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ullah SMA, Milon Islam Md, Mahmud S, Sheikh Nooruddin SM, Raju TU, Rezwanul Haque Md. Scalable telehealth services to combat novel coronavirus (COVID-19) pandemic. SN Comput Sci. 2020;2(1):18. doi: 10.1007/s42979-020-00401-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lather M, Singh P. Investigating brain tumor segmentation and detection techniques. Procedia Comput Sci. 2020;167:121–130. doi: 10.1016/j.procs.2020.03.189. [DOI] [Google Scholar]
- 7.Staff S. Covid-19: Double mutant strain could be considered a variant of concern, says top scientist (2021). Retrieved 15 April 2021, from https://scroll.in/latest/992323/covid-19-double-mutant-strain-could-be-considered-a-variant-of-concern-says-top-scientist
- 8.Zhou S, Greenspan H, Davatzikos C, Duncan J, Van Ginneken B, Madabhushi A, Prince J, Rueckert D. Summers R. A review of deep learning in medical imaging: imaging traits, technology trends, case studies with progress highlights, and future promises. 2020. [DOI] [PMC free article] [PubMed]
- 9.Gao J, Yang Y, Lin P, Park DS. Computer vision in healthcare applications. J Healthc Eng. 2018; [DOI] [PMC free article] [PubMed]
- 10.Porwal P, Pachade S, Kokare M, Deshmukh G, Son J, Bae W, et al. IDRiD: diabetic retinopathy—segmentation and grading challenge. Med Image Anal. 2020;59:101561. doi: 10.1016/j.media.2019.101561. [DOI] [PubMed] [Google Scholar]
- 11.Altaf F, Islam SMS, Akhtar N, Janjua NK. “Going deep in medical image analysis: Concepts, methods, challenges and future directions”. IEEE Access. 2019;7:99540–72.
- 12.Acampora G. Quantum machine intelligence. Quantum Mach Intell. 2019;1(1–2):1–3. doi: 10.1007/s42484-019-00006-5. [DOI] [Google Scholar]
- 13.Kiani B, Villanyi A, Lloyd S. Quantum medical imaging algorithms; 2020. arXiv.org. Retrieved 23 May 2020, from https://arxiv.org/abs/2004.02036.
- 14.Mayr A, Klambauer G, Unterthiner T, Hochreiter S. Deeptox: toxicity prediction using deep learning. Front Environ Sci. 2016 doi: 10.3389/fenvs.2015.00080. [DOI] [Google Scholar]
- 15.Orús R, Mugel S, Lizaso E. Quantum computing for finance: overview and prospects. Rev Phys. 2019;4:100028. doi: 10.1016/j.revip.2019.100028. [DOI] [Google Scholar]
- 16.Chen H, Engkvist O, Wang Y, Olivecrona M, Blaschke T. The rise of deep learning in drug discovery. Drug Discovery Today. 2018;23(6):1241–1250. doi: 10.1016/j.drudis.2018.01.039. [DOI] [PubMed] [Google Scholar]
- 17.Solenov D, Brieler J, Scherrer JF. The potential of quantum computing and machine learning to advance clinical research and change the practice of medicine. Mo Med. 2018;115(5):463–467. [PMC free article] [PubMed] [Google Scholar]
- 18.Rizwan I, Haque I, Neubert J. Deep learning approaches to biomedical image segmentation. Inform Med Unlocked. 2020;18:100297. doi: 10.1016/j.imu.2020.100297. [DOI] [Google Scholar]
- 19.Dunjko V, Taylor J, Briegel H. Quantum-enhanced machine learning. Phys Rev Lett. 2016;117(13). 10.1103/physrevlett.117.130501 [DOI] [PubMed]
- 20.Laumann T, Snyder A, Mitra A, Gordon E, Gratton C, Adeyemo B, Gilmore A, Nelson S, Berg J, Greene D, McCarthy J, Tagliazucchi E, Laufs H, Schlaggar B, Dosenbach N, Petersen S. On the stability of BOLD fMRI correlations. Cerebral Cortex. 2016. [DOI] [PMC free article] [PubMed]
- 21.Moore G. Cramming more components onto integrated circuits, Reprinted from Electronics, volume 38, number 8, April 19, 1965, pp.114 ff. IEEE Solid-State Circuits Soc Newslett. 2006;11(3):33–35.
- 22.Yanofsky N. An introduction to quantum computing. Proof Comput Agency. 2011 doi: 10.1007/978-94-007-0080-2_10. [DOI] [Google Scholar]
- 23.Imtiyaz S. Quantum adiabatic evolution for global optimization in big data; 2020. arXiv.org. Retrieved 23 May 2020, from https://arxiv.org/abs/1805.11479.
- 24.Chowdhury AN, Somma RD. Quantum algorithms for Gibbs sampling and hitting-time estimation. Quantum Info Comput. 2017;17:1–2.
- 25.Moreira C, Wichert A. Quantum-like Bayesian networks for modeling decision making. Front Psychol. 2016 doi: 10.3389/fpsyg.2016.00011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lee YT, Sidford A, Wong SC-W. A faster cutting plane method and its implications for combinatorial and convex optimization. In: Proceedings of 2015 IEEE 56th Annual Symposium on Foundations of Computer Science (FOCS), Berkeley, CA. New York: IEEE; 2015, p. 1049–1065
- 27.Arora S, Kale S. A combinatorial, primal-dual approach to semidefinite programs. In: Proceedings of of the 39th Annual ACM Symposium on Theory of Computing, San Diego, CA. New York: ACM; 2007, p. 227–236
- 28.Georgescu I, Ashhab S, Nori F. Quantum simulation. Rev Modern Phys. 2014;86(1):153–185. doi: 10.1103/revmodphys.86.153. [DOI] [Google Scholar]
- 29.de Lacy K, Noakes L, Twamley J, Wang J. Controlled quantum search. Quantum Inf Process. 2018;17(10). 10.1007/s11128-018-2031-6
- 30.Sentís G, Monràs A, Muñoz-Tapia R, Calsamiglia J, Bagan E. Unsupervised classification of quantum data. Phys Revi X. 2019;9(4).
- 31.Henderson M, Shakya S, Pradhan S, Cook T. Quanvolutional neural networks: powering image recognition with quantum circuits. 2019. [online] arXiv.org. Available at: [Accessed 21 July 2021].
- 32.Vabalas A, Gowen E, Poliakoff E, Casson A. Machine learning algorithm validation with a limited sample size. PLoS ONE. 2019;14(11):e0224365. doi: 10.1371/journal.pone.0224365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chen J, Wu L, Zhang J, Zhang L, Gong D, Zhao Y et al. Deep learning-based model for detecting 2019 novel coronavirus pneumonia on high-resolution computed tomography: a prospective study; 2020. 10.1101/2020.02.25.20021568 [DOI] [PMC free article] [PubMed]
- 34.Jin S, Wang B, Xu H, Luo C, Wei L, Zhao W et al. AI-assisted CT imaging analysis for COVID-19 screening: building and deploying a medical AI system in four weeks; 2020. 10.1101/2020.03.19.20039354 [DOI] [PMC free article] [PubMed]
- 35.Sabottke C, Spieler B. The effect of image resolution on deep learning in radiography. Radiol Artif Intell. 2020;2(1):e190015. 10.1148/ryai.2019190015 [DOI] [PMC free article] [PubMed]
- 36.Shi H, Han X, Jiang N, Cao Y, Alwalid O, Gu J, et al. Radiological findings from 81 patients with COVID-19 pneumonia in Wuhan, China: a descriptive study. Lancet Infect Dis. 2020;20(4):425–434. doi: 10.1016/s1473-3099(20)30086-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Li L, Qin L, Xu Z, Yin Y, Wang X, Kong B, et al. Artificial intelligence distinguishes COVID-19 from community acquired pneumonia on chest CT. Radiology. 2020 doi: 10.1148/radiol.2020200905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hani C, Trieu N, Saab I, Dangeard S, Bennani S, Chassagnon G, Revel M. COVID-19 pneumonia: a review of typical CT findings and differential diagnosis. Diagn Interv Imaging. 2020;101(5):263–268. doi: 10.1016/j.diii.2020.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sreedhar K. Enhancement of images using morphological transformations. Int J Comput Sci Inf Technol. 2012;4(1):33–50. doi: 10.5121/ijcsit.2012.4103. [DOI] [Google Scholar]
- 40.Hu X, Wang H, Vegesana A, Dube S, Yu K, Kao G, et al. Crowdsourcing detection of sampling biases in image datasets. Proc Web Conf. 2020 doi: 10.1145/3366423.3380063. [DOI] [Google Scholar]
- 41.Wanyan T, Zhang J, Ding Y. Azad A, Wang Z, Glicksberg B. Bootstrapping your own positive sample: contrastive learning with electronic health record data (2021). [online] arXiv.org. <https://arxiv.org/abs/2104.02932v1> Accessed 7 July 2021.
- 42.Liang S, Sun R, Lee JD, Srikant R. Adding one neuron can eliminate all bad local minima. In: 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, Canada; 2018
- 43.Singh D, Kumar V, Vaishali et al. Classification of COVID-19 patients from chest CT images using multi-objective differential evolution–based convolutional neural networks. Eur J Clin Microbiol Infect Dis. 2020. 10.1007/s10096-020-03901-z [DOI] [PMC free article] [PubMed]
- 44.Xu X, Jiang X, Ma C, Du P, Li X, Lv S et al. Deep learning system to screen coronavirus disease 2019 pneumonia; 2020. arXiv.org. Retrieved 22 May 2020, from https://arxiv.org/abs/2002.09334v1.
- 45.Buades A, Coll B, Morel J. Non-Local means denoising. Image Process Line. 2011;1:208–212.
- 46.Song Y, Zheng S, Li L, Zhang X, Zhang X, Huang Z et al. Deep learning enables accurate diagnosis of novel coronavirus (COVID-19) with CT images; 2020. 10.1101/2020.02.23.20026930 [DOI] [PMC free article] [PubMed]
- 47.Shan F, Gao Y, Wang J, Shi W, Shi N, Han M et al. Lung infection quantification of COVID-19 in CT images with deep learning; 2020. arXiv.org. Retrieved 22 May 2020, from https://arxiv.org/abs/2003.04655.
- 48.Barstugan M, Ozkaya U, Ozturk S. Coronavirus (COVID-19) classification using CT images by machine learning methods; 2020. arXiv.org. Retrieved 22 May 2020, from https://arxiv.org/abs/2003.09424v1.
- 49.Heinrich MP, Blendowski M, Oktay O. TernaryNet: faster deep model inference without GPUs for medical 3D segmentation using sparse and binary convolutions. Int J CARS. 2018;13:1311–1320. doi: 10.1007/s11548-018-1797-4. [DOI] [PubMed] [Google Scholar]
- 50.Islam MM, Islam MZ, Asraf A, Ding W. Diagnosis of COVID-19 from X-rays using combined CNN-RNN architecture with transfer learning; 2020
- 51.Zabirul Islam M, Islam MM, Asraf A. A combined deep CNN-LSTM network for the detection of novel coronavirus (COVID-19) using X-ray images. Inform Med Unlocked 2020; 20:100412 [DOI] [PMC free article] [PubMed]
- 52.Singh D, Kumar V, Kaur M. Densely connected convolutional networks-based COVID-19 screening model. Appl Intell. 2021 [DOI] [PMC free article] [PubMed]
- 53.Kadampur M, Al Riyaee S. Skin cancer detection: applying a deep learning based model driven architecture in the cloud for classifying dermal cell images. Inform Med Unlocked. 2020;18:100282. doi: 10.1016/j.imu.2019.100282. [DOI] [Google Scholar]
- 54.Baranov M. Image processing of biological liquids films for medical diagnostics. J Electron Sci Technol. 2020 doi: 10.1016/j.jnlest.2020.100027. [DOI] [Google Scholar]
- 55.Uesawa Y. Quantitative structure–activity relationship analysis using deep learning based on a novel molecular image input technique. Bioorg Med Chem Lett. 2018;28(20):3400–3403. doi: 10.1016/j.bmcl.2018.08.032. [DOI] [PubMed] [Google Scholar]
- 56.Gilmer J, Schoenholz S, Riley P, Vinyals O, Dahl G. Neural Message Passing for Quantum Chemistry. arXiv.org. Retrieved 22 May 2020, from https://arxiv.org/abs/1704.01212.
- 57.Aliper A, Plis S, Artemov A, Ulloa A, Mamoshina P, Zhavoronkov A. Deep learning applications for predicting pharmacological properties of drugs and drug repurposing using transcriptomic data. Mol Pharm. 2016;13(7):2524–2530. doi: 10.1021/acs.molpharmaceut.6b00248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Merkwirth C, Lengauer T. Automatic generation of complementary descriptors with molecular graph networks. J Chem Inform Model. 2005;45(5):1159–1168. doi: 10.1021/ci049613b. [DOI] [PubMed] [Google Scholar]
- 59.Islam MM, Azmat Ullah SM, Mahmud S, Taslim Uddin Raju SM. Breathing aid devices to support novel coronavirus (COVID-19) infected patients. SN Comput Sci. 2020;1(5):274. [DOI] [PMC free article] [PubMed]
- 60.Islam MM, Karray F, Alhajj R, Zeng J. A review on deep learning techniques for the diagnosis of novel coronavirus (COVID-19) IEEE Access. 2021;9:30551–30572. doi: 10.1109/ACCESS.2021.3058537. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated and/or analyzed during the current study are available in the GitHub repository, https://bit.ly/3xGUS8Q. The dataset does not consist of any confidential data.