Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jul 15;21(14):6095–6101. doi: 10.1021/acs.nanolett.1c01502

Extreme Ultraviolet Second Harmonic Generation Spectroscopy in a Polar Metal

Emma Berger †,‡,*, Sasawat Jamnuch §, Can B Uzundal †,‡, Clarisse Woodahl ∥, Hari Padmanabhan ⊥, Angelique Amado †,‡, Paul Manset #, Yasuyuki Hirata ○, Yuya Kubota ☆,□, Shigeki Owada ☆,□, Kensuke Tono ☆,□, Makina Yabashi ☆,□, Cuixiang Wang ◆, Youguo Shi ◆, Venkatraman Gopalan ⊥, Craig P Schwartz , Walter S Drisdell ¶,∇, Iwao Matsuda ⊞,▲, John W Freeland ⊕, Tod A Pascal §,●,&, Michael Zuerch †,‡,£,Œ,*
PMCID: PMC8323121  PMID: 34264679

Abstract

graphic file with name nl1c01502_0004.jpg

The coexistence of ferroelectricity and metallicity seems paradoxical, since the itinerant electrons in metals should screen the long-range dipole interactions necessary for dipole ordering. The recent discovery of the polar metal LiOsO3 was therefore surprising [as discussed earlier in Y. Shi et al., Nat. Mater. 2013, 12, 1024]. It is thought that the coordination preferences of the Li play a key role in stabilizing the LiOsO3 polar metal phase, but an investigation from the combined viewpoints of core-state specificity and symmetry has yet to be done. Here, we apply the novel technique of extreme ultraviolet second harmonic generation (XUV-SHG) and find a sensitivity to the broken inversion symmetry in the polar metal phase of LiOsO3 with an enhanced feature above the Li K-edge that reflects the degree of Li atom displacement as corroborated by density functional theory calculations. These results pave the way for time-resolved probing of symmetry-breaking structural phase transitions on femtosecond time scales with element specificity.

Keywords: X-ray nonlinear spectroscopy, polar metal, materials science, second harmonic generation

A central question of condensed matter physics is how the structure of a material gives rise to its function. One approach to this so-called “structure–function problem” is to ask how the elemental composition plays a role in a material’s emergent functionality. A symmetry-based perspective offers yet another valuable viewpoint. Here, we combine the insights of both approaches in a single experiment, namely extreme ultraviolet second harmonic generation (XUV-SHG), to explore the nonintuitive coexistence of polarity and metallicity in lithium osmate (LiOsO3). Although it was first predicted over 50 years ago that polar metals could form through a second-order phase transition, the first experimentally realized “ferroelectric-like” metal, LiOsO3, was discovered only recently.1,2 The search for polar metals has since expanded, motivated by prospects of multiferroics,3 electrodes in ferroelectric nanocapacitors,4 nonlinear optical media,5 polar superconductors,6−8 and thermoelectric devices.9 Recent works predicting asymmetric hysteresis in LiOsO3 thin films and revealing ferroelectric switching in a two-dimensional metal10 have generated significant recent excitement for the practical application of low-dimensional devices. Despite the numerous attempts to explain the coexistence of polarity and metallicity, there are still many unanswered questions as to how polar order can be stabilized in a metal.

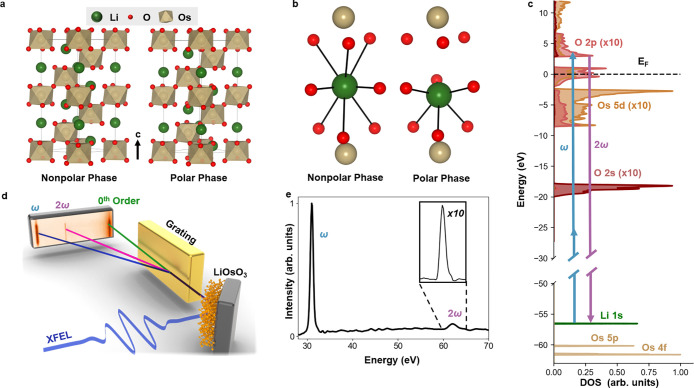
Since its discovery, LiOsO3 has become a prototypical polar metal. In this perovskite-structured material (ABO3), a continuous order–disorder phase transition occurs at a critical temperature of Tc = 140 K, where it transitions from an R3c nonpolar metallic to an R3c polar metallic phase through the loss of inversion symmetry (Figure 1a). Neutron diffraction,1 Raman spectroscopy,11 and optical spectroscopy12 have shown that the A2u soft phonon mode responsible for the transition involves a coordinated 0.5 Å displacement of Li atoms along the polar c-axis.11 To explain these observations, several theories have been developed.13−17 The decoupled electron mechanism hypothesis proposed by Puggioni et al. postulates that the soft phonon responsible for driving the “ferroelectric” transition is energetically decoupled from the electrons at the Fermi level responsible for the metallicity. In this picture, ineffective electron screening of long-range dipolar couplings stabilize the polar phase.9,12,18 Benedek et al. proposed a related mechanism that emphasizes short-range, atomic details.19 Here, ion-size mismatch effects and the local coordination preferences of the A-site Li atom are thought to drive the phase transition. With short-range interactions at the forefront, the itinerant electrons that are expected to screen the dipole–dipole forces are, thus, of secondary importance. In the high-temperature phase, the Li atom is coordinated to nine nearby O atoms via three short Li–O bonds and six long Li–O bonds. On the other hand, signatures of the polar metal phase include OsO6 octahedral rotations that shorten three of the longer Li–O bonds, and Li atoms displacements that shorten the three short Li–O bonds. The overall effect of these structural changes is to octahedrally coordinate the Li atom in the polar metal phase19 (Figure 1b). With regard to why all the Li atoms are displaced uniformly, their coordinated motion is thought to both minimize the number of faces Li octahedra share with Os octahedra and open up unscreened channels of anisotropic Coulomb interactions by which to minimize the free energy.13,15 Hence, the Li-coordination environment plays a determining role in the stabilization of the polar metal phase, but an experimental viewpoint that takes both broken symmetries and core-level specificity into account is lacking. The most common probe of broken inversion symmetry is optical second harmonic generation (SHG) spectroscopy, which has been applied previously to examine the nature of Os–O bonding in LiOsO3.20 However, not only is optical SHG non-element-specific, but a partial density of states (DOS) analysis reveals overwhelming contributions of Os 5d and O 2p character around the Fermi level (Figure 1c and Section 6 in the Supporting Information (SI)). In LiOsO3, the features of interest are Li–O acentric displacements. Given the orbital character of states around the Fermi surface, it is not surprising then that an order-of-magnitude weaker optical SHG signal was found in LiOsO3, compared to LiTaO3 and LiNbO3.20

Figure 1.

Figure 1

Open in a new tab

The structures of LiOsO3 in its nonpolar and polar phases, partial density of states calculations, and experimental scheme. (a) The hexagonal unit cell of LiOsO3 in its high-temperature nonpolar phase and low-temperature polar phase with the polar c-axis identified. (b) In the nonpolar phase, the Li atoms are symmetrically located between two OsO6 octahedra from above and below and in plane with 3 nearby O atoms from adjacent OsO6 octahedra. In the polar phase, an asymmetric displacement of Li atoms along the emergent polar c-axis results in octahedrally coordinated Li atoms. (c) Partial density of states calculations. Near the Fermi level are predominantly states of Os 2p and Os 5d character. The XUV-SHG experiment involves core-level electron excitations at 28–33 eV photon energy (ω) that are half-resonant with the Li 1s core state, resulting in second harmonic emission (2ω). Note the y-scale has broken axes between −50 eV and −30 eV. (d) Schematic of the experimental setup. The fundamental XUV beam is incident on the [120] plane of a LiOsO3 crystal under a 45° angle of incidence, with respect to the surface normal. The reflected beam is spectrally dispersed by a grating onto a detector, enabling simultaneous measurement of signals at the fundamental and SHG frequencies. (e) A characteristic spectrum measured at an incident XFEL energy of 31 eV, featuring peaks at both the fundamental and second harmonic. The inset shows the 2ω signal (×10) in detail.

To gain insight into the nature of the polar phase, we turn to extreme ultraviolet second harmonic generation (XUV-SHG) spectroscopy, which is a newly developed method viable for studying bulk-phase noncentrosymmetric masterials,21 surfaces,22,23 and buried interfaces24 in the XUV or the soft X-ray (SXR) regimes, where the objective is to perform SHG under resonant conditions, and in the hard X-ray regime, where a nonresonant approach is usually taken.25−27 In SXR- or XUV-SHG spectroscopy, the incident X-ray beam is resonant or half-resonant with a core-to-valence transition, such that the resulting resonantly enhanced, background-free signal is sensitive to core levels in the electronic structure. By energetically resolving the SHG emission, the symmetry breaking can be correlated to particular spectral features. The application of XUV-SHG spectroscopy to such short wavelengths requires the use of XUV photon sources capable of achieving high pulse intensities to drive the nonlinear light-matter response, for which X-ray free electron lasers (XFEL) are uniquely well-suited. The inherent intensity fluctuations of XFEL sources measure on a shot-to-shot basis enable measuring the nonlinear response via

graphic file with name nl1c01502_m001.jpg 1

where χeff(2) is the effective nonlinear susceptibility, dependent on crystal cut and experimental geometry, the incident beam is at a frequency-dependent intensity, I(ω), and SHG emission occurs with a frequency of 2ω. Here, the dielectric environment around Li in LiOsO3 below Tc is probed by tuning the incident XFEL photon energy to be half-resonant with energies around the Li K-edge at −56.6 eV (Figure 1c) with contributions from nearby Os semicore states. The energy-dependent χeff is extracted according to eq 1 and ab initio density functional perturbation theory (DFPT) simulations are used to relate the nonlinear response to the broken inversion symmetry. We find that the resultant nonlinear susceptibility suggests sensitivity to Li atomic displacements in the unit cell, but a lack of OsO6 octahedral rotations. Further, our results pave the way toward time- and temperature-dependent measurements of inversion symmetry-broken systems with core-level specificity.

Experimental Results

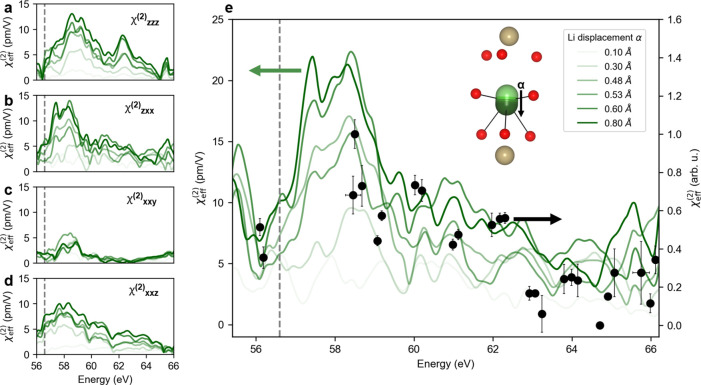
XUV-SHG spectroscopy was performed on samples of LiOsO3 in its polar metal phase at T = 62 K and in its high-temperature centrosymmetric phase at T = 160 K at the BL1 beamline of the SPring-8 Angstrom Compact Free Electron Laser (SACLA).28 A 30 fs p-polarized XUV beam was incident at 45°, with respect to the surface normal onto the [120] plane of LiOsO3. By tuning the incident photon energy to energies ranging from 28 eV to 33 eV, the incident photon was half-resonant with the Li 1s (−56.6 eV) level and close-by Os 4f (−61.6 eV) and 5p (−60.2 eV) levels, thus requiring two incident photons to access the valence states (Figure 1c). XUV-SHG spectra were collected by energy-dispersing the outgoing beam with a grating to simultaneously observe the fundamental and second harmonic beams using an imaging spectrometer (Figures 1d-e). Through nonlinear effects, a p-polarized fundamental photon can result in a nontrivial weighting of both s- and p-polarized frequency-doubled photons. An estimation of the relative contribution of both channels is provided in Section S1 in the SI, but further polarization analysis is beyond the scope of this work, since the two polarizations are not experimentally resolved. The χeff(2) spectrum was then extracted using eq 1 after binning and averaging spectra based on the photon energy and intensity of the driving fundamental pulse. The inherent jitter of the XFEL, both in frequency and intensity, allowed for a high-fidelity extraction of χeff(2ω) with significantly more data points, compared to refs (21−24). For the T = 62 K set of measurements, a quadratic function was fit to a plot of I(ω) vs I(2ω), at each energy where the second-order fit coefficient is modulo |χeff(2)(2ω)|2, with χeff(2ω) a rank-three tensor of four independent components (χzzz(2),χxxz, χzxx(2), and χxxy), because of point group symmetry (Figure 2e). For the measurements at 160 K, no SHG signal was discernible above the background noise, in accordance with the centrosymmetry of the LiOsO3 high-temperature phase. The lack of observable SHG above Tc further serves to rule out that the SHG from the low-temperature phase comes from broken inversion symmetry at the surface or harmonic contamination in the FEL beam.

Figure 2.

Figure 2

Open in a new tab

The energy-dependent nonlinear susceptibility across the Li K-edge. (a–d) χzzz(2), χzxx, χxxy(2), and χxxz across the Li K-edge. (e) The experimentally determined nonlinear susceptibility shown (black points) overlaid onto the calculated χeff(2)(2ω). For panels (a-e), the dashed gray line at 56.6 eV corresponds to the onset of the Li K edge: darker green corresponds to larger Li displacement along the polar axis (α) of the LiOsO3 polar phase as indicated by the inset in panel (e) and in the corresponding legend. Vertical error bars correspond to errors in the quadratic fit of eq 1, whereas horizontal error bars are a result of energy jitter of the FEL.

In order to relate the measured nonlinear susceptibility to unit cell structure, a tensor analysis considering the experiment geometry and crystal cut was performed to arrive at a mathematical expression for χeff(2). Further details of the experimental setup, data analysis, and sample preparation are described in sections S0–S4 in the SI.

According to the selection rules for SHG, electrons residing in Li 1s core states can transition to valence states of Os 5d character, whereas the Os 5p and Os 4f semicore states can transition to valence states of O 2p character (Figure 1c). The approximately 2 eV-wide gap in the DOS above the Fermi level (EF) has been previously assigned to the crystal-field splitting in Os 5d-like orbitals, but the nonzero DOS directly at EF is consistent with the metallic character of LiOsO3.16

To gain insight into how the measured spectra relate to the Li coordination environment, theoretical calculations of the LiOsO3 linear absorption were performed using the exciting full-potential all-electron-augmented linearized planewave software package based on first-principles density function theory (DFT).29 Two LiOsO3 periodic cell structures, corresponding to the nonpolar and polar phases, were used. The Brillouin zone was sampled with a 15 × 15 × 15 Γ-point centered k-point grid with the local density approximation functional.30 DFPT simulations within the random phase approximation were used to access excited states of the system. The formalism outlined by Sharma et al., as implemented within exciting, was used calculate the four active χijk(2) tensor elements (see Figures 2a–d), with the aforementioned k-point grid set.31 120 empty states were included in the ground-state calculation to account for the excited state at double the energy of the Li 1s core state. The background signal, which is the response from the valence electrons and is proportional to the inverse of energy (∼1/energy), was subtracted to obtain the effective susceptibility from the core state. The χeff was next calculated as a function of varying Li position along the polar axis, α, and compared to the experimental results (Figure 2e). Simulations with OsO6 displacements were also performed (see Section S9 in the SI) showing only little effect on the resulting XUV-SHG spectra. In addition, the core-level nonlinear susceptibility (see Section S8 in the SI), was calculated with the exclusion of Li 1s states (see Section S7 in the SI), the results of which suggest that the nonlinear response within the energy range probed is predominantly due to the transition from Li 1s core states to states above the Fermi level. Finally, the DFT calculations were repeated using the Vienna ab initio software package (VASP32), using a projector augmented wave (PAW) approach and a plane wave basis set of up to 400 eV to visualize the Kohn–Sham equation-generated charge densities within the LiOsO3 unit cell. Shown in Figure 3 are projections of this charge density surface onto the [110] plane through the middle of the hexagonal unit cell.

Figure 3.

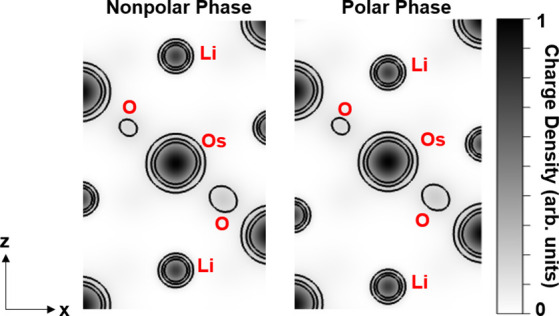
Figure 3

Open in a new tab

Charge densities within the LiOsO3 unit cell. Charge densities along the polar axis reveal inversion symmetry is broken in the polar phase as Li atoms are displaced vertically along the polar z-axis. An applied electric field along the z-axis further increases the magnitude of this asymmetry, whereas an applied electric field in the xy-plane increases it nontrivially. The black contours are drawn at 0.15 intervals of charge density units, from 0 to 0.6 arb.

Discussion

Absolute values of χeff(2) in the XUV are predicted to be on the order of 10 pm/V, which is in accordance with measured nonlinear susceptibilities of LiOsO3 and chemically similar LiTaO3 and LiNbO3 in the optical regime.20,33 The experimentally determined χeff shown in Figure 2e has several features to point out. DFT calculations in which the Li 1s states are removed from the simulation basis set indicate that the XUV-SHG signal in the 56–59 eV range is a result of transitions from Li 1s states (see Figure S7.1 in the SI). This is supported by the observation in Figure 2e that the spectral feature centered at 58 eV is highly sensitive to Li atom position within the unit cell. The increase in SHG signal measured experimentally suggests that XUV-SHG is sensitive to Li atomic displacements with core-level specificity. Furthermore, DFT simulations involving OsO6 octahedral rotations indicate that such motions have a very minimal affect the core-level χeff(2) spectrum (Figure S9.1). This observation, combined with the decreasing SHG response in the energy range above 60 eV corresponding to electronic transitions from Os semicore to O 2p states, suggests that inversion symmetry is largely maintained around the Os atoms.

Next, we turn to an analysis of how the XUV-SHG spectrum varies as a function of Li displacement α. The main feature at 58 eV increases in magnitude with asymmetry in the Li–O dipoles along the polar axis, resulting from one of two possible factors: (a) the mere increase in the asymmetric distortion enhances the XUV-SHG signal, or (b) as Li ions are displaced toward OsO6 octahedra, the aforementioned Li–O “long bonds” get shorter, leading to increased hybridization between orbitals of Li 2s and Os 2p character. This, in turn, gives more s-character to O 2p orbitals, thus opening up more selection-rule-allowed states for Li 1s electrons to transition into. The latter possibility is supported by DFT simulations since increased hybridization should lead to a downward shift in energy and a change in the density of states, which is observed in the appearance of a changing peak shape and a spectral shoulder at 57.5 eV as α increases.

To gain further insight into the inversion symmetry-breaking process, projections of the calculated charge density surface onto the [110] plane of the real space unit cell were examined. Shown in Figure 3 are slices of the charge density surfaces cut along the [110] plane in both the polar and nonpolar phases of LiOsO3. It is immediately apparent that the polar phase is characterized by broken inversion symmetry around the Li ions, as evidenced by the unequal relative displacements of each of the Li atoms to the central Os atom in the polar phase.

The plots in Figure 3 provide further qualitative physical intuition behind spectral features of the tensor elements shown in Figures 2a–d. Here, it should be noted that the ith index in χijk(2) corresponds to the Cartesian direction along which dipole oscillations are generated at with a frequency of 2ω by driving electric fields along the jthand kth directions. The broad feature at 58 eV observed in the calculated spectra for χzzz and χzxx(2) can be attributed to the polar displacement of Li atoms along the z-axis as the primary contributor to the broken inversion symmetry in LiOsO3. It can also be seen that χzzz and χxxz(2) increase in magnitude, but with a relatively unchanged spectral shape as α increases. In contrast, χ(2)zxx exhibits a nontrivial α-dependence. These observations can be contextualized by comparing the nonpolar and polar charge densities in Figure 3. Here, it is apparent that driving with a fundamental pulse along the z-direction will increase the asymmetry along the polar axis. Increasing α merely increases the amplitude of these oscillations. On the other hand, an incident laser beam polarized along the x-direction will alter the electron density with respect to the already present Li displacement in a complex way. Lastly, it is of note that χxxy changes minimally with α. This can again by explained by the observation that there are minimal polar displacements within the x–y plane for all atomic environments within the unit cell.

In summary, it is shown that XUV-SHG can selectively probe inversion-breaking symmetry in a bulk material with core-level specificity. Compared to optical SHG methods, XUV-SHG spectroscopy fills a key gap for studying structural asymmetries when the structural distortion is energetically separated from the Fermi surface and for probing symmetry-breaking in the spectral features of interest. For example, optical SHG would primarily probe Os–O acentric displacements, which obscures the Li–O acentric displacements that are the physics of interest. In addition, XUV-SHG offers the ability to access information on light atoms in a heavy-atom environment by making use of core-level resonances. A comparison of calculated charge density plots and theoretical simulations of the how the nonlinear susceptibility tensor elements vary as a function of Li displacement provide a qualitative picture for how microscopic asymmetries on unit cell length scales determine the nonlinear response. Open questions for future investigation are highlighted in three recent works. Shan et al.34 observed SHG due to electric quadrupolar effects above the polar ordering temperature up to 230 K, as a result of an extended critical fluctuation region. Such effects were not visible in XUV-SHG at 160 K, but may have been below the detection limit of this experiment. Through complementary theory calculations, Helk et al.23 noted that resonant and nonresonant contributions to SHG can be of the same order of magnitude in the XUV regime, because of allowed transitions from the valence band to high-energy continuum states. Further development of SHG methodology in the XUV and SXR regimes will be essential to deconvolute these contributions and to fully characterize element-specific responses. Lastly, we have recently demonstrated polarization-resolved XUV-SHG35 as a viable method to extract symmetry information from angle-resolved SHG responses with core-level specificity. Such a tool will add invaluable insight into systems like LiOsO3 where symmetry-arguments and angular anisotropies are central to structure–function relationships. We point out that the future of XUV-SHG spectroscopy lies in its potential to track the nonlinear response as a function of both temperature and time. The sensitivity to Li atom displacement above and below Tc demonstrated here highlight the viability for XUV-SHG for studying critical fluctuations, phase transitions, and interface physics in other condensed matter systems.

Acknowledgments

M.Z., C.P.S. and A.A. acknowledge support by the Max Planck Society (Max Planck Research Group). M.Z. acknowledges support by the Federal Ministry of Education and Research (BMBF), under“Make our Planet Great Again - German Research Initiative” (Grant No. 57427209 “QUESTforENERGY”) implemented by DAAD. J.W.F., H.P. and V.G. acknowledge Department of Energy Grant No. DE SC-0012375. W.S.D. acknowledges support from the Joint Center for Artificial Photosynthesis, a DOE Energy Innovation Hub, supported through the Office of Science of the U.S. Department of Energy, under Award No. DE-SC0004993. Measurements were performed at BL1 of SACLA with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2019B8066). This work was supported by the SACLA Basic Development Program 2018–2020. The authors would like to acknowledge the supporting members of the SACLA facility. Additional measurements were performed at beamline 6.3.2 of the Advanced Light Source, a U.S. DOE Office of Science User Facility (under Contract No. DE-AC02-05CH11231). This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy, under Contract No. DE-AC02-05CH11231. This work also used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation (Grant No. ACI-1548562). C. Wang and Y.S. acknowledge the National Natural Science Foundation of China (No. U2032204) and the Strategic Priority Research Program (B) of the Chinese Academy of Sciences (No. XDB33000000). C. Woodahl acknowledges support by the National Science Foundation REU Program (Grant No. 1852537). M.Z. acknowledges funding by the W. M. Keck Foundation, funding from the UC Office of the President within the Multicampus Research Programs and Initiatives (M21PL3263), and funding from Laboratory Directed Research and Development Program at Berkeley Lab (107573). We are grateful for input and discussion with David Attwood and Ramamoorthy Ramesh.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.1c01502.

  • Details about experimental methods, sample preparation, data processing, and theoretical calculations (PDF)

Author Contributions

A.A., P.M., Y.H., I.M., Y.K., S.O., K.T., M.Y., C.P.S., W.S.D., and J.W.F. performed the experiments at the SACLA free-electron laser. E.B., C.B.U., and M.Z. analyzed and interpreted the experimental data. C. Wang, and Y.S. synthesized the samples. H.P. and V.G. prepared and precharacterized the samples. S.J. and T.A.P. performed the simulations. W.S.D, A.A., and M.Z. performed linear reflectivity measurements at the Advanced Light Source. C. Woodahl. and C.B.U. analyzed the linear reflectivity data. M.Z., C.P.S., J.W.F., and W.S.D. conceived the experiment. M.Z. supervised the project. E.B. wrote the manuscript, under the supervision of M.Z. and with input from all authors.

The authors declare no competing financial interest.

Supplementary Material

nl1c01502_si_001.pdf (901.3KB, pdf)

References

  1. Shi Y.; Guo Y.; Wang X.; Princep A. J.; Khalyavin D.; Manuel P.; Michiue Y.; Sato A.; Tsuda K.; Yu S.; Arai M.; Shirako Y.; Akaogi M.; Wang N.; Yamaura K.; Boothroyd A. T. A Ferroelectric-like Structural Transition in a Metal. Nat. Mater. 2013, 12 (11), 1024–1027. 10.1038/nmat3754. [DOI] [PubMed] [Google Scholar]
  2. Anderson P. W.; Blount E. I. Symmetry Considerations on Martensitic Transformations: “Ferroelectric” Metals? (Physical Review Letters). Phys. Rev. Lett. 1965, 14 (7), 217–219. 10.1103/PhysRevLett.14.217. [DOI] [Google Scholar]
  3. Puggioni D.; Giovannetti G.; Capone M.; Rondinelli J. M. Design of a Mott Multiferroic from a Nonmagnetic Polar Metal. Phys. Rev. Lett. 2015, 115 (8), 087202. 10.1103/PhysRevLett.115.087202. [DOI] [PubMed] [Google Scholar]
  4. Puggioni D.; Giovannetti G.; Rondinelli J. M. Polar Metals as Electrodes to Suppress the Critical-Thickness Limit in Ferroelectric Nanocapacitors. J. Appl. Phys. 2018, 124 (17), 174102. 10.1063/1.5049607. [DOI] [Google Scholar]
  5. Edelstein V. M. Features of Light Reflection off Metals with Destroyed Mirror Symmetry. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83 (11), 113109. 10.1103/PhysRevB.83.113109. [DOI] [Google Scholar]
  6. Edelstein V. M. Magnetoelectric Effect in Polar Superconductors. Phys. Rev. Lett. 1995, 75 (10), 2004–2007. 10.1103/PhysRevLett.75.2004. [DOI] [PubMed] [Google Scholar]
  7. Edelstein V. M. Magnetoelectric Effect in Dirty Superconductors with Broken Mirror Symmetry. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 72 (17), 172501. 10.1103/PhysRevB.72.172501. [DOI] [Google Scholar]
  8. Enderlein C.; de Oliveira J. F.; Tompsett D. A.; Saitovitch E. B.; Saxena S. S.; Lonzarich G. G.; Rowley S. E. Superconductivity Mediated by Polar Modes in Ferroelectric Metals. Nat. Commun. 2020, 11 (4852), 1–10. 10.1038/s41467-020-18438-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Puggioni D.; Rondinelli J. M. Designing a Robustly Metallic Noncenstrosymmetric Ruthenate Oxide with Large Thermopower Anisotropy. Nat. Commun. 2014, 5 (3432), 1–9. 10.1038/ncomms4432. [DOI] [PubMed] [Google Scholar]
  10. Fei Z.; Zhao W.; Palomaki T. A.; Sun B.; Miller M. K.; Zhao Z.; Yan J.; Xu X.; Cobden D. H. Ferroelectric Switching of a Two-Dimensional Metal. Nature 2018, 560 (7718), 336–339. 10.1038/s41586-018-0336-3. [DOI] [PubMed] [Google Scholar]
  11. Jin F.; Wang L.; Zhang A.; Ji J.; Shi Y.; Wang X.; Yu R.; Zhang J.; Plummer E. W.; Zhang Q. Raman Interrogation of the Ferroelectric Phase Transition in Polar Metal LiOsO3. Proc. Natl. Acad. Sci. U. S. A. 2019, 116 (41), 20322–20327. 10.1073/pnas.1908956116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Laurita N. J.; Ron A.; Shan J. Y.; Puggioni D.; Koocher N. Z.; Yamaura K.; Shi Y.; Rondinelli J. M.; Hsieh D. Evidence for the Weakly Coupled Electron Mechanism in an Anderson-Blount Polar Metal. Nat. Commun. 2019, 10 (3217), 1–7. 10.1038/s41467-019-11172-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Xiang H. J. Origin of Polar Distortion in LiNbO3 -Type “Ferroelectric” Metals: Role of A -Site Instability and Short-Range Interactions. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90 (9), 094108. 10.1103/PhysRevB.90.094108. [DOI] [Google Scholar]
  14. Jin F.; Zhang A.; Ji J.; Liu K.; Wang L.; Shi Y.; Tian Y.; Ma X.; Zhang Q. Raman Phonons in the Ferroelectric-like Metal LiOsO3. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93 (6), 064303. 10.1103/PhysRevB.93.064303. [DOI] [Google Scholar]
  15. Liu H. M.; Du Y. P.; Xie Y. L.; Liu J. M.; Duan C. G.; Wan X. Metallic Ferroelectricity Induced by Anisotropic Unscreened Coulomb Interaction in LiOsO3. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91 (6), 064104. 10.1103/PhysRevB.91.064104. [DOI] [Google Scholar]
  16. Lo Vecchio I.; Giovannetti G.; Autore M.; Di Pietro P.; Perucchi A.; He J.; Yamaura K.; Capone M.; Lupi S. Electronic Correlations in the Ferroelectric Metallic State of LiOsO3. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93 (16), 1–5. 10.1103/PhysRevB.93.161113. [DOI] [Google Scholar]
  17. Sim H.; Kim B. G. First-Principles Study of Octahedral Tilting and Ferroelectric-like Transition in Metallic LiOsO3. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 201107. 10.1103/PhysRevB.89.201107. [DOI] [Google Scholar]
  18. Kim T. H.; Puggioni D.; Yuan Y.; Xie L.; Zhou H.; Campbell N.; Ryan P. J.; Choi Y.; Kim J. W.; Patzner J. R.; Ryu S.; Podkaminer J. P.; Irwin J.; Ma Y.; Fennie C. J.; Rzchowski M. S.; Pan X. Q.; Gopalan V.; Rondinelli J. M.; Eom C. B. Polar Metals by Geometric Design. Nature 2016, 533 (7601), 68–72. 10.1038/nature17628. [DOI] [PubMed] [Google Scholar]
  19. Benedek N. A.; Birol T. Ferroelectric” Metals Reexamined: Fundamental Mechanisms and Design Considerations for New Materials. J. Mater. Chem. C 2016, 4, 4000–4015. 10.1039/C5TC03856A. [DOI] [Google Scholar]
  20. Padmanabhan H.; Park Y.; Puggioni D.; Yuan Y.; Cao Y.; Gasparov L.; Shi Y.; Chakhalian J.; Rondinelli J. M.; Gopalan V. Linear and Nonlinear Optical Probe of the Ferroelectric-like Phase Transition in a Polar Metal, LiOsO3. Appl. Phys. Lett. 2018, 113, 122906. 10.1063/1.5042769. [DOI] [Google Scholar]
  21. Yamamoto S.; Omi T.; Akai H.; Kubota Y.; Takahashi Y.; Suzuki Y.; Hirata Y.; Yamamoto K.; Yukawa R.; Horiba K.; Yumoto H.; Koyama T.; Ohashi H.; Owada S.; Tono K.; Yabashi M.; Shigemasa E.; Yamamoto S.; Kotsugi M.; Wadati H.; Kumigashira H.; Arima T.; Shin S.; Matsuda I. Element Selectivity in Second-Harmonic Generation of GaFeO3 by a Soft-X-Ray Free-Electron Laser. Phys. Rev. Lett. 2018, 120, 223902. 10.1103/PhysRevLett.120.223902. [DOI] [PubMed] [Google Scholar]
  22. Lam R. K.; Raj S. L.; Pascal T. A.; Pemmaraju C. D.; Foglia L.; Simoncig A.; Fabris N.; Miotti P.; Hull C. J.; Rizzuto A. M.; Smith J. W.; Mincigrucci R.; Masciovecchio C.; Gessini A.; Allaria E.; De Ninno G.; Diviacco B.; Roussel E.; Spampinati S.; Penco G.; Di Mitri S.; Trovò M.; Danailov M.; Christensen S. T.; Sokaras D.; Weng T. C.; Coreno M.; Poletto L.; Drisdell W. S.; Prendergast D.; Giannessi L.; Principi E.; Nordlund D.; Saykally R. J.; Schwartz C. P. Soft X-Ray Second Harmonic Generation as an Interfacial Probe. Phys. Rev. Lett. 2018, 120, 023901. 10.1103/PhysRevLett.120.023901. [DOI] [PubMed] [Google Scholar]
  23. Helk T.; Berger E.; Jamnuch S.; Hoffmann L.; Kabacinski A.; Gautier J.; Tissandier F.; Goddet J.-P.; Chang H.-T.; Oh J.; Pemmaraju C. Das; Pascal T. A.; Sebban S.; Spielmann C.; Zuerch M. Table-Top Extreme Ultraviolet Second Harmonic Generation. Sci. Adv. 2021, 7, eabe2265. 10.1126/sciadv.abe2265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Schwartz C. P.; Raj S. L.; Jamnuch S.; Hull C. J.; Miotti P.; Lam K.; Nordlund D.; Uzundal C. B.; Pemmaraju C. Das Ångström-Resolved Interfacial Structure in Organic–Inorganic Junctions. Arxiv 2020, 2005.01905, 1–19. , accessed June 1, 2021. [Google Scholar]
  25. Shwartz S.; Fuchs M.; Hastings J. B.; Inubushi Y.; Ishikawa T.; Katayama T.; Reis D. A.; Sato T.; Tono K.; Yabashi M.; Yudovich S.; Harris S. E. X-Ray Second Harmonic Generation. Phys. Rev. Lett. 2014, 112, 163901. 10.1103/PhysRevLett.112.163901. [DOI] [PubMed] [Google Scholar]
  26. Fuchs M.; Trigo M.; Chen J.; Ghimire S.; Shwartz S.; Kozina M.; Jiang M.; Henighan T.; Bray C.; Ndabashimiye G.; Bucksbaum P. H.; Feng Y.; Herrmann S.; Carini G. A.; Pines J.; Hart P.; Kenney C.; Guillet S.; Boutet S.; Williams G. J.; Messerschmidt M.; Seibert M. M.; Moeller S.; Hastings J. B.; Reis D. A. Anomalous Nonlinear X-Ray Compton Scattering. Nat. Phys. 2015, 11, 964–970. 10.1038/nphys3452. [DOI] [Google Scholar]
  27. Yudovich S.; Shwartz S. Second-Harmonic Generation of Focused Ultrashort x-Ray Pulses. J. Opt. Soc. Am. B 2015, 32 (9), 1894–1900. 10.1364/JOSAB.32.001894. [DOI] [Google Scholar]
  28. Owada S.; Togawa K.; Inagaki T.; Hara T.; Tanaka T.; Joti Y.; Koyama T.; Nakajima K.; Ohashi H.; Senba Y.; Togashi T.; Tono K.; Yamaga M.; Yumoto H.; Yabashi M.; Tanaka H.; Ishikawa T. A Soft X-Ray Free-Electron Laser Beamline at SACLA: The Light Source, Photon Beamline and Experimental Station. J. Synchrotron Radiat. 2018, 25, 282–288. 10.1107/S1600577517015685. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Gulans A.; Kontur S.; Meisenbichler C.; Nabok D.; Pavone P.; Rigamonti S.; Sagmeister S.; Werner U.; Draxl C. Exciting: A Full-Potential All-Electron Package Implementing Density-Functional Theory and Many-Body Perturbation Theory. J. Phys.: Condens. Matter 2014, 26, 363202. 10.1088/0953-8984/26/36/363202. [DOI] [PubMed] [Google Scholar]
  30. Perdew J. P.; Zunger A. Self-Interaction Correction to Density-Functional Approximations for Many-Electron Systems. Phys. Rev. B: Condens. Matter Mater. Phys. 1981, 23 (10), 5048–5079. 10.1103/PhysRevB.23.5048. [DOI] [Google Scholar]
  31. Sharma S.; Ambrosch-Draxl C. Second-Harmonic Optical Response from First Principles. Phys. Scr. 2004, T109, 128–134. 10.1238/Physica.Topical.109a00128. [DOI] [Google Scholar]
  32. Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54 (16), 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  33. Schiek R.; Pertsch T. Absolute Measurement of the Quadratic Nonlinear Susceptibility of Lithium Niobate in Waveguides. Opt. Mater. Express 2012, 2 (2), 126–139. 10.1364/OME.2.000126. [DOI] [Google Scholar]
  34. Shan J.-Y.; de la Torre A.; Laurita N. J.; Zhao L.; Dashwood C. D.; Puggioni D.; Wang C. X.; Yamaura K.; Shi Y.; Rondinelli J. M.; Hsieh D. Evidence for an Extended Critical Fluctuation Region above the Polar Ordering Transition in LiOsO3. Phys. Rev. Res. 2020, 2, 033174. 10.1103/PhysRevResearch.2.033174. [DOI] [Google Scholar]
  35. Uzundal C. B.; Jamnuch S.; Berger E.; Woodahl C.; Manset P.; Hirata Y.; Sumi T.; Amado A.; Akai H.; Kubota Y.; Owada S.; Tono K.; Yabashi M.; Freeland J. W.; Schwartz C. P.; Drisdell W. S.; Matsuda I.; Pascal T. A.; Zong A.; Zuerch M.. Polarization-Resolved Extreme Ultraviolet Second Harmonic Generation from LiNbO3. Arxiv2021, No. (2104.01313), , accessed June 1, 2021. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl1c01502_si_001.pdf (901.3KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES