All Models are Wrong, but Many are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously

Abstract

Variable importance (VI) tools describe how much covariates contribute to a prediction model’s accuracy. However, important variables for one well-performing model (for example, a linear model f (x) = x^T β with a fixed coefficient vector β) may be unimportant for another model. In this paper, we propose model class reliance (MCR) as the range of VI values across all well-performing model in a prespecified class. Thus, MCR gives a more comprehensive description of importance by accounting for the fact that many prediction models, possibly of different parametric forms, may fit the data well. In the process of deriving MCR, we show several informative results for permutation-based VI estimates, based on the VI measures used in Random Forests. Specifically, we derive connections between permutation importance estimates for a single prediction model, U-statistics, conditional variable importance, conditional causal effects, and linear model coefficients. We then give probabilistic bounds for MCR, using a novel, generalizable technique. We apply MCR to a public data set of Broward County criminal records to study the reliance of recidivism prediction models on sex and race. In this application, MCR can be used to help inform VI for unknown, proprietary models.

1. Introduction

Variable importance (VI) tools describe how much a prediction model’s accuracy depends on the information in each covariate. For example, in Random Forests, VI is measured by the decrease in prediction accuracy when a covariate is permuted (Breiman, 2001; Breiman et al., 2001; see also Strobl et al., 2008; Altmann et al., 2010; Zhu et al., 2015; Gregorutti et al., 2015; Datta et al., 2016; Gregorutti et al., 2017). A similar “Perturb” VI measure has been used for neural networks, where noise is added to covariates (Recknagel et al., 1997; Yao et al., 1998; Scardi and Harding, 1999; Gevrey et al., 2003). Such tools can be useful for identifying covariates that must be measured with high precision, for improving the transparency of a “black box” prediction model (see also Rudin, 2019), or for determining what scenarios may cause the model to fail.

However, existing VI measures do not generally account for the fact that many prediction models may fit the data almost equally well. In such cases, the model used by one analyst may rely on entirely different covariate information than the model used by another analyst. This common scenario has been called the “Rashomon” effect of statistics (Breiman et al., 2001; see also Lecué, 2011; Statnikov et al., 2013; Tulabandhula and Rudin, 2014; Nevo and Ritov, 2017; Letham et al., 2016). The term is inspired by the 1950 Kurosawa film of the same name, in which four witnesses offer different descriptions and explanations for the same encounter. Under the Rashomon effect, how should analysts give comprehensive descriptions of the importance of each covariate? How well can one analyst recover the conclusions of another? Will the model that gives the best predictions necessarily give the most accurate interpretation?

To address these concerns, we analyze the set of prediction models that provide near-optimal accuracy, which we refer to as a Rashomon set. This approach stands in contrast to training to select a single prediction model, among a prespecified class of candidate models. Our motivation is that Rashomon sets (defined formally below) summarize the range of effective prediction strategies that an analyst might choose. Additionally, even if the candidate models do not contain the true data generating process, we may hope that some of these models function in similar ways to the data generating process. In particular, we may hope there exist well performing candidate models that place the same importance on a variable of interest as the underlying data generating process does. If so, then studying sets of well-performing models will allow us to deduce information about the data generating process.

Applying this approach to study variable importance, we define model class reliance (MCR) as the highest and lowest degree to which any well-performing model within a given class may rely on a variable of interest for prediction accuracy. Roughly speaking, MCR captures the range of explanations, or mechanisms, associated with well-performing models. Because the resulting range summarizes many prediction models simultaneously, rather a single model, we expect this range to be less affected by the choices that an individual analyst makes during the model-fitting process. Instead of reflecting these choices, MCR aims to reflect the nature of the prediction problem itself.

We make several, specific technical contributions in deriving MCR. First, we review a core measure of how much an individual prediction model relies on covariates of interest for its accuracy, which we call model reliance (MR). This measure is based on permutation importance measures for Random Forests (Breiman et al., 2001; Breiman, 2001), and can be expanded to describe conditional importance (see Section 8, as well as Strobl et al. 2008). We draw a connection between permutation-based importance estimates (MR) and U-statistics, which facilitates later theoretical results. Additionally, we derive connections between MR, conditional causal effects, and coefficients for additive models. Expanding on MR, we propose MCR, which generalizes the definition of MR for a class of models. We derive finite-sample bounds for MCR, which motivate an intuitive estimator of MCR. Finally, we propose computational procedures for this estimator.

The tools we develop to study Rashomon sets are quite general, and can be used to make finite-sample inferences for arbitrary characteristics of well-performing models. For example, beyond describing variable importance, these tools can describe the range of risk predictions that well-fitting models assign to a particular covariate profile, or the variance of predictions made by well-fitting models. In some cases, these novel techniques may provide finite-sample confidence intervals (CIs) where none have previously existed (see Section 5).

MCR and the Rashomon effect become especially relevant in the context of criminal recidivism prediction. Proprietary recidivism risk models trained from criminal records data are increasingly being used in U.S. courtrooms. One concern is that these models may be relying on information that would otherwise be considered unacceptable (for example, race, sex, or proxies for these variables), in order to estimate recidivism risk. The relevant models are often proprietary, and cannot be studied directly. Still, in cases where the predictions made by these models are publicly available, it may be possible to identify alternative prediction models that are sufficiently similar to the proprietary model of interest.

In this paper, we specifically consider the proprietary model COMPAS (Correctional Offender Management Profiling for Alternative Sanctions), developed by the company Northpointe Inc. (subsequently, in 2017, Northpointe Inc.,Courtview Justice Solutions Inc., and Constellation Justice Systems Inc. joined together under the name Equivant). Our goal is to estimate how much COMPAS relies on either race, sex, or proxies for these variables not measured in our data set. To this end, we apply a broad class of flexible, kernel-based prediction models to predict COMPAS score. In this setting, the MCR interval reflects the highest and lowest degree to which any prediction model in our class can rely on race and sex while still predicting COMPAS score relatively accurately. Equipped with MCR, we can relax the common assumption of being able to correctly specify the unknown model of interest (here, COMPAS) up to a parametric form. Instead, rather than assuming that the COMPAS model itself is contained in our class, we assume that our class contains at least one well-performing alternative model that relies on sensitive covariates to the same degree that COMPAS does. Under this assumption, the MCR interval will contain the VI value for COMPAS. Applying our approach, we find that race, sex, and their potential proxy variables, are likely not the dominant predictive factors in the COMPAS score (see analysis and discussion in Section 10).

The remainder of this paper is organized as follows. In Section 2 we introduce notation, and give a high level summary of our approach, illustrated with visualizations. In Sections 3 and 4 we formally present MR and MCR respectively, and derive theoretical properties of each. We also review related variable importance practices in the literature, such as retraining a model after removing one of the covariates. In Section 5, we discuss general applicability of our approach for determining finite-sample CIs for other problems. In Section 6, we present a general procedure for computing MCR. In Section 7, we give specific implementations of this procedure for (regularized) linear models, and linear models in a reproducing kernel Hilbert space. We also show that, for additive models, MR can be expressed in terms of the model’s coefficients. In Section 8 we outline connections between MR, causal inference, and conditional variable importance. In Section 9, we illustrate MR and MCR with a simulated toy example, to aid intuition. We also present simulation studies for the task of estimating MR for an unknown, underlying conditional expectation function, under misspecification. We analyze a well-known public data set on recidivism in Section 10, described above. All proofs are presented in the appendices.

2. Notation & Technical Summary

The label of “variable importance” measure has been broadly used to describe approaches for either inference (van der Laan, 2006; Díaz et al., 2015; Williamson et al., 2017) or prediction. While these two goals are highly related, we primarily focus on how much prediction models rely on covariates to achieve accuracy. We use terms such as “model reliance” rather than “importance” to clarify this context.

In order to evaluate how much prediction models rely on variables, we now introduce notation for random variables, data, classes of prediction models, and loss functions for evaluating predictions. Let $Z=(Y,X_1,X_2)\in \mathcal{Z}$ be a random variable with outcome $Y\in \mathcal{Y}$ and covariates $X=(X_1,X_2)\in \mathcal{X}$, where the covariate subsets $X_1\in {\mathcal{X}}_1$ and $X_2\in {\mathcal{X}}_2$ may each be multivariate. We assume that observations of Z are iid, that n ≥ 2, and that solutions to arg min and arg max operations exist whenever optimizing over sets mentioned in this paper (for example, in Theorem 4, below). Our goal is to study how much different prediction models rely on X₁ to predict Y.

We refer to our data set as Z = [ y X ], a matrix composed of a n-length outcome vector y in the first column, and a n × p covariate matrix X = [ X₁ X₂ ] in the remaining columns. In general, for a given vector v, let v_[j] denote its j^th element(s). For a given matrix A, let A′, A_[i,·], A_[·,j] and A_[i,j] respectively denote the transpose of A, the i^th row(s) of A, the j^th column(s) of A, and the element(s) in the i^th row(s) and j^th column(s) of A.

We use the term model class to refer to a prespecified subset $\mathcal{F}\subset \left\{f\right|f:\mathcal{X}\to \mathcal{Y}\}$ of the measurable functions from $\mathcal{X}$ to $\mathcal{Y}$. We refer to member functions $f\in \mathcal{F}$ as prediction models, or simply as models. Given a model f, we evaluate its performance using a nonnegative loss function $L:(\mathcal{F}\times \mathcal{Z})\to {\mathbb{R}}_{\ge 0}$. For example, L may be the squared error loss L_se(f, (y, x₁, x₂)) = (y − f (x₁, x₂))² for regression, or the hinge loss L_h(f, (y, x₁, x₂)) = (1 − y f (x₁, x₂))₊ for classification. We use the term algorithm to refer to any procedure $\mathcal{A}:{\mathcal{Z}}^n\to \mathcal{F}$ that takes a data set as input and returns a model $f\in \mathcal{F}$ as output.

2.1. Summary of Rashomon Sets & Model Class Reliance

Many traditional statistical estimates come from descriptions of a single, fitted prediction model. In contrast, in this section, we summarize our approach for studying a set of near-optimal models. To define this set, we require a prespecified “reference” model, denoted by f_ref, to serve as a benchmark for predictive performance. For example, f_ref may come from a flowchart used to predict injury severity in a hospital’s emergency room, or from another quantitative decision rule that is currently implemented in practice. Given a reference model f_ref, we define a population ϵ-Rashomon set as the subset of models with expected loss no more than ϵ above that of f_ref. We denote this set as $\mathcal{R}\left(ϵ\right):=\{f\in \mathcal{F}:\mathbb{E}L(f,Z)\le \mathbb{E}L(f_{\mathrm{ref}},Z)+ϵ\}$, where $\mathbb{E}$ denotes expectations with respect to the population distribution. This set can be thought of as representing models that might be arrived at due to differences in data measurement, processing, filtering, model parameterization, covariate selection, or other analysis choices (see Section 4).

Figure 1–A illustrates a hypothetical example of a population ϵ-Rashomon set. Here, the y-axis shows the expected loss of each model $f\in \mathcal{F}$, and the x-axis shows how much each model relies on X₁ for its predictive accuracy. More specifically, given a prediction model f, the x-axis shows the percent increase in f’s expected loss when noise is added to X₁. We refer to this measure as the model reliance (MR) of f on X₁, written informally as

$$MR\left(f\right):=\frac{\mathrm{Expected\; loss\; of}f\mathrm{under\; noise}}{\mathrm{Expected\; loss\; of}f\mathrm{without\; noise}}.$$ (2.1)

The added noise must satisfy certain properties, namely, it must render X₁ completely uninformative of the outcome Y, without altering the marginal distribution of X₁ (for details, see Section 3, as well as Breiman, 2001; Breiman et al., 2001).

Figure 1:

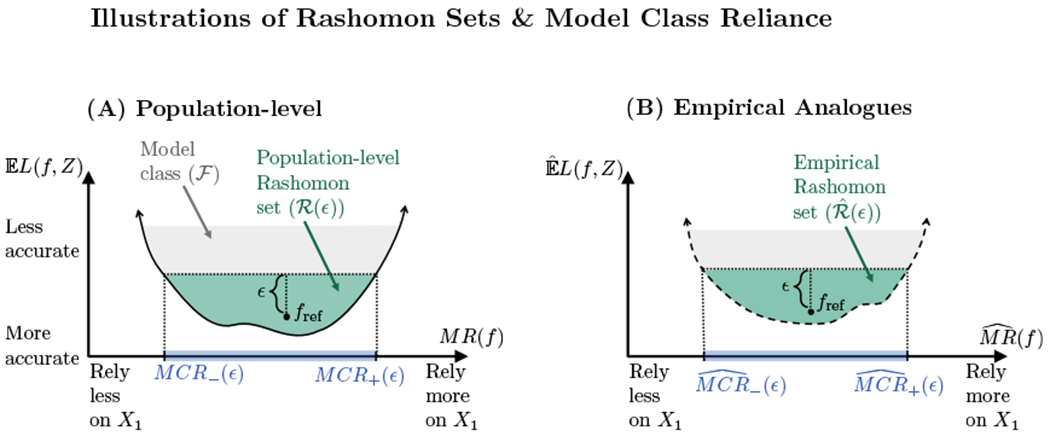
Rashomon sets and model class reliance – Panel (A) illustrates a hypothetical Rashomon set $\mathcal{R}\left(ϵ\right)$, within a model class $\mathcal{F}$. The y-axis shows the expected loss of each model $f\in \mathcal{F}$, and the x-axis shows how much each model f relies on X₁ (defined formally in Section 3). Along the x-axis, the population-level MCR range is highlighted in blue, showing the values of MR corresponding to well-performing models (see Section 4). Panel (B) shows the in-sample analogue of Panel (A). Here, the y-axis denotes the in-sample loss, $\widehat{\mathbb{E}}L(f,Z):=\frac{1}{n}{\sum }_{i=1}^{n}L(f,{\mathbf{Z}}_{[i,\cdot ]})$; the x-axis shows the empirical model reliance of each model $f\in \mathcal{F}$ on X₁ (see Section 3); and the highlighted portion of the x-axis shows empirical MCR (see Section 4).

Our central goal is to understand how much, or how little, models may rely on covariates of interest (X₁) while still predicting well. In Figure 1–A, this range of possible MR values is shown by the highlighted interval along the x-axis. We refer to an interval of this type as a population-level model class reliance (MCR) range (see Section 4), formally defined as

$$[{MCR}_{-}(ϵ),{MCR}_{+}(ϵ)]:=\left[\underset{f\in \mathcal{R}\left(ϵ\right)}{\min }MR\left(f\right),\underset{f\in \mathcal{R}\left(ϵ\right)}{\max }MR\left(f\right)\right].$$ (2.2)

To estimate this range, we use empirical analogues of the population ϵ-Rashomon set, and of MR, based on observed data (Figure 1–B). We define an empirical ϵ-Rashomon set as the set of models with in-sample loss no more than ϵ above that of f_ref, and denote this set by $\widehat{\mathcal{R}}\left(ϵ\right)$. Informally, we define the empirical MR of a model f on X₁ as

$$\widehat{MR}\left(f\right):=\frac{\text{In-sample loss of}f\text{under noise}}{\text{In-sample loss of}f\text{without noise}},$$ (2.3)

that is, the extent to which f appears to rely on X₁ in a given sample (see Section 3 for details). Finally, we define the empirical model class reliance as the range of empirical MR values corresponding to models with strong in-sample performance (see Section 4), formally written as

$$[{\widehat{MCR}}_{-}(ϵ),{\widehat{MCR}}_{+}(ϵ)]:=\left[\underset{f\in \widehat{\mathcal{R}}\left(ϵ\right)}{\min }\widehat{MR}\left(f\right),\underset{f\in \widehat{\mathcal{R}}\left(ϵ\right)}{\max }\widehat{MR}\left(f\right)\right].$$ (2.4)

In Figure 1–B, the above range is shown by the highlighted portion of the x-axis.

We make several technical contributions in the process of developing MCR.

• Estimation of MR, and population-level MCR: Given f, we show desirable properties of $\widehat{MR}(f)$ as an estimator of MR(f), using results for U-statistics (Section 3.1 and Theorem 5). We also derive finite sample bounds for population-level MCR, some of which require a limit on the complexity of $\mathcal{F}$ in the form of a covering number. These bounds demonstrate that, under fairly weak conditions, empirical MCR provides a sensible estimate of population-level MCR (see Section 4 for details).

• Computation of empirical MCR: Although empirical MCR is fully determined given a sample, the minimization and maximization in Eq 2.4 require nontrivial computations. To address this, we outline a general optimization procedure for MCR (Section 6). We give detailed implementations of this procedure for cases when the model class $\mathcal{F}$ is a set of (regularized) linear regression models, or a set of regression models in a reproducing kernel Hilbert space (Section 7). The output of our proposed procedure is a closed-form, convex envelope containing $\mathcal{F}$, which can be used to approximate empirical MCR for any performance level ϵ (see Figure 2 for an illustration). Still, for complex model classes where standard empirical loss minimization is an open problem (for example, neural networks), computing empirical MCR remains an open problem as well.

• Interpretation of MR in terms of model coefficients, and causal effects: We show that MR for an additive model can be written as a function of the model’s coefficients (Proposition 15), and that MR for a binary covariate X₁ can be written as a function of the conditional causal effects of X₁ on Y (Proposition 19).

• Extensions to conditional importance: We provide an extension of MR that is analogous to the notion of conditional importance (Strobl et al., 2008). This extension describes how much a model relies on the specific information in X₁ that cannot otherwise be gleaned from X₂ (Section 8.2).

• Generalizations for Rashomon sets: Beyond notions of variable importance, we also generalize our finite sample results for MCR to describe arbitrary characterizations of models in a population ϵ-Rashomon set. As we discuss in concurrent work (Coker et al., 2018), this generalization is analogous to the profile likelihood interval, and can, for example, be used to bound the range of risk predictions that well-performing prediction models may assign to a particular set of covariates (Section 5).

Figure 2:

Illustration of output from our empirical MCR computational procedure – Our computation procedure produces a closed-form, convex envelope that contains $\mathcal{F}$ (shown above as the solid, purple line), which bounds empirical MCR for any value of ϵ (see Eq 2.4). The procedure works sequentially, tightening these bounds as much as possible near the ϵ value of interest (Section 6). The results from our data analysis (Figure 8) are presented in the same format as the above purple envelope.

We begin in the next section by formally reviewing model reliance.

3. Model Reliance

To formally describe how much the expected accuracy of a fixed prediction model f relies on the random variable X₁, we use the notion of a “switched” loss where X₁ is rendered uninformative. Throughout this section, we will treat f as a pre-specified prediction model of interest (as in Hooker, 2007). Let $Z^{(a)}=(Y^{(a)},X_1^{(a)},X_2^{(a)})$ and $Z^{(b)}=(Y^{(b)},X_1^{(b)},X_2^{(b)})$ be independent random variables, each following the same distribution as Z = (Y, X₁, X₂). We define

$$e_{switch}\left(f\right):=\mathbb{E}L\{f,(Y^{\left(b\right)},X_1^{\left(a\right)},X_2^{\left(b\right)})\}$$

as representing the expected loss of model f across pairs of observations $(Z^{(a)},Z^{(b)})$ in which the values of $X_1^{(a)}$ and $X_1^{(b)}$ have been switched. To see this interpretation of the above equation, note that we have used the variables $(Y^{(b)},X_2^{(b)})$ from $Z^{(b)}$, but we have used the variable $X_1^{(b)}$ from an independent copy Z^(b). This is why we say that $X_1^{(a)}$ and $X_1^{(b)}$ have been switched; the values of ($Y^{(b)},X_1^{(a)},X_2^{(b)}$) do not relate to each other as they would if they had been chosen together. An alternative interpretation of e_switch(f) is as the expected loss of f when noise is added to X₁ in such a way that X₁ becomes completely uninformative of Y, but that the marginal distribution of X₁ is unchanged.

As a reference point, we compare e_switch(f) against the standard expected loss when none of the variables are switched, $e_{orig}(f):=\mathbb{E}L(f,(Y,X_1,X_2)).$ From these two quantities, we formally define model reliance (MR) as the ratio,

$$MR\left(f\right):=\frac{e_{\mathrm{switch}}\left(f\right)}{e_{\mathrm{orig}}\left(f\right)},$$ (3.1)

as we alluded to in Eq 2.1. Higher values of MR(f) signify greater reliance of f on X₁. For example, an MR(f) value of 2 means that the model relies heavily on X₁, in the sense that its loss doubles when X₁ is scrambled. An MR(f) value of 1 signifies no reliance on X₁, in the sense that the model’s loss does not change when X₁ is scrambled. Models with reliance values strictly less than 1 are more difficult to interpret, as they rely less on the variable of interest than a random guess. Interestingly, it is possible to have models with reliance less than one. For instance, a model f′ may satisfy MR(f′) < 1 if it treats X₁ and Y as positively correlated when they are in fact negatively correlated. However, in many cases, the existence of a model $f^{\prime }\in \mathcal{F}$ satisfying $MR(f^{\prime })<1$ implies the existence of another, better performing model $f^{″}\in \mathcal{F}$ satisfying $MR(f^{″})<1$ and e_orig(f″) ≤ e_orig(f′). That is, although models may exist with MR values less than 1, they will typically be suboptimal (see Appendix A.2).

Model reliance could alternatively be defined as a difference rather than a ratio, that is, as ${MR}_{\mathrm{difference}}(f):=e_{\mathrm{switch}}(f)-e_{\mathrm{orig}}(f).$ In Appendix A.5, we discuss how many of our results remain similar under either definition.

3.1. Estimating Model Reliance with U-statistics, and Connections to Permutation-based Variable Importance

Given a model f and data set $Z=[\mathbf{y}X]$, we estimate MR(f) by separately estimating the numerator and denominator of Eq 3.1. We estimate e_orig(f) with the standard empirical loss,

$${\widehat{e}}_{\mathrm{orig}}\left(f\right):=\frac{1}{n}\sum _{i=1}^{n}L\left\{f,\left({\mathbf{y}}_{\left[i\right]},{\mathbf{X}}_{1\left[i,\cdot \right]},{\mathbf{X}}_{2\left[i,\cdot \right]}\right)\right\}.$$ (3.2)

We estimate e_switch(f) by performing a “switch” operation across all observed pairs, as in

$${\widehat{e}}_{\mathrm{switch}}\left(f\right):=\frac{1}{n\left(n-1\right)}\sum _{i=1}^n\sum _{j\ne i}L\left\{f,\left({\mathbf{y}}_{\left[j\right]},{\mathbf{X}}_{1\left[i,\cdot \right]},{\mathbf{X}}_{2\left[j,\cdot \right]}\right)\right\}.$$ (3.3)

Above, we have aggregated over all possible combinations of the observed values for (Y, X₂) and for X₁, excluding pairings that are actually observed in the original sample. If the summation over all possible pairs (Eq 3.3) is computationally prohibitive due to sample size, another estimator of e_switch(f) is

$${\widehat{e}}_{\mathrm{divide}}\left(f\right):=\frac{1}{2\lfloor n/2\rfloor }\sum _{i=1}^{\lfloor n/2\rfloor }[L\left\{f,\left({\mathbf{y}}_{\left[i\right]},{\mathbf{X}}_{1\left[i+\lfloor n/2\rfloor ,\cdot \right]},{\mathbf{X}}_{2\left[i,\cdot \right]}\right)\right\}$$ (3.4)

$$+L\left\{f,\left({\mathbf{y}}_{\left[i+\lfloor n/2\rfloor \right]},{\mathbf{X}}_{1\left[i,\cdot \right]},{\mathbf{X}}_{2\left[i+\lfloor n/2\rfloor ,\cdot \right]}\right)\right\}].$$ (3.5)

Here, rather than summing over all pairs, we divide the sample in half. We then match the first half’s values for (Y, X₂) with the second half’s values for X₁ (Line 3.4), and vice versa (Line 3.5). All three of the above estimators (Eqs 3.2, 3.3 & 3.5) are unbiased for their respective estimands, as we discuss in more detail shortly.

Finally, we can estimate MR(f) with the plug-in estimator

$$\widehat{MR}\left(f\right):=\frac{{\widehat{e}}_{\mathrm{switch}}\left(f\right)}{{\widehat{e}}_{\mathrm{orig}}\left(f\right)},$$ (3.6)

which we define as the empirical model reliance of f on X₁. In this way, we formalize the empirical MR definition in Eq 2.3.

Again, our definition of empirical MR is very similar to the permutation-based variable importance approach of Breiman (2001), where Breiman uses a single random permutation and we consider all possible pairs. To compare these two approaches more precisely, let (π₁, … , π_n!} be a set of n-length vectors, each containing a different permutation of the set (1, …, n}. The approach of Breiman (2001) is analogous to computing the loss ${\sum }_{i=1}^{n}L\{f,({\mathbf{y}}_{[i]},{\mathbf{X}}_{1[{\pi }_{l_{[i]}},.]},{\mathbf{X}}_{2[i,.]})\}$ for a randomly chosen permutation vector π_l ∈ {π₁, … , π_n!}. Similarly, our calculation in Eq 3.3 is proportional to the sum of losses over all possible (n!) permutations, excluding the n unique combinations of the rows of X₁ and the rows of $[{\mathbf{X}}_2\mathbf{y}]$ that appear in the original sample (see Appendix A.3). Excluding these observations is necessary to preserve the (finite-sample) unbiasedness of ${\widehat{e}}_{\mathrm{switch}}(f)$.

The estimators ${\widehat{e}}_{\mathrm{orig}}(f)$, ${\widehat{e}}_{\mathrm{switch}}(f)$ and ${\widehat{e}}_{\mathrm{divide}}(f)$ all belong to the well-studied class of U-statistics. Thus, under fairly minor conditions, these estimators are unbiased, asymptotically normal, and have finite-sample probabilistic bounds (Hoeffding, 1948, 1963; Serfling, 1980; see also DeLong et al., 1988 for an early use of U-statistics in machine learning, as well as caveats in Demler et al., 2012). To our knowledge, connections between permutation-based importance and U-statistics have not been previously established.

While the above results from U-statistics depend on the model f being fixed a priori, we can also leverage these results to create uniform bounds on the MR estimation error for all models in a sufficiently regularized class $\mathcal{F}$. We formally present this bound in Section 4 (Theorem 5), after introducing required conditions on model class complexity. The existence of this uniform bound implies that it is feasible to train a model and to evaluate its importance using the same data. This differs from the classical VI approach of Random Forests (Breiman, 2001), which avoids in-sample importance estimation. There, each tree in the ensemble is fit on a random subset of data, and VI for the tree is estimated using the held-out data. The tree-specific VI estimates are then aggregated to obtain a VI estimate for the overall ensemble. Although sample-splitting approaches such as this are helpful in many cases, the uniform bound for MR suggests that they are not strictly necessary, depending on the sample size and the complexity of $\mathcal{F}$.

3.2. Limitations of Existing Variable Importance Methods

Several common approaches for variable selection, or for describing relationships between variables, do not necessarily capture a variable’s importance. Null hypothesis testing methods may identify a relationship, but do not describe the relationship’s strength. Similarly, checking whether a variable is included by a sparse model-fitting algorithm, such as the Lasso (Hastie et al., 2009), does not describe the extent to which the variable is relied on. Partial dependence plots (Breiman et al., 2001; Hastie et al., 2009) can be difficult to interpret if multiple variables are of interest, or if the prediction model contains interaction effects.

Another common VI procedure is to run a model-fitting algorithm twice, first on all of the data, and then again after removing X₁ from the data set. The losses for the two resulting models are then compared to determine the importance, or “necessity,” of X₁ (Gevrey et al., 2003). Because this measure is a function of two prediction models rather than one, it does not measure how much either individual model relies on X₁. We refer to this approach as measuring empirical Algorithm Reliance (AR) on X₁, as the model-fitting algorithm is the common attribute between the two models. Related procedures were proposed by Breiman et al. (2001); Breiman (2001), which measure the sufficiency of X₁.

As we discuss in Section 3.1, the permutation-based VI measure from RFs (Breiman, 2001; Breiman et al., 2001) forms the inspiration for our definition of MR. This RF VI measure has been the topic of empirical studies (Archer and Kimes, 2008; Calle and Urrea, 2010; Wang et al., 2016), and several variations of the measure have been proposed (Strobl et al., 2007, 2008; Altmann et al., 2010; Hapfelmeier et al., 2014). Mentch and Hooker (2016) use U-statistics to study predictions of ensemble models fit to subsamples, similar to the bootstrap aggregation used in RFs. Procedures related to “Mean Difference Impurity,” another VI measure derived for RFs, have been studied theoretically by Louppe et al. (2013); Kazemitabar et al. (2017). All of this literature focuses on VI measures for RFs, for ensembles, or for individual trees. Our estimator for model reliance differs from the traditional RF VI measure (Breiman, 2001) in that we permute inputs to the overall model, rather than permuting the inputs to each individual ensemble member. Thus, our approach can be used generally, and is not limited to trees or ensemble models.

Outside of the context of RF VI, Zhu et al. (2015) propose an estimand similar to our definition of model reliance, and Gregorutti et al. (2015, 2017) propose an estimand analogous to e_switch(f) − e_orig(f). These recent works focus on the model reliance of f on X₁ specifically when f is equal to the conditional expectation function of Y (that is, $f(x_1,x_2)=\mathbb{E}[Y|X_1=x_1,X_2=x_2]$). In contrast, we consider model reliance for arbitrary prediction models f. Datta et al. (2016) study the extent to which a model’s predictions are expected to change when a subset of variables is permuted, regardless of whether the permutation affects a loss function L. These VI approaches are specific to a single prediction model, as is MR. In the next section, we consider a more general conception of importance: how much any model in a particular set may rely on the variable of interest.

4. Model Class Reliance

Like many statistical procedures, our MR measure (Section 3) produces a description of a single predictive model. Given a model with high predictive accuracy, MR describes how much the model’s performance hinges on covariates of interest (X₁). However, there will often be many other models that perform similarly well, and that rely on X₁ to different degrees. With this notion in mind, we now study how much any well-performing model from a prespecified class $\mathcal{F}$ may rely on covariates of interest.

Recall from Section 2.1 that, in order to define a population ϵ-Rashomon set of near-optimal models, we must choose a “reference” model f_ref to serve as a performance benchmark. In order to discuss this choice, we now introduce more explicit notation for the population ϵ-Rashomon set, written as

$$\mathcal{R}\left(ϵ,f_{\mathrm{ref}},\mathcal{F}\right):=\left\{f\in \mathcal{F}:e_{\mathrm{orig}}\left(f\right)\le e_{\mathrm{orig}}\left(f_{\mathrm{ref}}\right)+ϵ\right\}.$$ (4.1)

Note that we write $\mathcal{R}(ϵ,f_{\mathrm{ref}},\mathcal{F})$ and $\mathcal{R}(ϵ)$ interchangeably when f_ref and $\mathcal{F}$ are clear from context. Similarly, we occasionally write empirical ϵ-Rashomon sets using the more explicit notation $\widehat{\mathcal{R}}(ϵ,f_{\mathrm{ref}},\mathcal{F}):=\{f\in \mathcal{F}:{\widehat{e}}_{\mathrm{orig}}(f)\le {\widehat{e}}_{\mathrm{orig}}(f_{\mathrm{ref}})+ϵ\}$, but typically abbreviate these sets as $\widehat{\mathcal{R}}(ϵ)$.

While f_ref could be selected by minimizing the in-sample loss, the theoretical study of $\mathcal{R}(ϵ,f_{\mathrm{ref}},\mathcal{F})$ is simplified under the assumption that f_ref is prespecified. For example, f_ref may come from a flowchart used to predict injury severity in a hospital’s emergency room, or from another quantitative decision rule that is currently implemented in practice. The model f_ref can also be selected using sample splitting. In some cases it may be desirable to fix f_ref equal to the best-in-class model $f\star :=\arg {\min }_{f\in \mathcal{F}}{e}_{orig}(f)$, but this is generally infeasible because f^⋆ is unknown. Still, for any $f_{\mathrm{ref}}\in \mathcal{F}$, the Rashomon set $\mathcal{R}(ϵ,f_{\mathrm{ref}},\mathcal{F})$ defined using f_ref will always be conservative in the sense that it contains the Rashomon set $\mathcal{R}(ϵ,f^{\star },\mathcal{F})$ defined using f^⋆.

We can now formalize our definitions of population-level MCR and empirical MCR by simply plugging in our definitions for MR(f) and $\widehat{MR}(f)$ (Section 3) into Eqs 2.2 & 2.4 respectively. Studying population-level MCR (Eq 2.2) is the main focus of this paper, as it provides a more comprehensive view of importance than measures from a single model. If MCR₊(ϵ) is low, then no well-performing model in $\mathcal{F}$ places high importance on X₁, and X₁ can be discarded at low cost regardless of future modeling decisions. If MCR₋(ϵ) is large, then every well-performing model in $\mathcal{F}$ must rely substantially on X₁, and X₁ should be given careful attention during the modeling process. Here, $\mathcal{F}$ may itself consist of several parametric model forms (for example, all linear models and all decision tree models with less than 6 single-split nodes). We stress that the range [MCR₋(ϵ), MCR₊(ϵ)| does not depend on the fitting algorithm used to select a model $f\in \mathcal{F}$. The range is valid for any algorithm producing models in $F$ F, and applies for any $f\in \mathcal{F}$.

In the remainder of this section, we derive finite sample bounds for population-level MCR, from which we argue that empirical MCR provides reasonable estimates of population-level MCR (Section 4.1). In Appendix B.7 we consider an alternate formulation of Rashomon sets and MCR where we replace the relative loss threshold in the definition of $\mathcal{R}(ϵ)$ with an absolute loss threshold. This alternate formulation can be similar in practice, but still requires the specification of a reference function f_ref to ensure that $\mathcal{R}(ϵ)$ and $\widehat{\mathcal{R}}(ϵ)$ are nonempty.

4.1. Motivating Empirical Estimators of MCR by Deriving Finite-sample Bounds

In this section we derive finite-sample, probabilistic bounds for MCR₊(ϵ) and MCR₋(ϵ). Our results imply that, under minimal assumptions, ${\widehat{MCR}}_{+}(ϵ)$ and ${\widehat{MCR}}_{-}(ϵ)$ are respectively within a neighborhood of MCR₊ (ϵ) and MCR₋(ϵ) with high probability. However, the weakness of our assumptions (which are typical for statistical-learning-theoretic analysis) renders the width of our resulting CIs to be impractically large, and so we use these results only to show conditions under which ${\widehat{MCR}}_{-}(ϵ)$ and ${\widehat{MCR}}_{-}(ϵ)$ form sensible point estimates. In Sections 9.1 & 10, below, we apply a bootstrap procedure to account for sampling variability.

To derive these results we introduce three bounded loss assumptions, each of which can be assessed empirically. Let b_orig, B_ind, B_ref, $B_{\mathrm{switch}}\in \mathbb{R}$ be known constants.

Assumption 1 (Bounded individual loss) For a given model $f\in \mathcal{F}$, assume that $0\le L(f,(y,x_1,x_2))\le B_{ind}\mathit{for\; any}(y,x_1,x_2)\in (\mathcal{Y}\times {\mathcal{X}}_1\times {\mathcal{X}}_2)$.

Assumption 2 (Bounded relative loss) For a given model $f\in \mathcal{F}$, assume that $|L(f,(y,x_1,x_2))-L(f_{\mathrm{ref}},(y,x_1,x_2)|\le B_{ref}\mathit{for\; any}(y,x_1,x_2)\in \mathcal{Z}$.

Assumption 3 (Bounded aggregate loss) For a given model $f\in \mathcal{F}$, assume that $\mathbb{P}\{0<b_{orig}\le {\widehat{e}}_{orig}(f)\}=\mathbb{P}\{{\widehat{e}}_{switch}(f)\le B_{switch}\}=1$.

Each assumption is a property of a specific model $f\in \mathcal{F}$. The notation B_ind and B_ref refer to bounds for any individual observation, and the notation b_orig and B_switch refer to bounds on the aggregated loss L in a sample. These boundedness assumptions are central to our finite sample guarantees, shown below.

Crucially, loss functions L that are unbounded in general may be used so long as L(f, (y, x₁, x₂)) is bounded on a particular domain. For example, the squared-error loss can be used if $\mathcal{Y}$ is contained within a known range, and predictions f (x₁, x₂) are contained within the same range for $(x_1,x_2)\in \mathcal{X}\times {\mathcal{X}}_2.$ We give example methods of determining B_ind in Sections 7.3.2 & 7.4.2. For Assumption 3, we can approximate b_orig by training a highly flexible model to the data, and setting b_orig equal to half (or any positive fraction) of the resulting cross-validated loss. To determine B_switch we can simply set B_switch = B_ind, although this may be conservative. For example, in the case of binary classification models for non-separable groups (see Section 9.1), no linear classifier can misclassify all observations, particularly after a covariate is permuted. Thus, it must hold that B_ind > B_switch. Similarly, if f_ref satisfies Assumption 1, then B_ref may be conservatively set equal to B_ind. If model reliance is redefined as a difference rather than a ratio, then a similar form of the results in this section will apply without Assumption 3 (see Appendix A.5).

Based on these assumptions, we can create a finite-sample upper bound for MCR₊(ϵ) and lower bound for MCR₋(ϵ). In other words, we create an “outer” bound that contains the interval [MCR₋(ϵ),MCR₊(ϵ)| with high probability.

Theorem 4 (“Outer” MCR Bounds) Given a constant ϵ ≥ 0, let $f_{+,ϵ}\in \arg {\max }_{\mathcal{R}(ϵ)}MR(f)$ and $f_{-,ϵ}\in \arg {\min }_{\mathcal{R}(ϵ)}MR(f)$ be prediction models that attain the highest and lowest model reliance among models in $\mathcal{R}(ϵ)$. If f_+,ϵ and f_−,ϵ satisfy Assumptions 1, 2 & 3, then

$$\mathbb{P}\left(MC{R}_{+}\left(ϵ\right)>{\widehat{MCR}}_{+}\left({ϵ}_{out}\right)+{\mathcal{Q}}_{out}\right)\le \delta ,and$$ (4.2)

$$\mathbb{P}\left(MC{R}_{-}\left(ϵ\right)<{\widehat{MCR}}_{-}\left({ϵ}_{out}\right)-{\mathcal{Q}}_{out}\right)\le \delta ,$$ (4.3)

where ${ϵ}_{out}:=ϵ+2B_{ref}\sqrt{\frac{\log (3{\delta }^{-1})}{2n}},{\mathit{and}\mathcal{Q}}_{\text{out}}:=\frac{B_{switch}}{b_{orig}}-\frac{B_{switch}-B_{ind}\sqrt{\frac{\log (6{\delta }^{-1})}{n}}}{b_{orig}+B_{ind}\sqrt{\frac{\log (6{\delta }^{-1})}{2n}}}$.

Eq 4.2 states that, with high probability, MCR₊(ϵ) is no higher than ${\widehat{MCR}}_{+}({ϵ}_{\mathrm{out}})$ added to an error term ${\mathcal{Q}}_{\mathrm{out}}$. As n increases, ϵ_out approaches ϵ and ${\mathcal{Q}}_{\mathrm{out}}$ approaches zero. One practical implication is that, roughly speaking, if ${\widehat{MCR}}_{+}(ϵ)\approx {\widehat{MCR}}_{+}({ϵ}_{\mathrm{out}})$, then the empirical estimator ${\widehat{MCR}}_{+}(ϵ)$ is unlikely to substantially underestimate MCR₊(ϵ). By similar reasoning, we can conclude from Eq 4.3 that if ${\widehat{MCR}}_{-}(ϵ)\approx {\widehat{MCR}}_{-}({ϵ}_{\mathrm{out}})$, then ${\widehat{MCR}}_{+}(ϵ)$ is unlikely to substantially overestimate MCR₋(ϵ). By setting ϵ = 0, Theorem 4 can also be used to create a finite-sample bound for the reliance of the unique (unknown) best-in-class model on X₁ (see Corollary 22 in Appendix A.4), although describing individual models is not the main focus of this paper.

We provide a visual illustration of Theorem 4 in Figure 3. A brief sketch of the proof is as follows. First, we enlarge the empirical ϵ-Rashomon set by increasing ϵ to ϵ_out, such that, by Hoeffding’s inequality, $f_{+,ϵ}\in \widehat{R}({ϵ}_{\mathrm{out}})$ with high probability. When $f_{+,ϵ}\in \widehat{R}({ϵ}_{\mathrm{out}})$, we know that ${\widehat{MR}}_{{}_{(f_{+,ϵ})}}\le {\widehat{MCR}}_{+}({ϵ}_{\mathrm{out}})$ by the definition of ${\widehat{MCR}}_{+}({ϵ}_{\mathrm{out}})$. Next, the term ${\mathcal{Q}}_{\mathrm{out}}$ leverages finite-sample results for U-statistics to account for estimation error of MR(f_+,ϵ) = MCR₊(ϵ) when using the estimator ${\widehat{MR}}_{{}_{(f_{+,ϵ})}}$. Thus, we can relate ${\widehat{MR}}_{{}_{(f_{+,ϵ})}}$ to both ${\widehat{MCR}}_{+}({ϵ}_{\mathrm{out}})$ and MCR₊(ϵ) in order to obtain Eq 4.2. Similar steps can be applied to obtain Eq 4.3.

Figure 3:

Illustration of terms in Theorems 4 and 6 – Above we show the relation between empirical MR (x-axis) and empirical loss (y-axis) for models f in a hypothetical model class $\mathcal{F}$. We mark f_ref by the black point. For each possible model reliance value r ≥ 0, the curved, dashed line shows the lowest possible empirical loss for a function in $f\in \mathcal{F}$ satisfying $\widehat{MR}(f)=r$. The set $\widehat{\mathcal{R}}(ϵ)$ contains all models in $\mathcal{F}$ within the dotted gray lines. To create the bounds from Theorem 4, we expand the empirical ϵ-Rashomon set by increasing ϵ to ϵ_out, such that f_+,ϵ (or f_−,ϵ) is contained in $\widehat{\mathcal{R}}({ϵ}_{\mathrm{out}})$ with high probability. We then add (or subtract) ${\mathcal{Q}}_{\mathrm{out}}$ to account for estimation error of $\widehat{MR}(f_{+,ϵ})$ (or $\widehat{MR}(f_{-,ϵ})$). These steps are illustrated above in blue, with the final bounds shown by the blue bracket symbols along the x-axis. To create the bounds for MCR₊(ϵ) (and MCR₋(ϵ)) in Theorem 6, we constrict the empirical ϵ-Rashomon set by decreasing ϵ to ϵ_in, such that all models with high expected loss are simultaneously excluded from $\widehat{\mathcal{R}}({ϵ}_{\mathrm{in}})$ with high probability. We then subtract (or add) ${\mathcal{Q}}_{\mathrm{in}}$ to simultaneously account for MR estimation error for models in $\widehat{\mathcal{R}}({ϵ}_{\mathrm{in}})$. These steps are illustrated above in purple, with the final bounds shown by the purple bracket symbols along the x-axis. For emphasis, below this figure we show a copy of the x-axis with selected annotations, from which it is clear that ${\widehat{MCR}}_{-}(ϵ)$ and ${\widehat{MCR}}_{+}(ϵ)$ are always within the bounds produced by Theorems 4 and 6. With high probability, ${\widehat{MCR}}_{-}(ϵ)$ and ${\widehat{MCR}}_{+}(ϵ)$ are within a neighborhood of MCR₋(ϵ) and MCR₊(ϵ) respectively.

The bounds in Theorem 4 naturally account for potential overfitting without an explicit limit on model class complexity (such as a covering number, Rademacher complexity, or VC dimension). Instead, these bounds depend on being able to fully optimize MR across sets in the form of $\widehat{\mathcal{R}}(ϵ)$. If we allow our model class $\mathcal{F}$ to become more flexible, then the size of $\widehat{\mathcal{R}}(ϵ)$ will also increase. Because the bounds in Theorem 4 result from optimizing over $\widehat{\mathcal{R}}(ϵ)$, increasing the size of $\widehat{\mathcal{R}}(ϵ)$ results in wider, more conservative bounds. In this way, Eqs 4.2 and 4.3 implicitly capture model class complexity.

So far, Theorem 4 lets us bound the range of MR values corresponding to models that predict well, but it does not tell us whether these bounds are actually attained. Similarly, we can conclude from Theorem 4 that [MCR₋(ϵ), MCR₊(ϵ)] is unlikely to exceed the estimated range [${\widehat{MCR}}_{-}(ϵ)$, ${\widehat{MCR}}_{+}(ϵ)$] by a substantial margin, but we cannot determine whether this estimated range is unnecessarily wide. For example, consider the models that drive the ${\widehat{MCR}}_{+}(ϵ)$ estimator: the models with strong in-sample accuracy, and high empirical reliance on X₁. These models’ in-sample performance could merely be the result of overfitting, in which case they do not tell us direct information about $\mathcal{R}(ϵ)$. Alternatively, even if all of these models truly do perform well on expectation (that is, even if they are contained in $\mathcal{R}(ϵ)$), the model with the highest empirical reliance on X₁ may merely be the model for which our empirical MR estimate contains the most error. Either of these scenarios can cause ${\widehat{MCR}}_{+}(ϵ)$ to be unnecessarily high, relative to MCR₊(ϵ).

Fortunately, both problematic scenarios are solved by requiring a limit on the complexity of $\mathcal{F}$. We propose a complexity measure in the form of a covering number, which allows us control a worst case scenario of either overfitting or MR estimation error. Specifically, we define the set of functions ${\mathcal{G}}_r$ as an r-margin-expectation-cover if for any $f\in \mathcal{F}$ and any distribution D, there exists $g\in {\mathcal{G}}_r$ such that

$${\mathbb{E}}_{Z\sim D}\left|L\left(f,Z\right)-L\left(g,Z\right)\right|\le r.$$ (4.4)

We define the covering number $N(\mathcal{F},r)$ to be the size of the smallest r-margin-expectation-cover for $\mathcal{F}$. In general, we use ${\mathbb{P}}_{V\sim D}$ and ${\mathbb{E}}_{V\sim D}$ to denote probabilities and expectations with respect to a random variable V following the distribution D. We abbreviate these quantities accordingly when V or D are clear from context, for example, as ${\mathbb{P}}_D$, ${\mathbb{P}}_V$, or simply $\mathbb{P}$. Unless otherwise stated, all expectations and probabilities are taken with respect to the (unknown) population distribution.

We first show that this complexity measure allows us to control the worst case MR estimation error, that is, the covering number $\mathcal{N}(\mathcal{F},r)$ provides a uniform bound on the error of $\widehat{MR}(f)$ for all $f\in \mathcal{F}$.

Theorem 5 (Uniform bound for $\widehat{MR}$) Given r > 0, if Assumptions 1 and 3 hold for all $f\in \mathcal{F}$, then

$$\mathbb{P}\left[\underset{f\in \mathcal{F}}{\sup }\left|\widehat{MR}\left(f\right)-MR\left(f\right)\right|>q\left(\delta ,r,n\right)\right]\le \delta ,$$

where

$$q\left(\delta ,r,n\right):=\frac{B_{switch}}{b_{orig}}-\frac{B_{switch}-\left\{B_{ind}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\sqrt{2}\right)\right)}{n}}+2r\sqrt{2}\right\}}{b_{orig}+\left\{B_{ind}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right\}}.$$ (4.5)

Theorem 5 states that, with high probability, the largest possible estimation error for MR(f) across all models in $\mathcal{F}$ is bounded by q(δ, r, n), which can be made arbitrarily small by increasing n and decreasing r. As we noted in Section 3.1, this means that it is possible to train a model and estimate its reliance on variables without using sample-splitting.

The covering number $\mathcal{N}(\mathcal{F},r)$ can also be used to limit the extent of overfitting (see Appendix B.5.1). As a result, it is possible to set an in-sample performance threshold low enough so that it will only be met by models with strong expected performance (that is, by models truly within $\mathcal{R}(ϵ)$). To implement this idea of a stricter performance threshold, we contract the empirical ϵ-Rashomon set by subtracting a buffer term from ϵ. This requires that we generalize the definition of an empirical ϵ-Rashomon set to $\widehat{R}(ϵ,f_{\mathrm{ref}},\mathcal{F}):=\{f_{\mathrm{ref}}\}\bigcup \{f\in \mathcal{F}:{\widehat{e}}_{\mathrm{orig}}(f)\le {\widehat{e}}_{\mathrm{orig}}(f_{\mathrm{ref}})+ϵ\}$ for $ϵ\in \mathbb{R}$, where the explicit inclusion of f_ref now ensures that $\widehat{R}(ϵ,f_{\mathrm{ref}},\mathcal{F})$ is nonempty, even for ϵ < 0. As before, we typically omit the notation f_ref and $\mathcal{F}$, writing $\widehat{R}(ϵ)$ instead.

We are now prepared to answer the questions of whether the bounds from Theorem 4 are actually attained, and of whether the estimated range $[{\widehat{MCR}}_{-}(ϵ),{\widehat{MCR}}_{+}(ϵ)]$ is unnecessarily wide. Our answer comes in the form of an upper bound on MCR₋(ϵ), and a lower bound on MCR₊(ϵ).

Theorem 6 (“Inner” MCR Bounds) Given constants ϵ ≥ 0 and r > 0, if Assumptions 1, 2 and 3 hold for all $f\in \mathcal{F}$, and then

$$\begin{array}{cc}\mathbb{P}\left({MCR}_{+}\left(ϵ\right)<{\widehat{MCR}}_{+}\left({ϵ}_{in}\right)-{\mathcal{Q}}_{in}\right)\le \delta ,& and\end{array}$$ (4.6)

$$\mathbb{P}\left(MC{R}_{-}\left(ϵ\right)>{\widehat{MCR}}_{-}\left({ϵ}_{in}\right)+{\mathcal{Q}}_{in}\right)\le \delta ,$$ (4.7)

where ${ϵ}_{in}:=ϵ-2B_{ref}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}-2r,\mathit{and}{\mathcal{Q}}_{in}=q\left(\frac{\delta }{2},r,n\right)$, as defined in Eq 4.5.

Theorem 6 can allow us to infer an “inner” bound that is contained within the interval [MCR₋(ϵ), MCR₊(ϵ)] with high probability. In Figure 3, we illustrate the result of Theorem 6, and give a sketch of the proof. This proof follows a similar structure to that of Theorem 4, but incorporates Theorem 5’s uniform bound on MR estimation error (${\mathcal{Q}}_{\mathrm{in}}$ term), as well as an additional uniform bound on the probability that any model has in-sample loss too far from its expected loss (ϵ_in term).

A practical implication of Theorem 6 is that, roughly speaking, if ${\widehat{MCR}}_{+}({ϵ}_{\mathrm{in}})\approx {\widehat{MCR}}_{+}(ϵ)$ then it is unlikely for the empirical estimator ${\widehat{MCR}}_{+(ϵ)}$ to substantially underestimate MCR₊(ϵ). Taken together with Theorem 4, we can conclude that, if ${\widehat{MCR}}_{+}({ϵ}_{\mathrm{in}})\approx {\widehat{MCR}}_{+}({ϵ}_{\mathrm{out}})$, then the estimator ${\widehat{MCR}}_{+}(ϵ)$ is unlikely either to overestimate or to underestimate MCR₊(ϵ) by very much. In large samples, it may be plausible to expect the condition ${\widehat{MCR}}_{+}({ϵ}_{\mathrm{in}})\approx {\widehat{MCR}}_{+}({ϵ}_{\mathrm{out}})$ to hold, since ϵ_in and ϵ_out both approach ϵ as n increases. In the same way, if ${\widehat{MCR}}_{-}({ϵ}_{\mathrm{in}})\approx {\widehat{MCR}}_{-}({ϵ}_{\mathrm{out}})$, we can conclude from Eqs 4.3 & 4.7 that the empirical estimator ${\widehat{MCR}}_{-}(ϵ)$ is unlikely to either overestimate or underestimate MCR₋(ϵ) by very much. For this reason, we argue that ${\widehat{MCR}}_{-}(ϵ)$ and ${\widehat{MCR}}_{+}(ϵ)$ form sensible estimates of population-level MCR – each is contained within a neighborhood of its respective estimand, with high probability. The secondary x-axis of Figure 3 gives an illustration of this argument.

5. Extensions of Rashomon Sets Beyond Variable Importance

In this section we generalize the Rashomon set approach beyond the study of MR. In Section 5.1, we create finite-sample CIs for other summary characterizations of near-optimal, or best-in-class models. The generalization also helps to illustrate a core aspect of the argument underlying Theorem 4: models with near-optimal performance in the population tend to have relatively good performance in random samples.

In Section 5.2, we review existing literature on near-optimal models.

5.1. Finite-sample Confidence Intervals from Rashomon Sets

Rather than describing how much a model relies on X₁, here we assume the analyst is interested in an arbitrary characteristic of a model. We denote this characteristic of interest as $\varphi :\mathcal{F}\to \mathbb{R}$. For example, if f_β is the linear model $f_{\beta }(x)=x^{\prime }\beta ,$ then ϕ may be defined as the norm of the associated coefficient vector (that is, $(\varphi (f_{\beta })={\Vert \beta \Vert }_2^2)$ or the prediction f_β would assign given a specific covariate profile x_new (that is $\varphi (f_{\beta })=f_{\beta }(x_{new})$).

Given a descriptor ϕ, we now show a general result that allows creation of finite-sample CIs for the best performing models $\mathcal{R}(ϵ)$. The resulting CIs are themselves based on empirical Rashomon sets.

Proposition 7 (Finite sample CIs from Rashomon sets) Let ${ϵ}^{\prime }:=ϵ+2B_{ref}\sqrt{\frac{\log (2^{\delta -1})}{2n}}$, let ${\widehat{\varphi }}_{-}({ϵ}^{\prime }):={\min }_{f\in \widehat{\mathcal{R}}({ϵ}^{\prime })}\varphi (f)$, and let ${\widehat{\varphi }}_{+}({ϵ}^{\prime }):={\max }_{f\in \widehat{\mathcal{R}}({ϵ}^{\prime })}\varphi (f)$.

If Assumption 2 holds for all $f\in \mathcal{R}(ϵ)$, then

$$\mathbb{P}\left[\left\{\varphi \left(f\right):f\in \mathcal{R}\left(ϵ\right)\right\}\subseteq \left[{\widehat{\varphi }}_{-}\left({ϵ}^{\prime }\right),{\widehat{\varphi }}_{+}\left({ϵ}^{\prime }\right)\right]\right]\ge 1-\delta .$$

Proposition 7 generates a finite-sample CI for the range of values ϕ(f) corresponding to well-performing models, $\{\varphi (f):f\in \mathcal{R}(ϵ)\}$. This CI, denoted by $[{\widehat{\varphi }}_{-}({ϵ}^{\prime }),{\widehat{\varphi }}_{+}({ϵ}^{\prime }),]$ can itself be interpreted as the range of values ϕ(f) corresponding to models f with empirical loss not substantially above that of f_ref. Thus, the interval has both a rigorous coverage rate and a coherent in-sample interpretation. The proof of Proposition 7 uses Hoeffding’s inequality to show that models in $\mathcal{F}$ are contained in $\widehat{\mathcal{R}}({ϵ}^{\prime })$ with high probability, that is, that models with good expected performance tend to perform well in random samples.

An immediate corollary of Proposition 7 is that we can generate finite-sample CIs for all best-in-class models $f^{\star }\in {\mathrm{arg\; min}}_{f\in \mathcal{F}}\mathbb{E}L(f,Z)$ by setting ϵ = 0. This corollary can be further strengthened if a single model f^⋆ is assumed to uniquely minimize $\mathbb{E}L(f,Z)$ over $f\in \mathcal{F}$ (see Appendix B.6).

Note that Proposition 7 implicitly assumes that ϕ(f) can be determined exactly for any model $f\in \mathcal{F}$, in order for the interval $[{\widehat{\varphi }}_{-}({ϵ}^{\prime }),{\widehat{\varphi }}_{+}({ϵ}^{\prime })]$ to be precisely determined. This assumption does not hold, for example, if ϕ(f) = MR(f), or if ϕ(f) = Var{f(X₁, X₂)}, as these quantities depend on both f and the (unknown) population distribution. In such cases, an additional correction factor must be incorporated to account for estimation error of ϕ(f), such as the ${\mathcal{Q}}_{\mathrm{out}}$ term in Theorem 4.

In concurrent work, Coker et al. (2018) show that profile likelihood intervals take the same form as the interval $[{\widehat{\varphi }}_{-}({ϵ}^{\prime }),{\widehat{\varphi }}_{+}({ϵ}^{\prime })]$ in Proposition 7. This means that a profile likelihood interval can also be expressed by minimizing and maximizing over an empirical Rashomon set. More specifically, consider the case where the loss function L is the negative of the known log likelihood function, and where f_ref is the maximum likelihood estimate of the “true model,” which in this case is f^⋆. If additional minor assumptions are met (see Appendix A.6 for details), then the (1 − δ)-level profile likelihood interval for ϕ(f^⋆) is equal to $[{\widehat{\varphi }}_{-}(\frac{{\mathcal{X}}_1,1-\delta }{2n}),{\widehat{\varphi }}_{+}(\frac{{\mathcal{X}}_1,1-\delta }{2n})]$, where (${\widehat{\varphi }}_{-}$ and ${\widehat{\varphi }}_{+}$ are defined as in Proposition 7, and ${\mathcal{X}}_{1,1-\delta }$ is the 1 − δ percentile of a chi-square distribution with 1 degree of freedom.

Relative to a profile likelihood approach, the advantage of Proposition 7 is that it does not require asymptotics, it does not require that the likelihood be known up to a parametric form, and it can be extended to study the set of near-optimal prediction models $\mathcal{R}(ϵ)$, rather than a single, potentially misspecified prediction model f^⋆. This is especially useful when different near-optimal models accurately describe different aspects of the underlying data generating process, but none capture it completely. The disadvantage of Proposition 7 is that the required performance threshold of ${ϵ}^{\prime }=ϵ+2B_{ref}\sqrt{\frac{\log (2\delta -1)}{2n}}$ decreases more slowly than the performance threshold of $\frac{{\mathcal{X}}_1,1-\delta }{2n}$ required in a profile likelihood interval. Because our results from Section 4.1 carry a similar disadvantage, we use these results primarily to motivate point estimates describing the Rashomon set $\mathcal{R}(ϵ)$.

Still, it is worth emphasizing the generality of Proposition 7. Through this result, Rashomon sets allow us to reframe a wide set of finite-sample inference problems as in-sample optimization problems. The implied CIs are not necessarily in closed form, but the approach still opens an exciting pathway for deriving non-asymptotic results. For example, they imply that existing methods for profile likelihood intervals might be able to be reapplied to achieve finite-sample results. For highly complex model classes where profile likelihoods are difficult to compute, such as neural networks or random forests, approximate inference is sometimes achieved via approximate optimization procedures (for example, Markov chain Monte Carlo for Bayesian additive regression trees, in Chipman et al., 2010). Proposition 7 shows that similar approximate optimization methods could be repurposed to establish approximate, finite-sample inferences for the same model classes.

5.2. Related Literature on the Rashomon Effect

Breiman et al. (2001) introduced the “Rashomon effect” of statistics as a problem of ambiguity: if many models fit the data well, it is unclear which model we should try to interpret. Breiman suggests that the ensembling many well-performing models together can resolve this ambiguity, as the new ensemble model may perform better than any of its individual members. However, this approach may only push the problem from the member level to the ensemble level, as there may also be many different ensemble models that fit the data well.

The Rashomon effect has also been considered in several subject areas outside of VI, including those in non-statistical academic disciplines (Heider, 1988; Roth and Mehta, 2002). Tulabandhula and Rudin (2014) optimize a decision rule to perform well under the predicted range of outcomes from any well-performing model. Statnikov et al. (2013) propose an algorithm to discover multiple Markov boundaries, that is, minimal sets of covariates such that conditioning on any one set induces independence between the outcome and the remaining covariates. Nevo and Ritov (2017) report interpretations corresponding to a set of well-fitting, sparse linear models. Meinshausen and Bühlmann (2010) estimate structural aspects of an underlying model (such as the variables included in that model) based on how stable those aspects are across a set of well-fitting models. This set of well-fitting models is identified by repeating an estimation procedure in a series of perturbed samples, using varying levels of regularization (see also Azen et al., 2001). Letham et al. (2016) search for a pair of well-fitting dynamical systems models that give maximally different predictions.

6. Calculating Empirical Estimates of Model Class Reliance

In this section, we propose a binary search procedure to bound the values of ${\widehat{MCR}}_{-}(ϵ)$ and ${\widehat{MCR}}_{+}(ϵ)$ (see Eq 2.4), which respectively serve as estimates of MCR₋(ϵ) and MCR₊(ϵ) (see Section 4.1). Each step of this search consists of minimizing a linear combination of ê_orig(f) and ê_switch(f) across $f\in \mathcal{F}$. Our approach is related to the fractional programming approach of Dinkelbach (1967), but accounts for the fact that the problem is constrained by the value of the denominator, ê_orig(f). We additionally show that, for many model classes, computing ${\widehat{MCR}}_{-}(ϵ)$ only requires that we minimize convex combinations of ê_orig(f) and ê_switch(f), which is no more difficult than minimizing the average loss over an expanded and reweighted sample (See Eq 6.2 & Proposition 11).

Computing ${\widehat{MCR}}_{+}(ϵ)$ however will require that we are able to minimize arbitrary linear combinations of ê_orig(f) and ê_switch(f). In Section 6.3, we outline how this can be done for convex model classes – classes for which the loss function is convex in the model parameter. Later, in Section 7, we give more specific computational procedures for when $\mathcal{F}$ is the class of linear models, regularized linear models, or linear models in a reproducing kernel Hilbert space (RKHS). We summarize the tractability of computing empirical MCR for different model classes in Table 1.

Table 1:

Tractability of empirical MCR computation for different model classes - For each case, we describe the tractability of computing ${\widehat{MCR}}_{-}$ and ${\widehat{MCR}}_{+}$ using our proposed approaches. Computing empirical MCR can be reduced to a sequence of optimization problems, the form of which are noted in parentheses within the above table.

Model class and loss function ($\mathcal{F}\&L$)	Computing ${\widehat{MCR}}_{-}$	Computing ${\widehat{MCR}}_{+}$
(L2 Regularized) Linear models, with the squared error loss	Highly tractable (QP1QC, see Sections 7.2 & 7.3)	Highly tractable (QP1QC, see Sections 7.2 & 7.3)
Linear models in a reproducing kernel Hilbert space, with the squared error loss	Moderately tractable (QP1QC, see Section 7.4.1)	Moderately tractable (QP1QC, see Section 7.4.1)
Cases where irrelevant covariates do not improve predictions	Moderately tractable (Convex optimization problems, see Proposition 11)	Potentially intractable
Cases where minimizing the empirical loss is a convex optimization problem	Potentially intractable (DC programs, see Section 6.3)	Potentially intractable (DC programs, see Section 6.3)

To simplify notation associated with the reference model f_ref, we present our computational results in terms of bounds on empirical MR subject to performance thresholds on the absolute scale. More specifically, we present bound functions b₋ and b₊ satisfying $b_{-}({ϵ}_{\mathrm{abs}})\le \widehat{MR}(f)\le b_{+}({ϵ}_{\mathrm{abs}})$ simultaneously for all $\{f,{ϵ}_{\mathrm{abs}}:{\widehat{e}}_{\mathrm{orig}}(f)\le {ϵ}_{\mathrm{abs}},f\in \mathcal{F},{ϵ}_{\mathrm{abs}}>0\}$ (Figures 2 & 8 show examples of these bounds). The binary search procedures we propose can be used to tighten these boundaries at a particular value ϵ_abs of interest.

Figure 8:

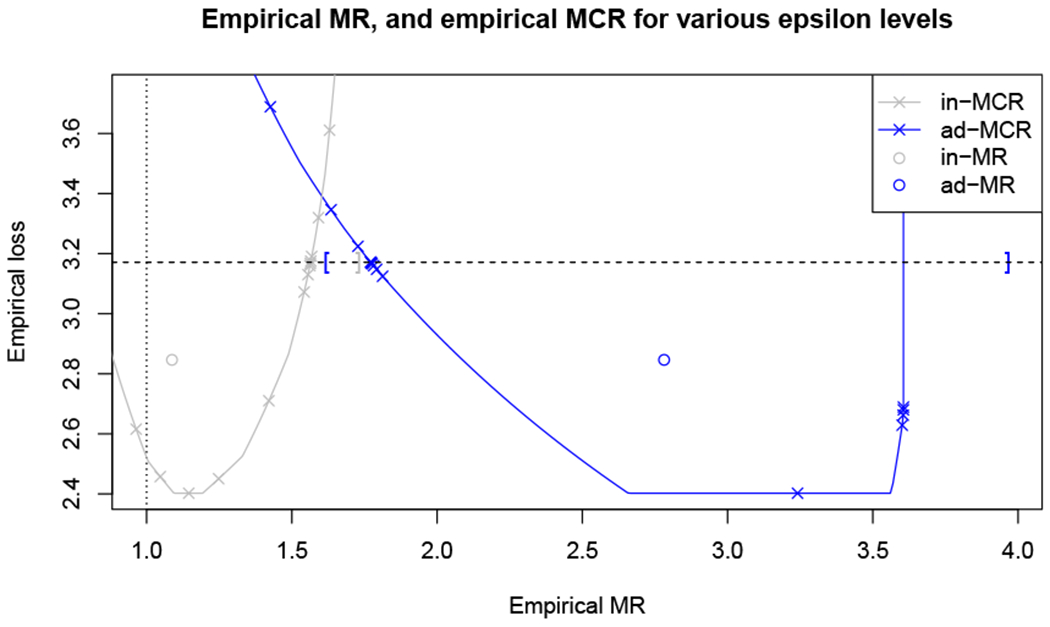
Empirical MR and MCR for Broward County criminal records data set - For any prediction model f, the y-axis shows empirical loss $({\widehat{e}}_{\mathrm{stnd}}(f))$ and the x-axis shows empirical reliance $(\widehat{MR}(f))$ on each covariate subset. Null reliance (MR equal to 1.0) is marked by the vertical dotted line. Reliances on different covariate subsets are marked by color (“admissible” = blue; “inadmissible” = gray). For example, model reliance values for f_ref are shown by the two circular points, one for “admissible” variables and one for “inadmissible” variables. MCR for different values of ϵ can be represented as boundaries on this coordinate space. To this end, for each covariate subset, we compute conservative boundary functions (shown as solid lines, or “bowls”) guaranteed to contain all models in the class (see Section 6). Specifically, all models in $f\in {\mathcal{F}}_{D,r_k}$ are guaranteed to have an empirical loss $({\widehat{e}}_{\mathrm{stnd}}(f))$ and empirical MR value $(\widehat{MR}(f))$ for “inadmissible variables” corresponding to a point within the gray bowl. Likewise, all models in ${\mathcal{F}}_{D,r_k}$ are guaranteed to have an empirical loss and empirical MR value for “admissible variables” corresponding to a point within the blue bowl. Points shown as “×” represent additional models in ${\mathcal{F}}_{D,r_k}$ discovered during our computational procedure, and thus show where the “bowl” boundary is tight. The goal of our computation procedure (see Section 6) is to tighten the boundary as much as possible near the ϵ value of interest, shown by the dashed horizontal line above. This dashed line has a y-intercept equal to the loss of the reference model plus the ϵ value of interest. Bootstrap CIs for MCR₋(ϵ) and MCR₊(ϵ) are marked by brackets.

We briefly note that as an alternative to the global optimization procedures we discuss below, heuristic optimization procedures such as simulated annealing can also prove useful in bounding empirical MCR. By definition, the empirical MR for any model in $\widehat{\mathcal{R}}(ϵ)$ forms a lower bound for ${\widehat{MCR}}_{+}(ϵ)$, and an upper bound for ${\widehat{MCR}}_{-}(ϵ)$. Heuristic maximization and minimization of empirical MR can be used to tighten these boundaries.

Throughout this section, we assume that $0<{\min }_{f\in \mathcal{F}}{ê}_{\mathrm{orig}}(f)$, to ensure that MR is finite.

6.1. Binary Search for Empirical MR Lower Bound

Before describing our binary search procedure, we introduce additional notation used in this section. Given a constant $\gamma \in \mathbb{R}$ and prediction model $fϵ\mathcal{F}$, we define the linear combination ${\widehat{h}}_{-,\gamma }$, and its minimizers (for example, ${\widehat{g}}_{-,\gamma },\mathcal{F}$), as

$${\widehat{h}}_{-,\gamma }\left(f\right):=\gamma {\widehat{e}}_{\text{orig}}\left(f\right)+{\widehat{e}}_{\text{switch}}\left(f\right),{\mathrm{and}\widehat{g}}_{-,\gamma ,\mathcal{F}}\in \underset{f\in \mathcal{F}}{\text{arg min}}{\widehat{h}}_{-,\gamma }\left(f\right).$$

We do not require that ${\widehat{h}}_{-,\gamma }$ is uniquely minimized, and we frequently use the abbreviated notation ${\widehat{g}}_{-,\gamma }$ when $\mathcal{F}$ is clear from context.

Our goal in this section is to derive a lower bound on $\widehat{MR}$ for subsets of $\mathcal{F}$ in the form of $\{f\in \mathcal{F}:{\widehat{e}}_{\mathrm{orig}}(f)\le {ϵ}_{abs}\}$. We achieve this by minimizing a series of linear objective functions in the form of ${\widehat{h}}_{-,\gamma }$, using a similar method to that of Dinkelbach (1967). Often, minimizing the linear combination ${\widehat{h}}_{-,\gamma }\left(f\right)$ is more tractable than minimizing the MR ratio directly.

Almost all of the results shown in this section, and those in Section 6.2, also hold if we replace ${\widehat{e}}_{\mathrm{switch}}$ with ${\widehat{e}}_{\mathrm{divide}}$ throughout (see Eq 3.5), including in the definition of $\widehat{MR}$ and ${\widehat{h}}_{-,\gamma }\left(f\right)$. The exception is Proposition 11, below, which we may still expect to approximately hold if we replace ${\widehat{e}}_{\mathrm{switch}}$ with ${\widehat{e}}_{\mathrm{divide}}$.

Given an observed sample, we define the following condition for a pair of values $\{\gamma ,{ϵ}_{\mathrm{abs}}\}\in \mathbb{R}\times {\mathbb{R}}_{>0}$, and argmin function ${\widehat{g}}_{-,\gamma }$:

Condition 8 (Criteria to continue search for $\widehat{MR}$ lower bound) ${\widehat{h}}_{-,\gamma }({\widehat{g}}_{-,\gamma })\ge 0$ and ${\widehat{e}}_{orig}(\widehat{g}-,\gamma )\le {ϵ}_{abs}$.

We are now equipped to determine conditions under which we can tractably create a lower bound for empirical MR.

Lemma 9 (Lower bound for $\widehat{MR}$) If $\gamma \in \mathbb{R}$ satisfies ${\widehat{h}}_{-,\gamma }({\widehat{g}}_{-,\gamma })\ge 0$, then

$$\frac{{\widehat{h}}_{-,\gamma }\left({\widehat{g}}_{-,\gamma }\right)}{{ϵ}_{\text{abs}}}-\gamma \le \widehat{MR}\left(f\right)$$ (6.1)

for all $f\in \mathcal{F}$ satisfying ${\widehat{e}}_{orig}(f)\le {ϵ}_{abs}$. It also follows that

$$-\gamma \le \widehat{MR}\left(f\right)\mathrm{for\; all}f\in \mathcal{F}.$$

Additionally, if $f={\widehat{g}}_{-,\gamma }$ and at least one of the inequalities in Condition 8 holds with equality, then Eq 6.1 holds with equality.

Lemma 9 reduces the challenge of lower-bounding $\widehat{MR}(f)$ to the task of minimizing the linear combination ${\widehat{h}}_{-,\gamma }\left(f\right)$. The result of Lemma 9 is not only a single boundary for a particular value of ϵ_abs, but a boundary function that holds all values of ϵ_abs > 0, with lower values of ϵ_abs leading to more restrictive lower bounds on $\widehat{MR}(f)$.

In addition to the formal proof for Lemma 9, we provide a heuristic illustration of the result in Figure 4, to aid intuition.

Figure 4:

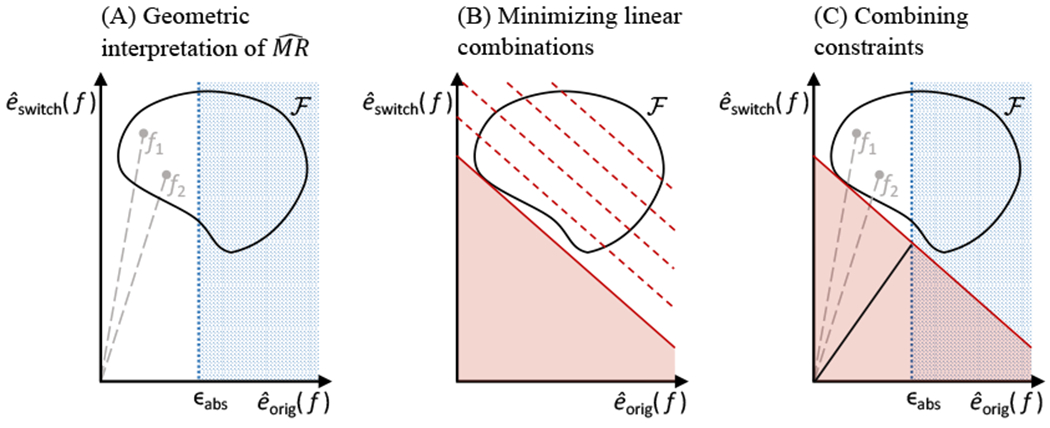
Above, we illustrate the geometric intuition for Lemma 9. In Panel (A), we show an example of a hypothetical model class $\mathcal{F}$, marked by the enclosed region. For each model $f\in \mathcal{F}$, the x-axis shows ${\widehat{e}}_{\mathrm{orig}}(f)$ and the y-axis shows ${\widehat{e}}_{\mathrm{switch}}(f)$. Here, we can see that the condition ${\min }_{f\in \mathcal{F}}{\widehat{e}}_{\mathrm{orig}}(f)>0$ holds. The blue dotted region marks models with higher empirical loss. We mark two example models within $\mathcal{F}$ as f₁ and f₂. The slopes of the lines connecting the origin to f₁ and f₂ are equal to $\widehat{MR}(f_1)$ and $\widehat{MR}(f_2)$ respectively. Our goal is to lower-bound the slope corresponding to $\widehat{MR}$ for any model f satisfying ê_orig(f) ≤ ϵ_abs. In Panel (B), we consider the linear combination ${\widehat{h}}_{-,\gamma }(f)=\gamma {\widehat{e}}_{\mathrm{orig}}(f)+{\widehat{e}}_{\mathrm{switch}}(f)$ for γ = 1. Above, contour lines of ${\widehat{h}}_{-,\gamma }$ are shown in red. The solid red line indicates the smallest possible value of ${\widehat{h}}_{-,\gamma }$ across $f\in \mathcal{F}$. Specifically, its y-intercept equals ${\min }_{f\in \mathcal{F}}{\widehat{h}}_{-,\gamma }(f)$. If we can determine this minimum, we can determine a linear border constraint on $\mathcal{F}$, that is, we will know that no points corresponding to models $f\in \mathcal{F}$ may lie in the shaded region above. Additionally, if ${\min }_{f\in \mathcal{F}}{\widehat{h}}_{-,\gamma }(f)\ge 0$ (see Lemma 9), then we know that the origin is either excluded by this linear constraint, or is on the boundary. In Panel (C), we combine the two constraints from Panels (A) & (B) to see that models $f\in \mathcal{F}$ satisfying ê_orig(f) ≤ ϵ_abs must, correspond to points in the white, unshaded region above. Thus, as long as the unshaded region does not contain the origin, any line connecting the origin to the a model f satisfying ê_orig(f) < ϵ_abs (for example, here, f₁, f₂) must, have a. slope at least, as high as that of the solid black line above. It. can be shown algebraically that the black line has slope equal to the left-hand side of Eq 6.1. Thus the left-hand side of Eq 6.1 is a lower bound for $\widehat{MR}(f)$ for all $\{f\in \mathcal{F}:{\widehat{e}}_{\mathrm{orig}}(f)\le {ϵ}_{\mathrm{abs}}\}$.

It remains to determine which value of γ should be used in Eq 6.1. The following lemma implies that this value can be determined by a binary search, given a particular value of interest for ϵ_abs.

Lemma 10 (Monotonicity for $\widehat{MR}$ lower bound binary search) The following monotonicity results hold:

1. ${\widehat{h}}_{-,\gamma }\left({\widehat{g}}_{-,\gamma }\right)$ is monotonically increasing in γ.

2. ${\widehat{e}}_{\mathit{orig}}\left({\widehat{g}}_{-,\gamma }\right)$ is monotonically decreasing in γ.

3. Given ϵ_abs, the lower bound from Eq 6.1, $\left\{\frac{{\widehat{h}}_{-,\gamma }({\widehat{g}}_{-,\gamma })}{{ϵ}_{abs}}-\gamma \right\}$, is monotonically decreasing in γ in the range where ${\widehat{e}}_{\mathit{orig}}\left({\widehat{g}}_{-,\gamma }\right)\le {ϵ}_{\mathit{abs}}$, and increasing otherwise.

Given a particular performance level of interest, ϵ_abs, Point 3 of Lemma 10 tells us that the value of γ resulting in the tightest lower bound from Eq 6.1 occurs when γ is as low as possible while still satisfying Condition 8. Points 1 and 2 show that if γ₀ satisfies Condition 8, and one of the equalities in Condition 8 holds with equality, then Condition 8 holds for all γ ≥ γ₀. Together, these results imply that we can use a binary search to determine the value of γ to be used in Lemma 9, reducing this value until Condition 8 is no longer met. In addition to the formal proof for Lemma 10, we provide an illustration of the result in Figure 5 to aid intuition.

Figure 5:

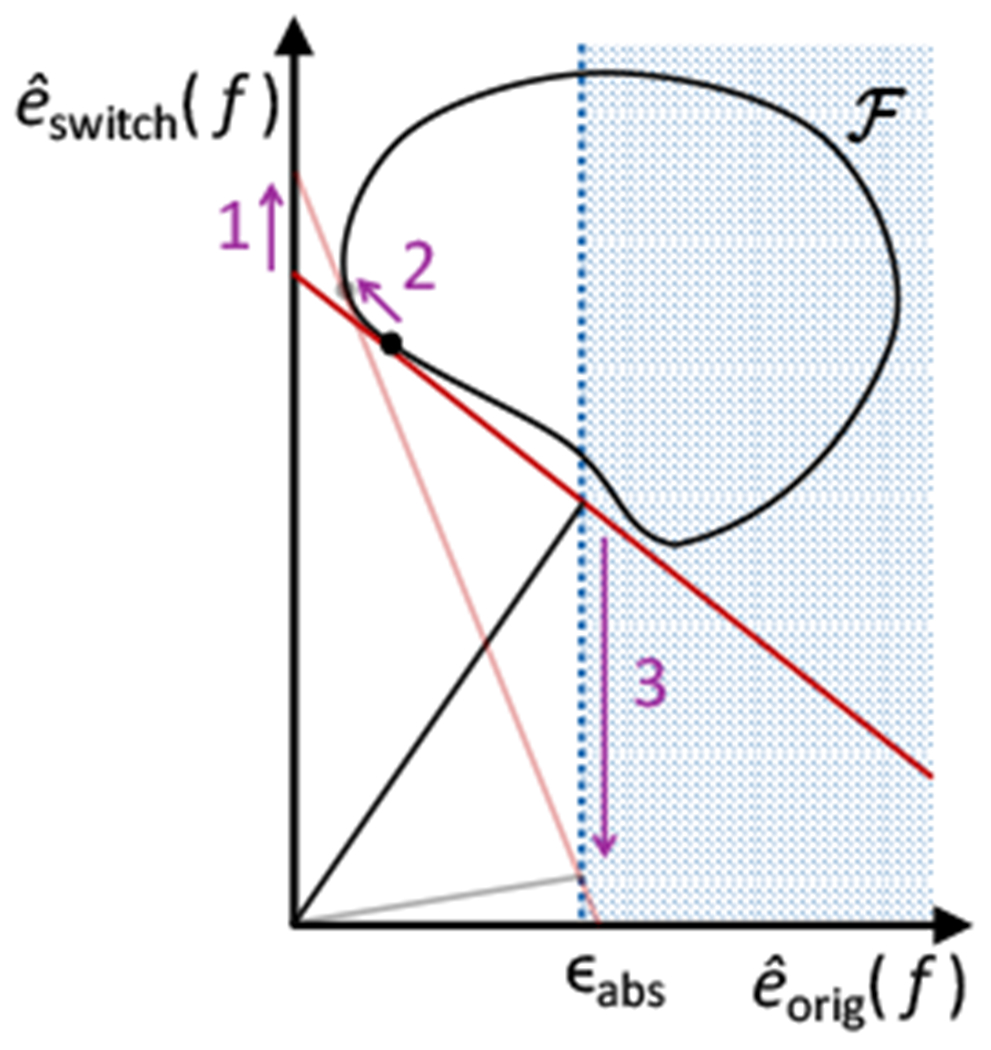
Monotonicity for binary search. Above we show a version of Figure 4–C for two alternative values of γ. This figure is meant, to add intuition for the monotonicity results in Lemma 10, in addition to the formal proof. Increasing γ is equivalent to decreasing the slope of the red line in Figure 4–C. We define two values γ₁ < γ₂, where γ₁ corresponds to the solid red line, above, and γ₂ corresponds to the semi-transparent, red line. The y-intercept values of these lines are equal to ${\widehat{h}}_{-,{\gamma }_1}({\widehat{g}}_{-,{\gamma }_1})$ and ${\widehat{h}}_{-,{\gamma }_2}({\widehat{g}}_{-,{\gamma }_2})$ respectively (see Figure 4–C caption). The solid and semi-transparent, black dots mark $({\widehat{g}}_{-,{\gamma }_1})$ and $({\widehat{g}}_{-,{\gamma }_2})$ respectively. Plugging γ₁ and γ₂ into Eq 6.1 yields two lower bounds for $\widehat{MR}$, marked by the slopes of the solid and semi-transparent, black lines respectively (see Figure 4–C caption). We see that (1) ${\widehat{h}}_{-,{\gamma }_1}({\widehat{g}}_{-,{\gamma }_1})\le {\widehat{h}}_{-,{\gamma }_2}({\widehat{g}}_{-,{\gamma }_2})$, that (2) ${\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_1})\ge {\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_2})\ge$, and that (3) the left-hand side of Eq 6.1 is decreasing in γ when ${\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_1})\le {ϵ}_{\mathrm{abs}}$. These three conclusions are marked by arrows in the above figure, with numbering matching the enumerated list in Lemma 10.

Next we present simple conditions under which the binary search for values of γ can be restricted to the nonnegative real line. This result substantially extends the computational tractability of our approach, as minimizing ${\widehat{h}}_{-,\gamma }$ for γ ≥ 0 is equivalent to minimizing a reweighted empirical loss over an expanded sample of size n²:

$${\widehat{h}}_{-,\gamma }\left(f\right)=\gamma {\widehat{e}}_{\text{orig}}\left(f\right)+{\widehat{e}}_{\text{switch}}\left(f\right)=\sum _{i=1}^n\sum _{j=1}^n{\omega }_{\gamma }\left(i,j\right)L\left\{f,\left({\mathbf{y}}_{\left[i\right]},{\mathbf{X}}_{1\left[j,\cdot \right]},{\mathbf{X}}_{2\left[i,\cdot \right]}\right)\right\},$$ (6.2)

where ${\omega }_{\gamma }\left(i,j\right)=\frac{\gamma 1\left(i=j\right)}{n}+\frac{1\left(i\ne j\right)}{n(n-1)}\ge 0$.

Proposition 11 (Nonnegative weights for $\widehat{MR}$ lower bound binary search) Assume that L and $\mathcal{F}$ satisfy the following conditions.

1. (Predictions are sufficient for computing the loss) The loss L{f, (Y, X₁, X₂)} depends on the covariates (X₁, X₂) only via the prediction function f, that is, $L\{f,(y,x_1^{(a)},x_2^{(a)})\}=L\{f,(y,x_1^{(b)},x_2^{(b)})\}$ whenever $f(x_1^{(a)},x_2^{(a)})=f(x_1^{(b)},x_2^{(b)})$.

2. (Irrelevant information does not improve predictions) For any distribution D satisfying X₁ ⊥_D (X₂, Y), there exists a function f_D satisfying

   $${\mathbb{E}}_{D}L\left\{f_D,\left(Y,X_1,X_2\right)\right\}=\underset{f\in \mathcal{F}}{\min }{\mathbb{E}}_{D}L\left\{f,\left(Y,X_1,X_2\right)\right\},$$

   and

   $$f_D(x_1^{\left(a\right)},x_2)=f_D(x_1^{\left(b\right)},x_2)forany{x}_1^{\left(a\right)},x_1^{\left(b\right)}\in {\mathcal{X}}_{1}and{x}_2\in {\mathcal{X}}_2.$$ (6.3)

Let γ = 0. Under the above assumptions, it follows that either (i) there exists a function ${\widehat{g}}_{-,0}$ minimizing ${\widehat{h}}_{-,0}$ that does not. satisfy Condition 8, or (ii) ${\widehat{e}}_{orig}(g-,0)\le {ϵ}_{\mathit{abs}}\mathit{and}{\widehat{MR}}_{(g-,0)}\le 1$ for any function ${\widehat{g}}_{-,0}$ minimizing ${\widehat{h}}_{-,0}$.

The implication of Proposition 11 is that, when the conditions of Proposition 11 are met, the search region for γ can be limited to the nonnegative real line, and minimizing ${\widehat{h}}_{-,\gamma }$ will be no harder than minimizing a reweighted empirical loss over an expanded sample (Eq 6.2). To see this, recall that for a fixed value of ϵ_abs we can tighten the boundary in Lemma 9 by conducting a binary search for the smallest, value of γ that satisfies Condition 8. If setting γ equal to 0 does not satisfy Condition 8, and the search for γ can be restricted to the nonnegative real line, where minimizing ${\widehat{h}}_{-,0}$ is more tractable (see Eq 6.2). Alternatively, if ${\widehat{e}}_{\mathrm{orig}}(g-,0)\le {ϵ}_{\mathrm{abs}}\text{and}{\widehat{MR}}_{(g-,0)}\le 1$, then we have identified a well-performing model g_−,0 with empirical MR no greater than 1. For ϵ_abs = ê_orig(f_ref) + ϵ, this implies that ${\widehat{MCR}}_{-}(ϵ)\le 1$, which is a sufficiently precise conclusion for most, interpretational purposes (see Appendix A.2).

Because of the fixed pairing structure used in ê_divide, Proposition 11 will not necessarily hold if we replace ê_switch with ê_divide throughout (see Appendix C.3). However, since ê_divide approximates ê_switch, we can expect Proposition 11 to hold approximately. The bound from Eq 6.1 still remains valid if we replace ê_switch with ê_divide and limit γ to the nonnegative reals, although in some cases it may not be as tight.

6.2. Binary Search for Empirical MR Upper Bound

We now briefly present a binary search procedure to upper bound $\widehat{MR}$, which mirrors the procedure from Section 6.1. Given a constant $\gamma \in \mathbb{R}$ and prediction model $f\in \mathcal{F}$, we define the linear combination ${\widehat{h}}_{+,\gamma }$, and its minimizers (for example, ${\widehat{g}}_{+,\gamma ,\mathcal{F}}$), as

$$\widehat{h}{}_{+,\gamma }\left(f\right):={\widehat{e}}_{\text{orig}}\left(f\right)+\gamma {\widehat{e}}_{\text{switch}}\left(f\right),\text{and}{\widehat{g}}_{+,\gamma ,\mathcal{F}}\in \underset{f\in \mathcal{F}}{\mathrm{arg\; min}}{\widehat{h}}_{+,\gamma }\left(f\right).$$

As in Section 6.1, ${\widehat{h}}_{+,\gamma }$ need not be uniquely minimized, and we generally abbreviate ${\widehat{g}}_{+,\gamma ,\mathcal{F}}$ as ${\widehat{g}}_{+,\gamma }$ when $\mathcal{F}$ is clear from context.

Given an observed sample, we define the following condition for a pair of values $\{\gamma ,{ϵ}_{\mathrm{abs}}\}\in {\mathbb{R}}_{\le 0}\times {\mathbb{R}}_{>0}$, and argmin function ${\widehat{g}}_{+,\gamma }$:

Condition 12 (Criteria to continue search for $\widehat{MR}$ upper bound) ${\widehat{h}}_{+,\gamma }\left({\widehat{g}}_{+,\gamma }\right)\ge 0$ and ${\widehat{e}}_{\mathit{orig}}\left({\widehat{g}}_{+,\gamma }\right)\le {ϵ}_{\mathit{abs}}$.

We can now develop a procedure to upper bound $\widehat{MR}$, as shown in the next lemma.

Lemma 13 (Upper bound for $\widehat{MR}$) If $\gamma \in \mathbb{R}$ satisfies γ ≤ 0 and ${\widehat{h}}_{+,\gamma }\left({\widehat{g}}_{+,\gamma }\right)\ge 0$, then

$$\widehat{MR}\left(f\right)\le \left\{\frac{{\widehat{h}}_{+,\gamma }\left({\widehat{g}}_{+,\gamma }\right)}{{ϵ}_{abs}}-1\right\}{\gamma }^{-1}$$ (6.4)

for all $f\in \mathcal{F}$ satisfying ê_orig(f) ≤ ϵ_abs. It also follows that

$$\widehat{MR}\left(f\right)\le \left|{\gamma }^{-1}\right|\mathit{for\; all}f\in \mathcal{F}.$$ (6.5)

Additionally, if $f={\widehat{g}}_{+,\gamma }$ and at least one of the inequalities in Condition 12 holds with equality, then Eq 6.4 holds with equality.

As in Section 6.1, it remains to determine the value of γ to use in Lemma 13, given a value of interest for ${ϵ}_{\mathrm{abs}}\ge {\min }_{f\in \mathcal{F}}{\widehat{e}}_{\text{orig}}\left(f\right)$. The next lemma tells us that the boundary from Lemma 13 is tightest when γ is as low as possible while still satisfying Condition 12.

Lemma 14 (Monotonicity for $\widehat{MR}$ upper bound binary search) The following monotonicity results hold:

1. ${\widehat{h}}_{+,\gamma }\left({\widehat{g}}_{+,\gamma }\right)$ is monotonically increasing in γ.

2. ${\widehat{e}}_{\mathit{orig}}\left({\widehat{g}}_{+,\gamma }\right)$ is monotonically decreasing in γ for γ ≤ 0, and Condition 12 holds for γ = 0 and ${ϵ}_{\mathit{abs}}\ge {\min }_{f\in \mathcal{F}}{\widehat{e}}_{\mathit{orig}}\left(f\right)$.

3. Given ϵ_abs, the upper boundary $\left\{\frac{{\widehat{h}}_{+,\gamma }\left({\widehat{g}}_{+,\gamma }\right)}{{ϵ}_{abs}}-1\right\}{\gamma }^{-1}$ is monotonically increasing in γ in the range where ${\widehat{e}}_{\mathit{orig}}\left({\widehat{g}}_{+,\gamma }\right)\le {ϵ}_{\mathit{abs}}$ and γ < 0, and decreasing in the range where ${\widehat{e}}_{\mathit{orig}}\left({\widehat{g}}_{+,\gamma }\right)>{ϵ}_{\mathit{abs}}$ and γ < 0.

Together, the results from Lemma 14 imply that we can use a binary search across $\gamma \in \mathbb{R}$ to tighten the boundary on $\widehat{MR}$ from Lemma 13.

6.3. Convex Models

In this section we show that empirical MCR can be conservatively computed when the loss function is convex in the model parameters – that is, when the models $f_{\theta }\in \mathcal{F}$ are indexed by a d-dimensional parameter $\theta \in \Theta \subseteq {\mathbb{R}}^d$, and when the loss function L(f_θ, (y, x₁, x₂)) is convex in θ for all $(x_1,x_2,y)\in {\mathcal{X}}_1\times ({\mathcal{X}}_2,\mathcal{Y})$.

Fortunately, neither Lemma 9 nor Lemma 13 require an exact minimum for ${\widehat{h}}_{-,\gamma }$ or ${\widehat{h}}_{+,\gamma }$. For Lemma 9, any lower bound on ${\widehat{h}}_{-,\gamma }$ is sufficient to determine a lower bound on MR(f). Likewise, for Lemma 13, any lower bound on ${\widehat{h}}_{+,\gamma }$ is sufficient to determine an upper bound on MR(f).

To find these lower bounds, we note that for “convex” model classes (defined above) the optimization problems in Sections 6.1 & 6.2 can be written either as convex optimization problems, or as difference convex function (DC) programs. A DC program is one that can be written as

$$\underset{\left\{\theta :c_{\mathrm{DC}}\left(\theta \right)\le k,\theta \in \Theta \right\}}{\min }{g}_{\mathrm{DC}}\left(\theta \right)-h_{\mathrm{DC}}\left(\theta \right),$$

where c_DC is a constraint function, $k\in {\mathbb{R}}^1$, and g_DC, h_DC, and c_DC are convex. Although precise solutions to DC problems are not always tractable, lower bounds can be attained by branch-and-bound (B&B) methods (Horst and Thoai, 1999). A simple B&B approach is to partition Θ into a set of simplexes. Within the j^th simplex, a lower bound on g_DC(θ)−h_DC(θ) can be determined by replacing h_DC with the hyperplane function h_j satisfying h_j (υ) = h_DC(υ) at each vertex υ of the j^th simplex. Within this partition, g_DC(θ) − h_DC(θ) is lower bounded by l_j := min_θ g_DC(θ) − h_j(θ), which can be computed as the solution to a convex optimization problem. Any partition for which l_j is found to be too high is disregarded. Once a bound l_j is computed for each partition, the partition with the lowest value l_j is selected to be subdivided further, and additional lower bounds are recomputed for each new, resulting partition. This procedure continues until a sufficiently tight lower bound is attained (for more detailed procedures, see Horst and Thoai, 1999).

This approach allows us to conservatively approximate bounds on $\widehat{MR}(f)$ in the form of Eq 6.1 & 6.4 by replacing ${\widehat{h}}_{-,\gamma }({\widehat{g}}_{-,\gamma })$ and ${\widehat{h}}_{+,\gamma }({\widehat{g}}_{+,\gamma })$ with lower bounds from the B&B procedure. Although it will always yield valid bounds, the procedure may converge slowly when the dimension of Θ is large, giving highly conservative results. For some special cases of model classes however, even high dimensional DC problems simplify greatly. We discuss these cases in the next section.

7. MR & MCR for Linear Models, Additive Models, and Regression Models in a Reproducing Kernel Hilbert Space

For linear or additive models, many simplifications can be made to our approaches for MR and MCR. To simplify the interpretation of MR, we show below that population-level MR for a linear model can be expressed in terms of the model’s coefficients (Section 7.1). To simplify computation, we show that the cost of computing empirical MR for a linear model grows only linearly in n (Section 7.1), even though the number of terms in the definition of empirical MR grows quadratically (see Eqs 3.3 & 3.6).

Moving on from MR, we show how empirical MCR can be computed for the class of linear models (Section 7.2), for regularized linear models (Section 7.3), and for regression models in a reproducing kernel Hilbert space (RKHS, Section 7.4). To do this, we build on the approach in Section 6 by giving approaches for minimizing arbitrary combinations of ê_switch(f) and ê_orig(f) across $f\in \mathcal{F}$. Even when the associated objective functions are non-convex, we can tractably obtain global minima for these model classes. We also discuss procedures to determine an upper bound B_ind on the loss for any observation when using these model classes (see Assumption 1).

Throughout this section, we assume that $\mathcal{X}\in {\mathbb{R}}^p$ for $p\in {\mathbb{Z}}^{+}$, that $\mathcal{Y}\subset {\mathbb{R}}^1$, and that L is the squared error loss function L(f, (y, x₁, x₂) = (y − f(x₁, x₂))². As in Section 6, we also assume that $0<{\min }_{f\in \mathcal{F}}{\widehat{e}}_{\mathit{orig}}\left(f\right)$, to ensure that empirical MR is finite.

7.1. Interpreting and Computing MR for Linear or Additive Models

We begin by considering MR for linear models evaluated with the squared error loss. For this setting, we can show both an interpretable definition of MR, as well as a computationally efficient formula for ê_switch(f).

Proposition 15 (Interpreting MR, and computing empirical MR for linear models) For any prediction model f, let e_orig(f), e_switch(f), ê_orig(f), and ê_swith(f) be defined based on the squared error loss L(f, (y, x₁, x₂)) := (y − f (x₁, x₂))² for $y\in \mathbb{R}$, $x_1\in {\mathbb{R}}^{p_1}$, and $x_2\in {\mathbb{R}}^{p_2}$, where p₁ and p₂ are positive integers. Let β = (β₁, β₂) and f_β satisfy ${\beta }_1\in {\mathbb{R}}^{p_1}$, ${\beta }_2\in {\mathbb{R}}^{p_2}$, and $f_{\beta }(x)=x^{\prime }\beta =x_1^{\prime }{\beta }_1+x_2^{\prime }{\beta }_2$. Then

$$MR(f_{\beta })=1+\frac{2}{e_{orig}(f_{\beta })}\left\{Co\upsilon \left(Y,X_1\right){\beta }_1-{\beta }_2^{\prime }Co\upsilon \left(X_2,X_1\right){\beta }_1\right\},$$ (7.1)

and, for finite samples,

$${\widehat{e}}_{switch}\left(f_{\beta }\right)=\frac{1}{n}\left\{{\mathbf{y}}^{\prime }\mathbf{y}-2{\left[\begin{array}{c}{{\mathbf{X}}^{\prime }}_1{\mathbf{W}}_{\mathbf{y}}\\ {{\mathbf{X}}^{\prime }}_2\mathbf{y}\end{array}\right]}^{\prime }\beta +{\beta }^{\prime }\left[\begin{array}{cc}{{\mathbf{X}}^{\prime }}_1{\mathbf{X}}_1& {{\mathbf{X}}^{\prime }}_1\mathbf{W}{\mathbf{X}}_2\\ {{\mathbf{X}}^{\prime }}_2\mathbf{W}{\mathbf{X}}_1& {{\mathbf{X}}^{\prime }}_2{\mathbf{X}}_2\end{array}\right]\beta \right\},$$ (7.2)

where $\mathbf{W}:=\frac{1}{n-1}({\mathbf{1}}_n{\mathbf{1}}_n^{\prime }-{\mathbf{I}}_n)$, 1_n is the n-length vector of ones, and I_n is the n × n identity matrix.

Eq 7.1 shows that model reliance for linear models can be interpreted in terms of the population covariances, the model coefficients, and the model’s accuracy. Gregorutti et al. (2017) show an equivalent formulation of Eq 7.1 under the stronger assumptions that f_β is equal to the conditional expectation function of Y (that is, $f_{\beta }=\mathbb{E}(Y|X=x)$), and the covariates X₁ and X₂ are centered.

Eq 7.2 shows that, although the number of terms in the definition of ê_switch grows quadratically in n (see Eq 3.3), the computational complexity of ê_switch(f_β) for a linear model f_β grows only linearly in n. Specifically, the terms ${\mathbf{X}}_1^{\prime }\mathbf{W}\mathbf{y}$ and ${\mathbf{X}}_1^{\prime }\mathbf{W}{\mathbf{X}}_2$ in Eq 7.2 can be computed as $\frac{1}{n-1}\left\{({\mathbf{X}}_1^{\prime }{\mathbf{1}}_n)({\mathbf{1}}_n^{\prime }\mathbf{y})-({\mathbf{X}}_1^{\prime }\mathbf{y})\right\}$ and $\frac{1}{n-1}\left\{({\mathbf{X}}_1^{\prime }{\mathbf{1}}_n)({\mathbf{1}}_n^{\prime }{\mathbf{X}}_2)-({\mathbf{X}}_1^{\prime }{\mathbf{X}}_2)\right\}$ respectively, where the computational complexity of each term in parentheses grows linearly in n.

As in Gregorutti et al. (2017), both results in Proposition 15 readily generalize to additive models of the form f_g1,g2 (X₁,X₂) := g₁ (X₁) + g₂(X₂), since permuting X₁ is equivalent to permuting g₁(X₁).

7.2. Computing Empirical MCR for Linear Models

Building on the computational result from the previous section, we now consider empirical MCR computation for linear model classes of the form

$${\mathcal{F}}_{\text{lm}}:=\left\{f_{\beta }:f_{\beta }\left(x\right)=x^{\prime }\beta ,\beta \in {\mathbb{R}}^p\right\}.$$

In order to implement the computational procedure from Sections 6.1 and 6.2, we must be able to minimize arbitrary linear combinations of ê_orig(f_β) and ê_switch(f_β). Fortunately, for linear models, this minimization reduces to a quadratic program, as we show in the next remark.

Remark 16 (Tractability of empirical MCR for linear model classes) For any $f_{\beta }\in {\mathcal{F}}_{\mathit{lm}}$ and any fixed coefficients ${\xi }_{\mathit{orig}},{\xi }_{\mathit{switch}}\in \mathbb{R}$, the linear combination

$${\xi }_{orig}{\widehat{e}}_{orig}\left(f_{\beta }\right)+{\xi }_{switch}{\widehat{e}}_{switch}\left(f_{\beta }\right)$$ (7.3)

is proportional in β to the quadratic function − 2q′β + β′Qβ, where

$$\mathbf{Q}:={\xi }_{orig}{\mathbf{X}}^{\prime }\mathbf{X}+{\xi }_{switch}\left[\begin{array}{cc}{\mathbf{X}}_1^{\prime }{\mathbf{X}}_1& {\mathbf{X}}_1^{\prime }\mathbf{W}{\mathbf{X}}_2\\ {\mathbf{X}}_2^{\prime }\mathbf{W}{\mathbf{X}}_1& {\mathbf{X}}_2^{\prime }{\mathbf{X}}_2\end{array}\right],\mathbf{q}:={\left({\xi }_{orig}{\mathbf{y}}^{\prime }\mathbf{X}+{\xi }_{switch}{\left[\begin{array}{c}{\mathbf{X}}_1^{\prime }\mathbf{W}\mathbf{y}\\ {\mathbf{X}}_2^{\prime }\mathbf{y}\end{array}\right]}^{\prime }\right)}^{\prime },$$

and $\mathbf{W}:=\frac{1}{n-1}({\mathbf{1}}_n{\mathbf{1}}_n^{\prime }-{\mathbf{I}}_n)$. Thus, minimizing ξ_origê_orig(f_β) + ξ_switchê_switch(f_β) is equivalent to an unconstrained (possibly non-convex) quadratic program.

Because our empirical MCR computation procedure from Sections 6.1 and 6.2 consists of minimizing a sequence of objective functions in the form of Eq 7.3, Remark 16 shows us that this procedure is tractable for the class of unconstrained linear models.

7.3. Regularized Linear Models

Next, we continue to build on the results from Section 7.2 to calculate boundaries on $\widehat{MR}$ for regularized linear models. We consider model classes formed by quadratically constrained subsets of ${\mathcal{F}}_{\text{lm}}$, defined as

$${\mathcal{F}}_{\text{lm},r_{\text{lm}}}:=\left\{f_{\beta }:f_{\beta }\left(x\right)=x^{\prime }\beta ,\beta ϵ{\mathbb{R}}^p,{\beta }^{\prime }{\mathbf{M}}_{\mathrm{l}\text{m}}\beta \le r_{\text{lm}}\right\},$$ (7.4)

where M_lm and r_lm are pre-specified. Again, this class describes linear models with a quadratic constraint on the coefficient vector.

7.3.1. Calculating MCR

As in Section 7.2, calculating bounds on $\widehat{MR}$ via Lemmas 9 & 13 requires that are able to minimizing linear combinations ξ_origê_orig(f_β) + ξ_switchê_switch (f_β) across $f_{\beta }\in {\mathcal{F}}_{\text{lm},r_{\text{lm}}}$ for arbitrary ${\xi }_{\mathrm{orig}},{\xi }_{\mathrm{switch}}\in \mathbb{R}$. Applying Remark 16, we can again equivalently minimize −2q′β + β′Qβ subject to the constraint in Eq 7.4:

$$\begin{array}{l}\text{minimize}-2{\mathbf{q}}^{\prime }\beta +{\beta }^{\prime }\mathbf{Q}\beta \\ \text{subject to}{\beta }^{\prime }{\mathbf{M}}_{\text{lm}}\beta \le r_{\text{lm}}.\end{array}$$ (7.5)

The resulting optimization problem is a (possibly non-convex) quadratic program with one quadratic constraint (QP1QC). This problem is well-studied, and is related to the trust region problem (Boyd and Vandenberghe, 2004; Pólik and Terlaky, 2007; Park and Boyd, 2017). Thus, the bounds on MCR presented in Sections 6.1 and 6.2 again become computationally tractable for the class of quadratically constrained linear models.

7.3.2. Upper Bounding the Loss

One benefit of constraining the coefficient vector (β′M_lmβ ≤ r_lm) is that it facilitates determining an upper bound B_ind on the loss function L(f_β, (y, x)) = (y − x′β)², which automatically satisfies Assumption 1 for all $f\in {\mathcal{F}}_{\text{lm},r_{\text{lm}}}$. The following lemma gives sufficient conditions to determine B_ind.

Lemma 17 (Loss upper bound for linear models) If M_lm is positive definite, Y is bounded within a known range, and there exists a known constant $r_{\mathcal{X}}$ such that $x^{\prime }{\mathbf{M}}_{lm}^{-1}x\le r_{\mathcal{X}}$ for all $x\in ({\mathcal{X}}_1\times {\mathcal{X}}_2)$, then Assumption 1 holds for the model class ${\mathcal{F}}_{lm,r_{lm}}$, the squared error loss function, and the constant

$$B_{ind}=\max \left[{\left\{\underset{y\in \mathcal{Y}}{\min }\left(y\right)-\sqrt{r\mathcal{X}{r}_{lm}}\right\}}^2,{\left\{\underset{y\in \mathcal{Y}}{\max }\left(y\right)-\sqrt{r\mathcal{X}{r}_{lm}}\right\}}^2\right].$$

In practice, the constant $r_{\mathcal{X}}$ can be approximated by the empirical distribution of X and Y. The motivation behind the restriction $x^{\prime }{\mathbf{M}}_{\mathrm{lm}}^{-1}x\le r_{\mathcal{X}}$ in Lemma 17 is to create complementary constraints on X and β. For example, if M_lm is diagonal, then the smallest elements of M_lm correspond to directions along which β is least restricted by β′M_lmβ ≤ r_lm (Eq 7.5), as well as the directions along which x is most restricted by $x^{\prime }{\mathbf{M}}_{\mathrm{lm}}^{-1}x\le r_{\mathcal{X}}$ (Lemma 17).

7.4. Regression Models in a Reproducing Kernel Hilbert Space (RKHS)

We now expand our scope of model classes by considering regression models in a reproducing kernel Hilbert space (RKHS), which allow for nonlinear and nonadditive features of the covariates. We show that, as in Section 7.3, minimizing a linear combination of ê_orig(f) and ê_switch(f) across models f in this class can be expressed as a QP1QC, which allows us to implement the binary search procedure of Sections 6.1 & 6.2.

First we introduce notation required to describe regression in a RKHS. Let D be a (R×p) matrix representing a pre-specified dictionary of R reference points, such that each row of D is contained in $\mathcal{X}={\mathbb{R}}^p$. Let k be a pre-specified positive definite kernel function, and let μ be a prespecified estimate of $\mathbb{E}Y$. Let K_D be the R × R matrix with K_D[i,j] = k(D_[i,·], D_[j,·]). We consider prediction models of the following form, where the distance to each reference point is used as a regression feature:

$${\mathcal{F}}_{\mathbf{D},r_k}=\left\{f_{\alpha }:f_{\alpha }\left(x\right)=\mu +\sum _{i=1}^{R}k\left(x,{\mathbf{D}}_{\left[i,\cdot \right]}\right){\alpha }_{\left[i\right]},{\Vert f_{\alpha }\Vert }_k\le r_k,\alpha ϵ{\mathbb{R}}^R\right\}.$$ (7.6)

Above, the norm ‖f_α‖_k is defined as

$${\Vert f_{\alpha }\Vert }_k:=\sum _{i=1}^R\sum _{j=1}^R{\alpha }_{\left[i\right]}{\alpha }_{\left[j\right]}k({\mathbf{D}}_{\left[i,\cdot \right]},{\mathbf{D}}_{\left[j,\cdot \right]})={\alpha }^{\prime }{\mathbf{K}}_{\mathbf{D}\alpha }.$$ (7.7)

In the next two sections, we show that bounds on empirical MCR can again be tractably computed for this class, and that the loss for models in this class can be feasibly upper bounded.

7.4.1. Calculating MCR

Again, calculating bounds on $\widehat{MR}$ from Lemmas 9 & 13 requires us to be able to minimize arbitrary linear combinations of ê_orig(f_α) and ê_switch(f_α).

Given a size-n sample of test observations Z = [ y X ], let K_orig be the n × R matrix with elements K_orig[i,j] = k (X_[i,·], D_[j,·]). Let Z_switch = [ y_switch X_switch ] be the (n(n − 1)) × (1 + p) matrix with rows that contain the set {(y_[i], X_1[j,·], X_2[i,·]) : i, j ∈ {1, … , n} and i ≠ j}. Finally, let K_switch be the n(n − 1) × R matrix with K_switch[i,j] = k (X_switch[i,·], D_[j,·]).

For any two constants ${\xi }_{\mathrm{orig}},{\xi }_{\mathrm{switch}}\in \mathbb{R}$, we can show that minimizing the linear combination ${\xi }_{\mathrm{orig}}{\widehat{e}}_{\mathrm{orig}}(f_{\alpha })+{\xi }_{\mathrm{switch}}{\widehat{e}}_{\mathrm{switch}}(f_{\alpha })$ over ${\mathcal{F}}_{\mathbf{D},r_k}$ is equivalent to the minimization problem

$$\text{minimize}\frac{{\xi }_{\text{orig}}}{n}{\Vert \mathbf{y}-\mu -{\mathbf{K}}_{\text{orig}}\alpha \Vert }_2^2+\frac{{\xi }_{\text{switch}}}{n\left(n-1\right)}{\Vert {\mathbf{y}}_{\text{switch}}-\mu -{\mathbf{K}}_{\text{switch}}\alpha \Vert }_2^2$$ (7.8)

$$\text{subject to}{\alpha }^{\prime }{\mathbf{K}}_{\mathbf{D}}\alpha <r_k.$$ (7.9)

Like Problem 7.5, Problem 7.8-7.9 is a QP1QC. To show Eqs 7.8–7.9, we first write ê_orig(f_α) as

$$\begin{gathered} {\widehat{e}}_{\text{orig}}\left(f_{\alpha }\right)=\frac{1}{n}{\sum _{i=1}^n\left\{{\mathbf{y}}_{\left[i\right]}-f_{\alpha }\left({\mathbf{X}}_{\left[i,\cdot \right]}\right)\right\}}^2 \\ =\frac{1}{n}{\sum _{i=1}^n\left\{{\mathbf{y}}_{\left[i\right]}-\mu -\sum _{j=1}^{R}k\left({\mathbf{X}}_{\left[i,\cdot \right]},{\mathbf{D}}_{\left[j,\cdot \right]}\right){\alpha }_{\left[j\right]}\right\}}^2 \\ =\frac{1}{n}{\sum _{i=1}^n\left\{{\mathbf{y}}_{\left[i\right]}-\mu -{{\mathbf{K}}^{\prime }}_{\text{orig}\left[i,\cdot \right]}\alpha \right\}}^2 \end{gathered}$$ (7.10)

$$=\frac{1}{n}{\Vert \mathbf{y}-\mu -{\mathbf{K}}_{\mathrm{orig}}\alpha \Vert }_2^2.$$ (7.11)

Following similar steps, we can obtain

$${\widehat{e}}_{\text{switch}}\left(f_{\alpha }\right)=\frac{1}{n\left(n-1\right)}{\Vert {\mathbf{y}}_{\text{switch}}-\mu -{\mathbf{K}}_{\text{switch}}\alpha \Vert }_2^2.$$

Thus, for any two constants ${\xi }_{\mathrm{orig}},{\xi }_{\mathrm{switch}}\in \mathbb{R}$, we can see that ξ_origê_orig(f_α)+ξ_switchê_switch(f_α) is quadratic in α. This means that we can tractably compute bounds on empirical MCR for this class as well.

7.4.2. Upper Bounding the Loss

Using similar steps as in Section 7.3.2, the following lemma gives sufficient conditions to determine B_ind for the case of regression in a RKHS.

Lemma 18 (Loss upper bound for regression in a RKHS) Assume that Y is bounded within a known range, and there exists a known constant r_D such that $\upsilon (x{)}^{\prime }{K}_D^{-1}\upsilon (x)\le r\mathbf{D}$ for all $x\in ({\mathcal{X}}_1\times {\mathcal{X}}_2)$, where $\upsilon :{\mathbb{R}}^p\to {\mathbb{R}}^R)$ is the function satisfying υ(x)_[i] = k(x, D_[i,·]). Under these conditions, Assumption 1 holds for the model class ${\mathcal{F}}_{\mathbf{D},r_k}$, the squared error loss function, and the constant

$$B_{ind}=\max \left[{\left\{\underset{y\in \mathcal{Y}}{\min }\left(y\right)-\left(\mu +\sqrt{r_{\mathbf{D}}{r}_k}\right)\right\}}^2,{\left\{\underset{y\in \mathcal{Y}}{\max }\left(y\right)+\left(\mu +\sqrt{r_{\mathbf{D}}{r}_k}\right)\right\}}^2\right].$$

Thus, for regression models in a RKHS, we can satisfy Assumption 1 for all models in the class.

8. Connections Between MR and Causality

Our MR approach can be fundamentally described as studying how a model’s behavior changes under an intervention on the underlying data. We aim to study the causal effect of this intervention on the model’s performance. This goal mirror’s the conventional causal inference goal of studying how an intervention on variables will change outcomes generated by a process in nature.

This section explores this connection to causal inference further. Section 8.1 shows that when the prediction model in question is the conditional expectation function from nature itself, MR reduces to commonly studied quantities in the causal literature. Section 8.2 proposes an alternative to MR that focuses on interventions, or data perturbations, that are likely to occur in the underlying data generating process.

8.1. Model Reliance and Causal Effects

In this section, we show a connection between population-level model reliance and the conditional average causal effect. For consistency with the causal inference literature, we temporarily rename the random variables (Y, X₁, X₂) as (Y, T, C), with realizations (y, t, c). Here, T := X₁ represents a binary treatment indicator, C := X₂ represents a set of baseline covariates (“C” is for “covariates”), and Y represents an outcome of interest. Under this notation, $e_{\mathrm{orig}}\left(f\right)$ represents the expected loss of a prediction function f, and $e_{\mathrm{switch}}\left(f\right)$ denotes the expected loss in a pair of observations in which the treatment has been switched. Let $f_0\left(t,c\right):=\mathbb{E}\left(Y|C=c,T=t\right)$ be the (unknown) conditional expectation function for Y, where we place no restrictions on the functional form of f₀.

Let Y₁ and Y₀ be potential outcomes under treatment and control respectively, such that $Y=Y_0\left(1-T\right)+Y_{1}T$. The treatment effect for an individual is defined as Y₁ − Y₀, and the average treatment effect is defined as $\mathbb{E}\left(Y_1-Y_0\right)$. Let $\mathrm{CATE}\left(c\right):=\mathbb{E}\left(Y_1-Y_0|C=c\right)$ be the (unknown) conditional average treatment effect of T for all patients with C = c. Causal inference methods typically assume $\left(Y_1-Y_0\right)\perp T|C$ (conditional ignorability), and $0<\mathbb{P}\left(T=1|C=c\right)<1$ for all values of c (positivity), in order for f₀ and CATE to be well defined and identifiable.

The next proposition quantifies the relation between the conditional average treatment effect function (CATE) and the model reliance of f₀ on X₁.

Proposition 19 (Causal interpretations of MR) For any prediction model f, let e_orig(f) and e_switch(f) be defined based on the squared error loss $L\left(f,\left(y,t,c\right)\right):={\left(y-f\left(t,c\right)\right)}^2$.

If $\left(Y_1-Y_0\right)\perp T|C$ (conditional ignorability) and $0<\mathbb{P}\left(T=1|C=c\right)<1$ for all values of c (positivity), then MR(f₀) is equal to

$$1+\frac{Var\left(T\right)}{{\mathbb{E}}_{T,C}Var\left(Y|T,C\right)}\sum _{t\in \left\{0,1\right\}}\left\{\mathbb{E}{\left(Y_1-Y_0|T=t\right)}^2+Var\left(CATE\left(C\right)|T=t\right)\right\},$$ (8.1)

where Var(T) is the marginal variance of the treatment assignment.

We see above that model reliance decomposes into several terms that are each individually important in causal inference: the treatment prevalence (via Var(T)); the variability in Y that is not explained by C or T; the magnitude of the average treatment effect, conditional on T; and the variance of the conditional average treatment effect across subgroups. For example, if all patients are treated, then scrambling the treatment in a random pair of observations has no effect on the loss. In this case we see that Var(T) = 0 and MR(f₀) = 1, indicating no reliance. When Var(T) > 0, a higher average treatment effect magnitude $(\mathbb{E}{(Y_1-Y_0|T=t)}^2)$ corresponds to f₀ requiring T more heavily to predict Y, all else equal. Similarly, if there is a high degree of treatment effect heterogeneity across subgroups (that is, when Var(CATE(C)|T = t) is large), the model f₀ will again use T more heavily when predicting Y. For example, a treatment may be important for predicting Y even if the average treatment effect is zero, so long as the treatment helps some subgroups more than others.

8.2. Conditional Importance: Adjusting for Dependence Between X₁ and X₂

One common scenario where multiple models achieve low loss is when the sets of predictors X₁ and X₂ are highly correlated, or contain redundant information. Models may predict well either through reliance on X₁, or through reliance on X₂, and so MCR will correctly identify a wide range of potential reliances on X₁. However, we may specifically be interested how much models rely on the information in X₁ that cannot alternatively be gleaned from X₂.

For example, age and accumulated wealth may be correlated, and both may be predictive of future promotion. We may wish to know the how much a model for predicting promotion relies on information that is uniquely available from wealth measurements.

To formalize this notion, we define an alternative to e_switch where noise is added to X₁ in a way that accounts for the dependence between X₁ and X₂. Given a fixed prediction model f, we ask: how well would the model f perform if the values of X₁ were scrambled across observations with the same value for X₂. Specifically, let $Z^{(a)}=(Y^{(a)},X_1^{(a)},X_2^{(a)})$ and $Z^{\left(b\right)}=\left(Y^{\left(b\right)},X_1^{\left(b\right)},X_2^{\left(b\right)}\right)$ denote a pair of independent random vectors following the same distribution as $Z=\left(Y,X_1,X_2\right)$, as in Section 3, and let

$$e_{\text{cond}}\left(f\right):={\mathbb{E}}_{X_2}{\mathbb{E}}_{(Y^{\left(b\right)},X_1^{\left(a\right)},X_2^{\left(b\right)})}\left[L\{f,(Y^{\left(b\right)},X_1^{\left(a\right)},X_2^{\left(b\right)})\}|X_2^{\left(a\right)}=X_2^{\left(b\right)}=X_2\right].$$ (8.2)

In words, e_cond(f) is the expected loss of a given model f across pairs of observations (Z^(a), Z^(b)) in which the values of $X_1^{(a)}$ and $X_1^{(b)}$ have been switched, given that these pairs match on X₂. This quantity can also be interpreted as the expected loss of f if noise were added to X₁ in such a way that X₁ was no longer informative of Y, given X₂, but that the joint distribution of the covariates (X₁, X₂) was maintained.

We then define conditional model reliance, or “core” model reliance (CMR) for a fixed function f as

$$CMR\left(f\right)=\frac{e_{\text{cond}}\left(f\right)}{e_{\text{orig}}\left(f\right)}.$$

That is, CMR is the factor by which the model’s performance degrades when the information unique to X₁ is removed. If X₁ ⊥ X₂, then X₁ contains no redundant information, and CMR and MR are equivalent. Otherwise, all else equal, CMR will decrease as X₂ becomes more predictive of X₁. Analogous to MCR, we define conditional MCR (CMCR) in the same way as in Eq 2.2, but with MR replaced with CMR. In comparison with MCR, CMCR will generally result in a range that is closer to 1 (null reliance).

An advantage of CMR is that it restricts the “noise-corrupted” inputs to be within the domain $\mathcal{X}$, rather than the expanded domain ${\mathcal{X}}_1\times {\mathcal{X}}_2$ considered by MR. This means that CMR will not be influenced by impossible combinations of x₁ and x₂, while MR may be influenced by them. Hooker (2007) discuss a similar issue, arguing that evaluations of a prediction model’s behavior in different circumstances should be weighted by, for example, how likely those circumstances are to occur.

A challenge facing the CMR approach is that matched pairs such as those in Eq 8.2 may occur rarely, making it difficult to estimate CMR nonparametrically. We explore this estimation issue next.

8.2.1. Estimation of CMR by Weighting, Matching, or Imputation

If the covariate space is discrete and low dimensional, nonparametric methods based on weighting or matching can be effective means of estimating CMR. Specifically, we can weight each pair of sample points i, j according to how likely the covariate combination $\left(X_{1\left[i,\cdot \right]},X_{2\left[j,\cdot \right]}\right)$ is to occur, as in

$${\widehat{e}}_{\text{weight}}(f):=\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j\ne i}\omega ({\mathbf{X}}_{1\left[i,\cdot \right]},{\mathbf{X}}_{2\left[j,\cdot \right]})\times L\{f,({\mathbf{Y}}_{\left[j\right]},{\mathbf{X}}_{1\left[i,\cdot \right]},{\mathbf{X}}_{2\left[j,\cdot \right]})\},$$

where $w\left(x_1,x_2\right):=\frac{\mathbb{P}\left(X_1=x_1|X_2=x_2\right)}{\mathbb{P}\left(X_1=x_1\right)}$ is an importance weight (see also Hooker, 2007). Here, pairs of observations corresponding to unlikely or impossible combinations of covariates are down-weighted or discarded, respectively. If the probabilities $\mathbb{P}\left(X_1=x_1|X_2=x_2\right)$ and $\mathbb{P}\left(X_1=x_1\right)$ are known, then ${\widehat{e}}_{weight}\left(f\right)$ is unbiased for e_cond(f) (see Appendix A.7).

Alternatively, if X₂ is discrete and low dimensional, we can restrict estimates of e_cond(f) to only consider pairs of sample observations in which X₂ is constant, or “matched,” as in

$${\widehat{e}}_{\text{match}}\left(f\right):=\frac{1}{n\left(n-1\right)}\sum _{i=1}^n\sum _{j\ne i}\frac{1\left({\mathbf{X}}_{2\left[j,\cdot \right]}={\mathbf{X}}_{2\left[i,\cdot \right]}\right)}{\mathbb{P}\left(X_2={\mathbf{X}}_{2\left[i,\cdot \right]}\right)}\times L\left\{f,\left({\mathbf{Y}}_{\left[j\right]},{\mathbf{X}}_{1\left[i,\cdot \right]},{\mathbf{X}}_{2\left[j,\cdot \right]}\right)\right\}.$$ (8.3)

This approach allows estimation of CMR without knowledge of the conditional distribution $\mathbb{P}\left(X_1=x_1|X_2=x_2\right)$. If the inverse probability weight $\mathbb{P}{\left(X_2={\mathbf{X}}_{2\left[i,\cdot \right]}\right)}^{-1}$ is known, then ê_match(f) is unbiased for e_cond(f) (see Appendix A.7). The weight $\mathbb{P}{\left(X_2={\mathbf{X}}_{2\left[i,\cdot \right]}\right)}^{-1}$ accounts for the fact that, for any given value x₂, the proportion of observations of X₂ taking the value x₂ will generally not be the same as the proportion of matched pairs $\left(X_2^{\left(a\right)},X_2^{\left(b\right)}\right)$ taking value the x₂, and so simply summing over all matched pairs would lead to bias. In practice, the proportion $\mathbb{P}\left(X_2={\mathbf{X}}_{2\left[i,\cdot \right]}\right)$ can be approximated as $\frac{1}{n-1}{\sum }_{j^{\prime }\ne i}1({\mathbf{X}}_{2[i,\cdot ]}={\mathbf{X}}_{2[j^{\prime },\cdot ]})$, with minor adjustments to Eq 8.3 to avoid dividing by zero. The resulting estimate is analogous to exact matching procedures commonly used in causal inference, which are known to work best when the covariates are discrete and low dimensional, in order for exact matches to be common (Stuart, 2010).

However, when the covariate space is continuous or high dimensional, we typically cannot estimate CMR nonparametrically. For such cases, we propose to estimate CMR under an assumption of homogeneous residuals. Specifically, we define μ₁ to be the conditional expectation function ${\mu }_1\left(x_2\right)=\mathbb{E}\left(X_1|X_2=x_2\right)$, and assume that the random residual X − μ₁(X₂) is independent of X₂. Under this assumption, it can be shown that

$$e_{\text{cond}}\left(f\right)=\mathbb{E}L\left[f,\left(Y^{\left(b\right)},\left\{X_1^{\left(a\right)}-{\mu }_1\left(X_2^{\left(a\right)}\right)\right\}+{\mu }_1\left(X_2^{\left(b\right)},X_2^{\left(b\right)}\right)\right)\right].$$

That is, e_cond(f) is equal to the expected loss of f across random pairs of observations (Z^(a), Z^(b)) in which the value of the residual terms (in curly braces) have been switched. Because of the independence assumption, no matching or weighting is required. If μ₁ is known, then we can again produce an unbiased estimate using the U-statistic

$${\widehat{e}}_{\text{impute}}\left(f\right):=\frac{1}{n\left(n-1\right)}\sum _{i=1}^n\sum _{j\ne i}L\left[f,({\mathbf{y}}_{\left[j\right]},\left\{{\mathbf{X}}_{1\left[i,\cdot \right]}-{\mu }_1\left({\mathbf{X}}_{2\left[i,\cdot \right]}\right)\right\}+{\mu }_1\left({\mathbf{X}}_{2\left[j,\cdot \right]},{\mathbf{X}}_{2\left[j,\cdot \right]}\right)\right].$$

This estimator aggregates over all pairs in our sample, switching the values of the residual terms (in curly braces) within each pair. In practice, when μ₁ is not known, an estimate of μ₁ can be achieved via regression or related machine learning techniques, and plugged in to the above equation. In this way, the assumption that $X-{\mu }_1\left(X_2\right)\perp X_2$ allows us to estimate CMR without explicitly modeling the joint distribution of X₁ and X₂.

In the existing literature, Strobl et al. (2008) introduce a similar procedure for estimating conditional variable importance. However, a formal comparison to Strobl et al. is complicated by the fact that the authors do not define a specific estimand, and that their approach is limited to tree-based regression models. Other existing approaches conditional importance approaches include methods for redefining X₁ and X₂ to induce approximate independence, before computing an importance measure analogous to MR. This can be done by reducing the total number of covariates used, and hence reducing how well any one variable can be predicted by the others (as in Gregorutti et al., 2017). Alternatively, variables in X₂ that are predictive of X₁ can be regrouped directly into X₁ (as in Toloşi and Lengauer, 2011; see also the discussion from Kirk, Lewin and Stumpf, in Meinshausen and Bühlmann 2010).

In summary, CMR allows us to see how much a model relies on the information uniquely available in X₁. While CMR is more difficult to estimate than MR, several tractable approaches exist when X₂ is discrete, or when a homogenous residual assumption can be applied. One may also consider extending CMR by conditioning only on a subset of X₂. For example, we may consider conditioning only on elements of X₂ that are believed to causally effect X₁, by changing the outer expectation in Eq 8.2. For simplicity, we focus on the base case of estimating MR in this paper. Similar results could potentially be carried over for CMR as well.

9. Simulations

In this section, we first present a toy example to illustrate the concepts of MR, MCR, and AR. We then present a Monte Carlo simulation studying the effectiveness of bootstrap CIs for MCR.

9.1. Illustrative Toy Example with Simulated Data

To illustrate the concepts of MR, MCR, and AR (see Section 3.2), we consider a toy example where $X=\left(X_1,X_2\right)\in {\mathbb{R}}^2$ , and Y ∈ {−1, 1} is a binary group label. Our primary goal in this section is to build intuition for the differences between these three importance measures, and so we demonstrate them here only in a single sample. We focus on the empirical versions of our importance metrics $(\widehat{MR},{\widehat{MCR}}_{-}\mathrm{and}{\widehat{MCR}}_{+})$, and compare them against AR, which is typically interpreted as an in-sample measure (Breiman, 2001), or as an intermediate step to estimate an alternate importance measure in terms of variable rankings (Gevrey et al., 2003; Olden et al., 2004).

We simulate $X|Y=-1$ from an independent, bivariate normal distribution with means $\mathbb{E}\left(X_1|Y=-1\right)=\mathbb{E}\left(X_2|Y=-1\right)=0$ and variances $Var\left(X_1|Y=-1\right)=Var\left(X_2|Y=-1\right)=\frac{1}{9}$. We simulate X|Y = 1 by drawing from the same bivariate normal distribution, and then adding the value of a random vector $\left(C_1,C_2\right):=\left(\cos \left(U\right),\sin \left(U\right)\right)$, where U is a random variable uniformly distributed on the interval $\left[-\pi ,\pi \right]$. Thus, (C₁, C₂) is uniformly distributed across the unit circle.

Given a prediction model $f:\mathcal{X}\to \mathbb{R}$, we use the sign of f(X₁, X₂) as our prediction of Y. For our loss function, we use the hinge loss $L\left(f,\left(y,x_1,x_2\right)\right)={\left(1-yf\left(x_1,x_2\right)\right)}_{+}$, where ${\left(a\right)}_{+}=a$ if a ≥ 0 and (a)₊ = 0 otherwise. The hinge loss function is commonly used as a convex approximation to the zero-one loss $L\left(f,\left(y,x_1,x_2\right)\right)=1\left[y\ne \mathrm{sign}\left\{f\left(x_1,x_2\right)\right\}\right]$.

We simulate two samples of size 300 from the data generating process described above, one to be used for training, and one to be used for testing. Then, for the class of models used to predict Y, we consider the set of degree-3 polynomial classifiers

$${\mathcal{F}}_{d3}=\{f_{\theta }:f_{\theta }\left(x_1,x_2\right)={\mathit{\theta }}_{\left[1\right]}+{\mathit{\theta }}_{\left[2\right]}{x}_1+{\mathit{\theta }}_{\left[3\right]}{x}_2+{\mathit{\theta }}_{\left[4\right]}{x}_1^2+{\mathit{\theta }}_{\left[5\right]}{x}_2^2+{\mathit{\theta }}_{\left[6\right]}{x}_1{x}_2+{\mathit{\theta }}_{\left[7\right]}{x}_1^3+{\mathit{\theta }}_{\left[8\right]}{x}_2^3+{\mathit{\theta }}_{\left[9\right]}{x}_1^2{x}_2+{\mathit{\theta }}_{\left[10\right]}{x}_1{x}_2^2;{\Vert {\mathit{\theta }}_{\left[-1\right]}\Vert }_2^2\le r_{d3}\},$$

where θ_[−1] denotes all elements of θ except θ_[1], and where we set r_d3 to the value that minimizes the 10-fold cross-validated loss in the training data. Let ${\mathcal{A}}_{d3}$ be the algorithm that minimizes the hinge loss over the (convex) feasible region $\{f_{\theta }:{\Vert {\mathit{\theta }}_{[-1]}\Vert }_2^2\le r_{d3}\}$. We apply ${\mathcal{A}}_{d3}$ to the training data to determine a reference model f_ref. Also using the training data, we set ϵ equal to 0.10 multiplied by the cross-validated loss of ${\mathcal{A}}_{d3}$, such that $\mathcal{R}(ϵ,f_{\mathrm{ref}},{\mathcal{F}}_{d3})$ contains all models in ${\mathcal{F}}_{d3}$ that exceed the loss of f_ref by no more than approximately 10% (see Eq 4.1). We then calculate empirical AR, MR, and MCR using the test observations.

We begin by considering the AR of ${\mathcal{A}}_{d3}$ on X₁. Calculating AR requires us to fit two separate models, first using all of the variables to fit a model on the training data, and then again using only X₂. In this case, the first model is equivalent to f_ref. We denote the second model as ${\widehat{f}}_2$. To compute AR, we evaluate f_ref and ${\widehat{f}}_2$ in the test observations. We illustrate this AR computation in Figure 6–A, marking the classification boundaries for f_ref and ${\widehat{f}}_2$ by the black dotted line and the blue dashed lines respectively, and marking the test observations by labelled points (“x” for Y = 1, and “o” for Y = −1). Comparing the loss associated with these two models gives one form of AR–an estimate of the necessity of X₁ for the algorithm ${\mathcal{A}}_{d3}$. Alternatively, to estimate the sufficiency of X₁, we can compare the reference model f_ref against the model resulting from retraining algorithm ${\mathcal{A}}_{d3}$ only using X₁. We refer to this third model as ${\widehat{f}}_1$, and mark its classification boundary by the solid blue lines in Figure 6–A.

Figure 6:

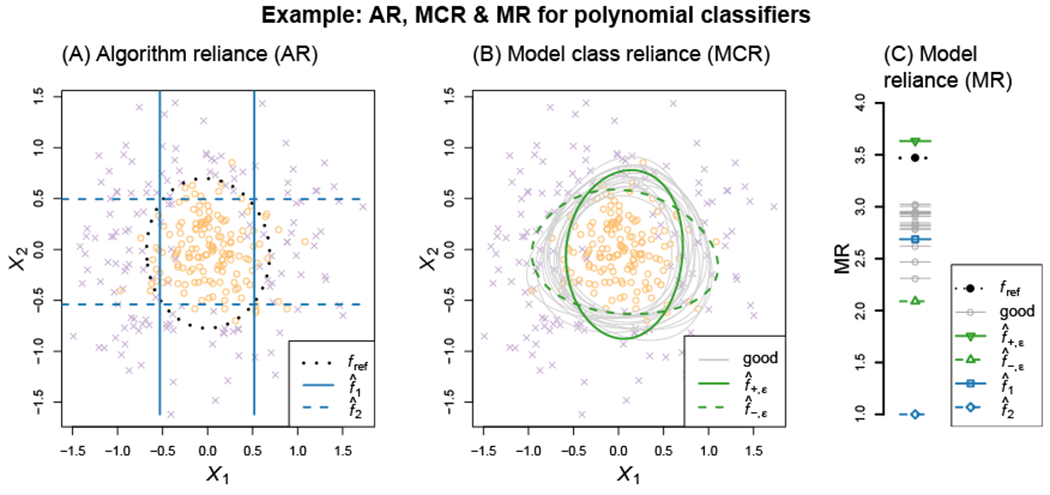
Example of AR, MCR & MR for polynomial classifiers. Panels (A) & (B) show the same 300 draws from a simulated data set, with the classification of each data point marked by “x” for Y = 1, and “o” for Y = −1. In Panel (A), for AR, we show single-feature models formed by dropping a covariate. Because these models take only a single input, we represent their classification boundaries as straight lines. In Panel (B), for MCR, we show the classification boundaries for several (two-feature) models with low in-sample loss. Of these models, the model with minimal dependence on X₁ is shown by the dashed green oval, and the model with maximal dependence on X₁ is shown by the solid green oval. Panel (C) shows the empirical model reliance on X₁ for each of the models in Panels (A) & (B). We see in Panel (C) that, as expected, no well-performing model relies (empirically) on X₁ more than ${\widehat{f}}_{+,ϵ}$ does, or relies (empirically) on X₁ less than ${\widehat{f}}_{-,ϵ}$ does. That is, no well-performing model has an empirical MR value greater than ${\widehat{MCR}}_{+}(ϵ)$, or less than ${\widehat{MCR}}_{-}(ϵ)$.

Each of the classifiers in Figure 6–A can also be evaluated for its reliance on X₁, as shown in Figure 6–C. Here, we use ê_divide in our calculation of $\widehat{MR}$ (see Eq 3.5). Unsurprisingly, the classifier fit without using X₁ (blue dashed line) has a model reliance of $\widehat{MR}\left({\widehat{f}}_2\right)=1$. The reference model f_ref (dotted black line) has a model reliance of $\widehat{MR}\left(f_{ref}\right)=3.47$. Each MR value has an interpretation contained to a single model. That is, $\widehat{MR}$ compares a single model’s behavior under different data distributions, rather than the AR approach of comparing different models’ behavior on marginal distributions from a single joint distribution.

We illustrate MCR in Figure 6–B. In contrast to AR, MCR is only ever a function of well-performing prediction models. Here, we consider the empirical ϵ-Rashomon set $\widehat{\mathcal{R}}\left(ϵ,f_{ref},{\mathcal{F}}_{d3}\right)$, the subset of models in ${\mathcal{F}}_{d3}$ with test loss no more than ϵ above that of f_ref. We show the classification boundary associated with 15 well-performing models contained in $\widehat{R}\left(ϵ,f_{ref},F_{d3}\right)$ by the gray solid lines. We also show two of the models in $\widehat{R}\left(ϵ,f_{ref},F_{d3}\right)$ that approximately maximize and minimize empirical reliance on X₁ among models in $\widehat{R}\left(ϵ,f_{ref},F_{d3}\right)$. We denote these models as ${\widehat{f}}_{+,ϵ}$ and ${\widehat{f}}_{-,ϵ}$, and mark them by the solid green and dashed green lines respectively. For every model shown in Figure 6–B, we also mark its model reliance in Figure 6–C. We can then see from Figure 6–C that $\widehat{MR}$ for each model in $\widehat{\mathcal{R}}\left(ϵ,f_{ref},{\mathcal{F}}_{d3}\right)$ is contained between $\widehat{MR}\left({\widehat{f}}_{-,ϵ}\right)$ and $\widehat{MR}\left({\widehat{f}}_{+,ϵ}\right)$, up to a small approximation error.

In summary, unlike AR, MCR is only a function of models that fit the data well.

9.2. Simulations of Bootstrap Confidence Intervals

In this section we study the performance of MCR under model class misspecification. Our goal will be to estimate how much the conditional expectation function $f_0\left(x\right)=\mathbb{E}\left(Y|X=x\right)$ relies on subsets of covariates. Given a reference model f_ref and model class $\mathcal{F}$, our ability to describe MR(f₀) will hinge on two conditions:

Condition 20 (Nearly correct model class) The class $\mathcal{F}$ contains a well-performing model $\tilde{f}\in \mathcal{R}\left(ϵ,f_{ref},\mathcal{F}\right)$ satisfying $MR\left(\tilde{f}\right)=MR\left(f_0\right)$ (see Eq 4.1).

Condition 21 (Bootstrap coverage) Bootstrap CIs for empirical MCR give appropriate coverage of population-level MCR.

Condition 20 ensures that the interval [MCR₋(ϵ),MCR₊(ϵ)] contains MR(f₀), and Condition 21 ensures that this interval can be estimated in finite samples. Condition 20 can also be interpreted as saying that the model reliance value of MR(f_c) is “well supported” by the class $\mathcal{F}$, even if $\mathcal{F}$ does not contain f₀. Our primary goal is to assess whether CIs derived from MCR can give appropriate coverage of MR(f₀), which depends on both conditions. As a secondary goal, we also would like to be able to assess Conditions 20 & 21 individually.

Verifying the above conditions requires that we are able to calculate population-level MCR. To this end, we draw samples with replacement from a finite population of 20,000 observations, in which MCR can also be calculated directly. To derive a CI based on MCR, we divide each simulated sample ${\mathcal{Z}}_s$ into a training subset and analysis subset. We use the training subset to fit a reference model f_ref,s, which is required for our definition of population-level MCR. We calculate a bootstrap CI by drawing 500 bootstrap samples from the analysis subset, and computing ${\widehat{MCR}}_{-}\left(ϵ\right)$ and ${\widehat{MCR}}_{+}\left(ϵ\right)$ in each bootstrap sample by optimizing over $\tilde{\mathcal{R}}\left(ϵ,f_{ref,s},\mathcal{F}\right)$. We then take the 2.5% percentile of ${\widehat{MCR}}_{-}\left(ϵ\right)$ values across bootstrap samples, and the 97.5% percentile of ${\widehat{MCR}}_{+}\left(ϵ\right)$ values across bootstrap samples, as the lower and upper endpoints of our CI, respectively. We repeat this procedure for both X₁ and X₂.

We generate data according to a model with increasing amounts of nonlinearity. For $\gamma \in \left\{0,0.1,0.2,0.3,0.4,0.5\right\}$, we simulate continuous outcomes as $Y=f_0\left(X\right)+E$, where f₀ is the function $f_0(\mathbf{x})={\sum }_{j=1}^{p}j{\mathbf{x}}_{[j]}-\gamma {\mathbf{x}}_{[j]}^2$ the covariate dimension p is equal to 2, with X₁ and X₂ defined as the first and second elements of X; the covariates X are drawn from a multivariate normal distribution with $\mathbb{E}\left(X_1\right)=\mathbb{E}\left(X_2\right)=0$, $\mathrm{Var}\left(X_1\right)=\mathrm{Var}\left(X_2\right)=0$, and $\mathrm{Cov}\left(X_1,X_2\right)=1/4$; and E is a normally distributed noise variable with mean zero and variance equal to ${\sigma }_E^2:=\mathrm{Var}\left(f_0\left(X\right)\right)$. We consider sample sizes of n = 400 and 800, of which n_tr = 200 or 300 observations are assigned to the training subset respectively.

To implement our approach, we use the model class ${\mathcal{F}}_{\mathrm{lm}}=\{f_{\beta }:f_{\beta }(\mathbf{x})={\beta }_{[1]}+{\sum }_{j=1}^2{\mathbf{x}}_{[j]}{\beta }_{[j+1]},\beta \in {\mathcal{R}}^3\}$. We set the performance threshold ϵ equal to $0.1\times {\sigma }_E^2$. We refer to this MCR implementation with ${\mathcal{F}}_{\mathrm{lm}}$ as “MCR-Linear.”

As a comparator method, we consider a simpler bootstrap approach, which we refer to as “Standard-Linear.” Here, we take 500 bootstrap samples from the simulated data ${\mathcal{Z}}_s$. In each bootstrap sample, indexed by b, we set aside n_tr training points to train a model $f_b\in {\mathcal{F}}_{\mathrm{lm}}$, and calculate $\widehat{MR}(f_b)$ from the remaining data points. We then create a 95% bootstrap percentile CI for MR(f₀) by taking the 2.5% and 97.5% percentiles of $\widehat{MR}(f_b)$ across b = 1, … , 500.

9.2.1. Results

Overall, we find that MCR provides more robust and conservative intervals for the reliance of f₀ on X₁ and X₂, relative to standard bootstrap approaches. We also find that higher sample size generally exacerbates coverage errors due to misspecification, as methods become more certain of biased results.

MCR-Linear gave proper coverage for up to moderate levels of misspecification (γ = 0.3), where Standard-Linear began to break down (Figure 7). For larger levels of misspecification (γ ≥ 0.4), both MCR-Linear and Standard-Linear failed to give appropriate coverage.

Figure 7:

MR Coverage - The y-axis shows coverage rate for the reliance of f₀ on either X₁ (left column) or X₂ (right column), where X₂ is simulated to be more influential that X₁. The x-axis shows increasing levels of misspecification (γ). All methods aim to have at least 95% coverage for each scenario (dashed horizontal line).

The increased robustness of MCR comes at the cost of wider CIs. Intervals for MCR-Linear were typically larger than intervals for Standard-Linear by a factor of approximately 2-4. This is partly due to the fact that CIs for MCR are meant to cover the range of values [MCR₋(ϵ), MCR₊(ϵ)] (defined using f_ref,s), rather than to cover a single point.

When investigating Conditions 20 & 21 individually, we find that the coverage errors for MCR-Linear were largely attributable to violations of Condition 20. Condition 21 appears to hold conservatively for all scenarios studied–within each scenario, at least 95.9% of bootstrap CIs contained population-level MCR.

These simulation results highlight an aspect of MCR that is both a strength and a weakness: MCR is generic. MCR does not assume a particular means by which misspecification may occur, and is less powerful than sensitivity analyses which make that assumption correctly. Nonetheless, MCR still appears to add robustness. For sufficiently strong signals, an informative interval may still be returned. In our applied data analysis, below, we see that this is indeed the case.

10. Data Analysis: Reliance of Criminal Recidivism Prediction Models on Race and Sex

Evidence suggests that bias exists among judges and prosecutors in the criminal justice system (Spohn, 2000; Blair et al., 2004; Paternoster and Brame, 2008). In an aim to counter this bias, machine learning models trained to predict recidivism are increasingly being used to inform judges’ decisions on pretrial release, sentencing, and parole (Monahan and Skeem, 2016; Picard-Fritsche et al., 2017). Ideally, prediction models can avoid human bias and provide judges with empirically tested tools. But prediction models can also mirror the biases of the society that generates their training data, and perpetuate the same bias at scale. In the case of recidivism, if arrest rates across demographic groups are not representative of underlying crime rate (Beckett et al., 2006; Ramchand et al., 2006; U.S. Department of Justice - Civil Rights Devision, 2016), then bias can be created in both (1) the outcome variable, future crime, which is measured imperfectly via arrests or convictions, and (2) the covariates, which include the number of prior convictions on a defendant’s record (Corbett-Davies et al., 2016; Lum and Isaac, 2016). Further, when a prediction model’s behavior and mechanisms are an opaque black box, the model can evade scrutiny, and fail to offer recourse or explanations to individuals rated as “high risk.”

We focus here on the issue of transparency, which takes an important role in the recent debate about the proprietary recidivism prediction tool COMPAS (Larson et al., 2016; Corbett-Davies et al., 2016). While COMPAS is known to not rely explicitly on race, there is concern that it may rely implicitly on race via proxies-variables statistically dependent with race (see further discussion in Section 11).

Our goal is to identify bounds for how much COMPAS relies on different covariate subsets, either implicitly or explicitly, under certain assumptions (defined below). We analyze a public data set of defendants from Broward County, Florida, in which COMPAS scores have been recorded (Larson et al., 2016). Within this data set, we only included defendants measured as African-American or Caucasian (3,373 in total) due to sparseness in the remaining categories. The outcome of interest (Y) is the COMPAS violent recidivism score. Of the available covariates, we consider three variables which we refer to as “admissible”: an individual’s age, their number of priors, and an indicator of whether the current charge is a felony. We also consider two variables which we refer to as “inadmissible”: an individual’s race and sex. Our labels of “admissible” and “inadmissible” are not intended to be legally precise-indeed, the boundary between these types of labels is not always clear (see Section 10.2). We compute empirical MCR and AR for each variable group, as well as bootstrap CIs for MCR (see Section 9.2).

To compute empirical MCR and AR, we consider a flexible class of linear models in a RKHS to predict the COMPAS score (described in more detail below). Given this class, the MCR range (See Eq 2.2) captures the highest and lowest degree to which any model in the class may rely on each covariate subset. We assume that our class contains at least one model that relies on “inadmissible variables” to the same extent that COMPAS relies either on “inadmissible variables” or on proxies that are unmeasured in our sample (analogous to Condition 20). We make the same assumption for “admissible variables.” These assumptions can be interpreted as saying that the reliance values of COMPAS are relatively “well supported” by our chosen model class, and allows us to identify bounds on the MR values for COMPAS. We also consider the more conventional, but less robust approach of AR (Section 3.2), that is, how much would the accuracy suffer for a model-fitting algorithm trained on COMPAS score if a variable subset was removed?

These computations require that we predefine our loss function, model class, and performance threshold. We define MR, MCR, and AR in terms of the squared error loss $L\left(f,\left(y,x_1,x_2\right)\right)={\left\{y-f\left(x_1,x_2\right)\right\}}^2$. We define our model class ${\mathcal{F}}_{\mathbf{D},r_k}$ in the form of Eq 7.6, where we determine D, μ, k, and r_k based on a subset $\mathcal{S}$ of 500 training observations. We set D equal to the matrix of covariates from $\mathcal{S}$; we set μ equal to the mean of Y in $\mathcal{S}$; we set k equal to the radial basis function $k_{\sigma s}(\mathbf{x},\tilde{\mathbf{x}})=\exp \left(-\frac{{\Vert \mathbf{x}-\tilde{\mathbf{x}}\Vert }^2}{2{\sigma }_s}\right)$, where we choose σ_s to minimize the cross-validated loss of a Nadaraya-Watson kernel regression (Hastie et al., 2009) fit to $\mathcal{S}$; and we select the parameters r_k by cross-validation on $\mathcal{S}$. We set ϵ equal to 0.1 times the cross-validated loss on $\mathcal{S}$. Also using $\mathcal{S}$, we train a reference model $f_{\mathrm{ref}}\in {\mathcal{F}}_{D,r_k}$ Using the held-out 2,873 observations, we then estimate MR(f_ref) and MCR for ${\mathcal{F}}_{D,r_k}$. To calculate AR, we train models from ${\mathcal{F}}_{D,r_k}$ using $\mathcal{S}$, and evaluate their performance in the held-out observations.

10.1. Results

Our results imply that race and sex play somewhere between a null role and a modest role in determining COMPAS score, but that they are less important than “admissible” factors (Figure 8). As a benchmark for comparison, the empirical MR of f_ref is equal to 1.09 for “inadmissible variables,” and 2.78 for “admissible variables.” The AR is equal to 0.94 and 1.87 for “inadmissible” and “admissible” variables respectively, roughly in agreement with MR. The MCR range for “inadmissible variables” is equal to [1.00, 1.56], indicating that for any model in ${\mathcal{F}}_{D,r_k}$ with empirical loss no more than ϵ above that of f_ref, the model’s loss can increase by no more than 56% if race and sex are permuted. Such a statement cannot be made solely based on AR or MR methods, as these methods do not upper bound the reliance values of well-performing models. The bootstrap 95% CI for MCR on “inadmissible variables” is [1.00, 1.73]. Thus, under our assumptions, if COMPAS relied on sex, race, or their unmeasured proxies by a factor greater than 1.73, then intervals as low as what we observe would occur with probability < 0.05.

For “admissible variables” the MCR range is equal to [1.77,3.61], with a 95% bootstrap CI of [1.62, 3.96]. Under our assumptions, this implies if COMPAS relied on age, number of priors, felony indication, or their unmeasured proxies by a factor lower than 1.77, then intervals as high as what we observe would occur with probability < 0.05. This result is consistent with Rudin et al. (2019), who find age to be highly predictive of COMPAS score.

It is worth noting that the upper limit of 3.61 maximizes empirical MR on “admissible variables” not only among well-performing models, but globally across all models in the class (see Figure 8, and Eq 6.5). In other words, it is not possible to find models in ${\mathcal{F}}_{D,r_k}$ that perform arbitrarily poorly on perturbed data, but still perform well on unperturbed data, and so the ratio of ê_switch(f) to ê_orig(f) has a finite upper bound. Because the regularization constraints of ${\mathcal{F}}_{D,r_k}$ preclude MR values higher than 3.61, the MR of COMPAS on “admissible variables” may be underestimated by empirical MCR. Note also that both MCR intervals are left-truncated at 1, as it is often sufficiently precise to conclude that there exists a well-performing model with no reliance on the variables of interest (that is, MR equal to 1; see Appendix A.2).

10.2. Discussion & Limitations

Asking whether a proprietary model relies on sex and race, after adjusting for other covariates, is related to the fairness metric known as conditional statistical parity (CSP). A decision rule satisfies CSP if its decisions are independent of a sensitive variable, conditional on a set of “legitimate” covariates C (Corbett-Davies et al., 2017; see also Kamiran et al., 2013). Roughly speaking, CSP reflects the idea that groups of people with similar covariates C are treated similarly (Dwork et al., 2012), regardless of the sensitive variable (for example, race or sex). However, the criteria becomes superficial if too many variables are included in C, and care should be taken to avoid including proxies for the sensitive variables. Several other fairness metrics have also been proposed, which often form competing objectives (Kleinberg et al., 2017; Chouldechova, 2017; Nabi and Shpitser, 2018; Corbett-Davies et al., 2017). Here, if COMPAS was not influenced by race, sex, or variables related to race or sex (conditional on a set of “legitimate” variables), it would satisfy CSP.

Unfortunately, it is often difficult to distinguish between “legitimate” (or “admissible”) variables and “illegitimate” variables. Some variables function both as part of a reasonable predictor for risk, and, separately, as a proxy for race. Because of disproportional arrest rates, particularly for misdemeanors and drug-related offenses (U.S. Department of Justice - Civil Rights Devision, 2016; Lum and Isaac, 2016), prior misdemeanor convictions may act as such a proxy (Corbett-Davies et al., 2016; Lum and Isaac, 2016).

Proxy variables for race (defined as being statistically dependent with race) that are unmeasured in our sample are also not the only reason that race could be predictive of COMPAS score. Other inputs to the COMPAS algorithm might be associated with race only conditionally on variables we categorize as “admissible.” However, our result from Section 10.1 that race has limited predictive utility for COMPAS score suggests that such conditional relationships are also limited.

11. Conclusion

In this article, we propose MCR as the upper and lower limit on how important a set of variables can be to any well-performing model in a class. In this way, MCR provides a more comprehensive and robust measure of importance than traditional importance measures for a single model. We derive bounds on MCR, which motivate our choice of point estimates. We also derive connections between permutation importance, U-statistics, conditional variable importance, and conditional causal effects. We apply MCR in a data set of criminal recidivism, in order to help inform the characteristics of the proprietary model COMPAS.

Several exciting areas remain open for future research. One research direction closely related to our current work is the development of exact or approximate MCR computation procedures for other model classes and loss functions. We have shown that, for model classes where minimizing the empirical loss is a convex optimization problem, MCR can be conservatively computed via a series of convex optimization problems. Further, we have shown that computing ${\widehat{MCR}}_{-}$ is often no more challenging that minimizing the empirical loss over a reweighted sample. General computation procedures for MCR are still an open research area.

Another direction is to consider MCR for variable selection. If MCR₊ is small for a variable, then no well-performing predictive model can heavily depend on that variable, indicating that it can be eliminated.

Our theoretical analysis of Rashomon sets depends on $\mathcal{F}$ and f_ref being prespecified. Above, we have actualized this by splitting our sample into subsets of size n₁ and n₂, using the first subset to determine $\mathcal{F}$ and f_ref, and conditioning on $\mathcal{F}$ and f_ref when estimating MCR in the second subset. As a result, the boundedness constants in our assumptions (B_ind, B_ref, B_switch, and b_orig) depend on $\mathcal{F}$, and hence on n₁. However, because our results are non-asymptotic, we have not explored how Rashomon sets behave when n₁ and n₂ grow at different rates. An exciting future extension of this work is to study sequences of triples $\{{ϵ}_{n_1},f_{{\mathrm{ref},n}_1},{\mathcal{F}}_{n_1}\}$ that change as n₁ increases, and the corresponding Rashomon sets $\mathcal{R}({ϵ}_{n_1},f_{{\mathrm{ref},n}_1},{\mathcal{F}}_{n_1})$, as this may more thoroughly capture how model classes are determined by analysts.

While we develop Rashomon sets with the goal of studying MR, Rashomon sets can also be useful for finite sample inferences about a wide variety of other attributes of best-in-class models (for example, Section 5). Characterizations of a Rashomon set itself may also be of interest. For example, in ongoing work, we are studying the size of a Rashomon set, and its connection to generalization of models and model classes (Semenova and Rudin, 2019). We are additionally developing methods for visualizing Rashomon sets (Dong and Rudin, 2019).

Appendix A. Miscellaneous Supplemental Sections

All labels for items in the following appendices begin with a letter (for example, Section A.2), while references to items in the main text contain only numbers (for example, Proposition 19).

A.1. Code

R code for our example in Section 9.1 and analysis in Section 10 is available at https://github.com/aaronjfisher/mcr-supplement.

A.2. Model Reliance Less than 1

While it is counterintuitive, it is possible for the expected loss of a prediction model to decrease when the information in X₁ is removed. Roughly speaking, a “pathological” model f_silly may use the information in X₁ to “intentionally” misclassify Y, such that e_switch(f_silly) < e_orig(f_silly) and MR(f_silly) < 1. The model f_silly may even be included in a population ϵ-Rashomon set (see Section 4) if it is still possible to predict Y sufficiently well from the information in X₂.

However, in these cases there will often exist another model that outperforms f_silly, and that has MR equal to 1 (i.e., no reliance on X₁). To see this, consider the case where $\mathcal{F}=\{f_{\theta }:\mathit{\theta }\in {\mathbb{R}}^d\}$ is indexed by a parameter θ. Let θ_silly and θ^⋆ be parameter values such that f_θsilly is equivalent to f_silly, and f_θ^⋆ is the best-in-class model. If f_θ^⋆ satisfies MR(f_θ^⋆) > 1 and if the model reliance function MR is continuous in θ, then there exists a parameter value θ₁ between θ_silly and θ^⋆ such that MR(f_θ1) = 1. Further, if the loss function L is convex in θ, then e_orig(f_θ^⋆) ≤ e_orig(f_silly), and any population ϵ-Rashomon set containing f_silly will also contain f_θ1.

A.3. Relating ${\widehat{e}}_{\mathrm{switch}}(f)$ to All Possible Permutations of the Sample

Following the notation in Section 3, let [π₁,…, π_n!} be a set of n-length vectors, each containing a different permutation of the set {1,…,n}. We show in this section that ${\widehat{e}}_{\mathrm{switch}}(f)$ is equal to the product of

$$\sum _{l=1}^{n!}\sum _{i=1}^{n}L\{f,({\mathbf{y}}_{\left[i\right]},X_{1[{\pi }_{l\left[i\right]},\cdot ]},X_{2\left[i,\cdot \right]})\}1({\pi }_{l\left[i\right]}\ne i),$$ (A.1)

and a proportionality constant that is only a function of n.

First, consider the sum

$$\sum _{l=1}^{n!}\sum _{i=1}^{n}L\{f,({\mathbf{y}}_{\left[i\right]},X_{1[{\pi }_{l\left[i\right]},\cdot ]},X_{2\left[i,\cdot \right]})\},$$ (A.2)

which omits the indicator function found in Eq A.1.

The summation in Eq A.2 contains n(n!) terms, each of which is a two-way combination of the form L{f, (y_[i], X_1[j,·], X_2[i,·])} for i,j ∈ {1, … n}. There are only n² unique combinations of this form, and each must occur in at least (n − 1)! of the n(n!) terms in Eq A.2. To see this, consider selecting two integer values $\tilde{i},\tilde{j}\in \{1,\dots n\}$, and enumerating all occurrences of the term $L\{f,({\mathbf{y}}_{[\tilde{i}]},{\mathbf{X}}_{1[\tilde{j},\cdot ]},{\mathbf{X}}_{2[\tilde{i},\cdot ]})\}$ within the sum in Eq A.2. Of the permutation vectors [π₁,…, π_n!}, we know that (n − 1)! of them place $\tilde{i}$ in the ${\tilde{j}}^{\mathit{th}}$ position, i.e., that satisfy ${\pi }_{l[\tilde{i}]}=\tilde{j}$. For each such permutation π_l, the inner summation in Eq A.2 over all possible values of i must include the term $L\{f,({\mathbf{y}}_{[\tilde{i}]},{\mathbf{X}}_{1[{\pi }_{l[\tilde{i}]},·]},{\mathbf{X}}_{2[\tilde{i},\cdot ]})\}=L\{f,({\mathbf{y}}_{[\tilde{i}]},{\mathbf{X}}_{1[\tilde{j},\cdot ]},{\mathbf{X}}_{2[\tilde{i},\cdot ]})\}$. Thus, Eq A.2 contains at least (n − 1)! occurrences of the term $L\{f,({\mathbf{y}}_{[\tilde{i}]},{\mathbf{X}}_{1[\tilde{j},\cdot ]},{\mathbf{X}}_{2[\tilde{i},\cdot ]})\}$.

So far, we have shown that each unique combination occurs at least (n − 1)! times, but it also follows that each unique combination must occur precisely (n − 1)! times. This is because each of the n² unique combinations must occur at least (n − 1)! times, which accounts for n²((n − 1)!) = n(n!) terms in total. As noted above, Eq has A.2 has only n(n)! terms, so there can be no additional terms. We can then simplify Eq A.2 as

$$\sum _{l=1}^{n!}\sum _{i=1}^{n}L\{f,({\mathbf{y}}_{\left[i\right]},X_{1[{\pi }_{l\left[i\right]},\cdot ]},X_{2\left[i,\cdot \right]})\}=\left(n-1\right)!\sum _{i=1}^n\sum _{j=1}^{n}L\{f,(y_{\left[i\right]},X_{1\left[j,\cdot \right]},X_{2\left[i,\cdot \right]})\}.$$

By the same logic, we can simplify Eq A.1 as

$$\begin{array}{l}\sum _{l=1}^{n!}\sum _{i=1}^{n}L\{f,({\mathbf{y}}_{\left[i\right]},X_{1[{\pi }_{l\left[i\right]},\cdot ]},X_{2\left[i,\cdot \right]})\}1({\pi }_{l\left[i\right]}\ne i)\\ =\left(n-1\right)!\left\{\sum _{i=1}^n\sum _{j=1}^{n}L\{f,({\mathbf{y}}_{\left[i\right]},X_{1\left[j,\cdot \right]},X_{2\left[i,\cdot \right]})\}1(j\ne i)\right\}\\ =\left(n-1\right)!\sum _{i=1}^n\sum _{j\ne 1}^{}L\{f,({\mathbf{y}}_{\left[i\right]},X_{1\left[j,\cdot \right]},X_{2\left[i,\cdot \right]})\},\end{array}$$

and Line A.3 is proportional to ê_switch(f) up to a function of n.

A.4. Bound for MR of the Best-in-class Prediction Model

Although describing individual models is not the primary focus of this work, a corollary of Theorem 4 is that we can create a probabilistic bound for the reliance of the (unknown) best-in-class model f^⋆ on X₁.

Corollary 22 (Bound on Best-in-class MR) Let $f^{\star }\in {\mathrm{arg\; min}}_{f\in \mathcal{F}}{e}_{\mathit{orig}}(f)$ be a prediction model that attains the lowest possible expected loss, and let f_+,ϵ and f_−,ϵ be defined as in Theorem 4· If f_+,ϵ and f_−,ϵ satisfy Assumptions 1, 2 and 3, then

$$\mathbb{P}\left(MR\left(f^{\star }\right)\in \left[{\widehat{\mathit{MCR}}}_{-}\left({ϵ}_{best}\right)-{\mathcal{Q}}_{best},{\widehat{\mathit{MCR}}}_{+}\left({ϵ}_{best}\right)+{\mathcal{Q}}_{best}\right]\right)\ge 1-\delta ,$$

where ${ϵ}_{best}:=2B_{ref}\sqrt{\frac{\log (6{\delta }^{-1})}{2n}},$ and ${\mathcal{Q}}_{best}:=\frac{B_{switch}}{b_{orig}}-\frac{B_{switch}-B_{ind}\sqrt{\frac{\log (12{\delta }^{-1})}{n}}}{b_{orig}+B_{ind}\sqrt{\frac{\log (12{\delta }^{-1})}{2n}}}.$

The above result does not require that f^⋆ be unique. If several models achieve the minimum possible expected loss, the above boundaries apply simultaneously for each of them. In the special case when the true conditional expectation function $\mathbb{E}(Y|X_1,X_2)$ is equal to f^⋆, then we have a boundary for the reliance of the function $\mathbb{E}(Y|X_1,X_2)$ on X₁. This reliance bound can also be translated into a causal statement using Proposition 19.

A.5. Ratios versus Differences in MR Definition

We choose our ratio-based definition of model reliance, $MR(f)=\frac{e_{\mathrm{switch}}(f)}{e_{\mathrm{orig}}(f)}$, so that the measure can be comparable across problems, regardless of the scale of Y. However, several existing works define VI measures in terms of differences (Strobl et al., 2008; Datta et al., 2016; Gregorutti et al., 2017), analogous to

$$M{R}_{\mathrm{difference}}\left(f\right):=e_{\mathrm{switch}}\left(f\right)-e_{\mathrm{orig}}\left(f\right).$$ (A.4)

While this difference measure is less readily interpretable, it has several computational advantages. The mean, variance, and asymptotic distribution of the estimator ${\widehat{MR}}_{\mathrm{difference}}(f):={\widehat{e}}_{\mathrm{switch}}(f)-{\widehat{e}}_{\mathrm{orig}}(f)$ can be easily determined using results for U-statistics, without the use of the delta method (Dorfman, 1938; Lehmann and Casella, 2006; see also Ver Hoef, 2012). Estimates in the form of ${\widehat{MR}}_{\mathrm{difference}}(f)$ will also be more stable when ${\min }_{f\in \mathcal{F}}{e}_{\mathrm{orig}}(f)$ is small, relative to estimates for the ratio-based definition of MR. To improve interpretability, we may also normalize MR_difference(f) by dividing by the variance of Y, which can be easily estimated without the use of models, as in Williamson et al. (2017).

Under the difference-based definition for MR (Eq A.4), the results from Theorem 4, Theorem 6, and Corollary 22 will still hold under the following modified definitions of ${\mathcal{Q}}_{\mathrm{out}}$, ${\mathcal{Q}}_{\mathrm{in}}$, and ${\mathcal{Q}}_{\mathrm{best}}$:

$${\mathcal{Q}}_{\mathrm{out},\mathrm{difference}}:=\left(1+\frac{1}{\sqrt{2}}\right)B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{n}},$$

$${\mathcal{Q}}_{\mathrm{in},\mathrm{difference}}:=B_{\mathrm{ind}}\left\{\sqrt{\frac{\log \left(8{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\sqrt{2}\right)\right)}{n}}+\sqrt{\frac{\log \left(8{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}\right\}+2r\left(\sqrt{2}+1\right),\mathrm{and}$$

$${\mathcal{Q}}_{\mathrm{best},\mathrm{difference}}:=\left(1+\frac{1}{\sqrt{2}}\right)B_{\mathrm{ind}}\sqrt{\frac{\log \left(12{\delta }^{-1}\right)}{n}}.$$

Respectively replacing ${\mathcal{Q}}_{\mathrm{out}}$, ${\mathcal{Q}}_{\mathrm{in}}$, ${\mathcal{Q}}_{\mathrm{best}}$, MR, and $\widehat{MR}$ with ${\mathcal{Q}}_{\mathrm{out,difference}}$, ${\mathcal{Q}}_{\mathrm{in,difference}}$, ${\mathcal{Q}}_{\mathrm{best,difference}}$, MR_difference and ${\widehat{MR}}_{\mathrm{difference}}$ entails only minor changes to the corresponding proofs (see Appendices B.3, B.5, and B.4). The results will also hold without Assumption 3, as is suggested by the fact that b_orig and B_switch do not appear in ${\mathcal{Q}}_{\mathrm{out,difference}}$, ${\mathcal{Q}}_{\mathrm{in,difference}}$, or ${\mathcal{Q}}_{\mathrm{best,difference}}$.

We also prove an analogous version of Theorem 5, on uniform bounds for ${\widehat{MR}}_{\mathrm{difference}}$, in Appendix B.5.1.

A.6. Rashomon Sets and Profile Likelihood Intervals

We note in Section 5.1 that, under certain conditions, the CIs returned from Proposition 7 take the same form as profile likelihood CIs (Coker et al., 2018). For completeness, we briefly review this connection. We assume here that models $f_{\theta }\in \mathcal{F}$ are indexed by a finite dimensional parameter vector θ ∈ Θ, where θ = (γ, ψ) contains a 1-dimensional parameter of interest $\gamma \in {\mathbb{R}}^1$, and a nuisance parameter ψ ∈ Ψ. We further assume and that e_orig(f_θ) is minimized by a unique parameter value θ^⋆ = (γ^⋆, ψ^⋆) ∈ Θ, and that our goal is to learn about γ^⋆.

If $s_{\theta }:={\int }_{\mathcal{Z}}\exp \{-L(f_{\theta },z)\}dz$ is finite for all θ ∈ Θ, we can convert L into the likelihood function $\mathcal{L}:(\mathcal{Z}\times \Theta )\to {\mathbb{R}}^1$ satisfying $\mathcal{L}(z;\theta )=\exp \{-L(f_{\theta },z)\}/s_{\theta }$. As an abbreviation, let $\mathcal{L}(\mathbf{Z};\theta )$ denote ${\prod }_{i=1}^n\mathcal{L}({\mathbf{Z}}_{[i,·]};\theta )$. Additionally, let $\widehat{\theta }:={\mathrm{arg\; min}}_{\theta \in \Theta }{\widehat{e}}_{\mathrm{orig}}(f_{\theta })$ be the empirical loss minimizer, and hence the maximum likelihood estimator of θ^⋆. If $\mathcal{L}$ is indeed the correct likelihood function, then θ^⋆ = (γ^⋆, ψ^⋆) corresponds to the true parameter vector. Further, if ϕ(f_θ) = ϕ(f_{(γ, ψ)}) = γ returns the parameter element of interest (γ), then the (1 − δ)-level profile likelihood interval for ϕ(f_θ^⋆) = γ^⋆ is

$$\begin{gathered} \mathrm{PLI}\left(\delta \right):=\left\{\gamma :\log \mathcal{L}\left(Z;\widehat{\theta }\right)-\log \mathcal{L}\left(Z;{\widehat{\theta }}_{\gamma }\right)\le \frac{{\mathcal{X}}_{1,1-\delta }}{2},\mathrm{where}{\widehat{\theta }}_{\gamma }=\underset{\left\{\theta \in \Theta :\varphi \left(f_{\theta }\right)=\gamma \right\}}{\mathrm{arg\; max}}\mathcal{L}\left(Z;\theta \right)\right\} \\ =\left\{\gamma :\exists {\widehat{\theta }}_{\gamma }\mathrm{satisfying}\varphi \left(f_{{\widehat{\theta }}_{\gamma }}\right)=\gamma \mathrm{and}\log \mathcal{L}\left(Z;\widehat{\theta }\right)-\log \mathcal{L}\left(Z;{\widehat{\theta }}_{\gamma }\right)\le \frac{{\mathcal{X}}_{1,1-\delta }}{2}\right\} \\ =\left\{\gamma :\exists {\widehat{\theta }}_{\gamma }\mathrm{satisfying}\varphi \left(f_{{\widehat{\theta }}_{\gamma }}\right)=\gamma \mathrm{and}{\widehat{e}}_{\mathrm{orig}}\left(f_{{\widehat{\theta }}_{\gamma }}\right)\le {\widehat{e}}_{\mathrm{orig}}\left(f_{\widehat{\theta }}\right)+\frac{{\mathcal{X}}_{1,1-\delta }}{2n}\right\} \\ =\left\{\gamma :\exists f_{{\widehat{\theta }}_{\gamma }}\mathrm{satisfying}\varphi \left(f_{{\widehat{\theta }}_{\gamma }}\right)=\gamma \mathrm{and}{f}_{{\widehat{\theta }}_{\gamma }}\in \widehat{\mathcal{R}}\left(\frac{{\mathcal{X}}_{1,1-\delta }}{2n},f_{\widehat{\theta }},\mathcal{F}\right)\right\} \end{gathered}$$ (A.5)

where ${\mathcal{X}}_{1,1-\delta }$ is the 1 − δ percentile of a chi-square distribution with 1 degree of freedom. If PLI(α) is indeed a contiguous interval, then maximizing and minimizing ϕ(f_θ) across models f_θ in the empirical Rashomon set in Eq A.5 yields the same interval.

A.7. Unbiased Estimates of CMR

We claim in Section 8.2 that both

$${\widehat{e}}_{\mathrm{match}}\left(f\right)=\frac{1}{n\left(n-1\right)}\sum _{i=1}^n\sum _{j\ne i}\frac{1\left(X_{2\left[j,\cdot \right]}=X_{2\left[i,\cdot \right]}\right)}{\mathbb{P}\left(X_2=X_{2\left[i,\cdot \right]}\right)}\times L\left\{f,\left({\mathbf{y}}_{\left[j\right]},X_{1\left[i,\cdot \right]},X_{2\left[j,\cdot \right]}\right)\right\}.$$

and

$${\widehat{e}}_{\mathrm{weight}}\left(f\right)=\frac{1}{n\left(n-1\right)}\sum _{i=1}^n\sum _{j\ne i}\frac{\mathbb{P}\left(X_1=X_{1\left[i,\cdot \right]}|X_2=X_{2\left[j,\cdot \right]}\right)}{\mathbb{P}\left(X_1=X_{1\left[i,\cdot \right]}\right)}\times L\left\{f,\left({\mathbf{y}}_{\left[j\right]},X_{1\left[i,\cdot \right]},X_{2\left[j,\cdot \right]}\right)\right\},$$

are unbiased for

$$e_{\mathrm{cond}}\left(f\right)={\mathbb{E}}_{X_2}\mathbb{E}\left[L\{f,(Y^{\left(b\right)},X_1^{\left(a\right)},X_2^{\left(b\right)})\}|X_2^{\left(a\right)}=X_2^{\left(b\right)},X_2\right].$$

To show that ê_match(f) is unbiased, we first note that each summation term in ê_match(f) has the same expectation. Following the notation in Section 3, let $Z^{\left(a\right)}=(Y^{\left(a\right)},X_1^{\left(a\right)},X_2^{\left(a\right)})$ and $Z^{\left(b\right)}=(Y^{\left(b\right)},X_1^{\left(b\right)},X_2^{\left(b\right)})$ be independent random variables following the same distribution as Z = (Y, X₁, X₂). The expectation of ê_match(f) is

$$\begin{array}{l}\mathbb{E}{\widehat{e}}_{\mathrm{match}}\left(f\right)=\mathbb{E}\left[\frac{1(X_2^{\left(a\right)}=X_2^{\left(b\right)})}{p_{x_2}(X_2^{\left(a\right)})}\times L\{f,(Y^{\left(b\right)},X_1^{\left(a\right)},X_2^{\left(b\right)})\}\right]\\ ={\mathbb{E}}_{X_2^{\left(a\right)}}\mathbb{E}\left[\frac{1(X_2^{\left(a\right)}=X_2^{\left(b\right)})}{p_{x_2}(X_2^{\left(a\right)})}\times L\{f,(Y^{\left(b\right)},X_1^{\left(a\right)},X_2^{\left(b\right)})\}|X_2^{\left(a\right)}\right]\\ ={\mathbb{E}}_{X_2^{\left(a\right)}}\left\{p_{x_2}(X_2^{\left(a\right)})\mathbb{E}\left[\frac{1}{p_{x_2}(X_2^{\left(a\right)})}\times L\{f,(Y^{\left(b\right)},X_1^{\left(a\right)},X_2^{\left(b\right)})\}|X_2^{\left(a\right)}=X_2^{\left(b\right)},X_2^{\left(a\right)}\right]+0\right\}\\ ={\mathbb{E}}_{X_2^{\left(a\right)}}\mathbb{E}\left[L\{f,(Y^{\left(b\right)},X_1^{\left(a\right)},X_2^{\left(b\right)})\}|X_2^{\left(a\right)}=X_2^{\left(b\right)},X_2^{\left(a\right)}\right]\\ =e_{\mathrm{cond}}\left(f\right).\end{array}$$

To show that ${\widehat{e}}_{\mathrm{weight}}(f)$ is unbiased, we similarly note that each summation term in ${\widehat{e}}_{\mathrm{weight}}(f)$ has the same expectation. Without loss of generality, we show the result for discrete variables (Y, X₁, X₂). Let ${\mathcal{Y}}_{x_2}$ be the domain of Y conditional on the event that X₂ = x₂. The expectation of ${\widehat{e}}_{\mathrm{weight}}(f)$ is

$$\begin{array}{l}\mathbb{E}{\widehat{e}}_{\mathrm{weight}}\left(f\right)=\sum _{x_2^{\left(b\right)}\in {\mathcal{X}}_2}\sum _{y^{\left(b\right)}\in {\mathcal{Y}}_{x_2^{\left(b\right)}}}\sum _{x_1^{\left(a\right)}\in {\mathcal{X}}_1}[L\{f,(y^{\left(b\right)},x_1^{\left(a\right)},x_2^{\left(b\right)})\}\left\{\frac{\mathbb{P}(X_1=x_1^{\left(a\right)}|X_2=x_2^{\left(b\right)})}{\mathbb{P}(X_1=x_1^{\left(a\right)})}\right\}\\ \times \mathbb{P}(X_1=x_1^{\left(a\right)})\mathbb{P}(Y=y^{\left(b\right)},X_2=x_2^{\left(b\right)})]\\ =\sum _{x_2^{\left(b\right)}\in {\mathcal{X}}_2}\mathbb{P}(X_2=x_2^{\left(b\right)})\sum _{y^{\left(b\right)}\in {\mathcal{Y}}_{x_2^{\left(b\right)}}}\sum _{x_1^{\left(a\right)}\in {\mathcal{X}}_1}[L\{f,(y^{\left(b\right)},x_1^{\left(a\right)},x_2^{\left(b\right)})\}\\ \times \mathbb{P}(X_1=x_1^{\left(a\right)}|X_2=x_2^{\left(b\right)})\mathbb{P}(Y=y^{\left(b\right)}|X_2=x_2^{\left(b\right)})]\\ ={\mathbb{E}}_{X_2^{\left(b\right)}}\mathbb{E}\left[\int L\{f,(Y^{\left(b\right)},X_1^{\left(a\right)},X_2^{\left(b\right)})\}|X_2^{\left(a\right)}=X_2^{\left(b\right)},X_2^{\left(b\right)})\right]\\ =e_{\mathrm{cond}}\left(f\right).\end{array}$$

Appendix B. Proofs for Statistical Results

We present proofs for our statistical results in this section, and conclude by presenting proofs for our computational results in Appendix C.

B.1. Lemma Relating Empirical and Population Rashomon Sets

Throughout the remaining proofs, it will be useful to express the definition of population ϵ-Rashomon sets in terms of the expectation of a single loss function, rather than a comparison of two loss functions. To do this, we simply introduce the “standardized” loss function $\tilde{L}$, defined as

$$\tilde{L}\left(f,z\right):=L\left(f,z\right)-L\left(f_{ref},z\right).$$ (B.1)

Above, recall from Section 2 that L(f, z) denotes L(f, (y, x₁, x₂)) for z = (y, x₁, x₂). Because we assume f_ref is prespecified and fixed, we omit notation for f_ref in the definition of $\tilde{L}$. We can now write

$$\begin{array}{l}\mathcal{R}\left(ϵ\right)=\left\{f_{\mathrm{ref}}\right\}\bigcup \left\{f\in \mathcal{F}:\mathbb{E}L\left(f,Z\right)\le \mathbb{E}L\left(f_{\mathrm{ref}},Z\right)+ϵ\right\}\\ =\left\{f_{\mathrm{ref}}\right\}\bigcup \left\{f\in \mathcal{F}:\mathbb{E}\tilde{L}\left(f,Z\right)\le ϵ\right\},\end{array}$$

and, similarly,

$$\widehat{\mathcal{R}}\left(ϵ\right)=\left\{f_{\mathrm{ref}}\right\}\bigcup \left\{f\in \mathcal{F}:\widehat{\mathbb{E}}\tilde{L}\left(f,Z\right)\le ϵ\right\}.$$

With this definition, the following lemma allows us to limit the probability that a given model $f_1\in \widehat{\mathcal{R}}\left(ϵ\right)$ is excluded from an empirical Rashomon set.

Lemma 23 For $ϵ\in \mathbb{R}$ and δ ∈ (0, 1), let ${ϵ}_1^{\prime }:=ϵ+2B_{ref}\sqrt{\frac{\log ({\delta }^{-1})}{2n}}$, and let $f_1\in \mathcal{R}\left(ϵ\right)$ denote a specific, possibly unknown prediction model. If f₁ satisfies Assumption 2, then

$$\mathbb{P}\{f_1\in \widehat{\mathcal{R}}({ϵ}_1^{\prime })\}\ge 1-\delta .$$

Proof If f_ref and f₁ are the same function, then the result holds trivially. Otherwise, the proof follows from Hoeffding’s inequality (Theorem 2 of Hoeffding, 1963). First, note that if f₁ satisfies Assumption 2, then $\tilde{L}(f_1)$ is bounded within an interval of length 2B_ref. Applying this in line B.3, below, we see that

$$\begin{array}{cc}\mathbb{P}\{f_1\notin \widehat{\mathcal{R}}({ϵ}_1^{\prime })\}=\mathbb{P}\left[\widehat{\mathbb{E}}\tilde{L}\left(f_1,Z\right)>{ϵ}_1^{\prime }\right]& \mathrm{from}{f}_1\notin \left\{f_{\mathrm{ref}}\right\}\\ =\mathbb{P}\left[\widehat{\mathbb{E}}\tilde{L}\left(f_1,Z\right)-ϵ>2B_{ref}\sqrt{\frac{\log \left({\delta }^{-1}\right)}{2n}}\right]& \mathrm{from\; definition\; of}{ϵ}_1^{\prime }\end{array}$$ (B.2)

$$\begin{array}{ll}\le \mathbb{P}\left[\widehat{\mathbb{E}}\tilde{L}\left(f_1,Z\right)-\mathbb{E}\tilde{L}\left(f_1,Z\right)>2B_{ref}\sqrt{\frac{\log \left({\delta }^{-1}\right)}{2n}}\right]& \mathrm{from}\mathbb{E}\tilde{L}\left(f_1,Z\right)\le ϵ\\ \le \exp \left\{-\frac{2n}{{\left(2B_{ref}\right)}^2}{\left[2B_{ref}\sqrt{\frac{\log \left({\delta }^{-1}\right)}{2n}}\right]}^2\right\}& \mathrm{from\; Hoeffding’s\; inequality}\end{array}$$ (B.3)

$$=\delta .$$ (B.4)

For the inequality used in Line B.3, see Theorem 2 of Hoeffding, 1963. ■

B.2. Lemma to Transform Between Bounds

The following lemma will help us translate from bounds for variables to bounds for differences and ratios of those variables. We will apply this lemma to transform from bounds on empirical losses to bounds on empirical model reliance, defined either in terms of a ratio or in terms of a difference.

Lemma 24 Let X, Z, μ_X ,μ_Z, k_X, $k_Z\in \mathbb{R}$ be constants satisfying |Z − μ_Z| ≤ k_Z and |X − μ_X| ≤ k_X, then

$$\left|\left(Z-X\right)-\left({\mu }_Z-{\mu }_X\right)\right|\le q_{difference}\left(k_Z,k_X\right),$$ (B.5)

where q_difference is the function

$$q_{difference}\left(k_Z,k_X\right):=k_Z+k_X.$$ (B.6)

Further, if there exists constants b_orig and B_switch such that 0 < b_orig ≤ X, μ_X and Z, μ_Z ≥ B_switch < ∞, then

$$\left|\frac{Z}{X}-\frac{{\mu }_Z}{{\mu }_X}\right|\le q_{ratio}\left(k_Z,k_X\right),$$ (B.7)

where q_ratio is the function

$$q_{ratio}\left(k_Z,k_X\right):=\frac{B_{switch}}{b_{orig}}-\frac{B_{switch}-k_Z}{b_{orig}+k_X}.$$ (B.8)

Proof Showing Eq B.5,

$$\begin{array}{l}\left|\left(Z-X\right)-\left({\mu }_Z-{\mu }_X\right)\right|\le \left|Z-{\mu }_Z\right|+\left|{\mu }_X-X\right|\\ \le k_Z+k_X.\end{array}$$

Showing Eq B.7, let A_z = max(Z, μ_z), a_X = min(X, μ_X), d_Z = |Z − μ_Z|, and d_X = |X − μ_X|. This implies that max(X, μ_X) = a_X + d_X and min(Z, μ_Z) = A_Z − d_Z. Thus, $\frac{Z}{X}$ and $\frac{\mu Z}{\mu X}$ are both bounded within the interval

$$\left[\frac{\min \left(Z,{\mu }_Z\right)}{\max \left(X,{\mu }_X\right)},\frac{\max \left(Z,{\mu }_Z\right)}{\min \left(X,{\mu }_X\right)}\right]=\left[\frac{A_Z-d_Z}{a_X+d_X},\frac{A_Z}{a_X}\right],$$

which implies

$$\left|\frac{Z}{X}-\frac{{\mu }_Z}{{\mu }_X}\right|\le \frac{A_Z}{a_X}-\frac{A_Z-d_Z}{a_X+d_X}.$$ (B.9)

Taking partial derivatives of the right-hand side, we get

$$\frac{\partial }{\partial a_X}\left(\frac{A_Z}{a_X}-\frac{A_Z-d_Z}{a_X+d_X}\right)=\frac{-A_Z}{a_X^2}+\frac{A_Z-d_Z}{{\left(a_X+d_X\right)}^2}\le 0,$$

$$\frac{\partial }{\partial A_Z}\left(\frac{A_Z}{a_X}-\frac{A_Z-d_Z}{a_X+d_X}\right)=\frac{1}{a_X}-\frac{1}{a_X+d_X}\ge 0,$$

$$\frac{\partial }{\partial d_X}\left(\frac{A_Z}{a_X}-\frac{A_Z-d_Z}{a_X+d_X}\right)=\frac{A_Z-d_Z}{{\left(a_X+d_X\right)}^2}>0,$$

$$\mathrm{and}\frac{\partial }{\partial d_Z}\left(\frac{A_Z}{a_X}-\frac{A_Z-d_Z}{a_X+d_X}\right)=\frac{1}{a_X+d_X}>0.$$

So the right-hand side of B.9 is maximized when d_Z, d_X, and A_Z are maximized, and when a_X is minimized. Thus, in the case where |Z − μ_Z| ≤ k_Z; |X − μ_X| ≤ k_X; 0 < b_orig ≤ X, μ_X ; and Z, μ_Z ≤ B_switch < ∞, we have

$$\begin{array}{l}\left|\frac{Z}{X}-\frac{\mu Z}{{\mu }_X}\right|\le \frac{A_Z}{a_X}-\frac{A_Z-d_Z}{a_X+d_X}\\ \le \frac{B_{\mathrm{switch}}}{b_{\mathrm{orig}}}-\frac{B_{\mathrm{switch}}-k_Z}{b_{\mathrm{orig}}+k_X}.\end{array}$$

B.3. Proof of Theorem 4

Proof We proceed in 4 steps.

B.3.1. Step 1: Show that $\mathbb{P}\left[\widehat{MR}\left(f_{+,ϵ}\right)\le {\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{OUT}}\right)\right]\ge 1-\frac{\delta }{3}.$

Consider the event that

$$\widehat{MR}\left(f_{+,ϵ}\right)\le {\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{out}}\right).$$ (B.10)

Eq B.10 will always hold if $f_{+,ϵ}\in \widehat{\mathcal{R}}({ϵ}_{\mathrm{out}})$, since ${\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{out}}\right)$ upper bounds the empirical model reliance for models in $\widehat{\mathcal{R}}\left({ϵ}_{\mathrm{out}}\right)$ by definition. Applying the above reasoning in Line B.11, below, we get

$$\mathbb{P}\left[\widehat{MR}\left(f_{+,ϵ}\right)>{\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{out}}\right)\right]\le \mathbb{P}\left[f_{+,ϵ}\notin \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{out}}\right)\right]$$ (B.11)

$$\le \frac{\delta }{3}\mathrm{from}{ϵ}_{\mathrm{out}}\mathrm{definition}\mathrm{and}\mathrm{Lemma}23.$$ (B.12)

B.3.2. Step 2: Conditional on $\widehat{MR}\left(f_{+,ϵ}\right)\le {\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{out}}\right)$, Upper Bound MR(f_+,ϵ) by ${\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{out}}\right)$ Added to an Error Term.

When Eq B.10 holds we have,

$$\begin{array}{l}\widehat{MR}\left(f_{+,ϵ}\right)\le {\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{out}}\right)\\ \widehat{MR}\left(f_{+,ϵ}\right)\le {\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{out}}\right)+\left\{MR\left(f_{+,ϵ}\right)-MR\left(f_{+,ϵ}\right)\right\}\\ MR\left(f_{+,ϵ}\right)\le {\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{out}}\right)+\left[MR\left(f_{+,ϵ}\right)-\widehat{MR}\left(f_{+,ϵ}\right)\right].\end{array}$$ (B.13)

B.3.3. Step 3: Probabilistically Bound the Error Term from Step 2.

Next we show that the bracketed term in Line B.13 is less than or equal to ${\mathcal{Q}}_{\mathrm{out}}$ with high probability. For $k\in \mathbb{R}$, let q_diference and q_ratio be defined as in Eqs B.6 and B.8. Let $q:\mathbb{R}\to \mathbb{R}$ be the function such that $q(k)=q_{\mathrm{ratio}}(k,\frac{k}{\sqrt{2}})$. Then

$$\begin{array}{l}{\mathcal{Q}}_{\mathrm{out}}=\frac{B_{\mathrm{switch}}}{b_{\mathrm{orig}}}-\frac{B_{\mathrm{switch}}-B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{n}}}{b_{\mathrm{orig}}+B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{2n}}}\\ =q_{\mathrm{ratio}}\left(B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{n}},B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{2n}}\right)\\ =q\left(B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{n}}\right).\end{array}$$

Applying this relation below, we have

$$\begin{array}{l}\mathbb{P}\left[MR\left(f_{+,ϵ}\right)-\widehat{MR}\left(f_{+,ϵ}\right)>{\mathcal{Q}}_{\mathrm{out}}\right]\\ \le \mathbb{P}\left[\left|MR\left(f_{+,ϵ}\right)-\widehat{MR}\left(f_{+,ϵ}\right)\right|>q\left(B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{n}}\right)\right]\\ \le \mathbb{P}[\left\{\left|{\widehat{e}}_{\mathrm{orig}}\left(f_{+,ϵ}\right)-e_{\mathrm{orig}}\left(f_{+,ϵ}\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{2n}}\right\}\\ \bigcup \left\{\left|{\widehat{e}}_{switch}\left(f_{+,ϵ}\right)-e_{switch}\left(f_{+,ϵ}\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{n}}\right\}]& \mathrm{from\; Lemma}24\\ \le \mathbb{P}\left[\left|{\widehat{e}}_{\mathrm{orig}}\left(f_{+,ϵ}\right)-e_{\mathrm{orig}}\left(f_{+,ϵ}\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{2n}}\right]\\ +\mathbb{P}\left[\left|{\widehat{e}}_{switch}\left(f_{+,ϵ}\right)-e_{switch}\left(f_{+,ϵ}\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{2n}}\right]& \mathrm{from\; the\; Union\; bound}\end{array}$$ (B.14)

$$\begin{array}{l}\le 2\exp \left\{-\frac{2n}{{\left(B_{\mathrm{ind}}-0\right)}^2}{\left[B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{2n}}\right]}^2\right\}\\ +2\exp \left\{-\frac{n}{{\left(B_{\mathrm{ind}}-0\right)}^2}{\left[B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{n}}\right]}^2\right\}& \mathrm{from\; Hoeffding\text{'}s\; bound\; for\; U-statistics}\end{array}$$ (B.15)

$$=\frac{2\delta }{6}+\frac{2\delta }{6}=\frac{2\delta }{3}.$$ (B.16)

In Line B.15, above, recall that ${\widehat{e}}_{\mathrm{orig}}(f_{+,ϵ})$ and ${\widehat{e}}_{\mathrm{switch}}(f_{+,ϵ})$ are both U-statistics. Note that $\mathbb{E}[{\widehat{e}}_{\mathrm{switch}}(f_{+,ϵ})]=e_{\mathrm{switch}}(f_{+,ϵ})$ because ${\widehat{e}}_{\mathrm{switch}}(f_{+,ϵ})$ is an average of terms, and each term has expectation equal to e_switch(f_+,ϵ). For the same reason, $\mathbb{E}[{\widehat{e}}_{\mathrm{orig}}(f_{+,ϵ})]=e_{\mathrm{orig}}(f_{+,ϵ})$. This allows us to apply Eq 5.7 of Hoeffding, 1963 (see also Eq 1 on page 201 of Serfling, 1980, in Theorem A) to obtain Line B.15.

Alternatively, if we instead define model reliance as MR_difference(f) = e_switch(f) − e_orig(f) (see Appendix A.5), define empirical model reliance as ${\widehat{MR}}_{\mathrm{difference}}(f):={\widehat{e}}_{\mathrm{switch}}(f)-{\widehat{e}}_{\mathrm{orig}}(f)$, and define

$${\mathcal{Q}}_{\mathrm{out,\; difference}}:=\left(1+\frac{1}{\sqrt{2}}\right)B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{n}}=q_{\mathrm{difference}}\left(B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{n}},B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{2n}}\right),$$

then the same proof holds without Assumption 3 if we replace MR, $\widehat{MR},{\mathcal{Q}}_{\mathrm{out}}$, respectively with MR_difference, ${\widehat{MR}}_{\mathrm{difference}},{\mathcal{Q}}_{\mathrm{out,difference}}$, and redefine $q:\mathbb{R}\to \mathbb{R}$ as the function $q(k)=q_{\mathrm{difference}}\left(k,\frac{k}{\sqrt{2}}\right)$.

Eqs B.14–B.16 also hold if we replace ê_switch throughout with ê_divide, including in Assumption 3, since the same bound can be used for both ê_switch and ê_divide (Eq 5.7 of Hoeffding, 1963; see also Theorem A on page 201 of Serfling, 1980).

B.3.4. Step 4: Combine Results to Show Eq 4.2

Finally, we connect the above results to show Eq 4.2. We know from Eq B.12 that Eq B.10 holds with high probability. Eq B.10 implies Eq B.13, which bounds MCR₊(ϵ) = MR(f_+,ϵ) up to a bracketed residual term. We also know from Eq B.16 that, with high probability, the residual term in Eq B.13 is less than ${\mathcal{Q}}_{out}=q\left(B_{\mathrm{ind}}\sqrt{\frac{\log (6{\delta }^{-1})}{n}}\right)$. Putting this together We can show Eq 4.2:

$$\begin{array}{l}\mathbb{P}\left(MC{R}_{+}\left(ϵ\right)>{\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{out}}\right)+{\mathcal{Q}}_{\mathrm{out}}\right)\\ =\mathbb{P}\left(MR\left(f_{+,ϵ}\right)>{\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{out}}\right)+{\mathcal{Q}}_{\mathrm{out}}\right)\\ \le \mathbb{P}\left[\left(\widehat{MR}\left(f_{+,ϵ}\right)>{\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{out}}\right)\right)\bigcup \left(MR\left(f_{+,ϵ}\right)-\widehat{MR}\left(f_{+,ϵ}\right)>{\mathcal{Q}}_{\mathrm{out}}\right)\right]& \mathrm{from\; Step}2\\ \le \mathbb{P}\left[\widehat{MR}\left(f_{+,ϵ}\right)>{\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{out}}\right)\right]+\mathbb{P}\left[MR\left(f_{+,ϵ}\right)-\widehat{MR}\left(f_{+,ϵ}\right)>{\mathcal{Q}}_{\mathrm{out}}\right]\\ \le \frac{\delta }{3}+\frac{2\delta }{3}=\delta .& \mathrm{from\; Steps}1\&3\end{array}$$ (B.17)

This completes the proof for Eq 4.2. For Eq 4.3 we can use the same approach, shown below for completeness. Analogous to Eq B.12, we have

$$\mathbb{P}\left[\widehat{MR}\left(f_{-,ϵ}\right)<{\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{out}}\right)\right]\le \frac{\delta }{3}.$$

Analogous to Eq B.13, when $\widehat{MR}\left(f_{-,ϵ}\right)\ge \widehat{MR}\left(f_{-,{ϵ}_{\mathrm{out}}}\right)$ we have

$$\begin{array}{l}\widehat{MR}\left(f_{-,ϵ}\right)\ge {\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{out}}\right)\\ \widehat{MR}\left(f_{-,ϵ}\right)\ge {\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{out}}\right)+\left\{MR\left(f_{-,ϵ}\right)-MR\left(f_{-,ϵ}\right)\right\}\\ \widehat{MR}\left(f_{-,ϵ}\right)\ge {\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{out}}\right)-\left[\widehat{MR}\left(f_{-,ϵ}\right)-MR\left(f_{-,ϵ}\right)\right].\end{array}$$

Analogous to Eq B.16, we have

$$\mathbb{P}\left[\widehat{MR}\left(f_{-,ϵ}\right)-MR\left(f_{-,ϵ}\right)>q\left(B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{n}}\right)\right]\le \frac{2\delta }{3}.$$ (B.18)

Finally, analogous to Eq B.17, we have

$$\begin{array}{l}\mathbb{P}\left(MC{R}_{-}\left(ϵ\right)<{\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{out}}\right)-{\mathcal{Q}}_{\mathrm{out}}\right)\\ \le \mathbb{P}\left[\left(\widehat{MR}\left(f_{-,ϵ}\right)<{\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{out}}\right)\right)\bigcup \left(\widehat{MR}\left(f_{-,ϵ}\right)-MR\left(f_{-,ϵ}\right)>q\left(B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{n}}\right)\right)\right]\end{array}$$ (B.19)

$$\begin{array}{l}\le \mathbb{P}\left[\widehat{MR}\left(f_{-,ϵ}\right)<{\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{out}}\right)\right]+\mathbb{P}\left[\widehat{MR}\left(f_{-,ϵ}\right)-MR\left(f_{-,ϵ}\right)>q\left(B_{\mathrm{ind}}\sqrt{\frac{\log \left(6{\delta }^{-1}\right)}{n}}\right)\right]\\ \le \frac{\delta }{3}+\frac{2\delta }{3}=\delta .\end{array}$$

Again, the same proof holds without Assumption 3 if we replace MR, $\widehat{MR},{\mathcal{Q}}_{\mathrm{out}}$ respectively with MR_difference, ${\widehat{MR}}_{\mathrm{difference}},{\mathcal{Q}}_{\mathrm{out,difference}}$, and redefine q as the function satisfying $q(k)=q_{\mathrm{difference}}\left(k,\frac{k}{\sqrt{2}}\right)$ in Eqs B.18 & B.19. ■

B.4. Proof of Corollary 22

Proof By definition, MR(f_−,ϵbest) ≤ MR(f^⋆) ≤ MR(f_+,ϵbest). Applying this relation in Line B.20, below, we see

$$\begin{array}{l}\mathbb{P}\left(MR\left(f^{\star }\right)\in \left[{\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{best}}\right)-{\mathcal{Q}}_{\mathrm{best}},{\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{best}}\right)+{\mathcal{Q}}_{\mathrm{best}}\right]\right)\\ =1-\mathbb{P}\left\{MR\left(f^{\star }\right)<{\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{best}}\right)-{\mathcal{Q}}_{\mathrm{best}}\bigcup MR\left(f^{\star }\right)>{\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{best}}\right)+{\mathcal{Q}}_{\mathrm{best}}\right\}\\ \ge 1-\mathbb{P}\left\{MR\left(f^{\star }\right)<{\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{best}}\right)-{\mathcal{Q}}_{\mathrm{best}}\right\}-\mathbb{P}\left\{MR\left(f^{\star }\right)>{\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{best}}\right)+{\mathcal{Q}}_{\mathrm{best}}\right\}\\ \ge 1-\mathbb{P}\left\{MR\left(f_{-,ϵ}\right)<{\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{best}}\right)-{\mathcal{Q}}_{\mathrm{best}}\right\}-\mathbb{P}\left\{MR\left(f_{+,ϵ}\right)>{\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{best}}\right)+{\mathcal{Q}}_{\mathrm{best}}\right\}\end{array}$$ (B.20)

$$\begin{array}{ll}\ge 1-\frac{\delta }{2}-\frac{\delta }{2}& \mathrm{from\; Theorem}4.\end{array}$$ (B.21)

To apply Theorem 4 in Line B.21, above, we note that ${\mathcal{Q}}_{\mathrm{best}}$ and ϵ_best are equivalent to the definitions of ${\mathcal{Q}}_{\mathrm{out}}$ and ϵ_out in Theorem 4, but with δ replaced by $\frac{\delta }{2}$.

Alternatively, if we define model reliance as MR_difference(f) = e_switch(f) − e_orig(f) (see Appendix A.5), and define empirical model reliance as ${\widehat{MR}}_{\mathrm{difference}}(f)={\widehat{e}}_{\mathrm{switch}}(f)-{\widehat{e}}_{\mathrm{orig}}(f)$, then let

$${\mathcal{Q}}_{\mathrm{best},\mathrm{difference}}:=\left(1+\frac{1}{\sqrt{2}}\right)B_{\mathrm{ind}}\sqrt{\frac{\log \left(12{\delta }^{-1}\right)}{n}}.$$

The term ${\mathcal{Q}}_{\mathrm{best,difference}}$ is equivalent to ${\mathcal{Q}}_{\mathrm{out,difference}}$ but with δ replaced with $\frac{\delta }{2}$. Under this difference-based definition of model reliance, Theorem 4 holds without Assumption 3 if we replace ${\mathcal{Q}}_{\mathrm{out}}$ with ${\mathcal{Q}}_{\mathrm{out,difference}}$ (see Section B.3), and so we can apply this altered version of Theorem 4 in Line B.21. Thus, Theorem 22 also holds without Assumption 3 if we replace MR, $\widehat{MR}$, and ${\mathcal{Q}}_{\mathrm{best}}$ respectively with MR_difference, ${\widehat{MR}}_{\mathrm{difference}}$, and ${\mathcal{Q}}_{\mathrm{best,difference}}$. ■

B.5. Proof of Theorems 5 & 6

We begin by proving Theorem 5, along with related results. We then apply these results to show Theorem 6.

B.5.1. Proof of Theorem 5, and Other Limits on Estimation Error, Based on Covering Number

The following theorem uses the covering number based on r-margin-expectation-covers to jointly bound empirical losses for any function $f\in \mathcal{F}$. Theorem 5 in the main text follows directly from Eq B.25, below.

Theorem 25 If Assumptions 1, 2 and 3 hold for all $f\in \mathcal{F}$, then for any r > 0

$${\mathbb{P}}_D\left[\underset{f\in \mathcal{F}}{\sup }\left|{\widehat{e}}_{\mathit{orig}}\left(f\right)-e_{\mathit{orig}}\left(f\right)\right|>B_{\mathit{ind}}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right]\le \delta ,$$ (B.22)

$${\mathbb{P}}_D\left[\underset{f\in \mathcal{F}}{\sup }\left|\widehat{\mathbb{E}}\tilde{L}\left(f,Z\right)-\mathbb{E}\tilde{L}\left(f,Z\right)\right|>2B_{ref}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right]\le \delta ,$$ (B.23)

$${\mathbb{P}}_D\left[\underset{f\in \mathcal{F}}{\sup }\left|{\widehat{e}}_{\mathit{switch}}\left(f\right)-e_{\mathit{switch}}\left(f\right)\right|>B_{\mathit{ind}}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{n}}+2r\right]\le \delta ,$$ (B.24)

$$\mathbb{P}\left[\underset{f\in \mathcal{F}}{\sup }\left|\frac{{\widehat{e}}_{\mathit{orig}}\left(f\right)}{{\widehat{e}}_{\mathit{switch}}\left(f\right)}-\frac{e_{\mathit{orig}}\left(f\right)}{e_{\mathit{switch}}\left(f\right)}\right|>{\mathcal{Q}}_4\right]\le \delta ,$$ (B.25)

$${\mathbb{P}}_D\left[\underset{f\in \mathcal{F}}{\sup }\left|\left\{{\widehat{e}}_{\mathit{switch}}\left(f\right)-{\widehat{e}}_{\mathit{orig}}\left(f\right)\right\}-\left\{e_{\mathit{switch}}\left(f\right)-e_{\mathit{orig}}\left(f\right)\right\}\right|>{\mathcal{Q}}_{4,\mathit{difference}}\right]\le \delta ,$$ (B.26)

where

$${\mathcal{Q}}_4:=q_{\mathit{ratio}}\left(B_{\mathit{ind}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\sqrt{2}\right)\right)}{n}}+2r\sqrt{2},B_{\mathrm{ind}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right),$$ (B.27)

$${\mathcal{Q}}_{4,\mathit{difference}}:=q_{\mathit{difference}}\left(B_{\mathit{ind}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\sqrt{2}\right)\right)}{n}}+2r\sqrt{2},B_{\mathit{ind}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right),$$ (B.28)

and q_ratio and q_difference are defined as in Lemma 24. For Eq B.26, the result is unaffected if we remove Assumption 3.

B.5.2. Proof of Eq B.22

Proof Let ${\mathcal{G}}_r$ be a r-margin-expectation-cover for $\mathcal{F}$ of size $\mathcal{N}(\mathcal{F},r)$. Let D_p denote the population distribution, let D_s be the sample distribution, and let D^⋆ be the uniform mixture of D_p and D_s, i.e., for any $z\in \mathcal{Z}$,

$${\mathbb{P}}_{D^{\star }}(Z\le z)=\frac{1}{2}{\mathbb{P}}_{D_p}(Z\le z)+\frac{1}{2}{\mathbb{P}}_{D_s}(Z\le z).$$ (B.29)

Unless otherwise stated, we take expectations and probabilities with respect to D_p. Since ${\mathcal{G}}_r$ is a r-margin-expectation-cover, we know that for any $f\in \mathcal{F}$ we can find a function $g\in {\mathcal{G}}_r$ such that ${\mathbb{E}}_{D^{\star }}|L(g,Z)-L(f,Z)|={\mathbb{E}}_{D^{\star }}|\tilde{L}(g,Z)-\tilde{L}(f,Z)|\le r,$ and

$$\begin{array}{l}\left|\widehat{\mathbb{E}}L\left(f,Z\right)-\mathbb{E}L\left(f,Z\right)\right|=\left|\widehat{\mathbb{E}}L\left(f,Z\right)-\mathbb{E}L\left(f,Z\right)+\left\{\widehat{\mathbb{E}}L\left(g,Z\right)-\widehat{\mathbb{E}}L\left(g,Z\right)\right\}+\left\{\mathbb{E}L\left(g,Z\right)-\mathbb{E}L\left(g,Z\right)\right\}\right|\end{array}$$ (B.30)

$$\begin{array}{l}\le \left|\widehat{\mathbb{E}}L\left(g,Z\right)-\mathbb{E}L\left(g,Z\right)\right|+\left|\mathbb{E}L\left(g,Z\right)-\mathbb{E}L\left(f,Z\right)\right|+\left|\widehat{\mathbb{E}}L\left(f,Z\right)-\widehat{\mathbb{E}}L\left(g,Z\right)\right|\\ \le \left|\widehat{\mathbb{E}}L\left(g,Z\right)-\mathbb{E}L\left(g,Z\right)\right|+{\mathbb{E}}_{D_p}\left|L\left(g,Z\right)-L\left(f,Z\right)\right|+{\mathbb{E}}_{D_s}\left|L\left(f,Z\right)-L\left(g,Z\right)\right|\\ =\left|\widehat{\mathbb{E}}L\left(g,Z\right)-\mathbb{E}L\left(g,Z\right)\right|+2{\mathbb{E}}_{D^{\star }}\left|L\left(g,Z\right)-L\left(f,Z\right)\right|\\ \le \left|\widehat{\mathbb{E}}L\left(g,Z\right)-\mathbb{E}L\left(g,Z\right)\right|+2r.\end{array}$$

Applying the above relation in Line B.31 below, we have

$$\begin{array}{l}\mathbb{P}\left(\underset{f\in \mathcal{F}}{\sup }\left|\widehat{\mathbb{E}}L\left(f,Z\right)-\mathbb{E}L\left(f,Z\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right)\\ =\mathbb{P}\left(\exists f\in \mathcal{F}:\left|\widehat{\mathbb{E}}L\left(f,Z\right)-\mathbb{E}L\left(f,Z\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right)\\ \le \mathbb{P}\left(\exists gϵG_r:\left|\widehat{\mathbb{E}}L\left(g,Z\right)-\mathbb{E}L\left(g,Z\right)\right|+2r>B_{\mathrm{ind}}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right)\end{array}$$ (B.31)

$$\begin{array}{l}=\mathbb{P}\left(\bigcup _{gϵG_r}\left|\widehat{\mathbb{E}}L\left(g,Z\right)-\mathbb{E}L\left(g,Z\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}\right)\\ \le \sum _{gϵG_r}\mathbb{P}\left(\left|\widehat{\mathbb{E}}L\left(g,Z\right)-\mathbb{E}L\left(g,Z\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}\right)& \mathrm{from\; the\; Union\; bound}\\ \le \mathcal{N}\left(\mathcal{F},r\right)2\exp \left[-\frac{2n}{{\left(B_{\mathrm{ind}}\right)}^2}{\left\{B_{\mathrm{ind}}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}\right\}}^2\right]& \mathrm{from\; Hoeffding’s\; inequality}\end{array}$$ (B.32)

$$\begin{array}{l}=\delta .\end{array}$$ (B.33)

To apply Hoeffding’s inequality (Theorem 2 of Hoeffding, 1963) in Line B.32, above, we use the fact that L(g, Z) is bounded within an interval of length B_ind. ■

B.5.3. Proof of Eq B.23

Proof The proof for Eq B.23 is nearly identical to the proof for Eq B.22. Simply replacing L and B_ind respectively with $\tilde{L}$ and (2B_ref) in Eqs B.30–B.33 yields a valid proof for Eq B.23. ■

B.5.4. Proof of Eq B.24

Proof Let F_D denote the cumulative distribution function for a distribution D. Let ${\tilde{D}}_s$ be the distribution such that

$$F_{{\tilde{D}}_p}\left(Y=y,X_1=x_1,X_2=x_2\right)=F_{D_p}\left(Y=y,X_2=x_2\right)F_{D_p}\left(X_1=x_1\right).$$

Let ${\tilde{D}}_p$ be the distribution satisfying

$${\mathbb{P}}_{{\tilde{D}}_s}\left(Y=y,X_1=x_1,X_2=x_2\right)=\frac{1}{n\left(n-1\right)}\sum _{i=1}^n\sum _{j\ne 1}\mathbf{1}\left({\mathbf{y}}_{\left[j\right]}=y,X_{1\left[i,\cdot \right]}=x_1,X_{2\left[j,\cdot \right]}=x_2\right).$$

Let ${\tilde{D}}^{\star }$ be the uniform mixture of ${\tilde{D}}_p$ and ${\tilde{D}}_s$, as in Eq B.29. Replacing e_orig, ê_orig, D_p, D_s, and ${\tilde{D}}^{\star }$ respectively with e_switch, ê_switch, ${\tilde{D}}_p$, ${\tilde{D}}_s$, and ${\tilde{D}}^{\star }$, we can follow the same steps as in the proof for Eq B.22. For any $f\in \mathcal{F}$, we know that there exists a function $g\in {\mathcal{G}}_r$ satisfying ${\mathbb{E}}_{{\tilde{D}}^{\star }}|L(g,Z)-L(f,Z)|\le r,$ which implies

$$\begin{array}{l}\left|{\widehat{e}}_{\mathrm{switch}}\left(f\right)-e_{\mathrm{switch}}\left(f\right)\right|=\left|{\widehat{e}}_{\mathrm{switch}}\left(f\right)-e_{\mathrm{switch}}\left(f\right)+\left\{{\widehat{e}}_{\mathrm{switch}}\left(g\right)-{\widehat{e}}_{\mathrm{switch}}\left(g\right)\right\}+\left\{e_{\mathrm{switch}}\left(g\right)-e_{\mathrm{switch}}\left(g\right)\right\}\right|\\ \le \left|{\widehat{e}}_{\mathrm{switch}}\left(g\right)-e_{\mathrm{switch}}\left(g\right)\right|+{\mathbb{E}}_{{\tilde{D}}_p}\left|L\left(g,Z\right)-L\left(f,Z\right)\right|+{\mathbb{E}}_{{\tilde{D}}_s}\left|L\left(f,Z\right)-L\left(g,Z\right)\right|\\ =\left|{\widehat{e}}_{\mathrm{switch}}\left(g\right)-e_{\mathrm{switch}}\left(g\right)\right|+2{\mathbb{E}}_{{\tilde{D}}^{\star }}\left|L\left(g,Z\right)-L\left(f,Z\right)\right|\\ \le \left|{\widehat{e}}_{\mathrm{switch}}\left(g\right)-e_{\mathrm{switch}}\left(g\right)\right|+2r.\end{array}$$

As a result,

$$\begin{array}{l}\mathbb{P}\left(\underset{f\in \mathcal{F}}{\sup }\left|{\widehat{e}}_{\mathrm{switch}}\left(f\right)-e_{\mathrm{switch}}\left(f\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{n}}+2r\right)\\ \le \mathbb{P}\left(\exists g\in {\mathcal{G}}_r:\left|{\widehat{e}}_{\mathrm{switch}}\left(g\right)-e_{\mathrm{switch}}\left(g\right)\right|+2r>B_{\mathrm{ind}}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{n}}+2r\right)\\ \le \sum _{g\in {\mathcal{G}}_r}\mathbb{P}\left(\left|{\widehat{e}}_{\mathrm{switch}}\left(g\right)-e_{\mathrm{switch}}\left(g\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{n}}\right)\\ \le \mathcal{N}\left(\mathcal{F},r\right)2\exp \left[-\frac{n}{{\left(B_{\mathrm{ind}}-0\right)}^2}{\left\{B_{\mathrm{ind}}\sqrt{\frac{\log \left(2{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{n}}\right\}}^2\right]\\ =\delta .\end{array}$$ (B.34)

In Line B.34, above, we apply Eq 5.7 of Hoeffding, 1963 (see also Eq 1 on page 201 of Serfling, 1980, in Theorem A), in the same way as in Eq B.15. ■

B.5.5. Proof for Eq B.25

Proof We apply Lemma 24 and Eq B.27 in Line B.36, below, to obtain

$$\begin{array}{l}\mathbb{P}\left[\underset{f\in \mathcal{F}}{\sup }\left|\frac{{\widehat{e}}_{\mathrm{orig}}\left(f\right)}{{\widehat{e}}_{\mathrm{switch}}\left(f\right)}-\frac{e_{\mathrm{orig}}\left(f\right)}{e_{\mathrm{switch}}\left(f\right)}\right|>{\mathcal{Q}}_4\right]\end{array}$$ (B.35)

$$\begin{array}{l}=\mathbb{P}\left(\exists f\in \mathcal{F}:\left|\frac{{\widehat{e}}_{\mathrm{orig}}\left(f\right)}{{\widehat{e}}_{\mathrm{switch}}\left(f\right)}-\frac{e_{\mathrm{orig}}\left(f\right)}{e_{\mathrm{switch}}\left(f\right)}\right|>{\mathcal{Q}}_4\right)\end{array}$$

$$\begin{array}{l}\le \mathbb{P}(\left\{\exists f\in \mathcal{F}:\left|{\widehat{e}}_{\mathrm{orig}}\left(f\right)-e_{\mathrm{orig}}\left(f\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right\}\end{array}$$ (B.36)

$$\begin{array}{l}\bigcup \left\{\exists f\in \mathcal{F}:\left|{\widehat{e}}_{\mathrm{switch}}\left(f\right)-e_{\mathrm{switch}}\left(f\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\sqrt{2}\right)\right)}{n}}+2r\sqrt{2}\right\})\end{array}$$

$$\begin{array}{l}=\mathbb{P}\left(\underset{f\in \mathcal{F}}{\sup }\left|{\widehat{e}}_{\mathrm{orig}}\left(f\right)-e_{\mathrm{orig}}\left(f\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right)\\ +\mathbb{P}(\underset{f\in \mathcal{F}}{\sup }\left|{\widehat{e}}_{\mathrm{switch}}\left(f\right)-e_{\mathrm{switch}}\left(f\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\sqrt{2}\right)\right)}{n}}+2r\sqrt{2})\end{array}$$

$$\begin{array}{ll}\le \frac{\delta }{2}+\frac{\delta }{2}.& \mathrm{from\; Eqs\; B.22\; and\; B.24}\end{array}$$ (B.37)

■

B.5.6. Proof for Eq B.26

Proof Finally, to show B.26, we apply the same steps as in Eqs B.35 through B.37. We apply Eq B.28 & Lemma 24 to obtain

$$\begin{array}{l}\mathbb{P}\left[\underset{f\in \mathcal{F}}{\sup }\left|\left\{{\widehat{e}}_{\mathrm{switch}}\left(f\right)-{\widehat{e}}_{\mathrm{orig}}\left(f\right)\right\}-\left\{e_{\mathrm{switch}}\left(f\right)-e_{\mathrm{orig}}\left(f\right)\right\}\right|>{\mathcal{Q}}_{4,\mathrm{difference}}\right]\\ \le \mathbb{P}(\left\{\exists f\in \mathcal{F}:\left|{\widehat{e}}_{\mathrm{orig}}\left(f\right)-e_{\mathrm{orig}}\left(f\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right\}\\ \bigcup \left\{\exists f\in \mathcal{F}:\left|{\widehat{e}}_{\mathrm{switch}}\left(f\right)-e_{\mathrm{switch}}\left(f\right)\right|>B_{\mathrm{ind}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\sqrt{2}\right)\right)}{2n}}+2r\sqrt{2}\right\})\\ \le \frac{\delta }{2}+\frac{\delta }{2}.\end{array}$$

■

B.5.7. Implementing Theorem 25 to Show Theorem 6

Proof Consider the event that

$$\exists {\widehat{f}}_{+,{ϵ}_{in}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{in}\right)}{\mathrm{arg\; max}}\widehat{MR}\left(f\right)\mathrm{such\; that}MC{R}_{+}\left(ϵ\right)<MR\left({\widehat{f}}_{+,{ϵ}_{in}}\right).$$ (B.38)

A brief outline of our proof for Eq 4.6 is as follows. We expect Eq B.38 to be unlikely due to the fact that ϵ_in < ϵ. If Eq B.38 does not hold, then the only way that ${\mathit{MCR}}_{+}(ϵ)<{\widehat{MCR}}_{+}({ϵ}_{\mathrm{in}})-{\mathcal{Q}}_{\mathrm{in}}$ holds is if there exists ${\widehat{f}}_{+,ϵin}\in {\text{arg max}}_{f\in \widehat{\mathcal{R}}({ϵ}_{in})}\widehat{MR}(f)$ which has an empirical MR that differs from its population-level MR by at least ${\mathcal{Q}}_{\mathrm{in}}$.

To show that Eq B.38 is unlikely, we apply Theorem 25:

$$\begin{array}{l}\mathbb{P}\left(\exists {\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; max}}\widehat{MR}\left(f\right):MC{R}_{+}\left(ϵ\right)<MR\left({\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\right)\right)\\ \le \mathbb{P}\left(\exists f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right):MC{R}_{+}\left(ϵ\right)<MR\left(f\right)\right)\\ =\mathbb{P}\left(\exists f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)\backslash f_{\mathrm{ref}}:MC{R}_{+}\left(ϵ\right)<MR\left(f\right)\right)& \mathrm{by}MC{R}_{+}\left(ϵ\right)\ge MR\left(f_{\mathrm{ref}}\right)\\ \le \mathbb{P}\left(\exists f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)\backslash f_{\mathrm{ref}}:\mathbb{E}\tilde{L}\left(f,Z\right)>ϵ\right)& \mathrm{by}MC{R}_{+}\left(ϵ\right)\mathrm{Def}\\ =\mathbb{P}\left(\exists f\in \mathcal{F},\mathbb{E}\tilde{L}\left(f,Z\right)>ϵ:\widehat{\mathbb{E}}\tilde{L}\left(f,Z\right)\le {ϵ}_{\mathrm{in}}\right)& \mathrm{by}\widehat{\mathcal{R}}\left(ϵ\right)\mathrm{Def}\\ =\mathbb{P}(\exists f\in \mathcal{F},\mathbb{E}\tilde{L}\left(f,Z\right)>ϵ:\\ \widehat{\mathbb{E}}\tilde{L}\left(f,Z\right)-ϵ\le -2B_{\mathrm{ref}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}-2r)& \mathrm{by}{ϵ}_{\mathrm{in}}\mathrm{Def}\end{array}$$ (B.39)

$$\begin{array}{l}\le \mathbb{P}(\exists f\in \mathcal{F},\mathbb{E}\tilde{L}\left(f,Z\right)>ϵ:\\ \widehat{\mathbb{E}}\tilde{L}\left(f,Z\right)-\mathbb{E}\tilde{L}\left(f,Z\right)\le -2B_{\mathrm{ref}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}-2r)\\ \le \mathbb{P}\left(\underset{f\in \mathcal{F}}{\sup }\left|\widehat{\mathbb{E}}\tilde{L}\left(f,Z\right)-\mathbb{E}\tilde{L}\left(f,Z\right)\right|\ge 2B_{\mathrm{ref}}\sqrt{\frac{\log \left(4{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right)\\ =\frac{\delta }{2}& \mathrm{by\; Thm}25.\end{array}$$ (B.40)

If Eq B.38 does not hold, we have

$$\begin{array}{ll}MC{R}_{+}\left(ϵ\right)\ge MR\left({\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\right)& \mathrm{for\; all}{\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\in \underset{fϵ\widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; max}}\widehat{MR}\left(f\right)\\ =\widehat{MR}\left({\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\right)-\left\{\widehat{MR}\left({\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\right)-MR\left({\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\right)\right\}& \mathrm{for\; all}{\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; max}}\widehat{MR}\left(f\right)\\ ={\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{in}}\right)-\left\{\widehat{MR}\left({\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\right)-MR\left({\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\right)\right\}& \mathrm{for\; all}{\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; max}}\widehat{MR}\left(f\right)\\ \ge {\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{in}}\right)-\underset{f\in \mathcal{F}}{\sup }\left|\widehat{MR}\left(f\right)-MR\left(f\right)\right|.\end{array}$$ (B.41)

Let q_ratio and q_difference be defined as in Lemma 24. Then

$$\begin{array}{l}{\mathcal{Q}}_{\mathrm{in}}=\frac{B_{\mathrm{switch}}}{b_{\mathrm{orig}}}-\frac{B_{\mathrm{switch}}-\left\{B_{\mathrm{ind}}\sqrt{\frac{\log \left(8{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\sqrt{2}\right)\right)}{n}}+2r\sqrt{2}\right\}}{b_{\mathrm{orig}}+\left\{B_{\mathrm{ind}}\sqrt{\frac{\log \left(8{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right\}}\\ =q_{\mathrm{ratio}}\left(B_{\mathrm{ind}}\sqrt{\frac{\log \left(8{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\sqrt{2}\right)\right)}{n}}+2r\sqrt{2},B_{\mathrm{ind}}\sqrt{\frac{\log \left(8{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right)\end{array}$$ (B.42)

Theorem 25 implies that the sup term in Eq B.41 is less than ${\mathcal{Q}}_{\mathrm{in}}$ with probability at least $1-\frac{\delta }{2}$. Now, examining the left-hand side of Eq 4.6, we see

$$\begin{array}{l}\mathbb{P}\left(MC{R}_{+}\left(ϵ\right)<{\widehat{MCR}}_{+}\left({ϵ}_{\mathrm{in}}\right)-{\mathcal{Q}}_{\mathrm{in}}\right)\\ \le \mathbb{P}[\left\{\exists {\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; max}}\widehat{MR}\left(f\right):MC{R}_{+}\left(ϵ\right)<MR\left({\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\right)\right\}\\ \bigcup \left\{\underset{f\in \mathcal{F}}{\sup }\left|\widehat{MR}\left(f\right)-MR\left(f\right)\right|>{\mathcal{Q}}_{\mathrm{in}}\right\}]& \mathrm{from\; Eq\; B.41}\\ \le \mathbb{P}\left[\exists {\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; max}}\widehat{MR}\left(f\right):MC{R}_{+}\left(ϵ\right)<MR\left({\widehat{f}}_{+,{ϵ}_{\mathrm{in}}}\right)\right]\\ +\mathbb{P}\left[\underset{f\in \mathcal{F}}{\sup }\left|\widehat{MR}\left(f\right)-MR\left(f\right)\right|>{\mathcal{Q}}_{\mathrm{in}}\right]& \mathrm{from\; the\; Union\; bound}\\ =\frac{\delta }{2}+\frac{\delta }{2}& \mathrm{from\; Eq\; B.40,\; Eq\; B.42,\; \&\; Theorem\; 25.}\end{array}$$ (B.43)

This completes the proof for Eq 4.6.

Alternatively, if we have defined model reliance as MR(f) = e_switch(f) − e_orig(f) (see Appendix A.5), with $\widehat{MR}(f)={\widehat{e}}_{\mathrm{switch}}(f)-{\widehat{e}}_{\mathrm{orig}}(f)$, and

$$\begin{array}{l}{\mathcal{Q}}_{\mathrm{in},\mathrm{difference}}=B_{\mathrm{ind}}\left\{\sqrt{\frac{\log \left(8{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\sqrt{2}\right)\right)}{n}}+\sqrt{\frac{\log \left(8{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}\right\}+2r\left(\sqrt{2}+1\right)\\ =q_{\mathrm{difference}}\left(B_{\mathrm{ind}}\sqrt{\frac{\log \left(8{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\sqrt{2}\right)\right)}{n}}+2r\sqrt{2},B_{\mathrm{ind}}\sqrt{\frac{\log \left(8{\delta }^{-1}\mathcal{N}\left(\mathcal{F},r\right)\right)}{2n}}+2r\right),\end{array}$$

then same proof of Eq 4.6 holds without Assumption 3 if we replace ${\mathcal{Q}}_{\mathrm{in}}$ with ${\mathcal{Q}}_{\mathrm{in},\mathrm{difference}}$, and apply Eq B.26 in Eq B.43.

For Eq 4.7 we can use the same approach. Consider the event that

$$\exists {\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; min}}\widehat{MR}\left(f\right):MC{R}_{-}\left(ϵ\right)>MR\left({\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\right).$$ (B.44)

Applying steps analogous to those used to derive Eq B.40, we have

$$\begin{array}{l}\mathbb{P}\left(\exists {\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; min}}\widehat{MR}\left(f\right):MC{R}_{-}\left(ϵ\right)>MR\left({\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\right)\right)\\ \le \mathbb{P}\left(\exists f\in \mathcal{F},\mathbb{E}\tilde{L}\left(f,Z\right)>ϵ:\widehat{\mathbb{E}}\tilde{L}\left(f,Z\right)\le {ϵ}_{\mathrm{in}}\right)\le \frac{\delta }{2}.\end{array}$$

Analogous to B.41, when Eq B.44 does not hold, we have have

$$\begin{array}{ll}MC{R}_{-}\left(ϵ\right)\le MR\left({\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\right)& \mathrm{for\; all}{\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; min}}\widehat{MR}\left(f\right)\\ =\widehat{MR}\left({\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\right)+\left\{MR\left({\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\right)-\widehat{MR}\left({\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\right)\right\}& \mathrm{for\; all}{\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; min}}\widehat{MR}\left(f\right)\\ ={\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{in}}\right)+\left\{MR\left({\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\right)-\widehat{MR}\left({\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\right)\right\}& \mathrm{for\; all}{\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; min}}\widehat{MR}\left(f\right)\\ \le {\widehat{MCR}}_{-}\left({ϵ}_{\mathrm{in}}\right)+\underset{f\in \mathcal{F}}{\sup }\left|MR\left(f\right)-\widehat{MR}\left(f\right)\right|\end{array}$$

Finally, analogous to Eq B.43,

$$\begin{array}{l}\mathbb{P}\left(MC{R}_{-}\left(ϵ\right)>\widehat{MCR}\left({ϵ}_{\mathrm{in}}\right)+{\mathcal{Q}}_{\mathrm{in}}\right)\\ \le \mathbb{P}[\left\{\exists {\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; min}}\widehat{MR}\left(f\right):MC{R}_{-}\left(ϵ\right)>MR\left({\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\right)\right\}\\ \bigcup \left\{\underset{f\in \mathcal{F}}{\sup }\left|\widehat{MR}\left(f\right)-MR\left(f\right)\right|>{\mathcal{Q}}_{\mathrm{in}}\right\}]\\ \le \mathbb{P}\left[\exists {\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\in \underset{f\in \widehat{\mathcal{R}}\left({ϵ}_{\mathrm{in}}\right)}{\mathrm{arg\; min}}\widehat{MR}\left(f\right):MC{R}_{-}\left(ϵ\right)>MR\left({\widehat{f}}_{-,{ϵ}_{\mathrm{in}}}\right)\right]\\ +\mathbb{P}\left[\underset{f\in \mathcal{F}}{\sup }\left|\widehat{MR}\left(f\right)-MR\left(f\right)\right|>{\mathcal{Q}}_{\mathrm{in}}\right]\\ =\frac{\delta }{2}+\frac{\delta }{2}.\end{array}$$ (B.45)

Under the difference-based definition of model reliance (see Appendix A.5), the same proof for Eq 4.7 holds without Assumption 3 if we replace MR, $\widehat{MR}$, & ${\mathcal{Q}}_{\mathrm{in}}$ respectively with MR_difference, ${\widehat{MR}}_{\mathrm{difference}}$, & ${\mathcal{Q}}_{\mathrm{in,difference}}$, and apply Eq B.26 in Eq B.45. ■

B.6. Proof of Proposition 7, and Corollary for a Unique Best-in-class Model.

We first introduce a lemma to describe the performance of any individual model in the population ϵ-Rashomon set.

Lemma 26 Let ${ϵ}_1^{\prime }:=2B_{ref}\sqrt{\frac{\log ({\delta }^{-1})}{2n}}$, and let the functions ${\widehat{\varphi }}_{-}$ and ${\widehat{\varphi }}_{+}$ be defined as in Proposition 7. Given a function $f_1\in \mathcal{R}(ϵ)$, if Assumption 2 holds for f₁, then

$$\mathbb{P}\left\{\varphi \left(f_1\right)\in \left[\widehat{\varphi }-\left({ϵ}_1^{\prime }\right),\widehat{\varphi }+\left({ϵ}_1^{\prime }\right)\right]\right\}\ge 1-\delta .$$

Proof Consider the event that

$$\varphi \left(f_1\right)\in \left[\widehat{\varphi }-\left({ϵ}_1^{\prime }\right),\widehat{\varphi }+\left({ϵ}_1^{\prime }\right)\right].$$ (B.46)

Eq B.46 will always hold if $f_1\in \widehat{\mathcal{R}}({ϵ}_1^{\prime })$, since the interval $\left[\widehat{\varphi }-\left({ϵ}_1^{\prime }\right),\widehat{\varphi }+\left({ϵ}_1^{\prime }\right)\right]$ contains ϕ(f) for any $f\in \widehat{\mathcal{R}}({ϵ}_1^{\prime })$ by definition. Thus,

$$\begin{array}{l}\mathbb{P}\left\{\varphi \left(f_1\right)\notin [\left[\widehat{\varphi }-\left({ϵ}_1^{\prime }\right),{\widehat{\varphi }}_{+}\left({ϵ}_1^{\prime }\right)\right]\right\}\le \mathbb{P}\left\{f_1\notin \widehat{\mathcal{R}}\left({ϵ}_1^{\prime }\right)\right\}\\ \le \delta & \mathrm{from\; Lemma\; 23.}\end{array}$$

■

B.6.1. Proof of Proposition 7

Proof Let $f_{-,ϵ,\varphi }\in {\mathrm{arg\; min}}_{f\in \mathcal{R}(ϵ)}\varphi (f)$ and $f_{+,ϵ,\varphi }\in {\mathrm{arg\; min}}_{f\in \mathcal{R}(ϵ)}\varphi (f)$ respectively denote functions that attain the lowest and highest values of ϕ(f) among models $f\in \mathcal{R}(ϵ)$. Applying the definitions of f_−,ϵ,ϕ and f_+,ϵ,ϕ in Line B.47, below, we have

$$\begin{array}{l}\mathbb{P}\left(\left\{\varphi \left(f\right):f\in \mathcal{R}\left(ϵ\right)\right\}\not\subset \left[{\widehat{\varphi }}_{-}\left({ϵ}^{\prime }\right),{\widehat{\varphi }}_{+}\left({ϵ}^{\prime }\right)\right]\right)\\ =\mathbb{P}\left(\left[\varphi \left(f_{-,ϵ,\varphi }\right),\varphi \left(f_{+,ϵ,\varphi }\right)\right]\not\subset \left[{\widehat{\varphi }}_{-}\left({ϵ}^{\prime }\right),{\widehat{\varphi }}_{+}\left({ϵ}^{\prime }\right)\right]\right)\\ =\mathbb{P}\left(\varphi \left(f_{-,ϵ,\varphi }\right)\notin \left[{\widehat{\varphi }}_{-}\left({ϵ}^{\prime }\right),{\widehat{\varphi }}_{+}\left({ϵ}^{\prime }\right)\right]\right)\bigcup \varphi \left(f_{+,ϵ,\varphi }\right)\notin \left[{\widehat{\varphi }}_{-}\left({ϵ}^{\prime }\right),{\widehat{\varphi }}_{+}\left({ϵ}^{\prime }\right)\right])\\ \le \mathbb{P}\left(\varphi \left(f_{-,ϵ,\varphi }\right)\notin \left[{\widehat{\varphi }}_{-}\left({ϵ}^{\prime }\right),{\widehat{\varphi }}_{+}\left({ϵ}^{\prime }\right)\right]\right)+\mathbb{P}\left(\varphi \left(f_{-,ϵ,\varphi }\right)\notin \left[{\widehat{\varphi }}_{-}\left({ϵ}^{\prime }\right),{\widehat{\varphi }}_{+}\left({ϵ}^{\prime }\right)\right]\right)\\ \le \frac{\delta }{2}+\frac{\delta }{2}=\delta \mathrm{from\; Lemma\; 26,\; and\; the\; definition\; of}{ϵ}^{\prime }=ϵ+2B_{\mathrm{ref}}\sqrt{\frac{\log \left(2{\delta }^{-1}\right)}{2n}}.\end{array}$$ (B.47)

■

B.6.2. Corollary for a Unique Best-in-Class Model

When the best-in-class model is unique, it can be described by the corollary below.

Corollary 27 Let ${\widehat{\varphi }}_{-}({ϵ}_0^{\prime }):={\min }_{f\in \widehat{\mathcal{R}}({ϵ}_1^{\prime })}\varphi (f)$ and ${\widehat{\varphi }}_{+}({ϵ}_1^{\prime }):={\max }_{f\in \widehat{\mathcal{R}}({ϵ}_1^{\prime })}\varphi (f)$, where ${ϵ}_0^{\prime }:=2B_{ref}\sqrt{\frac{\log ({\delta }^{-1})}{2n}}$. Let $f^{\star }\in {\mathrm{arg\; min}}_{f\in \mathcal{F}}{e}_{\mathit{orig}}(f)$ be the prediction model that uniquely attains the lowest possible expected loss. If f^⋆ satisfies Assumption 2, then

$$\mathbb{P}\left\{\varphi \left(f^{\star }\right)\in \left[{\widehat{\varphi }}_{-}\left({ϵ}_1^{\prime }\right),{\widehat{\varphi }}_{+}\left({ϵ}_1^{\prime }\right)\right]\right\}\ge 1-\delta .$$

Proof Since $f^{\star }\in \mathcal{R}(0)$, Corollary 27 follows immediately from Lemma 26.

Notice that by assuming f^⋆ is unique, we can use the threshold ${ϵ}_0^{\prime }:=2B_{\mathrm{ref}}\sqrt{\frac{\log ({\delta }^{-1})}{2n}}$, which is lower than the threshold of ${ϵ}^{\prime }=ϵ+2B_{\mathrm{ref}}\sqrt{\frac{\log (2{\delta }^{-1})}{2n}}$ with ϵ = 0, as in Proposition 7. In this way, assuming uniqueness allows a stronger statement than the one in Proposition 7. ■

B.7. Absolute Losses versus Relative Losses in the Definition of the Rashomon Set

In this paper we primarily define Rashomon sets as the models that perform well relative to a reference model f_ref. We can also study an alternate formulation of Rashomon sets by replacing the relative loss $\tilde{L}$ with the non-standardized loss L throughout. This results in a new interpretation of the Rashomon set $\mathcal{R}({ϵ}_{\mathrm{abs}},f_{\mathrm{ref}},\mathcal{F})=\{f_{\mathrm{ref}}\}\cup \{f\in \mathcal{F}:\mathbb{E}L(f,Z)\le {ϵ}_{\mathrm{abs}}\}$ as the union of f_ref and the subset of models with absolute loss L no higher than ϵ_abs, for ϵ_abs > 0. The process of computing empirical MCR is largely unaffected by whether L or $\tilde{L}$ is used, as it is simple to transform from one optimization problem to the other.

We still require the explicit inclusion of f_ref in empirical and population Rashomon sets to ensure that they are nonempty. However, in many cases, this inclusion becomes redundant when interpreting a Rashomon set (e.g., when ϵ ≥ 0, and $\mathbb{E}L(f_{\mathrm{ref}},Z)\le {ϵ}_{\mathrm{abs}}\}$.

Under the replacement of $\tilde{L}$ with L, we also replace Assumption 2 with Assumption 1 (whenever this is not redundant), and replace 2B_ref with B_ind in the definitions of ϵ_out, ϵ_best, ϵ_in, ϵ′ and ${ϵ}_1^{\prime }$ in Theorem 4, Corollary 22, Theorem 6, Proposition 7, and Corollary 27. This is because the motivation for the 2B_ref term is that $\tilde{L}(f_1)$ is bounded within an interval of length 2B_ref when f₁ satisfies Assumption 2. However, under Assumption 1, L(f₁) is bounded within an interval of length B_ind.

B.8. Proof of Proposition 15

Proof To show Eq 7.1 we start with e_orig(f_β),

$$\begin{array}{l}{e}_{\mathrm{orig}}(f_{\beta })=\mathbb{E}[{\{Y-X_1^{\prime }{\beta }_1-X_2^{\prime }{\beta }_2\}}^2]\\ =\mathbb{E}[{\{(Y-X_2^{\prime }{\beta }_2)-X_1^{\prime }{\beta }_1\}}^2]\\ =\mathbb{E}[{(Y-X_2^{\prime }{\beta }_2)}^2]-2\mathbb{E}[(Y-X_2^{\prime }{\beta }_2)X_1^{\prime }]{\beta }_1+{{\beta }^{\prime }}_{1}E[X_1{X}_1^{\prime }]{\beta }_1.\end{array}$$

For e_switch(f_β), we can follow the same steps as above:

$$\begin{array}{l}{e}_{\mathrm{switch}}(f_{\beta })={\mathbb{E}}_{Y^{(b)},X_1^{(a)},X_2^{(b)}}[{\{Y^{(b)}-X_1^{{(a)}^{\prime }}{\beta }_1-X_2^{{(b)}^{\prime }}{\beta }_2\}}^2]\\ =\mathbb{E}[{(Y^{(b)}-X_2^{{(b)}^{\prime }}{\beta }_2)}^2]-2\mathbb{E}[{(Y^{(b)}-X_2^{{(b)}^{\prime }}{\beta }_2)}^2]\mathbb{E}[X_1^{{(a)}^{\prime }}]{\beta }_1+{{\beta }^{\prime }}_1\mathbb{E}[X_1^{(a)}{X}_1^{{(a)}^{\prime }}]{\beta }_1.\end{array}$$

Since $(Y^{(b)},X_1^{(b)},X_2^{(b)})$ and $(Y^{(a)},X_1^{(a)},X_2^{(a)})$ each have the same distribution as (Y, X₁, X₂), we can omit the superscript notation to show Eq 7.1:

$$\begin{array}{l}{e}_{\mathrm{switch}}(f_{\beta })=\mathbb{E}[{(Y-X_2^{\prime }{\beta }_2)}^2]-2\mathbb{E}[Y-X_2^{\prime }{\beta }_2]\mathbb{E}[X_1^{\prime }]{\beta }_1+{\beta }_1^{\prime }\mathbb{E}[X_1{X}_1^{\prime }]{\beta }_1\\ e_{\mathrm{switch}}(f_{\beta })=e_{\mathrm{orig}}(f_{\beta })-2\mathbb{E}[Y-X_2^{\prime }{\beta }_2]\mathbb{E}[X_1^{\prime }]{\beta }_1+2\mathbb{E}[(Y-X_2^{\prime }{\beta }_2)X_1^{\prime }]{\beta }_1\\ e_{\mathrm{switch}}(f_{\beta })=e_{\mathrm{orig}}(f_{\beta })+2\mathrm{Cov}(Y-X_2^{\prime }{\beta }_2,X_1){\beta }_1\\ e_{\mathrm{switch}}(f_{\beta })=e_{\mathrm{orig}}(f_{\beta })+2\mathrm{Cov}(Y,X_1){\beta }_1-2{\beta }_2\mathrm{Cov}(X_2,X_1){\beta }_1.\end{array}$$

Dividing both sides by e_orig(f_β) gives the desired result.

Next, we can use a similar approach to show Eq 7.2:

$$\begin{array}{l}{\widehat{e}}_{\mathrm{switch}}\left(f_{\beta }\right)=\frac{1}{n\left(n-1\right)}\sum _{i=1}^n\sum _{j\ne 1}{\left({\mathbf{y}}_{\left[j\right]}-{\mathbf{X}}_{2\left[j,\cdot \right]}{\beta }_2-{\mathbf{X}}_{1\left[i,\cdot \right]}{\beta }_1\right)}^2\\ n\left(n-1\right){\widehat{e}}_{\mathrm{switch}}\left(f_{\beta }\right)=\sum _{i=1}^n\sum _{j\ne i}\left\{{\left({\mathbf{y}}_{\left[j\right]}-{\mathbf{X}}_{2\left[j,\cdot \right]}{\beta }_2\right)}^2-2\left({\mathbf{y}}_{\left[j\right]}-{\mathbf{X}}_{2\left[j,\cdot \right]}{\beta }_2\right)\left({\mathbf{X}}_{1\left[i,\cdot \right]}{\beta }_1\right)+{\left({\mathbf{X}}_{1\left[i,\cdot \right]}{\beta }_1\right)}^2\right\}\\ =\left(n-1\right){\sum _{i=1}^n\left({\mathbf{y}}_{\left[i\right]}-{\mathbf{X}}_{2\left[i,\cdot \right]}{\beta }_2\right)}^2\\ -2\left\{\sum _{i=1}^n\sum _{j\ne i}\left({\mathbf{X}}_{1\left[i,\cdot \right]}{\beta }_1\right)\left({\mathbf{y}}_{\left[j\right]}-X_{2\left[j,\cdot \right]}{\beta }_2\right)\right\}+\left(n-1\right){\sum _{i=1}^n\left(X_{1\left[i,\cdot \right]}{\beta }_1\right)}^2.\end{array}$$ (B.48)

Focusing on the term in braces,

$$\begin{array}{l}\sum _{i=1}^n\sum _{j\ne i}\left(X_{1\left[i,\cdot \right]}{\beta }_1\right)\left({\mathbf{y}}_{\left[j\right]}-X_{2\left[j,\cdot \right]}{\beta }_2\right)\\ =\sum _{i=1}^n\sum _{j=1}^n\left(X_{1\left[i,\cdot \right]}{\beta }_1\right)\left({\mathbf{y}}_{\left[j\right]}-X_{2\left[j,\cdot \right]}{\beta }_2\right)-\sum _{i=1}^n\left(X_{1\left[i,\cdot \right]}{\beta }_1\right)\left({\mathbf{y}}_{\left[j\right]}-X_{2\left[j,\cdot \right]}{\beta }_2\right)\\ =\sum _{i=1}^n\left(X_{1\left[i,\cdot \right]}{\beta }_1\right)\sum _{j=1}^n\left({\mathbf{y}}_{\left[j\right]}-X_{2\left[j,\cdot \right]}{\beta }_2\right)-\sum _{i=1}^n\left(X_{1\left[i,\cdot \right]}{\beta }_1\right)\left({\mathbf{y}}_{\left[j\right]}-X_{2\left[j,\cdot \right]}{\beta }_2\right)\\ =\left\{{\left(X_1{\beta }_1\right)}^{\prime }{\mathbf{1}}_n\right\}\left\{{\mathbf{1}}_n^{\prime }\left(\mathbf{y}-X_2{\beta }_2\right)\right\}-{\left(X_1{\beta }_1\right)}^{\prime }\left(\mathbf{y}-X_2{\beta }_2\right)\\ ={\left(X_1{\beta }_1\right)}^{\prime }\left({\mathbf{1}}_n{\mathbf{1}}_n^{\prime }-{\mathbf{I}}_n\right)\left(\mathbf{y}-X_2{\beta }_2\right).\end{array}$$ (B.49)

Plugging this into Eq B.48, and applying the sample linear algebra representations as in Eq B.49, we get

$$\begin{array}{l}n\left(n-1\right){\widehat{e}}_{\mathrm{switch}}\left(f_{\beta }\right)=\left(n-1\right){\Vert \mathbf{y}-X_2{\beta }_2\Vert }_2^2\\ -2{\left(X_1{\beta }_1\right)}^{\prime }\left({\mathbf{1}}_n{\mathbf{1}}_n^{\prime }-{\mathbf{I}}_n\right)\left(\mathbf{y}-X_2{\beta }_2\right)\\ +\left(n-1\right){\Vert X_1{\beta }_1\Vert }_2^2\\ n{\widehat{e}}_{\mathrm{switch}}\left(f_{\beta }\right)={\Vert \mathbf{y}-X_2{\beta }_2\Vert }_2^2\\ -2{\left(X_1{\beta }_1\right)}^{\prime }W\left(\mathbf{y}-X_2{\beta }_2\right)\\ +{\Vert X_1{\beta }_1\Vert }_2^2\\ ={\mathbf{y}}^{\prime }\mathbf{y}-2{\mathbf{y}}^{\prime }{X}_2{\beta }_2+{\beta }_2^{\prime }{X}_2^{\prime }{X}_2{\beta }_2\\ -2{\beta }_1^{\prime }{X}_1^{\prime }{W}_{\mathbf{y}}+2{\beta }_1^{\prime }{X}_1^{\prime }W{X}_2{\beta }_2\\ +{\beta }_1^{\prime }{X}_1^{\prime }{X}_1{\beta }_1\\ ={\mathbf{y}}^{\prime }\mathbf{y}-2{\left[\begin{array}{c}{X}_1^{\prime }{W}_{\mathbf{y}}\\ X_2^{\prime }\mathbf{y}\end{array}\right]}^{\prime }\beta +{\beta }^{\prime }\left[\begin{array}{cc}{X}_1^{\prime }{X}_1& X_1^{\prime }W{X}_2\\ X_2^{\prime }W{X}_1& X_2^{\prime }{X}_2\end{array}\right]\beta .\end{array}$$

■

B.9. Proof of Proposition 19

Proof First we consider e_orig(f₀). We briefly recall that the notation f₀(t, c) refers to the true conditional expectation function for both potential outcomes Y₁, Y₀, rather than the expectation for Y₀ alone.

Under the assumption that (Y₁, Y₀) ⊥ T|C, we have $f_0(t,c)=\mathbb{E}(Y|C=c,T=t)=\mathbb{E}(Y_t|C=c)$. Applying this, we see that

$$\begin{array}{l}{e}_{\mathrm{orig}}\left(f_0\right)=\mathbb{E}L\left(f_0,\left(Y,T,C\right)\right)\\ =\mathbb{E}L\left(f_0,\left(Y_T,T,C\right)\right)\\ ={\mathbb{E}}_T{\mathbb{E}}_{C|T}{\mathbb{E}}_{Y_T|C}[{\left\{Y_T-\mathbb{E}\left(Y_T|C\right)\right\}}^2]\\ ={\mathbb{E}}_T{\mathbb{E}}_{C|T}\mathrm{Var}\left(Y_T|C\right)\\ =q{\mathbb{E}}_{C|T=0}\mathrm{Var}\left(Y_0|C\right)+p{\mathbb{E}}_{C|T=1}\mathrm{Var}\left(Y_1|C\right),\end{array}$$ (B.50)

where $p:=\mathbb{P}(T=1)$ and $q:=\mathbb{P}(T=0)$.

Now we consider e_switch(f₀). Let $(Y_0^{(a)},Y_1^{(a)},T^{(a)},C^{(a)})$ and $(Y_0^{(b)},Y_1^{(b)},T^{(b)},C^{(b)})$ be a pair of independent random variable vectors, each with the same distribution as (Y₀, Y₁, T, C). Then

$$\begin{array}{l}{e}_{\mathrm{switch}}(f_0)={\mathbb{E}}_{T^{(b)},T^{(a)},C^{(b)},Y_{T^{(b)}}^{(b)}}[{\{Y_{T^{(a)}}^{(b)}-f_0(T^{(a)},C^{(b)})\}}^2]\\ ={\mathbb{E}}_{T^{(b)},T^{(a)},C^{(b)},Y_{T^{(b)}}^{(b)}}[{\{Y_{T^{(b)}}^{(b)}-\mathbb{E}(Y_{T^{(a)}}|C=C^{(b)})\}}^2]\\ ={\mathbb{E}}_{T^{(b)},T^{(a)}}{\mathbb{E}}_{C^{(b)}|T^{(b)}}{\mathbb{E}}_{Y_{T^{(b)}}^{(b)}|C^{(b)}}[{\{Y_{T^{(b)}}^{(b)}-\mathbb{E}(Y_{T^{(a)}}|C=C^{(b)})\}}^2].\end{array}$$

First we expand the outermost expectation, over T^(b), T^(a):

$$\begin{array}{l}{e}_{\mathrm{switch}}(f_0)\\ =\sum _{i,iϵ\{0,1\}}\mathbb{P}(T^{(b)}=i,T^{(a)}=j){\mathbb{E}}_{C^{(b)}|T^{(b)}=i}{\mathbb{E}}_{Y_i^{(b)}|C^{(b)}}[{\{Y_i^{(b)}-\mathbb{E}(Y_j|C=C^{(b)})\}}^2].\end{array}$$ (B.51)

Since T^(b) ⊥ T^(a), we can write

$$\begin{array}{l}\mathbb{P}(T^{(b)}=i,T^{(a)}=j)=\mathbb{P}(T^{(b)}=i)\mathbb{P}(T^{(a)}=j)\\ =p^{i+j}{q}^{2-i-j}.\end{array}$$

Plugging this into Eq B.51 we get

$$e_{\mathrm{switch}}(f_0)=\sum _{i,jϵ\{0,1\}}{p}^{i+j}{q}^{2-i-j}{\mathbb{E}}_{C^{(b)}|T^{(b)}=i}{\mathbb{E}}_{Y_i^{(b)}|C^{(b)}}[{\{Y_i^{(b)}-\mathbb{E}(Y_j|C=C^{(b)})\}}^2].$$

Since $(Y_0^{(b)},Y_1^{(b)},C^{(b)},T^{(b)})$ are the only random variables remaining, we can omit the superscript notation (e.g., replace C^(b) with C) to get

$$\begin{array}{l}{e}_{\mathrm{switch}}\left(f_0\right)=\sum _{i,jϵ\left\{0,1\right\}}{p}^{i+j}{q}^{2-i-j}{\mathbb{E}}_{C|T=i}{\mathbb{E}}_{Y_i|C}[{\left\{Y_i-\mathbb{E}\left(Y_i|C\right)\right\}}^2]\\ =:\sum _{i,jϵ\left\{0,1\right\}}{A}_{ij},\end{array}$$

where $A_{ij}=p^{i+j}{q}^{2-i-j}{\mathbb{E}}_{C|T=i}{\mathbb{E}}_{Y_i|C}[{\{Y_i-\mathbb{E}(Y_j|C)\}}^2]$. First, we consider A₀₀ and A₁₁:

$$\begin{array}{l}{A}_{00}=q^2{\mathbb{E}}_{C|T=0}{\mathbb{E}}_{Y_0|C}[{\left\{Y_0-\mathbb{E}\left(Y_0|C\right)\right\}}^2]\\ =q^2{\mathbb{E}}_{C|T=0}\mathrm{Var}\left(Y_0|C\right),\end{array}$$

and, similarly, $A_{11}=p^2{\mathbb{E}}_{C|T=1}\mathrm{Var}(Y_1|C)$.

Next we consider A₀₁ and A₁₀:

$$\begin{array}{l}{A}_{01}:=pq{\mathbb{E}}_{C|T=0}{\mathbb{E}}_{Y_0|C}[{\left\{Y_0-\mathbb{E}\left(Y_1|C\right)\right\}}^2]\\ =pq{\mathbb{E}}_{C|T=0}\left(\mathbb{E}\left(Y_0^2|C\right)-2\mathbb{E}\left(Y_0|C\right)\mathbb{E}\left(Y_1|C\right)+\mathbb{E}{\left(Y_1|C\right)}^2\right)\\ =pq{\mathbb{E}}_{C|T=0}\left(\mathrm{Var}\left(Y_0|C\right)+\mathbb{E}{\left(Y_0|C\right)}^2-2\mathbb{E}\left(Y_0|C\right)\mathbb{E}\left(Y_1|C\right)+\mathbb{E}{\left(Y_1|C\right)}^2\right)\\ =pq{\mathbb{E}}_{C|T=0}\left(\mathrm{Var}\left(Y_0|C\right)+{\left[\mathbb{E}\left(Y_1|C\right)-\mathbb{E}\left(Y_0|C\right)\right]}^2\right)\\ =pq{\mathbb{E}}_{C|T=0}\left(\mathrm{Var}\left(Y_0|C\right)+\mathrm{CATE}{\left(C\right)}^2\right),\end{array}$$

and, following the same steps,

$$A_{10}=pq{\mathbb{E}}_{C|T=1}\left(\mathrm{Var}\left(Y_1|C\right)+\mathrm{CATE}{\left(C\right)}^2\right).$$

Plugging in A₀₀, A₀₁, A₁₀, and A₁₁ we get

$$\begin{array}{l}{e}_{\mathrm{switch}}\left(f_0\right)=\left\{A_{00}+A_{11}\right\}\\ +\left[A_{01}+A_{10}\right]\\ =\left\{q^2{\mathbb{E}}_{C|T=0}\mathrm{Var}\left(Y_0|C\right)+p^2{\mathbb{E}}_{C|T=1}\mathrm{Var}\left(Y_1|C\right)\right\}\\ +\left[pq{\mathbb{E}}_{C|T=0}\left(\mathrm{Var}\left(Y_0|C\right)+\mathrm{CATE}{\left(C\right)}^2\right)+pq{\mathbb{E}}_{C|T=1}\left(\mathrm{Var}\left(Y_0|C\right)+\mathrm{CATE}{\left(C\right)}^2\right)\right]\end{array}$$

$$\begin{array}{l}=\left\{q\left(q+p\right){\mathbb{E}}_{C|T=0}\mathrm{Var}\left(Y_0|C\right)+p\left(p+q\right){\mathbb{E}}_{C|T=1}\mathrm{Var}\left(Y_1|C\right)\right\}\end{array}$$ (B.52)

$$\begin{array}{l}+pq\left[{\mathbb{E}}_{C|T=0}\left(\mathrm{CATE}{\left(C\right)}^2\right)+{\mathbb{E}}_{C|T=1}\left(\mathrm{CATE}{\left(C\right)}^2\right)\right]\end{array}$$ (B.53)

$$\begin{array}{l}=\left\{e_{\mathrm{orig}}\left(f_0\right)\right\}\end{array}$$ (B.54)

$$\begin{array}{l}+\mathrm{Var}\left(T\right)\left[{\mathbb{E}}_{C|T=0}\left(\mathrm{CATE}{\left(C\right)}^2\right)+{\mathbb{E}}_{C|T=1}\left(\mathrm{CATE}{\left(C\right)}^2\right)\right].\end{array}$$ (B.55)

In Lines B.52 and B.53, we consolidate terms involving ${\mathbb{E}}_{C|T=0}\mathrm{Var}\left(Y_0|C\right)$ and ${\mathbb{E}}_{C|T=1}\mathrm{Var}\left(Y_1|C\right)$. In Line B.54, we use p+q = 1 to reduce Line B.52 to the right-hand side of Eq B.50. Finally, in Line B.55, we use qp = Var(T). Dividing both sides by $e_{\mathrm{orig}}\left(f_0\right)={\mathbb{E}}_{T,C}\mathit{Var}\left(Y|T,C\right)$ gives the desired result. ■

Appendix C. Proofs for Computational Results

Almost all of the proofs in this section are unchanged if we replace ê_switch (f) with ê_divide(f) in our definitions of ĥ_−,γ, ĥ_+,γ, ĝ_−,γ, ĝ_+,γ, and $\widehat{MR}$. The only exception is in Appendix C.3.

Throughout the following proofs, we will make use of the fact that, for constants $a,b,c,d\in \mathbb{R}$ satisfying a ≥ c, the relation a + b ≤ c + d implies

$$\begin{array}{l}a+b\le c+d\\ a-c\le d-b\\ 0\le d-b\mathrm{since}0\le a-c\\ b\le d.\end{array}$$ (C.1)

We also make use of the fact that for any ${\gamma }_1,{\gamma }_2\in \mathbb{R}$, the definitions of ĝ_+,γ1 and ĝ_−,γ1 imply

$${\widehat{h}}_{+,{\gamma }_1}\left({\widehat{g}}_{+,{\gamma }_1}\right)\le {\widehat{h}}_{+,{\gamma }_1}\left({\widehat{g}}_{+,{\gamma }_2}\right),\mathrm{and}{\widehat{h}}_{-,{\gamma }_1}\left(g_{-,{\gamma }_1}\right)\le {\widehat{h}}_{-,{\gamma }_1}\left(g_{-,{\gamma }_2}\right).$$ (C.2)

Finally, for any two values ${\gamma }_1,{\gamma }_2\in \mathbb{R}$, we make use of the fact that

$$\begin{array}{l}{\widehat{h}}_{+,{\gamma }_1}\left(f\right)={\widehat{e}}_{\mathrm{orig}}\left(f\right)+{\gamma }_1{\widehat{e}}_{\mathrm{switch}}\left(f\right)\\ ={\widehat{e}}_{\mathrm{orig}}\left(f\right)+{\gamma }_2{\widehat{e}}_{\mathrm{switch}}\left(f\right)+\left\{{\gamma }_1{\widehat{e}}_{\mathrm{switch}}\left(f\right)-{\gamma }_2{\widehat{e}}_{\mathrm{switch}}\left(f\right)\right\}\\ ={\widehat{h}}_{+,{\gamma }_2}\left(f\right)+\left({\gamma }_1-{\gamma }_2\right){\widehat{e}}_{\mathrm{switch}}\left(f\right),\end{array}$$ (C.3)

and, by the same steps,

$${\widehat{h}}_{-,{\gamma }_1}\left(f\right)={\widehat{h}}_{-,{\gamma }_2}\left(f\right)+\left({\gamma }_1-{\gamma }_2\right){\widehat{e}}_{\mathrm{orig}}\left(f\right).$$ (C.4)

C.1. Proof of Lemma 9 (Lower Bound for MR)

Proof We prove Lemma 9 in 2 parts.

C.1.1. Part 1: Showing Eq 6.1 Holds for All $f\in \mathcal{F}$ Satisfying ê_orig(f) ≤ ϵ_abs.

If ĥ_−,γ (ĝ_−,γ) ≥ 0, then for any function $f\in \mathcal{F}$ satisfying ê_orig(f) ≤ ϵ_abs we know that

$$\begin{array}{c}\frac{1}{{ϵ}_{\mathrm{abs}}}\le \frac{1}{{\widehat{e}}_{\mathrm{orig}}\left(f\right)}\\ \frac{{\widehat{h}}_{-,\gamma }\left({\widehat{g}}_{-,\gamma }\right)}{{ϵ}_{\mathrm{abs}}}\le \frac{{\widehat{h}}_{-,\gamma }\left({\widehat{g}}_{-,\gamma }\right)}{{\widehat{e}}_{\mathrm{orig}}\left(f\right)}.\end{array}$$ (C.5)

Now, for any $f\in \mathcal{F}$ satisfying ê_orig(f) ≤ ϵ_abs, the definition of ĝ_−,γ implies that

$$\begin{array}{l}{\widehat{h}}_{-,\gamma }\left(f\right)\ge {\widehat{h}}_{-,\gamma }\left({\widehat{g}}_{-,\gamma }\right)\\ \gamma {\widehat{e}}_{\mathrm{orig}}\left(f\right)+{\widehat{e}}_{\mathrm{switch}}\left(f\right)\ge {\widehat{h}}_{-,\gamma }\left({\widehat{g}}_{-,\gamma }\right)\\ \gamma +\frac{{\widehat{e}}_{\mathrm{switch}}\left(f\right)}{{\widehat{e}}_{\mathrm{orig}}\left(f\right)}\ge \frac{{\widehat{h}}_{-,\gamma }\left({\widehat{g}}_{-,\gamma }\right)}{{\widehat{e}}_{\mathrm{orig}}\left(f\right)}\\ \gamma +\frac{{\widehat{e}}_{\mathrm{switch}}\left(f\right)}{{\widehat{e}}_{\mathrm{orig}}\left(f\right)}\ge \frac{{\widehat{h}}_{-,\gamma }\left({\widehat{g}}_{-,\gamma }\right)}{{ϵ}_{\mathrm{abs}}}& \mathrm{from\; Eq\; C.5}\\ \widehat{MR}\left(f\right)\ge \frac{{\widehat{h}}_{-,\gamma }\left({\widehat{g}}_{-,\gamma }\right)}{{ϵ}_{\mathrm{abs}}}-\gamma .\end{array}$$

C.1.2. Part 2: Showing that, if $f={\widehat{g}}_{-,\gamma }$, and at Least One of the Inequalities in Condition 8 Holds with Equality, then Eq 6.1 Holds with Equality.

We consider each of the two inequalities in Condition 8 separately. If ${\widehat{h}}_{-,\gamma }\left({\widehat{g}}_{-,\gamma }\right)=0$, then

$$\begin{array}{l}0=\gamma {\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,\gamma })+{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{-,\gamma })\\ \frac{-{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{-,\gamma })}{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,\gamma })}=\gamma .\end{array}$$

As a result

$$\frac{{\widehat{h}}_{-,\gamma }({\widehat{g}}_{-,\gamma })}{{ϵ}_{\mathrm{abs}}}-\gamma =\frac{0}{{ϵ}_{\mathrm{abs}}}-\left\{\frac{-{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{-,\gamma })}{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,\gamma })}\right\}=\widehat{\mathit{MR}}({\widehat{g}}_{-,\gamma }).$$

Alternatively, if ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{-,\gamma }\right)={ϵ}_{\mathrm{abs}}$, then

$$\frac{{\widehat{h}}_{-,\gamma }({\widehat{g}}_{-,\gamma })}{{ϵ}_{\mathrm{abs}}}-\gamma =\frac{\gamma {\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,\gamma })+{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{-,\gamma })}{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,\gamma })}-\gamma =\gamma +\frac{{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{-,\gamma })}{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,\gamma })}-\gamma =\widehat{\mathit{MR}}({\widehat{g}}_{-,\gamma }).$$

■

C.2. Proof of Lemma 10 (Monotonicity for MR Lower Bound Binary Search)

Proof We prove Lemma 10 in 3 parts.

C.2.1. Part 1: ${\widehat{h}}_{-,\gamma }\left({\widehat{g}}_{-,\gamma }\right)$ is Monotonically Increasing in γ.

Let ${\gamma }_1,{\gamma }_2\in \mathbb{R}$ satisfy γ₁ < γ₂. We have assumed that $0<{\widehat{e}}_{\mathrm{orig}}\left(f\right)$ for any $f\in \mathcal{F}$. Thus, for any $f\in \mathcal{F}$ we have

$$\begin{array}{c}{\gamma }_1{\widehat{e}}_{\mathrm{orig}}(f)+{\widehat{e}}_{\mathrm{switch}}(f)<{\gamma }_2{\widehat{e}}_{\mathrm{orig}}(f)+{\widehat{e}}_{\mathrm{switch}}(f)\\ \widehat{h}-,{\gamma }_1(f)<\widehat{h}-,{\gamma }_2(f).\end{array}$$ (C.6)

Applying this, we have

$$\begin{array}{ll}\hfill {\widehat{h}}_{-},{\gamma }_1({\widehat{g}}_{-},{\gamma }_1)\le {\widehat{h}}_{-},{\gamma }_1({\widehat{g}}_{-},{\gamma }_2)& \mathrm{from\; Eq\; C.2}\\ \hfill \le {\widehat{h}}_{-},{\gamma }_2({\widehat{g}}_{-},{\gamma }_2)& \mathrm{from\; Eq\; C.6.}\end{array}$$

This result is analogous to Lemma 3 from Dinkelbach (1967).

C.2.2. Part 2: ${\widehat{e}}_{\mathrm{ORIG}}\left({\widehat{g}}_{-,\gamma }\right)$ is Monotonically Decreasing in γ.

Let ${\gamma }_1,{\gamma }_2\in \mathbb{R}$ satisfy γ₁ < γ₂. Then

$$\begin{array}{cc}{\widehat{h}}_{-,{\gamma }_1}({\widehat{g}}_{-,{\gamma }_1})\le {\widehat{h}}_{-,{\gamma }_1}({\widehat{g}}_{-,{\gamma }_2})& \mathrm{from\; Eq\; C.2}\hfill \\ {\widehat{h}}_{-,{\gamma }_2}({\widehat{g}}_{-,{\gamma }_1})+({\gamma }_1-{\gamma }_2){\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_1})\le {\widehat{h}}_{-,{\gamma }_2}({\widehat{g}}_{-,{\gamma }_2})+({\gamma }_1-{\gamma }_2){\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_2})& \mathrm{from\; Eq\; C.4}\hfill \\ ({\gamma }_1-{\gamma }_2){\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_1})\le ({\gamma }_1-{\gamma }_2){\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_2})& \mathrm{from\; Eqs\; C.1\; \&\; C.2}\hfill \\ {\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_1})\ge {\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_2}).\end{array}$$

C.2.3. Part 3: $\left\{\frac{{\widehat{h}}_{-,\gamma }\left({\widehat{g}}_{-,\gamma }\right)}{{ϵ}_{\mathrm{ABS}}}-\gamma \right\}$ is Monotonically Decreasing in γ in the Range Where ${\widehat{e}}_{\mathrm{ORIG}}\left({\widehat{g}}_{-,\gamma }\right)\le {ϵ}_{\mathrm{ABS}}$, and Increasing Otherwise.

Suppose ${\gamma }_1<{\gamma }_2$ and ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{-,{\gamma }_1}\right)$, ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{-,{\gamma }_2}\right)\le {ϵ}_{\mathrm{abs}}$. Then, from Eq C.2,

$$\begin{array}{l}{\widehat{h}}_{-,{\gamma }_2}\left({\widehat{g}}_{-,{\gamma }_2}\right)\le {\widehat{h}}_{-,{\gamma }_2}\left({\widehat{g}}_{-,{\gamma }_1}\right)\\ {\widehat{h}}_{-,{\gamma }_2}\left({\widehat{g}}_{-,{\gamma }_2}\right)\le {\widehat{h}}_{-,{\gamma }_1}\left({\widehat{g}}_{-,{\gamma }_1}\right)+\left({\gamma }_2-{\gamma }_1\right){\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{-,{\gamma }_1}\right)& \mathrm{from\; Eq\; C.4}\\ {\widehat{h}}_{-,{\gamma }_2}\left({\widehat{g}}_{-,{\gamma }_2}\right)\le {\widehat{h}}_{-,{\gamma }_2}\left({\widehat{g}}_{-,{\gamma }_1}\right)+\left({\gamma }_2-{\gamma }_1\right){ϵ}_{\mathrm{abs}}& \mathrm{from}{\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{-,{\gamma }_1}\right)\le {ϵ}_{\mathrm{abs}}\\ \frac{{\widehat{h}}_{-,{\gamma }_2}\left({\widehat{g}}_{-,{\gamma }_2}\right)}{{ϵ}_{\mathrm{abs}}}-{\gamma }_2\le \frac{{\widehat{h}}_{-,{\gamma }_1}\left({\widehat{g}}_{-,{\gamma }_1}\right)}{{ϵ}_{\mathrm{abs}}}-{\gamma }_1.\end{array}$$

Similarly, if ${\gamma }_1<{\gamma }_2$ and ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{-,{\gamma }_1}\right)$, ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{-,{\gamma }_2}\right)\le {ϵ}_{\mathrm{abs}}$. Then, from Eq C.2

$$\begin{array}{l}{\widehat{h}}_{-,{\gamma }_1}\left({\widehat{g}}_{-,{\gamma }_1}\right)\le {\widehat{h}}_{-,{\gamma }_1}\left({\widehat{g}}_{-,{\gamma }_2}\right)\\ {\widehat{h}}_{-,{\gamma }_1}\left({\widehat{g}}_{-,{\gamma }_1}\right)\le {\widehat{h}}_{-,{\gamma }_2}\left({\widehat{g}}_{-,{\gamma }_2}\right)+\left({\gamma }_1-{\gamma }_2\right){\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{-,{\gamma }_2}\right)& \mathrm{from\; Eq\; C.4}\\ {\widehat{h}}_{-,{\gamma }_1}\left({\widehat{g}}_{-,{\gamma }_1}\right)\le {\widehat{h}}_{-,{\gamma }_2}\left({\widehat{g}}_{-,{\gamma }_2}\right)+\left({\gamma }_1-{\gamma }_2\right){ϵ}_{\mathrm{abs}}& \mathrm{from}{\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{-,{\gamma }_1}\right)\ge {ϵ}_{\mathrm{abs}}\\ \frac{{\widehat{h}}_{-,{\gamma }_1}\left({\widehat{g}}_{-,{\gamma }_1}\right)}{{ϵ}_{\mathrm{abs}}}-{\gamma }_2\le \frac{{\widehat{h}}_{-,{\gamma }_2}\left({\widehat{g}}_{-,{\gamma }_2}\right)}{{ϵ}_{\mathrm{abs}}}-{\gamma }_2.\end{array}$$

■

C.3. Proof of Proposition 11 (Nonnegative Weights for MR Lower Bound Binary Search)

Proof Let ${\gamma }_1:=\frac{1}{n-1}$. First we show that there exists a function ${\widehat{g}}_{-,{\gamma }_1}$ minimizing ${\widehat{h}}_{-,{\gamma }_1}$ such that $\widehat{MR}\left({\widehat{g}}_{-,{\gamma }_1}\right)=1$. Let D_s denote the sample distribution of the data, and let D_m be the distribution satisfying

$$\begin{array}{l}{\mathbb{P}}_{D_m}\left\{\left(Y,X_1,X_2\right)=\left(Y,X_1,X_2\right)\right\}={\mathbb{P}}_{D_s}\left\{\left(Y,X_2\right)=\left(y,x_2\right)\right\}\times {\mathbb{P}}_{D_s}\left(X_1=x_1\right)\\ =\frac{1}{n^2}\sum _{i=1}^{n}1\left({\mathbf{y}}_{\left[i\right]}=y\mathrm{and}{\mathbf{X}}_{2\left[i\right]}=x_2\right)\sum _{j=1}^{n}1\left({\mathbf{X}}_{1\left[j\right]}=x_1\right).\end{array}$$

From ${\gamma }_1=\frac{1}{n-1}$ and Eq 6.2, we see that

$$\begin{array}{l}{\widehat{h}}_{-,{\gamma }_1}\left(f\right)=\sum _{i=1}^n\sum _{j=1}^{n}L\left\{f,\left({\mathbf{y}}_{\left[i\right]},{\mathbf{X}}_{1\left[j\right]},{\mathbf{X}}_{2\left[i\right]}\right)\right\}\times \left\{\frac{{\gamma }_{1}1\left(i=j\right)}{n}+\frac{1\left(i\ne j\right)}{n\left(n-1\right)}\right\}\\ =\sum _{i=1}^n\sum _{j=1}^{n}L\left\{f,\left({\mathbf{y}}_{\left[i\right]},{\mathbf{X}}_{1\left[j\right]},{\mathbf{X}}_{2\left[i\right]}\right)\right\}\times \left\{\frac{1}{n\left(n-1\right)}\right\}.\\ \propto {\mathbb{E}}_{D_m}L\left\{f,\left(Y,X_1,X_2\right)\right\}.\end{array}$$

Thus, from Condition 2 of Proposition 11, we know there exists a function ${\widehat{g}}_{-,{\gamma }_1}$ that minimizes ${\widehat{h}}_{-,{\gamma }_1}$ with ${\widehat{g}}_{-,{\gamma }_1}\left(x_1^{\left(a\right)},x_2\right)={\widehat{g}}_{-,{\gamma }_1}\left(x_1^{\left(b\right)},x_2\right)$ for any $x_1^{\left(a\right)},x_1^{\left(b\right)}\in {\mathcal{X}}_1$ and $x_2\in {\mathcal{X}}_2$. Condition 1 of Proposition 11 then implies that $L\left\{{\widehat{g}}_{-,{\gamma }_1},\left(y,x_1^{\left(a\right)},x_2\right)\right\}=L\left\{{\widehat{g}}_{-,{\gamma }_1},\left(y,x_1^{\left(b\right)},x_2\right)\right\}$ for any $x_1^{\left(a\right)},x_1^{\left(b\right)}\in {\mathcal{X}}_1$, $x_2\in {\mathcal{X}}_2$, and $y\in \mathcal{Y}$. We apply this result in Line C.7, below, to show that loss of model ${\widehat{g}}_{-,{\gamma }_1}$ is unaffected by permuting X₁ within our sample:

$$\begin{array}{l}{\widehat{e}}_{\text{switch}}\left({\widehat{g}}_{-,{\gamma }_1}\right)=\frac{1}{n}\sum _{i=1}^n\frac{1}{n-1}\sum _{j\ne i}L\left\{{\widehat{g}}_{-,{\gamma }_1},\left({\mathbf{y}}_{\left[i\right]},{\mathbf{X}}_{1\left[j\right]},{\mathbf{X}}_{2\left[j\right]}\right)\right\}\\ =\frac{1}{n}\sum _{i=1}^n\frac{1}{n-1}\sum _{j\ne i}L\left\{{\widehat{g}}_{-,{\gamma }_1},\left({\mathbf{y}}_{\left[i\right]},{\mathbf{X}}_{1\left[j\right]},{\mathbf{X}}_{2\left[j\right]}\right)\right\}\\ =\frac{1}{n}\sum _{i=1}^{n}L\left\{{\widehat{g}}_{-,{\gamma }_1},\left({\mathbf{y}}_{\left[i\right]},{\mathbf{X}}_{1\left[j\right]},{\mathbf{X}}_{2\left[j\right]}\right)\right\}\\ ={\widehat{e}}_{\text{orig}}\left({\widehat{g}}_{-,{\gamma }_1}\right).\end{array}$$ (C.7)

It follows that $\widehat{MR}\left({\widehat{g}}_{-,{\gamma }_1}\right)=1$. To show the result of Proposition 11, let γ₂ = 0. For any function ${\widehat{g}}_{-,{\gamma }_2}$ minimizing ${\widehat{h}}_{-,{\gamma }_2}$, we know that

$$\begin{array}{cc}{\widehat{h}}_{-,{\gamma }_2}\left({\widehat{g}}_{-,{\gamma }_2}\right)\le {\widehat{h}}_{-,{\gamma }_2}\left({\widehat{g}}_{-,{\gamma }_1}\right)& \mathrm{from\; the\; definition\; of}{\widehat{g}}_{-,{\gamma }_2}\hfill \\ 0+{\widehat{e}}_{\mathrm{switch}}\left({\widehat{g}}_{-,{\gamma }_2}\right)\le 0+{\widehat{e}}_{\mathrm{switch}}\left({\widehat{g}}_{-,{\gamma }_1}\right)& \mathrm{from}{\gamma }_2=0\mathrm{and\; the\; definition\; of}{\widehat{h}}_{-,{\gamma }_2}.\hfill \end{array}$$ (C.8)

From γ₂ ≤ γ₁, and Part 2 of Lemma 10, we know that

$${\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_2})\ge {\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_1}).$$ (C.9)

Combining Eqs C.8 and C.9, we have

$$\widehat{MR}({\widehat{g}}_{-,{\gamma }_2})=\frac{{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{-,{\gamma }_2})}{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_2})}\le \frac{{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{-,{\gamma }_1})}{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{-,{\gamma }_1})}=\widehat{MR}({\widehat{g}}_{-,{\gamma }_1})=1.$$ (C.10)

Since ${\widehat{h}}_{-,{\gamma }_2}\left({\widehat{g}}_{-,{\gamma }_2}\right)={\widehat{e}}_{\mathrm{switch}}\left({\widehat{g}}_{-,{\gamma }_2}\right)\ge 0$ by definition, Condition 8 holds for γ₂, ϵ_abs and ${\widehat{g}}_{-,{\gamma }_2}$ if and only if ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{-,{\gamma }_2}\right)\le {ϵ}_{\mathrm{abs}}$. This, combined with Eq C.10, completes the proof.

The same result does not necessarily hold if we replace ê_switch with ê_divide in our definitions of ${\widehat{h}}_{-,\gamma }$, $\widehat{MR}$, and ${\widehat{MCR}}_{-}$. This is because ê_divide does not correspond to the expectation over a distribution in which X₁ is independent of X₂ and Y, due to the fixed pairing structure used in ê_divide. Thus, Condition 2 of Proposition 11 will not apply. ■

C.4. Proof of Lemma 13 (Upper Bound for MR)

Proof We prove Lemma 13 in 2 parts.

C.4.1. Part 1: Showing Eq 6.4 Holds for All $f\in \mathcal{F}$ Satisfying ${\widehat{e}}_{\mathrm{ORIG}}\left(f\right)\le {ϵ}_{\mathrm{ABS}}$

If ${\widehat{h}}_{+,\gamma }\left({\widehat{g}}_{+,\gamma }\right)\ge 0$, then for any function $f\in \mathcal{F}$ satisfying ${\widehat{e}}_{\mathrm{orig}}\left(f\right)\le {ϵ}_{\mathrm{abs}}$ we know that

$$\begin{array}{c}\frac{1}{{ϵ}_{\mathrm{abs}}}\le \frac{1}{{\widehat{e}}_{\mathrm{orig}}(f)}\\ \frac{{\widehat{h}}_{+,\gamma }({\widehat{g}}_{+,\gamma })}{{ϵ}_{\mathrm{abs}}}\le \frac{{\widehat{h}}_{+,\gamma }({\widehat{g}}_{+,\gamma })}{{\widehat{e}}_{\mathrm{orig}}(f)}.\end{array}$$ (C.11)

Now, if γ ≤ 0, then for any $f\in \mathcal{F}$ satisfying ${\widehat{e}}_{\mathrm{orig}}\left(f\right)\le {ϵ}_{\mathrm{abs}}$, the definition of ĝ_+,γ implies

$$\begin{array}{l}{\widehat{h}}_{+,\gamma }(f)\ge {\widehat{h}}_{+,\gamma }({\widehat{g}}_{+,\gamma })\\ {\widehat{e}}_{\mathrm{orig}}(f)+\gamma {\widehat{e}}_{\mathrm{switch}}(f)\ge {\widehat{h}}_{+,\gamma }({\widehat{g}}_{+,\gamma })\\ 1+\gamma \frac{{\widehat{e}}_{\mathrm{switch}}(f)}{{\widehat{e}}_{\mathrm{orig}}(f)}\ge \frac{{\widehat{h}}_{+,\gamma }({\widehat{g}}_{+,\gamma })}{{\widehat{e}}_{\mathrm{orig}}(f)}\\ 1+\gamma \frac{{\widehat{e}}_{\mathrm{switch}}(f)}{{\widehat{e}}_{\mathrm{orig}}(f)}\ge \frac{{\widehat{h}}_{+,\gamma }({\widehat{g}}_{+,\gamma })}{{ϵ}_{\mathrm{abs}}}& \mathrm{from\; Eq\; C.11}\\ 1+\gamma \widehat{MR}(f)\ge \frac{{\widehat{h}}_{+,\gamma }({\widehat{g}}_{+,\gamma })}{{ϵ}_{\mathrm{abs}}}\\ \widehat{MR}(f)\le \left\{\frac{{\widehat{h}}_{+,\gamma }({\widehat{g}}_{+,\gamma })}{{ϵ}_{\mathrm{abs}}}-1\right\}{\gamma }^{-1}.\end{array}$$

C.4.2. Part 2: Showing that if f = ĝ_+,γ, and at Least One of the Enequalities in Condition 12 Holds with Equality, then Eq 6.4 Holds with Equality.

We consider each of the two inequalities in Condition 12 separately. If ${\widehat{h}}_{+,\gamma }\left({\widehat{g}}_{+,\gamma }\right)=0$, then

$$\begin{array}{l}0={\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,\gamma })+\gamma {\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,\gamma })\\ -\gamma {\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,\gamma })={\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,\gamma })\\ -\left\{\frac{{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,\gamma })}{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,\gamma })}\right\}=\frac{1}{\gamma }.\end{array}$$

As a result,

$$\left\{\frac{{\widehat{h}}_{+,\gamma }({\widehat{g}}_{+,\gamma })}{{ϵ}_{\mathrm{abs}}}-1\right\}{\gamma }^{-1}=\left\{\frac{0}{{ϵ}_{\mathrm{abs}}}-1\right\}\left\{\frac{{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,\gamma })}{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,\gamma })}\right\}=\widehat{\mathit{MR}}({\widehat{g}}_{+,\gamma }).$$

Alternatively, if ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{+,\gamma }\right)\le {ϵ}_{\mathrm{abs}}$, then

$$\begin{array}{l}\left\{\frac{{\widehat{h}}_{+,\gamma }({\widehat{g}}_{+,\gamma })}{{ϵ}_{\mathrm{abs}}}-1\right\}{\gamma }^{-1}=\left\{\frac{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,\gamma })+\gamma {\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,\gamma })}{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,\gamma })}-1\right\}{\gamma }^{-1}=\left\{1+\gamma \frac{{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,\gamma })}{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,\gamma })}-1\right\}{\gamma }^{-1}\\ \hfill =\widehat{\mathit{MR}}({\widehat{g}}_{+,\gamma }).\hfill \end{array}$$

■

C.5. Proof of Lemma 14 (Monotonicity for MR Upper Bound Binary Search)

Proof We prove Lemma 14 in 3 parts.

C.5.1. Part 1: ${\widehat{h}}_{+,\gamma }\left({\widehat{g}}_{+,\gamma }\right)$ is Monotonically Increasing in γ.

Let ${\gamma }_1<{\gamma }_2\in \mathbb{R}$ satisfy ${\gamma }_1\le {\gamma }_2$. We have assumed that $0\le {\widehat{e}}_{\mathrm{orig}}\left(f\right)$ for any $f\in \mathcal{F}$. Thus, for any $f\in \mathcal{F}$ we have

$$\begin{array}{c}{\widehat{e}}_{\mathrm{orig}}(f)+{\gamma }_1{\widehat{e}}_{\mathrm{switch}}(f)<{\widehat{e}}_{\mathrm{orig}}(f)+{\gamma }_2{\widehat{e}}_{\mathrm{switch}}(f)\\ {\widehat{h}}_{+,{\gamma }_1}(f)<{\widehat{h}}_{+,{\gamma }_2}(f).\end{array}$$ (C.12)

Applying this, we have

$$\begin{array}{ll}\hfill {\widehat{h}}_{+,{\gamma }_1}({\widehat{g}}_{+,{\gamma }_1})\le {\widehat{h}}_{+,{\gamma }_1}({\widehat{g}}_{+,{\gamma }_2})& \mathrm{from\; Eq\; C.2}\\ \hfill \text{<}{\widehat{h}}_{+,{\gamma }_2}({\widehat{g}}_{+,{\gamma }_2})& \mathrm{from\; Eq\; C.12.}\end{array}$$

C.5.2. Part 2: ${\widehat{e}}_{\mathrm{ORIG}}\left({\widehat{g}}_{+,{\gamma }_2}\right)$ is Monotonically Decreasing in γ for γ ≤ 0, and Condition 12 Holds for γ = 0 and ${ϵ}_{\mathrm{ABS}}\ge {\min }_{f\in \mathcal{F}}{\widehat{e}}_{\mathrm{ORIG}}\left(f\right)$.

Let ${\gamma }_1<{\gamma }_2\in \mathbb{R}$ satisfy γ₁ < γ₂ ≤ 0. Then

$$\begin{array}{cc}{\widehat{h}}_{+,{\gamma }_1}({\widehat{g}}_{+,{\gamma }_1})\le {\widehat{h}}_{+,{\gamma }_1}({\widehat{g}}_{+,{\gamma }_2})& \hfill \mathrm{from\; Eq\; C.2}\\ {\widehat{h}}_{+,{\gamma }_1}({\widehat{g}}_{+,{\gamma }_1})+({\gamma }_1-{\gamma }_2){\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,{\gamma }_1})\le {\widehat{h}}_{+,{\gamma }_2}({\widehat{g}}_{+,{\gamma }_2})+({\gamma }_1-{\gamma }_2){\widehat{e}}_{\mathrm{switch}}(g_{\gamma 2})& \hfill \mathrm{from\; Eq\; C.3}\\ ({\gamma }_1-{\gamma }_2){\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,{\gamma }_1})\le ({\gamma }_1-{\gamma }_2){\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,{\gamma }_2})& \hfill \mathrm{from\; Eqs\; C.1}\&\mathrm{C.2}\\ {\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,{\gamma }_1})\ge {\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,{\gamma }_2})\\ {\gamma }_2{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,{\gamma }_1})\le {\gamma }_2{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,{\gamma }_2})& \hfill \mathrm{from}{\gamma }_2\le 0.\end{array}$$ (C.13)

Now we are equipped to show the result that ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{+,{\gamma }_2}\right)$ is monotonically decreasing in γ for γ ≤ 0:

$$\begin{array}{cc}{\widehat{h}}_{+,\gamma 2}({\widehat{g}}_{+,\gamma 2})\le {\widehat{h}}_{+,{\gamma }_2}({\widehat{g}}_{+,{\gamma }_1})& \hfill \mathrm{from\; Eq\; C.2}\\ {\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_2})+{\gamma }_2{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,\gamma 2})+{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_1})+{\gamma }_2{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,{\gamma }_1})\\ {\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_2})+{\gamma }_2{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,{\gamma }_1})& \hfill \mathrm{from\; Eqs\; C.1}\&\mathrm{C.13.}\end{array}$$ (C.14)

To show that Condition 12 holds for γ = 0 and ${\min }_{f\in \mathcal{F}}{\widehat{e}}_{\mathrm{orig}}\left(f\right)\le ϵ{}_{\mathrm{abs}}$, we first note that $h_{0,+}\left(g_{0,+}\right)={\widehat{e}}_{\mathrm{orig}}\left(g_{0,+}\right)$, which is positive by assumption. Second, we note that

$${\widehat{e}}_{\mathrm{orig}}(g_0{}_{,+})=h_{0,+}(g_0{}_{,+})=\underset{f\in \mathcal{F}}{\min }{h}_{0,+}(f)=\underset{f\in \mathcal{F}}{\min }{\widehat{e}}_{\mathrm{orig}}(f)\le {ϵ}_{\mathrm{abs}}.$$

C.5.3. Part 3: $\left\{\frac{{\widehat{h}}_{+,\gamma }\left({\widehat{g}}_{+,\gamma }\right)}{{ϵ}_{\mathrm{ABS}}}-1\right\}{\gamma }^{-1}$ is Monotonically Increasing in γ in the Range Where ${\widehat{e}}_{\mathrm{ORIG}}\left({\widehat{g}}_{+,\gamma }\right)\le {ϵ}_{\mathrm{ABS}}$ and γ < 0, and Decreasing in the Range Where ${\widehat{e}}_{\mathrm{ORIG}}\left({\widehat{g}}_{+,\gamma }\right)>{ϵ}_{\mathrm{ABS}}$ and γ < 0.

To prove the first result, suppose that γ₁ < γ₂ < 0 and ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{+,{\gamma }_1}\right)$, ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{+,{\gamma }_2}\right)\le {ϵ}_{\mathrm{abs}}$. This implies

$$\begin{array}{c}\frac{1}{{\gamma }_2}<\frac{1}{{\gamma }_1}\\ \frac{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_1})-{ϵ}_{\mathrm{abs}}}{{\gamma }_2}<\frac{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_1})-{ϵ}_{\mathrm{abs}}}{{\gamma }_1}.\end{array}$$ (C.15)

Then, starting with Eq C.2,

$$\begin{array}{l}{\widehat{h}}_{+,{\gamma }_2}({\widehat{g}}_{+,{\gamma }_2})\le {\widehat{h}}_{+,{\gamma }_2}({\widehat{g}}_{+,{\gamma }_1})\\ {\widehat{h}}_{+,{\gamma }_2}({\widehat{g}}_{+,{\gamma }_2})\le {\gamma }_2{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,\gamma 1})+{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_1})\\ \frac{{\widehat{h}}_{+,{\gamma }_2}({\widehat{g}}_{+,{\gamma }_2})-{ϵ}_{\mathrm{abs}}}{{\gamma }_2}\ge {\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,\gamma 1})+\frac{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_1})-{ϵ}_{\mathrm{abs}}}{{\gamma }_2}\\ \hfill \ge {\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,{\gamma }_1})+\frac{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_1})-{ϵ}_{\mathrm{abs}}}{{\gamma }_1}\hfill & \mathrm{from\; Eq\; C.15}\\ \hfill \text{=}\frac{({\widehat{h}}_{+,{\gamma }_1})({\widehat{g}}_{+,\gamma 2})-{ϵ}_{\mathrm{abs}}}{{\gamma }_1}.\hfill \end{array}$$

Diving both sides of the above equation by ϵ_abs proves that $\left\{\frac{{\widehat{h}}_{+,\gamma }\left({\widehat{g}}_{+,\gamma }\right)}{{ϵ}_{\mathrm{abs}}}-1\right\}{\gamma }^{-1}$ is monotonically decreasing in γ in the range where ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{+,\gamma }\right)\le {ϵ}_{\mathrm{abs}}$ and γ < 0.

To prove the second result we proceed in the same way. Suppose that γ₁ < γ₂ < 0 and ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{+,{\gamma }_1}\right)$ ; ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{+,\gamma }\right)\ge {ϵ}_{\mathrm{abs}}$. This implies

$$\begin{array}{c}\frac{1}{{\gamma }_2}<\frac{1}{{\gamma }_1}\\ \frac{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_2})-{ϵ}_{\mathrm{abs}}}{{\gamma }_2}<\frac{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_2})-{ϵ}_{\mathrm{abs}}}{{\gamma }_1}.\end{array}$$ (C.16)

Then, starting with Eq C.2,

$$\begin{array}{l}{\widehat{h}}_{+,{\gamma }_1}({\widehat{g}}_{+,{\gamma }_1})\le {\widehat{h}}_{+,{\gamma }_1}({\widehat{g}}_{+,{\gamma }_2})\\ {\widehat{h}}_{+,{\gamma }_1}({\widehat{g}}_{+,{\gamma }_1})\le {\gamma }_1{\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,\gamma 2})+{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_2})\\ \frac{{\widehat{h}}_{+,{\gamma }_1}({\widehat{g}}_{+,{\gamma }_1})-{ϵ}_{\mathrm{abs}}}{{\gamma }_1}\ge {\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,\gamma 2})+\frac{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_2})-{ϵ}_{\mathrm{abs}}}{{\gamma }_2}\\ \hfill \ge {\widehat{e}}_{\mathrm{switch}}({\widehat{g}}_{+,{\gamma }_2})+\frac{{\widehat{e}}_{\mathrm{orig}}({\widehat{g}}_{+,{\gamma }_2})-{ϵ}_{\mathrm{abs}}}{{\gamma }_2}\hfill & \mathrm{from\; Eq\; C.16}\\ \hfill \text{=}\frac{({\widehat{h}}_{+,{\gamma }_1})({\widehat{g}}_{+,\gamma 2})-{ϵ}_{\mathrm{abs}}}{{\gamma }_2}.\hfill \end{array}$$

Diving both sides of the above equation by ϵ_abs proves that $\left[\left\{\frac{{\widehat{h}}_{+,\gamma }\left({\widehat{g}}_{+,\gamma }\right)}{{ϵ}_{\mathrm{abs}}}-1\right\}{\gamma }^{-1}\right]$ is monotonically decreasing in γ in the range where ${\widehat{e}}_{\mathrm{orig}}\left({\widehat{g}}_{+,\gamma }\right)>{ϵ}_{\mathrm{abs}}$ and γ < 0. ■

C.6. Proof of Remark 16 (Tractability of Empirical MCR for Linear Model Classes)

Proof To show Remark 16, we apply Proposition 15 to see that

$$\begin{array}{l}{\xi }_{\mathrm{orig}}{\widehat{e}}_{\mathrm{orig}}(f_{\beta })+{\xi }_{\mathrm{switch}}{\widehat{e}}_{\mathrm{switch}}(f_{\beta })\\ =\frac{{\xi }_{\mathrm{orig}}}{n}{\Vert \mathbf{y}-\mathbf{X}\beta \Vert }_2^2+{\xi }_{\mathrm{switch}}{\widehat{e}}_{\mathrm{switch}}(f_{\beta })\\ =\frac{{\xi }_{\mathrm{orig}}}{n}({\mathbf{y}}^{\prime }\mathbf{y}-2{\mathbf{y}}^{\prime }X\beta +{\beta }^{\prime }{X}^{\prime }\mathbf{X}\beta )\\ +\frac{{\xi }_{\mathrm{switch}}}{n}\left\{{\mathbf{y}}^{\prime }\mathbf{y}-2\left[\begin{array}{c}{\mathbf{X}}_1^{\prime }\mathbf{W}\mathbf{y}\\ {\mathbf{X}}_2^{\prime }\mathbf{y}\end{array}\right]\beta +{\beta }^{\prime }\left[\begin{array}{cc}{\mathbf{X}}_1^{\prime }{\mathbf{X}}_1& {\mathbf{X}}_2^{\prime }\mathbf{W}{\mathbf{X}}_2\\ {\mathbf{X}}_2^{\prime }\mathbf{W}{\mathbf{X}}_1& {\mathbf{X}}_2^{\prime }{\mathbf{X}}_2\end{array}\right]\beta \right\}\\ {\propto }_{\beta }-2{\mathbf{q}}^{\prime }\beta +{\beta }^{\prime }\mathbf{Q}\beta .\end{array}$$

■

C.7. Proof of Lemma 17 (Loss Upper Bound for Linear Models)

Proof Under the conditions in Lemma 17 and Eq 7.5, we can construct an upper bound on $L\left(f_{\beta ,}\left(y,x\right)\right)={\left(y-x^{\prime }\beta \right)}^2$ by either maximizing or minimizing x′β. First, we consider the maximization problem

$$\underset{\beta ,x\in {\mathbb{R}}^p}{\max }{x}^{\prime }\beta \mathrm{subjeted\; to}{x}^{\prime }{\mathbf{M}}_{\mathrm{lm}}^{-1}x\le r_{\mathcal{X}}\mathrm{and}{\beta }^{\prime }{\mathbf{M}}_{\mathrm{lm}}\beta \le r_{\mathrm{lm}}.$$ (C.17)

We can see that both constraints hold with equality at the solution to this problem. Next, we apply the change of variables $\tilde{x}=\frac{1}{\sqrt{{}^r\mathcal{X}}}{D}^{\frac{-1}{2}}{U}^{\prime }x$ and $\tilde{\beta }=\frac{1}{\sqrt{r_{\mathrm{lm}}}}{D}^{\frac{1}{2}}{U}^{\prime }\beta$, where $UD{U}^{\prime }=M_{\mathrm{lm}}$ is the eigendecomposition of M_lm. We obtain

$$\underset{\tilde{\beta },\tilde{x}\in {\mathbb{R}}^p}{\max }{\tilde{x}}^{\prime }\tilde{\beta }\sqrt{r_{\mathcal{X}}{r}_{\mathrm{lm}}}\mathrm{subject\; to}{\tilde{x}}^{\prime }\tilde{x}=1\text{and}{\tilde{\beta }}^{\prime }\tilde{\beta }=1,$$

which has an optimal objective value equal to $\sqrt{{}^r\mathcal{X}{}^r\mathrm{lm}}$. By negating the objective in Eq C.17, we see that the minimum possible value of x′β, subject to the constraints in Eq 7.5 and Lemma 17, is found at $-\sqrt{{}^r\mathcal{X}{}^r\mathrm{lm}}$. Thus, we know that

$$L(f,(y,x_1,x_2))\le \max \left[{\left\{\left(\underset{y\in \mathcal{Y}}{\min }y\right)-\sqrt{r_{\mathcal{X}}{r}_{\mathrm{lm}}}\right\}}^2,{\left\{\left(\underset{y\in \mathcal{Y}}{\max }y\right)+\sqrt{r_{\mathcal{X}}{r}_{\mathrm{lm}}}\right\}}^2\right],$$

for any $(y,x_1,x_2)\in (\mathcal{Y},{\mathcal{X}}_1,{\mathcal{X}}_2)$. ■

C.8. Proof of Lemma 18 (Loss Upper Bound for Regression in a RKHS)

This proofs follows a similar structure as the proof in Section C.7. From the assumptions of Lemma 18, we know from Eq 7.7 that the largest possible output from a model $f_{\alpha }\in {\mathcal{F}}_{D,r_k}$ is

$$\begin{array}{ll}\mu +\underset{x\in {\mathbb{R}}^R,\alpha \in {\mathbb{R}}^R}{\max }\sum _{i=1}^{R}k(x,{\mathbf{D}}_{[i,1]}){\alpha }_{[i]}& \mathrm{subjected\; to}\upsilon {(x)}^{\prime }{\mathbf{K}}_{\mathbf{D}}^{-1}\upsilon (x)\le r_D\text{and}{\alpha }^{\prime }{\mathbf{K}}_{\mathbf{D}}\alpha \le r_k\\ =\mu +\underset{x\in {\mathbb{R}}^R,\alpha \in {\mathbb{R}}^R}{\max }\upsilon (x{)}^{\prime }\alpha & \mathrm{subjected\; to}\upsilon {(x)}^{\prime }{\mathbf{K}}_{\mathbf{D}}^{-1}\upsilon (x)\le r_D\text{and}{\alpha }^{\prime }{\mathbf{K}}_{\mathbf{D}}\alpha \le r_k\\ \le \mu +\underset{\mathbf{z},\alpha \in {\mathbb{R}}^R}{\max }{\mathbf{z}}^{\prime }\alpha & \mathrm{subjected\; to}{\mathbf{z}}^{\prime }{\mathbf{K}}_{\mathbf{D}}^{-1}\mathbf{z}\le r_D\text{and}{\alpha }^{\prime }{\mathbf{K}}_{\mathbf{D}}\alpha \le r_k.\end{array}$$

The above problem can be solved in the same way as Eq C.17, and has a solution at $(\mu +\sqrt{r_D{r}_k})$. The smallest possible model output will similarly be lower bounded by − $(\mu +\sqrt{r_D{r}_k})$. Thus, B_ind is less than or equal to

$$\max \left[{\left\{\underset{y\in \mathcal{Y}}{\min }(y)-(\mu +\sqrt{r_D{r}_k})\right\}}^2,{\left\{\underset{y\in \mathcal{Y}}{\max }(y)+(\mu +\sqrt{r_D{r}_k})\right\}}^2\right].$$