How will mass-vaccination change COVID-19 lockdown requirements in Australia?

Abstract

Background

To prevent future outbreaks of COVID-19, Australia is pursuing a mass-vaccination approach in which a targeted group of the population comprising healthcare workers, aged-care residents and other individuals at increased risk of exposure will receive a highly effective priority vaccine. The rest of the population will instead have access to a less effective vaccine.

Methods

We apply a large-scale agent-based model of COVID-19 in Australia to investigate the possible implications of this hybrid approach to mass-vaccination. The model is calibrated to recent epidemiological and demographic data available in Australia, and accounts for several components of vaccine efficacy.

Findings

Within a feasible range of vaccine efficacy values, our model supports the assertion that complete herd immunity due to vaccination is not likely in the Australian context. For realistic scenarios in which herd immunity is not achieved, we simulate the effects of mass-vaccination on epidemic growth rate, and investigate the requirements of lockdown measures applied to curb subsequent outbreaks. In our simulations, Australia’s vaccination strategy can feasibly reduce required lockdown intensity and initial epidemic growth rate by 43% and 52%, respectively. The severity of epidemics, as measured by the peak number of daily new cases, decreases by up to two orders of magnitude under plausible mass-vaccination and lockdown strategies.

Interpretation

The study presents a strong argument for a large-scale vaccination campaign in Australia, which would substantially reduce both the intensity of future outbreaks and the stringency of non-pharmaceutical interventions required for their suppression.

Funding

Australian Research Council; National Health and Medical Research Council.

Introduction

The Australian response to the COVID-19 pandemic has been very effective to date. Strict control measures, including travel restrictions and social distancing, successfully suppressed the initial pandemic wave in Australia (March – June 2020) [1], as well as several secondary outbreaks across the states, most notably in Victoria (June – September 2020) [2]. However, as vaccines become available a more refined response is needed, given the need to balance population health against the high socio-economic impacts of local, regional and nation-wide lockdowns.

The national COVID-19 vaccine rollout strategy developed by the Australian Government commenced in late February 2021, aiming to vaccinate a significant portion of the Australian population (the majority of the adult population) by the end of October 2021 [3]. The first phase of the strategy targets priority groups with the BNT162b2 (Pfizer/BioNTech) vaccine, while the remainder of the population will receive the ChAdOx1 nCoV-19 (Oxford/AstraZeneca) vaccine during phases two and three. Both of these vaccines have demonstrated high clinical efficacy [4], [5]. However, between August 2020 and January 2021, there has been a substantial increase in vaccine hesitancy in Australia, with 21.7% of surveyed Australians responding that “they probably or definitely would not get a safe and effective COVID-19 vaccine in January 2021” [6]. Furthermore, over April–June 2021, the vaccine rollout strategy in Australia has been significantly revised due to health risks attributed to administering the ChAdOx1 nCoV-19 (Oxford/AstraZeneca) vaccine to individuals in specific age groups. As a result, from mid-June 2021 this vaccine is no longer recommended to Australians younger than 60, who instead became eligible for the BNT162b2 (Pfizer/BioNTech) vaccine.

Thus, many questions remain. Is herd immunity achievable with current vaccination approaches? To what extent can the strict lockdown rules be relaxed with a partial mass vaccination? Is there an optimal but feasible balance between the vaccination efforts and social distancing practice? What is the impact of the revised vaccine rollout strategy? In this work, we approach these questions with a large-scale agent-based model (ABM) of COVID-19 transmission, case-targeted non-pharmaceutical interventions, lockdowns, and mass-vaccination in the context of Australia, using the latest available information.

There are several specific challenges in modelling COVID-19 vaccination campaigns: the complexity and burden of non-pharmaceutical interventions (NPIs); the heterogeneity of the population; country-specific demographics; logistical and supply constraints; as well as unknown vaccine characteristics. The heterogeneity of the Australian population has been shown to unevenly affect the spread of respiratory diseases across different social contexts and wider jurisdictions [1], [7]. We can therefore expect complex trade-offs between NPIs and vaccination interventions, covering overlapping but not identical parts of the population. These effects may be difficult to predict for situations in which the vaccine efficacy differs with respect to reducing susceptibility, preventing symptoms of infection, and limiting further transmission of the virus. Some of the available vaccines, most notably BNT162b2 (Pfizer/BioNTech), have shown a high efficacy against documented infection, as well as symptomatic and severe disease [4]. However, comprehensive results across multiple efficacy components are still lacking. In this work, we account for differences in vaccine efficacy for the two distinct vaccine types approved for distribution in Australia: a priority vaccine, (e.g.., BNT162b2), and a general vaccine, (e.g., ChAdOx1 nCoV-19).

In order to capture population heterogeneity, we adapted a previously developed and validated high-resolution ABM of mitigation and control of the COVID-19 pandemic in Australia [1], [7]. This model included a range of dynamically adjustable NPIs, such as travel restrictions, case isolation, home quarantine and mandated social distancing (lockdown). Here, we extended the ABM to include several detailed vaccination measures. These extensions included an explicit account of separate components of vaccination efficacy (susceptibility, disease, and infectiousness), and changeable levels of age-stratified mass-vaccination coverage with the general and priority vaccines.

This paper addresses several open questions surrounding vaccination in Australia. Firstly, we investigate the feasibility of herd immunity following a mass-vaccination campaign. This is addressed by varying vaccination coverage with different vaccine efficacy combinations. Secondly, we quantify the benefit of the general vaccine in scenarios where all priority vaccine supplies are consumed by considering different levels of general vaccination distributed in addition to a fixed realistic priority vaccination coverage. Finally, we quantify to what extent mass-vaccination can reduce or eliminate the need for lockdowns by varying lockdown compliance levels for various extents of vaccination coverage.

Methods

Simulating COVID-19 in Australia

Our approach to simulating COVID-19 in Australia follows that of our previous work [1]. This model is implemented within a high-precision simulator comprising about 23.4 million stochastically generated software agents. These artificial “agents” represent the population in Australia, with attributes of an anonymous individual (e.g., age, residence, gender, workplace, susceptibility and immunity to diseases), and contact rates within different social contexts (e.g., households, household clusters, neighbourhoods, classrooms, workplaces). The set of agents, i.e., the surrogate population, is generated to match the average characteristics of the Australian Census and the Australian Curriculum, Assessment and Reporting Authority data, including commuting patterns between the places of residence (i.e., census statistical areas) and work or study (i.e., census destination zones) [8], [9], [10]. Furthermore, the model is calibrated to key COVID-19 characteristics, using age-dependent contact and transmission rates (scaled to match the COVID-19 reproductive number $R_0$ by the scaling factor $\kappa$), the fraction of symptomatic cases (set as 0.134 for children, and 0.669 for adults), the probabilities of transmission for asymptomatic/presymptomatic and symptomatic agents, and other parameters specifying the natural disease history model (see below) [1].

A discrete-time simulation scenario progresses by updating agents’ states over time, starting from an initial distribution of infection, seeded by imported cases dependent on the incoming international air traffic (using data from the Australian Bureau of Infrastructure, Transport and Regional Economics) [8], [9]. Unless travel restrictions (i.e., border closures) are imposed by a scenario, at each time step this process probabilistically introduces new infections within a 50 km radius of every international airport, in proportion to the average daily number of incoming passengers at that airport (using a binomial distribution) [1], [8], [9]. By simulating interactions within all the mixing contexts in the surrogate population in 12-hour cycles (“day” and “night”), with respect to work, study and other activities, a specific outbreak, originated at particular points, is traced over time. A typical distribution of local transmissions (distinct from overseas acquired cases), traced from the simulation, has been cross-validated with the genomic surveillance data in Australia [7].

The following modifications were made to our model of COVID-19 disease natural history and case ascertainment:

• •Infectious incubation times ($T_{\text{inc}}$) calibrated to the findings of Lauer et al. [11] who inferred log-normally distributed incubation times with mean 5.5 days.
• •An infectious asymptomatic or symptomatic period ($T_{\text{symp}}$), following incubation, lasting between 7 days and 14 days (uniformly distributed), based on estimates of the replication-competent viral shedding period used to support guidance on case isolation periods published by the United States Centre for Disease Control and Prevention (CDC, see [12] and references therein [13]).
• •Differentiation between “asymptomatic infectivity” and “pre-symptomatic infectivity”. In the previous iteration of the model used in Chang et al. [1], asymptomatic and pre-symptomatic individuals had reduced infectivity to contacts. That assumption was modified in this work, for which pre-symptomatic cases are assumed to be as infectious as symptomatic cases (with respect to viral load), while those who remain asymptomatic throughout the course of disease have reduced infectivity (a factor of 0.5 is applied to the force of infection exerted on contacts). This change reflects the general finding that pre-symptomatic transmission is responsible for a substantial amount of COVID-19 spread (up to 50% of transmission), and allows a parsimonious calibration of disease natural history, reproductive ratio, and generation interval [14], [15].
• •To simulate the imperfect detection of cases in a scenario with high levels of voluntary population screening, we introduce two case detection probabilities, one for symptomatic case detection and the other for pre-symptomatic and asymptomatic detection. For symptomatic cases, the probability of detection per day is set to 0.23, while for pre-symptomatic and asymptomatic cases, the probability of detection per day is 0.01.

Interventions are specified via suitably defined macro- and micro-parameters constraining agent interactions and transmission probabilities. These constraints represent assumptions on how non-pharmaceutical (e.g., social distancing) or pharmaceutical (e.g., vaccine efficacy) interventions reduce the infection spread. For example, social distancing compliance can be set at 80% at the macro-level, while micro-distancing contacts during a lockdown can be reduced to 10% within workplaces and 25% within communities (cf. Table S3).

Model calibration

Because the models of disease natural history and case ascertainment were modified, we re-calibrated the model used by Chang et al. [1] to approximately match the case incidence data recorded during the first and second waves of COVID-19 in Australia and the global reproduction number of $R_0\approx 2.995\%\text{CI}[2.39,3.44]$ [16] (see Supplementary Material).

Mass-vaccination simulations

In our mass-vaccination scenarios, we used an age-stratified vaccine allocation scheme. Starting with no individuals vaccinated, the algorithm allocates new immunisations randomly according to the following ratio: 100:10:1, which correspond to [age $\ge 65$] : [$18\le \text{age}<65$] : [age $<18$ ]. That is, for every 100 individuals aged over 64 years, 10 individuals aged between 18 and 64 years are immunised and one individual under the age of 18 years is immunised. This allocation ratio applies unless there are no remaining unvaccinated individuals in an age category, in which case vaccines are allocated to the remaining age categories according to the same specified proportions until the specified number of immunisations is depleted or all individuals over the age of 18 are immunised, whichever occurs first. The priority vaccines are distributed first, followed by the general vaccines. In practice, due to the age distribution in our model of the Australian population (based on the 2016 ABS Census) this means that all individuals aged over 64 years (i.e., 65+) are immunised unless there are fewer than $3.9\times {10}^6$ total immunisations. In our hybrid mass-vaccination scenarios, we assume at least $5\times {10}^6$ priority immunisations, so the entire population over the age of 64 years is immunised with the priority vaccine, while the remaining immunisations are distributed between children and adults under 65 in a ratio of 10/1 (adults/children). All immunisations are allocated on day 0 of each outbreak simulation. Note that because our allocation procedure terminates after all individuals aged 18 or older are immunised, the maximum number of vaccinated children is 1/10 of the population between 18 and 64, or 1.4M children vaccinated. This accounts for approximately 25% of the population under 18, reflecting the tighter regulations on vaccine approval for these age groups worldwide, which are currently relaxing for adolescents over the age of 12. Therefore, the maximum number of immunisations is capped at 19.3M, leaving approximately 4.2M children unvaccinated.

Growth rate estimation

Throughout this work, we report growth rates estimated from incidence data produce by the ABM or collected from government case reports. To estimate growth rates, we fit each case incidence timeseries to a delayed exponential function:

$$I\left(t\right)=\exp \left(\lambda \right(t-\Delta t\left)\right),$$ (1)

where $\lambda$ is the exponential growth rate of case incidence, and the delay $\Delta t$ accounts for transient stochastic effects during the early stages of outbreaks as well as delays in detection of new cases.

Role of the funding source

The funders of the study had no role in the study design; the collection, analysis, and interpretation of data; the writing of the Article; and in the decision to submit the paper for publication. The corresponding author had full access to all the data in the study and had final responsibility for the decision to submit for publication.

Results

We present our results in three sections, first covering questions related to herd immunity and vaccine efficacy, then the effect of mass-vaccination on epidemic growth rate, and lastly the effects of future lockdowns in conjunction with prepandemic mass-vaccination. Section A investigates the feasibility of achieving herd immunity given the existing known and unknown aspects of COVID-19 vaccine efficacy. For clinical efficacy values of 0.9 and 0.6 (corresponding to conservative estimates for the priority and the general vaccine, respectively), we use a homogeneous approximation to calculate the coverage required to achieve herd immunity as a function of vaccine efficacy against susceptibility, symptom expression, and onward transmission. We then compare the results of our ABM to the homogeneous approximation for a subset of vaccine efficacy values. Section B describes the effects of realistic simulated mass vaccination regimes on epidemic growth rate. In scenarios where herd immunity is not achieved, we compute the growth rate of cumulative incidence for different levels of vaccination coverage, in combination with case-targeted NPIs. Section C investigates outbreak suppression in mass-vaccination scenarios and shows how vaccination can reduce the fraction of the population required to be in lockdown to achieve suppression of case incidence.

A. Herd immunity requirements: coverage and efficacy

For the purposes of modelling the effects of vaccination on the spread of COVID-19 and evaluating the requirements for herd immunity, three main components of vaccine efficacy constitute important unknown factors:

• •Efficacy for susceptibility ($\text{VEs}$) determines the level of immunity vaccination imparts to those susceptible to the virus. In the ABM this parameter reduces the probability of becoming infected if exposed.
• •Efficacy for disease ($\text{VEd}$) determines the expression of illness in those who are vaccinated and subsequently become infected. In the ABM this parameter reduces the probability of expressing symptoms if infected.
• •Efficacy for infectiousness ($\text{VEi}$) reduces the potential for vaccinated individuals to transmit the virus if infected. In the ABM, this parameter reduces the force of infection produced by infected individuals who are vaccinated.

The practical bounds of the efficacy terms ($\text{VEs}$, $\text{VEi}$, and $\text{VEd}$) are only partially constrained by the clinical efficacy ($\text{VEc}$) reported in clinical trials, since:

$$\text{VEc}=\text{VEd}+\text{VEs}-\text{VEs}\text{VEd}.$$ (2)

The clinical efficacy, $\text{VEc}$, is defined as the reduction in presentation of clinical disease in the vaccine group relative to the control. The vaccine efficacy for an individual’s susceptibility and disease, $\text{VEs}$ and $\text{VEd}$, are constrained by the clinical efficacy, $\text{VEc}$, through Eq.  (2); however, the vaccine efficacy for infectiousness, $\text{VEi}$, is left undefined by clinical trial data. Although unreported, it is crucial for $\text{VEi}$ to be defined in order to compute the population-level vaccine efficacy, $\text{VE}$, for a given proportion of the population vaccinated. For defined values of the input parameters (coverage, $\text{VEi}$, $\text{VEs}$, and $\text{VEd}$), $\text{VE}$ can be estimated from a homogeneous approximation of population mixing (see Supplementary Material) and the necessary vaccine coverage threshold for herd immunity can then be estimated by computing the effective reproductive number, $R$, after vaccination:

$$R=R_0(1-\text{VE}),$$ (3)

where $R_0$ is the basic reproductive ratio in a completely susceptible population, and herd immunity is achieved when $R<1$. In the Supplementary Material Fig. S1, we provide herd immunity thresholds in the $\text{VEi}\times \text{coverage}$ plane for different combinations of $\text{VEd}$ and $\text{VEs}$ constrained through Eq.  (2), with $R_0=2.75$ to match the basic reproductive ratio used in our ABM.

These results show that, for herd immunity in a homogeneous system, the general vaccine (with $\text{VEc}=0.6$) must produce a substantial reduction in the transmission potential of infected individuals, with an efficacy for infectiousness ($\text{VEi}$) on the same order of efficacy for susceptibility ($\text{VEs}$) and disease ($\text{VEd}$). On the other hand, Fig. S1b illustrates that a priority vaccine with clinical efficacy of $90\%$ ($\text{VEc}=0.9$) could produce herd immunity with vaccination coverage between $64\%$ and $86\%$. Moreover, as long as $\text{VEs}\ge \text{VEd}$, this result can be achieved without a substantial contribution from the unknown effect of the vaccine on reducing infectiousness (i.e., $\text{VEi}$).

Of course, Australia is not a homogeneous system with respect to population mixing patterns, and the true vaccine allocation strategy is intentionally heterogeneous, first prioritising those in high-risk age groups and prioritising children last. For these reasons, we expected our ABM to produce results differing from those estimated by the homogeneous approximation. To match our scenarios to the Australian context, which has consistently maintained case-targeted non-pharmaceutical interventions, we performed a systematic scan of efficacy parameters both with and without combinations of detected case isolation, home quarantine of household contacts, and international travel restrictions. While the proposed vaccination regime in Australia involves both priority and general vaccines, initially we treat each separately in order to reduce the complexity of the parameter space.

Therefore, the results presented in this section are not directly applicable to proposed vaccination levels in Australia, but can be used to guide intuition with respect to the influence of different efficacy combinations and potential deviation from estimates based on homogeneous approximations.

For a given mass-vaccination scenario, the ABM mimics the current government roll-out policy by allocating immunisations using an age-stratified system. In this system, individuals aged 65 and older are preferentially vaccinated, with second preference for those aged 18 - 64 years, and third preference for those under the age of 18 (see Methods). We do not explicitly simulate partial vaccination (i.e., using one dose only), with the number of individuals immunised corresponding to the prospective number of completed vaccine treatment schedules. In this analysis we relax the condition that limits vaccine allocation to only 25% of the child population, instead limiting allocation only by the number of vaccines distributed. We made this choice to ensure that our parameter sweeps were not bounded by the limitations currently in place on vaccination of children, allowing a more complete scan of the parameter space available to the model and an effective identification of herd immunity thresholds.

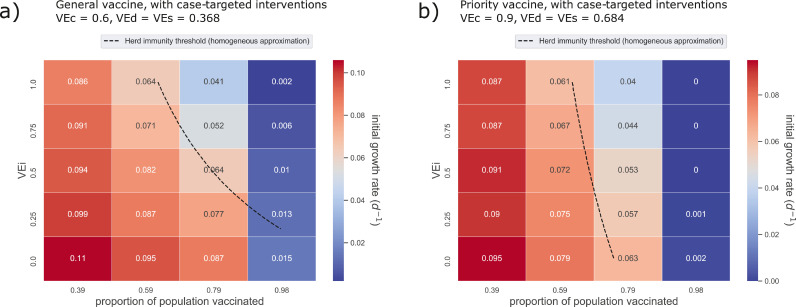
Our full results are given in the Supplementary Material Tables S5 through S16, and are summarised here below. Note that in the ABM, due to continuous introductions of cases from overseas, the clustering of children into school contact networks, and age-stratified vaccine roll-out, the vaccine coverage required for herd immunity is substantially higher than predicted by the homogeneous approximation (Fig. 1).

Fig. 1.

Simulations suggest that herd immunity is unlikely to be attained by either the general or the priority vaccine alone. The incidence growth rates shown here computed from results of the ABM over a range of values for coverage and vaccine efficacy against infectiousness ($\text{VEi}$) for the general vaccine (a, $\text{VEc}=0.6$) and the priority vaccine (b, $\text{VEc}=0.9$). Here, central values of efficacy against disease and susceptibility were used ($\text{VEd}=\text{VEs}=1-\sqrt{1-\text{VEc}}$), and case-targeted NPIs were applied in addition to vaccination.

Our results show that the general vaccine ($\text{VEc}=0.6$) alone cannot feasibly induce herd immunity, even when combined with targeted non-pharmaceutical interventions. Specifically, the general vaccine by itself (without case-targeted NPIs) can only produce herd immunity if efficacy for infectiousness (VEi) is above 0.5 (i.e., on the order of VEd and VEs, see Fig. S2a, with a coverage threshold between $80\%$ and $98\%$ corresponding to a nonlinear drop in epidemic growth rate, after which growth rapidly approaches zero. This result suggests that even if all individuals over 18 were vaccinated, and VEi were sufficiently high, a portion of the child population would need to be immunised in order to achieve herd immunity. However, there are still significant benefits for feasible ranges of vaccine coverage and efficacy.

Notably, peak prevalence can be reduced by a factor of two without the need for case-targeted interventions, with central values of $\text{VEd}$ and $\text{VEs}$ (i.e., when $\text{VEd}=\text{VEs}=1-\sqrt{1-\text{VEc}}=0.368$), a reasonable value of $\text{VEi}\approx 0.5$, and only $40\%$ population coverage (Tab. S6). Referring to Fig. S3a, increasing this vaccine coverage to approximately $80\%$ reduces peak prevalence by 83–$88\%$ (Tab. S6) and delays the peak by several weeks (Tab. S7). By combining case-targeted interventions with this $80\%$ coverage, the general vaccine can dramatically slow the spread of the virus. For VEi = 0.5, growth rate is reduced by 53% from the baseline value of 0.137$d^{-1}$ for unmitigated outbreaks down to 0.064$d^{-1}$ (Fig. 1a, Tab. 2). Even when herd immunity is not reached, this reduction in epidemic growth rate corresponds to large reductions in epidemic intensity as measured by the peak number of concurrent active cases (Fig. S4a).

Table 2.

Growth rates of daily incidence for eight different intervention scenarios. For each scenario, growth rates were computed for 110 realisations. The values shown here are ensemble means from each scenario, as well as the 5% and 95% quantiles of the growth rate distribution from each set of realisations and the 95% bootstrap confidence interval for the mean.

scenario	mean growth rate	quantiles [5%, 95%]	95% CI (mean, bootstrap)
no intervention	0.137	[0.128, 0.146]	[0.1356, 0.1376]
targeted NPIs only	0.118	[0.110, 0.127]	[0.1171, 0.1189 ]
priority vaccine (5M)	0.104	[0.097, 0.112]	[0.1034, 0.1052]
general vaccine (11.5M)	0.091	[0.083 0.099]	[0.0901, 0.0917]
priority vaccine (10M)	0.085	[0.076, 0.092]	[0.0843, 0.0859]
priority 10M, general 2.5M	0.078	[0.072, 0.087]	[0.0771, 0.0787]
priority 10M, general 6.1M	0.067	[0.061, 0.072]	[0.0666, 0.0679]
priority 10M, general 9.3M	0.057	[0.052, 0.062]	[0.0562, 0.0573]

The priority vaccine ($\text{VEc}=0.9$), produces similar benefits with a vaccine coverage as low as 60% and central efficacy values of $\text{VEs}=\text{VEd}=0.684$, $\text{VEi}\in [0.5,0.75]$ (Figures S2b and S3b). In combination with targeted interventions, our simulations suggest that the priority vaccine could produce herd immunity, with a coverage threshold between $80\%$ and $98\%$. This threshold exists even if efficacy against infectiousness is negligible (VEi $\approx$ 0), with the coverage required for herd immunity decreasing gradually with higher VEi (Fig. 1b). However, the current vaccination rollout in Australia constrains the maximum coverage of the priority vaccine, relying on a combination of priority and general vaccines. Therefore, substantial uptake of the less-effective general vaccine will be required if the benefits of the priority vaccine are to be realised for the whole population. For a more feasible coverage of $40\%$, the priority vaccine combined with case targeted NPIs reduces the epidemic growth rate by $34\%$ (with VEi = 0.5) and delays the peak by approximately 40 days (Fig. 1b, Fig. S4b, Tab. S16). As a benchmark value, note that our simulations show case-targeted interventions alone decrease growth rate by 14% relative to unmitigated outbreaks (Tab. 2).

To summarise, herd immunity is possible in principle for both general and priority vaccines, however, it requires coverage levels above 80% (of the entire population) regardless of whether or not case-targeted NPIs are implemented. Furthermore, for the general vaccine, herd immunity is not achievable at any coverage for VEi < 0.5, which is an optimistic upper bound for the general vaccine [17]. The results of the ABM are qualitatively consistent with the homogeneous approximation, but indicate that heterogeneity produces substantial quantitative differences in the coverage levels required for herd immunity. These levels are higher than what is currently achievable under the existing mass-vaccination strategy in Australia. Assuming limited vaccination in the Australian population younger than 18, overall vaccination coverage is constrained to less than 80%, even if the entire adult population is vaccinated.

B. Effects of hybrid mass-vaccination on epidemic growth

To investigate the possible effects of realistic mass-vaccination strategies on epidemic growth dynamics, we selected central values of efficacy for the priority vaccine ($\text{VEi}=\text{VEs}=\text{VEd}=0.684$) and general vaccine ($\text{VEi}=\text{VEs}=\text{VEd}=0.368$), and simulated initial epidemic growth in eight different scenarios (Tab. 1). We find that realistic hybrid vaccination campaigns systematically reduce epidemic growth rate with increasing coverage (by up to a factor of two). However, we do not identify a distinct coverage level beyond which growth rate decreases sharply (i.e., a herd immunity threshold).

Table 1.

Selected vaccination scenarios simulated with the ABM. The numbers under “priority immunisations” and “general immunisations” correspond to the number of individuals who have undergone a full vaccination regime (i.e., a two-dose regime for the priority vaccine). *TR: travel restrictions (ban on international travel), CI: case isolation (in-home isolation of detected cases), HQ: home quarantine (in-home isolation for household contacts of detected cases).

scenario	targeted NPIs	priority immunisations	general immunisations
no intervention	nil	nil	nil
targeted NPIs only	TR, CI, HQ*	nil	nil
priority vaccine (5M)	”	$5\times {10}^6$	nil
general vaccine (11.5M)	”	nil	$11.5\times {10}^6$
priority vaccine (10M)	”	${10}^7$	nil
priority 10M, general 2.5M	”	${10}^7$	$2.5\times {10}^6$
priority 10M, general 6.1M	”	${10}^7$	$6.1\times {10}^6$
priority 10M, general 9.3M	”	${10}^7$	$9.3\times {10}^6$

To improve the realism of our model for simulating hybrid vaccination scenarios, we use the latest estimates of coverage with the priority vaccine (enough has been purchased at the time of writing to vaccinate up to 10M individuals, or approximately $40\%$ of the population), and the general vaccine. We assume that the general vaccine will not be subject to supply constraints, with coverage limited instead by uptake. To reflect the current situation in Australia where the disease is currently controlled, we do not simulate a progressive vaccine rollout during the outbreak. We made the decision not to simulate progressive rollout for two reasons:

• 1.The timescale of COVID-19 outbreaks and the associated policy response has so far been much faster than the timescale of vaccination (substantial changes in vaccination levels require weeks or months, while outbreaks have typically triggered lockdown implementation within days).
• 2.Simulating progressive rollout requires several additional degrees of freedom, so that capturing the details of progressive rollout increases the complexity of the model without substantially improving the insight available from the results it generates.

Instead, we explore different coverage levels as a proxy for timing of the next epidemic wave between the beginning and end of the protracted vaccination campaign. We compare scenarios ranging from a relatively small number of priority vaccine immunisations (5M two-dose vaccinations), to an optimistic endpoint scenario with 10M priority (two-dose) immunisations and an additional 9.3M general immunisations, for coverage of 82% (100% of the adult population, and 25% of the population aged less than 18 years).

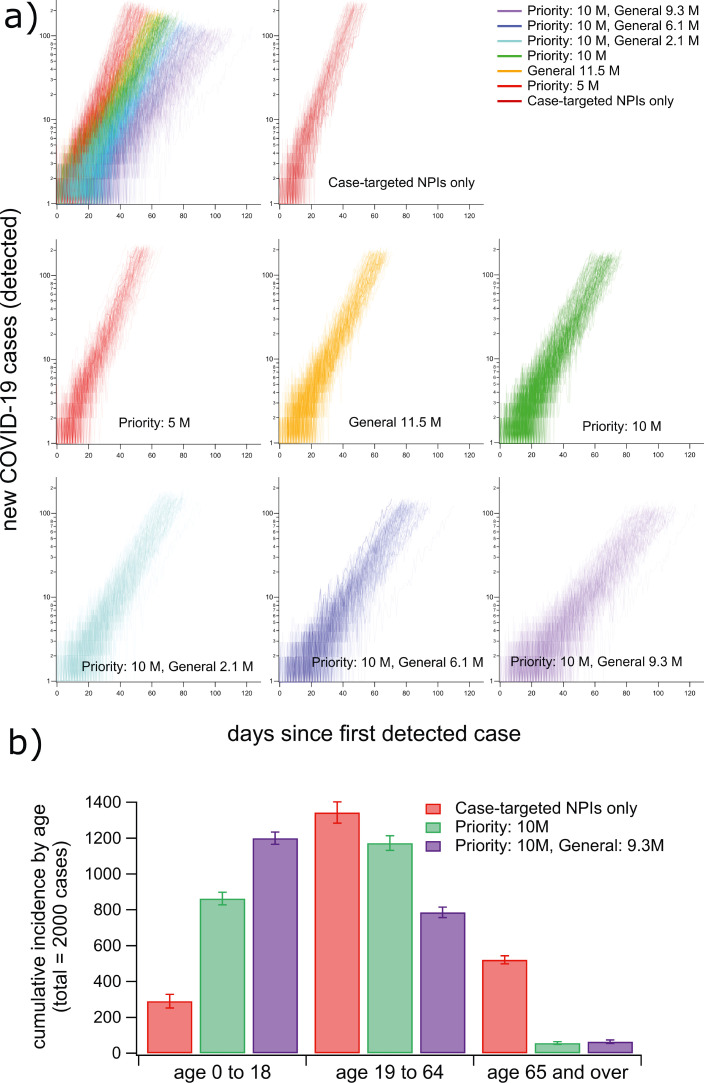
For each scenario, we simulated 110 realisations of outbreaks and estimated the expected growth rate of cumulative incidence for the first 2 000 cases (Fig. 2). To do so, we computed the incidence growth rate of each realisation (see Methods) and estimated the mean growth rate over all realisations of each mass-vaccination scenario (Tab. 2). Initial growth of case incidence decreases gradually as vaccination levels increase (Fig. 2). With 10M priority immunisations (maximum projected supply), the growth rate decreased by 28% relative to the rate computed with targeted NPIs only. At a feasible endpoint condition with $82\%$ of the population vaccinated (10M priority and 9.3M general immunisations), the average growth rate decreases by $52\%$ (from 0.118$d^{-1}$ with targeted NPIs only, to 0.057$d^{-1}$ with vaccination). In this scenario, the lockdown compliance required for epidemic suppression decreased by 43% (from $\approx 70\%$ with targeted NPIs only to $\approx 40\%$ with 82% vaccination coverage).

Fig. 2.

Hybrid vaccination programs produce up to a two-fold reduction of the epidemic growth rate. Individual incidence trajectories are colour-coded by mass-vaccination scenario (110 trajectories are shown for each). Each trajectory ends at the time the lockdown trigger condition was reached (cumulative incidence exceeding 2000 cases). The plots in (a) show log-scaled incidence trajectories for each vaccination scenario. Subplot (b) shows the distribution of the first 2000 cases in the three age groups used to prioritise vaccination in three representative scenarios (error bars show standard deviations over 110 realisations). Summary growth rate statistics for each scenario are given in Tab. 2.

Log-scaled plots of initial case incidence (Fig. 2a) clearly demonstrate the lack of a defined herd immunity threshold within the set of plausible scenarios we investigated. This is not surprising given that the levels of vaccine coverage reached are lower than those required for herd immunity with either vaccine individually (Fig 1). The distribution of the first 2000 cases between age groups suggests that systematically placing children at low priority for immunisation increases the required threshold for nonlinear reductions in epidemic growth rate (Fig. 2b), consistent with our results for single vaccine types (Fig. 1). Based on the risk-averse precedent for COVID-19 response in Australia, it is plausible that even the relatively slow spreading rates we calculate for the endpoint vaccination scenario would lead to some level of lockdown imposition, which we address in the following section.

C. Effects of mass-vaccination on lockdown requirements

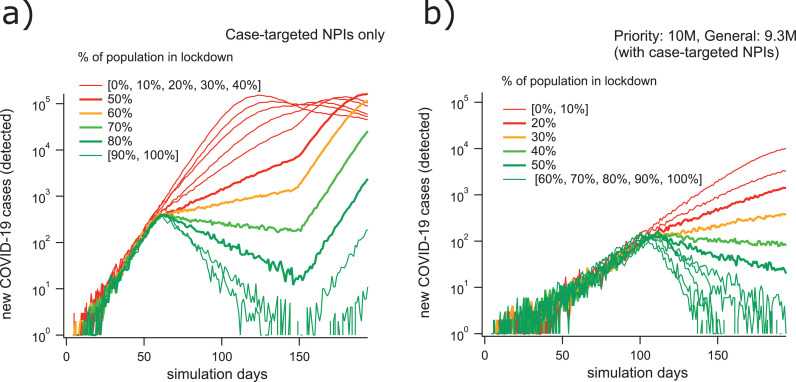
For the realistic vaccination scenarios given in Tab. 1, we estimated the level of lockdown compliance required to suppress epidemic growth. In each scenario, the population-scale physical distancing (lockdown) measures were enacted when the epidemic reached cumulative incidence of 2 000 cases. Choosing this relatively high threshold for the implementation of lockdown allows us to illustrate how epidemic dynamics depend on vaccination levels, and how these dynamics respond to the implementation of lockdown restrictions (Fig. 3). Incidence initially increases exponentially, and the growth rate is reduced after the imposition of lockdown restrictions (occurring at approximately day 50 in Fig. 3a, and at day 120 in Fig. 3b). If enough of the population complies with physical distancing measures, the growth rate becomes negative and the conditions for eventual suppression are met. In concordance with our previous work [1], this threshold lies between 60% and 70% compliance when only NPIs are considered. In these simulations, vaccination systematically decreased the fraction of the population required to maintain physical distancing restrictions in order to suppress epidemic spread. Summary results shown in Fig. 4 demonstrate how this compliance threshold depends on the level of vaccination. At the endpoint condition of 10M priority immunisations and 9.3M general immunisations, the lockdown compliance threshold drops to approximately 40% (Figures 3b and 4).

Fig. 3.

Our simulations suggest that realistic hybrid vaccinations strategies reduce the required intensity of lockdowns (mandated physical distancing) by a factor of two. Timeseries plots of representative case incidence trajectories for the scenario with targeted NPIs only (a) demonstrate a lockdown compliance threshold for elimination lying between 60% and 70%. Similar plots for the vaccination scenario with 10M priority vaccinations (VEc = 0.9; VEi = VEs = VEd = 0.684) and 9.3M general vaccinations (VEc = 0.6; VEi = VEs = VEd = 0.368), in addition to case-targeted NPIs, (b) show a lockdown compliance threshold for elimination lying between 30% and 40%.

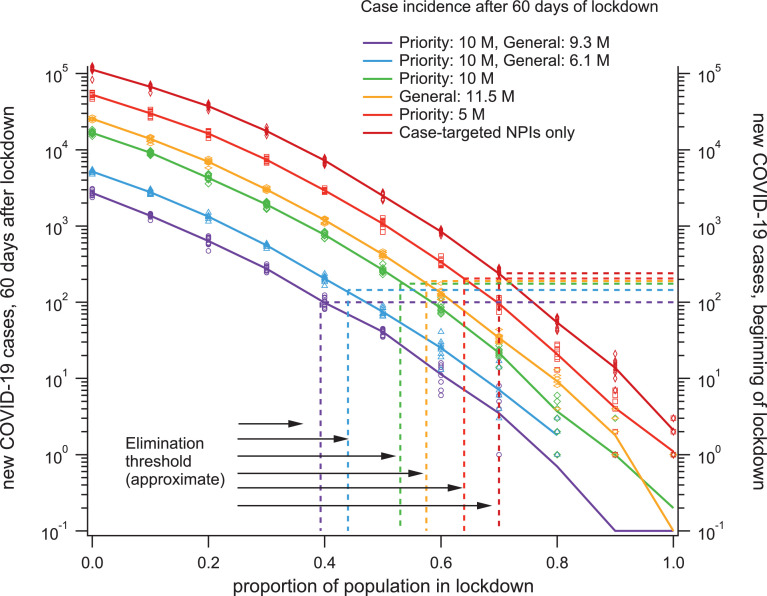
Fig. 4.

The intensity of lockdown required for gradual elimination of the virus steadily decreases with increasing vaccination levels. Solid lines connect ensemble averages of case incidence 60 days into the lockdown period for each scenario (left y-axis) while the values recorded from each individual simulation are shown as symbols. Each horizontal dashed line corresponds to the average incidence at the onset of lockdown (right y axis) for the vaccination scenario labelled with the same colour. The vertical dashed lines correspond to the approximate proportion of the population in lockdown required for case incidence to decrease, in each vaccination scenario.

In the Supplementary Material, we show results obtained for higher general vaccine efficacy (raised from VEc = 0.6 to VEc = 0.75, Fig. S7a), demonstrating that this approximate threshold was not sensitive within this range to the precise efficacy value used for the general vaccine. In addition, we carried out sensitivity analysis in terms of efficacy against infectiousness for the priority vaccine, contrasting higher (VEi = 0.684) and lower levels (VEi = 0.5). The corresponding results, summarised in Supplementary Fig. S7b, show that the reported outcomes are robust to this change as well.

Finally, we examined the sensitivity of our results to the priority structure of vaccine rollout (Figures S7b and S7c). Specifically, we re-parameterised the priority schedule to invert the prioritisation of individuals aged 65 or older relative to those aged 18-64, while holding constant the total vaccinated proportion in each age group. The requirements of lockdown under this inverted priority structure are practically invariant (Fig. S8). This result reflects a low sensitivity of the model to priority levels when overall vaccination coverage remains unchanged.

In addition to reducing the lockdown compliance threshold, vaccination reduces the growth rate of the epidemic even in the absence of lockdown restrictions, so incidence levels during outbreaks decrease dramatically for the same proportion of the population complying with physical distancing. For example, Fig. 4 demonstrates that, 60 days after the beginning of lockdown, the complete vaccination program consistently decreases case incidence by almost two orders of magnitude, independently to the proportion of the population complying. Such a difference in case incidence could be expected to have a dramatic impact on the projected strain to medical infrastructure, even without considering vaccine efficacy for severe disease. Additionally, Fig. 2 and Fig. 4 demonstrate that, due to slower epidemic growth with vaccination, case incidence at the onset of lockdown decreases from approximately 250 cases per day (targeted NPIs only), down to 100 cases per day (completed vaccination program). Taken together, these results indicate that vaccination would allow for shorter, less restrictive physical distancing mandates, if such measures were required in order to suppress subsequent outbreaks.

Discussion

Stochastic agent-based models have been established as robust tools for tracing fine-grained effects of complex intervention policies in diverse epidemic and pandemic settings [18], [19]. ABM studies have produced policy recommendations developed for the control of COVID-19 outbreaks, which have been adopted broadly by the WHO [20].

Typically, ABMs simulate each individual separately, aiming to account for heterogeneity of demographic and epidemic conditions, as well as details of social interactions and mobility patterns. This approach has a relatively high computational cost, driven by calibration of numerous internal ABM parameters [1], [21] and reconstruction of mobility patterns. However, ABMs offer an important advantage, combining both behavioural and mechanical adequacy of the model mechanism. Behavioural adequacy is verified by comparing simulated and actual epidemic patterns. Mechanical adequacy ensures, in addition, that the natural history of the disease progresses in concordance with the known estimates of incubation periods, serial and generation intervals, and other key parameters. Two ABMs, verified with respect to both behavioural and mechanical adequacy, provided a strong foundation for our study: ACEMod developed to simulate influenza pandemics [8], and AMTraC-19 created to simulate COVID-19 [1].

Our early COVID-19 study [1] compared several non-pharmaceutical intervention strategies and identified the minimal levels of social distancing required to control the pandemic. A compliance rate below 70% was found to be inadequate for any duration of social distancing, while a compliance at the 90% level was shown to control the disease within 13-14 weeks, when coupled with other restrictions. In another study we modelled pre-pandemic vaccination and targeted antiviral prophylaxis for influenza pandemics in Australia [22]. However, the COVID-19 pandemic demands new intervention protocols, optimised for given vaccine efficacy and coverage [23], [24], and accounting for logistical constraints, limited supply and hesitancy.

An early investigation by Bartsch et al. modelled trade-offs between the vaccine efficacy and vaccination coverage, before and during an epidemic in the USA [23]. The work showed that in order to prevent an epidemic, the efficacy has to be at least 60% when vaccination coverage is perfect (100%), and when the latter reduces to 60%, the necessary efficacy threshold increases to 80%. During an ongoing epidemic, higher efficacy thresholds were found to be needed to significantly reduce peak severity. The study conducted by Moore et al. modelled several vaccine components, in particular distinguishing between the vaccine types that may reduce susceptibility by inhibiting viral transmission (thus, indirectly protecting the individual) and the vaccine types that directly protect only the vaccinated individual by reducing the probability of developing severe symptoms [24]. Importantly, this study suggested that vaccinating older age groups initially may prevent a second wave within the UK, but only if the vaccine reduces both transmission and disease. Even in this optimistic scenario, only a highly efficacious vaccine, delivered to at least 70% of the population, was shown to succeed without NPIs. A high level of vaccination was also shown to be required in France, based on the ABM developed by Hoertel et al. who reported that vaccinating only priority groups (e.g., older adults) would be insufficient to lift NPIs [25]. Recent evidence from statistical modelling strongly suggests that indirect protection of unvaccinated individuals can indeed occur. However, identification of herd immunity thresholds using statistical models is hindered by many factors including lack of knowledge regarding the levels of natural immunity imparted by recovery from infection, the constantly changing effects of individual behaviour, and the influence of state-imposed mitigation policies [26].

Thus, while it is clear that vaccination cannot provide herd immunity without mass population coverage, to what extent coverage requirements can be alleviated by maintaining some (relaxed) level of social distancing and other suppression measures in a highly heterogeneous demographic setting remains an open and country-specific question. This question becomes more complex when several vaccines are considered, each with a different combination of efficacy against susceptibility, infectiousness and disease.

In attempting to reduce uncertainty of this complex space, we considered different mass vaccination scenarios tailored to the current situation in Australia, while varying the key intervention parameters. As a result, we identified several salient trade-offs between the (pre-pandemic) vaccination and (future) lockdown requirements. Qualitatively, these trade-offs are not dissimilar to those reported by Bartsch et al. [23], however, the thresholds which we quantified for Australia are specific for a more refined, hybrid, mass vaccination campaign (with priority and general vaccines). We also reinforce the findings of Moore et al. [24] with respect to separate components of the vaccine efficacy: future outbreaks become preventable only when the distributed vaccines avert transmission as well as disease. Crucially, no combination of realistic vaccine efficacy values was found to completely eliminate the pandemic threat in Australia without population-scale NPIs, under the feasible vaccination coverage extents that we simulated. This is somewhat different from the results of Moore et al. [24], where such an outcome was shown to be theoretically possible in UK, but only by adopting a highly efficacious vaccine. The necessity of partial lockdowns is in concordance with the analysis of Hoertel et al. [25], which highlighted the difficulties in lifting NPIs under realistic vaccination strategies considered in France.

In the main analysis we used a relatively high level of efficacy against infectiousness for the priority vaccine (VEi = 0.684). Recent studies such as that of Harris et al. [17] narrowed the estimates of VEi for BNT162b2 to a lower level (VEi $\approx$ 0.5). In order to verify robustness of our results to changes in VEi between higher and lower levels, we carried out an additional sensitivity analysis which confirmed that the reported outcomes persist across this range of VEi values (Fig. S7).

There is a remaining uncertainty about the clinical efficacy of ChAdOx1 nCoV-19 (Oxford/AstraZeneca) vaccine under different vaccine administration schedules. An interim analysis of four randomised controlled trials carried out in three countries (Brazil, South Africa, and the UK) between April and November 2020 suggested a vaccine efficacy of 62.1% (95% CI: 41.0–75.7) in participants who received two standard doses separated by four weeks [27]. When two standard doses were separated by 12 weeks or longer, the vaccine efficacy was observed to be higher at 81.3% (95% CI: 60.3–91.2) [28]. However, the follow-up study did not explicitly account for seasonal effects and variation between the trial countries in terms of the epidemic intensity (as well as circulating viral variants). In addition, these trials were not designed to discriminate between vaccine efficacies by dose interval, and therefore, these encouraging “post-hoc exploratory findings could be biased” [29]. Given the reported wide confidence intervals and a possible bias, we considered two settings for efficacy of the general vaccine. Firstly, we adopted a conservative estimate for the efficacy VEc = 0.6 (i.e., 60%), while varying different components of the efficacy in a broader range. Secondly, we explored a more optimistic setting, VEc = 0.75 (assuming an optimal dose separation regime). We found that our results regarding the lockdown compliance rate required for elimination did not change when we increased the efficacy of the general vaccine from VEc = 0.6 to VEc = 0.75 for the originally planned rollout strategy which followed the allocation ratio of 100:10:1 (for 65+ : 18-64 : <18 age groups, Fig. S8).

The optimistic setting for general vaccine (VEc = 0.75) was also used in sensitivity analysis of

• (a)the effects of changing infectiousness efficacy for the priority vaccine from a higher (VEi = 0.684) to a lower level (VEi = 0.5), for the original allocation ratio 100:10:1 (cf. Figures S7a and S7b), and
• (b)the impact of the adjusted rollout strategy based on the revised allocation ratios, while maintaining the more conservative level of efficacy against infectiousness (VEi = 0.5) for the priority vaccine (cf. Figures S7b and S7c).

This comparative analysis confirmed the overall robustness of our results based on the latest available information, including (i) an optimistic setting of efficacy of the general vaccine (VEc = 0.75), (ii) a conservative level of efficacy against infectiousness for the priority vaccine (VEi = 0.5), and (iii) an adopted rollout strategy adjusted for the revised allocation ratios.

Our finding, that herd immunity is not attained even when a large proportion (82%) of the population is vaccinated, can be explained as a consequence of two correlated sources of heterogeneity. The first is structural, and occurs due to the unavoidable clustering of children in schools and classrooms. The second is imposed by the choice to place children at low priority for immunisation (due to typically low disease severity in this cohort). In Australia, school-aged children (aged from 5 to 18 years), comprise approximately 15% of the total population (with about 5% composed of children under the age of 5). Therefore, even with 82% of the population vaccinated, roughly three quarters of the child population will remain fully susceptible to the virus. Of those who are vaccinated, very few (if any) will receive the priority vaccine. In our ABM, the result is an interconnected subpopulation with high susceptibility. During outbreaks, this produces deviations from the homogeneous approximation in the form of heterogeneous epidemic spread strongly biased towards school-aged children. While the source of this deviation is produced in our model by the policy decision not to vaccinate large numbers of children, the general result is similar to those related to discretionary differences between clustered social groups with high levels of vaccine scepticism or hesitancy [30]. Therefore, changing health recommendations regarding vaccination of young people may not be sufficient to correct such deviations, which may also be influenced heavily by public opinion and the social clustering of those with similar views.

It has been widely established that children are at much lower risk of severe COVID-19 disease. However, estimates of transmission rates among children are made difficult by the relatively low rate of symptom expression in young cohorts [31]. The current advice from the United States CDC suggests an emerging consensus that transmission rates in young people are similar to those in the adult population [32]. In our model of COVID-19 transmission, we did not truncate the susceptibility or infectiousness of children but we did assume a lower rate of symptom expression, in line with the available evidence [1].

Taken together, these factors mean that age-stratified vaccine prioritisation represents a trade-off: by comprehensively vaccinating older adults with the priority vaccine, the system ensures lower levels of severe disease in the highest-risk cohort, even with low levels of coverage. However, our results demonstrate that this may come at the cost of precluding eventual herd immunity as the virus continues to spread slowly among the (largely asymptomatic) young cohort. Meehan et al. simulated optimised vaccination strategies and demonstrated that in order to achieve herd immunity, those at highest risk of transmission must be targeted for immunisation [33]. In our model, infections in children produce a high transmission risk, despite presenting a low risk of symptomatic disease. In this context, and given the current uncertainty with respect to efficacy of COVID-19 vaccines on transmission, our results demonstrate that the Australian strategy trades possible herd immunity for a reduction in severe case load potential.

Limitations and future work

In comparison with [1], our model included a more refined natural history of the disease, calibrated to recent outbreaks which occurred after the first wave in Australia. Nevertheless, the model does not explicitly capture in-hotel quarantine, hospitalisations, and in-hospital transmissions. This limitation is offset by the fact that in Australia’s vaccination plan, healthcare and border control professionals are included in the priority vaccination phase, carried out in a pre-pandemic mode. We also do not systematically quantify mortality rates, and do not elaborate on the expanding disease surveillance capacity and standard clinical pathways in Australia [34].

As we pointed out, no herd immunity is attainable under currently feasible conditions. This outcome has several ramifications beyond the direct consequences of future partial lockdowns. On the one hand, the main reason for the inadequate collective immunity is the existence of highly clustered, networked communities (e.g., educational, religious and community groups, etc.). This highlights the need for a more sophisticated simulation of contact networks, in addition to the workplace/school environments generated from the census data. On the other hand, the lack of herd immunity may affect the behaviour of the “free-riders” who typically exploit the collective protection of mass immunisation while not committing to the vaccination themselves. This may create a feedback loop, reducing vaccine hesitancy in the near- to mid-term, and generating long-term oscillatory dynamics in vaccine adoption [35].

Another caveat is that our ABM population is matched to the latest Australian Census data, which was collected in 2016. This produces a model population of 23.4M individuals, which is smaller than the current Australian population by approximately 2M people. Due to this discrepancy, the coverage proportions defined for fixed numbers of vaccines are slightly inflated in our simulations (by about 8%), relative to what would be achieved with the current population count. Because we did not identify a threshold in epidemic severity as a function of vaccine coverage in our hybrid scenarios, we do not expect this discrepancy to qualitatively alter our results.

Finally, our simulations treat the entire population as initially susceptible, not accounting for the influence of pre-existing immunity in the population produced by previous waves of COVID-19 in Australia. The effective suppression of these previous outbreaks has kept cumulative confirmed case totals below 1% of the total population, so we do not expect this simplifying assumption to influence our results.

Conclusion

In this work, we extended a high-resolution agent-based model of COVID-19 mitigation and control to simulate the effects of coupled vaccination and non-pharmaceutical strategies on future outbreaks in Australia. We found that, combined with case-targeted interventions, a completed mass-vaccination campaign using both a 90% effective vaccine for priority populations and a 60% effective vaccine for the general population would dramatically slow viral spread but would not produce herd immunity. If a community transmission outbreak were to occur during or after the vaccination campaign, population-scale non-pharmaceutical interventions (i.e., lockdown) would be necessary to curb transmission. In our simulations, the required extent and duration of these measures decreased gradually with the level of vaccination coverage obtained by the time of the outbreak. For realistic endpoint conditions, with 82% of the population vaccinated, the required lockdown intensity decreased by 43% and and initial epidemic growth rate decreased by 52%. Due to coupling between these two factors (broadening of the epidemic curve and increased effectiveness of nonpharmaceutical interventions), the severity of epidemics as measured by the peak number of new cases over a 24hr period decreased by up to two orders of magnitude under plausible mass-vaccination campaign endpoint conditions.

With respect to the prognosis for future outbreaks of COVID-19 in Australia, several important questions remain unaddressed by our study. Because we did not model the effect of vaccination on hospital case load, medical infrastructure, and mortality, our results do not directly inform estimates of the trade-off between the socioeconomic costs of lockdown and the human cost of allowing a low level of COVID-19 transmission. Finally, at the time of writing, several SARS-CoV-2 variants of concern have been identified. Among them, variant B.1.1.7 (Alpha), which emerged in the United Kingdom and has spread globally, was associated with increased transmission potential: specifically, its $R_0$ was estimated to be 43-90% (95% CrI: 38–130%) higher than reproduction number of preexisting variants [36]. Variant B.1.351 (Beta), originally identified in South Africa, has been provisionally associated with lower rates of neutralisation by polyclonal antibodies, and variant P.1 (Gamma), thought to have originated in Brazil, has been associated with a major outbreak in a population thought to be effectively immune [37], [38]. Most recently, variant B.1.617.2 (Delta), first detected in India, has become the dominant strain in many countries, increasing risk of household transmission by approximately 60% compared to the Alpha variant [39]. Given the currently low level of understanding about the implications of these variants in future outbreak scenarios, our results should be viewed as optimistic guidelines that assume the continuing vaccination efforts can keep pace with the evolution of SARS-CoV-2.

Contributors

CZ and MP conceived and co-supervised the study, designed the computational experiments and drafted the original Article. CZ and OMC developed the agent-based model. CZ implemented intervention strategies. All authors developed and calibrated the COVID-19 epidemiological model, and performed sensitivity analysis. SLC and CZ carried out the computational experiments and analysis, verified the underlying data, and prepared all figures. All authors had full access to all the data in the study. All authors contributed to the editing of the Article, and read and approved the final Article.

Data sharing

Post-processing source data and supplementary data are provided with this Article. The full data can be made available to approved bona fide researchers after their host institution has signed a Data Access/Confidentiality Agreement with the University of Sydney. Mediated access will enable data to be shared and results to be confirmed without unduly compromising the University’s ability to commercialise the software. To the extent that this data sharing does not violate the commercialisation and licensing agreements entered into by the University of Sydney, the data will be made publicly available after the appropriate licensing terms agreed.

Declaration of interests

We declare no competing interests.

Declaration of Competing Interest

The authors declare no conflict of interest.

Appendix A. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/