Abstract
In alchemical free energy (FE) simulations, annihilation and creation of atoms are generally achieved with the soft-core potential that shifts the inter-particle separations. While this soft-core potential eliminates the numerical instability occurring near the two end states of the transformation, it makes the hybrid Hamiltonian to vary non-linearly with respect to the parameter λ which interpolates between the Hamiltonians representing the two end states. This complicates FE estimation by Bennett acceptance ratio (BAR), free energy perturbation (FEP) and thermodynamic integration (TI) methods, and thus reducing their calculation efficiency. In this work, we develop a new type of repulsive soft-core potential, called Gaussian soft-core (GSC) potential, with two parameters controlling its maximum and width. The main advantage of this potential is the linearity of the hybrid Hamiltonian with respect to λ, thus permitting the direct application of BAR, FEP, TI and other variant FE methods. The accuracy and efficiency of the GSC potential are demonstrated by comparing the free energies of annihilation determined for 13 small molecules and an alchemical mutation of a protein side chain. In addition, in combination with a TI integrand (∂H/ ∂λ) estimation strategy, we show that GSC can considerably reduce the number of λ simulations compared to the commonly used separation-shifted soft-core potential.
Graphical Abstract
I. INTRODUCTION
Alchemical free energy (FE) simulation is a widely used approach for determining the free energies of small molecule solvation,1–4 ligand binding5–10 and side chain modifications of proteins and nucleic acids.11–15 In general, the alchemical transformation is achieved by linearly interpolating between the two end-state Hamiltonians with a coupling parameter λ and performing simulations at several fixed λ values for increased overlap of configurations between them. The FE of the transformation is then calculated by applying the thermodynamic integration (TI),16 free energy perturbation (FEP)17 or Bennett acceptance ratio (BAR) method.18 Over the past decade, considerable efforts have improved the alchemical FE calculation. Notable examples are the automation of alchemical calculation protocols,19–24 improved configuration sampling,25–33 the use of polarizable force-fields and electronic structure methods34–37 and the solution of many longstanding issues, such as the net charge of transformation,38–40 multiple protonation and tautomeric states41 and scaffold hopping.42 Beyond these efforts, it remains a challenge to eliminate the issue of “end-point catastrophe,”43–45 which occurs due to the physical overlap of solvent molecules with the newly created or annihilated atoms of the transformation.46 Although other approaches are possible,47–52 the soft-core potential44–45 is most common for circumventing this issue.
The separation-shifted scaling potential,44 referred to herein as conventional soft-core (CSC) potential, is often used to eliminate the end-point problem by shifting the inter-particle distances between the solute and solvent atoms and scaling their interactions in a λ-dependent manner. Although the CSC potential has been adopted in many molecular simulation packages, including CHARMM,53 AMBER,54 NAMD,55 GROMACS56 and GROMOS,57 its explicit λ-dependence complicates the evaluation of FE and reduces the overall efficiency of the calculations. For example, in the BAR and FEP methods, the potential energies at different λ values must be evaluated in a post-processing or on-the-fly manner.58 This is particularly tedious with the multistate Bennett acceptance ratio (MBAR)59 and weighted histogram analysis methods (WHAM).60
This work presents the development of a Gaussian-type soft-core (GSC) potential which eliminates the weakness of the CSC potential described above. The main difference of GSC from CSC is that the GSC potential is introduced as an ad hoc repulsion between the transformed solute and the surrounding solvent molecules. Consequently, the hybrid Hamiltonian retains its linearity with respect to λ, allowing direct application of the TI, FEP and BAR methods. The parametric nature of GSC then makes it possible to reduce the number of λ simulations compared to CGC. Taking these advantages, we have developed several protocols for efficient alchemical FE simulations. Below, we describe the GSC potential developed as well as the different FE simulation methods. Then, the developed method is tested against the CSC potential, followed by a summary of the paper.
II. THEORY
A. Alchemical free energy calculation methods
In alchemical FE simulations, the hybrid Hamiltonian Hλ is constructed by interpolating between the two end-state Hamiltonians, H0 and H1. Although non-linear interpolation is possible,45, 61–62 linear interpolation is predominantly used, as
| (1) |
where λ varies between 0 and 1. Then, the simulations are performed at fixed λ value, during which the configurations of the system are saved for post-processing calculation of FE using the TI, FEP and BAR methods. Below, each of the different FE methods used in this work is briefly discussed to facilitate the discussion.
Thermodynamics integration (TI):
In the TI method, the free energy difference (ΔF) between the two end states is determined by integrating the free energy gradient along the entire transformation between λ = 0 and 1,
| (2) |
where F(1)(λ) refers the first order derivative of F(λ) with respect to λ, i.e., ∂F/∂λ, and 〈… 〉λ represents an ensemble average in the Hλ phase space. In this equation, if the total number of atoms and their masses are conserved between the two end states, ∂H/∂λ can be replaced with the potential energy derivative ∂U/∂λ. Further, it is equal to the potential energy difference (ΔU = U1 − U0) for the Hamiltonian in eq. (1). Then,
| (3) |
In practice, the integration is carried out by a numerical quadrature based on the simulations performed at N discrete λ states,
| (4) |
where F(j) and w(j) are the j-th order derivative of free energy and its associated weight, determined up to the mi-th order. In the integration, although other quadrature methods are possible,63–65 the trapezoidal and Simpson’s rules are the most common. In the present work, the trapezoidal rule was applied to all TI calculations.
Free energy perturbation (FEP):
In the FEP method,17 the FE difference between two λ values is determined by an exponential average of their potential energy gap, as
| (5) |
where β−1 = kBT and kB and T are the Boltzmann constant and Kelvin temperature, respectively. In FE evaluation, the double-wide sampling (DW-FEP) is usually performed by perturbing the systems at λ1 and λ2 to their mid-point λ value.66 Then, the total FE value is determined as the summation over all the intermediate FE values,
| (6) |
In this equation, represents the forward perturbation FE from λi to and the backward perturbation FE from λi+1 to , where is a value between λi and λi+1, most commonly a mid-point value.
Bennett acceptance ratio (BAR) method:
The BAR method18 determines the ΔF value by iteratively solving the following equation,
| (7) |
where f(x) = 1/[1 + exp(βx)], and Q refers to the partition function. The value of C, thus ΔF, is determined by maximizing the overlap between the weighted density distributions of the two states, i.e., . The BAR method predicts the ΔF value with a minimum variance and thus is usually more reliable and efficient than TI and FEP.67–68 However, unlike FEP, BAR requires that the simulations must be performed at least at the two λ values to determine the FE value between them, and that the configurations sampled must have a sufficient overlap between the different λ states.18, 69–72
B. Soft-core potentials
Separation-shifted soft-core potentials:
The separation-shifted scaling potential, i.e., conventional soft-core (CSC) potential in this work,44 was developed to eliminate the singularity of the Lennard-Jones (LJ) potential at zero inter-particle separation. The modified LJ potentials are
| (8a) |
and
| (8b) |
where is the well depth of the LJ potential, the inter-particle distance at the LJ minimum, δ the shift parameter and “prime” indicates the summation only for the solute-solvent pairs. Since CSC does not alter the (hybrid) Hamiltonians at λ=0 and 1, it produces a correct FE value. The CSC potential can also be applied to the electrostatic interactions. However, its rigorous implementation in the context of the particle mesh Ewald (PME) summation is not straightforward. For example, both the real and reciprocal space terms have to be evaluated with the soft-core potential for a correct cancellation of the reciprocal space terms within the real-space cutoff, while in the most implementation, only the real space terms are evaluated with the soft-core potential.73–74 Although this does not cause problems at the two end states, they lead to incorrect estimates of Coulomb interactions at intermediate λ states. For this and other reasons as described by Steinbrecher et al.,61 we have not considered its application to the electrostatic interactions in this work and have performed all simulations using the two-step annihilation process in Figure 1.
Figure 1.
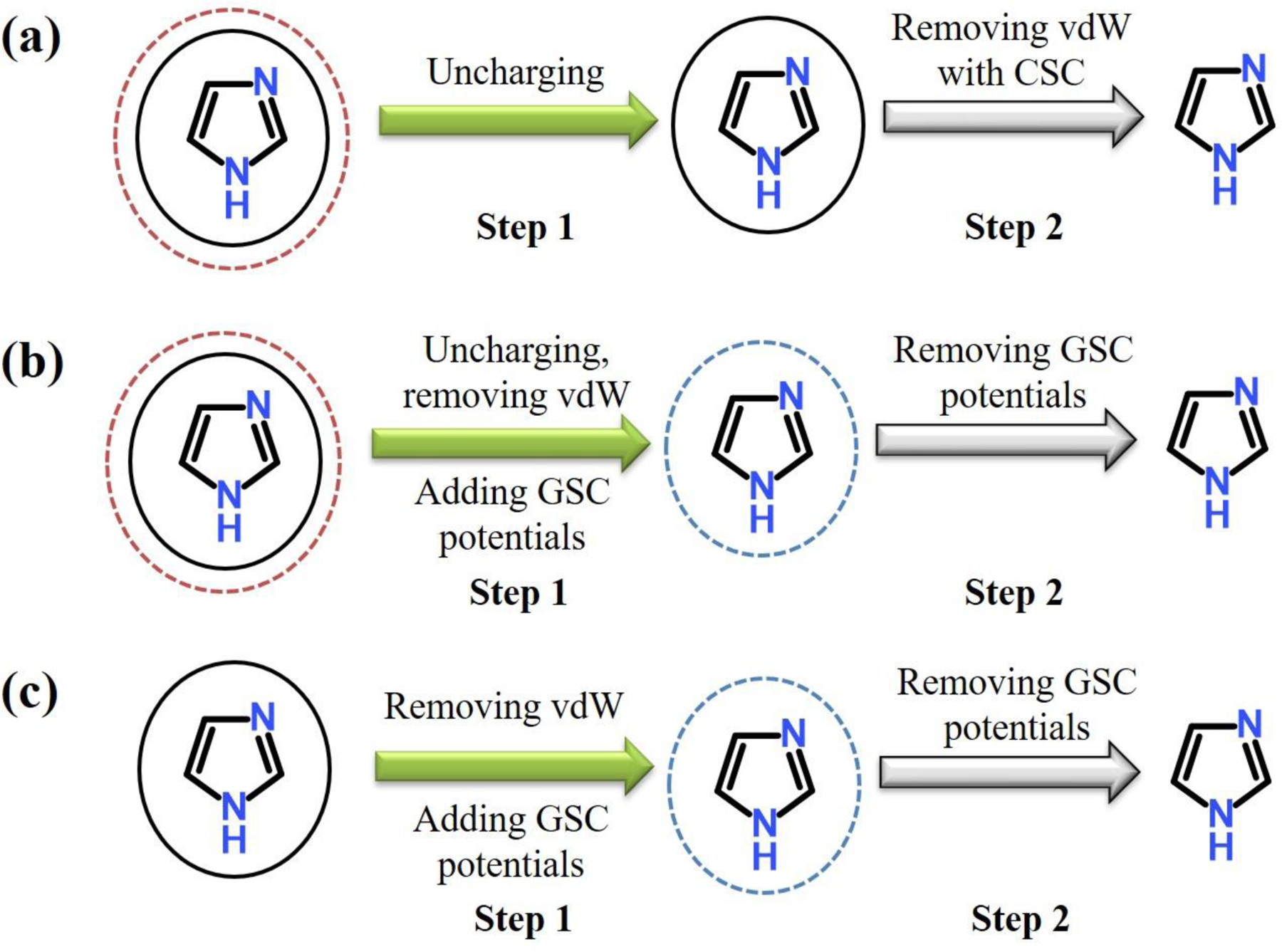
Two-step annihilation protocols of solutes in water. (a) In the CSC protocol, the first step (Step 1) removes the electrostatic interactions of solute with solvents, and the second step (Step 2) removes the van der Waals (vdW) interactions with CSC potential. (b) In this GSC protocol, the first step (Step 1) removes the electrostatic and vdW interactions of solute with solvents, while GSC repulsion is turned on. The GSC repulsion is removed in the second step (Step 2). (c) For solute without charges, vdW interaction is removed in two steps with the GSC potential. The first step removes the vdW interaction of solute with solvents, while GSC repulsion is turned on. The GSC repulsion is turned off in the second step.
Despite its wide use, CSC has several shortcomings. First, because of the explicit λ-dependence of the LJ potentials (eq. (8)), the derivative ∂U/∂λ for TI requires the evaluation of two additional terms, as
| (9) |
For FEP and BAR, eqs. (5) and (7) involve a tedious evaluation of the potential energies at different λ values in a post-processing or on-the-fly manner. In the absence of CSC, on the other hand, their corresponding values can be simply determined for any pairs of λ values based on the U0 and U1 values recorded during each λ simulation.58 Second, when multiple atoms are added or deleted, the TI integrand for the vdW transformation is highly non-linear with the transformation of the solute. For this reason, simulations at many intermediate λ states must be performed to accurately describe the curvature of the TI integrand over the entire range of λ between 0 and 1.58 These issues can be mitigated by several different soft-core potentials developed,75–76 such as, the “cap potential” which softens LJ interactions at short inter-particle separation.76 Although it removes the explicit λ-dependence of ∂U/∂λ, it leads to heavily skewed ΔU distributions near the end states76 and requires more λ simulations.
Gaussian-type soft-core (GSC) potentials:
Based on the above discussion, the requirements that the newly developed soft-core potential must meet are as follows: First, the soft-core potential should not alter the Hamiltonians at the two end states. Second, the linearity of the hybrid Hamiltonian must be kept for direct application of TI, FEP and BAR. In other words, the hybrid Hamiltonian should be a linear function of λ as in eq. (1). Finally, the new soft-core potential should produce a smooth alchemical transformation. That is, ∂U/∂λ should vary smoothly with respect to λ. For example, when both Coulomb and LJ interactions are turned on, CSC occasionally produces unexpected minima at certain λ values. This can lead to a sudden jump in ∂U/∂λ and thus, unreliable FE estimation.75
These requirements are satisfied with GSC potential developed in this work, which are added to the regular non-bonded interaction energy, Unb (i.e., a sum of the unmodified electrostatic and van der Waals interactions) as
| (10a) |
and
| (10b) |
where X = 2 or 4. In the equation, “prime” indicates the summation only between the solute-solvent pairs, where the solute refers to the entire solute or a part of it that is alchemically transformed. The total non-bonded interaction energy of the entire system in eq. (1) is then
| (11) |
In eq. (10), α and β are the user-provided parameters defining the maximum and width of the repulsion, respectively. The equation is general and allows for an easy control of the GSC terms in the different alchemical transformation simulations as presented in Supporting Information. In such simulation, since GSC is only applied to the solute-solvent pairs, the overhead of the GSC potential is negligible. Moreover, when α=0, its evaluation can be skipped. In this study, when GSC is turned on, X = 4, α = 5 kcal/mol and β = 5. Otherwise, α is set to zero (i.e., no GSC potential).
Because of the different behavior of GSC from CSC, the protocol of the alchemical transformation requires certain modifications (Figures 1 and S1). For example, when annihilating a solute, the transformation is carried out in two steps. In the first step, the LJ and Coulomb interactions of solute with solvents are removed by setting the ε and charge values of the solute to zero, while the GSC repulsion is turned on. In the end of this step, the solute is purely represented by the GSC potential, forming a cavity around it. In the second step, the GSC potential is turned off to complete the annihilation. In this step, although the solvents can penetrate the solute as λ approaches 1, they do not cause any singularity in the energy. Thus, numerical stability is guaranteed in the simulation as well as in the FE evaluation. As described in the Results and Discussion section, we can also use this penetration to reduce the number of λ simulations needed. Details on how the two-step annihilation is performed are presented in the Supporting Information. In Figure 2, we also show how the GSC repulsion interacts with the LJ term when the LJ interaction is switched off while GSC is turn on as λ changes from 0 to 1.
Figure 2.
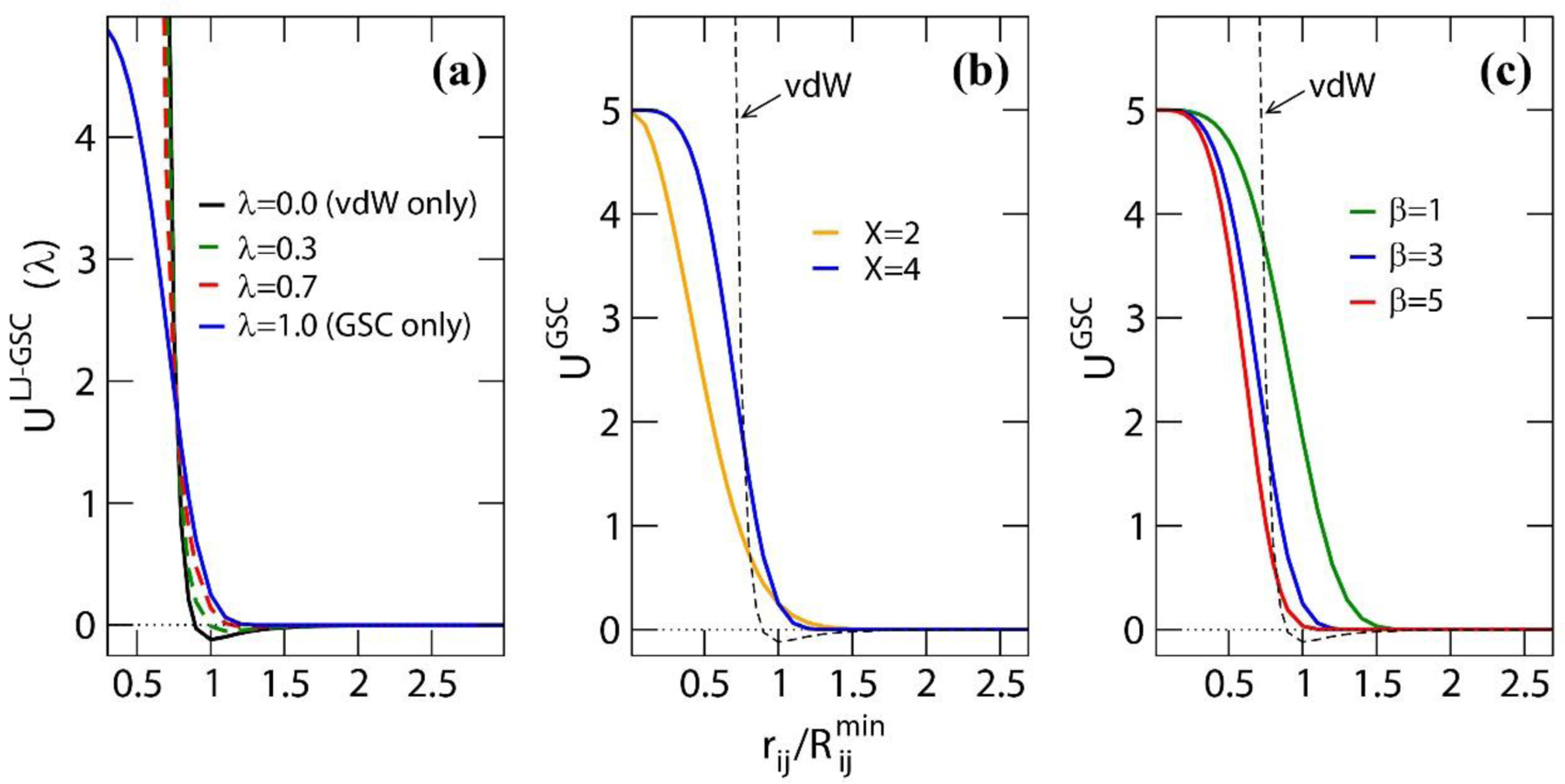
(a) The interaction of the GSC repulsion with the Lennard-Jones (LJ) potential at different λ values. In the plot, ULJ−GSC(λ) = (1 − λ)ULJ + λUGSC, i.e., the process occurs such that the Lennard-Jones potential is turned off while the GSC repulsion is turned on. The εij value used for the LJ potential is 0.12 kcal/mol, and for GSC, α = 5 kcal/mol, β = 3 and X=4. Comparison of the GSC potentials (b) between X=2 and 4, in which α = 5 kcal/mol and β = 3, and (c) between the different β values with α = 5 kcal/mol and X=4. In (b) and (c), the van der Waals interaction potential (εij = 0.12 kcal/mol) is also shown.
C. Combining TI with DW-FEP
The FEP equation (e.g., eq. (5)) can be differentiated with respect to λ.77 For a hybrid Hamiltonian that is a linear function of λ, its first order derivative becomes the weighted ensemble average of ΔU (i.e., U1 − U0) sampled at λ′,
| (12a) |
| (12b) |
where … |λ′ denotes the value estimated based on the simulation at λ′. The accuracy of the predicted value then depends on the overlap of the configurations sampled at λ′ to those at λ.76, 78–79 Several alchemical FE calculation methods have been developed by applying the same principle.78–83
Eq. (12) proposes a simple strategy for determining the range of λ values, at which the FE value can be reliably estimated using the sampled configurations at λ′. The same strategy can also be used to determine the number of λ simulations and their λ values. For example, based on the configurations sampled at λ1 and λ2, the values can be determined using eq. (12) at any λ value. Then, as shown in Figure 3, their difference, i.e.,
| (13) |
has a minimum between λ1 and λ2. If the minimum is smaller than a threshold which can be determined on the basis of the accuracy of the FE value desired, e.g., 1 kcal/mol, the DW-FEP calculation is performed to the λ value at the minimum. Then, the error of the FE value is . If the minimum is greater than the threshold and/or if a higher accuracy of FE is desired, an additional simulation is performed at this λ value. This process is iterated until the desired accuracy of FE is reached. Previously, Tidor and Karplus applied this combined FEP/TI approach to improve the TI quadrature.83 Hereafter, we refer this method to as the TI integrand prediction-guided DW-FEP (simply, IPDW-FEP) method. Compared to the commonly used mid-point DW-FEP, which is a de facto non-optimized version, IPDW-FEP considers the asymmetry of the alchemical transformation and is more general.
Figure 3.
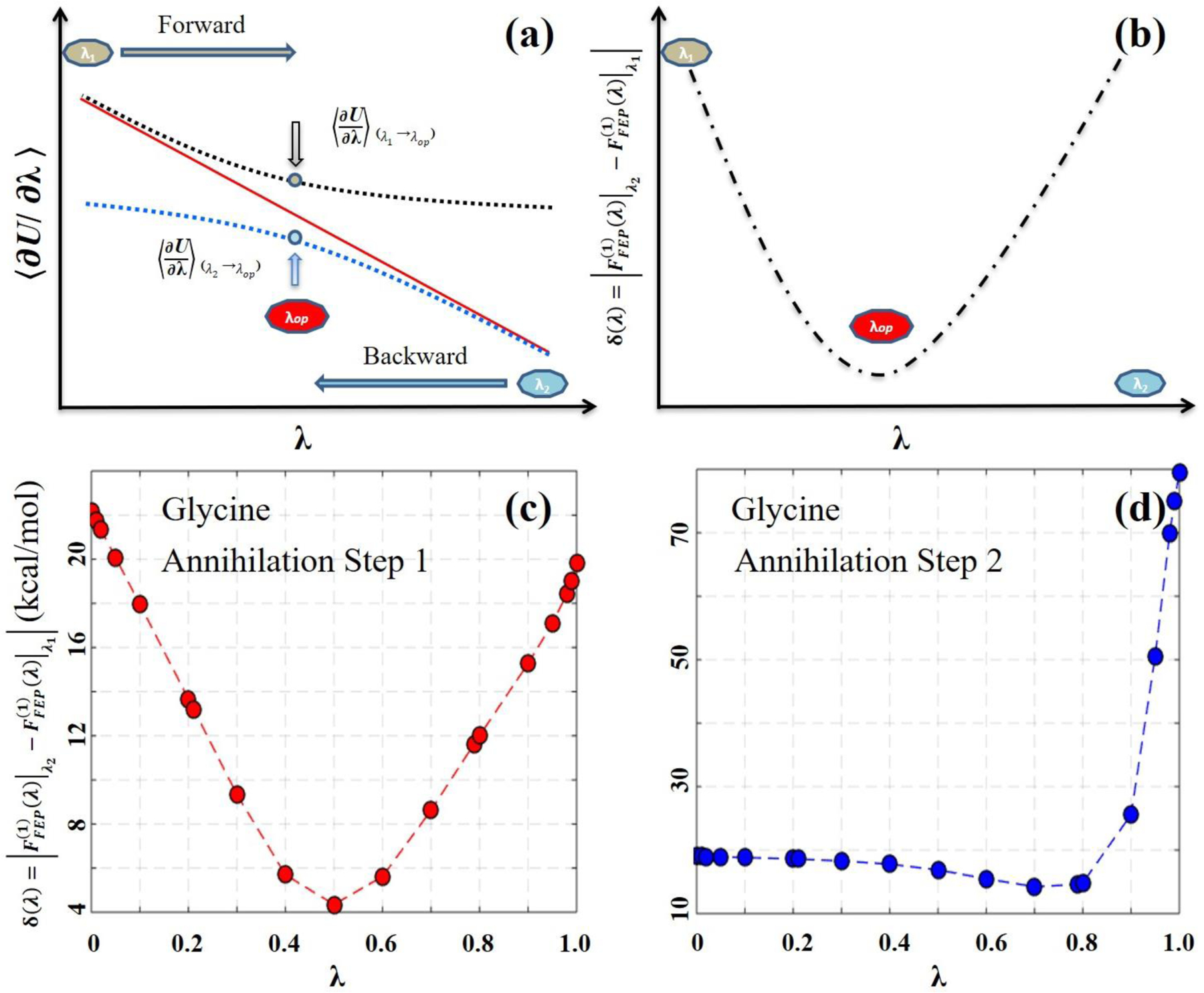
Schematic illustration to identify an optimal λ value for the IPDW-FEP method. (a) The original and predicted TI integrands. The solid red line represents the original TI integrands determined from each λ simulation. The dashed blue lines represent the TI integrands predicted based on the configurations sampled at the two end-point λ values, i.e., λ0 and λ1. (b) The difference between the two predicted TI integrands, i.e., δ(λ) of eq. (13). The arrows in (a) indicate the λ value at the minimum of δ(λ) in (b), at which the DW-FEP calculation yields a minimum FE error.
III. COMPUTATIONAL DETAILS
The GSC methods and protocols developed were tested using 13 small molecular systems and one protein system, i.e., insulin-like growth factor receptor kinase (IGF-1RK).84 The 13 molecular systems, which cover diverse functional groups, charge states and large solvation FE variations, were annihilated in water. For the protein system, phosphorylation modification of IGF-1RK (i.e., Tyr-to-pTyr modification) was simulated. The same transformation was also performed in water.
The PERT module available in the CHARMM program (version c41a2)53 was used in all simulations with the relevant modification for the GSC potentials. The CHARMM36 force fields85 and the TIP3P water model86 were used to describe the system. In the protein system, the CMAP backbone correction potential87–88 was also used. Each small molecule was solvated with the 40 Å cubic water box and the protein with the 80 Å rhombic dodecahedron water box. The details of the protein system preparation were described in our recent study.12 All molecular dynamics (MD) simulations were performed with 2 femtosecond (fs) integration time step, leapfrog Verlet and the Nosé-hoover thermostat89 at 300K. The SHAKE algorithm was applied to all bonds involving hydrogen atoms.90 The switching function was applied between 8 Å and 10 Å for the LJ interactions and the PME method91 for the electrostatic interactions, respectively.
For each small molecule, the alchemical simulations were performed using both the CSC and GSC protocols presented in Figure 1. In the CSC protocol, the Coulomb interactions of the solutes were removed first, followed by the removal of the LJ interactions with the CSC potential. In the GSC protocol, the Coulomb and LJ interactions were removed first, during which the GSC repulsion was turned on. The GSC potential was then removed in the second step. In both protocols, at the end of the annihilation, the solute has only the bonded terms (i.e., bond, angle and dihedral terms). Therefore, the free energy (FE) of solvation requires the computation of the free energy to restore the Coulomb and van der Waals interactions of the solute in vacuum. In the present study, such calculation was performed for each solute in vacuum by following the CSC protocol (Figure 1a). Thus determined solvation free energies are presented in Table 1. Each step of the transformation was accomplished with a total of 19 λ simulations at λ =0.0, 0.01, 0.02, 0.05, 0.2, , 0.3, 0.4, 0.5, 0.6, 0.7, , 0.8, 0.9, 0.95, 0.98, 0.99 and 1.0. At each λ value, the MD simulation was carried out for 2 nanosecond (ns) and the U0, U1 and ∂U/∂λ values were recorded at each MD step. The values recorded were then sampled with an interval of 2 ps from the last 1.5 ns simulation to construct an uncorrelated dataset. Finally, different FE calculation methods, including TI, BAR, DW-FEP, IPDW-FEP methods, were applied to determine the FE change, in which the free energy value and its error were determined by the bootstrapping strategy.92 The Tyr-to-pTyr mutation was simulated with the 3-step protocols (Figure S1).
Table 1.
Free energies (in kcal/mol) of small molecule solvation in water. For each molecule, the annihilation free energies (∆Fwater) were computed in water by following the CSC (Figure 1a) and GSC protocols (Figure 1b). Their free energies were determined by the TI method for the CSC protocol, and the TI, BAR, DW-FEP and IPDW-FEP methods for the GSC protocol, respectively. To correct the bonded terms, the same annihilation free energies were determined in vacuum (Figure 1c) using the TI method. The free energies thus determined are provided in Table S1. The solvation free energies reported were then .
|
a |
a |
||||||
|---|---|---|---|---|---|---|---|
| ID | Molecule | Charge | TI | TI | BAR | DW-FEP | IPDW-FEP |
| Monoatomic ions | |||||||
| 1 | K+ | +1 | −71.41 | −71.35 | −71.38 | −71.47 | −71.43 |
| 2 | Cl− | −1 | −92.15 | −91.96 | −91.99 | −91.98 | −92.00 |
| 3 | Na+ | +1 | −92.02 | −92.14 | −92.12 | −92.10 | −92.12 |
| 4 | Ca2+ | +2 | −367.86 | −367.77 | −367.90 | −367.77 | −367.79 |
| Small molecules | |||||||
| 5 | Glycine | 0 | −9.74 | −9.39 | −9.69 | −9.69 | −9.69 |
| 6 | Ethanol | 0 | −5.69 | −5.45 | −5.72 | −5.73 | −5.73 |
| 7 | Imidazole | 0 | −10.35 | −10.20 | −10.47 | −10.49 | −10.49 |
| 8 | Imidazolium | −1 | −51.39 | −51.48 | −51.77 | −51.80 | −51.80 |
| 9 | Methylamine | 0 | −4.10 | −3.97 | −4.16 | −4.15 | −4.14 |
| 10 | Methylammonium | −1 | −60.89 | −60.63 | −60.80 | −60.82 | −60.81 |
| 11 | Acetic acid | 0 | −3.81 | −4.04 | −4.30 | −4.28 | −4.30 |
| 12 | Acetate ion | −1 | −98.06 | −98.04 | −98.32 | −98.38 | −98.39 |
| 13 | Phospho-tyrosine | −2 | −209.10 | −209.33 | −209.69 | −209.93 | −209.88 |
| MSD b | 0.06 | −0.13 | −0.16 | −0.15 | |||
| MUD b | 0.17 | 0.18 | 0.21 | 0.21 | |||
All annihilation simulations were carried out in two steps, in which each step was accomplished by 19 λ simulations, i.e., a total of 38 λ simulations to complete the entire annihilation of an solute molecule. Thus, for the computation of solvation free energy of each small molecule, a total of 76 λ simulations were performed. For the monoatomic ions, by definition.
The mean signed and mean unsigned deviations (MSD and MUD) relative to the CSC TI results.
IV. RESULTS AND DISCUSSION
A. Accuracy of the GSC potential
The accuracy of the GSC potential was examined by comparing the free energies (FEs) of small molecule solvation in water determined for the 13 molecules using both the GSC and CSC potentials (Table 1). The solvation free energies were computed based on the free energies of solute annihilation in water and a correction term in vacuum (Table S1). Since the objective of this work is to compare the newly developed GSC potential to the CSC potential, unless otherwise specified, the remainder of this work focuses on the free energy values determined from the annihilation of the solute in water. In Tables S1 and S2, the FE values of solute annihilation determined using the TI method are presented. For the GSC protocol, the FE values determined from X=2 and 4 (eq. (10)) are compared in Table S3.
The GSC protocol reproduced all the results of the CSC protocol with 0.06 kcal/mol mean-signed (MSD) and 0.17 kcal/mol mean-unsigned deviations (MUD) for the TI method. The BAR and FEP methods also reproduced the CSC results with an accuracy similar to the TI method (Tables 1 and S1). Finally, in Table 2, we compare the FE change of a tyrosine phosphorylation between the CSC and GSC potentials. For this comparison, we applied a double decoupling scheme as presented in Figure S1. The result shows that the GSC protocol reproduces the free energy change of the side chain mutation with only 0.53 kcal/mol difference between the two protocols. Together, the results presented suggest that GSC is as accurate as CSC and independent of the FE methods employed.
Table 2.
Free energies of the Try-to-pTyr mutation in water and in IGF-1RK, determined by the TI method and the three-step transformation process presented in Figure S1.a The energy is in the unit of kcal/mol.
|
a |
b |
|||||||
|---|---|---|---|---|---|---|---|---|
| Total c | Step 1 | 2 | 3 | Totalc | Step 1 | 2 | 3 | |
| ΔF (water) d | −205.99 ± 0.16 | 15.41 ± 0.02 | 5.33 ± 0.12 | −226.73 ± 0.11 | −206.09 ± 0.16 | 17.92 ± 0.02 | 11.46 ± 0.11 | −235.47 ± 0.11 |
| ΔF (IGF-1RK) e | −212.24 ± 0.27 | 14.77 ± 0.03 | 3.82 ± 0.19 | −230.83 ± 0.18 | −212.87 ± 0.29 | 21.25 ± 0.04 | 13.01 ± 0.17 | −247.13 ± 0.23 |
| ΔΔF (Stability) f | −6.25 | −6.78 | ||||||
In the CSC protocol, Step 1 removes the charge of the solute, Step 2 transforms the vdW parameters of the solute to those of the transformed solute with CSC and Step 3 introduces the charge of the transformed solute, respectively (Figure S1a).
In the GSC protocol, Step 1 removes the charge and the vdW interactions of the solute with the introduction of the solute GSC potential, Step 2 transforms the solute GSC potential to the transformed solute’s GSC potential and Step 3 introduces the charge and the vdW interactions of the transformed solute with the removal of the GSC potential, respectively (Figure S1b).
“Total” refers the total FE change of the entire transformation.
Free energies of the mutation in water. Each step was achieved with 19 λ simulations.
Free energies of the mutation in the protein IGF-1RK. Each step was achieved with 11 λ simulations.
The relative free energy between protein and water, i.e., ∆∆F = ∆F (IGF-1RK) −∆F (water), in each step as well as the entire transformation.
B. Efficiency of the CSC versus GSC protocols
To examine the efficiency of the GSC potential, we systematically vary the number of λ states used in the FE evaluation between N=2, 3, 6, 11 and 19. First, the efficiency of CSC and GSC on calculating the total annihilation free energies are compared in Tables 3 and 4. When TI was applied, the overall accuracy and efficiency were similar between the two protocols. Both protocols required at least 6 λ simulations in Step 1 and 11 λ simulations in Step 2 to yield MUD < 0.3 kcal/mol relative to their respective reference FE values (i.e., N=19 values). Figure S2 compares the TI integrands of all systems determined by the CSC and GSC protocols. In Step 1, the integrands change almost linearly over the entire range of λ for both protocols (Figure S2a and S2b). This explains why their FE values can be reliably determined with few λ simulations by TI. In Step 2, their TI integrands show a large curvature around λ=0.9 (Figures S2c and d). Consequently, they require 11 λ simulations to accurately capture the changes in the TI integrands.
Table 3.
Accuracy of the TI method for the different numbers of λ simulations for Steps 1 and 2 of the CSC protocol in water (Figure 1a).a The energy is in the unit of kcal/mol.
|
(Step 1) |
(Step 2) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N=2 | 3 | 6 | 11 | 19 | N=2 | 3 | 6 | 11 | 19 | |
| 1. K+ | 77.37 | 74.10 | 73.51 | 73.46 | 73.56 | −1.96 | −2.01 | −2.12 | −2.12 | −2.14 |
| 2. Cl− | 99.41 | 95.97 | 94.91 | 94.77 | 94.75 | 13.30 | −7.44 | −4.12 | −3.18 | −2.60 |
| 3. Na+ | 97.78 | 94.60 | 93.86 | 93.79 | 93.67 | −1.08 | −1.48 | −1.62 | −1.62 | −1.66 |
| 4. Ca2+ | 350.47 | 369.48 | 368.72 | 369.25 | 369.17 | −0.72 | −1.15 | −1.29 | −1.32 | −1.31 |
| 5. Glycine | −46.42 | −48.47 | −48.92 | −48.99 | −48.99 | 11.85 | −5.10 | −1.82 | −1.16 | −0.92 |
| 6. Ethanol | 13.86 | 12.42 | 12.16 | 12.10 | 12.12 | −8.27 | −3.83 | −1.66 | −1.22 | −1.14 |
| 7. imidazole | 16.74 | 15.25 | 14.90 | 14.86 | 14.85 | −6.70 | −2.64 | −0.57 | −0.18 | −0.20 |
| 8. Imidazolium− | 14.56 | 12.80 | 12.49 | 12.51 | 12.55 | −5.70 | −1.69 | 0.35 | 0.78 | 0.77 |
| 9. Methylamine | −6.74 | −7.87 | −8.09 | −8.12 | −8.12 | −5.53 | −2.75 | −1.39 | −1.02 | −0.87 |
| 10. Methylammonium− | 45.12 | 42.79 | 42.60 | 42.58 | 42.60 | −5.53 | −2.69 | −1.29 | −0.95 | −0.85 |
| 11. Acetic acid | 79.69 | 77.88 | 77.62 | 77.37 | 77.40 | −9.33 | −4.21 | −1.68 | −1.15 | −1.05 |
| 12. Acetate ion− | 151.13 | 148.02 | 146.84 | 146.72 | 146.49 | −8.86 | −4.03 | −1.70 | −1.23 | −0.99 |
| 13. Phospho-tyrosine2− | 244.52 | 237.72 | 233.78 | 232.90 | 231.83 | 72.26 | −37.88 | −22.30 | 18.60 | −17.53 |
| MSD b | 1.97 | 0.99 | 0.19 | 0.10 | −9.28 | −3.57 | −0.82 | −0.19 | ||
| MUD b | 4.85 | 0.99 | 0.28 | 0.13 | 9.48 | 3.64 | 0.84 | 0.20 | ||
The λ values in the N=2, 3, 6 and 11-point λ simulation results are: for N=2, λ=0 and 1; for N=3, λ=0, 0.5 and 1; for N=6, λ=0, 0.2, 0.4, 0.6, 0.8 and 1; and for N=11, λ=0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1, respectively.
MSD and MUD are relative to the N=19 simulation results of each step.
Table 4.
Accuracy of the TI method for the different numbers of λ simulations for the Steps 1 and 2 of the GSC protocol in water (Figure 1b).a The energy is in the unit of kcal/mol.
|
(Step 1) |
(Step 2) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N=2 a | 3 | 6 | 11 | 19 | N=2 | 3 | 6 | 11 | 19 | |
| 1. K+ | 74.07 | 74.08 | 74.58 | 74.90 | 75.21 | −6.05 | −4.40 | −3.93 | −3.89 | −3.87 |
| 2. Cl− | 97.15 | 97.17 | 97.31 | 97.48 | 97.65 | −9.76 | −6.69 | −5.84 | −5.74 | −5.70 |
| 3. Na+ | 91.72 | 93.18 | 93.98 | 94.38 | 94.78 | −4.03 | −2.99 | −2.69 | −2.65 | −2.65 |
| 4. Ca2+ | 339.04 | 368.20 | 369.80 | 370.06 | 370.43 | −4.06 | −3.05 | −2.73 | −2.68 | −2.66 |
| 5. Glycine | −38.54 | −39.49 | −39.39 | −39.38 | −39.36 | −42.00 | −23.35 | −13.25 | −11.04 | −10.91 |
| 6. Ethanol | 22.14 | 21.03 | 20.82 | 20.80 | 20.80 | −39.87 | −22.03 | −12.40 | −10.20 | −10.06 |
| 7. imidazole | 25.59 | 24.48 | 24.21 | 24.19 | 24.20 | −41.12 | −22.32 | −12.25 | −9.94 | −9.71 |
| 8. Imidazolium− | 23.16 | 21.91 | 21.82 | 21.80 | 21.94 | −36.69 | −19.80 | −10.70 | −8.66 | −8.54 |
| 9. Methylamine | −1.19 | −1.87 | −1.94 | −1.98 | −1.99 | −25.85 | −14.36 | −8.40 | −7.26 | −7.13 |
| 10. Methylammonium− | 49.79 | 48.81 | 48.84 | 48.87 | 48.80 | −26.68 | −14.79 | −8.60 | −7.36 | −7.31 |
| 11. Acetic acid | 87.56 | 86.21 | 86.56 | 86.46 | 86.43 | −37.72 | −20.86 | −11.83 | −9.94 | −9.85 |
| 12. Acetate ion− | 157.69 | 156.28 | 155.51 | 155.32 | 155.27 | −36.37 | −20.26 | −11.75 | −9.89 | −9.79 |
| 13. Phospho-tyrosine2− | 254.84 | 252.81 | 250.51 | 249.75 | 249.69 | −97.92 | −61.15 | −41.10 | −35.73 | −35.17 |
| MSD b | −1.60 | −0.08 | −0.10 | −0.09 | −21.91 | −8.67 | −1.70 | −0.13 | ||
| MUD b | 3.95 | 0.81 | 0.30 | 0.13 | 21.91 | 8.67 | 1.70 | 0.13 | ||
The λ values in the N=2, 3, 6 and 11-point λ simulation results are: for N=2, λ=0 and 1; for N=3, λ=0, 0.5 and 1; for N=6, λ=0, 0.2, 0.4, 0.6, 0.8 and 1; and for N=11, λ=0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1, respectively.
MSD and MUD are relative to the N=19 simulation results of each step.
Next, we applied the mid-point perturbation version of the DW-FEP method (also known as the simple overlap sampling method93) to both steps of the GSC protocol and to Step 1 of the CSC protocol. Here, the DW-FEP method was not applied to Step 2 of the CSC protocol, because it required to reevaluate the energies at the perturbed λ values for each saved coordinate. Note that all the FE values reported are based on the energies saved in each MD step followed by construction of an uncorrelated dataset (See Computational Details). The results are presented in Table 5. For GSC, with the exception of N=2, most of the computed FEs are in an error of 0.5 kcal/mol from the reference N=19 values, and 6 λ simulations are needed to achieve MUE < 0.3 kcal/mol in each step. Together, a total of 12 λ simulations reproduce all annihilation FE values. In Table S4, the BAR method was also tested and produced results comparable to the DW-FEP method. However, at several N=2 and 3 cases, it failed to converge due to the poor configuration overlap. For CSC with DW-FEP, 6 λ simulations are needed to reproduce its reference values (Table 5). Overall, the DW-FEP method is more efficient than the TI method in Step 2 of the GSC protocol, whereas Step 1 shows similar efficiency between the different FE methods tested.
Table 5.
Accuracy of the DW-FEP method for the different numbers of λ simulations for Steps 1 and 2 of the GSC protocol and Step 1 of the CSC protocol (Figure 1).a All free energies are in the unit of kcal/mol.
|
(Step 1) |
(Step 2) |
(Step 1) |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N=2 | 3 | 6 | 11 | 19 | N=2 | 3 | 6 | 11 | 19 | N=2 | 3 | 6 | 11 | 19 | |
| 1. K+ | 75.83 | 75.75 | 75.09 | 75.16 | 75.32 | −3.83 | −3.84 | −3.86 | −3.87 | −3.85 | 76.32 | 73.34 | 73.36 | 73.43 | 73.47 |
| 2. Cl− | 101.05 | 98.98 | 97.70 | 97.67 | 97.63 | −5.86 | −5.77 | −5.75 | −5.71 | −5.65 | 96.05 | 95.22 | 94.72 | 94.72 | 94.66 |
| 3. Na+ | 97.50 | 95.33 | 94.84 | 94.78 | 94.73 | −2.68 | −2.64 | −2.64 | −2.64 | −2.63 | 99.23 | 95.04 | 93.78 | 93.79 | 93.74 |
| 4. Ca2+ | 338.07 | 365.15 | 370.49 | 370.49 | 370.42 | −2.69 | −2.71 | −2.68 | −2.66 | −2.65 | 350.87 | 369.03 | 369.75 | 369.43 | 369.84 |
| 5. Glycine | −39.22 | −39.42 | −39.32 | −39.35 | −39.37 | −12.99 | −11.27 | −10.69 | −10.66 | −10.60 | −48.75 | −49.02 | −49.00 | −49.01 | −49.00 |
| 6. Ethanol | 20.95 | 20.83 | 20.79 | 20.79 | 20.79 | −12.45 | −10.57 | −9.83 | −9.77 | −9.78 | 12.28 | 12.03 | 12.10 | 12.09 | 12.08 |
| 7. imidazole | 23.63 | 24.13 | 24.15 | 24.18 | 24.19 | −12.06 | −10.36 | −10.83 | −9.55 | −9.41 | 14.71 | 14.85 | 14.84 | 14.85 | 14.82 |
| 8. Imidazolium− | 24.24 | 22.31 | 21.80 | 21.79 | 21.97 | −11.25 | −9.21 | −8.37 | −8.29 | −8.24 | 13.36 | 12.42 | 12.46 | 12.50 | 12.52 |
| 9. Methylamine | −1.92 | −1.99 | −1.95 | −1.98 | −1.99 | −7.03 | −7.00 | −6.97 | −7.03 | −6.94 | −8.10 | −8.14 | −8.14 | −8.13 | −8.12 |
| 10. Methylammonium− | 50.34 | 48.70 | 48.89 | 48.88 | 48.80 | −8.23 | −7.48 | −7.17 | −7.15 | −7.11 | 41.55 | 42.53 | 42.59 | 42.59 | 42.61 |
| 11. Acetic acid | 86.31 | 86.14 | 86.52 | 86.46 | 86.42 | −13.42 | −10.98 | −9.75 | −9.62 | −9.60 | 77.68 | 77.45 | 77.54 | 77.35 | 77.38 |
| 12. Acetate ion− | 155.74 | 155.41 | 155.24 | 155.29 | 155.35 | −10.92 | −9.79 | −9.59 | −9.53 | −9.53 | 147.88 | 147.65 | 146.67 | 146.67 | 146.49 |
| 13. Phospho-tyrosine2− | 247.45 | 248.27 | 249.64 | 249.65 | 249.76 | −47.27 | −38.64 | −35.32 | −34.61 | −34.64 | 243.29 | 236.84 | 233.07 | 232.74 | 232.07 |
| MSD b | −1.85 | −0.34 | −0.01 | −0.02 | −2.31 | −0.74 | −0.22 | −0.04 | 0.29 | 0.51 | 0.09 | 0.04 | |||
| MUD b | 3.59 | 0.78 | 0.09 | 0.06 | 2.31 | 0.74 | 0.22 | 0.04 | 3.39 | 0.70 | 0.14 | 0.12 | |||
The λ values in the N=2, 3, 6 and 11-point λ simulation results are: for N=2, λ=0 and 1; for N=3, λ=0, 0.5 and 1; for N=6, λ=0, 0.2, 0.4, 0.6, 0.8 and 1; and for N=11, λ=0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1, respectively.
MSD and MUD are relative to the N=19 simulation results of each step.
Finally, to test the reproducibility and efficiency of the GSC potential, we compared the free energies of the annihilation of solute’s vdW interactions in Step 2 of the CSC protocol (Figure 1a). In the comparison, the FE values from Step 2 of the CSC protocol (Table 3) were used for CSC, and for GSC, additional two-step annihilation simulations were performed (Figure 1c). In the first step, the vdW interactions of the solute were removed, while the GSC potential was turned on. The second step was the same as Step 2 of the GSC protocol shown in Figure 1b. The results are presented in Table S5. First, GSC reproduces the CSC results with 0.07 kcal/mol MUD for DW-FEP and 0.15 kcal/mol MUD for TI. Second, DW-FEP requires fewer λ simulations than TI. For example, in Step 1, DW-FEP using two λ simulations (i.e., λ=0 and 1) reproduces the N=19 λ simulation results with 0.04 kcal/mol MUD and using a single simulation at λ=0.95 with 0.08 kcal/mol MUD, while TI requires 6 λ simulations for MUD < 0.3 kcal/mol; with 3 λ simulations, MUD is 0.32 kcal/mol. Together, DW-FEP requires a total of 7 λ simulations (i.e., 1 simulation for Step 1 and 6 simulations for Step 2) to produce the FE values of the vdW annihilation with MUD < 0.3 kcal/mol. Below we also discuss how to minimize the number of λ simulations required for Step 2 of the GSC protocol.
C. Understanding efficiency of the GSC potential
The efficiency of GSC can be understood by comparing the TI integrands estimated using eq. (12) to those directly determined from each λ simulation. In Figures 4a and b, this comparison is made using glycine as an example. In Step 1, the TI integrands estimated from 3 λ simulations at λ=0, 0.5 and 1 reproduce the TI integrands directly determined from 19 λ simulations. The robustness of eq. (12) in this case is due to the quasi-linearity of the TI integrands over the entire range of λ values. The same principle can be applied to Step 1 of the CSC protocol. In Step 2 of GSC, despite the high curvature around λ=0.9, three λ simulations at λ=0, 0.5 and 1 reproduce the TI integrands between λ=0 and 1 (Figure 4b). This explains why DW-FEP predicts the FE change with reasonably high accuracy even at N=3, while TI severely underestimates the FE value. This approach is similar to the approach used by Tidor and Karplus,83 but is different from the extended TI approach by de Ruiter and Oostenbrink,78 which uses the CSC potential and requires the evaluation of ∂U/∂λ values at non-simulated λ values on the fly or after simulations.
Figure 4.
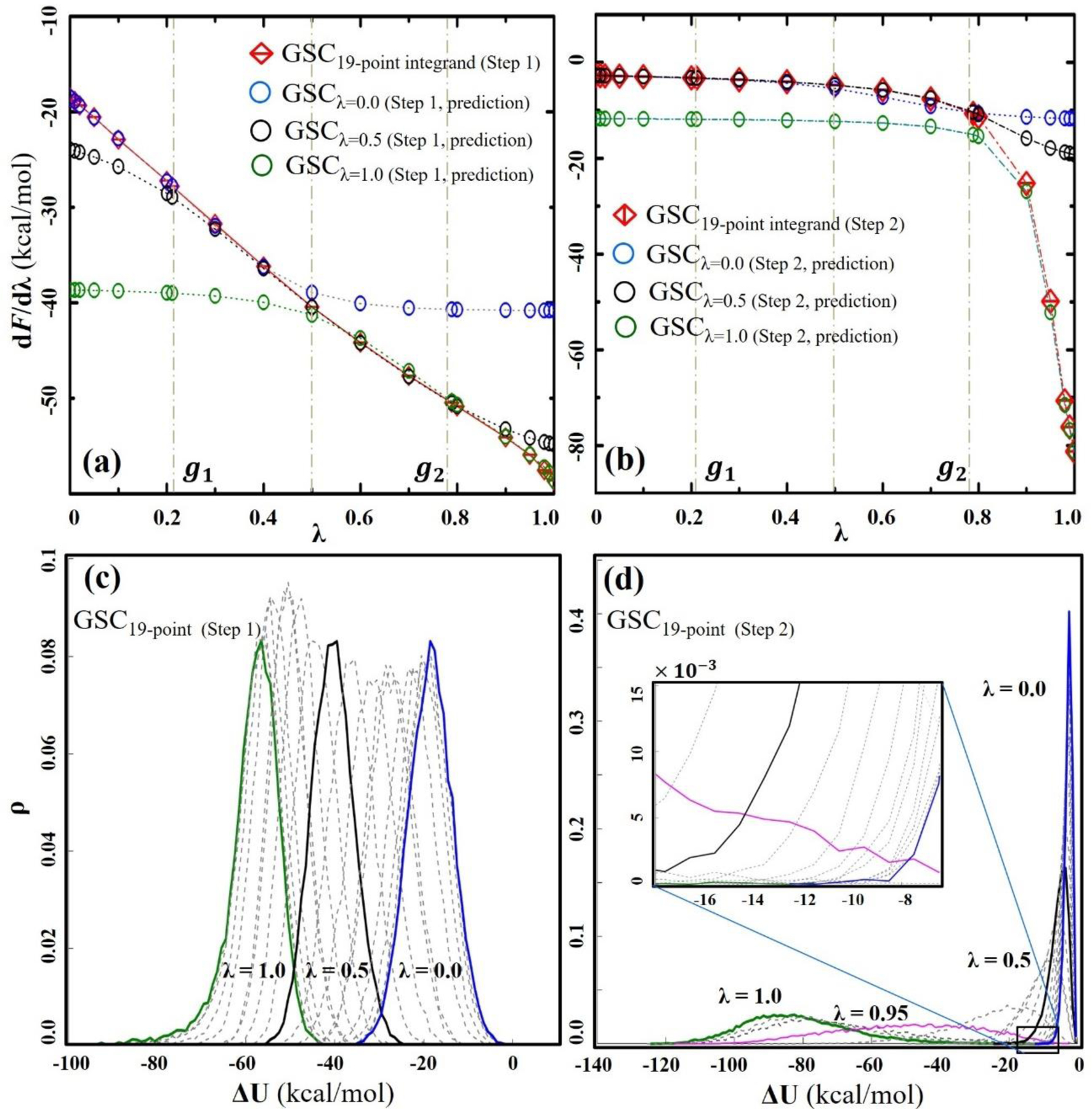
TI integrands and ρ(ΔU) distributions of glycine annihilation with GSC. (a) and (b) show the TI integrands for the first and second annihilation steps, respectively. The integrands directly determined from each λ simulation are colored in red (i.e., the reference TI integrands). The TI integrands predicted based on eq. (12) are represented with different colors: blue for λ=0; black for λ=0.5; and green for λ=1.0, respectively. (c) and (d) show the ΔU distributions for the first and second annihilation steps, respectively. To highlight the overlap between the different λ simulations, several distributions are displayed with different colors indicated and the remaining distributions are shown in gray.
The predictability of eq. (12) can be examined by analyzing the probability density of the energy gap, ρ(ΔU), determined from each λ simulation (Figure 4c and d). In agreement with the quasi-linear TI integrands in Step 1, all the density distributions are of the Gaussian shape with a similar width (Figure 4c). This suggests that the solvent molecules response linearly to the elimination of the solute-solvent interaction. A nonlinear response contributes to the long tail of the density distribution at large λ values. This occurs because the GSC repulsion, which is turned on during the first step of the annihilation, prevents physical overlapping between the solute and the surrounding solvents, so that the solvents only have to respond to pure repulsion around the solute.
The density distribution analysis allows the determination of the number of λ simulations and their respective λ values necessary to cover the entire range of the energy gaps with sufficient overlap between them. For example, in the case of glycine, the simulations at λ=0, 0.5 and 1 show ample overlap between them (Figure 4c). For this reason, the 3 simulations are sufficient to accurately determine FE values in most cases using TI (Tables 3 and 4) and DW-FEP (Table 5). There are a few exceptions. For example, in the case of Ca2+, its ρ(ΔU) distributions are too narrow to cover the entire range of ΔU with three λ states, and at least 6 λ simulations are needed to have some overlap between them (Figure S2f). The importance of the overlap of the density distribution has previously been discussed in the context of FEP and BAR methods.69, 72 Together, 3 λ simulations are sufficient in Step 1 of the neutral and singly charged molecule annihilation, while at least 6 λ simulations are needed for the annihilation of highly charged solutes.
In Step 2 of the GSC protocol, the density distribution changes drastically from a narrow distribution at λ=0 to a wide distribution at λ > 0.9 (Figure 5d). This widening occurs because the GSC repulsion decreases with the increase of λ. For example, for α=5 kcal/mol, the maximum of the GSC repulsion is 0.25 kcal/mol at λ=0.95. As it is less than 1/2 kBT, solvent atoms can easily overcome this repulsion and overlap with the solute atoms. Since the determination of annihilation FE requires sampling of the solvent configurations that overlap with the solute molecule as well as that exclude the solute’s volume (i.e., the solute cavity), this feature of GSC around λ=0.95 allows the sampling of both types of solvent configurations and offers a unique advantage for predicting the TI integrands over a broad range of λ values. Indeed, the configurations sampled at λ=0.95 accurately predict the TI integrand over the entire range of λ (Figure S3c), and the FE values determined only have 0.5 kcal/mol of MUE (See the last two columns of Table S6).
D. Locating λ values with minimal FE errors for DW-FEP
The TI integrand and density distribution analyses described above suggest a practical approach for determining the λ value with minimal error in DW-FEP. As illustrated in Figure 3, the integrands are overestimated in the increasing direction of λ and are underestimated in the opposite direction, following the Gibbs-Bogoliubov model.94 Consequently, if the TI integrands predicted from two λ simulations are compared, their difference (eq. (13)) has a minimum between the two λ values. When the minimum is below a certain threshold, the DW-FEP calculation can be performed to the λ value at the minimum. Otherwise, an additional simulation is performed at this λ value to improve the accuracy of the FE value. In this work, this approach is called the integrand prediction-guided DW-FEP (IPDW-FEP) method.
The advantage of IPDW-FEP is evident in Step 2 of the alchemical transformation with GSC (Table S7). On the other hand, Step 1 displays an efficiency similar to the mid-point DW-FEP (Table 5), due to the similar shape and variance of the ρ(ΔU) distributions (Figure 5c). By analyzing the different behaviors of the ρ(ΔU) distributions, we can optimize the number of λ simulations and their respective λ values in each of the two transformation steps. With a total of 7 λ simulations (i.e., 5 simulations in Step 1 at λ=0.1, 0.3, 0.5, 0.7 and 0.9 and 2 simulations in Step 2 at λ=0.5 and 0.95), the FE values determined are with MUD < 0.3 kcal/mol (Table S8). The total number of λ simulations can be further reduced if the accuracy criterion of 1 kcal/mol is used. For example, with a total of 5 λ simulations (i.e., 3 simulations in Step 1 at λ=0.1, 0.5 and 0.9 and 2 simulations in Step 2 at λ=0.5 and 0.95), MSD and MUD values of the determined FE values are −0.51 kcal/mol and 0.61 kcal/mol, respectively (Table S6). In this case, we note that the FEs of Step 2 are still based on the two simulations at λ=0.5 and 0.95.
E. Limitations of the GSC potential.
The developed GSC potential is has several limitations. First of all, GSC is not compatible with the single-step annihilation protocol, in which Coulomb and vdW interactions are turned off simultaneously while the CSC potential is applied to both types of interactions to avoid singularity. When the PME method is used, the single-step protocol requires a rigorous implementation of the CSC potential for correct cancellation of the reciprocal space terms by the real space terms at intermediate λ states. In addition, when proper parameters are not used for the soft-core potentials, they results in an incomplete cancelling between the Coulomb and the vdW interactions at short interparticle distance, and in some cases, the two particles collapse.61 This does not occur with two-step annihilation process. In addition, the advantage of GSC makes it possible to perform the entire transformation with fewer λ simulations than the transformation with CSC. Especially, as presented in this study, only two λ simulations in the second step produce a very reliably free energy estimate.
Second, while the functional form of GSC (eq. (10)) is well suited for the dual-topology alchemical transformation, it is not optimal for the single-topology parameter interpolation (PI) scheme adopted in AMBER.95 Obviously, GSC can be applied to the PI scheme by interpolating the GSC parameters (i.e., α, β, and ) but this negates the advantage of GSC. For example, as the parameter-interpolated GSC potentials depend on λ, the TI calculation requires the explicit evaluation of the derivative of GSC with respect to λ. We can get around this limitation by interpolating only the α value, while making the β and parameters λ-independent, for example, by taking a geometric or arithmetic mean of their two end-state values. This simplifies the TI integrand calculations. Nevertheless, for FEP and BAR, the energy must still be reevaluated at the perturbed λ values for each saved coordinate.
V. CONCLUSION
This paper presents a new type of soft-core potential, called Gaussian soft-core (GSC) potential, and associated alchemical simulation protocols. Several features of GSC make it an attractive alternative to the conventional separation-shifted soft-core potential. First, the GSC potential prevents the configuration overlap between solute and solvent molecules without explicit modification of Lennard-Jones potentials. This simplifies the calculation of ∂U/ ∂λ and permits a straightforward determination of the free energy values using any of the thermodynamic integration (TI), free energy perturbation (FEP) and Bennett acceptance ratio (BAR) methods. The effectiveness and accuracy of GSC are demonstrated by systematically comparing the annihilation free energies of 13 model systems and the free energy of a protein side chain modification. Second, the parametric nature of GSC allows the control of the range of solvent configuration sampling, especially in the annihilation of the GSC potential (i.e., the second step of the annihilation of solute). As we have demonstrated, this feature allows a significant reduction of the number of λ simulations without losing accuracy of the determined FE values. By combining the prediction of the TI integrands and double-wide FEP (DW-FEP) method, we show that GSC can reduce the overall computational expense by more than 60 % compared with the traditional soft-core potential.
Supplementary Material
ACKNOWLEDGEMENT
This research was financed by the University of Texas at Arlington, the Swedish Research Council (VR 2015-04114 to K.N. and VR 2019-00608 to Y.L.) and the National Institute of General Medical Sciences of the National Institute of Health (R01 GM132481 to K.N.). Computer resources were provided by the Swedish National Infrastructure for Computing (SNIC) at the High Performance Computing Center North (HPC2N), by the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, and by the Oak Ridge Leadership Computing Facility, which is supported by the Office of Science of the Department of Energy under Contract DE-AC05-00OR22725.
Footnotes
SUPPORTING INFOMRATION
The Supporting Information is available free of charge via the internet at [https://pubs.acs.org/doi/10.1021/acs.jctc.0c00163].
Utility of the GSC potential; Free energies of solute annihilation in water and vacuum determined using different annihilation protocols and free energy methods; Table for the TI method; Comparison of the different β parameter values; Accuracy of BAR method; Free energy of van der Waals term annihilation using the GSC potential; IPDW-FEP method using 5 λ simulations; The performance of IPDW-FEP method; IPDW-FEP method using 7 λ simulations; Three-step alchemical transformation protocol; Comparison of TI integrands; TI integrands of glycine annihilation in water; TI integrands for tyrosine to phosphor-tyrosine transformation
REFERENCES
- 1.Matos GDR; Kyu DY; Loeffler HH; Chodera JD; Shirts MR; Mobley DL, Approaches for Calculating Solvation Free Energies and Enthalpies Demonstrated with an Update of the FreeSolv Database. J. Chem. Eng. Data 2017, 62 (5), 1559–1569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Shirts MR; Pande VS, Solvation free energies of amino acid side chain analogs for common molecular mechanics water models. J. Chem. Phys 2005, 122 (13). [DOI] [PubMed] [Google Scholar]
- 3.Shirts MR; Pitera JW; Swope WC; Pande VS, Extremely precise free energy calculations of amino acid side chain analogs: Comparison of common molecular mechanics force fields for proteins. J. Chem. Phys 2003, 119 (11), 5740–5761. [Google Scholar]
- 4.Grossfield A; Ren PY; Ponder JW, Ion Solvation Thermodynamics from Simulation with a Polarizable Force Field. J. Am. Chem. Soc 2003, 125 (50), 15671–15682. [DOI] [PubMed] [Google Scholar]
- 5.Kuang GL; Wang X; Halldin C; Nordberg A; Langstrom B; Agren H; Tu YQ, Theoretical study of the binding profile of an allosteric modulator NS-1738 with a chimera structure of the α 7 nicotinic acetylcholine receptor. Phys. Chem. Chem. Phys 2016, 18 (40), 28003–28009. [DOI] [PubMed] [Google Scholar]
- 6.Aldeghi M; Heifetz A; Bodkin MJ; Knapp S; Biggin PC, Accurate calculation of the absolute free energy of binding for drug molecules. Chem. Sci 2016, 7 (1), 207–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Michel J; Essex JW, Prediction of protein-ligand binding affinity by free energy simulations: assumptions, pitfalls and expectations. J. Comput. Aid. Mol. Des 2010, 24 (8), 639–658. [DOI] [PubMed] [Google Scholar]
- 8.Mobley DL; Chodera JD; Dill KA, Confine-and-Release Method: Obtaining Correct Binding Free Energies in the Presence of Protein Conformational Change. J. Chem. Theory Comput 2007, 3 (4), 1231–1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Woo HJ; Roux B, Calculation of absolute protein-ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci. U.S.A 2005, 102 (19), 6825–6830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sham YY; Chu ZT; Tao H; Warshel A, Examining methods for calculations of binding free energies: LRA, LIE, PDLD‐LRA, and PDLD/S‐LRA calculations of ligands binding to an HIV protease. Proteins 2000, 39 (4), 393–407. [PubMed] [Google Scholar]
- 11.Xu Y; Villa A; Nilsson L, The free energy of locking a ring: Changing a deoxyribonucleoside to a locked nucleic acid. J. Comput. Chem 2017, 38 (15), 1147–1157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Li Y; Nam K, Dynamic, structural and thermodynamic basis of insulin-like growth factor 1 kinase allostery mediated by activation loop phosphorylation. Chem. Sci 2017, 8 (5), 3453–3464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Graf MMH; Maurer M; Oostenbrink C, Free-Energy Calculations of Residue Mutations in a Tripeptide Using Various Methods to Overcome Inefficient Sampling. J. Comput. Chem 2016, 37 (29), 2597–2605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Seeliger D; de Groot BL, Protein Thermostability Calculations Using Alchemical Free Energy Simulations. Biophys. J 2010, 98 (10), 2309–2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kollman PA, Free Energy Calculations: Applications to Chemical and Biochemical Phenomena. Chem. Rev 1993, 93 (7), 2395–2417. [Google Scholar]
- 16.Kirkwood JG, Statistical mechanics of fluid mixtures. J. Chem. Phys 1935, 3 (5), 300–313. [Google Scholar]
- 17.Zwanzig RW, High-Temperature Equation of State by a Perturbation Method.1. Nonpolar Gases. J. Chem. Phys 1954, 22 (8), 1420–1426. [Google Scholar]
- 18.Bennett CH, Efficient Estimation of Free Energy Differences from Monte Carlo Data. J. Comput. Phys 1976, 22 (2), 245–268. [Google Scholar]
- 19.Rackers JA; Wang Z; Lu C; Laury ML; Lagardere L; Schnieders MJ; Piquemal JP; Ren PY; Ponder JW, Tinker 8: Software Tools for Molecular Design. J. Chem. Theory Comput 2018, 14 (10), 5273–5289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lee TS; Cerutti DS; Mermelstein D; Lin C; LeGrand S; Giese TJ; Roitberg A; Case DA; Walker RC; York DM, GPU-Accelerated Molecular Dynamics and Free Energy Methods in Amber18: Performance Enhancements and New Features. J. Chem. Inf Model 2018, 58 (10), 2043–2050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gapsys V; de Groot BL, Alchemical Free Energy Calculations for Nucleotide Mutations in Protein-DNA Complexes. J. Chem. Theory Comput 2017, 13 (12), 6275–6289. [DOI] [PubMed] [Google Scholar]
- 22.Loeffler HH; Michel J; Woods C, FESetup: Automating Setup for Alchemical Free Energy Simulations. J. Chem. Inf. Model 2015, 55 (12), 2485–2490. [DOI] [PubMed] [Google Scholar]
- 23.Klimovich PV; Mobley DL, A Python tool to set up relative free energy calculations in GROMACS. J. Comput. Aid. Mol. Des 2015, 29 (11), 1007–1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liu S; Wu YJ; Lin T; Abel R; Redmann JP; Summa CM; Jaber VR; Lim NM; Mobley DL, Lead optimization mapper: automating free energy calculations for lead optimization. J. Comput. Aid. Mol. Des 2013, 27 (9), 755–770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Vilseck JZ; Armacost KA; Hayes RL; Goh GB; Brooks CL, Predicting Binding Free Energies in a Large Combinatorial Chemical Space Using Multisite lambda Dynamics. J. Phys. Chem. Lett 2018, 9 (12), 3328–3332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Macdonald HEB; Cave-Ayland C; Ross GA; Essex JW, Ligand Binding Free Energies with Adaptive Water Networks: Two-Dimensional Grand Canonical Alchemical Perturbations. J. Chem. Theory Comput 2018, 14 (12), 6586–6597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jiang W; Thirman J; Jo S; Roux B, Reduced Free Energy Perturbation/Hamiltonian Replica Exchange Molecular Dynamics Method with Unbiased Alchemical Thermodynamic Axis. J. Phys. Chem. B 2018, 122 (41), 9435–9442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bhati AP; Wan S; Coveney PV, Ensemble-Based Replica Exchange Alchemical Free Energy Methods: The Effect of Protein Mutations on Inhibitor Binding. J. Chem. Theory Comput 2019, 15 (2), 1265–1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sidler D; Schwaninger A; Riniker S, Replica exchange enveloping distribution sampling (RE-EDS): A robust and accurate method to calculate multiple free energy differences from a single simulation. J. Chem. Phys 2016, 145, 154114. [DOI] [PubMed] [Google Scholar]
- 30.Raman EP; Lakkaraju SK; Denny RA; MacKerell AD, Estimation of relative free energies of binding using pre-computed ensembles based on the single-step free energy perturbation and the site-identification by Ligand competitive saturation approaches. J. Comput. Chem 2017, 38 (15), 1238–1251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Armacost KA; Goh GB; Brooks CL, Biasing Potential Replica Exchange Multisite lambda-Dynamics for Efficient Free Energy Calculations. J. Chem. Theory Comput 2015, 11 (3), 1267–1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zheng L; Chen M; Yang W, Simultaneous escaping of explicit and hidden free energy barriers: Application of the orthogonal space random walk strategy in generalized ensemble based conformational sampling. J. Chem. Phys 2009, 130 (23), 234105. [DOI] [PubMed] [Google Scholar]
- 33.Christ CD; van Gunsteren WF, Enveloping distribution sampling: A method to calculate free energy differences from a single simulation. J. Chem. Phys 2007, 126 (18), 184110. [DOI] [PubMed] [Google Scholar]
- 34.Hudson PS; Boresch S; Rogers DM; Woodcock HL, Accelerating QM/MM Free Energy Computations via Intramolecular Force Matching. J. Chem. Theory Comput 2018, 14 (12), 6327–6335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Olsson MA; Ryde U, Comparison of QM/MM Methods To Obtain Ligand-Binding Free Energies. J. Chem. Theory Comput 2017, 13 (5), 2245–2253. [DOI] [PubMed] [Google Scholar]
- 36.Bradshaw RT; Essex JW, Evaluating Parametrization Protocols for Hydration Free Energy Calculations with the AMOEBA Polarizable Force Field. J. Chem. Theory Comput 2016, 12 (8), 3871–3883. [DOI] [PubMed] [Google Scholar]
- 37.König G; Hudson PS; Boresch S; Woodcock HL, Multiscale Free Energy Simulations: An Efficient Method for Connecting Classical MD Simulations to QM or QM/MM Free Energies Using Non-Boltzmann Bennett Reweighting Schemes. J. Chem. Theory Comput 2014, 10 (4), 1406–1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chen W; Deng Y; Russell E; Wu Y; Abel R; Wang L, Accurate Calculation of Relative Binding Free Energies between Ligands with Different Net Charges. J. Chem. Theory Comput 2018, 14 (12), 6346–6358. [DOI] [PubMed] [Google Scholar]
- 39.Lin YL; Aleksandrov A; Simonson T; Roux B, An Overview of Electrostatic Free Energy Computations for Solutions and Proteins. J. Chem. Theory Comput 2014, 10 (7), 2690–2709. [DOI] [PubMed] [Google Scholar]
- 40.Rocklin GJ; Mobley DL; Dill KA; Hünenberger PH, Calculating the binding free energies of charged species based on explicit-solvent simulations employing lattice-sum methods: An accurate correction scheme for electrostatic finite-size effects. J. Chem. Phys 2013, 139 (18), 184103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.de Oliveira C; Yu HY; Chen W; Abele R; Wang LL, Rigorous Free Energy Perturbation Approach to Estimating Relative Binding Affinities between Ligands with Multiple Protonation and Tautomeric States. J. Chem. Theory Comput 2019, 15, 424–435. [DOI] [PubMed] [Google Scholar]
- 42.Wang L; Deng Y; Wu Y; Kim B; LeBard DN; Wandschneider D; Beachy M; Friesner R; Abel R, Accurate Modeling of Scaffold Hopping Transformations in Drug Discovery. J. Chem. Theory Comput 2017, 13 (1), 42–54. [DOI] [PubMed] [Google Scholar]
- 43.Pitera JW; van Gunsteren WF, A Comparison of Non-Bonded Scaling Approaches for Free Energy Calculations. Mol. Simulat 2002, 28 (1–2), 45–65. [Google Scholar]
- 44.Zacharias M; Straatsma TP; McCammon JA, Separation-Shifted Scaling, a New Scaling Method for Lennard-Jones Interactions in Thermodynamic Integration. J. Chem. Phys 1994, 100 (12), 9025–9031. [Google Scholar]
- 45.Beutler TC; Mark AE; van Schaik RC; Gerber PR; van Gunsteren WF, Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chem. Phys. Lett 1994, 222 (6), 529–539. [Google Scholar]
- 46.Beveridge DL; DiCapua FM, Free Energy Via Molecular Simulation: Applications to Chemical and Biomolecular Systems. Annual Review of Biophysics and Biophysical Chemistry 1989, 18, 431–492. [DOI] [PubMed] [Google Scholar]
- 47.Naden LN; Shirts MR, Linear Basis Function Approach to Efficient Alchemical Free Energy Calculations. 2. Inserting and Deleting Particles with Coulombic Interactions. J. Chem. Theory Comput 2015, 11 (6), 2536–2549. [DOI] [PubMed] [Google Scholar]
- 48.Naden LN; Pham TT; Shirts MR, Linear Basis Function Approach to Efficient Alchemical Free Energy Calculations. 1. Removal of Uncharged Atomic Sites. J. Chem. Theory Comput 2014, 10 (3), 1128–1149. [DOI] [PubMed] [Google Scholar]
- 49.Pearlman DA; Kollman PA, The Lag between the Hamiltonian and the System Configuration in Free-Energy Perturbation Calculations. J. Chem. Phys 1989, 91 (12), 7831–7839. [Google Scholar]
- 50.Straatsma TP; Zacharias M; McCammon JA, Holonomic Constraint Contributions to Free-Energy Differences from Thermodynamic Integration Molecular-Dynamics Simulations. Chem. Phys. Lett 1992, 196 (3–4), 297–302. [Google Scholar]
- 51.Lin C; Wood RH, Free Energy of Solvation of a Small Lennard-Jones Particle. J. Comput. Chem 1994, 15 (2), 149–154. [Google Scholar]
- 52.Boresch S; Bruckner S, Avoiding the van der Waals Endpoint Problem Using Serial Atomic Insertion. J. Comput. Chem 2011, 32 (11), 2449–2458. [DOI] [PubMed] [Google Scholar]
- 53.Brooks BR; Brooks CL III; MacKerell AD Jr.; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M; Fischer S; Gao J; Hodoscek M; Im W; Kuczera K; Lazaridis T; Ma J; Ovchinnikov V; Paci E; Pastor RW; Post CB; Pu JZ; Schaefer M; Tidor B; Venable RM; Woodcock HL; Wu X; Yang W; York DM; Karplus M, CHARMM: The Biomolecular Simulation Program. J. Comput. Chem 2009, 30 (10), 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Salomon-Ferrer R; Case DA; Walker RC, An overview of the Amber biomolecular simulation package. Wires Comput. Mol. Sci 2013, 3 (2), 198–210. [Google Scholar]
- 55.Phillips JC; Braun R; Wang W; Gumbart J; Tajkhorshid E; Villa E; Chipot C; Skeel RD; Kalé L; Schulten K, Scalable molecular dynamics with NAMD. J. Comput. Chem 2005, 26 (16), 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Hess B; Kutzner C; van der Spoel D; Lindahl E, GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput 2008, 4 (3), 435–447. [DOI] [PubMed] [Google Scholar]
- 57.Christen M; Hünenberger PH; Bakowies D; Baron R; Bürgi R; Geerke DP; Heinz TN; Kastenholz MA; Kräutler V; Oostenbrink C; Peter C; Trzesniak D; van Gunsteren WF, The GROMOS software for biomolecular simulation: GROMOS05. J. Comput. Chem 2005, 26 (16), 1719–1751. [DOI] [PubMed] [Google Scholar]
- 58.de Ruiter A; Boresch S; Oostenbrink C, Comparison of thermodynamic integration and Bennett acceptance ratio for calculating relative protein-ligand binding free energies. J. Comput. Chem 2013, 34 (12), 1024–1034. [DOI] [PubMed] [Google Scholar]
- 59.Shirts MR; Chodera JD, Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys 2008, 129 (12), 124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kumar S; Rosenberg JM; Bouzida D; Swendsen RH; Kollman PA, The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J. Comput. Chem 1992, 13 (8), 1011–1021. [Google Scholar]
- 61.Steinbrecher T; Joung I; Case DA, Soft-Core Potentials in Thermodynamic Integration: Comparing One- and Two-Step Transformations. J. Comput. Chem 2011, 32 (15), 3253–3263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Steinbrecher T; Mobley DL; Case DA, Nonlinear scaling schemes for Lennard-Jones interactions in free energy calculations. J. Chem. Phys 2007, 127 (21), 214108. [DOI] [PubMed] [Google Scholar]
- 63.Bruckner S; Boresch S, Efficiency of Alchemical Free Energy Simulations. II. Improvements for Thermodynamic Integration. J. Comput. Chem 2011, 32 (7), 1320–1333. [DOI] [PubMed] [Google Scholar]
- 64.Hummer G; Szabo A, Calculation of free-energy differences from computer simulations of initial and final states. J. Chem. Phys 1996, 105 (5), 2004–2010. [Google Scholar]
- 65.Paliwal H; Shirts MR, A Benchmark Test Set for Alchemical Free Energy Transformations and Its Use to Quantify Error in Common Free Energy Methods. J. Chem. Theory Comput 2011, 7 (12), 4115–4134. [DOI] [PubMed] [Google Scholar]
- 66.Jorgensen WL; Ravimohan C, Monte Carlo simulation of differences in free energies of hydration. J. Chem. Phys 1985, 83 (6), 3050–3054. [Google Scholar]
- 67.Shirts MR; Bair E; Hooker G; Pande VS, Equilibrium free energies from nonequilibrium measurements using maximum-likelihood methods. Phys. Rev. Lett 2003, 91 (14), 140601. [DOI] [PubMed] [Google Scholar]
- 68.Shirts MR; Pande VS, Comparison of efficiency and bias of free energies computed by exponential averaging, the Bennett acceptance ratio, and thermodynamic integration. J. Chem. Phys 2005, 122 (14), 144107. [DOI] [PubMed] [Google Scholar]
- 69.Bruckner S; Boresch S, Efficiency of Alchemical Free Energy Simulations. I. A Practical Comparison of the Exponential Formula, Thermodynamic Integration, and Bennett’s Acceptance Ratio Method. J. Comput. Chem 2011, 32 (7), 1303–1319. [DOI] [PubMed] [Google Scholar]
- 70.König G; Bruckner S; Boresch S, Unorthodox Uses of Bennett’s Acceptance Ratio Method. J. Comput. Chem 2009, 30 (11), 1712–1718. [DOI] [PubMed] [Google Scholar]
- 71.König G; Brooks BR; Thiel W; York DM, On the convergence of multi-scale free energy simulations. Mol. Simulat 2018, 44 (13–14), 1062–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Lu ND; Kofke DA, Accuracy of free-energy perturbation calculations in molecular simulation. I. Modeling. J. Chem. Phys 2001, 114 (17), 7303–7311. [Google Scholar]
- 73.Anwar J; Heyes DM, Robust and accurate method for free-energy calculation of charged molecular systems. J. Chem. Phys 2005, 122 (22), 224117. [DOI] [PubMed] [Google Scholar]
- 74.Klimovich PV; Shirts MR; Mobley DL, Guidelines for the analysis of free energy calculations. J. Comput. Aid. Mol. Des 2015, 29 (5), 397–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Gapsys V; Seeliger D; de Groot BL, New Soft-Core Potential Function for Molecular Dynamics Based Alchemical Free Energy Calculations. J. Chem. Theory Comput 2012, 8 (7), 2373–2382. [DOI] [PubMed] [Google Scholar]
- 76.Buelens FP; Grubmüller H, Linear-Scaling Soft-Core Scheme for Alchemical Free Energy Calculations. J. Comput. Chem 2012, 33 (1), 25–33. [DOI] [PubMed] [Google Scholar]
- 77.Torrie GM; Valleau JP, Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella Sampling. J. Comput. Phys 1977, 23 (2), 187–199. [Google Scholar]
- 78.de Ruiter A; Oostenbrink C, Extended Thermodynamic Integration: Efficient Prediction of Lambda Derivatives at Nonsimulated Points. J. Chem. Theory Comput 2016, 12 (9), 4476–4486. [DOI] [PubMed] [Google Scholar]
- 79.Li H; Yang W, Forging the missing link in free energy estimations: λ-WHAM in thermodynamic integration, overlap histogramming, and free energy perturbation. Chem. Phys. Lett 2007, 440 (1–3), 155–159. [Google Scholar]
- 80.Leitgeb M; Schroder C; Boresch S, Alchemical free energy calculations and multiple conformational substates. J. Chem. Phys 2005, 122 (8), 084109. [DOI] [PubMed] [Google Scholar]
- 81.Ota N; Stroupe C; Ferreira-da-Silva JMS; Shah SA; Mares-Guia M; Brunger AT, Non-Boltzmann thermodynamic integration (NBTI) for macromolecular systems: Relative free energy of binding of trypsin to benzamidine and benzylamine. Proteins 1999, 37 (4), 641–653. [DOI] [PubMed] [Google Scholar]
- 82.Ota N; Brunger AT, Overcoming barriers in macromolecular simulations: non-Boltzmann thermodynamic integration. Theor. Chem. Acc 1997, 98 (4), 171–181. [Google Scholar]
- 83.Tidor B; Karplus M, Simulation Analysis of the Stability Mutant R96h of T4 Lysozyme. Biochemistry 1991, 30 (13), 3217–3228. [DOI] [PubMed] [Google Scholar]
- 84.Li R; Pourpak A; Morris SW, Inhibition of the Insulin-like Growth Factor-1 Receptor (IGF1R) Tyrosine Kinase as a Novel Cancer Therapy Approach. J. Med. Chem 2009, 52 (16), 4981–5004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Huang J; MacKerell AD Jr., CHARMM36 all-atom additive protein force field: validation based on comparison to NMR data. J. Comput. Chem 2013, 34 (25), 2135–2145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML, Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79 (2), 926–935. [Google Scholar]
- 87.MacKerell AD Jr.; Feig M; Brooks CL III, Improved Treatment of the Protein Backbone in Empirical Force Fields. J. Am. Chem. Soc 2004, 126 (3), 698–699. [DOI] [PubMed] [Google Scholar]
- 88.MacKerell AD Jr.; Feig M; Brooks CL III, Extending the treatment of backbone energetics in protein force fields: Limitations of gas‐phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem 2004, 25 (11), 1400–1415. [DOI] [PubMed] [Google Scholar]
- 89.Martyna GJ; Tobias DJ; Klein ML, Constant pressure molecular dynamics algorithms. J. Chem. Phys 1994, 101 (5), 4177–4189. [Google Scholar]
- 90.Ryckaert JP; Ciccotti G; Berendsen HJC, Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys 1977, 23 (3), 327–341. [Google Scholar]
- 91.Essmann U; Perera L; Berkowitz ML; Darden T; Lee H; Pedersen LG, A Smooth Particle Mesh Ewald Method. J. Chem. Phys 1995, 103 (19), 8577–8593. [Google Scholar]
- 92.Efron B, Bootstrap Methods: Another Look at the Jackknife. Ann. Stat 1979, 7 (1), 1–26. [Google Scholar]
- 93.Lu ND; Kofke DA; Woolf TB, Improving the efficiency and reliability of free energy perturbation calculations using overlap sampling methods. J. Comput. Chem 2004, 25 (1), 28–40. [DOI] [PubMed] [Google Scholar]
- 94.Bogoliubov NN; Soloviev VG, On a Variational Principle in the Many Body Problem. Dokl. Akad. Nauk. Sssr 1959, 124 (5), 1011–1014. [Google Scholar]
- 95.Giese TJ; York DM, A GPU-Accelerated Parameter Interpolation Thermodynamic Integration Free Energy Method. J. Chem. Theory Comput 2018, 14 (3), 1564–1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


