The Promise of Prediction: Biomechanical Analyses in Neuro-Ophthalmology

Biomechanics is the study of the mechanical interaction of solids and/or fluids with internal and external forces in the context of biology. It has long been a mainstay in the cardiovascular and orthopedic fields, where it has been used to analyze and predict the mechanical and biological mechanisms underlying bone fractures, hard and soft tissue remodeling, and blood flow through arterial stents and aneurysms. Biomechanical techniques are critical in optimizing cardiac and orthopedic implant designs for maximum clinical efficacy and life.

Ocular biomechanics primarily has been focused on diseases of the cornea, trabecular meshwork, sclera, and optic nerve head with limited use in the vitreous, lens, and iris. It has provided insight into disease processes and surgical outcome in various eye disorders. For example, in glaucoma, ocular biomechanics has been used to analyze and predict the importance of the sclera in determining the biomechanics of the lamina cribrosa, the site of axonal damage in glaucoma.

Biomechanical engineers use cutting-edge engineering-based computational and experimental techniques to investigate the interaction of ocular tissues with their surroundings, and the forces that are common in the eye are intraocular pressure, tensile and torsional muscle tractions, blood flow and vascular pressures, external traumatic forces, cerebrospinal fluid pressure, and tissue growth pressures. The tools bioengineers use include finite element modeling, a computational technique to split complex geometries such as the lamina cribrosa into small regularly shaped elements, for which loading, mechanical stress (force distribution), and mechanical strain (local deformation) are calculated individually. The results of each of these simple elemental responses are then added up, or superposed, into the overall response of the structure. Experimental measures of tissue deformation under load can now be obtained with imaging techniques, such as ultrasound biomicroscopy, optical coherence tomography, and magnetic resonance imaging, and these observations can be used to validate computational biomechanics simulations.

The structural geometries in the human body are much more complex than typical engineered structures, such as bridges and airplane wings (Fig. 1). Biological tissue stiffness is inherently complex in that it changes with orientation (anisotropy), the rate of loading (viscoelasticity), and with the level of stretch or compression (hyperelasticity). Computational models require accurate representations of tissue geometry, loading and constraints on the modeled structure, and compliance or stiffness of the tissue constituents. These are often very difficult to obtain, especially for tiny structures in the eye (1) or those buried in the brain. Important factors such as fluid pressures or blood flow are nearly impossible to measure using current technology. When accurate representations of the model inputs are unavailable, simple representative geometries, coupled with simplifying assumptions on the loading and tissue material properties can still be used to construct models that reveal fundamental relationships regarding the responses of tissues to load (2).

FIG. 1.

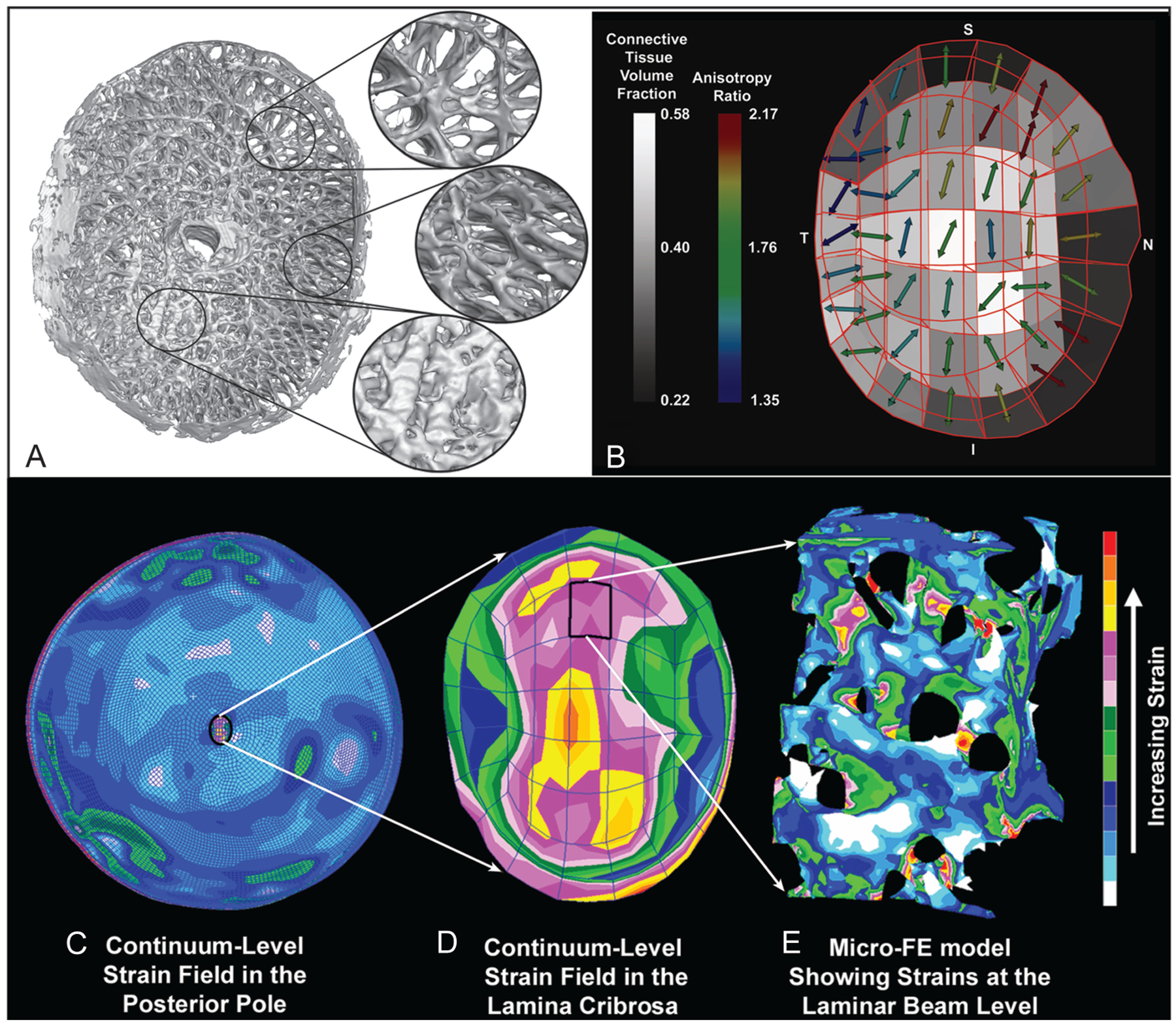
Regional differences in laminar microarchitecture in a normal eye and regional laminar density and anisotropy mapping. Characterization of the laminar microarchitecture (A) uses the element boundaries of a continuum finite mesh to partition the lamina cribrosa connective tissue into 45 subregions (B). The connective tissue volume fraction (CTVF) for each region is expressed as a percentage and mapped to a grayscale value in the background. The arrows indicate the pre-dominant orientation of the laminar beams in each region, with higher values (color-coded) indicating regions in which the beams are more highly oriented. Note that in the peripheral regions of the lamina, the beams are tethered radially into the scleral canal wall. Complexities in the posterior pole biomechanical response. C. The image shows the strain distribution in a macroscale model of the connective tissues of the posterior pole of the eye. Note that thickness variations in the sclera give rise to a nonuniform distribution of tensile strain within the scleral shell, and that the strains are lower in the sclera than in the more compliant lamina cribrosa. D. A detail is shown of the strain field within the macroscale representation of the lamina cribrosa derived from the individual mapping of laminar CTVF and beam orientation shown in (B). Although this portion of the model has been assigned regional material properties related to the amount and orientation of the laminar beams shown in (B), the continuum description represents a bulk homogenization of the specific microarchitecture in each element and only approximates the overall strain field. E. The distribution of mechanical strain at the microscale in the laminar beam microarchitecture demonstrates that strains concentrate focally in individual lamina cribrosa beams and around individual axonal pores. Adapted from Roberts et al (1) and Downs et al (2).

Until recently, neuro-ophthalmology has been largely left out of the revolution in ocular biomechanical analysis. In this issue of the Journal of Neuro-Ophthalmology, Wang et al (3) have applied biomechanics to investigate the mechanisms underlying bitemporal hemianopia in optic chiasmal compression. In this computational study, the authors used both macro- and micro-scale finite element models (FEMs) to estimate the mechanical strains (tensile stretch and compression) in the optic chiasm due to pituitary tumor growth-driven compression. The results demonstrated that the stresses estimated by the macroscale (optic nerve) model are reasonable in view of the limited experimental data available for validation, but these stresses are unable to explain bitemporal hemianopia. To generate this visual field defect, separation of the insult to nasal and temporal optic nerve axons is required, which could only be explained by the microscale model of compression of 2 axons oriented either in parallel or perpendicularly. The central aspect of the optic chiasm always experienced higher compressive strains than the peripheral portions when compressed from beneath by tumor growth. In models of individual axons, strains in the nasal (crossed) nerve fibers were always much larger than in temporal (uncrossed) nerve fibers, providing a mechanical explanation for the selective neuronal damage that results in bitemporal hemianopia.

A critical aspect of all biomechanical modeling analyses is validation. All FEMs simulate a condition and yield results, but validation is required to know how well those results mimic the simulated condition. Validation is the process by which a model is constructed and refined using known data and then subsequently exercised to predict the behavior of several new conditions for which the results are not known apriori. A model is only considered valid for prediction when it can accurately predict mechanical behavior across a range of conditions and loadings, which have been checked for accuracy against experimental measurements and observations of the structure’s actual mechanical response. Unvalidated models can provide some insight in limited circumstances but only in the context of describing one of the potentially limitless possible scenarios that could explain the behavior being modeled.

In the study by Wang et al (3), there are no validating data to support the results, as geometry, boundary conditions, and material properties such as anisotropy and viscoelasticity become more problematic at the cell scale. Therefore, the presented strain estimates can only serve as a computational experiment that must be further investigated and validated using experimental measures. The authors acknowledged that the results reflect one scenario that could explain the clinical finding of bitemporal hemianopia, that is, these modeling results are speculative. Yet, the study does demonstrate the power of biomechanical modeling as a tool to investigate difficult clinical problems. Even speculative modeling results can drive further hypothesis-forming steps and experimental studies designed to validate the models’ predictions, a form of reverse validation. Welcome to the wonderful world of biomechanics.