Abstract
We present a class of pulsed third-spin-assisted recoupling (P-TSAR) magic-angle-spinning (MAS) solid-state NMR techniques that achieve efficient polarization transfer over long distances to provide important restraints for structure determination. These experiments utilize second-order cross terms between strong 1H-13C and 1H-15N dipolar couplings to achieve 13C-13C and 13C-15N polarization transfer, similar to the principle of continuous-wave (CW) TSAR experiments. However, in contrast to the CW-TSAR experiments, these P-TSAR experiments require much less radiofrequency (rf) energy and allow a much simpler routine for optimizing the rf field strength. We call the techniques PULSAR (PULSed proton Asissted Recoupling) for homonuclear spin pairs. For heteronuclear spin pairs, we improve the recently introduced PERSPIRATIONCP (Proton-Enhanced Rotor-echo Short Pulse IRradiATION Cross-Polarization) experiment by shifting the pulse positions and removing z-filters, which significantly broaden the bandwidth and increase the efficiency of polarization transfer. We demonstrate the PULSAR and PERSPIRATIONCP techniques on the model protein GB1, and found cross peaks for distances as long as 10 and 8 Å for 13C-13C and 15N-13C spin pairs, respectively. We then apply these methods to the amyloid fibrils formed by the peptide hormone glucagon, and show that long-range correlation peaks are readily observed to constrain intermolecular packing in this cross-β fibril. We provide an analytical model for the PULSAR and PERSPIRATIONCP experiments to explain the measured and simulated chemical shift dependence and pulse flip angle dependence of polarization transfer. These two techniques are useful for measuring long-range distance restraints to determine the three-dimensional structures of proteins and other biological macromolecules.
Graphical Abstract
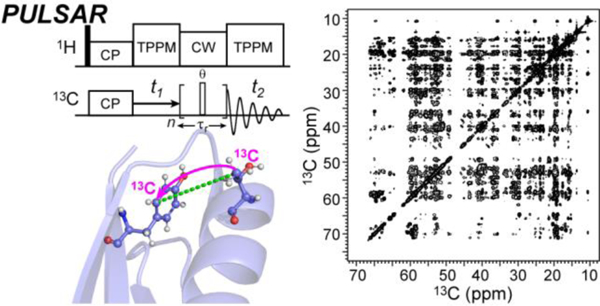
Introduction
Magic-angle-spinning (MAS) solid-state nuclear magnetic resonance (SSNMR) spectroscopy produces high-resolution spectra by averaging orientation-dependent nuclear spin interactions such as chemical shift anisotropy (CSA), dipolar couplings, and quadrupolar couplings. MAS SSNMR is uniquely suited among spectroscopic techniques to provide atomic-resolution structural information of insoluble, non-crystalline biological macromolecules such as membrane proteins 1–4, amyloid fibrils 5–13, and cell walls 14–17. Once chemical shift assignment is complete, three-dimensional structure determination predominantly relies on inter-atomic distance restraints, which are measured through internuclear dipolar couplings. Under MAS, dipolar couplings are reintroduced using tailored radiofrequency (rf) pulse sequences or a careful choice of spinning frequency 18. Heteronuclear dipolar couplings and distances can be measured using the Rotational Echo DOuble Resonance (REDOR) technique 19 and the related Transferred Echo DOuble Resonance (TEDOR) 20–21, while homonuclear dipolar couplings and distances are typically measured qualitatively using spin diffusion techniques such as Proton-Driven Spin-Diffusion (PDSD) 22, Dipolar-Assisted Rotational Resonance (DARR) 23–24 and COmbined R2νn Driven spin diffusion (CORD) 25. Higher magnetic field strengths are advantageous for obtaining higher spectral resolution and sensitivity. However, at higher fields the larger isotropic chemical shift differences weaken the spin diffusion mechanism. Moreover the larger CSA requires faster MAS to suppress, thus further weakening the dipolar couplings that drive homonuclear polarization transfer. In addition, nuclei with low gyromagnetic ratios (γ) have weak dipolar couplings, which make it difficult to measure the long distances that are especially useful for restraining three-dimensional structures. Therefore, it is important to develop improved pulse sequences for high-field fast MAS conditions to achieve efficient long-range polarization transfer 26.
Third-Spin-Assisted Recoupling (TSAR) experiments are a class of techniques that transfer polarization between low-γ nuclei A and B 27. This transfer occurs via cross terms in the second-order average Hamiltonian between the H–A and H–B dipolar couplings, which are generally much stronger than the direct A-B dipolar coupling. In continuous-wave TSAR (CW-TSAR) experiments, the homonuclear variant is known as Proton-Asisted Recoupling (PAR) 28 whereas the heteronuclear variant is called Proton-Asissted Insensitive Nuclei Cross Polarization (PAINCP) 29–30. The CW irradiation in these experiments requires carefully optimized rf field strengths on both the 1H channel and the heteronuclear channels. This is usually achieved by an extensive multidimensional search of the rf field strengths, without which the polarization transfer efficiency can easily fall well below the theoretical maximum 31. Moreover, mixing times of 10–30 ms are usually required to detect long-range 13C-13C and 15N-13C correlation peaks. The extended high-power CW irradiation on two to three channels can damage the NMR probe and heat-sensitive biological samples. These two practical drawbacks have limited the use of the PAR and PAINCP experiments, despite their theoretical ability for long-range spin polarization transfer, compared to the simpler spin diffusion experiments.
Here we introduce pulsed TSAR (P-TSAR) techniques that achieve efficient polarizarion transfer over long distances using low rf energy and simple optimization routines. These P-TSAR experiments rely on a pulsed spin-lock 32, in contrast to CW-TSAR experiments, which utilize a CW spin-lock. We demonstrate these techniques on a model protein, the β1 immunoglobulin binding domain of protein G (GB1), and apply them to the amyloid fibrils formed by the peptide hormone glucagon 12. We then show by numerical simulations, average Hamiltonian Theory 33 and an analytical model that these P-TSAR experiments have the same essential spin dynamics as CW-TSAR: they have vanishing first-order average Hamiltonians and rely on trilinear terms of the kind and in the second-order average Hamiltonian to mediate polarization transfer. We call the homonuclear experiment PULSed proton-Asissted Recoupling (PULSAR) (Fig. 1a) and the heteronuclear experiment Proton-Enhanced Rotor-echo Short Pulse IRradiATION (PERSPIRATIONCP). The latter was introduced recently by us 34 but is now significantly improved by altering the timing of the spin-lock pulses to better refocus the magnetization at the end of each rotor period (Fig. 1c, Fig. S1). This pulse timing change obviates the need for z-filters and increases the bandwidth of P-TSAR transfer. Most importantly, P-TSAR experiments use only 10–20% of the rf duty cycle of their CW-TSAR analogs on the low-frequency channels and are robust against variations in the heteronuclear rf powers.
Figure 1.
P-TSAR pulse sequences developed in this study (a, c), together with previously published CW-TSAR pulse sequences (b, d). (a) 2D 13C-13C PULSAR. (b) 2D 13C-13C PAR 28. (c) 2D 15N-13C PERSPIRATIONCP with spin-lock pulses in the center of the rotor period. (d) 2D 15N-13C PAINCP 28.
Materials and Methods
SSNMR experiments were conducted on Bruker Avance III HD 600 MHz (14.1 T) and Avance II 800 MHz (18.8 T) spectrometers equipped with triple-resonance 1H/13C/15N 3.2 mm MAS probes. All experiments were carried out under 20 kHz MAS. 13C, 15N-labeled microcrystalline GB1 was expressed, purified and precipitated as previously described 35–36. Most GB1 spectra were measured on a 13C, 15N-labeled GB1 that was H/D exchanged. About 20 mg protein was packed into a 3.2 mm Bruker MAS rotor. Site-specifically 13C, 15N-labeled glucagon peptide was purchased from Biopeptek Pharmaceuticals (Malvern, PA) and fibrillized in pH 2 solution at 21˚C for 7 days at a concentration of 8 mg/ml 12. A total of 5 mg fibril was packed into a 3.2 mm rotor. For the anhydrous model compound formyl-Met–Leu–Phe (f-MLF) 37, 2.8 mg peptide was center-packed in a 3.2 mm rotor.
PULSAR and PERSPIRATIONCP experiments (Appendix S4,5) were conducted at a set temperature of 278 K for GB1 and 258–263 K for f-MLF and hydrated glucagon fibrils. At 20 kHz MAS, the actual sample temperature was estimated to be 15 K higher than the set temperature due to frictional heating 38. Two-Pulse Phase Modulation (TPPM) 1H decoupling 39 was applied at an rf field of 71–83 kHz during 13C detection. For 2D 13C-13C PULSAR experiments on GB1, the direct acquisition times were 21.5 ms and 16.1 ms for the 600 and 800 MHz spectra, respectively, whereas the indirect dimension maximum 13C evolution times were 9.9 ms and 7.4 ms, respectively. For 2D 13C-13C PULSAR experiments on glucagon at 800 MHz, the direct dimension acquisition time was 15.3 ms while the indirect dimension 13C evolution time was 7.4 ms. For the 2D 15N-13C PERSPIRATIONCP experiment on GB1 at 600 MHz, the 13C acquisition time was 11.9 ms and the maximum 15N evolution time was 10.2 ms. For the 2D 15N-13C PERSPIRATIONCP experiment on glucagon at 600 MHz, the 13C acquisition time was 11.9 ms and the 15N maximum evolution time was 6.6 ms. Most 2D experiments took 0.9–2.5 days, except for the PERSPIRATIONCP experiment on glucagon, which took 3.6 days. A pseudo-3D PERSPIRATIONCP experiment was conducted on the 800 MHz spectrometer in which one indirect dimension varied the 13C rf carrier frequency from 0 to 200 ppm in 2.5 ppm increments, and the other indirect dimension varied the spin-lock pulse flip angles for both 13C and 15N from 0 to 360º in 15º increments. For the spin-lock pulses, the 13C and 15N rf field strengths were 50 kHz and 38.8 kHz, respectively, while the 1H CW rf irradiation was 56–59 kHz during PULSAR and PERSPIRATIONCP polarization transfer.
All 2D spectra were processed in TopSpin (Bruker BioSpin) and assigned in Sparky 40. The distance upper limits were set to 10 Å for the 13C-13C cross peaks in the PULSAR spectra and 8 Å for the 13C-15N cross peaks in the PERSPIRATIONCP spectra. We calculated the GB1 structure using CYANA 2.1 41. The (ϕ, ψ) torsion angles were predicted from backbone chemical shifts using the TALOS-N software 42. The angular uncertainty was set to twice the uncertainty given by TALOS-N. The structure calculation consisted of a total of 100 independent runs with 70,000 torsion angle steps each. The ten structures with the lowest target function were included in the final ensemble.
Numerical simulations of the PULSAR and PERSPIRATIONCP polarization transfer dynamics were conducted using SpinEvolution 43. Analytical calculations and data analysis were performed using home-written MATLAB and Python scripts, which are provided in the Supporting Information. The magnetization trajectories and Bloch spheres were generated in MATLAB.
Results
Demonstration of PULSAR and PERSPIRATIONCP experiments on a microcrystalline protein
Fig. 1 and Fig. S1 show the pulse sequences for PULSAR and PERSPIRATIONCP and their CW-TSAR counterparts. Both P-TSAR experiments use pulses with a flip angle θ at the center of each rotor period on the low-frequency channels. CW decoupling occurs on the 1H channel during the mixing time. As in PAR and PAINCP, the 1H decoupling field strength is chosen to avoid the rotary resonance condition, ω1= ωr, as well as avoiding the CP matching condition with the heteronuclear channels. We conducted all experiments under 20 kHz MAS and used rf field strengths of 35–50 kHz for the θ-pulses.
We first demonstrate the PULSAR and PERSPIRATIONCP experiments on the model protein GB1 on a 600 MHz spectrometer (Fig. 2). We placed the 13C carrier frequency at 43 ppm, in the middle of the aliphatic region, and the 15N carrier frequency at 122 ppm, in the middle of the amide region. We varied the spin-lock pulse flip angle from 90° to 165°, and found 150° pulses to give maximum polarization transfer in a broadband fashion. The aliphatic 13C chemical shift range for which signal intensity is observed is about 9 kHz (60 ppm). Intensity is also observed in the aromatic and carbonyl regions of the spectrum. At 600 MHz, the aliphatic-carbonyl chemical shift difference is ~20 kHz (130 ppm). Smaller flip angles reduced the chemical shift range of polarization transfer, whereas larger flip angles decreased the total transferred magnetization. The optimal 1H rf field strength during the 13C and 15N P-TSAR period is slightly less than for both PULSAR and PERSPIRATIONCP experiments, consistent with numerical simulations (Fig. S2). The 2D 13C-13C PULSAR spectrum shows a large number of long-range correlations in every region of the 2D spectrum. These include aliphatic-aliphatic, aliphatic-aromatic, aliphatic-carbonyl, aromatic-aromatic correlations (Fig. 2a, b). Some of the cross peaks correspond to distances of 8 Å or more, such as T25-Y3 (Fig. 2c). Similarly, the 2D 15N-13C PERSPIRATIONCP spectrum showed many long-range correlations (Fig. 2d, e) such as V54-L7, which has a distance of 6 Å (Fig. 2f). We compared the performance of PULSAR with PAR on the 600 MHz spectrometer (Fig. S3). Relative to a 10 ms 2D PAR spectrum, the 10 ms PULSAR spectrum shows roughly equivalent sensitivity while the 20 ms PULSAR spectrum has significantly lower sensitivity than the 10 ms PAR due to relaxation. However, the 20 ms PULSAR spectrum displays many long-range cross peaks that are absent or very weak in the 10 ms PULSAR or PAR spectra. Both PULSAR experiments required less rf power than the PAR experiment.
Figure 2.
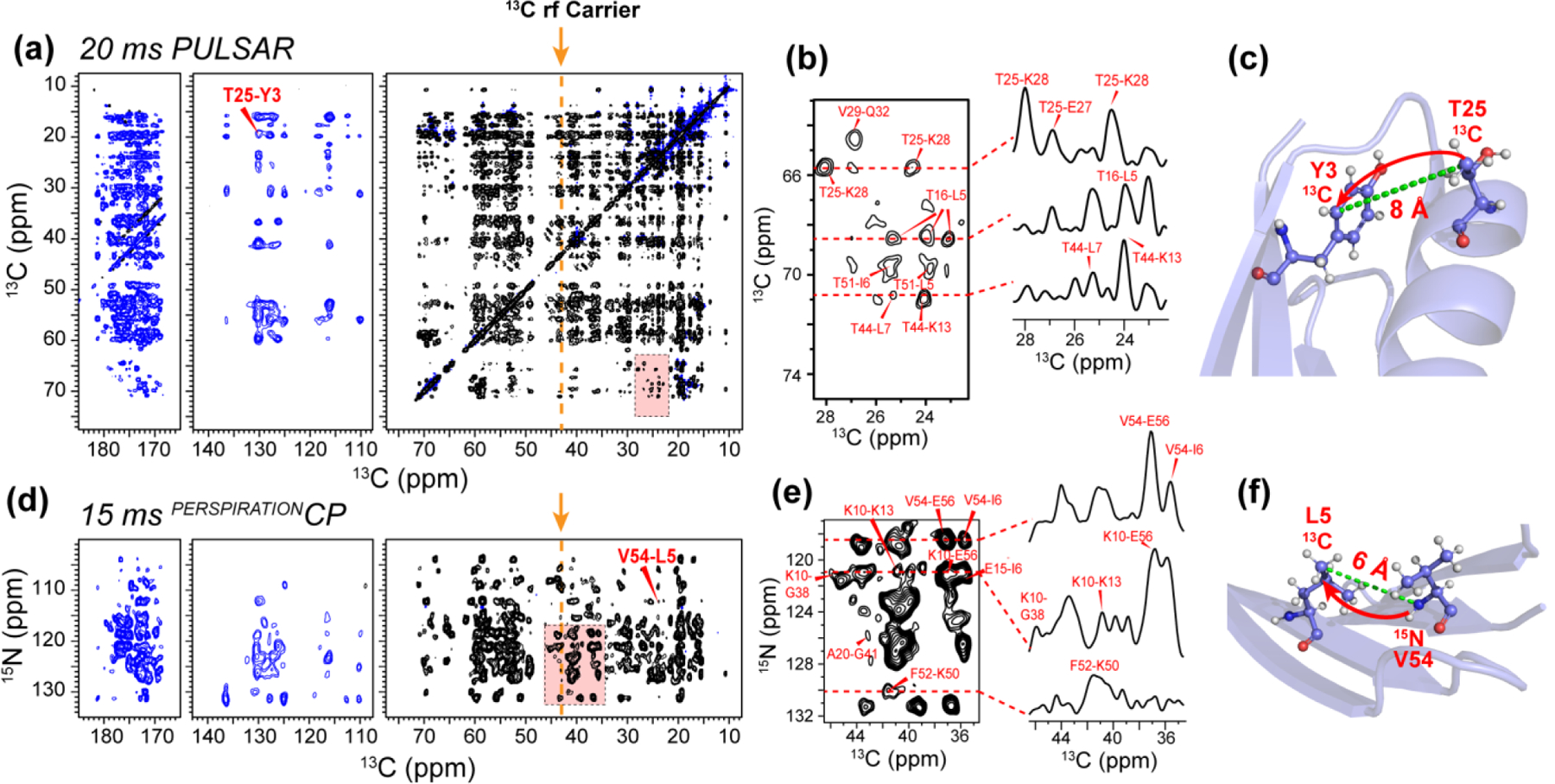
2D 13C-13C PULSAR and 15N-13C PERSPIRATIONCP spectra of GB1 measured on the 600 MHz spectrometer. The 13C rf carrier frequency was set at 42 ppm (orange arrow and dashed line). Positive intensities are shown in black and negative intensities are shown in blue. (a) 2D 13C PULSAR spectrum measured with 20 ms mixing and 150º recoupling pulses. The indirect dimension evolution time was 9.9 ms, while the direct dimension acquisition time was 21.5 ms. (b) Selected zoomed-in area and 1D cross sections of the PULSAR spectrum, showing some of the medium-range, long-range, and intermolecular correlation peaks. (c) GB1 structure, indicating one of the long-range contacts, between T25 and Y3, observed in the PULSAR spectrum. (d) 2D 15N-13C PERSPIRATIONCP spectrum measured with 15 ms mixing and 150˚ recoupling pulses. The 15N maximum evolution time was 10.2 ms while the direct dimension 13C acquisition time was 11.9 ms. (e) Selected zoomed-in area and 1D cross sections of the PERSPIRATIONCP spectrum, showing some of the medium-range, long-range, and intermolecular correlation peaks. (f) GB1 structure, indicating one of the long-range contacts, between V54 and L7, whose cross peak is observed in (d).
Because of the enhanced sensitivity and resolution provided by higher magnetic fields, we next conducted PULSAR experiments on an 800 MHz spectrometer, where the aliphatic chemical shifts span a range of 12 kHz and the aliphatic-carbonyl chemical shift separation increases to 26 kHz. To achieve the same offset-dependent polarization transfer as the 600 MHz spectra, one would need to spin the samples at 27 kHz. Since this is not feasible using 3.2 mm MAS rotors and nitrogen gas for spinning, we kept the MAS rate at 20 kHz and varied the pulse flip angle to optimize polarization transfer in the spectral region of interest. With 150º pulses, 13C magnetization from the aliphatic carbons gave positive transfer to other aliphatic carbons, negative transfer to aromatic carbons (110–156 ppm), and positive transfer to carbonyl carbons (172–182 ppm) (Fig. 3a, c). With 210º pulses, the transfer profile has a null in the aromatic region and negative intensities in the carbonyl region (Fig. 3b). Similarly long distances were observed as spectra measured at 600 MHz.
Figure 3.
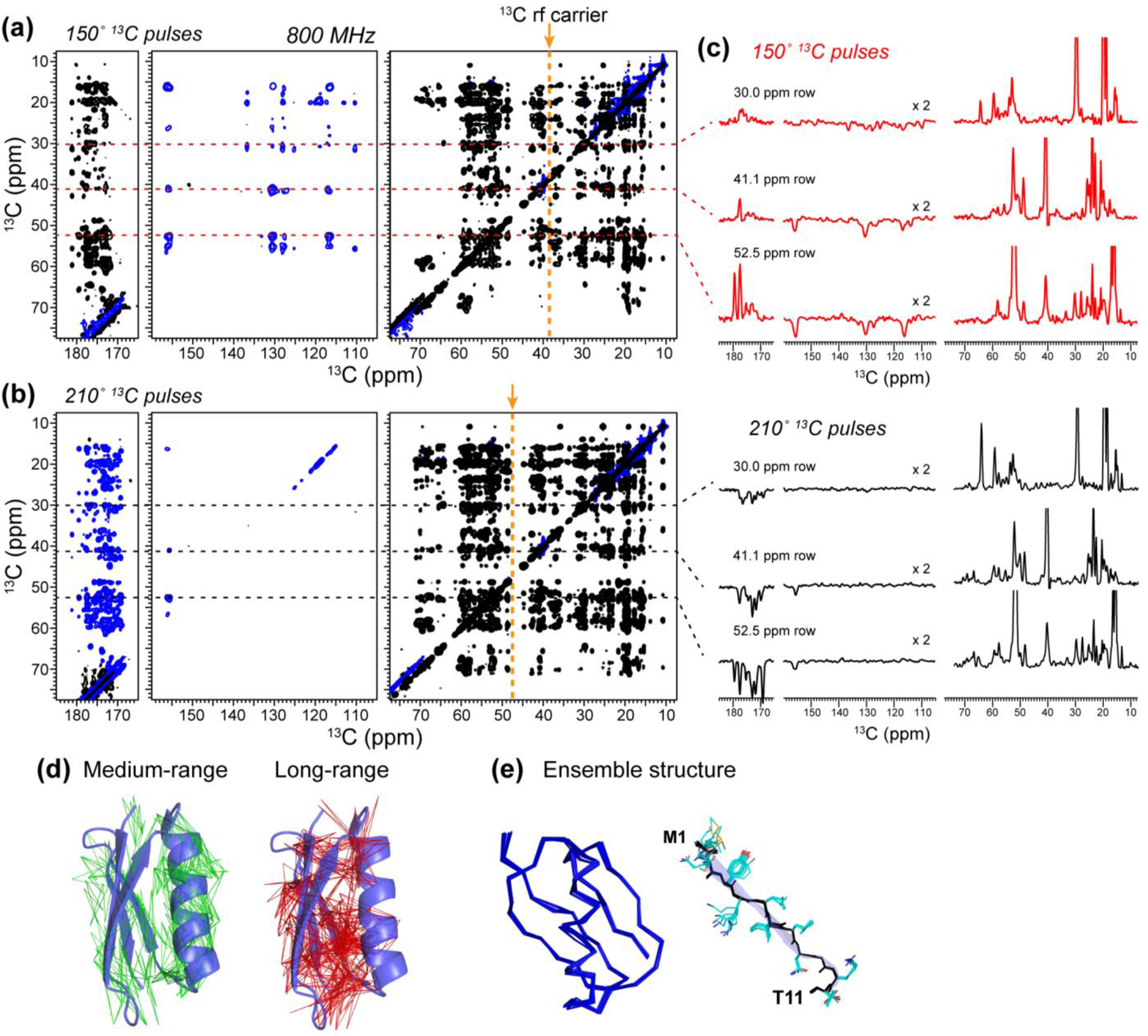
2D 13C-13C PULSAR spectra of GB1 measured at 800 MHz to investigate the offset dependence of the experiment. (a) 2D spectrum measured using 150º spin-lock pulses. (b) 2D spectrum measured using 210˚ spin-lock pulses. The rf fields were 50 kHz for 13C and 56 kHz for 1H and the mixing time was 20 ms. Both spectra were measured using a maximum evolution time of 7.4 ms and direct acquisition time of 15.3 ms. (c) Corresponding 1D cross sections illustrating the signal-to-noise ratios of the two spectra. The aromatic region was processed with Gaussian broadening to enhance the sensitivity, while the aliphatic and carbonyl regions were processed using a qsine window function to enhance the resolution. (d) 112 medium-range (green) and 176 long-range (red) correlations in GB1 obtained from these PULSAR and PERSPIRATIONCP spectra. (e) Lowest-energy ensemble of GB1 structures calculated based on the distance constraints obtained from the PULSAR and PERSPIRATIONCP spectra. The backbone ensemble shows that P-TSAR distance restraints combined with (ϕ, ψ) torsion angles are sufficient to determine the 3D structure of the protein. The M1-T11 β-strand is shown on the right to illustrate the sidechain conformations constrained by the long-range correlations.
These 2D 13C-13C and 15N-13C correlation spectra yielded a total of 100 sequential, 112 medium-range (2 < |i-j| < 5), and 176 long-range ( |i-j| > 5) distance restraints (Fig. 3d). Combining these restraints with (ϕ, ψ) torsion angles obtained from backbone chemical shifts, we calculated the GB1 structure. We set the upper distance limits to 10 Å for PULSAR cross peaks and 8 Å for PERSPIRATIONCP cross peaks. These upper limits were estimated by finding cross peaks corresponding to the longest distance in the high-resolution NMR structure of GB1 44 and ensuring that this upper limit does not cause restraint violations in the structure calculation. The medium-range restraints are particularly useful for determining the secondary structure, since i to i + 2 cross peaks are expected for β-strands while i to i + 3 or 4 cross peaks are expected for α-helices. The long-range restraints helped to define both the backbone fold and the sidechain conformations. The ten lowest-energy structures display a backbone RMSD of 0.4 ± 0.1 Å and a heavy-atom RMSD of 1.3 ± 0.2 Å (Fig. 3e). Therefore, these 13C-13C PULSAR and 15N-13C PERSPIRATIONCP restraints are sufficient to solve the high-resolution structure of GB1.
Application of P-TSAR to glucagon amyloid fibrils
To test the ability of the PULSAR and PERSPIRATIONCP experiments for structure determination of non-crystalline proteins, we applied them to the amyloid fibrils formed by the peptide hormone glucagon 12. Glucagon is used as a pharmaceutical compound to treat severe hypoglycemia. At the high concentrations required for intravenous administration, it fibrillizes rapidly 45 into cross-β structures. This fibrillization tendency has limited glucagon’s formulation to a dry powder, to be mixed in acidic solution immediately prior to injection. Understanding the atomic structure of glucagon fibrils is thus important for designing glucagon analogs that resist fibril formation. We measured the 2D PULSAR and PERSPIRATIONCP spectra of a glucagon fibril containing nine 13C, 15N-labeled residues (Fig. 4a). The 2D 13C-13C PULSAR spectrum was measured at 800 MHz using a 12.5 ms mixing time while the 2D 15N-13C PERSPIRATIONCP spectrum was measured at 600 MHz using a 15 ms mixing time (Fig. 4b, c). Many medium-range intramolecular cross peaks were observed, such as T5Cβ-Q3Cβ and Q24Cγ-L26Cδ1. This is consistent with the location of i and i + 2 sidechains on the same side of the β-sheet plane. We also detected long-range correlations such as T5Cα-M27Cα and T5Cα-L26Cδ in the PULSAR spectrum and G4N-N28Cβ and W25N-M27Cε cross peaks in the 15N-13C correlation spectra. These long-range correlations can only be assigned to intermolecular contacts, based on additional experiments of isotopically diluted samples 12. Therefore, the long-range correlations define the antiparallel packing of β-strands. Intra-residue backbone 15N to sidechain 13C correlations are also observed for bulky sidechains such as Q24N-W25Cζ3. These restraints combine with intermolecular correlations involving the same W25 sidechain to determine the rotameric structure of the bulky sidechain (Fig. 4d, e).
Figure 4.
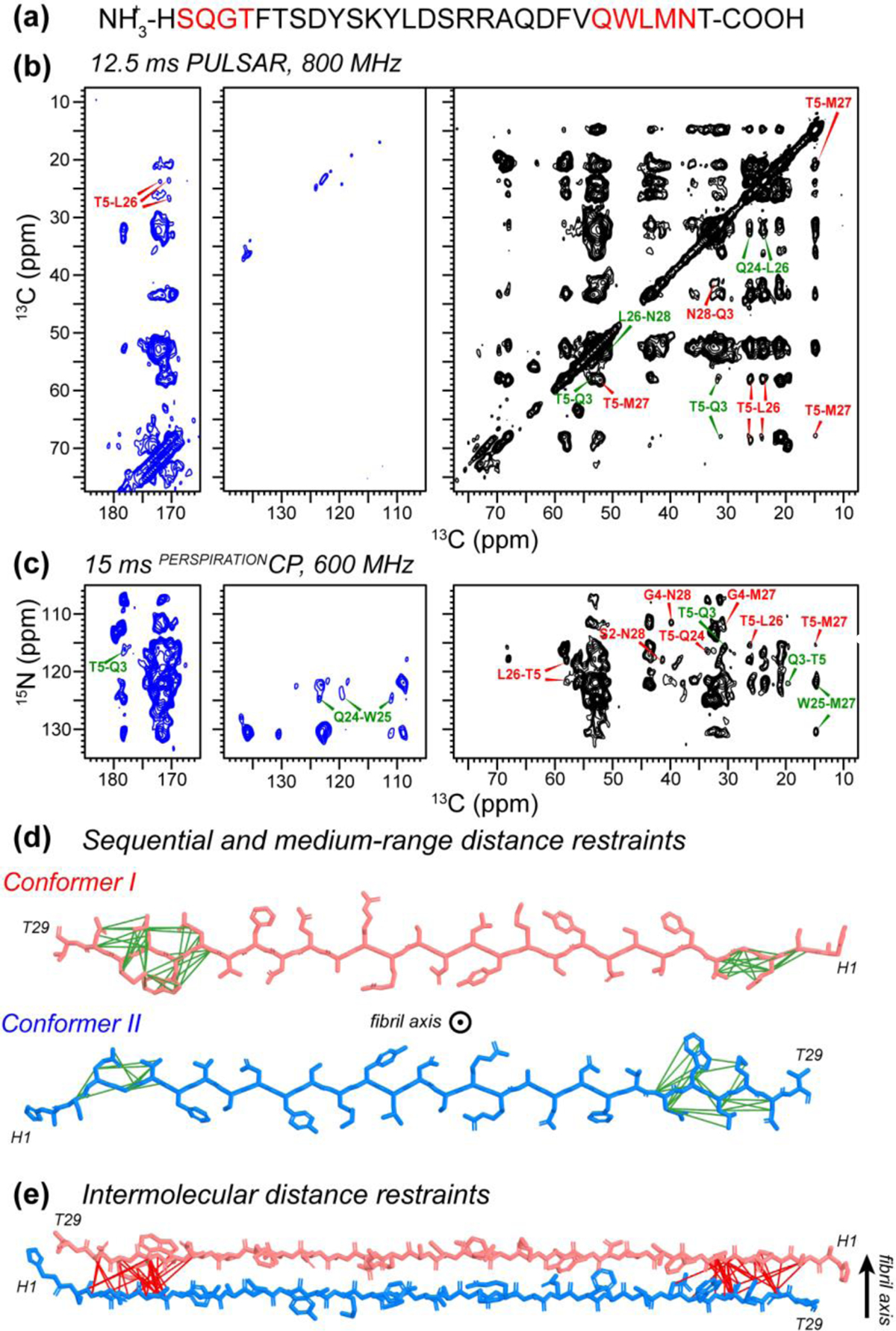
2D PULSAR and PERSPIRATIONCP spectra of glucagon fibrils for obtaining distance restraints. (a) Amino acid sequence of glucagon. 13C, 15N-labeled residues are shown in red. (b) 12.5 ms 2D 13C PULSAR spectrum, measured on the 800 MHz spectrometer using 150º 13C recoupling pulses. The spectrum was measured with a maximum evolution time of 2.6 ms and a direct acquisition time of 12.3 ms. (c) 15 ms 2D 15N-13C PERSPIRATIONCP spectrum, measured on the 600 MHz spectrometer using 150º 13C and 15N recoupling pulses. The t1 evolution time was 6.6 ms while the direct dimension acquisition time was 11.9 ms. (d) Sequential and medium-range intramolecular correlations found in the PULSAR and PERSPIRATIONCP spectra. These correlations help to define the rotameric conformation of sidechains such as W25. (e) Intermolecular correlations define antiparallel hydrogen bonding of the β-strands along the fibril axis.
Numerical simulations of CW-TSAR and P-TSAR experiments
We conducted numerical simulations to understand the chemical shift offset and rf field dependences of the P-TSAR experiments compared to CW-TSAR. A 7-spin system was used for PULSAR and PAR while an 8-spin system was used for PERSPIRATIONCP and PAINCP. These spin systems were taken from amino acid Met to represent the backbone and sidechain structure of a typical residue (Fig. 5a, d). For PULSAR and PERSPIRATIONCP experiments, we simulated the polarization transfer as a function of 13C chemical shift offset of the observed (sink) spins and as a function of the pulse flip angle. For PAR and PAINCP experiments, we simulated the transfer efficiency as a function of the rf field strength. Representative simulation scripts are given in Supporting Information Appendix S1.
Figure 5.
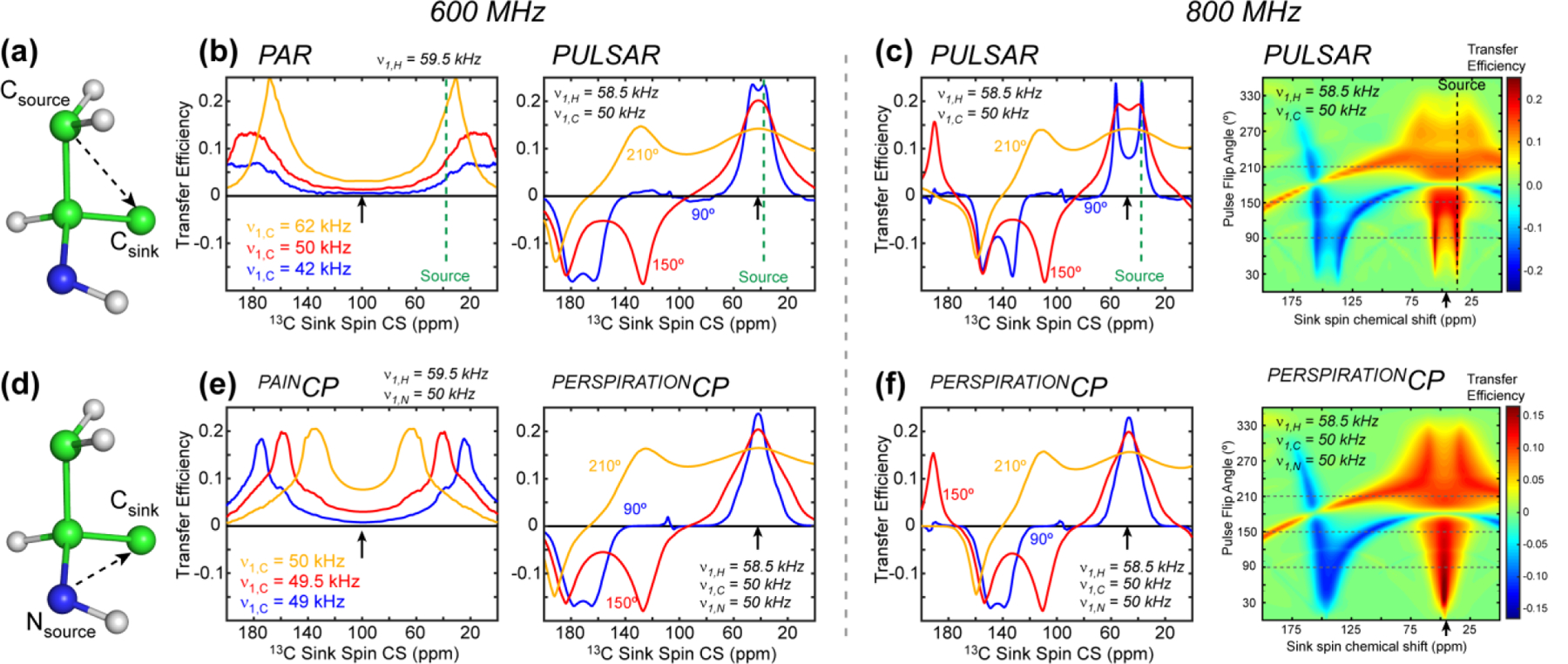
Numerical simulations of the chemical shift dependence of TSAR experiments. A mixing time of 20 ms was used in all simulations. (a) 7-spin system for simulating the PAR and PULSAR 13C-13C polarization transfer. The 15N spin is excluded in these simulations. (b) PAR and PULSAR efficiencies at 600 MHz as a function of the observed 13C chemical shifts. The 13C rf carrier frequency is denoted with a black arrow while the 13C source spin chemical shift is denoted with a green dashed line. (c) PULSAR transfer efficiency at 800 MHz. Right: 2D contour map of the PULSAR transfer efficiency as a function of sink spin chemical shift and pulsed spin-lock flip angle. (d) 8-spin system used for simulating PAINCP and PERSPIRATIONCP 15N-13C polarization transfer. (e) PAINCP and PERSPIRATIONCP efficiencies at 600 MHz as a function of the observed 13C chemical shifts. (f) PERSPIRATIONCP transfer efficiencies at 800 MHz. Right: 2D contour plot of the PERSPIRATIONCP transfer efficiency as a function of sink-spin chemical shift and pulse flip angle.
PAR transfer is optimized when the source and sink spin have similar 13C chemical shift offsets. With the 13C rf carrier frequency at 100 ppm, the PAR polarization transfer from a CH2 carbon at 40 ppm is efficient to aliphatic signals near the source 13C chemical shift and to carbonyl carbons. However, the polarization transfer is minimal at ~100 ppm (Fig. 5b, left). Over the range of 13C rf field strength from 62 to 42 kHz, stronger rf fields give higher polarization transfer efficiencies. 15N-13C PAINCP exhibits a similar offset dependence (Fig. 5e, left), but the transfer efficiency is much more sensitive to the 13C rf field strength: much higher transfer efficiency is found at a 13C rf field of 50 kHz than at 49 kHz, while 1H and 15N rf fields are held constant at 59.5 kHz and 50 kHz, respectively. The same modest 13C rf field change also changed the offset at which maximum transfer occurs, from 60 ppm to 30 ppm. Thus, PAINCP is extremely sensitive to both the rf field strength and the chemical shift offset.
Compared to these CW-TSAR polarization transfer profiles, the P-TSAR experiments give more broadband transfer and are less sensitive to the rf field strength. Maximum PULSAR transfer is also found when the source and sink spin have similar chemical shift offsets (Fig. 5b, right, Fig. 5c). However, unlike PAR, there are other matching conditions that can accomplish polarization transfer. Prudent choice of pulse flip-angle and carrier frequency can allow an experiment to have a much wider range of chemical shift offsets with efficient transfer. At 600 MHz, when the 13C carrier frequency is set to 38 ppm, the optimal 13C flip angle is ~150°, at which efficient transfer is found for all three regions of the 13C spectra: aliphatic, aromatic, and carbonyl (Fig. 5b, right). When the flip angle increases to 210˚, the aromatic signals becomes positive while the carbonyl intensities vanish. At 800 MHz, the highest polarization transfer is found at a flip angle of 210˚, where positive transfer is observed from 0–130 ppm and negative transfer is observed for carbonyl carbons (Fig. 5c). The 15N-13C PERSPIRATIONCP transfer profiles (Fig. 5e, right, Fig. 5f) are similar to the PULSAR transfer profiles.
Average Hamiltonian analysis of P-TSAR
To further understand the mechanism of polarization transfer in PULSAR and PERSPIRATIONCP, we analyzed their average Hamiltonians 33 using a similar approach to the CW-TSAR treatment 28, 30. For clarity, we first analyze PERSPIRATIONCP; explanations on how the analysis changes for PULSAR are given in the main text and Supporting Information. We consider a three-spin system consisting of one 1H, one 15N and one 13C. The 1H spin is subjected to CW rf irradiation while δ-function pulses with flip angles θC and θN are applied at the center of each rotor period to 13C and 15N, respectively (Fig. 1a, c). The Zeeman-truncated internal Hamiltonian for PERSPIRATIONCP is
| (1) |
Here and are the sum of the isotropic chemical shift offset and chemical shift anisotropy (CSA) of 13C and 15N, , and are heteronuclear dipolar couplings, and ω1,H is the 1H CW rf field strength. The Dirac δ-function specifies the 13C and 15N pulses in the middle of each rotor period, . MAS introduces time-dependence in the CSA and dipolar couplings, which is not explicitly shown in Eq. (1).
We transform this Hamiltonian into the interaction frame defined by the rf pulses for 1H and the frame defined by both rf pulses and isotropic chemical shift offset for 13C and 15N. We neglect 1H isotropic chemical shift because CW irradiation truncates chemical shift evolution. In contrast, the heteronuclear spins undergo chemical shift evolution between pulses. This interaction-frame transformation can be written as:
| (2) |
Here represents all the terms in Eq. (1) except for the rf pulses and the 15N and 13C isotropic chemical shift. The interaction-frame transformations in Eq. (2) each only affect one spin. As such, we can separately transform each one-spin operator in the Hamiltonian, and multiply the results together to obtain the two-spin product operators. We thus calculate the effect of the interaction frame transformation on the product operators , , and .
For the 1H spin we consider the interaction frame of the 1H CW rf irradiation. Similar to the treatment of PAR 28, we rotate to so that the spin-lock direction is . We convert product operators to spherical tensor operators:
| (3) |
The propagator for the 13C rf pulse and isotropic shift is:
| (4) |
where n is the number of elapsed pulses defined by the floor function: is x rounded down to the nearest integer. Since any series of successive rotations is equivalent to a single rotation about a new axis, we define a pulsed spin-lock axis in the x-z plane, at an angle from the x-axis towards the z-axis, and call the net rotation about this axis in each rotor period . Each 13C spin in the system has a distinct isotropic chemical shift, and thus also has a distinct pulsed spin-lock direction and net rotation per rotor period . The propagator in Eq. (4) can then be simplified as:
| (5) |
We next consider the interaction-frame transformation of :
| (6) |
Similar to 1H, we rotate to to make the pulsed spin-lock direction , and convert product operators to spherical tensor operators:
| (7) |
Here, for clarity, we have dropped the primes for the rotated axes on the spherical tensor operators. The interaction-frame 15N operators are identical to Eq. (4)-(7) except with all C replaced by N: the 15N spin has its own pulsed spin-lock direction , and the interaction-frame is given by an analogous equation to Eq. (7). The interaction-frame Hamiltonian (Eq. (2)) can thus be calculated by replacing the spin operators in Eq. (1) with their interaction-frame representations, Eq. (3) and (7):
| (8) |
In Eq. (8) is the Kronecker delta and n is the number of elapsed pulses. Terms 1 and 2 are the 13C-1H and 15N-1H dipolar couplings, term 3 is the 13C and 15N CSA, term 4 is the 1H chemical shift, and term 5 is the 15N-13C dipolar coupling.
To apply average Hamiltonian theory (AHT) 33, there must be an integer N such that is periodic with period . This requires , , and to be integer multiples of 2π. We assume that such an integer N exists, that there is no rotary resonance recoupling, i.e. , and that neither the 13C nor 15N rf field strengths fulfill Hartman-Hahn matching conditions with the 1H rf field, i.e. , where is an integer. Under these conditions, the first-order average Hamiltonian is zero because term 4 integrates over to zero, terms 3 and 5 integrate over each rotor period between pulses to zero, and terms 1 and 2 can also be proven to vanish to first order (Supporting Information 1).
For homonuclear polarization transfer by PULSAR, the internal Hamiltonian is identical to the heteronuclear Hamiltonian in Eq. (1) except for an additional “flip-flop” term, . Numerical simulations (Fig. S4) indicate that 13C-13C dipolar couplings have minimal effect on P-TSAR transfer, therefore we neglect the “flip-flop” term in this discussion. A full treatment of the first-order average Hamiltonian of homonuclear dipolar couplings can be found in Supporting Information 2.
Because the first-order average Hamiltonian is zero, the second-order average Hamiltonian is expected to dominate. As in CW-TSAR28, 30, we attribute P-TSAR transfer to the cross-term between terms 1 and 2 in Eq. (8) in the second-order average Hamiltonian:
| (9) |
Here and are numbers of elapsed pulses in t1 and t2, and the commutator = 0 unless , in which case . As we show in Supporting Information 3, the double integral is zero unless , or equivalently
| (10) |
for some integer l. Equation (10) can be satisfied in three ways:
If the zero-quantum matching condition, for integer , is met, Eq. (10) will be satisfied with the additional condition that . The 1×2 cross term (Eq. 9) then produces terms in the second-order average Hamiltonian with spin product operators and . These zero-quantum terms can induce polarization transfer from N to C and vice-versa without a change in sign, while the proton acts as a bystander.
If the double-quantum matching condition, for integer , is met, Eq. (10) will be satisfied with the additional condition that . The 1×2 cross term (Eq. 9) then produces double-quantum product operators and . These double-quantum terms can induce transfer from N to C and vice-versa, with a change in sign, while the proton acts as a bystander.
For any and , satisfies Eq. (10). The spin operator would be . This longitudinal term commutes with both the zero-quantum and double-quantum terms from cases 1 and 2, and will not accomplish any transfer.
A direct analogy can thus be drawn between CW-TSAR and P-TSAR. In both cases, cross terms in the second-order average Hamiltonian between the H–A and H–B dipolar couplings produce double-quantum terms of the form or zero-quantum terms of the form in the interaction-frame. In CW-TSAR there are CW spin-locks on all channels, while for P-TSAR it is a pulsed spin-lock for the A and B channels. In both cases, matching conditions on the low-frequency channels dictate when TSAR transfer occurs, and whether it is positive-intensity transfer for the zero-quantum condition or negative-intensity transfer for the double-quantum condition.
Relation between chemical shift offset, pulse flip angle, and polarization transfer in P-TSAR
The matching conditions in P-TSAR are based on the time-averaged pulsed spin-lock flip angles and . These flip angles are functions of the applied pulse flip angles on each channel and the isotropic offset of each spin. To best design P-TSAR experiments, we now consider how the choices of pulse flip angle and rf carrier frequencies dictate the chemical shifts that survive the pulsed spin-lock and fulfill the zero-quantum or double-quantum matching conditions.
Consider a single spin at a chemical shift offset Ω subjected to a train of rf pulses with flip angle θ about the x-axis at the center of each rotor period. This spin undergoes three successive rotations per rotor period (Fig. 6a): a rotation about the z-axis during the two free evolution periods (1 to 2 and 3 to 4), sandwiching a rotation about the x-axis during the pulse (2 to 3). These three successive rotations can be expressed as:
| (11) |
The net effect of the three rotations is equivalent to a single rotation of angle φ about the pulsed spin-lock axis (Fig. 6b), which can be defined as the rotation operator . This rotation is repeated many times during the pulsed spin-lock period (Fig. 6c), so that only magnetization along the spin-lock axis will be fully retained (Fig. 6d) while magnetization that is perpendicular to the effective spin-lock axis will precess to a different position on the Bloch sphere at the end of each rotor period (Fig. 6e). Any magnetization that is not parallel to the axis thus decays rapidly and can be discarded. Placing the spin-lock pulses in the center of each rotor period ensures that the spin-lock axis lies in the xz-plane; any initial y-magnetization is dephased during the spin-lock, thus allowing quadrature detection of the indirect dimension. However, x’ is not necessarily along x, but is instead in the xz-plane, therefore only a portion of the initial x-magnetization is properly spin-locked while the rest is dephased:
| (12) |
The initial x-magnetization, Mx, can be expressed in the x’ and z’ basis by projection (Fig. 6b). The time-dependent trajectory of Mx can then be expressed as two oscillating x’ and z’ components:
| (13) |
Magnetization along z’ is perpendicular to the spin-lock axis and decays rapidly. A pulsed spin-lock will scale down magnetization by a factor of , with a different direction of for each isochromat (Fig. S5). This “read-in” loss is followed by a “read-out” loss in which magnetization is projected from the spin-lock direction back to the x-axis for detection (Fig. 7a). Treating the rf pulse as finite rather than a δ-function pulse gives a more accurate pulsed spin-lock profile (Fig. 7b, Supporting Information 4). For small pulse flip angles, the “read-in” and “read-out” losses are minimal for spins on resonance or at an rf offset near nωr. For pulse flip angles near 360º, losses are minimal on resonance and at an rf offset of about 1.5ωr. The pulsed spin-lock bandwidth increases as the nominal pulse flip angle increases from 0º to 180º or decreases from 360º to 180º.
Figure 6.
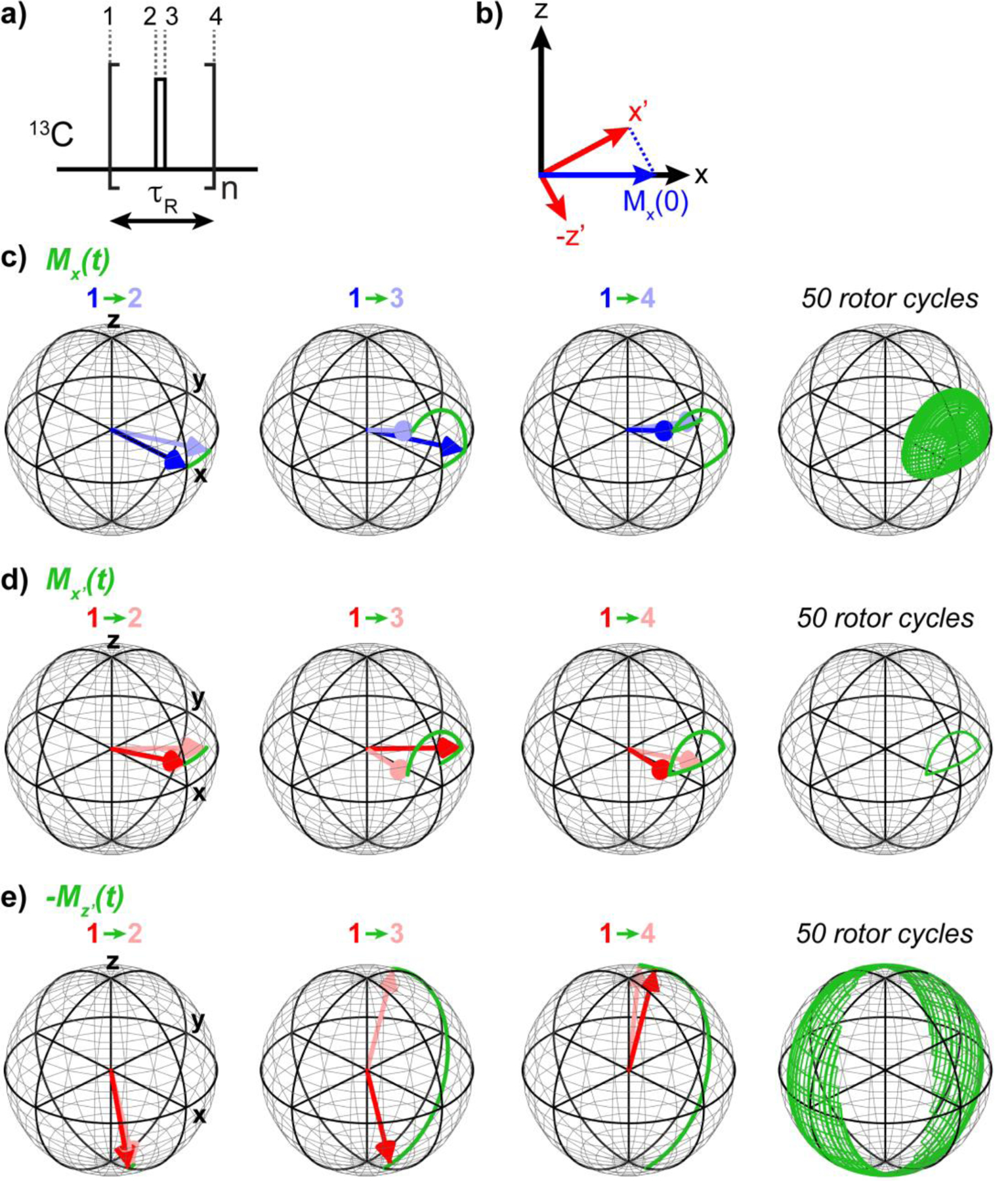
Magnetization trajectories under pulsed spin-lock. (a) Diagram of the basic pulsed spin-lock unit. The free evolution periods of 1→2 and 3→4 rotate the magnetization around the z-axis due to the isotropic chemical shift offset, while the rf pulse during 2→3 rotates the magnetization around the x-axis. (b) The pulsed spin-lock axis is tilted from the x-axis in the xz-plane. The initial x-magnetization, Mx(0), has components along the x’ and z’ axes. (c-e) Magnetization trajectories under pulsed spin-lock, calculated in MATLAB using an rf field of 50 kHz, a pulse flip angle of 90º, and a chemical shift offset of 17.5 ppm. (c) Trajectory of x-magnetization. The initial and final locations are not at the same spot on the Bloch sphere. (d) Trajectory of . This magnetization begins and ends the rotor period at the same position on the Bloch sphere, hence it is spin-locked. (e) Trajectory of . This magnetization traces out a broad trajectory, indicating rapid decay.
Figure 7.
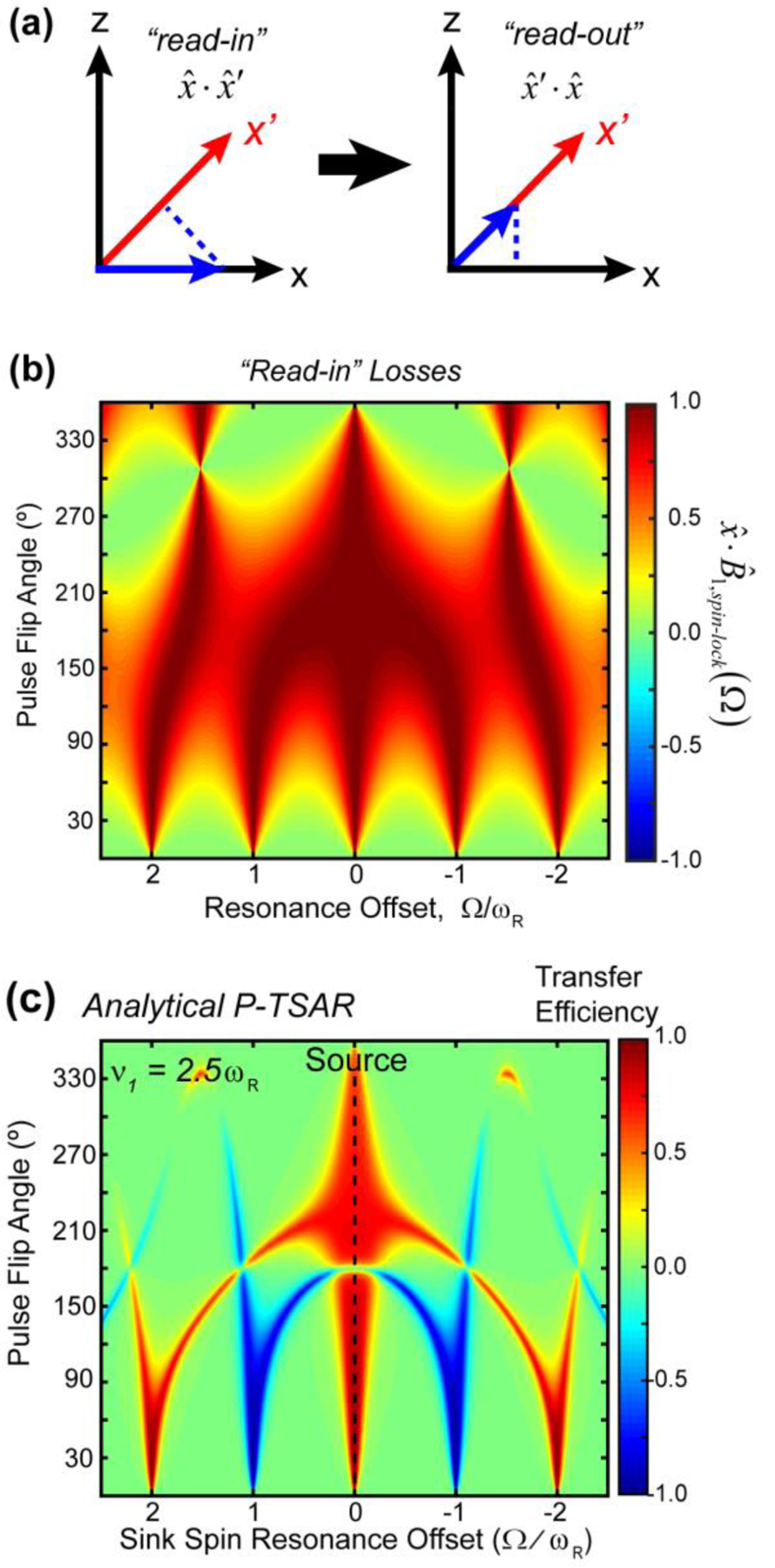
“Read-in” and “read-out” losses associated with a pulsed spin-lock. (a) “Reading in” and “reading out” of the pulsed spin-lock causes magnetization losses due to projection of one axis onto the other. (b) Contour plot showing the “read-in” losses as a function of pulse flip angle and resonance offset. 50 kHz rf pulses were used in these calculations. (c) Calculated P-TSAR efficiencies as a function of the sink-spin offset. The source spin (C1) was placed on resonance. Positive transfer occurs at the zero-quantum condition (φC1 = φC2) while negative transfer occurs at the double-quantum condition (φC1 + φC2 = 2π).
This analytical model not only gives the pulsed spin-lock axis, but also the net rotation, , during each rotor period. For visualization purposes, we can convert this into a time-averaged pulsed spin-lock field strength ωSL:
| (14) |
This time-averaged spin-lock field is analogous to the CW spin-lock field in PAR and PAINCP. From the average Hamiltonian analysis, the P-TSAR sequences have double- and zero-quantum matching conditions for integer values of l. The zero-quantum condition leads to positive transfer intensities while the double-quantum condition leads to negative transfer intensities. This differs from typical implementations of CW-TSAR experiments, which only fulfill zero-quantum matching conditions.
To model the P-TSAR transfer, we combine the “read-in” and “read-out” losses with the matching conditions: the overall transfer efficiency from spin A to B is the product of three factors: the “read-in” loss , projection of one spin’s spin-lock axis onto the other, , and the “read-out” loss . These three factors are further multiplied by Lorentzian functions centered at the zero- and double-quantum matching conditions. Finally, we include a scaling factor to account for the finite pulse length, which reduces the effective transfer time for long pulses:
| (15) |
Eq. (15) was used to calculate the polarization transfer efficiencies (Fig. 7c, 8c) with a Lorentzian width ε = 0.05ωr. This width was chosen empirically by varying ε in the analytical model until the local bandwidth is consistent with numerical simulations and experiments. The resulting polarization transfer profile (Fig. 8c) has a nearly identical chemical shift and flip-angle dependence as that obtained from numerical simulation (Fig. 8b). Positive transfer is maximized when the source and sink spins have the same absolute offset. Negative transfer is obtained when the sink spin is ~ωr away from the carrier for small flip angles, but splits into two separate branches for larger flip angles. A nominal flip angle of 180º gives vanishing transfer. With flip angles larger than 180º, the bandwidth for positive zero-quantum transfer is significantly larger than for smaller flip angles.
Figure 8.
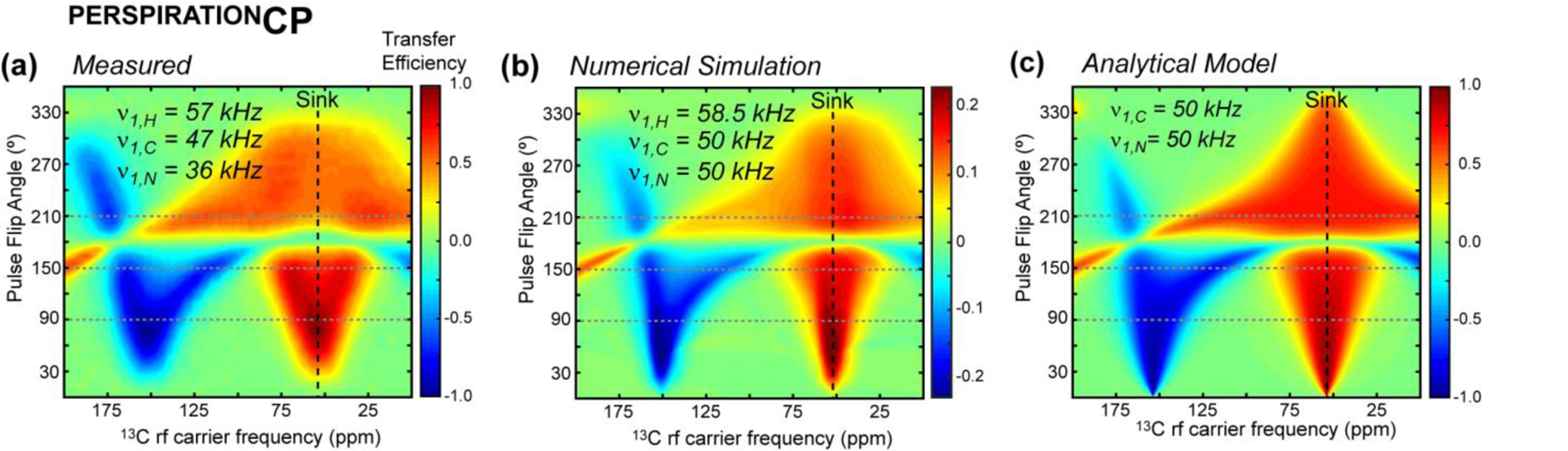
Measured, simulated, and calculated PERSPIRATIONCP polarization transfer efficiencies as a function of the 13C rf carrier frequency and pulse flip angle. The experiments were conducted on an 800 MHz spectrometer under 20 kHz MAS. Calculations were conducted for the same conditions. (a) Measured PERSPIRATIONCP efficiencies of f-MLF as a function of 13C carrier frequency and 13C pulse flip angle. The 2D heat map is generated from 25 × 80 1D spectra measured as a function of 13C pulsed flip angles (0˚ to 360˚ in 15˚ increments) and rf carrier frequencies (0 to 200 ppm in 2.5 ppm increments.) The integrated Cα band intensities (46 ppm to 59 ppm) of the spectra are represented in the plot. The rf field strengths of the PERSPIRATIONCP block are 57 kHz, 47 kHz, and 36 kHz for 1H, 13C and 15N, respectively. (b) Numerical simulations of PERSPIRATIONCP polarization transfer from an on-resonance 15N to 13Cα. (c) PERSPIRATIONCP transfer efficiencies calculated using the analytical model.
To test the isotropic shift dependence of P-TSAR, we carried out a pseudo-3D PERSPIRATIONCP experiment on the model peptide formyl-Met-Leu-Phe (f-MLF), in which we varied the 13C rf carrier frequency and pulse flip angle in the two indirect dimensions. Fig. 8a plots the integrated intensity of the three Cα peaks as a function of these two parameters, with representative 1D spectra shown in Fig. S6. Remarkably, the experiment gives the same qualitative features as predicted in the numerical simulations and the analytical model. Maximum positive transfer occurs when the source and sink spin chemical shift offsets are both small, while maximum negative transfer occurs when the 13C carrier is about away from the sink spins for small pulse flip angles.
Discussion
Our first implementation of the heteronuclear PERSPIRATIONCP experiment (Fig. S1d) 34 placed the spin-lock pulses at the end of each rotor period. This timing refocuses the magnetization of spins that are on resonance or at ~nωr from the carrier frequency for small flip angles, but does not refocus other off-resonance magnetization. Off-resonance signals have both x- and y-components at the end of the pulsed spin-lock period, which require a z-filter before and after this period to obtain clean, in-phase x-magnetization. Omitting these z-filters results in spectra with severe phase distortion. Inclusion of the z-filters leads to significant “read-in” and “read-out” losses by discarding the y-component (Fig. S7a). Spins that are ~0.5ωr off-resonance for small flip angles do not survive the pulsed spin-lock and therefore do not contribute to polarization transfer (Fig. S7b, c). PERSPIRATIONCP with pulses at the end of each rotor period results in low transfer efficiency above 60 ppm and below 20 ppm and no transfer for aromatic signals at 110–140 ppm. Centering the spin-lock pulses in the rotor period refocuses magnetization along an axis in the xz-plane. This allows us to remove the z-filters, which facilitates quadrature detection and broadens the bandwidth of these experiments.
Previous studies have shown that a pulsed spin-lock can extend the coherence lifetime in solids by about 10-fold compared to a spin echo 32, 46–48. These past implementations of pulsed spin-locks to solids used simple spin systems such as CaF2 49, sometimes in the absence of MAS 47–48, or dealt with amino acids with a single 13C label, 46 for which spectral resolution and bandwidth were not of concern. In this study, we demonstrate the use of a pulsed spin-lock in the presence of significant isotropic shift dispersion, wherein maximizing the pulsed spin-lock bandwidth is of utmost importance to enable the detection of as many long-range correlations as possible. By placing a pulse in the center of each rotor-period, we make the sideband spacing significantly larger compared to previous MAS pulsed spin-lock experiments that pulsed only every 20 rotor periods for similar spinning frequencies 46. Moreover, our careful choice of the pulse flip angle maximizes the breadth of the envelope of magnetization that survives the pulsed spin-lock compared to experiments that use flip angles less than 90° in order to maximize the relaxation time constant. Importantly, in contrast to previous work that uses a pulsed spin-lock to extend coherence time for greater sensitivity32, 46, 49–51, here we use a pulsed spin-lock to generate distinct average Hamiltonians along the pulsed spin-lock directions that accomplish internuclear transfer.
The excellent agreement between our analytical model, numerical simulations, and measured polarization transfer profiles (Fig. 8) indicates that once a 1H CW field strength is chosen, the main factors dictating polarization transfer are the pulse flip angle and the chemical shift offset that fulfill the zero- or double-quantum matching conditions, Eq. (10). These matching conditions are well-predicted by our analytical model, hence the 13C flip angle and carrier frequency can be chosen by inspecting the calculated analytical 2D map for a given magnetic field strength and MAS frequency (Appendix S3). Once the 13C carrier frequency and pulse flip angle are chosen, PULSAR can be optimized with only two steps. First, we optimize the 1H CW rf field with a 1D experiment that includes a Cα selective echo before the P-TSAR block, by maximizing the non-Cα intensities (Fig. S1a). At an MAS rate of 20 kHz, we found that a 1H CW field of ~57 kHz, which is just under 3 times the spinning speed, worked reliably for all samples and conditions. The 1H power is briefly optimized by varying the power by 2 dB. We observed a broad maximum with multiple suitable 1H power levels. The main power level we used would lead to a ~30% intensity loss for an error of ~0.7 dB. We then optimized the 13C pulse length to again maximize the transferred intensity in the desired spectral regions. PERSPIRATIONCP experiments require an additional step of optimizing the 15N pulse length with respect to the 13C pulse length, which is simple once the 13C flip angle has been selected. Importantly, these optimization steps are uncoupled from each other and can be run independently. Separate optimization of 13C and 15N powers revealed that a 0.5 dB change leads to a 30% loss of transfer efficiency, similar to cross polarization. Finally, for the 13C rf field strengths in the PULSAR and PERSPIRATIONCP experiments, as long as they are larger than the chemical shift offset, increasing the rf field strengths further do not improve the polarization transfer efficiency significantly. Instead, the pulse flip angle is the more important variable to optimize, to achieve both broadband transfer and high-efficiency transfer.
This optimization routine is much faster and easier than the multi-parameter optimization for CW-TSAR due to the extreme sensitivity of PAR and PAINCP’s matching conditions to rf field strengths, spin geometry, and 1H density. Even for a given sample, different spin pairs have different optimal rf field strengths. Moreover, the rf field strengths that result in good polarization transfer for CW-TSAR experiments are inter-dependent. Such multidimensional parameter searches are very time-consuming, especially for 2D correlation experiments. For example, a recent investigation involving the 2D 15N-15N PAR experiment conducted 29 × 29 = 841 separate 2D’s to search for the optimal 1H and 15N CW spin-lock field strengths 52. Simulations can facilitate this parameter search, but often show significant discrepancies from experiments 31. The optimized parameters can also change significantly between samples, which make it difficult to implement CW-TSAR experiments on low-sensitivity biological samples. In comparison, P-TSAR experiments do not require sample-specific optimization; the matching conditions are easily predicted using analytical theory, and the user can choose the pulse flip angle and rf carrier frequency in advance. Moreover, the 1H CW field strength in P-TSAR experiments is only weakly coupled to other parameters, which further simplifies the optimization of P-TSAR experiments.
Conclusions
We have introduced two pulsed third-spin-assisted recoupling (P-TSAR) experiments that efficiently transfer polarization between homonuclear and heteronuclear spin pairs using a low rf duty cycle. The PULSAR and the improved PERSPIRATIONCP experiments are demonstrated on GB1 and glucagon amyloid fibrils and give rise to many long-range correlations that restrain the 3D structures of proteins. Using numerical simulations and analytical theory, we found that the first-order average Hamiltonian for the P-TSAR experiments is averaged to zero, apart from a homonuclear dipolar coupling term that has negligible effects on P-TSAR. We found that the second-order average Hamiltonian yields non-zero cross terms between the 1H-13C1 (1H-15N) and 1H-13C2 (1H-13C) dipolar couplings, which drive polarization transfer. These properties are the same as the PAR and PAINCP experiments. P- and CW-TSAR experiments give similar long-range contacts, but P-TSAR experiments use 5–10 fold less rf energy than their CW counterparts, and are much easier to optimize. The current study demonstrates these P-TSAR experiments on 600 and 800 MHz spectrometers under 20 kHz MAS, but the methodology can be extended to other magnetic field strengths, MAS frequency regimes, and spin pairs.
Supplementary Material
Acknowledgements
This work is supported by NIH grants AG059661 and P41-GM132079 to M.H. M.D.G. is supported by an NIH Ruth L. Kirschstein Individual National Research Service Award (1F31AI133989).
Footnotes
Supporting Information Available
• Additional derivations of the average Hamiltonian of P-TSAR experiments;
• Calculations of the finite-pulse spin-lock sequence;
• Figures of pulse sequences, numerical simulations of polarization transfer efficiencies, magnetization trajectories, and measured PERSPIRATIONCP transfer efficiencies;
• Additional 2D 13C correlation spectra comparing PULSAR and PAR performances.
• Table of atomic coordinates used for simulating the polarization transfer efficiency;
• SpinEvolution simulation scripts;
• MATLAB scripts for calculating the PULSAR transfer efficiency;
• Bruker pulse programs for PULSAR and PERSPIRATIONCP;
This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Wang SL; Munro RA; Shi LC; Kawamura I; Okitsu T; Wada A; Kim SY; Jung KH; Brown LS; Ladizhansky V., Solid-state NMR spectroscopy structure determination of a lipid-embedded heptahelical membrane protein. Nature Methods 2013, 10, 1007–1012. [DOI] [PubMed] [Google Scholar]
- 2.Möbius K; Kazemi S; Güntert P; Jakob A; Heckel A; Becker-Baldus J; Glaubitz C., Global response of diacylglycerol kinase towards substrate binding observed by 2D and 3D MAS NMR. Sci. Rep 2019, 9, 3995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jekhmane S; Medeiros-Silva J; Li J; Kümmerer F; Müller-Hermes C; Baldus M; Roux B; Weingarth M., Shifts in the selectivity filter dynamics cause modal gating in K+ channels. Nat. Commun 2019, 10, 123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mandala VS; Loftis AR; Shcherbakov AA; Pentelute BL; Hong M., Atomic Structures of Closed and Open Influenza B M2 Proton Channel Reveal the Conduction Mechanism. Nat. Struc. Mol. Biol 2020, 27, 160–167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Paravastu AK; Leapman RD; Yau W-M; Tycko R., Molecular structural basis for polymorphism in Alzheimer’s β-amyloid fibrils. Proc. Natl. Acad. Sci. USA 2008, 105, 18349–18354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wasmer C; Lange A; Van Melckebeke H; Siemer AB; Riek R; Meier BH, Amyloid fibrils of the HET-s(218–289) prion form a beta solenoid with a triangular hydrophobic core. Science 2008, 319, 1523–1526. [DOI] [PubMed] [Google Scholar]
- 7.Bertini I; Gonnelli L; Luchinat C; Mao J; Nesi A., A New Structural Model of Aβ40 Fibrils. J. Am. Chem. Soc 2011, 133, 16013–16022. [DOI] [PubMed] [Google Scholar]
- 8.Lu JX; Qiang W; Yau WM; Schwieters CD; Meredith SC; Tycko R., Molecular structure of β-amyloid fibrils in Alzheimer’s disease brain tissue. Cell 2013, 154, 1257–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Colvin MT; Silvers R; Ni QZ; Can TV; Sergeyev I; Rosay M; Donovan KJ; Michael B; Wall J; Linse S, et al. , Atomic Resolution Structure of Monomorphic Aβ42 Amyloid Fibrils. J. Am. Chem. Soc. 2016, 138, 9663–9674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wälti MA; Ravotti F; Arai H; Glabe CG; Wall JS; Böckmann A; Güntert P; Meier BH; Riek R., Atomic-resolution structure of a disease-relevant Aβ(1–42) amyloid fibril. Proc. Natl. Acad. Sci. USA 2016, 113, E4976–E4984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tuttle MD; Comellas G; Nieuwkoop AJ; Covell DJ; Berthold DA; Kloepper KD; Courtney JM; Kim JK; Barclay AM; Kendall A, et al. , Solid-state NMR structure of a pathogenic fibril of full-length human α-synuclein. Nat. Struct. Mol. Biol 2016, 23, 409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gelenter MD; Smith KJ; Liao SY; Mandala VS; Dregni AJ; Lamm MS; Tian Y; Xu W; Pochan DJ; Tucker TJ, et al. , The peptide hormone glucagon forms amyloid fibrils with two coexisting b-strand conformations. Nat. Struc. Mol. Biol 2019, 26, 592–598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dregni AJ; Mandala VS; Wu H; Elkins MR; Wang HK; Hung I; DeGrado WF; Hong M., In vitro 0N4R tau fibrils contain a monomorphic b-sheet core enclosed by dynamically heterogeneous fuzzy coat segments. Proc. Natl. Acad. Sci. U.S.A 2019, 116, 16357–16366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Phyo P; Gu Y; Hong M., Impact of acidic pH on plant cell wall polysaccharide structure and dynamics: insights into the mechanism of acid growth in plants from solid-state NMR. Cellulose 2019, 26, 291–304. [Google Scholar]
- 15.Wang T; Park YB; Caporini MA; Rosay M; Zhong L; Cosgrove DJ; Hong M., Sensitivity-enhanced solid-state NMR detection of expansin’s target in plant cell walls. Proc. Natl. Acad. Sci. U. S. A 2013, 110, 16444–16449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kang X; Kirui A; Muszyński A; Widanage MCD; Chen A; Azadi P; Wang P; Mentink-Vigier F; Wang T., Molecular architecture of fungal cell walls revealed by solid-state NMR. Nat. Commun 2018, 9, 2747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Romaniuk JAH; Cegelski L., Peptidoglycan and Teichoic Acid Levels and Alterations in Staphylococcus aureus by Cell-Wall and Whole-Cell Nuclear Magnetic Resonance. Biochemistry 2018, 57, 3966–3975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.De Paëpe G., Dipolar recoupling in magic angle spinning solid-state nuclear magnetic resonance. Annu. Rev. Phys. Chem 2012, 63, 661–684. [DOI] [PubMed] [Google Scholar]
- 19.Gullion T; Schaefer J., Rotational-echo double-resonance NMR. J. Magn. Reson 1989, 81, 196–200. [DOI] [PubMed] [Google Scholar]
- 20.Hing AW; Vega S; Schaefer J., Transferred-echo double-resonance NMR. J. Magn. Reson 1992, 96, 205–209. [Google Scholar]
- 21.Jaroniec CP; Filip C; Griffin RG, 3D TEDOR NMR Experiments for the Simultaneous Measurement of Multiple Carbon–Nitrogen Distances in Uniformly 13C,15N-Labeled Solids. J. Am. Chem. Soc 2002, 124, 10728–10742. [DOI] [PubMed] [Google Scholar]
- 22.Bloembergen N., On the interaction of nuclear spins in a crystalline lattice. Physica 1949, 15, 386–426. [Google Scholar]
- 23.Takegoshi K; Nakamura S; Terao T., 13C–1H dipolar-assisted rotational resonance in magic-angle spinning NMR. Chem. Phys. Lett 2001, 344, 631–637. [Google Scholar]
- 24.Morcombe CR; Gaponenko V; Byrd RA; Zilm KW, Diluting abundant spins by isotope edited radio frequency field assisted diffusion. J. Am. Chem. Soc 2004, 126, 7196–7197. [DOI] [PubMed] [Google Scholar]
- 25.Hou G; Yan S; Trébosc J; Amoureux J-P; Polenova T., Broadband homonuclear correlation spectroscopy driven by combined R2nv sequences under fast magic angle spinning for NMR structural analysis of organic and biological solids. J. Magn. Reson 2013, 232, 18–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Demers J-P; Chevelkov V; Lange A., Progress in correlation spectroscopy at ultra-fast magic-angle spinning: Basic building blocks and complex experiments for the study of protein structure and dynamics. Solid State Nucl. Magn. Reson 2011, 40, 101–113. [DOI] [PubMed] [Google Scholar]
- 27.Paul S; Takahashi H; Hediger S; De Paëpe G, Chapter Three - Third Spin-Assisted Recoupling in SSNMR: Theoretical Insights and Practicable Application to Biomolecular Structure Determination. In Annu. Rep. NMR Spectrosc, Webb GA, Ed. Academic Press: 2015; Vol. 85, pp 93–142. [Google Scholar]
- 28.De Paëpe G; Lewandowski JR; Loquet A; Böckmann A; Griffin RG, Proton assisted recoupling and protein structure determination. J. Chem. Phys 2008, 129, 245101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lewandowski JR; De Paëpe G; Griffin RG, Proton Assisted Insensitive Nuclei Cross Polarization. J. Am. Chem. Soc 2007, 129, 728–729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.De Paëpe G; Lewandowski JR; Loquet A; Eddy M; Megy S; Böckmann A; Griffin RG, Heteronuclear proton assisted recoupling. J. Chem. Phys 2011, 134, 095101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Donovan KJ; Jain SK; Silvers R; Linse S; Griffin RG, Proton-Assisted Recoupling (PAR) in Peptides and Proteins. J. Phys. Chem. B 2017, 121, 10804–10817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ostroff ED; Waugh JS, Multiple Spin Echoes and Spin Locking in Solids. Phys. Rev. Lett 1966, 16, 1097–1098. [Google Scholar]
- 33.Haeberlen U; Waugh JS, Coherent Averaging Effects in Magnetic Resonance. Phys. Rev 1968, 175, 453–467. [Google Scholar]
- 34.Gelenter MD; Hong M., Efficient 15N-13C Polarization Transfer by Third-Spin-Assisted Pulsed Cross-Polarization Magic-Angle-Spinning NMR for Protein Structure Determination. J. Phys. Chem. B 2018, 122, 8367–8379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Franks WT; Zhou DH; Wylie BJ; Money BG; Graesser DT; Frericks HL; Sahota G; Rienstra CM, Magic-angle spinning solid-state NMR spectroscopy of the beta1 immunoglobulin binding domain of protein G (GB1): 15N and 13C chemical shift assignments and conformational analysis. J. Am. Chem. Soc 2005, 127, 12291–12305. [DOI] [PubMed] [Google Scholar]
- 36.Gelenter MD; Wang T; Liao S-Y; O’Neill H; Hong M., 2H–13C correlation solid-state NMR for investigating dynamics and water accessibilities of proteins and carbohydrates. J. Biomol. NMR 2017, 68, 257–270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hong M; Griffin RG, Resonance Assignment for Solid Peptides by Dipolar-Mediated 13C/15N Correlation Solid-State NMR. J. Am. Chem. Soc 1998, 120, 7113–7114. [Google Scholar]
- 38.Bernard GM; Goyal A; Miskolzie M; McKay R; Wu Q; Wasylishen RE; Michaelis VK, Methylammonium lead chloride: A sensitive sample for an accurate NMR thermometer. J. Magn. Reson 2017, 283, 14–21. [DOI] [PubMed] [Google Scholar]
- 39.Bennett AE; Rienstra CM; Auger M; Lakshmi KV; Griffin RG, Heteronuclear decoupling in rotating solids. J. Chem. Phys 1995, 103, 6951–6958. [Google Scholar]
- 40.Lee W; Tonelli M; Markley JL, NMRFAM-SPARKY: enhanced software for biomolecular NMR spectroscopy. Bioinformatics 2015, 31, 1325–1327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Güntert P; Mumenthaler C; Wüthrich K., Torsion angle dynamics for NMR structure calculation with the new program Dyana. J. Mol. Biol 1997, 273, 283–298. [DOI] [PubMed] [Google Scholar]
- 42.Shen Y; Bax A., Protein backbone and sidechain torsion angles predicted from NMR chemical shifts using artificial neural networks. J. Biomol. NMR 2013, 56, 227–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Veshtort M; Griffin RG, SPINEVOLUTION: A powerful tool for the simulation of solid and liquid state NMR experiments. J. Magn. Reson 2006, 178, 248–282. [DOI] [PubMed] [Google Scholar]
- 44.Wylie BJ; Sperling LJ; Nieuwkoop AJ; Franks WT; Oldfield E; Rienstra CM, Ultrahigh resolution protein structures using NMR chemical shift tensors. Proc. Natl. Acad. Sci. USA 2011, 108, 16974–16979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gratzer WB; Bailey E; Beaven GH, Conformational states of glucagon. Biochem. Biophys. Res. Commun 1967, 28, 914–919. [DOI] [PubMed] [Google Scholar]
- 46.Petkova AT; Tycko R., Sensitivity Enhancement in Structural Measurements by Solid State NMR through Pulsed Spin Locking. J. Magn. Reson 2002, 155, 293–299. [DOI] [PubMed] [Google Scholar]
- 47.Schmidt-Rohr K; Saalwachter K; Liu SF; Hong M., High-sensitivity 2H-NMR in solids by 1H detection. J. Am. Chem. Soc 2001, 123, 7168–7169. [DOI] [PubMed] [Google Scholar]
- 48.Hong M; Yamaguchi S., Sensitivity-Enhanced Static 15N NMR of Solids by 1H Indirect Detection. J. Magn. Reson 2001, 150, 43–48. [DOI] [PubMed] [Google Scholar]
- 49.Rhim WK; Burum DP; Elleman DD, Multiple-Pulse Spin Locking in Dipolar Solids. Phys. Rev. Lett 1976, 37, 1764–1766. [Google Scholar]
- 50.Suwelack D; Waugh JS, Quasistationary magnetization in pulsed spin-locking experiments in dipolar solids. Phys. Rev. B 1980, 22, 5110–5114. [Google Scholar]
- 51.Rhim WK; Burum DP; Elleman DD, Calculation of spin–lattice relaxation during pulsed spin locking in solids. J. Chem. Phys 1978, 68, 692–695. [Google Scholar]
- 52.Donovan KJ; Silvers R; Linse S; Griffin RG, 3D MAS NMR Experiment Utilizing Through-Space 15N–15N Correlations. J. Am. Chem. Soc 2017, 139, 6518–6521. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


