Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2022 Aug 1.
Published in final edited form as: J Neurosci Methods. 2021 Jun 19;360:109267. doi: 10.1016/j.jneumeth.2021.109267

Automated Segmentation of Choroidal Layers from 3-Dimensional Macular Optical Coherence Tomography Scans

Kyungmoo Lee a,b, Alexis K Warren c, Michael D Abràmoff a,b,c,d,e,f,g, Andreas Wahle a,b, S Scott Whitmore c,e, Ian C Han c,e, John H Fingert c,e, Todd E Scheetz a,c,d,e, Robert F Mullins c,e, Milan Sonka a,b,c, Elliott H Sohn c,e,*
PMCID: PMC8324559  NIHMSID: NIHMS1716914  PMID: 34157370

Abstract

Background:

Changes in choroidal thickness are associated with various ocular diseases, and the choroid can be imaged using spectral-domain optical coherence tomography (SD-OCT) and enhanced depth imaging OCT (EDI-OCT).

New Method:

Eighty macular SD-OCT volumes from 80 patients were obtained using the Zeiss Cirrus machine. Eleven additional control subjects had two Cirrus scans done in one visit along with enhanced depth imaging (EDI-OCT) using the Heidelberg Spectralis machine. To automatically segment choroidal layers from the OCT volumes, our graph-theoretic approach was utilized. The segmentation results were compared with reference standards from two independent graders, and the accuracy of automated segmentation was calculated using unsigned/signed border positioning/thickness errors and Dice similarity coefficient (DSC). The repeatability and reproducibility of our choroidal thicknesses were determined by intraclass correlation coefficient (ICC), coefficient of variation (CV), and repeatability coefficient (RC).

Results:

The mean unsigned/signed border positioning errors for the choroidal inner and outer surfaces are 3.39 ± 1.26 μm (mean ± standard deviation)/−1.52 ± 1.63 μm and 16.09 ± 6.21 μm/4.73 ± 9.53 μm, respectively. The mean unsigned/signed choroidal thickness errors are 16.54 ± 6.47 μm/6.25 ± 9.91 μm, and the mean DSC is 0.949 ± 0.025. The ICC (95% confidence interval), CV, RC values are 0.991 (0.977–0.997), 2.48%, 14.25 μm for the repeatability and 0.991 (0.977–0.997), 2.49%, 14.30 μm for the reproducibility studies, respectively.

Comparison with Existing Method(s):

The proposed method outperformed our previous method using choroidal vessel segmentation and inter-grader variability.

Conclusions:

This automated segmentation method can reliably measure choroidal thickness using different OCT platforms.

1. Introduction

The choroid is the vascular layer between the retina and the sclera that provides oxygen and nourishment to the outer layers of the retina (Chirco et al., 2017; Sohn et al., 2014). Spectral-domain optical coherence tomography (SD-OCT) provides rapid, non-invasive, cross-sectional images of the retina and choroid with high axial resolution and has become a standard clinical and research tool (Mrejen and Spaide, 2013; Whitmore et al., 2015; Wojtkowski et al., 2012). Visualization of the choroid can be optimized using enhanced depth imaging OCT (EDI-OCT) (Ikuno et al., 2011), which is acquired by placing an imaging focal point known as a zero-delay line, to the choroid, or swept-source OCT (SS-OCT) which uses a tunable, longer wavelength laser that enables deeper tissue penetration (Chen et al., 2016). Changes in choroidal thickness are associated with various ocular diseases such as age-related macular degeneration (AMD) (Bakall et al., 2013; Manjunath et al., 2011; Tozer et al., 2013; Whitmore et al., 2015), high myopia (Fujiwara et al., 2009), and central serous chorioretinopathy (Chin et al., 2015; Imamura et al., 2009; Kim et al., 2011; Maruko et al., 2010).

Previous studies have demonstrated the feasibility of manual choroidal layer segmentation of OCT scans (Sacconi et al., 2017; Yin et al., 2010; Zhang et al., 2012), but manual segmentation is labor intensive and susceptible to effects due to subjectivity of the graders. To overcome these issues, automated methods have been developed using various image processing techniques. Several groups have proposed 2D segmentation methods for choroidal layers of EDI-OCT or SS-OCT scans. The 2D approaches are appropriate for 2D OCT scans consisting of a single B-scan (a 2D image in the XZ plane, e.g., Fig. 1A), but they are not suitable for 3D OCT scans consisting of multiple B-scans since the 2D approaches identify choroidal boundaries on each individual B-scan separately, which have the potential to segment discontinuous choroidal layers between adjacent B-scans (Hussain et al., 2018; Masood et al., 2019; Vupparaboina et al., 2015; Zhang et al., 2020). Wang et al. reported an automated 3D segmentation method, which takes into account choroidal layers on adjacent B-scans, but this requires long computational time (43.29 minutes) for each SS-OCT scan (Wang et al., 2017).

Fig. 1.

Fig. 1.

Open in a new tab

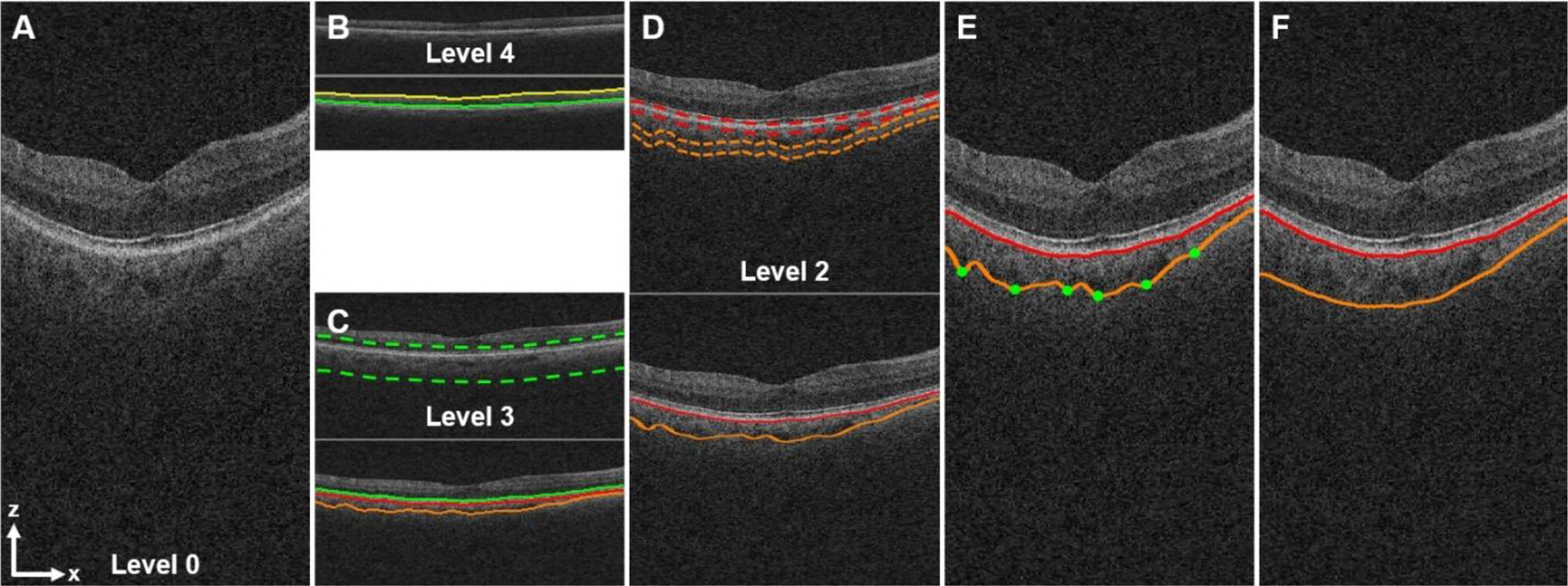
Automated multiscale segmentation of the choroidal layer from a 3D macular SD-OCT scan using the LOGISMOS method. (A) Full-resolution central B-scan image (level 0, height: 1024 voxels). (B) Segmentation of the inner limiting membrane (ILM, yellow line) and the boundary of myoid and ellipsoid of inner segments (BMEIS, green line) from the OCT volume (level 4, height: 64 voxels) down-sampled in the z-direction by a factor of 16. (C) Segmentation of the BMEIS (green line) and the choroidal layer (red, orange lines) from the OCT volume (level 3, height: 128 voxels) down-sampled by a factor of 8 using the sub-OCT volume (dotted green lines) determined by the BMEIS in level 4 up-scaled by a factor of 2. (D) Segmentation of the choroidal layer from the OCT volume (level 2, height: 256 voxels) down-sampled by a factor of 4 using 2 sub-OCT volumes (dotted red, orange lines) defined by the choroidal layer in level 3 up-scaled by a factor of 2. (E) Segmentation of the choroidal layer from the full-resolution OCT volume (level 0). The green dots show control points for thin plate spline fitting. (F) Image (A) overlaid with the final, smoothed choroidal layer segmentation.

Previously, our research group reported an automated 3D choroidal layer segmentation method (Zhang et al., 2012) using choroidal vessel segmentation, but it was prone to relatively large segmentation errors since the vessel segmentation is not reliable in low signal choroidal OCT images. Thus, we developed a novel, reliable, memory-efficient, automated 3D choroidal layer segmentation method for macular SD-OCT scans and evaluated it in terms of accuracy, repeatability, and reproducibility.

2. Materials and Methods

2.1. Human Subjects and Data Acquisition

This study received approval from the institutional review board of the University of Iowa and adhered to the tenets of the Declaration of Helsinki.

To develop this algorithm, subjects were recruited from the glaucoma clinics at the University of Iowa Hospitals and Clinics. Both eyes of all patients had SD-OCT scans but only one eye was randomly chosen from each subject for analysis in this study. Fovea-centered SD-OCT image volumes (200 × 200 × 1024 voxels, 6.0 × 6.0 × 2.0 mm) were acquired from a Cirrus OCT instrument (Cirrus™ HD-OCT, Carl Zeiss Meditec, Inc., Dublin, CA) and exported as raw files (.img) using Cirrus Research Browser software.

To evaluate our choroidal layer segmentation method in terms of accuracy, our results were compared with reference standards created by averaging, in the axial direction, manual tracings (z-values in the pixel domain) obtained from two independent graders (AKW, KL). The manual tracings were performed in three B-scan images (horizontal line scans number 50, 100, 150) for each volumetric OCT scan using our custom software which can draw a 2D B-spline using several control points marked by a grader.

Additionally, eleven young subjects without any ocular disease had macular Cirrus SD-OCT scan performed twice in one visit as well as 61 line scan Spectralis (Heidelberg Engineering, Heidelberg, Germany) EDI-OCT scan (768 × 61 × 496 voxels, 9.2 × 7.8 × 1.9 mm) to evaluate our novel segmentation method in terms of repeatability and reproducibility.

2.2. Automated Segmentation of Choroidal Layers

The choroidal layer is bounded anteriorly by Bruch’s membrane (BM) and posteriorly by the choroid-sclera interface (CSI). To automatically segment the choroidal layer from a macular SD-OCT image volume, we utilized our layered optimal graph image segmentation for multiple objects and surfaces (LOGISMOS) method (Li et al., 2006; Sonka and Abramoff, 2016; Yin et al., 2010) using a multiresolution approach, during which choroidal layer surfaces are sequentially detected at 5 levels of resolution in a coarse-to-fine manner. The analysis starts with level 4 (coarsest, low resolution) and progresses to the finest full resolution level 0. The LOGISMOS method can simultaneously segment multiple surfaces by finding the minimum s - t cut of the weighted graph which is composed of the nodes corresponding to image voxels and the arcs associating graph nodes with costs. Graph nodes are an integral element of the graph-theoretic approach (Li et al., 2006). Our method starts by segmenting the inner limiting membrane (ILM) and the boundary of myoid and ellipsoid of inner segments (BMEIS) from the macular OCT image volume (level 4) down-sampled in the z-direction by a factor of 16 (Fig. 1B). To simultaneously detect these surfaces, a double surface 3D graph search approach (Li et al., 2006; Sonka and Abramoff, 2016; Yin et al., 2010) was applied using edge-based cost functions of the dark-to-bright transition from top to bottom of the down-sampled OCT image volume. The cost functions are the z-directional inverted gradient magnitudes of the OCT voxel intensities, which are smoothed in the x-, z-directions by a 2D Gaussian filter (σ = 1 voxel). Segmentation of the BMEIS, BM, and CSI in level 3 was performed from the sub-OCT image volume region (dotted green lines of Fig. 1C), ranging from 30 μm (2 voxels) above the BMEIS in level 4 up-scaled by a factor of 2 to 400 μm (26 voxels) below the BMEIS. A triple surface 3D graph search approach (Li et al., 2006; Sonka and Abramoff, 2016; Yin et al., 2010) was employed using edge-based cost functions of the dark-to-bright transition for the BMEIS, CSI and that of the bright-to-dark transition for the BM. The z-directional first derivatives of the vesselness values obtained by a Hessian matrix analysis (Sato et al., 1998) were added to the CSI cost function since the CSI is located below choroid blood vessels. Segmentation of the BM and CSI in level 2 was performed from the sub-OCT image volumes with a height of 86 μm (11 voxels) (dotted red and orange lines of Fig. 1D) based on the BM and CSI segmented in level 3 up-scaled by a factor of 2 using a single surface 3D graph search method (Li et al., 2006; Sonka and Abramoff, 2016; Yin et al., 2010). The BM and CSI in levels 1, 0 were consequently detected using the same manner. Finally, the choroidal layer in the full-resolution OCT image volume was obtained by smoothing the CSI using thin plate spline fitting (Donato and Belongie, 2002) (Figs. 1E, 1F). The point (green dot) indicating the thickest location between the BM and CSI surfaces in the patch of 600 μm (20 voxels) by 600 μm (20 voxels) was selected, and 100 control points in total were used to create a thin plate spline.

After detecting binary choroidal vessels using a multiscale Hessian matrix analysis followed by vessel probability thresholding, our previous method (Zhang et al., 2012) automatically segmented 3D choroidal layers by enveloping the binary choroidal vessels. In addition to now incorporating an edge-based cost function for the 3D graph search approach, our newly proposed method utilizes vessel probability values as a vesselness-based cost function to directly segment choroidal layers.

2.3. Statistical Analysis

To evaluate our automated choroidal layer segmentation method, our results were compared with the reference standards created by averaging in the z-direction the manual tracings obtained from two independent graders. The accuracy of our segmentation results was estimated by unsigned/signed border positioning/thickness errors and Dice similarity coefficient (DSC) (Zou et al., 2004). The unsigned/signed border positioning/thickness errors are calculated by measuring the z-directional unsigned/signed Euclidean distances between our segmentation results and the reference standards. If our segmented surface is located above the reference standard, the signed border positioning error is negative, otherwise positive. If our choroidal thickness is thinner than the reference standard, the signed thickness error is negative, otherwise positive. The DSC is calculated by measuring the spatial overlap between our segmented choroidal layer (A) and the reference standard (B), which is defined as DSC(A, B) = 2(A ∩ B) / (A + B). To validate our choroidal layer segmentation method, the unsigned/signed border positioning/thickness errors and DSCs were compared with the unsigned/signed border positioning/thickness differences and DSCs between the two manual tracings. A paired t-test was used in the 95% confidence interval to compare the two measurements, and a Bland-Altman plot was utilized to analyze the agreement between the two measurements (Bland and Altman, 1986).

The repeatability (between repeated Cirrus SD-OCT scans) and the reproducibility (between Spectralis EDI-OCT and Cirrus SD-OCT scans) of choroidal thicknesses were determined by intraclass correlation coefficient (ICC), coefficient of variation (CV), and repeatability coefficient (RC). The ICC is a statistic representing agreements between two measurements, which is calculated on the basis of a two-way random model for analysis of variance (ANOVA) using statistical software (R version 4.0.0, The R Foundation for Statistical Computing) (Shrout and Fleiss, 1979). The CV is defined as a normalized measure of dispersion of two measurements, which is calculated by dividing the standard deviation of two measurements by the mean of the two measurements (Mwanza et al., 2010). The RC is defined as the value of an interval within which 95% of the differences of two measurements lie, which is measured by multiplying the standard deviation of the differences of the two measurements by 1.96 (Bland and Altman, 1986).

3. Results

One hundred Cirrus macular SD-OCT image volumes from 100 patients were randomly obtained from our database system, but 20 volumes were excluded since two independent graders (AKW, KL) could not adequately delineate Bruch’s membrane (BM) or choroid-sclera interface (CSI) because of choroidal neovascularization (CNV), large drusen, and/or fluid. Thus, 80 Cirrus macular SD-OCT image volumes (38 right eyes, 42 left eyes) without significant pathological change in the retina and choroid were used for measurement of the accuracy of our proposed method. The mean age of the cohort was 71.8 ± 10.9 (mean ± standard deviation) years, and 34 subjects were male (42.5%). For measurement of repeatability and reproducibility using our proposed method, two macular Cirrus SD-OCT scans were obtained at the same visit along with Spectralis EDI-OCTs from an additional cohort of 11 young subjects (10 female) with a mean age of 31.3 years.

The mean choroidal thicknesses from graders 1, 2, reference standard, our previous (Zhang et al., 2012) and proposed methods are 208.75 ± 54.31 μm, 206.43 ± 58.73 μm, 207.60 ± 56.00 μm, 128.18 ± 49.35 μm, and 208.85 ± 54.88 μm, respectively. There was no significant difference between the two graders (p = 0.19) or between the reference standard and our proposed method (p = 0.26). The choroidal thickness from our proposed method was significantly thicker than that from our previous method (p < 0.01).

Table 1 shows mean unsigned/signed border positioning/thickness errors and mean DSCs between our previous vs. proposed choroidal layer segmentations and the reference standards, and between the manual tracings of two graders. Our proposed approach showed significantly better performance (p < 0.01) than our previous method in all error metrics except the unsigned/signed border positioning errors of BM. There was no significant difference for the unsigned border positioning error of BM (p = 0.20), and the previous method showed a significantly smaller signed border positioning error of BM (p < 0.01). While the unsigned border positioning errors of BM, CSI, and unsigned thickness error from our proposed approach are significantly smaller than those from the manual tracings of two graders (p < 0.01), the signed border positioning errors of BM, CSI, signed thickness error, and DSC from our proposed approach are significantly larger (p < 0.01).

Table 1.

Error metrics between our previous vs. proposed choroidal layer segmentation algorithms and the reference standard (RS), and between the manual tracings of two independent graders. The bold font shows a statistically significant improvement of the previous or proposed method (p < 0.01).

Previous Method vs. RS Proposed Method vs. RS Grader 1 vs. 2
Mean Unsigned Border Positioning Error of BM (μm) 3.85 ± 3.54 3.39 ± 1.26 4.68 ± 1.61
Mean Signed Border Positioning Error of BM (μm) 0.03 ± 3.87 −1.52 ± 1.63 1.08 ± 2.72
Mean Unsigned Border Positioning Error of CSI (μm) 80.62 ± 62.50 16.09 ± 6.21 23.73 ± 10.71
Mean Signed Border Positioning Error of CSI (μm) −79.39 ± 63.59 4.73 ± 9.53 −1.24 ± 15.92
Mean Unsigned Thickness Error (μm) 80.16 ± 62.73 16.54 ± 6.47 23.90 ± 10.54
Mean Signed Thickness Error (μm) −79.43 ± 63.31 6.25 ± 9.91 −2.33 ± 15.76
Mean Dice Similarity Coefficient (DSC, unitless) 0.743 ± 0.176 0.949 ± 0.025 0.926 ± 0.035
Open in a new tab

As shown in the Bland-Altman plots (Fig. 2), the choroidal thicknesses obtained by our previous method are thinner than the reference standards with a larger variation. While the choroidal thickness differences between our proposed method and the reference standard are slightly larger than those between two graders, the proposed method has less variation.

Fig. 2.

Fig. 2.

Open in a new tab

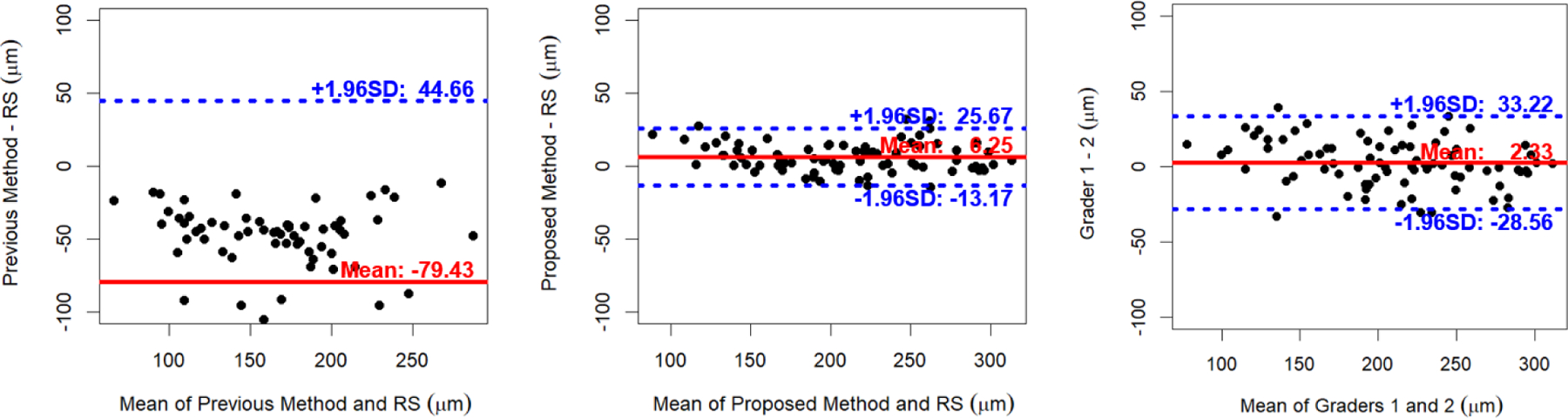
Bland-Altman plots of choroidal thicknesses between our previous vs. proposed choroidal layer segmentations and the reference standard (RS) and between the manual tracings of two independent graders for 80 macular SD-OCT scans.

To demonstrate the range of segmentation accuracy across the previous method, proposed method, two graders, and reference standard, Fig. 3 shows three cropped B-scan images of macular SD-OCT volumes overlaid with our best and worst choroidal layer segmentations having the minimum (4.45 μm) and maximum (19.30 μm) sums of the mean unsigned border positioning errors of BM and CSI.

Fig. 3.

Fig. 3.

Open in a new tab

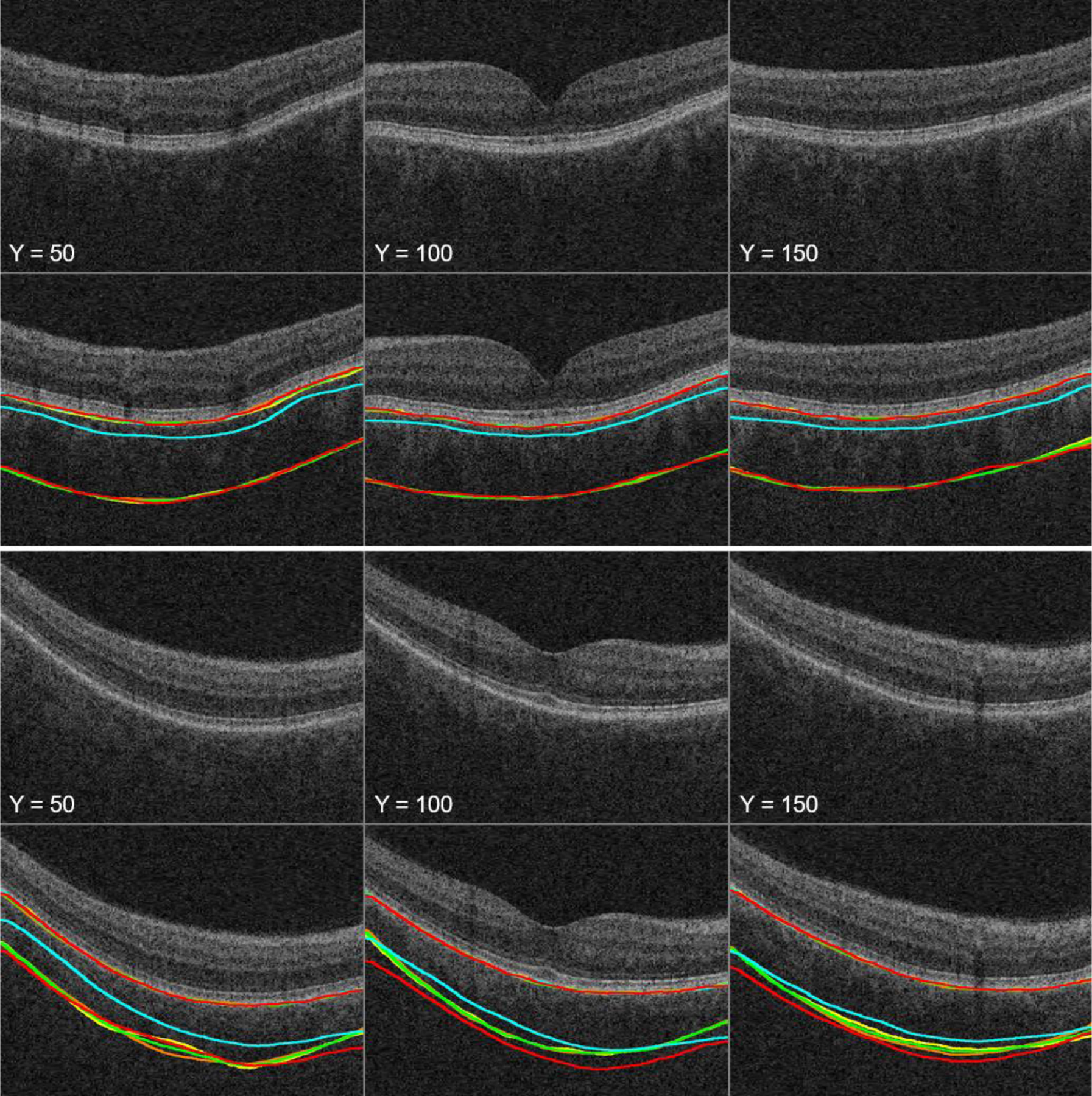
Three cropped B-scan images of macular SD-OCT volumes overlaid with our best (top two rows) and worst (bottom two rows) choroidal layer segmentations (yellow line: grader 1, orange line: grader 2, green line: reference standard, cyan line: our previous method, red line: our proposed method).

The mean choroidal thicknesses of the circular region (radius r ≤ 3.0 mm) originated on the fovea for the repeated SD-OCT and EDI-OCT scans are 292.73 ± 53.37 μm/294.34 ± 54.89 μm and 292.46 ± 53.80 μm (Fig. 4). The mean choroidal thicknesses of the repeated SD-OCT scans are not significantly different (p = 0.35), and those of the first/second repeated SD-OCT scans and EDI-OCT scans are not significantly different either (p = 0.87, 0.36). Table 2 and Fig. 5 show the ICC, CV, RC values and Bland-Altman plots of our choroidal thicknesses between the repeated macular SD-OCT scans for the repeatability and between the macular SD-OCT and EDI-OCT scans for the reproducibility (Giavarina, 2015; Bland and Altman, 1986).

Fig. 4.

Fig. 4.

Open in a new tab

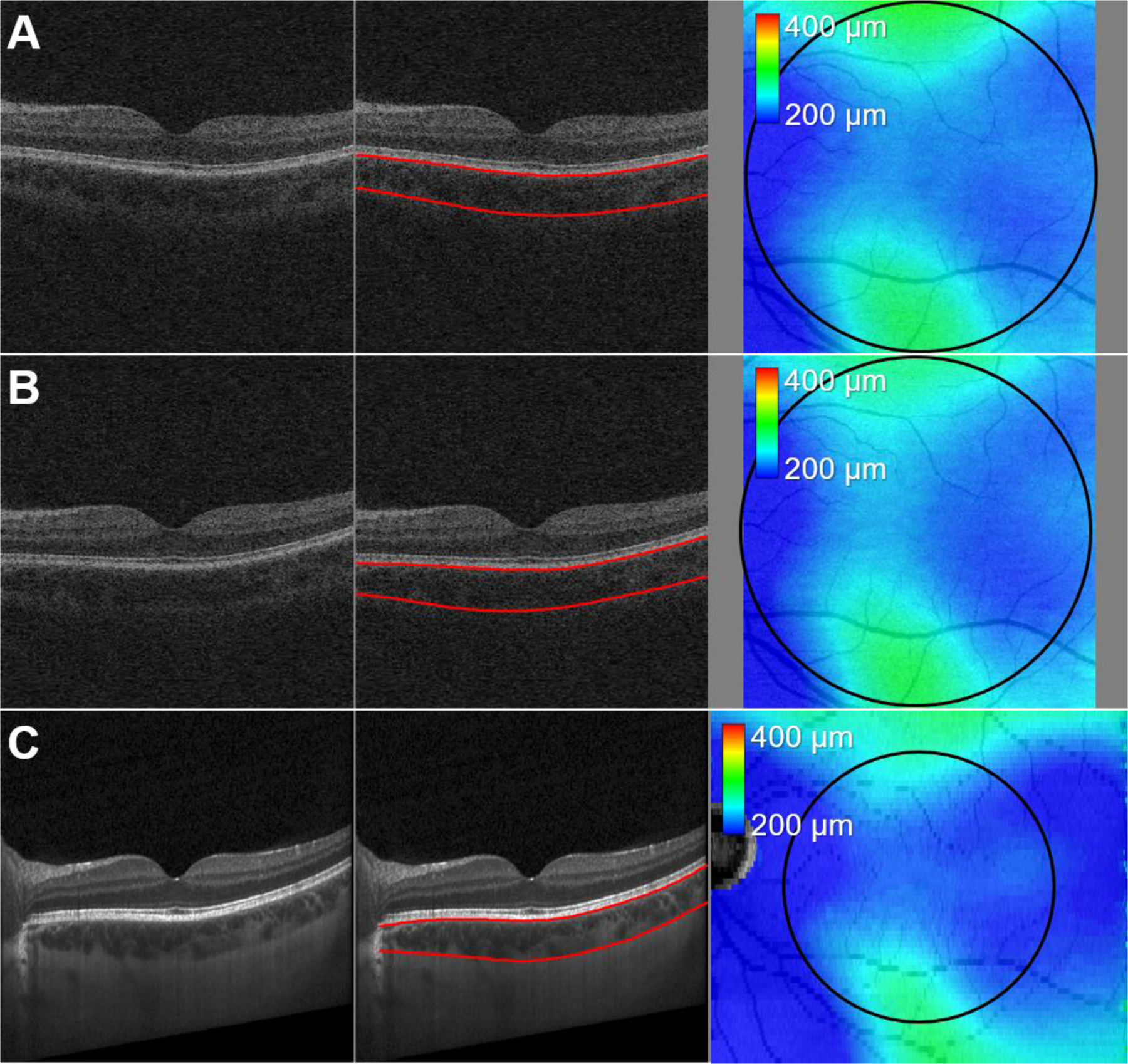
Central B-scan images of (A, B) repeated macular Cirrus SD-OCT volumes (6.0 × 6.0 × 2.0 mm) and (C) Spectralis EDI-OCT volume (9.2 × 7.8 × 1.9 mm) of the same eye overlaid with our proposed choroidal layer segmentations (red lines). The black circle on the choroidal thickness map is originated on the fovea, and its radius is 3.0 mm.

Table 2.

Intraclass correlation coefficient (ICC), coefficient of variation (CV), and repeatability coefficient (RC) values of our proposed choroidal thicknesses between repeated Cirrus SD-OCT scans for repeatability and between Cirrus SD-OCT and Spectralis EDI-OCT scans for reproducibility.

SD-OCT 1 vs. SD-OCT 2 SD-OCT 1 vs. EDI-OCT SD-OCT 2 vs. EDI-OCT
Intraclass Correlation Coefficient (ICC, 95% Confidence Interval) 0.991 (0.977–0.997) 0.991 (0.977–0.997) 0.987 (0.967–0.995)
Coefficient of Variation (CV, %) 2.48 2.49 2.99
Repeatability Coefficient (RC, μm) 14.25 14.30 17.20
Open in a new tab

Fig. 5.

Fig. 5.

Open in a new tab

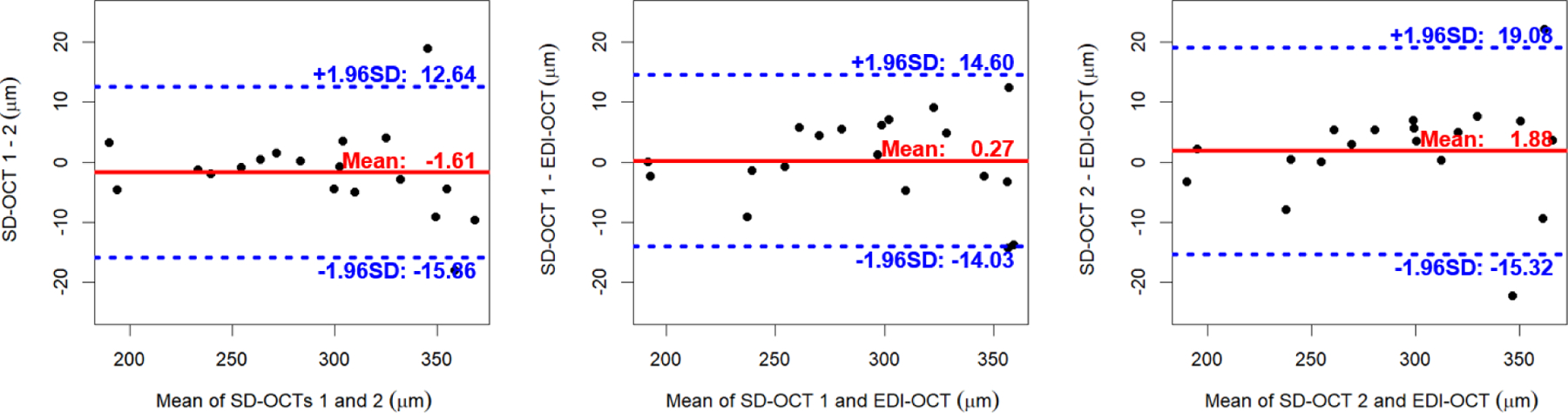
Bland-Altman plots of choroidal thicknesses between repeated Cirrus macular SD-OCT scans for repeatability and between Cirrus SD-OCT and Spectralis EDI-OCT scans for reproducibility.

While our previous method required 6.58 ± 0.61 minutes of running time and 18.5 GB of computer memory (RAM) per single OCT volume on the PC (OS: Microsoft Windows 10 ×64, CPU: Intel® Core™ i7-4790, RAM: 32.0 GB), our proposed method required 1.22 ± 0.36 minutes and 2.0 GB, notable processing time speedup and decrease of computer memory demands. The computer memory usage was measured by checking the peak memory while running the algorithm.

4. Discussion and Conclusions

Measurement of choroidal thickness, whose changes are associated with various ocular diseases, is clinically important. In this study, we have proposed a novel, reliable, memory-efficient, automated 3D choroidal layer segmentation method for macular SD-OCT scans and evaluated it in terms of accuracy, repeatability, and reproducibility. Our proposed automated choroidal layer segmentation method for 3D macular SD-OCT scans significantly outperformed our previously published method (Zhang et al., 2012) using choroid vessel segmentation in terms of mean unsigned/signed border positioning errors of CSI, mean unsigned/signed thickness errors, and mean DSC (p < 0.01). There was no significant difference in the BM unsigned border positioning error between our proposed and previous methods (p = 0.20), which is not surprising as BM has a clear boundary; thus, even our previous method could detect this well. Compared with BM, the boundary for CSI is less clear, especially on Cirrus scans without dedicated EDI imaging; thus, segmentation of CSI had larger unsigned/signed border positioning errors using our previous method but was substantially improved with the proposed method. As shown in the Bland-Altman plots of Fig. 2, the choroidal thicknesses obtained with our proposed method performed better compared with our previous method and also performed well compared with the inter-grader variability of manual segmentations.

Our proposed choroidal layer segmentation method also worked well for macular EDI-OCT scans from a different machine on an additional cohort of young, normal subjects. The ICC, CV, RC values of Table 2 and the Bland-Altman plots of Fig. 5 showed excellent agreements of our choroidal thicknesses between repeated macular SD-OCT scans for repeatability and between macular Zeiss SD-OCT and Heidelberg EDI-OCT scans for reproducibility.

Our proposed automated choroidal layer segmentation method was compared with published 2D/3D segmentation methods using EDI-OCT or SS-OCT based on the error metric values provided by their papers. Masood et al. introduced a deep learning-based segmentation method using morphological operations and convolutional neural networks from Spectralis EDI-OCT scans (Masood et al., 2019). The mean unsigned/signed border positioning errors were 5.42 ± 0.98 μm/1.68 ± 3.94 μm for BM and 11.27 ± 4.10 μm/10.92 ± 5.85 μm for CSI, and the mean DSC was 0.974 ± 0.023. While our proposed method showed a better performance than this method in terms of the unsigned/signed border positioning errors of BM and the signed border positioning error of CSI, the deep learning-based method exhibited lower unsigned border positioning error of CSI and the DSC compared with our proposed approach, which is not surprising since the Spectralis EDI-OCT scans depict choroidal layers with less speckle noise and higher contrast than Cirrus SD-OCT scans. Unsigned errors describe local border inaccuracies whereas signed errors attest to consistent border positioning offsets. Zhang et al. introduced another deep learning-based segmentation method using a biomarker infused global-to-local network from DRI OCT-1 Atlantis SS-OCT scans (Topcon, Tokyo, Japan) (Zhang et al., 2020). The deep learning-based method worked well for automated segmentation of complex choroidal layers. The mean unsigned border positioning error of combined BM and CSI was 18.84 μm, and the mean DSC was 0.908. Our proposed method showed a better performance for both error metrics than this method. Hussain et al. proposed an automated choroidal layer segmentation method using the Dijkstra shortest path algorithm from Spectralis EDI-OCT scans (Hussain et al., 2018). Its mean BM, CSI unsigned border positioning errors, unsigned thickness error, and DSC are 7.29 ± 2.93 μm, 30.07 ± 24.53 μm, 31.51 ± 22.97 μm, and 0.929, respectively. Our proposed method outperformed this method for all error metrics. The Hussain’s method is a 2D segmentation method having a limitation on segmentation of 3D choroidal layers since it does not include the contextual information between adjacent B-scans. Vupparaboina et al. reported another 2D choroidal layer segmentation method from Spectralis EDI-OCT scans by measuring the structural dissimilarity between choroid and sclera by structural similarity (SSIM) index followed by enveloping the thresholded index region (Vupparaboina et al., 2015). Its mean unsigned/signed border positioning errors of CSI and DSC are 19.15 ± 15.98 μm, −15.31 ± 17.97 μm, and 0.955 ± 0.017. While this method showed a slightly larger DSC value, our proposed method showed smaller unsigned/signed border positioning errors of CSI. The Vupparaboina’s method used only 5 EDI-OCT scans for validation and required 6–12 minutes per scan of running time, which is 4.9–9.8 times slower than our proposed method. Want et al. presented an automated 3D segmentation method using the level set framework from DRI OCT-1 Atlantis SS-OCT scans (Wang et al., 2017). Its mean unsigned/signed border positioning errors of CSI and DSC are 5.64 ± 4.60 μm, 4.13 ± 4.29 μm, and 0.90 ± 0.04. While this method showed smaller unsigned/signed border positioning errors of CSI, our proposed method showed a larger DSC value. The SS-OCT scans also depict choroidal layers with higher-than-Cirrus contrast, similar to the EDI-OCT scans. The drawback of this method is its long computational time (43.29 minutes) compared with our proposed method (1.22 ± 0.36 minutes).

There are several limitations of the proposed method for automated segmentation of choroidal layers from macular SD-OCT scans. The first is that a relatively small number of OCT scans were used for this study. More OCT scans with the manual tracings of more than 3 B-scans per volume scan from multiple graders are required for more reliable validation of our proposed method. The second one is that the proposed method does not work well for the OCT scans with weak signal in the choroid for which the CSI is not clearly visible by retinal specialists. A study on the association between the SD-OCT signal strength in the choroid and the accuracy of our proposed method would be beneficial. The third is that the proposed method does not work well for OCT scans with large retinal and/or choroidal alterations such as pigment epithelial detachment (Fig. 6), choroidal neovascularization, or large drusen. Fortunately, this method can be still used in studies without these pathologies, e.g., comparisons of different populations, genetic-based correlations, early stage non-exudative AMD patients, and those with other diseases such as diabetes and glaucoma when there is no significant alteration of the outer retina/RPE layers. This is a considerable improvement over our previously published method (Zhang et al., 2012), which now has relatively limited value as the new method generates choroidal thickness substantially closer to those of the manual graders. In addition to edge-based and vesselness-based cost functions for our proposed method, deep learning-based cost functions would be helpful for segmentation of the complex choroidal layers, and future work will compare AI-based algorithms to the one proposed here.

Fig. 6.

Fig. 6.

Open in a new tab

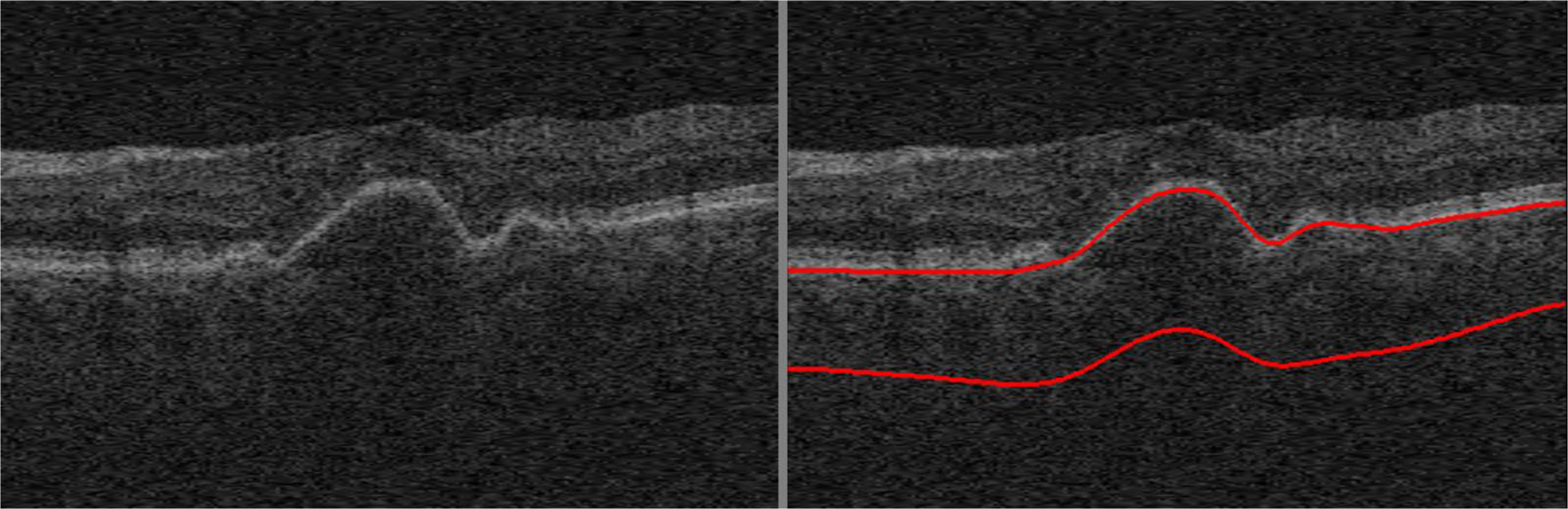
Mis-segmented choroidal layer of our proposed method because of pigment epithelial detachment.

We have proposed a new, automated choroidal layer segmentation method of 3D macular SD-OCT scans and validated it by measuring various error metrics and comparing with the inter-grader variability of two independent, manual graders. For this study, the proposed method showed better performance than our previous method and the inter-grader variability. The proposed method provides a rapid, convenient, automated way of segmenting the choroid from SD-OCT scans, which may be clinically useful for analysis and monitoring of various choroidal diseases.

HIGHLIGHTS.

  • Novel, memory-efficient, 3D automated choroidal layer segmentation method for OCTs

  • Multiscale segmentation from macular scans using LOGIMOS method

  • Works on Cirrus and Heidelberg machines (good results observed with images from other OCT machines)

  • High reliability/reproducibilty demonstrates significant superiority to previous method

  • Could be useful clinically for analysis and monitoring of choroidal diseases, e.g. AMD

Acknowledgements

We appreciate the excellent assistance of Teresa Kopel and Brice Critser in image acquisition and management. This study was supported by the National Institutes of Health grants R01-EY026547, P30-EY025580, R01-EB004640; Research to Prevent Blindness; MDA is the Watzke Professor of Ophthalmology.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Declaration of Competing Interest: Michael D. Abràmoff: Personal Financial Interest (IDx), Consultant (IDx), Patent (University of Iowa); Milan Sonka: Patent (University of Iowa); All other authors: None

References

  1. Bakall B, Folk JC, Boldt HC, Sohn EH, Stone EM, Russell SR, Mahajan VB, 2013. Aflibercept therapy for exudative age-related macular degeneration resistant to bevacizumab and ranibizumab. Am. J. Ophthalmol 156, 15–22.e1. 10.1016/j.ajo.2013.02.017. [DOI] [PubMed] [Google Scholar]
  2. Bland JM, Altman DG, 1986. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1, 307–10. 10.1016/s0140-6736(86)90837-8. [DOI] [PubMed] [Google Scholar]
  3. Chen Q, Niu S, Yuan S, Fan W, Liu Q, 2016. Choroidal vasculature characteristics based choroid segmentation for enhanced depth imaging optical coherence tomography images. Med. Phys 43, 1649. 10.1118/1.4943382. [DOI] [PubMed] [Google Scholar]
  4. Chin EK, Almeida DR, Roybal CN, Niles PI, Gehrs KM, Sohn EH, Boldt HC, Russell SR, Folk JC, 2015. Oral mineralocorticoid antagonists for recalcitrant central serous chorioretinopathy. Clin. Ophthalmol 9, 1449–56. 10.2147/Opth.S86778. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chirco KR, Sohn EH, Stone EM, Tucker BA, Mullins RF, 2017. Structural and molecular changes in the aging choroid: implications for age-related macular degeneration. Eye (Lond.) 31, 10–25. 10.1038/eye.2016.216. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Donato G, Belongie S, 2002. Approximate thin plate spline mappings. Computer Vision-ECCV 2002. 2352, 21–31. 10.1007/3-540-47977-5_2. [DOI] [Google Scholar]
  7. Fujiwara T, Imamura Y, Margolis R, Slakter JS, Spaide RF, 2009. Enhanced depth imaging optical coherence tomography of the choroid in highly myopic eyes. Am. J. Ophthalmol 148, 445–50. 10.1016/j.ajo.2009.04.029. [DOI] [PubMed] [Google Scholar]
  8. Hussain MA, Bhuiyan A, Ishikawa H, Smith RT, Schuman JS, Kotagiri R, 2018. An automated method for choroidal thickness measurement from enhanced depth imaging optical coherence tomography images. Comput. Med. Imaging Graph 63, 41–51. 10.1016/j.compmedimag.2018.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ikuno Y, Maruko I, Yasuno Y, Miura M, Sekiryu T, Nishida K, Iida T, 2011. Reproducibility of retinal and choroidal thickness measurements in enhanced depth imaging and high-penetration optical coherence tomography. Invest. Ophthalmol. Vis. Sci 52, 5536–40. 10.1167/iovs.10-6811. [DOI] [PubMed] [Google Scholar]
  10. Imamura Y, Fujiwara T, Margolis R, Spaide RF, 2009. Enhanced depth imaging optical coherence tomography of the choroid in central serous chorioretinopathy. Retina. 29, 1469–73. 10.1097/IAE.0b013e3181be0a83. [DOI] [PubMed] [Google Scholar]
  11. Giavarina D, 2015. Understanding Bland Altman analysis. Biochem. Med 25, 141–51. 10.11613/BM.2015.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kim SW, Oh J, Kwon SS, Yoo J, Huh K, 2011. Comparison of choroidal thickness among patients with healthy eyes, early age-related maculopathy, neovascular age-related macular degeneration, central serous chorioretinopathy, and polypoidal choroidal vasculopathy. Retina. 31, 1904–11. 10.1097/IAE.0b013e31821801c5. [DOI] [PubMed] [Google Scholar]
  13. Li K, Wu XD, Chen DZ, Sonka M, 2006. Optimal surface segmentation in volumetric images - a graph-theoretic approach. IEEE Trans. Pattern Anal. Mach. Intell 28, 119–34. 10.1109/Tpami.2006.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Manjunath V, Goren J, Fujimoto JG, Duker JS, 2011. Analysis of choroidal thickness in age-related macular degeneration using spectral-domain optical coherence tomography. Am. J. Ophthalmol 152, 663–8. 10.1016/j.ajo.2011.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Maruko I, Iida T, Sugano Y, Ojima A, Ogasawara M, Spaide RF, 2010. Subfoveal choroidal thickness after treatment of central serous chorioretinopathy. Ophthalmology. 117, 1792–9. 10.1016/j.ophtha.2010.01.023. [DOI] [PubMed] [Google Scholar]
  16. Masood S, Fang RG, Li P, Li HT, Sheng B, Mathavan A, Wang XN, Yang P, Wu Q, Qin J, Jia WP, 2019. Automatic choroid layer segmentation from optical coherence tomography images using deep learning. Sci. Rep 9, 3058. 10.1038/s41598-019-48368-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Mrejen S, Spaide RF, 2013. Optical coherence tomography: imaging of the choroid and beyond. Surv. Ophthalmol 58, 387–429. 10.1016/j.survophthal.2012.12.001. [DOI] [PubMed] [Google Scholar]
  18. Mwanza JC, Chang RT, Budenz DL, Durbin MK, Gendy MG, Shi W, Feuer WJ, 2010. Reproducibility of peripapillary retinal nerve fiber layer thickness and optic nerve head parameters measured with Cirrus HD-OCT in glaucomatous eyes. Invest. Ophthalmol. Vis. Sci 51, 5724–30. 10.1167/iovs.10-5222. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Sacconi R, Deotto N, Merz T, Morbio R, Casati S, Marchini G, 2017. SD-OCT choroidal thickness in advanced primary open-angle glaucoma. J. Glaucoma 26, 523–7. 10.1097/Ijg.0000000000000661. [DOI] [PubMed] [Google Scholar]
  20. Sato Y, Nakajima S, Shiraga N, Atsumi H, Yoshida S, Koller T, Gerig G, Kikinis R, 1998. Three-dimensional multi-scale line filter for segmentation and visualization of curvilinear structures in medical images. Med. Image Anal 2, 143–68. 10.1016/s1361-8415(98)80009-1. [DOI] [PubMed] [Google Scholar]
  21. Shrout PE, Fleiss JL, 1979. Intraclass correlations: uses in assessing rater reliability. Psychol. Bull 86, 420–8. 10.1037/0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
  22. Sohn EH, Khanna A, Tucker BA, Abramoff MD, Stone EM, Mullins RF, 2014. Structural and biochemical analyses of choroidal thickness in human donor eyes. Invest. Ophthalmol. Vis. Sci 55, 1352–60. 10.1167/iovs.13-13754. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Sonka M, Abramoff MD, 2016. Quantitative analysis of retinal OCT. Med. Image Anal 33, 165–9. 10.1016/j.media.2016.06.001. [DOI] [PubMed] [Google Scholar]
  24. Tozer K, Roller AB, Chong LP, Sadda S, Folk JC, Mahajan VB, Russell SR, Boldt HC, Sohn EH, 2013. Combination therapy for neovascular age-related macular degeneration refractory to anti-vascular endothelial growth factor agents. Ophthalmology. 120, 2029–34. 10.1016/j.ophtha.2013.03.016. [DOI] [PubMed] [Google Scholar]
  25. Vupparaboina KK, Nizampatnam S, Chhablani J, Richhariya A, Jana S, 2015. Automated estimation of choroidal thickness distribution and volume based on OCT images of posterior visual section. Comput. Med. Imaging Graph 46, 315–27. 10.1016/j.compmedimag.2015.09.008. [DOI] [PubMed] [Google Scholar]
  26. Wang C, Wang YX, Li YM, 2017. Automatic choroidal layer segmentation using Markov random field and level set method. IEEE J. Biomed. Health Inform 21, 1694–702. 10.1109/Jbhi.2017.2675382. [DOI] [PubMed] [Google Scholar]
  27. Whitmore SS, Sohn EH, Chirco KR, Drack AV, Stone EM, Tucker BA, Mullins RF, 2015. Complement activation and choriocapillaris loss in early AMD: implications for pathophysiology and therapy. Prog. Retin. Eye Res 45, 1–29. 10.1016/j.preteyeres.2014.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Wojtkowski M, Kaluzny B, Zawadzki RJ, 2012. New directions in ophthalmic optical coherence tomography. Optom. Vis. Sci 89, 524–42. 10.1097/OPX.0b013e31824eecb2. [DOI] [PubMed] [Google Scholar]
  29. Yin Y, Zhang XM, Williams R, Wu XD, Anderson DD, Sonka M, 2010. LOGISMOS-layered optimal graph image segmentation of multiple objects and surfaces: cartilage segmentation in the knee joint. IEEE Trans. Med. Imaging 29, 2023–37. 10.1109/Tmi.2010.2058861. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Zhang H, Yang J, Zhou K, Fang L, Li F, Hu Y, Zhao Y, Zhang X, Liu J, 2020. Automatic segmentation and visualization of choroid in OCT with knowledge infused deep learning. arXiv. arXiv:2002.04712v1. [DOI] [PubMed] [Google Scholar]
  31. Zhang L, Lee K, Niemeijer M, Mullins RF, Sonka M, Abramoff MD, 2012. Automated segmentation of the choroid from clinical SD-OCT. Invest. Ophthalmol. Vis. Sci 53, 7510–9. 10.1167/iovs.12-10311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Zou KH, Warfield SK, Bharatha A, Tempany CMC, Kaus MR, Haker SJ, Wells WM, Jolesz FA, Kikinis R, 2004. Statistical validation of image segmentation quality based on a spatial overlap index. Acad. Radiol 11, 178–89. 10.1016/S1076-6332(03)00671-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES