Abstract
Meta-analysis is a practical and powerful analytic tool that enables a unified statistical inference across the results from multiple studies. Notably, researchers often report the results on multiple related markers in each study (e.g., various α-diversity indices in microbiome studies). However, univariate meta-analyses are limited to combining the results on a single common marker at a time, whereas existing multivariate meta-analyses are limited to the situations where marker-by-marker correlations are given in each study. Thus, here we introduce two meta-analysis methods, multi-marker meta-analysis (mMeta) and adaptive multi-marker meta-analysis (aMeta), to combine multiple studies throughout multiple related markers with no priori results on marker-by-marker correlations. mMeta is a statistical estimator for a pooled estimate and its standard error across all the studies and markers, whereas aMeta is a statistical test based on the test statistic of the minimum p-value among marker-specific meta-analyses. mMeta conducts both effect estimation and hypothesis testing based on a weighted average of marker-specific pooled estimates while estimating marker-by-marker correlations non-parametrically via permutations, yet its power is only moderate. In contrast, aMeta closely approaches the highest power among marker-specific meta-analyses, yet it is limited to hypothesis testing. While their applications can be broader, we illustrate the use of mMeta and aMeta to combine microbiome studies throughout multiple α-diversity indices. We evaluate mMeta and aMeta in silico and apply them to real microbiome studies on the disparity in α-diversity by the status of HIV infection. The R package for mMeta and aMeta is freely available at https://github.com/hk1785/mMeta.
Keywords: Multi-marker meta-analysis, Adaptive meta-analysis, Random effects meta-analysis, Non-parametric meta-analysis, Meta-analysis for α-diversity indices, Meta-analysis for microbiome studies
Introduction
Meta-analysis represents a statistical method to summarize and combine the results from multiple related studies. In the early years, meta-analysis was mostly a descriptive review of prior studies1, yet it has later been greatly reinforced with the functionality to make a unified statistical inference across studies (e.g., a pooled estimate and its standard error). The major benefits of meta-analysis are its practical use and improved statistical power as it requires only the summary statistics (e.g., study-specific estimates and their standard errors) for implementation and integrates information across studies. For these reasons, meta-analysis has been increasingly employed in many academic fields, such as biology, medicine, psychology, education and economics2. Especially in the fields of high-dimensional data analysis, meta-analysis has been proven as a powerful analytic tool to discover novel markers by aggregating possibly small effects across studies and thus making a detectable pooled effect3,4,5.
In this paper, we especially pay attention to the situation where researchers report the results on multiple, distinct but related, markers in each study; as such, the summary data (e.g., effect estimates and their standard errors) can be organized in a two-dimensional array [Table 1], where the first dimension is for individual studies, and the second dimension is for multiple markers. Here, the multiple markers are different measurements (distinct) that have a common goal (related). For example, the multiple, distinct but related, markers are many different α-diversity indices in human microbiome studies, such as Species richness, Shannon6, Simpson7, Inverse Simpson7,8, Chao19, ACE10, phylogenetic diversity (PD)11, phylogenetic entropy (PE)12 and phylogenetic quadratic entropy (PQE)13,14, for a common goal of measuring true α-diversity. Here, the human microbiome refers to the entire ecosystem of all microbes residing in and on the human body. The roles of the microbiome on human health or disease have been increasingly studied by the recent advance in high-throughput sequence technologies. For example, the microbial α-diversity of the human microbiome have been surveyed to evaluate its association with a variety of host phenotypes (or disease status). In human microbiome studies, multiple α-diversity indices have been individually surveyed to evaluate the association between microbial diversity and a host phenotype (or disease status) because there is no single best α-diversity index which is superior to the other indices in all contexts8,15. Therefore, it will be worthwhile if we can make an overall conclusion on ‘α-diversity’ in a global sense while jointly considering multiple α-diversity indices.
Table 1.
An illustration of the summary data for mMeta and aMeta in a two-dimensional array.
| Marker 1 | Marker 2 | … | Marker Q-1 | Marker Q | |
|---|---|---|---|---|---|
| Study 1 | () | () | … | () | () |
| Study 2 | () | () | … | () | () |
| … | … | … | … | … | … |
| Study K-1 | () | () | … | () | () |
| Study K | () | () | … | () | () |
Suppose that there are K studies and Q markers, where () denotes the effect estimate and its standard error for the k-th study (k = 1, …, K) and the j-th marker (j = 1, …, Q).
However, univariate meta-analysis can combine the results only on a single common marker across studies, which is referred to in this paper as a single-marker (or marker-specific) meta-analysis. The single-marker meta-analyses are useful in making specific conclusions on each particular marker, but are subject to a substantial loss of power because of the requisite multiple testing correction for multiple simultaneous tests. The results from single-marker meta-analyses can also vary by markers, and we note that the approach that reports significant results while hiding non-significant results (a.k.a. cherry-picking or p-hacking) is detrimental to our science making it flooded with false discoveries because of the issue of invisible multiplicity. On the contrary, multivariate meta-analysis can combine multiple studies throughout multiple related markers, and thus can make an overall conclusion across all the studies and markers with no need for multiple testing correction. However, existing frequentist methods for multivariate meta-analysis can be implemented only when marker-by-marker correlations (a.k.a. within-study covariances) are given from each study while assuming that they are fixed with no error to ensure identifiability of the other parameters in the model16,17. In reality, researchers rarely report the results on marker-by-marker correlations as they often analyze multiple markers individually, not using a joint statistical model, or simply omit them due to a lack of scholarly attention16. Of course, if individual study data are available, we can estimate ad hoc marker-by-marker correlations, yet such analyses fall in the class of pooled analysis, instead of meta-analysis, where the practical benefit of requiring only the summary statistics for implementation disappears. On the other hand, existing Bayesian methods for multivariate meta-analysis can be implemented by incorporating a prior information on the correlations, for example, through the inverse-Wishart prior, into a parametric variance covariance structure via Markov Chain Monte Carlo methods17,18, yet any prior information on the correlations lacks in practice. Any violation on the parametric variance covariance structure can result in invalid statistical inference.
Thus, here we introduce two meta-analysis methods, namely, multi-marker meta-analysis (mMeta) and adaptive multi-marker meta-analysis (aMeta), that can be implemented using only the summary statistics (i.e., effect estimates and their standard errors) with no priori results on marker-by-marker correlations to combine multiple studies throughout multiple related markers. mMeta is a statistical estimator for a pooled estimate and its standard error across all the studies and markers, whereas aMeta is a statistical test based on the test statistic of the minimum p-value among multiple marker-specific meta-analyses19. mMeta conducts both effect estimation and hypothesis testing in a unified approach based on a weighted average of marker-specific pooled estimates while estimating marker-by-marker correlations using a permutation method, yet its power is only moderate among multiple marker-specific meta-analyses due to the central tendency of its weighted averaging scheme. In contrast, aMeta closely approaches the highest power among multiple marker-specific meta-analyses due to the high adaptivity to the most significant result of the minimum p-value statistic, yet it is limited to hypothesis testing with no estimation facilities (i.e., purely a test for significance). Therefore, mMeta is better interpreted with the direction and size of the pooled estimate, while aMeta is more powerful to make novel discoveries.
The machinery of mMeta and aMeta starts with combining the results on each marker across studies (i.e., single-marker meta-analysis), and then combines the results from marker-specific meta-analyses to make an overall conclusion across markers. Individual studies are usually heterogeneous to each other because of the difference in their underlying study characteristics, such as study design, ethnicity, sequencing and other unknown sources; hence, we developed mMeta and aMeta as random effects meta-analysis methods to account for the heterogeneity across studies. We estimate the heterogeneity variance using the Sidik and Jonkman (SJ) estimator (a.k.a. the robust variance estimator or the sandwich variance estimator)20 because the SJ estimator gives a robust estimate based on a refinement using an initial estimate of the heterogeneity variance. We adopted a semi-parametric group permutation method21 to estimate marker-by-marker correlations for mMeta and to generate the null statistic values of the minimum p-value statistic for aMeta. We also adopted the Han and Eskin’s modified random effects meta-analysis22 which assumes no heterogeneity under H0 because the assumption of the traditional null hypothesis that the heterogeneity exists even under H0 can be overly conservative. Notably, the summary statistics are not usually available in a balanced way across all the studies and markers (i.e., the summary data in [Table 1] can be missing for some studies or markers); hence, we developed mMeta and aMeta to robustly handle missing summary data.
The methodological novelty of mMeta and aMeta, mostly lies in the implementation of multivariate meta-analysis with no priori results on marker-by-marker correlations and the use of minimum p-value statistic in the context of multivariate meta-analysis. The other methodological aspects of mMeta and aMeta are mostly multivariate extensions of the existing approaches in univariate meta-analysis. We illustrate the use of mMeta and aMeta to combine multiple microbiome association studies with the results on multiple α-diversity indices. We evaluate mMeta and aMeta in silico, and also apply them to 15 real microbiome studies on the disparity in microbial α-diversity by the status of HIV infection. While mMeta and aMeta require only the summary statistics [Table 1] for implementation, many studies report different forms of effect estimates or degrees of significance making the conventional meta-analysis challenging. Thus, finally, we discuss such practical limitations as well as potential extensions to other multi-marker studies.
mMeta and aMeta can be implemented using the R package, mMeta, which is freely available at https://github.com/hk1785/mMeta. In the software manual on the webpage, we described detailed implementation procedures (e.g., pre-requisite libraries, installation, functions, arguments) and outputs (e.g., graphical representations) including example data and codes.
Methods
Here, we describe the methodological details on mMeta and aMeta. We begin with the description of the prior single-marker meta-analysis to combine multiple studies on a single common marker (see Single-marker meta-analysis) as well as the Han and Eskin’s modified random effects meta-analysis that assumes no heterogeneity under H0 (see Han and Eskin’s modified random effects meta-analysis). Then, we describe our proposed methods, mMeta (see Multi-marker meta-analysis (mMeta)) and aMeta (see Adaptive multi-marker meta-analysis (aMeta)), to jointly consider multiple related markers. We also describe the implications of mMeta and aMeta in the human microbiome research field to combine multiple α-diversity indices to make an overall conclusion on ‘α-diversity’ in a global sense (see α-diversity indices). Finally, we describe how mMeta and aMeta can handle missing summary data from prior studies (see A simple modification to robustly handle missing summary data from prior studies).
Single-marker meta-analysis
Suppose that we conduct a meta-analysis with K independent studies on a single common marker, and let and denote the estimated study-specific effect (e.g., regression coefficient) and its standard error, respectively, for k = 1, …, K. Here, the true study-specific effects (denoted as βk’s) tend to be heterogeneous across studies due to the difference in their underlying study characteristics (e.g., study design, ethnicity, sequencing, etc). Therefore, we consider a random effects meta-analysis model to account for the heterogeneity across studies (Eq. 1)23.
| (1) |
where βk’s are the true study-specific effects treated as random to account for the heterogeneity across studies, and ek’s are within-study errors. Here, the within-study error (ek) is assumed to follow a normal distribution N(0, ), in which is the within-study variance that can be simply estimated by the square of the estimated study-specific standard error (). The true study-specific effect (βk) is assumed to follow a normal distribution N(μ, τ2), in which μ is the pooled effect across studies and τ2 is the between-study variance (a.k.a. the heterogeneity variance). While there have been a variety of methods to estimate the heterogeneity variance (τ2), we employ the SJ estimator20 for our proposed methods because of its simplicity and robustness as supported by many follow-up studies 2,24,25. The SJ estimator gives a refinement to the usual weighted least squares estimator by using a residual variance as an initial (rough) estimate of the heterogeneity variance (Eq. 2)20.
| (2) |
where . Then, the study-specific weights are updated using the initial estimate of the heterogeneity variance (Eq. 2) as for k = 1, …, K, and then, the SJ estimator is formulated with (Eq. 3)20.
| (3) |
where W is a K × K diagonal matrix of the weights, W = diag( is a K × 1 vector of 1’s, I = (1,…,1)T, and is a K × 1 vector of the estimated study-specific effects, . The refinement using the initial estimate of the heterogeneity variance leads that the SJ estimator () more robustly estimates the heterogeneity variance than the ones with no refinement20,24,25. In addition, the SJ estimator is non-iterative and produces a non-negative variance estimate all the time with no need to truncate a negative estimate to zero. Therefore, the SJ estimator is computationally efficient and straightforward20,24,25.
Here, we are particularly interested in estimating the pooled effect across studies (μ) and testing the null hypothesis of no pooled effect against the alternative hypothesis of some pooled effect, that is, H0: μ = 0 vs. H1: μ ≠ 0. In tradition, the pooled effect is estimated as a weighted average of study-specific effects (Eq. 4)23.
| (4) |
where . By its formula (Eq. 4), we can infer that the study-specific effects () are weighted more for the studies with smaller within-study variance () than the studies with larger within-study variance. This indicates, for example, that the study-specific effects () are weighted more for the studies with larger sample sizes than the studies with smaller sample sizes since the standard error () decreases as the sample size increases. We can also infer that the pooled effect () is larger when the between-study variance () is smaller. This indicates that the pooled effect () is large when the individual studies are similar in their underlying study characteristics (e.g., study design, ethnicity, sequencing, etc), but it is vice versa when they are dissimilar in their underlying study characteristics.
The most commonly used approach to obtain the p-value and the confidence interval for is a parametric method that calculates the p-value as P(|| > N(0,1)) and the 95% confidence interval as 1.96×, where is the standard error of estimated as . However, to estimate marker-by-marker correlations for mMeta (see Multi-marker meta-analysis (mMeta)) and because of the unknown limiting distribution of the minimum p-value statistic for aMeta (see Adaptive multi-marker meta-analysis (aMeta)), we instead employ a group permutation method proposed by Follmann and Proschan (1999)21 for our proposed methods. The group permutation method is semi-parametric assuming only that the distribution of is symmetric. The symmetry of the distribution is usually less demanding than a full distributional assumption, and it is satisfied by many common distributions (e.g., normal distribution, t-distribution). The symmetric enables the sign of to be equally likely positive or negative under H0, and thus we can generate the null values of ’s by randomly assigning −1 or +1 to the absolute values of ’s. Follmann and Proschan (1999)21 called this method as a group permutation method as it corresponds to flipping the labels of treatment and control groups in each clinical trial, and permuting possible combinations of the signs across trials. There are 2K possible permutations of the signs, and either all the 2K permutations or a large number of randomly selected permutations (e.g., 5,000 permutations) leads to reliable estimates26. However, a limitation of the group permutation method is that the number of all possible permutations (2K) is small for a small number of studies (i.e., a small K) so that it might not produce a reliable p-value for a small K due to a high discreteness of the exact null distribution. For example, the number of all possible permutations for K = 5 is only 25 = 32; hence, there are only 32 discrete null statistic values that are compared with the observed statistic value for K = 5. Therefore, we set the smallest possible value of K as K = 10 for our proposed methods.
Suppose that there are R permutations of the signs. For each permutation (r = 1, …, R), we can compute the null values of (denoted as for k = 1, …, K) by assigning the signs of ±1’s to the absolute values of ’s, and then compute the null values of (denoted as ) using and for k = 1, …, K through Eq. 2, 3 and 4. We can then compute the p-value as the proportion of the null values of for r = 1, …, R) equal to or more extreme than the observed value of , and the 95% confidence interval for as the interval between 2.5% and 97.5% quantile values among the null values of for r = 1, …, R) around the observed value of 21. We organized all the detailed computational procedures in Algorithm 1. Single-marker meta-analysis.
Han and Eskin’s modified random effects meta-analysis
Han and Eskin (2011)22 addressed an important issue of assuming no heterogeneity under H0, and testing [H0: μ = 0 and τ2 = 0 vs. H1: μ ≠ 0 or τ2 > 0]. Here, [H0: μ = 0 and τ2 = 0] indicates no pooled effect and no heterogeneity under H0, which is equivalent to no effect across all studies under H0[H0:βk = 0 for all k’s in {1, …, K}], while [H1: μ ≠ 0 or τ2 > 0] indicates some pooled effect or some heterogeneity under H1, which is equivalent to some effect for at least one study under H1[H1: βk ≠ 0 for some k’s in {1, …, K}]. Therefore, [H0: μ = 0 and τ2 = 0 vs. H1: μ ≠ 0 or τ2 > 0] is equivalent to [H0:βk = 0 for all k’s in {1, …, K} vs. H1:βk ≠ 0 for some k’s in {1, …, K}], and we can see that the assumption of no heterogeneity under H0 also holds in the latter representation because βk’s are all equivalently zeros under H0.
Importantly, [H0: μ = 0 and τ2 = 0] indicates the traditional null hypothesis in random effects meta-analysis [H0: μ = 0], but [H0: μ = 0] does not necessarily indicate [H0: μ = 0 and τ2 = 0]. In addition, [H1: μ ≠ 0] indicates [H1: μ ≠ 0 or τ2 > 0], but [H1: μ ≠ 0 or τ2 > 0] does not necessarily indicate [H1: μ ≠ 0]. Therefore, [H0: μ = 0 and τ2 = 0 vs. H1: μ ≠ 0 or τ2 > 0] is less conservative than [H0: μ = 0 vs. H1: μ ≠ 0], which indicates that the Han and Eskin’s modified random effects meta-analysis is more powerful than the traditional random effects meta-analysis.
As described in Han and Eskin (2011)22, we also notice that the assumption of the traditional null hypothesis that the heterogeneity exists even under H0 can be overly conservative. That is, if we suppose that βk’s are real numbers and K is finite, μ = 0 is likely to indicate βk = 0 for all k’s in {1, …, K} because there is no perfect cancelling-out of non-zero βk’s to make μ = 0 in probability, and thus, the assumption of no heterogeneity under H0 does not comport a realistic difference against the traditional null hypothesis. Therefore, the Han and Eskin’s modified random effects meta-analysis can be considered to improve power while relaxing the conservative assumption of the heterogeneity under H0. We adopt the Han and Eskin’s modification for mMeta and aMeta, for which we set the permuted (null) heterogeneity estimates as all zeros ( = 0 for r = 1, …, R) (see Option 1 (default) in Algorithm 1. Single-marker meta-analysis), while providing the traditional hypothesis testing in random effects meta-analysis as a user option in our software package (see Option 2 in Algorithm 1. Single-marker meta-analysis).
Algorithm 1.
Single-marker meta-analysis
| Inputs. The estimated study-specific effect () and its standard error () for k = 1, …, K. |
| Options. ‘Option 1 (default)’ assumes the absence of the heterogeneity under H0 for testing [H0: μ = 0 and τ2 = 0 vs. H1: μ ≠ 0 or τ2 ≠ 0]; ‘Option 2’ assumes the existence of the heterogeneity under H0 for testing [H0: μ = 0 vs. H1: μ ≠ 0]. |
| Outputs. The main outcomes to be reported are and the p-value and the 95% confidence interval for , and the ancillary outcomes to be stored for the following analyses are for r = 1, …, R. |
| 1. Generate a K × R matrix (denoted as S) including its elements with the randomly generated ±1’s. |
| 2. Compute the null values of βk (denoted as ) as | for k = 1, …, K & r = 1, …, R, where Sk,r is the (k, r)-th element of S. |
| 3. If ‘Option 1 (default)’, = 0 for r = 1, …, R. If ‘Option 2’, compute the null values of (denoted as ) using based on Eq. 2 and 3 for r = 1, …, R. |
| 4. Compute the null values of μ (denoted as ) using , and based on Eq. 4 for r = 1, …, R. |
| 5. Compute the observed pooled effect (denoted as ) using and for k = 1, …, K through Eq. 2, 3, 4. |
| 6. Compute the p-value as and the 95% confidence interval for as [φ(0.025)+, φ(0.975)+], where I(·) is an indicator function, and φ(0.025) and φ(0.975) are 2.5% and 97.5% quantile values in {}, respectively. |
Multi-marker meta-analysis (mMeta)
Now, we suppose that there are multiple, distinct but related, markers of interest such as the α-diversity indices (e.g., Species richness, Shannon, Simpson, Inverse Simpson, Chao1, ACE, PD, PE, PQE) in microbiome studies. Let Q denote the total number of markers, and and (j = 1, …, Q) denote the marker-specific pooled effect and its standard error estimated through the single-marker meta-analysis. For example, if there are six α-diversity indices (e.g., Species richness, Shannon, Simpson, PD, PE, PQE) to be surveyed, Q equals to 6. Moreover, the results on all the Q markers do not need to be reported in all individual prior studies (for more details, see A simple modification to robustly handle missing summary data from prior studies). That is, in the above example, the results on all the six α-diversity indices do not necessarily need to be reported in all individual prior studies.
Here, we are interested in estimating the pooled effect across all the studies and markers (denoted as μA) and testing H0:μA = 0 vs. H1:μA ≠ 0 in order to make an overall conclusion in effect direction and size on a common goal shared by the underlying multiple markers (e.g., an overall conclusion on ‘α-diversity’ by combining multiple α-diversity indices). One may want to estimate μA as a weighted average of marker-specific pooled effects such that , where and is the between-marker variance estimate. This approach is simply the traditional meta-analysis to combine multiple markers instead of the multiple studies in (Eq. 4). However, the multiple markers (e.g., α-diversity indices) are correlated to each other because of their semantic and technical relatedness8; hence the traditional meta-analysis based on the independence assumption (Eq. 4) cannot be directly used to combine multiple correlated markers23. Therefore, here we first estimate the marker-by-marker (Q × Q) covariance matrix (denoted as V) to account for the correlations across markers. For this, we apply the same permuted signs to all different markers (i.e., we generate S in Step 1 in Algorithm 1 only once, and apply the same S to all different markers for the following steps), and calculate pairwise covariances across markers using the permuted (null) marker-specific pooled effects as (Eq. 5).
| (5) |
where is the (j, j’)-th element of the Q × Q covariance matrix () and () and () are the permuted (null) pooled effects for the j-th and j’-th markers, respectively, for j = 1, …, Q and j’ = 1, …, Q. Then, we estimate as in (Eq. 6).
| (6) |
where . This is also the weighted average of marker-specific pooled effects like (Eq. 4)23, but importantly, here we applied the weights based on the estimated marker-by-marker covariance matrix () to account for the correlations across markers.
For each permutation (r = 1, …, R), we can compute the null values of (denoted as ) using for j = 1, …, Q through Eq. 5 and 6. We can then compute the p-value as the proportion of the null values of for r = 1, …, R) equal to or more extreme than the observed value of , and the 95% confidence interval for as the interval between 2.5% and 97.5% quantile values among the null values of for r = 1, …, R) around the observed value of . We organized all the detailed computational procedures in Algorithm 2. mMeta.
Algorithm 2.
mMeta
| Inputs: The estimated marker-specific pooled effect () and the permuted (null) pooled effects () obtained based on the single-marker meta-analysis (Algorithm 1) for each marker (j = 1, …, Q). |
| Outputs: , the p-value and the 95% confidence interval for . |
| 1. Compute the marker-by-marker (Q × Q) covariance matrix (denoted as ), by calculating pairwise covariances across markers as = Cov[()], where is the (j, j’)-th element of for j = 1, …, Q and j’ = 1, …, Q (Eq. 5). |
| 2. Compute the null values of μA (denoted as ) using for j = 1, …, Q and based on Eq. 6 for r = 1, …, R. |
| 3. Compute the observed pooled effect (denoted as ) using for j = 1, …, Q and based on Eq. 6. |
| 4. Compute the p-value as and the 95% confidence interval for as [φ(0.025)+, φ(0.975)+], where I(·) is an indicator function, and φ(0.025) and φ(0.975) are 2.5% and 97.5% quantile values in {}, respectively. |
Adaptive multi-marker meta-analysis (aMeta)
Again, mMeta is an approach to make a breadth of statistical inferences (i.e., effect estimation and hypothesis testing) based on a weighted average of marker-specific pooled effects () (Eq. 6). The mechanism of weighted averaging is a natural way to combine multiple effects, but its central tendency can make mMeta a compromise among the multiple surveyed markers in performance. Especially, for a sparsity situation when only a few markers among many markers have significant signals, mMeta can lose power because the weighted average effect is diluted from many weak signals. Therefore, we introduce another meta-analysis method for multi-marker studies, aMeta, which is in the context of taking the strongest evidence of significance among single-marker meta-analyses instead of averaging marker-specific pooled effects, and testing H0:μj = 0 for all j’s in {1, …, Q} vs. H1:μj ≠ 0 for some j’s in {1, …, Q}.
Let Pj denote the estimated marker-specific p-value based on the single-marker meta-analysis for each marker (j = 1, …, Q). We formulate the test statistic of aMeta as the minimum p-value among Pj’s (Eq. 7).
| (7) |
This minimum p-value statistic reflects only the most significant signal, ignoring all the other signals, among multiple surveyed markers, and thus enables aMeta to adaptively approach the highest power among single-marker meta-analyses. However, the major limitation of aMeta is that it is only for hypothesis testing with no effect estimation facilities.
The use of the minimum p-value statistic19 has also been widely used in many prior tests15,27,28,29,30 along with a permutation method partly because of the unknown properties on its limiting behavior, but, distinctively, aMeta is in the context of meta-analysis which requires only the summary statistics for implementation. We organized all the detailed computational procedures to calculate the p-value based on the minimum p-value statistic (Eq 7) in Algorithm 3. aMeta.
Algorithm 3.
aMeta
| Inputs: The estimated marker-specific p-value (Pj) and the permuted (null) pooled effects () obtained based on the single-marker meta-analysis (Algorithm 1) for each marker (j = 1, …, Q). |
| Outputs: The p-value for aMeta. |
| 1. Compute the null values of Pj (denoted as ) as = , where r = 1, …, R and = 1, …, R, for each marker (j = 1, …, Q). |
| 2. Compute the null statistic values of TaMeta (denoted as ) as , for r = 1, …, R (Eq. 7). |
| 3. Compute the observed statistic value (denoted as TaMeta) as (Eq. 7). |
| 4. Compute the p-value for aMeta as , where I(·) is an indicator function. |
α-diversity indices
mMeta and aMeta can be broadly applied to any set of multiple related markers, depending on the availability of the summary statistics from prior studies and/or investigators’ interest. As a demonstration, we investigate six α-diversity indices, Species richness, Shannon6, Simpson7, PD11, PE12 and PQE13,14, in our simulations and real data applications. We show the formulas for these α-diversity indices in [Table 2]. These α-diversity indices have a common goal of measuring microbial diversity in a community (i.e., within-sample diversity), but are also distinguished by different weighting schemes based on microbial abundance and/or phylogenetic tree information8,15 [Table 2]. That is, the Species richness, Shannon and Simpson indices are non-phylogenetic indices which do not incorporate phylogenetic tree information8,15 [Table 2]. The Species richness is the total number of the species present in a sample, and it is the simplest form of α-diversity based only on the presence/absence information of species with no weights in relative abundance, while the Shannon and Simpson indices apply additional weights in relative abundance [Table 2]. Therefore, in an association analysis between microbial diversity and a host phenotype (or disease status), the Species richness suits the situation when the species associated with the host phenotype are rare species, while the Shannon and Simpson indices suit the situation when the associated species are common species. In contrast, PD, PE and PQE indices are phylogenetic indices which incorporate phylogenetic tree information12,15,31 [Table 2]. The PD index is simply the total length of the branches in the phylogenetic tree that belong to the species present in a sample with no weights in relative abundance [Table 2]. Instead, the PE and PQE indices apply additional weights in relative abundance [Table 2]. Therefore, the PD index suits the situation when the species associated with the host phenotype are rare species with high phylogenetic difference, while the PE and PQE indices suit the situation when the associated species are common species with high phylogenetic difference. Importantly, mMeta and aMeta are to make a statistical inference on the microbial α-diversity in general throughout different forms of α-diversity while robustly suiting diverse unknown association patterns.
Table 2.
Formulas for the non-phylogenetic and phylogenetic α-diversity indices.
| Non-phylogenetic indices | Phylogenetic indices | ||
|---|---|---|---|
| Richness | S | PD | |
| Shannon | PE | ||
| Simpson | PQE | ||
S is the total number of species present in a sample, wt is the relative abundance of the t-th species, and lt is the length of the branches that belong to the t-th species in the phylogenetic tree for t = 1, …, S.
Richness, Shannon, Simpson, PD, PE and PQE represent the Species richness, Shannon, Simpson, PD, PE and PQE indices, respectively.
A simple modification to robustly handle missing summary data from prior studies
The summary statistics are not usually available in a balanced way across all the studies and markers, and it has been a general challenge in multivariate meta-analysis17. That is, for example, some studies can report the results on the Species richness, PE and PQE while other studies can report the results on Shannon, PD and PE or so. Therefore, here we provide some flexibility to our methods’ implementation. For this, we simply modified our software package while setting K in Algorithm 1. Single-marker meta-analysis including the subscript j as Kj for j = 1, …, Q. This simple modification allows the number of studies to vary by markers, and makes mMeta and aMeta to be able to use all available summary data with no error in their implementation. Thus, this modification should make mMeta and aMeta much more practical in case of the imbalance in available markers from prior studies.
Simulations
Here, we describe our simulation experiments to evaluate the performance of our proposed multi-marker meta-analyses, mMeta and aMeta, in terms of type I error and power. For the methods to calculate the p-value, we surveyed the parametric method based on the asymptotic normality that N(0,1) under H023 as well as the semi-parametric group permutation method21 that we adopted for mMeta and aMeta. For the methods to estimate the heterogeneity variance, we surveyed the DerSimonian and Laird (DL) estimator (a.k.a. the method of moments estimator, and the mostly cited estimator in meta-analysis)2,23 as well as the SJ estimator17 that we adopted for mMeta and aMeta. We surveyed the six α-diversity indices, Species richness, Shannon6, Simpson7, PD11, PE12 and PQE13,14 [Table 2].
Simulation design
As in prior studies27,30, we simulated the count table across samples and species per study (denoted as Mk for k = 1, …, K) based on the Dirichlet-multinomial distribution32. For this, we employed the 100 common operational taxonomic units (OTUs) and their phylogenetic tree in the respiratory-tract microbiome data33 as surrogates for 100 microbial species. Then, we estimated their proportions and dispersion to reflect real microbial composition27. We surveyed 10, 20 and 30 studies, respectively (i.e., K=10, 20 or 30). We applied the estimated proportions and dispersion for the same 100 OTUs to each study. To reflect the heterogeneity in sample size and sequencing depth across studies, we randomly generated the sample size per study (denoted as nk) and the total read count per study based on the discrete uniform distributions from 50 to 100 samples and from 1,000 to 5,000 total reads, respectively. Then, we generated Gaussian responses for the host phenotype based on the linear regression model (Eq. 8).
| (8) |
where the subscripts, k, i, and h represent a study (k = 1, …, K), a sample (i = 1, …, nk), and a species (h = 1, …, 100), respectively, yk,i is the Gaussian responses for the host phenotype, and are two covariates generated based on the Bernoulli distribution with success probability of 1/2 and the standard normal distribution N(0, 1), respectively, is the (i, h)-th element of the simulated count table (Mk), ζ is the set of associated species, βk is the true study-specific effect, εk,i is an error generated based on N(0, 1), and scale(·) is the standardization function to have mean 0 and variance 1. To estimate type I errors, we set βk = 0 for k = 1, …, K, which satisfies the null hypothesis for both the traditional random effects meta-analysis and the Han and Eskin’s modified random effects meta-analysis. To estimate powers, we set βk = 1 for k = 1, …, K while selecting the set of associated species (ζ) (Eq. 8) as S1) ζ = {the 10 rarest species}, S2) ζ = {10 randomly selected species}, S3) ζ = {the 10 most common species} or S4) ζ = {species in a randomly selected cluster among 10 clusters partitioned by partitioning-around-medoids (PAM) algorithm}15,28,29,30. The first three scenarios reflect the situations when rare, random and common species, respectively, are truly associated with the host phenotype. The PAM algorithm groups phylogenetically close species in the phylogenetic tree together34, and thus the fourth scenario reflects the situation when phylogenetically close species are truly associated with the host phenotype.
We computed the six α-diversity indices, Species richness, Shannon6, Simpson7, PD11, PE12 and PQE13,14, based on their formulas [Table 2] and the same simulated count table and phylogenetic tree for each sample in each study, and denote them as for j {Richness, Shannon, Simpson, PD, PE, PQE}, k = 1, …, K, and i = 1, …, n. Then, to estimate study-specific effects and their standard errors for each α-diversity index, we considered the linear regression model (Eq. 9).
| (9) |
where and βj,k are the regression coefficients for the covariates, and , and the α-diversity index, , respectively, for j {Richness, Shannon, Simpson, PD, PE, PQE}. We estimated the regression coefficients and their standard errors for each α-diversity index in each study based on the least squares estimation adjusting for and , and denote them as and . Finally, we performed meta-analysis using ’s and ’s to combine multiple studies for each marker using the single-marker meta analyses and throughout all different markers using mMeta and aMeta.
Simulation results
Type I error
Table 3 reports the empirical type I error rates at the significance level of 5% for the single-marker meta-analyses for each α-diversity index and the multi-marker meta-analyses, mMeta and aMeta. Here, we find well-controlled type I error rates (≤ 5%) for all the single-marker or multi-marker meta-analyses based on the asymptotic normality or the group permutation, based on the DL estimator or the SJ estimator, with or without the assumption of heterogeneity under H0, and for any number of studies [Table 3]; as such, all the surveyed methods are statistically valid.
Table 3.
Empirical type I error rates using different meta-analysis methods (Unit: %)
| Methods | Asymptotic method (Het. under H0) | Permutation method (Het. under H0) | Permutation method (No het. under H0) | |||
|---|---|---|---|---|---|---|
| DL | SJ | DL | SJ | DL | SJ | |
| K = 10 | ||||||
| Richness | 1.49 | 0.72 | 4.91 | 4.89 | 4.94 | 4.85 |
| Shannon | 1.63 | 0.80 | 5.15 | 5.08 | 5.17 | 5.10 |
| Simpson | 1.61 | 0.86 | 4.86 | 4.89 | 4.87 | 4.86 |
| PD | 1.68 | 0.76 | 5.09 | 4.99 | 5.11 | 5.03 |
| PE | 1.64 | 0.86 | 4.93 | 4.96 | 4.97 | 5.00 |
| PQE | 1.53 | 0.74 | 4.95 | 4.95 | 4.91 | 4.87 |
| mMeta | - | - | 1.54 | 1.60 | 1.54 | 1.57 |
| aMeta | - | - | 3.83 | 3.84 | 3.87 | 3.68 |
| K = 20 | ||||||
| Richness | 1.67 | 0.80 | 4.87 | 4.95 | 4.83 | 4.93 |
| Shannon | 1.50 | 0.64 | 4.86 | 4.84 | 4.88 | 4.88 |
| Simpson | 1.60 | 0.67 | 4.97 | 4.94 | 4.96 | 4.97 |
| PD | 1.62 | 0.68 | 4.98 | 5.06 | 4.94 | 5.08 |
| PE | 1.66 | 0.76 | 4.87 | 4.85 | 4.88 | 4.89 |
| PQE | 1.74 | 0.74 | 4.98 | 4.97 | 5.02 | 4.96 |
| mMeta | - | - | 1.89 | 1.93 | 1.89 | 1.94 |
| aMeta | - | - | 3.66 | 3.71 | 3.72 | 3.77 |
| K = 30 | ||||||
| Richness | 1.52 | 0.62 | 4.85 | 4.93 | 4.85 | 4.95 |
| Shannon | 1.51 | 0.67 | 4.65 | 4.71 | 4.64 | 4.78 |
| Simpson | 1.63 | 0.74 | 4.81 | 4.82 | 4.85 | 4.86 |
| PD | 1.68 | 0.65 | 4.94 | 4.96 | 4.96 | 4.98 |
| PE | 1.59 | 0.74 | 4.93 | 4.93 | 4.96 | 5.00 |
| PQE | 1.66 | 0.70 | 4.88 | 4.97 | 4.95 | 4.94 |
| mMeta | - | - | 1.92 | 1.89 | 1.92 | 1.90 |
| aMeta | - | - | 3.38 | 3.44 | 3.41 | 3.48 |
[Asymptotic method (Het. under H0)] represents the p-value calculation method based on the asymptotic normality and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; [Permutation method (Het. under H0)] represents the group permutation method and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; [Permutation method (No het. under H0)] represents the group permutation method and for the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0.
DL and SJ represents the DerSimonian Laird (method of moments) estimator and the Sidik and Jonkman (robust variance or sandwich variance) estimator, respectively.
Richness, Shannon, Simpson, PD, PE and PQE represent the Species richness, Shannon, Simpson, PD, PE and PQE indices, respectively.
For additional reference, we can observe that the empirical type I error rates are lower than the significance level of 5% for the asymptotic method with the assumption of heterogeneity under H0 [Table 3] consequently leading to low statistical power (see Power), as expected by the conservative assumption that the heterogeneity exists even under H022. In contrast, for the single-marker meta-analysis, we can observe that the empirical type I error rates are close to the significance level of 5% for the group permutation method whether the assumption of heterogeneity under H0 exists or not [Table 3]; hence, for the group permutation method, the assumption of heterogeneity under H0 does not affect the empirical type I error rates, but only improves statistical power (see Power). In addition, for the multi-marker meta-analyses, we can observe that the empirical type I error rates are lower than the significance level of 5%. This might be because our simulation design gives ideal marker-by-marker correlations by calculating all the α-diversity indices based on their formulas using individual study data [Table 2], while our multi-marker meta-analyses estimate the marker-by-marker correlations based on summary-level statistics. Furthermore, our simulation is designed to give the validity to all individual single-marker meta-analyses [H0:μj = 0 for all j’s in {1, …, Q}], which is more conservative than the null hypothesis of mMeta [H0:μA = 0] consequently leading to low statistical power for mMeta (see Power).
Power
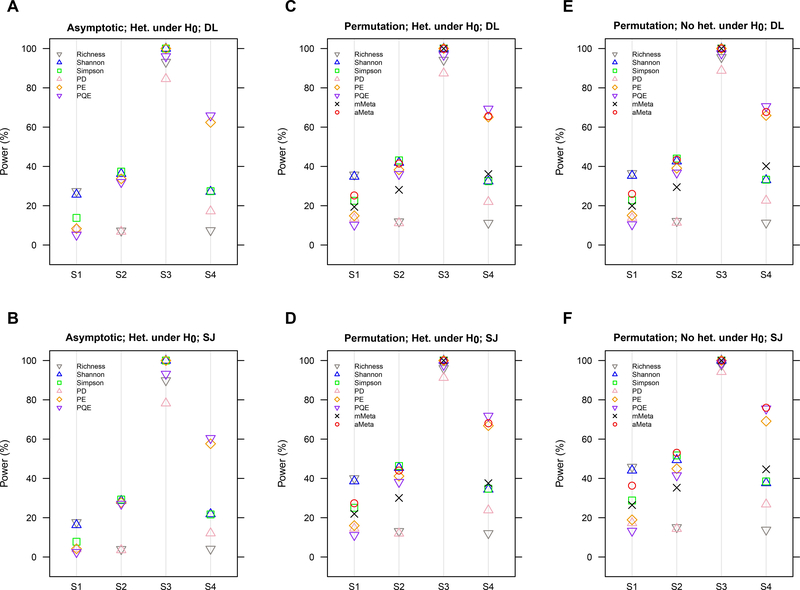
Figure 1, Figure S1 and Figure S2 report the power estimates for the single-marker meta-analyses for each α-diversity index and the multi-marker meta-analyses, mMeta and aMeta for 20 (K = 20), 10 (K=10) and 30 (K=30) studies, respectively. In general, the power increases as the number of studies increases [Figure S1 < Figure 1 < Figure S2], but the comparative powers among different methods are the same irrespective of the number of studies [Figure 1, Figure S1–S2]. Thus, to save space, we moved the power estimates for 10 (K=10) [Figure S1] and 30 (K=30) [Figure S2] studies to Appendix.
Figure 1. Power estimates using different meta-analysis methods for 20 studies (K=20) (Unit: %). A. The method based on the asymptotic normality using DL estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; B. The method based on the asymptotic normality using SJ estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; C. The group permutation method using DL estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; D. The group permutation method using SJ estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; E. The group permutation method using DL estimator and for the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0; F. The group permutation method using SJ estimator and for the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0.
* S1. ζ = {the 10 rarest species}; S2. ζ = {10 randomly selected species}; S3. ζ = {the 10 most common species}; S4. ζ = {species in a randomly selected cluster among 10 clusters partitioned by PMA algorithm}, where ζ is the set of associated species (Eq. 8). * Richness, Shannon, Simpson, PD, PE and PQE represent the Species richness, Shannon, Simpson, PD, PE and PQE indices, respectively.
To compare powers among different p-value calculation methods and heterogeneity variance estimators, the group permutation method is more powerful than the method based on the asymptotic normality [Figure 1A,B < Figure 1C,D] as expected by the results on their empirical type I error rates [Table 3], while the SJ estimator is more powerful than the DL estimator [Figure 1A,C,E < Figure 1B,D,F]; as such, the combination of the group permutation method and the SJ estimator gives the highest power. For additional reference, we found that the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0 is more powerful than the traditional random effects meta-analysis for the existence of heterogeneity under H0 [Figure 1C,D < Figure 1E,F].
To compare powers among single-marker meta-analyses, the Species richness and the Shannon index are most powerful when rare species are associated with the host phenotype [Figure 1: S1], the Shannon and Simpson indices are most powerful when random or common species are associated with the host phenotype [Figure 1: S2 & S3], and the PQE index is most powerful when phylogenetically relevant species are associated with the host phenotype [Figure 1: S4], as expected by the difference in their weighting schemes in relative abundance and the use or non-use of phylogenetic tree information [Table 2]. This indicates that the performance of single-marker meta-analyses can vary by markers and the underlying association patterns.
To evaluate powers for the multi-marker meta-analyses compared with the single-marker meta-analyses, mMeta remains at a medium power level among multiple single-marker meta-analyses, as expected by the central tendency of its weighted averaging scheme (Eq. 6) [Figure 1], while aMeta robustly approaches the highest power among multiple single-marker meta-analyses, as expected by the high adaptivity of its minimum p-value statistic (Eq. 7) [Figure 1].
In summary, mMeta is moderately powerful across all different association patterns, while aMeta is highly powerful across all different association patterns [Figure 1]. In contrast, the single-marker meta-analyses are highly sensitive to the chosen α-diversity index and the underlying association pattern [Figure 1]. Therefore, aMeta is most attractive in power especially because the true association pattern is usually unknown in practice. However, aMeta is limited to hypothesis testing, while mMeta conducts both effect estimation and hypothesis testing; hence, mMeta can be better interpreted with a breadth of statistical inference facilities including the pooled estimate and its confidence interval and p-value. All the possible results and interpretations for mMeta and aMeta are addressed in the following section with real data applications.
Real data applications
Here, we illustrate the use of our proposed multi-marker meta-analyses, mMeta and aMeta, through the meta-analysis for 15 gut microbiome studies on the disparity in microbial α-diversity by the status of HIV infection (i.e., HIV uninfected (HIV-) vs. HIV infected (HIV+) individuals)35,36,37,38,39,40,41,42,43,44,45,46,47,48,49. These 15 gut microbiome studies are also the ones surveyed in Tuddenham et al. (2019)50 for the single-marker meta-analyses on the Species richness and Shannon index, respectively. Although the meta-analysis requires only the summary statistics from prior studies, we actually could obtain all the 16S ribosomal RNA (rRNA) gene sequence data and metadata for each study from public databases or study authors.
We processed the raw 16S rRNA gene sequence data using the same procedures performed in Tuddenham et al. (2019) based on standard bioinformatics tools to construct the count table across samples and OTUs and the phylogenetic tree for each study, where we used the OTUs as surrogates for microbial species. To briefly describe the data processing procedures50, the paired-end read sequences from the Illumina platform were merged using FLASH51 and went through quality controls using Trimmomatic52 and PyNAST53, while the amplicon sequences from the Roche/454 platform went through quality controls using Acacia54. Then, the primers were trimmed and the chimeras were screened using UCLUST55, the human genome contaminants were filtered using Bowtie256, and the chloroplast and mitochondrial contaminants were filtered using the RDP classifier57. Then, the OTU table and the phylogenetic tree for each study were constructed using Resphera Insight and PyNAST53. We rarefied the OTU table for each study to an even level of total reads per sample, meant to control for differing total reads per sample, while minimizing sample loss due to insufficient total reads [Table S1].
While using the same reprocessing pipeline for all the studies can lead to a smaller between-study variance and thus a larger pooled effect (Eq. 4) than using different reprocessing procedures, we can still find that the studies are heterogeneous in many other characteristics, such as country, study design, sample size, sample type, targeted variable region, sequencing platform, and sequencing depth [Table S1]. Thus, to account for the possible heterogeneity across studies, the random effects meta-analysis could be better suited than the fixed effects meta-analysis. We surveyed two different random effects meta-analysis approaches, 1) the traditional random effects meta-analysis for the heterogeneity under H0 and 2) the Han and Eskin’s modified random effects meta-analysis for no heterogeneity under H0, respectively.
The α-diversity indices to be included in the meta-analysis depends on the availability of the summary statistics from prior studies. Yet, for a demonstration purpose, which is possible as we have all the individual study data, we computed all the six α-diversity indices, Species richness, Shannon6, Simpson7, PD11, PE12 and PQE13,14 for each sample in each study. Then, we fitted the simple logistic regression model to evaluate the disparity in each α-diversity index for each study by the status of HIV infection (i.e., HIV uninfected (HIV-) individuals coded as 0 vs. HIV infected (HIV+) individuals coded as 1), and obtained the summary statistics, regression coefficient estimate and its standard error, for each study on each α-diversity index.
Figure 2 reports the results for each study on each α-diversity index and the results for the single-marker meta-analyses based on the SJ estimator20 and the group permutation method21 to combine all the studies on each α-diversity index. Here, we can first see that for a given α-diversity index, the results are not consistent across studies [Figure 2]. For example, for the Species richness, Dubourg et al. (2016), Noguera-Julian et al. (2016), Pinto-Cardoso et al. (2017), Serrano-Villar et al. (2017a), Vesterbacka et al. (2017) and Villanueva-Millán et al. (2017) are statistically significant at the significance level of 5%, while the other studies are not statistically significant [Figure 2A]. For the Species richness again, Lozupone et al. (2013) estimate a positive association (i.e., HIV infected (HIV+) individuals have a higher microbial α-diversity than HIV uninfected (HIV-) individuals), while the other studies estimate negative associations [Figure 2A]. Therefore, we need the single-marker meta-analyses for an overall conclusion on each α-diversity index. However, here we can find that the results for the single-marker meta-analyses are not also consistent across α-diversity indices [Figure 2]. For example, the PQE index is not statistically significant, while the other α-diversity indices are statistically significant [Figure 2]. For additional reference, we found that the Han and Eskin’s modified random effects meta-analyses for the assumption of no heterogeneity under H0 produces smaller p-values than the traditional random effects meta-analyses for the existence of heterogeneity under H0 [Figure 2], which also confirms our simulation results [Figure 1C,D < Figure 1E,F].
Figure 2. The forest plot: the results for each study on each α-diversity index, and the results for the single-marker meta-analyses based on the combination of the SJ estimator and the group permutation method to combine all the studies on each α-diversity index. A. Species richness; B. Shannon index; C. Simpson index; D. PD index; E. PE index; F. PQE index.
* Overall(Het. under H0) represents the traditional random effects meta-analysis for the existence of heterogeneity under H0, and Overall(No het. under H0) represents the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0.
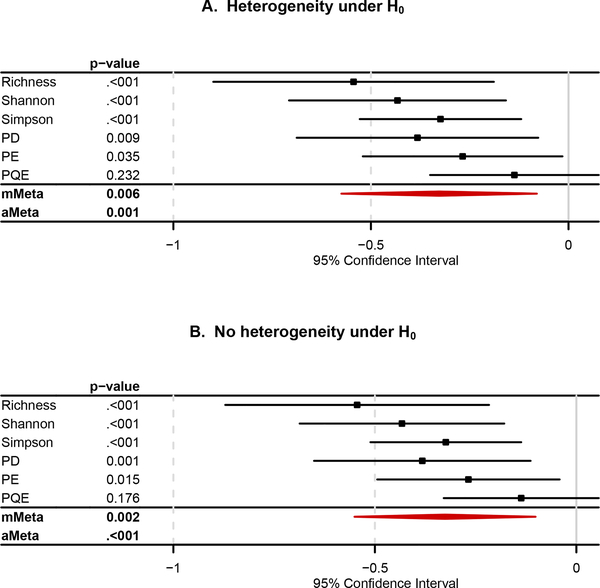
Figure 3 reports the results for the multi-marker meta-analyses, mMeta and aMeta, together with the single-marker meta-analyses that are also reported in [Figure 2]. Again, the results for the single-marker meta-analyses are not consistent across α-diversity indices, and thus, we cannot be sure about the association between microbial α-diversity and the status of HIV infection [Figure 3]. Therefore, we need the multi-marker meta-analyses, mMeta and aMeta, for an overall conclusion across all the studies and α-diversity indices. We interpret the results for mMeta and aMeta [Figure 3] as follows: 1) Based on mMeta, we found a statistically significant association between microbial α-diversity and the status of HIV infection, and estimated that HIV infected (HIV+) individuals have a lower microbial α-diversity than HIV uninfected (HIV-) individuals [Figure 3]; 2) Based on aMeta, we found a statistically significant association between microbial α-diversity and the status of HIV infection [Figure 3].
Figure 3.
The results for the single-marker meta-analyses and the multi-marker meta-analyses, mMeta and aMeta, based on the combination of the SJ estimator and the group permutation method. A. The traditional random effects meta-analysis for the existence of heterogeneity under H0. B. The Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0.
Here, we can find that mMeta is better interpreted in effect direction with the additional facility of the pooled estimate, yet aMeta produces a smaller p-value than mMeta, which also confirms our simulation results that aMeta is more powerful than mMeta [Figure 1C,D,E,F]. Again, we found that the Han and Eskin’s modified random effects meta-analyses for the assumption of no heterogeneity under H0 [Figure 3B] produces smaller p-values than the traditional random effects meta-analyses for the existence of heterogeneity under H0 [Figure 3A].
For additional reference, we reported all the p-values for the single-marker and multi-marker meta-analyses based on different p-value calculation methods and heterogeneity variance estimators, and the traditional random effects meta-analysis for the existence of heterogeneity under H0 and the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0 in [Table S2]. Here, we found that the real data applications [Table S2] confirm the simulation results [Figure 1], while matching the methods with smaller (or larger) p-values in the real data applications [Table S2] to the same methods with lower (or higher) power estimates in the simulation results [Figure 1].
Discussion
In this paper, we introduced two multi-marker meta-analyses, mMeta and aMeta, to combine multiple studies throughout multiple related markers. We illustrated in our simulations that mMeta is moderately powerful across all different association patterns, while aMeta is highly powerful across all different association patterns. In the same context, we also found in our real data applications that aMeta produces smaller p-values than mMeta. Therefore, aMeta is more attractive than mMeta for powerful discoveries. However, mMeta is a statistical estimator that conducts both effect estimation and hypothesis testing in a unified approach based on a weighted average of marker-specific pooled estimates, while aMeta is purely a test for significance. Therefore, mMeta is better interpreted with a breadth of statistical inference tools including the pooled estimate and its confidence interval and p-value.
Since aMeta is more powerful than mMeta, it is possible that aMeta produces a significant p-value while mMeta does not. While such results are seemingly conflicting, they are distinguished in interpretation as follows: at least one marker-specific pooled effect has statistical significance by aMeta for the hypothesis testing of [H0:μj = 0 for all j’s in {1, …, Q} vs. H1:μj ≠ 0 for some j’s in {1, …, Q}], while the pooled effect across all the studies and markers has no statistical significance by mMeta for the hypothesis testing of [H0:μA = 0 vs. H1:μA ≠ 0]. Furthermore, such results can provide a critical insight that only a few markers among many markers might have significant signals and/or the marker-specific pooled effects might be inconsistent in direction. The reason is because aMeta takes only the strongest evidence of significance into its minimum p-value statistic, while mMeta combines all the directions and sizes of marker-specific pooled effects into its weighted averaging scheme; as such, the sparsity in significance and the directionality of underlying markers substantially matter for mMeta, while they do not matter for aMeta.
We also surveyed different p-value calculation methods and heterogeneity variance estimators. We found in our simulations and real data applications that the group permutation method and the SJ estimator, geared up to mMeta and aMeta, give higher powers and smaller p-values than the method based on the asymptotic normality and the DL estimator, respectively. In light of Han and Eskin (2011), we described that the existence of heterogeneity even under H0 for the traditional random effects meta-analysis can be overly conservative. We also found in our simulations and real data applications that the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0 give higher powers and smaller p-values than the traditional random effects meta-analysis for the existence of heterogeneity under H0. Therefore, we adopted the Han and Eskin’s modification for mMeta and aMeta, while providing a user option in our software package for the traditional random effects meta-analysis.
Throughout the paper, we illustrated the use of mMeta and aMeta to combine multiple microbiome studies with the results on multiple α-diversity indices. However, the application of mMeta and aMeta is not restricted to the microbiome studies or the α-diversity indices. mMeta and aMeta are the multi-marker meta-analyses in general to combine multiple studies with the results on multiple related markers. Thus, mMeta and aMeta can be employed as long as we have the summary statistics, effect estimates and their standard errors, across multiple studies and multiple related markers. For example, we can imagine that there are multiple studies on the effect of an environmental exposure (or drug use) on liver function, and they report the results for multiple serum markers on liver function (e.g., alanine transaminase, aspartate transaminase, alkaline phosphatase, gamma-glutamyl transferase). It is also reasonable to suppose that the studies are heterogeneous, the multiple serum markers are correlated because of their biological relatedness, and the results are not always balanced across all the studies and markers. Then, in this example, mMeta and aMeta can be used to make a conclusion on the effect of an environmental exposure (or drug use) on the ‘liver function’ in a global, while accounting for study characteristics and utilizing all available information. We encourage further studies on the possible extensions and applications of mMeta and aMeta.
We described that selecting candidate markers for mMeta and aMeta depends on the availability of the summary statistics from prior studies, scientific justifications and/or investigators’ interest. We also surveyed the six α-diversity indices, Species richness, Shannon, Simpson, PD, PE and PQE in our simulations and real data applications. The reason is because they have a common goal of measuring microbial diversity in a community but are also distinguished by different weighting schemes based on microbial abundance and/or phylogenetic tree information; as a result, we could demonstrate varying performances by markers as well as the overall conclusion across markers using mMeta and aMeta. However, the six α-diversity indices are not always available from prior studies while other indices can be available from prior studies. Furthermore, researchers may have different interests and thoughts on selecting candidate markers for mMeta and aMeta. Therefore, it is debatable which selection rules are most reasonable. In spite that there are no set criteria for selecting candidate markers, we suggest delineating the selection rules you use so that future readers can evaluate if the selection rules are reasonable. To us, it is not reasonable to deliberately select only the markers that have strong association signals just to avoid some dilution from weak association signals and make a strong overall conclusion using mMeta or aMeta. Such an ex post facto selection overstates the results that are prone to multiple potential testing issues and thus hardly reproducible58. To us, it is more reasonable to select all the markers that are available from prior studies only with some inevitable exclusions, for example, due to some practical limitations.
We would also like to notice that, in practice, many studies report different forms of effect estimates or degrees of significance. For example, most of the 15 microbiome studies in our real data applications reported stratified effect estimates (e.g., mean, median, and interquartile range for each case or control group), not the estimates on difference or association, and p-values. Moreover, many of the 15 microbiome studies reported only the graphs (e.g., box plots, bar/line charts with error bars) with no numbers. While mMeta and aMeta require only the effect estimates and their standard errors for implementation, they are still hard to obtain in practice. Although such limitations are not unique to mMeta and aMeta (i.e., many other meta-analysis methods have such limitations), it is necessary to develop a more flexible and practical meta-analysis method that can deal with many different types of summary data, yet we did not fully achieve such a goal in this paper.
Besides, while p-values are useful tools in hypothesis testing, we suggest investigators to report confidence intervals as they are better informed by revealing the range of parameter values that are likely to exist. We also suggest reporting the effect estimates and their standard errors as well as the confidence intervals in numbers to better facilitate future meta-analysis. Moreover, developing a database for summary data plays a crucial role in meta-analysis as well. Thus, we included the effect estimates and standard errors for the six α-diversity indices, Species richness, Shannon, Simpson, PD, PE and PQE, from the15 microbiome studies in our R packages, mMeta.
Supplementary Material
Figure S1. Power estimates using different meta-analysis methods for 10 studies (K=10) (Unit: %). A. The method based on the asymptotic normality using DL estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; B. The method based on the asymptotic normality using SJ estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under h; C. The group permutation method using DL estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; D. The group permutation method using SJ estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; E. The group permutation method using DL estimator and for the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0; F. The group permutation method using SJ estimator and for the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0. * S1. ζ = {the 10 rarest species}; S2. ζ = {10 randomly selected species}; S3. ζ = {the 10 most common species}; S4. ζ = {species in a randomly selected cluster among 10 clusters partitioned by PMA algorithm}, where ζ is the set of associated species (Eq. 8). * Richness, Shannon, Simpson, PD, PE and PQE represent the Species richness, Shannon, Simpson, PD, PE and PQE indices, respectively.
Figure S2. Power estimates using different meta-analysis methods for K=30 (Unit: %). A. The method based on the asymptotic normality using DL estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; B. The method based on the asymptotic normality using SJ estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; C. The group permutation method using DL estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; D. The group permutation method using SJ estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; E. The group permutation method using DL estimator and for the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0; F. The group permutation method using SJ estimator and for the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0. * S1. ζ = {the 10 rarest species}; S2. ζ = {10 randomly selected species}; S3. ζ = {the 10 most common species}; S4. ζ = {species in a randomly selected cluster among 10 clusters partitioned by PMA algorithm}, where ζ is the set of associated species (Eq. 8). * Richness, Shannon, Simpson, PD, PE and PQE represent the Species richness, Shannon, Simpson, PD, PE and PQE indices, respectively.
Acknowledgements
This study was supported in part by NIH grants, U24OD023382 (Environmental Influences of Child Health Outcomes (ECHO) Data Analysis Center) and 1P30AI094189 (Johns Hopkins University Center for AIDS Research). The data used in this study are from work that was supported by the HIV Microbiome Re-analysis Consortium. The contents of the paper are solely the responsibility of the authors and do not necessarily represent the official views of NIH.
Footnotes
Conflict of Interest
The authors declare no conflict of interest.
Data Availability Statement
The summary data (i.e., effect estimates and standard errors) for the six α-diversity indices, Species richness, Shannon, Simpson, PD, PE and PQE, from the15 microbiome studies we used in our real data application can be found in our R packages, mMeta, at https://github.com/hk1785/mMeta.
References
- 1.Glass GV. Primary, secondary, and meta-analysis of research. Educ Res. 1976:(5)10:3–8. [Google Scholar]
- 2.DerSimonian R, Laird NM. Meta-analysis in clinical trials revisited. Control Clin Trials. 2015:45:139–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Eichler EE, Flint J, Gibson G, Kong A, Leal SM, Moore JH, Nadeau JH. Missing heritability and strategies for finding the underlying causes of complex disease. Nat Rev Genet. 2010:11:446–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lee S, Teslovich TM, Boehnke M, Lin X. General framework for meta-analysis of rare variants in sequencing association studies. Am J Hum Genet. 2013:93:42–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Liu DJ, Peloso GM, Zhan X, Holmen OL, Zawistowski M, Feng S, Nikpay M, Auer PL, Goel A, Zhang H, et al. Meta-analysis of gene-level tests for rare variant association. Nat Genet 2014:46:200–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shannon CE. A mathematical theory of communication. Bell Syst Tech J. 1948:27:379–423 & 623–656. [Google Scholar]
- 7.Simpson EH. Measurement of diversity. Nature 1949:163:688. [Google Scholar]
- 8.Hill MO. Diversity and evenness: a unifying notation and its consequences. Ecology 1973:54:427–432. [Google Scholar]
- 9.Chao A Non-parametric estimation of the number of classes in a population. Scand J Stat. 1984:11:265–270. [Google Scholar]
- 10.Chao A, Lee S. Estimating the number of classes via sample coverage. J Am Stat Assoc. 1992:87:210–217. [Google Scholar]
- 11.Faith DP. Conservation evaluation and phylogenetic diversity. Biol Conserv. 1992:61:1–10. [Google Scholar]
- 12.Allen B, Kon M, Bar-Yam Y. A new phylogenetic diversity measure generalizing the Shannon index and its application to phyllostomid bats. Am Nat. 2009:174(2):236–243. [DOI] [PubMed] [Google Scholar]
- 13.Rao CR. Diversity and dissimilarity coefficients: a unified approach. Theor Popul Biol. 1982:21(1):24–43. [Google Scholar]
- 14.Warwick RM, Clarke KR. New ‘biodiversity’ measures reveal a decrease in taxonomic distinctness with increasing stress. Mar Ecol Prog Ser. 1995:129(1):301–305. [Google Scholar]
- 15.Koh H An adaptive microbiome α-diversity-based association analysis method. Sci Rep. 2018;8(18026). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ishak K, Platt R, Joseph L, Hanley J. Impact of approximating or ignoring within-study covariances in multivariate meta-analyses. Stat Med. 2008;27(5):670–686. [DOI] [PubMed] [Google Scholar]
- 17.Jackson D, Riley R, White IR. Multivariate meta-analysis: potential and promise. Stat Med. 2011;30(20):2481–2498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lunn DJ, Thomas A, Best N, Spiegelhalter D. WinBUGS - a Bayesian modeling framework: concepts, structure, and extensibility. Stat Comput. 2000;10(4):325–337. [Google Scholar]
- 19.Tippett LHC. The methods of statistics. London: Williams and Norgate; 1931. [Google Scholar]
- 20.Sidik K, Jonkman JN. A note on variance estimation in random effects meta-regression. J Biophrm Stat. 2005:15(5):823–838. [DOI] [PubMed] [Google Scholar]
- 21.Follmann DA, Proschan MA. Valid inference in random effects meta-analysis. Biometrics. 1999:55:732–737. [DOI] [PubMed] [Google Scholar]
- 22.Han B, Eskin E. Random-effects model aimed at discovering associations in meta-analysis of genome-wide association studies. Am J Hum Genet. 2011:88(5):586–598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.DerSimonian R, Laird NM. Meta-analysis in clinical trials. Control Clin Trials. 1986:7(3):177–188. [DOI] [PubMed] [Google Scholar]
- 24.IntHout J, Ioannidis JPA, Borm G. The Hartung-Knapp-Sidik-Jonkman method for random effects meta-analysis is straightforward and considerably outperforms the standard DerSimonian-Laird method. BMC Med Res Methodol. 2014:14(25). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Veroniki AA, Jackson D, Viechtbauer W, Bender R, Bowden J, Knapp G, Kuss O, Higgins JPT, Langan D, Salanti G. Methods to estimate the between-study variance and its uncertainty in meta-analysis. Res Syn Meth. 2016:7:55–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dwass M Modified randomization tests for nonparametric hypotheses. Ann Math Statist. 1957:28(1):181–187. [Google Scholar]
- 27.Zhao N, Chen J, Carroll IM, Ringel-Kulka T, Epstein MP, Zhou H, Zhou JJ, Ringel Y, Li H, Wu MC. Testing in microbiome-profiling studies with MiRKAT, the microbiome regression-based kernel association test. Am J Hum Genet. 2015;96(5):797–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Koh H, Blaser MJ, Li H. A powerful microbiome-based association test and a microbial taxa discovery framework for comprehensive association mapping. Microbiome. 2017;5(45). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Koh H, Livanos AE, Blaser MJ, Li H. A highly adaptive microbiome-based association test for survival traits. BMC Genom. 2018;19(210). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Koh H, Li Y, Zhan X, Chen J, Zhao N. A distance-based kernel association test based on the generalized linear mixed model for correlated microbiome studies. Front Genet. 2019;458(10). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.McCoy CO, Matsen FA IV. Abundance-weighted phylogenetic diversity measures distinguish microbial community states and are robust to sampling depth. PeerJ 2013:1(e157). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mosimann JE. On the compound multinomial distribution, the multivariate β-distribution, and correlations among proportions. Biometrika. 1962;49(1/2):65–82. [Google Scholar]
- 33.Charlson ES, Chen J, Custers-Allen R, Bittinger K, Li H, Sinha R, Hwang J, Bushman FD, Collman RG. Disordered microbial communities in the upper respiratory tract of cigarette smokers. PLoS One. 2010;5(12). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Reynolds AP, Richards G, de la Iglesia B, Rayward-Smith VJ. Clustering rules: A comparison of partitioning and hierarchical clustering algorithms. J Math Model Algorithms. 2006;5(4):474–504. [Google Scholar]
- 35.Dillon SM, Lee EJ, Kotter CV, Austin GL, Dong Z, Hecht DK, Gianella S, Siewe B, Smith DM, Landay AL, Robertson CE, Frank DN, Wilson CC. An altered intestinal mucosal microbiome in HIV-1 infection is associated with mucosal and systemic immune activation and endotoxemia. Mucosal Immunol. 2014:7:983–994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dinh DM, Volpe GE, Duffalo C, Bhalchandra S, Tai AK, Kane AV, Wanke CA, Ward HD. Intestinal microbiota, microbial translocation, and systemic inflammation in chronic HIV infection. J Infect Dis. 2015:211(1):19–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dubourg G, Lagier JC, Hüe S, Surenaud M, Bachar D, Robert C, Michelle C, Ravaux I, Mokhtari S, Million M, Stein A, Brougui P, Levy Y, Raoult D. Gut microbiota associated with HIV infection is significantly enriched in bacteria tolerant to oxygen. BMJ Open Gastroenterol. 2016:3(1):e000080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lozupone CA, Li M, Campbell TB, Flores SC, Linderman D, Gebert MJ, Knight R, Fontenot AP, Palmer BE. Alterations in the gut microbiota associated with HIV-1 infection. Cell Host Microbe. 2013:14(3):329–339 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Monaco CL, Gootenberg DB, Zhao G, Handley SA, Ghebremichael MS, Lim ES, Lankowski A, Baldridge MT, Wilen CB, Flagg M, Norman JM, Keller BC, Luévano JM, Wang D, Boum Y, Martin JN, Hunt PW, Bangsberg DR, Siedner MJ, Kwon DS, Virgin HW. Altered virome and bacterial microbiome in human immunodeficiency virus-associated acquired immunodeficiency syndrome. Cell Host Microbe. 2016:19(3):311–322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mutlu EA, Keshavarzian A, Losurdo J, Swanson G, Siewe B, Forsyth C, French A, DeMarais P, Sun Y, Koenig L, Cox S, Engen P, Chakradeo P, Abbasi R, Gorenz A, Burns C,Landay A. A compositional look at the human gastrointestinal microbiome and immune activation parameters in HIV infected subjects. PLoS Pathog. 2014:10(2):e1003829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Noguera-Julian M, Rocafort M, Guillén Y, Rivera J, Casadellà M, Nowak P, Hidebrand F, Zeller G, Parera M, Bellido R, Rodríguez C, Carrillo J, Mothe B, Coll J, Bravo I, Estany C, Herrero C, Saz J, Sirera G, Torrela A, Navarro J, Crespo M, Brander C, Negredo E, Blanco J, Guarner F, Calle ML, Bork P, Sönnerborg A, Clotet B, Paredes R. Gut microbiota linked to sexual preference and HIV infection. EBioMedicine. 2016:5:135–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Nowak P, Troseid M, Avershina E, Barqasho B, Neogi U, Holm K, Hov JR, Noyan K, Vesterbacka J, Svärd J, Rudi K, Sönnerborg A. Gut microbiota diversity predicts immune status in HIV-1 infection. AIDS. 2015:29(18):2409–2418. [DOI] [PubMed] [Google Scholar]
- 43.Nowak RG, Bentzen SM, Ravel J, Crowell TA, Dauda W, Ma B, Liu H, Blattner WA, Baral SD, Charurat ME, TRUSTRV368 Study Group. Rectal microbiota among HIV-uninfected, untreated HIV, and treated HIV-infected in Nigeria. AIDS. 2017:31(6):857–862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pinto-Cardoso S, Lozupone C, Briceño O, Alva-Hernández S, Téllez N, Adriana A, Murakami-Ogasawara A, Reyes-Terán G. Fecal bacterial communities in treated HIV infected individuals on two antiretroviral regimens. Sci Rep. 2017:7:(43741). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Serrano-Villar S, Vázquez-Castellanos JF, Vallejo A, Latorre A, Sainz T, Ferrando-Martinez S, Rojo D, Martinez-Botas J, Del Romero J, Madrid N, Leal M, Mosele JI, Motilva MJ, Barbas C, Ferrer M, Moya A, Moreno S, Gosalbes MJ, Estrada V. The effects of prebiotics on microbial dysbiosis, butyrate production and immunity in HIV-infected subjects. Mucosal Immunol. 2017a:10(5):1279–93. [DOI] [PubMed] [Google Scholar]
- 46.Serrano-Villar S, Vásquez-Domínguez E, Pérez-Molina JA, Sainz T, de Benito A, Latorre A, Moya A, Gosalbes MJ, Moreno S. HIV, HPV, and microbiota: partners in crime? AIDS. 2017b:31(4):591–594. [DOI] [PubMed] [Google Scholar]
- 47.Vesterbacka J, Rivera J, Noyan K, Parera M, Neogi U, Calle M, Paredes R, Sönnerborg A, Noguera-Julian M, Nowak P. Richer gut microbiota with distinct metabolic profile in HIV infected elite controllers. Sci Rep. 2017:7(1):6269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Villanueva-Millán MJ, Pérez-Matute P, Recio-Fernández E, Rosales JML, Oteo JA. Differential effects of antiretrovirals on microbial translocation and gut microbiota composition of HIV-infected patients. J Int AIDS Soc. 2017:20(1):21526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Yu G, Fadrosh D, Ma B, Ravel J, Goedert JJ. Anal microbiota profiles in HIV-positive and HIV-negative MSM. AIDS. 2014:28:753–760. [DOI] [PubMed] [Google Scholar]
- 50.Tuddenham SA. Koay WLA, Zhao N, White JR, Ghanem KG, Sears CL, HIV Microbiome Re-analysis Consortium. The impact of human immunodeficiency virus infection on gut microbiota α-diversity: an individual-level meta-analysis. Clin Infect Dis. 2020:70(4):615–627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Magoč T, Salzberg SL. FLASH: fast length adjustment of short reads to improve genome assemblies. Bioinformatics. 2011:27(21):2957–2963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bolger AM, Lohse M, Usadel B. Trimmomatic: a flexible trimmer for Illumina sequence data. Bioinformatics. 2014:30(15):2114–2120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Caporaso JG, Bittinger K, Bushman FD, DeSantis TZ, Andersen GL, Knight R. PyNAST: a flexible tool for aligning sequences to a template alignment. Bioinformatics. 2010:26(2):266–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Bragg L, Stone G, Imelfort M, Hugenholtz P, Tyson GW. Fast, accurate error-correction of amplicon pyrosequences using Acacia. Nat Methods. 2012:9:425–426. [DOI] [PubMed] [Google Scholar]
- 55.Edgar RC, Haas BJ, Clemente JC, Quince C, Knight R. UCHIME improves sensitivity and speed of chimera detection. Bioinformatics 2011:27(16):2194–2200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Langmead B, Salzberg SL. Fast gapped-read alignment with Bowtie 2. Nat Methods. 2012:9:357–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Wang Q, Garrity GM, Tiedje JM, Cole JR. Naive Bayesian classifier for rapid assignment of rRNA sequences into the new bacterial taxonomy. Appl Environ Microbiol. 2007:73(16):5261–5267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Gelman A, Loken E. The statistical crisis in science. Am Sci. 2014;102:460–465. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Power estimates using different meta-analysis methods for 10 studies (K=10) (Unit: %). A. The method based on the asymptotic normality using DL estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; B. The method based on the asymptotic normality using SJ estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under h; C. The group permutation method using DL estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; D. The group permutation method using SJ estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; E. The group permutation method using DL estimator and for the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0; F. The group permutation method using SJ estimator and for the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0. * S1. ζ = {the 10 rarest species}; S2. ζ = {10 randomly selected species}; S3. ζ = {the 10 most common species}; S4. ζ = {species in a randomly selected cluster among 10 clusters partitioned by PMA algorithm}, where ζ is the set of associated species (Eq. 8). * Richness, Shannon, Simpson, PD, PE and PQE represent the Species richness, Shannon, Simpson, PD, PE and PQE indices, respectively.
Figure S2. Power estimates using different meta-analysis methods for K=30 (Unit: %). A. The method based on the asymptotic normality using DL estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; B. The method based on the asymptotic normality using SJ estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; C. The group permutation method using DL estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; D. The group permutation method using SJ estimator and for the traditional random effects meta-analysis for the existence of heterogeneity under H0; E. The group permutation method using DL estimator and for the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0; F. The group permutation method using SJ estimator and for the Han and Eskin’s modified random effects meta-analysis for the assumption of no heterogeneity under H0. * S1. ζ = {the 10 rarest species}; S2. ζ = {10 randomly selected species}; S3. ζ = {the 10 most common species}; S4. ζ = {species in a randomly selected cluster among 10 clusters partitioned by PMA algorithm}, where ζ is the set of associated species (Eq. 8). * Richness, Shannon, Simpson, PD, PE and PQE represent the Species richness, Shannon, Simpson, PD, PE and PQE indices, respectively.
Data Availability Statement
The summary data (i.e., effect estimates and standard errors) for the six α-diversity indices, Species richness, Shannon, Simpson, PD, PE and PQE, from the15 microbiome studies we used in our real data application can be found in our R packages, mMeta, at https://github.com/hk1785/mMeta.