Abstract
Objective:
This study classifies sleep stages from a single lead electrocardiogram (ECG) using beat detection, cardiorespiratory coupling in the time-frequency domain and a deep convolutional neural network (CNN).
Approach:
An ECG-derived respiration (EDR) signal and synchronous beat-to-beat heart rate variability (HRV) time series were derived from the ECG using previously described robust algorithms. A measure of cardiorespiratory coupling (CRC) was extracted by calculating the coherence and cross-spectrogram of the EDR and HRV signal in five-minute windows. A CNN was then trained to classify the sleep stages (wake, rapid-eye-movement (REM) sleep, non-REM (NREM) light sleep and NREM deep sleep) from the corresponding CRC spectrograms. A support vector machine was then used to combine the output of CNN with the other features derived from the ECG, including phase-rectified signal averaging (PRSA), sample entropy, as well as standard spectral and temporal HRV measures. The MIT-BIH Polysomnographic Database (SLPDB), the PhysioNet/Computing in Cardiology Challenge 2018 database (CinC2018) and the Sleep Heart Health Study (SHHS) database, all expert-annotated for sleep stages, were used to train and validate the algorithm.
Main results:
Ten-fold cross validation results showed that the proposed algorithm achieved an accuracy (Acc) of 75.4% and a Cohen’s kappa coefficient of κ = 0.54 on the out of sample validation data in the classification of Wake, REM, NREM light and deep sleep in SLPDB. This rose to Acc = 81.6% and κ = 0.63 for the classification of Wake, REM sleep and NREM sleep and Acc = 85.1% and κ = 0.68 for the classification of NREM sleep versus REM/wakefulness in SLPDB.
Significance:
The proposed ECG-based sleep stage classification approach that represents the highest reported results on non-electroencephalographic data and uses datasets over 10 times larger than those in previous studies. By using a state-of-the-art QRS detector and deep learning model, the system does not require human annotation and can therefore be scaled for mass analysis.
1. Introduction
The earliest detailed description of the various stages of sleep, based on the electroencephalogram (EEG), was provided by Loomis et al. (1936, 1937) in the mid-1930s. In the early 1950s Aserinsky and Kleitman (1953) identified rapid-eye-movement (REM) sleep, which is related to dreaming. Sleep has been traditionally divided into two broad types: non-REM (NREM) and REM sleep. The sleep staging criteria were standardized in 1968 by Rechtschaffen and Kales (1968) (the ‘R&K rules’), based mostly on EEG changes, and dividing 30 s epochs of NREM sleep into a four further stages (stage I, stage II, stage III, stage IV). In 2004, the American Academy of Sleep Medicine (AASM) standards commissioned the AASM Visual Scoring Task Force to review the R&K scoring system and to combine stages III and IV into stage N3 (Iber et al. (2007)).
Currently, the gold standard in terms of sleep disorder diagnosis is a sleep study, or an overnight polysomnogram (PSG) which includes multiple EEG electrodes, as well as electromyograms, electrooculargrams, pulse oximetry (usually on the finger tip), respiratory bands across the upper chest and lower abdomen, as well as actigraphy, audio and video at times. PSG studies are therefore cumbersome, intrusive and expensive. This combination of physical and psychological discomfort tends to inhibit a restful night’s sleep and leads to poor compliance beyond a single night of evaluation. Even relatively simple home study equipment can lead to a significant disturbance and inconvenience (Roebuck et al. (2014)). Moreover, it is well known that a single night’s sleep, or even several nights of sleep, may not be sufficient to asses the quality of sleep of a subject (Wohlgemuth et al. (1999); Herbst et al. (2010)). In response to these issues, actigraphic devices have often been used, although actigraphy has been shown to be a poor estimator of sleep onset latency and it has not been validated for measuring sleep stages (Martin and Hakim (2011)). Actigraphy is also prone to overestimating sleep in certain patient groups, and although it has been shown to be accurate in measuring total sleep time among healthy subjects (with a sensitivity above 90%, the ability to detect sleep is substantially reduced in patients with disturbed sleep (those who have frequent arousals and reduced total sleep time). Finally, we note that wrist worn devices do not capture torso movements (such as sleep) and provide poor measurements of physiology compared to devices attached to the torso.
The enormity of data that can be captured during sleep leads to another issue, that human scoring of the data is time consuming and also expensive. High inter-rater variabilities also confound the problem of manual scoring. (The overall agreement as measured by Cohen’s Kappa (κ) coefficient ranges from 0.6 to 0.9 depending on the sleep scoring guidelines and population being (Crowell et al. (1997, 2002); Stepnowsky et al. (2004); Ferri et al. (2005); Rosa et al. (2006); Saito et al. (2006).) An automated approach to assessing sleep from multiple nights of data is therefore important. In Roebuck et al. (2014) we provide an extensive review of most of the approaches to automated sleep analysis and their practical applications. The work presented here is focused on a high compliance, unobtrusive approach to monitoring physiological correlates of sleep, namely the electrocardiogram (ECG). Modern electrocardiographic patches can provide accurate physiological information pertinent to sleep and facilitate high compliance. Notably, both respiration and heart rate variability, which changes with sleep stages and sleep related health problems (such as sleep apnea), can be captured by such devices.
We are not the first to suggest the ECG is a potential vehicle for revealing approximate sleep structure. (We do not claim it provides a true resolution of 30 second epochs of sleep, as is tradition in sleep scoring, as noted later on.) Thomas et al. (2005) developed an automated measure of cardiopulmonary coupling (CPC) during sleep using the power in specific bands of the single-lead electrocardiographic signal. The CPC, or as it is sometimes called, cardiorespiratory coupling (CRC), was measured using the power in specific bands of the cross-spectral density between the ECG-derived respiration signal (EDR) and the respiratory sinus arrhythmia signal (RSA) derived from ECG. The energy in specific bands was then thresholded (in an unspecified way) to produce an output of wakefulness/REM sleep (WR), unstable/CAP sleep, or stable/NCAP sleep. The authors reported a value of κ = 0.627 on a training set and κ = 0.439 on a test set, where the training and test sets included 35 polysomnograms each, selected from a total of 900 polysomnograms acquired at Beth Israel Deaconess Medical Center during December 2003 to July 2005. No cross validation or bootstrapping of the 900 patients was performed.
Long et al. (2014) described a dissimilarity measure which was computed between two respiratory effort signal segments with the same number of consecutive breaths. Using a set of 48 healthy subjects, a linear discriminant classifier and a ten-fold cross validation they reported an out-of-sample value of κ = 0.48 for three-stage classification (Wake, REM sleep and NREM sleep) and of κ = 0.41 for 4-stage classification (Wake, REM sleep, light sleep and deep sleep). Their method therefore exhibited a moderate ability to distinguish between sleep stages, with the exception of substantial confusion between REM sleep and wakefulness.
Fonseca et al. (2015) proposed a sleep stage classification algorithm based on heart rate variability (HRV) calculated from ECG and respiratory effort from respiratory inductance plethysmography (RIP). A total of 142 features were extracted from cardiac and respiratory activity, and from cardiorespiratory interaction (CRI) using a sliding window (of undefined length) centered on each 30 s epoch. A multi-class Bayesian linear discriminant with time-varying prior probabilities was used for classification. The authors reported an out of sample performance using ten-fold cross validation of κ = 0.49 and an accuracy (Acc) of 69% in the four-class classification of Wake, REM, light and deep sleep and κ = 0.56 and Acc = 80% in the three class problem of differentiating, Wake, REM sleep and NREM sleep.
In 2017, Fonseca et al. (2017) subsequently reported a new sleep stage classifier based on a conditional random field model. From ECG and RIP signals, 33 respiratory features, 81 cardiac features and 3 CRI features were extracted. A total of 342 recordings from 180 subjects were used for training and validation using ten-fold cross validation. Four separate non-complementary two-class detection tasks were considered: N3, NREM, REM and Wake separately, in a “one versus all” approach. They reported an out of sample κ = 0.41 and Acc = 87.4% for N3 detection, κ = 0.55 and Acc = 78.7% for NREM, κ = 0.51 and Acc = 88.5% for REM and κ = 0.51 and Acc = 85.7% for Wake detection.
Tataraidze et al. (2016) presented a three-step classifier for sleep stages using ECG and RIP signals. At first a gradient boosted machine and a random forest classifier were used in parallel to process the features extracted from ECG and RIP, followed by a linear discriminant analysis (LDA) to predict class probabilities. Then a simple linear combination was used to make prediction. The algorithm was tested on a polysomnography dataset with 625 subjects with five-fold cross-validation. A value of κ = 0.57 and an accuracy of 71.4% in the four-class classification of Wake, REM, light and deep sleep was reported.
Yoon et al. (2017) developed an automatic algorithm to determine REM sleep by ECG. After obtained 14 HRV parameters from ECG, a principal component analysis (PCA) was applied to extract the principal components where the first principal component was used to represent the major fluctuation reflected by the pattens of a sleep cycle. The algorithm was trained on a set of 26 subjects and evaluated on a validation set of 25 subjects. They reported a value of κ = 0.63 and 0.61, an accuracy of 87.1% and 87.0% for the training and validation sets respectively in the two-class classification of REM and NREM including N1,N2,N3 and wakefulness.
Wei et al. (2018) described a neural network approach applied to the ECG to classify the sleep stages into one of three classes; Wake, REM and NREM. A total of 11 features were extracted from the raw ECG and were presented to a 4-layer neural network. Cross-validation was used on the MIT-BIH Polysomnographic Database for validation. An accuracy of 77% and κ = 0.56 were reported for the three-class problem.
In the work presented in this article, the coherence and cross-spectrogram of the EDR and RSA signals were calculated on a 5-min epoch basis. Rather than selecting predetermined frequencies and optimizing amplitude or power thresholds, a convolutional neural network (CNN) was used to automatically identify the most relevant time-frequency cross spectral and coherence features associated with a given sleep stage. CNNs were originally developed to provide rotationally invariant spatial filters for images. Since the spectrogram is a matrix of numbers with spatiotemporal correlations that are similar to images, with specific subregions forming features indicative of specific physiological states, the CNN is a natural framework for identifying such features. A support vector machine (SVM) was then used to combine the output of the CNN with the other features derived from ECG, based upon heart rate variability, and signal quality indices (SQI) to produce a classification of sleep stage.
2. Methods
2.1. Dataset
For this work we used three databases: 1. the MIT-BIH Polysomnographic Database (SLPDB, Goldberger A L et al. (2000), 2. the Physionet/Computing in Cardiology Challenge 2018 training database (CinC2018tDB, Ghassemi M M et al. (2018)) and 3. the Sleep Heart Health Study visit 1 (SHHSv1) database (Quan et al. (1997)). The SLPDB database includes 18 recordings from 16 subjects of multiple physiological signals during sleep, containing over 80 hours of four-, six-, and seven-channel polysomnographic recordings, each with a single channel of of ECG annotated beat-by-beat, and EEG and respiration signals annotated with respect to sleep stages and apnea. The CinC2018 training database includes 994 subjects who were monitored at Massachusetts General Hospital (MGH) sleep laboratories for the diagnosis of sleep disorders, containing over 7660 hours of a variety of physiological signals recorded as they slept through the night including EEG, electrooculography (EOG), electromyography (EMG), ECG, and oxygen saturation (SaO2) together with arousal and sleep stages annotations. The SHHS database is a multi-center cohort study implemented by the National Heart & Lung Blood Institute to determine the cardiovascular and other consequences of sleep-disordered breathing. In all, 6,441 men and women aged 40 years and older were enrolled between 1995 and 1998 to take part in SHHS Visit 1, including 5793 recordings (SHHSv1). During 2001 to 2003, a second polysomnogram (SHHSv2) was created using 3295 of the original participants. The entirety of the 5793 recordings in the SHHSv1 database was used without exclusion. Only the ECG signal was used in this study as an input and the expert sleep stages as targets/class labels.
The sleep stage annotations include six categories: wake, REM sleep, sleep stage 1, sleep stage 2, sleep stage 3 and sleep stage 4 in the SLPDB; wake, REM sleep, sleep stage 1, sleep stage 2, sleep stage 3 and undefined in the CinC2018tDB database; and wake, REM sleep, sleep stage 1, sleep stage 2, sleep stage 3 and sleep stage 4 in the SHHSv1 database). In this study, we combined sleep stage 1 and sleep stage 2, denoted NREM light sleep and combined sleep stage 3 and sleep stage 4, denoted NREM deep sleep. Data epochs were therefore classified into four categories, or ‘states’; Wake, REM sleep, NREM light sleep and NREM deep sleep. The data were annotated in non-overlapping 30 seconds epochs by experts. Since 30 seconds is too short an interval to contain a sufficient number of heart beats for estimating autonomic activity, we used five-min windows for an epoch, sliding the window forward every one minute in SLPDB and CinC2018tDB, but using non-overlapped window in SHHSv1 to keep the number of total epochs tractable. An epoch was selected only when the annotations within the five-min window belonged to the same state. This prevented the inclusion of multiple sleep stages in a single epoch and reduced the effect of nonstationarities. A total of 2,829 epochs were selected in SLPDB, 261,946 epochs in CinC2018tDB, and 400,547 epochs in SHHSv1 database, as shown in Table 1.
Table 1:
Distribution of epochs by state for each database used in this study
| database | Wake | REM | NREM light | NREM deep | Total |
|---|---|---|---|---|---|
| SLPDB | 914 (32%) | 185 (7%) | 1585 (56%) | 145 (5%) | 2829 |
| CinC2018tDB | 34711 (13%) | 37593 (14%) | 160748 (61%) | 28894 (11%) | 261946 |
| SHHSv1 | 130688 (33%) | 60234 (15%) | 167343 (42%) | 42282 (11%) | 400547 |
2.2. Preprocessing
The ECG signals were preprocessed by a finite impulse response (FIR) lowpass filter with a band stop at 22Hz and a FIR highpass filter and with at corner frequency of 1.2Hz. A state-of-the-art QRS detector (jqrs) was used for ECG R-peak detection (Johnson et al. (2015)). The detector consists of a window-based peak energy detector, which is extremely robust to noise. An ECG signal quality index (bSQI), which assesses the signal quality or noise levels of the signals, was extracted from the ECG and used to accept the epochs for further processing or reject the epochs if the signal quality of ECG was too low to be trusted (Li et al. (2008)). A sliding 10-second window was used, evaluated every second with a nine second overlap. If the value of the signal quality index was lower than a preset threshold, the epoch was rejected.
2.3. Cardiorespiratory coupling spectrogram calculation
After R-peak detection and derivation of the RR tachograms, RSA and EDR time series were extracted. Outliers due to false or missed R-peak detection were removed using a sliding window average filter with a length of 41 data points. Central points lying outside 20% of the window average were rejected. The resulting normal-to-normal (NN) interval series and its associated EDR signal were then linearly resampled at 4 Hz, so that the five-min epoch contained 1200 samples. The cross-spectral power and coherence of these two signals were calculated over a 512-sample (128-second) window. Then the 512-sample sliding window was advanced every 40 samples (10-seconds) to obtain 18 cross-spectral estimates. By placing the cross-spectral curves in order of time, we obtained a CRC spectrogram of dimensions 50×18, where the frequency range was from 0 Hz to 0.4 Hz (taken 50 points) and the time window was five minutes. An example of a CRC spectrogram for each sleep stage is shown in Figure 1. The CRC spectrogram for each state, average over all epochs in SLPDB, is shown in Figure 2.
Figure 1:
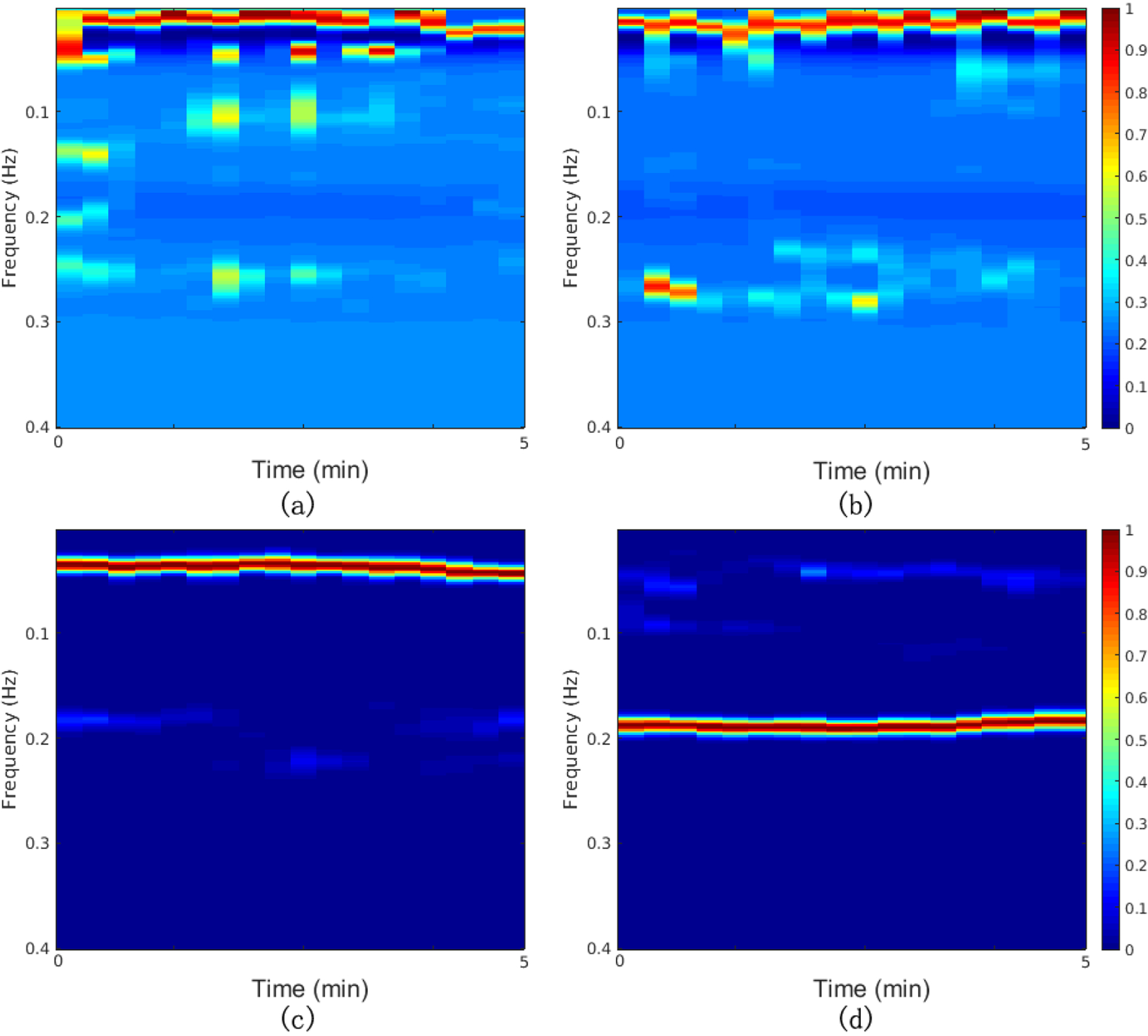
Examples of CRC spectrograms for each sleep state: (a) Wake; (b) REM sleep; (c) NREM light sleep; (d) NREM deep sleep. Hotter colors indicate higher cross spectral coherence (inherently normalized between 0 and 1)
Figure 2:
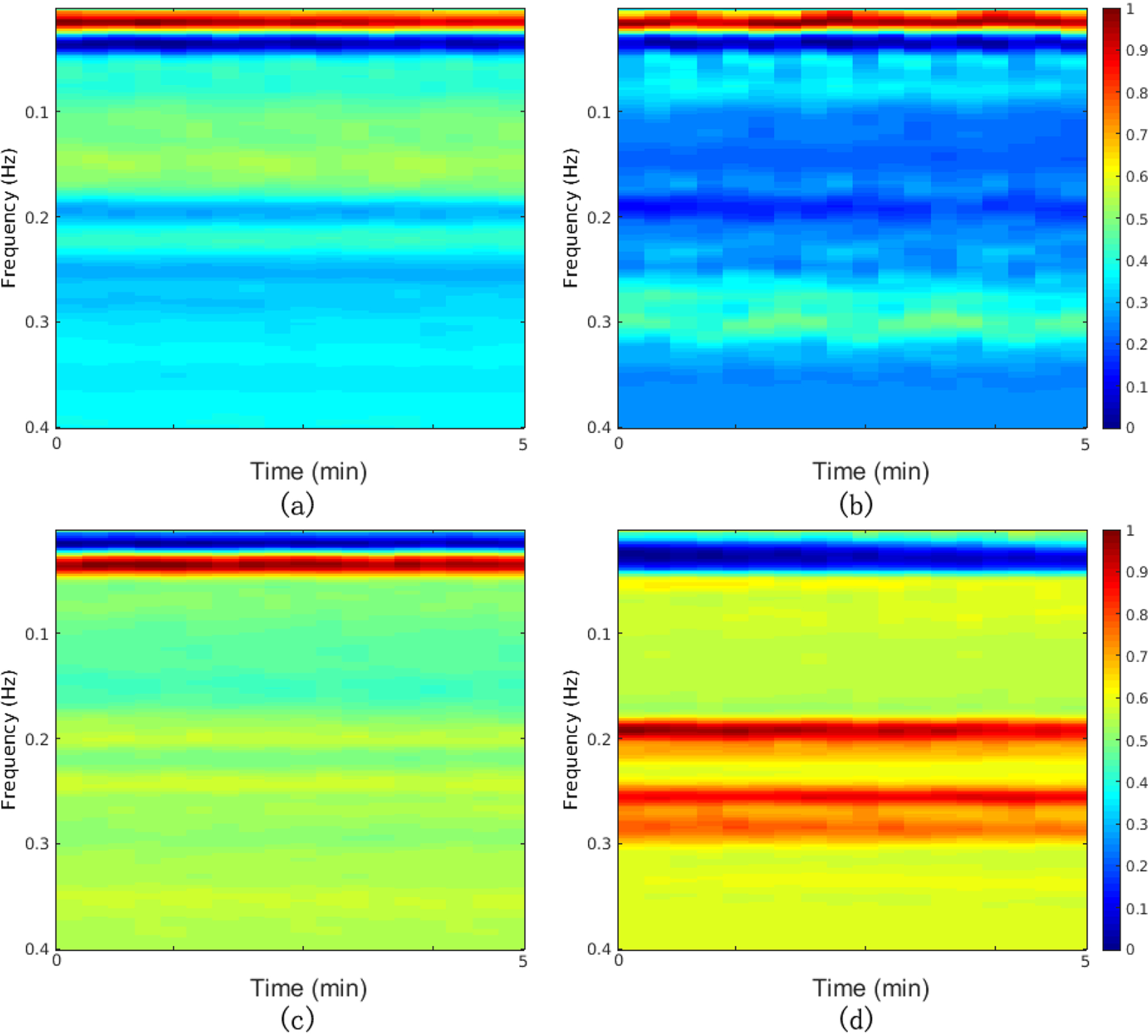
Average of CRC spectrogram over all epochs in SLPDB for each state: (a) Wake; (b) REM sleep; (c) NREM light sleep; (d) NREM deep sleep. Hotter colors indicate higher cross spectral coherence (inherently normalized between 0 and 1)
2.4. Convolutional neural network implementation
The CNN toolbox used in this study was written in Matlab R2016b (Vedaldi and Lenc (2015), MatConvNet: CNNs for MATLAB (2016)). The CNN model used consisted of three convolutional layers, two max pooling layers (implemented after the first and the second convolutional layer), a rectified linear unit (ReLU) layer and finally a fully connected layer, as shown in Figure 3. An n × m sized map is convolved with the input image at each convolutional layer, resulting in an output with n − 1 × m − 1 reduction in size from the input. The 2×2 max pooling layer downsamples the input by a factor of two in both directions, dropping 75% of data size while retaining most discernible features for classification. The final layer of convolution computes the input into a single value, which after increasing nonlinear properties by the ReLU layer, is passed into the fully connected layer thereby producing the final resulting probabilities for each class. Figure 3 illustrates this architecture.
Figure 3:
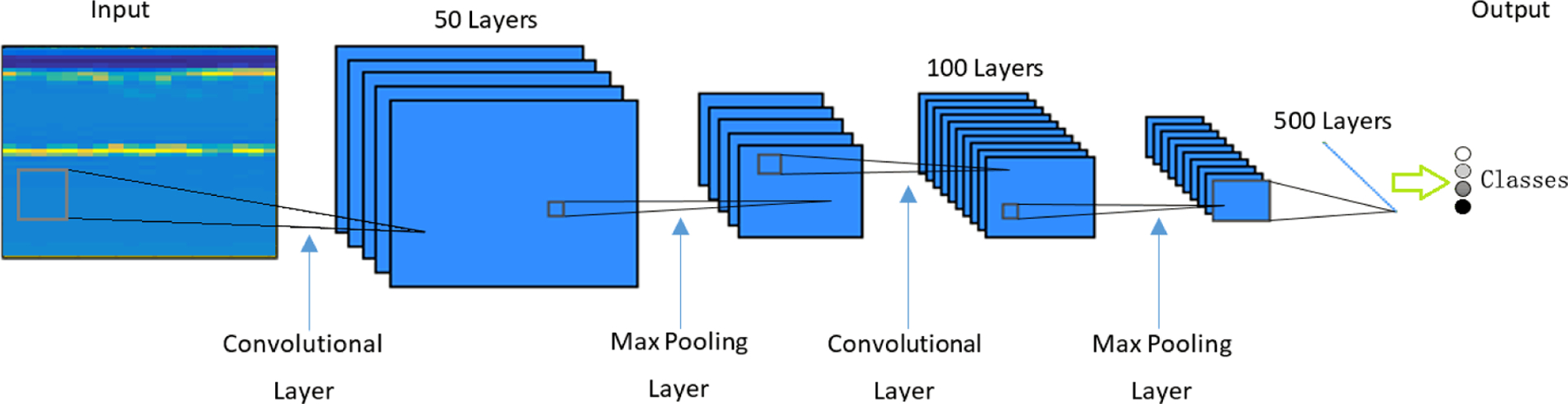
Convolutional neural network structure.
2.5. Additional features
In order to capture information not present in the cross spectral coherence, we also calculated several HRV metrics (Vest et al. (2018)). These included deceleration and acceleration capacity from phase-rectified signal averaging (PRSA, Campana et al. (2010)), sample entropy (Costa et al. (2005)), and other HRV metrics (standard deviation of NN intervals (SDNN) and the ratio of low frequency and high frequency spectral power (LF/HF-ratio)). We also included several novel indices including the ratio of the sum of the two maximal coherent cross-power peaks in the low-frequency band (0.01–0.1 Hz) to the sum of the two maximal peaks in the high-frequency band (0.1–0.4 Hz), the ratio of the energy between the low-frequency and high-frequency band, and the signal quality index.
2.6. Support vector machine
To combine the above features and produce a final sleep stage class probability, a SVM classifier was used (Chang and Lin (2011); LibSVM – a library for support vector machines (2016)). The SVM employed a Gaussian radial basis function kernel, defined by: K(xn, xm) = exp(γ||xn−xm||2), where γ controls the width of the Gaussian and plays a role in controlling the flexibility of the resulting classifier. xn and xm are two vectors expressed in the initial feature space. We used the LibSVM libraries, which decouples the multiclass classification problem to several two-class problems and a voting strategy is then used: each binary classification is considered to be a voting entity, where votes can be cast for all data samples. A sample is designated to be in a class with the maximum number of votes.
The probability outputs of CNN were fed into the SVM at its input, together with the individual HRV features extracted from the same five-min ECG, as described in section 2.5.
2.7. K-fold cross-validation
The 16 subjects in SLPDB, and the recordings from CinC2018tDB and SHHSv1 were randomly allocated into ten subsets (folds, K=10) of data respectively. Grouping was performed by subject number rather than by the total epochs, (i.e. stratified by subject) so that the data from one subject would not appear in both the training fold or the test fold. K−1 folds of the dataset were used for training, after which the network was saved, it was tested on the remaining (validation) fold. This process was repeated K times with each of the K folds tested and the results were averaged or accumulated.
2.8. Evaluation method
The classification accuracy (Acc) and Cohen’s Kappa (κ) were used to evaluate the performance of the algorithm. The Acc is defined as follows:
where q is the number of categories, N is the total number of epochs and nkk is the number of correct classification. Cohen’s Kappa is then calculated by:
where , , pkk represents the percentage of epochs classified into category k by the algorithm and by the annotated label; pk+ and p+k represent the percentage of epochs assigned to category k by the algorithm and annotated label respectively.
3. Results
Table 2 shows the performance of the ten-fold cross validation in SLPDB. The four classes, or states, are Wake, REM sleep, NREM light sleep and NREM deep sleep. The three classes are broken into two categories: (a) Wake, REM sleep and NREM sleep; and (b) Wake and REM combined, NREM light sleep, and NREM deep sleep. The two class problem combines Wake and REM sleep as one class and NREM sleep as the other. The average values are the average accuracy of the held-out fold in the ten validation runs. The accumulation accuracy and κ were obtained by accumulating the results from every validation fold.
Table 2:
Performance of ten-fold cross validation in SLPDB
| training folds | validation fold | |||
|---|---|---|---|---|
| Acc average (%) | Acc average (%) | Acc accumulation (%) | κ | |
| 4 classes | 86.9±0.7 | 75.6±9.0 | 75.4 | 0.54 |
| 3 classes(a) | 92.8±0.8 | 81.7±7.5 | 81.6 | 0.63 |
| 3 classes(b) | 91.5±0.4 | 79.7±10.1 | 79.8 | 0.61 |
| 2 classes | 93.8±0.4 | 85.0±6.5 | 85.1 | 0.68 |
An accuracy of 75.4% and a Cohen’s kappa coefficient of 0.54 on out of sample validation in the classification of Wake, REM, light and deep sleep was obtained. For the three class problem an Acc = 81.6% and κ = 0.63 for the classification of Wake, REM sleep and NREM sleep and Acc = 85.1% and κ = 0.68 for the classification of NREM sleep vs REM/wakefulness was found. The confusion matrix are tabled in the Appendix.
Table 3 shows the performance of the ten-fold cross validation in CinC2018tDB. An accuracy (Acc) of 65.6% and a Cohen’s kappa coefficient of 0.31 on out of sample validation in the classification of Wake, REM, light and deep sleep was achieved. For the three class problem an Acc = 76.5% and κ = 0.42 for the classification of Wake, REM sleep and NREM sleep and Acc = 79.4% and κ = 0.48 for the classification of NREM sleep vs REM/wakefulness was accomplished.
Table 3:
Performance of ten-fold cross validation in CinC2018tDB
| training folds | validation fold | |||
|---|---|---|---|---|
| Acc average (%) | Acc average (%) | Acc accumulation (%) | κ | |
| 4 classes | 68.8±0.2 | 65.6±1.3 | 65.6 | 0.31 |
| 3 classes(a) | 79.2±0.1 | 76.5±1.0 | 76.5 | 0.42 |
| 3 classes(b) | 72.2±0.1 | 68.2±1.2 | 68.2 | 0.36 |
| 2 classes | 81.3±0.1 | 79.4±0.9 | 79.4 | 0.48 |
Table 4 shows the performance of the ten-fold cross validation in SHHSv1. An accuracy (Acc) of 65.9% and a Cohen’s kappa coefficient of 0.47 on out of sample validation in the classification of Wake, REM, light and deep sleep was achieved. For the three class problem an Acc = 75.3% and κ = 0.57 for the classification of Wake, REM sleep and NREM sleep and Acc = 80.8% and κ = 0.61 for the classification of NREM sleep vs REM/wakefulness was accomplished.
Table 4:
Performance of ten-fold cross validation in SHHSv1
| training folds | validation fold | |||
|---|---|---|---|---|
| Ace average (%) | Ace average (%) | Ace accumulation (%) | κ | |
| 4 classes | 67.0±0.1 | 65.9±0.7 | 65.9 | 0.47 |
| 3 classes(a) | 76.3±0.1 | 75.3±0.5 | 75.3 | 0.57 |
| 3 classes (b) | 72.3±0.1 | 71.6±0.4 | 71.6 | 0.49 |
| 2 classes | 81.4±0.1 | 80.8±0.3 | 80.8 | 0.61 |
Figure 4 illustrates the output of our new approach to automated sleep structure identification for the two, three and four-class problem.
Figure 4:
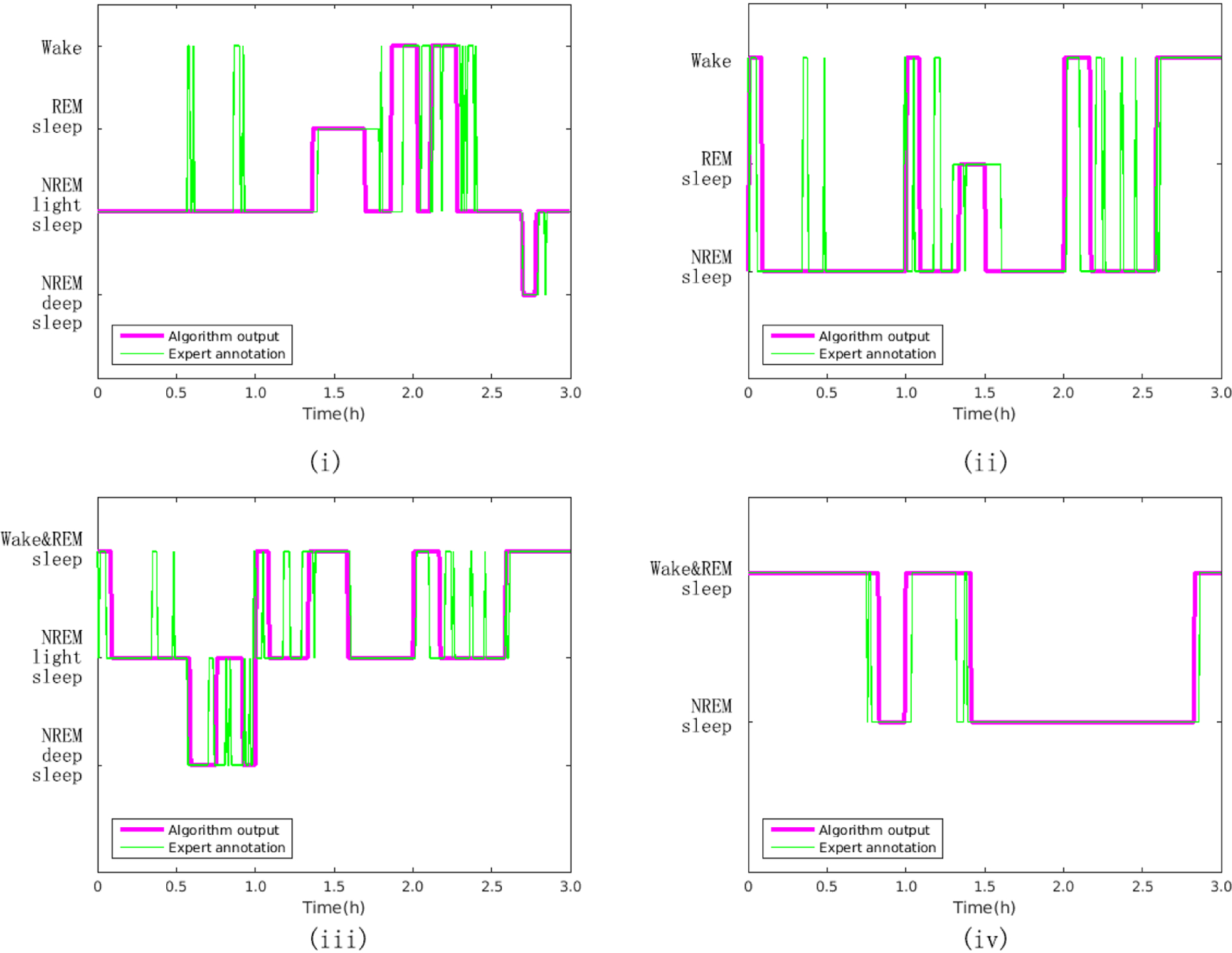
A comparison of expert-scored hypnograms and the output from the proposed approach for the (i) four class problem, (ii) three class problem (a), (iii) three class problem (b), and (iv) two class problem. Note that each epoch is five minutes for the algorithm output and 30 seconds for the expert annotation, so rapid changes between epochs (less than 5 minutes) are undetectable.
Table 5 shows the performance when different SQI thresholds were used to exclude noisy epochs in SLPDB.
Table 5:
Performance (Acc accumulation %) on validation fold by SQI-threshold selection in SLPDB
| SQI-threshold | - | 0.80 | 0.90 | 0.95 |
| epochs | 2829 | 2814 | 2774 | 2658 |
| SQI values | 0.985±0.07 | 0.988±0.05 | 0.989±0.04 | 0.992±0.03 |
| 4 classes | 75.4 | 76.3 | 76.3 | 75.9 |
| 3 classes(a) | 81.6 | 82.5 | 82.6 | 82.0 |
| 3 classes(b) | 79.8 | 80.2 | 80.0 | 79.9 |
| 2 classes | 85.1 | 85.2 | 85.0 | 84.7 |
4. Discussion and Conclusions
In this article we have presented a new approach to ECG-based sleep stage classification. Our results provide the highest accuracy compared to the state of the art Fonseca et al. (2015), with a 6.4% increase in accuracy and 0.05 increase in Cohen’s kappa for the four class problem, a 1.6% increase in accuracy and 0.07 increase in Cohen’s kappa for the three class problem, and the highest reported two class results (see Table 2). A comparison with the latest algorithms was shown in table 6.
Table 6:
A comparison with the latest sleep staging algorithms
| Work | Signals used | Database | Subjects (Recordings) | classes | k-fold | Ace | κ |
|---|---|---|---|---|---|---|---|
| Long et al. (2014) | RIP | part of SIESTA | 48 out of 584 | 4 classes | 10-fold | 64.9 | 0.41 |
| Fonseca et al. (2015) | ECG+RIP | part of SIESTA | 48 out of 584 | 4 classes | 10-fold | 69 | 0.49 |
| Tataraidze et al. (2016) | ECG+RIP | part of SHHSv1 | 625 out of 5793 | 4 classes | 5-fold | 71.4 | 0.57 |
| our work | ECG | SLPDB | 16 (18) | 4 classes | 10-fold | 75.4 | 0.54 |
| out work | ECG | SHHSv1 | 5793 | 4 classes | 10-fold | 65.9 | 0.47 |
| Fonseca et al. (2015) | ECG+RIP | part of SIESTA | 48 out of 584 | 3 classes | 10-fold | 80 | 0.56 |
| Long et al. (2014) | RIP | part of SIESTA | 48 out of 584 | 3 classes | 10-fold | 77.1 | 0.48 |
| Wei et al. (2018) | ECG | SLPDB | 16 (18) | 3 classes | 10-fold* | 77 | 0.56 |
| our work | ECG | SLPDB | 16 (18) | 3 classes | 10-fold | 81.6 | 0.63 |
| out work | ECG | SHHSv1 | 5793 | 3 classes | 10-fold | 75.3 | 0.57 |
| Thomas et al. (2005) | ECG | private | 35train+35test+15test | 2 classes | - | - | 0.439 |
| Fonseca et al. (2017) | ECG+RIP | part of SIESTA+private | 180 (342) | 2 classes | 10-fold | 78.71 | 0.55 |
| Yoon et al. (2017) | ECG | private | 26train+25test | 2 classes | - | 87.03 | 0.61 |
| our work | ECG | SLPDB | 16 (18) | 2 classes | 10-fold | 85.1 | 0.68 |
| out work | ECG | SHHSv1 | 5793 | 2 classes | 10-fold | 80.8 | 0.61 |
10-fold by epochs, not by recordings
Aside from the improved results over earlier studies, there are several features of our method that make it superior to previously reported best in class (Fonseca et al. (2015)). First, previous authors required the recording of a respiratory inductance plethysmography. This can be energy consuming, annoying for the user and require expert placement of electrodes. Respiratory signals in themselves are notoriously difficult signals to interpret and generalization to consumer use is probably impossible (and in all likelihood why no clinical grade consumer respiratory band devices have come to the market).
In this work, we used the cross-spectral power to measure the amplitudes coupling of EDR and RSA, and used coherence to reveal the phase relationship between these signals. It has been shown that although the amplitudes can be subject and pathology dependent, the phase changes with sleep stages is consistent across populations (Thomas et al. (2005)). The product of the cross-spectrogram and the coherence can then be used as a quantitative measure of the cardiopulmonary coupling. However, we note that there are other measures of cardio-respiratory coupling that may prove useful quantities to measure in this context. Bartsch et al. (2012, 2014) demonstrated three independent forms of cardio-respiratory coupling, such as RSA, cardio-respiratory phase synchronization (CRPS) and time delay stability analysis (TDS) and the stratification patterns with transitions across sleep stages. Comparing with RSA, the sensitivity of CRPS to sleep-stage transitions is 10 times higher. Specifically, the CRPS reflects the degree of clustering of heartbeats at specific relative phases within each breathing cycle, and the TDS quantifies the stability of the time-delay with which bursts in the activity in one system are consistently followed by corresponding bursts in the other system.
Recently research has addressed sleep staging from the perspective of network physiology (Bashan et al. (2012), Bartsch et al. (2015), Ivanov and Bartsch (2014), D’Agostino and Scala (2014) and Ivanov et al. (2016)). Bashan et al. (2012) developed a framework to probe interactions among diverse systems and identify physiological networks. They found that each physiological state was characterized by a specific network structure, demonstrating an interplay between network topology and physiological function. Bartsch et al. (2015) systematically studied how diverse physiologic systems in the human organism dynamically interact and collectively behave to produce distinct physiologic states and functions. The authors used TDS to identify and quantify networks of physiologic interactions from long-term continuous, multi-channel physiological recordings and found a sleep-stage stratification pattern for brain-brain, brain-organ and organ-organ networks. In this paper we studied the physiologic interactions among heart and respiration with cardiorespiratory coupling of EDR and RSA extracted from ECG without an explicit modelling of this system. In that sense it represents a non-parametric approach. The interactions of the cardiopulmonary system were converted to a CRC spectrogram and the different sleep stages of light sleep, deep sleep, REM sleep and wake exhibited characteristic differences in the CRC spectrogram which could then be classified by the proposed deep learning architecture.
We also note that with a cross spectral approach, the noise present during respiration is removed, since incoherent noise exhibits a very low amplitude or nonexistent signal in our time-frequency plot. This lack of signal due to noise becomes a useful signal for us, and in fact including this in the CNN leads to higher accuracies/κ. This indicates that certain sleep stages exhibit more noise than others, and this noise level can be learned, if it doesn’t swamp the signal.
We also note that the use of a time-frequency approach allows us to identify relatively short periods of physiology (like sleep stages) and to capture nonstationary events. Since sleep stages are defined to be assessed on 30 second epochs, and indeed, events can happen on a shorter time-scale, a method that can spot these (such as arousals) is essential in sleep analysis. In this study we used a relatively long window of 5-minute epoch to generate the CRC spectrogram for sleep staging analysis. To evaluate our algorithm on a 30-second basis, we slide the 5-min window forward every 30-second to match the annotation of the 30-second epoch centred on the 5-min window. In this way we were able to match the epochs generated through traditional sleep staging approaches. Of course, this leads to a slight low-pass filtering effect that may dampen out shot term sudden shifts since data from the surrounding epochs are used, but the evaluation of a 30s epoch-by-epoch basis is still valid. The classification performance of the algorithm was tested by a 10-fold cross validation in the SLPDB. The results showed an Acc = 66.2% and κ = 0.36 on out of sample validation in the classification of Wake, REM, light and deep sleep, Acc = 73.6% and κ = 0.44 for the classification of Wake, REM sleep and NREM sleep and Acc = 76.1% and κ = 0.47 for the classification of NREM sleep vs REM/wakefulness. In the last decade or so there have been attempts to develop HRV metrics from shorter term windows, such as Phase Rectified Signal Averaging (Bauer et al. (2006)). Most recently, Hou et al. (2016) presented a new approach on 30 seconds epochs during sleep. The authors constructed a complex network from short-term HRV based on a visibility graph algorithm and extracted four network measure parameters across sleep stages. However, these measures do not capture the interactions between respiration and heart rate, and so would not be useful in our analysis here.
Perhaps most importantly, we note that the use of a QRS detector in our work is important. Previous studies using ECG data have often used hand annotations of beat locations. As we have previously shown (Oster and Clifford, 2015), the use of algorithms trained and tested on hand annotations significantly over-estimates the accuracy of the resultant algorithms and leads to a substandard approach in reality. For this reason, we have not included comparisons with other sleep staging algorithms based on ECG - it would be unfair to compare any technique which requires hand annotation of QRS complexes. In such scenarios, one might as well have recorded the EEG and had experts read the EEG. Since the accuracy of the EDR and RSA signals derived from ECG depend on the quality of the QRS detector, the accurate estimation of the HRV features and derivation of the CRC are naturally also a function of the quality of the ECG and the accuracy of the QRS detector. Poor QRS detection performance is therefore likely to result in poor sleep staging classification. To illustrate the effect of different QRS detectors on sleep staging from automated ECG analysis, we compared the results when using an open source QRS detector, wqrs (Zong et al. (2003)), which is sensitive to noise. The 10-fold cross validation approach results in the SLPDB resulted in an out of sample four-class Acc = 73.1% and κ = 0.51 (Wake, REM, NREM light sleep and NREM deep sleep), a three-class Acc = 77.7% and κ = 0.56 (Wake, REM and NREM sleep) and a two-class Acc = 81.6% and κ = 0.61 (NREM sleep vs REM/wakefulness). These results are a modest but important 2–4% lower than the results using jqrs. However, we note that the CRC, which provides an estimate of the cardiopulmonary coupling, is in some sense robust to noise, since only coherent signals in both the respiration and heart rate will be detected. In some sense this has somewhat (although not entirely) mitigated the issue of noise. However, noisy segments of ECG are likely to be correlated to movements, which themselves are correlated with less deep sleep stages or wakefulness. This bias is likely to be learned by the deep learning architecture and therefore must be considered carefully in the context of the population on which the algorithm is trained. (This is of course true for all sleep staging approaches, regardless of which signals are used for sleep staging.) Therefore, using as accurate a beat detection algorithm as possible is still important.
Finally, we note that we have demonstrated robustness of the approach presented here across three databases with over 10 times as many patients as any previous study. The use of an automated QRS detector made this approach possible.
There is one key limitation to our study in that we used relatively specific patient cohorts. Since abnormal conditions can reduce the inter-class agreement level of experts, then training becomes more difficult. Although this does not always directly impact on the eventual diagnosis, it can be significant for automated classification systems, which may disproportionately weight incorrectly labeled epochs during training. Inter-rater reliability/agreement has been shown to vary enormously, with κ coefficient values ranging between 0.6 and 0.9 (Crowell et al. (1997, 2002); Stepnowsky et al. (2004); Ferri et al. (2005); Rosa et al. (2006); Saito et al. (2006)). Taking this into consideration, we can see that the κ values we obtain of 0.54 to 0.68 are as good as can be expected.
In general, in order to ascertain if the method described here provides enough information to be diagnostically useful for any given condition, the output from this method will have to be fed to another classifier (or expert). Sleep stages in themselves are rather uninformative, yet statistics derived from them are correlated with a range of conditions. For example, patients with Major Depressive Disorder exhibit shortened latency to the onset of REM sleep (REM latency), an increased percentage of the night in REM sleep, a longer duration of the first REM period, and decreased amount of slow-wave sleep (Krystal (2012)).
It may therefore be possible to identify a proxy for ECG-related REM-like sleep from our algorithm, and then identify thresholds for a given patient population, that although different to EEG-based REM thresholds, may never-the-less provide enough predictive power for patient screening or follow-up. On an individual basis, the ECG-based sleep structure estimate may be even more informative, allowing the user to identify treatment-related improvements on a long term basis, something which is not feasible with EEG-based systems, since the user rarely tolerates more than a few nights of such measurements and expert-application of the electrodes is often needed.
In conclusion, we have described an improved system for estimating sleep structure from a cardiovascular time series that is robust to noise, and in fact takes advantage of the noise in the ECG to aid classification accuracy. The system described outperforms current reported systems and in general it could apply to any pulsatile signal from which a beat onset and a respiratory modulation can be observed, such as the photoplethysmogram. Perhaps most notably, the results provided here do not require human annotation and can therefore be scaled for mass analysis without restriction beyond the modest storage and computational power requirements of earlier works.
Acknowledgements
The authors wish to acknowledge the National Institutes of Health (Grant # NIH 5R01HL136205-02), National Heart, Lung, and Blood Institute and Emory University for their financial support of this research. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Institutes of Health, National Heart, Lung, and Blood Institute or Emory University.
Appendix
Table 7:
Appendix - Confusion matrix of the four class problem of ten-fold cross validation in SLPDB
| Annotation algorithm | Wake | REM | Light Sleep | Deep Sleep |
|---|---|---|---|---|
| Wake | 703 | 73 | 140 | 27 |
| REM | 21 | 15 | 30 | 0 |
| Light Sleep | 181 | 96 | 1398 | 101 |
| Deep Sleep | 9 | 1 | 17 | 17 |
Table 8:
Appendix - Confusion matrix of the two class problem of ten-fold cross validation in SLPDB
| Annotation algorithm | Wake & REM | NREM Sleep |
|---|---|---|
| Wake & REM | 857 | 181 |
| NREM Sleep | 242 | 1549 |
Table 9:
Appendix - Confusion matrix of the four class problem of ten-fold cross validation in SHHSv1
| Annotation algorithm | Wake | REM | Light Sleep | Deep Sleep |
|---|---|---|---|---|
| Wake | 95538 | 12891 | 16350 | 2198 |
| REM | 6950 | 23221 | 7700 | 356 |
| Light Sleep | 27913 | 24099 | 139875 | 34395 |
| Deep Sleep | 287 | 23 | 3418 | 5333 |
Table 10:
Appendix - Confusion matrix of the two class problem of ten-fold cross validation in SHHSv1
| Annotation algorithm | Wake & REM | NREM Sleep |
|---|---|---|
| Wake & REM | 149783 | 35832 |
| NREM Sleep | 41139 | 173793 |
References
- Aserinsky E and Kleitman N (1953). Regularly occurring periods of eye motility, and concomitant phenomena, during sleep, Science 118: 273–274. [DOI] [PubMed] [Google Scholar]
- Bartsch RP, Liu KK, Bashan A and Ivanov PC (2015). Network physiology: how organ systems dynamically interact, Plos One 10(11): e0142143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartsch RP, Liu KK, Ma QD and Ivanov PC (2014). Three independent forms of cardio-respiratory coupling: transitions across sleep stages, Computing in Cardiology Conference (CinC), 2014, IEEE, 781–784. [PMC free article] [PubMed] [Google Scholar]
- Bartsch RP, Schumann AY, Kantelhardt JW, Penzel T and Ivanov PC (2012). Phase transitions in physiologic coupling, Proceedings of the National Academy of Sciences 109(26): 10181–10186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bashan A, Bartsch RP, Kantelhardt JW, Havlin S and Ivanov PC (2012). Network physiology reveals relations between network topology and physiological function, Nature Communications 3: 702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer A, Kantelhardt JW, Barthel P, Schneider R, Mäkikallio T, Ulm K, Hnatkova K, Schömig A, Huikuri H, Bunde A et al. (2006). Deceleration capacity of heart rate as a predictor of mortality after myocardial infarction: cohort study, The Lancet 367(9523): 1674–1681. [DOI] [PubMed] [Google Scholar]
- Campana L, Owens R, Clifford GD, Pittman SD and Malhotra A (2010). Phase-rectified signal averaging as a sensitive index of autonomic changes with aging, Journal of Applied Physiology 108(6): 1668–1673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C and Lin C (2011). LIBSVM: A library for support vector machines, ACM Transactions on Intelligent Systems and Technolog 2(27): 1:27. [Google Scholar]
- Costa M, Goldberger AL and Peng CK (2005). Multiscale entropy analysis of biological signals, Phys Rev E Stat Nonlin Soft Matter Phys 71: 021906:1–18. [DOI] [PubMed] [Google Scholar]
- Crowell DH, Brooks LJ, Colton T, Corwin MJ, Hoppenbrouwers TT, Hunt CE, Kapuniai LE, Lister G, Neuman MR, Peucker M, Ward SL, Weese-Mayer DE and Willinger M (1997). Infant polysomnography: reliability. Collaborative Home Infant Monitoring Evaluation (CHIME) Steering Committee., Sleep 20(7): 553–60. [PubMed] [Google Scholar]
- Crowell DH, Kulp TD, Kapuniai LE, Hunt CE, Brooks LJ, Weese-Mayer DE, Silvestri J, Ward SD, Corwin M, Tinsley L, Peucker M and CHIME Study Group (2002). Infant polysomnography: reliability and validity of infant arousal assessment., Journal of Clinical Neurophysiology 19(5): 469–483. [DOI] [PubMed] [Google Scholar]
- D’Agostino G and Scala A (2014). Networks of networks: the last frontier of complexity, Vol. 340, Springer. [Google Scholar]
- Ferri R, Bruni O, Miano S, Smerieri A, Spruyt K and Terzano MG (2005). Inter-rater reliability of sleep cyclic alternating pattern (CAP) scoring and validation of a new computer-assisted CAP scoring method, Clinical Neurophysiology 116(3): 696–707. [DOI] [PubMed] [Google Scholar]
- Fonseca P, den Teuling N, Long X and Aarts RM (2017). Cardiorespiratory sleep stage detection using conditional random fields, IEEE Journal of Biomedical and Health Informatics 21(4): 956–966. [DOI] [PubMed] [Google Scholar]
- Fonseca P, Long X, Radha M, Haakma R, Aarts RM and Rolink J (2015). Sleep stage classification with ecg and respiratory effort, Physiol. Meas 36: 2027–2040. [DOI] [PubMed] [Google Scholar]
- Ghassemi MM, Moody B, Lehman LH, Song C, Li Q, Sun H, , Westover MB and Clifford GD (2018). You snooze, you win: the physionet/computing in cardiology challenge 2018, Computing in Cardiology 45: 1–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberger AL, Amaral LAN, Glass L, Hausdorff JM, Ivanov P Ch, Mark RG, Mietus JE, Moody GB, Peng C-K and Stanley HE (2000). PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals, Circulation 101(23): e215–e220. [DOI] [PubMed] [Google Scholar]
- Herbst E, Metzler TJ, Lenoci M, McCaslin SE, Inslicht S, Marmar CR and Neylan TC (2010). Adaptation effects to sleep studies in participants with and without chronic posttraumatic stress disorder., Psychophysiology 47(6): 1127–1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou F, Li F, Wang J and Yan F (2016). Visibility graph analysis of very short-term heart rate variability during sleep, Physica A: Statistical Mechanics and its Applications 458: 140–145. [Google Scholar]
- Iber C, Ancoli-Israel S, Chesson A and Quan SF (2007). The AASM Manual for the Scoring of Sleep and Associated Events: Rules, Terminology and Technical Specifications, Westchester, IL: American Academy of Sleep Medicine. [Google Scholar]
- Ivanov PC and Bartsch RP (2014). Network physiology: mapping interactions between networks of physiologic networks, Networks of Networks: the last Frontier of Complexity, Springer, 203–222. [Google Scholar]
- Ivanov PC, Liu KK and Bartsch RP (2016). Focus on the emerging new fields of network physiology and network medicine, New Journal of Physics 18(10): 100201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson AE, Behar J,Andreotti F,Clifford GD and Oster J (2015). Multimodal heart beat detection using signal quality indices, Physiological Measurement 36(8): 1665–1677. [DOI] [PubMed] [Google Scholar]
- Krystal AD (2012). Psychiatric disorders and sleep., Neurologic Clinics 30(4): 1389–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Q, Mark RG and Clifford GD (2008). Robust Heart Rate Estimation from Multiple Asynchronous Noisy Sources using Signal Quality Indices and a Kalman Filter, Physiological Measurement 29(1): 15–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LibSVM – a library for support vector machines (2016). URL: https://www.csie.ntu.edu.tw/cjlin/libsvm/
- Long X, Yang J, Weysen T, Haakma R, Foussier J, Fonseca P and Aarts RM (2014). Measuring dissimilarity between respiratory effort signals based on uniform scaling for sleep staging, Physiological Measurement 35(12): 2529–2542. [DOI] [PubMed] [Google Scholar]
- Loomis AL, Harvey EN and Hobart G (1936). Electrical potentials of the human brain, J. Exp. Psychol 19: 249279. [Google Scholar]
- Loomis AL, Harvey EN and Hobart G (1937). Cerebral states during sleep, as studied by human brain potentials, J. Exp. Psychol 21: 127–144. [Google Scholar]
- Martin JL and Hakim AD (2011). Wrist actigraphy., Chest 139(6): 1514–1527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MatConvNet: CNNs for MATLAB (2016). URL: http://www.vlfeat.org/matconvnet/
- Oster J and Clifford GD (2015). Impact of the presence of noise on RR interval-based atrial fibrillation detection, Journal of Electrocardiology 48(6): 947–951. [DOI] [PubMed] [Google Scholar]
- Quan SF, Howard BV, Iber C, Kiley JP, Nieto FJ, O’connor GT, Rapoport DM, Redline S, Robbins J, Samet JM et al. (1997). The sleep heart health study: design, rationale, and methods, Sleep 20(12): 1077–1085. [PubMed] [Google Scholar]
- Rechtschaffen A and Kales A (1968). A manual of standardized terminology, techniques and scoring system for sleep stages of human subjects, Los Angeles, CA: UCLA Brain Information Service/Brain Research Institute. [Google Scholar]
- Roebuck A, Monasterio V, Gederi E, Osipov M, Behar J, Malhotra A, Penzel T and Clifford GD (2014). A review of signals used in sleep analysis., Physiological Measurement 35(1): R1–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosa A, Alves GR, Brito M, Lopes MC and Tufik S (2006). Visual and automatic cyclic alternating pattern (CAP) scoring: inter-rater reliability study., Arquivos de Neuro-psiquiatria 64(3A): 578–581. [DOI] [PubMed] [Google Scholar]
- Saito Y, Sozu T, Hamada C and Yoshimura I (2006). Effective number of subjects and number of raters for inter-rater reliability studies, Statistics in Medicine 25(9): 1547–1560. [DOI] [PubMed] [Google Scholar]
- Stepnowsky CJ, Berry C and Dimsdale JE (2004). The effect of measurement unreliability on sleep and respiratory variables., Sleep 27(5): 990–995. [DOI] [PubMed] [Google Scholar]
- Tataraidze A, Korostovtseva L, Anishchenko L, Bochkarev M and Sviryaev Y (2016). Sleep architecture measurement based on cardiorespiratory parameters, Engineering in Medicine and Biology Society (EMBC), 2016 IEEE 38th Annual International Conference of the, IEEE, 3478–3481. [DOI] [PubMed] [Google Scholar]
- Thomas RJ, Mietus JE, Peng C-K and Goldberger AL (2005). An electrocardiogram-based technique to assess cardiopulmonary coupling during sleep, SLEEP 28(9): 1151–1161. [DOI] [PubMed] [Google Scholar]
- Vedaldi A and Lenc K (2015). Matconvnet: Convolutional neural networks for matlab, Proceedings of the 23rd ACM International Conference on Multimedia, pp. 689–692. [Google Scholar]
- Vest AN, Da Poian G, Li Q, Liu C, Nemati S, Shah AJ and Clifford GD (2018). An open source benchmarked toolbox for cardiovascular waveform and interval analysis, Physiological Measurement 39(10): 105004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei R, Zhang X, Wang J and Dang X (2018). The research of sleep staging based on single-lead electrocardiogram and deep neural network, Biomedical Engineering Letters 8(1): 87–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wohlgemuth WK, Edinger JD, Fins AI and Sullivan RJ (1999). How many nights are enough? The short-term stability of sleep parameters in elderly insomniacs and normal sleepers, Psychophysiology 36(2): 233–244. [PubMed] [Google Scholar]
- Yoon H, Hwang SH, Choi J-W, Lee YJ, Jeong D-U and Park KS (2017). Rem sleep estimation based on autonomic dynamics using r–r intervals, Physiological Measurement 38(4): 631–651. [DOI] [PubMed] [Google Scholar]
- Zong W, Moody G-B and Jiang D (2003). A robust open-source algorithm to detect onset and duration of QRS complexes, Comput in Cardiol 30: 737–740. [Google Scholar]


